Optimization Study of Soil Organic Matter Mapping Model in Complex Terrain Areas: A Case Study of Mingguang City, China
Abstract
1. Introduction
2. Materials and Methods
2.1. Study Area
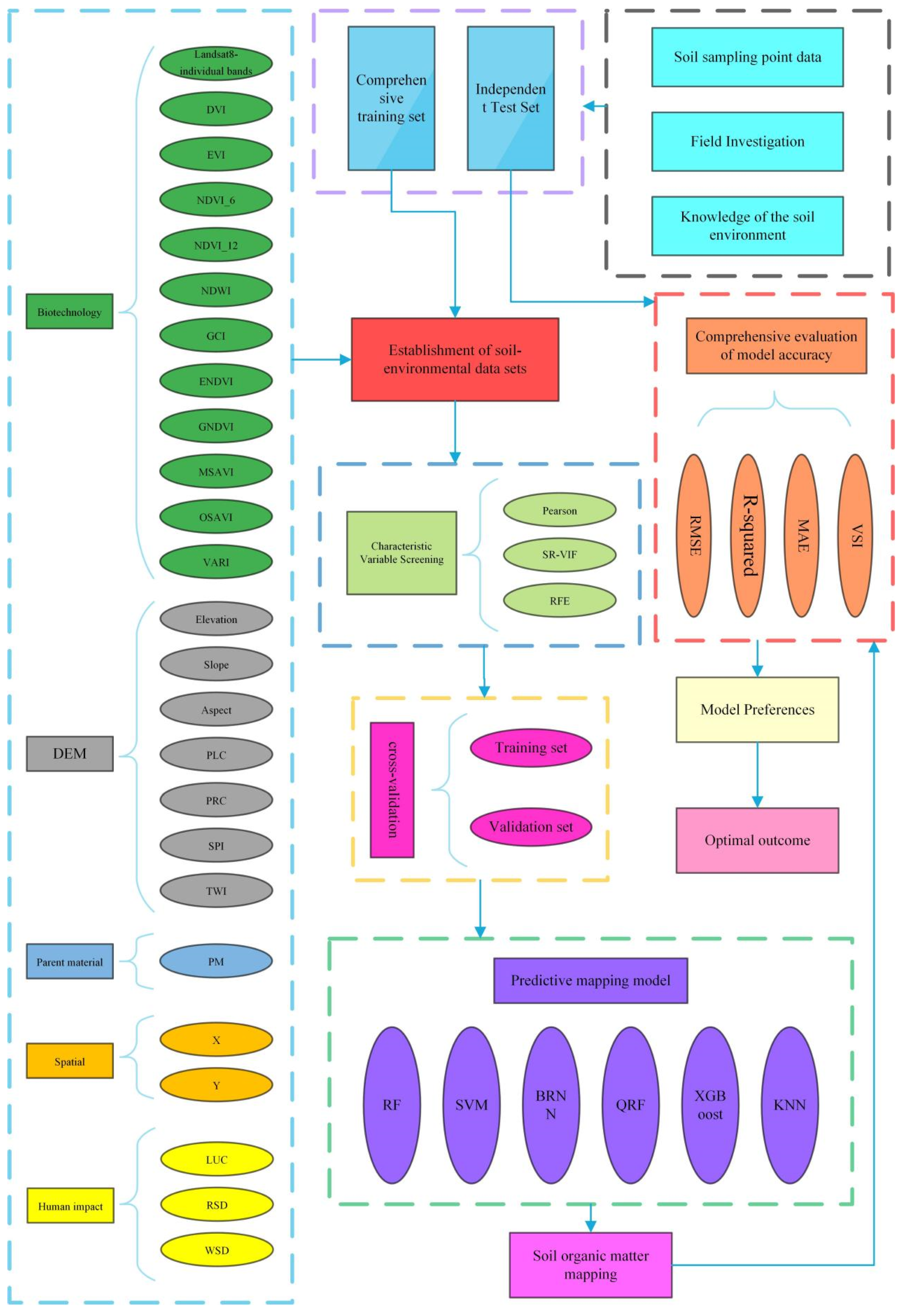
2.2. Database and Methodology
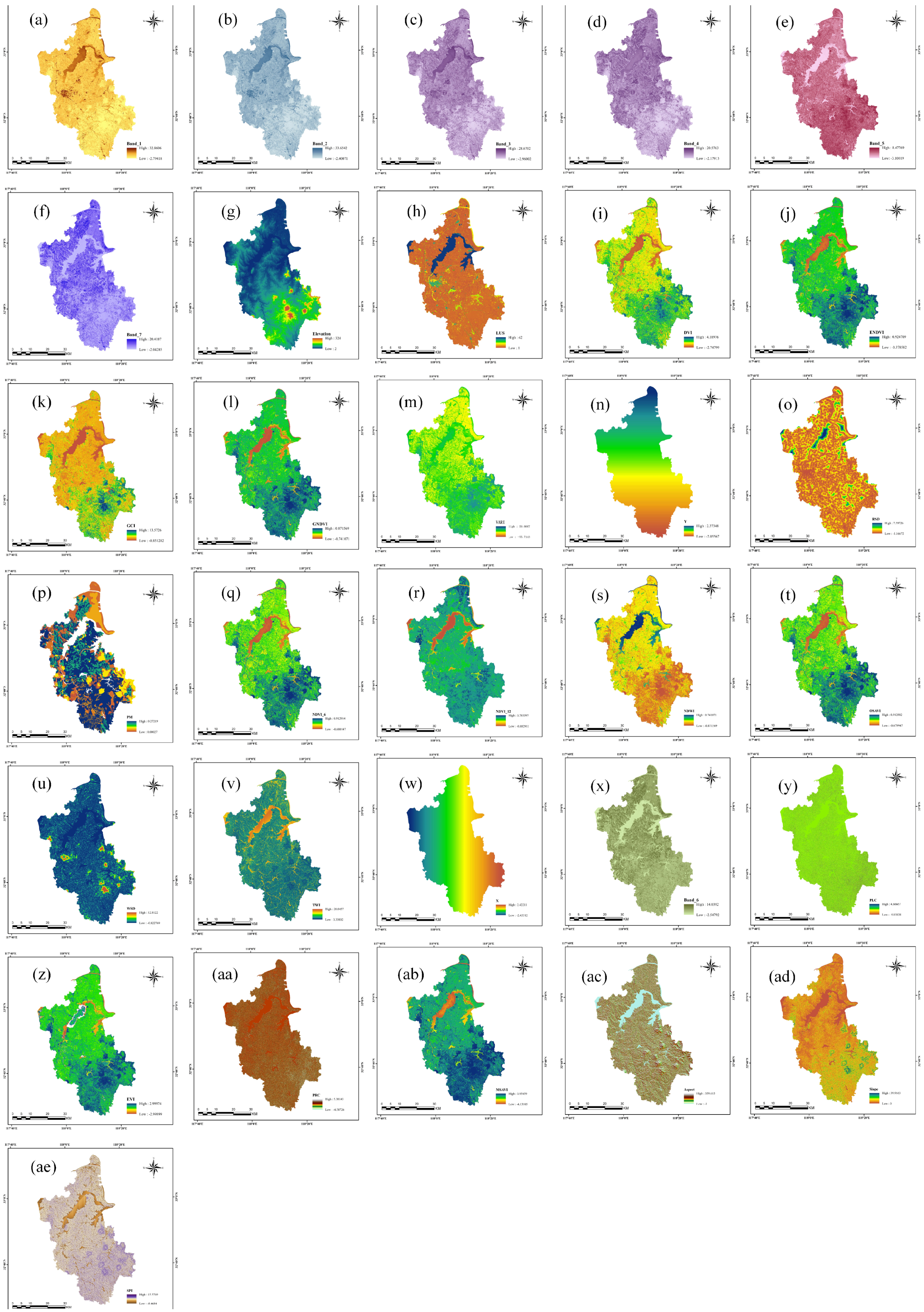
2.3. Extraction of Organic Matter Influencing Factors
2.3.1. Biological Factors
2.3.2. Terrain Factors
2.3.3. Parent Material Factors
2.3.4. Anthropogenic Factors
2.3.5. Spatial Factors
2.4. Model Building
2.4.1. Modeling Method
k-Nearest Neighbor (KNN) Algorithm
Support Vector Machine
Random Forest
Quantile Random Forest
XGBoost
Neural Network
2.4.2. Variable Selection
2.4.3. Accuracy Verification
3. Results and Analysis
3.1. Selection of Limiting Factors of SOM
3.1.1. PCC Selection Results
3.1.2. SR-VIF Selection Results
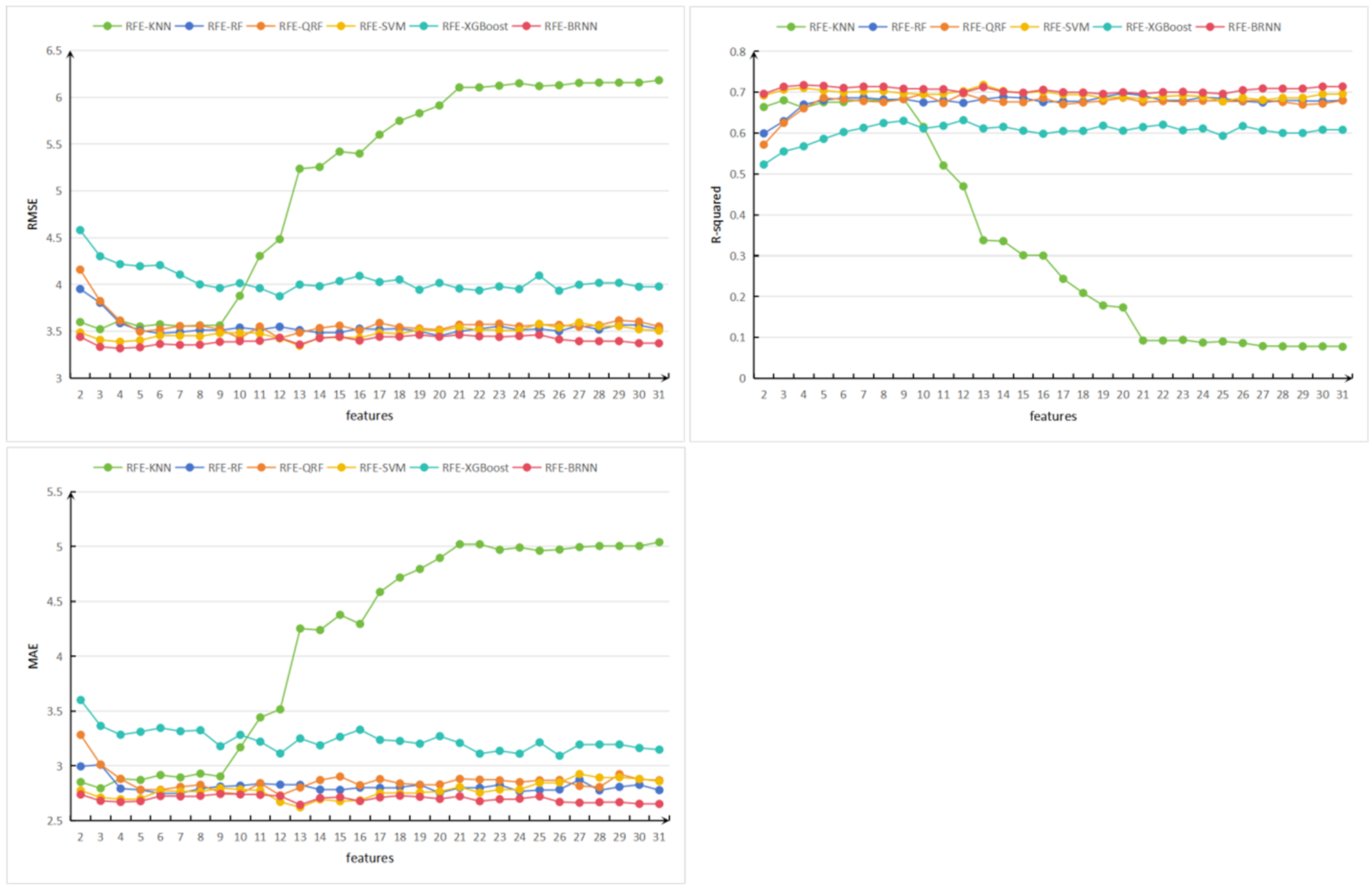
3.1.3. RFE Selection Results
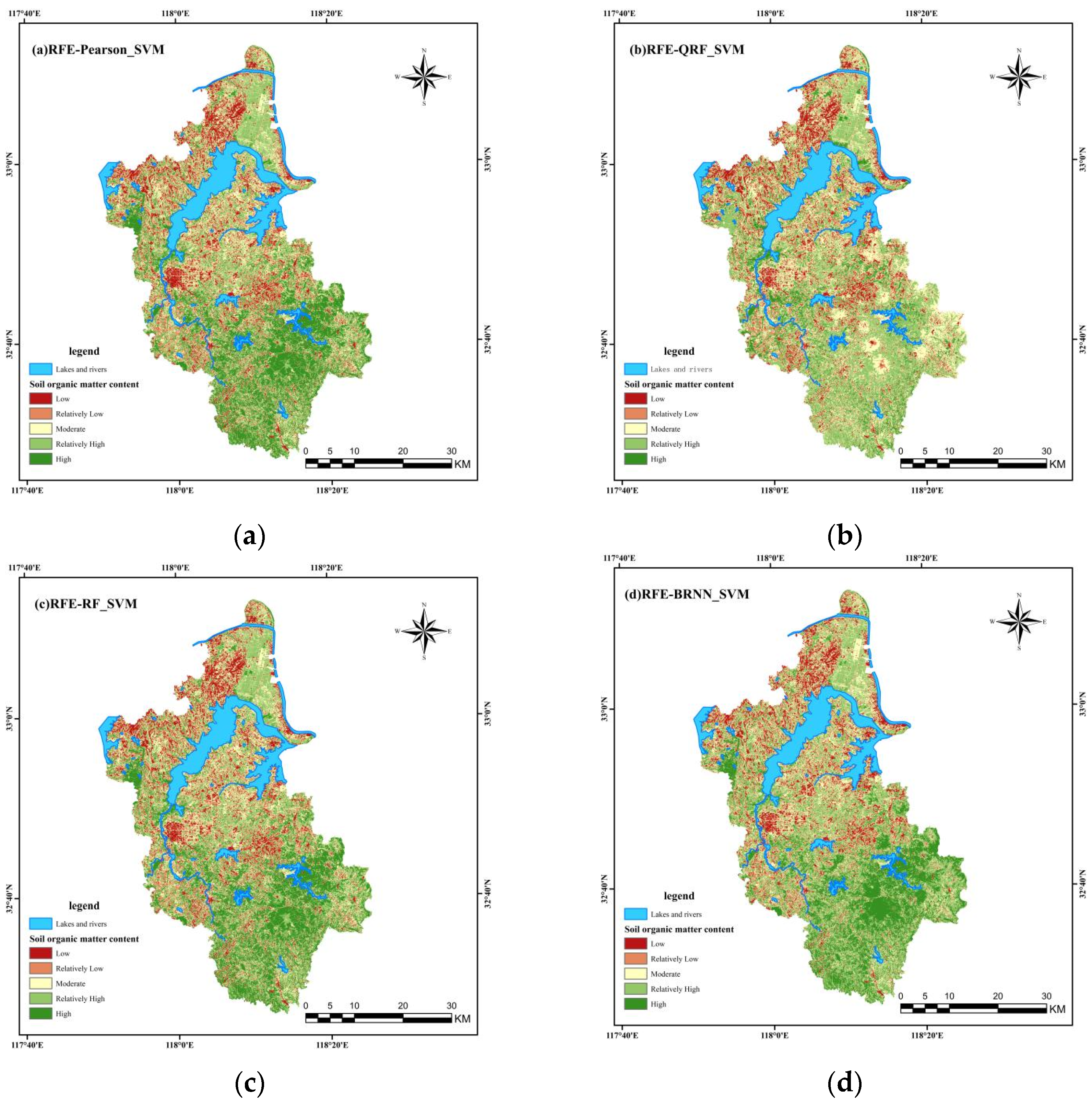
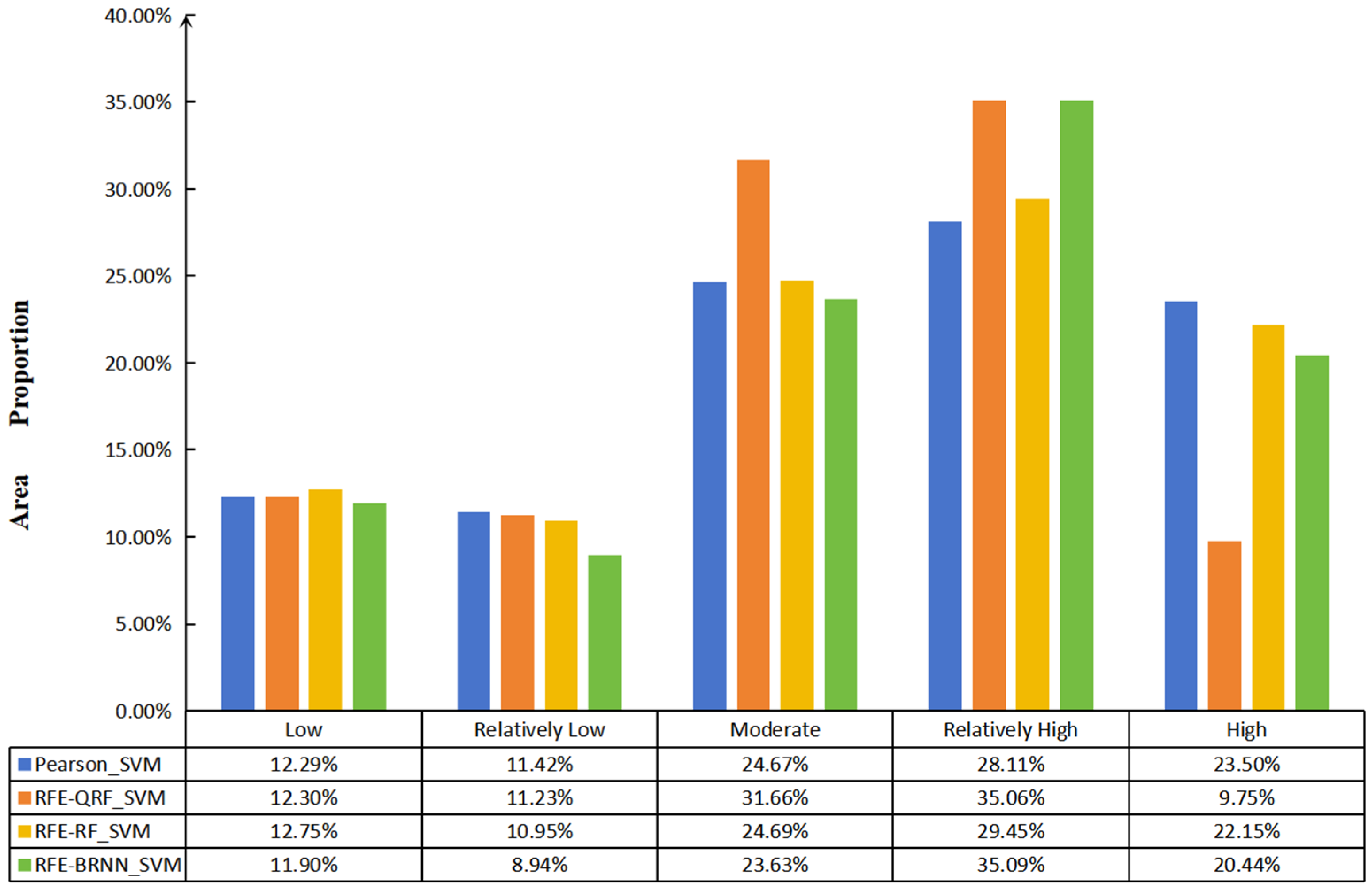
3.2. SOM Mapping
3.3. Performance Evaluation of Combined Models
3.3.1. Combined Model Training Accuracy
3.3.2. Test Set Accuracy
3.3.3. Comprehensive Performance
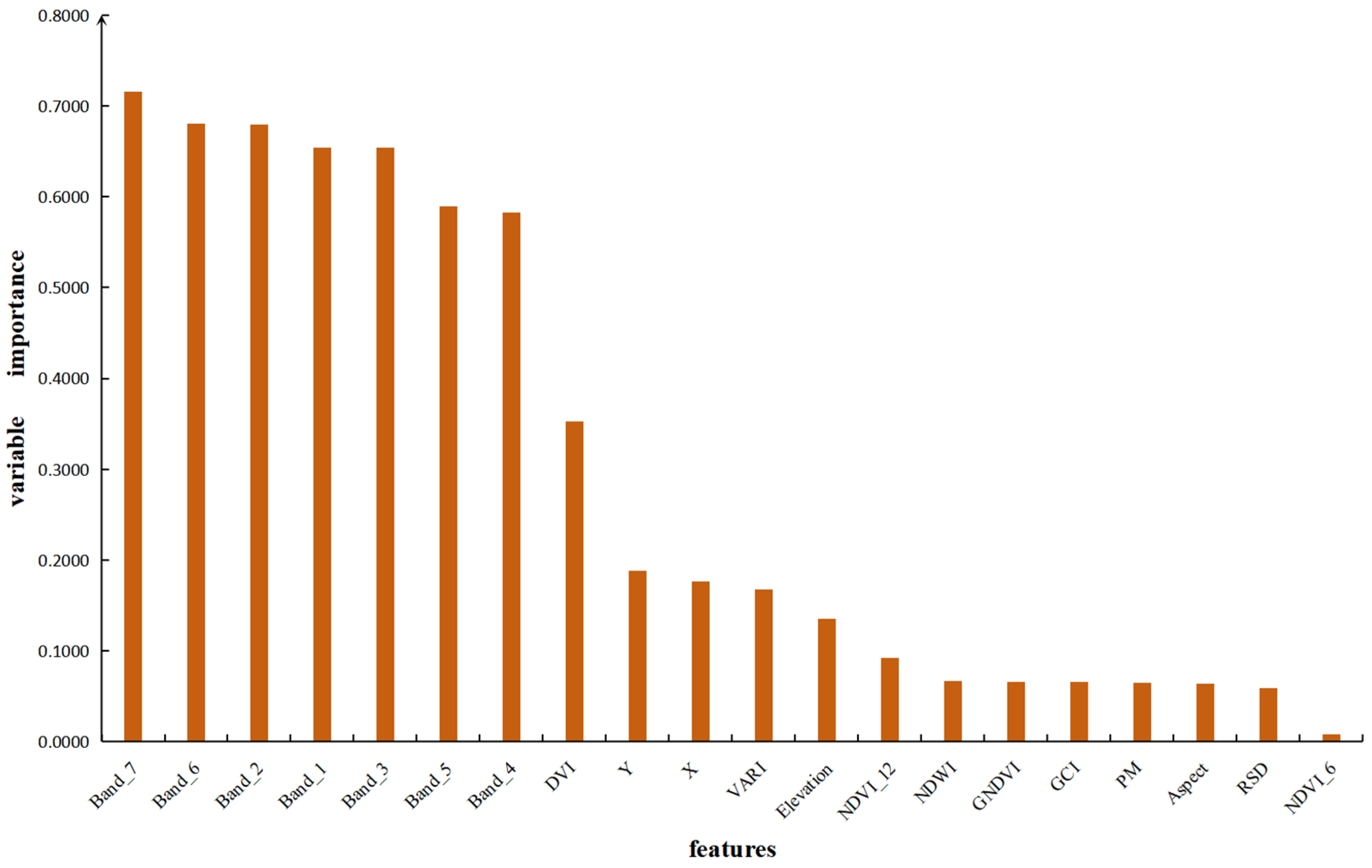
3.4. Optimal Variable Contribution Analysis
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
| Factors | Pearson | Factors | Pearson |
|---|---|---|---|
| Band_1 | −0.790 | RSD | 0.215 |
| Band_2 | −0.809 | MSAVI | −0.024 |
| Band_3 | −0.795 | PM | −0.254 |
| Band_4 | −0.753 | NDVI_6 | −0.026 |
| Band_5 | −0.759 | NDVI_12 | 0.148 |
| Band_6 | −0.810 | NDWI | −0.204 |
| Band_7 | −0.834 | OSAVI | −0.026 |
| Elevation | −0.321 | Slope | 0.051 |
| LUS | −0.171 | PLC | 0.104 |
| DVI | −0.579 | PRC | −0.042 |
| ENDVI | −0.167 | Aspect | −0.249 |
| EVI | −0.037 | SPI | 0.017 |
| GCI | 0.199 | WSD | 0.017 |
| GNDVI | 0.204 | TWI | −0.066 |
| VARI | −0.268 | X | 0.172 |
| Y | 0.244 |
| Stepwise Variable Combination | AIC |
|---|---|
| Band_5 + DVI + Band_1 + Band_2 + Band_3 + Band_6 + Band_7 + NDWI + Elevation + LUS + ENDVI + EVI + GCI + RSD + MSAVI + PM + NDVI_6 + NDVI_12 + OSAVI + Slope + PLC + PRC + Aspect + SPI + WSD + TWI + VARI + X + Y | 314.69 |
| Band_5 + DVI + Band_1 + Band_2 + Band_3 + Band_6 + Elevation + LUS + ENDVI + RSD + MSAVI + PM + NDVI_6 + NDVI_12 + OSAVI + Slope + PLC + PRC + Aspect + SPI + WSD + TWI + VARI + X + Y | 306.77 |
| Band_5 + DVI + Band_1 + Band_2 + Band_3 + Band_6 + Elevation + LUS + ENDVI + PM + NDVI_6 + NDVI_12 + OSAVI + PLC + PRC + Aspect + SPI + WSD + TWI + VARI + X + Y | 301.18 |
| Band_5 + Band_1 + Band_2 + Band_3 + Band_6 + Elevation + LUS + ENDVI + PM + NDVI_6 + NDVI_12 + OSAVI + Aspect + SPI + WSD + TWI + VARI + X + Y | 295.96 |
| Band_5 + Band_2 + Band_3 + Band_6 + Elevation + LUS + ENDVI + PM + NDVI_6 + NDVI_12 + OSAVI + Aspect + SPI + WSD + TWI + VARI + X + Y | 294.40 |
| Band_5 + Band_2 + Band_3 + Band_6 + Elevation + LUS + ENDVI + PM + NDVI_6 + NDVI_12 + OSAVI + SPI + WSD + VARI + Y | 290.07 |
| Band_5 + Band_2 + Band_3 + Band_6 + Elevation + LUS + ENDVI + PM + NDVI_12 + OSAVI + SPI + WSD + Y | 287.47 |
| Band_5 + Band_2 + Band_3 + Elevation + ENDVI + PM + NDVI_12 + OSAVI + SPI + WSD + Y | 286.13 |
| Factors | Iinear Regression Coefficient | VIF |
|---|---|---|
| Band_5 | −12.782 | 26.023 |
| Band_2 | −9.110 | 16.079 |
| Band_3 | 7.117 | 32.159 |
| Elevation | −0.095 | 1.805 |
| ENDVI | −151.364 | 7.266 |
| PM | −7.202 | 1.620 |
| NDVI_12 | 4.928 | 1.661 |
| OSAVI | 125.731 | 13.555 |
| SPI | 0.179 | 1.123 |
| WSD | 1.378 | 1.164 |
| Y | −0.850 | 2.329 |

References
- Yazdanshenas, H.; Tavili, A.; Jafari, M.; Shafeian, E. Evidence for relationship between carbon storage and surface cover characteristics of soil in rangelands. Catena 2018, 167, 139–146. [Google Scholar] [CrossRef]
- Picariello, E.; Baldantoni, D.; Izzo, F.; Langella, A.; De Nicola, F. Soil organic matter stability and microbial community in relation to different plant cover: A focus on forests characterizing Mediterranean area. Appl. Soil Ecol. 2021, 162, 103897. [Google Scholar] [CrossRef]
- Mallah Nowkandeh, S.; Noroozi, A.A.; Homaee, M. Estimating soil organic matter content from Hyperion reflectance images using PLSR, PCR, MinR and SWR models in semi-arid regions of Iran. Environ. Dev. 2018, 25, 23–32. [Google Scholar] [CrossRef]
- Gu, X.; Wang, Y.; Sun, Q.; Yang, G.; Zhang, C. Hyperspectral inversion of soil organic matter content in cultivated land based on wavelet transform. Comput. Electron. Agric. 2019, 167, 105053. [Google Scholar] [CrossRef]
- Zhao, X.; Zhao, D.; Wang, J.; Triantafilis, J. Soil organic carbon (SOC) prediction in Australian sugarcane fields using Vis–NIR spectroscopy with different model setting approaches. Geoderma Reg. 2022, 30, e00566. [Google Scholar] [CrossRef]
- Horta, A.; Azevedo, L.; Neves, J.; Soares, A.; Pozza, L. Integrating portable X-ray fluorescence (pXRF) measurement uncertainty for accurate soil contamination mapping. Geoderma 2021, 382, 114712. [Google Scholar] [CrossRef]
- McBratney, A.B.; Santos, M.M.; Minasny, B. On digital soil mapping. Geoderma 2003, 117, 3–52. [Google Scholar] [CrossRef]
- Dalal, R.; Henry, R. Simultaneous determination of moisture, organic carbon, and total nitrogen by near infrared reflectance spectrophotometry. Soil Sci. Soc. Am. J. 1986, 50, 120–123. [Google Scholar] [CrossRef]
- Bond-Lamberty, B.; Hengl, T.; Mendes de Jesus, J.; Heuvelink, G.B.M.; Ruiperez Gonzalez, M.; Kilibarda, M.; Blagotić, A.; Shangguan, W.; Wright, M.N.; Geng, X.; et al. SoilGrids250m: Global gridded soil information based on machine learning. PLoS ONE 2017, 12, e0169748. [Google Scholar]
- Zhao, D.; Arshad, M.; Wang, J.; Triantafilis, J. Soil exchangeable cations estimation using Vis-NIR spectroscopy in different depths: Effects of multiple calibration models and spiking. Comput. Electron. Agric. 2021, 182, 105990. [Google Scholar] [CrossRef]
- Keskin, H.; Grunwald, S.; Harris, W.G. Digital mapping of soil carbon fractions with machine learning. Geoderma 2019, 339, 40–58. [Google Scholar] [CrossRef]
- De Sousa, L.; Poggio, L.; Batjes, N.; Heuvelink, G.; Kempen, B.; Riberio, E.; Rossiter, D. SoilGrids 2.0: Producing quality-assessed soil information for the globe with quantified spatial uncertainty. Soil 2021, 7, 217–240. [Google Scholar]
- Zeng, P.; Song, X.; Yang, H.; Wei, N.; Du, L. Digital Soil Mapping of Soil Organic Matter with Deep Learning Algorithms. ISPRS Int. J. Geo Inf. 2022, 11, 299. [Google Scholar] [CrossRef]
- Wang, T. Research on Spatial Prediction of Soil TextureBased on GF-1 Image and Machine Learning: A Case Study of Mingguang City. Master’s Thesis, Anhui Agricultural University, Hefei, China, 2023. [Google Scholar]
- Tobler, W.R. A computer movie simulating urban growth in the Detroit region. Econ. Geogr. 1970, 46 (Suppl. S1), 234–240. [Google Scholar] [CrossRef]
- Sereni, L.; Guenet, B.; Lamy, I. Mapping risks associated with soil copper contamination using availability and bio-availability proxies at the European scale. Environ. Sci. Pollut. Res. 2022, 30, 19828–19844. [Google Scholar] [CrossRef] [PubMed]
- Wanghe, K.; Guo, X.; Luan, X.; Li, K. Assessment of Urban Green Space Based on Bio-Energy Landscape Connectivity: A Case Study on Tongzhou District in Beijing, China. Sustainability 2019, 11, 4943. [Google Scholar] [CrossRef]
- Minasny, B.; McBratney, A.B. Digital soil mapping: A brief history and some lessons. Geoderma 2016, 264, 301–311. [Google Scholar] [CrossRef]
- Dobos, E.; Montanarella, L.; Nègre, T.; Micheli, E. A regional scale soil mapping approach using integrated AVHRR and DEM data. Int. J. Appl. Earth Obs. Geoinf. 2001, 3, 30–42. [Google Scholar] [CrossRef]
- Grinand, C.; Arrouays, D.; Laroche, B.; Martin, M.P. Extrapolating regional soil landscapes from an existing soil map: Sampling intensity, validation procedures, and integration of spatial context. Geoderma 2008, 143, 180–190. [Google Scholar] [CrossRef]
- Akumu, C.E.; Johnson, J.A.; Etheridge, D.; Uhlig, P.; Woods, M.; Pitt, D.G.; McMurray, S. GIS-fuzzy logic based approach in modeling soil texture: Using parts of the Clay Belt and Hornepayne region in Ontario Canada as a case study. Geoderma 2015, 239–240, 13–24. [Google Scholar] [CrossRef]
- Sena, N.C.; Veloso, G.V.; Fernandes-Filho, E.I.; Francelino, M.R.; Schaefer, C.E.G.R. Analysis of terrain attributes in different spatial resolutions for digital soil mapping application in southeastern Brazil. Geoderma Reg. 2020, 21, e00268. [Google Scholar] [CrossRef]
- Silveira, C.T.; Oka-Fiori, C.; Santos, L.J.C.; Sirtoli, A.E.; Silva, C.R.; Botelho, M.F. Soil prediction using artificial neural networks and topographic attributes. Geoderma 2013, 195–196, 165–172. [Google Scholar] [CrossRef]
- Sharma, A. Integrating terrain and vegetation indices for identifying potential soil erosion risk area. Geo Spat. Inf. Sci. 2010, 13, 201–209. [Google Scholar] [CrossRef]
- Pei, T.; Qin, C.-Z.; Zhu, A.X.; Yang, L.; Luo, M.; Li, B.; Zhou, C. Mapping soil organic matter using the topographic wetness index: A comparative study based on different flow-direction algorithms and kriging methods. Ecol. Indic. 2010, 10, 610–619. [Google Scholar] [CrossRef]
- Heung, B.; Bulmer, C.E.; Schmidt, M.G. Predictive soil parent material mapping at a regional-scale: A Random Forest approach. Geoderma 2014, 214–215, 141–154. [Google Scholar] [CrossRef]
- Bormann, H.; Klaassen, K. Seasonal and land use dependent variability of soil hydraulic and soil hydrological properties of two Northern German soils. Geoderma 2008, 145, 295–302. [Google Scholar] [CrossRef]
- Rossiter, D.G.; Liu, J.; Carlisle, S.; Zhu, A.X. Can citizen science assist digital soil mapping? Geoderma 2015, 259–260, 71–80. [Google Scholar] [CrossRef]
- Ziadat, F.M. Land suitability classification using different sources of information: Soil maps and predicted soil attributes in Jordan. Geoderma 2007, 140, 73–80. [Google Scholar] [CrossRef]
- Hui, D.; Adhikari, K.; Hartemink, A.E.; Minasny, B.; Bou Kheir, R.; Greve, M.B.; Greve, M.H. Digital Mapping of Soil Organic Carbon Contents and Stocks in Denmark. PLoS ONE 2014, 9, e105519. [Google Scholar]
- Mansuy, N.; Thiffault, E.; Paré, D.; Bernier, P.; Guindon, L.; Villemaire, P.; Poirier, V.; Beaudoin, A. Digital mapping of soil properties in Canadian managed forests at 250m of resolution using the k-nearest neighbor method. Geoderma 2014, 235–236, 59–73. [Google Scholar] [CrossRef]
- Wu, W.; Li, A.-D.; He, X.-H.; Ma, R.; Liu, H.-B.; Lv, J.-K. A comparison of support vector machines, artificial neural network and classification tree for identifying soil texture classes in southwest China. Comput. Electron. Agric. 2018, 144, 86–93. [Google Scholar] [CrossRef]
- Awad, M.; Khanna, R.; Awad, M.; Khanna, R. Support vector machines for classification. In Efficient Learning Machines: Theories, Concepts, and Applications for Engineers and System Designers; Apress: Berkeley, CA, USA, 2015; pp. 39–66. [Google Scholar]
- Grimm, R.; Behrens, T.; Märker, M.; Elsenbeer, H. Soil organic carbon concentrations and stocks on Barro Colorado Island—Digital soil mapping using Random Forests analysis. Geoderma 2008, 146, 102–113. [Google Scholar] [CrossRef]
- Meinshausen, N.; Ridgeway, G. Quantile regression forests. J. Mach. Learn. Res. 2006, 7, 983–999. [Google Scholar]
- Vaysse, K.; Lagacherie, P. Using quantile regression forest to estimate uncertainty of digital soil mapping products. Geoderma 2017, 291, 55–64. [Google Scholar] [CrossRef]
- Lu, Q.; Tian, S.; Wei, L. Digital mapping of soil pH and carbonates at the European scale using environmental variables and machine learning. Sci. Total Environ. 2023, 856, 159171. [Google Scholar] [CrossRef] [PubMed]
- Hateffard, F.; Dolati, P.; Heidari, A.; Zolfaghari, A.A. Assessing the performance of decision tree and neural network models in mapping soil properties. J. Mt. Sci. 2019, 16, 1833–1847. [Google Scholar] [CrossRef]
- Behrens, T.; Förster, H.; Scholten, T.; Steinrücken, U.; Spies, E.D.; Goldschmitt, M. Digital soil mapping using artificial neural networks. J. Plant Nutr. Soil Sci. 2005, 168, 21–33. [Google Scholar] [CrossRef]
- Tien Bui, D.; Pradhan, B.; Lofman, O.; Revhaug, I.; Dick, O.B. Landslide susceptibility assessment in the Hoa Binh province of Vietnam: A comparison of the Levenberg–Marquardt and Bayesian regularized neural networks. Geomorphology 2012, 171–172, 12–29. [Google Scholar] [CrossRef]
- Camera, C.; Zomeni, Z.; Noller, J.S.; Zissimos, A.M.; Christoforou, I.C.; Bruggeman, A. A high resolution map of soil types and physical properties for Cyprus: A digital soil mapping optimization. Geoderma 2017, 285, 35–49. [Google Scholar] [CrossRef]
- Nabiollahi, K.; Golmohamadi, F.; Taghizadeh-Mehrjardi, R.; Kerry, R.; Davari, M. Assessing the effects of slope gradient and land use change on soil quality degradation through digital mapping of soil quality indices and soil loss rate. Geoderma 2018, 318, 16–28. [Google Scholar] [CrossRef]
- Cohen, I.; Huang, Y.; Chen, J.; Benesty, J.; Benesty, J.; Chen, J.; Huang, Y.; Cohen, I. Pearson correlation coefficient. In Noise Reduction in Speech Processing; Springer: Berlin/Heidelberg, Germany, 2009; pp. 1–4. [Google Scholar]
- Mondejar, J.P.; Tongco, A.F. Estimating topsoil texture fractions by digital soil mapping—A response to the long outdated soil map in the Philippines. Sustain. Environ. Res. 2019, 29, 31. [Google Scholar] [CrossRef]
- Mosleh, Z.; Salehi, M.H.; Jafari, A.; Borujeni, I.E.; Mehnatkesh, A. The effectiveness of digital soil mapping to predict soil properties over low-relief areas. Environ. Monit. Assess. 2016, 188, 195. [Google Scholar] [CrossRef] [PubMed]
- Hamzehpour, N.; Shafizadeh-Moghadam, H.; Valavi, R. Exploring the driving forces and digital mapping of soil organic carbon using remote sensing and soil texture. Catena 2019, 182, 104141. [Google Scholar] [CrossRef]
- Brungard, C.W.; Boettinger, J.L.; Duniway, M.C.; Wills, S.A.; Edwards, T.C. Machine learning for predicting soil classes in three semi-arid landscapes. Geoderma 2015, 239–240, 68–83. [Google Scholar] [CrossRef]
- Zhao, Z.-D.; Zhao, M.-S.; Lu, H.-L.; Wang, S.-H.; Lu, Y.-Y. Digital Mapping of Soil pH Based on Machine Learning Combined with Feature Selection Methods in East China. Sustainability 2023, 15, 12874. [Google Scholar] [CrossRef]
- Piikki, K.; Söderström, M. Digital soil mapping of arable land in Sweden—Validation of performance at multiple scales. Geoderma 2019, 352, 342–350. [Google Scholar] [CrossRef]
- Brus, D.J.; Kempen, B.; Heuvelink, G.B.M. Sampling for validation of digital soil maps. Eur. J. Soil Sci. 2011, 62, 394–407. [Google Scholar] [CrossRef]
- Srisomkiew, S.; Kawahigashi, M.; Limtong, P. Digital mapping of soil chemical properties with limited data in the Thung Kula Ronghai region, Thailand. Geoderma 2021, 389, 114942. [Google Scholar] [CrossRef]
- Chicco, D.; Warrens, M.J.; Jurman, G. The coefficient of determination R-squared is more informative than SMAPE, MAE, MAPE, MSE and RMSE in regression analysis evaluation. Peerj Comput. Sci. 2021, 7, e623. [Google Scholar] [CrossRef] [PubMed]
- Schober, P.; Boer, C.; Schwarte, L.A. Correlation coefficients: Appropriate use and interpretation. Anesth. Analg. 2018, 126, 1763–1768. [Google Scholar] [CrossRef]
- Overholser, B.R.; Sowinski, K.M. Biostatistics primer: Part 2. Nutr. Clin. Pract. 2008, 23, 76–84. [Google Scholar] [CrossRef] [PubMed]
- Yang, R.-M.; Liu, L.-A.; Zhang, X.; He, R.-X.; Zhu, C.-M.; Zhang, Z.-Q.; Li, J.-G. The effectiveness of digital soil mapping with temporal variables in modeling soil organic carbon changes. Geoderma 2022, 405, 115407. [Google Scholar] [CrossRef]
- Chen, S.; Richer-de-Forges, A.C.; Leatitia Mulder, V.; Martelet, G.; Loiseau, T.; Lehmann, S.; Arrouays, D. Digital mapping of the soil thickness of loess deposits over a calcareous bedrock in central France. Catena 2021, 198, 105062. [Google Scholar] [CrossRef]
- Vaysse, K.; Lagacherie, P. Evaluating Digital Soil Mapping approaches for mapping GlobalSoilMap soil properties from legacy data in Languedoc-Roussillon (France). Geoderma Reg. 2015, 4, 20–30. [Google Scholar] [CrossRef]
- Guo, P.-T.; Li, M.-F.; Luo, W.; Tang, Q.-F.; Liu, Z.-W.; Lin, Z.-M. Digital mapping of soil organic matter for rubber plantation at regional scale: An application of random forest plus residuals kriging approach. Geoderma 2015, 237–238, 49–59. [Google Scholar] [CrossRef]
- Lehmann, J.; Kleber, M. The contentious nature of soil organic matter. Nature 2015, 528, 60–68. [Google Scholar] [CrossRef] [PubMed]
- Schmidt, M.W.I.; Torn, M.S.; Abiven, S.; Dittmar, T.; Guggenberger, G.; Janssens, I.A.; Kleber, M.; Kögel-Knabner, I.; Lehmann, J.; Manning, D.A.C.; et al. Persistence of soil organic matter as an ecosystem property. Nature 2011, 478, 49–56. [Google Scholar] [CrossRef] [PubMed]
- Tiessen, H.; Cuevas, E.; Chacon, P. The role of soil organic matter in sustaining soil fertility. Nature 1994, 371, 783–785. [Google Scholar] [CrossRef]
- Kempen, B.; Brus, D.; Stoorvogel, J. Three-dimensional mapping of soil organic matter content using soil type–specific depth functions. Geoderma 2011, 162, 107–123. [Google Scholar] [CrossRef]
- Rossi, G.; Ferrarini, A.; Dowgiallo, G.; Carton, A.; Gentili, R.; Tomaselli, M. Detecting complex relations among vegetation, soil and geomorphology. An in-depth method applied to a case study in the Apennines (Italy). Ecol. Complex. 2014, 17, 87–98. [Google Scholar] [CrossRef]
- Vincent, S.; Lemercier, B.; Berthier, L.; Walter, C. Spatial disaggregation of complex Soil Map Units at the regional scale based on soil-landscape relationships. Geoderma 2018, 311, 130–142. [Google Scholar] [CrossRef]
- Camacho, M.E.; Quesada-Román, A.; Mata, R.; Alvarado, A. Soil-geomorphology relationships of alluvial fans in Costa Rica. Geoderma Reg. 2020, 21, e00258. [Google Scholar] [CrossRef]
- Pereira, G.W.; Valente, D.S.M.; de Queiroz, D.M.; Santos, N.T.; Fernandes-Filho, E.I. Soil mapping for precision agriculture using support vector machines combined with inverse distance weighting. Precis. Agric. 2022, 23, 1189–1204. [Google Scholar] [CrossRef]
- Heung, B.; Ho, H.C.; Zhang, J.; Knudby, A.; Bulmer, C.E.; Schmidt, M.G. An overview and comparison of machine-learning techniques for classification purposes in digital soil mapping. Geoderma 2016, 265, 62–77. [Google Scholar] [CrossRef]
- Nketia, K.A.; Asabere, S.B.; Ramcharan, A.; Herbold, S.; Erasmi, S.; Sauer, D. Spatio-temporal mapping of soil water storage in a semi-arid landscape of northern Ghana—A multi-tasked ensemble machine-learning approach. Geoderma 2022, 410, 115691. [Google Scholar] [CrossRef]
- Mulder, V.L.; de Bruin, S.; Schaepman, M.E.; Mayr, T.R. The use of remote sensing in soil and terrain mapping—A review. Geoderma 2011, 162, 1–19. [Google Scholar] [CrossRef]
- Goossens, R.; Van Ranst, E. The use of remote sensing to map gypsiferous soils in the Ismailia Province (Egypt). Geoderma 1998, 87, 47–56. [Google Scholar] [CrossRef]
- Mahmoudabadi, E.; Karimi, A.; Haghnia, G.H.; Sepehr, A. Digital soil mapping using remote sensing indices, terrain attributes, and vegetation features in the rangelands of northeastern Iran. Environ. Monit. Assess. 2017, 189, 500. [Google Scholar] [CrossRef] [PubMed]
- Kane, E.S.; Hockaday, W.C.; Turetsky, M.R.; Masiello, C.A.; Valentine, D.W.; Finney, B.P.; Baldock, J.A. Topographic controls on black carbon accumulation in Alaskan black spruce forest soils: Implications for organic matter dynamics. Biogeochemistry 2010, 100, 39–56. [Google Scholar] [CrossRef]
- Du Preez, C.C.; Van Huyssteen, C.W.; Mnkeni, P.N. Land use and soil organic matter in South Africa 2: A review on the influence of arable crop production. S. Afr. J. Sci. 2011, 107, 1–8. [Google Scholar] [CrossRef]
- Riley, H.; Pommeresche, R.; Eltun, R.; Hansen, S.; Korsaeth, A. Soil structure, organic matter and earthworm activity in a comparison of cropping systems with contrasting tillage, rotations, fertilizer levels and manure use. Agric. Ecosyst. Environ. 2008, 124, 275–284. [Google Scholar] [CrossRef]
- Xue, J.; Su, B. Significant Remote Sensing Vegetation Indices: A Review of Developments and Applications. J. Sens. 2017, 2017, 1353691. [Google Scholar] [CrossRef]
- Haboudane, D.; Miller, J.R.; Tremblay, N.; Zarco-Tejada, P.J.; Dextraze, L. Integrated narrow-band vegetation indices for prediction of crop chlorophyll content for application to precision agriculture. Remote Sens. Environ. 2002, 81, 416–426. [Google Scholar] [CrossRef]
- Lu, M.-y.; Liu, Y.; Liu, G.-j. Precise prediction of soil organic matter in soils planted with a variety of crops through hybrid methods. Comput. Electron. Agric. 2022, 200, 107246. [Google Scholar] [CrossRef]
- Sanchez, P.A.; Ahamed, S.; Carré, F.; Hartemink, A.E.; Hempel, J.; Huising, J.; Lagacherie, P.; McBratney, A.B.; McKenzie, N.J.; Mendonça-Santos, M.D.L. Digital soil map of the world. Science 2009, 325, 680–681. [Google Scholar] [CrossRef] [PubMed]
- Brevik, E.C.; Calzolari, C.; Miller, B.A.; Pereira, P.; Kabala, C.; Baumgarten, A.; Jordán, A. Soil mapping, classification, and pedologic modeling: History and future directions. Geoderma 2016, 264, 256–274. [Google Scholar] [CrossRef]


| Data Types | Environmental Factor | Definition | Spatial Resolution | Source |
|---|---|---|---|---|
| Biotechnology | Band_1 | Landsat8-individual bands | 30 m | USGS |
| Band_2 | ||||
| Band_3 | ||||
| Band_4 | ||||
| Band_5 | ||||
| Band_6 | ||||
| Band_7 | ||||
| DVI | Difference Vegetation Index | Remote sensing image-derived data | ||
| EVI | Enhanced Vegetation Index | |||
| NDVI_6 | Normalized Difference Vegetation Index-June | |||
| NDVI_12 | Normalized Difference Vegetation Index-December | |||
| NDWI | Normalized Difference Water Index | |||
| GCI | Green Chlorophyll Vegetation Index | |||
| ENDVI | Extended normalized difference vegetation index | |||
| GNDVI | Normalized Green Difference Vegetation Index | |||
| MSAVI | Modified Soil Adjustment Vegetation Index | |||
| OSAVI | Optimization Of Soil Regulatory Vegetation Index | |||
| VARI | Visible-band Difference Vegetation Index | |||
| Topographical | Elevation | Digital elevation model model | Geospatial Data Cloud | |
| Slope | Degree of surface inclination | DEM-derived data | ||
| Aspect | The direction in which the slope faces | |||
| PLC | Plan Curvature | |||
| PRC | Profile Curvature | |||
| SPI | Stream Power Index | |||
| TWI | Topographic Wetness Index | |||
| Parent material | PM | Soil map deep-dive | Local soil map | |
| Spatial | X | Longitudes | Data from the Third Territorial Survey | |
| Y | Dimension | |||
| Human impact | LUC | Land Use Structure | ||
| RSD | Residential Site Distance | |||
| WSD | Water Source Distance |
| Variable Filtering | Learning Model | Training_RMSE | Training_Q-Squared | Training_MAE | Testing-RMSE | Testing-Q-Squared | Testing-MAE |
|---|---|---|---|---|---|---|---|
| All | KNN | 6.107 | 0.099 | 5.090 | 6.121 | 0.213 | 5.163 |
| SVM | 3.639 | 0.694 | 3.071 | 3.546 | 0.722 | 2.875 | |
| RF | 3.365 | 0.721 | 2.767 | 3.587 | 0.721 | 2.983 | |
| QRF | 3.413 | 0.715 | 2.800 | 3.977 | 0.684 | 3.273 | |
| XGBoost | 3.741 | 0.668 | 2.971 | 3.917 | 0.660 | 3.162 | |
| BRNN | 3.377 | 0.723 | 2.765 | 3.674 | 0.701 | 3.129 | |
| Pearson | KNN | 6.075 | 0.114 | 5.025 | 6.032 | 0.242 | 5.101 |
| SVM | 3.549 | 0.714 | 2.951 | 3.586 | 0.719 | 2.935 | |
| RF | 3.329 | 0.729 | 2.747 | 3.718 | 0.711 | 3.045 | |
| QRF | 3.407 | 0.719 | 2.819 | 3.752 | 0.723 | 3.121 | |
| XGBoost | 3.593 | 0.692 | 2.896 | 3.721 | 0.694 | 3.013 | |
| BRNN | 3.384 | 0.726 | 2.775 | 3.709 | 0.695 | 3.108 | |
| SR | KNN | 5.652 | 0.250 | 4.548 | 6.011 | 0.202 | 4.943 |
| SVM | 3.105 | 0.771 | 2.535 | 3.494 | 0.732 | 2.900 | |
| RF | 3.392 | 0.711 | 2.757 | 3.774 | 0.693 | 3.104 | |
| QRF | 3.377 | 0.715 | 2.803 | 3.818 | 0.702 | 3.122 | |
| XGBoost | 3.423 | 0.694 | 2.718 | 3.893 | 0.665 | 3.175 | |
| BRNN | 3.078 | 0.760 | 2.507 | 3.658 | 0.703 | 3.108 | |
| SR-VIF | KNN | 5.892 | 0.215 | 4.804 | 6.450 | 0.085 | 5.278 |
| SVM | 6.010 | 0.134 | 4.984 | 6.537 | 0.059 | 5.300 | |
| RF | 5.475 | 0.233 | 4.387 | 5.744 | 0.289 | 4.488 | |
| QRF | 5.368 | 0.275 | 4.271 | 5.638 | 0.297 | 4.329 | |
| XGBoost | 5.963 | 0.223 | 4.711 | 6.848 | 0.106 | 5.658 | |
| BRNN | 5.892 | 0.133 | 4.840 | 6.513 | 0.064 | 5.318 | |
| RFE-KNN | KNN | 3.437 | 0.708 | 2.844 | 3.488 | 0.734 | 0.940 |
| SVM | 3.343 | 0.728 | 2.711 | 3.388 | 0.765 | 2.789 | |
| RF | 3.500 | 0.698 | 2.836 | 3.726 | 0.693 | 2.993 | |
| QRF | 3.535 | 0.688 | 2.848 | 3.895 | 0.669 | 3.142 | |
| XGBoost | 3.954 | 0.633 | 3.136 | 4.457 | 0.594 | 3.644 | |
| BRNN | 3.307 | 0.830 | 2.704 | 3.397 | 0.749 | 2.866 | |
| RFE-SVM | KNN | 4.755 | 0.431 | 3.832 | 5.091 | 0.445 | 4.017 |
| SVM | 3.278 | 0.755 | 2.622 | 3.517 | 0.730 | 2.894 | |
| RF | 3.323 | 0.723 | 2.716 | 3.464 | 0.745 | 2.839 | |
| QRF | 3.334 | 0.730 | 2.734 | 3.414 | 0.759 | 2.765 | |
| XGBoost | 3.545 | 0.691 | 2.878 | 4.087 | 0.630 | 3.324 | |
| BRNN | 3.249 | 0.750 | 2.657 | 3.726 | 0.692 | 3.158 | |
| RFE-RF | KNN | 6.057 | 0.121 | 4.997 | 6.084 | 0.217 | 5.111 |
| SVM | 3.470 | 0.728 | 2.826 | 3.504 | 0.730 | 2.874 | |
| RF | 3.343 | 0.724 | 2.745 | 3.537 | 0.729 | 2.857 | |
| QRF | 3.375 | 0.715 | 2.797 | 3.723 | 0.720 | 3.039 | |
| XGBoost | 3.470 | 0.708 | 2.676 | 3.698 | 0.697 | 2.821 | |
| BRNN | 3.324 | 0.730 | 2.691 | 3.585 | 0.716 | 2.985 | |
| RFE-QRF | KNN | 4.825 | 0.414 | 3.862 | 5.068 | 0.449 | 3.986 |
| SVM | 3.379 | 0.728 | 2.693 | 3.441 | 0.742 | 2.808 | |
| RF | 3.346 | 0.717 | 2.726 | 3.470 | 0.743 | 2.860 | |
| QRF | 3.374 | 0.716 | 2.737 | 3.501 | 0.740 | 2.842 | |
| XGBoost | 3.604 | 0.688 | 2.882 | 3.675 | 0.705 | 2.872 | |
| BRNN | 3.352 | 0.729 | 2.714 | 3.562 | 0.719 | 3.034 | |
| RFE-XGBoost | KNN | 4.825 | 0.414 | 3.862 | 5.068 | 0.449 | 3.986 |
| SVM | 3.379 | 0.728 | 2.693 | 3.441 | 0.742 | 2.808 | |
| RF | 3.346 | 0.717 | 2.726 | 3.470 | 0.743 | 2.860 | |
| QRF | 3.374 | 0.716 | 2.737 | 3.501 | 0.740 | 2.842 | |
| XGBoost | 3.604 | 0.688 | 2.882 | 3.675 | 0.705 | 2.872 | |
| BRNN | 3.352 | 0.729 | 2.714 | 3.562 | 0.719 | 3.034 | |
| RFE-BRNN | KNN | 3.397 | 0.716 | 2.688 | 3.602 | 0.717 | 3.011 |
| SVM | 3.376 | 0.724 | 2.727 | 3.367 | 0.767 | 2.761 | |
| RF | 3.296 | 0.732 | 2.675 | 3.740 | 0.690 | 2.999 | |
| QRF | 3.243 | 0.738 | 2.628 | 3.841 | 0.678 | 3.030 | |
| XGBoost | 3.629 | 0.682 | 2.864 | 4.518 | 0.582 | 3.555 | |
| BRNN | 3.313 | 0.730 | 2.709 | 3.395 | 0.748 | 2.865 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mei, S.; Tong, T.; Zhang, S.; Ying, C.; Tang, M.; Zhang, M.; Cai, T.; Ma, Y.; Wang, Q. Optimization Study of Soil Organic Matter Mapping Model in Complex Terrain Areas: A Case Study of Mingguang City, China. Sustainability 2024, 16, 4312. https://doi.org/10.3390/su16104312
Mei S, Tong T, Zhang S, Ying C, Tang M, Zhang M, Cai T, Ma Y, Wang Q. Optimization Study of Soil Organic Matter Mapping Model in Complex Terrain Areas: A Case Study of Mingguang City, China. Sustainability. 2024; 16(10):4312. https://doi.org/10.3390/su16104312
Chicago/Turabian StyleMei, Shuai, Tong Tong, Shoufu Zhang, Chunyang Ying, Mengmeng Tang, Mei Zhang, Tianpei Cai, Youhua Ma, and Qiang Wang. 2024. "Optimization Study of Soil Organic Matter Mapping Model in Complex Terrain Areas: A Case Study of Mingguang City, China" Sustainability 16, no. 10: 4312. https://doi.org/10.3390/su16104312
APA StyleMei, S., Tong, T., Zhang, S., Ying, C., Tang, M., Zhang, M., Cai, T., Ma, Y., & Wang, Q. (2024). Optimization Study of Soil Organic Matter Mapping Model in Complex Terrain Areas: A Case Study of Mingguang City, China. Sustainability, 16(10), 4312. https://doi.org/10.3390/su16104312









