Economic Analysis of Gas Turbine Using to Increase Efficiency of the Organic Rankine Cycle
Abstract
:1. Introduction
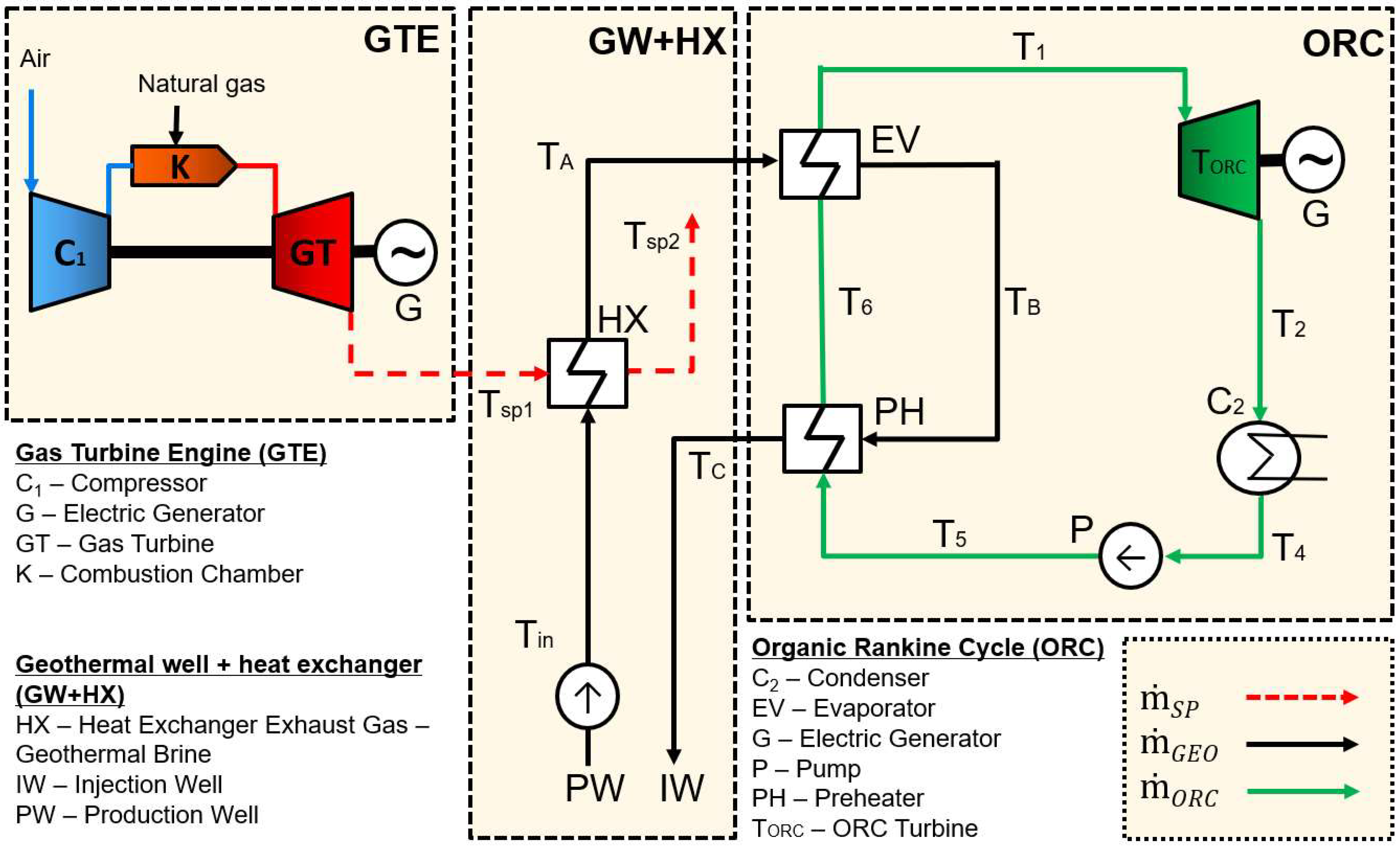
2. System Configuration and Modeling
2.1. Energy Analysis
- The specific enthalpy (h1) and specific entropy (s1) were calculated using the evaporation pressure of dry saturated steam (with a quality of x = 1).
- Considering the isentropic expansion of the vaporized working fluid in the turbine, the specific enthalpy (h2s) was determined based on the specific entropy (s1) and the condensing pressure.
- The specific enthalpy (h3) was determined using the condensation pressure for dry saturated steam (with a quality of x = 1).
- The specific enthalpy (h4) was determined based on the condensing pressure for the liquid state, specifically on the saturation line (with a quality of x = 0).
- Considering the isentropic compression of the working fluid in the pump (s4 = s5) based on specific entropy s4 and evaporation pressure, specific enthalpy h5s was determined.
- The specific enthalpy (h6) was determined based on the evaporation pressure for the liquid state, specifically on the boundary line.
- ORC efficiency:
- Power of the ORC cycle:
- Electrical power of the designed ORC power plant:
2.2. Economic Analysis
- ORC pump [59]:
- ORC preheater [60]:
- ORC evaporator [61]:
- ORC turbine [60]:
- ORC Condenser [62]:
- IO—investment expenditure, USD;
- CF—yearly cash flow, USD/year;
- GT—gas turbine;
- F—working fluid;
- Conf—configuration.
- TSP2 = (240, 245, 250) °C;
- Tgeo_in = (80–130) °C;
- TC = (60, 65, 70) °C.
- Inc—operational income, USD;
- OCost—operational cost, USD.
- pel—electricity price, USD/MWh;
- nhour—operational number of hours in year: 7446 h;
- png—natural gas price, USD/kg;
- varOM—variable operation and maintenance cost, USD;
- fixOM—fixed operation and maintenance cost, USD.
- pTG—gas turbine price, USD/kW;
- pHE—heat exchanger price, USD.
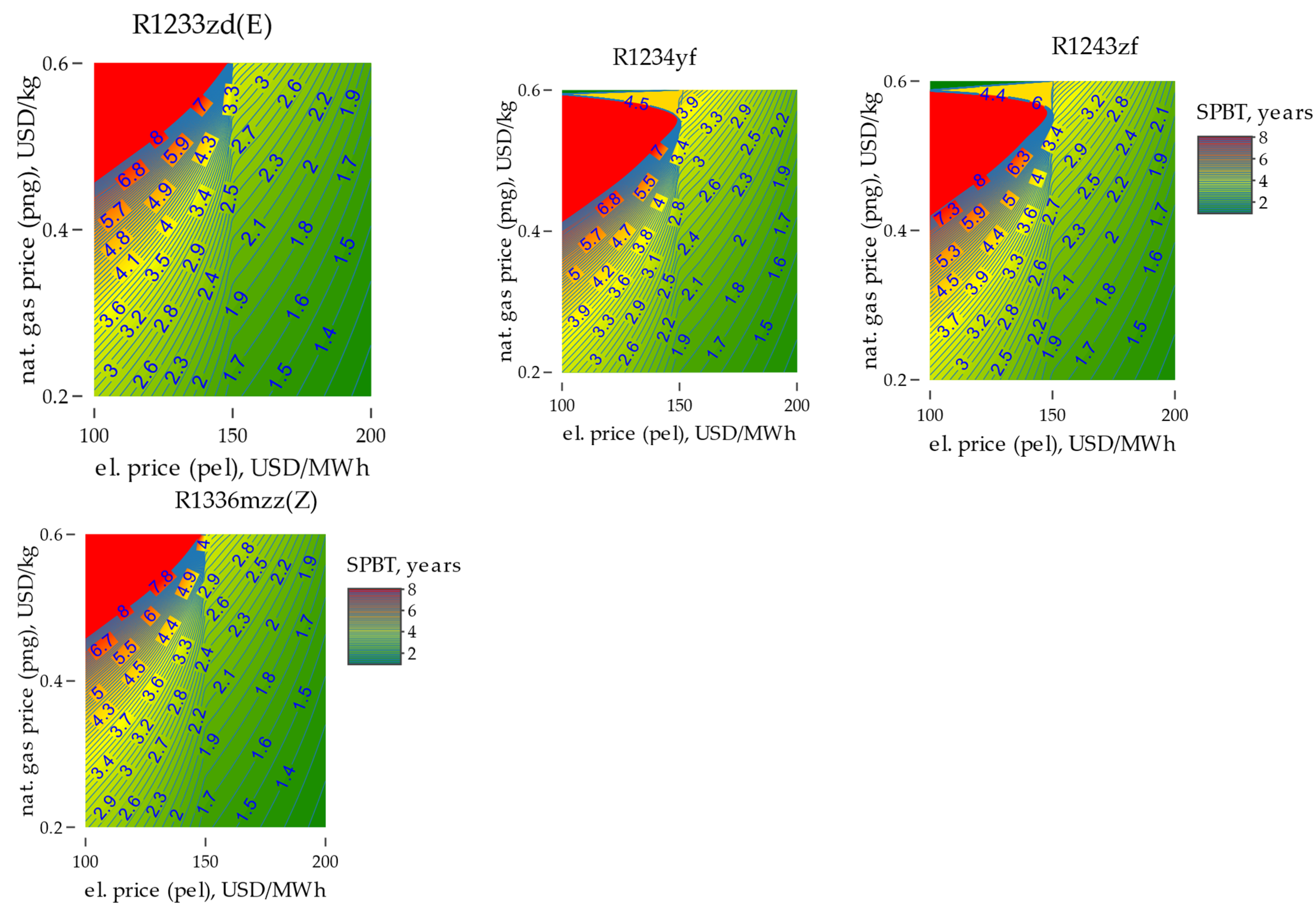
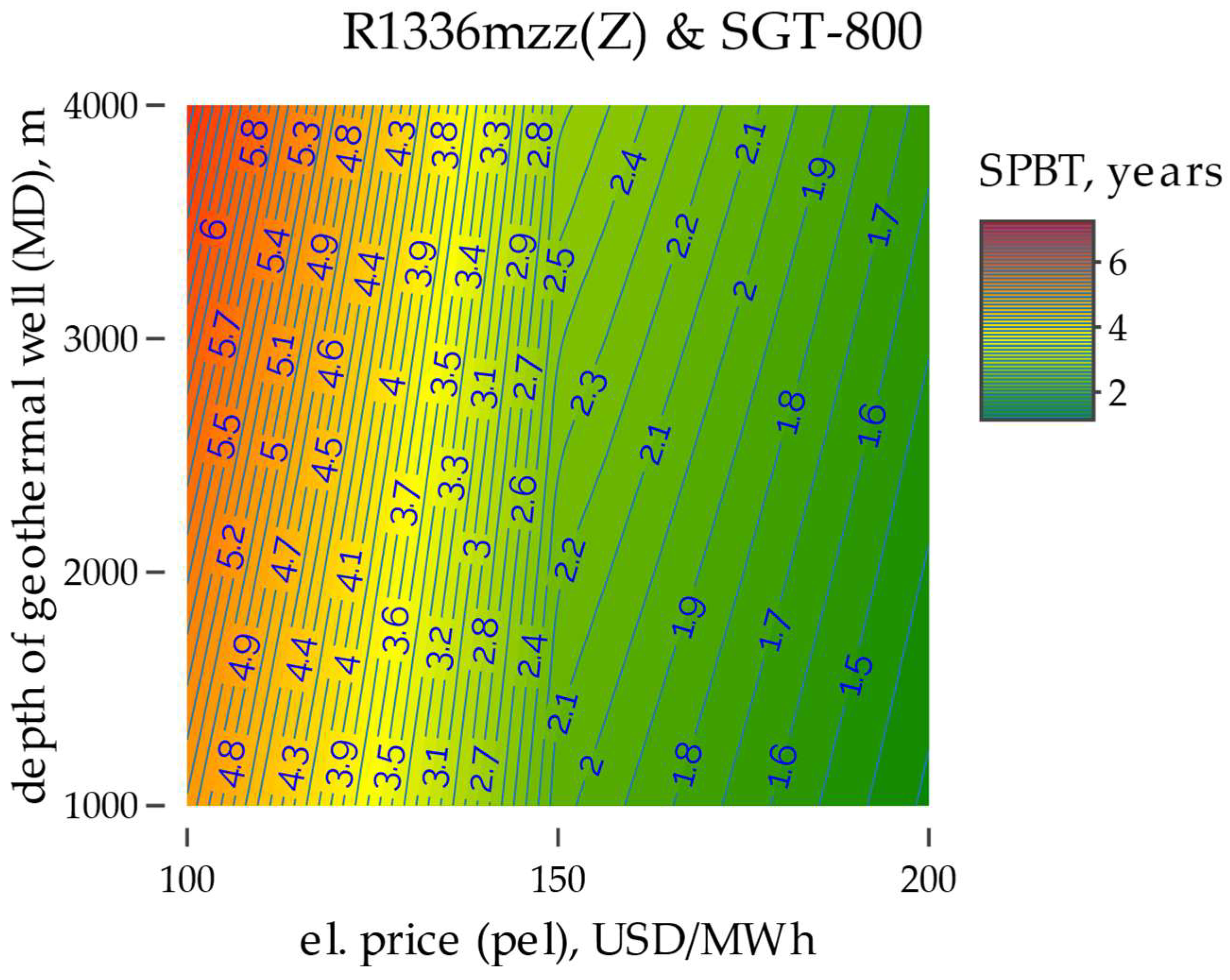
3. Results
4. Conclusions
Funding
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Nomenclature
| Symbols | |
| heat flux [kW] | |
| equipment power [kW] | |
| log mean temperature difference [K] | |
| A | heat transfer area [m2] |
| CF | yearly cash flow [USD/yr] |
| fixOM | fixed operation and maintenance costs [USD] |
| Inc | operational income [USD] |
| IO | investment expenditure [USD] |
| MC | depth of the geothermal well [m] |
| N | system power [kW] |
| Nhour | operational number of hours in year [h] |
| OCost | operational cost [USD] |
| pel | electricity price [USD/MWh] |
| pHE | heat exchanger price [USD] |
| png | natural gas price [USD/kg] |
| pTG | gas turbine price [USD/kW] |
| T | temperature [K] |
| U | overall heat transfer coefficient [kW/m2·K] |
| varOM | variable operation and maintenance costs [USD] |
| Z | equipment investment cost [USD] |
| η | efficiency [- or %] |
| Subscripts | |
| 1,…,6,A,B,C | thermodynamic state points |
| C | condenser |
| Conf | configuration |
| E | evaporator |
| el | electrical |
| F | working fluid |
| g | generator |
| GEO | geothermal |
| HX | heat exchanger |
| i | internal |
| IN | at inlet |
| m | mechanical |
| OUT | at outlet |
| P | pump |
| PH | preheater |
| SP | exhaust gases from gas turbine |
| T | turbine |
| Abbreviation | |
| GT | gas turbine |
| GT-ORC | gas turbine–ORC combined system |
| GW | geothermal well |
| GWC | geothermal well cost |
| HC | hydrocarbon |
| HCFO | hydrochlorofluoroolefin |
| HFC | hydrofluorocarbon |
| HFO | hydrofluoroolefins |
| MM | hexamethyldisiloxane |
| ORC | organic Rankine cycle |
| SPBT | simple payback time |
| VER | vapor expansion ratio |
References
- Augustyn, A.; Kamiński, J. A Review of Methods Applied for Wind Power Generation Forecasting. Polityka Energ.-Energy Policy J. 2018, 21, 139–150. [Google Scholar] [CrossRef]
- Kaszyński, P.; Komorowska, A.; Kamiński, J. Regional Distribution of Hard Coal Consumption in the Power Sector under Selected Forecasts of EUA Prices. Gospod. Surowcami Miner.-Miner. Resour. Manag. 2019, 35, 113–134. [Google Scholar] [CrossRef]
- Tocci, L.; Pal, T.; Pesmazoglou, I.; Franchetti, B. Small Scale Organic Rankine Cycle (ORC): A Techno-Economic Review. Energies 2017, 10, 413. [Google Scholar] [CrossRef]
- Kulpa, J.; Olczak, P.; Stecuła, K.; Sołtysik, M. The Impact of RES Development in Poland on the Change of the Energy Generation Profile and Reduction of CO2 Emissions. Appl. Sci. 2022, 12, 11064. [Google Scholar] [CrossRef]
- Dyczko, A.; Kamiński, P.; Stecuła, K.; Prostański, D.; Kopacz, M.; Kowol, D. Thermal and Mechanical Energy Storage as a Chance for Energy Transformation in Poland. Polityka Energ.-Energy Policy J. 2021, 24, 43–60. [Google Scholar] [CrossRef]
- Kulpa, J.; Kamiński, P.; Stecuła, K.; Prostański, D.; Matusiak, P.; Kowol, D.; Kopacz, M.; Olczak, P. Technical and Economic Aspects of Electric Energy Storage in a Mine Shaft—Budryk Case Study. Energies 2021, 14, 7337. [Google Scholar] [CrossRef]
- Petrollese, M.; Cocco, D. Robust Optimization for the Preliminary Design of Solar Organic Rankine Cycle (ORC) Systems. Energy Convers. Manag. 2019, 184, 338–349. [Google Scholar] [CrossRef]
- Fatigati, F.; Vittorini, D.; Di Bartolomeo, M.; Cipollone, R. Experimental Characterization of a Small-Scale Solar Organic Rankine Cycle (ORC) Based Unit for Domestic Microcogeneration. Energy Convers. Manag. 2022, 258, 115493. [Google Scholar] [CrossRef]
- Gilani, H.A.; Hoseinzadeh, S.; Esmaeilion, F.; Memon, S.; Garcia, D.A.; Assad, M.E.H. A Solar Thermal Driven ORC-VFR System Employed in Subtropical Mediterranean Climatic Building. Energy 2022, 250, 123819. [Google Scholar] [CrossRef]
- Yu, H.; Helland, H.; Yu, X.; Gundersen, T.; Sin, G. Optimal Design and Operation of an Organic Rankine Cycle (ORC) System Driven by Solar Energy with Sensible Thermal Energy Storage. Energy Convers. Manag. 2021, 244, 114494. [Google Scholar] [CrossRef]
- Matuszewska, D.; Kuta, M.; Górski, J. The Environmental Impact of Renewable Energy Technologies Shown in Case of ORC-Based Geothermal Power Plant. IOP Conf. Ser. Earth Environ. Sci. 2019, 214, 012142. [Google Scholar] [CrossRef]
- Jankowski, M.; Borsukiewicz, A.; Wiśniewski, S.; Hooman, K. Multi-Objective Analysis of an Influence of a Geothermal Water Salinity on Optimal Operating Parameters in Low-Temperature ORC Power Plant. Energy 2020, 202, 117666. [Google Scholar] [CrossRef]
- Ziółkowski, P.; Hyrzyński, R.; Lemański, M.; Kraszewski, B.; Bykuć, S.; Głuch, S.; Sowiżdżał, A.; Pająk, L.; Wachowicz-Pyzik, A.; Badur, J. Different Design Aspects of an Organic Rankine Cycle Turbine for Electricity Production Using a Geothermal Binary Power Plant. Energy Convers. Manag. 2021, 246, 114672. [Google Scholar] [CrossRef]
- Chitgar, N.; Hemmati, A.; Sadrzadeh, M. A Comparative Performance Analysis, Working Fluid Selection, and Machine Learning Optimization of ORC Systems Driven by Geothermal Energy. Energy Convers. Manag. 2023, 286, 117072. [Google Scholar] [CrossRef]
- Żołądek, M.; Figaj, R.; Sornek, K. Energy Analysis of a Micro-Scale Biomass Cogeneration System. Energy Convers. Manag. 2021, 236, 114079. [Google Scholar] [CrossRef]
- Świerzewski, M.; Kalina, J.; Musiał, A. Techno-Economic Optimization of ORC System Structure, Size and Working Fluid within Biomass-Fired Municipal Cogeneration Plant Retrofitting Project. Renew. Energy 2021, 180, 281–296. [Google Scholar] [CrossRef]
- Braimakis, K.; Charalampidis, A.; Karellas, S. Techno-Economic Assessment of a Small-Scale Biomass ORC-CHP for District Heating. Energy Convers. Manag. 2021, 247, 114705. [Google Scholar] [CrossRef]
- Mascuch, J.; Novotny, V.; Spale, J.; Vodicka, V.; Zeleny, Z. Experience from Set-up and Pilot Operation of an in-House Developed Biomass-Fired ORC Microcogeneration Unit. Renew. Energy 2021, 165, 251–260. [Google Scholar] [CrossRef]
- Witanowski, Ł.; Klonowicz, P.; Lampart, P.; Ziółkowski, P. Multi-Objective Optimization of the ORC Axial Turbine for a Waste Heat Recovery System Working in Two Modes: Cogeneration and Condensation. Energy 2023, 264, 126187. [Google Scholar] [CrossRef]
- Lecompte, S.; Oyewunmi, O.A.; Markides, C.N.; Lazova, M.; Kaya, A.; den Broek, M.; De Paepe, M. Case Study of an Organic Rankine Cycle (ORC) for Waste Heat Recovery from an Electric Arc Furnace (EAF). Energies 2017, 10, 649. [Google Scholar] [CrossRef]
- Marchionni, M.; Fatigati, F.; Di Bartolomeo, M.; Di Battista, D.; Petrollese, M. Experimental and Numerical Dynamic Investigation of an ORC System for Waste Heat Recovery Applications in Transportation Sector. Energies 2022, 15, 9339. [Google Scholar] [CrossRef]
- Fatigati, F.; Vittorini, D.; Wang, Y.; Song, J.; Markides, C.N.; Cipollone, R. Design and Operational Control Strategy for Optimum Off-Design Performance of an ORC Plant for Low-Grade Waste Heat Recovery. Energies 2020, 13, 5846. [Google Scholar] [CrossRef]
- Bianchi, M.; Branchini, L.; De Pascale, A.; Melino, F.; Ottaviano, S.; Peretto, A.; Torricelli, N.; Zampieri, G. Performance and Operation of Micro-ORC Energy System Using Geothermal Heat Source. Energy Procedia 2018, 148, 384–391. [Google Scholar] [CrossRef]
- Galanis, N.; Cayer, E.; Roy, P.; Denis, E.; Désilets, M. Electricity Generation from Low Temperature Sources. J. Appl. Fluid Mech. 2009, 2, 55–67. [Google Scholar]
- Tempesti, D.; Manfrida, G.; Fiaschi, D. Thermodynamic Analysis of Two Micro CHP Systems Operating with Geothermal and Solar Energy. Appl. Energy 2012, 97, 609–617. [Google Scholar] [CrossRef]
- Hung, T.C.; Shai, T.Y.; Wang, S.K. A Review of Organic Rankine Cycles (ORCs) for the Recovery of Low-Grade Waste Heat. Energy 1997, 22, 661–667. [Google Scholar] [CrossRef]
- Chen, H.; Goswami, D.Y.; Stefanakos, E.K. A Review of Thermodynamic Cycles and Working Fluids for the Conversion of Low-Grade Heat. Renew. Sustain. Energy Rev. 2010, 14, 3059–3067. [Google Scholar] [CrossRef]
- Saleh, B.; Koglbauer, G.; Wendland, M.; Fischer, J. Working Fluids for Low-Temperature Organic Rankine Cycles. Energy 2007, 32, 1210–1221. [Google Scholar] [CrossRef]
- Quoilin, S.; Declaye, S.; Tchanche, B.F.; Lemort, V. Thermo-Economic Optimization of Waste Heat Recovery Organic Rankine Cycles. Appl. Therm. Eng. 2011, 31, 2885–2893. [Google Scholar] [CrossRef]
- Özcan, Z.; Ekici, Ö. A Novel Working Fluid Selection and Waste Heat Recovery by an Exergoeconomic Approach for a Geothermally Sourced ORC System. Geothermics 2021, 95, 102151. [Google Scholar] [CrossRef]
- Di Marcoberardino, G.; Invernizzi, C.M.; Iora, P.; Arosio, L.; Canavese, M.; Lunghi, A.; Mazzei, A. Thermal Stability and Thermodynamic Performances of Pure Siloxanes and Their Mixtures in Organic Rankine Cycles. Energies 2022, 15, 3498. [Google Scholar] [CrossRef]
- Liu, W.; Meinel, D.; Wieland, C.; Hartmut, S. Investigation of Hydrofluoroolefins as Potential Working Fluids in Organic Rankine Cycle for Geothermal Power Generation. Energy 2014, 67, 106–116. [Google Scholar] [CrossRef]
- Matuszewska, D.; Sztekler, K.; Gorski, J. An Influence of Low-Stability Region on Dense Gas Phenomena and Their Peculiarities in the ORC Fluids. MATEC Web Conf. 2014, 18, 03005. [Google Scholar] [CrossRef]
- Wang, W.; Dai, X.; Shi, L. Influence of Thermal Stability on Organic Rankine Cycle Systems Using Siloxanes as Working Fluids. Appl. Therm. Eng. 2022, 200, 117639. [Google Scholar] [CrossRef]
- Nami, H.; Ertesvåg, I.S.; Agromayor, R.; Riboldi, L.; Nord, L.O. Gas Turbine Exhaust Gas Heat Recovery by Organic Rankine Cycles (ORC) for Offshore Combined Heat and Power Applications—Energy and Exergy Analysis. Energy 2018, 165, 1060–1071. [Google Scholar] [CrossRef]
- Yağlı, H.; Koç, Y.; Koç, A.; Görgülü, A.; Tandiroğlu, A. Parametric Optimization and Exergetic Analysis Comparison of Subcritical and Supercritical Organic Rankine Cycle (ORC) for Biogas Fuelled Combined Heat and Power (CHP) Engine Exhaust Gas Waste Heat. Energy 2016, 111, 923–932. [Google Scholar] [CrossRef]
- Raninga, M.; Mudgal, A.; Patel, V.K.; Patel, J. Design of ORC-RO System for Utilizing Waste Heat from Flue Gases of Coal-Fired Thermal Power Plant. Mater. Today Proc. 2023, 77, 105–110. [Google Scholar] [CrossRef]
- Di Battista, D.; Mauriello, M.; Cipollone, R. Waste Heat Recovery of an ORC-Based Power Unit in a Turbocharged Diesel Engine Propelling a Light Duty Vehicle. Appl. Energy 2015, 152, 109–120. [Google Scholar] [CrossRef]
- Douvartzides, S.; Karmalis, I. Working Fluid Selection for the Organic Rankine Cycle (ORC) Exhaust Heat Recovery of an Internal Combustion Engine Power Plant. IOP Conf. Ser. Mater. Sci. Eng. 2016, 161, 12087. [Google Scholar] [CrossRef]
- Carcasci, C.; Winchler, L. Thermodynamic Analysis of an Organic Rankine Cycle for Waste Heat Recovery from an Aeroderivative Intercooled Gas Turbine. Energy Procedia 2016, 101, 862–869. [Google Scholar] [CrossRef]
- Khaljani, M.; Khoshbakhti Saray, R.; Bahlouli, K. Thermodynamic and Thermoeconomic Optimization of an Integrated Gas Turbine and Organic Rankine Cycle. Energy 2015, 93, 2136–2145. [Google Scholar] [CrossRef]
- Lecompte, S.; Huisseune, H.; den Broek, M.; Vanslambrouck, B.; De Paepe, M. Review of Organic Rankine Cycle (ORC) Architectures for Waste Heat Recovery. Renew. Sustain. Energy Rev. 2015, 47, 448–461. [Google Scholar] [CrossRef]
- Xiao, G.; Chen, J.; Ni, M.; Cen, K. A Solar Micro Gas Turbine System Combined with Steam Injection and ORC Bottoming Cycle. Energy Convers. Manag. 2021, 243, 114032. [Google Scholar] [CrossRef]
- Köse, Ö.; Koç, Y.; Yağlı, H. Performance Improvement of the Bottoming Steam Rankine Cycle (SRC) and Organic Rankine Cycle (ORC) Systems for a Triple Combined System Using Gas Turbine (GT) as Topping Cycle. Energy Convers. Manag. 2020, 211, 112745. [Google Scholar] [CrossRef]
- Bidini, G.; Desideri, U.; Di Maria, F.; Baldacci, A.; Papale, R.; Sabatelli, F. Optimization of an Integrated Gas Turbine–Geothermal Power Plant. Energy Convers. Manag. 1998, 39, 1945–1956. [Google Scholar] [CrossRef]
- Astina, I.M.; Pastalozi, M.; Sato, H. An Improved Hybrid and Cogeneration Cycle for Enhanced Geothermal Systems. In Proceedings of the World Geothermal Congress 2010, Bali, Indonesia, 25–30 April 2010. [Google Scholar]
- Jawad Kadhim, H.; Abbas, A.; Kadhim, T.; Rashid, F. Evaluation of Gas Turbine Performance in Power Plant with High-Pressure Fogging System. Math. Model. Eng. Probl. 2023, 10, 605–612. [Google Scholar] [CrossRef]
- Hammid, S.; Naima, K.; Ikumapayi, O.M.; Kezrane, C.; Liazid, A.; Asad, J.; Rahman, M.H.; Rashid, F.L.; Hussien, N.A.; Menni, Y. Overall Assessment of Heat Transfer for a Rarefied Flow in a Microchannel with Obstacles Using Lattice Boltzmann Method. Comput. Model. Eng. Sci. 2024, 138, 273–299. [Google Scholar] [CrossRef]
- Ren, J.; Cao, Y.; Long, Y.; Qiang, X.; Dai, Y. Thermodynamic Comparison of Gas Turbine and ORC Combined Cycle with Pure and Mixture Working Fluids. J. Energy Eng. 2019, 145, 05018002. [Google Scholar] [CrossRef]
- Matuszewska, D.; Olczak, P. Evaluation of Using Gas Turbine to Increase Efficiency of the Organic Rankine Cycle (ORC). Energies 2020, 13, 1499. [Google Scholar] [CrossRef]
- Olczak, P.; Jaśko, P.; Kryzia, D.; Matuszewska, D.; Fyk, M.I.; Dyczko, A. Analyses of Duck Curve Phenomena Potential in Polish PV Prosumer Households’ Installations. Energy Rep. 2021, 7, 4609–4622. [Google Scholar] [CrossRef]
- Franco, A.; Vaccaro, M. Numerical Simulation of Geothermal Reservoirs for the Sustainable Design of Energy Plants: A Review. Renew. Sustain. Energy Rev. 2014, 30, 987–1002. [Google Scholar] [CrossRef]
- Sun, J.; Liu, Q.; Duan, Y. Effects of Reinjection Temperature on Thermodynamic Performance of Dual-Pressure and Single-Pressure Geothermal ORCs. Energy Procedia 2019, 158, 6016–6023. [Google Scholar] [CrossRef]
- Siemens/Reliable Gas Turbines. 2023. Available online: https://www.siemens-energy.com/global/en/offerings/power-generation/gas-turbines.html (accessed on 31 May 2023).
- NIST. NIST Reference Fluid Thermodynamic and Transport Properties Database (REFPROP); National Institute of Standards and Technology: Gaithersburg, MD, USA, 2019. [Google Scholar]
- Bahrami, M.; Pourfayaz, F.; Kasaeian, A. Low Global Warming Potential (GWP) Working Fluids (WFs) for Organic Rankine Cycle (ORC) Applications. Energy Rep. 2022, 8, 2976–2988. [Google Scholar] [CrossRef]
- Zhao, S.; Abed, A.M.; Deifalla, A.; Al-Zahrani, A.; Aryanfar, Y.; García Alcaraz, J.L.; Galal, A.M.; Sai, W. Competitive Study of a Geothermal Heat Pump Equipped with an Intermediate Economizer for Various ORC Working Fluids. Case Stud. Therm. Eng. 2023, 45, 102954. [Google Scholar] [CrossRef]
- DiPippo, R. Geothermal Power Plants Principles Applications Case Studies and Environmental Impact, 3rd ed.; Butterworth-Heinemann: Oxford, UK, 2013. [Google Scholar]
- Nazari, N.; Heidarnejad, P.; Porkhial, S. Multi-Objective Optimization of a Combined Steam-Organic Rankine Cycle Based on Exergy and Exergo-Economic Analysis for Waste Heat Recovery Application. Energy Convers. Manag. 2016, 127, 366–379. [Google Scholar] [CrossRef]
- Ghaebi, H.; Namin, A.; Rostamzadeh, H. Exergoeconomic Optimization of a Novel Cascade Kalina/Kalina Cycle Using Geothermal Heat Source and LNG Cold Energy Recovery. J. Clean. Prod. 2018, 189, 279–296. [Google Scholar] [CrossRef]
- Li, Z.X.; Ehyaei, M.A.; Kamran Kasmaei, H.; Ahmadi, A.; Costa, V. Thermodynamic Modeling of a Novel Solar Powered Quad Generation System to Meet Electrical and Thermal Loads of Residential Building and Syngas Production. Energy Convers. Manag. 2019, 199, 111982. [Google Scholar] [CrossRef]
- Aliehyaei, M.; Ahmadi, A.; El Haj Assad, M.; Rosen, M. Investigation of an Integrated System Combining an Organic Rankine Cycle and Absorption Chiller Driven by Geothermal Energy: Energy, Exergy, and Economic Analyses and Optimization. J. Clean. Prod. 2020, 258, 120780. [Google Scholar] [CrossRef]
- Yağlı, H.; Koç, Y.; Kalay, H. Optimisation and Exergy Analysis of an Organic Rankine Cycle (ORC) Used as a Bottoming Cycle in a Cogeneration System Producing Steam and Power. Sustain. Energy Technol. Assess. 2021, 44, 100985. [Google Scholar] [CrossRef]
- Gimelli, A.; Luongo, A.; Muccillo, M. Efficiency and Cost Optimization of a Regenerative Organic Rankine Cycle Power Plant through the Multi-Objective Approach. Appl. Therm. Eng. 2017, 114, 601–610. [Google Scholar] [CrossRef]
- A Pequot Publication. Gas Turbine World 2021 GTW Handbook; A Pequot Publication: Fairfield, CT, USA, 2021. [Google Scholar]
- U.S. Energy Information Administration. Capital Cost and Performance Characteristic Estimates for Utility Scale Electric Power Generating Technologies; U.S. Energy Information Administration: Washington, DC, USA, 2020. [Google Scholar]
- Lukawski, M.Z.; Anderson, B.J.; Augustine, C.; Capuano, L.E.; Beckers, K.F.; Livesay, B.; Tester, J.W. Cost Analysis of Oil, Gas, and Geothermal Well Drilling. J. Pet. Sci. Eng. 2014, 118, 1–14. [Google Scholar] [CrossRef]
- Shokati, N.; Ranjbar, F.; Yari, M. Exergoeconomic Analysis and Optimization of Basic, Dual-Pressure and Dual-Fluid ORCs and Kalina Geothermal Power Plants: A Comparative Study. Renew. Energy 2015, 83, 527–542. [Google Scholar] [CrossRef]
- Gołdasz, A.; Matuszewska, D.; Olczak, P. Technical, Economic, and Environmental Analyses of the Modernization of a Chamber Furnace Operating on Natural Gas or Hydrogen. Int. J. Hydrog. Energy 2022, 47, 13213–13225. [Google Scholar] [CrossRef]
| Type of the Gas Turbine (GT) | Gas Turbine SGT-50 | Gas Turbine SGT-100 | Gas Turbine SGT-300 | Gas Turbine SGT-400 |
|---|---|---|---|---|
| Fuel | Natural gas, liquid fuel, dual fuel | |||
| Gross efficiency | 26% | 30.2% | 30.6% | 34.8% |
| Heat rate | 15,148 kJ/kWh | 11,914 kJ/kWh | 11,773 kJ/kWh | 10,355 kJ/kWh |
| Turbine speed | 25,500 rpm | 17,384 rpm | 14,010 rpm | 9500 rpm |
| Pressure ration | 7.0:1 | 14.0:1 | 13.7:1 | 16.8:1 |
| Exhaust mass flow | 9.5 kg/s | 19.5 kg/s | 30.2 kg/s | 39.4 kg/s |
| Exhaust temperature | 600 °C | 545 °C | 542 °C | 555 °C |
| Power | 2 MWe | 5.1 MWe | 7.9 MWe | 12.9 MWe |
| Type of the Gas Turbine (GT) | Gas Turbine SGT-800 | Gas Turbine SGT-A05 KB5S | Gas Turbine SGT-A05 KB7S | Gas Turbine SGT-A05 KB7HE |
| Fuel | Natural gas, liquid fuel, dual fuel | |||
| Gross efficiency | 41.1% | 29.7% | 32.3% | 33.2% |
| Heat rate | 8759 kJ/kWh | 12,137 kJ/kWh | 11,152 kJ/kWh | 10,848 kJ/kWh |
| Turbine speed | 6600 rpm | 14,200 rpm | 14,600 rpm | 14,600 rpm |
| Pressure ration | 21.1:1 | 10.3:1 | 13.9:1 | 14.1:1 |
| Exhaust mass flow | 135.5 kg/s | 15.4 kg/s | 21.3 kg/s | 21.4 kg/s |
| Exhaust temperature | 596 °C | 560 °C | 494 °C | 522 °C |
| Power | 62.5 MWe | 4.0 MWe | 5.4 MWe | 5.8 MWe |
| Working Fluid (F) | Chemical Class | Tbp (K) | TCR (K) | PCR (MPa) | ASHRAE Safety Group | ASHRAE Flammability | ASHRAE Toxicity | ODP | GWP |
|---|---|---|---|---|---|---|---|---|---|
| R600a | HC | 272.66 | 424.13 | 3.796 | A3 | Yes (highly flammable) | No | 0 | 3 |
| R134a | HFC | 247,08 | 374.21 | 4.0593 | A1 | Non-flammable | No | 0 | 1430 |
| R152a | HFC | 249.13 | 386.41 | 4.5168 | A2 | Yes (medium flammable) | No | 0 | 124 |
| R227ea | HFC | 256.81 | 374.9 | 2.925 | A1 | Non-flammable | No | 0 | 3230 |
| R245fa | HFC | 288.29 | 427.16 | 3.651 | A1 | Non-flammable | No | 0 | 1030 |
| R1224yd(Z) | HCFO | 287.77 | 428.69 | 3.337 | - | Flammable | Relatively non-toxic | 0 | 0.88 |
| R1233zd(E) | HCFO | 291.41 | 439.6 | 3.6237 | A3 | Yes (highly flammable) | Acceptable toxicity | 0 | 7 |
| R1234yf | HFO | 243.7 | 367.85 | 3.3822 | A2L | Yes (low flammable) | No | 0 | 4 |
| R1243zf | HFO | 247.73 | 376.93 | 3.5179 | - | Yes (highly flammable) | Toxic | 0 | 149 |
| R1336mzz(Z) | HFO | 306.6 | 444.5 | 2.903 | A3 | Yes (highly flammable) | No | 0 | 9 |
| Equipment | Heating Fluid Type | Heating Fluid Phase | Heated Fluid Type | Heated Fluid Phase | U [kW/m2·K] |
|---|---|---|---|---|---|
| Heat exchanger | Exhaust gas | Gas | Geothermal brine | Liquid | 0.2 |
| Evaporator | Geothermal brine | Liquid | Organic fluid | Liquid/vapor | 0.9 |
| Preheater | Geothermal brine | Liquid | Organic fluid | Liquid | 0.9 |
| Condenser | Organic fluid | Vapor/liquid | Water | Liquid | 1.0 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Matuszewska, D. Economic Analysis of Gas Turbine Using to Increase Efficiency of the Organic Rankine Cycle. Sustainability 2024, 16, 75. https://doi.org/10.3390/su16010075
Matuszewska D. Economic Analysis of Gas Turbine Using to Increase Efficiency of the Organic Rankine Cycle. Sustainability. 2024; 16(1):75. https://doi.org/10.3390/su16010075
Chicago/Turabian StyleMatuszewska, Dominika. 2024. "Economic Analysis of Gas Turbine Using to Increase Efficiency of the Organic Rankine Cycle" Sustainability 16, no. 1: 75. https://doi.org/10.3390/su16010075
APA StyleMatuszewska, D. (2024). Economic Analysis of Gas Turbine Using to Increase Efficiency of the Organic Rankine Cycle. Sustainability, 16(1), 75. https://doi.org/10.3390/su16010075








