How to Price Catastrophe Bonds for Sustainable Earthquake Funding? A Systematic Review of the Pricing Framework

Abstract

Earthquake contingency costs in traditional insurance cannot provide sufficient earthquake funding for a country because they often differ significantly from actual losses. Over the last three decades, this approach has been replaced by linking earthquake insurance to bonds in the capital market; this is now known as the earthquake catastrophe bond (ECB). Through the ECB, contingency costs become larger and more sustainable earthquake funds. Unfortunately, there are challenges in ECB issuance, as the pricing framework does not yet have standard rules and still needs to be studied. Therefore, the objective of this study is to systematically review how the ECB pricing framework is designed. The method used in this review is PRISMA. First, articles aiming to design an ECB pricing framework were collected from the Scopus, Science Direct, and Dimensions databases on 22 March 2023. Then, the results were selected, resulting in eleven relevant articles. Then, the articles’ pricing frameworks were reviewed based on variables, methods, trigger events, coupon and redemption value payment schemes, and the model solution forms. Finally, several research opportunities for academics are also outlined. This research constitutes a reference for ECB issuers during the pricing process and can motivate academics to design more useful ECB pricing models.

1. Introduction

Earthquakes are very frequent. An earthquake may be happening right now. However, not all earthquakes can be felt directly. Generally, when an earthquake is very strong, everyone can feel it [1]. Earthquakes of this magnitude are often referred to as extreme earthquakes.

Extreme earthquakes are rare but result in significant economic losses and fatalities [2,3]. Based on data from the International Disaster Database, between 1997 and 2021 (https://www.emdat.be, accessed on 27 October 2022), a single earthquake incident resulted in an average economic loss of 1,266,348,909 USD and 961 fatalities. On average, earthquakes cause a larger number of losses and fatalities than other catastrophes, as shown in

Table 1. Average economic losses and fatalities from a single catastrophe by type.

Type of Catastrophe	Losses (USD)	Fatalities (People)
Earthquakes	1,266,348,909	961
Extreme temperatures	157,529,668	352
Storms	662,920,441	87
Droughts	461,086,035	51
Landslides	21,412,879	48
Floods	258,287,739	47
Volcanic activity	24,887,188	13
Wildfires	392,804,851	7

.

Significant earthquake losses place a burden on a country’s budget [4,5,6,7]. As a result, between 1992 and 2000, many countries used traditional insurance mechanisms to obtain contingency costs for their earthquake responses. However, traditional earthquake insurance mechanisms are generally ineffective because the contingency costs are less significant than the actual losses [8,9]. For example, in 1992, Turkey used earthquake insurance to cope with an earthquake in Erzincan with a magnitude of 6.8 Mw [10]. Unfortunately, the contingency cost was only USD 10.8 million, or 1.44% of the losses incurred; in other words, the nominal contingency cost was small and did not sufficiently cover actual losses. Then, in 1993, an earthquake with a magnitude of 7.7 Mw occurred in Okushiri (Japan) [11]. However, the insurance could only provide a contingency cost of USD 16 million or 1.6% of the actual loss. Again, this nominal figure did not sufficiently cover the actual losses incurred. Thus, an innovative new mechanism must be developed to replace the traditional earthquake insurance mechanism [12,13,14].

Over the last three decades, earthquake-prone countries, i.e., countries traversed by tectonic plates, have attempted to develop a new earthquake insurance mechanism that more effectively provides post-earthquake contingency costs [15,16]. To date, these countries and the World Bank have focused on mechanisms that link the country’s earthquake insurance with financial instruments in the capital market [17,18]. In other words, a country’s earthquake risk is partially or fully shared with investors via financial instruments in the capital market. This has become known as earthquake-insurance-linked securities (EILS). The most successful financial instruments in EILS are bonds [19,20,21]. Compared to other financial instruments, bonds can raise significant funds quickly; however, they also involve moderate levels of risk [14]. This mechanism is known as the earthquake catastrophe bond (ECB).

Several earthquake-prone countries have used the ECB as a source of contingency costs. A visualization of ECB-using countries is shown in Figure 1. Figure 1 shows that the first country to use the ECB was Mexico in 2006, with CAT-Mex special-purpose vehicles (SPV) [13,22]. They obtained a USD 160 million contingency fund to finance earthquake events that might occur over the next three years. Then, Mexico again made use of the three-year ECBs in 2009 and 2017 and the two-year ECB in 2018. The three ECBs were issued by SPV MultiCAT-Mexico [23], IBRD CAR 113 [24], and IBRD 118–119 [25], respectively. More specifically, the contingency costs of each issue were USD 290, 120, and 260 million, respectively. Mexico’s plan was then followed by neighboring countries, such as Chile, Peru, and Colombia. All three countries used the ECB in 2018 [26]. Chile used the three-year term ECB issued by IBRD CAT 116 with a contingency cost of USD 500 million. Then, through IBRD CAR 120, Peru issued a two-year ECB with a contingency cost of USD 200 million, and, through IBRD CAR 117, Colombia issued a three-year ECB with a contingency cost of USD 400 million. Finally, in 2019, the Philippines used the three-year ECB issued by IBRD 123 with a contingency cost of USD 75 million [25]. In other words, contingency costs for earthquake funding via the ECB appear to total USD 75 to 500 million. This amount is enormous and can better cover the actual losses that occur than traditional earthquake insurance mechanisms. This indicates that the ECB is more effective in providing post-earthquake funding for a country [27,28].

Even though several countries have issued ECBs, there are fundamental obstacles at the issuance stage that must be continuously studied, namely, the fair price setting stage [14,29]. This is a tricky stage because the pricing framework integrates financial and earthquake risk variables. Several researchers conducted systematic literature reviews (SLRs) of the fair pricing framework for the ECB or of catastrophic bonds (CAT bonds) in general; these researchers include Cannabaro et al. [30], Linnerooth-Bayer and Amendola [31], Skees et al. [32], Sukono et al. [33], and Anggraeni et al. [34]. Cannabaro et al. [30] introduced the terminology and simplified the pricing of CAT bonds for the first time. The differences between traditional bonds and CAT bonds are also explained therein. Then, Linnerooth-Bayer and Amendola discussed a loss-sharing system in catastrophic state funding through linkages with financial securities in the capital market [31]. They found that bonds are the most effective security in such a loss-sharing system. Then, Skees et al. [32] explained the importance of post-catastrophe funding through CAT bonds in low-income countries; countries that have successfully used CAT bonds are also described in this study. Sukono et al. [33] reviewed how the compound Poisson process (CPP) was used in pricing CAT bonds. The review includes the type of CPP used, models of the time of claim occurrence, and new research that can be conducted in the future. Finally, Anggraeni et al. [34] examined how extreme value theory was applied to ECB pricing. They found five articles on this topic. In addition, other results show that the ECB with two triggers is better implemented than that with one trigger. This makes sense, given that the present increasing annual extreme earthquake frequency will increase the probability of ECB claim events. Hence, it will decrease investor interest in buying ECB. One means of overcoming this problem involves using a two-trigger ECB. In this type of ECB, the claim event happens when two triggers occur; this also increases the probability of a claim event. Therefore, under these conditions, ECB will be more attractive to investors.

Based on the problems raised above, the objective of this study is to systematically review how the ECB pricing framework is designed. Specifically, the following eight research questions (RQs) will be examined:

• RQ1: What financial risk variables are involved in ECB pricing?
• RQ2: What earthquake risk variables are involved in ECB pricing?
• RQ3: What are the main methods used to model financial risk variables?
• RQ4: What are the main methods used to model earthquake risk variables?
• RQ5: What type of claim trigger index is used?
• RQ6: What are payment schemes of coupon and redemption value from the ECB?
• RQ7: What are the solution forms of the ECB’s pricing models?
• RQ8: What is the method of determining the solution for a model that does not have a closed form?

Meanwhile, the novelty of this study is that the methods used to price the ECB are not limited. In other words, there is no limit to the method used. This method was chosen so that the study’s results provide a general overview of the problem. In addition, the research questions explored in this study have never been considered in previous works. The review uses the Preferred Reporting Items for Systematic Review and Meta-Analyses (PRISMA) method, which makes use of a detailed flowchart to increase the compatibility between the articles obtained and the topics studied [35]. There are three main stages in this process: collecting, selecting, and reviewing articles. All stages were conducted independently, without conflict of interest, to minimize bias. The article collection stage was conducted based on the examined criteria via the Scopus, Science Direct, and Dimensions databases search engines. Then, articles obtained during this stage were selected in the next stage by reading the abstracts and full texts of all of the articles. Finally, the review stage was conducted based on the ECB pricing frameworks used in the articles. After the review was conducted, we also analyzed and discussed future research opportunities. This research presents several options for developing the ECB’s pricing framework, which other researchers could pursue. This research can provide insights into the ECB pricing framework and motivate other researchers to design more helpful frameworks.

2. Research Methodology

In this study, the Preferred Reporting Items for Systematic Review and Meta-Analyses (PRISMA, see the Supplementary Material) method was used to review how to price the ECB. This method was chosen because it uses a detailed flowchart to increase the suitability of the articles obtained for the topics studied [35].

This method has three stages. The first stage involves article collection. Article collection was conducted based on specific criteria. The article collection criteria used in this study are as follows:

(a)

Article type: a research or conference article written in English.

(b)

The article was published before 22 March 2023 in a peer-reviewed international journal indexed by Scopus, Science Direct, or Dimensions.

(c)

The article contains the following words in the title, abstract, or keywords: “Earthquake” AND (“Catastrophe Bond” OR “Catastrophic Bond” OR “CAT Bond”) AND (“Pricing” OR “Price” OR “Valuation” OR “Valuing”).

All criteria were confirmed to be fulfilled independently, without conflict of interest, in order to minimize bias. The fulfillment of criteria (a) to (c) was assessed using a search engine from the Scopus, Science Direct, and Dimensions databases. The words in point (c) were entered into the article search field. Before the search button was pressed, the advanced search icon was selected. Then, the type of article, the language, and the source type were selected to be those described in points (a) and (b).

The second stage ©s article selection. This stage was conducted manually, to ensure that the selected articles were accurate and relevant. The selected articles aim to model ECB price. The stages of article selection are as follows [33,36]:

(a)

Removal of duplicate and unavailable articles

Articles that have been collected may be simultaneously indexed in more than one database. Thus, duplicates are possible, so the duplicates must be deleted. In addition, it is possible that the articles that have been collected are not available to the publishers. Therefore, those unavailable articles were also deleted.

(b)

Selection of articles in the title and abstract sections

At this stage, the selection of articles was conducted by reading the title and abstract sections. These parts of the articles were chosen because they best represent the article. In addition, this approach shortens the selection time. Articles whose titles and abstracts do not relate to the research topic were excluded at this stage.

(c)

Selection of articles through reading all sections thoroughly

The articles obtained from stage two were reselected by reading them thoroughly, one by one. This step was conducted to ensure that the selected articles are relevant to the research topic. The articles obtained at this stage were then reviewed.

The final stage is the article review. The stage is conducted based on research questions presented in Section 1.

3. Results

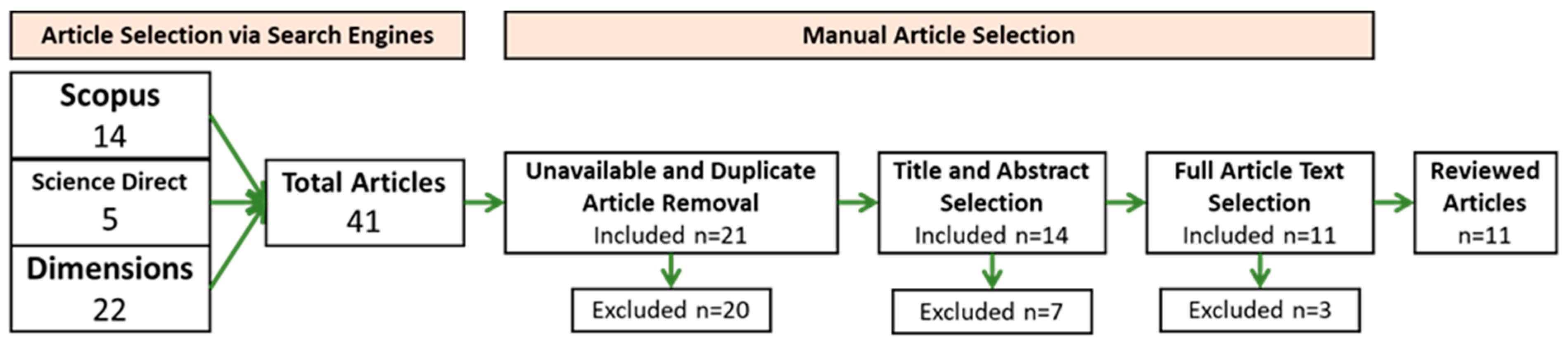
3.1. Article Collection and Selection Results

The numbers of articles that met collection criteria (a) to (c) from the Scopus, Science Direct, and Dimensions databases are 14, 5, and 22, respectively. In other words, 41 articles in total were obtained from the three databases. These results are summarized in

Table 2. Summary of article collection via search engines in the Scopus, Science Direct, and Dimensions databases.

Article Database	The Number of Articles
Scopus	14
Science Direct	5
Dimensions	22
Total	41

.

After the articles were collected, these articles were selected manually. The removal of unavailable and duplicate articles resulted in the removal of four articles that were not available and sixteen articles that were duplicated. In other words, twenty articles were deleted, and the remaining twenty-one were reselected for the title and abstract selection stage. This stage resulted in fourteen articles that met the objective criteria for modeling ECB prices. These articles were then selected for the manual full-text selection stage. This final stage resulted in eleven articles that met the criteria. In other words, three articles were deemed not to be appropriate based on the full text: Tao et al. [37], Wu and Zou [38], and Ismail [39]. Tao et al. [37] discussed the determination of insurance premiums through ECBs, while Wu and Zou [38] and Ismail [39] designed frameworks for calculating the probability of earthquake severity. Thus, the full texts of eleven articles were reviewed. These were written by Romaniuk [40], Zimbidis et al. [41], Shao et al. [42], Gunardi and Setiawan [43], Tang and Yuan [44], Hofer et al. [45], Kang et al. [46], Wei et al. [9], Mistry and Lombardi [47], Aghdam et al. [48], and Anggraeni et al. [49]. Primary information data for these eleven articles can be accessed at https://bit.ly/3Kwof5j (accessed on 24 March 2023). A visual summary of the results of the collection and selection of articles is presented in Figure 2.

3.2. Description of Articles

A geographical description of the eleven articles, based on the authors’ country of affiliation, is shown in Figure 3.

Figure 3 shows that, in general, the country affiliations of the authors are earthquake-prone countries. This shows that ECB price modeling research is actively carried out in earthquake-prone countries. For example, China, Indonesia, Iran, the USA, and Greece are among the top ten countries in terms of both the author’s affiliation and the highest number of earthquakes in the world today.

Next, a description of the eleven articles based on their annual publication frequencies and number of citations is given in

Table 3. Descriptions of eleven articles based on their publication years and the number of citations.

No.	Author(s)	Year	Number of Citations
1	Romaniuk [40]	2003	9
2	Zimbidis et al. [41]	2007	32
3	Shao et al. [42]	2015	17
4	Gunardi and Setiawan [43]	2015	3
5	Tang and Yuan [44]	2019	11
6	Hofer et al. [45]	2020	13
7	Kang et al. [46]	2022	0
8	Mistry and Lombardi [47]	2022	2
9	Wei et al. [9]	2022	5
10	Aghdam et al. [48]	2022	0
11	Anggraeni et al. [49]	2023	0

. Table 3 shows that the publication of articles about ECB pricing shows an increasing tendency. The study of this topic began in 2003 and became more popular in 2015 and 2016. Table 3 also shows that the article by Zimbidis et al. [41] is the most widely cited. In other words, based on the number of citations, this article is the most relevant to the issue of ECB price modeling.

Next, is a description of the popular topics that are often covered in the eleven articles. Popular topics are measured by the frequency of relevant words that appear in all articles; they are visually presented in Figure 4, which was produced using VosViewer software version 1.6.17. The visualization also provides the associations of all the words. Only words with a frequency occurrence of more than one are shown, in order to simplify the figure.

The circle size represents the number of times the word appears in the eleven articles. The bigger the circle, the more frequently the words are discussed; likewise, smaller circles represent fewer mentions. Furthermore, the connecting lines between the circles represent relationships between the words. The more connecting lines in a circle, the more associations between this word and other words. The circle’s color represents the word cluster; circles of the same color indicate that the words are in the same cluster. Finally, the distance between the circles represents the strength of the link between the words in them. The smaller the distance between the circles, the stronger the association between the words.

Figure 4 shows circles with the words “earthquake” and “catastrophe bond”, which have large sizes, short connecting lines, and belong to different clusters. This shows that the two words have a strong connection and are among the eleven articles’ most frequently discussed topics. Another cluster of words (“pricing”, “model”, “formula”, “application”, and “case study”) represents the research objectives of the articles; it indicates that, apart from ECB price modeling (formulation), the eleven articles’ models also carry out analyses of their application, as well as case studies. There is also a cluster comprised of the words “magnitude”, “loss”, “depth”, and “spatial”, which show the relevant earthquake risk variables. This indicates that the standard earthquake risk variables involved in ECB price modeling are magnitude, depth, loss, and spatiality. Then, there is a circle including the words “interest”, “coupon”, and “stochastic interest rate”, which shows the financial risk variables involved. Finally, there is a circle comprising the words “extreme value theory”, “Monte Carlo method”, “Cox–Ingersoll–Ross”, and “generalized extreme value”, which refer to the ECB’s price modeling methods. This circle indicates that these theories are commonly used theories in ECB price modeling.

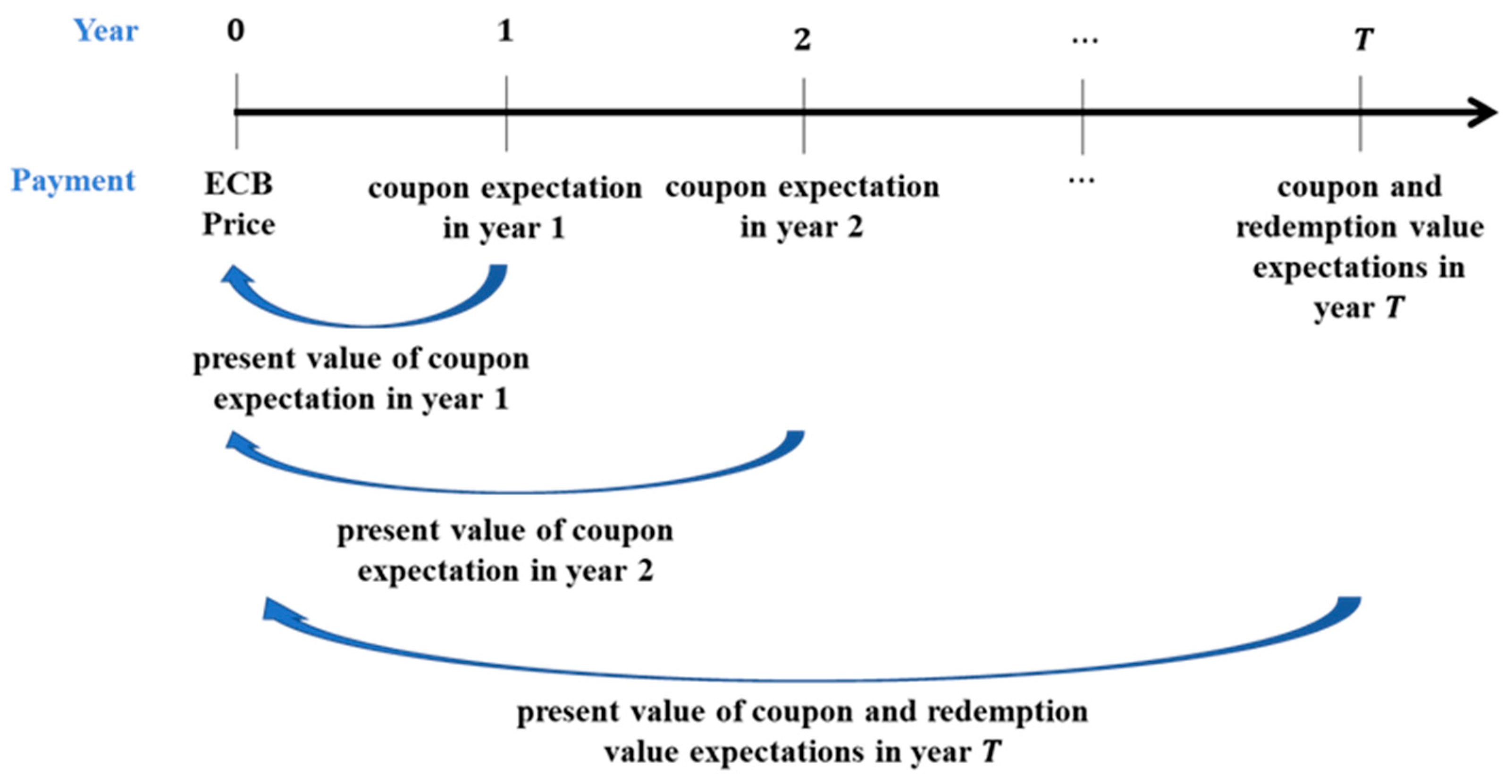
3.3. Pricing Framework Analysis

The ECB’s pricing mechanism is generally similar to traditional bond pricing. The difference is that, in ECB pricing, the coupon and redemption value payments are based on the existence of the claim-triggering event. In the eleven articles, ECB pricing is generally conducted using the expected value principle. This means that the coupon per period and the redemption value from the ECB are represented as random variables with the domain of time and image of proportion. The calculation of the $T$-year ECB price with a coupon paid annually is shown in Figure 5.

Figure 5 shows that the ECB price is the sum of the present values of the coupon’s random variable expectations for each year and the present value of the redemption value’s random variable expectation. It is mathematically expressed as follows:

$$P_T=K_T+R_T,$$

(1)

where $T$ represents the ECB period (year), $P_T$ is the ECB price with a period of $T$, $K_T$ represents the present value of the expected coupon each year until $T$ year, and $R_T$ represents the present value of the expected redemption value in year $T$.

Furthermore, an analysis of the ECB pricing framework from the eleven articles is conducted based on the eight research questions presented in Section 1. First, we analyzed the problems articulated in RQ1 and RQ2. The eleven articles reviewed generally assume that financial risk variables are independent of earthquake risk variables. In other words, financial risk variables do not affect earthquake risk variables and vice versa, i.e., the nominal interest rate does not affect the frequency of earthquakes, and earthquake losses do not affect the inflation rate. The results for RQ1 and RQ2 regarding the involvement of financial and earthquake risk variables in ECB pricing are presented in

Table 4. Financial and earthquake risk variables used in eleven articles.

Author(s)	Financial Risk Variables	Earthquake Risk Variables
Romaniuk [40]	$F_T$, $T$, $r_c$, ${\mathcal{S}}_t$	${\tau }_N$, $\gamma$
Zimbidis et al. [41]	$F_T$, $T$, $r_c$, $c_k$, $C_k$, $e$, $i_k$	$M_k$
Shao et al. [42]	$F_T$, $T$, $r_k$, $c_k$, $C_k$, $e$, ${\pi }_k$	$M_k$, $D_k$
Gunardi and Setiawan [43]	$F_T$, $T$, $r_{c,t}$, $c$, $e$, $C_k$	$M_k$
Tang and Yuan [44]	$F_T$, $T$, $r_{c,t}$, $c_k$, $C_k$	$N_t$, $\lambda$, $X_i$, $L_t$
Hofer et al. [45]	$F_T$, $T$, $r_{c,t}$, $c$, $C_k$	$N_t$, ${\lambda }_t$, $X_i$, $L_t$, $W_j$, ${\rho }_a$
Kang et al. [46]	$F_T$, $T$, $r_{c,t}$, $D_t$	$N_t$, $\lambda$, $X_i$, $L_t$
Mistry and Lombardi [47]	$F_T$, $T$, $r_{c,t}$, $c$, $C_k$	$N_t$, $\lambda$, $X_i$, $L_t$, $W_j$, ${\tau }_L$, ${\rho }_b$
Wei et al. [9]	$F_T$, $T$, $r_{c,t}$, $c$, $C_k$	$N_t$, $\lambda$, $X_i$, $L_t$, $Y_i$, $M_t$, ${\tau }_a$, ${\tau }_b$
Aghdam et al. [48]	$F_T$, $T$, $r_{c,t}$	$N_t$, $\lambda$, $X_i$, $L_t^{\mathrm{*}}$
Anggraeni et al. [49]	$F_T$, $T$, $r_{c,t}$, $c_k$, $e$, $C_k$	$N_t$, $\lambda$, $M_k$, $D_k$, $W_j$

, and the descriptions are provided in

Table 5. Notational descriptions of financial and earthquake risk variables used in the eleven articles.

Variable	Description
$F_T$	Redemption value in year $T$
$T$	The term of ECB
$r_k$	The nominal interest rate at the end of the $k$-th year, $k=1,2,\dots ,T$, which is inconstant and compounded once
$r_c$	The nominal interest rate, which is constant and continuously compounding
$r_{c,t}$	The nominal interest rate at time $t$, $t\in \left[0,T\right]$, which is inconstant and continuously compounding
$c$	The constant coupon rate
$c_k$	The inconstant coupon rate at the end of the $k$-th year, $k=1,2,\dots ,T$
$C_k$	The coupon at the end of the $k$-th year, $k=1,2,\dots ,T$
$e$	The extra premium loading rate compounded continuously within one year
${\pi }_k$	The inconstant inflation rate at the end of the $k$-th year, $k=1,2,\dots ,T$
$i_k$	The inconstant return rate from bank deposits at the end of the $k$-th year, $k=1,2,\dots ,T$
${\mathcal{S}}_t$	The inconstant underlying asset at time $t$, $t\in \left[0,T\right]$
$D_t$	The liability worth of sponsors at time $t$, $t\in \left[0,T\right]$
$N_t$	The number of earthquakes that occur until time $t$, $t\in \left[0,T\right]$
$\lambda$	The constant intensity of earthquakes
${\lambda }_t$	The inconstant intensity of earthquakes at time $t$, $t\in \left[0,T\right]$
$X_i$	The financial loss of the $i$-th earthquake, $i=1,2,\dots ,N_t$
$L_t$	The aggregate earthquake financial until time $t$, $t\in \left[0,T\right]$
$L_t^{*}$	The aggregate earthquake financial with jumping until time $t$, $t\in \left[0,T\right]$
$Y_i$	the magnitude of the $i$-th earthquake, $i=1,2,\dots ,N_t$
$M_t$	The maximum magnitude of earthquake until time $t$, $t\in \left[0,T\right]$
$M_k$	The maximum magnitude of earthquake at the end of the $k$-th year, $k=1,2,\dots ,T$
$D_k$	The annual earthquake depth corresponding to $M_k$ at the end of the $k$-th year, $k=1,2,\dots ,T$
$W_j$	The $j$-th region zone insured in the ECB
${\tau }_N$	The first time an earthquake has occurred since the ECB was published
${\tau }_L$	The first time the earthquake loss exceeds its threshold value
${\tau }_a$	The first time the aggregate loss or maximum magnitude of the earthquake exceeds its threshold value
${\tau }_b$	The first time the aggregate loss and maximum magnitude of the earthquake exceed the threshold value
${\rho }_a$	The correlation of ground movement between insured zones in the ECB
${\rho }_b$	The spatial seismic hazard in terms of peak ground acceleration (PGA)
$\gamma$	The average time between two consecutive earthquake events

.

Table 4 shows that the essential financial risk variables used are the redemption value ($F_T$), the term ($T$), and the nominal interest rate ($r_k$, $r_c$, $r_{c,t}$) of the ECB. The redemption value is expressed in three schemes, an explanation of which is given in the next results. Then, the nominal interest rate is expressed in three forms as follows:

(a)

$r_k$ represents the nominal interest rate at the end of $k$-th years, $k=1,2,\dots ,T$, which is inconstant and is compounded once a year. The value of this nominal interest rate fluctuates only on an annual basis. This form is used by Shao et al. [42].

(b)

$r_c$ represents the annual nominal interest rate, which is constant and compounded continuously. The value of this interest rate is the same throughout the life of the ECB. This form is used by Romaniuk [40] and Zimbidis et al. [41].

(c)

$r_{c,t}$ represents the nominal interest rate at time $t$, $t\in [0,T]$, which is inconstant and compounds continuously. This form is used by Gunardi and Setiawan [43], Tang and Yuan [44], Hofer et al. [45], Wei et al. [9], Kang et al. [46], Aghdam et al. [48], Mistry and Lombardi [47], and Anggraeni et al. [49].

Almost all of the articles involve the coupon rate when designing ECB pricing frameworks ($C_k$). Only Romaniuk [40], Kang et al. [46], and Aghdam et al. [48] did not make use of it. The coupon rate is divided into two forms, as follows:

(a)

$c_k$ represents the inconstant coupon rate at the end of $k$-year, $k=\mathrm{1,2},\dots ,T$. This coupon rate is used by Zimbidis et al. [41], Shao et al. [42], Tang and Yuan [44], and Anggraeni et al. [49].

(b)

$c$ represents the constant coupon rate. This coupon rate is used by Gunardi and Setiawan [43], Hofer et al. [45], Mistry and Lombardi [47], and Wei et al. [9].

Several articles add other financial risk variables, as follows:

(a)

Zimbidis et al. [41], Shao et al. [42], Gunardi and Setiawan [43], and Anggraeni et al. [49] involved extra premium loading ($e$). This variable is added to increase compensation to investors so that the ECB becomes more attractive.

(b)

Shao et al. [42] added an inconstant inflation rate to the model (${\pi }_k$) so that returns from investors are more accurate.

(c)

Zimbidis et al. [41] used a variable deposit interest rate ($i_k$) due to the reinvestment of ECB sales proceeds from investors into risk-free assets.

(d)

Romaniuk [40] added the assumption that the value of the ECB assets is inconstant (${\mathcal{S}}_t$).

(e)

Kang et al. [46] involved the variable annual liability of the sponsor ($D_t$).

Table 4 shows that, in general, almost all articles considered the variable frequency of earthquakes $N_t$. Only Romaniuk [40], Zimbidis et al. [41], Shao et al. [42], and Gunardi and Setiawan [43] did not consider it. The earthquake frequency variable has an intensity parameter. The intensity parameter describes the average frequency of earthquakes in a specific time interval. Two forms of intensity parameters are used. The two forms are as follows:

(a)

$\lambda$ represents the constant earthquake intensity. This means that the average earthquake frequency is assumed to be the same for each time interval of the same length. This form of the parameter is used by Tang and Yuan [44], Kang et al. [46], Wei et al. [9], Aghdam et al. [48], Mistry and Lombardi [47], and Anggraeni et al. [49].

(b)

${\lambda }_t$ represents the inconstant earthquake intensity at time $t$, $t\in \left[0,T\right]$. This means that the average frequency of earthquakes for each interval of the same length can differ. This parameter shape is used by Hofer et al. [45].

The other earthquake risk variables considered are as follows:

(a)

Financial loss

The financial loss represents the economic loss experienced due to the earthquake. Out of the eleven articles, six use this variable: Tang and Yuan [44], Hofer et al. [45], Kang et al. [46], Mistry and Lombardi [47], Wei et al. [9], and Aghdam et al. [48]. This variable is used in three forms, namely $X_i$, $L_t$, and $L_t^{*}$. $X_i$ with $i=\mathrm{1,2},\dots ,N_t$ represents the financial loss from the $i$-th single earthquake, $L_t$ with $t\in [0,T]$ represents the aggregate financial loss from the earthquake until time $t$, and $L_t^{*}$ is a form specifically from $L_t$ with a jumping number of losses.

(b)

Earthquake magnitude

Out of the eleven articles, five use earthquake magnitude variables, namely, Zimbidis et al. [41], Shao et al. [42], Gunardi and Setiawan [43], Wei et al. [9], and Anggraeni et al. [49]. This variable is divided into three forms, namely $Y_i$, $M_k$, and $M_t$. $Y_i$ with $i=1,2,\dots ,N_t$ represents the magnitude of the i-th single earthquake, $M_k$ with $k=\mathrm{1,2},\dots ,T$ represents the maximum magnitude of the earthquake in year $k$, and $M_t$ is the form specifically from $M_k$ with a continuous time index.

(c)

Earthquake Epicenter Depth

Only two articles used the $D_k$ epicenter depth variable, namely, Shao et al. [42] and Anggraeni et al. [49]. Specifically, $D_k$ represents the lowest epicenter depth of the earthquake until year $k$ with $k=\mathrm{1,2},\dots ,T$.

(d)

Earthquake-prone zone

Three of the eleven articles considered the zone variable of $W_j$, namely Hofer et al. [45], Mistry and Lombardi [47], and Anggraeni et al. [49]. This variable is added because these three articles set ECB prices for different regions within a country. Furthermore, Hofer et al. [45] accounted for the correlation of ground movement between the insured zones in the ECB (${\rho }_a$), and Mistry and Lombardi [47] considered the spatial seismic hazard in terms of peak ground acceleration (PGA) (${\rho }_b$).

Furthermore, an analysis of the answers to RQ3 and RQ4 regarding the primary methods for describing financial and earthquake risks in ECB pricing is given in

Table 6. Methods for describing financial and earthquake risk variables in the eleven articles.

Author(s)	Main Methods Used to Model Financial Risk	Main Methods Used to Model Earthquake Risk
Romaniuk [40]	Geometrical Brownian Motion	Exponential Distribution
Zimbidis et al. [41]	Geometrical Brownian Motion	Block Maxima
Shao et al. [42]	ARIMA (1, 1, 1), ARIMA (1, 0, 0), Cox–Ingersoll–Ross Model	Block Maxima, Gamma Distribution
Gunardi and Setiawan [43]	Cox–Ingersoll–Ross Model	Block Maxima
Tang and Yuan [44]	Vasicek Model	Block Maxima, Peaks Over Threshold, Homogeneous Compound Poisson Process
Hofer et al. [45]	Cox–Ingersoll–Ross Model	Inhomogeneous Compound Poisson Process, Ground Motion Prediction Equation
Kang et al. [46]	Lee–Yu Model, Cox–Ingersoll–Ross Model, Asset-Liability Management Model	Lognormal Distribution, Compound Negative Binomial Process
Mistry and Lombardi [47]	Cox–Ingersoll–Ross Model	High Spatial Resolution Hazard and Exposure Model, Homogeneous Compound Poisson Process
Wei et al. [9]	Cox–Ingersoll–Ross Model	Peaks Over Threshold, Homogeneous Compound Poisson Process, Copula
Aghdam et al. [48]	Cox–Ingersoll–Ross Model	Homogeneous Compound Poisson Jumping Process
Anggraeni et al. [49]	Singh’s Fuzzy Time Series	K-Means Clustering Method, Peaks Over Threshold, Homogeneous Compound Poisson Process, Copula

.

Table 6 shows the following information regarding the main methods used to model financial risk variables:

(a)

Almost all articles that consider the nominal interest rate variable $r_{c,t}$ described it using the Cox–Ingersoll–Ross model, proposed by Cox et al. [50]. This model is widely used because the estimated nominal interest rate is guaranteed to be positive. It generally corresponds to the actual situation, except in Japan and Switzerland. Meanwhile, some studies do not use the Cox–Ingersoll–Ross model to describe the nominal interest rate. Shao et al. [42] used the ARIMA model (1, 1, 1), and Tang and Yuan [44] used the Vasicek model [51].

(b)

Each article involves an inconstant coupon rate $c_k$ used a different method to describe it. Zimbidis et al. [41] used geometrical Brownian motion, Tang and Yuan [44] used the Vasicek model, Shao et al. [42] used the Cox–Ingersoll–Ross model, and Anggraeni et al. [49] used Singh’s Fuzzy Time Series [52].

(c)

The inflation rate included by Shao et al. [42] was accommodated using the ARIMA model (1, 0, 0).

(d)

The dynamical ECB asset in Romaniuk [40] was described using geometrical Brownian motion.

(e)

The liability variable in the study conducted by Kang et al. [46] was accommodated using Lee and Yu’s model [6] and its extension, namely, the Asset-Liability Management Model.

Table 6 shows the following information regarding the main methods used to model earthquake risk variables:

(a)

Six articles used the compound Poisson process to model the frequency, financial loss, and magnitude of earthquakes in an integrated manner. These articles were written by Tang and Yuan [44], Hofer et al. [45], Mistry and Lombardi [47], Wei et al. [9], Aghdam et al. [48], and Anggraeni et al. [49]. This method is an efficient means of modeling all three variables. The compound Poisson process has two forms: the homogeneous and inhomogeneous compound Poisson processes. The differences and similarities between the two are given in

Table 7. Differences and similarities between the homogeneous and inhomogeneous compound Poisson processes.

Compound Poisson Process Type	Difference	Similarity
Homogeneous	$N_t~$Homogeneous Poisson $\left(\lambda t\right)$	$X_i~i.i.d.$ and $Y_i~i.i.d$
Inhomogeneous	$N_t~\mathrm{I}\mathrm{n}\mathrm{h}\mathrm{o}\mathrm{m}\mathrm{o}\mathrm{g}\mathrm{e}\mathrm{n}\mathrm{e}\mathrm{o}\mathrm{u}\mathrm{s} \mathrm{P}\mathrm{o}\mathrm{i}\mathrm{s}\mathrm{s}\mathrm{o}\mathrm{n} \left({\lambda }_{t}t\right)$

.

Table 7 shows that the homogeneous compound Poisson process uses the assumption of constant earthquake intensity ($\lambda$), while the other uses the assumption of inconstant earthquake intensity (${\lambda }_t$). Moreover, the financial losses ($X_i$) and magnitudes ($Y_i$) of single earthquakes are assumed not to affect each other. In addition to the compound Poisson process, another model uses a compound negative-binomial process, namely Kang et al. [46].

(b)

The articles generally modeled the financial loss and magnitude of the $i$-th earthquake ($X_i$ and $Y_i$) using the extreme value theory through the block maxima and peaks over threshold methods. This indicates that only earthquakes with financial losses and extreme magnitudes are considered in the data selection. Apart from these two methods, some articles used other approaches to model the loss and magnitude of the $i$-th earthquake. Romaniuk [40] and Kang et al. [46] used exponential and lognormal distributions to model financial loss, respectively. Finally, Shao et al. [42] used the gamma distribution to model earthquake magnitudes.

(c)

Various methods are used to account for earthquake-prone-zone variables. Anggraeni et al. [49] used the K-means clustering algorithm to model the earthquake-prone zone ($W_j$). Hofer et al. [45] used the ground motion prediction equation proposed by Bindi et al. [53]. Mistry and Lombardi [47] accommodated it using a high-spatial-resolution hazard and exposure model.

Furthermore, an analysis of answers to RQ5, regarding the type of claim trigger index used, is given in

Table 8. The type of claim trigger index used in the eleven articles.

Author(s)	Type of Claim Trigger Index
	Indemnity	Parametric
	Aggregate Losses	Magnitude	Depth
Romaniuk [40]	$\surd$	-	-
Zimbidis et al. [41]	-	$\surd$	-
Shao et al. [42]	-	$\surd$	$\surd$
Gunardi and Setiawan [43]	-	$\surd$	-
Tang and Yuan [44]	$\surd$	-	-
Hofer et al. [45]	$\surd$	-	-
Kang et al. [46]	$\surd$		-
Mistry and Lombardi [47]	$\surd$		-
Wei et al. [9]	$\surd$	$\surd$	-
Aghdam et al. [48]	$\surd$	-	-
Anggraeni et al. [49]	-	$\surd$	$\surd$

.

Table 8 shows three types of claim trigger events used in the eleven articles: indemnity index, parametric, and combination. The indemnity index is based on the actual earthquake losses, both physical and economic. In contrast, the parametric index is an index based on the geological severity of the earthquake, i.e., the magnitude or depth of the earthquake. Six articles used the indemnity index as measured by aggregate earthquake losses, namely Romaniuk [40], Tang and Yuan [44], Hofer et al. [45], Kang et al. [46], Mistry and Lombardi [47], Wei et al. [9], and Aghdam et al. [48]. It is the most commonly used type of claim trigger, and it has the advantage of high regulatory acceptance [54]. Four articles used a parametric index, as measured by magnitude or a combination of magnitude and depth. The magnitude was used by Zimbidis et al. [41] and Gunardi and Setiawan [43], while a combination of magnitude and depth was used by Shao et al. [42] and Anggraeni et al. [49]. The parametric index has the advantages of a high level of transparency and fast measurement [55]. Finally, one article, by Wei et al. [9], used a combination of indemnity and parametric indices measured from the aggregate losses and magnitudes of earthquakes. The simultaneous use of indemnity and parametric indices has the advantage of accurately depicting earthquake severity because it is measured financially and geologically [9,14].

Furthermore, an analysis of the answers to RQ6, regarding the coupon and redemption value of payment schemes of the ECB, is given in

Table 9. The coupon and redemption value of payment schemes.

Author(s)	Coupon Payment Scheme	Redemption Value Payment Scheme
Romaniuk [40]	-	$F_T=\left\{\begin{array}{cc}0& ;{\tau }_N\le T\\ {\mathcal{S}}_T& ;{\tau }_N>T\end{array}\right.$
Zimbidis et al. [41]	$C_k=\left\{\begin{array}{cc}3c_{k}F& ;0.0<M_k\le 5.4\hfill \\ 2c_{k}F& ;5.4<M_k\le 5.8\hfill \\ c_{k}F& ;5.8<M_k\le 6.2\hfill \\ 0& ;M_k>6.2\hfill \end{array}\right.$	$F_T=\left\{\begin{array}{cc}F& ;0.0<M_T\le 6.6\hfill \\ \frac{2}{3}F& ;6.6<M_T\le 7.0\hfill \\ \frac{1}{3}F& ;7.0<M_T\le 7.4\hfill \\ 0& ;M_T>7.4\hfill \end{array}\right.$
Shao et al. [42]	$C_k=\left\{\begin{array}{cc}2.8c_{k}F& ;0.0<M_k\le {\mu }_1,D_k>{\delta }_1\hfill \\ 2.6c_{k}F& ;0.0<M_k\le {\mu }_1,D_k\le {\delta }_1\hfill \\ 1.9c_{k}F& ;{\mu }_1<M_k\le {\mu }_2,D_k>{\delta }_2\hfill \\ 1.6c_{k}F& ;{\mu }_1<M_k\le {\mu }_2,D_k\le {\delta }_2\hfill \\ 0.6c_{k}F& ;{\mu }_2<M_k\le {\mu }_3,D_k>{\delta }_3\hfill \\ 0.5c_{k}F& ;{\mu }_2<M_k\le {\mu }_3,D_k\le {\delta }_3\hfill \\ 0& ;M_k>{\mu }_3,D_k>0\hfill \end{array}\right.$	$F_T=\left\{\begin{array}{cc}F& ;0.0<M_T\le {\mu }_4\hfill \\ 0.85F& ;{\mu }_4<M_T\le {\mu }_5,D_T>{\delta }_4\hfill \\ 0.8F& ;{\mu }_4<M_T\le {\mu }_5,D_T\le {\delta }_4\hfill \\ 0.6F& ;{\mu }_5<M_T\le {\mu }_6,D_T>{\delta }_5\hfill \\ 0.55F& ;{\mu }_5<M_T\le {\mu }_6,D_T\le {\delta }_5\hfill \\ 0.2F& ;M_T>{\mu }_6,D_T>0\hfill \end{array}\right.$
Gunardi and Setiawan [43]	$C_k=\left\{\begin{array}{cc}cF& ;0<M_k\le {\mu }_1\hfill \\ cF(1-w_1)& ;{\mu }_1<M_k\le {\mu }_2\hfill \\ ⋮& ⋮\\ cF\left(1-{\displaystyle \sum _{m=1}^{q-1}}{w}_m\right)& ;{\mu }_{q-1}<M_k\le {\mu }_q\hfill \\ ⋮& ⋮\\ cF\left(1-{\displaystyle \sum _{m=1}^n}{w}_m\right)& ;M_k>{\mu }_n\hfill \end{array}\right.$	$F_T=\left\{\begin{array}{cc}F& ;0<M_T\le {\eta }_1\hfill \\ F(1-y_1)& ;{\eta }_1<M_T\le {\eta }_2\hfill \\ ⋮& ⋮\\ F\left(1-{\displaystyle \sum _{m=1}^{q-1}}{y}_m\right)& ;{\eta }_{q-1}<M_T\le {\eta }_q\hfill \\ ⋮& ⋮\\ F\left(1-{\displaystyle \sum _{m=1}^n}{y}_m\right)& ;M_T>{\eta }_n\hfill \end{array}\right.$
Tang and Yuan [44]	$C_k=F\mathrm{\Pi }\left(L_{k-1}\right)\exp \left(c_k+c\right)$	$F_T=F\mathrm{\Pi }\left(L_T\right)$
Hofer et al. [45]	$C_k=\left\{\begin{array}{cc}0& ;L_k>{\mu }_L\hfill \\ cF& ;L_k\le {\mu }_L\hfill \end{array}\right.$	$F_T=\left\{\begin{array}{cc}0& ;L_T>{\mu }_L\hfill \\ F& ;L_T\le {\mu }_L\hfill \end{array}\right.$
Kang et al. [46]	-	$F_T=\left\{\begin{array}{cc}\eta F& ;L_T>{\mu }_L\hfill \\ F& ;L_T\le {\mu }_L\hfill \end{array}\right.$
Mistry and Lombardi [47]	$C_k=\left\{\begin{array}{cc}0& ;L_k>{\mu }_L\hfill \\ cF& ;L_k\le {\mu }_L\hfill \end{array}\right.$	$F_T=\left\{\begin{array}{cc}\eta F& ;L_T>{\mu }_L\hfill \\ F& ;L_T\le {\mu }_L\hfill \end{array}\right.$ for zero-coupon ECB $F_T=F$ for coupon-paying ECB
Wei et al. [9]	$C_k=\left\{\begin{array}{cc}0& ;\min \{\mathcal{t}\in \left[0,k\right]:L_{\mathcal{t}}>{\mu }_L \mathrm{o}\mathrm{r} M_{\mathcal{t}}>{\mu }_M\}\le k\hfill \\ cF& ;\min \{\mathcal{t}\in \left[0,k\right]:L_{\mathcal{t}}>{\mu }_L \mathrm{o}\mathrm{r} M_{\mathcal{t}}>{\mu }_M\}>k\hfill \end{array}\right.$	$F_T=\left\{\begin{array}{cc}0& ;\min \{t\in \left[0,T\right]|L_t>{\mu }_L \mathrm{a}\mathrm{n}\mathrm{d} M_t>{\mu }_M\}\le T\hfill \\ F& ;\min \{t\in \left[0,T\right]|L_t>{\mu }_L \mathrm{a}\mathrm{n}\mathrm{d} M_t>{\mu }_M\}>T\hfill \end{array}\right.$
Aghdam et al. [48]	-	$F_T=\left\{\begin{array}{cc}0& ;L_T^{*}>\mu \hfill \\ F& ;L_T^{*}\le \mu \hfill \end{array}\right.$
Anggraeni et al. [49]	$C_k=\left\{\begin{array}{cc}0& ;M_k>{\mu }_M\hfill \\ c_{k}F& ;M_k\le {\mu }_M\hfill \end{array}\right.$	$F_T=\left\{\begin{array}{cc}F& ;0.0<M_T<5.0,D_T>0\hfill \\ f_{!}F& ;5.0\le M_T<6.0,D_T\ge 300\hfill \\ f_{2}F& ;5.0\le M_T<6.0,70\le D_T<300\hfill \\ f_{3}F& ;5.0\le M_T<6.0,0<D_T<70\hfill \\ f_{4}F& ;6.0\le M_T<7.0,D_T\ge 300\hfill \\ f_{5}F& ;6.0\le M_T<7.0,70\le D_T<300\hfill \\ f_{6}F& ;6.0\le M_T<7.0,0<D_T<70\hfill \\ f_{7}F& ;7.0\le M_T<8.0,D_T\ge 300\hfill \\ f_{8}F& ;7.0\le M_T<\mathrm{8.0,70}\le D_T<300\hfill \\ f_{9}F& ;7.0\le M_T<8.0,0<D_T<70\hfill \\ 0& ;M_T\ge 8.0,D_T>0\hfill \end{array}\right.$

.

Table 9 shows three payment schemes of the ECB redemption value and coupons used in the eleven articles: binary, piecewise, and continuous. These are explained in brief as follows:

(a)

The binary scheme provides two possible payments of redemption values and coupons. If the claim of the ECB occurs within its term, the coupons and redemption values are paid in proportion or not at all. More specifically, the value of this proportion is in the interval $\left(\mathrm{0,1}\right)$ and is measured in various ways using various methods. The notation of the proportion value in Table 9 is written as $\eta$ [46,47]. Then, if a claim for ECB does not occur within its term, the coupons and redemption values are paid in full to the investor.

(b)

The piecewise scheme provides more than two possible coupon and redemption value payments. Many of these possibilities are countable. The minimum value of the coupons and redemption values is zero. This value is obtained when the claim trigger index exceeds its maximum limit. Then, the maximum value of the coupon is two to three times that of the standard coupon ($c_{k}F$ or $cF$). Then, the maximum value of the redemption value is $F$. These maximum values of coupons and redemption values occur when the claim trigger index value is in the interval with the smallest values. The notation of the proportion of coupon or redemption value payments in Table 9 is written as $1-\sum _{m=1}^n{w}_m$ [43], $1-\sum _{m=1}^n{y}_m$ [43], and $\{f_1,f_2,\dots f_9\}$ [49].

(c)

The continuous schema provides many uncountable possibilities. This scheme’s coupons and redemption values are represented by descending and continuous functions of non-negative real numbers. Table 9 shows the proportion of coupons and redemption values as $\mathrm{\Pi }\left(L_t\right)$ [44].

Claim-trigger index values, such as $\left\{{\mu }_1,{\mu }_2\dots ,{\mu }_6\right\},$ $\left\{{\delta }_1,{\delta }_2,\dots ,{\delta }_5\right\},$ $\left\{{\eta }_1,{\eta }_2,\dots ,{\eta }_n\right\},$ $\left\{{\mu }_L\right\},$ and $\left\{{\mu }_M\right\}$, are determined first by analyzing historical data. A balance is sought between marketability and profit. Some articles explicitly include claim-trigger index values, namely Zimbidis et al. [41] and Anggraeni et al. [49].

Furthermore, an analysis of the answers to RQ7 and RQ8, regarding the solution form of the model and the method of determining the solution, is given in

Table 10. Model solution form and its determination method.

Author(s)	Model Solution Form	Solution Determination Method
Romaniuk [40]	It has no closed-form solution	Iterative Stochastic Method, Monte Carlo Method
Zimbidis et al. [41]	It has no closed-form solution	Monte Carlo Method
Shao et al. [42]	It has no closed-form solution	Monte Carlo Method
Gunardi and Setiawan [43]	It has no closed-form solution	Monte Carlo Method
Tang and Yuan [44]	It has no closed-form solution	Wang Transformation Method
Hofer et al. [45]	It has no closed-form solution	Monte Carlo Method
Kang et al. [46]	It has no closed-form solution	Monte Carlo Method
Mistry and Lombardi [47]	It has no closed-form solution	Monte Carlo Method
Wei et al. [9]	It has a closed-form solution	-
Aghdam et al. [48]	It has no closed-form solution	Chebyshev Basis, Spectral Method, Expansion of the Gauss–Laguerre Quadrature
Anggraeni et al. [49]	It has no closed-form solution	Monte Carlo Method

.

Table 10 shows that the models generally do not have a closed solution form. Only Wei et al. [9] present a model with this form. This means that the solution determination is not conducted analytically; however, some alternative methods do achieve this. In general, the alternative method used in almost all articles is the Monte Carlo method. Moreover, Romaniuk [40] combined it with the stochastic iteration method. Aside from the Monte Carlo or its combination with other methods, Tang and Yuan [44] used the Wang transformation method. Finally, Aghdam et al. [48] used the Chebyshev basis, spectral method, and the expansions of the Gauss–Laguerre quadrature.

4. Discussion

Intriguingly, articles about catastrophic bond price modeling generally use the indemnity index as the trigger type for their claim. Consequently, the methods used to model the index are very similar for each type of catastrophe [56,57]. For example, Deng et al. [26] and Ibrahim et al. [29], respectively, modeled drought and flood catastrophe bond prices with an indemnity index. However, even though the types of catastrophes are different, the method used to model the index is the same, namely, a homogeneous compound Poisson process. The articles that use parametric indexes as their claim trigger type generally use a different method, because the method used must be adapted to the parametric characteristics of the type of catastrophe studied. For example, Hofer et al. [45] used the Ground Motion Prediction Equation to measure the severity of ground motion in earthquakes in earthquake hazard bonds, and Li et al. [58] used a point process to measure the maximum point precipitation in flood catastrophe bonds.

Moreover, not all insurers who cover state catastrophe risk divert it into catastrophe bonds alone. Other insurers, albeit only a few, create portfolios that contain several other financial instruments, which are referred to as catastrophe derivatives [59]. This portfolio is intended to increase the expected return from transferring risk to the capital market as compensation that will be given to investors. However, it should be noted that an increase in expected losses accompanies an increase in expected returns.

This study also identified several areas for future research. The eleven extant articles on ECB price modeling are still open to development. This development can be achieved by involving new variables or using new methods not considered in previous studies. Some of the model developments that can be conducted in the future are as follows:

(a)

Each country has a different resilience level when facing the risk of earthquakes. This resilience includes economic resilience and mitigation when an earthquake occurs [60]. In this regard, countries with low resilience should logically have higher ECB prices and vice versa. Therefore, this resilience variable can be considered in the development of new models. By including this variable, earthquake severity can be measured better so that the estimated ECB price will be fairer.

(b)

Earthquake-prone-zone clustering, as seen in Hofer et al. [45], Mistry and Lombardi [47], and Anggraeni et al. [49], generally still used earthquake severity attributes in the form of magnitude and depth. The clustering of earthquake-prone zones can also use other attributes, such as the distance of the zones from active faults, volcanoes, or subduction areas. Therefore, this can be used as a research opportunity in the future.

(c)

Almost every model used the Monte Carlo method to determine the solution for the ECB pricing model. This method has weaknesses in terms of computation time efficiency. In other words, the determination of the solution is computed hundreds to thousands of times iteratively. Therefore, developing a more efficient model solution determination method constitutes a further area for future research. For example, studies may use the method of approximating the cumulative distribution function of the compound Poisson process developed by Chaubey et al. [61] and Reijnen et al. [62]. This method makes the computational process faster because it is based on the parameter values of the compound Poisson process.

(d)

The ARIMA and Vasicek models that describe inconstant nominal interest rates or coupon rates can produce negative values. This problem is overcome by the Cox–Ingersoll–Ross model, where the forecast value is guaranteed to be positive. However, the volatility described in this model does not consider jumps when economic crashes occasionally occur [49]. Therefore, future research may seek to address this problem.

(e)

The financial and earthquake risk variables included in the eleven articles are assumed to be independent. However, both are possibly correlated. Therefore, considering the correlation of both represents a further future research opportunity.

5. Conclusions

This research systematically reviewed the extant articles on the ECB pricing framework. Based on examined criteria, articles were collected and selected from the Scopus, Science Direct, and Dimensions databases on 22 March 2023. This process resulted in eleven relevant articles. Then, the articles were reviewed; this process included descriptive analysis, an analysis of the pricing framework, and a discussion of future research opportunities.

The descriptive analysis shows that research on the design of the ECB pricing framework is generally actively conducted in earthquake-prone countries. Our analysis of the pricing framework shows that the ECB price is generally expressed as the sum of the present value of the expected annual coupon random variable and the present value of the expected redemption value random variable. In addition, the model analysis shows that the financial risk variable is independent of the earthquake risk variable. Furthermore, the most popular financial risk variables are described using the Cox–Ingersoll–Ross model, while the most well-known earthquake risk variables are modeled using a compound Poisson process. Three claim-trigger indices are used for ECBs: the indemnity index, the parametric index, and a combination of both. Each index has its advantages and disadvantages. Moreover, there are three coupon and redemption value payment schemes for the ECB: binary, piecewise, and continuous. The three schemes are designed based on claim-trigger index values obtained from historical data. Almost no models have a closed-solution form, so the solution is generally sought using an alternative Monte Carlo method. Finally, five model developments can be explored in the future. These developments involve using new variables (e.g., economic and mitigations resilience) or methods (CIR with jumping processes) that previous studies did not consider.

This research can provide insights into the ECB pricing framework and motivate other researchers to design a fairer ECB pricing framework.