1. Introduction
With the characteristics of safety, high efficiency, convenience, and environmental protection, public transportation has become an effective transportation mode to alleviate urban transportation problems [
1]. It has become a general consensus to prioritize the development of public transportation [
2]. The development of regular bus routes and bus vehicle configuration issues are not only related to the costs and benefits of the bus company but also have an essential relationship with the service level of buses and passenger satisfaction [
3,
4]. The core of bus allocation is the optimization of departure intervals to meet passenger flow demand. Therefore, the optimization of bus departure intervals is of positive significance for the sustainable development of the public transport system. Bus vehicle configuration and bus departure intervals are closely related. Bus vehicle configuration refers to the number and type of vehicles configured on the bus route. The minimum bus departure interval is subject to the number of vehicles configured on the bus route and the bus operation time. How to determine an optimal departure frequency and optimize the social benefits of bus services while ensuring the basic benefits of bus operators is a question worthy of discussion. The bus vehicle configuration of bus lines should meet the departure frequency of the peak period. Therefore, the problem of bus line vehicle allocation is able to be transformed into the problem of optimizing the departure frequency of bus lines during peak hours.
Many scholars have conducted in-depth research on the optimization of bus vehicle configuration and departure intervals. The two-level programming model that considers the benefits of bus operators and passengers has been commonly used. Di Zhen [
5] considered the revenue of bus companies as the upper-level objective; the minimum weighted total cost of travel time and cost of passengers was the lower-level objective, and government behavior was used as a constraint to establish a two-level programming model for the bus line vehicle allocation problem. Zhao Shuzhi [
6] established a multi-model bus route allocation optimization model based on the weighted sum of bus operator costs and bus service levels. Liu Tao [
3] researched public transport timetables and vehicle scheduling problems and developed a bi-objective, bi-level programming model. The upper objective is to minimize the total operating cost and the total travel time of passengers from the perspective of the bus operator. The lower model is for a traffic distribution issue based on the departure time and vehicle capacity constraints. Filipe Monnerat [
7] researched fleet management problems and established a vehicle and driver assignment model with an objective function of minimizing the total cost. Liujiang Kang [
8] developed three integer linear programming models (ILPM) to describe bus and driver scheduling problems with meantime windows for a single bus line. M.A. Goberna [
9] dealt with solutions problems for uncertain multi-objective convex programs, which allowed the data of the objective function and the constraints to be uncertain.
However, uncertainty realizations play an important role in real-world applications [
10]. There are many uncertain factors in the operation of public transportation: the service time windows and passenger demand of different stops cannot be accurately estimated. During the development of bus lines and bus vehicle allocations, these variables are typically estimated on the basis of historical data or experience, so that a relatively reliable result is obtained; this will result in large errors. In order to decrease the error, the methods for optimization under uncertain factors have been widely studied over past decades [
10]. Real decisions are generally made under the state of indeterminacy [
11]. Randomness, grayness, and fuzziness are three inseparable uncertain factors that affect real decisions [
12]. There are two mathematical systems for modeling the indeterminacy: one is probability theory [
13], and the other is uncertainty theory [
11]. Probability is interpreted as frequency, while uncertainty is interpreted as personal belief degree [
11]. Frequency is the empirical basis of probability theory, while belief degree is the empirical basis of uncertainty theory. Savage [
14] said a rational man behaved as if he used subjective probabilities. In other words, a rational person is expected to hold belief degrees that follow the laws of uncertainty theory rather than probability theory. In order to minimize the error of indeterminacy and unify the descriptions of grayness, randomness, and fuzziness as three inseparable uncertain factors, Liu Baoding [
15] put forward the uncertainty theory in 2007 and continuously improved it to form a standardized axiomatic mathematical system. Liu [
16] introduced uncertain variables when considering programming problems in 2009 and proposed uncertain programming. Stochastic uncertainty is caused by parameter variations but also from an epistemic uncertainty caused by a lack of knowledge about the system.
The uncertainty theory represented by uncertain programming has been widely and successfully applied in the fields of transportation, logistics, and finance [
10,
16,
17]. The applications of uncertainty theory in transportation problems mainly include vehicle scheduling problems, critical road problems, etc. Jiao Dengya [
18] built an uncertain programming model based on Liu Baoding’s research to solve the logistics of the vehicle scheduling problem with uncertain factors, which took into account the uncertainty of the demand for goods and the travel time among the delivery points. A genetic algorithm that can effectively solve the uncertain programming model of vehicle scheduling is designed. Liu Wusheng [
19] used the bus IC card data to analyze the passenger flow uncertainty of bus stops and proposed a probabilistic derivation model and algorithm, without applying it to bus vehicle allocation, operation scheduling, and other issues. Wei Ming [
20] constructed a bi-level programming model for solving uncertain bus scheduling problems. The constraints such as depot capacities, fueling, and emissions of polluting gases are considered in the bi-level programming model. The genetic algorithm for solving the upper and lower models is designed, the concept of satisfactory solutions is introduced, and a set of satisfactory solutions produced by the lower programming are compared and selected by the upper programming, and then the best bus dispatching plan as well as the corresponding vehicle purchase plan are generated. Lin Chen [
21] established uncertain goal programming models for bicriteria solid transportation problems: the transportation cost and time, conveyance capacities, supplies, and demands were regarded as uncertain variables in the model. By applying some properties of uncertainty theory, the chance-constrained goal programming model and the expected value goal programming model can be, respectively, transformed into the corresponding deterministic equivalents [
21]. Based on uncertainty theory, Jun Guo [
22] proposed a vehicle scheduling method considering the dynamic departure interval and vehicle configuration of electric buses (EBs). An uncertain bi-level programming model (UBPM) was established, which took the total cost of passenger travel (CP) as the upper objective function and the total cost of EBs (CB) as the lower. Bing Zhang [
23] established a two-level planning model that takes the maximum total revenue of the bus company as the upper-level goal and the minimum total travel cost of passengers as the lower-level goal and used uncertainty theory to study and design customized bus routes with uncertain factors. Bin Zhan [
24] established a bi-level programming model to determine the frequency of the bus vehicles and non-uniform interval optimization considering the uncertainty of passenger demand, without considering the uncertainty of bus travel time.
The vehicle scheduling problem is well known as an NP-hard problem; in order to solve the problem, Lu Sun [
25] considered the vehicle scheduling problem with an uncertain processing time and proposed a hybrid cooperative co-evolution algorithm (hccEA). The results prove the efficiency and effectiveness of hccEA, and future research will apply the algorithm on multiple objectives of the uVSP (uncertain vehicle scheduling problem). Hannah Bakker [
10] reviewed multi-stage optimization under uncertainty; problems requiring a sequence of decisions considering uncertainty in reality are of crucial relevance in real-world applications, e.g., vehicle scheduling, supply chain planning, or finance. While models for multi-stage optimization under uncertainty have often been addressed from a specific application-driven point of view (pre-determining the style of uncertainty representation and solution methodology), the classification possibilities and insights shown in this review can form the basis of an undistorted and consistent model for the analysis of multi-stage uncertainty problems considering potentials of a variety of uncertainty models, solution methods, and evaluation techniques [
10]. Federica Ciccullo [
26] developed a method to link supply uncertainty and sustainable supply chain strategies, which has a positive effect on logistics and transportation. However, when sustainability is a desirable attribute or an order winner, companies might implement sustainable practices aiming at reducing supply uncertainty rather than for sustainability goals.
To sum up, although many scholars have conducted in-depth research on the optimization of bus vehicle configuration, and the uncertain theory has been widely and successfully applied in the fields of transportation and logistics, few results have been obtained using the uncertainty theory to study bus vehicle configuration problems. This paper considers the uncertainty of the number of passengers at the bus station and the bus operation time, as well as the cost and benefits of bus operators and bus passengers. An uncertain bi-level programming model is established with a view to providing theoretical support for bus departure time problems. The structure of the thesis is to briefly introduce the uncertainty theory, then build an uncertain bi-level programming model for the bus departure time problem, and design a solution algorithm. No. 207 bus line of Nanchang city, China, is taken as an example for case analysis, and the last section is the research conclusion.
5. Discussions and Conclusions
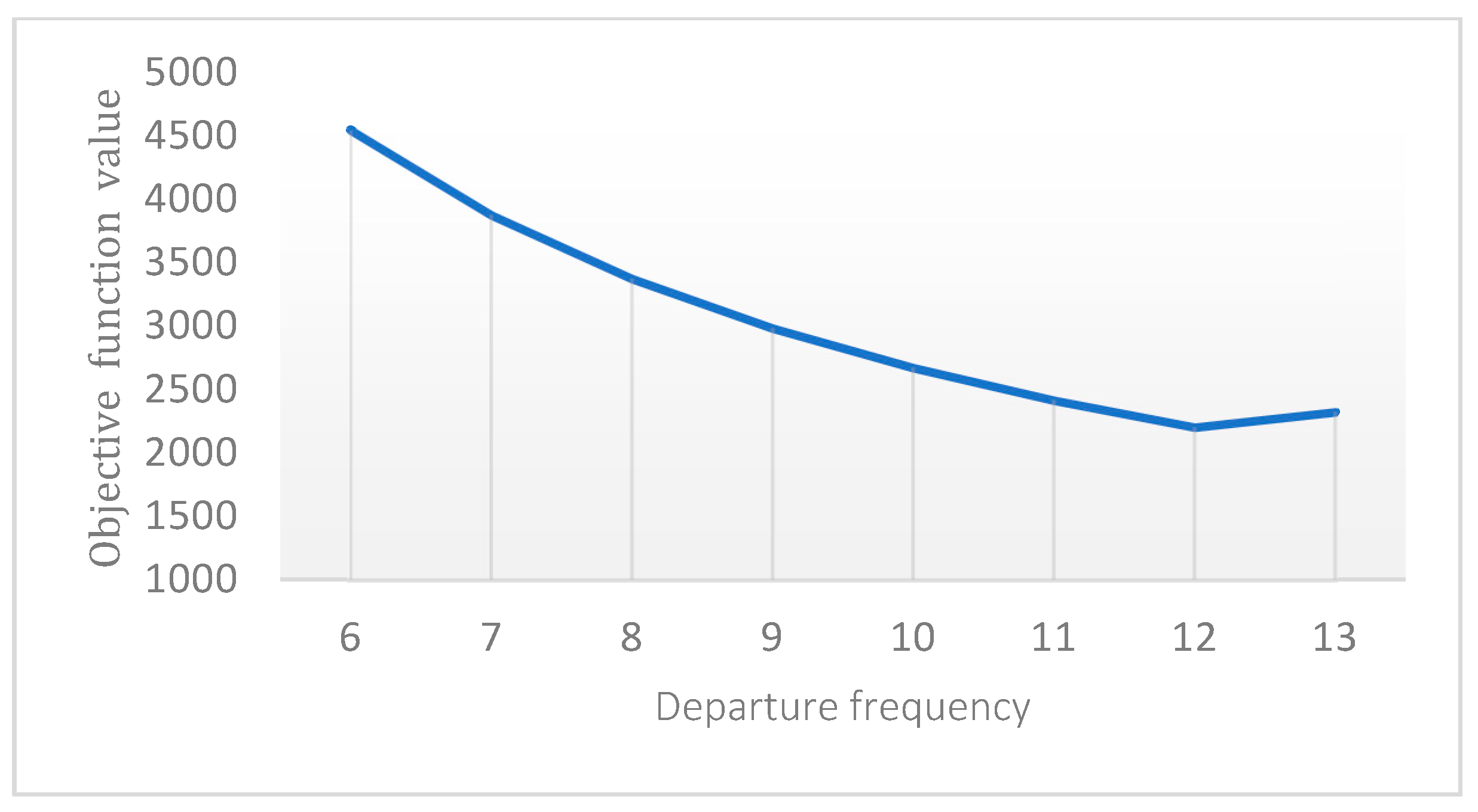
This paper investigated the basic data of bus route 207 of Nanchang city, China, and optimized the departure frequency and departure interval of the bus route in the morning peak hour based on uncertainty theory and a bi-level programming model. The uncertainty of passenger arrival and bus operation time was taken into account, combined with actual operation conditions. After determining the optimal departure frequency, the differences between uniform and non-uniform scheduling are studied and analyzed. Nanchang 207 bus line was taken as an example to optimize the departure frequency and scheduling in the morning peak hour. The optimal departure frequency in the morning peak hour is 12 times. The overall index value of the route non-uniform scheduling during peak hours increased by 0.06 and 9.23% compared with uniform scheduling. The analysis results show that the effect of the non-uniform scheduling is obvious.
Moreover, taking integers of model variables is conducive to the solution of the model and improves the practicability of the model. At the same time, the upper-level programming model can intuitively reflect the mutual influence and mutual restriction between the bus companies and passengers in the public transportation system. The problem of bus line departure frequency and scheduling has a positive effect on improving the efficiency of public transportation, reducing operating costs, and promoting the sustainable development of the public transportation system. This paper considers the uncertainty of the number of passengers at the bus station and the bus operation time and also considers the cost and benefits of bus operators as well as bus passengers. The uncertainty bi-level programming model for departure frequency of a bus line is more consistent with reality. Although the uncertain theory has been widely and successfully applied in the fields of transportation [
16,
17,
18,
19,
20,
21,
22,
23,
24], the results of using the uncertainty theory to study the bus vehicle configuration problems are few. Therefore, this article provides a theoretical support for bus operators to optimize route operations.
However, the model assumptions are relatively ideal, and some influencing factors are not reflected in the model and need to be further discussed in future research. Nanchang Public Transport Group only provided the number of card swipes but unfortunately did not provide passenger attribute information. If relevant data can be obtained in the future, in-depth analysis of the impact of passenger attributes and economic and social background on public transportation travel can be conducted. The social (in) equity and housing along the bus line are not considered in the research. The captive riders of public transport are often middle-to-low-income residents, with high-income residents (the choice riders) often choosing to drive to reach various destinations. Housing price/cost is often a good indicator for the income level of residents living there and the probability of residents’ transit utility. Moreover, the optimization of transit location should consider the very people living along the transit lines, which can be relatively accurately reflected by housing costs/prices. In [
29,
30,
31], housing and transit costs have been examined. Transit optimization is often a social equity issue that should be discussed in the future along with housing since they are often intertwined with each other in affecting (in) equity. The coupling factors of passenger travel demand and vehicle scheduling, the location, environment, platform capacity, passenger waiting time, and other attributes of the bus stop should also be fully considered. Zhichao Cao [
32] considered the constraints of the vehicle with regard to capacity in shuttle bus service timetabling and vehicle scheduling. Man Li [
33] considered the function of rail transit line capacity and load distribution strategy, the passenger flow congestion in a train delay scenario. When considering passengers choosing a bus, the model assumes that as long as the number of passengers in the bus does not reach the maximum capacity, then passengers could get on the bus, without considering the impact of the crowded situations in vehicles on passenger choice, which also affects the reliability of model calculation results. This study only analyzes departure frequency and scheduling and considers the uncertain variables of the number of passengers at the bus stop as well as running time; the optimization problem under multiple uncertain factors, such as the number of passengers at the bus stop, bus line assignments, and driving timetables, which constitute the optimization problem of driving operation plans, needs further research. The size of the test population and the flow frequency are not fully considered in the present manuscript; deeper work will be carried out in the future. In addition, the optimization of public transportation networks and regional dispatching considering uncertain factors are also worthy of discussion. Additionally, the situation especially in COVID-19 times, when the utilization of public transport is being re-defined to address the new safety standards, is not considered in the manuscript, which can be discussed in further research.
To summarize the research, this paper considers the uncertainty of the number of passengers at the bus stop and the bus operation time and also considers the cost and benefits of bus operators as well as bus passengers. An uncertain bi-level programming model was established with a view to providing theoretical support for bus departure time problems. The case study of bus route 207 of Nanchang city, China, shows the proposed uncertain bi-level programming model is effective for addressing the departure frequency problem of bus lines. As mentioned in the previous paragraph, this study has some limitations. Model assumptions and more influencing factors need to be further considered and improved.