Clustering Analysis of Classified Performance Evaluation of Higher Education in Shanghai Based on Topsis Model

Abstract

Diversification is a fundamental attribute of higher education. With the continuous expansion of the scale, universities and colleges have paid more attention to developing in diversified ways. Diversification is an important way to promote sustainable development of universities and colleges. Sustainable development is the endogenous impetus for the long-term development of higher education. The implementation of classified performance evaluation on higher education is beneficial to optimize fund and resource allocation for different types of universities and colleges, to effectively promote the diversified construction and sustainable development of higher education. Therefore, it becomes extremely important in the reform of higher education in China. It classifies universities and colleges into different types and then implements performance evaluation on the objects of the same type. In this paper, a classified performance evaluation indicator system is established for different types of universities and colleges. Topsis model is used to calculate the relative adjacency between the evaluated objects and the optimal and inferior solutions of all objects. A systematic clustering algorithm is made to analyze and evaluate the performance of universities and colleges in the same type. An automatic system is developed to analyze data from 62 universities and colleges in Shanghai. It provides advice and guidance for the development strategy of higher education.

1. Introduction

Diversification is a fundamental attribute of higher education. Although it is difficult to define and measure, and even more difficult to compare among universities and colleges, it has become an important trend in the development of higher education [1]. Diversification is an important way to promote sustainable development of universities and colleges [2]. Sustainable development is the endogenous impetus for the long-term development of higher education [3]. United Nations Educational, Scientific and Cultural Organization (UNESCO) points out that diversification is a trend in the development of higher education in the 21st century [4]. Objectively speaking, diversification in higher education can meet various needs of economic and social development for high-quality talents and personalization requirements [5]. However, a unified evaluation system is often used to evaluate all universities and colleges of different types and levels in China for a long time, it leads to a serious homogenization problem in higher education. Now, more attention is paid to diversified construction and sustainable development in higher education in China. How to carry out diversified construction better and promote sustainable development has become a significant task in the reform of higher education in China.

Since 1993, some official documents have put forward the objective and requirement of establishing the classification system, implementing classification management, and promoting characteristic development of universities and colleges in China, such as the National Medium and Long-term Education Reform and Development Plan (2010–2020), the Opinions on Accelerate the Reform of Education System, the Thirteenth Five-Year Plan for the National Education [6,7,8]. However, from the practice of higher education reform, the homogenization tendency of the development in universities and colleges exists due to simple evaluation standard. The implementation of classified performance evaluation contributes to more efficient diversified construction and sustainable development in universities and colleges [9]. In 2020, Ministry of Education of China proposed an overall plan for education evaluation reform in the new era. It places special emphasis on promoting classified performance evaluation, guiding different types of universities and colleges to position themselves scientifically, and developing characteristically [10]. Classified performance evaluation encourages universities and colleges to develop in personalized and characteristic way instead of in a homogenized way. Different from general evaluation, universities, and colleges are classified into different types in classified performance evaluation. It establishes a scientific evaluation indicator system according to the development characteristics and running goals of different types of universities and colleges. It places emphasis on evaluation of universities and colleges of the same type. The evaluation results reflect the realistic problems existing in different types of universities and colleges. The implementation of classified performance evaluation aims to promote the construction of higher education. Meanwhile, it motivates universities and colleges to involve in evaluation more actively. It is urgent to carry out theoretical and practical research on classified performance evaluation of universities and colleges.

This paper proposes a clustering algorithm of classified performance evaluation of universities and colleges based on Topsis model (Technique for Order Preference by Similarity to an Ideal Solution). A classified performance evaluation indicator system is established for different types of universities and colleges. Topsis model is used to calculate relative adjacency between the evaluated objects and optimal and inferior solutions of all objects in the same type according to the classification evaluation indicator systems. The systematic clustering algorithm is then used to cluster and analyze universities and colleges of the same type. An automatic classified performance evaluation system is implemented with data from 62 universities and colleges in Shanghai. It provides advice and guidance for scientific development strategy in universities and colleges.

2. Related Works

The performance of higher education mainly refers to the effective allocation and use of resources in higher education. It affects the level of scientific research, affects the quality of talents, and even reflects the potential of technological innovation in a country. The performance evaluation of higher education can promote continuous improvement of internal management in order to improve the efficiency of running universities and colleges [11]. However, the management of universities and colleges is a complicated system. Diversification is a fundamental attribute of higher education. Running level, developing orientation, developing stage, discipline focus, geography location, and social needs are diversified in various universities and colleges. The performance evaluation of higher education is a multi-attribute comprehensive work [12]. The United States and the United Kingdom have conducted performance evaluations of higher education earlier and have established specialized institutions to carry out research in performance evaluation [13].

So far, the research on performance evaluation of higher education mainly focuses on evaluation indicator system and evaluation methods. It usually evaluates the performance of universities and colleges with harmonized standards, in which the evaluation indicators include scientific research, faculty resources, international level, and social service [14]. It sometimes involves social reputation, technical innovation, campus infrastructure construction, knowledge transfer, research management organization, etc. [15]. It produces some university rankings. However, the current rankings in higher education usually evaluates universities and colleges with evaluation indicator system of a harmonized standard. To a certain extent, the evaluation indicator system with harmonized standards guides and promotes the development of higher education [16]. However, it is a little homogenized to universities and colleges of different types, which ignores the differentiation development in them. Some universities and colleges develop themselves according to the homogenized evaluation indicator system in order to get good rankings, which results to homogenization in higher education development [17]. For example, they all pursue developing comprehensively and on large scale and set up similar talent cultivation mode, cultivation objectives, curriculum system, etc. [18]. The homogenization development is adverse for universities and colleges to form their own characteristics. In the long run, it will be difficult to meet the needs of diversified development in the society.

In 1976, UNESCO formulated the International Standard Classification of Education (ISCED). Universities and colleges are classified into three types, academic research type, professional application type, and vocational skill type, which cultivate different types of students [19]. Carnegie Foundation for the Advancement of Teaching proposes the Carnegie classification of institutions of higher education, which classifies universities and colleges in US into some categories: Large Research Universities, Smaller Doctorate-Granting Universities, Comprehensive Institutions, Baccalaureate Institutions, Associate Degree Institutions, Specialized Institutions, and Vocational/Technical Institutions [20]. U-Map, the tool for European classification of higher education Institution, classifies European higher education institutions through dimensions of teaching and learning, research, knowledge exchange, international orientation, and regional engagement [21]. In some countries, universities and colleges are classified into different types according to their own characteristics. Universities and colleges are classified into three types in Germany: University, University of Applied Sciences, and University of Arts and Music [22]. Universities and colleges are classified into four types in England: Ancient University, Red Brick University, Plate Glass University, and Post-1992 University [23]. Universities and colleges are classified into three types in France: University, Grandeecole Universite, and Institut Universitaire Detechnologie [24]. However, there is no detailed evaluation indicator system for different types of universities and colleges in the above classifications.

The current performance evaluation methods of higher education usually include Linear Weighted Sum method (LWS), Balanced Score Card method (BSC), Data Envelopment Analysis method (DEA), Fuzzy Comprehensive Evaluation method (FCE), Analytical Hierarchy Process method (AHP), Principal Components Analysis method (PCA), Factor Analysis Method (FAM), etc. [25,26]. However, they do not have enough artificial intelligence. Different performance evaluation indicator systems and different evaluation methods will bring various results.

Linear Weighted Sum method is often used in university and college rankings [27]. The weights of indicators are determined by the opinions of some experts or some algorithms. The performance value is calculated by linear weighted accumulation. Some highly influential rankings include Times Higher Education World University Rankings (THE), Quacquarelli Symonds World University Rankings (QS), U.S. News & World Report Best Global Universities Rankings (USNWR), Shanghai Ranking Academic Ranking of World Universities (ARWU), etc. [28,29,30]. Other types of world university rankings include Essential Science Indicators Rankings (ESI) in US, Nature Index Rankings (NI) in UK, Moscow International University Ranking (MosIUR) in Russia, Webometrics Rankings of World Universities (WRWU) in Spain, SCImago Institutions Rankings (SIR) in Spain, CWUR World University Rankings (CWUR) in Saudi Arabia, CWTS Leiden Ranking (CWTS) in the Netherlands, Multi-dimensional Global University Ranking (U-Multirank) in the European Union, Assessment of Higher Education Learning Outcomes (AHELO) in Organization for Economic Cooperation and Development, OECD, etc. [31,32,33].

Balanced Score Card method was proposed by Robert Kaplan in Harvard University and David Norton in Nolan Norton Institute in the 1990s [34]. It is widely used in the performance management of enterprises. At present, it is applied to the performance evaluation of universities and colleges. The performance evaluation indicator system is established based on the four knowledge dimensions, financial, customer, internal business processes, learning, and growth [35]. The method helps to improve the performance management system for universities and colleges and to form the strategic vision, theme, and objectives [36].

Data Envelopment Analysis method was proposed by A. Charnes and W. W. Cooper in 1978 [37]. It is widely used in the performance management of industries. It shows advantages in dealing with multi-indicators of inputs and outputs. The output-oriented DEA method is a suitable method to evaluate the performance of non-profit organizations with multiple inputs and outputs indicators. It is used to evaluate the performance of 19 academic departments of Indian Institute of Technology [38]. It is also used to evaluate the performance of some universities in China, Malaysia, etc. [39]. The DEA method can analyze sensitivity of indicators by changing the input and output indicators, and can easily set weights of indicators by linear optimization algorithm [40]. However, DEA method expresses the relative ratio of input and output indicators instead of the actual development level of universities and colleges. Its performance evaluation ability declines when the number of indicators increase [41].

The performance evaluation indicator system usually includes two types of indicators, quantitative indicators and qualitative indicators. Experts are invited to evaluate the value of qualitative indicators. Thus, the evaluation value will be affected by the individual experience and standards, etc. The evaluation value is sometimes sensitive and ambiguous [42]. Therefore, a Fuzzy Comprehensive Evaluation method is introduced to evaluate the performance of universities and colleges more professionally. Membership function fuzzy synthetic evaluation matrix is introduced to transform qualitative evaluation into quantitative evaluation, eliminating ambiguity, and subjectivity [43]. It optimizes the method how to set the weight and evaluation value of each indicator.

Analytical Hierarchy Process method was proposed by T. L. Saaty in University of Pittsburgh in the 1970s [44]. It is a hierarchical analysis method to deal with complicated decision-making problems with component elements in different levels. AHP method is used to evaluate the performance of some universities and colleges in Greek [45]. It is used to calculate the weight of each performance indicator in some financial and economic universities and colleges in China [46].

Principal Components Analysis method is a multivariate statistical analysis method that converts multiple indicators into fewer comprehensive independent ones [47]. It is widely used in the fields of economics and management science. In multi-indicator systems, there are always dependencies among indicators, which reveal overlapping information [48]. PCA takes the idea of dimension reduction to simplify the situation. Several principal independent indicators are chosen to represent the whole components, which contain information as much as possible in the system. It is widely used to set up and optimize the performance evaluation indicator system of universities and colleges [49].

Factor Analysis Method is proposed by C. E. Spearman. It is a statistical method used to describe variability among observed, correlated variables in terms of a potentially lower number of unobserved variables called factors [50]. It is used to set up and optimize the performance evaluation indicator system of universities and colleges.

Topsis model is a common method which is commonly used for multi-objective decision making [51]. It calculates the relative adjacency between evaluated objects and the optimal and inferior solutions of all objects [52]. According to the principle of Topsis model, the ideal evaluation object is the one in which all data of evaluation indicators are closest to the optimal ones and farthest from the inferior ones. It can be used in the field of performance evaluation in higher education, advantageously comparing with other evaluation method. Firstly, there is no strict restriction in data of evaluated objects, including the type of data, the sample size, etc. Secondly, the data of evaluated objects with different meaning have various units and valid ranges, which is called dimensions. The Topsis method standardizes dimensions in advance to eliminate the impact of various dimensions. Thirdly, it is better to do comparative analysis of different evaluated objects. It introduces evaluation indicators of various dimensions for comprehensive evaluation.

The systematic clustering algorithm classifies evaluated objects on their own characteristics. The evaluated objects with higher similarity are grouped into one category, which is called a cluster, while those with lower similarity are grouped into different cluster [53]. The number of clusters is determined based on the similarity of evaluated objects instead of being set in advance. The number of evaluated objects in each cluster is calculated by the systematic clustering algorithm. The systematic clustering algorithm effectively solves the classification problem of multiple indicators, avoiding subjectivity and arbitrariness.

In order to solve the homogenization problems in the current evaluation, this paper proposes a clustering algorithm of classified performance evaluation of universities and colleges based on Topsis model. The algorithm advocates implementing classified performance evaluation according to different types of universities and colleges, which encourages them to develop themselves in personalized and characteristic ways.

3. Proposed Method

The clustering algorithm of classified performance evaluation of universities and colleges based on Topsis model aims to promote the development characteristics and running goals of universities and colleges. To a large extent, it solves the homogenization problems in current evaluation, which helps to better diversify construction and sustainable development in higher education in China. The clustering algorithm consists of four parts. First, determine the number of classification types of universities and colleges. In this paper, two classification types are identified as examples, one for universities focusing on scientific research and the other for colleges focusing on technical skills. Then, design a classified performance evaluation indicator system for two types of universities and colleges. Topsis model is then used to calculate the relative adjacency between evaluated objects and the optimal and inferior solutions of all objects. After that, systematic cluster algorithm is used to analyze and evaluate the performance of universities and colleges in the same type. An automatic system is developed to analyze data from universities and colleges.

3.1. Classified Performance Evaluation Indicator System

In accordance with the development characteristics and running goals, the classified performance evaluation indicator system contains two sets of evaluation indicators with the principles of dominance, measurability, systematicity, scientificity, and practicality, one for universities focusing on scientific research, the other for colleges focusing on technical skills. From the perspective of diversification, non-uniform evaluation standards are adopted for different types of universities and colleges according to their special history and current situations. The evaluation standards not only reflect the general character and the inherent features of higher education but also reflect the individual characteristics of universities and colleges. Different evaluation standards correspond to different development goals, construction tasks, policy support, talent cultivation types, and education quality. From the perspective of sustainability, it is necessary to pay attention not only to current status, but also to the development and improvement of universities and colleges. The indicators of development increment, such as the growth ratio of faculty team, teaching resources, research projects, etc., in the evaluation period, reflects the notion of sustainability.

The design principles of the classified performance evaluation indicator system follows four points. First, quantitative indicators are combined with qualitative indicators. Second, indicators about scale are combined with indicators about quality. Third, indicators about external performance are combined with internal improvement. Fourth, indicators about the total amount are combined with indicators about per capita. Fifth, indicators about accumulation are combined with indicators about development increment.

This paper uses evaluation indicators from Classified Performance Evaluation Indicator System for universities and colleges in Shanghai, which was revised and promulgated in 2022 [54]. The content of Classified Performance Evaluation Indicator System is shown in

Table 1. Classified performance evaluation indicator system.

Primary	Secondary	Tertiary (Observation Point)
		Classification Type 1: Universities Focusing on Scientific Research	Classification Type 1: Colleges Focusing on Technical Skills
Running Direction and Management Level	Running Direction	Implementation of moral education	Same
		Cultural heritage and innovation	Same
		…	…
	Management Level	Planning management	Same name with different content
		Teaching quality assurance	Same
		Financial management	Same
		…	…
Running Condition and Resources	Faculty Team	--	Student-teacher ratio
		Number of outstanding talents	Same name with different content
		Number of outstanding teaching and research teams	Same name with different content
		--	Ratio of full-time teachers who possess profound professional theory and solid professional skills and rich experience
		--	Ratio of part-time teachers in enterprises
		--	Professional practice in enterprises for full-time teachers
		Ratio of full-time teachers with oversea learning experiences	--
		…	…
	Teaching Resource	Average number of courses per undergraduate students	Average number of courses per college students
		--	Ratio of practice courses
		Number of excellent courses	Same name with different content
		Number of high-quality teaching materials published at national level	Number of teaching materials published focusing on vocational education
		…	…
	Platforms	Number of research and experiment platforms	Same name with different content
		Number of innovation and entrepreneurial bases or projects	Same name with different content
		…	…
	Research Projects	Amount of science and technology funds (RMB)	Same name with different content
		Number of science and research projects	Number of entrusted projects of enterprises and institutions
		…	…
Running Quality	Disciplines	Optimization of discipline distribution	Optimization of major distribution
		Number of excellent disciplines	Number of excellent majors
		Ratio of excellent disciplines or majors	Ratio of majors integrated with industry and education
		…	…
	Innovation Achievement	Number of student awards	Same name with different content
		Number of teaching achievement awards	Same name with different content
		Number of academic papers published domestically and internationally	--
		Number of distinguished patents	--
		Number of research awards	Same name with different content
		…	…
	International Exchange	Ratio of international students with academic qualifications	Ratio of international students
		Ratio of students who study or work as intern abroad	Same
		Number of sino-foreign institutions	Number of colleges with mutual recognition of credits
		--	Number of cultivation programs abroad
		…	…
	Social Service	Number of transformations of achievement	Same name with different content
		…	…

. It contains three primary indicators, including Running Direction and Management Level, Running Condition, and Resources, and Running Quality. Each primary indicator is composed of several secondary indications, ten secondary indicators in all. Each secondary indicator contains some observation points, which can be considered as tertiary indicators, the weight of which can be calculated in Topsis Model later. The percentage of the tertiary indicators that reflect distinguishing characteristics of each type of university and college is about 30%. The diversification of the classified performance evaluation indicator system is mainly listed in the following aspects.

First, each set of the evaluation indicators has some different tertiary indicators since development characteristics and running goals are different for different types of universities and colleges. For example, the tertiary indicator, ratio of part-time teachers in enterprises is only available in the type of colleges focusing on technical skills. Compared to the universities focusing on scientific research, the colleges pay more attention on practical operations.

Second, the weight of the same indicator may be different in each set. For example, the secondary indicator, Research Projects, is available in both sets of classified performance evaluation indicator of universities and colleges. The value of the weight is a little larger in the indicator for universities focusing on scientific research than that for the colleges focusing on technical skills according to the calculation result of Topsis model. Relatively speaking, the colleges focusing on technical skills pay more attention on talent cultivation.

Third, each set of evaluation indicators has some similar primary, secondary, and even tertiary indicators, while the real meaning of similar indicators for each set is different. It reflects the characteristics of different types of universities and colleges. These indicators may be inconsistent both in names and content, or the same name with inconsistent content. For example, the tertiary indicator, Number of Outstanding Talents, is available in both sets of classified performance evaluation indicator of universities and colleges. It includes the number of academicians of the Chinese Academy of Sciences (CAS), the Chinese Academy of Engineering (CAE), members of the National Academy of Sciences (NAS), members of the Academia Europaea, etc., as the content of the indicator for universities focusing on scientific research. However, it includes the number of masters of technical skills, craftsmen of the Nation, directors and members of teaching guidance committee of China Ministry of Education (MOE), etc., as the content of indicator for colleges focusing on technical skills.

Fourth, the evaluation criteria of the same indicator may be different in each set. For example, some tertiary indicators in Platform are available in both sets of classified performance evaluation indicator of universities and colleges. Due to the different evaluation criteria, the evaluation value is different even if the data of the indicator is identical.

Fifth, the classified performance evaluation indicator system takes into account completeness and simplicity. The evaluation indicators need cover to reflect all aspects of the performance of universities and colleges, which leads to complexity. At the same time, too complicated indicator system makes performance evaluation more difficult. Focusing on too much detail may not reflect the performance of universities and colleges scientifically. It is necessary to balance the contradiction of completeness and simplicity appropriately.

The classified performance evaluation indicator system is dynamic. Universities and colleges, government, experts, etc., are consulted for their opinion every year. Minor revision and improvement are made accordingly. Major revision may be made every five years.

The classified performance evaluation indicator system encourages various types of universities and colleges to develop themselves in personalized and characteristic ways in order to meet the needs of diversified social requirements.

3.2. Topsis Model

Topsis model is a common method which is widely used in the field of multi-objective decision making. It calculates the relative adjacency between evaluated objects and the optimal and inferior solutions of all objects. Since there is no strict limitation in sample size, Topsis model can be used in the field of performance evaluation in higher education. According to the principle of Topsis model, the ideal evaluation object is the one in which all data of evaluation indicators are closest to the optimal ones and farthest from the inferior ones. The steps are shown as below.

1.

Establish a decision matrix;

If there are n evaluated objects, which are known as samples, and p evaluation indicators, an n ∗ p decision matrix $X_l$ is established as (1).

$$X_l=\left[\begin{array}{cc}\begin{array}{cc}{x}_{11}& x_{12}\\ x_{21}& x_{22}\end{array}& \begin{array}{cc}\cdots & x_{1p}\\ \cdots & x_{2p}\end{array}\\ \begin{array}{cc}\begin{array}{c}⋮\\ x_{i1}\\ ⋮\end{array}& \begin{array}{c}⋮\\ x_{i2}\\ ⋮\end{array}\\ x_{n1}& x_{n2}\end{array}& \begin{array}{cc}\begin{array}{c}⋮\\ x_{ij}\\ ⋮\end{array}& \begin{array}{c}⋮\\ x_{ip}\\ ⋮\end{array}\\ \cdots & x_{np}\end{array}\end{array}\right]$$

(1)

2.

Standardize the decision matrix;

Since each evaluation indicator has an individual meaning, there are various units and valid ranges. It is completely ignored for some evaluation indicators with small values in range. Therefore, it is necessary to standardize the decision matrix $X_l^{\prime }$ in (2).

$$X_l^{\prime }=\left[\begin{array}{cc}\begin{array}{cc}{x}_{11}^{\prime }& x_{12}^{\prime }\\ x_{21}^{\prime }& x_{22}^{\prime }\end{array}& \begin{array}{cc}\cdots & x_{1p}^{\prime }\\ \cdots & x_{2p}^{\prime }\end{array}\\ \begin{array}{cc}\begin{array}{c}⋮\\ x_{i1}^{\prime }\\ ⋮\end{array}& \begin{array}{c}⋮\\ x_{i2}^{\prime }\\ ⋮\end{array}\\ x_{n1}^{\prime }& x_{n2}^{\prime }\end{array}& \begin{array}{cc}\begin{array}{c}⋮\\ x_{ij}^{\prime }\\ ⋮\end{array}& \begin{array}{c}⋮\\ x_{ip}^{\prime }\\ ⋮\end{array}\\ \cdots & x_{np}^{\prime }\end{array}\end{array}\right]$$

(2)

In the standardization decision matrix, $x_{ij}^{\prime }=\frac{x_{ij}}{{{\displaystyle \sum }}_{i=1}^n{x}_{ij}^2} x_{ij}\in X_l$.

3.

Establish a weight vector;

In order to determine the influence of each indicator in performance evaluation, it is important to set a weight to each indicator, which can be calculated through entropy method, fuzzy analytic hierarchy process method (FAHP), principal component analysis method (PCA), etc. [55,56]. In this paper, the entropy method is used to determine the weight of each evaluation indicator. The weight vector W is set as (3).

$$W=[w_1\hspace{1em}{w}_2\hspace{1em}\cdots \cdots \hspace{1em}{w}_p]$$

(3)

4.

Establish a weighted standardization decision matrix;

$$X_l^{″}=W\ast X_l^{\prime }=\left[\begin{array}{cc}\begin{array}{cc}{w}_1{x}_{11}^{\prime }& w_2{x}_{12}^{\prime }\\ w_1{x}_{21}^{\prime }& w_2{x}_{22}^{\prime }\end{array}& \begin{array}{cc}\cdots \cdots & w_p{x}_{1p}^{\prime }\\ \cdots \cdots & w_p{x}_{2p}^{\prime }\end{array}\\ \begin{array}{cc}\begin{array}{c}⋮\\ w_1{x}_{i1}^{\prime }\\ ⋮\end{array}& w_2\begin{array}{c}⋮\\ x_{i2}^{\prime }\\ ⋮\end{array}\\ w_1{x}_{n1}^{\prime }& w_2{x}_{n2}^{\prime }\end{array}& \begin{array}{cc}\begin{array}{c}⋮\\ w_j{x}_{ij}^{\prime }\\ ⋮\end{array}& \begin{array}{c}⋮\\ w_p{x}_{ip}^{\prime }\\ ⋮\end{array}\\ \cdots \cdots & w_p{x}_{np}^{\prime }\end{array}\end{array}\right]=\left[\begin{array}{cc}\begin{array}{cc}{r}_{11}& r_{12}\\ r_{21}& r_{22}\end{array}& \begin{array}{cc}\cdots & r_{1p}\\ \cdots & r_{2p}\end{array}\\ \begin{array}{cc}\begin{array}{c}⋮\\ r_{i1}\\ ⋮\end{array}& \begin{array}{c}⋮\\ r_{i2}\\ ⋮\end{array}\\ r_{n1}& r_{n2}\end{array}& \begin{array}{cc}\begin{array}{c}⋮\\ r_{ij}\\ ⋮\end{array}& \begin{array}{c}⋮\\ r_{ip}\\ ⋮\end{array}\\ \cdots & r_{np}\end{array}\end{array}\right]={\left(r_{ij}\right)}_{n\ast p}$$

(4)

The standardization decision matrix $X_l^{″}$ is defined as (4). $x_{ij}^{\prime }\in X_l^{\prime }, w_j\in W$, which is the weight of the jth evaluation indicator, $r_{ij}=w_j{x}_{ij}^{\prime }$, $i\in \left[1,n\right], j\in \left[1,p\right]$.

5.

Identify the optimal and the inferior solutions of all evaluated objects;

The optimal solution set $S_j^{+}$ and the inferior solution set $S_j^{-}$ of classified performance evaluation indicators are obtained according to the weighted standardization decision matrix.

The $S_j^{+}$ and $S_j^{-}$ are defined as (5) if the jth evaluation indicator is positive.

$$\{\begin{array}{c}{S}_j^{+}=max\left\{r_{ij}|i=1,2,\dots ,n\right\}\\ S_j^{-}=min\left\{r_{ij}|i=1,2,\dots ,n\right\}\end{array}j\in J^{+}$$

(5)

The $S_j^{+}$ and $S_j^{-}$ are defined as (6) if the jth evaluation indicator is negative.

$$\{\begin{array}{c}{S}_j^{+}=min\left\{r_{ij}|i=1,2,\dots ,n\right\}\\ S_j^{-}=max\left\{r_{ij}|i=1,2,\dots ,n\right\}\end{array}j\in J^{-}$$

(6)

$J^{+}$ is the positive efficiency indicator set. $J^{-}$ is the negative efficient indicator set.

6.

Calculate the ideal distance between evaluated objects and optimal and inferior solutions;

The ideal distance between evaluation objects and optimal solution $S{d}_i^{+}$ and inferior solution $S{d}_i^{-}$ is defined as (7),$i\in \left[1,n\right]$.

$$\{\begin{array}{c}S{d}_i^{+}=\sqrt{{\displaystyle {\displaystyle \sum }_{j=1}^p}{w}_j{\left(r_{ij}-S_j^{+}\right)}^2}\\ S{d}_i^{-}=\sqrt{{\displaystyle {\displaystyle \sum }_{j=1}^p}{w}_j{\left(r_{ij}-S_j^{-}\right)}^2}\end{array}$$

(7)

7.

Calculate the relative adjacency η_i.

The relative adjacency is defined as (8), ${\eta }_i\in \left[0,1\right]$, $i\in \left[1,n\right]$. The greater the value of relative adjacency, the better the evaluated object is, and vice versa. Evaluated objects can be ranked by the value of the relative adjacency.

$${\eta }_i=\frac{S{d}_i^{-}}{S{d}_i^{+}+S{d}_i^{-}}$$

(8)

3.3. Systematic Clustering Algorithm

On the basis of classified performance evaluation indicator system and the relative adjacency calculated by Topsis model, systematic clustering algorithm can be used to evaluate the performance of universities and colleges of the same type. The performance of universities and colleges in the same cluster is more similar, while those in the different clusters are less similar.

If n samples are divided into m clusters, set $G_i i\in \left[1,m\right]$ as each cluster, $n_i$ as the number of samples in cluster $G_i$, ${\overline{Y}}^{\left(i\right)}$ as the centre of cluster $G_i$, $Y_j^{\left(i\right)}$ as the jth sample in cluster $G_i$. Define Sum of Squares of Deviations (SSD) of each cluster as (9), which indicates discreteness of samples in one cluster.

$$SS{D}_i={\displaystyle \sum }_{j=1}^{n_i}{\left(Y_j^{\left(i\right)}-{\overline{Y}}^{\left(i\right)}\right)}^{\prime }\left(Y_j^{\left(i\right)}-{\overline{Y}}^{\left(i\right)}\right)$$

(9)

The total SSD is defined as (10).

$$SSD={\displaystyle \sum }_{k=1}^{m}SS{D}_i={\displaystyle \sum }_{k=1}^m{\displaystyle \sum }_{i=1}^{n_i}{\left(Y_j^{\left(i\right)}-{\overline{Y}}^{\left(i\right)}\right)}^{\prime }\left(Y_j^{\left(i\right)}-{\overline{Y}}^{\left(i\right)}\right)$$

(10)

In the process of clustering, if two clusters $G_p$ and $G_q$ are integrated into a new cluster $G_r$, with the number of samples $n_p$, $n_q$, $n_r$, and the Sum of Squares of Deviations $SS{D}_p$, $SS{D}_q$, $SS{D}_r$, define the distance between $G_p$ and $G_q$ as $SSD{T}_{pq}$ in (11). Define the distance between $G_r$ and other clusters as (12).

$$SSD{T}_{pq}^2=SS{D}_r-(SS{D}_p+SS{D}_q)$$

(11)

$$SSD{T}_{kr}^2=\frac{n_k+n_p}{n_k+n_r} SSD{T}_{kp}^2+\frac{n_k+n_q}{n_k+n_r} SSD{T}_{kq}^2-\frac{n_p+n_q}{n_k+n_r} SSD{T}_{pq}^2$$

(12)

When the $SSD{T}_{pq}^2$ reaches a local minimum value and $SSD{T}_{kr}^2$ reaches a local maximum value, $G_p$ and $G_q$ can be integrated. At this point, $SS{D}_r$ of $G_r$ increases least while the discreteness between G_r and other clusters increase most. The total $SSD$ of all samples will increase with the decreasing number of clusters.

The steps of systematic clustering algorithm are as below. Set each sample as one cluster firstly. Then Integrate two clusters into one according to (11) and (12). Repeat the above step until all samples are integrated into one.

The workflow of the systematic clustering algorithm of classified performance evaluation of universities and colleges (SCACPE) is as follows (Algorithm 1).

Algorithm 1: SCACPE (Systematic Clustering Algorithm of Classified Performance Evaluation of Universities and Colleges)

Input: Samples (the set of universities and colleges), Attributes (the set of classified performance evaluation indicators) Output: Clusters of universities and colleges Workflow: SCACPE (Samples, Attributes) Begin Set each sample as one cluster; Repeat 2. Calculate $SS{D}_i$ of each cluster; 3. For each ($SS{D}_i$) 4.   Calculate $SSD{T}_{ij}^2$ between $SS{D}_i$ and other clusters; 5.   For each (integrated cluster i and cluster j as cluster r) 6.     Calculate $SSD{T}_{kr}^2$ between $SS{D}_r$ and other clusters; 7.   If ($SSD{T}_{ij}^2$ = local minimum & $SSD{T}_{kr}^2$ = local maximum) 8.         Return clusters i and cluster j; 9. Integrated cluster i and cluster j into one new cluster; 10. Until only one cluster is generated End

The time complexity of algorithm SCACPE is O [cardinal (Attributes) ∗ cardinal (Samples) ∗ Log2cardinal (Samples)]. Cardinal (Attributes) is the cardinal number of the set of classified performance evaluation indicator. Cardinal (Samples) is the cardinal number of the set of samples.

4. Application

4.1. Data Selection

In order to ensure authenticity, reliability, and authority, the related data in classified performance evaluation come from following parts.

• Official statistic data from Ministry of Education of China and Shanghai Municipal Education Commission, including Educational Statistics Yearbook of China, Compilation of Basic Statistics of Universities and Colleges directly under the Ministry of Education of China, Analysis Report on Education and Teaching Data of Universities and Colleges directly under the Ministry of Education of China, Basic Level Statistic Report of Higher Education, Annual Statistic Report of Science and Technology of Universities and Colleges, Platform of Data Collection and Management of Talent Cultivation in Higher Education, etc.
• Officially released information for public use in official website, including National Data Monitor Platform for Higher Education Quality, Platform of Data Collection and Management of Talent Cultivation in Higher Vocational Colleges, etc.
• Materials submitted by the universities and colleges including Report of Innovation Information Collection of each university and college, etc.
• Information from third-party organizations, including Shanghai Soft Science Education Information Consulting Company, Elsevier B.V. Company, Clarivate Company, etc.

All the data are focusing on tertiary indicators. They are subject to vigorous verification.

It needs to set performance evaluation period. It is known that the output of higher education shows hysteretic characteristics. If the evaluation period is too short, it is difficult to obtain an effective correlation of evaluation indicators and the real performance of universities and colleges. If the evaluation period is too long, it is unfavorable to adjust resource allocation and to improve running practices. Referring to the evaluation periods of about three to eight years in other countries, and the actual situation of universities and colleges, the evaluation period is set to five years. The first evaluation period is 2008 to 2012. Classified performance evaluation is continuously implemented with a five-year period.

The classified performance evaluation is implemented on 62 universities and colleges in Shanghai, which are identified into two types: one for universities focusing on scientific research and the other for colleges focusing on technical skills. Data of continuous five years are collected from 2017 to 2021, and are integrated into the basic information table of universities and colleges in the database. The table structure is shown in

Table 2. Table structure of basic information of universities and college.

No	Meaning	Name	Type	Primary Key	Foreign Key	Default Value	…
1	University or college ID	UCID	char	Yes	Yes	NULL	…
2	University or college name	UCName	varchar	No	No	NULL	…
3	University or college type	UCType	char	No	No	NULL	…
4	Number of faculty	Faculty	smallint	No	No	NULL	…
5	Number of college students	CLStudent	mediumint	No	No	NULL	…
6	Number of undergraduate students	UDGStudent	mediumint	No	No	NULL	…
7	Number of graduate students	GStudent	mediumint	No	No	NULL	…
8	Number of doctoral students	DStudent	mediumint	No	No	NULL	…
9	Number of academicians of the Chinese Academy of Sciences	AcademicianCAS	smallint	No	No	NULL	…
10	Number of academicians of the Chinese Academy of Engineering	AcademicianCAE	smallint	No	No	NULL	…
11	Number of members of the National Academy of Sciences	memberNAS	smallint	No	No	NULL	…
12	Number of masters of technical skills	masterTS	smallint	No	No	NULL	…
13	Number of craftsmen of the Nation	craftsmenNA	smallint	No	No	NULL	…
14	Number of national-level teaching team	NLteachingteam	smallint	No	No	NULL	…
15	Number of innovation team of Ministry of Education	InnoteamMOE	smallint	No	No	NULL	…
16	Number of national laboratories	NLaboratory	smallint	No	No	NULL	…
17	Number of high-level think tanks	HLthinktank	smallint	No	No	NULL	…
18	Number of National Natural Science Fund	NNSFund	smallint	No	No	NULL	…
19	Number of National Social Science Fund	NSSFund	smallint	No	No	NULL	…
20	Number of National Teaching Achievement Award	NTeachingAAward	smallint	No	No	NULL	…
…	…	…	…	No	No	NULL	…
162	Number of patent transforms	PatentTFS	mediumint	No	No	NULL	…
163	Number of national decision-making and consulting reports	NDSCReport	mediumint	No	No	NULL	…
164	Number of provincial expert advice reports	PEAReport	mediumint	No	No	NULL	…
165	Year	Year	mediumint	No	No	NULL	…

, which defines 161 classified performance evaluation attributes together with some primary key and foreign keys.

Some pre-processing works, such as data cleaning, data integration, data transformation, data reduction, etc., shall be done in advance [57].

4.2. Data Pre-Processing Based on Topsis Model

After establishing and standardizing decision matrix according to the average value of data of continuous five years for universities focusing on scientific research and colleges focusing on technical skills separately, the entropy method is used to determine the weight of each evaluation indicator for universities and colleges in (13) and (14).

$$W_{university}=\left[\begin{array}{cc}\begin{array}{cc}0.123& 0.026\end{array}& \begin{array}{cc}\cdots \cdots & 0.019\end{array}\end{array}\right]$$

(13)

$$W_{college}=\left[\begin{array}{cc}\begin{array}{cc}0.134& 0.023\end{array}& \begin{array}{cc}\cdots \cdots & 0.018\end{array}\end{array}\right]$$

(14)

A weighted standardization decision matrix is established. The optimal and the inferior solution sets of universities or colleges are identified separately. The ideal distance between evaluated samples and optimal and inferior solutions of universities or colleges is calculated. The relative adjacency is calculated. The scores of universities and colleges based on Topsis model in 2017–2021 are shown in

Table 3. The scores of universities and colleges in 2017~2021.

Classification Type	Name	Scores of Universities and Colleges (%)
		2017	2018	2019	2020	2021
University focusing on scientific research	University 1	47.27	60.80	76.76	82.66	83.26
	University 2	48.57	59.89	80.99	80.28	80.39
	University 3	42.42	62.32	69.19	78.20	78.36
	University 4	46.56	58.48	55.91	66.59	63.58
	University 5	41.53	58.30	54.30	63.40	70.35
	…	…	…	…	…	…
	University 21	32.74	43.14	43.59	41.74	43.14
	University 22	42.50	53.63	60.55	45.58	40.36
	University 23	38.08	51.72	52.17	43.41	50.31
College focusing on technical skills	College 1	54.30	64.52	75.32	77.53	78.88
	College 2	58.79	64.13	69.27	68.01	77.72
	College 3	61.44	63.71	67.96	71.24	77.33
	College 4	55.43	57.65	63.22	60.25	68.54
	College 5	51.22	58.60	67.28	57.62	68.61
	…	…	…	…	…	…
	College 38	45.67	35.48	43.05	54.31	68.50
	College 39	46.45	33.55	36.78	59.83	67.05

.

4.3. Clustering Algorithm of Classified Performance Evaluation

According to the scores of 23 universities and 39 colleges based on Topsis model in 2017–2021 in Table 3, systematic clustering algorithm is made for comprehensive analysis to evaluate the performance of universities and colleges of the same type.

The clustering diagram of universities focusing on scientific research is shown in Figure 1, with one node representing one clustering process. With the transect method and the actual situation of universities and colleges in Shanghai, the relative distance is set to 0.010. The 23 universities in Shanghai are clustered into three levels. There are six universities in level 1, six universities in level 2, and eleven universities in level 3.

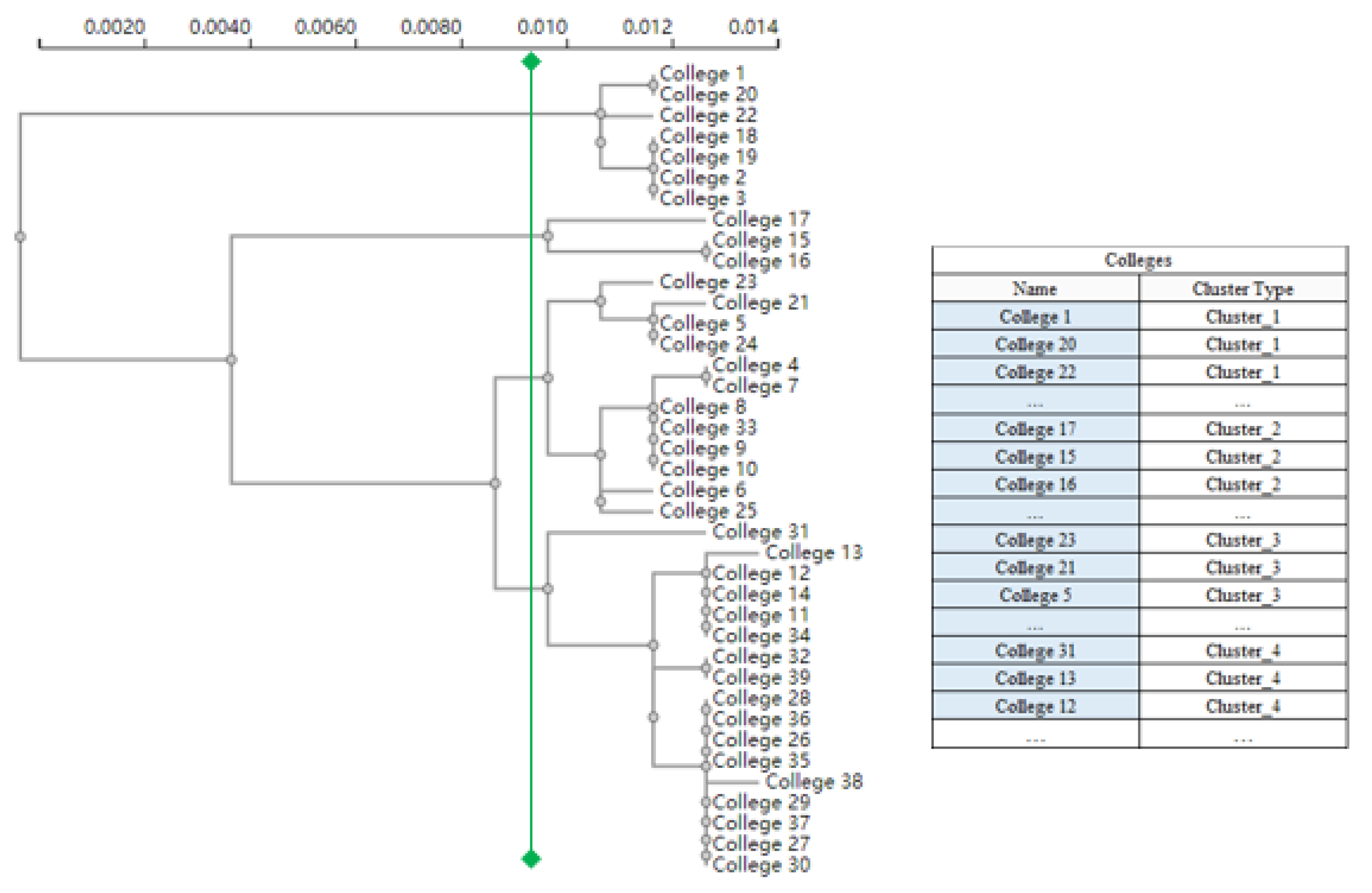
The clustering diagram of colleges focusing on technical skills is shown in Figure 2. According to a relative distance of 0.010, the 39 colleges in Shanghai are clustered into four levels. There are seven colleges in level 1, three colleges in level 2, twelve colleges in level 3, and seventeen colleges in level 4.

4.4. Classified Performance Evaluation Result Analysis

Classified Performance Evaluation is implemented in 23 universities focusing on scientific research and 39 colleges focusing on technical skills in Shanghai in 2022. On the basis of continuous research and practice, data of continuous five years from 2017 to 2021 are collected for analysis. A classified performance evaluation indicator system is established. Topsis model is used to calculate relative adjacency. A systematic clustering algorithm is made for comprehensive analysis to evaluate the performance of universities and colleges of the same type.

Take 23 universities focusing on scientific research as an example. Through clustering algorithm of classified performance evaluation, when the threshold value is set to 0.010, there are six universities in level 1 with high performance, which account for about 26.09% of the total universities. It includes four comprehensive universities (66.67%), one university of science and engineering (16.67%), and one normal university (16.67%). There are six universities in level 2 with medium performance, accounting for about 26.09% of the total universities. It includes one university of science and engineering (16.67%), two medical universities (33.33%), two universities of liberal arts, economic and management (33.33%), and one university of arts and sports (16.67%). There are eleven universities in level 3 with relatively low performance, accounting for about 47.82% of the total universities. It includes three comprehensive universities (27.27%), four universities of science and engineering (45.45%), two universities of liberal arts, economic and management (18.18%), and two universities of arts and sports (18.18%). Among all the universities, 57.14% of comprehensive universities are in level 1 with high performance, 42.86% of them are in level 3 with relatively low performance. 16.67% of universities of science and engineering are in level 1 with high performance, 16.67% of them are in level 2 with medium performance, and 66.67% of them are in level 3 with relatively low performance. 50.00% of universities of liberal arts, economic, and management are in level 2 with medium performance, 50% of them are in level 3 with relatively low performance. 33.33% of universities of arts and sports are in level 2 with medium performance, 66.67% of them are in level 3 with relatively low performance.

Based on the above data, the performance of universities under the Ministry of Education is usually stable with relatively higher performance. There are about half of the universities with relatively low performance, which are expected to improve the performance effectively.

By analyzing the evaluation indicators of universities, it shows as follows.

First, the number of outstanding disciplines in top-ranked universities is significantly higher than other universities. The outstanding disciplines are the top 50 disciplines in QS, or the top 1% disciplines in ESI. They act as pioneers in the process of disciplines development in universities. They drive the common development of other relevant disciplines while enhancing themselves. There are breakthroughs in one or two fields to be famous worldwide, and then the overall quality of universities improves slowly. Most outstanding disciplines develop gradually in the development of universities, which are the foundation of universities. Therefore, universities can focus on discipline development and strengthen the advantages.

Second, some top-ranked universities and medium-ranked universities collaborate with each other closely, such as interdisciplinary collaborations, scientific research platform collaborations, etc. There are some advantageous disciplines in the top-ranked and medium-ranked universities. The advantageous disciplines are the top 500 disciplines in QS, or the top 1% of disciplines in ESI. The outstanding and advantageous disciplines collaborate closely to make the university improve effectively. The collaboration of these disciplines is beneficial to the development of universities.

Third, the top-ranked universities have an obvious advantage in the number of outstanding talents, funds, science, and research achievements and government support, etc., comparing to the other universities. These aspects are important for the development of universities focusing on scientific research.

Fourth, some indicators of development increment, such as the growth ratio of the faculty team, teaching resources, research projects, etc., have a slight impact on performance. Two universities enter different clusters due to a little difference in these increment indicators while most other indicator values are similar. From the perspective of sustainability, these evaluation indicators can reflect the potential of university development.

5. Discussion and Conclusions

This paper proposes a new method of clustering analysis of classified performance evaluation of universities and colleges based on Topsis model. The classified performance evaluation indicator system is established for different types of universities and colleges. Topsis model is used to calculate the relative adjacency between the evaluated objects and the optimal and inferior solutions of all objects. Systematic clustering algorithm is made for comprehensive analysis to evaluate the performance of universities and colleges in the same type. An automatic system is developed to analyze data from 62 universities and colleges in Shanghai.

The study of the method helps to reveal the performance and the development stage of universities and colleges. It is helpful for educational administrative department to develop new optimized strategies for higher education. It helps to improve the efficiency of funds and resource allocation, to void homogeneous competition, and to promote alliance and collaboration among universities and colleges, so as to effectively promote the diversified construction and sustainable development of higher education.

Based on the result of classified performance evaluation, specific policies shall be implemented in universities and colleges in Shanghai effectively as follows.

First, establish funding classification support and management model to allocate funds efficiently. Universities and colleges can serve the country and society more effectively, and enhance social recognition and international influence.

Second, establish short-term, medium-term, and long-term classified evaluation systems based on achievements of discipline construction, quality of talent cultivation, international influence, national serving strategies, etc. Concentrate resources on constructing outstanding and advantageous disciplines to drive the development of universities and colleges.

Third, create University and College Community to form strong alliances and collaboration among universities and colleges, and to avoid homogenization.

Fourth, encourage construction of interdisciplinary Integration in universities and colleges. Promote the mutual development of disciplines.

The clustering analysis of classified performance evaluation of higher education is in initial stage. The relevant work is under exploration. It lacks effective reference and experience, and needs more knowledge to support. As far as the algorithm is concerned, latest data of continuous five years are collected from 2017 to 2021. It evaluates the performance of universities within one certain period of time. In the future, a rolling five-year period is considered to evaluate the performance of universities and colleges more dynamically and sustainably. In addition, we will take further research on outliers in the clustering algorithm to make the clustering of universities and colleges more scientifically. The complexity of the algorithm is considered be reduced in the future.