Abstract
With the rapid development of information technology and communication technology, several online recovery platforms have introduced offline channels to encourage customers to participate in product acquisition and improve profits. Motivated by this reverse supply chain practice, we develop a game theory model under three scenarios (single offline channel, single online channel, and dual-channel structures) to assess the effect of a newly added offline channel for online recovery platforms and explore the factors that have significant impacts on the dual-channel strategy for recovery platforms. We conduct static analyses to solve the model and perform a numerical study to examine the robustness of the results. The results reveal that a recovery platform can always gain more profit and set lower recovery prices under the dual-channel structure. However, the relatively high shipping cost might cause the recovery platform to recover a smaller quantity under the dual-channel structure compared with the single offline channel structure. In addition, the recovery platform is more likely to adopt a dual-channel structure with low shipping cost, high average hassle cost or hassle cost uncertainty, and less uncertainty on the reservation value. Moreover, the recovery platform can use the price difference between online and offline channels as a tool to split product holders and induce them to choose the most appropriate channel. Our findings highlight the profit and recovery quantity benefits brought by the dual-channel structure, and provide management insights for recovery platforms.
1. Introduction
Recently, with the rapid development of information technology and the shortened life-cycles of electrical and electronic equipment, the large amount of wasted electrical and electronic equipment (WEEE) has become a serious problem [1,2]. According to the United Nations [3], globally, consumers generated almost 45 million tons of electronic WEEE in 2017. Moreover, a report by Greenpeace (2019) predicts that the number of discarded electronic products in China will reach 27.22 million tons by 2030 [4]. Such a large amount of WEEE has great economic value to human beings. For example, according to the report by Greenpeace (2019), it is estimated that if 85% of computers and mobile phones could be recycled, the total value of the recovered metals would reach CNY 130 billion [4]. On the other hand, if WEEE is not appropriately collected and disposed of, not only are a large number of resources wasted, but the environment will also be greatly harmed by the leakage of multitudinous hazardous materials from the e-waste, such as mercury, arsenic, and cadmium [5].
In order to gain the residual value of WEEE and protect the environment, many recycling practices have emerged. With the fast development of the Internet, many enterprises, such as Aihuishou, Huishoubao, and Huishouge, try to collect and resell WEEE online. However, because of the inconvenience of recovery and the opaqueness of the price-setting process by these online recovery platforms, acceptance of the recovery mode through online channels is not high yet, and a large amount of WEEE is still retained or abandoned. Hence, increasing the recovery quantity and improving profits have become major challenges for these online recovery platforms.
A promising solution to the above problem for online recovery platforms is to make use of an offline channel for recovery, as well. In reality, many of the online recovery platforms mentioned above, which recover used products through online channels, have now begun to collect WEEE through both online and offline channels (i.e., physical stores), to obtain higher recovery volumes and achieve higher profits (e.g., Aihuishou, http://www.aihuishou.com/, accessed on 29 November 2019). However, online recovery platforms also face considerable challenges when implementing a dual-channel recovery structure, for example, the pricing of both recovery channels to maximize profits with the given cost structure of the recovery channels. Moreover, many studies have explored the effects of the dual-channel structure on platforms’ profit performance. However, only a few studies have taken recovery quantity into account. In this paper, we measure the impact of the newly added offline channel on the performance of online recovery platforms; more specifically, we examine the corresponding improvements in the recovery quantities and profits.
In addition, online recovery platforms’ dual-channel strategies are impacted by many factors. For example, factors such as the hassle cost incurred by the product holder when traveling to physical stores, the shipping cost for mailing the used products, and the uncertainty of the value of the product holder’s reservation of their own used products, all have significant impacts on the decisions and operations of recovery platforms’ dual-channel strategies.
However, to the best of our knowledge, there are limited analyses that focuses on the impact of these factors on the dual-channel strategies of recovery platforms. In this paper, we build a stylized model to solve these questions and explicitly figure out the impact of these factors on the decisions and performance of recovery platforms.
This paper is inspired by the extensive popularity of online recovery platforms, such as Aihuishou and Huishoubao in China, Gazelle in America, and O2recycle in the UK. Nowadays, major online recovery platforms offer both offline and online channels to consumers in China (www.aihuishou.com, accessed on 29 November 2019). This paper hopes to answer the above questions using an online recovery platform that collects used products from customers through both online and offline channels. More specifically, this research attempts to address the following questions: What is the optimal pricing strategy for both the offline and online channels of online recovery platforms, after adding an offline recovery channel? Can recovery quantity and profit be increased after introducing the dual-channel structure? Under what circumstances would improvements in profits using the dual-channel structure be more significant? Finally, what are the impacts of various factors on the recovery performance of recovery platforms?
By creating an analytical model and performing extensive numerical studies to explore these issues, the main contributions of this research are summarized as follows: First, we incorporate both recovery quantities and profits in this research. Second, we further examine factors that impact the performance of the dual channel in a reverse supply chain, unlike former research, which mainly explored forward supply chains and dis not consider these factors. Third, we figure out a feasible solution to maximize recovery platforms’ profits under a dual-channel structure, and we find that the dual-channel structure can always help recovery platforms gain more profits.
The rest of this study is organized as follows. We review the relevant literature in Section 2. In Section 3, we establish three models, each for a specific recovery channel structure, and explicitly derive the optimal decisions of each model. In Section 4, we conduct a comparison of the results among the models and perform comparative static analyses. Extensive numerical studies are conducted in Section 5. Finally, we conclude the paper and suggest directions for future research in Section 6. All proof is available in the Appendix A.
2. Literature Review
Our work investigates the management of offline and online channels for an online recovery platform in reverse supply chains. Our research is most closely related to three streams of literature, including online recovery platform management, channel management in reverse supply chains, and omnichannel operations. In the following sections, we review each stream of literature.
Several online e-waste recycling platforms, such as Gazelle in the USA, O2recycle in the UK, FLIP4NEW in Germany, and Aihuishou in China, have been established to provide alternative ways to recover used products, and have attracted the attention of a number of scholars. For example, Zuo et al. (2019) and Gu et al. (2019) both investigate a recycling mode that is composed of an online platform for booking collection appointments and an offline logistics platform for waste pick-up at an appointed place, which is an online-to-offline (O2O) system [6,7]. Zuo et al. (2019) study three cases in China and summarize that the O2O WEEE collection is popular in the capital market and among customers because it can eliminate information asymmetry, reduce transaction costs, and realize higher collection quantity and economic value [6]. Gu et al. (2019) examine the environmental benefits of O2O WEEE collection using material flow analysis and life cycle assessment [7]. Their results indicate that the recovery of unsubsidized WEEE shows the highest potential environmental benefit because of the high value of precious metals. Furthermore, Wang et al. (2018) investigate four “Internet +” recycling modes, and suggest that online recycling platforms should enhance the interaction between online and offline channels, the diversification of profit making, the instructions for online recycling platform operations, and the application of smart machines to improve profits [8]. Hahler et al. (2017) construct a sequential online acquisition model between the recommerce provider and product holders. They discover that the recommerce provider could take advantage of their last mover advantage to gain the greatest bargaining potential [9]. Except for Hahler et al. (2017), most of the papers on this topic explore the online platform issue in a qualitative way [9]. On the contrary, we construct a stylized model to study the strategic game between the online recovery platform and product holders when the online recovery platform introduces an offline recovery channel and adopts a dual-channel strategy.
In the literature on dual-channel management in reverse supply chains, many researchers have studied the optimal recovery channel choice, as well as the competition and coordination issues in a reverse supply chain. Hong et al. (2013) investigate three hybrid channel structures for collecting used products from customers and find that the manufacturer and the retailer hybrid channel structure is optimal for the manufacturer [10]. He et al. (2019) investigate recovery efficiency, as well as customer behavior, in a closed-loop supply chain with competitive collection [11]. That is, the manufacturer and the retailer compete in collecting used products, and customers perceive different levels of convenience for each collection channel. The authors find that collection competition does nothing to improve recovery efficiency. Huang et al. (2013) also study a dual recycling channel model in a closed-loop supply chain, within which a retailer and a third party compete to collect used products [12]. Their results indicate that a dual-recycling channel structure would be better than a single recycling channel structure for both consumers and manufacturers, only when the competition in recycling is less intense. Wang et al. (2019) investigate a hybrid closed-loop supply chain with competition in the recycling and product markets [13]. They consider three competition scenarios chosen by the manufacturers (i.e., the manufacturers do not establish a complete CLSC, and the remanufacturer takes the entire recycling business instead; the manufacturers establish their own collection networks and compete with the remanufacturer; and the manufacturers outsource the collection business to the retailer, and the retailer and remanufacturer compete in the recycling market) in their research. It is found that the manufacturer will always participate in recycling, and the optimal collection channel depends on the unit cost of self-collection and the compensation from outsourcing-collection.
The above literature provides perspectives and theories to better understand channel choice and management in reverse supply chains. However, these studies mainly consider traditional dual-channel recycling structures, which are commonly composed of a manufacturer, a retailer, or a third-party collector/remanufacturer. Recently, with the rise of the Internet and the prosperity of e-commerce, some research has also begun to consider a new dual-channel structure in reverse supply chains, that is, the co-existence of a traditional offline and an online recycling channel. Feng et al. (2017) consider a two-echelon reverse supply chain with dual-recycling channels where the dominant recyclable dealer has to design the optimal reverse channel structure [14]. The two channels are competitive. Moreover, by considering the consumer’s preference for the online channel in the model, they examine three scenarios: a single traditional recycling channel, a single online-recycling channel, and a hybrid dual-recycling channel. It is found that the dual-recycling channel always outperforms its single-channel counterparts from the recyclable dealer’s and the system’s perspectives. Li et al. (2019) investigate the recovery performance of a mixed offline and online recycling channel structure with stochastic demand for remanufactured products in a two-echelon closed-loop supply chain [15]. They find that a mixed recycling channel system could benefit the remanufactures but hurt the recycler. Huang et al. (2017) consider dual-recycling channel decision in a closed-loop supply chain with cost disruptions, where a manufacturer and a third-party collector collect the used products through an online channel and an offline channel, respectively [16]. They show that the dual-channel structure dominates single-channel structure when there is positive cost disruption for new products. All the above research considers the online and offline channels to be managed by different entities. However, we consider both the offline and online channel to be operated by the same entity (i.e., a recovery platform) and explore the interaction of the online and offline channel and their impact on the recovery platform’s recovery quantity and profits. We also explicitly model the acquisition process by incorporating the offline hassle cost, the reservation value uncertainty of product holders regarding their used products, and the online shipping cost into the models, which are not considered in previous papers.
In addition, this paper is also related to the literature in the relatively new field of omnichannel operations, which is a recent trend across retailing companies and aims to provide a seamless shopping experience to customers through the alignment of the retailers’ multiple sales channels. Harsha et al. (2019) summarizes the new capabilities enabled by omnichannel retail. Moreover, several papers explore the mechanism underlying omnichannel operations from various perspectives [17]. For example, Gao et al. (2017) study how retailers can effectively deliver online and offline information to omnichannel consumers, and consider three information mechanisms, i.e., physical showrooms, virtual showrooms, and the availability of information in an omnichannel retailing environment [18]. Jing (2018) further demonstrates that showrooming could intensify the competition between offline and online retailers [19]. Furthermore, Gao et al. (2017) establish a stylized model to explore the impact of BOPS on store operations while the retailer offers customers the option to buy online and pick up in store (BOPS), and identify the conditions under which BOPS is profitable [20]. Nageswaran et al. (2020) and Jin et al. (2020) both consider retailers’ return policy strategies in omnichannel operations [21,22]. The above research mainly considers omnichannel operations in a forward supply chain; however, our paper contributes to this literature stream by considering omnichannel operations in a reverse supply chain, where an online recovery platform starts to operate in both online and offline channels to collect used products and improve profits. Furthermore, unlike the scenario where a seller decides on whether they should create a new channel in a forward supply chain, our work aims not only to increase profits for recovery platforms, but also to realize higher recovery quantities by implementing a dual-channel strategy. However, our results show that in some cases, a higher recovery quantity would be not necessarily be realized upon introducing a new channel.
Our research contributes to the above three streams of literature in three important ways. First, unlike the previous literature conducted in a qualitative way, we build a game model in a dual-channel reverse supply chain to examine the optimal channel strategy and pricing strategy for online recovery platforms and product holders. Second, we incorporate the offline hassle costs, the reservation value uncertainty of the product holders, and the online shipping costs into the models to analyze the strategic game between the online recovery platforms and product holders. Third, unlike the previous literature, which focuses on profit maximization, our work focuses on both profit for the recovery platform and recovery quantity upon implementing the dual-channel strategy.
3. Model
3.1. Problem Description and Basic Assumptions
We consider an online recovery platform that collects used products from customers through the internet, i.e., the online channel, and construct a model based on information asymmetry theory and transaction cost economics theory. Examples of such online recovery platforms include Gazelle in the USA, O2recycle in the UK, Aihuishou in China, etc. Moreover, as there exists information asymmetry regarding the value of customers’ used products, hassle costs for recovery platform, and information asymmetry regarding the recovery prices of used products for the customer, the online recovery platform utilizes both online and offline channels to collect used products from customers to attract more customers and improve profits, that is, it adopts a dual-channel strategy. In addition, we also consider a case wherein the recovery platform collects used products through a single offline channel, to make our analysis more complete. Such a single offline channel may present a reverse logistic channel for a traditional recycler, in practice. In summary, we consider three different recovery channel models in our study, i.e., the single offline channel model, the single online channel model, and the dual-channel model. Under these three channel structures, their exists shipping costs in the online channel and hassle costs in the offline channel; these are associated with transaction cost economics theory and might greatly influence the recovery action and the profits of the recovery platform. Each of these channel models is illustrated in Figure 1.
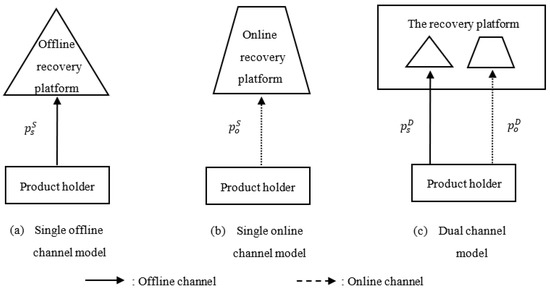
Figure 1.
Three kinds of recovery model.
We next describe the acquisition process and the decisions made by the recovery platform and the used product holders for each channel structure. In brief, our model involves a game between the product holder and recovery platform, where the recovery platform determines the recovery prices of the used product for each of its recovery channels, and the product holders choose between turning in their used products through online or offline channels (if both channels are available), or keeping the product instead. More specifically, when the recovery platform collects the used products through the single offline channel, the product holder visits a physical store and turns in their used products. They incurs a hassle cost . We consider a heterogenous used product holder population in which may differ across used product holders [23,24]. Specifically, for tractability, we assume that is uniformly distributed in , where is the upper bound of the product holder’s hassle cost in our analytical model. Afterwards, we use a more general distribution of hassle cost in the numerical study. The recovery platform decides on the offline channel recovery price .
For the single online channel model, the used product is required to be mailed to a designated site, or the used product is recovered via a door-to-door service by the recovery platform. The recovery platform incurs a cost per-unit shipping , which is exogenously determined by an outside express market. The used product holder also incurs a hassle cost . However, as the shipping cost is undertaken by the recovery platform when the used product holders turn in their used product directly online, this online hassle cost is much smaller than the offline hassle cost . Therefore, without loss of generality, we normalize to zero, hereafter. Moreover, the recovery platform determines the online channel recovery price .
Finally, when the recovery platform utilizes both online and offline channels to collect the used products, the product holder chooses between the online channel and offline channel to turn in their used products, given the anticipation of the recovery platform’s online and offline channel price and , the associated costs of each channel, etc.
Specifically, we consider the acquisition process of an individual used product holder to submit a single used product to the recovery platform in our model. As the whole operation of product return can be seen as a collection of such independent acquisition processes, this allows us to focus on the return of a single used product to derive our main insights.
We assume that a single used product is associated with an intrinsic value , which is determined by the features of the product itself, such as the brand, quality, etc. Practically, the product holders may be heterogeneous with respect to the reservation value of the same used product. For example, each product holder may evaluate the used product using different criteria, such as the service condition, the degree of care, special meaning, knowledge of production cost, the state of the second-hand market, etc. Therefore, we assume that is randomly deviated from the product’s intrinsic value and follows distribution and density . In particular, to obtain the results of tractability, we assume that is uniformly distributed in , where is assumed to guarantee a positive reservation value. Moreover, the reservation value represents the product holder’s private information, but its distribution is common knowledge.
The recovery platform resells the acquired used product on the second-hand market. As in Hahler and Fleischmann (2017), we assume that the recovery platform is a price taker on the resell market [9], i.e., the market price for a specific used product of a certain quality is fixed. Let denote the margin of the resell market price minus the reprocessing and distribution costs, which include the costs for cleaning and data deletion, refurbishing, marketing and shipment, etc. Note that though depends on the actual quality of the submitted product, because we capture the acquisition process of a single product submission but do not explicitly include this dependence in our notation, for ease of exposition.
Similarly to Feng et al. (2017), we make the following specific modeling assumptions to ensure the tractability of our results and their accordance with reality [14].
Assumption 1.
.
Assumption 1 implies that the shipping cost is no higher than the upper bound of hassle cost . Note that the shipping cost is undertaken by the recovery platform in the online channel, and the hassle cost refers to the cost that the product holder incurs for submitting the used product through the offline channel. If the shipping cost is too high, the recovery platform will transfer part of the shipping cost to the product holder by lowering the online channel recovery price, which may cause fewer product holders to submit their used products through the online channel. In extreme cases, it becomes meaningless to acquire used products through the online channel. Thus, Assumption 1 is presented to ensure both offline and online channels are attractive to the product holders, as well as to the recovery platform.
Table 1 summarizes the notations used in our model.

Table 1.
Summary of notations.
3.2. Optimization Problems and Decision Analysis
In this section, we present the analysis and optimal decisions for the three recovery channel models based on game theory. Specifically, we use superscript and to represent the single-channel model and dual-channel model, respectively. Moreover, we use subscript and to denote the offline channel and online channel, respectively. For each model, we study the strategic interaction between the recovery platform and the product holder, and derive the optimal decisions of each entity via backward deduction.
3.2.1. Single Offline Channel Model
In this scenario, the product holder submits their used product only through the offline channel. Specifically, they incur a hassle cost (e.g., searching for and traveling to the store). Their net utility is . The product holder will recover the used product if, and only if, . Otherwise, they would keep it. We first characterize the recovery quantity under the single offline channel using utility theory. Therefore, the total recovery quantity in the single offline channel model is:
According to (1), the recovery platform’s profit with the single offline channel is:
Note that is concave in . In (2) above, the recovery platform maximizes its profit by optimally determining the recovery price . By applying the first-order condition (FOC) with respect to in (2), we obtain the optimal price in the single offline channel model as follows:
Correspondingly, by substituting into (1) and (2), the optimal recovery quantity and profit for the single offline channel model are obtained as follows, respectively.
3.2.2. Single Online Channel Model
When the single online recovery channel is provided, the product holder can only submit their used product through the online channel. Specifically, they mail the used product to a designated site or make an order on the website, and wait for the staff to pick up it. Recall that we normalize the product holder’s online hassle cost to zero. Therefore, the utility of the product holder in this scenario is given by . The product holder would be able to to participate in recovery if, and only if, . Otherwise, the product holder would keep the used product. The expression of the recovery quantity under the single online channel model is as follows:
Based on the recovery quantity expressed in (6), we write the recovery platform’s problem as follows:
Likewise, is concave in . Thus, we apply FOC with respect to in (7) and obtain the optimal price in the single online channel model
Correspondingly, by substituting into (6) and (7), the optimal recovery quantity and profit in the case of the single online channel are:
Upon comparing the results of two single-channel structures, we find that the recovery platform makes more profit under single online channel recovery when the shipping cost is smaller than the average hassle cost, i.e., . With a relatively low shipping cost , the product holder would benefit more from online recovery compared to the single offline channel model. Therefore, the recovery quantity and corresponding profit with the single online channel structure could both be higher in this case.
Furthermore, it is easy to determine the impacts of different parameters on the recovery platform’s decisions and their corresponding profits under the two single-channel models, using Equations (3)–(5) and (8)–(10). Under the single offline channel model, a higher hassle cost for product holders would result in an increase in recovery price but the degradation of recovery performance. Similarly, under the single online channel model, the recovery price would decrease with the shipping cost , directly resulting in a decline in recovery quantity and a reduction in profit for the online recovery platform. In addition, value uncertainty would decrease recovery prices, reduce recovery quantities, and harm profits under both the single offline channel and the online channel model. This implies that under value uncertainty circumstances, the recovery platform would lower its recovery prices and obtain a higher profit margin, though they would recover fewer products in this case.
Finally, the recovery price difference under two single-channel recovery models, i.e., , increases with the upper bounds of both the hassle cost and the shipping cost . Under the single offline channel model, when the upper bound of the hassle cost is higher, the number of product holders who are willing to submit their used products is smaller. Thus, the recovery platform has to provide a high recovery price to attract more product holders. Similarly, for the single online channel model, the recovery platform will make the product holder undertake part of the shipping cost through price transferring. Therefore, a higher shipping cost would result in a lower online recovery price.
3.2.3. Dual-Channel Model
In this scenario, the product holder makes a choice between using the offline channel or the online channel, or keeping the product while taking the reservation value and hassle cost into account (See in Figure 2). Specifically, the product holder (i) would recover their used product through the offline channel when and are both satisfied, (ii) would choose the online channel if the conditions and hold, or (iii) would keep the product under other circumstances. Therefore, the recovery quantities of the offline and online channels for the recovery platform and are:
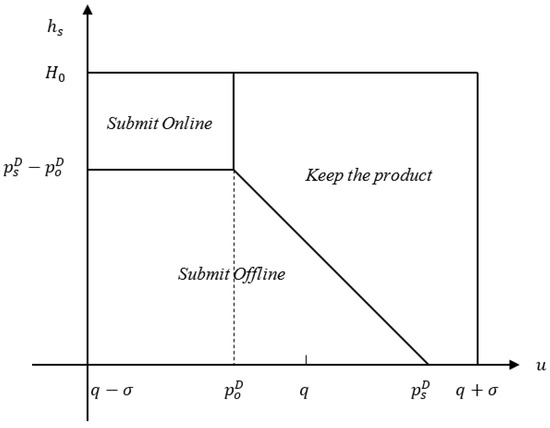
Figure 2.
The product holder’s different choice options under the dual-channel model.
Given the recovery quantities of the offline and online channels in (11) and (12), we formulate the recovery platform’s problem as follows:
Similarly, is concave in and . By applying the FOCs of with respect to and in (13), respectively, we obtain
Though it is challenging to derive the closed form of the optimal offline and online recovery prices and for the recovery platform from (14) and (15), we can simplify the above equations by applying and let . Moreover, by rearranging the corresponding terms, we obtain:
Furthermore, by substituting into (14) and simplifying the terms by letting , we obtain:
Equation (17) reflects the relationship between the optimal offline and online recovery prices differences (i.e., ) for the recovery platform and the model parameters under the dual-channel model. To make our results consistent with reality, similarly to Matsui (2023), we further present the following assumption [25].
Assumption 2.
.
Assumption 2 shows that the recovery price difference should be no higher than the upper bound of the hassle cost. If the highest hassle cost that the product holder undertakes is even lower than the recovery price difference , the product holder would never choose the online channel to submit their used products, and the dual-channel model would degenerate into the a single offline channel model.
Next, by substituting (16) into (11) and (12) and combining this with , we obtain:
Notice that both the offline and online recovery quantities should be non-negative. Therefore, combined with Assumption 2, we know that must be satisfied. In other words, the rational value of should range from 0 to , where .
Though it is difficult to derive the closed form of from the solution to the non-linear maximum function of Equation (20), and there may be multiple roots that satisfy Equation (17). We find that there is a unique solution that is feasible and optimal for our dual-channel model. Specifically, this result is shown in Proposition 1.
Proposition 1.
There is a unique feasible solution
to the profit maximization problem for the recovery platform’s dual-channel model. More specifically,
is the first positive root of Equation (17).
Proof.
See Appendix A for details of the proof of Proposition 1. □
Proposition 1 implies that there is a unique feasible solution to the optimal pricing problem for the recovery platform with a dual-channel structure. When the price difference is equal to , the recovery platform could realize profit maximization. In addition, because and , we further infer that is within the range of from Equation (17).
Proposition 2.
The recovery platform’s optimal recovery prices, recovery quantities for the offline and online channels, and profit under the dual-channel model are shown in Equations (21)–(25), respectively.
Finally, we summarize the recovery platform’s optimal decisions and corresponding profits under the three kinds of channel model in Table 2.

Table 2.
The optimal decisions and corresponding profits of the recovery platform under the three kinds of channel model.
4. Comparative Static Analyses
In this section, we first compare the optimal recovery prices, quantities, and profits under three different channel models to derive the main insights of our research.
Proposition 3.
The recovery prices of the offline channel and online channel under the dual-channel model are both lower than those of any single-channel model, i.e., and Moreover, the total recovery quantity under the dual-channel model is higher than that under the single online channel model, However, when the shipping cost is high, the total recovery quantity under the dual-channel model is less than that under the single offline channel model, i.e., when , .
Proof.
See Appendix A for details of the proof of Proposition 3. □
Proposition 3 implies that the recovery platform would lower both his offline and online recovery prices after introducing the dual-channel model. Moreover, compared to the single online channel model, the recovery platform would recover more used products under the dual-channel model. This may explain the recent phenomenon whereby typical online recovery platforms, such as Aihuishou, construct offline channels to recover used products. However, as the last part of Proposition 3 shows, with respect to the recovery quantity, the dual-channel model outperforms the single offline channel model only when the shipping cost is relatively smaller than the average offline hassle cost. Otherwise, the single offline channel is better. Nevertheless, as we will show in the numerical studies presented in the next section, this condition is easily satisfied in practice, as the recovery platform commonly employs a third-party express service, which is characterized by large-scale economy and high efficiency. Therefore, the recovery platform will commonly recover more used products when it adopts the dual-channel model.
Next, we explore whether the dual-channel strategy would increase the recovery platform’s profit compared to the two single-channel models.
Proposition 4.
The recovery platform’s optimal profit realized using the dual-channel model is higher than that using both the single online channel model and single offline channel model, i.e., , .
Proof.
See Appendix A for details of the proof of Proposition 4. □
Proposition 4 implies that adopting a dual-channel strategy improves the recovery platform’s profits compared to any single online channel or single offline channel model. Proposition 4 shows that the recovery platform would lower its recovery prices for each channel, and can simultaneously achieve a higher recovery quantity most of the time. As a result, the recovery platform can achieve a higher profit under the dual-channel model. However, note that in our model, we do not explicitly consider the fixed costs of establishing an offline (online) channel, and the profit improvement can be seen as the maximum acceptable cost of establishing a new offline (online) channel for the recovery platform.
Next, we perform comparative static analyses to study the impacts of different parameters on the recovery platform’s decisions and corresponding profits under the dual-channel model. First, we explore how the parameters affect the recovery platform’s offline and online channel recovery price differences.
Proposition 5.
The optimal recovery price difference
increases with the shipping cost and the product holder’s reservation value uncertainty associated with their used products, i.e., and , and decreases with the upper bound of the hassle cost , i.e., .
Proof.
See Appendix A for details of the proof of Proposition 5. □
Proposition 5 indicates that the higher shipping cost, greater value uncertainty, or a lower upper bound of the hassle cost would spur the recovery platform to increase its recovery price difference under the dual-channel model. When the shipping cost increases, the recovery platform would decrease its online channel recovery price, resulting in a larger recovery price difference. Moreover, as increases, the recovery platform would increase its online channel recovery price, but its offline channel recovery price may increase or decrease at a slower pace (see details in Proposition 6). Therefore, the recovery price difference between the two channels decreases with . However, notice that only represents the upper bound of the hassle cost. We will explicitly analyze the impacts of the average hassle cost and the variation in the recovery price difference numerically to derive more insights in the next section. In addition, while the value uncertainty of the product holder is relatively high, the recovery platform also inclines to differentiate the online channel and offline channel by setting a higher price gap between the two channels. Therefore, in this way, the recovery platform can split the product holders based on their product holders’ features and induce them to choose the most appropriate channel.
To explore the monotonicity of the optimal recovery prices with respect to the parameters, we present the following proposition.
Proposition 6.
The optimal recovery price of the online channel decreases with the shipping cost and value uncertainty , i.e., and , and increases with the upper bound of the hassle cost , i.e., . Moreover, the variations in the optimal offline channel recovery price with , , and are both less than those in the online channel recovery price. In other words, , , and .
Proof.
See Appendix A for details of the proof of Proposition 6. □
Proposition 6 reflects how the parameters in the dual-channel model impact on the recovery platform’s optimal recovery prices. Because the recovery platform has to undertake the shipping cost when product holders turn in their used products online, the optimal recovery price of the online channel decreases with . Moreover, an interesting finding here is that the optimal recovery price of the online channel decreases with the upper bound of the product holders’ offline hassle cost. As the product holders’ offline hassle cost increases, the recovery platform will raise the online recovery price to attract more product holders to submit their products online. Furthermore, we find that the optimal online channel price decreases with the value uncertainty . This implies as the value uncertainty increases, the recovery platform will be more cautious to avoid pricing too high for its online channel (though we also observe that the recovery price may increase in value uncertainty first when we consider that the reservation value follows a normal distribution in our numerical analysis in the next section). However, as we show in Proposition 5, the recovery platform will incline to differentiate its online channel from its offline channel in this case, since the price difference between the online and offline channel increases.
With respect to the offline channel price, though we are uncertain about the monotonicity of the optimal offline recovery prices with respect to the parameters, we find that the magnitude of the variation in the optimal offline recovery prices with the parameters is smaller than that of the online channel prices, or that they even vary in the opposite direction with the parameters. Therefore, the joint effect of variations in the online and offline recovery prices determines the variation in the offline and online channel recovery price difference with the model parameters, as shown in Proposition 5, reflecting the interaction between the recovery platform’s online and offline channels.
We then examine variations in the optimal recovery quantities and profits of the recovery platform with the parameters , , and . The results are shown in Proposition 7 and Proposition 8, respectively.
Proposition 7.
The total recovery quantity decreases with the shipping cost and the upper bound of the hassle cost , i.e., and . Moreover, if , decreases with .
Proof.
See Appendix A for details of the proof of Proposition 7. □
Corollary 1.
If , decreases with .
Proof.
Because , achieves its maximum when . It is easy to derive that if , decreases with . □
Proposition 7 indicates that increases in both the online channel shipping cost and the offline channel hassle cost leads to a decrease the total recovery quantity under the dual-channel model. Moreover, when the margin is slightly higher, the total recovery quantity also decreases with the reservation value uncertainty. Note that the condition in Corollary 1 is easily satisfied in reality. We conclude that the total recovery quantity decreases with in most cases. Note that the optimal recovery quantities under the single online and offline channels both decrease in value uncertainty (See Table 2), which implies that value uncertainty is not beneficial to recovering used products in most cases.
Proposition 8.
The optimal profit decreases with the shipping cost and the upper bound of the offline channel hassle cost , i.e., and . Moreover, if when equals , the optimal profit decreases with within the interval , or else decreases, and then, increases with within the interval .
Proof.
See Appendix A for details of the proof of Proposition 8. □
Proposition 8 indicates that the high shipping cost and the high average offline channel hassle cost both decrease the optimal profit of the recovery platform realized under the dual-channel model. In addition, Proposition 8 shows that generally, the level of value uncertainty also harms the recovery platform’s profit as it becomes larger, or the recovery platform’s profit presents a “U-shape” with the value uncertainty within its reasonable range. That is, when the value uncertainty is high, the recovery platform’s profit may also increase in value uncertainty.
In reality, because the value uncertainty is commonly relatively small, it decreases the recovery quantity and harms the recovery platform’s profit, as shown in Table 2 and Propositions 7 and 8. The typical electronics online recovery platforms, such as Aihuishou, offer upfront quality assessment on their websites to be completed before the acquisition process so that product holders can answer questions to decrease their value uncertainty. In this process, the product holder commonly has to answer several questions about their used product, such as the exact model (memory size, color, etc.), the integrity of functionality, the year of usage, the maintenance state, etc. In this way, the product holder can reduce their used product reservation value uncertainty and the recovery platform can reduce profit loss.
5. Numerical Study
The above discussion is analyzed under the assumption that hassle cost and the valuation of the used product both follow a uniform distribution, which is mathematically easy to handle and enables us to obtain critical insights. In this section, we re-examine whether our results are robust when considering more general distributions numerically. More specifically, we assume that the hassle cost follows a truncated-normal distribution derived from an underlying normal distribution with mean and variance . In addition, the product holder’s reservation value of the used product also follows a truncated normal distribution with mean and variance . and are independent random variables. In the following sections, we first derive the parameter estimations in Section 5.1, and then, conduct explicit numerical analyses in Section 5.2.
5.1. Parameters Estimations
Let us begin with the margin of the used product and the distribution of . In reality, recovery platforms such as Aihuishou commonly sell recovered products to a second-hand sales platform such as JD, Yihaodian, or Xianyu (Zuo et al. 2019 [6]). In fact, there are three common ways to process the recovered products: (1) environmental disassembling for low-quality products; (2) transferring to a cooperative recycler for medium-quality products; and (3) selling in the second-hand market after repair for high-quality products. However, we focus on the selling activities of the recovery platforms in the second-hand market, as these are the main activities of recovery platforms and it provides ease of exposition. We take into account one type of smart phone that is popular in such second-hand markets in China, i.e., the MI 8. On Paipai, one of the major second-hand online platforms in China, the MI 8 has received more than 5800 reviews, and its approval rate is as high as 96%.
We estimate the margin of the used product by selecting a number of sales samples of the MI 8 with the same configuration from Paipai, and then, averaging the selling price. Therefore, we obtain . Moreover, we obtain an estimation of the product holder’s expectation of the reservation value and the variance using Aihuishou’s revaluation system. Specifically, by inputting different features, such as the integrity of screen display, screen appearance, and border backplane, into Aihuishou’s revaluation system, we can obtain the corresponding estimated value of the used products. Then, we use this as an approximation of the product holder’s expectation and the variance of the reservation value of their used product. In this way, we obtain an estimation of and .
Next, we estimate the parameter values of the hassle cost . As the product holders have to travel to a physical store and turn in their used products, the hassle cost commonly consists of two parts: the traffic cost and the timing cost.
We take the Aihuishou stores in Changsha as our main reference for estimating the hassle cost parameter values and . Currently, there are eight offline Aihuishou stores in Changsha, and they are all located in regional shopping centers whose radiation radiuses could be as large as 10 km. Therefore, these stores are far away from each other. We consider three different kinds of transportation mode by which product holders travel to these stores, including walking, public transportation, and taxis. Each mode is chosen by product holders who live within a certain distance of the store. Specifically, we consider three different radiation radiuses around the shopping centers, i.e., 1 km, 3 km, and 10 km. The proportions of product holders available within each radiation radius are assumed to be 65%, 25%, and 10% (data source: https://wiki.mbalib.com/zh-tw/Business_District, accessed on 29 November 2020).
We explicitly estimate the traffic cost for each kind of transportation mode. The results are presented in Table 3. Moreover, we use the per capita hourly wage of Changsha to estimate the timing cost, which is CNY 32 per hour. The time that the product holders spend traveling to the store is estimated to be 10, 10, and 22 min for the three transportation modes, respectively. Moreover, we assume that on average, each product holder spends about 30 min in store. As a result, when the product holder recovers offline, their total timing cost is calculated as the per capita hourly wage multiplied by the total time, which includes the round-trip time on the road and the waiting time in the store.

Table 3.
Estimation of the hassle cost parameters and .
We obtain the total cost for each kind of product holder by adding the traffic cost and the timing cost. Finally, we estimate by calculating the weighted hassle cost, where the weight is the product holder proportion of each radiation radius. In addition, the variance of hassle cost is similarly estimated. We finally obtain and using the above process.
Finally, we use the shipping cost , which is the basic rate for most of the express companies in China.
5.2. Numerical Results
Using the basic parameter values estimated in Section 5.1, we conduct numerical studies to investigate the impacts of various model parameters on the online recovery platform’s optimal decisions and profits under different channel structures.
We start by varying the shipping cost from 8 to 20 and fixing the other parameter values to the basic values selected above. Figure 3a–c show the impact of varying on the recovery platform’s optimal recovery prices, quantities, and profits under three different channel structures. This result confirms Propositions 3 and 4. Furthermore, we observe that the reduction in is greater than that in as increases. In addition, the offline channel recovery price under the dual-channel model increases with in Figure 3a. As under the dual-channel structure, in order to offset the negative effect of increasing shipping costs, the recovery platform can increase its offline recovery price and decrease its online recovery price to attract more customers to submit their used products through the offline channel to increase its profits. Therefore, the recovery price difference between the offline channel and the online channel is higher as increases under the dual-channel model, which is consistent with Propositions 5. We also find from Figure 3b that both and decrease with , and nearly at the same pace, though the reduction in is indeed slightly faster than that in . Additionally, as we can clearly see from Figure 3c, the profit decline under the dual-channel model is more significant than that under the single online channel model, which implies that the advantage of the dual-channel structure for the recovery platform is weakened in . As shipping cost only influences the performance of the online channel, the increase in shipping cost can have a negative effect on both the dual-channel model and the single online channel model. The recovery platform needs to control its shipping cost within a reasonable interval to improve its performance and profits.
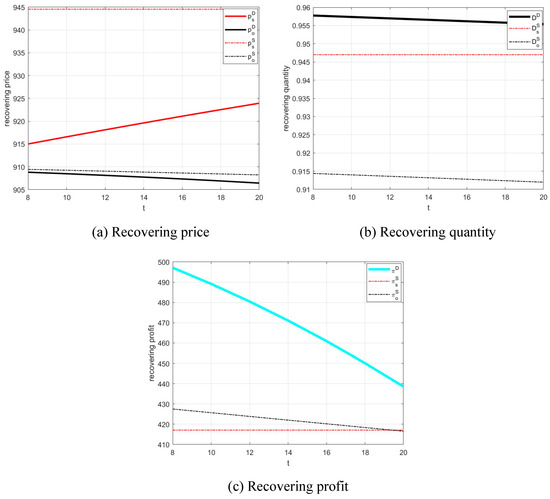
Figure 3.
The impacts of shipping cost on the recovery platform’s optimal decisions and profits under different recovery channel structures.
We next vary the average hassle cost within [30, 50] and fix the other parameter values. Figure 4 presents how the average hassle cost affects the recovery platforms’ optimal decisions and profit. Note that the recovery performance under the single online channel model is unaffected by the hassle cost parameters and . We find that the dual-channel model still outperforms the single-channel models for different average hassle cost, as both the total recovery quantity and the profit are higher under the dual-channel model. Moreover, as we can see in Figure 4a, , , and all increase with , which confirms Proposition 3. However, the increases in and are both slower than that in , which is consistent with Proposition 6. This implies that the recovery prices under the dual-channel model are less sensitive to changes in the average hassle cost relative to the single offline channel recovery price. As under dual-channel structure, the recovery platform can use the online channel to attract more product holders, and does not need to raise the prices for each channel as much as it would under the single offline channel. In addition, we also find from Figure 4a that increases more slowly than , resulting in a larger price difference between the online and offline channels as the average hassle cost increases. Because a hassle cost is incurred only when product holders submit their used products offline, the recovery price of the offline channel is more sensitive relative to the online channel when the average hassle cost changes. From Figure 4b,c, we find that the decreases with the recovery quantity and profit under the dual-channel model are less significant than those under the single offline channel model (i.e., and ), which confirms Propositions 7 and 8. This result illustrates that the benefit of the dual-channel structure for the recovery platform increases with the average hassle cost. When is high, product holders are less inclined to submit their used products offline, which leads to low recovery quantity and profit for the single offline channel model. However, under the dual-channel model, the recovery platform provides an alternative channel for product holders to submit their used products, which prevents profit loss to a greater extent than the single offline channel model. Therefore, the recovery platform should adopt a dual-channel structure to reduce the negative effects of reduced recovery quantity and recovery profit brought by hassle cost.
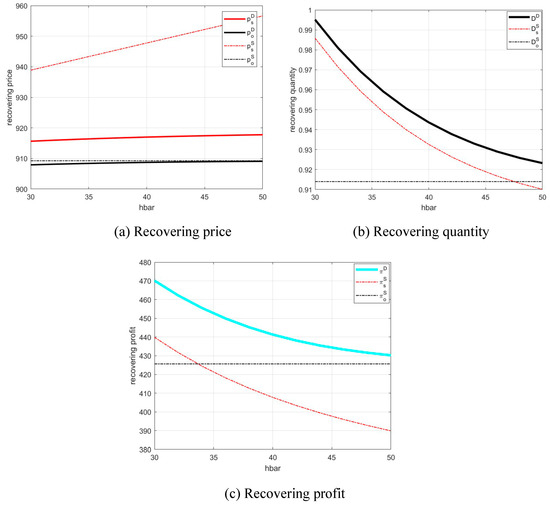
Figure 4.
The impact of the average hassle cost on the recovery platform’s optimal decisions and profits under different recovery channel structures.
To observe the effect of hassle cost uncertainty among product holders on the recovery platform’s optimal decisions and profits under the three recovery channel models, we vary the standard deviation of the hassle cost . Figure 5 presents variation in the recovery prices, quantities, and profits for the recovery platform with hassle cost uncertainty under the three models. As shown in Figure 5, the dual-channel model also outperforms the single-channel models with regard to the recovery quantity and profits, which confirms Propositions 3 and 4. Moreover, in Figure 5a, we observe that slightly increases with , whereas and both decrease with . The reason is that hassle cost only occurs in the offline channel, and when the recovery platform only uses the offline channel, they need to increase the recovery price to compensate customers’ increasing hassle costs. When the recovery platform uses the dual-channel structure, they can split the product holders based on their products’ features and induce them to choose the most appropriate channel. In addition, decreases faster than , resulting in a smaller price difference between the online and offline channels as the hassle cost uncertainty increases. This shows that under the dual-channel model, the optimal offline channel price is also more sensitive to hassle cost uncertainty than that of the online channel because the hassle cost is only incurred offline. As we can see in Figure 5b,c, the recovery quantities and and the profits and all increase with , implying that the recovery platform could benefit more from greater variance in the hassle cost among product holders under the dual-channel model and the single offline channel model. In addition, Figure 5c shows that the recovery platform can gain more profit by adopting the dual-channel structure with increasing relative to the single offline channel model; this implies that the recovery platform should adopt the dual-channel structure when the variance in hassle cost for product holders is much larger.
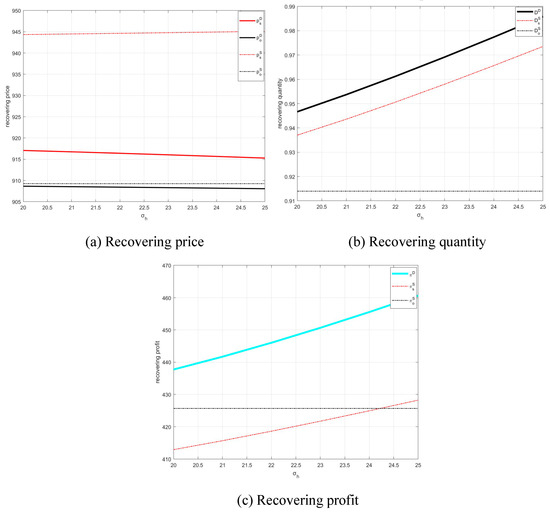
Figure 5.
The impact of hassle cost uncertainty on the recovery platform’s optimal decisions and profit under different recovery channel structures.
To showcase how value uncertainty affects recovery performance, we vary the standard deviation of valuation and fix the other parameters. Figure 6 presents the variation in the recovery platform’s optimal decisions and profit with the product holders’ reservation value uncertainty under the three kinds of channel model. Similar to the above analyses and consistent with Proposition 3 and 4, Figure 6 also shows that the performance of the dual-channel model dominates that of any single-channel model.
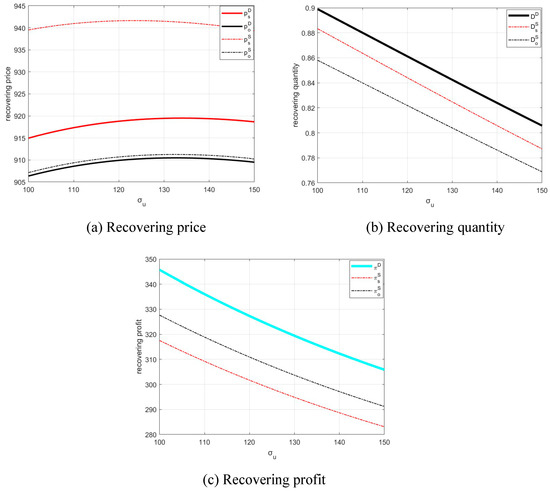
Figure 6.
The impact of value uncertainty on the recovery platform’s optimal decisions and profits under different recovery channel structures.
Moreover, as we can see from Figure 6b,c, the recovery platform will undergo a loss in recovery quantities and profits under high value uncertainty in all three kinds of channel structure, which is consistent with our predictions in Propositions 7 and 8. Under the dual-channel structure, the recovery platform can split product holders based on their products’ features to reduce their value uncertainty. Finally, profit improvement under the dual-channel structure is less significant with higher value uncertainty, as we see from Figure 6c. This indicates that when the recovery platform is confronted with high value uncertainty, the recovery platform can use the dual-channel structure to split its customers based on their products’ features and induce them to choose the most appropriate channel. In this way, the recovery platform can make the profit improvement from the dual-channel structure more significant.
6. Conclusions
6.1. Summary
In this paper, we examine the optimal channel strategy and pricing decisions of online recovery platforms, such as Aihuishou, who previously recovered products only through online channels and recently set up an offline channel. By taking several closely related factors into account, including the product holders’ offline hassle costs when they submit their used products offline, the shipping costs undertaken by the recovery platform when the product holders submit their products online, and the reservation values of the product holders’ used products, we establish three recovery channel models, i.e., the single offline channel model, the single online channel model, and the dual-channel model, to investigate the strategic game between the recovery platform and the product holders. The recovery platform sets the recovery price for each channel, and the product holders choose between submitting online or offline, or keeping the product. After deriving the optimal recovery prices for each channel of the three different models, we conduct both comparative static analyses and a numerical study to derive the main insights, which we summarize as follows.
First, we show that after establishing the dual-channel structure, the recovery platform could lower both its online and offline recovery prices, compared to any single-channel structure. Moreover, the dual-channel structure outperforms any single-channel structure in terms of the recovery platform’s profit. However, the recovery quantity of the dual-channel structure may not be higher than that of the single offline channel model when the shipping cost is relatively high. As our starting point is to investigate the effect of adding offline channel to an online recovery platform, our results show that it would improve both the online recovery platform’s recovery quantity and profits, as we expected.
Second, the shipping cost in the online channel and the offline hassle cost are the main impediments to recovery platforms’ ability to improve their recovery quantity and profits. Moreover, product holder’s reservation value uncertainty regarding their used products is also harmful to the recovery platform’s recovery quantity and profits. Therefore, in practice, the recovery platform builds long-term relationships with large express companies and recommends the nearest offline store to product holders to mitigate the negative effects of the shipping cost and offline hassle cost. In addition, a more detailed and accessible pre-valuation system is also built to ease the loss arising from value uncertainty.
Third, compared to the single-channel models, the price difference between the online and offline channels under the dual-channel structure can be used by the recovery platform as a tool to split product holders based on their products’ features and induce them to choose the most appropriate channel. As a result, we can see that the price difference increases with the shipping cost, the average offline hassle cost, and value uncertainty. However, it decreases with hassle cost uncertainty. Because a hassle cost is incurred only offline, the offline channel prices are more sensitive relative to those of the online channel. Overall, given the cost structure of recovery channels, recovery platforms could take advantage of the interplay between channels to formulate corresponding pricing strategies and maximize their profits.
Finally, we find the conditions under which profit improvement under the dual-channel model is higher, relative to any single-channel model. Specifically, when the shipping cost is small, either the hassle cost or the hassle cost uncertainty is high, or the value uncertainty is low, and the profit improvement brought about by introducing the dual-channel structure is enhanced. Therefore, the recovery platform should use the dual-channel structure in these cases.
6.2. Managerial Implications
There are many important management implications of our results. First, the recovery platform can adjust its recovery price based on shipping cost and hassle cost. When there exists increasing shipping costs, the recovery platform can adopt the dual-channel structure and decrease its online recovery price to induce customers to submit their products offline. Second, the recovery platform can earn more profits using the single offline channel and dual-channel structure with greater variance in hassle costs among product holders. Third, the recovery platform should use the dual-channel structure to offset the negative influence brought about by value uncertainty, as adding the offline channel can help to decrease customers’ value uncertainty. Moreover, under the dual-channel structure, the recovery platform can split product holders based on their products’ features and induce them to choose the most appropriate channel. Therefore, the recovery platform should increase its offline channel and adapt a dual-channel structure to increase its profits.
In practice, in order to increase its recovery quantity and profits, the recovery platform needs to take several actions. First, the recovery platform should reach an agreement with express companies that includes the shipping cost. In the meantime, the recovery platform needs to reasonably set up its offline store to reduce the influence brought by offline hassle cost. In addition, a pre-valuation system can be built by the recovery platform to reduce product holders’ value uncertainty. Taking Aihuishou as an example, the platform has signed agreements with JD Logistics, China Post, and SF Express to reduce shipping costs. In addition, the platform has developed a pre-valuation system that collects basic information on products, and then, prices the product to reduce the influence brought about by customers’ value uncertainty. Furthermore, the platform has increased its offline stores to reduce hassle cost, with the number of offline store increasing from 730 in 2020 to 1920 in 2022, and the platform achieved its first annual profit in 2022.
6.3. Future Research Directions
There are a few limitations to this study, as well as future research directions. One of the limitations is that we only consider one recovery platform without any competition in our model. Considering the competition between different recovery platforms and exploring its impacts on recovery quantity and profits could be a potential future research direction. Moreover, another future research direction could be to explore how to solve two-sided information asymmetry problems between recovery platforms and product holders, as online recovery platforms cannot observe the value of used products until they receive them, and product holders do not know the price setting process when they submit their products online. In addition, as the value of used electric products perishes quickly, the recovery price of used electric products also changes quickly; analyzing the dynamic strategic pricing interplay between platforms and product holders would also be an interesting research topic. We shall address these topics in future research.
Author Contributions
Writing—original draft, W.Z. and X.H.; Writing—review & editing, W.Z. and F.W.; Supervision, F.W.; Funding acquisition, F.W. All authors have read and agreed to the published version of the manuscript.
Funding
The authors gratefully acknowledge the financial support provided by the National Nature Science Foundation of China (Grant No. 71972184).
Data Availability Statement
No new data were created or analyzed in this study. Data sharing is not applicable to this article.
Conflicts of Interest
The authors declare no conflict of interest.
Appendix A
Proof of Proposition 1.
Given the expression of , where and , we take the first and second derivatives of with respect to , respectively, and obtain:
From Equation (A2), we know that the second derivative of decreases with . It is easy to see that , which implies that increases with when and decreases with when . Moreover, is at maximum at . Because , there are two feasible solutions for , which we denote as and , respectively. Without loss of generality, we assume that <. According to the sign of , we can derive the variation in with as follows:
- (1)
- when , , decreases with ;
- (2)
- when , , decreases with ;
- (3)
- when , , decreases with .
Thus, obtains its local maximum at . Moreover, we can easily derive that as we assume that in Assumption 1. In addition, note that ; therefore, should not be larger than , i.e., . As a result, since it is the local maximum value of the function within the interval . There is only one positive root of within the interval , or equivalently, the interval .
By substituting , , , and into , the profit function is reformulated as:
Upon applying the first- and second-order conditions of (3) with respect to , we obtain:
Therefore, the optimal price difference should satisfy , and . From the discussion of the monotonicity of above, should fall into the interval . Notice that there is only one root within the interval , is feasible and unique, and realizes its maximum at . Moreover, it is easy to see that is the first positive root of . □
Proof of Proposition 3.
By comparing the optimal recovery prices under the dual-channel model with that under the single offline channel model and single online channel model, respectively, we obtain:
As we assume that in Assumption 1, and combined with Assumption 2, and , we obtain . Therefore, and are proven.
By comparing the optimal recovery quantities under the dual-channel model with those under the single offline channel model and single online channel model, we obtain:
Combined with the results stating that , it is also easy to see that is satisfied. From Equation (A9), when , i.e., , holds. □
Proof of Proposition 4.
By comparing the optimal profits of the recovery platform under the dual-channel model with those under the two single-channel models, respectively, we obtain:
Based on the result stating that , it is easy to see from Equation (A10) that . Moreover, because is optimal at , and is irrelevant to , . Therefore, is proven. □
Proof of Proposition 5.
According to the implicit function theorem, we obtain:
First, by taking the first-order derivative of with respect to , we obtain:
From Equation (A15), we can see that and . According to the result stating that and the quadratic form of , it is easy to derive that is satisfied. Combined with the result from the proof of Proposition 1 and Equation (A12), we can see that .
Second, combined with , and Equation (A13), it is easy to derive .
Lastly, according to , we can see that . Therefore, . Combined with and Equation (A14), we obtain: . □
Proof of Proposition 6.
By taking the first-order partial derivative of with respect to , , and , respectively, we obtain:
Combined with the results , , and from proposition 5 and the result , it is easy to derive that , , and .
Similarly, by taking the first-order partial derivative of with respect to , , and , respectively, it is easy to see that:
□
Proof of Proposition 7.
First, we analyze the impacts of the shipping cost on the recovery quantities. By taking the first-order partial derivative of with respect to , we obtain:
According to , , and Equation (A12), we can also see that . By calculating . Recall that and . Then, we can see that , which means that . Therefore, combined with the assumption 1 and the result that , we can derive that from Equation (A22).
Then, by taking the first-order derivative of with respect to , we obtain:
Combined with the results and , it is easy to derive that .
Finally, we take the first-order derivative of with respect to , and obtain:
Let and note that ; therefore, . Moreover, . As a result, if and , decreases with . Combined with the result , we can see that decreases with when . □
Proof of Proposition 8.
By taking the first-order derivatives of with respect to and , respectively, we obtain and . According to the positive of and the assumption 2 , . We obtain and .
Moreover, by taking the first-order derivatives of with respect to , we see that . Let ; by taking the first-order derivative of with respect to , we obtain . Therefore, increases with . Note that . Therefore, if , then within the interval , and decreases with ; otherwise, decreases, and then, increases with within the interval . □
References
- Wang, Z.; Zhang, B.; Yin, J.; Zhang, X. Willingness and behavior towards e-waste recycling for residents in Beijing city, China. J. Clean. Prod. 2011, 19, 977–984. [Google Scholar] [CrossRef]
- Yu, J.; Williams, E.; Ju, M. Analysis of material and energy consumption of mobile phones in China. Energy Policy 2010, 38, 4135–4141. [Google Scholar] [CrossRef]
- The Global e-Waste Monitor 2017. Available online: https://bit.ly/2CpNqSE (accessed on 29 November 2019).
- GreenPeace. Awakening the Sleeping Treasure: China Discarded Electronics Recycling Economy Potential Report. Available online: https://www.greenpeace.org.cn/sleeping-treasure-the-recycling-of-mobile-phones-activity/ (accessed on 29 November 2019).
- Julander, A.; Lundgren, L.; Skare, L.; Grandér, M.; Palm, B.; Vahter, M.; Lidén, C. Formal recycling of e-waste leads to increased exposure to toxic metals: An occupational exposure study from Sweden. Environ. Int. 2014, 73, 243–251. [Google Scholar] [CrossRef] [PubMed]
- Zuo, L.S.; Wang, C.; Sun, Q. Sustaining WEEE collection business in China: The case of online to offline (O2O) development strategies. Waste Manag. 2019, 101, 222–230. [Google Scholar] [CrossRef] [PubMed]
- Gu, F.; Zhang, W.J.; Guo, J.F.; Hall, P. Exploring “internet+recycling”: Mass balance and life cycle assessment of a waste management channel associated with a mobile application. Sci. Total Environ. 2019, 649, 172–185. [Google Scholar] [CrossRef]
- Wang, H.D.; Han, H.G.; Liu, T.T.; Tian, X.; Xu, M.; Wu, Y.; Gu, Y.; Liu, Y.; Zuo, T. “Internet +” recyclable resources: A new recycling mode in China. Resour. Conserv. Recycl. 2018, 134, 44–47. [Google Scholar] [CrossRef]
- Hahler, S.; Fleischmann, M. Strategic grading in the product acquisition process of a reverse supply chain. Prod. Oper. Manag. 2017, 26, 1498–1511. [Google Scholar] [CrossRef]
- Hong, X.P.; Wang, Z.J.; Wang, D.Z.; Zhang, H. Decision models of closed-loop supply chain with remanufacturing under hybrid dual-channel collection. Int. J. Adv. Manuf. Technol. 2013, 68, 1851–1865. [Google Scholar] [CrossRef]
- He, Q.D.; Wang, N.M.; Yang, Z.; He, Z.; Jiang, B. Competitive collection under channel inconvenience in closed-loop supply chain. Eur. J. Oper. Res. 2019, 275, 155–166. [Google Scholar] [CrossRef]
- Huang, M.; Song, M.; Lee, L.H.; Ching, W.K. Analysis for strategy of closed-loop supply chain with dual recycling channel. Int. J. Prod. Econ. 2013, 144, 510–520. [Google Scholar] [CrossRef]
- Wang, N.; He, Q.; Jiang, B. Hybrid closed-loop supply chains with competition in recycling and product markets. Int. J. Prod. Econ. 2019, 217, 246–258. [Google Scholar] [CrossRef]
- Feng, L.; Govindan, K.; Li, C. Strategic planning: Design and coordination for dual-recycling channel reverse supply chain considering consumer behavior. Eur. J. Oper. Res. 2017, 260, 601–612. [Google Scholar] [CrossRef]
- Li, C.F.; Feng, L.P.; Luo, S.Y. Strategic introduction of an online recycling channel in the reverse supply chain with a random demand. J. Clean. Prod. 2019, 236, 76–83. [Google Scholar] [CrossRef]
- Huang, Y.T.; Wang, Z.J. Dual-Recycling Channel Decision in a Closed-Loop Supply Chain with Cost Disruptions. Sustainability 2017, 9, 2004. [Google Scholar] [CrossRef]
- Harsha, P.; Subramanian, S.; Uichanco, J. Dynamic Pricing of Omnichannel Inventories. Manuf. Serv. Oper. Manag. 2019, 21, 47–65. [Google Scholar] [CrossRef]
- Gao, F.; Su, X.M. Online and Offline Information for Omnichannel Retailing. Manuf. Serv. Oper. Manag. 2017, 19, 84–98. [Google Scholar] [CrossRef]
- Jing, B. Showrooming and Webrooming: Information Externalities Between Online and Offline Sellers. Mark. Sci. 2018, 37, 469–483. [Google Scholar] [CrossRef]
- Gao, F.; Su, X.M. Omnichannel Retail Operations with Buy-Online-and-Pick-up-in-Store. Manag. Sci. 2017, 63, 2478–2492. [Google Scholar] [CrossRef]
- Nageswaran, L.; Cho, S.H.; Scheller-Wolf, A. Consumer Return Policies in Omnichannel Operations. Manag. Sci. 2020, 66, 5558–5575. [Google Scholar] [CrossRef]
- Jin, D.; Caliskan-Demirag, O.; Chen, F.; Huang, M. Omnichannel retailers’ return policy strategies in the presence of competition. Int. J. Prod. Econ. 2020, 225, 107595. [Google Scholar] [CrossRef]
- Cao, J.; So, K.C.; Yin, S. Impact of an “online-to-store” channel on demand allocation, pricing and profitability. Eur. J. Oper. Res. 2016, 248, 234–245. [Google Scholar] [CrossRef]
- Cao, K.Y.; Wang, J.; Dou, G.W.; Zhang, Q. Optimal trade-in strategy of retailers with online and offline sales channels. Comput. Ind. Eng. 2018, 123, 148–156. [Google Scholar] [CrossRef]
- Matsui, K. Dual-recycling channel reverse supply chain design of recycling platforms under acquisition price competition. Int. J. Prod. Econ. 2023, 259, 108769. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).