PSO-BP-Based Morphology Prediction Method for DED Remanufactured Deposited Layers
Abstract
1. Introduction
- Simulation results differ significantly from experimental results.
- The generalizability of the process conclusions obtained varies depending on the additive manufacturing equipment used.
- The training of neural networks often requires a large amount of experimental work, which can be time-consuming and costly.
- Using neural networks to predict the quality of deposited layers can suffer from slow convergence and the tendency to get stuck in local minima.
2. Methods
2.1. Directed Energy Deposition
2.1.1. Quality Connotation of Directed Energy Deposition
2.1.2. Analysis of Influencing Factors of Deposited Layer Quality
- Effect of the laser power on deposited layer quality
- Effect of the scanning speed on deposited layer quality
- Effect of the powder flow rate on deposited layer quality
2.2. Construction of Directed Energy Deposition Layer Quality Model Based on PSO-BP Neural Network
2.2.1. Construction of PSO-BP Network
- Determine the structure and particle dimensions of the neural network
- Setting of particle swarm algorithm parameters

- Determination of fitness function

- Update the speed and position of particles to generate new populations.
- Update the individual optimal value Pb and global optimal value Gb of the particles, and then proceed to the next step when the maximum iteration times are reached; otherwise, return to the previous step to continue the iteration.
- Map the global optimal value Pg generated in the previous step to the weight and threshold of the BP neural network. Perform network training to further update weights and thresholds until the error meets the accuracy requirements.
- Use test samples to check the accuracy of network prediction.
2.2.2. Deposited Layer Quality Control System
3. Case Study
3.1. Formation of the Deposited Layer
3.2. Experimental Data Acquisition
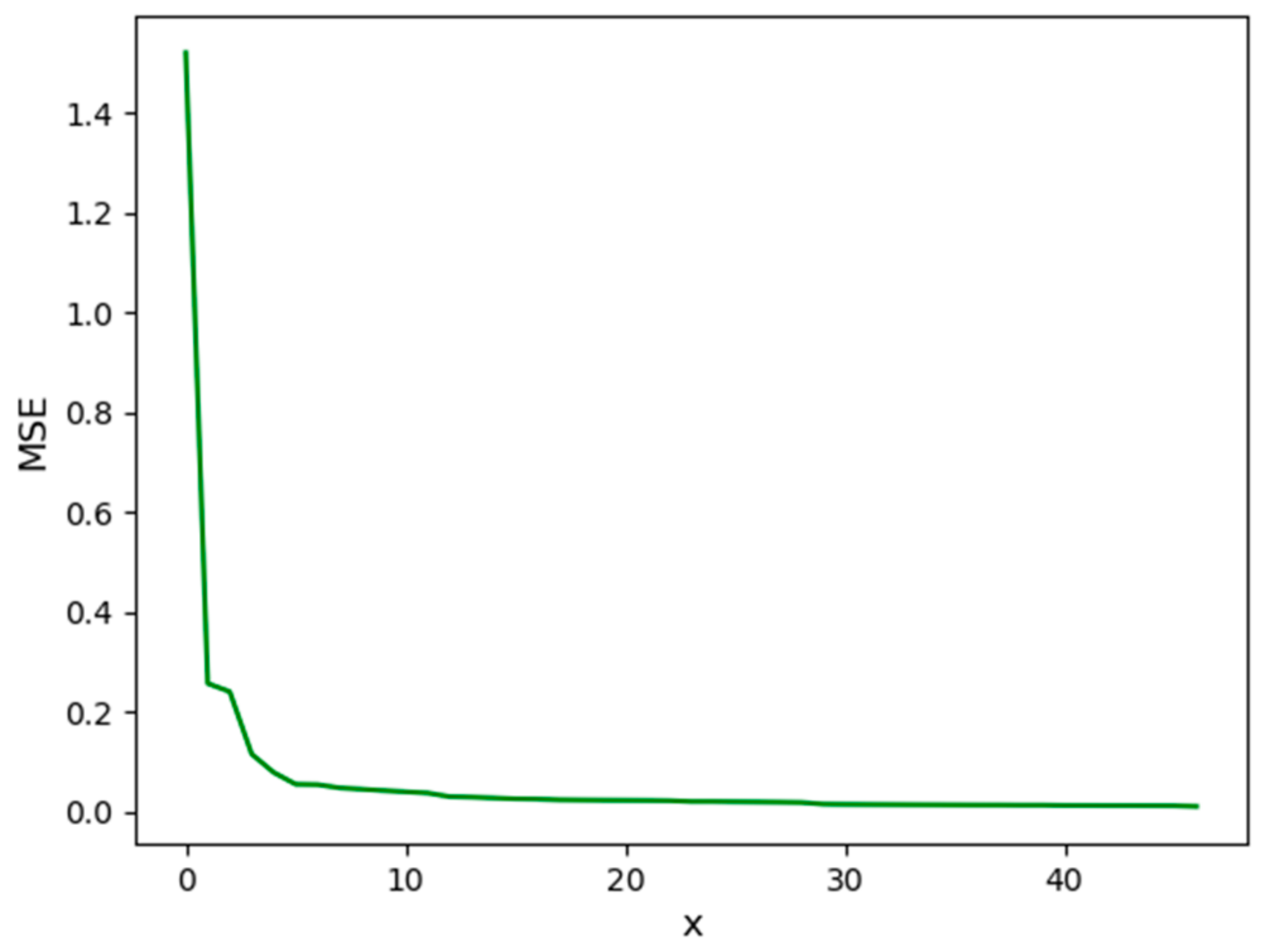
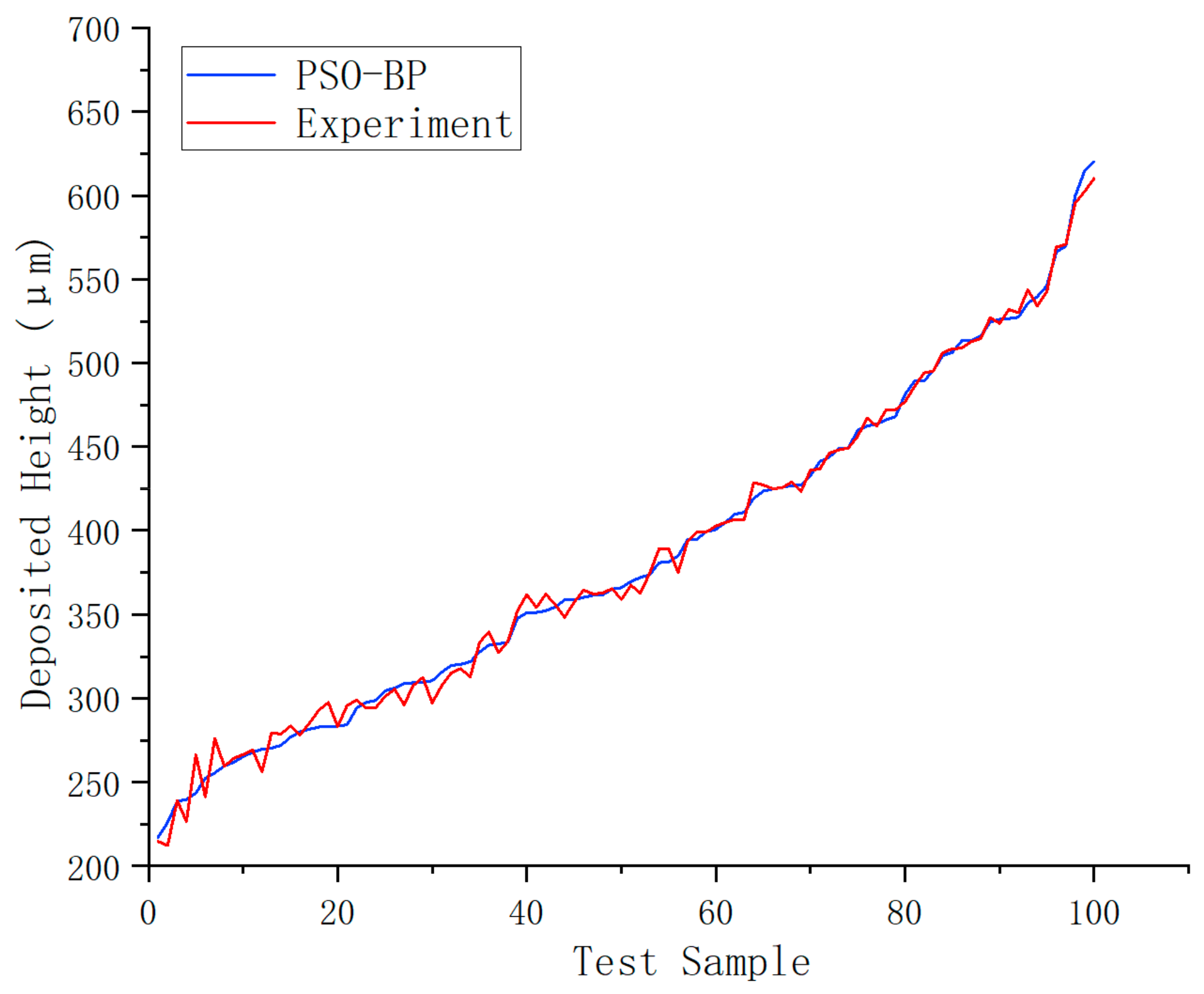
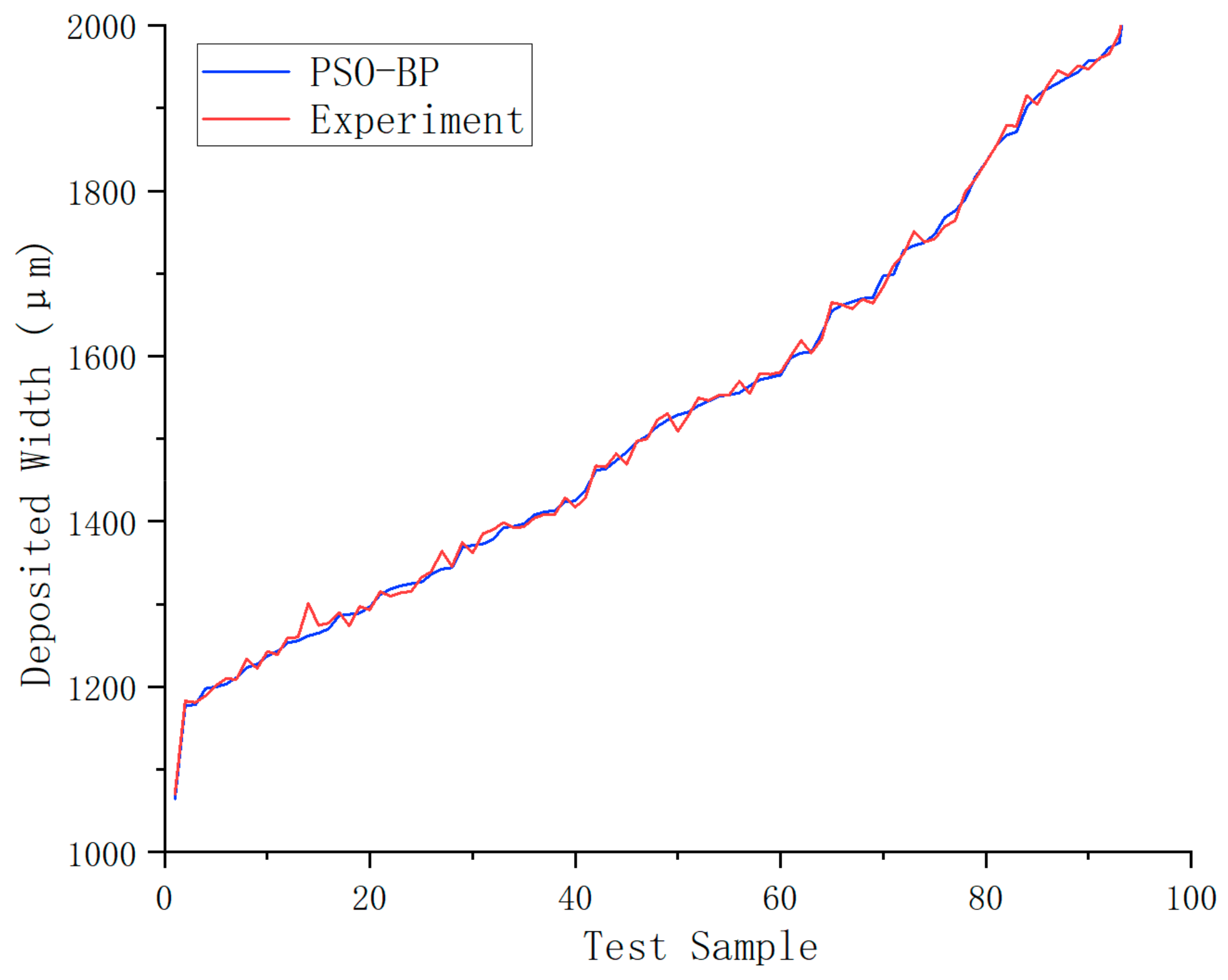
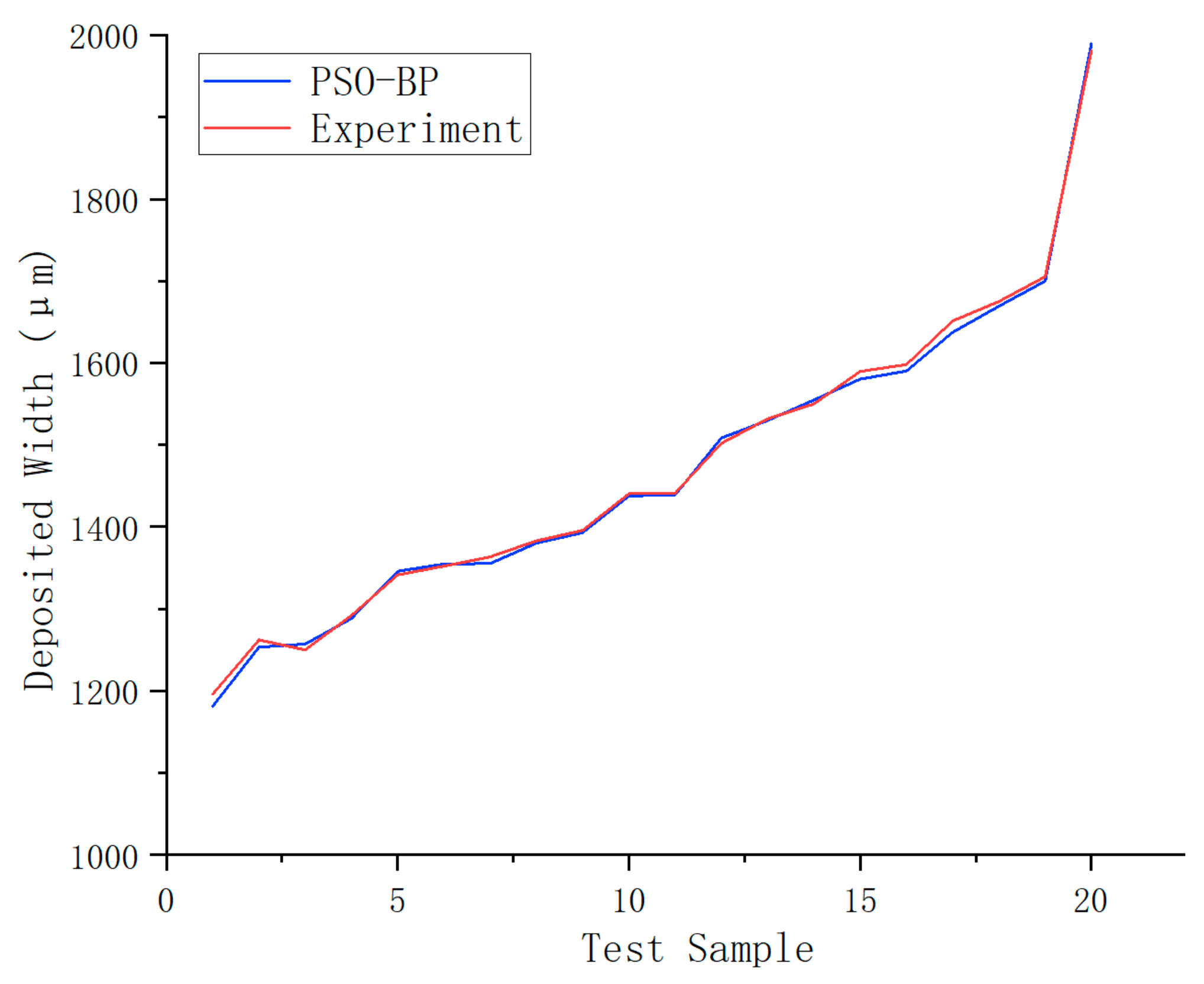
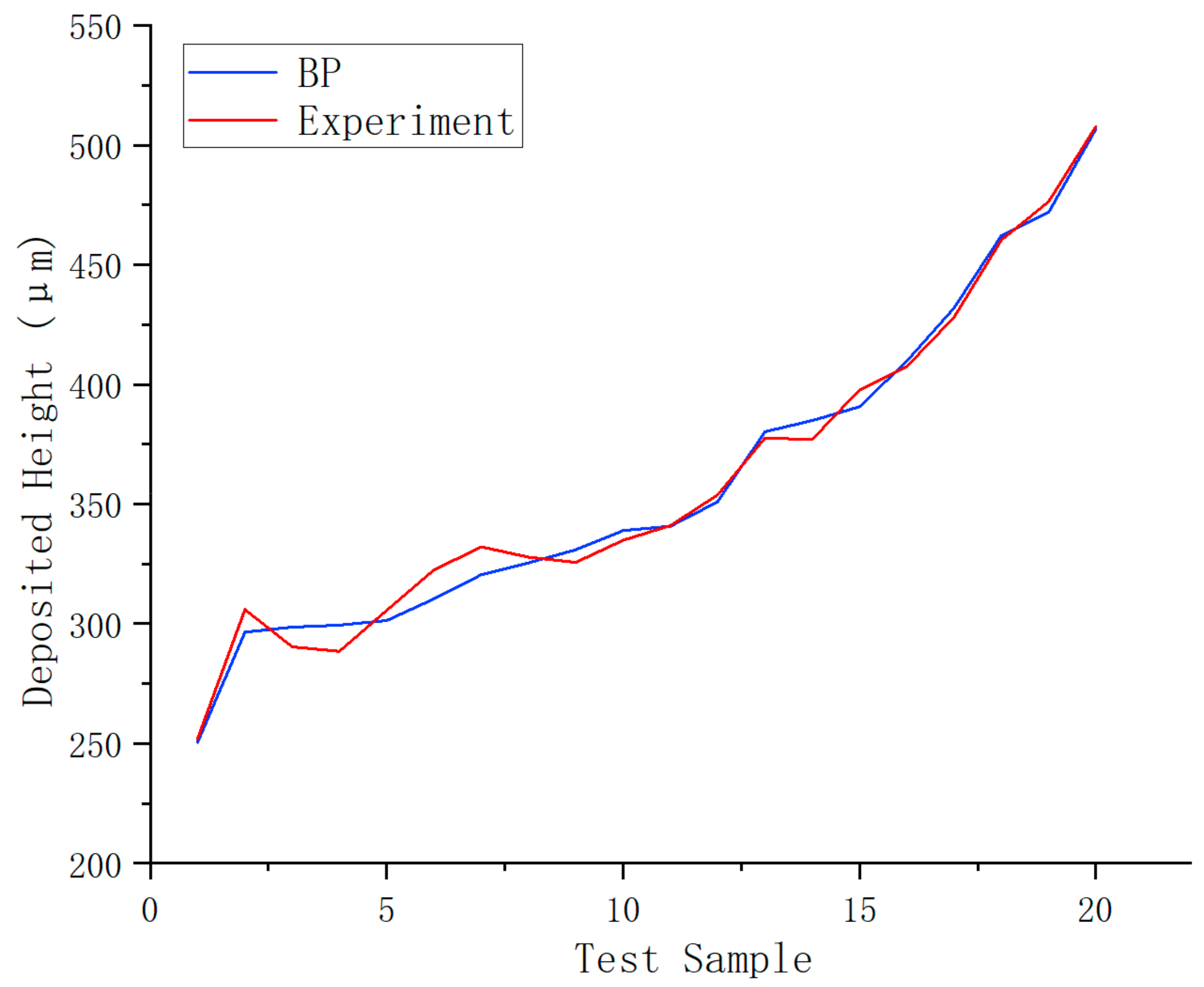
4. Results
5. Discussion
6. Conclusions
- Selecting appropriate neural networks and optimization algorithms can help further improve the prediction accuracy of the model.
- In addition to the morphology of the sediment layer, its mechanical properties, internal defects, and other quality indicators are also important. Neural networks can be further developed to conduct in-depth research in these areas.
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Jiang, X.Y.; Song, B.X.; Li, L.; Dai, M.; Zhang, H. The customer satisfaction-oriented planning method for redesign parameters of used machine tools. Int. J. Prod. Res. 2019, 57, 1146–1160. [Google Scholar] [CrossRef]
- Jiang, X.Y.; Li, J.Z.; Lu, Y.T.; Tian, G. Design of Reverse Logistics Network for Remanufacturing Waste Machine Tools Based on Multi-Objective Gray Wolf Optimization Algorithm. IEEE Access 2020, 8, 141046–141056. [Google Scholar] [CrossRef]
- Zhao, J.X.; Wang, G.; Wang, X.Y.; Luo, H.; Wang, L.; Rong, Y. Multicomponent multiphase modeling of dissimilar laser cladding process with high-speed steel on medium carbon steel. Int. J. Heat Mass Transf. 2020, 148, 118990. [Google Scholar] [CrossRef]
- Li, Z.N.; Chen, C.Z.; He, Q.S. Influence of Cu on microstructure and wear resistance of TiC/TiB/TiN reinforced composite coating fabricated by laser cladding. Mater. Chem. Phys. 2012, 133, 741–745. [Google Scholar] [CrossRef]
- Tanigawa, D.; Funada, Y.; Abe, N.; Tsukamoto, M.; Hayashi, Y.; Yamazaki, H.; Tatsumi, Y.; Yoneyama, M. Suppression of dilution in Ni-Cr-Si-B alloy cladding layer by controlling diode laser beam profile. Opt. Laser Technol. 2018, 99, 326–332. [Google Scholar] [CrossRef]
- Jelvani, S.; Razavi, R.S.; Barekat, M.; Dehnavi, M. Empirical-Statistical Modeling and Prediction of Geometric Characteristics for Laser-Aided Direct Metal Deposition of Inconel 718 Superalloy. Met. Mater. Int. 2020, 5, 668–681. [Google Scholar] [CrossRef]
- Erfanmanesh, M.; Abdollah-Pour, H.; Mohammadian-Semnani, H.; Shoja-Razavi, R. An empirical-statistical model for laser cladding of WC-12Co powder on AISI 321 stainless steel. Opt. Laser Technol. 2017, 97, 180–186. [Google Scholar] [CrossRef]
- Aghili, S.E.; Shamanian, M. Investigation of powder fed laser cladding of NiCr-chromium carbides single-tracks on titanium aluminide substrate. Opt. Laser Technol. 2019, 119, 105652. [Google Scholar] [CrossRef]
- Li, X.B.; Li, T.; Shi, B.W.; Wang, D.; Adnan, M.; Lu, H. The influence of substrate tilt angle on the morphology of laser cladding layer. Surf. Coat. Technol. 2020, 391, 125706. [Google Scholar] [CrossRef]
- Amine, T.; Newkirk, J.W.; Liou, F. Investigation of effect of process parameters on multilayer builds by direct metal deposition. Appl. Therm. Eng. 2014, 73, 500–511. [Google Scholar] [CrossRef]
- Amine, T.; Newkirk, J.W.; Liou, F. Methodology for Studying Effect of Cooling Rate During Laser Deposition on Microstructure. J. Mater. Eng. Perform. 2015, 24, 3129–3136. [Google Scholar] [CrossRef]
- Emamian, A.; Farshidianfar, M.H.; Khajepour, A. Thermal monitoring of microstructure and carbide morphology in direct metal deposition of Fe-Ti-C metal matrix composites. J. Alloy. Compd. 2017, 207, 20–28. [Google Scholar] [CrossRef]
- Palavra, A.; Coelho, B.N.; Hosson, J.T.M.; Lima, M.S.F.; Carvalho, S.M.; Costa, A.R. Laser surface treatment for enhanced titanium to carbon fiber-reinforced polymer adhesion. J. Braz. Soc. Mech. Sci. Eng. 2017, 39, 2917–2924. [Google Scholar] [CrossRef]
- Jaritngam, P.; Tangwarodomnukun, V.; Qi, H.; Dumkum, C. Surface and subsurface characteristics of laser polished Ti6Al4V titanium alloy. Opt. Laser Technol. 2020, 126, 106102. [Google Scholar] [CrossRef]
- Dumkum, C.; Jaritngam, P.; Tangwarodomukun, V. Surface characteristics and machining performance of TiAlN-, TiN- and AlCrN-coated tungsten carbide drills. Proc. Inst. Mech. Eng. Part B J. Eng. Manuf. 2019, 233, 1075–1086. [Google Scholar] [CrossRef]
- Tan, H.; Chen, J.; Zhang, F.Y.; Lin, X.; Huang, W. Process analysis for laser solid forming of thin-wall structure. Int. J. Mach. Tools Manuf. 2010, 39, 376–381. [Google Scholar] [CrossRef]
- Reddy, L.; Preston, S.P.; Shipway, P.H.; Davis, C.; Hussain, T. Process parameter optimisation of laser clad iron based alloy: Predictive models of deposition efficiency, porosity and dilution. Surf. Coat. Technol. 2018, 349, 198–207. [Google Scholar] [CrossRef]
- El Cheikh, H.; Courant, B.; Branchu, S.; Hascoët, J.-Y.; Guillén, R. Analysis and prediction of single laser tracks geometrical characteristics in coaxial laser cladding process. Opt. Laser Eng. 2012, 50, 413–422. [Google Scholar] [CrossRef]
- Wang, X.L.; Deng, D.W.; Hu, Y.B.; Liu, Z.-C. Analytical modeling and experimental investigation of laser clad geometry. Opt. Eng. 2017, 56, 1212–1220. [Google Scholar] [CrossRef]
- Onwubolu, G.C.; Davim, J.P.; Oliveira, C.; Cardoso, A. Prediction of clad angle in laser cladding by power using response surface methodology and scatter search. Opt. Laser Technol. 2011, 39, 1130–1134. [Google Scholar] [CrossRef]
- Marimuthu, S.; Triantaphyllou, A.; Antar, M.; Wimpenny, D.; Morton, H.; Beard, M. Laser polishing of selective laser melted components. Int. J. Mach. Tools Manuf. 2015, 95, 97–104. [Google Scholar] [CrossRef]
- Wang, J.H.; Han, F.Z.; Ying, W.S. Prediction and verification of the single cladding layer thickness for laser solid forming. In Proceedings of the International Conference on Advanced Functional Materials And Composites (Icafmc2018), Barcelona, Spain, 5–7 September 2018; p. 24. [Google Scholar]
- Wang, J.H.; Han, F.Z.; Chen, S.F.; Ying, W.-s. A novel model of laser energy attenuation by powder particles for laser solid forming. Int. J. Mach. Tools Manuf. 2019, 145, 103440. [Google Scholar] [CrossRef]
- Xu, Z.M.; Wu, H.B.; Hong, Z.H. Quality prediction of laser cladding based on evolutionary neural network. Appl. Mech. Mater. 2011, 44–47, 1012–1017. [Google Scholar] [CrossRef]
- Alimardani, M.; Toyserkani, E. Prediction of laser solid freeform fabrication using neuro-fuzzy method. Appl. Soft Comput. 2008, 8, 316–323. [Google Scholar] [CrossRef]
- Varol, T.; Canakci, A.; Ozsahin, S.; Erdemir, F.; Ozkaya, S. Artificial neural network-based prediction technique for coating thickness in Fe-Al coatings fabricated by mechanical milling. Part. Sci. Technol. 2018, 36, 742–750. [Google Scholar] [CrossRef]
- Gao, J.L.; Wang, C.; Hao, Y.B.; Wang, X.; Zhao, K.; Ding, X. Prediction of molten pool temperature and processing quality in laser metal deposition based on back propagation neural network algorithm. Opt. Laser Technol. 2022, 155, 108363. [Google Scholar] [CrossRef]
- Li, H.Y.; Chen, H.; Wu, Y.; Yong, C.; Wei, Y. Prediction of two-dimensional topography of laser cladding based on neural network. Int. J. Mod. Phys. B 2019, 33, 1940034. [Google Scholar]
- Weglowski, M.S.; Blacha, S.; Phillips, A. Electron beam welding—Techniques and trends—Review. Vacuum 2016, 130, 72–79. [Google Scholar] [CrossRef]
- Tian, Y.S.; Chen, C.Z.; Li, S.T.; Huo, Q.H. Research progress on laser surface modification of titanium alloys. Appl. Surf. Sci. 2005, 242, 177–184. [Google Scholar] [CrossRef]
- Liu, H.; Ge, C.; Zhou, W.; Zhou, W. Research progress on crack control of laser clad composite coating. Heat Treat. Met. 2018, 8, 228–232. [Google Scholar]
- Liu, J.L.; Yu, H.J.; Chen, C.Z.; Weng, F.; Dai, J. Research and development status of laser cladding on magnesium alloys: A review. Opt. Lasers Eng. 2017, 93, 195–210. [Google Scholar] [CrossRef]
- Gaumann, M.; Henry, S.; Cleton, F.; Wagnière, J.-D.; Kurz, W. Epitaxial laser metal forming: Analysis of microstructure formation. Mater. Sci. Eng. A-Struct. Mater. Prop. Microstruct. Process. 1999, 271, 232–241. [Google Scholar] [CrossRef]
- Wang, Z.Q.; Palmer, T.A.; Beese, A.M. Effect of processing parameters on microstructure and tensile properties of austenitic stainless steel 304L made by directed energy deposition additive manufacturing. Acta Mater. 2016, 110, 226–235. [Google Scholar] [CrossRef]
- Dai, D.H.; Gu, D.D. Influence of thermodynamics within molten pool on migration and distribution state of reinforcement during selective laser melting of AlN/AlSi 10Mg composites. Int. J. Mach. Tools Manuf. 2016, 100, 14–24. [Google Scholar] [CrossRef]






| C | Cr | Si | Ni | Mn | Fe | |
|---|---|---|---|---|---|---|
| Fe304 | 0.03 | 18.0 | 0.1 | 10 | 0.3 |
| Laser Power (W) | Powder Flow Rate (mm/min) | Scanning Speed (g/min) |
|---|---|---|
| 600 | 240 | 6 |
| 700 | 360 | 8 |
| 800 | 480 | 10 |
| 900 | 600 | 12 |
| 1000 | 720 | 14 |
| Prediction Error | AAE | MSE | VAF | |
|---|---|---|---|---|
| PSO-BP | 1.329% | 6.48 | 67.65 | 99.67% |
| BP | 4.314% | 21.12 | 1116.15 | 92.88% |
| GA-BP | 2.692% | 13.81 | 328.31 | 98.81% |
| GWO-BP | 3.475% | 17.38 | 617.25 | 97.30% |
| CNN | 1.816% | 9.71 | 145.56 | 98.62% |
| RNN | 2.247% | 11.68 | 277.18 | 97.59% |
| Prediction Error | AAE | MSE | VAF | |
|---|---|---|---|---|
| PSO-BP | 0.442% | 8.27 | 99.53 | 99.92% |
| BP | 2.052% | 34.04 | 1489.21 | 97.94% |
| GA-BP | 1.348% | 25.85 | 887.19 | 98.01% |
| GWO-BP | 1.533% | 27.91 | 1098.13 | 98.92% |
| CNN | 0.795% | 15.08 | 350.09 | 99.11% |
| RNN | 0.584% | 9.69 | 263.61 | 99.68% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, Z.; Jiang, X.; Song, B.; Yang, G.; Liu, W.; Liu, T.; Ni, Z.; Zhang, R. PSO-BP-Based Morphology Prediction Method for DED Remanufactured Deposited Layers. Sustainability 2023, 15, 6437. https://doi.org/10.3390/su15086437
Wang Z, Jiang X, Song B, Yang G, Liu W, Liu T, Ni Z, Zhang R. PSO-BP-Based Morphology Prediction Method for DED Remanufactured Deposited Layers. Sustainability. 2023; 15(8):6437. https://doi.org/10.3390/su15086437
Chicago/Turabian StyleWang, Zisheng, Xingyu Jiang, Boxue Song, Guozhe Yang, Weijun Liu, Tongming Liu, Zhijia Ni, and Ren Zhang. 2023. "PSO-BP-Based Morphology Prediction Method for DED Remanufactured Deposited Layers" Sustainability 15, no. 8: 6437. https://doi.org/10.3390/su15086437
APA StyleWang, Z., Jiang, X., Song, B., Yang, G., Liu, W., Liu, T., Ni, Z., & Zhang, R. (2023). PSO-BP-Based Morphology Prediction Method for DED Remanufactured Deposited Layers. Sustainability, 15(8), 6437. https://doi.org/10.3390/su15086437





