Using the Morgenstern–Price Method and Cloud Theory to Invert the Shear Strength Index of Tailings Dams and Reveal the Coupling Deformation and Failure Law under Extreme Rainfall
Abstract
1. Introduction
2. Methodology
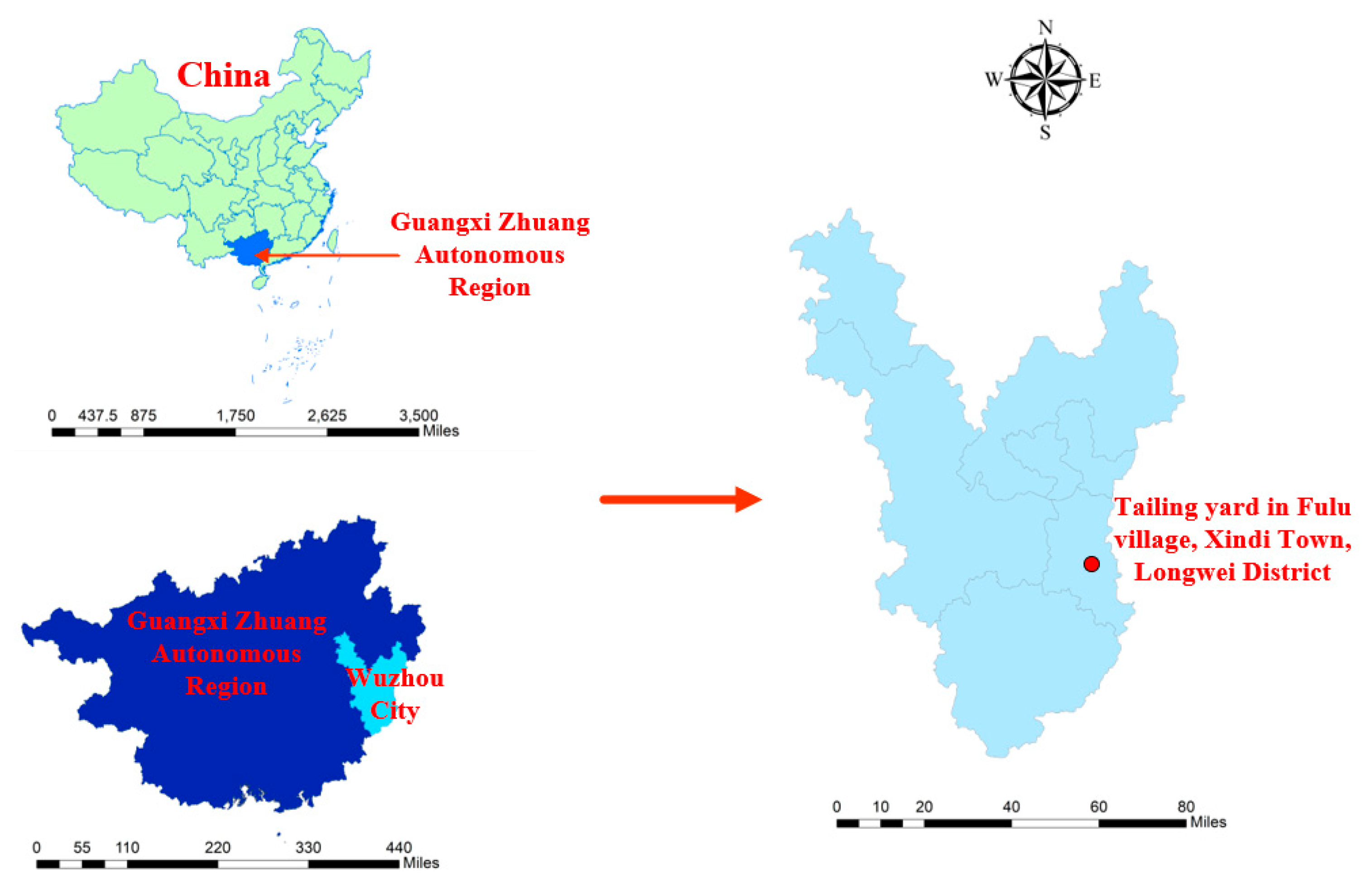
2.1. Engineering Background
2.1.1. Engineering Geological Conditions of the Tailings Stacking Field
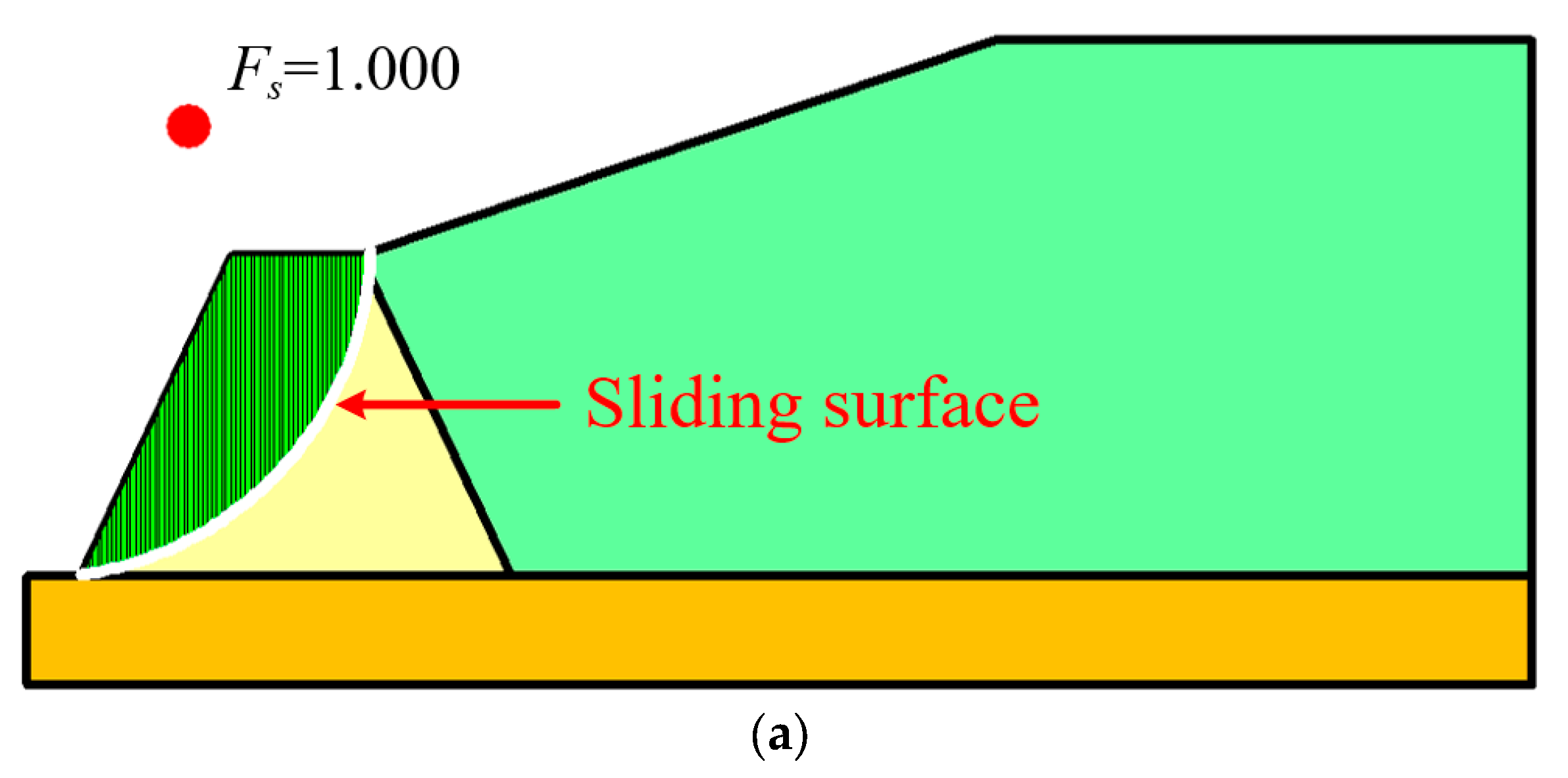
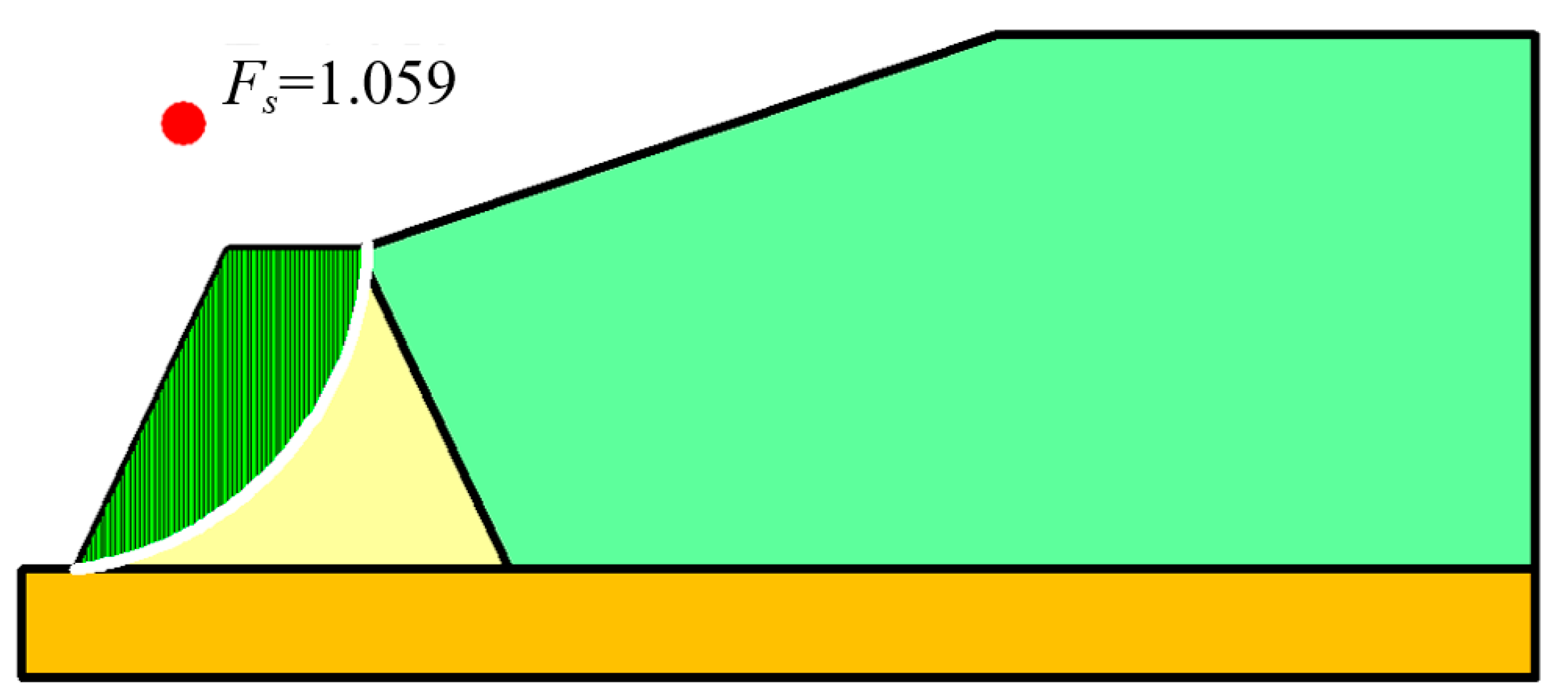
2.1.2. Judgement of the Unstable State of the Tailings Dam
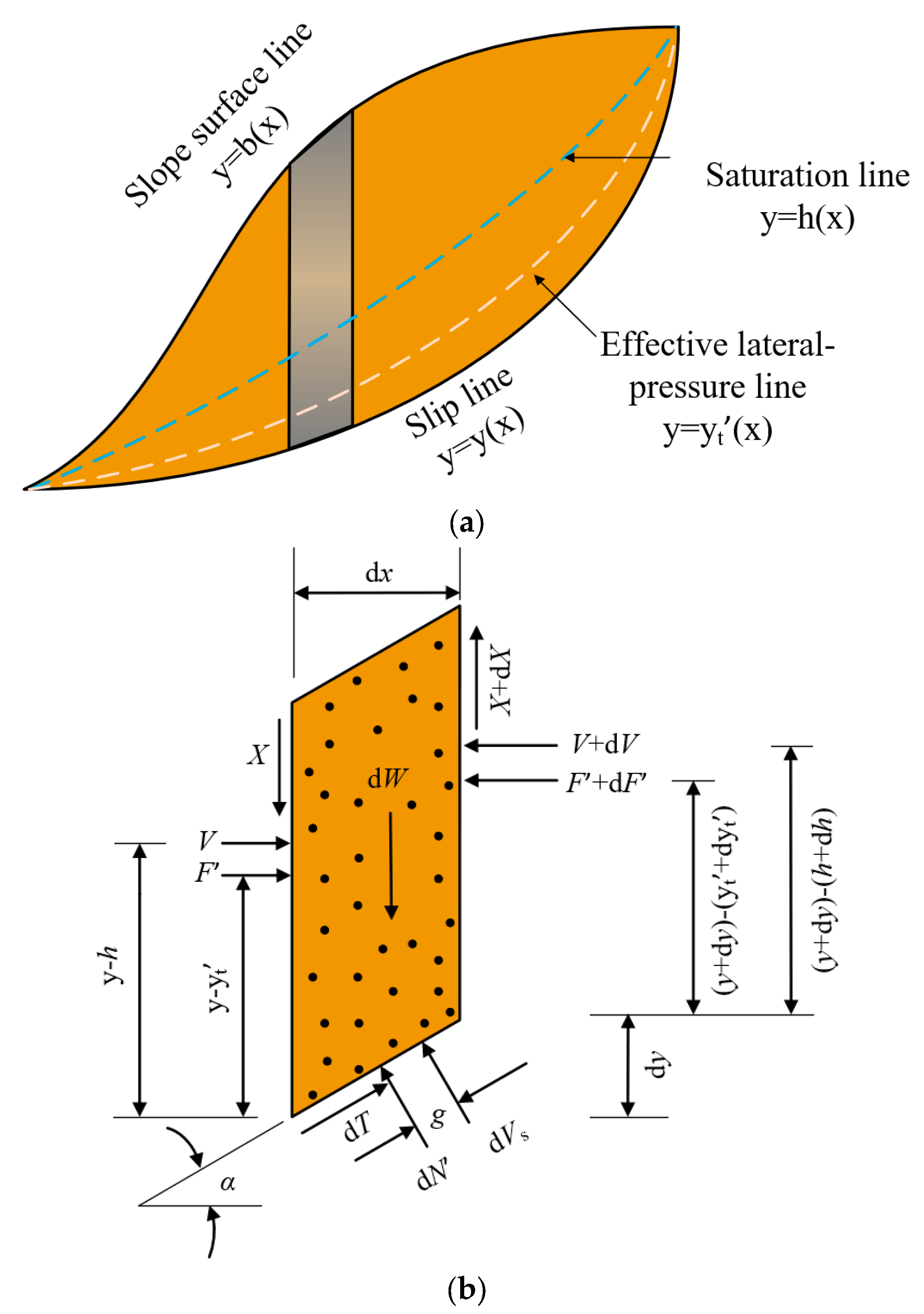
2.2. Morgenstern–Price Method
2.3. Cloud Theory
2.4. Rainfall Conditions
2.5. Theoretical Model Construction
3. Results and Discussion
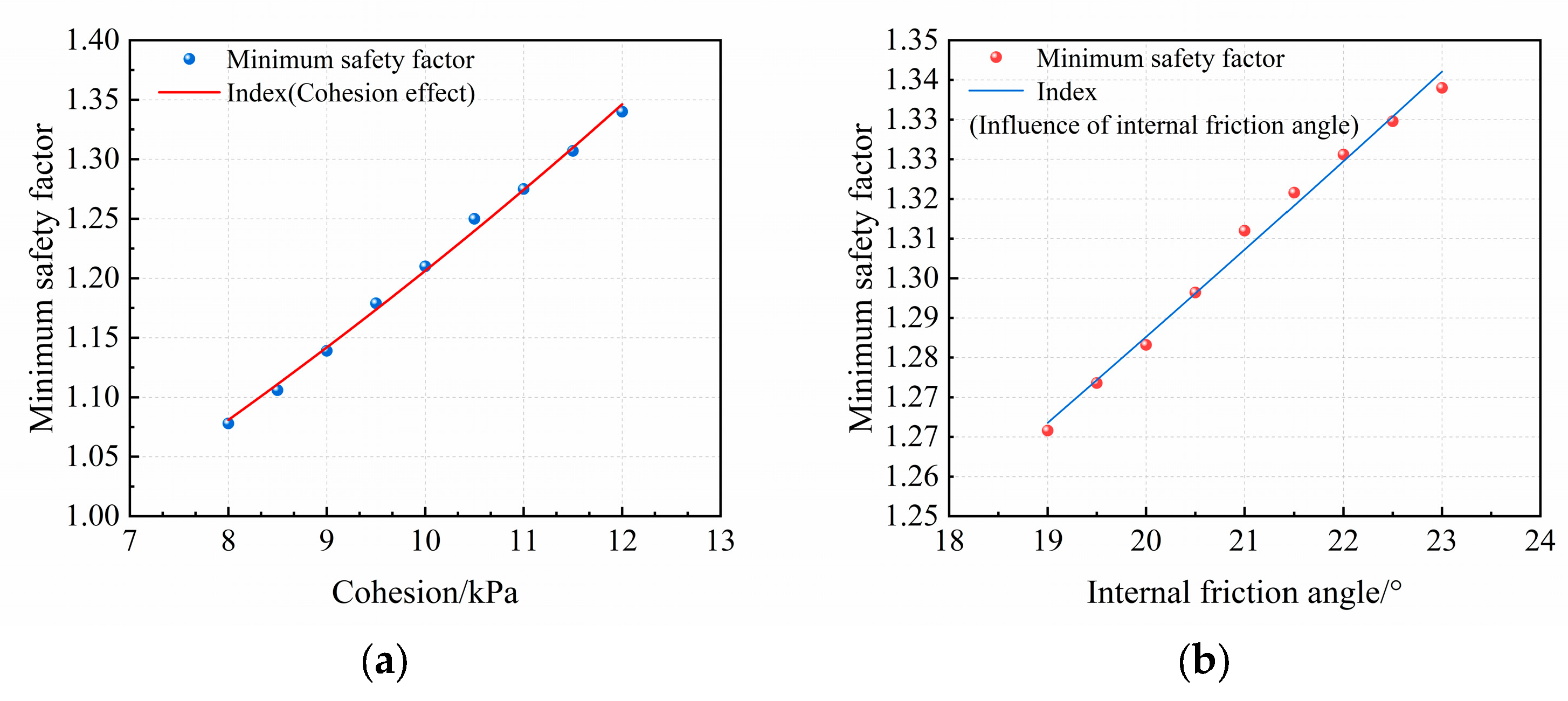
3.1. Sensitivity Analysis of Shear Strength Parameters for Tailings Dams
3.2. Theoretical Tailings Dam Cohesion Parameter Inversion Based on the Cloud Model
3.2.1. Select Parameter Range
3.2.2. Selection of Training Samples and Calculation of Safety Factor
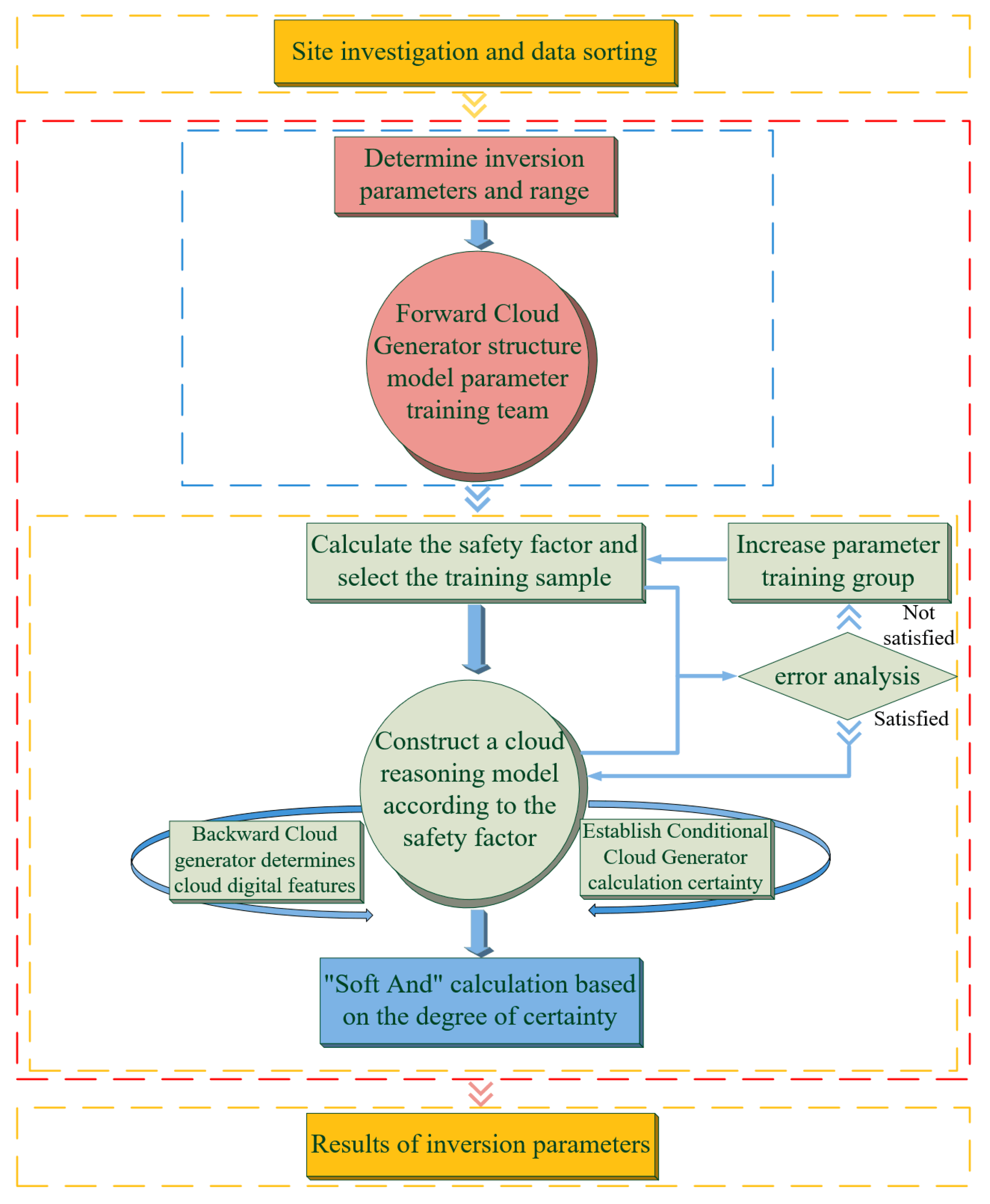
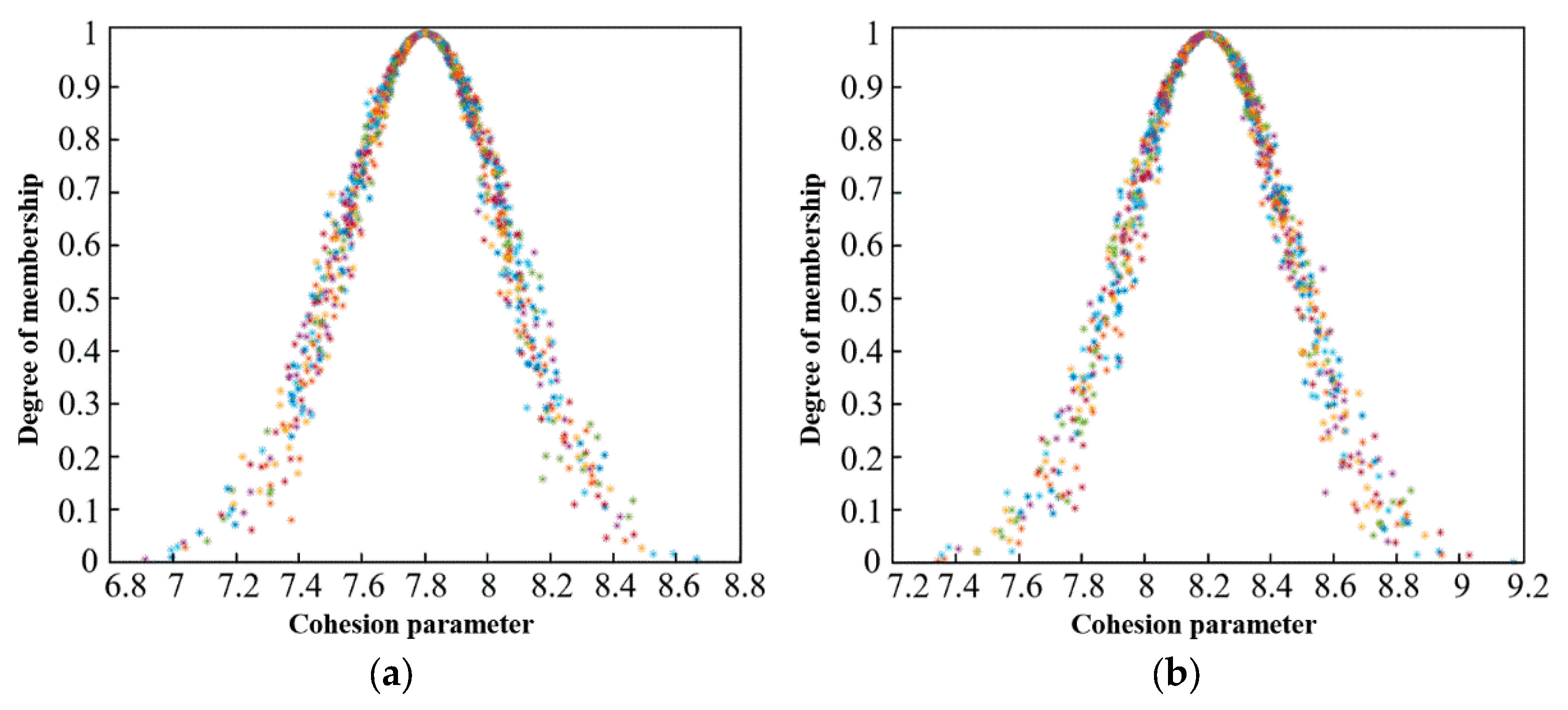
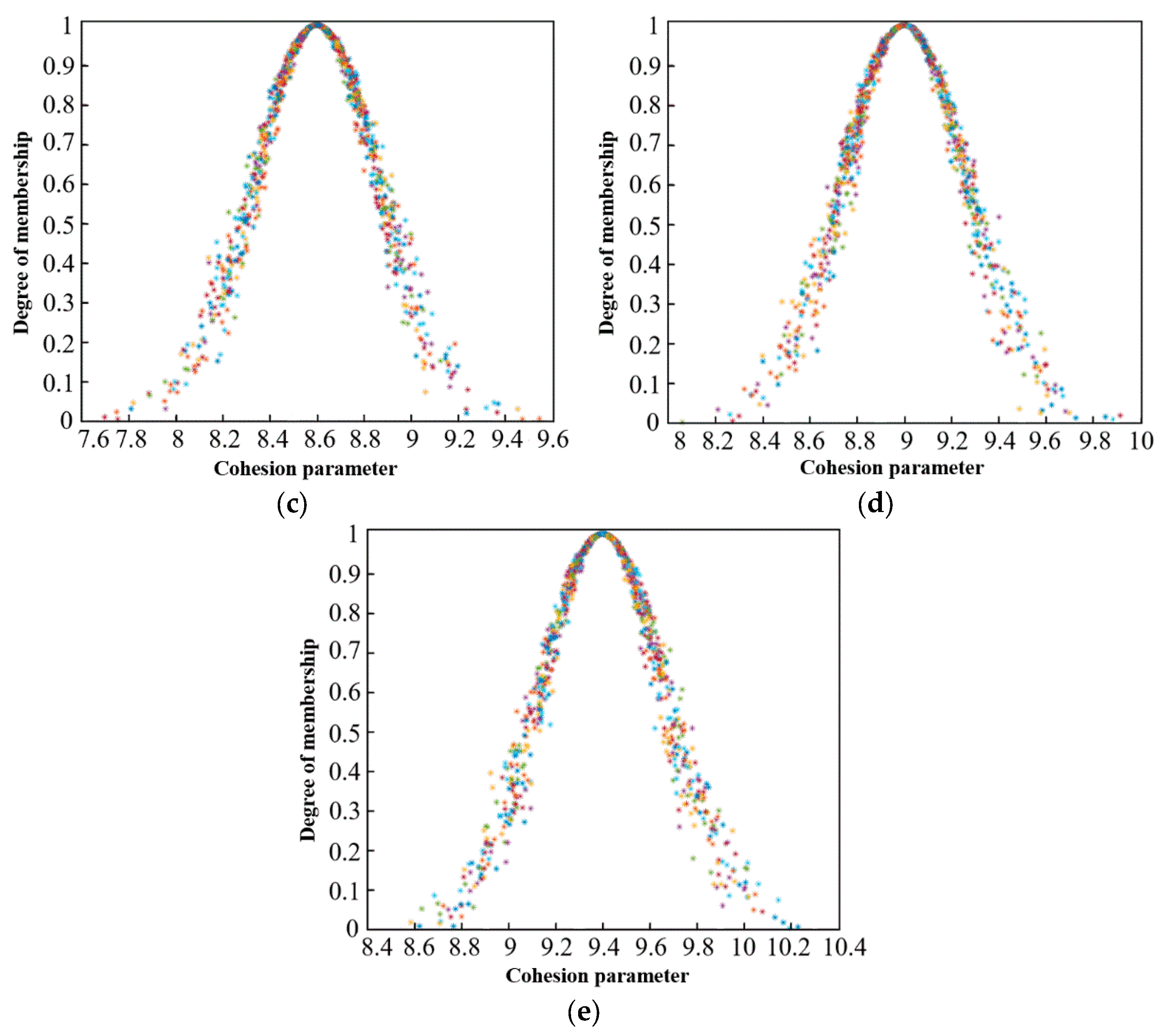
3.2.3. Uncertain Cloud Reasoning
- (1)
- If only one group of uncertainties is greater than 0, the output is directly generated by the inverse cloud generator;
- (2)
- If there are 2 degrees of certainty of confirmation (Ki and Ki+1) greater than 0, when using these 2 degrees of certainty to activate the corresponding rules consequent, select the 2 cloud droplets generated and cover these 2 cloud droplets with a virtual cloud. Then, the output method of cohesion C is Formula (24):
- (3)
- When more than three uncertainties are greater than 0, the expectation Ex of the virtual cloud is generated directly by the inverse cloud generator, and the value of Ex is the output value of cohesion C.
3.2.4. Verification of the Inversion Method of Strength Parameters
3.3. Analysis of the Deformation Destruction Characteristics of a Tail Mine Dam under Extreme Rainfall Conditions
4. Conclusions
- (1)
- The correlation between cohesion C and safety factor Fs is significant. The safety factor of a tailings dam is obtained by the Morgenstern–Price method, and the specific cohesion parameters are inversed by using cloud theory within the corresponding cohesion C range. The final calculation result is 8.6901 kPa, which overcomes the problem that the fuzziness and randomness of the quantitative cohesion value are transferred to the qualitative concept of the safety factor;
- (2)
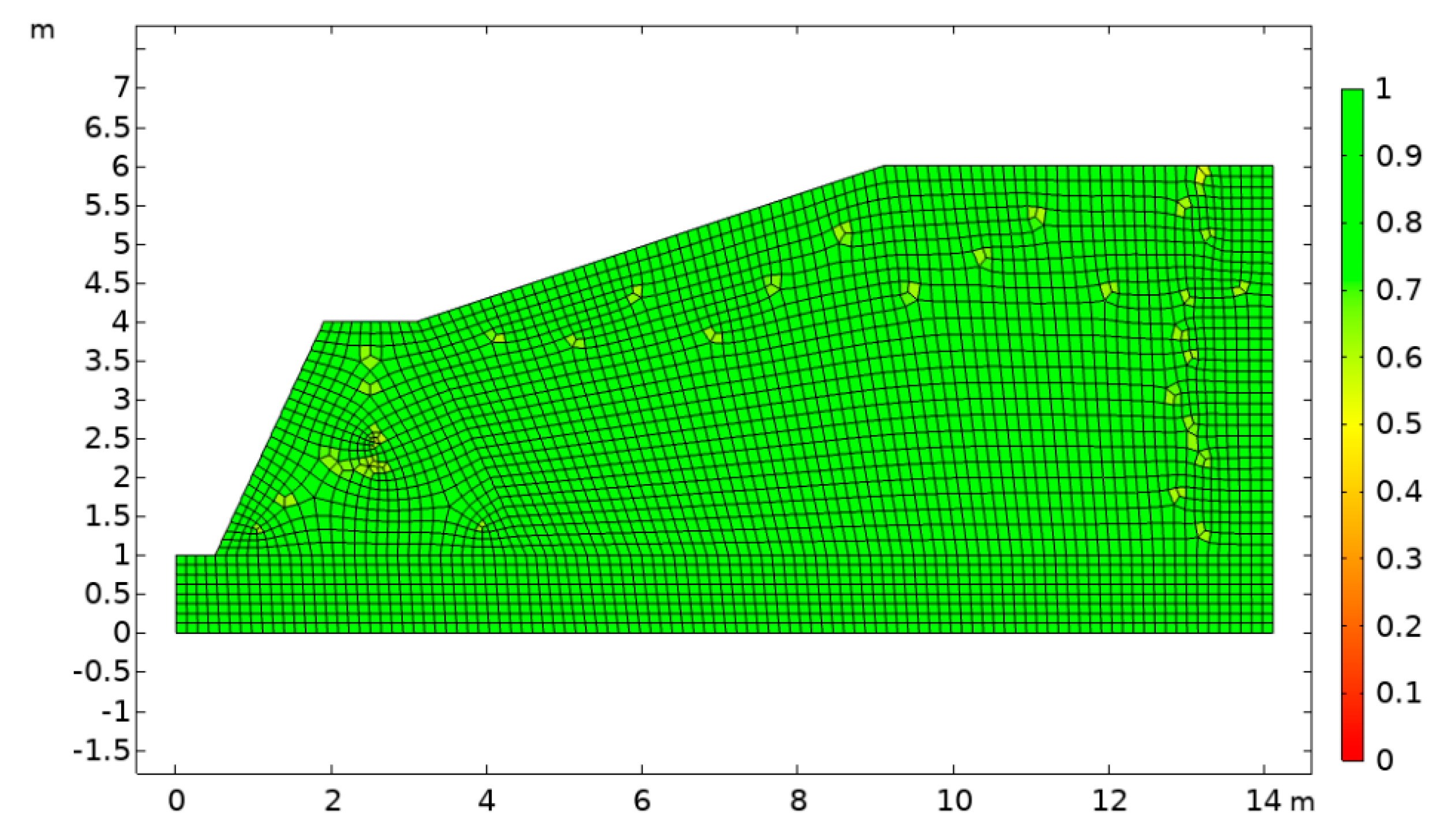
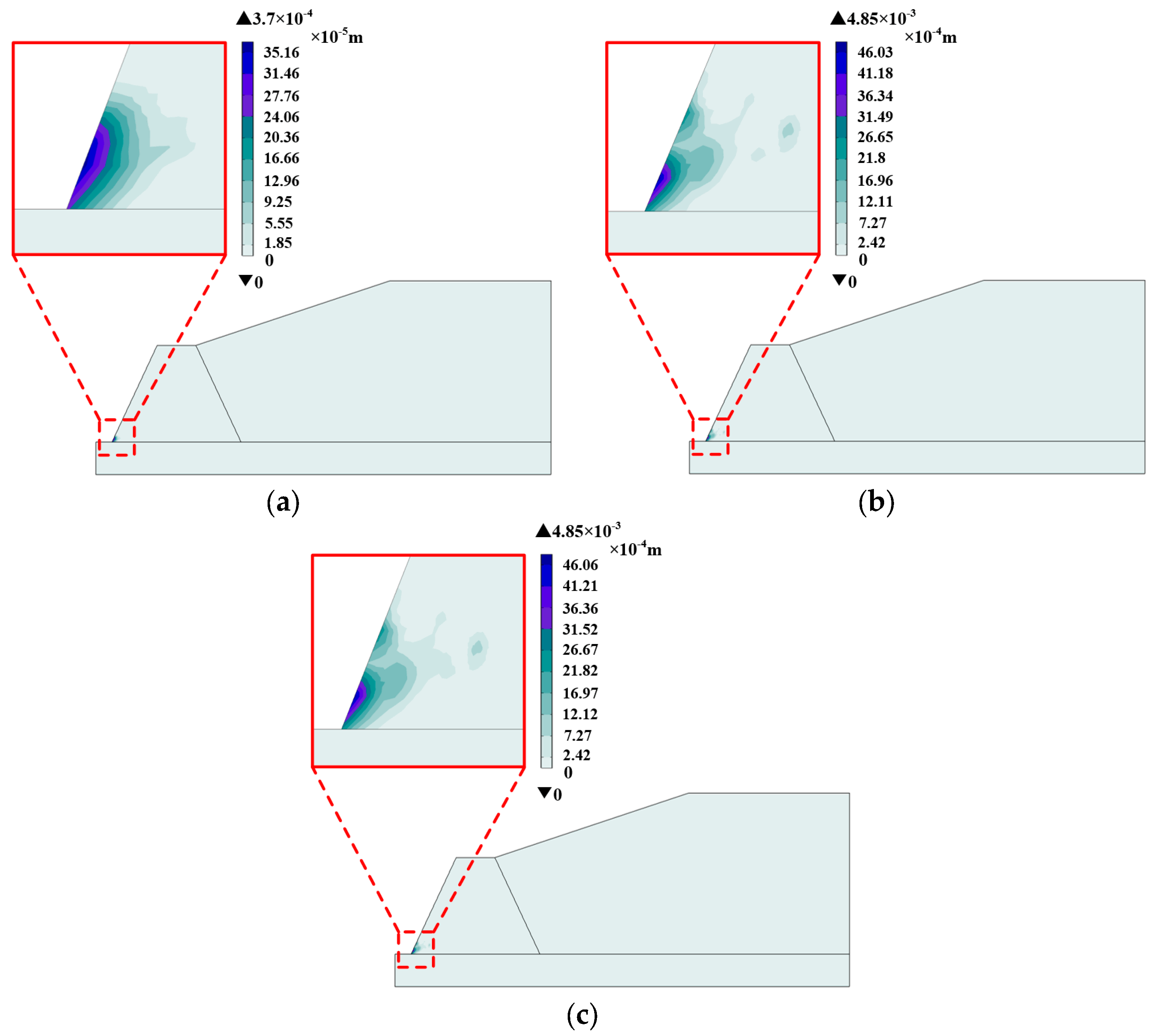
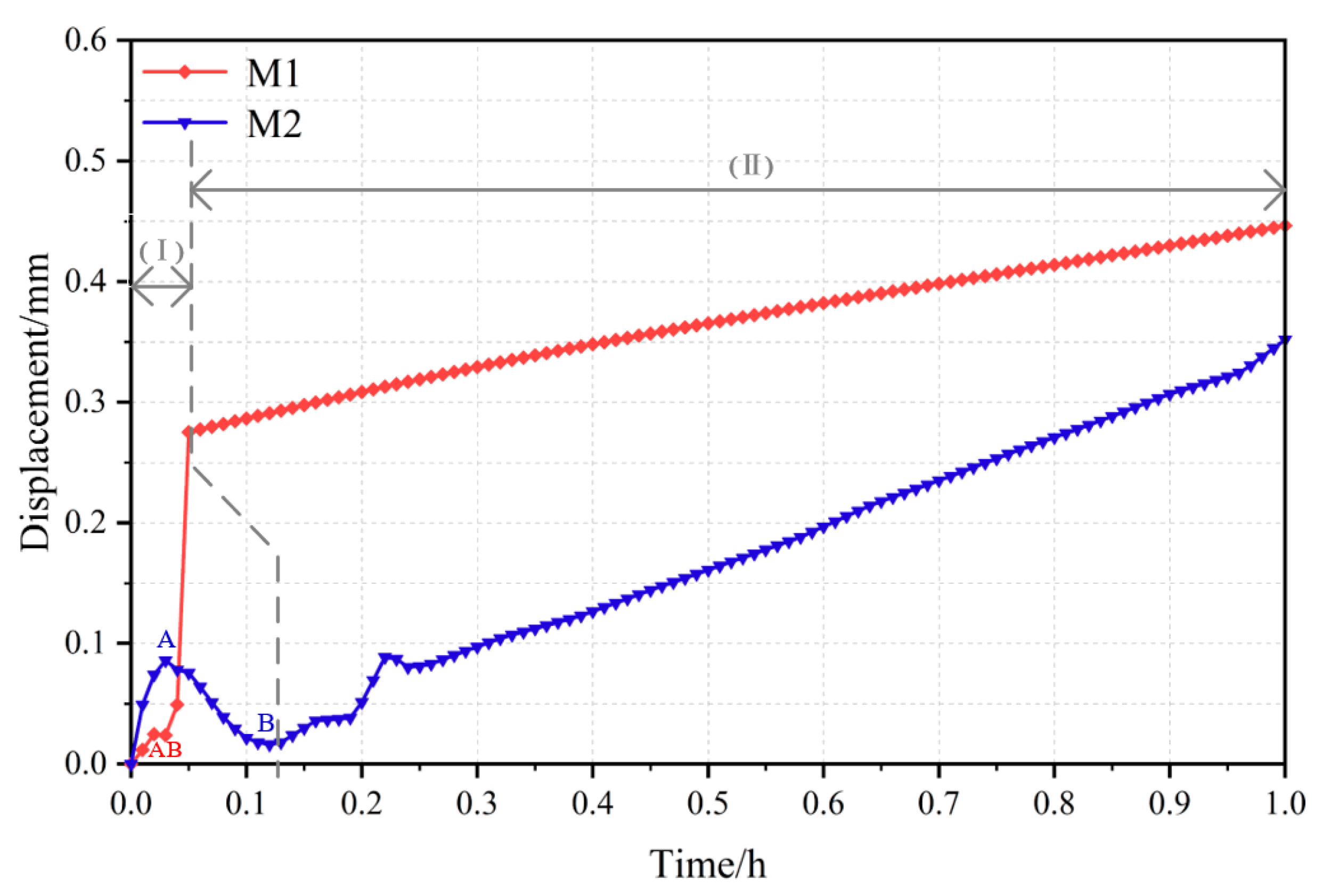
- The characteristics of coupling deformation and failure under extreme rainfall conditions are as follows: the plastic deformation area gradually develops on the inside of the tailings dam after dampness and softening, and the area gradually expands. The dam toe and abutment area have obvious displacement, and the whole displacement field gradually transfers from the accumulative tailings to the tailings dam with the rainfall, which intensifies the deformation and damage of the tailings dam. The seepage of rainwater and the hydrodynamic force generated by runoff drive the deformation and failure of tailings dams, and the deformation and failure of tailings dams provide a dominant transport path for rainwater seepage;
- (3)
- Under extreme rainfall conditions, the dam toe and abutment are high-risk areas. They should be taken as the target areas for priority prevention and control. In actual projects, measures such as the drainage or covering of the dam surface should be taken to avoid damage to the rainwater acceleration tailings dam.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Burritt, R.L.; Christ, K.L. Water risk in mining: Analysis of the Samarco dam failure. J. Clean. Prod. 2018, 178, 196–205. [Google Scholar] [CrossRef]
- Dong, L.; Deng, S.; Wang, F. Some developments and new insights for environmental sustainability and disaster control of tailings dam. J. Clean. Prod. 2020, 269, 122270. [Google Scholar] [CrossRef]
- Hancock, G. A method for assessing the long-term integrity of tailings dams. Sci. Total Environ. 2021, 779, 146083. [Google Scholar] [CrossRef] [PubMed]
- Pacheco, F.; Oliveira, M.; Oliveira, M.; Libanio, M.; Valle, J.F.; Melo, S.M.; Pissarra, T.; Melo, M.; Valera, C.; Fernandes, L. Water security threats and challenges following the rupture of large tailings dams. Sci. Total Environ. 2022, 834, 155285. [Google Scholar] [CrossRef] [PubMed]
- Buch, A.; Niemeyer, J.; Marques, E.; Silva-Filho, E. Ecological risk assessment of trace metals in soils affected by mine tailings. J. Hazard Mater. 2021, 403, 123852. [Google Scholar] [CrossRef]
- Clarkson, L.; Williams, D. An Overview of Conventional Tailings Dam Geotechnical Failure Mechanisms. Min. Met. Explor. 2021, 38, 1305–1328. [Google Scholar] [CrossRef]
- Piciullo, L.; Storrøsten, E.; Liu, Z.; Nadim, F.; Lacasse, S. A new look at the statistics of tailings dam failures. Eng. Geol. 2022, 303, 106657. [Google Scholar] [CrossRef]
- Owen, J.; Kemp, D.; Lèbre, É.; Svobodova, K.; Pérez, M.G. Catastrophic tailings dam failures and disaster risk disclosure. Int. J. Disaster Risk Reduct. 2020, 42, 101361. [Google Scholar] [CrossRef]
- Rico, M.; Benito, G.; Diez-Herrero, A. Floods from tailings dam failures. J. Hazard Mater. 2008, 154, 79–87. [Google Scholar] [CrossRef]
- Hatje, V.; Pedreira, R.; Rezende, C.; Schettini, C.; Souza, G.; Marin, D.; Hackspacher, P. The environmental impacts of one of the largest tailing dam failures worldwide. Sci. Rep. 2017, 7, 10706. [Google Scholar] [CrossRef]
- Dong, L.; Tong, X.; Li, X.; Zhou, J.; Wang, S.; Liu, B. Some developments and new insights of environmental problems and deep mining strategy for cleaner production in mines. J. Clean. Prod. 2019, 210, 1562–1578. [Google Scholar] [CrossRef]
- Čarman, M.; Jemec Auflič, M.; Komac, M. Landslides at a uranium mill tailing deposit site Boršt (Slovenia) detected by radar interferometry. Landslides 2014, 11, 527–536. [Google Scholar] [CrossRef]
- Jia, Y.; Xu, B.; Chi, S.; Xiang, B.; Xiao, D.; Zhou, Y. Joint back analysis of the creep deformation and wetting deformation parameters of soil used in the Guanyinyan composite dam. Comput. Geotech. 2018, 96, 167–177. [Google Scholar] [CrossRef]
- Yu, X.; Gong, B.; Tang, C. Study of the slope deformation characteristics and landslide mechanisms under alternating excavation and rainfall disturbance. Bull. Eng. Geol. Environ. 2021, 80, 7171–7191. [Google Scholar] [CrossRef]
- Yu, Y.; Zhang, B.; Yuan, H. An intelligent displacement back-analysis method for earth-rockfill dams. Comput. Geotech. 2007, 34, 423–434. [Google Scholar] [CrossRef]
- Lin, X.; Zhang, L.; Yang, Z.; Li, P.; Li, T. Inversion analysis of the shear strength parameters for a high loess slope in the limit state. J. Mt. Sci. 2020, 18, 252–264. [Google Scholar] [CrossRef]
- Daftaribesheli, A.; Ataei, M.; Sereshki, F. Assessment of rock slope stability using the Fuzzy Slope Mass Rating (FSMR) system. Appl. Soft. Comput. 2011, 11, 4465–4473. [Google Scholar] [CrossRef]
- Luo, Z.; Xie, C.; Jia, N.; Yang, B.; Cheng, G. Safe roof thickness and span of stope under complex filling body. J. Cent. South. Univ. 2013, 20, 3641–3647. [Google Scholar] [CrossRef]
- Xie, C.; Jia, N.; He, L. Study on the Instability Mechanism and Grouting Reinforcement Repair of Large-Scale Underground Stopes. Adv. Civ. Eng. 2020, 10, 8832012. [Google Scholar] [CrossRef]
- Kang, F.; Xu, B.; Li, J.; Zhao, S. Slope stability evaluation using Gaussian processes with various covariance functions. Appl. Soft. Comput. 2017, 60, 387–396. [Google Scholar] [CrossRef]
- Li, D.; Liu, C.; Gan, W. A new cognitive model: Cloud model. Int. J. Intell. Syst. 2009, 24, 357–375. [Google Scholar] [CrossRef]
- Wang, G.; Xu, C.; Li, D. Generic normal cloud model. Inform. Sci. 2014, 280, 1–15. [Google Scholar] [CrossRef]
- Wang, M.; Wang, X.; Liu, Q.; Shen, F.; Jin, J. A novel multi-dimensional cloud model coupled with connection numbers theory for evaluation of slope stability. Appl. Math. Model. 2020, 77, 426–438. [Google Scholar] [CrossRef]
- Wang, Y.; Yin, X.; Jing, H.; Liu, R.; Su, H. A novel cloud model for risk analysis of water inrush in karst tunnels. Environ. Earth Sci. 2016, 75, 1–3. [Google Scholar] [CrossRef]
- Yao, X.; Deng, H.; Zhang, T.; Qin, Y. Multistage fuzzy comprehensive evaluation of landslide hazards based on a cloud model. PLoS ONE 2019, 14, e0224312. [Google Scholar] [CrossRef]
- He, X.; Wang, J.; Feng, J.; Yan, Z.; Miao, S.; Zhang, Y.; Xia, J. Observational and modeling study of interactions between urban heat island and heatwave in Beijing. J. Clean. Prod. 2020, 247, 119169. [Google Scholar] [CrossRef]
- Naveendrakumar, G.; Vithanage, M.; Kwon, H.; Chandrasekara, S.; Iqbal, M.; Pathmarajah, S.; Fernando, W.; Obeysekera, J. South Asian perspective on temperature and rainfall extremes: A review. Atmos. Res. 2019, 225, 110–120. [Google Scholar] [CrossRef]
- Zipser, E.; Liu, C. Extreme Convection vs. Extreme Rainfall: A Global View. Curr. Clim. Change Rep. 2022, 7, 121–130. [Google Scholar] [CrossRef]
- Du, C.; Liang, L.; Yi, F.; Niu, B. Effects of Geosynthetic Reinforcement on Tailings Accumulation Dams. Water 2021, 13. [Google Scholar] [CrossRef]
- Kang, C.; Chen, S.; Chan, D.; Tfwala, S. Numerical modeling of large-scale dam breach experiment. Landslides 2020, 17, 2737–2754. [Google Scholar] [CrossRef]
- Gonzalez, F.; Raval, S.; Taplin, R.; Timms, W.; Hitch, M. Evaluation of Impact of Potential Extreme Rainfall Events on Mining in Peru. Nat. Resour. Res. 2018, 28, 393–408. [Google Scholar] [CrossRef]
- Nazrien, N.J.; Mohd, T.A.; Razali, I.; Abd, R.N.; Wan, M.W.; Karim, O.A.; Mat, D.S.; Awang, S.; Mohd, M. The Effect of Extreme Rainfall Events on Riverbank Slope Behaviour. Front. Env. Sci. 2022, 10, 176. [Google Scholar] [CrossRef]
- Zhao, N.; Hu, B.; Yi, Q.; Yao, W.; Ma, C. The Coupling Effect of Rainfall and Reservoir Water Level Decline on the Baijiabao Landslide in the Three Gorges Reservoir Area, China. Geofluids 2017, 12, 3724867. [Google Scholar] [CrossRef]
- Yeh, H.; Tsai, Y. Effect of Variations in Long-Duration Rainfall Intensity on Unsaturated Slope Stability. Water 2018, 10, 479. [Google Scholar] [CrossRef]
- Gui, R.; He, G. The Effects of Internal Erosion on the Physical and Mechanical Properties of Tailings under Heavy Rainfall Infiltration. Appl. Sci. 2021, 11, 9496. [Google Scholar] [CrossRef]
- Yang, Y.; Cai, R.; Zhang, G.; Su, S.; Liu, W. Evaluating and analyzing the stability of loess slope using intermittent rainfall and various rainfall patterns. Arab. J. Geosci. 2022, 15, 218. [Google Scholar] [CrossRef]
- Jiang, X.; Wörman, A.; Chen, P.; Huang, Q.; Chen, H. Mechanism of the progressive failure of non-cohesive natural dam slopes. Geomorphology 2020, 363, 107198. [Google Scholar] [CrossRef]
- Hu, W.; Xin, C.; Li, Y.; Zheng, Y.; van Asch, T.; McSaveney, M. Instrumented flume tests on the failure and fluidization of tailings dams induced by rainfall infiltration. Eng. Geol. 2021, 294, 106401. [Google Scholar] [CrossRef]
- Xu, J.; Ueda, K.; Uzuoka, R. Evaluation of failure of slopes with shaking-induced cracks in response to rainfall. Landslides 2021, 19, 119–136. [Google Scholar] [CrossRef]
- Tian, S.; Dai, X.; Wang, G.; Lu, Y.; Chen, J. Formation and evolution characteristics of dam breach and tailings flow from dam failure: An experimental study. Nat. Hazards 2021, 107, 1621–1638. [Google Scholar] [CrossRef]
- Zhong, Q.; Chen, S.; Mei, S.; Cao, W. Numerical simulation of landslide dam breaching due to overtopping. Landslides 2017, 15, 1183–1192. [Google Scholar] [CrossRef]
- Xie, C.; Nguyen, H.; Choi, Y.; Jahed, A.D. Optimized functional linked neural network for predicting diaphragm wall deflection induced by braced excavations in clays. Geosci. Front. 2022, 13, 101313. [Google Scholar] [CrossRef]
- Qiu, X.; Li, J.; Jiang, H.; Ou, J.; Ma, J. Evolution of the Transient Saturated Zone and Stability Analysis of Slopes under Rainfall Conditions. KSCE J. Civ. Eng. 2022, 26, 1618–1631. [Google Scholar] [CrossRef]
- Khan, K.; Wang, C.; Khan, M.; Liang, Z.; Li, S.; Li, B. Influence of rainfall infiltration on the stability of unsaturated coal gangue accumulated slope. J. Mt. Sci. 2021, 18, 1696–1709. [Google Scholar] [CrossRef]
- Zhou, C.; Ai, D.; Huang, W.; Xu, H.; Ma, L.; Chen, L.; Wang, L. Emergency Survey and Stability Analysis of a Rainfall-Induced Soil-Rock Mixture Landslide at Chongqing City, China. Front. Earth Sci. 2021, 9, 774200. [Google Scholar] [CrossRef]
- Wu, K.; Chen, N.; Hu, G.; Han, Z.; Ni, H.; Rahman, M. Failure mechanism of the Yaoba loess landslide on 5 March 2020: The early-spring dry spell in Southwest China. Landslides 2021, 18, 3183–3195. [Google Scholar] [CrossRef]
- Li, S.; Yuan, L.; Yang, H.; An, H.; Wang, G. Tailings dam safety monitoring and early warning based on spatial evolution process of mud-sand flow. Saf. Sci. 2020, 124, 104579. [Google Scholar] [CrossRef]
- Xie, C.; Nguyen, H.; Bui, X.; Nguyen, V.; Zhou, J. Predicting roof displacement of roadways in underground coal mines using adaptive neuro-fuzzy inference system optimized by various physics-based optimization algorithms. J. Rock Mech. Geotech. 2021, 13, 1452–1465. [Google Scholar] [CrossRef]
- Sun, G.; Cheng, S.; Jiang, W.; Zheng, H. A global procedure for stability analysis of slopes based on the Morgenstern-Price assumption and its applications. Comput. Geotech. 2016, 80, 97–106. [Google Scholar] [CrossRef]
- Ouyang, W.; Liu, S.; Yang, Y. An improved morgenstern-price method using gaussian quadrature. Comput. Geotech. 2022, 148, 104754. [Google Scholar] [CrossRef]
- Liu, X.; Zhang, M.; Sun, Z.; Zhang, H.; Zhang, Y. Comprehensive evaluation of loess collapsibility of oil and gas pipeline based on cloud theory. Sci. Rep. 2021, 11, 15422. [Google Scholar] [CrossRef]
- Cao, W.; Deng, J.; Yang, Y.; Zeng, Y.; Liu, L. Water Carrying Capacity Evaluation Method Based on Cloud Model Theory and an Evidential Reasoning Approach. Mathematics 2022, 10, 266. [Google Scholar] [CrossRef]
- Zhang, H.; Wang, T.; Ding, Z.; Zhang, X.; Han, L. Uncertainty analysis of impact factors of eco-environmental vulnerability based on cloud theory. Ecol. Indic. 2020, 110, 105864. [Google Scholar] [CrossRef]
- Wu, D.; Deng, T.; Duan, W.; Zhang, W. A coupled thermal-hydraulic-mechanical application for assessment of slope stability. Soils Found. 2019, 59, 2220–2237. [Google Scholar] [CrossRef]
- Wang, T.; Li, S.; Xu, Z.; Hu, J.; Pan, D.; Xue, Y. Risk assessment of water inrush in karst tunnels excavation based on normal cloud model. Bull. Eng. Geol. Environ. 2018, 78, 3783–3798. [Google Scholar] [CrossRef]
- Cao, J.; Xie, C.; Hou, Z. Spatiotemporal distribution patterns and risk characteristics of heavy metal pollutants in the soil of lead–zinc mines. Environ. Sci. Eur. 2022, 34, 1–14. [Google Scholar] [CrossRef]
- Zou, J.; Zhang, R.; Zhou, F.; Zhang, X. Hazardous area reconstruction and law analysis of coal spontaneous combustion and gas coupling disasters in goaf based on DEM-CFD. ACS. Omega 2023, 8, 2685–2697. [Google Scholar] [CrossRef]
- Cao, J.; Xie, C.; Hou, Z. Transport patterns and numerical simulation of heavy metal pollutants in soils of lead-zinc ore mines. J. Mt. Sci.-Engl. 2021, 18, 2345–2356. [Google Scholar] [CrossRef]







| Cohesion (kPa) | Fs | |
|---|---|---|
| 1C | 7.50131 | 0.943 |
| 8.30150 | 1.027 | |
| 7.70046 | 0.976 | |
| 7.40259 | 0.939 | |
| 7.89953 | 0.979 | |
| 8.00075 | 1.006 | |
| 8.20211 | 1.023 | |
| 7.60060 | 0.952 | |
| Ex1C | 7.8 | 1.000 |
| Cohesion (kPa) | Fs | |
|---|---|---|
| 2C | 8.00480 | 1.006 |
| 8.10081 | 1.021 | |
| 8.30078 | 1.030 | |
| 8.40121 | 1.035 | |
| 7.79991 | 0.998 | |
| 7.90093 | 0.979 | |
| 8.50072 | 1.043 | |
| 8.60047 | 1.050 | |
| Ex2C | 8.2 | 1.023 |
| Cohesion (kPa) | Fs | |
|---|---|---|
| 3C | 8.40168 | 1.035 |
| 8.50064 | 1.043 | |
| 8.70093 | 1.061 | |
| 8.80129 | 1.070 | |
| 8.20208 | 1.023 | |
| 8.30044 | 1.030 | |
| 9.00298 | 1.084 | |
| 8.90135 | 1.079 | |
| Ex3C | 8.6 | 1.05 |
| Cohesion (kPa) | Fs | |
|---|---|---|
| 4C | 8.80021 | 1.070 |
| 8.90051 | 1.079 | |
| 9.10094 | 1.094 | |
| 9.20022 | 1.104 | |
| 8.60354 | 1.050 | |
| 8.70189 | 1.061 | |
| 9.30214 | 1.109 | |
| 9.40796 | 1.113 | |
| Ex4C | 9 | 1.066 |
| Cohesion (kPa) | Fs | |
|---|---|---|
| 5C | 9.20095 | 1.104 |
| 9.30010 | 1.109 | |
| 9.50246 | 1.122 | |
| 9.60023 | 1.136 | |
| 9.00350 | 1.091 | |
| 9.10623 | 1.094 | |
| 9.70047 | 1.144 | |
| 9.80063 | 1.152 | |
| Ex5C | 9.4 | 1.103 |
| 1C | 2C | 3C | 4C | 5C | ||
|---|---|---|---|---|---|---|
| Fs | Ex | 1.000 | 1.023 | 1.050 | 1.066 | 1.103 |
| En | 0.252 | 0.0194 | 0.0217 | 0.020 | 0.202 | |
| He | 0.0030693 | 0.0023693 | 0.0025607 | 0.0025000 | 0.0025006 |
| Cloud Representation of Qualitative Concept of Rule Antecedents of Fs | Cloud Representation of Qualitative Concept of Rule Consequent of C |
|---|---|
| PREAC1 = PRE (1.000, 0.0252, 0.0030693) | POSTBC1 = POST (7.8, 0.266, 0.0266) |
| PREAC2 = PRE (1.023, 0.0194, 0.0023693) | POSTBC2 = POST (8.2, 0.266, 0.0266) |
| PREAC3 = PRE (1.050, 0.0217, 0.0025607) | POSTBC3 = POST (8.6, 0.266, 0.0266) |
| PREAC4 = PRE (1.066, 0.0200, 0.0025000) | POSTBC4 = POST (9.0, 0.266, 0.0266) |
| PREAC5 = PRE (1.103, 0.0202, 0.0025006) | POSTBC5 = POST (9.4, 0.266, 0.0266) |
| Material | Bulk Density ρ (kg/m3) | Young’s Modulus E (Pa) | Poisson’s Ratio μ | Cohesion C (kPa) | Internal Friction Angle φ (°) | Hydraulic Conductivity K (m/s) |
|---|---|---|---|---|---|---|
| Tailings dam | 2200 | 2.0 × 107 | 0.28 | 9.56 | 23.1 | 4.1 × 10−5 |
| Tailings | 2820 | 3.5 × 107 | 0.27 | 9.80 | 26.6 | 5.5 × 10−5 |
| Foundation | 2300 | 3.0 × 107 | 0.30 | 30.00 | 25.0 | 1.5 × 10−7 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, Z.; Xie, C.; Xiong, G.; Shen, J.; Yang, B. Using the Morgenstern–Price Method and Cloud Theory to Invert the Shear Strength Index of Tailings Dams and Reveal the Coupling Deformation and Failure Law under Extreme Rainfall. Sustainability 2023, 15, 6106. https://doi.org/10.3390/su15076106
Chen Z, Xie C, Xiong G, Shen J, Yang B. Using the Morgenstern–Price Method and Cloud Theory to Invert the Shear Strength Index of Tailings Dams and Reveal the Coupling Deformation and Failure Law under Extreme Rainfall. Sustainability. 2023; 15(7):6106. https://doi.org/10.3390/su15076106
Chicago/Turabian StyleChen, Ziwei, Chengyu Xie, Guanpeng Xiong, Jinbo Shen, and Baolin Yang. 2023. "Using the Morgenstern–Price Method and Cloud Theory to Invert the Shear Strength Index of Tailings Dams and Reveal the Coupling Deformation and Failure Law under Extreme Rainfall" Sustainability 15, no. 7: 6106. https://doi.org/10.3390/su15076106
APA StyleChen, Z., Xie, C., Xiong, G., Shen, J., & Yang, B. (2023). Using the Morgenstern–Price Method and Cloud Theory to Invert the Shear Strength Index of Tailings Dams and Reveal the Coupling Deformation and Failure Law under Extreme Rainfall. Sustainability, 15(7), 6106. https://doi.org/10.3390/su15076106








