Extending Quality Function Deployment and Analytic Hierarchy Process under Interval-Valued Fuzzy Environment for Evaluating Port Sustainability

Abstract

To confront the related problems of environmental protection, energy saving, and carbon reduction, sustainability has been a prominent issue for enterprises seeking to meet the requirements of the Earth Summit’ sustainable development goals (SDGs). Basically, sustainability evaluation of enterprises must be considered from environmental, social, and economic perspectives, recognized as quality requirements. Numerous enterprises, especially for international ports, must pay attention to these requirements in expressing their corporate social responsibility (CSR) for decreasing marine pollution. Practically, the three requirements may be dependent under uncertain environments, and rationally evaluated by fuzzy multi-criteria decision-making (FMCDM) with dependent evaluation criteria (DEC). In other words, evaluating port sustainability, containing location expanding, should belong to FMCDM with DEC. For DEC under uncertain environments, fuzzy extension of the analytic network process (ANP) is a feasible solution to solve the above problems. However, fuzzy computations of ANP are heavily complicated; thus, we desire to combine quality function deployment (QFD) with the analytic hierarchy process (AHP) under the interval-valued fuzzy environment (IVFE) into a hybrid method for evaluating port sustainability. In numerous multi-criteria decision-making (MCDM) efforts, AHP was often extended into FMCDM to encompass the imprecision and vagueness of data, but the extension was properly used for FMCDM with independent evaluation criteria (IDEC). Herein, QFD is utilized to express the dependent relationships between criteria, and thus transforms IDEC into DEC for the evaluation of port sustainability. Through the hybrid method, QFD is combined with AHP to replace ANP under IVFE, the complicated ties of ANP-corresponding interval-valued fuzzy numbers (IVFNs) are overcome, and the problem of evaluating port sustainability is rationally solved.

1. Introduction

Recently, sustainability has become an essential issue for enterprises due to environmental protection, energy saving, and carbon reduction on a global scale. Therefore, enterprises must implement corporate social responsibility (CSR) with regard to sustainability issues to achieve the requirements of the Earth Summit’s sustainable development goals (SDGs). For instance, giant international ports heavily influence marine pollution owing to their operations; thus, evaluating port sustainability will be important. Basically, evaluating port sustainability is considered from the perspective of three varied quality requirements: environmental, social, and economic [1]. Criteria ratings of evaluating port sustainability are assessed from the three aspects and thus criteria should be mutually dependent. Additionally, evaluating port sustainability is often undertaken under uncertain environments, and thus this kind of problem belongs to fuzzy multi-criteria decision-making (FMCDM) [2] with dependent evaluation criteria (DEC). FMCDM is from multi-criteria decision-making (MCDM) [3] and the fuzzy extension of MCDM. To perform FMCDM with DEC, the analytic network process (ANP) proposed by Saaty [4] may be extended under fuzzy environments, but there as complicated relationships of hierarchical structure in ANP puzzle decision-makers. On the other hand, the analytic hierarchy process (AHP) [5] over ANP is easy with respect to computation and realization for decision-makers, but AHP is merely used in MCDM with independent evaluation criteria (IDEC). To utilize AHP in evaluating port sustainability—a FMCDM problem with DEC— AHP is combined with quality function deployment (QFD) [6] and extended under the interval-valued fuzzy environment (IVFE) [7]. By the assistant of QFD, the relationships between DEC are presented in FMCDM and related weights of DEC are derived. Then AHP can be utilized in FMCDM with DEC according to related weights of DEC. In other words, combining QFD with AHP under IVFE into a hybrid method will replace ANP to solve the problem of evaluating port sustainability containing sustainability evaluation of port expanding locations. Taiwan is an island country that has only rare resources and a small area, so the gross domestic product (GDP) of Taiwan relies on international trade, hence the importance of international ports. In Taiwan, the international ports are Kaohsiung port, Taichung port, and Taipei port. Evidently, evaluating port sustainability—the FMCDM problem with DEC—is essential and presented as follows.

For evaluating port sustainability, related problems belongs to MCDM [3] with DEC, among which $A_1,A_2,\dots ,A_m$ were alternatives, $C_1,C_2,\dots ,C_n$ were DEC, $G_{ij}$ was the rating of $A_i$ over $C_j$, and $W_j$ was the weight of $C_j$ for $i=1,2,\dots ,m$; $j=1,2,\dots ,n$. During alternative ratings and criteria weights assessed in imprecision and vagueness situations, the problems should belong to FMCDM [2] in MCDM, where ratings and weights are displayed by linguistic terms [8,9] and then represented by fuzzy numbers [10]. In the past, FMCDM [11] with IDEC was proverbially used, but FMCDM having DEC might be scarcely discussed due to their complicated computations. Recently, FMCDM with DEC have been mentioned, incrementally, owing to their necessary consideration. For identifying relationships of DEC, QFD [6] is useful, through the connections between quality requirements and function solutions, to gain criteria weights. In QFD [12], user opinions denote quality requirements, and expert assistants indicate function solutions. The quality requirement priorities of QFD are presented in an important level matrix, and relationships between quality requirements and function solutions of QFD are expressed in a relation matrix. Through the two above matrices, importance and relationship of DEC are connected and then criteria weights are aggregated by QFD. For imprecision, subjectivity, or vagueness data, QFD was expanded into fuzzy quality function deployment (FQFD) [13] as well; thus, elements of the above matrices in FQFD are expressed by fuzzy numbers. Due to the characteristics of fuzzy numbers, the related computations of FQFD [14,15] are complex and it is difficult to combine the important level matrix with the relation matrix. For instance, Liang’s FQFD [16] had demonstrated the hard computation because the criterion weight was a pooled fuzzy number (PFN) [10] constructed from the multiplication of two trapezoidal fuzzy numbers (TRFNs) [17]. Practically, these computations used in interval-valued fuzzy numbers (IVFNs) [18,19] will be more complex than others. IVFNs are from interval-valued fuzzy sets (IVFSs) [20,21] and utilized in numerous fields [22,23]. However, hard operations of pooled fuzzy numbers (PFNs) constructed from IVFNs in generalizing QFD under the fuzzy environment were commonly necessary to derive criteria weights in FMCDM with DEC under IVFE. Therefore, related computations of IVFNs must be mentioned to resolve the ties of PFNs.

Some were devoted to FMCDM with IDEC under IVFE [7] for grasping more messages than triangular fuzzy numbers (TFNs) or TRFNs, but FMCDM having DEC for IVFNs was still rare. Herein, we generalize QFD and AHP [5] under IVFE [20] in FMCDM with DEC for sustainability evaluation of port expanding locations. AHP [5] was often generalized under fuzzy environment into fuzzy AHP, such as in the approaches of Chang [24], Zhu, Jing, and Chang [25], and Wang [26]. In these above fuzzy extensions of AHP, Chang expressed an extent analysis for FMCDM [27] constructed on TFNs. Chang’s operations, except for the extent analysis, were the fuzzy improvement of classical AHP [5,28] or the application of fuzzy approximate division [29,30]. Extent analysis [24] was the main contribution of Chang, but it had one drawback in computation which made the possibility degrees for fuzzy pairwise comparison ratios confused. Wang [26] indicated that the possibility degrees attained through Chang’s computation might be negative. Then Zhu et al. [25] proposed an improvement to the possibility degrees to ameliorate Chang’s drawback. However, the confusion of deriving possibility degrees denoted by Wang still persisted despite the improvement [26].

To tackle Chang’s and Zhu et al.’s drawbacks, Wang [26] used representative utility functions [31,32] to extend AHP on TFNs. Wang’s method was simpler than Chang’s and Zhu et al.’s on fuzzy computations, but Wang’s was not applying IVFNs [33,34]. In addition to above methods, some researchers [35,36,37] generalized AHP under the fuzzy environment by hesitant fuzzy preference relations. The preference relations are utilized to derive priority weights in interval ratios, which are not used in IVFNs. Herein, a utility representative function of IVFNs is applied to compute priority representation vectors of fuzzy pairwise comparison matrices (FPWCMs). Obviously, AHP based on the utility representative function is extended under IVFE into fuzzy AHP in FMCDM. Unfortunately, fuzzy AHP is merely suitable for FMCDM with IDEC, whereas ANP [4] is a method for DEC. In fact, the difference between AHP and ANP is in their hierarchical structures. The former is used in independent hierarchical structures, but the latter is utilized in dependent hierarchical structures. Evidently, ANP is more complicated than AHP with regard to computation, and thus ANP is also harder in fuzzy extension than AHP. For FMCDM with DEC, QFD combined with AHP in this paper are extended under IVFE to replace fuzzy ANP for the sustainability evaluation of port expanding locations. Through improving Lee’s [38,39] extended fuzzy preference relation, Wang [40] associated QFD with simple additive weighting (SAW) [41], and Wang et al. [42] combined QFD with a technique for order preference by similarity to ideal solution (TOPSIS) [3] for FMCDM with DEC in IVFNs to grasp more messages. In data specifications, SAW and TOPSIS are different from AHP. AHP is used in data consisting of relative ratios, whereas SAW and TOPSIS are utilized in messages composed of general values. In other words, data specification commonly determines the use of decision-making method. For sustainability evaluation of port expanding locations, we associate QFD with AHP to replace ANP under IVFNs due to collected data being relative ratios in a numerical example.

To describe clearly, related notions of IVFNs are shown in Section 2. In Section 3, extending QFD and AHP under IVFNs are displayed to FMCDM with DEC for the sustainability evaluation of port expanding locations. Then, a numerical example for the sustainability evaluation of port expanding locations is presented in Section 4. Finally, conclusions are described in Section 5.

2. Preliminaries

In this section, related notions of IVFNs [10] are denoted below.

Definition 1.

An interval-valued fuzzy set (IVFS), $A$, according to Gorzalczany [43] is defined on $(-\infty ,\infty )$ as $A$ = $\{x,[{\mu }_{A^L}(x),{\mu }_{A^U}(x)]\},$ $x\in (-\infty ,\infty )$, ${\mu }_{A^L},{\mu }_{A^U}:$$(-\infty ,\infty )\to [0,1]$, ${\mu }_{A^L}(x)\le {\mu }_{A^U}(x),$ $\forall x\in (-\infty ,\infty )$, ${\mu }_A(x)=[{\mu }_{A^L}(x),{\mu }_{A^U}(x)]$, $x\in (-\infty ,\infty )$, where ${\mu }_{A^L}(x)$ 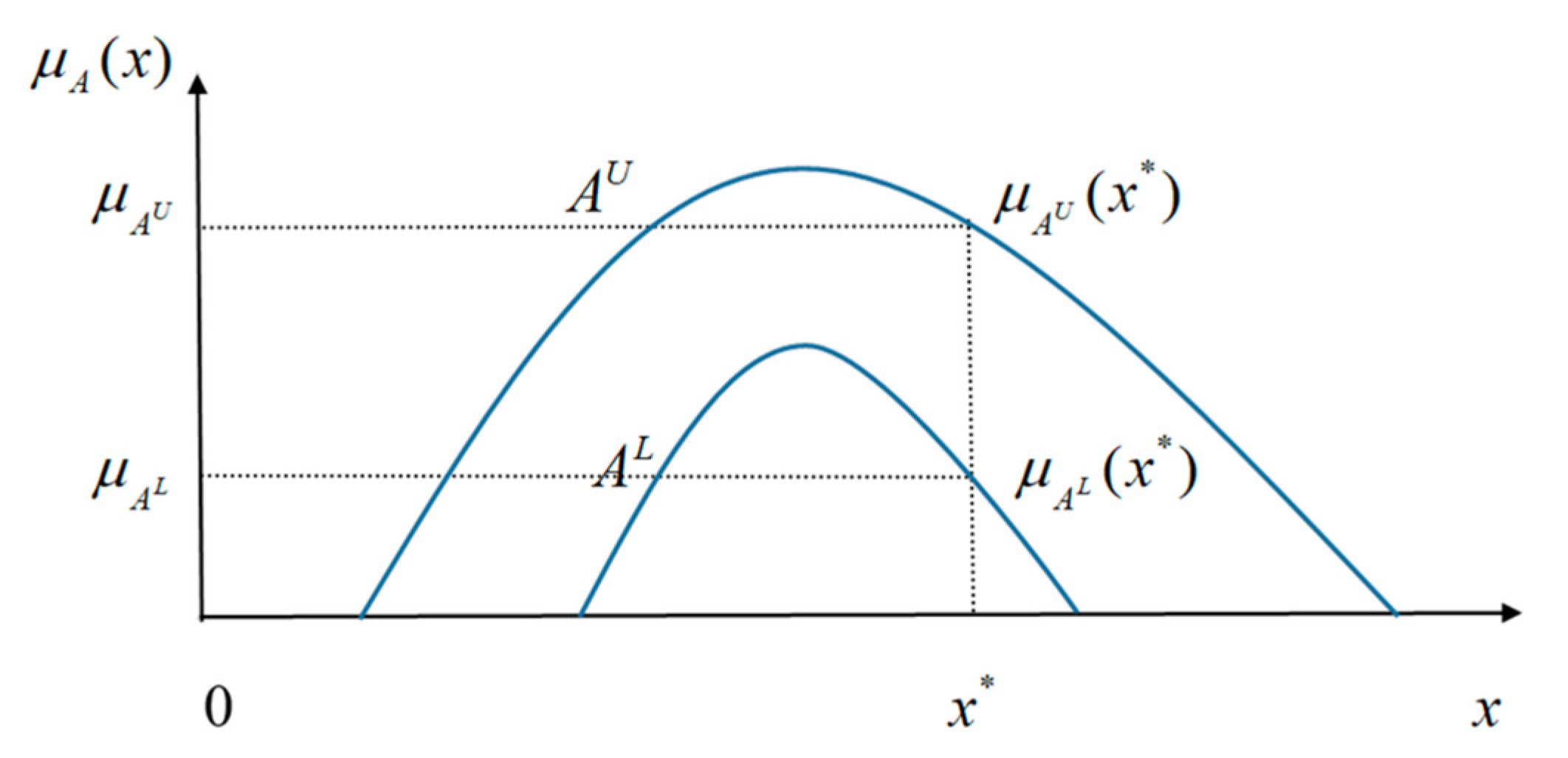is the lower limit of membership degree and ${\mu }_{A^U}(x)$ is the upper limit of membership degree. In addition, the membership degree of $A$ in $x^{*}$ is expressed by $\left[{\mu }_{A^L}\right(x^{*}), {\mu }_{A^U}(x^{*}\left)\right]$ in Figure 1, where ${\mu }_{A^L}\left(x^{*}\right)$ and ${\mu }_{A^U}\left(x^{*}\right)$, respectively, denote the minimum and maximum grades of membership in $x^{*}$.

Definition 2.

A triangular interval-valued fuzzy number(TIVFN), $A$, proposed by Yao and Lin [44] is presented as $A$ = $[A^L,A^U]$ = $[(a_l^L,a_h^L,a_u^L;w_A^L),(a_l^U,a_h^U,a_u^U;w_A^U=1)]$ in Figure 2, where $A_{}^L$ and $A_{}^U$, respectively, indicate the lower and upper parts of the TIVFN, and $A_{}^L$$\subseteq$$A_{}^U$.

Based on Figure 3, the related lemmas [45] of an interval-valued fuzzy number (IVFN), $A$, are expressed in the following.

Lemma 1.

$A$ is a crisp value if $a_l^L$ = $a_l^U$ = $a_h^L=a_h^U$ = $a_u^L$ = $a_u^U$.

Lemma 2.

$A$ belongs to TFNs if $A_{}^L$ = $A_{}^U$(i.e., $a_l^L$ = $a_l^U$ = $a_l$, $a_h^L=a_h^U$ = $a_h$, and $a_u^L$ = $a_u^U$ = $a_u$). Hence $A$ is a triplet $(a_l,a_h,a_u)$.

Lemma 3.

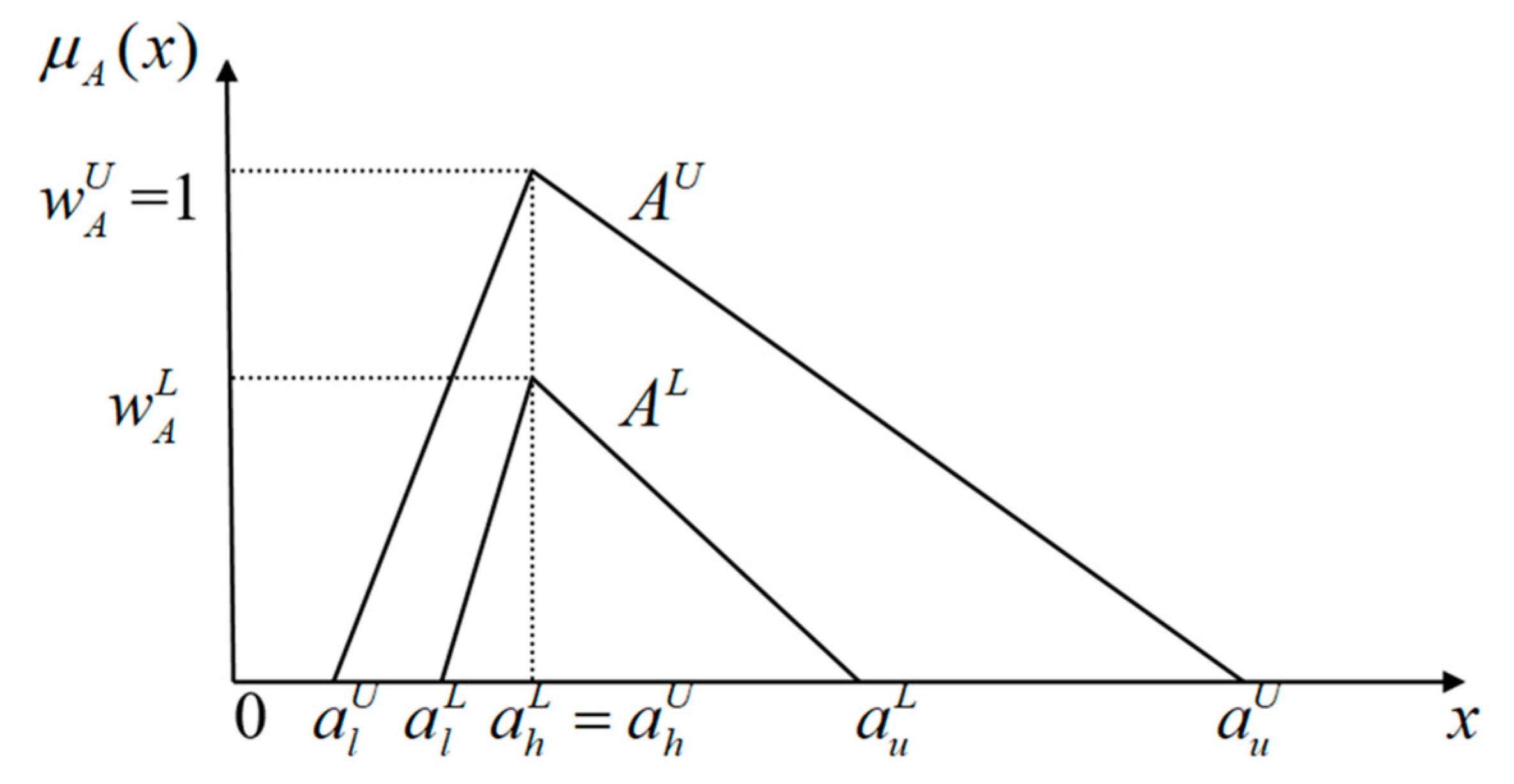
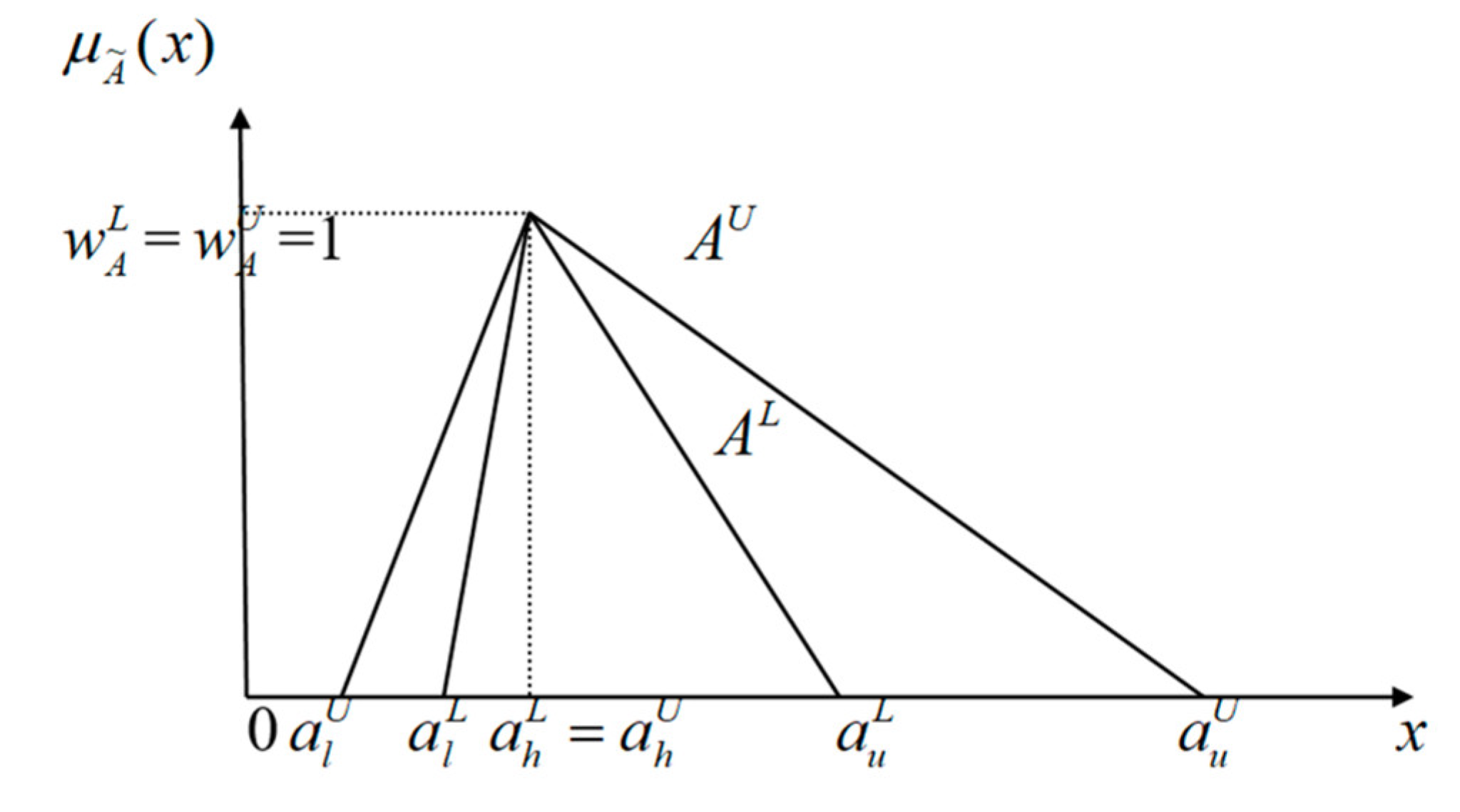
$A$ = $[A^L,A^U]$ = $((a_l^U,a_l^L),(a_h^L=a_h^U),(a_u^L,a_u^U))$ is a general TIVFN as shown as Figure 3 if $w_A^L$ = $w_A^U$ = 1 and $a_h^L=a_h^U$.

Furthermore, a general TIVFN, $A$, has two piecewise linear membership functions ${\mu }_{A^L}\left(x\right)$ and ${\mu }_{A^U}\left(x\right)$ defined by

$${\mu }_{A^L}(x)=\left\{\begin{array}{cc}\frac{x-a_l^L}{a_h^L-a_l^L}\hfill & a_l^L\le x\le a_h^L\hfill \\ \frac{a_u^L-x}{a_u^L-a_h^L}& a_h^L\le x\le a_u^L\hfill \\ 0 \hfill & otherwise\hfill \end{array}\right. \mathrm{and} {\mu }_{A^U}(x)=\left\{\begin{array}{cc}\frac{x-a_l^U}{a_h^U-a_l^U}\hfill & a_l^U\le x\le a_h^U\hfill \\ \frac{a_u^U-x}{a_u^U-a_h^U}\hfill & a_h^U\le x\le a_u^U\hfill \\ 0\hfill & otherwise\hfill \end{array}\right., \mathrm{where} a_h^L=a_h^U.$$

Let $((a_l^U,a_l^L),(a_h^L=a_h^U=a_h),(a_u^L,a_u^U))$ be the general TIVFN $A$. Herein, general triangular IVFNs (TIVFNs) are used to express IVFNs on the following computations.

Definition 3.

Let$A$ = $[A^L,A^U]$ be an IVFN. Then ${(A^L)}_{\alpha }^{-}$, ${(A^L)}_{\alpha }^{+}$, ${(A^U)}_{\alpha }^{-}$, and ${(A^U)}_{\alpha }^{+}$ extended from Lee’s [38,39] are, respectively, displayed as ${(A^L)}_{\alpha }^{-}=\underset{{\mu }_{A^L}(z)\ge \alpha }{\inf (z)}$, ${(A^L)}_{\alpha }^{+}=\underset{{\mu }_{A^L}(z)\ge \alpha }{\sup (z)}$, ${(A^U)}_{\alpha }^{-}=\underset{{\mu }_{A^U}(z)\ge \alpha }{\inf (z)}$, and ${(A^U)}_{\alpha }^{+}=\underset{{\mu }_{A^U}(z)\ge \alpha }{\sup (z)}$.

Definition 4.

A fuzzy preference relation (FPR) $R$ [46,47] is a fuzzy subset of $\Re \times \Re$ with a membership function ${\mu }_R(A,B)$ representing the preference degree of fuzzy numbers $A$ over $B$. (i) $R$ is reciprocal if ${\mu }_R(A,B)=1-{\mu }_R(B,A)$ for fuzzy numbers $A$ and $B$. (ii) $R$ is transitive if ${\mu }_R(A,B)\ge \frac{1}{2}$ and ${\mu }_R(B,C)\ge \frac{1}{2}$ $\Rightarrow$ ${\mu }_R(A,C)\ge \frac{1}{2}$ for fuzzy numbers $A$, $B$, and $C$. (iii) $R$ is a total ordering relation [48,49] if $R$ is both reciprocal and transitive on fuzzy numbers. As $A$ is compared with $B$ by $R$ [12], $A$ is smaller than $B$ if ${\mu }_R(A,B)<\frac{1}{2}$, whereas $A$ is bigger than $B$ if ${\mu }_R(A,B)>\frac{1}{2}$. Otherwise, $A$ is equal to $B$ if ${\mu }_R(A,B)=\frac{1}{2}$.

Definition 5.

An extended FPR (EFPR), $R^{\prime }$, is an extended fuzzy subset of $\Re \times \Re$ with membership function $-\infty \le {\mu }_{R^{\prime }}(A,B)\le \infty$ stands for the preference degree of fuzzy numbers $A$ over $B$[38,39]. (i) $R^{\prime }$ is reciprocal if ${\mu }_{R^{\prime }}(A,B)=-{\mu }_{R^{\prime }}(B,A)$ for fuzzy numbers $A$ and $B$. (ii) $R^{\prime }$ is transitive if ${\mu }_{R^{\prime }}(A,B)\ge 0$ and ${\mu }_{R^{\prime }}(B,C)\ge 0\Rightarrow$${\mu }_{R^{\prime }}(A,C)\ge 0$ for fuzzy numbers $A$, $B$, and $C$. (iii) $R^{\prime }$ is additive if ${\mu }_{R^{\prime }}(A,C)={\mu }_{R^{\prime }}(A,B)+{\mu }_{R^{\prime }}(B,C)$. (iv) $R^{\prime }$ is a total ordering relation if $R^{\prime }$ is reciprocal, transitive, and additive. Based on $R^{\prime }$, $A$ is smaller than $B$ if ${\mu }_{R^{\prime }}(A,B)<0$, whereas $A$ is bigger than $B$ if ${\mu }_{R^{\prime }}(A,B)>0$. Moreover, $A$ is equal to $B$ if ${\mu }_{R^{\prime }}(A,B)=0$.

Definition 6.

Let$A$ and $B$ be two general fuzzy numbers. Based on Lee [38,39], the EFPR ${\mu }_{R^{\prime }}(A,B)$ of $A$ over $B$ is defined as ${\displaystyle {\int }_0^1({(A-B)}_{\alpha }^{-}+}{(A-B)}_{\alpha }^{+})d\alpha$.

Definition 7.

For two IVFNs $A$ = $[A^L,A^U]$ and $B$ = $[B^L,B^U]$, the EFPR [40] ${\mu }_{P*}(A,B)$ of $A$ over $B$ is improved as $\frac{1}{2}{\displaystyle {\int }_0^1({(A^U-B^U)}_{\alpha }^{-}+{(A^L-B^L)}_{\alpha }^{-}+}{(A^L-B^L)}_{\alpha }^{+}+{(A^U-B^U)}_{\alpha }^{+})d\alpha$.

Lemma 4.

As$A$ = $((a_l^U,a_l^L),a_h,(a_u^L,a_u^U))$ and $B$ = $((b_l^U,b_l^L),b_h,(b_u^L,b_u^U))$ are two TIVFNs, the EFPR ${\mu }_{P*}(A,B)$ is yielded as $\frac{(a_l^U-b_u^U)+(a_l^L-b_u^L)+4(a_h-b_h)+(a_u^L-b_l^L)+(a_u^U-b_l^U)}{4}$.

Definition 8.

Let$A$ = $((a_l^U,a_l^L),a_h,(a_u^L,a_u^U))$ and $B$ = $((b_l^U,b_l^L),b_h,(b_u^L,b_u^U))$ be two TIVFNs. The addition computation $\oplus$ [15] for the two TIVFNs is $A$$\oplus$$B$ = $((a_l^U+b_l^U,a_l^L+b_l^L),a_h+b_h,(a_u^L+b_u^L,a_u^U+b_u^U))$.

Definition 9.

The multiplication computation $\otimes$ [15] of a real number, $\beta$, and a TIVFN $A$ = $((a_l^U,a_l^L),a_h,(a_u^L,a_u^U))$ is $\beta$$\otimes$$A$ = $\beta$$\otimes$$((a_l^U,a_l^L),a_h,(a_u^L,a_u^U))$ = $((\beta a_l^U,\beta a_l^L),\beta a_h,(\beta a_r^L,\beta a_r^U))$.

Definition 10.

Let $U_e(A)$ be the utility representative value of an IVFN, $A$, constructed on a utility representative function $U_e()$ and presented as $U_e(A)$ = $\frac{1}{2}{\mu }_{P*}(A,0)$ = $\frac{1}{4}({\displaystyle {\int }_0^1({(A^L)}_{\alpha }^{-}}+{(A^L)}_{\alpha }^{+})d\alpha +{\displaystyle {\int }_0^1({(A^U)}_{\alpha }^{-}}+{(A^U)}_{\alpha }^{+})d\alpha )$.

Lemma 5.

Let $U_e(A)$ be the utility representative value of a TIVFN $A$ = $((a_l^U,a_l^L),a_h,(a_u^L,a_u^U))$ from $U_e()$. Based on Definition 10, $U_e(A)$ = $\frac{1}{2}{\mu }_{P*}(A,0)$ = $\frac{a_l^U+a_l^L+4a_h+a_u^L+a_u^U}{8}$. As $A$ is a crisp value $a$ expressed by an IVFN $((a,a),a,(a,a))$, $U_e(A)$ is equal to $\frac{a+a+4a+a+a}{8}$(=$a$). It is said that the utility representative function can be also used in crisp values.

Definition 11.

For IVFNs $A_1,A_2,\dots ,A_n$, their sum is defined as ${{\displaystyle \tilde{\sum }}}_{i=1}^n{A}_i=A_1\oplus A_2\oplus \dots \oplus A_n$, where ${\displaystyle \tilde{\sum }}$, being the sum computation of fuzzy numbers, is discriminated from $\sum$, being the sum computation of crisp values.

3. QFD and AHP Extended under IVFE for Sustainability Evaluation of Port Expanding Locations

To FMCDM with DEC, QFD and AHP are extended under IVFE for the sustainability evaluation of port expanding locations. Related computations are expressed below.

In the interval-valued FMCDM problem, weights $W_1,W_2,\dots ,W_n$ of DEC (i.e., technical solutions) $C_1,C_2,\dots ,C_n$ can be yielded by extending QFD under IVFE. $D_1,D_2,\dots ,D_t$ are quality requirements assessed through users, and $W{D}_{kq}$ is a fuzzy important level of quality requirement $D_k$ evaluated by the $q$th user, where $k=1,2,\dots ,t$; $q=1,2,\dots ,s$. $W{D}_k$ is fuzzy important levels of $D_k$ after aggregating the opinions of all users. Thus, $W{D}_k$ = $\frac{1}{s}\otimes (W{D}_{k1}\oplus W{D}_{k2}\oplus \dots \oplus W{D}_{ks})$, $\forall k$, and then $WD$ = $\left[W{D}_1,W{D}_2,\dots ,W{D}_t\right]$ is a fuzzy important level matrix.

In QFD, weights of DEC are gained by associating $WD$ with a relation matrix $R$ that expresses the relationships between quality requirements over function solutions. To the relation matrix $R$, $R_{kjv}$ evaluated by the $v$th expert indicates the fuzzy relationship strength rating for $D_k$ over $C_j$, where $k=1,2,\dots ,t$; $j=1,2,\dots ,n$; $v=1,2,\dots ,f$. Then, $R_{kj}$ = $\frac{1}{f}\otimes (R_{kj1}\oplus R_{kj2}\oplus \dots \oplus R_{kjf})$ is the mean of relationship strength rating for $D_k$ over $C_j$, $\forall k,j$. In addition,

$$\begin{gathered} C_1{C}_2\dots C_n \\ R=\begin{array}{c}{D}_1\\ D_2\\ ⋮\\ D_t\end{array}\left[\begin{array}{cccc}{R}_{11}& R_{12}& \cdots & R_{1n}\\ R_{21}& R_{22}& \cdots & R_{2n}\\ ⋮& ⋮& \cdots & ⋮\\ R_{t1}& R_{t2}& \cdots & R_{tn}\end{array}\right] \end{gathered}$$

(1)

represents the relation matrix for quality requirements over function solutions after aggregating all experts’ opinions. Based on the above, $W$ is yielded by generating QFD under fuzzy environment into a weight matrix, and thus

$$W=\frac{1}{t}\left[W{D}_1,W{D}_2,\dots ,W{D}_t\right]\left[\begin{array}{cccc}{R}_{11}& R_{12}& \cdots & R_{1n}\\ R_{21}& R_{22}& \cdots & R_{2n}\\ ⋮& ⋮& \cdots & ⋮\\ R_{t1}& R_{t2}& \cdots & R_{tn}\end{array}\right]=\left[W_1,W_2,\dots ,W_n\right]$$

(2)

where

$$W_j=\frac{1}{t}\left[W{D}_1,W{D}_2,\dots ,W{D}_t\right]\left[\begin{array}{c}{R}_{1j}\\ R_{2j}\\ ⋮\\ R_{tj}\end{array}\right]=\frac{1}{t}\otimes (W{D}_1\otimes R_{1j}\oplus W{D}_2\otimes R_{2j}\oplus \dots \oplus W{D}_t\otimes R_{tj}), \forall j.$$

Practically, multiplying two fuzzy numbers [50] would form a PFN. In generalizing QFD under fuzzy environment, corresponding computations of PFNs may be necessary but complicated, especially for the environment constructed on IVFNs. For instance, $W{D}_k$ = $((w{d}_{kl}^U,w{d}_{kl}^L),w{d}_{kh},(w{d}_{ku}^L,w{d}_{ku}^U))$ and $R_{kj}$ = $((r_{kjl}^U,r_{kjl}^L),r_{kjh},(r_{kju}^L,r_{kju}^U))$, $\forall k,j$. $W{D}_k\otimes R_{kj}$ = $((P_{kj}^U,P_{kj}^L),Q_{kj},(Z_{kj}^L,Z_{kj}^U);(F_{kj}^L,F_{kj}^U),(T_{kj}^L,T_{kj}^U);(Y_{kj}^L,Y_{kj}^U),(V_{kj}^L,V_{kj}^U))$, $\forall k,j$. Moreover, the membership function of $W{D}_k\otimes R_{kj}$ [40] is presented as

$${\mu }_{W{D}_k\otimes R_{kj}}(x)=\left\{\begin{array}{ccc}\frac{\{-F_{kj}^U+{[{(F_{kj}^U)}^2-4(P_{kj}^U-x)T_{kj}^U]}^{1/2}\}}{2T_{kj}^U}\hfill & if\hfill & P_{kj}^U\le x\le Q_{kj}\hfill \\ \frac{\{-F_{kj}^L+{[{(F_{kj}^L)}^2-4(P_{kj}^L-x)T_{kj}^L]}^{1/2}\}}{2T_{kj}^L}\hfill & if\hfill & P_{kj}^L\le x\le Q_{kj}\hfill \\ 1\hfill & if\hfill & x=Q_{kj}\hfill \\ \frac{\{Y_{kj}^L-{[{(Y_{kj}^L)}^2-4(Z_{kj}^L-x)V_{kj}^L]}^{1/2}\}}{2V_{kj}^L}\hfill & if\hfill & Q_{kj}\le x\le Z_{kj}^L\hfill \\ \frac{\{Y_{kj}^U-{[{(Y_{kj}^U)}^2-4(Z_{kj}^U-x)V_{kj}^U]}^{1/2}\}}{2V_{kj}^U}\hfill & if\hfill & Q_{kj}\le x\le Z_{kj}^U\hfill \\ 0\hfill & & otherwise\hfill \end{array}\right.$$

(3)

where

• $P_{kj}^L=w{d}_{kl}^L{r}_{kjl}^L$, $P_{kj}^U=w{d}_{kl}^U{r}_{kjl}^U$,
• $Q_{kj}=w{d}_{kh}{r}_{kjh}$,
• $Z_{kj}^L=w{d}_{ku}^L{r}_{kju}^L$, $Z_{kj}^U=w{d}_{ku}^U{r}_{kju}^U$,
• $F_{kj}^L=w{d}_{kl}^L(r_{kjh}-r_{kjl}^L)+r_{kjl}^L(w{d}_{kh}-w{d}_{kl}^L)$, $F_{kj}^U=w{d}_{kl}^U(r_{kjh}-r_{kjl}^U)+r_{kjl}^U(w{d}_{kh}-w{d}_{kl}^U)$,
• $T_{kj}^L=(w{d}_{kh}-w{d}_{kl}^L)(r_{kjh}-r_{kjl}^L)$, $T_{kj}^U=(w{d}_{kh}-w{d}_{kl}^U)(r_{kjh}-r_{kjl}^U)$,
• $Y_{kj}^L=w{d}_{ku}^L(r_{kju}^L-r_{kjh})+r_{kju}^L(w{d}_{ku}^L-w{d}_{kh})$, $Y_{kj}^U=w{d}_{ku}^U(r_{kju}^U-r_{kjh})+r_{kju}^U(w{d}_{ku}^U-w{d}_{kh})$,
• $V_{kj}^L=(w{d}_{ku}^L-w{d}_{kh})(r_{kju}^L-r_{kjh})$, $V_{kj}^U=(w{d}_{ku}^U-w{d}_{kh})(r_{kju}^U-r_{kjh})$.

Based on above, the PFN $W{D}_k\otimes R_{kj}$ would not be a TIVFN. It is evident that corresponding computations of PFNs for FMCDM are hard. To resolve the hard computation above, the EFPR values (i.e., utility representative values) of the fuzzy important levels over their comparison basis are substituted for the fuzzy important levels in quality requirements. Due to $W{D}_k$ ($\forall k$) > 0, the common comparison basis of the preference relations for IVFNs is assumed as 0. The utility representative value of $W{D}_k$ yielded as $U_e(W{D}_k)$ = $\frac{w{d}_{kl}^U+w{d}_{kl}^L+4w{d}_{kh}+w{d}_{ku}^L+w{d}_{ku}^U}{8}$ denote the preference degree of $W{D}_k$ over 0, $\forall k$. Through the relative preference degrees of fuzzy important levels over 0, $W^{\prime }$ is assumed to be the adjusted fuzzy weight matrix for yielding DEC, and thus

$$W^{\prime }=\frac{1}{t}\otimes \left[U_e(W{D}_1),U_e(W{D}_2),\dots ,U_e(W{D}_t)\right]\left[\begin{array}{cccc}{R}_{11}& R_{12}& \cdots & R_{1n}\\ R_{21}& R_{22}& \cdots & R_{2n}\\ ⋮& ⋮& \cdots & ⋮\\ R_{t1}& R_{t2}& \cdots & R_{tn}\end{array}\right]=\left[{W_1}^{\prime },{W_2}^{\prime },\dots ,{W_n}^{\prime }\right],$$

(4)

where ${W_j}^{\prime }$ = $\frac{1}{t}\otimes \left[U_e(W{D}_1),U_e(W{D}_2),\dots ,U_e(W{D}_t)\right]$$\left[\begin{array}{c}{R}_{1j}\\ R_{2j}\\ ⋮\\ R_{tj}\end{array}\right]$ $=\frac{1}{t}\otimes (U_e(W{D}_1)\otimes R_{1j}\oplus U_e(W{D}_2)\otimes R_{2j}\oplus \dots \oplus U_e(W{D}_t)\otimes R_{tj})$, $\forall j$.

${W_j}^{\prime }$ is a TIVFN due to $U_e(W{D}_k)$ being a crisp value and $R_{kj}$ being a TIVFN $\forall k,j$. Then, the adjusted fuzzy weight ${W_j}^{\prime }$, being a TIVFN, is recognized as the representation values of $W_j$ and used in interval-valued FMCDM with DEC, $\forall j$.

The utility representative function $U_e()$ in previous descriptions is utilized for adjusted fuzzy weights, and also used in extending AHP under the fuzzy environment. In fuzzy extension of AHP, yielding priority vectors of FPWCMs for weights are critical, but related works are hard. Herein, the priorities from the fuzzy pairwise comparison matrix (FPWCM) of IDEC based on evaluation objective are unnecessary because adjusted fuzzy weights are gained for DEC. Practically, ANP [4] is more suitable than AHP [5] for the consideration of DEC. However, the fuzzy extended computation of ANP is very complicated. Hence, the computation of QFD is substituted for yielding priorities of pairwise weight comparison matrix in AHP. For traditional AHP, several approximating solutions [5], including normalization of row arithmetic averages (NRA), were proposed to derive the eigenvector of AHP. These approximating computations might be easy in obtaining the eigenvectors of pairwise comparison matrices; however, extended under fuzzy environment, they were still complicated and hard. For instance, the simplest NRA of the approximating solutions extended under fuzzy environment expresses the computation difficulty. Hence, the other approximating computations will be also hard, and related demonstrations are presented as follows.

For sustainability evaluation of port expanding locations, let

$$G_j={(g_{uvj})}_{m\times m}=\left[\begin{array}{cccc}{g}_{1j}/g_{1j}& g_{1j}/g_{2j}& \cdots & g_{1j}/g_{mj}\\ g_{2j}/g_{1j}& g_{2j}/g_{2j}& \cdots & g_{2j}/g_{mj}\\ ⋮& ⋮& \cdots & ⋮\\ g_{mj}/g_{1j}& g_{mj}/g_{2j}& \cdots & g_{mj}/g_{mj}\end{array}\right]$$

(5)

Be a $m\times m$ pairwise comparison matrix for $m$ alternatives (i.e., locations) based on the $j$th criterion in AHP, where $g_{uvj}$ = $g_{uj}/g_{vj}$ denotes the rating ratio of location $u$ over location $v$ based on criterion $j$, and $g_{vuj}={(g_{uvj})}^{-1}$ for $u=1,2,\dots ,m$; $v=1,2,\dots ,m$; $j=1,2,\dots ,n$. In NRA [5], the $u$th priority $g_{uj}$ of $G_j$ is computed as $g_{uj}=\frac{{\displaystyle {\sum }_{v=1}^m{g}_{uvj}}}{{\displaystyle {\sum }_{u=1}^m{\displaystyle {\sum }_{v=1}^m{g}_{uvj}}}}$. The computation is difficult as the process is transferred in extending AHP under fuzzy environment. Herein, ${\tilde{G}}_j$ = ${(G_{uvj})}_{m\times m}$ is a FPWCM of locations based on the $j$th criterion, and $G_{uj}$ stands for the $u$th fuzzy priority in ${\tilde{G}}_j$. For NRA being extended under fuzzy environment, $G_{uj}$ = $({{\displaystyle \tilde{\sum }}}_{v=1}^m{G}_{uvj})\otimes {({{\displaystyle \tilde{\sum }}}_{u=1}^m{{\displaystyle \tilde{\sum }}}_{v=1}^m{G}_{uvj})}^{-1}$, where $G_{uvj}$ denotes the fuzzy rating ratio of location $u$ over location $v$ based on criterion $j$, and $G_{vuj}$ = ${(G_{uvj})}^{-1}$, $\forall u,v$. Due to $G_{uvj}$ being a fuzzy number, both ${{\displaystyle \tilde{\sum }}}_{v=1}^m{G}_{uvj}$ and ${{\displaystyle \tilde{\sum }}}_{u=1}^m{{\displaystyle \tilde{\sum }}}_{v=1}^m{G}_{uvj}$ are fuzzy numbers as well. Based on the above, $G_{uj}$ derived is hard because addition and division of fuzzy numbers are not easy, $\forall u,v$. Despite approximating computation, division for fuzzy numbers does not exist truly. Therefore, the utility representative function of Section 3 is also used in approximating computations of NRA to yield the priorities of FPWCMs because $({{\displaystyle \tilde{\sum }}}_{v=1}^m{G}_{uvj})\otimes {({{\displaystyle \tilde{\sum }}}_{u=1}^m{{\displaystyle \tilde{\sum }}}_{v=1}^m{G}_{uvj})}^{-1}$ is fuzzy multiplication, similar as Chou’s [32] multiplication operation, where ${({{\displaystyle \tilde{\sum }}}_{u=1}^m{{\displaystyle \tilde{\sum }}}_{v=1}^m{G}_{uvj})}^{-1}$ is the multiplicative inverse of ${{\displaystyle \tilde{\sum }}}_{u=1}^m{{\displaystyle \tilde{\sum }}}_{v=1}^m{G}_{uvj}$.

Based on the above, Wang [26] proposed the representative utility function for NRA computation about TFNs. Similar to Wang’s computations, the priority representation ${g_{uj}}^{\prime }$ through the utility representative function is

$${g_{uj}}^{\prime }=\frac{U_e(G_{uj})}{{\displaystyle {\sum }_{u=1}^m{U}_e(G_{uj})}}=\frac{U_e({{\displaystyle \tilde{\sum }}}_{v=1}^m{G}_{uvj})\times U_e({({{\displaystyle \tilde{\sum }}}_{u=1}^m{{\displaystyle \tilde{\sum }}}_{v=1}^m{G}_{uvj})}^{-1})}{{\displaystyle {\sum }_{u=1}^m(U_e({{\displaystyle \tilde{\sum }}}_{v=1}^m{G}_{uvj})\times U_e({({{\displaystyle \tilde{\sum }}}_{u=1}^m{{\displaystyle \tilde{\sum }}}_{v=1}^m{G}_{uvj})}^{-1}))}}=\frac{U_e({{\displaystyle \tilde{\sum }}}_{v=1}^m{G}_{uvj})}{{\displaystyle {\sum }_{u=1}^m{U}_e({{\displaystyle \tilde{\sum }}}_{v=1}^m{G}_{uvj})}}$$

(6)

with $G_{uvj}$ being an IVFN stands for the rating ratio of location $u$ over location $v$ based on criterion $j$ in the corresponding FPWCM, $\forall u,v,j$. Let $G_j$ = ${({g_{1j}}^{\prime },{g_{2j}}^{\prime },\dots ,{g_{mj}}^{\prime })}^T$—that is the transpose of $({g_{1j}}^{\prime },{g_{2j}}^{\prime },\dots ,{g_{mj}}^{\prime })$—be the priority representative vector composed of ${g_{1j}}^{\prime },{g_{2j}}^{\prime },\dots ,{g_{mj}}^{\prime }$, $\forall j$. In addition, the priority representative matrix $G$ is formatted as

$$G=G_1\cup G_2\cup \dots \cup G_n=\left[\begin{array}{cccc}{g_{11}}^{\prime }& {g_{12}}^{\prime }& \cdots & {g_{1n}}^{\prime }\\ {g_{21}}^{\prime }& {g_{22}}^{\prime }& \cdots & {g_{2n}}^{\prime }\\ ⋮& ⋮& \cdots & ⋮\\ {g_{m1}}^{\prime }& {g_{m2}}^{\prime }& \cdots & {g_{mn}}^{\prime }\end{array}\right].$$

(7)

With $W^{\prime }$ and $G$, the alternative performance indices are derived. Let $PA$ = ${(p{a}_1,p{a}_2,\dots ,p{a}_m)}^T$ be the performance index vector, where ${(p{a}_1,p{a}_2,\dots ,p{a}_m)}^T$ is the transpose of $(p{a}_1,p{a}_2,\dots ,p{a}_m)$. Let

$$PA=G\times {(W^{\prime })}^T=\left[\begin{array}{cccc}{g_{11}}^{\prime }& {g_{12}}^{\prime }& \cdots & {g_{1n}}^{\prime }\\ {g_{21}}^{\prime }& {g_{22}}^{\prime }& \cdots & {g_{2n}}^{\prime }\\ ⋮& ⋮& \cdots & ⋮\\ {g_{m1}}^{\prime }& {g_{m2}}^{\prime }& \cdots & {g_{mn}}^{\prime }\end{array}\right]\left[\begin{array}{c}{W_1}^{\prime }\\ {W_2}^{\prime }\\ ⋮\\ {W_n}^{\prime }\end{array}\right]=\left[\begin{array}{c}p{a}_1\\ p{a}_2\\ ⋮\\ p{a}_m\end{array}\right],$$

(8)

where $p{a}_u$ = ${{\displaystyle \tilde{\sum }}}_{j=1}^n{g}_{uj}\otimes {W_j}^{\prime }$$=(g_{u1}\otimes {W_1}^{\prime })\oplus (g_{u2}\otimes {W_2}^{\prime })\oplus \dots \oplus (g_{un}\otimes {W_n}^{\prime })$ is the performance index of alternative $u$, $\forall u$. Due to $p{a}_1$, $p{a}_2$, …, $p{a}_m$ being IVFNs, alternatives are ranked according to $U_e(p{a}_1)$, $U_e(p{a}_2)$,…,$U_e(p{a}_m)$. Then, extending QFD and AHP under IVFE for sustainability evaluation of port expanding locations is finished because the optimal alternative is determined.

Moreover, preference consistency [51] of FPWCMs was important. Hence, Wang’s [17] consistency computations of IVFNs are applied to yield the consistency test of FPWCMs in this paper. To the consistency test, the consistency ratio (CR) indicates the ratio of consistency index (CI) over random index (RI). For AHP [5], the values of RI based on varied ranks are presented in

Table 1. The values of RI based on varied ranks.

Ranks	1	2	3	4	5	6	7	8	9	10
RI’s values	0	0	0.58	0.9	1.12	1.24	1.32	1.41	1.45	1.49

below. Commonly, CR < 0.1 denotes that the pairwise comparison matrix conforms to preference consistency.

Through Wang [17], CI between criteria and locations for criterion $j$ is yielded as ${\lambda }_{\max \_j}={\displaystyle {\sum }_{u=1}^m\frac{{\displaystyle {\sum }_{v=1}^m(U_e(G_{uvj}})\times {g_{vj}}^{\prime })}{m\times {g_{uj}}^{\prime }}}$ and $C{I}_{Between criteria and locations for criterion j}=\frac{1}{t}\times \frac{{\lambda }_{\max \_j}-m}{m-1}$. Moreover, $C{R}_{Between criteria and locations for criterion j}=\frac{C{I}_{Between criteria and locations for criterion j}}{R{I}_m}$, $\forall j$. Then CR of the whole hierarchy (i.e., CRH) is derived as CRH = $\frac{{\displaystyle {\sum }_{j=1}^n(U_e({W_j}^{\prime })\times C{I}_{Between criteria and locations for criterion j})}}{{\displaystyle {\sum }_{j=1}^n(U_e({W_j}^{\prime })\times R{I}_m)}}$. As CRH < 0.1, the related FPWCMs for sustainability evaluation of port expanding locations conforms to preference consistency of the whole hierarchy. Generally, weight consistency of pairwise comparison matrices in CRH should be also taken into consideration for AHP. However, the weights of DEC had derived by extending QFD; thus, the weights are not considered in CRH of extending QFD and AHP for FMCDM with DEC.

4. Illustrating Example for Sustainability Evaluation of Taipei Port’s Expanding Locations with DEC

In Taiwan, three main harbors are Kaohsiung port, Taichung port, and Taipei port. For these harbors, Taipei port, established in 1993, is relatively new compared to the others, and thus numerous corresponding expansions are necessary. To Taipei port’s expanding on sustainability, three candidate locations based on criteria are assessed. In QFD, three fundamental aspects are recognized as quality requirements being environmental ($D_1$), social ($D_2$), and economic ($D_3$), evaluated by thirty professional users, and $W{D}_1,W{D}_2,W{D}_3$ are, respectively, the fuzzy importance levels of these requirements. Herein, criteria are considered to be four function solutions that are compatible ($C_1$), feasible ($C_2$), recyclable ($C_3$), and stable ($C_4$), employed by ten experts. The function solutions and the previous quality requirements are tightly connected, as shown on Figure 4. to indicate the relationships between DEC. Moreover, corresponding fuzzy weights $W_1,W_2,W_3,W_4$ are yielded in the sustainability evaluation problem of candidate locations for Taipei port’s expanding.

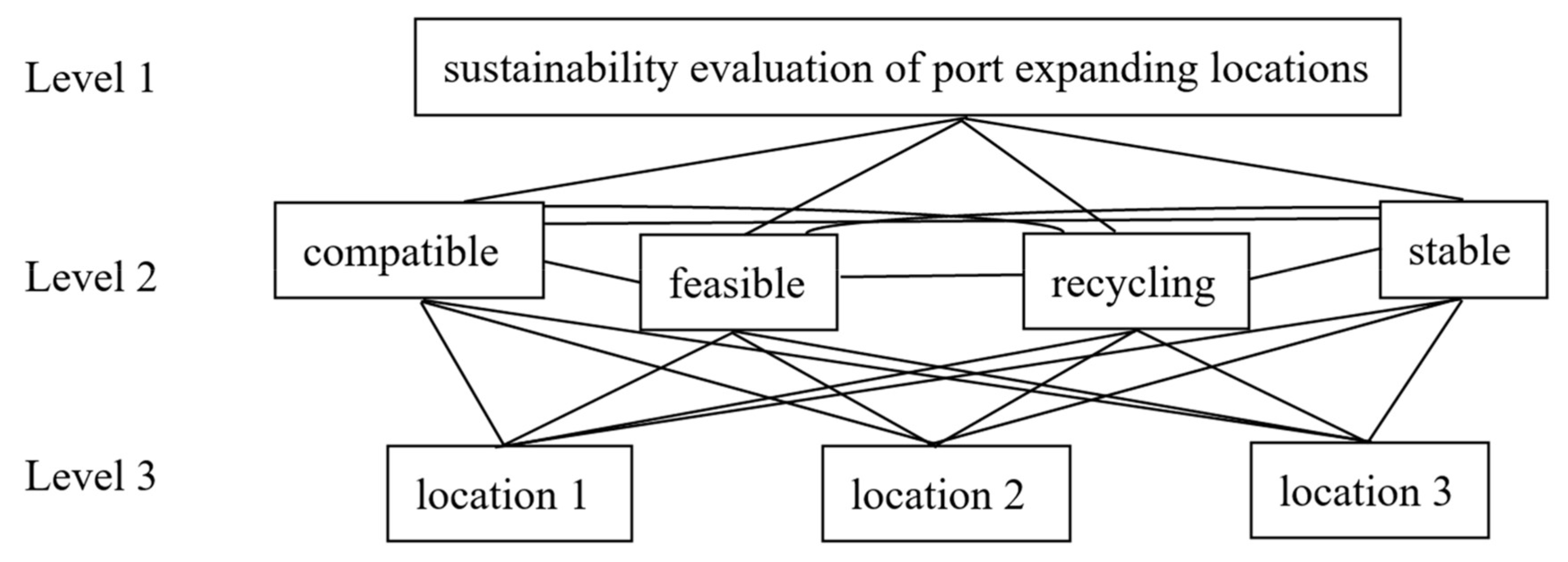
Based on the above, the related hierarchical structure is presented in Figure 5, where sustainability evaluation of port expanding locations is denoted in Level 1, DEC are indicated in Level 2, and candidate locations are displayed in Level 3. According to the hierarchical structure for the sustainability evaluation of port expanding locations, it is evident that the four evaluation criteria are dependent. AHP is not enough to resolve the sustainability evaluation problem with dependent criteria, whereas ANP may be used in the situation. However, ANP is more complicated than AHP on computation, and experts take much time to determine relative weights in the rating process. To simplify computations of DEC for experts, QFD is combined with AHP for replacing ANP on sustainability evaluation of port expanding locations. Further, DEC compatible, feasible, recycling, and stable are conceptualized functions. In fact, these DEC, through the system analysis assistant, can be subdivided and added according to the necessary experts. In other words, these DEC are conceptually formed and flexibly adjusted to conform to the requirements of evaluation.

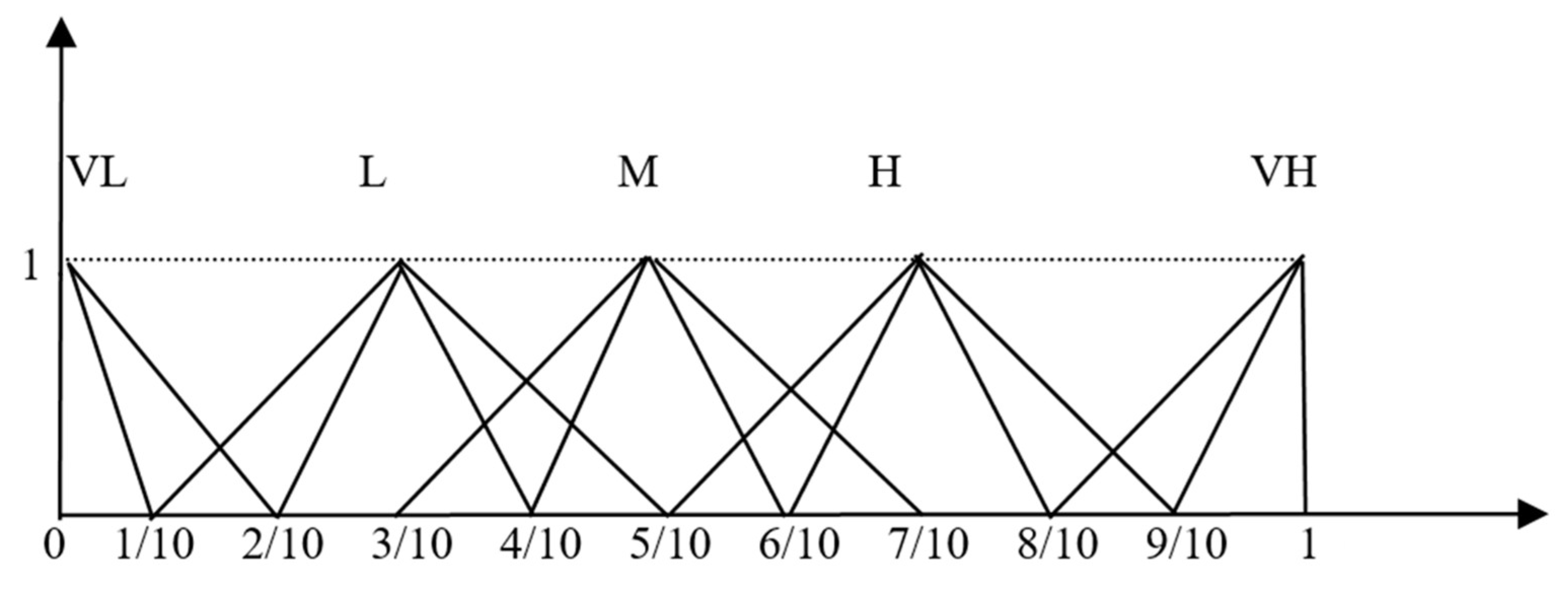
Through QFD, importance levels are measured from a linguistic term set {very low (VL), low (L), medium (M), high (H), very high (VH)}. These linguistic terms and corresponding IVFNs are shown in

Table 2. Linguistic evaluation terms and corresponding IVFNs.

Linguistic Terms	IVFNs
VL	((0, 0), 0, (1/10, 2/10))
L	((1/10, 2/10), 3/10, (4/10, 5/10))
M	((3/10, 4/10), 5/10, (6/10, 7/10))
H	((5/10, 6/10), 7/10, (8/10, 9/10))
VH	((8/10, 9/10), 1, (1, 1))

. In addition, linguistic assessments employed through professional users containing crews of harbors, shipping companies, and shipping agents are displayed in

Table 3. Linguistic assessments for quality requirements of candidate locations for port expanding.

Quality Requirements	Linguistic Assessments from Users
	VL	L	M	H	VH
Environmental	3	1	4	9	13
Social	5	6	3	6	10
Economic	0	1	7	9	13

, and fuzzy importance levels of quality requirements according to entries of Table 2 and Table 3 are aggregated in

Table 4. Fuzzy importance levels for quality requirements of candidate locations for port expanding.

Quality Requirements	Fuzzy Importance Levels
Environmental	((0.540, 0.630), 0.720, (0.777, 0.833, 2.830))
Social	((0.417, 0.500), 0.583, (0.650, 0.717, 2.308))
Economic	((0.570, 0.670), 0.770, (0.827, 0.883, 3.015))

. Moreover, the relationships between IVFNs of Table 2 are shown in Figure 6.

Through entries of Table 4, utility representative values of fuzzy importance levels are computed in

Table 5. Utility representative values of fuzzy importance levels of candidate locations for port expanding.

Quality Requirements	Relative Preference Degrees
Environmental	0.7075
Social	0.5771
Economic	0.7538

.

Herein, linguistic relationship strength assessments for quality requirements over function solutions are shown in

Table 6. Linguistic relationship strength assessments for quality requirements over function solutions.

Linguistic Assessments	Environmental					Social					Economic
	VL	L	M	H	VH	VL	L	M	H	VH	VL	L	M	H	VH
Compatible	1	0	1	3	5	1	1	1	1	6	3	1	0	1	5
Feasible	1	0	3	3	3	0	1	0	4	5	1	3	0	3	3
Recycling	1	2	2	2	3	1	2	6	1	0	1	0	2	2	5
Stable	1	1	0	3	5	1	2	3	1	3	1	1	1	1	6

, and the table is gained by experts containing managers of harbors, shipping companies, and shipping agents through the previous linguistic term set. Then, linguistic relationship strength ratings of Table 6 are derived to construct a relation matrix. This is presented in

Table 7. A relation matrix for three quality requirements over four function solutions.

	Compatible	Feasible
Environmental	((0.58, 0.67), 0.76, (0.81, 0.86))	((0.48, 0.57), 0.66, (0.73, 0.80))
Social	((0.57, 0.66), 0.75, (0.79, 0.83))	((0.61, 0.71), 0.81, (0.86, 0.91))
Economic	((0.46, 0.53), 0.60, (0.65, 0.70))	((0.42, 0.51), 0.60, (0.67, 0.74))
	Recycling	Stable
Environmental	((0.42, 0.51), 0.60, (0.67, 0.74))	((0.56, 0.65), 0.74, (0.79, 0.84))
Social	((0.25, 0.34), 0.43, (0.53, 0.63))	((0.40, 0.49), 0.58, (0.65, 0.72))
Economic	((0.56, 0.65), 0.74, (0.79, 0.84))	((0.57, 0.66), 0.75, (0.79, 0.83))

.

According to entries of Table 5 and Table 7, an adjusted fuzzy weight matrix is expressed in

Table 8. The adjusted fuzzy weight matrix.

${W_1}^{\prime }$	${W_2}^{\prime }$
((0.3620, 0.4181), 0.4743, (0.5063, 0.5384))	((0.3361, 0.3991), 0.4622, (0.5059, 0.5496))
${W_3}^{\prime }$	${W_4}^{\prime }$
((0.2878, 0.3490), 0.4101, (0.4584, 0.5068))	((0.3522, 0.4134), 0.4745, (0.5098, 0.5451))

.

As the adjusted fuzzy weight matrix is yielded, the opinions of related users in the available questionnaires are indicated by pairwise comparison ratios that are absolute unimportance (=1/9), very strong unimportance (=1/7), essential unimportance (=1/5), weak unimportance (=1/3), equal importance (=1), weak importance (=3), essential importance (=5), very strong importance (=7), and absolute importance (=9). Then, the pairwise comparison ratios are aggregated into TIVFNs shown in FPWCMs of candidate locations based on evaluation criteria. For the FPWCM of candidate locations, let $q_{uvjk}$ denote the relative rating ratio of location $u$ over location $v$ based on criterion $j$ employed by the $k$th user, $\forall u,v,j,k$. The converting formula, through sample mean and sample standard deviation [52], is indicated as

$$G_{uvj}=((g_{uvjl}^U,g_{uvjl}^L),g_{uvjh},(g_{uvjr}^L,g_{uvjr}^U)),$$

(9)

where

$$\begin{array}{c}{g}_{uvjl}^U=\hfill \\ \left\{\begin{array}{c}{\min }_{k=1,2,\dots ,t}(q_{uvjk}) if \min ({\min }_{k=1,2,\dots ,t}(q_{uvjk}),\frac{1}{t}{\displaystyle {\sum }_{k=1}^t{q}_{uvjk}}-{(\frac{{\displaystyle {\sum }_{k=1}^t(q_{uvjk}}-\frac{1}{t}{\displaystyle {\sum }_{k=1}^t{q}_{uvjk}}{)}^2}{t-1})}^{1/2})<0\hfill \\ \min ({\min }_{k=1,2,\dots ,t}(q_{uvjk}),\frac{1}{t}{\displaystyle {\sum }_{k=1}^t{q}_{uvjk}}-{(\frac{{\displaystyle {\sum }_{k=1}^t(q_{uvjk}}-\frac{1}{t}{\displaystyle {\sum }_{k=1}^t{q}_{uvjk}}{)}^2}{t-1})}^{1/2})\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}otherwise\hfill \end{array}\right.,\hfill \\ g_{uvjl}^L=\max ({\min }_{k=1,2,\dots ,t}(q_{uvjk}),\frac{1}{t}{\displaystyle {\sum }_{k=1}^t{q}_{uvjk}}-{(\frac{{\displaystyle {\sum }_{k=1}^t(q_{uvjk}}-\frac{1}{t}{\displaystyle {\sum }_{k=1}^t{q}_{uvjk}}{)}^2}{t-1})}^{1/2}),\hfill \\ g_{uvjh}=\frac{1}{t}{\displaystyle {\sum }_{k=1}^t{q}_{uvjk}},\hfill \\ g_{uvjr}^L=\min ({\max }_{k=1,2,\dots ,t}(q_{uvjk}),\frac{1}{t}{\displaystyle {\sum }_{k=1}^t{q}_{uvjk}}+{(\frac{{\displaystyle {\sum }_{k=1}^t(q_{uvjk}}-\frac{1}{t}{\displaystyle {\sum }_{k=1}^t{q}_{uvjk}}{)}^2}{t-1})}^{1/2}), \mathrm{and}\hfill \\ g_{uvjr}^U=\max ({\max }_{k=1,2,\dots ,t}(q_{uvjk}),\frac{1}{t}{\displaystyle {\sum }_{k=1}^t{q}_{uvjk}}+{(\frac{{\displaystyle {\sum }_{k=1}^t(q_{uvjk}}-\frac{1}{t}{\displaystyle {\sum }_{k=1}^t{q}_{uvjk}}{)}^2}{t-1})}^{1/2}).\hfill \end{array}$$

In addition, $G_{vuj}={(G_{uvj})}^{-1}$$\approx ((1/g_{uvjr}^U,1/g_{uvjr}^L),1/g_{uvjh},(1/g_{uvjl}^L,1/g_{uvjl}^U))$ expresses the multiplicative inverse of $G_{uvj}$, where $u=1,2,3$; $v=1,2,3$; $j=1,2,3,4$. As $t$ = 190, four FPWCMs representing these candidate locations of port expanding based on four criteria including compatible, feasible, recycling, and stable items are indicated as

Table 9. FPWCM for locations based on compatible item.

C1	A1	A2	A3
A1	((1, 1), 1, (1, 1))	((0.1111, 0.3282), 2.7305, (5.1328, 9))	((0.1111, 0.3756), 2.4663, (4.5570, 9))
A2	((0.1111, 0.1948), 0.3662, (3.0473, 9))	((1, 1), 1, (1, 1))	((0.1111, 0.2254), 2.3348, (4.4443, 9))
A3	((0.1111, 0.2194), 0.4055, (2.6624, 9))	((0.1111, 0.2250), 0.4283, (4.4374, 9))	((1, 1), 1, (1, 1))

,

Table 10. FPWCM for locations based on feasible item.

C2	A1	A2	A3
A1	((1, 1), 1, (1, 1))	((0.1111, 0.3082), 2.5423, (4.7765, 9))	((0.1111, 0.2050), 2.3403, (4.4756, 9))
A2	((0.1111, 0.2094), 0.3933, (3.2488, 9))	((1, 1), 1, (1, 1))	((0.1111, 0.2555), 2.3144, (4.3732, 9))
A3	((0.1111, 0.2234), 0.4273, (4.8789, 9))	((0.1111, 0.2287), 0.4321, (3.9132, 9))	((1, 1), 1, (1, 1))

,

Table 11. FPWCM for locations based on recycling item.

C3	A1	A2	A3
A1	((1, 1), 1, (1, 1))	((0.1111, 0.2046), 2.6532, (5.1019, 9))	((0.1111, 0.1599), 2.5004, (4.8410, 9))
A2	((0.1111, 0.1960), 0.3769, (4.8883, 9))	((1, 1), 1, (1, 1))	((0.1111, 0.1126), 2.5530, (4.9934, 9))
A3	((0.1111, 0.2066), 0.3999, (6.2552, 9))	((0.1111, 0.2003), 0.3917, (8.8814, 9))	((1, 1), 1, (1, 1))

and

Table 12. FPWCM for locations based on stable item.

C4	A1	A2	A3
A1	((1, 1), 1, (1, 1))	((0.1111, 0.4846), 2.9130, (5.3414, 9))	((0.1429, 0.1894), 2.6487, (5.1080, 9))
A2	((0.1111, 0.1872), 0.3433, (2.0635, 9))	((1, 1), 1, (1, 1))	((0.1111, 0.2324), 2.6628, (5.0933, 9))
A3	((0.1111, 0.1958), 0.3775, (5.2786, 7))	((0.1111, 0.1963), 0.3755, (4.3034, 9))	((1, 1), 1, (1, 1))

, respectively.

According to entries of the four tables above, the priority representation vectors of three port expanding locations based on compatible, feasible, recycling, and stable items are, respectively, derived as (0.4117,0.3223,0.2661)${}^T$, (0.3978,0.3234,0.2788)${}^T$, (0.3804,0.3204,0.2991)${}^T$, and (0.4180,0.3212,0.2608)${}^T$. Moreover, CI = 0.0070 and CR = 0.0121 < 0.1 for the FPWCM of three locations based on compatible item, CI = 0.0072 and CR = 0.0124 < 0.1 for the FPWCM of three locations based on feasible item, CI = 0.0084 and CR = 0.0145 < 0.1 for the FPWCM of three locations based on recycling item, and CI = 0.0073 and CR = 0.0125 < 0.1 for the FPWCM of three locations based on stable item. Evidently, these FPWCMs conform to preference consistency. Then, CRH is yielded as

$$\begin{gathered} U_e({W_1}^{\prime })=\frac{0.3620+0.4181+4\times 0.4743+0.5063+0.5384}{8}=0.4652, \\ {U}_e({W_2}^{\prime })=\frac{0.3361+0.3991+4\times 0.4622+0.5059+0.5496}{8}=0.4550, \\ {U}_e({W_3}^{\prime })=\frac{0.2878+0.3490+4\times 0.4101+0.4584+0.5068}{8}=0.4053, \\ {U}_e({W_4}^{\prime })=\frac{0.3522+0.4134+4\times 0.4745+0.5098+0.5451}{8}=0.4648, \mathrm{and} \mathrm{then} \\ \mathrm{CRH}=\frac{0.4652\times 0.0070+0.4550\times 0.0072+0.4053\times 0.0084+0.4648\times 0.0073}{0.4652\times 0.58+0.4550\times 0.58+0.4053\times 0.58+0.4648\times 0.58}=0.0128 < 0.1. \end{gathered}$$

Therefore, the whole hierarchy for the sustainability evaluation of port expanding locations satisfies preference consistency as well.

From the entries of Table 8 and the priority representation vectors of three port expanding locations based on four sustainability evaluation criteria, the performance indices are derived as

$$\begin{array}{c}PA=G\times {(W^{\prime })}^T\hfill \\ =\left[\begin{array}{cccc}0.4117& 0.3978& 0.3804& 0.4180\\ 0.3223& 0.3234& 0.3204& 0.3212\\ 0.2661& 0.2788& 0.2991& 0.2608\end{array}\right]\left[\begin{array}{c}((0.3620,0.4181),0.4743,(0.5063,0.5384))\\ ((0.3361,0.3991),0.4622,(0.5059,0.5496))\\ ((0.2878,0.3490),0.4101,(0.4584,0.5068))\\ ((0.3522,0.4134),0.4745,(0.5098,0.5451))\end{array}\right]\hfill \\ =\left[\begin{array}{c}((0.5394,0.6364),0.7335,(0.7972,0.8609))\\ ((0.4307,0.5085),0.5862,(0.6375,0.6887))\\ ((0.3680,0.4347),0.5015,(0.5459,0.5902))\end{array}\right].\hfill \end{array}$$

Therefore,

$$\begin{array}{c}{U}_e(p{a}_1)=\frac{0.5394+0.6364+4\times 0.7335+0.7972+0.8609}{8}=0.7210,\hfill \\ U_e(p{a}_2)=\frac{0.4307+0.5085+4\times 0.5862+0.6375+0.6887}{8}=0.5763, \mathrm{and}\hfill \\ U_e(p{a}_3)=\frac{0.3680+0.4347+4\times 0.5015+0.5459+0.5902}{8}=0.4931.\hfill \end{array}$$

The ranking result of three candidates is $A_1$ > $A_2$ > $A_3$, owing to the representation values of above performance indices for the sustainability evaluation of port expanding locations. Obviously, location 1 is the best one with respect to the sustainability evaluation problem. Moreover, the sensitivity analysis of adjusted weights, according to the above computations, is yielded from a linear programming model as follows. The model is formatted as

$$\begin{array}{cc}\mathrm{Max}:\hfill & 0.4117\times U_e({W_1}^{\prime })+0.3978\times U_e({W_2}^{\prime })+0.3804\times U_e({W_3}^{\prime })+0.4180\times U_e({W_4}^{\prime }),\hfill \\ \mathrm{s}.\mathrm{t}.\hfill & 0.4117\times U_e({W_1}^{\prime })+0.3978\times U_e({W_2}^{\prime })+0.3804\times U_e({W_3}^{\prime })+0.4180\times U_e({W_4}^{\prime })\le 0.7210\hfill \\ & 0.3223\times U_e({W_1}^{\prime })+0.3234\times U_e({W_2}^{\prime })+0.3204\times U_e({W_3}^{\prime })+0.3212\times U_e({W_4}^{\prime })\le 0.7210\hfill \\ & 0.2661\times U_e({W_1}^{\prime })+0.2788\times U_e({W_2}^{\prime })+0.2991\times U_e({W_3}^{\prime })+0.2608\times U_e({W_4}^{\prime })\le 0.7210\hfill \\ & 0.4652 – 0.1\le U_e({W_1}^{\prime })\le 0.4652+0.1,\hfill \\ & 0.4550 – 0.1\le U_e({W_2}^{\prime })\le 0.4550+0.1,\hfill \\ & 0.4053 – 0.1\le U_e({W_3}^{\prime })\le 0.4053+0.1, \mathrm{and}\hfill \\ & 0.4648 – 0.1\le U_e({W_4}^{\prime })\le 0.4648+0.1.\hfill \end{array}$$

To avoid criteria weights being 0, four constraints of adjusted weight values on utility representative function are added. Hence, the scopes of $U_e({W_1}^{\prime })$, $U_e({W_2}^{\prime })$, $U_e({W_3}^{\prime })$, and $U_e({W_4}^{\prime })$ are, respectively, 0.4652 $\pm$0.1, 0.4550 $\pm$ 0.1, 0.4053 $\pm$ 0.1, and 0.4648 $\pm$ 0.1. Then sensitivity analysis of adjusted weights yielded by the sensitivity report of Excel 16.0 is presented in

Table 13. Sensitivity analysis of adjusted weights in tolerance being 0.1.

Adjusted Weights	Final Values	Reduced Costs	Objective Coefficients	Allowable Increase Values	Allowable Decrease Values
Compatible	0.552805852	0	0.41165873	0	0
Feasible	0.355	0	0.397812847	0	1 × 1030
Recycling	0.3053	0	0.380432089	0	1 × 1030
Stable	0.5648	0	0.417958866	1 × 1030	0

.

Through the entries of Table 13, it is obvious that the original values of adjusted weights on utility representative function are stable because these allowable increase and allowable decrease values are almost fixed. In fact, the stable situations are also shown in the tolerance values. For instance, the scopes of $U_e({W_1}^{\prime })$, $U_e({W_2}^{\prime })$, $U_e({W_3}^{\prime })$, and $U_e({W_4}^{\prime })$ are revised as 0.4652 $\pm$0.4, 0.4550 $\pm$ 0.4, 0.4053 $\pm$ 0.4, and 0.4648 $\pm$ 0.4. That is to say, four constraints of adjusted weight values on utility representative function are 0.4652 − 0.4 $\le U_e({W_1}^{\prime })\le$ 0.4652 + 0.4, 0.4550 − 0.4 $\le U_e({W_2}^{\prime })\le$ 0.4550 + 0.4, 0.4053 − 0.4 $\le U_e({W_3}^{\prime })\le$ 0.4053 + 0.4, and 0.4648 − 0.4 $\le U_e({W_4}^{\prime })\le$ 0.4648 + 0.4. At that time, the sensitivity analysis of adjusted weights yielded by the sensitivity report of Excel 16.0 is expressed in

Table 14. Sensitivity analysis of adjusted weights in tolerance being 0.4.

Adjusted Weights	Final Values	Reduced Costs	Objective Coefficients	Allowable Increase Values	Allowable Decrease Values
Compatible	0.815367564	0	0.41165873	0	0
Feasible	0.055	0	0.397812847	0	1 × 1030
Recycling	0.0053	0	0.380432089	0	1 × 1030
Stable	0.8648	0	0.417958866	1 × 1030	0

.

Similar to Table 13, these allowable increase and allowable decrease values in Table 14 are the same entries as well. Practically, the hybrid method combining QFD with AHP under IVFE is compared with other FMCDM ones presented in the following

Table 15. Comparisons of the hybrid method and other FMCDM ones.

Comparisons	The Hybrid Method	Fuzzy ANP	Fuzzy TOPSIS [42]	Fuzzy AHP [17]
Applications	FMCDM with DEC	FMCDM with DEC	FMCDM with IDEC	FMCDM with IDEC
Operations	Medium	Complexity	Simplicity	Simplicity
Data attributes	Relative ratios	Relative ratios	General numbers	Relative ratios

.

Through comparisons of Table 15, it is evident that characteristics of the hybrid method are suitable to FMCDM with DEC and used in relative ratios. Although the method may not the simplest one for operations due to combination of QFD and AHP, easier single methods are utilized in FMCDM with IDEC. Moreover, the time complexity for fuzzy computation to yield the priority representations of $n\times n$ FPWCMs is $n$ for IVFNs by the utility representative function, similar to that of Wang [26] for TFNs, whereas the time complexity of Chang’s method [24] on fuzzy computation is $n^2$ for TFNs. As $n$ is a positive integer, $n$$\le$$n^2$. Hence, a hybrid method combining QFD with AHP under IVFE is better than Chang’s with respect to the time complexity for fuzzy computation and is able to be used for IVFNs.

5. Conclusions

International ports are important resources for lots of countries, and thus evaluating port sustainability containing sustainability evaluation of port expanding locations is imperative to avoid future trade barriers because related barrier problems concerning environmental protection, energy saving, and carbon reduction between a country and others may occur, violating the Earth Summit’s SDGs’. Based on the above, an example of the sustainability evaluation of Taipei’s port expanding locations in the previous section is illustrated to describe the situation of evaluating port sustainability. In the illustrating example, extending QFD under IVFE through the utility representation function is used to yield adjusted weights of DEC. Additionally, location performance ratings by extending AHP with the utility representation function are derived under IVFE, and then the adjusted criteria weights and performance ratings along all the evaluation criteria for each location are integrated into performance indices as ranking references. According to utility representation function, computations of extending QFD and AHP under IVFE are easy to derive in interval-valued FMCDM with DEC for the sustainability evaluation of port expanding locations. Herein, DEC for decision-making, being conceptually presented by feasible, compatible, recycling, and stable aspects in the short term, are tightly connected with environmental, social, and economic requirements. Practically, these DEC for decision-making in the future, especially in the long term, are added or sub-divided due to proposals based on the environmental, social, and economic requirements of decision-makers to reserve conceptualization and flexibility for evaluating port sustainability. In other words, DEC for evaluation are conceptualized and flexibly changed to reflect varied environmental, social, and economic requirements for sustainability. Further, the evaluation result of port sustainability is an important reference by which to finish the corresponding task in short term decision-making, and an essential foundation to establish advanced facilities in long term decision-making because new investments are needed, and more technologies will be developed in the future. For sustainability, the technologies of offshore platforms [53,54,55] and offshore wind power [56,57,58,59] will possibly be useful to support the ongoing development in ports. These above technologies, respectively, involve floating structures and green energies for sustainability. In fact, the hybrid method, combining AHP with QFD via computations of previous sections to replace ANP under IVFE, can be used in these kinds of FMCDM problems with DEC owing to environmental, social, and economic requirements. After all, extending QFD and AHP under IVFE for the sustainability evaluation of port expanding locations has three strengths: decision-making with DEC, easy computation, and gaining more information than others. Therefore, the hybrid method should be widely applied to the sustainability evaluation problems of numerous fields, not merely those limited to a specific scope.