Spatial and Temporal Dynamics of Drought and Waterlogging in Karst Mountains in Southwest China
Abstract
1. Introduction
2. Materials and Methods
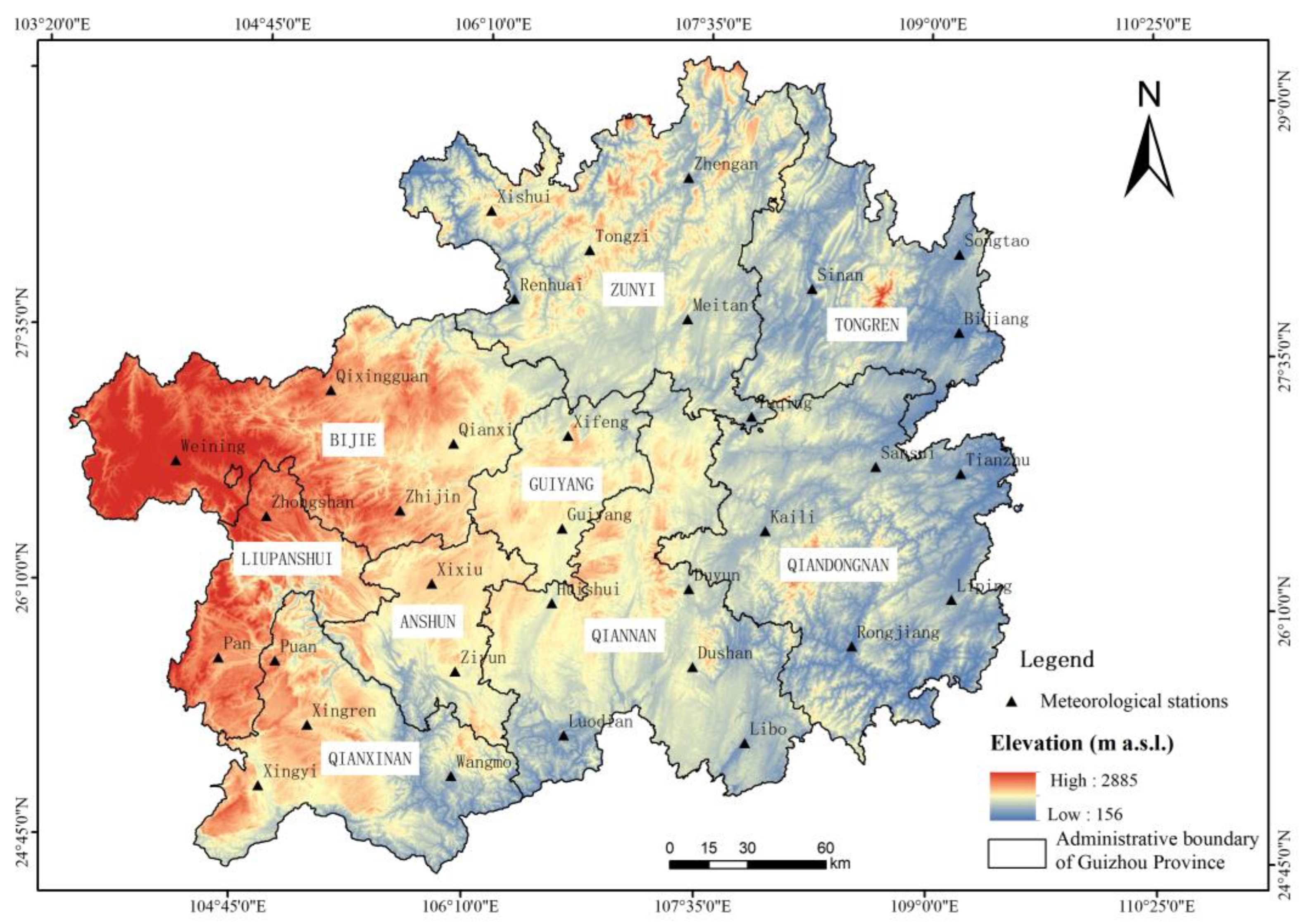
2.1. Study Area
2.2. Data Collection and Analysis
2.2.1. Data Sources
2.2.2. Z Index Calculation
2.2.3. Calculation of Normalized Difference Drought and Waterlogging Index
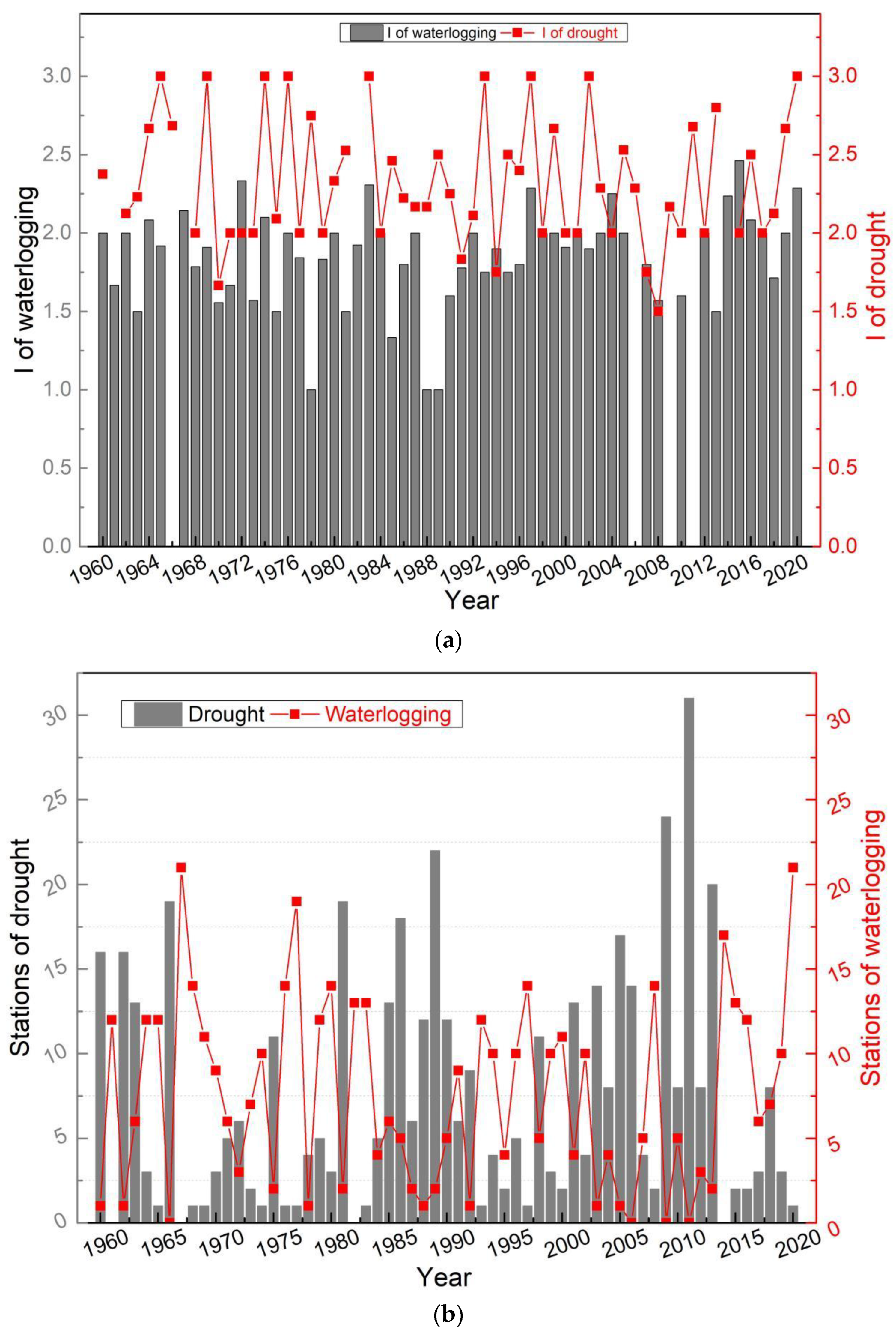
2.2.4. Intensity of Drought and Waterlogging
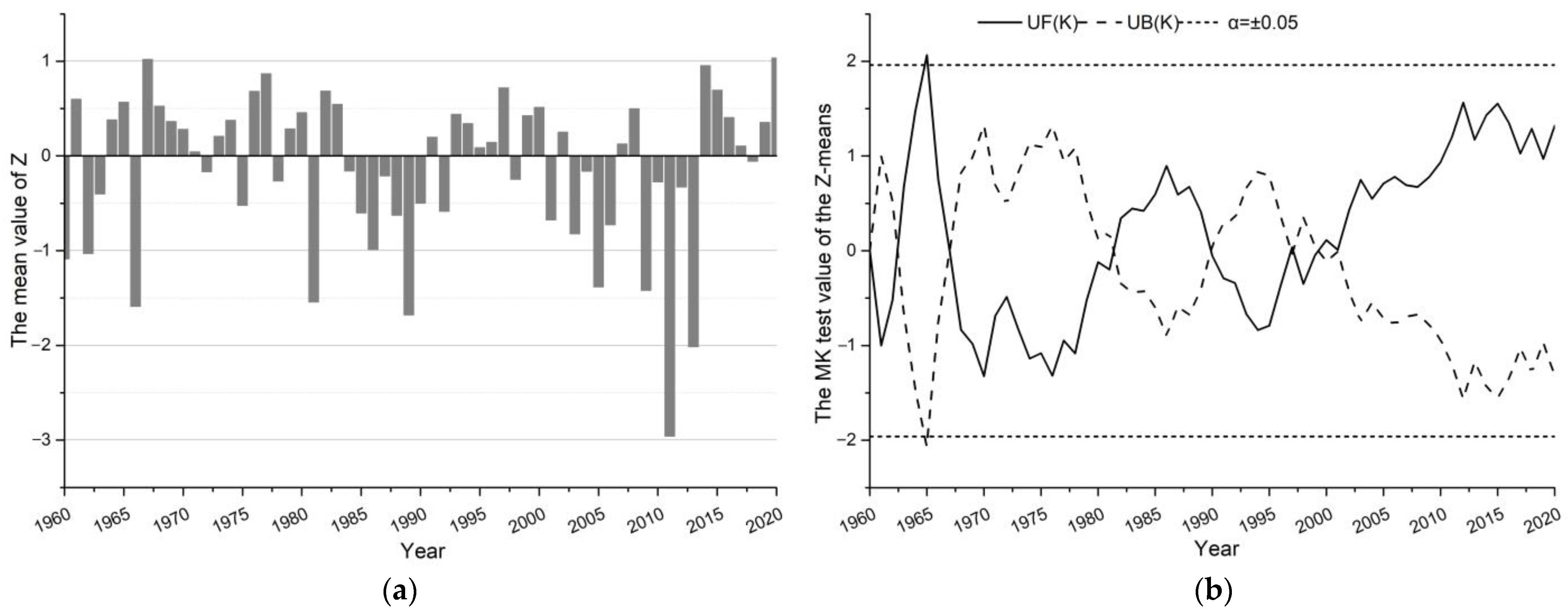
2.2.5. MK Test
2.2.6. Topographical Analysis
3. Results
3.1. Interannual Characteristics of Drought and Waterlogging
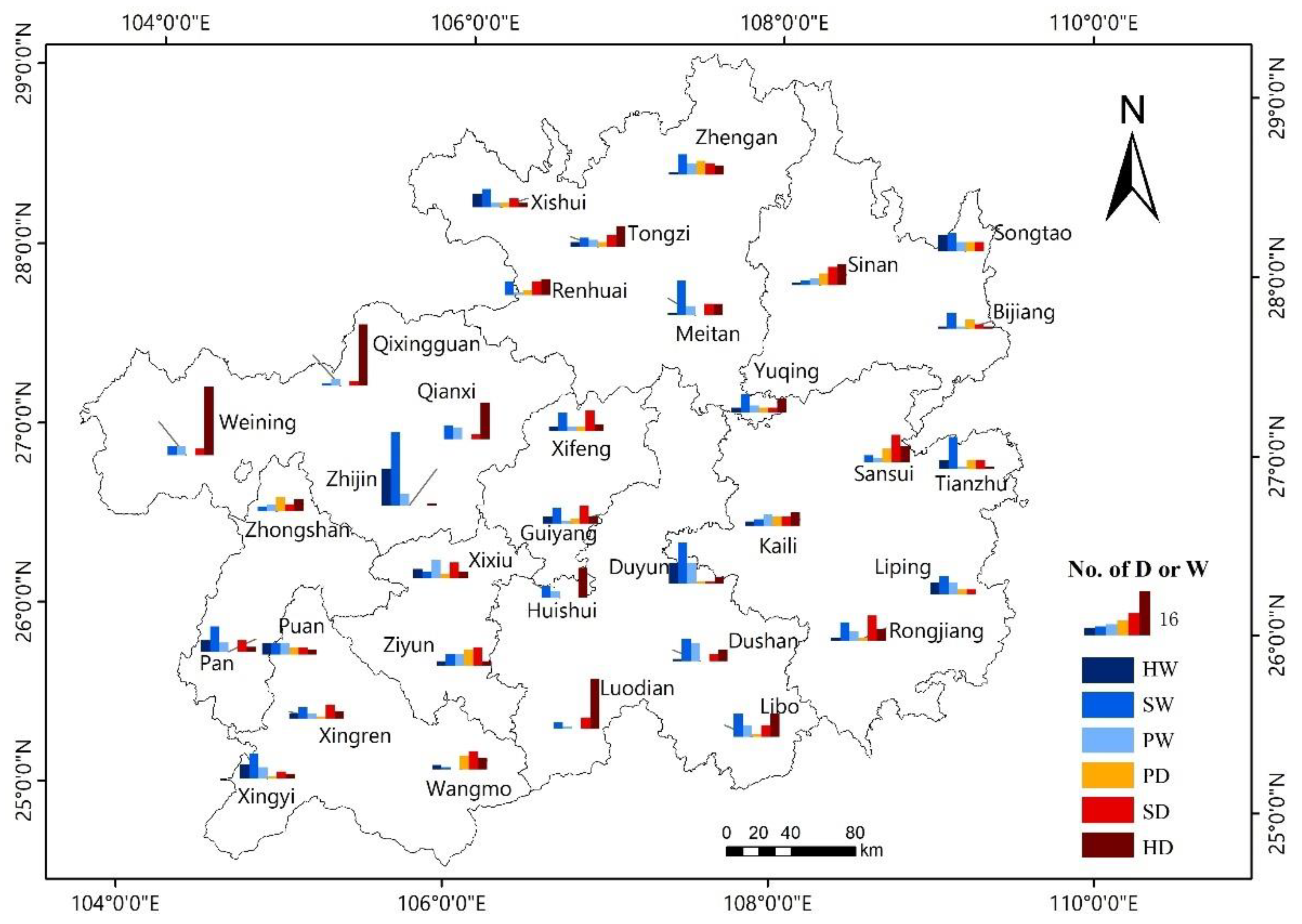
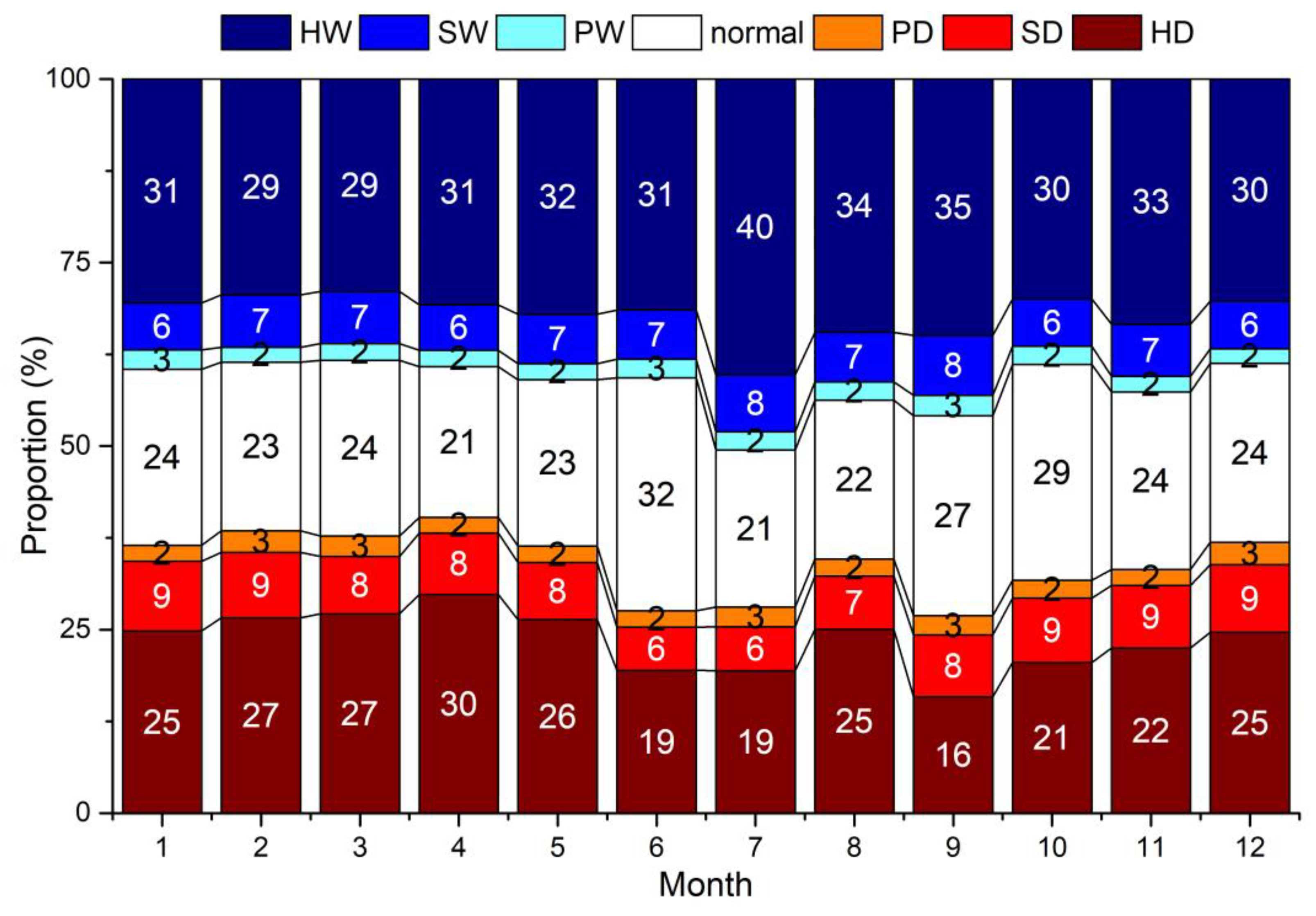
3.2. Characteristics of Monthly Drought and Waterlogging
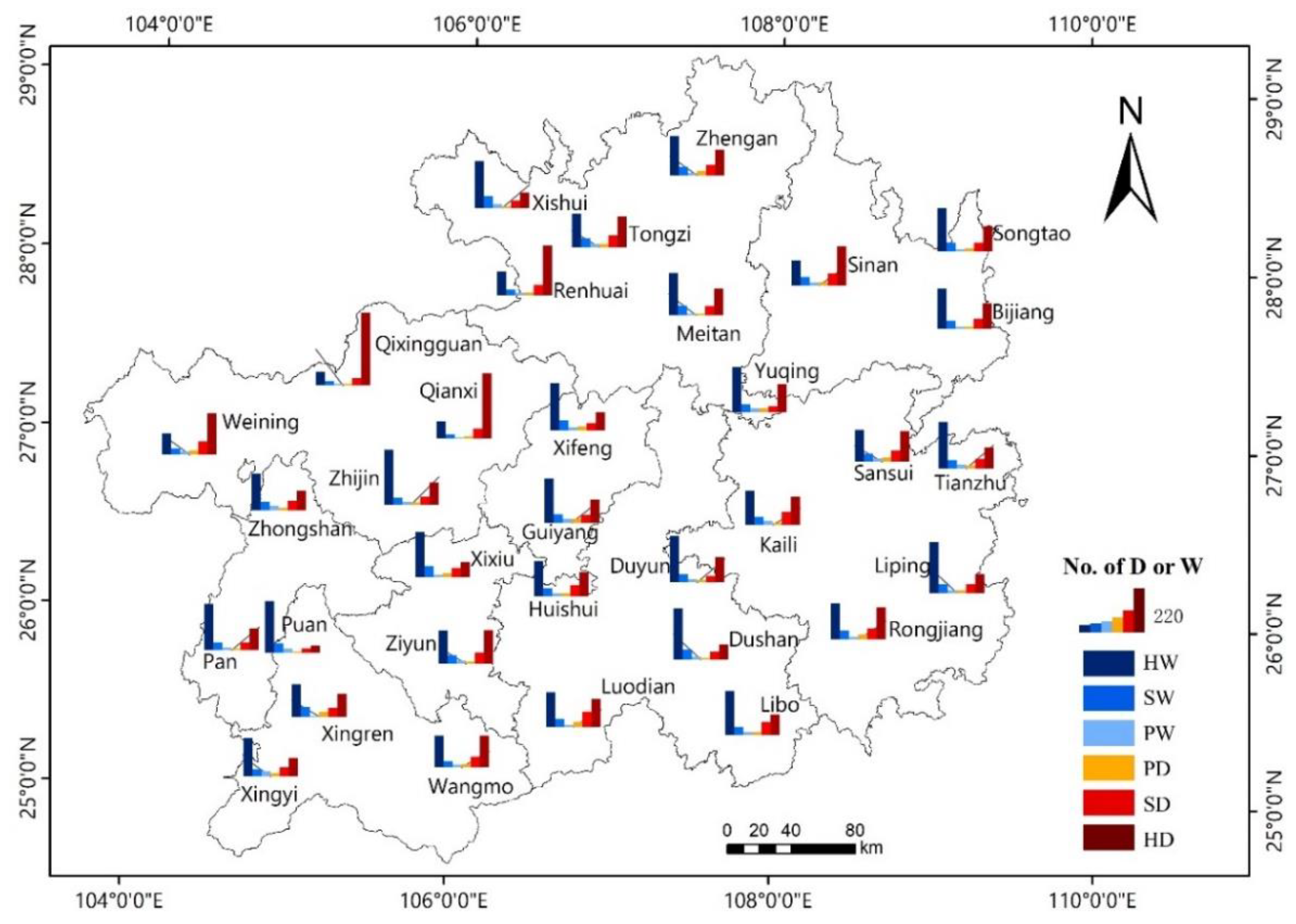
3.3. Relationship between Terrain and Annual Drought and Waterlogging
4. Discussion
4.1. The Spatiotemporal Pattern of Waterlogging and Drought in Guizhou
4.2. The Correlated Factors of Waterlogging and Drought in Karst Mountains
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Stokes, T.; Griffiths, P. An Overview of the Karst Areas in British Columbia, Canada. Geosci. Can. 2019, 46, 49–66. [Google Scholar] [CrossRef]
- Geekiyanage, N.; Goodale, U.; Cao, K.-F.; Kitajima, K. Plant ecology of tropical and subtropical karst ecosystems. Biotropica 2019, 51, 626–640. [Google Scholar] [CrossRef]
- Goldscheider, N.; Chen, Z.; Auler, A.; Bakalowicz, M.; Broda, S.; Drew, D.; Hartmann, J.; Jiang, G.; Moosdorf, N.; Stevanovic, Z.; et al. Global distribution of carbonate rocks and karst water resources. Hydrogeol. J. 2020, 28, 1661–1677. [Google Scholar] [CrossRef]
- Covington, M.; Martin, J.; Toran, L.; Macalady, J.; Sekhon, N.; Sullivan, P.; García, Á.; Heffernan, J.; Graham, W. Carbonates in the Critical Zone. Earth Future 2023, 11, e2022EF002765. [Google Scholar] [CrossRef]
- Olarinoye, T.; Gleeson, T.; Marx, V.; Seeger, S.; Adinehvand, R.; Allocca, V.; Andreo, B.; Apaéstegui, J.; Apolit, C.; Arfib, B.; et al. Global karst springs hydrograph dataset for research and management of the world’s fastest-flowing groundwater. Sci. Data 2020, 7, 59. [Google Scholar] [CrossRef] [PubMed]
- Ford, D.; Williams, P. Karst Geomorphology and Hydrology; John Wiley & Sons: Hoboken, NJ, USA, 2007; Volume 346. [Google Scholar]
- Khoury, I.; Boithias, L.; Labat, D. A Review of the Application of the Soil and Water Assessment Tool (SWAT) in Karst Watersheds. Water 2023, 15, 954. [Google Scholar] [CrossRef]
- Goldscheider, N. A holistic approach to groundwater protection and ecosystem services in karst terrains. Carbonates Evaporites 2019, 34, 1241–1249. [Google Scholar] [CrossRef]
- Athamrie, A.; Tadesse, C.; Abebe, T. Drought and Flood Extreme Events and Management Strategies in Ethiopia. J. Geogr. Nat. Disasters 2022, 12, 248. [Google Scholar] [CrossRef]
- Liu, B.; Chen, C.; Lian, Y.; Chen, J.; Chen, X. Long-term Change of Wet and Dry Climatic Conditions in the Southwest Karst Area of China. Glob. Planet. Chang. 2015, 127, 1–11. [Google Scholar] [CrossRef]
- Pang, J.; Zhang, H. Global map of a comprehensive drought/flood index and analysis of controlling environmental factors. Nat. Hazards 2022, 1–27. [Google Scholar] [CrossRef]
- Gutiérrez, F. A review on natural and human-induced geohazards and impacts in karst. Earth Sci. Rev. 2014, 138, 61–88. [Google Scholar] [CrossRef]
- Najib, K.; Jourde, H.; Pistre, S. A methodology for extreme groundwater surge predetermination in carbonate aquifers: Groundwater flood frequency analysis. J. Hydrol. 2008, 352, 1–15. [Google Scholar] [CrossRef]
- Bailly-Comte, V.; Borrell Estupina, V.; Jourde, H.; Pistre, S. A conceptual semidistributed model of the Coulazou River as a tool for assessing surface water-karst groundwater interactions during flood in Mediterranean ephemeral rivers. Water Resour. Res. 2012, 48, 9534. [Google Scholar] [CrossRef]
- Pei, J.; Li, Q. Land Use and Soil and Water Loss in Typical Karst Mountain Area. Bull. Soil Water Conserv. 2006, 26, 94–99. (In Chinese) [Google Scholar]
- Li, Y.; Wang, S.; Rong, L. Problems of karst rocky desertification in southwest China. Resour. Environ. Yangtze Basin 2003, 12, 593–598. (In Chinese) [Google Scholar]
- Luo, L.; Wu, Y.; Li, H.; Xing, D.; Zhou, Y.; Xia, A. Drought Induced Dynamic Traits of Soil Water and Inorganic Carbon in Different Karst Habitats. Water 2022, 14, 3837. [Google Scholar] [CrossRef]
- Moradi, H.; Rahmati, M.; Karimi, H. Evaluating the Effects of Meteorological Drought on the Karstic Aquifers with Karst Development in Different Conditions. J. Water Soil Sci. 2018, 22, 255–266. [Google Scholar] [CrossRef]
- Wang, Y.; Liang, L.; Jing, J.; Luo, F.; Wang, A. Characteristic of Drought and Flood in the Dian-Qian-Gui Karst Areas Based on TRMM-Z Index. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2020, XLII-3/W10, 917–924. [Google Scholar] [CrossRef]
- Fragoso-Servón, P.; Bautista, F.; Frausto, O.; Pereira Corona, A. Characterization of karst depressions (shape, size and density) at 1:50,000 scale and the associated type of flood in the State of Quintana Roo, Mexico. Rev. Mex. Cienc. Geol. 2014, 31, 127–137. [Google Scholar]
- Huang, W.; Yang, X.; Li, M.; Zhang, X.; Wang, M.; Dai, S.; Ma, J. Evolution characteristics of seasonal drought in the south of China during the past 58 years based on standardized precipitation index. Trans. Chin. Soc. Agric. Eng. 2010, 26, 50–59. [Google Scholar] [CrossRef]
- Zhou, W.; Liu, D.; Zhang, J.; Jiang, S.; Xing, S.; Wang, J.; Cheng, Y.; Chen, N. Identification and frequency analysis of drought–flood abrupt alternation events using a daily-scale standardized weighted average of the precipitation index. Front. Environ. Sci. 2023, 11, 1142259. [Google Scholar] [CrossRef]
- Chloé, O.; Olioso, A.; Carrière, S.; Boulet, G.; Chalikakis, K.; Chanzy, A.; Charlier, J.-B.; Combemale, D.; Davi, H.; Emblanch, C.; et al. An evapotranspiration model driven by remote sensing data for assessing groundwater resource in karst watershed. Sci. Total Environ. 2021, 781, 146706. [Google Scholar] [CrossRef]
- Faiz, M.; Zhang, Y.; Zhang, X.; Ma, N.; Aryal, S.; Trinh Thi, V.H.; Baig, F.; Naz, F. A composite drought index developed for detecting large-scale drought characteristics. J. Hydrol. 2021, 605, 127308. [Google Scholar] [CrossRef]
- Kong A Siou, L.; Fleury, P.; Johannet, A.; Borrell Estupina, V.; Pistre, S.; Dörfliger, N. Performance and complementarity of two systemic models (reservoir and neural networks) used to simulate spring discharge and piezometry for a karst aquifer. J. Hydrol. 2014, 519, 3178–3192. [Google Scholar] [CrossRef]
- Nerantzaki, S.; Nikolaidis, N. The response of three Mediterranean karst springs to drought and the impact of climate change. J. Hydrol. 2020, 591, 125296. [Google Scholar] [CrossRef]
- Pu, J.; Zhao, X.; Dong, P.; Wang, Q.; Yue, Q. Extracting Information on Rocky Desertification from Satellite Images: A Comparative Study. Remote Sens. 2021, 13, 2497. [Google Scholar] [CrossRef]
- Zhang, J.; Dai, M.; Wang, L.; Zeng, C.; Su, W. The challenge and future of rocky desertification control in Karst areas in Southwest China. Solid Earth Discuss. 2015, 7, 3271–3292. [Google Scholar] [CrossRef]
- Molina Paniagua, M.; Melo, P.H.; Ramírez-Barahona, S.; Ortiz Rodriguez, A.; Monro, A.; Burelo-Ramos, C.; Gómez-Domínguez, H. How Diverse Are the Mountain Karst Forests of Mexico? bioRxiv 2023, 3, 530643. [Google Scholar] [CrossRef]
- Wang, Z.; Liu, S.; Su, Y. Spatial-Temporal Characteristics of Soil Erosion and Erosion Hotspots in Guiyang City of Karst Plateau Mountainous Region in 2008–2018. J. Soil Water Conserv. 2020, 34, 94–102+110. (In Chinese) [Google Scholar] [CrossRef]
- Cinkus, G.; Mazzilli, N.; Jourde, H. KarstID: An R Shiny application for the analysis of karst spring discharge time series and the classification of karst system hydrological functioning. Environ. Earth Sci. 2023, 82, 136. [Google Scholar] [CrossRef]
- Rad, S.; Junfeng, D.; Jingxuan, X.; Zitao, L.; Linyan, P.; Wan, Z.; Lin, L. Lijiang flood characteristics and implication of karst storage through Muskingum flood routing via HEC-HMS, S. China. Hydrol. Res. 2022, 53, 1480–1493. [Google Scholar] [CrossRef]
- Wu, Q.; Zheng, W.; Rao, C.; Wang, E.; Yan, W. Soil Quality Assessment and Management in Karst Rocky Desertification Ecosystem of Southwest China. Forests 2022, 13, 1513. [Google Scholar] [CrossRef]
- Yao, B.; Yue, X.-j.; Huang, P.; Li, Y.-h. The Qing-Long model: China provides a solution to the karst rocky desertification challenge. Acta Ecol. Sin. 2022. [Google Scholar] [CrossRef]
- Huang, Q.; Cai, Y. Spatial pattern of Karst rock desertification in the Middle of Guizhou Province, Southwestern China. Environ. Geol. 2007, 52, 1325–1330. [Google Scholar] [CrossRef]
- Fan, Z.; Li, J.; Yue, T.-X.; Zhou, X.; Lan, A. Scenarios of land cover in Karst area of Southwestern China. Environ. Earth Sci. 2015, 74, 6407–6420. [Google Scholar] [CrossRef]
- Gao, J.; Jiang, Y.; Anker, Y. Contribution analysis on spatial tradeoff/synergy of Karst soil conservation and water retention for various geomorphological types: Geographical detector application. Ecol. Indic. 2021, 125, 107470. [Google Scholar] [CrossRef]
- Xiong, H.; Wang, S.; Rong, L.; Cheng, A.; Li, Y. Effects of extreme drought on plant species in karst area of Guizhou province, southwest China. Chin. J. Appl. Ecol. 2011, 22, 1127–1134. [Google Scholar]
- Yuan, D.; Cai, G. The Study of Karst Environment; Chongqing Publisher: Chongqing, China, 1988. [Google Scholar]
- Lu, H.; Chen, S.; Zhang, C. Characteristics and generation mechanism of flood disaster in karst basin: A case study of the houzhai river in Guizhou. Trop. Geogr. 2012, 32, 352–356. [Google Scholar]
- Zhao, Z.; Xiong, K.; Chen, H.; Zhou, W.; Meng, H.; Wang, X.; Xue, Z. Effect of Drought on Soil Animal in Karst Rocky Desertification Ecological Rehabilitation Areas in Guizhou. Southwest China J. Agric. Sci. 2011, 24, 1167–1172. (In Chinese) [Google Scholar] [CrossRef]
- Bai, S.; Mo, T.; Shi, J.; Zhou, Y. Spatial and temporal variations of rainfall days with different intensities in Guizhou in recent 50 years (in Chinese). South North Water Transf. Water Sci. Technol. 2015, 13, 220–224. (In Chinese) [Google Scholar] [CrossRef]
- Yu, F.; Ningbo, C.; Yanmei, X.; Zhenping, Z.; Junqin, W. Temporal and spatial distribution characteristics of meteorological drought in Guizhou Province. J. Arid. Land Resour. Environ. 2015, 29, 82–86. (In Chinese) [Google Scholar] [CrossRef]
- Zhao, Y.; Park, C.; Son, S.W. Importance of Diabatic Heating for the Eastward-Moving Heavy Rainfall Events along the Yangtze River, China. J. Atmos. Sci. 2022, 80, 151–165. [Google Scholar] [CrossRef]
- Zhao, Y.; Lin, D.; Li, Z.; Wang, Y. Quantitative Attribution of Vertical Motion Responsible for Summer Heavy Rainfall Over North China. J. Geophys. Res. Atmos. 2022, 127, e2021JD035765. [Google Scholar] [CrossRef]
- Zhao, Y.; Chen, D.; Li, J.; Chen, D.; Yi, C.; Li, J.; Qin, R. Enhancement of the summer extreme precipitation over North China by interactions between moisture convergence and topographic settings. Clim. Dyn. 2020, 54, 2713–2730. [Google Scholar] [CrossRef]
- Jain, V.; Pandey, R.; Jain, M.; Byun, H.-R. Comparison of drought indices for appraisal of drought characteristics in the Ken River Basin. Weather. Clim. Extrem. 2015, 8, 1–11. [Google Scholar] [CrossRef]
- Dogan, S.; Berktay, A.; Singh, V. Comparison of multi-monthly rainfall-based drought severity indices, with application to semi-arid Konya closed basin, Turkey. J. Hydrol. 2012, 470–471, 255–268. [Google Scholar] [CrossRef]
- Shahabfar, A.; Ghulam, A.; Eitzinger, J. Drought monitoring in Iran using the perpendicular drought indices. Int. J. Appl. Earth Obs. Geoinf. 2012, 18, 119–127. [Google Scholar] [CrossRef]
- Zhang, H.; Yang, J. Characteristics and Models of Regional Drought Evolution in Guizhou; China Water Conservancy and Hydropower Press: Beijing, China, 2014. [Google Scholar]
- Wen, K.; Luo, N. China Meteorological Disasters: Guizhou Volume; Meteorological Press: Beijing, China, 2006. (In Chinese) [Google Scholar]
- Water-Resources-Department-of-Guizhou. Guizhou Water Resources Bulletin from 2000 to 2020. Available online: http://mwr.guizhou.gov.cn/sjfb/slsj/202211/t20221117_77132741.html (accessed on 10 July 2021).
- Chen, Y.; Chang, J.; Huang, S.; Wang, Y.; Guo, A. Variation characteristics of drought in Weihe River Basin based on Palmer drought severity index. J. Nat. Disasters 2014, 23, 29–37. (In Chinese) [Google Scholar] [CrossRef]
- Pirnia, A.; Golshan, M.; Darabi, H.; Adamowski, J.; Rozbeh, S. Using the Mann–Kendall test and double mass curve method to explore stream flow changes in response to climate and human activities. J. Water Clim. Chang. 2018, 10, 725–742. [Google Scholar] [CrossRef]
- Huang, Q.; Fan, J. Detecting Runoff Variation of the Mainstream in Weihe River. J. Appl. Math. 2013, 2013, 356474. [Google Scholar] [CrossRef]
- Tang, G.; Na, J.; Cheng, W. Progress of Digital Terrain Analysis on Regional Geomorphology in China. Acta Geod. Cartogr. Sin. 2017, 46, 1570–1591. (In Chinese) [Google Scholar] [CrossRef]
- Esteban, E.; Castilho, C.; Melgaço, K.; Costa, F. The other side of droughts: Wet extremes and topography as buffers of negative drought effects in an Amazonian forest. New Phytol. 2020, 229, 1995–2006. [Google Scholar] [CrossRef]
- He, Z.; Liang, H.; Yang, Z. Study on the driven mechanism of hydrologic drought based on the lithology-combined structure of the Karst drainage basin in South China. J. Water Clim. Chang. 2021, 12, 3714–3733. [Google Scholar] [CrossRef]
- Ren, J.; Wang, W.; Wei, J.; Li, H.; Li, X.; Liu, G.; Chen, Y.; Ye, S. Evolution and prediction of drought-flood abrupt alternation events in Huang-Huai-Hai River Basin, China. Sci. Total Environ. 2023, 869, 161707. [Google Scholar] [CrossRef]
- Qiao, Y.; Xu, W.; Meng, C.; Liao, X.; Qin, L. Increasingly Dry/Wet Abrupt Alternation Events in a Warmer World: Observed Evidence from China during 1980–2019. Int. J. Climatol. 2022, 42, 6429–6440. [Google Scholar] [CrossRef]
- Dixon, R.K.; Solomon, A.M.; Brown, S.; Houghton, R.A.; Trexier, M.C.; Wisniewski, J. Carbon Pools and Flux of Global Forest Ecosystems. Science 1994, 263, 185. [Google Scholar] [CrossRef]
- McMahon, S.M.; Dietze, M.C.; Hersh, M.H.; Moran, E.V.; Clark, J.S. A Predictive Framework to Understand Forest Responses to Global Change. In Year in Ecology and Conservation Biology 2009; Blackwell Publishing: Oxford, UK, 2009; Volume 1162, pp. 221–236. [Google Scholar]


| Z Index | Level of the Drought or Waterlogging | |||
|---|---|---|---|---|
| Z > 1.645 | Heavy waterlogging (HW) | SW and above (SWA) | Waterlogging (W) | |
| 1.037 < Z ≤ 1.645 | Severe waterlogging (SW) | |||
| 0.842 < Z ≤ 1.037 | Partial waterlogging (PW) | |||
| −0.842 < Z ≤ 0.842 | Normal | |||
| −1.037 < Z ≤ −0.842 | Partial drought (PD) | Drought (D) | ||
| −1.645 < Z ≤ −1.037 | Severe drought (SD) | SD and above (SDA) | ||
| Z ≤ −1.645 | Heavy drought (HD) | |||
| Administrative Sub-Division | DW Proportion (%) | ||||||
|---|---|---|---|---|---|---|---|
| HD | SD | PD | Normal | PW | SW | HW | |
| Anshun | 4.10 | 12.30 | 7.38 | 54.10 | 10.66 | 6.56 | 4.92 |
| Bijie | 30.33 | 2.87 | 0 | 35.66 | 6.97 | 17.62 | 6.56 |
| Guiyang | 4.92 | 13.93 | 3.28 | 59.02 | 2.46 | 12.30 | 4.10 |
| Liupanshui | 5.74 | 6.56 | 4.92 | 62.30 | 5.74 | 10.66 | 4.10 |
| Qiandongnan | 6.23 | 10.82 | 5.57 | 56.07 | 5.57 | 11.80 | 3.93 |
| Qiannan | 17.38 | 4.59 | 0.66 | 50.49 | 8.52 | 15.08 | 3.28 |
| Qianxinan | 4.94 | 8.23 | 4.53 | 62.14 | 4.94 | 9.05 | 6.17 |
| Tongren | 5.46 | 7.65 | 7.10 | 61.20 | 4.37 | 9.29 | 4.92 |
| Zunyi | 9.02 | 7.38 | 3.83 | 57.92 | 4.92 | 13.66 | 3.28 |
| DW | L Value in Equation (10) | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Entire Province | Anshun | Bijie | Guiyang | Qiandongnan | Qiannan | Qianxinan | Tongren | Zunyi | Liupanshui | |
| D | 0.32 | 0.54 | 1.92 * | 0.46 | 1.28 | 1.49 | 0.9 | 0.92 | 1.04 | 0.25 |
| W | 0.06 | −0.97 | −2.37 ** | −0.87 | −0.55 | −1.47 | −1.22 | −0.8 | −1.36 | −1.16 |
| Sub-Divisions | Month | Ratio | Month | Ratio | Month | Ratio | |||
|---|---|---|---|---|---|---|---|---|---|
| SDA | SWA | SDA | SWA | SDA | SWA | ||||
| Anshun | 1 | 0.35 | 0.35 | 5 | 0.20 | 0.45 | 9 | 0.40 | 0.33 |
| Bijie | 0.62 | 0.18 | 0.50 | 0.25 | 0.22 | 0.48 | |||
| Guiyang | 0.14 | 0.52 | 0.20 | 0.57 | 0.49 | 0.26 | |||
| Liupanshui | 0.30 | 0.43 | 0.32 | 0.35 | 0.16 | 0.54 | |||
| Qiandongnan | 0.31 | 0.41 | 0.33 | 0.39 | 0.26 | 0.42 | |||
| Qiannan | 0.35 | 0.34 | 0.29 | 0.42 | 0.20 | 0.45 | |||
| Qianxinan | 0.22 | 0.46 | 0.30 | 0.41 | 0.27 | 0.44 | |||
| Tongren | 0.31 | 0.38 | 0.36 | 0.38 | 0.13 | 0.40 | |||
| Zunyi | 0.36 | 0.36 | 0.40 | 0.37 | 0.22 | 0.45 | |||
| Anshun | 2 | 0.25 | 0.36 | 6 | 0.28 | 0.52 | 10 | 0.31 | 0.45 |
| Bijie | 0.70 | 0.17 | 0.30 | 0.39 | 0.53 | 0.27 | |||
| Guiyang | 0.16 | 0.49 | 0.32 | 0.38 | 0.22 | 0.48 | |||
| Liupanshui | 0.25 | 0.42 | 0.07 | 0.66 | 0.00 | 0.02 | |||
| Qiandongnan | 0.33 | 0.38 | 0.33 | 0.40 | 0.32 | 0.39 | |||
| Qiannan | 0.37 | 0.34 | 0.24 | 0.46 | 0.24 | 0.39 | |||
| Qianxinan | 0.22 | 0.44 | 0.01 | 0.00 | 0.19 | 0.46 | |||
| Tongren | 0.37 | 0.41 | 0.31 | 0.39 | 0.39 | 0.36 | |||
| Zunyi | 0.34 | 0.37 | 0.32 | 0.41 | 0.30 | 0.37 | |||
| Anshun | 3 | 0.23 | 0.40 | 7 | 0.26 | 0.48 | 11 | 0.29 | 0.42 |
| Bijie | 0.71 | 0.11 | 0.25 | 0.47 | 0.64 | 0.17 | |||
| Guiyang | 0.09 | 0.58 | 0.39 | 0.30 | 0.10 | 0.61 | |||
| Liupanshui | 0.38 | 0.34 | 0.12 | 0.59 | 0.36 | 0.41 | |||
| Qiandongnan | 0.32 | 0.38 | 0.30 | 0.40 | 0.25 | 0.45 | |||
| Qiannan | 0.39 | 0.34 | 0.01 | 0.83 | 0.25 | 0.43 | |||
| Qianxinan | 0.25 | 0.42 | 0.30 | 0.43 | 0.26 | 0.41 | |||
| Tongren | 0.36 | 0.38 | 0.36 | 0.32 | 0.35 | 0.37 | |||
| Zunyi | 0.28 | 0.40 | 0.33 | 0.39 | 0.27 | 0.45 | |||
| Anshun | 4 | 0.31 | 0.40 | 8 | 0.35 | 0.40 | 12 | 0.26 | 0.39 |
| Bijie | 0.69 | 0.14 | 0.27 | 0.46 | 0.61 | 0.18 | |||
| Guiyang | 0.17 | 0.59 | 0.51 | 0.25 | 0.10 | 0.53 | |||
| Liupanshui | 0.55 | 0.27 | 0.16 | 0.59 | 0.24 | 0.35 | |||
| Qiandongnan | 0.30 | 0.41 | 0.34 | 0.40 | 0.28 | 0.40 | |||
| Qiannan | 0.34 | 0.39 | 0.31 | 0.40 | 0.37 | 0.34 | |||
| Qianxinan | 0.32 | 0.41 | 0.29 | 0.44 | 0.25 | 0.43 | |||
| Tongren | 0.37 | 0.38 | 0.37 | 0.35 | 0.39 | 0.38 | |||
| Zunyi | 0.36 | 0.39 | 0.33 | 0.40 | 0.35 | 0.39 | |||
| Topographic Factors | 5 km | 10 km | 15 km | |||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Factor | Window Size | Value | HW | W | SWA | PD | HD | SDA | PD | PW |
| Terrain relief | 9 × 9 | Min | 0.49 ** | 0.35 * | 0.39 * | 0.33 | −0.2 | −0.19 | 0.38 * | −0.08 |
| Mean | −0.01 | 0 | 0.06 | 0.34 | −0.18 | −0.13 | 0.39 * | −0.2 | ||
| 7 × 7 | Min | 0.39 * | 0.26 | 0.29 | 0.29 | −0.21 | −0.21 | 0.28 | 0 | |
| Mean | −0.01 | 0 | 0.06 | 0.34 | −0.18 | −0.12 | 0.40 * | −0.2 | ||
| 5 × 5 | Min | 0.44 * | 0.36 * | 0.38 * | 0.24 | −0.15 | −0.18 | 0.21 | 0.03 | |
| Max | −0.19 | −0.04 | 0 | 0.34 | −0.35 * | −0.32 | 0.19 | −0.1 | ||
| Mean | −0.02 | −0.01 | 0.05 | 0.34 | −0.17 | −0.11 | 0.40 * | −0.2 | ||
| 3 × 3 | Min | 0.35 | 0.35 * | 0.37 * | 0.18 | −0.15 | −0.15 | 0.02 | 0.03 | |
| Max | 0.03 | 0.15 | 0.18 | 0.35 * | −0.35 * | −0.36 * | 0.17 | 0.02 | ||
| Mean | −0.02 | 0 | 0.05 | 0.34 | −0.16 | −0.1 | 0.39 * | −0.2 | ||
| Slope change rate | Min | 0.06 | −0.1 | −0.04 | 0.33 | −0.1 | −0.1 | 0.36 * | −0.38 * | |
| Max | −0.01 | 0.1 | 0.12 | 0.40 * | −0.37 * | −0.35 * | 0.34 | −0.04 | ||
| Mean | −0.01 | 0.02 | 0.07 | 0.36 * | −0.21 | −0.19 | 0.39 * | −0.1 | ||
| Elevation | Min | 0.13 | 0.07 | 0.03 | −0.36 * | 0.37 * | 0.25 | −0.39 * | 0.22 | |
| Surface roughness | Min | 0.02 | −0.08 | −0.08 | 0.29 | 0.06 | 0.12 | 0.08 | −0.383 * | |
| Mean | −0.08 | −0.04 | 0.01 | 0.32 | −0.13 | −0.08 | 0.39 * | −0.18 | ||
| Slope | Max | 0.01 | 0.11 | 0.14 | 0.3 | −0.35 * | −0.35 * | 0.22 | 0 | |
| Min | −0.1 | −0.2 | −0.17 | 0.29 | 0.06 | 0.12 | 0.08 | −0.38 * | ||
| Mean | −0.03 | −0.02 | 0.04 | 0.35 * | −0.16 | −0.1 | 0.40 * | −0.21 | ||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dai, L.; Zhao, Y.; Yin, C.; Mao, C.; Zhang, P.; Zhou, F.; Yu, X. Spatial and Temporal Dynamics of Drought and Waterlogging in Karst Mountains in Southwest China. Sustainability 2023, 15, 5545. https://doi.org/10.3390/su15065545
Dai L, Zhao Y, Yin C, Mao C, Zhang P, Zhou F, Yu X. Spatial and Temporal Dynamics of Drought and Waterlogging in Karst Mountains in Southwest China. Sustainability. 2023; 15(6):5545. https://doi.org/10.3390/su15065545
Chicago/Turabian StyleDai, Li, Yuhan Zhao, Changying Yin, Chunyan Mao, Ping Zhang, Fang Zhou, and Xianyun Yu. 2023. "Spatial and Temporal Dynamics of Drought and Waterlogging in Karst Mountains in Southwest China" Sustainability 15, no. 6: 5545. https://doi.org/10.3390/su15065545
APA StyleDai, L., Zhao, Y., Yin, C., Mao, C., Zhang, P., Zhou, F., & Yu, X. (2023). Spatial and Temporal Dynamics of Drought and Waterlogging in Karst Mountains in Southwest China. Sustainability, 15(6), 5545. https://doi.org/10.3390/su15065545





