Sustainability of Using Steel Fibers in Reinforced Concrete Deep Beams without Stirrups
Abstract
1. Introduction
2. Shear Strength Models of SFRC Deep Beams
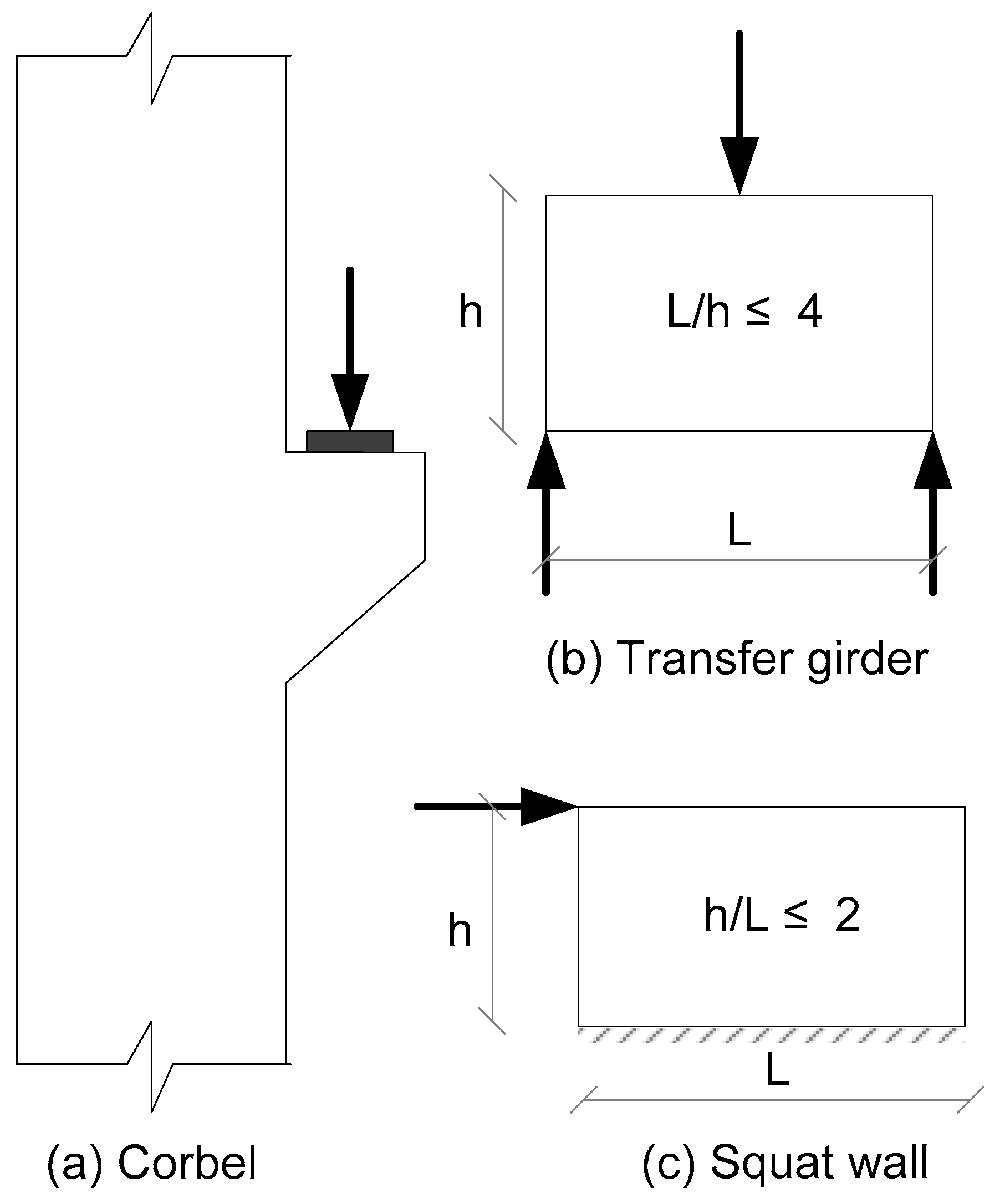
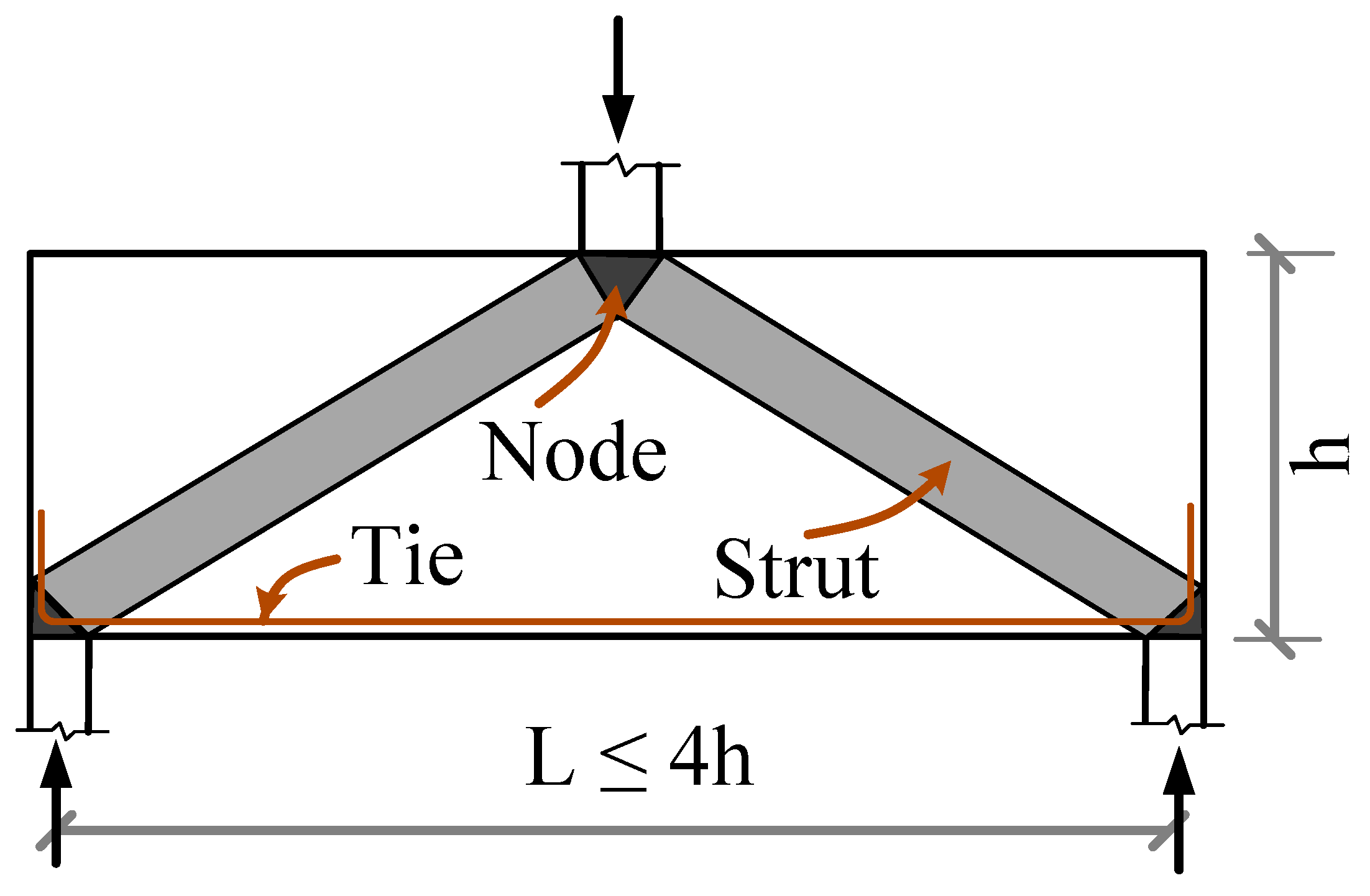
2.1. Background
2.2. Available Shear Strength Models
3. Research Significance
4. Methodology
4.1. Available Experimental Database
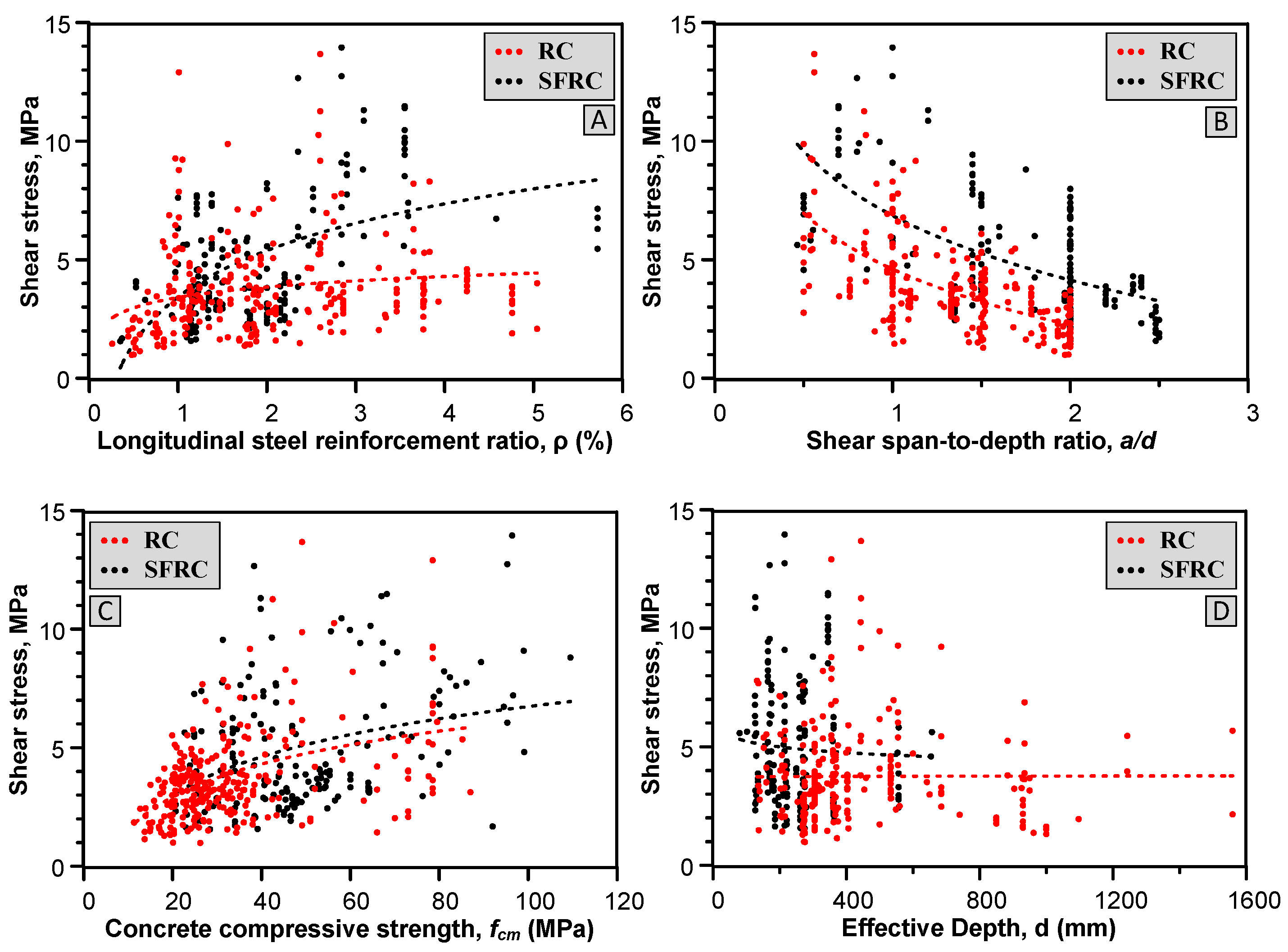
4.2. Comparison between RC and SFRC Databases
4.3. Development of the Nonlinear Regression-Based Model and Features Selection
4.4. Derivation and Evaluation of the Nonlinear Regression Model
5. Results and Discussions
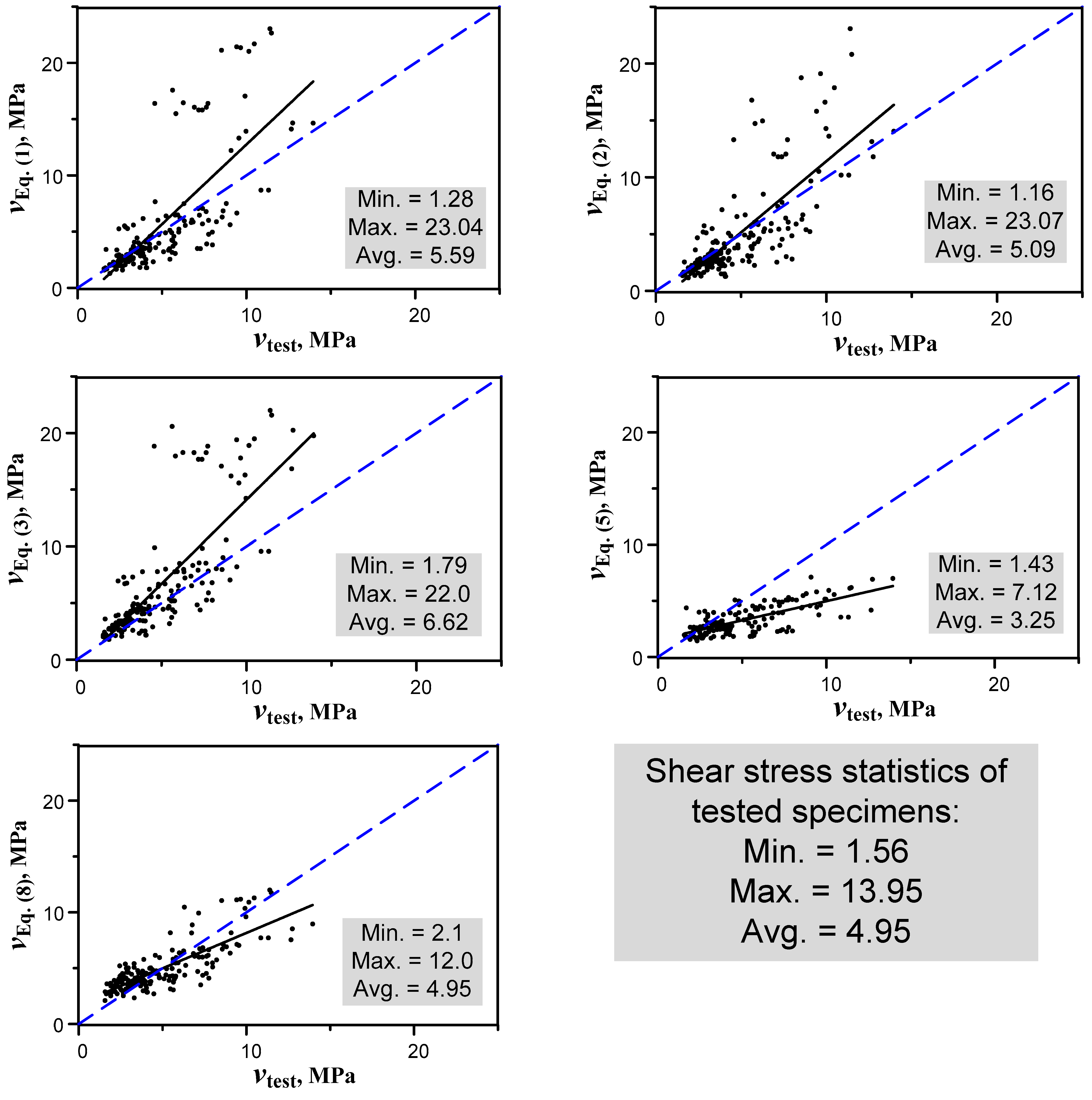
5.1. Performance of the Proposed Model
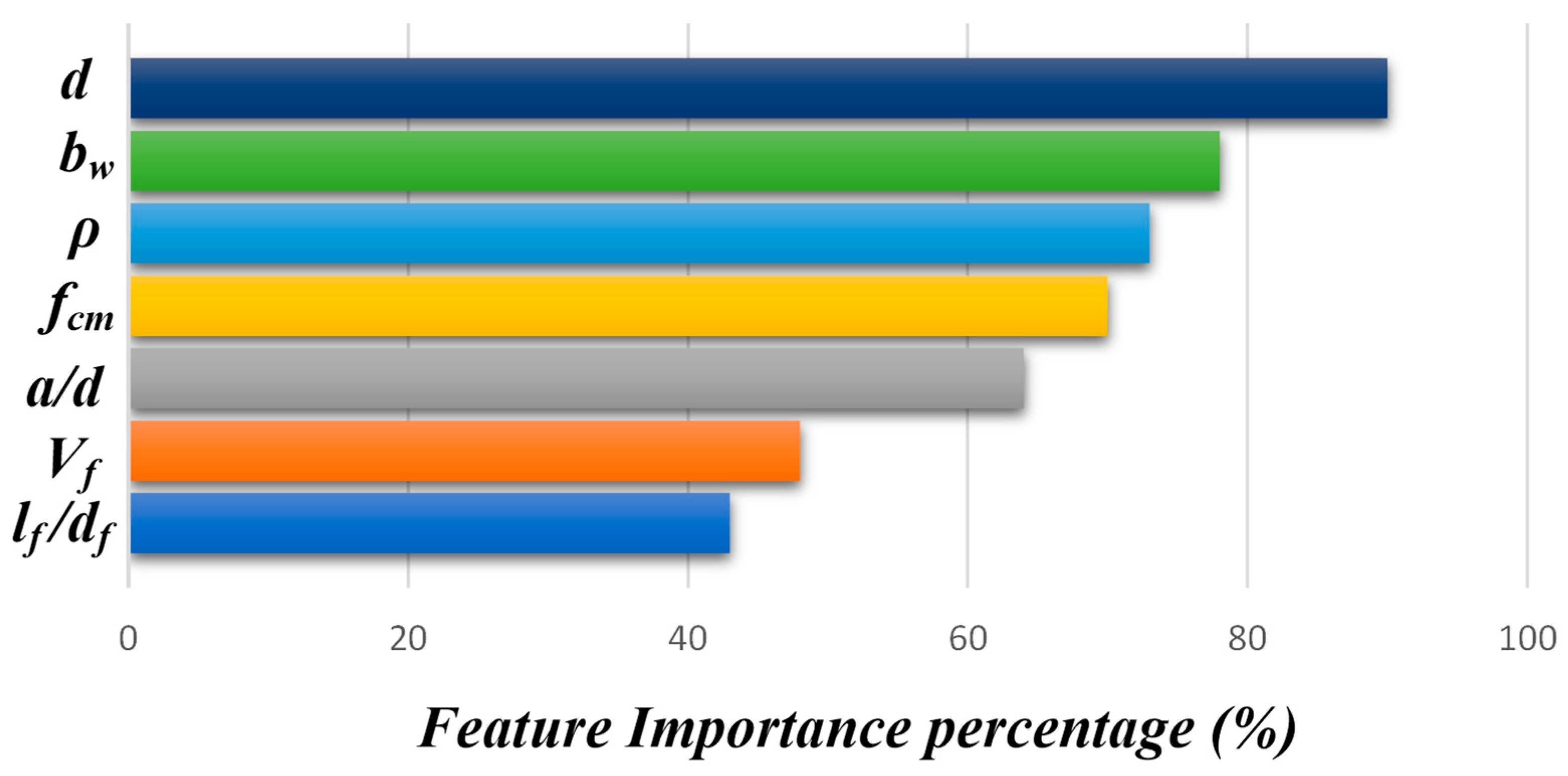
5.2. Importance of Key Parameters
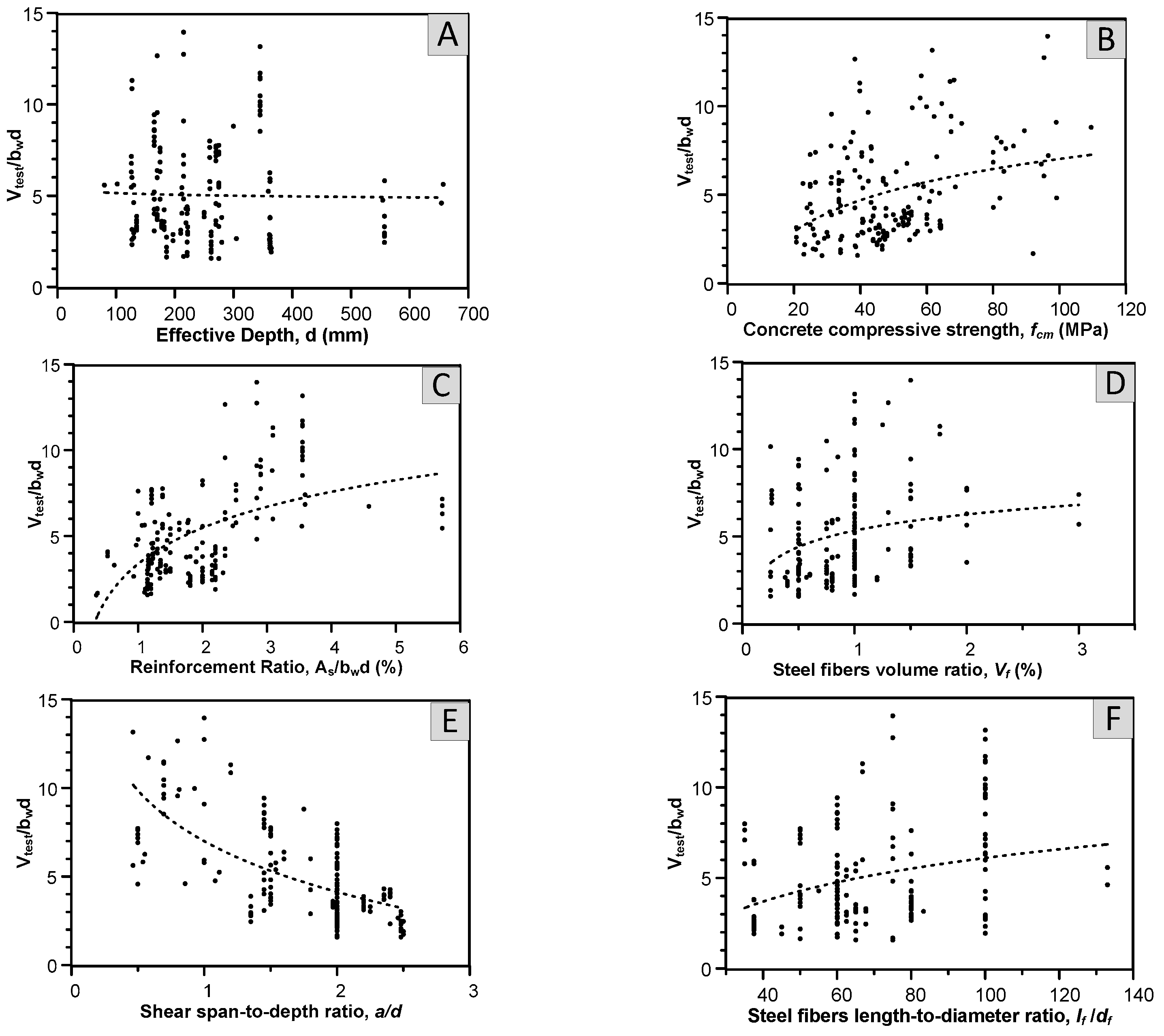
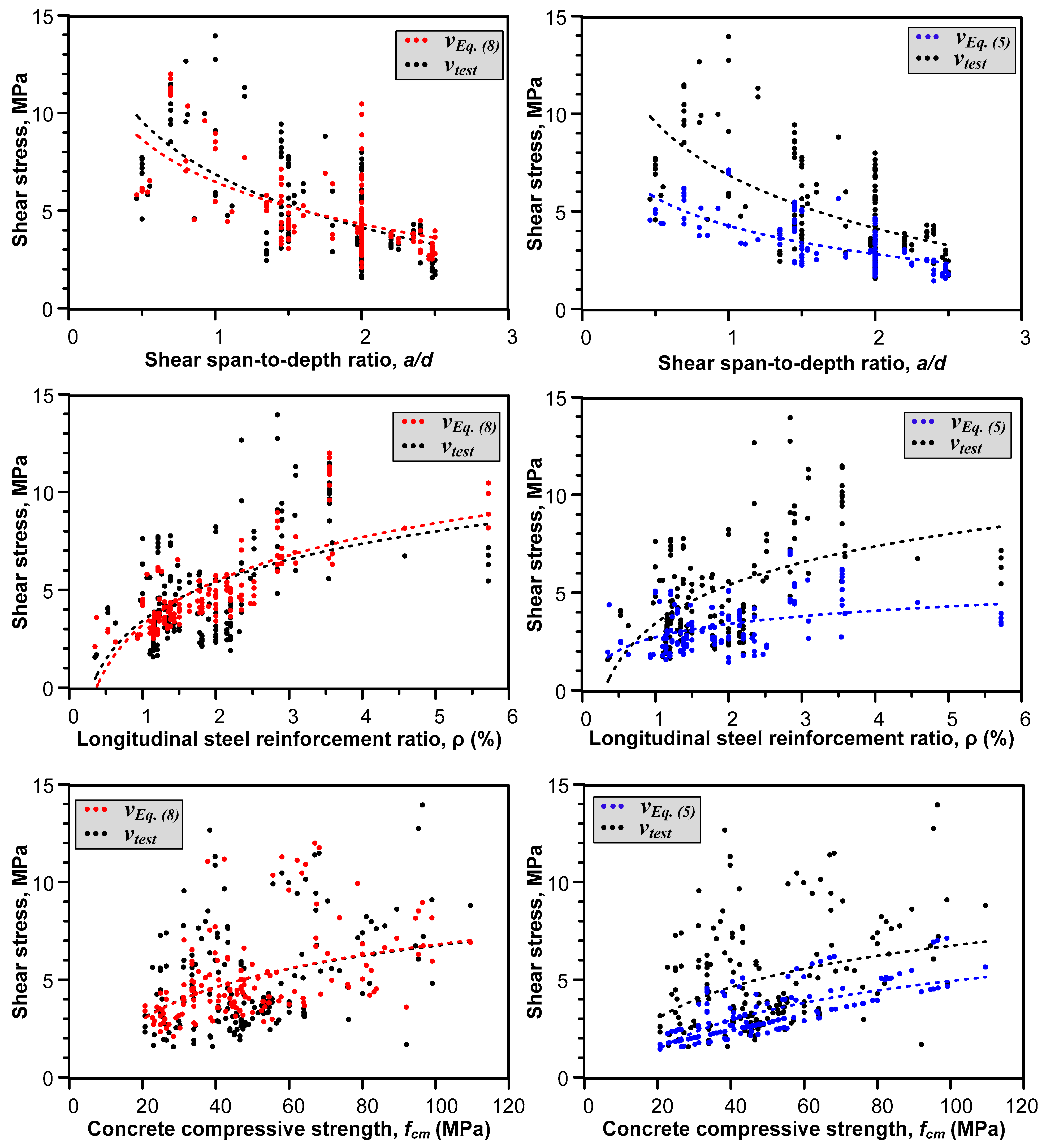
5.3. Effect of Selected Parameters on the Proposed Model
6. Summary and Conclusions
- Longitudinal steel reinforcement significantly boosts the shear strength of SFRC deep beams without stirrups. This can be justified, as the steel fibers improve deep beams’ capacity to carry loads by helping them bridge cracks.
- Even though the shear stresses are inversely related to the span-to-depth ratio, SFRC deep beams experience higher shear loads than RC deep beams because when the span-to-depth ratio of beams rises, the failure mode shifts from crushing of struts to diagonal shear failure.
- The results also show that the concrete compressive strength and depth of beams have only a small impact on the performance of SFRC and RC beams, which is understandable given that the strut-and-tie model, which primarily relies on the concrete compressive strength, provides the most accurate simulation of the shear strength of deep beams.
- A survey was conducted to explore the input parameters of the available shear strength models in literatures, and the investigation revealed the three variables , and are significant to quantify the shear strength contribution of steel reinforcement, concrete, and steel fibers ratio. Therefore, these three variables were utilized to build the proposed shear strength model for SFRC deep beams without stirrups.
- The proposed model outperformed the other equations in the literature, since it was able to anticipate the shear strength of SFRC deep beams with the lowest RMSE (=1.58) and lowest scatteredness, demonstrating the model’s high accuracy.
- The shear stresses predictions using the proposed model revealed that the trendlines of a/d, , and versus the predicted shear stresses match the test results in terms of the average fitting line and the scatteredness of data. This demonstrates the suggested model’s superior performance when considering various crucial factors that affect the shear strength of SFRC deep beams without stirrups.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Dabiri, H.; Daneshvar, K.; Karakouzian, M.; Farhangi, V. Application of Machine Learning to Predict the Mechanical Characteristics of Concrete Containing Recycled Plastic-Based Materials. Appl. Sci. 2023, 13, 2033. [Google Scholar] [CrossRef]
- Chao, S.-H. Size Effect on Ultimate Shear Strength of Steel Fiber-Reinforced Concrete Slender Beams. ACI Struct. J. 2020, 117, 145–158. [Google Scholar] [CrossRef]
- ACI 318; Building Code Requirements for Structural Concrete (ACI 318-19) and Commentary (ACI 318R-19). American Concrete Institute: Farmington Hills, MI, USA, 2019.
- Dang, T.D.; Tran, D.T.; Nguyen-Minh, L.; Nassif, A.Y. Shear resistant capacity of steel fibres reinforced concrete deep beams: An experimental investigation and a new prediction model. Structures 2021, 33, 2284–2300. [Google Scholar] [CrossRef]
- Ashour, S.A.; Hasanain, G.S.; Wafa, F.F. Shear Behavior of High-Strength Fiber Reinforced Concrete Beams. ACI Struct. J. 1992, 89, 176–184. [Google Scholar] [CrossRef]
- Li, V.C.; Ward, R.J.; Hamza, A.M. Steel and Synthetic Fibers as Shear Reinforcement. ACI Mater. J. 1992, 89, 499–508. [Google Scholar] [CrossRef]
- Mansur, M.A.; Ong, K.C.G.; Paramasivam, P. Shear Strength of Fibrous Concrete Beams Without Stirrups. J. Struct. Eng. 1986, 112, 2066–2079. [Google Scholar] [CrossRef]
- Cho, S.-H.; Kim, Y.-I. Effects of Steel Fibers on Short Beams Loaded in Shear. ACI Struct. J. 2003, 10, 765–774. [Google Scholar]
- Gebretsadik, B.; Jadidi, K.; Farhangi, V.; Karakouzian, M. Application of Ultrasonic Measurements for the Evaluation of Steel Fiber Reinforced Concrete. Eng. Technol. Appl. Sci. Res. 2021, 11, 6662–6667. [Google Scholar] [CrossRef]
- Narayanan, R.; Darwish, I.Y.S. Use of Steel fibers as shear reinforcement. ACI Struct. J. 1987, 84, 216–227. [Google Scholar] [CrossRef]
- Kwak, Y.K.; Eberhard, M.O.; Kim, W.S.; Kim, J. Shear Strength of Steel Fiber-Reinforced Concrete Beams without Stirrups. ACI Struct. J. 2002, 99, 530–538. [Google Scholar] [CrossRef]
- Shahnewaz, M.; Alam, M.S. Genetic algorithm for predicting shear strength of steel fiber reinforced concrete beam with parameter identification and sensitivity analysis. J. Build. Eng. 2020, 29, 101205. [Google Scholar] [CrossRef]
- Lim, T.Y.; Paramasivam, P.; Lee, S.L. Shear and moment capacity of reinforced steel-fibre-concrete beams. Mag. Concr. Res. 1987, 39, 148–160. [Google Scholar] [CrossRef]
- Narayan, R.; Darwish, I.Y.S. Fiber Concrete Deep Beams in Shear. ACI Struct. J. 1988, 85, 141–149. [Google Scholar] [CrossRef]
- Shin, S.-W.; Oh, J.-G.; Ghosh, S.K. Shear Behavior of Laboratory-Sized High-Strength Concrete Beams Reinforced With Bars and Steel Fibers. Spec. Publ. 1994, 142, 181–200. [Google Scholar] [CrossRef]
- Murty, D.S.R.; Venkatacharyulu, T. Fibre Reinforced Concrete Beams Subjected to Shear Force.(Retroactive Coverage). In Proceedings of the International Symposium on Fiber Reinforced Concrete, Madras, India, 16–19 December 1987; pp. 1.125–1.132. [Google Scholar]
- Adebar, P.; Mindess, S.; Pierre, D.S.; Olund, B. Shear Tests of Fiber Concrete Beams without Stirrups. ACI Struct. J. 1997, 94, 68–76. [Google Scholar]
- Batson, G.; Jenkins, E.; Spatney, R. Steel Fibers as Shear Reinforcement in Beams. ACI J. 1972, 69, 640–644. [Google Scholar]
- Imam, M.; Vandewalle, L.; Mortelmans, F. Shear capacity of steel fiber high-strength concrete beams. ACI Spec. Pub. 1994, 149, 227–242. [Google Scholar]
- Tahenni, T.; Chemrouk, M.; Lecompte, T. Effect of steel fibers on the shear behavior of high strength concrete beams. Constr. Build. Mater. 2016, 105, 14–28. [Google Scholar] [CrossRef]
- Kang, T.H.-K.; Kim, W.; Kwak, Y.-K.; Hong, S.-G. Shear Testing of Steel Fiber-Reinforced Lightweight Concrete Beams without Web Reinforcement. ACI Struct. J. 2011, 108, 553. [Google Scholar] [CrossRef]
- Gali, S.; Subramaniam, K.V.L. Shear Behavior of Slender and Non-Slender Steel Fiber-Reinforced Concrete Beams. ACI Struct. J. 2019, 116, 149–158. [Google Scholar] [CrossRef]
- Cucchiara, C.; La Mendola, L.; Papia, M. Effectiveness of stirrups and steel fibres as shear reinforcement. Cem. Concr. Compos. 2004, 26, 777–786. [Google Scholar] [CrossRef]
- Zhao, J.; Liang, J.; Chu, L.; Shen, F. Experimental Study on Shear Behavior of Steel Fiber Reinforced Concrete Beams with High-Strength Reinforcement. Materials 2018, 11, 1682. [Google Scholar] [CrossRef]
- Manju, R.; Sathya, S.; Sylviya, B. Shear strength of high-strength steel fibre reinforced concrete rectangular beams. IJCIET 2017, 8, 1716–1729. [Google Scholar]
- Roberts, T.; Ho, N. Shear failure of deep fibre reinforced concrete beams. Int. J. Cem. Compos. Light. Concr. 1982, 4, 145–152. [Google Scholar] [CrossRef]
- Spinella, N.; Colajanni, P.; La Mendola, L. Nonlinear Analysis of Beams Reinforced in Shear with Stirrups and Steel Fibers. ACI Struct. J. 2012, 109, 53–64. [Google Scholar] [CrossRef]
- Chalioris, C.; Sfiri, E. Shear Performance of Steel Fibrous Concrete Beams. Procedia Eng. 2011, 14, 2064–2068. [Google Scholar] [CrossRef]
- Dupont, D.; Vandewalle, L. Shear Capacity of Concrete Beams Containing Longitudinal Reinforcement and Steel Fibers. Spec. Publ. 2003, 216, 79–94. [Google Scholar] [CrossRef]
- Jindal, R.L. Shear and Moment Capacities of Steel Fiber Reinforced Concrete Beams. Spec. Publ. 1984, 81, 1–16. [Google Scholar]
- Garcia, S.; Pereira, A.; Pierott, R. Shear Strength of Sand-Lightweight Concrete Deep Beams with Steel Fibers. ACI Struct. J. 2021, 118, 203–214. [Google Scholar] [CrossRef]
- Xue, X.; Hua, X.; Zhou, J. Test and prediction of shear strength for the steel fiber–reinforced concrete beams. Adv. Mech. Eng. 2019, 11, 1687814019840551. [Google Scholar] [CrossRef]
- Li, X.K.; Li, C.Y.; Zhao, M.L.; Yang, H.; Zhou, S.Y. Testing and Prediction of Shear Performance for Steel Fiber Reinforced Expanded-Shale Lightweight Concrete Beams without Web Reinforcements. Materials 2019, 12, 1594. [Google Scholar] [CrossRef]
- Padmarajaiah, S.K.; Ramaswamy, A. Behavior of Fiber-Reinforced Prestressed and Reinforced High-Strength Concrete Beams Subjected to Shear. ACI Struct. J. 2001, 98, 752–761. [Google Scholar] [CrossRef]
- Lakavath, C.; Pidapa, V.; Joshi, S.S. Shear Behavior Of Steel Fiber Reinforced Precast Prestressed Concrete Beams. In Proceedings of the International Conference on Composite Materials and Structures- ICCMS 2017, Hyderabad, India, 27–29 December 2017. [Google Scholar]
- Parmentier, B.; Cauberg, N.; Vandewalle, L. Shear Resistance of Macro-Synthetic and Steel Fibre Reinforced Concrete Beams Without Stirrups. In Proceedings of the 8th RILEM International Symposium on Fibre Reinforced Concrete: Challenges and Opportunities, Guimaraes, Portugal, 19–21 September 2012; pp. 19–21. [Google Scholar]
- Uomoto, T.; Weerarathe, R.K.; Furukoshi, H.; Fujino, H. Shear Strength of Reinforced Concrete Beams with Fiber Reinforcement, Proceedings, Third Internal RILEM Symposium on Developments in Fiber Reinforced Cement and Concrete, Sheffield, RILEM Technical Committee 49-TFR; Sheffield University Press Unit: Sheffield, UK, 1986; pp. 553–562. [Google Scholar]
- Moody, K.; Viest, I.; Elstner, R.; Hognestad, E. Shear Strength of Reinforced Concrete Beams Part 2-Tests of Restrained Beams without Web Reinforcement. ACI 1955, 51, 417–434. [Google Scholar]
- Moody, K.; Viest, I.; Elstner, R.; Hognestad, E. Shear Strength of Reinforced Concrete Beams Part 1-Tests of Simple Beams. ACI 1954, 51, 317–332. [Google Scholar]
- Morrow, J.; Viest, I.M. Shear Strength of Reinforced Concrete Frame Members without Web Reinforcement. ACI J. Proc. 1957, 53, 833–869. [Google Scholar] [CrossRef]
- Chang, T.S.; Kesler, C.E. Static and fatigue strength in shear of beams with tensile reinforcement. ACI J. 1958, 54, 1033–1057. [Google Scholar]
- Watstein, D.; Mathey, R.G. Strains in beams having diagonal cracks. ACI J. 1958, 55, 717–728. [Google Scholar]
- Rodriguez, J.J.; Bianchini, A.C.; Viest, I.M.; Kesler, C.E. Shear Strength of Two-Span Continous Reinforced Concrete Beams. ACI J. Proc. 1959, 5, 1089–1130. [Google Scholar]
- De Cossio, R.D.; Siess, C.P. Behavior and strength in shear of beams and frames without web reinforcement. ACI J. Proc. 1960, 56, 695–736. [Google Scholar]
- Leonhardt, F.; Walther, R. The Stuttgart Shear Tests. CACA Transl. 1961, 1964, 49–54. [Google Scholar]
- Mathey, R.G.; Watstein, D. Shear strength of beams without web reinforcement containing deformed bars of different yield strengths. ACI J. Proc. 1963, 60, 183–208. [Google Scholar]
- de Paiva, H.A.R.; Siess, C.P. Strength and Behavior of Deep Beams in Shear. J. Struct. Div. 1965, 91, 22. [Google Scholar] [CrossRef]
- Kani, G.N.J. How safe are our large reinforced concrete beams? ACI J. 1967, 64, 128–141. [Google Scholar]
- Ramakrishnan, V.; Ananthanarayana, Y. Ultimate strength of deep beams in shear. ACI J. Proc. 1968, 65, 87–98. [Google Scholar]
- Manuel, R. Failure of deep beams. ACI Spec. Publ. 1974, 42, 15. [Google Scholar]
- Smith, K.; Vantsiotis, A. Shear strength of deep beams. ACI J. Proc. 1982, 79, 201–213. [Google Scholar]
- Mphonde, A.G.; Frantz, G.C. Shear tests of high-and low-strength concrete beams without stirrups. ACI J. Proc. 1984, 81, 350–357. [Google Scholar]
- Rogowsky, D.M.; MacGregor, J.G.; Ong, S.Y. Tests of Reinforced Concrete Deep Beams. ACI 1986, 83, 10. [Google Scholar]
- Ahmad, S.H.; Lue, D. Flexure-shear interaction of reinforced high strength concrete beams. ACI Struct. J. 1987, 84, 330–341. [Google Scholar]
- Lehwalter, N. Bearing Capacity of Concrete Compression Struts in Truss-Systems, Exemplified by the Case of Short Beams. Ph.D. Thesis, Darmstadt, Germany, 1988. [Google Scholar]
- Walraven, J.; Lehwalter, N. Size Effects in Short Beams Loaded in Shear. ACI Struct. J. 1994, 9, 585–593. [Google Scholar]
- Xie, Y.; Ahmad, S.H.; Yu, T.; Hino, S.; Chung, W. Shear Ductility of Reinforced Concrete Beams of Normal and High-Strength Concrete. ACI Struct. J. 1994, 91, 140–149. [Google Scholar] [CrossRef]
- Tan, K.H.; Kong, F.K.; Teng, S.; Guan, L. High-Strength Concrete Deep Beams with Effective Span and Shear Span Variations. ACI Struct. J. 1995, 92, 395–405. [Google Scholar] [CrossRef]
- Shin, S.W.; Lee, K.S.; Moon, J.I.; Ghosh, S.K. Shear Strength of Reinforced High-Strength Concrete Beams with Shear Span-to-Depth Ratios between 1.5 and 2.5. ACI Struct. J. 1999, 96, 549–556. [Google Scholar] [CrossRef]
- Tan, K.H.; Lu, H.Y. Shear Behavior of Large Reinforced Concrete Deep Beams and Code Comparisons. ACI Struct. J. 1999, 96, 836–846. [Google Scholar] [CrossRef]
- Pendyala, R.S.; Mendis, P. Experimental study on shear strength of high-strength concrete beams. ACI Struct. J. 2000, 97, 564–571. [Google Scholar]
- Adebar, P. One-way shear strength of large footings. Can. J. Civ. Eng. 2000, 27, 553–562. [Google Scholar] [CrossRef]
- Oh, J.K.; Shin, S.W. Shear Strength of Reinforced High-Strength Concrete Deep Beams. ACI Struct. J. 2001, 98, 164–173. [Google Scholar] [CrossRef]
- Lertsrisakulrat, T.; Niwa, J.; Yanagawa, A.; Matsuo, M. Concept of Concrete Compressive Fracture Energy in RC Deep Beams without Transverse Reinforcement; Japan Concrete Institute: Tokyo, Japan, 2001; Volume 23, pp. 97–102. [Google Scholar]
- Yang, K.-H.; Chung, H.-S.; Lee, E.-T.; Eun, H.-C. Shear characteristics of high-strength concrete deep beams without shear reinforcements. Eng. Struct. 2003, 25, 1343–1352. [Google Scholar] [CrossRef]
- Tan, K.H.; Cheng, G.H.; Cheong, H.K. Size effect in shear strength of large beams—Behaviour and finite element modelling. Mag. Concr. Res. 2005, 57, 497–509. [Google Scholar] [CrossRef]
- Seliem, H.; Hosny, A.; Dwairi, H.; Rizkalla, S. Shear behavior of concrete beams reinforced with MMFX steel without web rein-forcement. In NC State University Final Report; Project No. IS-06-08; Constructed Facilities Laboratory, North Carolina State University: Raleigh, NC, USA, 2006; 21p. [Google Scholar]
- Zhang, N.; Tan, K.-H. Size effect in RC deep beams: Experimental investigation and STM verification. Eng. Struct. 2007, 29, 3241–3254. [Google Scholar] [CrossRef]
- Tan, K.-H.; Cheng, G.-H.; Zhang, N. Experiment to mitigate size effect on deep beams. Mag. Concr. Res. 2008, 60, 709–723. [Google Scholar] [CrossRef]
- Ismail, K.S. Shear Behaviour of Reinforced Concrete Deep Beams; The University of Sheffield: Sheffield, UK, 2016. [Google Scholar]
- Joint ACI-ASCE Committee 445. Recent Approaches to Shear Design of Structural Concrete. J. Struct. Eng. 1998, 124, 1375–1417. [Google Scholar] [CrossRef]

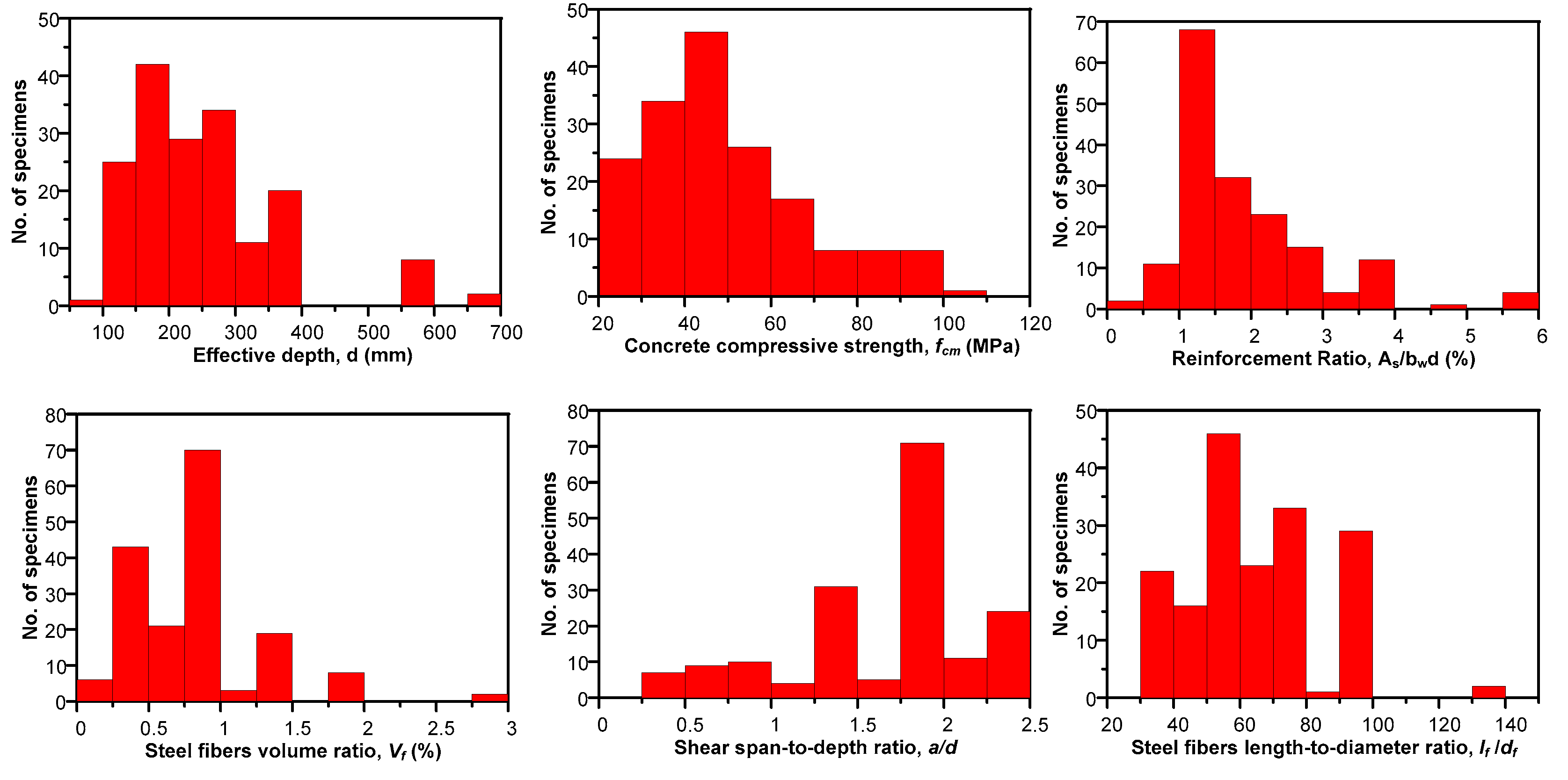
| Reference | No. of Specimens | d (mm) |
(MPa) | ρ (%) | Vf (%) | a/d | lf/df |
|---|---|---|---|---|---|---|---|
| [6] | 1 | 102 | 22.7 | 1.1 | 1.0 | 1.5 | 60 |
| [7] | 2 | 197 | 29.1;29.9 | 1.34 | 0.5; 0.75 | 2.0 | 60 |
| [13] | 5 | 221 | 34 | 1.1; 2.2 | 0.5; 1.0 | 1.5; 2.5 | 60 |
| [10] | 8 | 130; 126 | 49–78.8 | 2.0, 5.72 | 0.25–2.0 | 2.0 | 100;133 |
| [5] | 8 | 215 | 92–99.1 | 0.37–4.58 | 0.5–1.5 | 1.0;2.0 | 75 |
| [14] | 9 | 345 | 37.8–68.2 | 3.55 | 0.25–1.0 | 0.7–0.93 | 100 |
| [15] | 2 | 175 | 80 | 3.59 | 0.5; 1.0 | 2.0 | 100 |
| [16] | 4 | 186 | 23–26 | 1.2 | 0.5; 1.0 | 2.0 | 50;100 |
| [17] | 6 | 557 | 40.8–56.5 | 2.15 | 0.4–1.5 | 1.35 | 60;100 |
| [11] | 3 | 212 | 30.8–68.6 | 1.5 | 0.5;0.75 | 2.0 | 62.5 |
| [18] | 3 | 127 | 39.8 | 3.09 | 1.76 | 1.2;1.8 | 66.8 |
| [19] | 1 | 300 | 109.5 | 3.08 | 0.75 | 1.75 | 75 |
| [20] | 9 | 135 | 60–64.2 | 1.16 | 0.5;1.0 | 2.2 | 65;80 |
| [21] | 2 | 210 | 44.6;57.2 | 1.5 | 0.5 | 2.0 | 62.5 |
| [22] | 4 | 222 | 40.4–45.6 | 1.43 | 0.5;0.75 | 1.8;2.25 | 80 |
| [23] | 2 | 219 | 40.9;43.2 | 1.9 | 1.0;2.0 | 2.0 | 60 |
| [24] | 4 | 260 | 34.5–37.1 | 2.52 | 0.5–2.0 | 2.0 | 35 |
| [25] | 3 | 175 | 82–83.8 | 1.0 | 0.5–1.5 | 1.5 | 80 |
| [26] | 6 | 170 | 31.3;38.3 | 2.35 | 0.85;1.3 | 0.8–2.4 | 100 |
| [27] | 1 | 219 | 80 | 1.91 | 1.0 | 2.0 | 55 |
| [28] | 1 | 275 | 28.4 | 0.35 | 0.5 | 2.0 | 75 |
| [8] | 12 | 165 | 25.3–89.4 | 1.3;2.9 | 0.5;1.0 | 1.45 | 60 |
| [29] | 11 | 260–305 | 26.5–50 | 0.93–1.64 | 0.25–0.75 | 1.54–2.48 | 45–80 |
| [30] | 4 | 127 | 20.7 | 2.0 | 1.0 | 2.0;2.4 | 62.5–100 |
| [31] | 6 | 360–657 | 33.5 | 1.06–1.78 | 1.0 | 0.46–1.11 | 60 |
| [32] | 9 | 275 | 24.9–31.2 | 0.63–2.47 | 1.0–3.0 | 1.5;2.0 | 60 |
| [33] | 18 | 362 | 38.4–47.4 | 1.11–2.32 | 0.4–1.2 | 1.0–2.0 | 37.5 |
| [34] | 9 | 170;178 | 52.5–54.6 | 1.23;1.35 | 0.5–1.5 | 1.97;2.35 | 80 |
| [35] | 4 | 250 | 53.1;55.4 | 0.53 | 0.5;1.0 | 2.4 | 50 |
| [36] | 8 | 270 | 40.4;43.2 | 1.21 | 0.26;0.51 | 0.5;1.5 | 50 |
| [37] | 7 | 80–280 | 45.8–51.5 | 2.0–3.54 | 0.75;1.5 | 2.0 | 60;67.7 |
| Total | 172 |
| Statistical Measure | Features | |||||
|---|---|---|---|---|---|---|
| d (mm) | bw (mm) | a/d | fcm (MPa) | ρ (%) | Vu (kN) | |
| Mean | 425 | 183 | 1.35 | 33.5 | 2.02 | 283.4 |
| Median | 356 | 178 | 1.36 | 27.9 | 1.82 | 220.8 |
| Mode | 305 | 178 | 1 | 31.4 | 1.13 | 192.7 |
| Standard deviation | 234 | 64 | 0.4 | 16.7 | 1.1 | 206 |
| Minimum | 132 | 51 | 0.5 | 11.3 | 0.26 | 20.7 |
| Maximum | 1559 | 460 | 2 | 87 | 5.04 | 1240 |
| Count | 281 | 281 | 281 | 281 | 281 | 281 |
| Reference | Variable | Parameter | Note |
|---|---|---|---|
| [10] | X1 | X2 is dependent on X1, therefore, X2 will be dropped | |
| X2 | |||
| X3 | |||
| [5] | X4 | ||
| X5 | |||
| X6 | |||
| [6] | X7 | ||
| [11] | X8 | X8 is dependent on X1, therefore, X8 will be dropped | |
| [12] | X9 | ||
| X10 | |||
| Proposed in this study | X11 | ||
| X12 |
| Variable | X1 | X3 | X4 | X5 | X6 | X7 | X9 | X10 | X11 | X12 |
|---|---|---|---|---|---|---|---|---|---|---|
| X1 | 1 | |||||||||
| X3 | 0.23 | 1 | ||||||||
| X4 | 0.20 | 0.96 | 1 | |||||||
| X5 | −0.04 | −0.75 | −0.78 | 1 | ||||||
| X6 | 0.10 | 0.24 | 0.23 | −0.05 | 1 | |||||
| X7 | 0.29 | 0.69 | 0.78 | −0.26 | 0.32 | 1 | ||||
| X9 | 0.12 | 0.23 | 0.23 | −0.05 | 0.99 | 0.33 | 1 | |||
| X10 | 0.70 | 0.45 | 0.50 | −0.10 | 0.17 | 0.73 | 0.18 | 1 | ||
| X11 | 0.10 | 0.23 | 0.23 | −0.05 | 1.00 | 0.33 | 0.99 | 0.17 | 1 | |
| X12 | 0.79 | 0.03 | 0.06 | 0.04 | −0.05 | 0.20 | −0.04 | 0.69 | −0.05 | 1 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Almasabha, G.; Murad, Y.; Alghossoon, A.; Saleh, E.; Tarawneh, A. Sustainability of Using Steel Fibers in Reinforced Concrete Deep Beams without Stirrups. Sustainability 2023, 15, 4721. https://doi.org/10.3390/su15064721
Almasabha G, Murad Y, Alghossoon A, Saleh E, Tarawneh A. Sustainability of Using Steel Fibers in Reinforced Concrete Deep Beams without Stirrups. Sustainability. 2023; 15(6):4721. https://doi.org/10.3390/su15064721
Chicago/Turabian StyleAlmasabha, Ghassan, Yasmin Murad, Abdullah Alghossoon, Eman Saleh, and Ahmad Tarawneh. 2023. "Sustainability of Using Steel Fibers in Reinforced Concrete Deep Beams without Stirrups" Sustainability 15, no. 6: 4721. https://doi.org/10.3390/su15064721
APA StyleAlmasabha, G., Murad, Y., Alghossoon, A., Saleh, E., & Tarawneh, A. (2023). Sustainability of Using Steel Fibers in Reinforced Concrete Deep Beams without Stirrups. Sustainability, 15(6), 4721. https://doi.org/10.3390/su15064721








