Abstract
In this article, new multiple-production systems based on the micro-combined cooling, heating and power (CCHP) cycle with biomass heat sources are presented. In this proposed system, absorption refrigeration cycle subsystems and a water softener system have been used to increase the efficiency of the basic cycle and reduce waste. Comprehensive thermodynamic modeling was carried out on the proposed system. The validation of subsystems and the optimization of the system via the genetic algorithm method was carried out using Engineering Equation Solver (EES) software. The results show that among the components of the system, the dehumidifier has the highest exergy destruction. The effect of the parameters of evaporator temperature 1, ammonia concentration, absorber temperature, heater temperature difference, generator 1 pressure and heat source temperature on the performance of the system was determined. Based on the parametric study, as the temperature of evaporator 1 increases, the energy efficiency of the system increases. The maximum values of the energy efficiency and exergy of the whole system in the range of heat source temperatures between 740 and 750 K are equal to 74.2% and 47.7%. The energy and exergy efficiencies of the system in the basic mode are equal to 70.68% and 44.32%, respectively, and in the optimization mode with the MOOD mode, they are 87.91 and 49.3, respectively.
1. Introduction
One of the important aspects in energy production is the design of power generation systems based on renewable energy sources in such a way that fewer pollutants are produced. Biomass is one of the sources of renewable energy. One type of wooden waste is sawdust. Sawdust production has increased all over the world; sawdust is used in wood products, and sawdust waste is used as biomass [1]. On the other hand, the use of biomass increases greenhouse gases. Therefore, improving the performance of systems will increase the ratio of energy produced per unit of fuel consumed. From 2006 to 2030, the need for energy and power will increase by about 40% [2]. With the increase in global demand, the price of energy and the cost of its maintenance and environmental concerns will increase. Therefore, the use of CCHP systems is a suitable solution to meet the increasing demand for energy [3].
In this research, the chemical analysis of urban waste in Hamedan was carried out, and the heating value of urban waste incineration was estimated. In this way, an approximate amount of energy obtained could be obtained before designing the system [4]. In this research, different compositions of air and steam as a reactor input were examined, and fixed-base gasifier behavior in different situations was specified, which demonstrated that the best air–steam composition which achieved the best heat valuation was 12.26 (lb/s) for air input and 9.989 (lab/s) for steam input [5]. In this research, we first studied renewable energies, followed by technologies related to biogas systems. Biogas systems have been referred to in research regarding landfill, and their utilization in this type of scheme has been discussed comprehensively. For this purpose, the input source of this system was considered as the volume of garbage in the city of Germi, which was used as the study area. In the next step, the amount of garbage produced in this city was extracted, and the Landfill software was used for methane production potential assessment from this system, and the Homer software was used for the economic analysis and reliability evaluation. The most important results relate to the payback period, which is about 10 years, and the amount of electricity produced per year, which is 11,658.265 MWh [6]. In this study, the study area of Hamadan city was considered to have average urban waste production of about 420 tons/month. Homer software was used to analyze the amount of electricity produced, and economic and environmental analyses were also carried out. One of the outstanding results of this research is that it was found that the production of electrical energy is 229,735 kW/year. Electricity generation with biomass resources will reduce Co2 and Co emissions by 77.2 and 7.96 kg/year, respectively. That cost of energy (COE) for this system is 0.177 USD/kWh [7].
Geng, D. and Gao, X [8] proposed the thermodynamic and exergoeconomic optimization of a novel cooling, desalination and power multi-generation system based on ocean thermal energy. This study proposed a novel combined cooling, desalination and power (CCDP) system consisting of an open-ocean thermal energy conversion (OTEC) cycle, a dual-Kalina cycle, an ejector refrigeration cycle (ERC) and reverse osmosis (RO) desalination. Wang et al. [9] presented the techno-economic and techno-environmental assessment and multi-objective optimization of a new CCHP system based on waste heat recovery from the regenerative Brayton cycle. Xing, L. and Li, J [10] proposed a biomass/geothermal-hybrid-driven poly-generation plant centered on cooling, heating, power and hydrogen production with CO2 capture. The results of these numerical investigations showed that the system supplied net power of almost 22.23 MW, a 34.13 MW heating effect, a cooling effect of 96.40 MW, plus hydrogen generation of 124 kg/h. Additionally, the rate of CO2 capture was 4.32 kg/s. The exergy efficiency and energy efficiency of the system were estimated to be 17.87% and 79.47%, respectively. In addition, the plant had a total product cost rate of 1.162 USD/s and a sustainability index of 1.218. Wang et al. [11] presented the bi-level sizing optimization of a distributed solar hybrid CCHP system considering economic, energy and environmental objectives. Delgado et al. [12] presented an integration of cycles via absorption for the production of desalinated water and cooling. Askari et al. [13] presented the exergo-economic analysis of two novel combined ejector heat pump/humidification–dehumidification desalination systems.
In this study, a new multiple-generation system based on a micro-CCHP cycle with a biomass heat source is presented. In this proposed system, absorption refrigeration cycle subsystems and a water softener system were used in order to increase the efficiency of the basic cycle and reduce waste. In this research, the microturbine system was modeled with a biomass generator, which was used to model the thermodynamic relationships governing the various components of the studied system. The general goal of this research was to increase the energy efficiency and exergy of the system, and to achieve this goal, the waste heat of the generator after recovery was used as the starter of the absorption refrigeration cycle.
2. Materials and Methods
To carry out this project, related articles were studied. The modeling and validation of each cycle used were carried out in EES software. Finally, modeling of the overall system and optimization of the overall system with the genetic algorithm method with single-objective and multi-objective functions were carried out in EES software.
2.1. Analysis of the Proposed System
Figure 1 shows the schematic view of the proposed system. Air and biomass enter the combustion chamber, and the gases produced from burning are transferred to the boiler during this phase and increase the temperature of the water in the boiler. The two-phase water–ammonia mixture taken out of the generator enters the separator. A water–ammonia vapor solution enters the turbine to generate power. The mixed fluid enters the heat exchanger to start the ERC cycle with isobutane, as the working fluid, losing heat. Then, the fluid passes through pump to compensate for the pressure drop applied to the fluid while passing through the turbine and pressure relief valve. As the working fluid passes through the generator, the temperature of the fluid increases, and the Kalina cycle is completed. The high-pressure fluid and the fluid coming out of evaporator with low pressure are mixed and condensed in the ejector. The condensed fluid coming out of the ejector loses its energy by passing through the heat exchanger and starts the vapor compression heat pump cycle (VCHPC) with the working fluid, R141b. The output fluid from the heat exchanger is separated into streams. One of the currents produces cooling by passing through the evaporator. The other flow passes through the pump and heat exchanger and completes the ERC cycle. The saturated liquid turns into saturated vapor at a constant temperature while passing through the heat exchanger. Additionally, by passing through the compressor, the fluid pressure increases. The saturated vapor is cooled by passing through the heater and turns into a saturated liquid. The refrigerant pressure decreases by passing through the pressure relief valve, and the VCHPC cycle is completed.
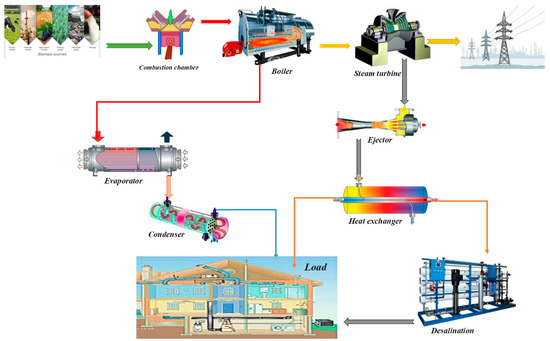
Figure 1.
Schematic view of the proposed system.
In this project, we used the closed-air open-water system (CAOWS) model. The humidification–dehumidification (HDH) system includes three main parts: humidification, dehumidification, and a heat source. In this system, water travels through an open loop and air through a closed loop. First, in the dehumidifier, salt water enters the system, and then, the preheated salt water enters the heat exchanger, is reheated in the heat exchanger during states 28–29 and enters the humidifier. In the humidifier, the air is in direct contact with the salt water, and the moist and warm air flow coming out of the humidifier enters the dehumidification chamber. In the dehumidifier, the air is in indirect contact with cold salt water. Additionally, when the air passes over the cold surfaces, it is distilled and recycled, and fresh water is produced.
The heat of the output water from the Kalina cycle generator is used to start the ARS cycle. The water vapor coming out of the evaporator, after passing through the heat exchanger, enters the absorber and is mixed with the thick solution of lithium bromide water (state 44), and a dilute solution is produced. After passing through the heat exchanger, the pumped diluted solution enters the generator, and due to receiving heat, some of the solutions evaporate and enter the condenser.
In this article, for a better evaluation of the proposed system, first, each subsystem was modeled, and energy and exergy analyses were performed on them. Additionally, to check the performance of the freshwater production system, the effective parameters of that system were defined. Then, thermodynamic modeling, mass, energy, and exergy balance equations of the proposed system were presented. In the following sections, a parametric study was conducted to investigate the effect of parameters on the system performance, and finally, the optimal thermodynamic conditions were calculated to determine the maximum energy efficiency and exergy of the overall system. EES software was used as the main tool in all calculations.
The following assumptions were considered in system modeling:
- Minor changes in pressure were ignored.
- All modeling was checked in stable conditions.
- All processes were one-dimensional and adiabatic, and nothing was carried out during the process.
- The velocity of entering and leaving the fluid in the ejector was equal.
- Kinetic and potential exergy was omitted.
- The power required for pumping or suctioning fluid into the desalination system was omitted.
- The temperature of fresh water leaving the dehumidifier was equal to the average temperature of the air entering and exiting the dehumidifier.
- The state of the output flow from the condenser and evaporator was saturated.
The data in Table 1 were used to evaluate the performance of the proposed system.
Assuming stable conditions for each control volume shown in Figure 1, the mass and energy balance for each system component is as follows [14]:
Mass balance:
x is the concentration of NH3 and LiBr in NH3-H2O and LiBr-H2O solutions. Energy balance:
The efficiency of the first law of the proposed system is calculated as follows:
Exergy destruction is one of the important parameters in exergy analysis. The exergy destruction rate for a control volume in a steady state is calculated as follows:
The total exergy is equal to the sum of physical and chemical exergy:
Chemical exergy is the standard fluid.
Physical exergy for biomass burning is calculated as follows:
The chemical exergy equation of ideal gases resulting from biomass burning is as follows:
The physical exergy of air and biomass at the state is 1.2 times zero. Biomass chemical exergy is calculated from the following equation [15]:
The efficiency of the second law for each component of the system is calculated as follows:
The efficiency of the second law (exergy) of the proposed system is calculated as follows:
To calculate the heat produced from biomass burning in the chamber, the following equation is used:
The value of HHVf can be calculated as follows [16]:

Table 1.
ARS cycle validation results with reference [17].
Table 1.
ARS cycle validation results with reference [17].
| Parameter | Calculated Value | [17] | Error % |
|---|---|---|---|
| COP | 0/535 | 0/5654 | 5/3 |
| f | 4/438 | 4/33 | 2/4 |
| (kg/s) | 12/24 | 12/5 | 2/08 |
| (kW) | 392/9 | 384/41 | 1/41 |
| (kW) | 232/8 | 241 | 3/4 |
| (kW) | 210/2 | 225/57 | 6/8 |
| (kW) | 370/3 | 378/87 | 2/2 |
2.2. Desalination System
The effective parameters in the freshwater production system are defined as follows [18]:
GOR: This coefficient is equal to the ratio of the latent heat of evaporation of produced fresh water to the heat input to the system. This parameter is an effective parameter to determine the amount of water produced and the amount of heat required for the system.
The maximum temperature of the system is equal to the temperature of the fluid leaving the heater. In this project, salt water passes through the heater.
- The lowest temperature of the system: the temperature of the salt water entering the dehumidifier has the lowest temperature of the desalination system.
ε (humidifying and dehumidifying efficiency): this parameter is equal to the ratio of the actual enthalpy difference to the maximum value of the enthalpy difference.
HCR: Due to the changes in fluid mass in the humidifier and dehumidifier, the parameter HCR (heat capacity ratio) is defined [19].
This parameter is equal to the ratio of the greatest possible enthalpy difference in cold flow to the greatest possible enthalpy difference in hot flow. This parameter is defined separately for humidifiers and dehumidifiers.
Based on the value of HCR and considering the input conditions to the dehumidifier or dehumidifier constant, the amount of irreversibility can be reduced [19].
2.3. Ejector
The ejector is a part of the system that converts the mechanical energy (pressure) of moving steam into kinetic energy (velocity) using convergence divergence. This factor creates a low-pressure area in the ejector, and as a result, the secondary flow is sucked into the ejector. When the fluid flow passes through the throat, the fluid is condensed, and the kinetic energy is converted into pressure. Figure 2 shows a schematic of the ejector and the profile of pressure and speed changes. To perform ejector calculations, Equations (21)–(26) are used [20,21]:
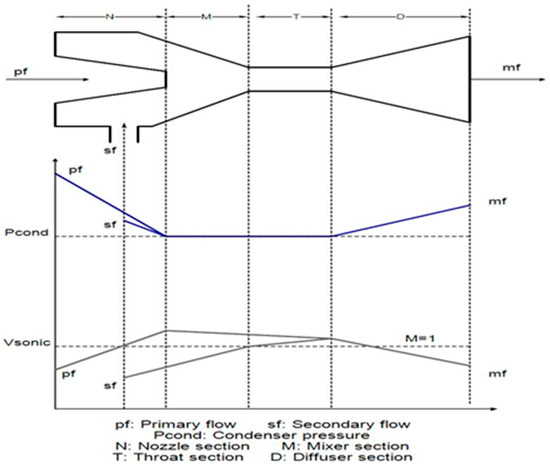
Figure 2.
The schematic view of the ejector and the profile of pressure and speed changes.
3. Results
3.1. Validation
The validation results of the Kalina cycle in the CCHP system with reference to (Sun et al., 2014 [22]) are presented in Table 2.

Table 2.
Kalina cycle validation with reference [22].
As can be seen from Table 2, the percentage of Kalina cycle validation is between 0.6 and 4%; this amount of difference is acceptable for numerical analysis.
The validation of the ERC and VCHPC cycle in the CCHP system was completed with reference [23]; the results are also presented in Table 3. According to the difference percentage, the calculated values are acceptable. The performance coefficient of the ERC and VCHPC cycle is 4.548 and 23.56, respectively.

Table 3.
Validation of ERC and VCHPC cycle in the CCHP system with reference [23].
In Figure 3, the validation of the CCHP cycle second-law efficiency change chart in terms of heat source temperature changes is shown with reference to [24]. The largest difference between the calculated values and the values specified in the reference [24] is related to the temperature of 560 °K, and the percentage of this difference is about 4.3%.
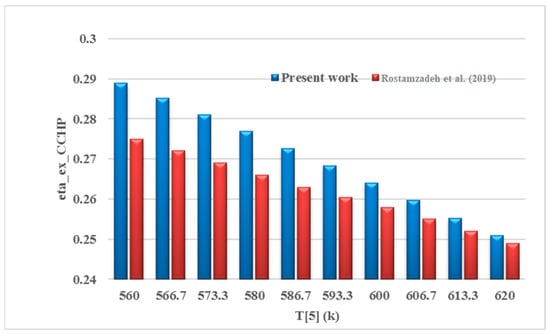
Figure 3.
Validation of the diagram of the efficiency changes of the second law of the CCHP cycle according to the temperature changes of the heat source with reference [24].
The results of the ARS cycle validation with reference [17] are presented in Table 1. According to Table 4, the percentage range of differences obtained is 1 to 6 percent. In Figure 4, the validation of the ARS cycle coefficient of performance (COP) graph is shown regarding the evaporator temperature with reference [17].

Table 4.
Optimal performance of the system in different modes and parameters.
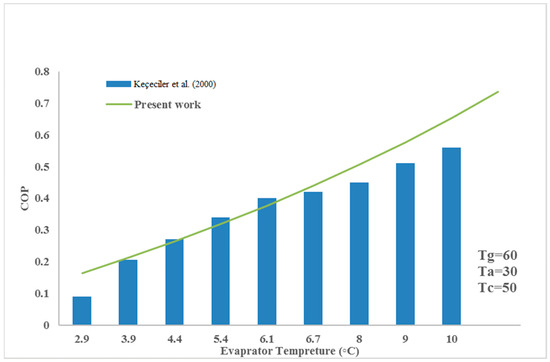
Figure 4.
Validation of the ARS cycle coefficient of performance (COP) graph regarding the evaporator temperature with reference [17].
In Figure 5, the validation of the desalination system is shown in the form of a graph of changes in the gained output ratio (GOR) compared to the heat capacity ratio of the dehumidifier (HCRd) [25]. According to the figure, it can be seen that in HCRd = 1, the performance of the GOR has the highest value. In this system, the dehumidifier has the most irrecoverable properties. Additionally, the maximum performance of the system occurs when the dehumidifier conditions are in equilibrium. Theoretically, this state is represented by HCRd = 1.
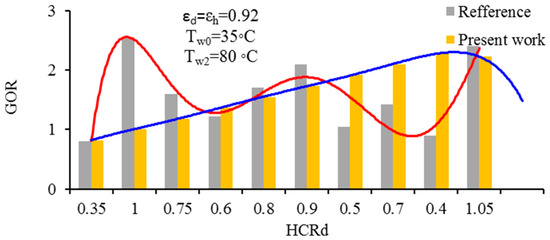
Figure 5.
Validation of the graph of GOR changes relative to HCRd with reference [25].
3.2. Parametric Study Results
The effect of some effective parameters in the system (evaporator temperature 1, ammonia concentration, absorber temperature, heater temperature difference, generator 1 pressure and heat source temperature) on the energy efficiency and exergy of the system was investigated.
3.3. The Effect of Evaporator 1 Temperature on the Energy Efficiency and Exergy of the System
As shown in Figure 6, changes in energy efficiency and exergy compared to the temperature of evaporator 1 were investigated. By increasing the temperature of the evaporator, the cooling capacity of the CCHP cycle increases and increases the pressure of the secondary fluid entering the ejector. As a result, the temperature of the fluid in the VCHPC cycle increases, the amount of power consumed in the compressor decreases, and the heat transferred to the HDH system increases. Additionally, by increasing the temperature of evaporator 1, the exergy of the product will increase more than the required exergy. Therefore, the exergy efficiency of the whole system increases.
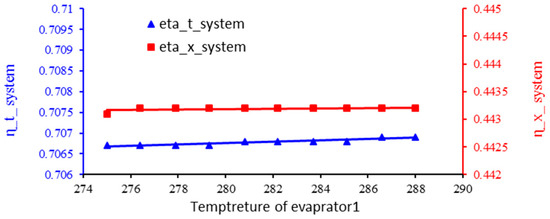
Figure 6.
Effect of evaporator temperature change on energy and exergy efficiency of the system.
3.4. The Effect of Ammonia Concentration on the Energy Efficiency and Exergy of the System
Figure 7 shows the changes in the energy efficiency and exergy of the whole system in relation to the changes in ammonia concentration. As the concentration of NH3 increases, the heat capacity of the Kalina cycle agent fluid (NH3-H2O) decreases; as a result, with the increase in NH3 concentration, the production power and cooling load produced in CCHP and the amount of heat transferred to the HDH system and the exergy of the product are reduced and irreversible. The number of systems increases. As a result, the energy efficiency and exergy of the system decrease. Changes in ammonia concentration will not affect the production cooling load in the absorption refrigeration cycle.
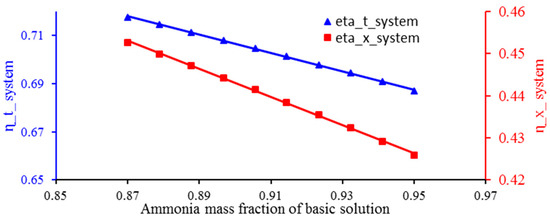
Figure 7.
Effect of ammonia concentration on energy and exergy efficiency of the system.
3.5. Effect of Absorber Temperature on Energy Efficiency and Exergy of the System
Figure 8 shows the changes in energy efficiency and exergy of the system in relation to the temperature changes in the absorber. As the temperature of the condenser increases, the work completed in the pump increases. As a result, the net productive work in the system decreases. Additionally, the heat transfers in the condenser decreases, and the energy efficiency decreases. As the temperature of the condenser increases, the increase in exergy required by the system will be greater than the exergy of the product of the system, and the irreparability of the system will increase. As a result, the exergy efficiency decreases.
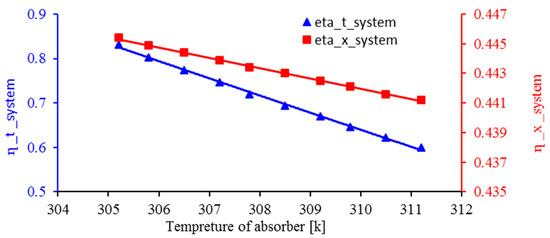
Figure 8.
Effect of absorber temperature change on energy and exergy efficiency of the system.
3.6. Effect of Heater Temperature Difference on Energy Efficiency and Exergy of the System
In Figure 9, the changes in the energy efficiency and exergy of the system are shown in relation to the temperature difference in the heater. Changing the temperature difference in the heater will not affect the cooling load and the production power of the system. By increasing the temperature difference in the heater, less heat is transferred to the HDH system, and as a result, the produced freshwater flow is reduced to a small amount. Additionally, the exergy of the product is reduced in HDH. So, with the increase in the heater temperature difference, the energy efficiency and exergy of the system will decrease.
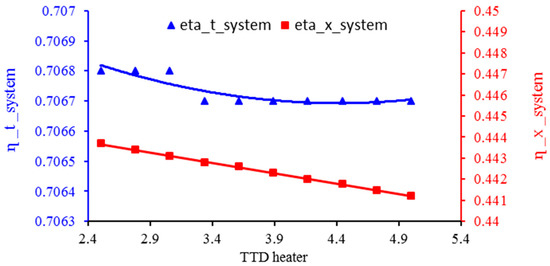
Figure 9.
Effect of heat exchanger temperature change on energy and exergy efficiency of the system.
3.7. The Effect of Generator Pressure on Energy Efficiency and Exergy of the System
Figure 10 shows the changes in the energy efficiency and exergy of the system compared to the pressure changes in the generator. By increasing the inlet pressure turbine, more work is produced in the turbine, and more heat is transferred to the ERC cycle. Therefore, the amount of cooling and power and freshwater production increases, and the energy efficiency of the system increases. By increasing the inlet pressure turbine, the exergy of the system product increases more than the exergy required by the system, and the exergy efficiency of the system increases.
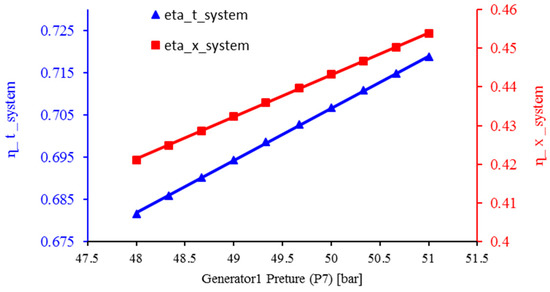
Figure 10.
Effect of generator pressure change on energy and exergy efficiency of the system.
3.8. The Effect of Heat Source Temperature on Energy Efficiency and Exergy of the System
In Figure 11, the changes in the energy efficiency and exergy of the system are shown in relation to the temperature of the heat source. As the temperature of the heat source increases, more heat is transferred to the system, and the fluid pressure entering the turbine increases. Additionally, the capacity of power generation and cooling in the system increases, and the amount of freshwater production remains almost constant. As a result, the energy efficiency of the system increases. Additionally, as the temperature of the heat source increases, the maximum amount of work obtainable from the system (product exergy) will increase more than the fuel exergy. As a result, the exergy efficiency of the system increases with the increase in the temperature of the heat source.
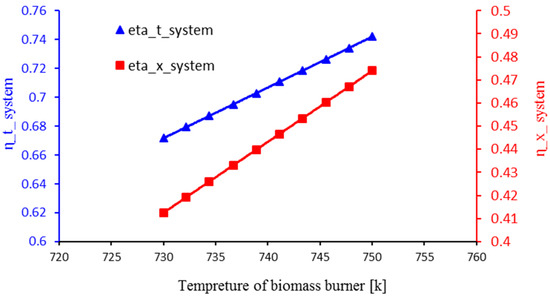
Figure 11.
Effect of heat source temperature on energy and exergy efficiency of the system.
3.9. Optimization Results
In the design of thermal systems, the optimization of thermodynamic conditions is used to determine the maximum efficiency of energy and exergy. In this article, the genetic algorithm method was used in EES software. The genetic algorithm method can be suitable compared to other methods available in the software. In the single-objective optimization method, the objective function is to determine the maximum energy efficiency or exergy of a system, but in multi-objective optimization, the objective function is to simultaneously determine the maximum energy efficiency and exergy of a system (Zare et al., 2012 [25]). The ranges of thermodynamic parameters for optimization are the same ranges examined in the parametric study of a system. For the system presented in this research, the maximum of the multi-objective function is expressed as follows:
In Figure 12 and Table 4, the optimization results of the single-objective and multi-objective algorithms are presented, and the values of energy efficiency and exergy in the initial state and different modes (MOOD {w1 = w2 = 0.5}, EEOD, TEOD) were examined.
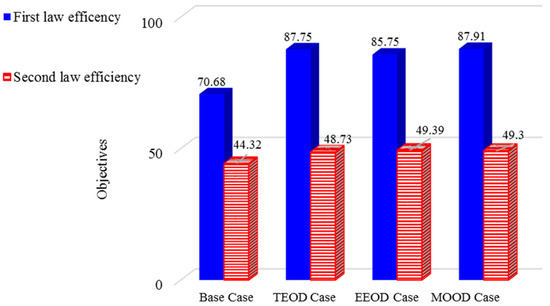
Figure 12.
Optimal performance of the system in different modes.
The results regarding system optimization in different modes are as follows:
- Comparing the optimization results between the basic study and TEOD shows that in the TEOD mode, energy efficiency and exergy efficiency improved by 24.15% and 9.9%. In this case, from the point of view of the first law, the results are very satisfactory.
- The comparison of the optimization results between the basic study and EEOD shows that in EEOD, the energy efficiency and exergy efficiency improved by 21.32% and 11.43%. Compared to the TEOD mode, this mode is very satisfactory from the point of view of the second law of results.
- The comparison of the optimization results between the basic study and MOOD shows that in MOOD, the energy efficiency and exergy efficiency improved by 24.37% and 11.23%. In this case, the net production power, the heat of the evaporators and the amount of freshwater produced increased compared to the initial state.
4. Conclusions
The purpose of this project was to improve CCHP efficiency and reduce waste. For this purpose, we added an absorption refrigeration cycle to the system, which starts with the output of generator 1. Additionally, we used biomass as a heat source and the heat produced in the CCHP cycle to produce fresh water via the desalination–humidifier–dehumidifier system. The effect of heat source temperature parameters, evaporator temperature, ammonia concentration, generator pressure, absorber temperature, and heater temperature difference on the system performance was investigated. To achieve the best performance of the system, the optimization of the system was achieved with the method of single-objective and multi-objective genetic algorithms. The important results obtained are summarized as follows:
- The maximum amount of energy efficiency and exergy of the whole system in the range of heat source temperature between 740 and 750 is equal to 74.2 and 47.7.
- The dehumidifier plays an important role in the freshwater production system. By increasing the dehumidifier performance coefficient (HCRd), the performance of the water softener system (GOR) increases.
- By increasing the temperature of the thermal pool, the temperature of the evaporator improves the overall system performance and increases the energy efficiency and exergy of the system.
- An increase in the concentration of ammonia in the Kalina cycle agent fluid solution and an increase in the temperature difference in the heater (decreasing the efficiency of the heater) will decrease the energy efficiency and exergy of the overall system.
- The flow rate of fresh water produced in the optimal conditions of the overall system was calculated as 0.5 g/s. For future work, the following topics could be addressed:
A thermo-mechanical energy level approach integrated with exergoeconomic optimization.
The energetic and exergetic analysis of a biomass-fueled CCHP system integrated with other heat resources.
Multi-criteria evaluation biomass-fueled CCHP system.
Author Contributions
T.H.H. and Y.A.S.: Conceptualization, Supervision, writing—Reviewing and Editing. A.K.K.: Writing, Visualization, Investigation, K.S.M.: Writing, Visualization, Investigation, I.K.: Writing, Visualization, Investigation, A.H.A. and E.M.M.: Methodology, Reviewing, original draft preparation. O.C. and R.M. and D.Ø.M.: Reviewing, editing, methodology. All authors have read and agreed to the published version of the manuscript.
Funding
This study is Supported via funding from Prince Sattam bin Abdulaziz University project number (PSAU/2023/1444).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
All data used to support the findings of this study are included within the article.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Al-Sulaiman, F.A.; Dincer, I.; Hamdullahpur, F. Energy and exergy analyses of a biomass trigeneration system using an organic Rankine cycle. Energy 2012, 45, 975–985. [Google Scholar] [CrossRef]
- Kearnry, D. EIA’s Outlook Through 2035; U.S. Energy Information Administration (EIA): Washington, DC, USA, 2010.
- Wu, D.W.; Wang, R.Z. Combined cooling, heating and power: A review. Prog. Energy Combust. Sci. 2006, 32, 459–495. [Google Scholar] [CrossRef]
- Alayi, R.; Rouhi, H. Techno-economic analysis of electrical energy generation from urban waste in Hamadan, Iran. Int. J. Des. Nat. Ecodynamics 2020, 15, 337–341. [Google Scholar] [CrossRef]
- Alayi, R.; Sobhani, E.; Najafi, A. Analysis of environmental impacts on the characteristics of gas released from biomass. Anthropog. Pollut. 2020, 4, 1–14. [Google Scholar]
- Alayi, R.; Sadeghzadeh, M.; Shahbazi, M.; Seyednouri, S.R.; Issakhov, A. Analysis of 3E (energy-economical-environmental) for biogas production from landfill: A case study. Int. J. Chem. Eng. 2022, 2022, 3033701. [Google Scholar] [CrossRef]
- Alayi, R.; Jahangeri, M.; Monfared, H. Optimal location of electrical generation from urban solid waste for biomass power plants. Anthropog. Pollut. 2020, 4, 44–51. [Google Scholar]
- Geng, D.; Gao, X. Thermodynamic and exergoeconomic optimization of a novel cooling, desalination and power multigeneration system based on ocean thermal energy. Renew. Energy 2023, 202, 17–39. [Google Scholar] [CrossRef]
- Wang, A.; Wang, S.; Ebrahimi-Moghadam, A.; Farzaneh-Gord, M.; Moghadam, A.J. Techno-economic and techno-environmental assessment and multi-objective optimization of a new CCHP system based on waste heat recovery from regenerative Brayton cycle. Energy 2021, 241, 122521. [Google Scholar] [CrossRef]
- Xing, L.; Li, J. Proposal of biomass/geothermal hybrid driven poly-generation plant centering cooling, heating, power, and hydrogen production with CO2 capturing: Design and 3E evaluation. Fuel 2022, 330, 125593. [Google Scholar] [CrossRef]
- Wang, J.; Chen, B.; Che, Y. Bi-level sizing optimization of a distributed solar hybrid CCHP system considering economic, energy, and environmental objectives. Int. J. Electr. Power Energy Syst. 2023, 145, 108864. [Google Scholar] [CrossRef]
- Delgado-Gonzaga, J.; Rivera, W.; Juárez-Romero, D. Integration of cycles by absorption for the production of desalinated water and cooling. Appl. Therm. Eng. 2023, 220, 119718. [Google Scholar] [CrossRef]
- Askari, I.B.; Shahsavar, A. The exergo-economic analysis of two novel combined ejector heat pump/humidification-dehumidification desalination systems. Sustain. Energy Technol. Assess. 2022, 53, 102561. [Google Scholar] [CrossRef]
- Bejan, A.; Tsatsaronis, G.; Moran, M.J. Thermal Design and Optimization; John Wiley & Sons: Hoboken, NJ, USA, 1995. [Google Scholar]
- Szargut, J. Exergy Method: Technical and Ecological Applications; WIT Press: Billerica, MA, USA, 2005; Volume 18. [Google Scholar]
- Basu, P. Combustion and Gasification in Fluidized Beds; CRC Press: Boca Raton, FL, USA, 2006. [Google Scholar]
- Keçeciler, A.; Acar, H.; Doğan, A. Thermodynamic analysis of the absorption refrigeration system with geothermal energy: An experimental study. Energy Convers. Manag. 2000, 41, 37–48. [Google Scholar] [CrossRef]
- Narayan, G.P.; Sharqawy, M.H.; Leinhard, V.J.H.; Zubair, S.M. Thermodynamic analysis of humidification dehumidification desalination cycles. Desalin. Water Treat. 2010, 16, 339–353. [Google Scholar] [CrossRef]
- Narayan, G.P.; Lienhard, V.J.H.; Zubair, S.M. Entropy generation minimization of combined heat and mass transfer devices. Int. J. Therm. Sci. 2010, 49, 2057–2066. [Google Scholar] [CrossRef]
- Ghaebi, H.; Parikhani, T.; Rostamzadeh, H.; Farhang, B. Proposal and assessment of a novel geothermal combined cooling and power cycle based on Kalina and ejector refrigeration cycles. Appl. Therm. Eng. 2018, 130, 767–781. [Google Scholar] [CrossRef]
- Rostamzadeh, H.; Rostamzadeh, J.; Matin, P.S.; Ghaebi, H. Novel dual-loop bi-evaporator vapor compression refrigeration cycles for freezing and air-conditioning applications. Appl. Therm. Eng. 2018, 138, 563–582. [Google Scholar] [CrossRef]
- Sun, F.; Zhou, W.; Ikegami, Y.; Nakagami, K.; Su, X. Energy–exergy analysis and optimization of the solar-boosted Kalina cycle system 11 (KCS-11). Renew. Energy 2014, 66, 268–279. [Google Scholar] [CrossRef]
- Sag, N.B.; Ersoy, H.; Hepbasli, A.; Halkaci, H. Energetic and exergetic comparison of basic and ejector expander refrigeration systems operating under the same external conditions and cooling capacities. Energy Convers. Manag. 2015, 90, 184–194. [Google Scholar] [CrossRef]
- Rostamzadeh, H.; Ebadollahi, M.; Ghaebi, H.; Shokri, A. Comparative study of two novel micro-CCHP systems based on organic Rankine cycle and Kalina cycle. Energy Convers. Manag. 2019, 183, 210–229. [Google Scholar] [CrossRef]
- Zare, V.; Mahmoudi, S.; Yari, M.; Amidpour, M. Thermoeconomic analysis and optimization of an ammonia–water power/cooling cogeneration cycle. Energy 2012, 47, 271–283. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).