Next Article in Journal
What Are the Binding Constraints for a Knowledge-Based Economy in Qatar?
Next Article in Special Issue
Family Dwelling House Localization in Poland as a Factor Influencing the Economic Effect of Rainwater Harvesting System with Underground Tank
Previous Article in Journal
The Sustainability of Emerging Social Vulnerabilities: The Hikikomori Phenomenon in Southern Italy
Previous Article in Special Issue
Modeling of Fuzzy Cognitive Maps with a Metaheuristics-Based Rainfall Prediction System
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Sustainability
Volume 15
Issue 5
10.3390/su15053870
sustainability-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles thumb_up
...
Endorse textsms
...
Comment
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

Pioneer Use of Pseudo Sub-Daily Timestep Model for Rainwater Harvesting Analysis: Acceptance over Hourly Model and Exploring Accuracy of Different Operating Algorithms

by
Monzur A. Imteaz
*,
Hassaan Ahmad
and
Iqbal Hossain
Department of Civil and Construction Engineering, Swinburne University of Technology, Hawthorn, VIC 3122, Australia
*
Author to whom correspondence should be addressed.
Sustainability 2023, 15(5), 3870; https://doi.org/10.3390/su15053870
Submission received: 31 January 2023 / Revised: 9 February 2023 / Accepted: 16 February 2023 / Published: 21 February 2023
(This article belongs to the Special Issue Sustainable Rainwater Management: Challenges and Perspectives)
Browse Figures
Versions Notes

Abstract

:
This study investigates the effectiveness of a pseudo sub-daily timestep model, which uses 6-hourly variable demands and daily rainfall values split into four equal 6-hourly portions. To assess the achievements through such sub-daily model, simulations were conducted using 6-hourly YBS (yield before storage), 6-hourly YAS (yield after storage), daily YBS and daily YAS models using rainfall data from a station near Melbourne (Australia) city under different input conditions. Results from the developed models were compared with the results of an earlier developed hourly timestep model, which considered hourly rainfall data and hourly variable rainwater demands. From the results, it is found that the results of YAS models are more accurate compared to the results of YBS models. Considering only potential water savings, daily YAS model results are very similar to the 6-hourly YAS model results.

1. Introduction

Rainwater harvesting systems have been in use for many centuries in different parts of the world where decent rainfall amounts are common and other suitable water sources are scarce [1,2,3,4,5,6]. With the development of urban areas having centralised the water supply system, at one stage, the primitive rainwater harvesting systems became less important, except in remote areas where other sources of water are either scarce, not easily accessible or expensive. However, in recent years, rainwater harvesting has again gained attention as the urban water authorities are struggling to cope with the ever-increasing water demands due to urban population increases. In addition, the effects of climate change and increases in rainfall variability, which affect surface water sources, exerted further pressure on the urban water supply. However, a complete dependence on harvested rainwater is not likely, mainly due to the quality issue. Moreover, in most cases, the quantity would not be enough to meet the total household demands. Water supply authorities are promoting the installation of household rainwater tanks to alleviate the total potable water demand, which comes with robust water treatments and costs. In the contemporary world, as the sustainability focus receives priority, domestic rainwater tanks are becoming an integral part of new city design. In a non-urban setup where space is usually abundant, optimisation of rainwater tank size is not crucial. However, in a typical urban setup, the space is limited, and expensive optimisation of rainwater tank size is important, which has resulted in many relevant studies.
As the salient features of rainwater harvesting analysis are the water savings potential and the optimum size of the tank, most of the authors focused on exploring either the optimum size or water savings potential through certain tank size(s) [1,2,3,4,5,6,7,8,9]. As in some periods of the year the installed rainwater tank may not be able to satisfy the intended demand, some researchers studied the reliability of the rainwater tank in augmenting water supply [10,11,12]. As rainwater tank installation and maintenance costs are significant in many regions, some researchers studied the economic feasibility of rainwater tanks in specific regions considering rainwater availability and the price of potential water savings in specific regions [1,10,13,14,15,16].
Rainwater tanks not only save the potable water, they also save energy; through the savings of potable water, the energy used to produce and deliver that potable water is saved indirectly. With the ever-increasing demands of energy, such indirect energy savings help the energy suppliers, and, consequently, there have been several studies on this subject [17,18,19,20]. Some studies even considered optimized energy consumption and scheduling for different home appliances [21,22]. However, most of the end-users do not try to comprehend such energy savings. Moreover, in many regions, the currently low cost of water coupled with high cost of rainwater tank installation makes it economically unfeasible. Imteaz et al. [23] presented a detailed study showing the relationship between the increase in water price and reductions in the payback period of rainwater tank installation costs. They have shown that the payback period reduces exponentially with the increase of water price. Nonetheless, it is to be noted that rainwater tanks render great intangible benefits towards global sustainability. To overcome users’ unwillingness to implement rainwater tanks, some authorities offer different incentives to end-users, which resulted in several studies on appropriate incentives [15,24,25]. To the above-mentioned negative factors, a further dilemma has recently been added, namely, the unknown consequences of impending climate change, which will likely result in significant changes in rainfall intensity and distribution. Several researchers focused on evaluating rainwater savings potential and reliability under future climate change scenarios [26,27,28,29].
All the above-mentioned studies require a reliable tool to be used for estimating rainwater tank outcomes. It is to be noted that among the prevailing analysis methods for rainwater harvesting, a continuous water balance model is most widely acceptable due to its accuracy and easy to use [30]. However, the timestep of such modelling simulations is a crucial factor; like other mathematical modelling tasks, longer timestep simulations do not produce accurate results. Nowadays, with the availability of proper scientific instrumentations, in order to achieve accurate results, most of the studies on rainwater harvesting use daily timestep models; although, in some cases, researchers were compelled to use monthly timestep models due to the unavailability of daily rainfall data [2,7]. Imteaz and Boulomytis [30] discussed the shortcomings of such monthly timestep analyses. Daily timestep models are also not free from potential inaccuracies due to two major factors: (i) a constant water demand is considered for the whole day; whereas water demands significantly vary throughout the day; and (ii) a bulk amount is deducted as demand from the stored water either at the end of the day or at the beginning of the day, both of which are likely to cause inaccuracies. The analysis which considers deduction of demand after adding the runoff is called ‘yield after storage’ (YAS) and the analysis which considers deduction of demand before adding the runoff is called ‘yield before storage’ (YBS). Several studies reported that the YAS algorithm underestimates water savings; whereas the YBS algorithm overestimates potential water savings [3,31], which can be only ascertained through using a sub-daily/hourly timestep model. Zhang et al. [3], comparing the results of daily and hourly timestep models, reported that in regard to water saving efficiency, a daily model using YAS provides underestimations up to 9.3%; whereas a daily model using YBS provides overestimations up to 4.9%. However, for most of the regions, hourly rainfall data is not available, which prevents use of the hourly timestep model. To overcome this issue, this study proposes to use a pseudo sub-daily timestep model and compares the pseudo sub-daily timestep model results with hourly timestep model results to explore the reliability of using such a sub-daily timestep model. Finally, the achieved accuracies are compared with the accuracies of daily timestep models using both the mentioned algorithms (YAS and YBS). Accuracies were assessed both in regard to potential water savings and reliability. The research question here is whether a pseudo sub-daily model is superior to a daily timestep model and, if yes, with which algorithm?

2. Methodology and Data

The operating algorithm of a daily water balance model has been used and described in several studies such as [9,32]. Earlier, the daily water balance algorithm used in Imteaz et al. [9] was modified to incorporate hourly rainfall data and hourly variable rainwater demands. The details of the development of hourly timestep model are described in Imteaz and Boulomytis [30]. In brief, the operational sequence of the calculations is as follows: the main input data is rainfall (i.e., daily, 6-hourly or hourly), and from the incoming rainfall amount, a certain percentage is deducted, which comprises all the associated losses (evaporation, spillage and/or leak). The runoff from the roof is calculated by multiplying roof area with the rainfall excess (after deduction). This incoming runoff volume is added with the accumulated runoffs in the tank (with specific volume) from earlier time periods. From the stored water in the tank, the user-specified demand is deducted in each timestep. In the YAS method, this deduction is performed after adding the runoff from the current timestep; whereas, in the YBS method, this deduction is performed before adding the runoff from the current timestep. If, at any timestep, the accumulated rainwater becomes more than the specified tank size (i.e., tank is full), the subsequent runoff amounts will no longer be added with the accumulated stored water, and will instead be considered lost (i.e., overflow) from the system. On the other hand, if the stored water in the tank becomes zero, no more deductions will occur from these zero amounts (i.e., stored water will not be calculated as negative), and in such case the specified rainwater demand is expected to be fulfilled from normal town water supply. The model eventually calculates the total of such water needed in a year for the selected scenario. In the hourly timestep model, in addition to providing hourly rainfall data, hourly variable demands are also provided. A typical hourly distribution of demands (as % of total daily demand) is shown in Figure 1 as per Beal [33].
For the stakeholders who do not have hourly rainfall data, this study proposes the use of a pseudo sub-daily model and data. For the sub-daily model, a 6-hour timestep is considered and the demands distribution presented by Beal [33] is converted to 6-hour blocks: midnight to 6 am, 6 am to 12 noon, 12 noon to 6 pm and 6 pm to midnight. Table 1 shows the six-hourly distributions of daily total demand as percentage. Daily rainfall can be spread in numerous different ways; with the current knowledge, it is not possible to split daily rainfall data to similar sub-daily blocks. As such, for the current study, the daily rainfall data was split into four equal blocks (i.e., 6-hourly). Such an assumption will at least alleviate the errors incurred due to daily deductions or additions of a bulk amount either at the beginning of the day (YBS algorithm) or at the end of the day (YAS algorithm). Sub-daily models were also developed using both the algorithms, i.e., 6-hourly YAS (demand deducted after the addition of rainfall) and 6-hourly YBS (demand deducted before the addition of rainfall).
Hourly rainfall data for several recent years from 2004 to 2020 were collected from the Australian Bureau of Meteorology (http://www.bom.gov.au/climate/data/) (accessed on 1 January 2023) for a location near northwest of Melbourne, Australia. Daily rainfall data is freely downloadable from the mentioned website; however, hourly data can be collected from the same organisation through special request. The selected rain gauge station is located at Essendon Airport, about 10 km northwest of Melbourne CBD. To explore the variations in results due to different weather conditions from the collected rainfall data, three years were identified as dry, average and wet years. In most of the studies [9,10,23,24,26,28,30] where weather variations are investigated, the three distinct conditions (dry, average and wet) were considered. In very rare cases (i.e., [34]) more than three weather conditions (dry, mild dry, average, mild wet and wet) were considered. Consideration of five weather variabilities is justified when there are many years of data (in the mentioned study there was 100 years of data). However, in the current study, as there was only 17 years of data, three weather conditions were considered. In Australia, the dry, average and wet years are defined as the years having close to 10 percentile, 50 percentile and 90 percentile annual rainfall amount, respectively. For the selected station, based on historical annual rainfall data, the 10 percentile, 50 percentile and 90 percentile rainfall amounts are 422.7 mm, 603.8 mm and 758.8 mm, respectively. The selected years and the corresponding annual rainfall amounts are presented in the Table 2. For use in the daily timestep model, hourly rainfall data for the selected years were converted to daily rainfall data by simply adding the amounts in each 24 h.
Overall characteristics of the rainfall station, as well as historical rainfall information, are provided in Table 3. Figure 2 shows the annual (Figure 2a), monthly (Figure 2b) and daily (Figure 2c) rainfall data series for the selected years.
All the developed models (hourly, daily YAS, daily YBS, 6-hourly YAS and 6-hourly YBS) were separately simulated with the corresponding rainfall data for the selected years, along with other rainwater tank related data such as roof area, tank volume, rainwater demand and percentage loss from the rainfall. To explore a best model, several comparisons are presented in two stages. In the first stage, daily YAS and daily YBS models’ results were compared with the corresponding hourly timestep model. For these comparisons, three different tank volumes (2000 L, 5000 L and 10,000 L) and two different rainwater demands (300 and 400 L/day) were considered. In the second stage, the 6-hourly models’ (YAS and YBS) results were compared with hourly timestep model results, obviously considering the hourly timestep model as the most accurate. A constant roof area of 200 m2 was considered for all the simulations. As per Imteaz et al. [9], a runoff loss of 10% was considered for all the simulations. Reliability is defined as the ratio of number of timesteps when harvested rainwater was able to fulfil the intended demand to the total number of timesteps (i.e., 365 or 366 for a daily timestep model) in a year.

3. Results

Simulated results from the hourly timestep model and daily timestep models (YAS and YBS) are compared in regard to annual water savings and reliability of fulfilling demand. It is to be mentioned that annual water savings and reliability are the salient features of rainwater tank outcomes. Comparisons are shown for different simulations comprising different combinations of tank sizes and total rainwater demands under three weather conditions (dry, average and wet).

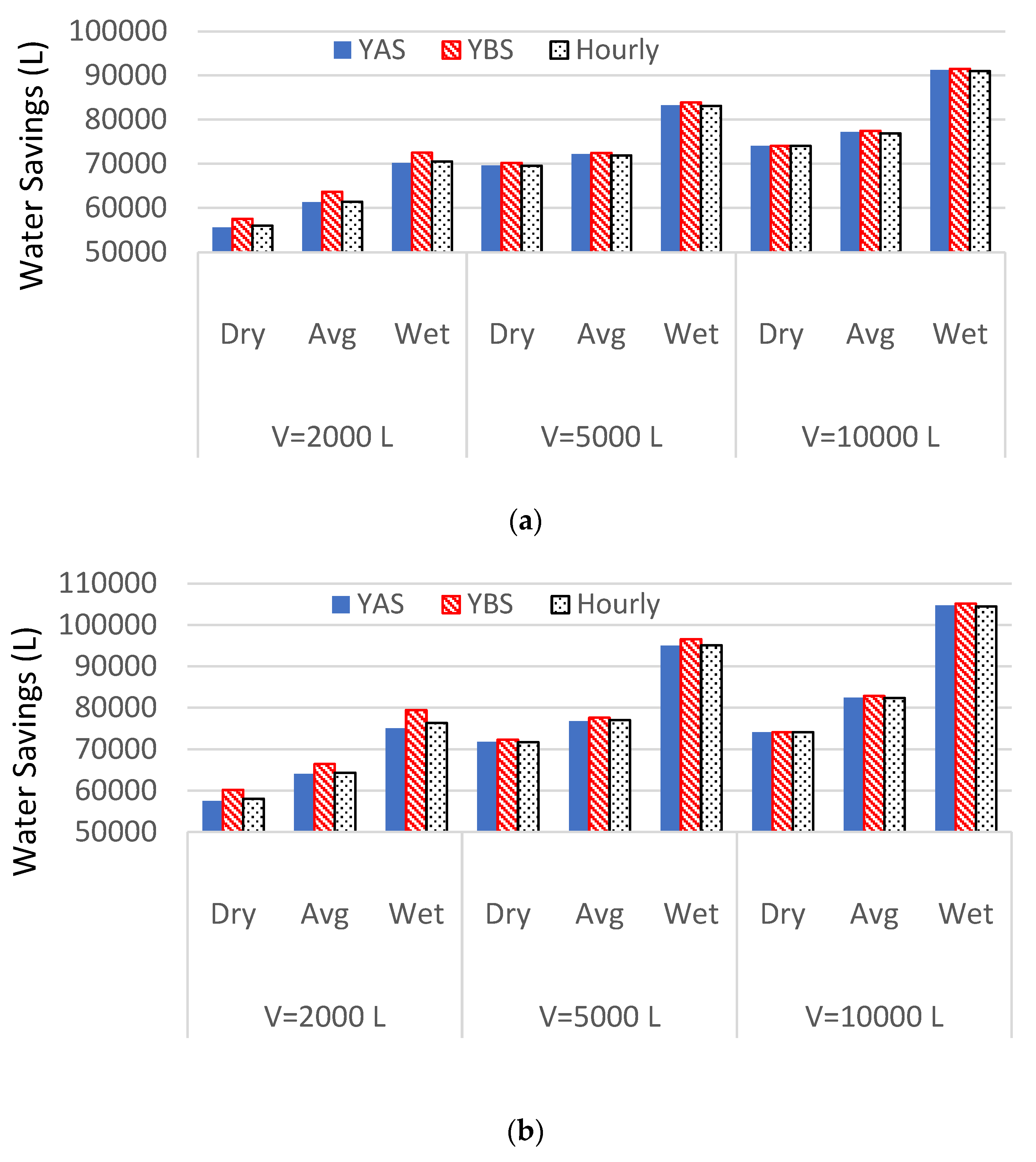
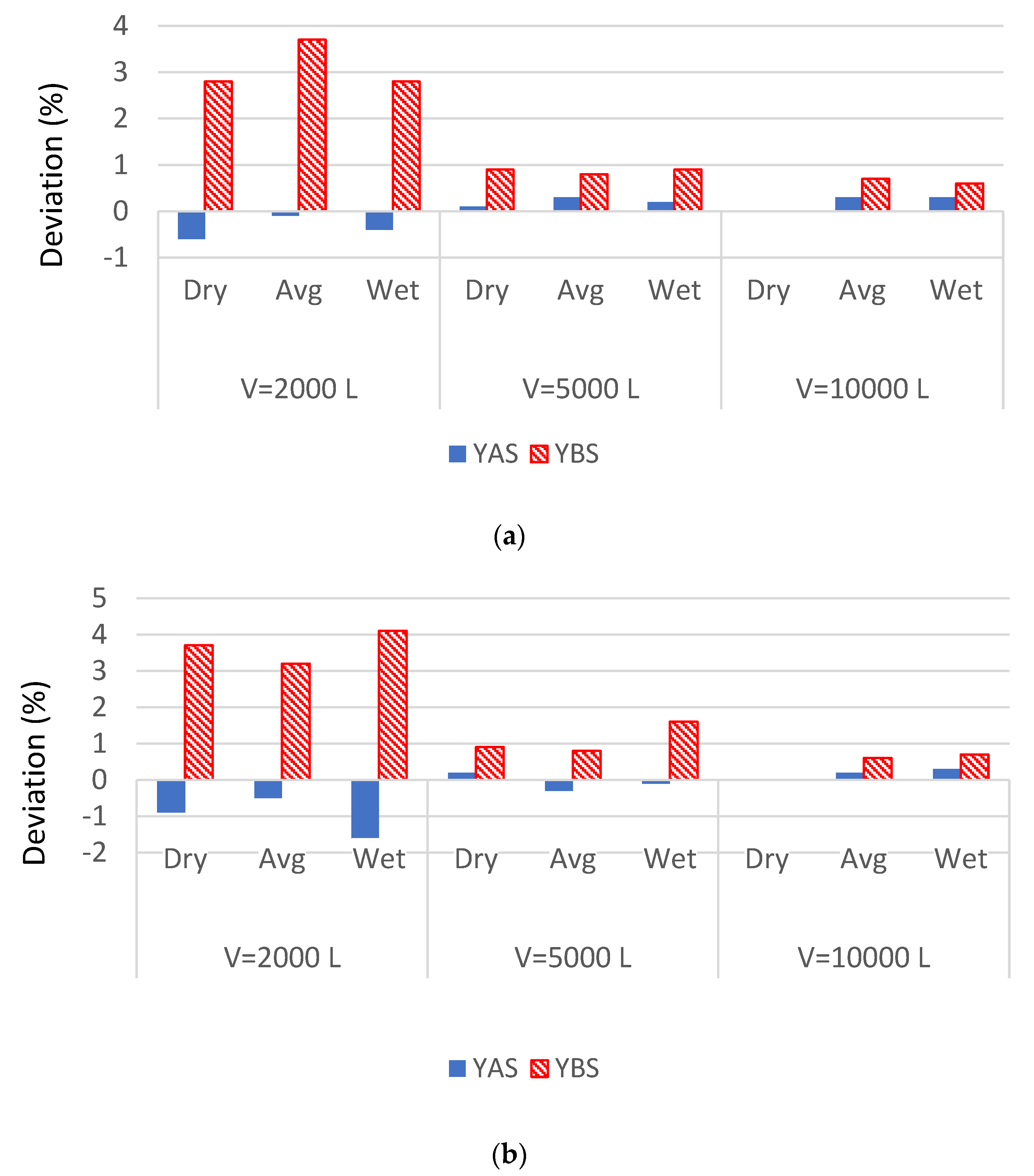
3.1. Comparison with Daily (YAS and YBS) Models

To explore the accuracy of YAS/YBS models, as mentioned earlier, the daily timestep models were simulated with the mentioned set of input parameters (roof area, tank size, rainwater demand) under three different weather conditions. With similar input data, an hourly timestep model was also simulated, except that, for the hourly timestep model, daily demand was split into hourly demands (as per Figure 1) spread over 24 h and, instead of daily rainfall data, hourly rainfall data for the same station and same year were used. Figure 3 shows the simulated results of annual water savings with the three models (YAS-daily, YBS-daily and hourly) for rainwater demands of 300 L/day (Figure 3a) and 400 L/day (Figure 3b). As the potential annual water savings amounts are quite large, the differences among the three look apparently insignificant.
For better visualisation of the differences, Figure 4a,b shows the percent deviation of each model (YAS/YBS) results compared to the hourly timestep model results. Considering the hourly timestep model results as standard, the daily timestep models’ results are compared with the hourly timestep model results. From the figures it is clear that daily YBS model always overestimates the annual water savings.
Overestimations through YBS model were also reported by Lade et al. [31]) and Zhang et al. [3]. However, underestimations through the YAS model, as were reported by Lade et al. [31] and Zhang et al. [3], are not always the case as per the current study; it depends on the other factors, especially tank size and weather condition. As per the current study, YAS’s overestimations are mainly for bigger tank sizes. However, for those overestimations, discrepancies are insignificant (less than 1%). In general, for a smaller tank size, which is more prone to overflow, the differences are significant. From the figures, it is found that with the YBS model, the daily timestep model produced discrepancies are <1% for a 10-kL tank, <2% for a 5-kL tank and <5% for a 2-kL tank; whereas, with the YAS model, the same discrepancies are <0.5% for both the 10-kL and 5-kL tanks and <2% for a 2-kL tank. As such, it can be concluded that for such water balance modelling, the YAS modelling algorithm is more accurate than the YBS modelling algorithm. The following section presents more analysis on the differences between a 6-hourly timescale model, a daily YAS model and an hourly timestep model. It is to be noted that for an hourly timestep model, it is understood that the effect withdrawal after/before storage will be insignificant. In this study, for the hourly timestep model, the YAS concept was used.

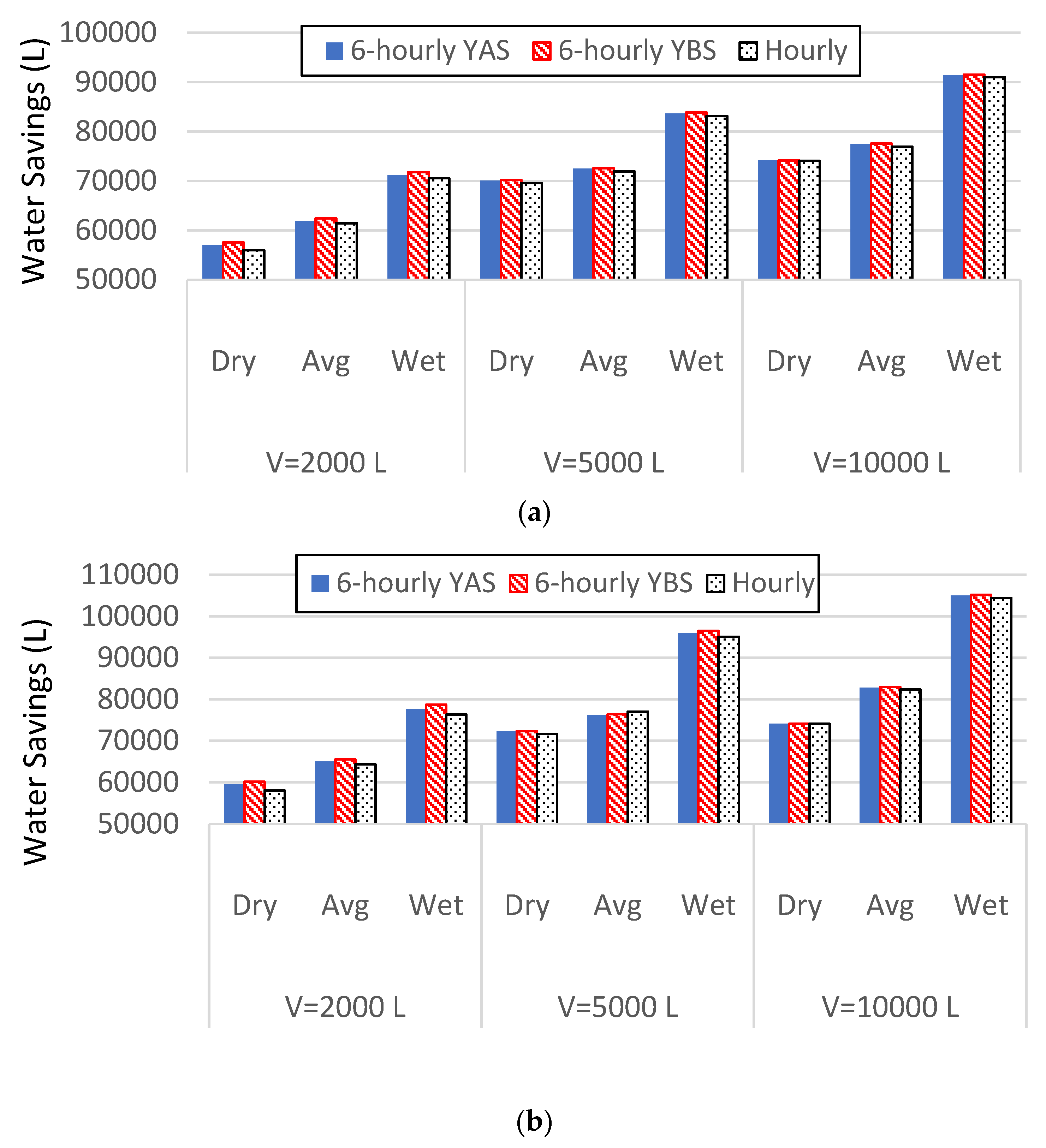
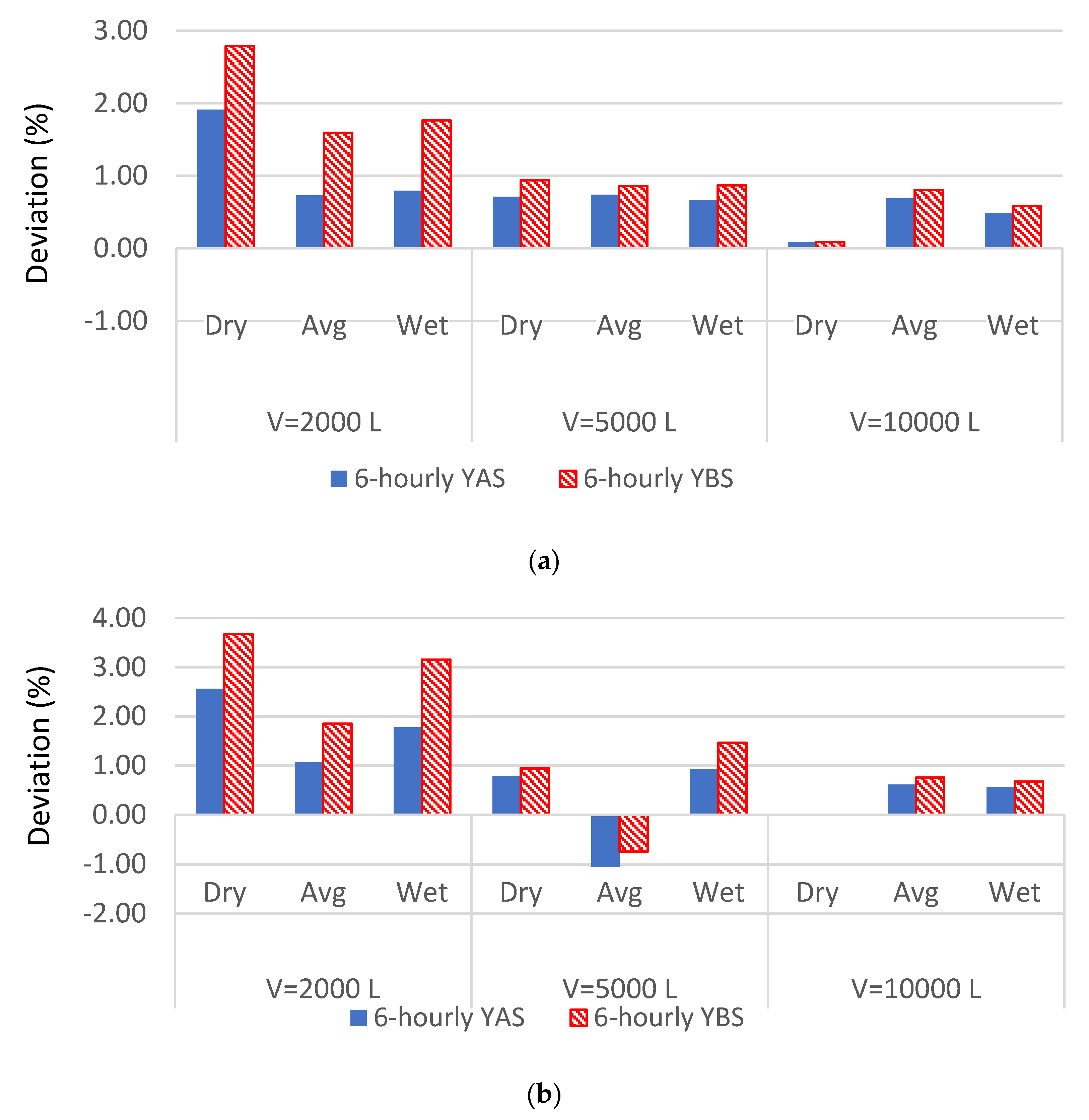
3.2. Comparisons with 6-Hourly (YAS and YBS) Timestep Models

Six-hourly timestep models were simulated with the same set of input parameters (roof area, tank size, rainwater demand) and rainfall data under three different weather conditions. Results from the models’ simulations were compared with the hourly timestep model results, which is the same as mentioned in the preceding section. Figure 5 shows the simulated results of annual water savings with the three models (6-hourly YAS, 6-hourly YBS and hourly) for rainwater demands of 300 L/day (Figure 5a) and 400 L/day (Figure 5b). Similar to that which mentioned in the preceding section, as the potential annual water savings amounts are quite large, the differences among the three look apparently insignificant.
For better visualisation of the differences, Figure 6a,b shows the percent deviation of each model (YAS/YBS) results compared to the hourly timestep model results. Considering the hourly timestep model results as standard, the 6-hourly timestep models’ results are compared with the hourly timestep model results. From the figures, it is clear that both the 6-hourly YBS and 6-hourly YAS models always overestimate the annual water savings, except in one scenario (in an average year with higher demand and a tank of 5000 L) where both the models underestimate annual water savings. However, for both models, the overestimations are insignificant, especially for larger tank sizes.
From the figures, it is found that for both models, under a low demand scenario (300 L/day), the 6-hourly model produced discrepancies are always <1% for tank sizes of 5 kL and 10 kL. For a smaller tank (2 kL), the 6-hourly YAS model-produced discrepancies are <1% in average and wet years, and <2% in dry year; whereas the 6-hourly YBS model produced discrepancies are <2% in average and wet years, and <3% in dry year. For a higher demand (400 L/day) scenario with a 2-kL tank, the 6-hourly YAS model produced discrepancies are ~1%, <2% and <3% in average, wet and dry years, respectively. On the contrary, for the same scenario, the 6-hourly YBS model produced discrepancies are <2%, ~3% and <4% in average, wet and dry years, respectively. As such, it can be concluded that for such water balance modelling, the YAS modelling algorithm is more accurate than the YBS modelling algorithm. It is to be noted that Zhang et al. [3] also reported that YAS modelling results provide more accurate results compared to YBS modelling. Another observation which is clear from the presented figures is that the YAS model always underestimates the annual water savings, which is justified via the fact that rainwater supply starts after overflow (i.e., when tank is full), which provides a relatively larger volume of overflow and a smaller volume of savings compared with the YBS concept.

3.3. Comparisons for Reliability Values

Models were simulated to calculate the reliabilities under the same scenarios mentioned above with varying tank sizes, demands and weather conditions. Table 4 shows the calculated reliabilities for all the scenarios using daily YAS, 6-hourly YAS, 6-hourly YBS and hourly models. The daily YBS model was discarded in this stage as, regarding potential water savings, the daily YBS model was found to be less accurate than the daily YAS model, which is elaborated in the preceding sections. From the calculated values, it is clear that reliability values are very close through the 6-hourly YAS and 6-hourly YBS models. However, the reliability values are slightly lower than the corresponding reliability values calculated through the hourly model. The maximum underestimation from all the studied scenarios is 3.6%. However, reliability values calculated through the daily YAS model are much lower compared to the hourly model. The maximum underestimation from all the studied scenarios is 10% and, in most cases, underestimations are more than 5%. As such, it can be concluded that regarding reliability, the daily YAS model is not quite accurate.

4. Conclusions

It is obvious that calculations with shorter timestep models will produce more accurate results. However, due to the lack of shorter timestep rainfall data, most of the studies on rainwater harvesting systems used either daily or monthly timestep. Recently, with the availability of hourly rainfall data in a few locations, some researchers used the hourly timestep model. However, for the vast majority of the areas/countries, the hourly data is not available. On the other hand, using the daily timestep model is not likely to render accurate results due to the fact that in the daily model, a single amount is considered as the daily rainwater demand, which is deducted either at the end or beginning of the day; whereas water demand significantly varies during a day and consideration of such diurnal variation is not possible without adopting a sub-daily timestep model. As such, in order to enhance the accuracy of the models’ estimations using daily rainfall data, this study proposed a pseudo sub-daily model, which uses the daily rainfall data but uses sub-daily variable demands. Following a water balance modelling technique, the pseudo sub-daily model was developed for a timestep of 6-h. From a local study, an hourly variation of demand was converted to a 6-hourly variation, which was used in the developed model along with daily rainfall data split into four equal amounts. As two prevailing concepts exist with respect to the operating algorithm, both the YAS and YBS concepts were used for the development of the 6-hourly model. For the verification of the 6-hourly models, the results were compared with earlier developed hourly model results. Moreover, to discuss the improvements detected in the sub-daily model, the results were compared with daily timestep models’ (YAS and YBS) results. Hourly rainfall data for several recent years from a rainfall station near Melbourne city was collected from the Australian Bureau of Meteorology. To assess the potential differences of results due to varying weather conditions, three years were selected as dry, average and wet years. Hourly rainfall values were summed up to facilitate conversion to 6-hourly and daily rainfall values. The models were simulated with corresponding rainfall data for varying rainwater demands and tank sizes for the three selected years. For each comparison, the results from the hourly timestep model were considered the most accurate. From the comparisons, it is clear that in regard to annual water savings, deviations of daily YBS model results are much higher than the deviations of daily YAS model results if compared to hourly timestep model results. Moreover, a similar tendency is observed for 6-hourly timestep models, i.e., YAS model results are closer to hourly timestep model results. It is to be noted that in regard to annual water savings, results obtained through a 6-hourly YAS model are similar to the results through a daily YAS model. However, in regard to calculations of reliability, results of the daily YAS model are far inferior compared to the results of the 6-hourly YAS model. As such, it can be concluded that if an hourly timestep model is not possible due to non-availability of hourly rainfall data, the developed pseudo 6-hourly timestep model should be used instead of a daily timestep model to achieve higher accuracies in rainwater harvesting analysis. To use this 6-hourly model, the daily demand value can easily be converted to the 6-hourly demand value using water usage patterns from local water supply authorities.

Author Contributions

Conceptualization, M.A.I.; methodology, M.A.I.; formal analysis, H.A.; investigation, H.A.; resources, M.A.I.; data curation, I.H.; writing—original draft preparation, H.A. and I.H.; writing—review and editing, M.A.I.; supervision, M.A.I.; project administration, M.A.I. All authors have read and agreed to the published version of the manuscript.

Funding

This research received no external funding.

Institutional Review Board Statement

Not applicable.

Informed Consent Statement

Not applicable.

Data Availability Statement

The data presented in this study are available through contacting the first author.

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. Khan, Z.; Alim, M.A.; Rahman, M.M.; Rahman, A. A continental scale evaluation of rainwater harvesting in Australia, Resources. Conserv. Recycl. 2021, 167, 105378. [Google Scholar] [CrossRef]
  2. Shadeed, S.; Alawna, S. Optimal Sizing of Rooftop Rainwater Harvesting Tanks for Sustainable Domestic Water Use in the West Bank, Palestine. Water 2021, 13, 573. [Google Scholar] [CrossRef]
  3. Zhang, S.; Jing, X.; Yue, T.; Wang, J. Performance assessment of rainwater harvesting systems: Influence of operating algorithm, length and temporal scale of rainfall time series. J. Clean. Prod. 2020, 253, 120044. [Google Scholar] [CrossRef]
  4. Bailey, R.T.; Beikmann, A.; Kottermair, M.; Taboroši, D.; Jenson, J.W. Sustainability of rainwater catchment systems for small island communities. J. Hydrol. 2018, 557, 137–146. [Google Scholar] [CrossRef]
  5. Lopes, V.A.; Marques, G.F.; Dornelles, F.; Medellin-Azuara, J. Performance of rainwater harvesting systems under scenarios of non-potable water demand and roof area typologies using a stochastic approach. J. Clean. Prod. 2017, 148, 304–313. [Google Scholar] [CrossRef]
  6. Guizani, M. Storm Water harvesting in Saudi Arabia: A multipurpose water management alternative. Water Resour. Manag. 2016, 30, 1819–1833. [Google Scholar] [CrossRef]
  7. Lizárraga-Mendiola, L.; Vázquez-Rodríguez, G.; Blanco-Piñón, A.; Rangel-Martínez, Y.; González-Sandoval, M. Estimating the Rainwater Potential per Household in an Urban Area: Case Study in Central Mexico. Water 2015, 7, 4622–4637. [Google Scholar] [CrossRef] [Green Version]
  8. Bocanegra-Martínez, A.; Ponce-Ortega, J.M.; Nápoles-Rivera, F.; Serna-González, M.; Castro-Montoya, A.J.; El-Halwagi, M.M. Optimal design of rainwater collecting systems for domestic use into a residential development. Resources. Conserv. Recycl. 2014, 84, 44–56. [Google Scholar] [CrossRef]
  9. Imteaz, M.A.; Adeboye, O.; Rayburg, S.; Shanableh, A. Rainwater harvesting potential for southwest Nigeria using daily water balance model. Resources. Conserv. Recycl. 2012, 62, 51–55. [Google Scholar] [CrossRef]
  10. Bashar, M.Z.I.; Karim, M.R.; Imteaz, M.A. Reliability and Economic Analysis of Urban Rainwater Harvesting: A Comparative Study within Six Major Cities of Bangladesh. Resour. Conserv. Recycl. 2018, 133, 146–154. [Google Scholar] [CrossRef]
  11. Mehrabadi, M.H.R.; Saghafian, B.; Fashi, F.H. Assessment of residential rainwater harvesting efficiency for meeting non-potable water demands in three climate conditions. Resour. Conserv. Recycl. 2013, 73, 86–93. [Google Scholar] [CrossRef]
  12. Basinger, M.; Montalto, F.A.; Lall, U. A rainwater harvesting system reliability model based on nonparametric stochastic rainfall generator. J. Hydrol. 2010, 392, 105–118. [Google Scholar] [CrossRef]
  13. Ali, S.; Zhang, S.; Yue, T. Environmental and economic assessment of rainwater harvesting systems under five climatic conditions of Pakistan. J. Clean. Prod. 2020, 259, 120–829. [Google Scholar] [CrossRef]
  14. Alim, M.A.; Rahman, A.; Tao, Z.; Samali, B.; Khan, M.M.; Shirin, S. Feasibility analysis of a small-scale rainwater harvesting system for drinking water production at Werrington, New South Wales, Australia. J. Clean. Prod. 2020, 270, 122437. [Google Scholar] [CrossRef]
  15. Imteaz, M.A.; Moniruzzaman, M. Spatial variability of reasonable government rebates for rainwater tank installations: A case study for Sydney, Resources. Conserv. Recycl. 2018, 133, 112–119. [Google Scholar] [CrossRef]
  16. Jing, X.; Zhang, S.; Zhang, J.; Wang, Y.; Wang, Y. Assessing efficiency and economic viability of rainwater harvesting systems for meeting non-potable water demands in four climatic zones of China. Resour. Conserv. Recycl. 2017, 126, 74–85. [Google Scholar] [CrossRef]
  17. Basheer, M.; Elagib, N.A. Temporal analysis of water-energy nexus indicators for hydropower generation and water pumping in the Lower Blue Nile Basin. J. Hydrol. 2019, 578, 124085. [Google Scholar] [CrossRef]
  18. Wurthmann, K. Assessing storage requirements, water and energy savings, and costs associated with a residential rainwater harvesting system deployed across two counties in Southeast Florida. J. Environ. Manag. 2019, 252, 109673. [Google Scholar] [CrossRef] [PubMed]
  19. Chiu, Y.R.; Tsai, Y.L.; Chiang, Y.C. Designing rainwater harvesting systems cost-effectively in a urban water-energy saving scheme by using a GIS-simulation based design system. Water 2015, 7, 6285–6300. [Google Scholar] [CrossRef] [Green Version]
  20. Vieira, A.S.; Beal, C.D.; Ghisi, E.; Stewart, R.A. Energy intensity of rainwater harvesting systems: A review. Renew. Sustain. Energy Rev. 2014, 34, 225–242. [Google Scholar] [CrossRef] [Green Version]
  21. Waseem, M.; Lin, Z.; Liu, S.; Zhang, Z.; Aziz, T.; Khan, D. Fuzzy compromised solution-based novel home appliances scheduling and demand response with optimal dispatch of distributed energy resources. Appl. Energy 2021, 290, 116761. [Google Scholar] [CrossRef]
  22. Waseem, M.; Lin, Z.; Liu, S.; Sajjad, I.A.; Aziz, T. Optimal GWCSO-based home appliances scheduling for demand response considering end-users comfort. Electr. Power Syst. Res. 2020, 187, 106477. [Google Scholar] [CrossRef]
  23. Imteaz, M.A.; Shanableh, A.; Rahman, A.; Ahsan, A. Optimisation of Rainwater Tank Design from Large Roofs: A Case Study in Melbourne, Australia. Resources. Conserv. Recycl. 2011, 55, 1022–1029. [Google Scholar] [CrossRef]
  24. Paudel, U.; Imteaz, M.A. Spatial Variability of Reasonable Government Rebates for Rainwater Tank Installations: A Case Study for Adelaide. In Sustainability Perspectives: Science, Policy and Practice; Khaiter, P.A., Erechtchoukova, M.G., Eds.; Springer: Berlin/Heidelberg, Germany, 2019; Chapter 13; ISBN 978-3-030-19549-6. [Google Scholar] [CrossRef]
  25. Gómez, Y.D.; Teixeira, L.G. Residential rainwater harvesting: Effects of incentive policies and water consumption over economic feasibility. Resour. Conserv. Recycl. 2017, 127, 56–67. [Google Scholar] [CrossRef]
  26. Imteaz, M.A.; Paudel, U.; Santos, C. Impacts of climate change on weather and spatial variabilities of potential water savings from rainwater tanks. J. Clean. Prod. 2021, 311, 127491. [Google Scholar] [CrossRef]
  27. Santos, C.; Imteaz, M.A.; Ghisi, E.; Matos, C. The effect of climate change on domestic rainwater harvesting. Sci. Total Environ. 2020, 729, 138967. [Google Scholar] [CrossRef]
  28. Imteaz, M.A.; Moniruzzaman, M. Potential impacts of climate change on future rainwater tank outcomes: A case study for Sydney. J. Clean. Prod. 2020, 273, 123095. [Google Scholar] [CrossRef]
  29. Haque, M.M.; Rahman, A.; Samali, B. Evaluation of climate change impacts on rainwater harvesting. J. Clean. Prod. 2016, 137, 60–69. [Google Scholar] [CrossRef]
  30. Imteaz, M.A.; Boulomytis, V.T.G. Improvement of rainwater harvesting analysis through an hourly timestep model in comparison with a daily timestep model. Water Resour. Manag. 2022, 36, 2611–2622. [Google Scholar] [CrossRef]
  31. Lade, O.; Oloke, D.; Chinyio, E.; Fullen, M. Use of multi-criteria decision analysis methods for water supply problems: A framework for improved rainwater harvesting. J. Environ. Sci. Eng. A 2012, 1, 909–917. [Google Scholar]
  32. Eroksuz, E.; Rahman, A. Rainwater tanks in multi-unit buildings: A case study for three Australian cities. Resour. Conserv. Recycl. 2010, 54, 1449–1452. [Google Scholar] [CrossRef]
  33. Beal, C.; South East Queensland Residential End Use Study: Final Report. Urban Water Security Research Alliance 2011, Technical Report No. 47. Available online: http://www.urbanwateralliance.org.au/publications/UWSRA-tr47.pdf (accessed on 15 July 2022).
  34. Imteaz, M.A.; Khan, M.S. Pioneer attempt of incorporating four variables in generalised equations for predicting water savings through rainwater tanks. Urban Water J. 2022, 19, 714–731. [Google Scholar] [CrossRef]
Sustainability 15 03870 g001 550
Figure 1. Diurnal distribution of typical household water demand.
Figure 1. Diurnal distribution of typical household water demand.
Sustainability 15 03870 g001
Sustainability 15 03870 g002a 550Sustainability 15 03870 g002b 550
Figure 2. (a) Annual rainfall timeseries for the study period. (b) Monthly rainfall timeseries for the study period. (c) Daily rainfall timeseries for the study period.
Figure 2. (a) Annual rainfall timeseries for the study period. (b) Monthly rainfall timeseries for the study period. (c) Daily rainfall timeseries for the study period.
Sustainability 15 03870 g002aSustainability 15 03870 g002b
Sustainability 15 03870 g003 550
Figure 3. Potential annual water savings with daily YAS, daily YBS and hourly models for: (a) demand = 300 L/day and (b) demand = 400 L/day.
Figure 3. Potential annual water savings with daily YAS, daily YBS and hourly models for: (a) demand = 300 L/day and (b) demand = 400 L/day.
Sustainability 15 03870 g003
Sustainability 15 03870 g004 550
Figure 4. Expected deviations in annual water savings calculations with daily YAS and daily YBS models compared to hourly model results for: (a) demand = 300 L/day and (b) demand = 400 L/day.
Figure 4. Expected deviations in annual water savings calculations with daily YAS and daily YBS models compared to hourly model results for: (a) demand = 300 L/day and (b) demand = 400 L/day.
Sustainability 15 03870 g004
Sustainability 15 03870 g005 550
Figure 5. Potential annual water savings with 6-hourly YAS, 6-hourly YBS and hourly models for: (a) demand = 300 L/day and (b) demand = 400 L/day.
Figure 5. Potential annual water savings with 6-hourly YAS, 6-hourly YBS and hourly models for: (a) demand = 300 L/day and (b) demand = 400 L/day.
Sustainability 15 03870 g005
Sustainability 15 03870 g006 550
Figure 6. Expected deviations in annual water savings calculations with 6-hourly YAS and 6-hourly YBS models compared to hourly model results for: (a) demand = 300 L/day and (b) demand = 400 L/day.
Figure 6. Expected deviations in annual water savings calculations with 6-hourly YAS and 6-hourly YBS models compared to hourly model results for: (a) demand = 300 L/day and (b) demand = 400 L/day.
Sustainability 15 03870 g006
Table
Table 1. Distribution of daily total demand in 6-hourly blocks.
Table 1. Distribution of daily total demand in 6-hourly blocks.
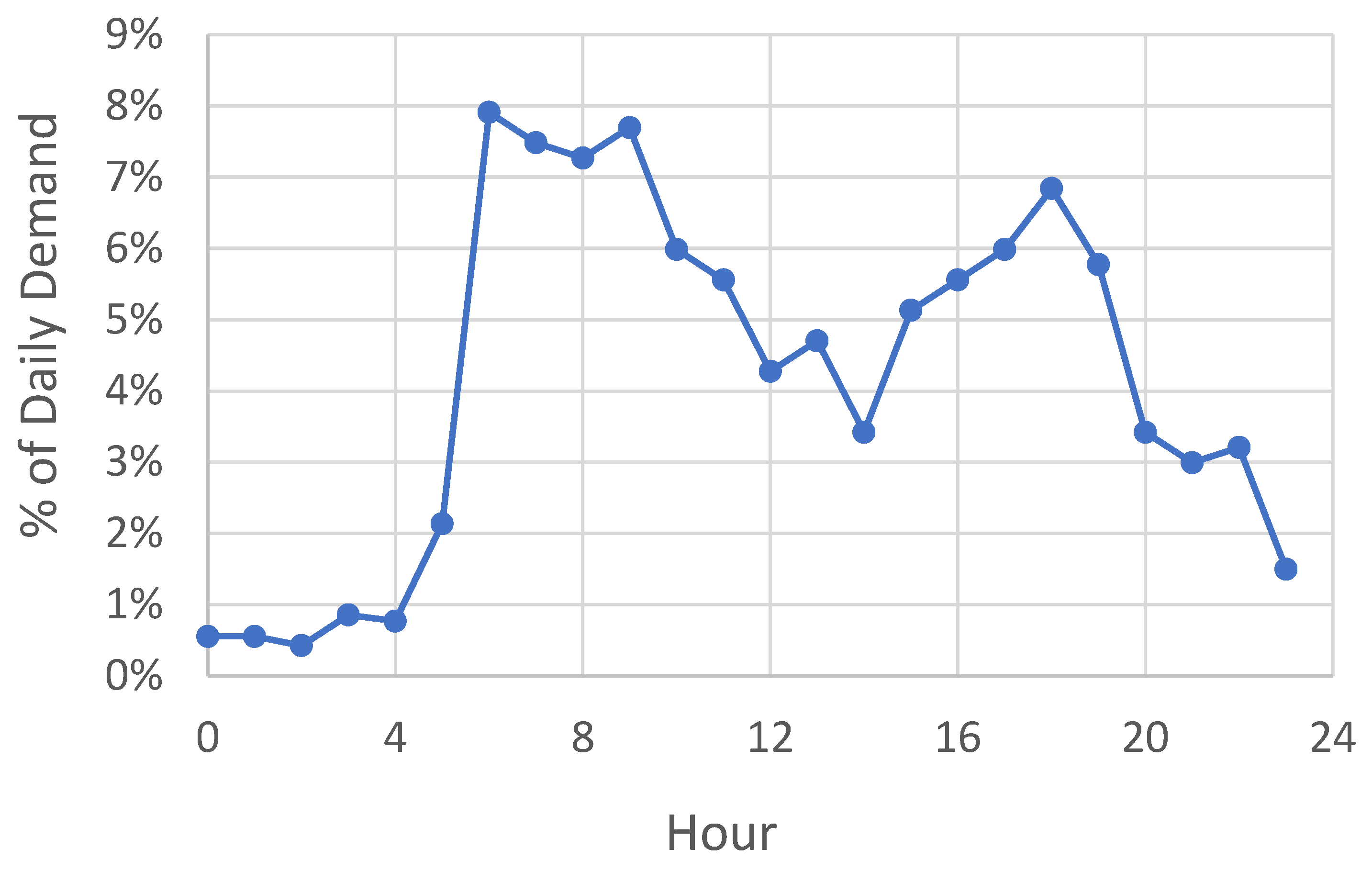
Period% of Total Demand
Midnight—6 a.m.5
6 a.m.—12 noon42
12 noon—6 p.m.29
6 p.m.—midnight24
Midnight—6 a.m.5
Table
Table 2. Selected years and corresponding annual rainfall amounts.
Table 2. Selected years and corresponding annual rainfall amounts.
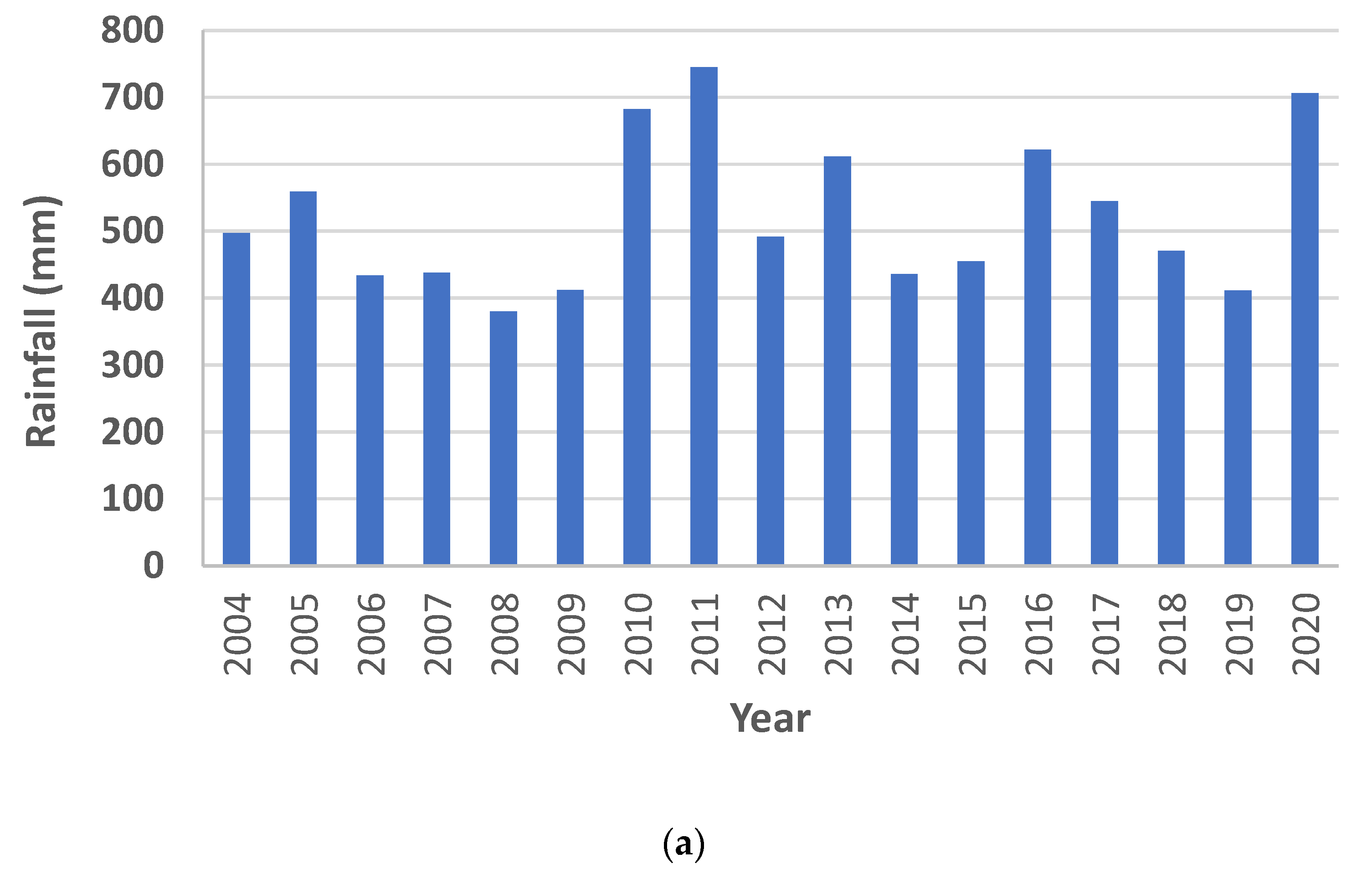
WeatherYearAnnual Rainfall (mm)
Dry2019406.0
Average2017551.6
Wet2011731.0
Table
Table 3. Station and historical rainfall information.
Table 3. Station and historical rainfall information.
ParameterValue
Station latitude and longitude37.73° S and 144.91° N
Station elevation78 m
Historical mean annual rainfall587 mm
Highest annual rainfall817.9 mm
Lowest annual rainfall350.4 mm
Table
Table 4. Calculated reliability values under different scenarios with different models.
Table 4. Calculated reliability values under different scenarios with different models.
Tank Size
(kL)		Weather ConditionDaily YAS Model6-Hourly YAS Model6-Hourly YBS ModelHourly Model
Daily Demand (L/day)Daily Demand (L/day)Daily Demand (L/day)Daily Demand (L/day)
300400300400300400300400
2Dry45.231.550.137.850.538.650.839.4
2Avg48.535.354.241.054.541.456.043.8
2Wet57.342.263.249.663.850.364.352.2
5Dry60.343.062.947.363.047.363.348.8
5Avg60.044.964.348.864.549.065.652.6
5Wet71.857.875.262.775.463.175.765.0
10Dry65.244.766.748.666.748.667.350.5
10Avg65.249.669.353.669.453.770.156.1
10Wet80.366.982.769.882.769.983.071.4
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

Share and Cite

MDPI and ACS Style

Imteaz, M.A.; Ahmad, H.; Hossain, I. Pioneer Use of Pseudo Sub-Daily Timestep Model for Rainwater Harvesting Analysis: Acceptance over Hourly Model and Exploring Accuracy of Different Operating Algorithms. Sustainability 2023, 15, 3870. https://doi.org/10.3390/su15053870

AMA Style

Imteaz MA, Ahmad H, Hossain I. Pioneer Use of Pseudo Sub-Daily Timestep Model for Rainwater Harvesting Analysis: Acceptance over Hourly Model and Exploring Accuracy of Different Operating Algorithms. Sustainability. 2023; 15(5):3870. https://doi.org/10.3390/su15053870

Chicago/Turabian Style

Imteaz, Monzur A., Hassaan Ahmad, and Iqbal Hossain. 2023. "Pioneer Use of Pseudo Sub-Daily Timestep Model for Rainwater Harvesting Analysis: Acceptance over Hourly Model and Exploring Accuracy of Different Operating Algorithms" Sustainability 15, no. 5: 3870. https://doi.org/10.3390/su15053870

APA Style

Imteaz, M. A., Ahmad, H., & Hossain, I. (2023). Pioneer Use of Pseudo Sub-Daily Timestep Model for Rainwater Harvesting Analysis: Acceptance over Hourly Model and Exploring Accuracy of Different Operating Algorithms. Sustainability, 15(5), 3870. https://doi.org/10.3390/su15053870

Note that from the first issue of 2016, this journal uses article numbers instead of page numbers. See further details here.

Article Metrics

Back to TopTop