Multi-Scale Integration and Distribution of Soil Organic Matter Spatial Variation in a Coal–Grain Compound Area
Abstract
1. Introduction
2. Materials and Methods
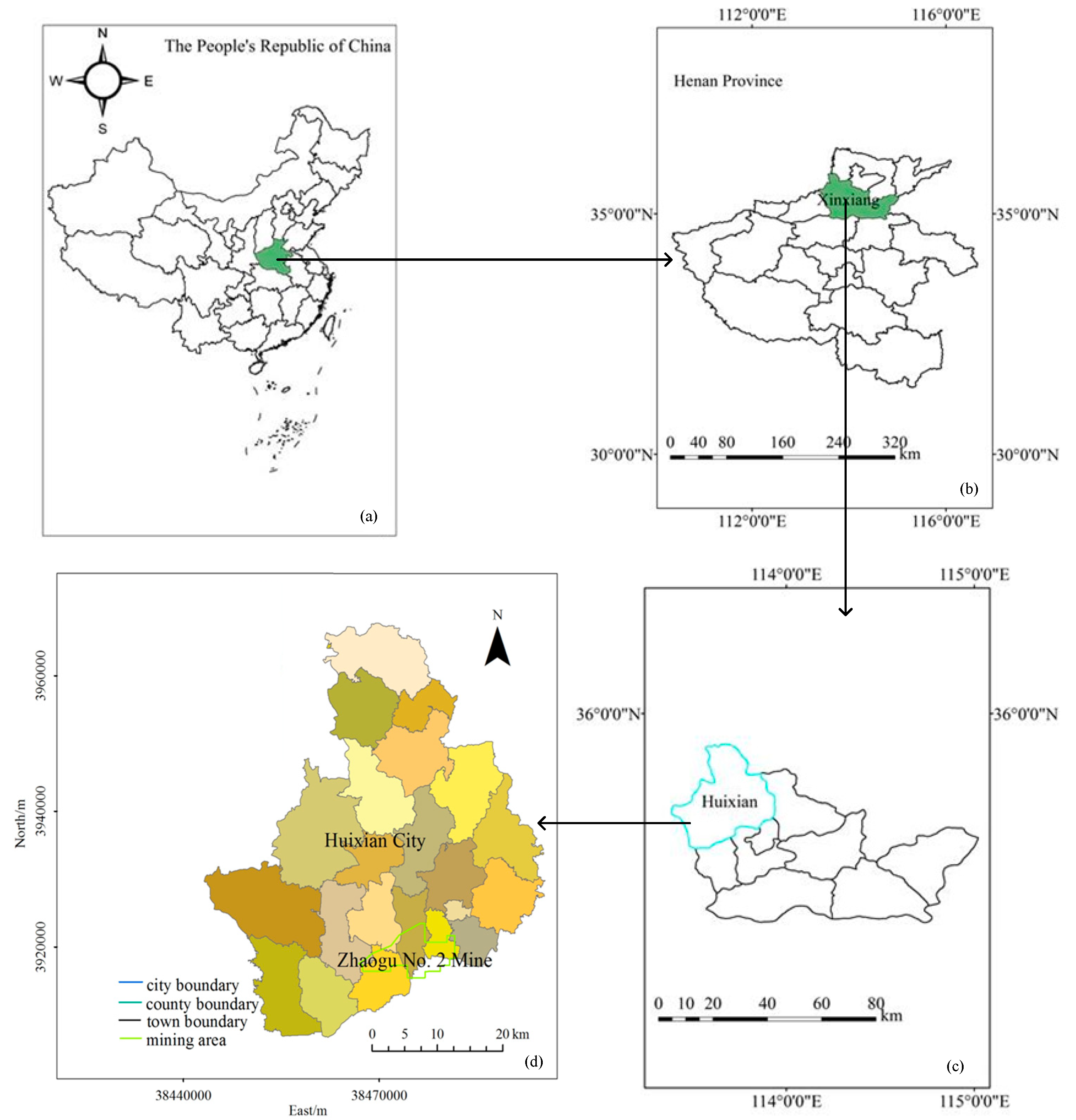
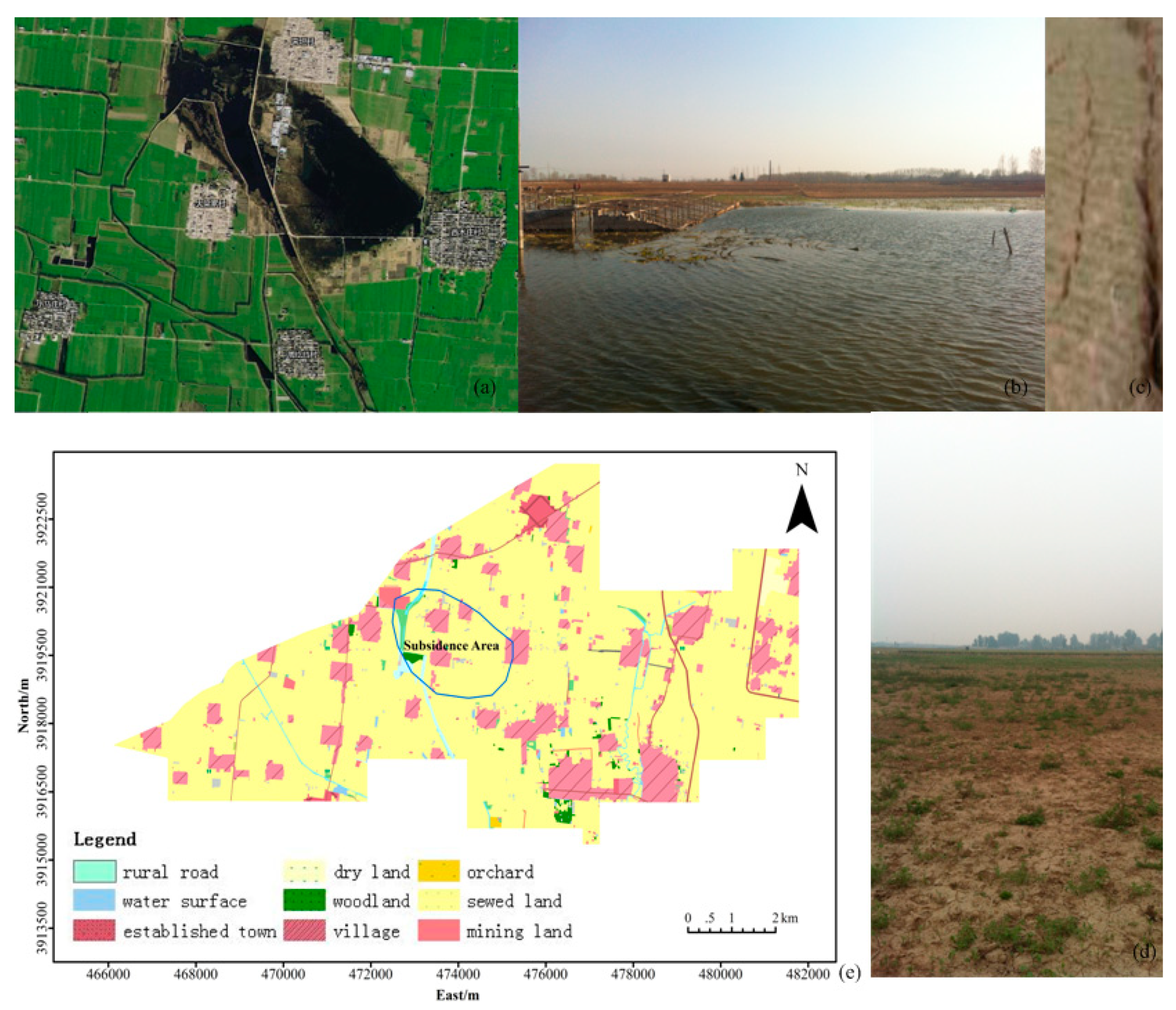
2.1. Study Area
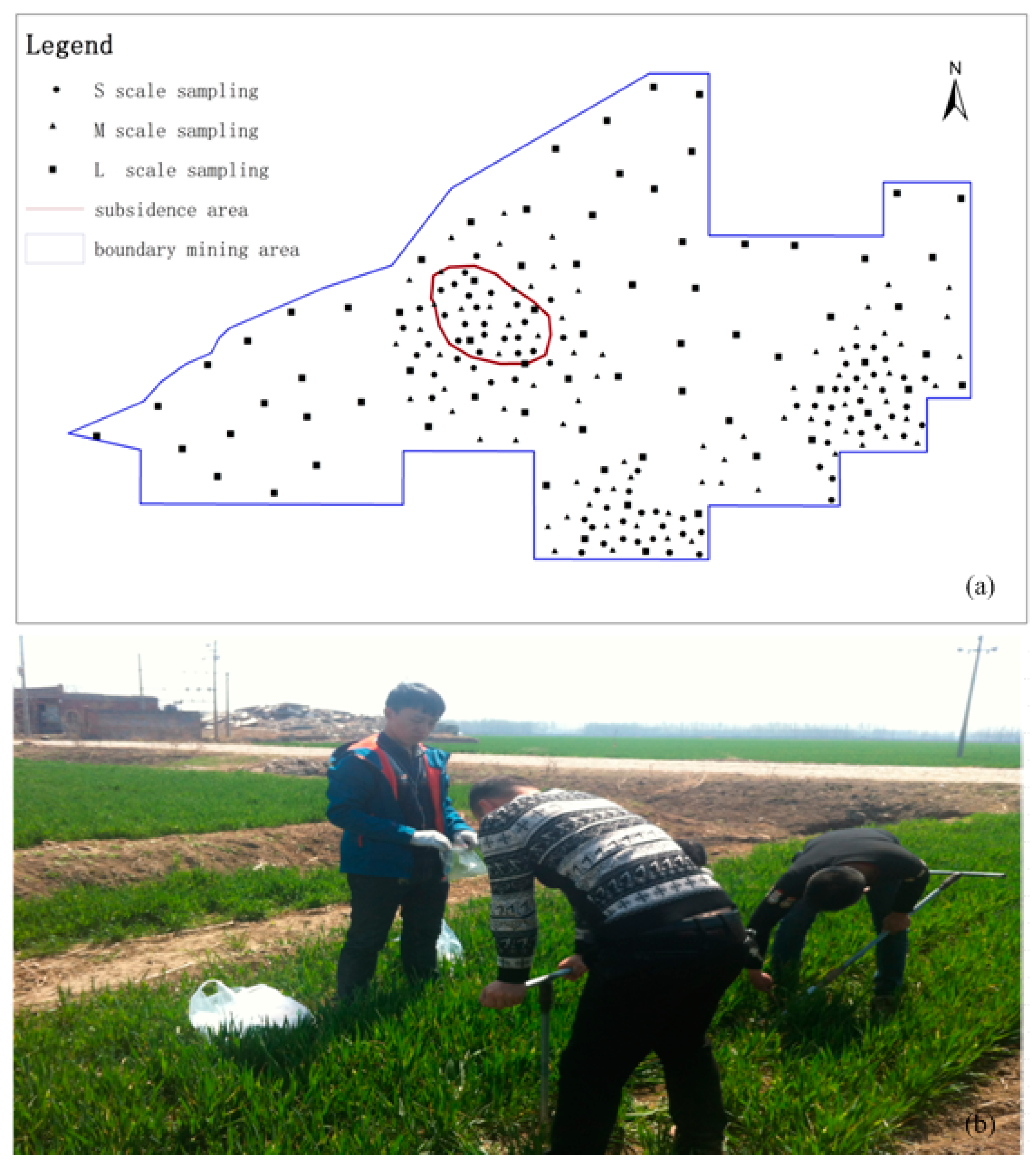
2.2. Soil Sampling
2.3. Research Methods
2.3.1. Semivariogram Model
2.3.2. Multiscale Nested Model
2.3.3. Model Test Method
2.4. Data Processing and Analysis
3. Results
3.1. SOM Content at Different Scales
3.2. Spatial Structure Analysis of SOM at Different Scales
3.3. Multiscale Integration of SOM
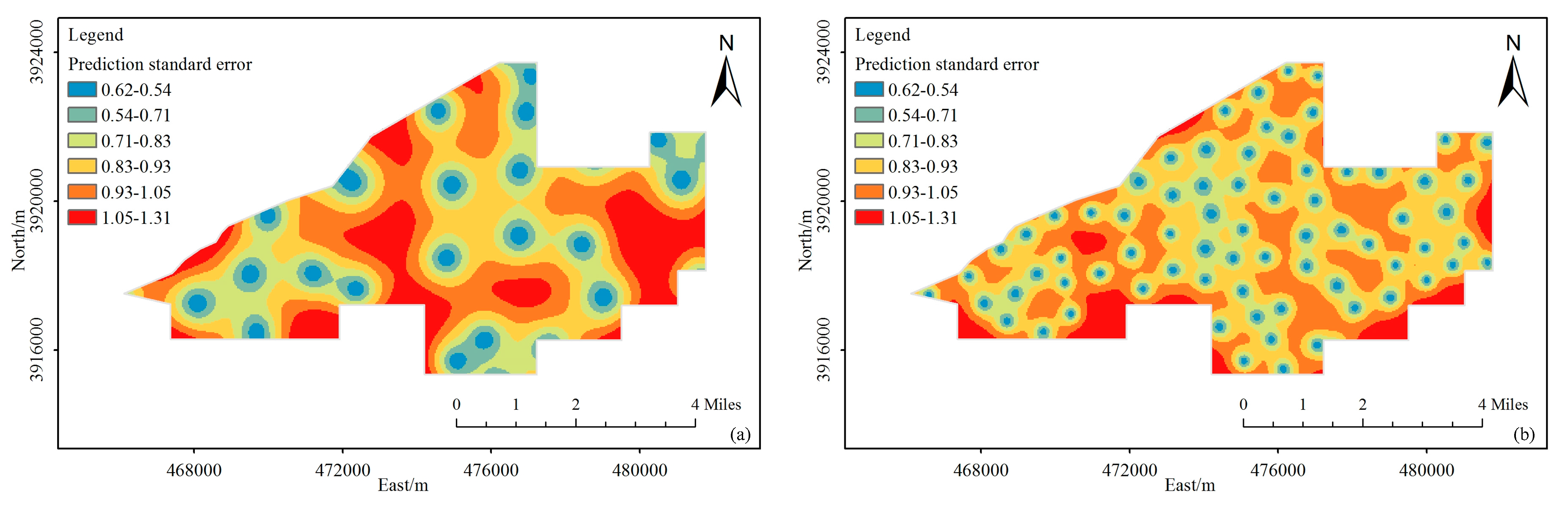
3.4. Accuracy Verification
3.5. Spatial Distribution of SOM
4. Discussion
4.1. Effect of Sample Size on the Spatial Variability in SOM
4.2. Effect of Soil Type on SOM
4.3. Other Factors Affecting SOM
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Liu, X.; Bai, Z.; Zhou, W.; Cao, Y.; Zhang, G. Changes in soil properties in the soil profile after mining and reclamation in an opencast coal mine on the Loess Plateau, China. Ecol. Eng. 2017, 98, 228–239. [Google Scholar] [CrossRef]
- Guo, J.; Zhang, Y.; Huang, H.; Yang, F. Deciphering soil bacterial community structure in subsidence area caused by underground coal mining in arid and semiarid area. Appl. Soil Ecol. 2021, 163, 103916. [Google Scholar] [CrossRef]
- Zhang, H.; Liu, W.; Zhang, H.; Fan, L.; Ma, S. Spatial distribution of soil organic matter in a coal mining subsidence area. Acta Agric. Scand. Sect. B—Soil Plant Sci. 2019, 70, 117–127. [Google Scholar] [CrossRef]
- Wang, Y.; Luo, C.; Zhang, W.; Meng, X.; Liu, Q.; Zhang, X.; Liu, H. Remote Sensing Prediction Model of Cultivated Land Soil Organic Matter Considering the Best Time Window. Sustainability 2022, 15, 469. [Google Scholar] [CrossRef]
- Ivanova, S.; Vesnina, A.; Fotina, N.; Prosekov, A. An Overview of Carbon Footprint of Coal Mining to Curtail Greenhouse Gas Emissions. Sustainability 2022, 14, 15135. [Google Scholar] [CrossRef]
- Ahirwal, J.; Maiti, S.K. Assessment of soil properties of different land uses generated due to surface coal mining activities in tropical Sal (Shorea robusta) forest, India. Catena 2016, 140, 155–163. [Google Scholar] [CrossRef]
- Ahirwal, J.; Maiti, S.K. Restoring coal mine degraded lands in India for achieving the United Nations-Sustainable Development Goals. Restor. Ecol. 2021, 30, e13606. [Google Scholar] [CrossRef]
- Sun, J.; Guo, E.; Yang, X.; Kong, Y.; Yang, L.; Liu, H.; Lin, X. Seasonal and spatial variations in soil biochemical properties in areas with different degrees of mining subsidence in Central China. SSRN. 2022, 508, 21. [Google Scholar] [CrossRef]
- De Valck, J.; Williams, G.; Kuik, S. Does coal mining benefit local communities in the long run? A sustainability perspective on regional Queensland, Australia. Resour. Policy 2021, 71, 102009. [Google Scholar] [CrossRef]
- Ahirwal, J.; Pandey, V.C. Restoration of mine degraded land for sustainable environmental development. Restor. Ecol. 2020, 29, e13268. [Google Scholar] [CrossRef]
- Li, S.; Wang, J.; Zhang, M.; Tang, Q. Characterizing and attributing the vegetation coverage changes in North Shanxi coal base of China from 1987 to 2020. Resour. Policy 2021, 74, 102331. [Google Scholar] [CrossRef]
- Ma, Q.; Wu, J.; He, C.; Fang, X. The speed, scale, and environmental and economic impacts of surface coal mining in the Mongolian Plateau. Resour. Conserv. Recycl. 2021, 173, 105730. [Google Scholar] [CrossRef]
- Jarašiūnas, G.; Kinderiene, I. Impact of agro-environmental systems on soil erosion processes and soil properties on hilly landscape in Western Lithuania. J. Environ. Eng. Landsc. Manag. 2015, 24, 60–69. [Google Scholar] [CrossRef]
- Wang, J.; Zhang, J.; Feng, Y. Characterizing the spatial variability of soil particle size distribution in an underground coal mining area: An approach combining multi-fractal theory and geostatistics. Catena 2019, 176, 94–103. [Google Scholar] [CrossRef]
- Nie, X.; Hu, Z.; Ruan, M.; Zhu, Q.; Sun, H. Remote-Sensing Evaluation and Temporal and Spatial Change Detection of Ecological Environment Quality in Coal-Mining Areas. Remote Sens. 2022, 14, 345. [Google Scholar] [CrossRef]
- Arefieva, O.; Nazarkina, A.V.; Gruschakova, N.V.; Skurikhina, J.E.; Kolycheva, V.B. Impact of mine waters on chemical composition of soil in the Partizansk Coal Basin, Russia. Int. Soil Water Conserv. Res. 2019, 7, 57–63. [Google Scholar] [CrossRef]
- Liao, Q.; Liu, X.; Xiao, M. Ecological Restoration and Carbon Sequestration Regulation of Mining Areas—A Case Study of Huangshi City. Int. J. Environ. Res. Public Health 2022, 19, 4175. [Google Scholar] [CrossRef]
- Omeka, M.E.; Igwe, O.; Unigwe, C.O. An integrated approach to the bioavailability, ecological, and health risk assessment of potentially toxic elements in soils within a barite mining area, SE Nigeria. Environ. Monit. Assess. 2022, 194, 1–30. [Google Scholar] [CrossRef]
- Ignacy, D. Comprehensive method of assessing the flood threat of artificially drained mine subsidence areas for identification and sustainable repair of mining damage to the aquatic environment. Water Resour. Ind. 2021, 26, 100153. [Google Scholar] [CrossRef]
- Zerizgh, T.; Guo, Q.; Tian, L.; Wei, R.; Zhao, C. An integrated approach to quantify ecological and human health risks of soil heavy metal contamination around coal mining area. Sci. Total Environ. 2022, 814, 152653. [Google Scholar] [CrossRef]
- Ma, K.; Zhang, Y.; Ruan, M.; Guo, J.; Chai, T. Land Subsidence in a Coal Mining Area Reduced Soil Fertility and Led to Soil Degradation in Arid and Semi-Arid Regions. Int. J. Environ. Res. Public Health 2019, 16, 3929. [Google Scholar] [CrossRef]
- Donnell, M.S.O.; Manier, D.J. Spatial Estimates of Soil Moisture for Understanding Ecological Potential and Risk: A Case Study for Arid and Semi-Arid Ecosystems. Land 2022, 11, 1856. [Google Scholar] [CrossRef]
- Long, L.; Liu, Y.; Chen, X.; Guo, J.; Li, X.; Guo, Y.; Zhang, X.; Lei, S. Analysis of Spatial Variability and Influencing Factors of Soil Nutrients in Western China: A Case Study of the Daliuta Mining Area. Sustainability 2022, 14, 2793. [Google Scholar] [CrossRef]
- Iskandar, I.; Suryaningtyas, D.T.; Baskoro, D.P.T.; Budi, S.W.; Gozali, I.; Saridi, S.; Masyhuri, M.; Dultz, S. The regulatory role of mine soil properties in the growth of revegetation plants in the post-mine landscape of East Kalimantan. Ecol. Indic. 2022, 139, 108877. [Google Scholar] [CrossRef]
- Liu, F.; Wang, X.; Chi, Q.; Tian, M. Spatial variations in soil organic carbon, nitrogen, phosphorus contents and controlling factors across the “Three Rivers” regions of southwest China. Sci. Total Environ. 2021, 794, 148795. [Google Scholar] [CrossRef]
- Kaminski, M.; Smolka, G. Clausal Tableaux for Hybrid PDL. Electron. Notes Theor. Comput. Sci. 2021, 278, 99–113. [Google Scholar] [CrossRef]
- Wang, Z.; Wang, G.; Zhang, G.; Wang, H.; Ren, T. Effects of land use types and environmental factors on spatial distribution of soil total nitrogen in a coalfield on the Loess Plateau, China. Soil Tillage Res. 2021, 211, 105027. [Google Scholar] [CrossRef]
- Pelegrino, M.H.P.; Silva, S.H.G.; de Faria, Á.J.G.; Mancini, M.; Teixeira, A.F.D.S.; Chakraborty, S.; Weindorf, D.C.; Guilherme, L.R.G.; Curi, N. Prediction of soil nutrient content via pXRF spectrometry and its spatial variation in a highly variable tropical area. Precis. Agric. 2021, 23, 18–34. [Google Scholar] [CrossRef]
- Xu, T.; Yi, S.; Zhou, Y.; Li, Q.; Liu, Y. Temporal and Spatial Changes and Driving Forces of Soil Properties in Subtropical Mountainous Areas from 2017 to 2020: A Case Study of Baokang County, Hubei Province, China. Land 2022, 11, 1735. [Google Scholar] [CrossRef]
- Voltr, V.; Menšík, L.; Hlisnikovský, L.; Hruška, M.; Pokorný, E.; Pospíšilová, L. The Soil Organic Matter in Connection with Soil Properties and Soil Inputs. Agronomy 2021, 11, 779. [Google Scholar] [CrossRef]
- Bennett, J.M.; Melland, A.R.; Eberhard, J.F.; Paton, C.; Clewett, J.F.; Newsome, T.; Baillie, C. Rehabilitating open-cut coal mine spoil for a pasture system in south east Queensland, Australia: Abiotic soil properties compared with unmined land through time. Geoderma Reg. 2021, 25, e00364. [Google Scholar] [CrossRef]
- Hu, W.; Shen, Q.; Zhai, X.; Du, S.; Zhang, X. Impact of environmental factors on the spatiotemporal variability of soil organic matter: A case study in a typical small Mollisol watershed of Northeast China. J. Soils Sediments 2021, 21, 736–747. [Google Scholar] [CrossRef]
- Crookston, B.S.; Yost, M.A.; Bowman, M.; Veum, K.; Cardon, G.; Norton, J. Soil health spatial-temporal variation influence soil security on Midwestern, U.S. farms. Soil Secur. 2021, 3, 100005. [Google Scholar] [CrossRef]
- Tang, S.; Du, C.; Nie, T. Inversion Estimation of Soil Organic Matter in Songnen Plain Based on Multispectral Analysis. Land 2022, 11, 608. [Google Scholar] [CrossRef]
- Angst, G.; Mueller, K.E.; Nierop, K.G.J.; Simpson, M.J. Plant- or microbial-derived? A review on the molecular composition of stabilized soil organic matter. Soil Biol. Biochem. 2021, 156, 108189. [Google Scholar] [CrossRef]
- Witzgall, K.; Vidal, A.; Schubert, D.I.; Höschen, C.; Schweizer, S.A.; Buegger, F.; Pouteau, V.; Chenu, C.; Mueller, C.W. Particulate organic matter as a functional soil component for persistent soil organic carbon. Nat. Commun. 2021, 12, 1–10. [Google Scholar] [CrossRef]
- Bradford, M.A.; Wood, S.A.; Addicott, E.T.; Fenichel, E.P.; Fields, N.; González-Rivero, J.; Jevon, F.V.; Maynard, D.S.; Oldfield, E.E.; Polussa, A.; et al. Quantifying microbial control of soil organic matter dynamics at macrosystem scales. Biogeochemistry 2021, 156, 19–40. [Google Scholar] [CrossRef]
- Chen, L.; Liu, L.; Qin, S.; Yang, G.; Fang, K.; Zhu, B.; Kuzyakov, Y.; Chen, P.; Xu, Y.; Yang, Y. Regulation of priming effect by soil organic matter stability over a broad geographic scale. Nat. Commun. 2019, 10, 1–10. [Google Scholar] [CrossRef]
- Weng, Z.H.; Lehmann, J.; Van Zwieten, L.; Joseph, S.; Archanjo, B.S.; Cowie, B.; Thomsen, L.; Tobin, M.J.; Vongsvivut, J.; Klein, A.; et al. Probing the nature of soil organic matter. Crit. Rev. Environ. Sci. Technol. 2021, 52, 4072–4093. [Google Scholar] [CrossRef]
- Sun, X.; Gao, L.; Ren, H.; Ye, Y.; Li, A.; Stafford-Smith, M.; Connor, J.D.; Wu, J.; Bryan, B.A. China’s progress towards sustainable land development and ecological civilization. Landsc. Ecol. 2018, 33, 1647–1653. [Google Scholar] [CrossRef]
- Zhang, Z.; Ding, J.; Zhu, C.; Wang, J.; Ma, G.; Ge, X.; Li, Z.; Han, L. Strategies for the efficient estimation of soil organic matter in salt-affected soils through Vis-NIR spectroscopy: Optimal band combination algorithm and spectral degradation. Geoderma 2020, 382, 114729. [Google Scholar] [CrossRef]
- Zhang, H.; Liu, W.; Zhang, Q.; Huang, X. Three-Dimensional Spatial Distribution and Influential Factors of Soil Total Nitrogen in a Coal Mining Subsidence Area. Sustainability 2022, 14, 7897. [Google Scholar] [CrossRef]
- Bouasria, A.; Namr, K.I.; Rahimi, A.; Ettachfini, E.M. Geospatial Assessment of Soil Organic Matter Variability at Sidi Bennour District in Doukkala Plain in Morocco. J. Ecol. Eng. 2021, 22, 120–130. [Google Scholar] [CrossRef]
- Bhunia, G.S.; Shit, P.K.; Maiti, R. Comparison of GIS-based interpolation methods for spatial distribution of soil organic carbon (SOC). J. Saudi Soc. Agric. Sci. 2018, 17, 114–126. [Google Scholar] [CrossRef]
- Usowicz, B.; Lipiec, J. Spatial variability of saturated hydraulic conductivity and its links with other soil properties at the regional scale. Sci. Rep. 2021, 11, 829. [Google Scholar] [CrossRef]
- Yang, M.; Gao, X.; Zhao, X.; Wu, P. Scale effect and spatially explicit drivers of interactions between ecosystem services—A case study from the Loess Plateau. Sci. Total. Environ. 2021, 785, 147389. [Google Scholar] [CrossRef]
- Yang, J.; Wang, J.; Xu, C.; Liao, X.; Tao, H. Modeling the spatial relationship between rice cadmium and soil properties at a regional scale considering confounding effects and spatial heterogeneity. Chemosphere 2021, 287, 132402. [Google Scholar] [CrossRef]
- Paterson, S.; Minasny, B.; McBratney, A. Spatial variability of Australian soil texture: A multiscale analysis. Geoderma 2018, 309, 60–74. [Google Scholar] [CrossRef]
- Jenerette, G.D.; Wu, J.; Grimm, N.B.; Hope, D. Points, patches, and regions: Scaling soil biogeochemical patterns in an urbanized arid ecosystem. Glob. Chang. Biol. 2006, 12, 1532–1544. [Google Scholar] [CrossRef]
- Suriyavirun, N.; Krichels, A.H.; Kent, A.D.; Yang, W.H. Microtopographic differences in soil properties and microbial community composition at the field scale. Soil Biol. Biochem. 2019, 131, 71–80. [Google Scholar] [CrossRef]
- Hu, K.; Wang, S.; Li, H.; Huang, F.; Li, B. Spatial scaling effects on variability of soil organic matter and total nitrogen in suburban Beijing. Geoderma 2014, 226–227, 54–63. [Google Scholar] [CrossRef]
- Aghasi, B.; Jalalian, A.; Khademi, H.; Toomanian, N. Sub-basinscale spatial variability of soil properties in Central Iran. Arab. J. Geosci. 2017, 10, 136. [Google Scholar] [CrossRef]
- Kraemer, F.B.; Sainz, D.; Morrás, H.; Carfagno, P.; Eiza, M.; Fernández, P.; Chagas, C. Soil structure and glyphosate fate under no-till management in the Pampa region. I. Soil structural anisotropy and hydro-physical behavior. Soil Tillage Res. 2022, 221, 105410. [Google Scholar] [CrossRef]
- Benavides-Bravo, F.G.; Soto-Villalobos, R.; Cantú-González, J.R.; Aguirre-López, M.A.; Benavides-Ríos, Á.G. A Quadratic–Exponential Model of Variogram Based on Knowing the Maximal Variability: Application to a Rainfall Time Series. Mathematics 2021, 9, 2466. [Google Scholar] [CrossRef]
- Panagea, I.S.; Berti, A.; Čermak, P.; Diels, J.; Else, A.; Kusá, H.; Piccoli, I.; Poesen, J.; Stoate, C.; Tits, M.; et al. Soil Water Retention as Affected by Management Induced Changes of Soil Organic Carbon: Analysis of Long-Term Experiments in Europe. Land 2021, 10, 1362. [Google Scholar] [CrossRef]
- Piccini, C.; Francaviglia, R.; Marchetti, A. Predicted Maps for Soil Organic Matter Evaluation: The Case of Abruzzo Region (Italy). Land 2020, 9, 349. [Google Scholar] [CrossRef]
- Du, Z.; Gao, B.; Ou, C.; Du, Z.; Yang, J.; Batsaikhan, B.; Dorjgotov, B.; Yun, W.; Zhu, D. A Quantitative Analysis of Factors Influencing Organic Matter Concentration in the Topsoil of Black Soil in Northeast China Based on Spatial Heterogeneous Patterns. ISPRS Int. J. Geo-Inf. 2021, 10, 348. [Google Scholar] [CrossRef]
- Shi, W.; Wang, J.; Li, X.; Xu, Q.; Jiang, X. Multi-fractal characteristics of reconstructed landform and its relationship with soil erosion at a large opencast coal-mine in the loess area of China. Geomorphology 2021, 390, 107859. [Google Scholar] [CrossRef]
- Qi, Q.; Zhang, D.; Zhang, M.; Tong, S.; Wang, W.; An, Y. Spatial distribution of soil organic carbon and total nitrogen in disturbed Carex tussock wetland. Ecol. Indic. 2020, 120, 106930. [Google Scholar] [CrossRef]
- Yang, Q.-Y.; Yang, J.-S.; Liu, G.-M. [Scale-dependency of spatial variability of soil available nutrients]. J. Appl. Ecol. 2011, 22, 431–436. [Google Scholar]
- Qin, J.; Liu, M.; Deng, Z.; Gu, S.; Gao, J. Spatial Variability of Soil Moisture at Different Scales in Sandy Loam in Northern Henan Province. J. Irrig. Drain. 2019, 38, 10–16. [Google Scholar]

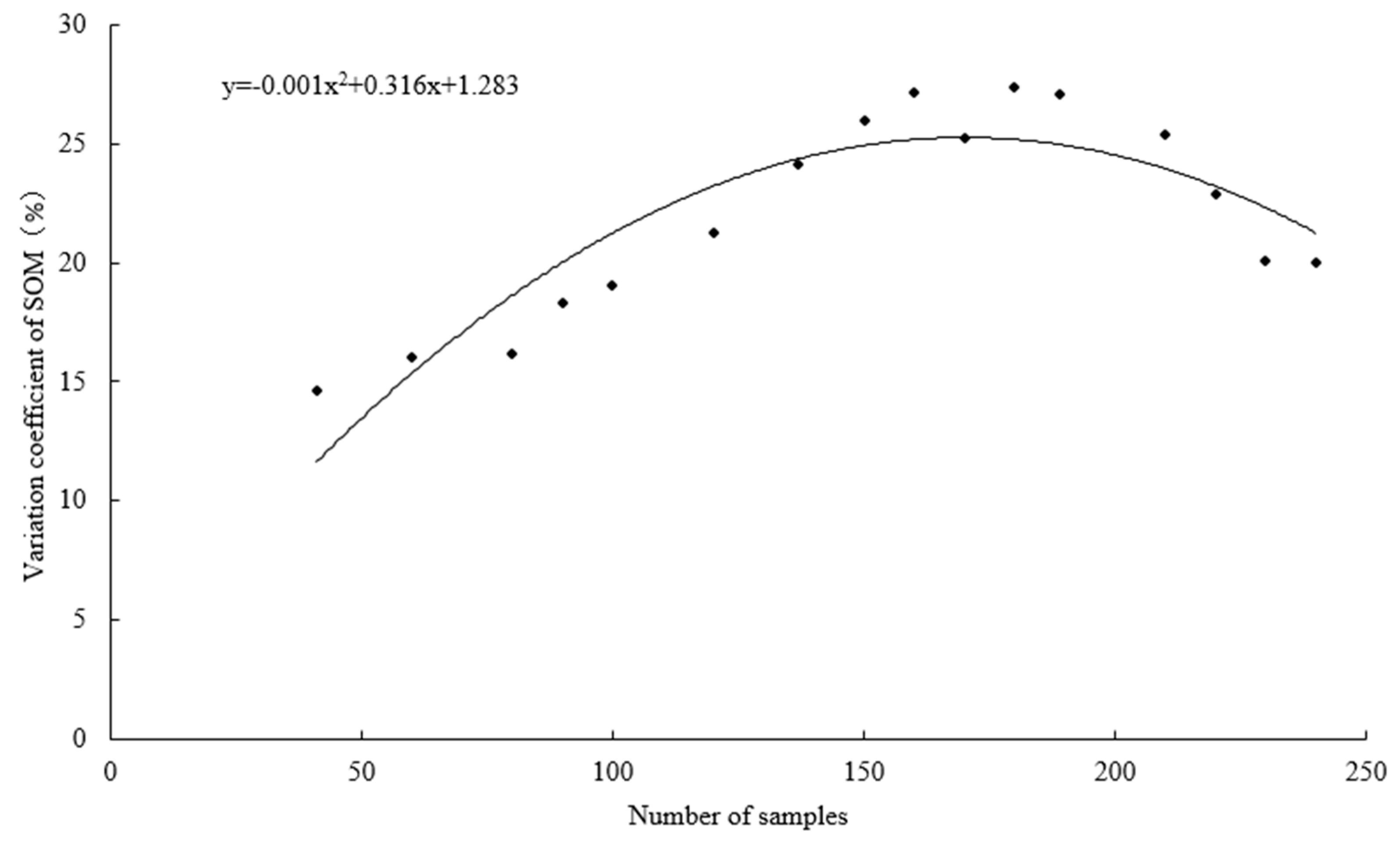
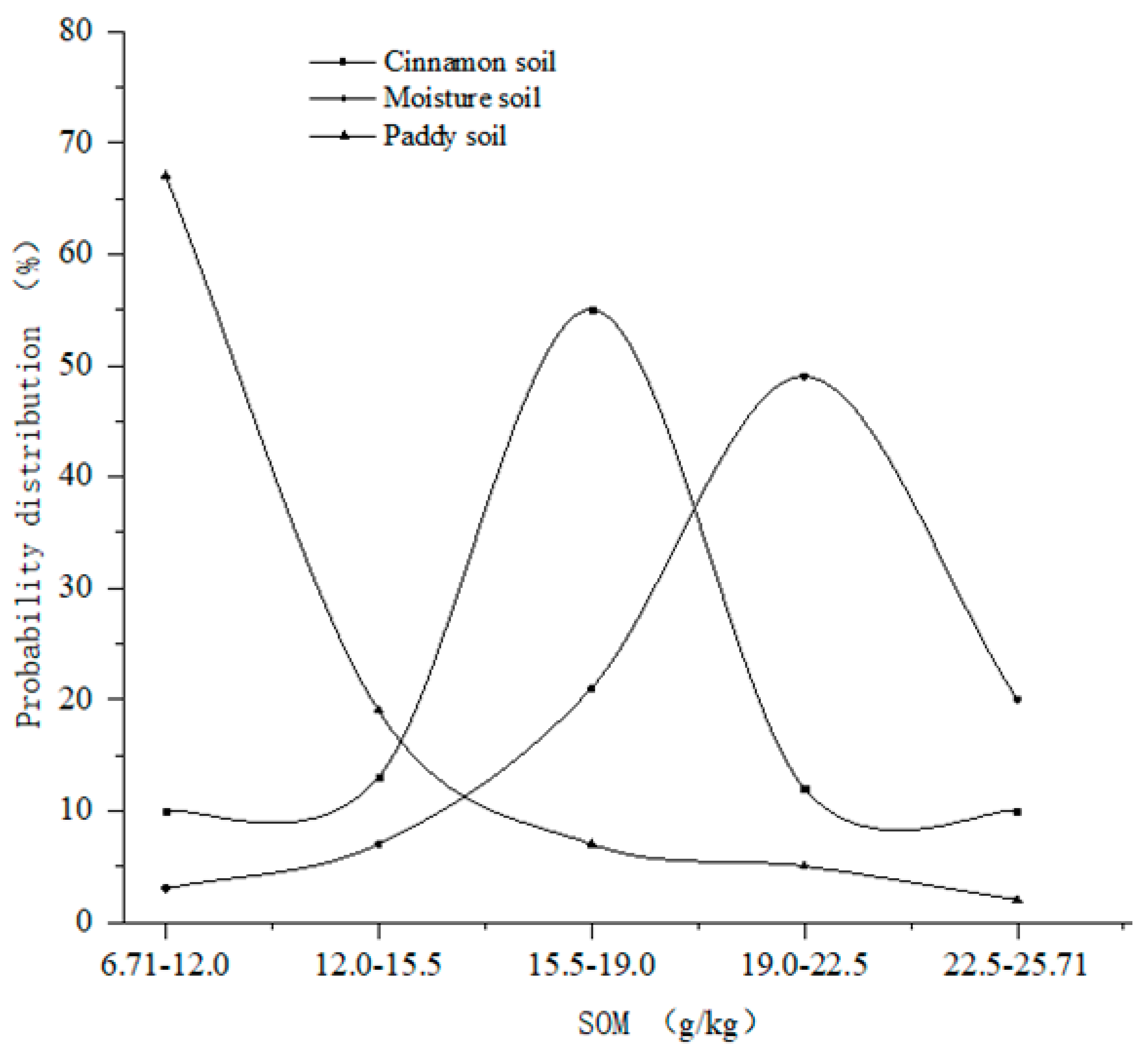
| Item | Scales a | Samples | Max | Min | Mean | SD | Median | Kurtosis | Skewness | K-S (p) | CV (%) b |
|---|---|---|---|---|---|---|---|---|---|---|---|
| SOM (g·kg−1) | L | 72 | 26.35 | 10.26 | 15.92 | 3.66 | 15.61 | 0.341 | 0.043 | 0.866 | 28.07 |
| M | 76 | 24.26 | 10.92 | 14.94 | 2.93 | 14.32 | 0.613 | −0.291 | 0.916 | 14.93 | |
| S | 79 | 23.61 | 11.13 | 13.62 | 2.01 | 13.38 | 0.695 | −0.306 | 0.969 | 14.31 |
| Scales | Main Variable Direction/° | Main Range/m | Secondary Range/m | Anisotropy Ratio |
|---|---|---|---|---|
| L | 90 | 2460 | 2460 | 1.000 |
| 135 | 2496 | 2473 | 1.009 | |
| 180 | 2460 | 2460 | 1.000 | |
| 225 | 2314 | 2438 | 0.949 | |
| M | 44 | 1126 | 1167 | 0.965 |
| 89 | 1253 | 1197 | 1.047 | |
| 134 | 1083 | 1106 | 0.979 | |
| 179 | 1324 | 1289 | 1.027 | |
| S | 142 | 621 | 621 | 1.000 |
| 187 | 656 | 643 | 1.020 | |
| 232 | 621 | 621 | 1.000 | |
| 277 | 661 | 673 | 0.982 |
| Item | Scales | Model | Determination Coefficient | Residual | Range (m) | C0 | C0 + C | C0/C0 + C% |
|---|---|---|---|---|---|---|---|---|
| SOM | L | Exponential | 0.431 | 0.160 | 2460 | 0.207 | 0.413 | 50.12 |
| M | Exponential | 0.462 | 0.126 | 1135 | 0.106 | 0.357 | 29.70 | |
| S | Spherical | 0.397 | 0.182 | 621 | 0.132 | 0.402 | 32.84 |
| Item | Interpolation | I Value | P |
|---|---|---|---|
| SOM | Ordinary Kriging | 2.369 | 2.406 |
| Fit Model | 0.561 | 0.529 |
| Methods | Max | Min | Mean | CV(%) |
|---|---|---|---|---|
| Measured value | 26.35 | 10.26 | 15.92 | 28.07 |
| Ordinary Kriging | 24.19 | 12.36 | 15.76 | 24.03 |
| Fit model | 26.93 | 11.13 | 15.92 | 26.56 |
| Type of Soil | Number (a) | Mean (g/kg) | Standard Deviation | CV(%) |
|---|---|---|---|---|
| cinnamon soil | 73 | 20.14 | 3.32 | 15.61 |
| moisture soil | 68 | 10.16 | 2.93 | 30.26 |
| paddy soil | 59 | 18.29 | 2.35 | 11.44 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, H.; Liu, W.; Hu, Q.; Huang, X. Multi-Scale Integration and Distribution of Soil Organic Matter Spatial Variation in a Coal–Grain Compound Area. Sustainability 2023, 15, 3780. https://doi.org/10.3390/su15043780
Zhang H, Liu W, Hu Q, Huang X. Multi-Scale Integration and Distribution of Soil Organic Matter Spatial Variation in a Coal–Grain Compound Area. Sustainability. 2023; 15(4):3780. https://doi.org/10.3390/su15043780
Chicago/Turabian StyleZhang, Huijuan, Wenkai Liu, Qingfeng Hu, and Xiaodong Huang. 2023. "Multi-Scale Integration and Distribution of Soil Organic Matter Spatial Variation in a Coal–Grain Compound Area" Sustainability 15, no. 4: 3780. https://doi.org/10.3390/su15043780
APA StyleZhang, H., Liu, W., Hu, Q., & Huang, X. (2023). Multi-Scale Integration and Distribution of Soil Organic Matter Spatial Variation in a Coal–Grain Compound Area. Sustainability, 15(4), 3780. https://doi.org/10.3390/su15043780






