1. Introduction
In the design process of new mines and reconstruction and upgrading of mines, the design of mining methods is an important part and is the core of the whole design work, which directly determines the subsequent technical personnel allocation, production organization management and industrial supporting facilities [
1,
2,
3]. Choosing the most appropriate mining method to mine the deposit is very important to the safety, economy and environmental protection of mining operations and affects the benefits and long-term development of mining companies [
4].
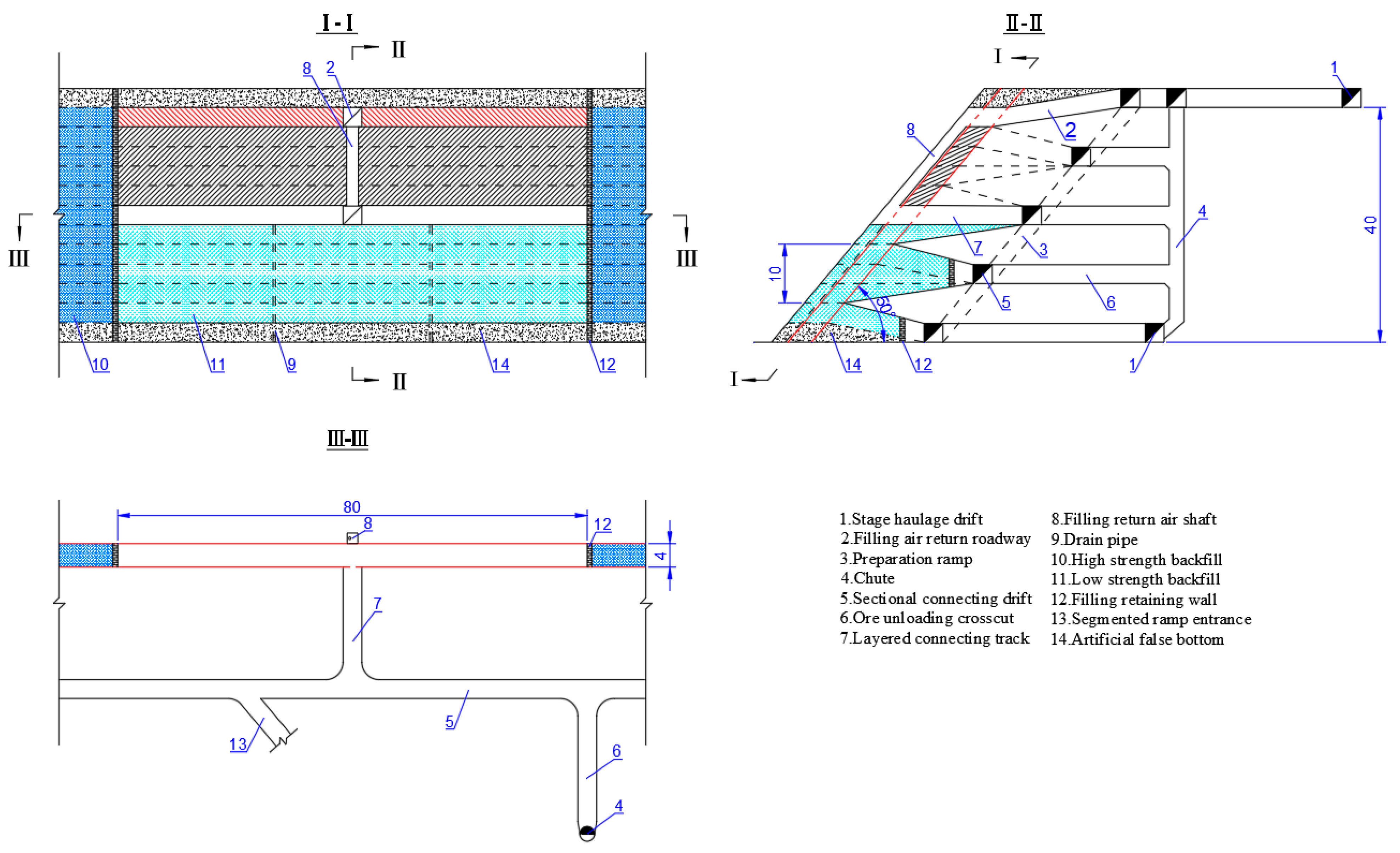
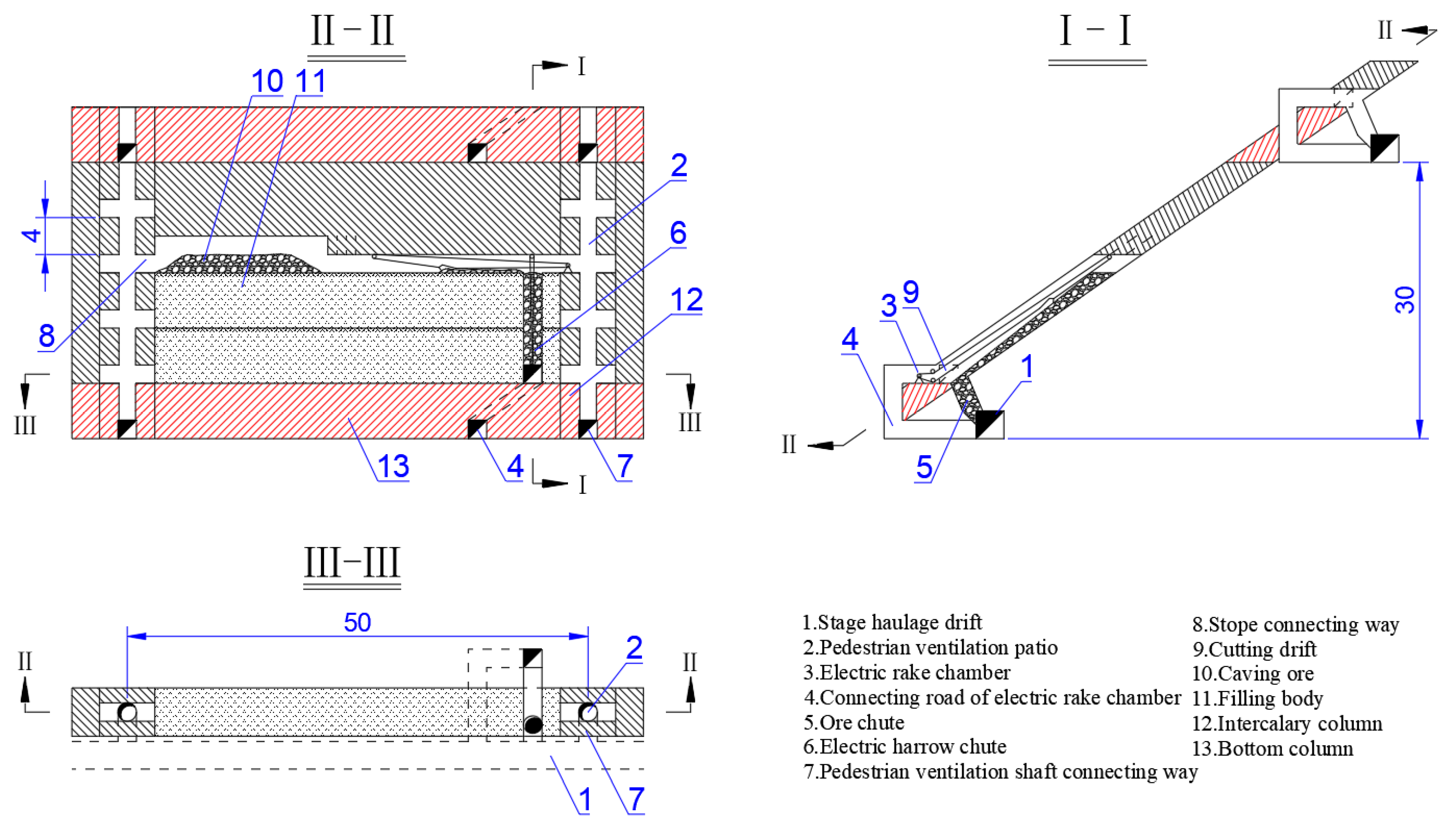
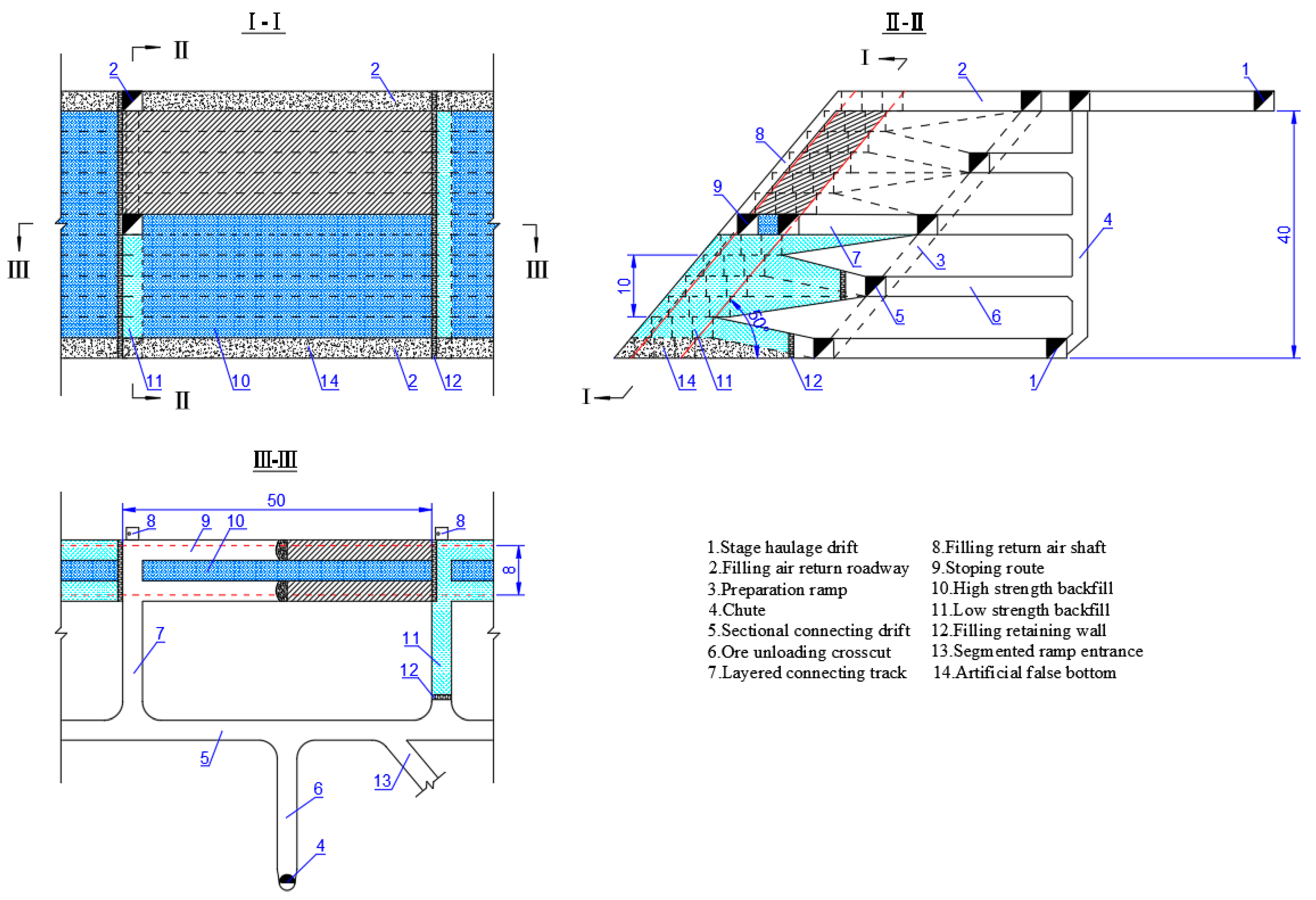
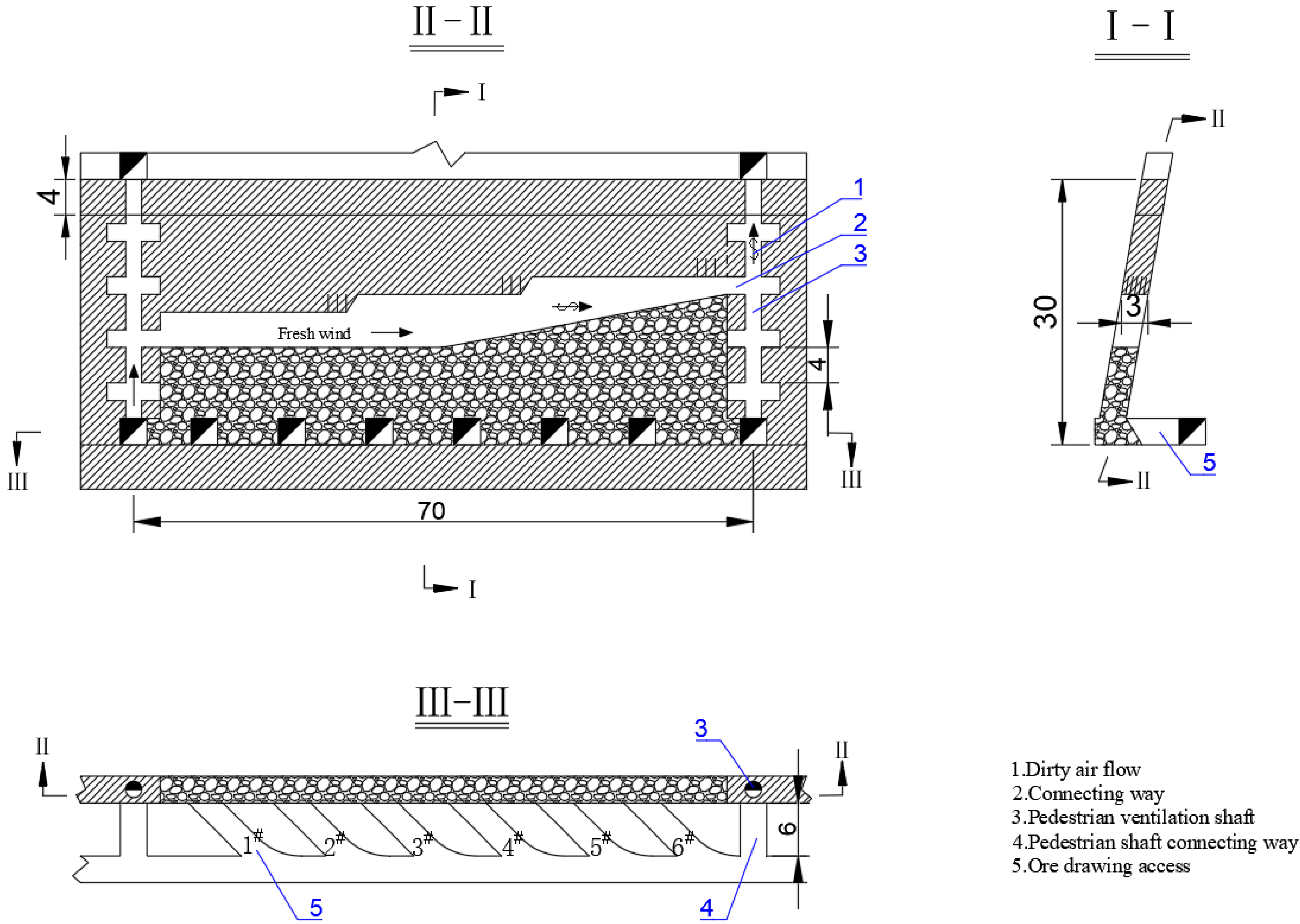
For a continuous orebody with regular shape, the most appropriate mining method can be selected by comparing the advantages and disadvantages and the economic and technical indicators. However, taking the difficult-to-mine complicated orebody (DCO) (see
Figure 1) as example, it was greatly affected by faults and joint fissures, leading to obvious branching and compounding phenomenon. Since it is difficult to determine the optimal plan through traditional methods for DCO, more reliance is placed on the experience of design decision-makers and limited data, through the comprehensive comparison of various indicators. This is typical of Multiple Attribute Decision Making (MADM).
Multiple Attribute Decision Making refers to the decision making problem of selecting the best alternative or ranking under a condition of considering multiple indicators [
5]. In order to solve such problems, researchers have developed a variety of multi criteria decision-making methods; typical representative methods include the Analytic Hierarchy Process [
6], Entropy method [
7], CRITIC method [
8], TOPSIS method [
9], GST (Grey Target Decision) method [
10], DEA method [
11], VIKOR method [
12], Fuzzy comprehensive evaluation method [
13], etc.
However, with increase in the complexity and scientific requirements of evaluation, a single decision-making method cannot guarantee optimal or accurate results [
14,
15]. Under this background, researchers have explored and developed mixed decision-making methods, for example, mixtures of Analytic Hierarchy Process and fuzzy, Entropy weight method and TOPSIS, Analytic Hierarchy Process, fuzzy set and VIKOR, fuzzy set and TOPSIS, etc.
In the field of mining engineering, many experts rely on these decision-making methods to optimize mining methods, for example, Karimnia [
16] proposed the fuzzy analytical hierarchy process method, the most suitable method selected for Iran’s Qapliq salt mine. Yavuz [
17] used the AHP method and fuzzy multiple attribute decision-making method, respectively, in a lignite mine located in Istanbul, carried out sensitivity analysis of the two methods and concluded that the Room and pillar method with filling is the most appropriate method. Qinqiang Guo [
18] used the mixed method of AHP to determine the index weight and TOPSIS to rank, selecting the most suitable mining method from the Soft Broken Complex Orebody, and achieved very good results, Iphar [
19] is committed to developing a mobile application, integrating several decision-making methods, and the optimal mining method can be obtained by inputting the original parameters for reference by engineering researchers.
However, in view of the complexity of mining method selection, simple expert scoring cannot fully reflect the fuzzy information, and the cognitive differences between different experts are easy to cause distortion of results. In terms of sorting, different ranging methods may have different results. In this case, the development of fuzzy set theory provides a good idea for solving such problems [
20]. Bajić [
21] transformed the indicators into triangular fuzzy numbers, constructed a fuzzy decision matrix and a fuzzy performance matrix, used to select the optimal alternative, and verified this through sensitivity analysis. Memori [
22] uses the TOPSIS method based on intuitionistic fuzzy sets, providing an accurate sustainable ranking of suppliers and a relevant solution for sustainable sourcing decisions that is validated through a real-world case study. Narayanamoorthy [
23] selected the best scheme for the selection of industrial robots by using a combination of Interval-valued intuitionistic hesitant fuzzy entropy and VIKOR.
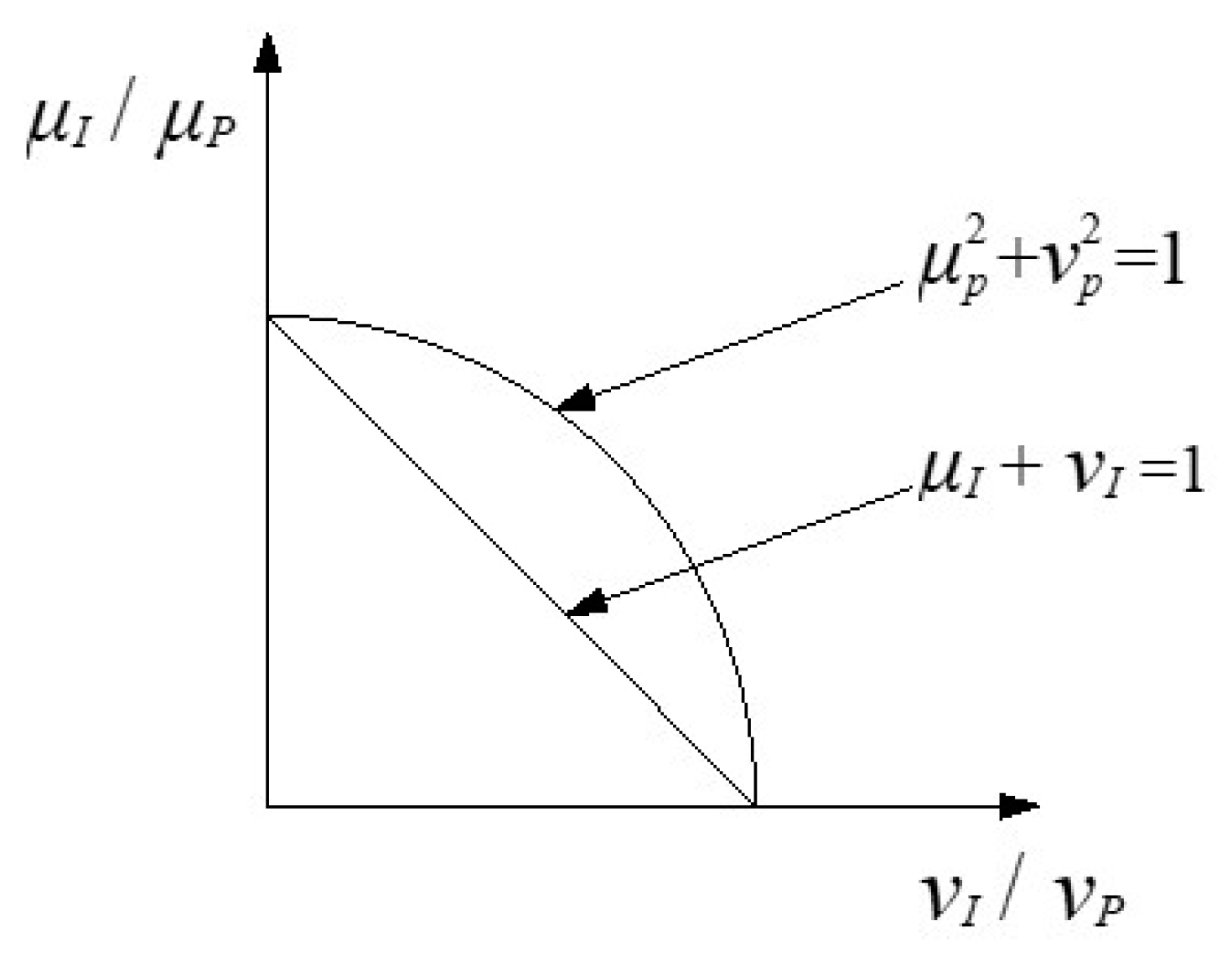
Pythagorean fuzzy sets (PFS) generalized by Yager [
24] is a new method to deal with fuzzy problems. Its main contribution is to go beyond the limit that the sum of membership and no membership of fuzzy sets is less than 1 (see
Figure 2). Compared with other fuzzy sets such as intuitionistic fuzzy sets, it can more fully and accurately represent uncertain information [
25]. In view of this, this paper introduces a TOPSIS method based on PFS [
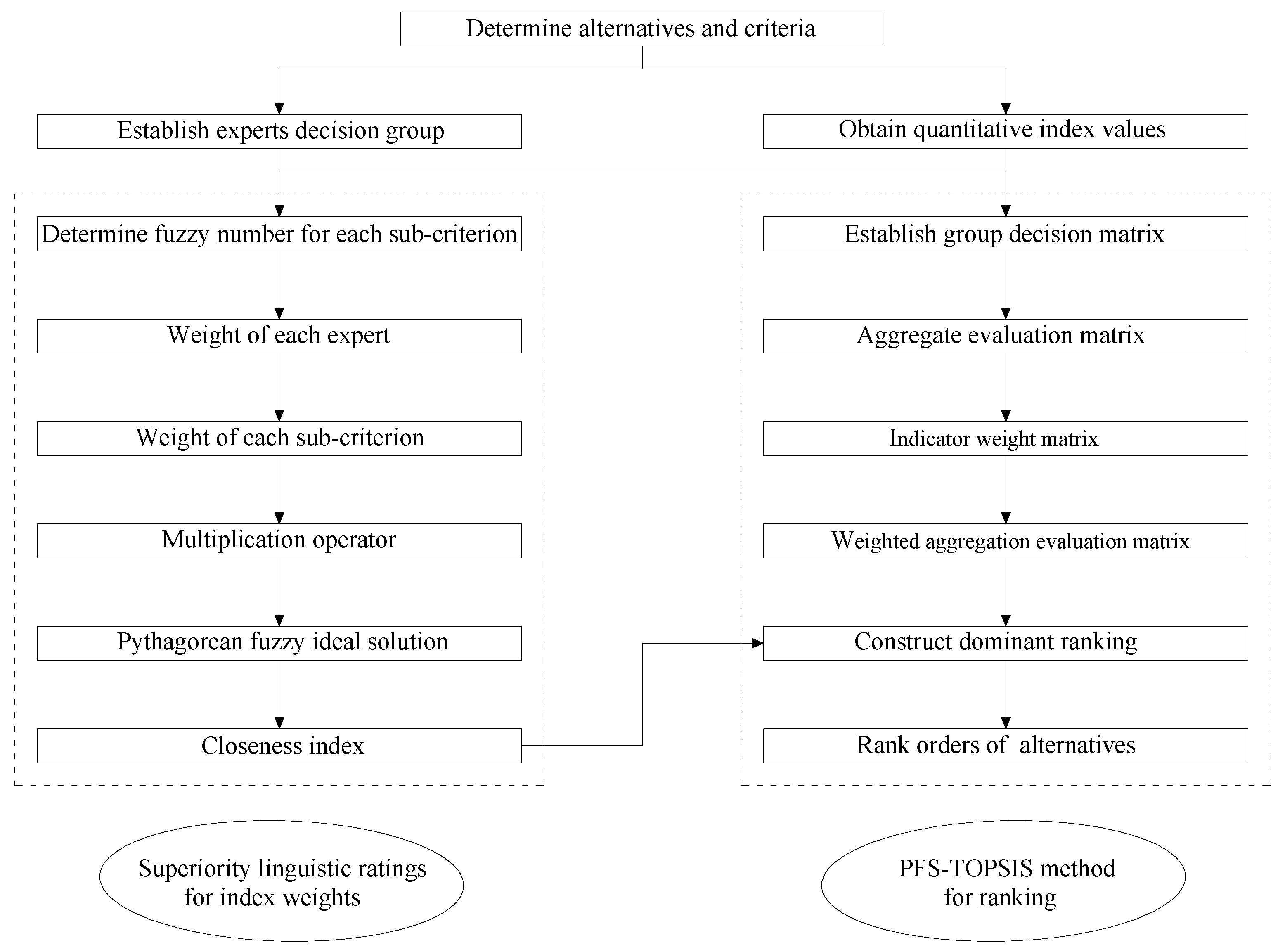
26]. The framework of this PFS–TOPSIS method is illustrated (see
Figure 3), which is used for mining method decision-making for the Suichang Gold Mine in Zhejiang Province, China, and has achieved good results in actual production.
2. Methods Introduction
2.1. Introduction of PFS Method
Definition 1. Let X be a universe of discourse [27,28]. The PFS ξ on X is given by Equation (1).where the functions μξ(x):X → [0, 1] and νξ(x): X → [0, 1] define the degree of membership and the degree of non-membership of the element x∈X to the set ξ, respectively, with the condition that 0 ≤ (μξ(x))2 + (νξ(x))2 ≤ 1,∀x∈X. πξ(x) =is called the degree of indeterminacy of element x∈X. For convenience, they are called (μξ(x), νξ(x))
and a Pythagorean fuzzy number (PFN) denoted by ξ = (μξ,νξ,) [
29].
Definition 2. For the collection ξi = (μξ,νξ,) (i = 1,2,……n) of the of PFNs with the weight vector w = (w1 w2……wn) of ξi(i = 1,2,……n) such that, the Pythagorean fuzzy weighted averaging (PFWA) operator and the Pythagorean fuzzy weighted geometric (PFWG) operator can be defined as in Equations (2) and (3), respectively [30]. Definition 3. Let A and B be PFSs of X = {x1, x2, … xn} [27]. Then, the sum of A and B is defined as Equation (4). The product of A and B is defined as Equation (5). 2.2. Introduction of TOPSIS Method
The TOPSIS method was developed by Hwang [
31], first put forward in 1981, and is a method of ranking according to the closeness of a limited number of evaluation objects to the ideal target. After years of development, dozens of derivative methods have been created by combining various mathematical theories, and have been widely used in various fields such as economic, management, engineering, medicine, etc. Its core ideas and steps are as follows [
32]:
- (1)
Quantification of evaluation indicators, converting natural language into numbers, and ensuring a certain distinction between good and bad, D is the evaluation objective and X is the evaluation index. The characteristic matrix is defined as Equation (6).
- (2)
Normalize the characteristic matrix, obtain the normalized vector rij and establish the normalized matrix about the normalized vector. This is defined as Equation (7).
- (3)
Normalize the value vij by calculating the weight; weight normalization matrix is defined as Equation (8).
- (4)
Determine ideal solution A+ and anti-ideal solution A−; in the ideal solution and anti-ideal solution, J1 is the optimal value of profitability index set expressed on the i index; J2 is the worst value of the i index of the loss index set. A+ and A− are defined as Equations (9) and (10).
- (5)
Calculate the distance S+ from the target to the ideal solution A+ and the distance S− from the target to the ideal solution A−. The distances are defined as Equation (11).
- (6)
Calculate the closeness index of the ideal solution. It is defined as Equation (12).
- (7)
Ranking according to the size of the ideal pasting progress.
2.3. Distance Measures and Similarity Measures for PFS
Distance measure for PFSs is a term that describes the difference between PFS. Let A and B be PFSs of X = {x1, x2,…xn} with three parameters μ(x), ν(x) and π(x). Here, some distance measures (DM) are presented for PFSs.
The normalized Hamming distance is defined as Equation (13).
The normalized Euclidean distance is defined as Equation (14).
The normalized Hausdorff distance is defined as Equation (15).
For convenience, the above is called formula
d1,
d2 and
d3, and
d4 is defined as Equation (16).
Like measure distance, similarity distance is also an important parameter between fuzzy sets. Let
f be a monotone decreasing function. Then, the similarity measure between PFSs
A and
B can be defined as Equation (17).
By defining
f, different similarity measures are obtained. Here, some simple methods are introduced. When
f(
x) = 1 −
x, the similarity measure is defined as Equation (18).
When
f(
x) = 1/(1 +
x), the similarity measure is defined as Equation (19).
2.4. PFS–TOPSIS Method for MADM
The Pythagorean fuzzy set has a broader value space than the traditional fuzzy set and can represent uncertain information in more detail. In addition, with better adaptability, the combination with other MADM methods has achieved many successful cases. TOPSIS is a classic evaluation or ranking method. Based on this, this section introduced a TOPSIS method based on the PFS. The detailed procedure is presented in the following:
Step 1: First, determine alternatives, criteria and experts, and also determine the corresponding transformation relationship between natural language and fuzzy numbers.
Step 2: Establish a group decision matrix scored by experts R =
, which can be defined as Equation (20).
This represents PFS formed by
n experts’ evaluation of a certain index of a certain scheme. For convenience, (
μAi(
Cj)
k,
νAi(
Cj)
k,
πAi(
Cj)
k) is represented by (
,
,
). Therefore, the group decision matrix is obtained as Equation (21).
Step 3: Since the knowledge level, experience and focus of each expert are different, the importance of each expert is different, so the weight
σk of each expert should be determined according to certain standards. At the same time, for the evaluation of the same indicator of the same scheme, the individual opinions of all experts need to be aggregated into a general evaluation view, i.e., transforming a PFS
into a Pythagorean fuzzy number
xij = (
μAi(
Cj),
νAi(
Cj),
πAi(
Cj)). For convenience, this is expressed as
xij = (
μij νij πij); this transformation process is realized through the Python fuzzy aggregated averaging (PFWA) operator, which can be defined as Equation (22).
At the same time, the aggregation evaluation matrix can be obtained as Equation (23).
Step 4: All criteria may not have equal importance, so it is necessary to assign weight to indicators. This step is also determined by experts. Let
be a PFN, which is used to indicate the evaluation and scoring of the
j indicator by the
k expert. Different experts’ evaluation and scoring of an indicator also need to be aggregated into a Pythagorean fuzzy number
wj = (
μj νj πj). This process is also implemented through the Python fuzzy aggregated averaging (PFWA) operator as in Equation (24).
At the same time, construct a weight matrix for all indicators W, W= (w1 w2…wm).
Step 5: After the aggregation evaluation matrix and index weight matrix are obtained, the weighted aggregation Python fuzzy decision matrix (PFDM) can be obtained through the multiple operator
RWA = (
xWij)
l×m, where
xWij = (
μWij,
νWij,
πWij), the multiplication operator, is as in Equation (25).
The weighted aggregated PFDM can be constructed as in Equation (26).
Step 6: Let
J1 and
J2 be the collection of benefit-type criteria and cost-type criteria. The Pythagorean fuzzy positive ideal solution (PFPIS)
A+ and the Pythagorean fuzzy negative ideal solution (PFNIS)
A− are as in Equations (27)–(30).
Step 7: After obtaining PFPIS and PFNIS, the next step is to calculate the distance between each scheme and the optimal solution
D (
Ai,
A+) and the worst solution
D (
Ai,
A−). The normalized hamming distance formula is used. Then, the proximity between the alternatives and PFPIS is obtained and the calculation formula is as in Equation (31).
Step 8: According to the calculated closeness, rank each alternative from high to low and select the best one.
4. Discussion
The selection of mining method is very important and complex. In this paper, through a TOPSIS method based on PFS, the MUH is selected as the final scheme among the four mining methods suitable for Suichang Gold Mine. By combining the advantages of PFS which can fully represent fuzzy information with the advantages of TOPSIS ranking science, an ideal result is achieved.
However, due to the importance and particularity of mining method decision making, the above models and calculations cannot fully guarantee the scientific accuracy of the results. In fact, as TOPSIS methods that rank according to the proximity of good and bad solutions, the core influencing factors are the distance between the scheme and the positive and negative ideal solutions, as well as the ranking method. As mentioned above, there are many methods to measure the distance between PFS and each method has its own advantages and disadvantages and the most suitable application [
35,
36,
37,
38]. In terms of sorting, Hadi-Vencheh [
39] believes that the traditional closeness index rank may not be able to produce an optimal alternative, being close to the PIS and far from the NIS. Consequently, they introduced the revised closeness index as Equation (35).
Mahanta [
31] adopted a method of ranking by similarity in their article. It is defined in Equations (29) and (30).
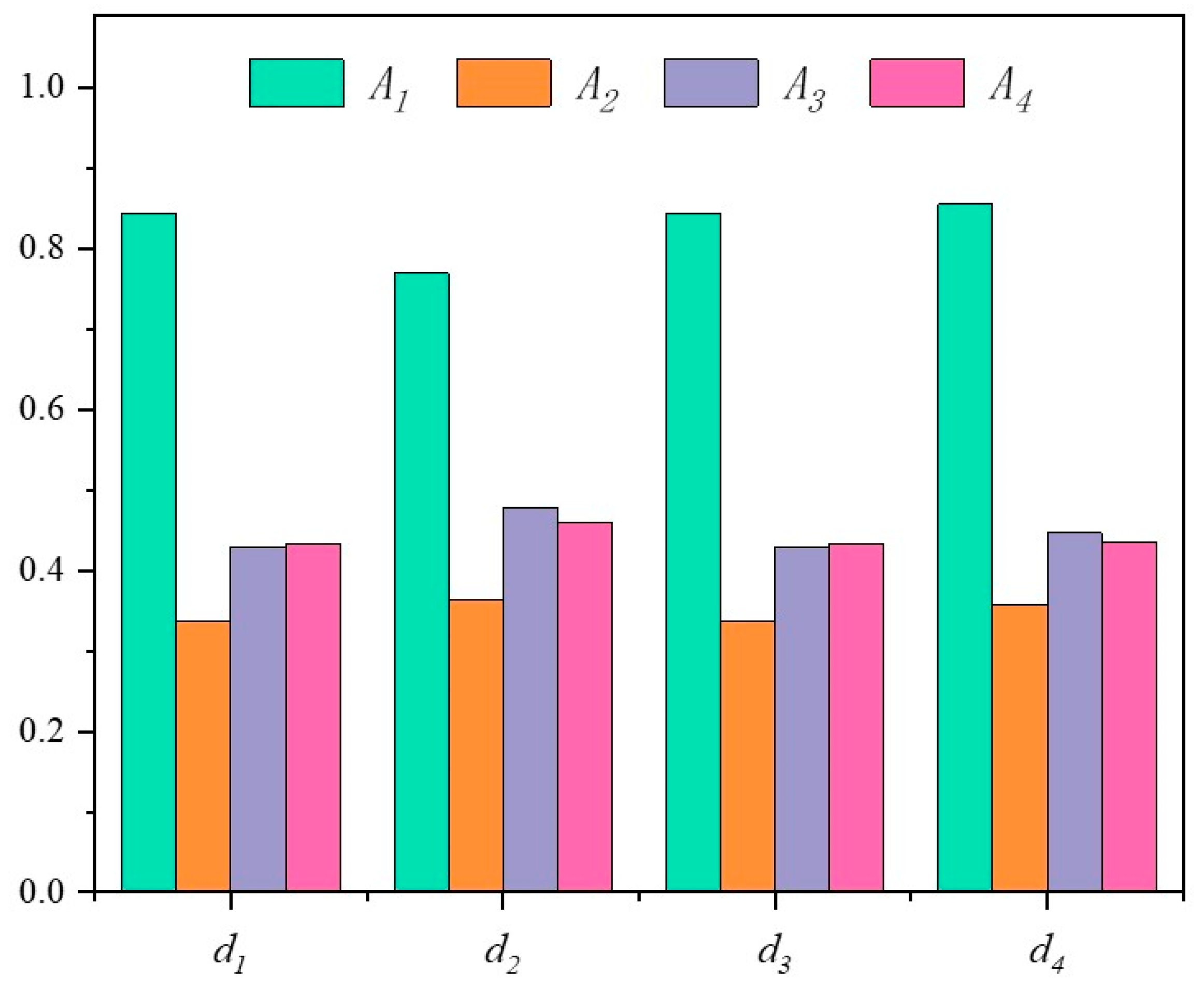
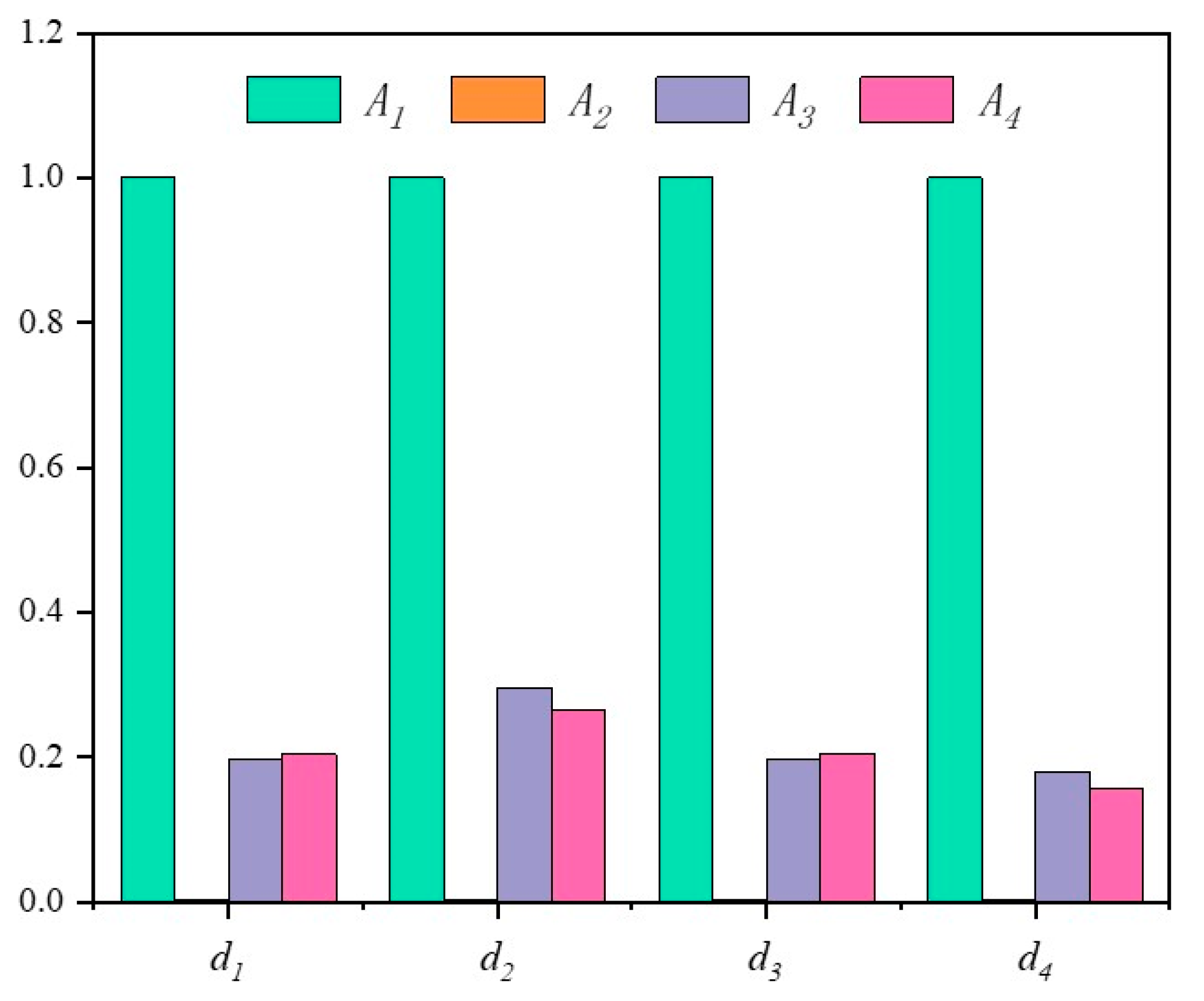
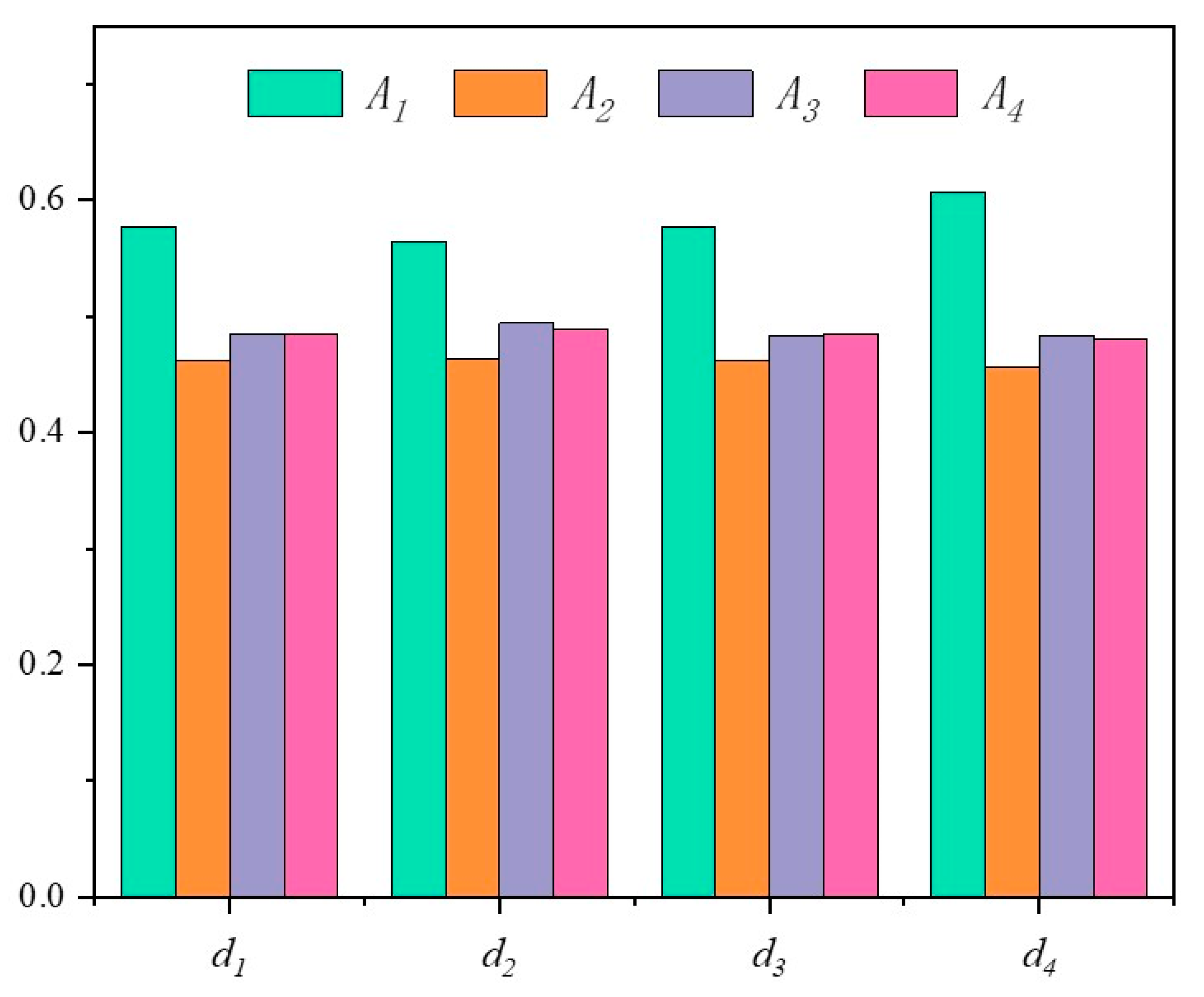
In view of this, the stability of the above results is analyzed through the four distance measures and three ranking methods mentioned above (see
Figure 11,
Figure 12 and
Figure 13), as shown in
Table 8 and
Table 9, and the data in
Figure 12 have been normalized.
It can be seen from the analysis results that the best scheme obtained by changing the distance measures and ranking methods is still the MUH, so it can be considered that the results are accurate. In fact, in the actual production of Suichang Gold Mine, the application of this method has also achieved the ideal results of safety, efficiency and environmental protection.
Whether it can be considered that the model is universal and can be generalized in mining method optimization, the answer is obviously unknown. As is known, the factors that need to be considered in the optimization of mining methods are not completely fuzzy information, e.g., the recovery rate, cut ratio and other factors have certain empirical values. Therefore, the perfect solution is to build a corresponding transformation relationship between the exact value and the PFS and to build a mining method optimization model that combines fuzzy information with accurate data.