Numerical Study on the Influence of Block Physical Characteristics on Landslide Migration Using Three-Dimensional Discontinuous Deformation Analysis
Abstract
:1. Introduction
2. Theory and Methods
2.1. DDA Method
2.2. Contact Detection Scheme
2.3. Method of Determining Contact Points
2.4. Judgment of Block Contact
2.5. Calculation of Normal Force
2.6. Calculation of Shear Force
2.7. Calculation of Frictional Force
2.8. Calculation of Block Rotation
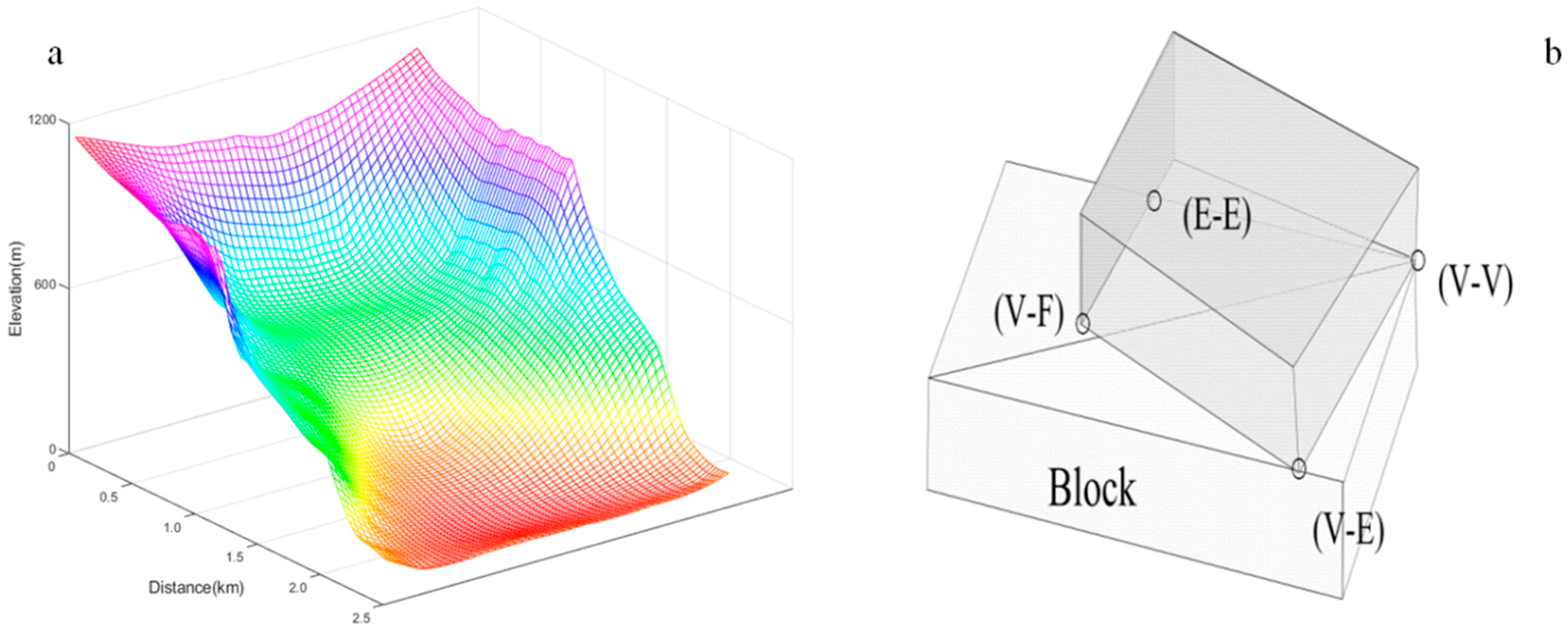
3. Terrain Settings
4. Validation of Parameters
5. Results and Discussion
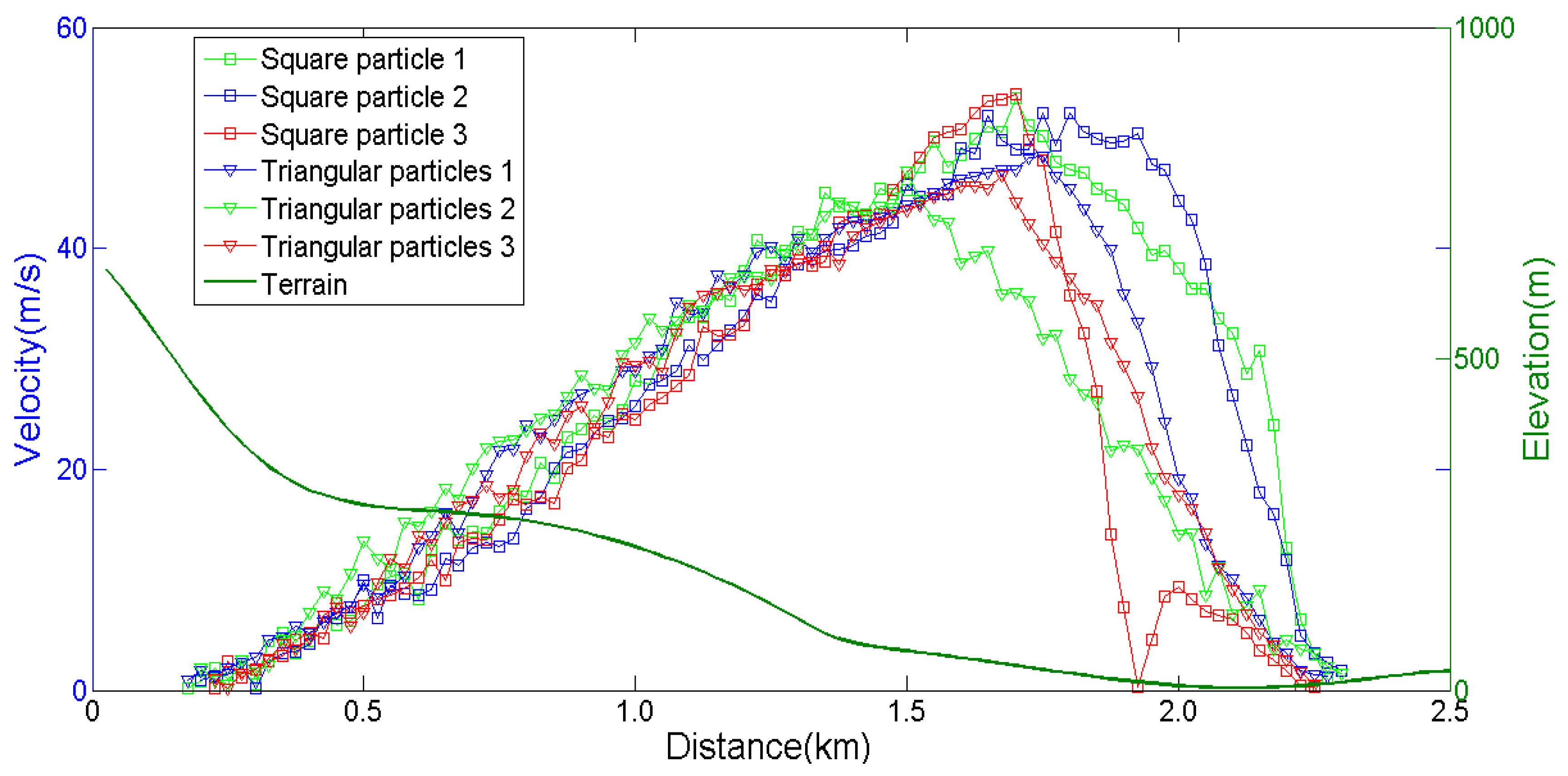
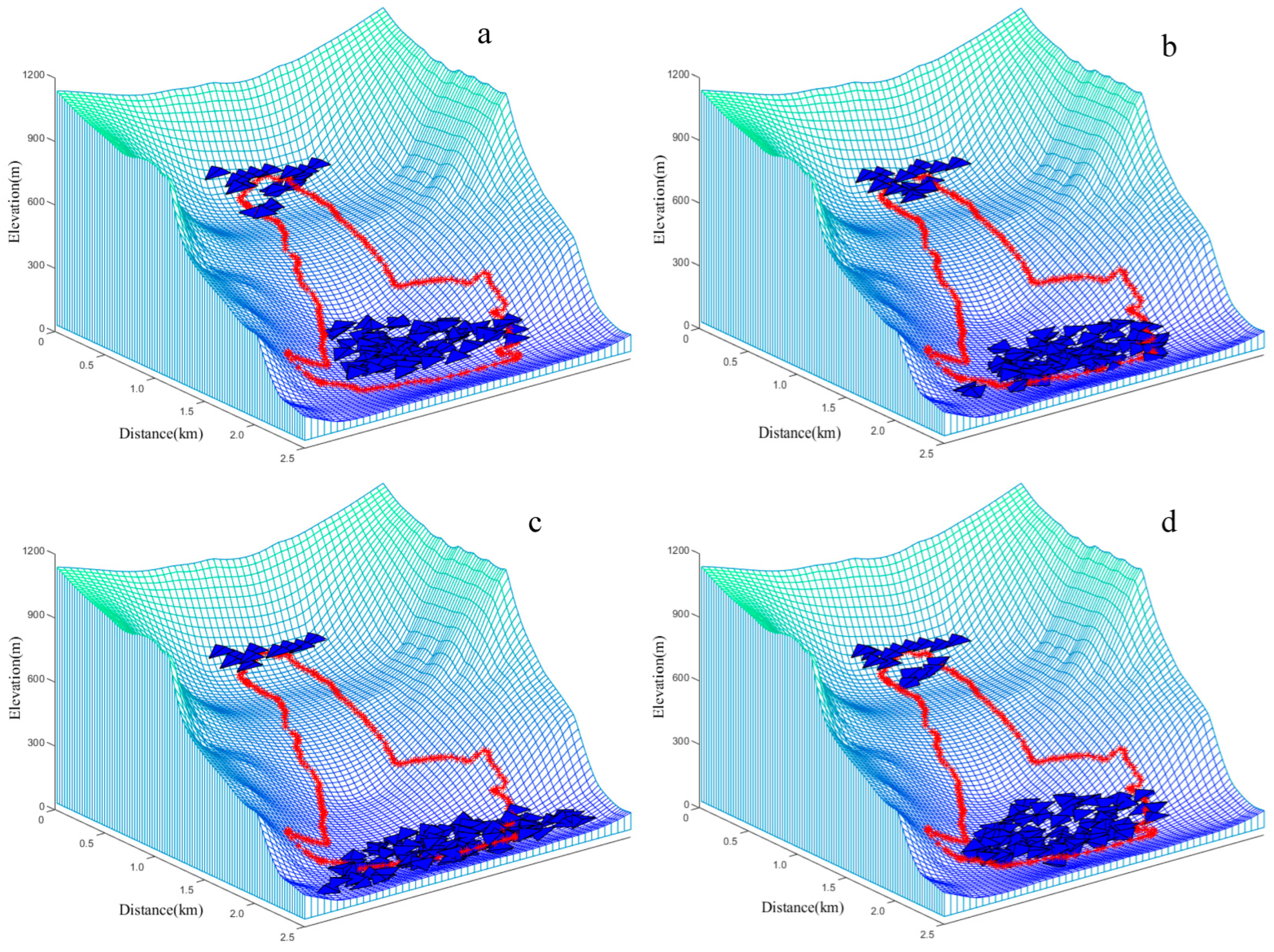
5.1. Results of Analysis
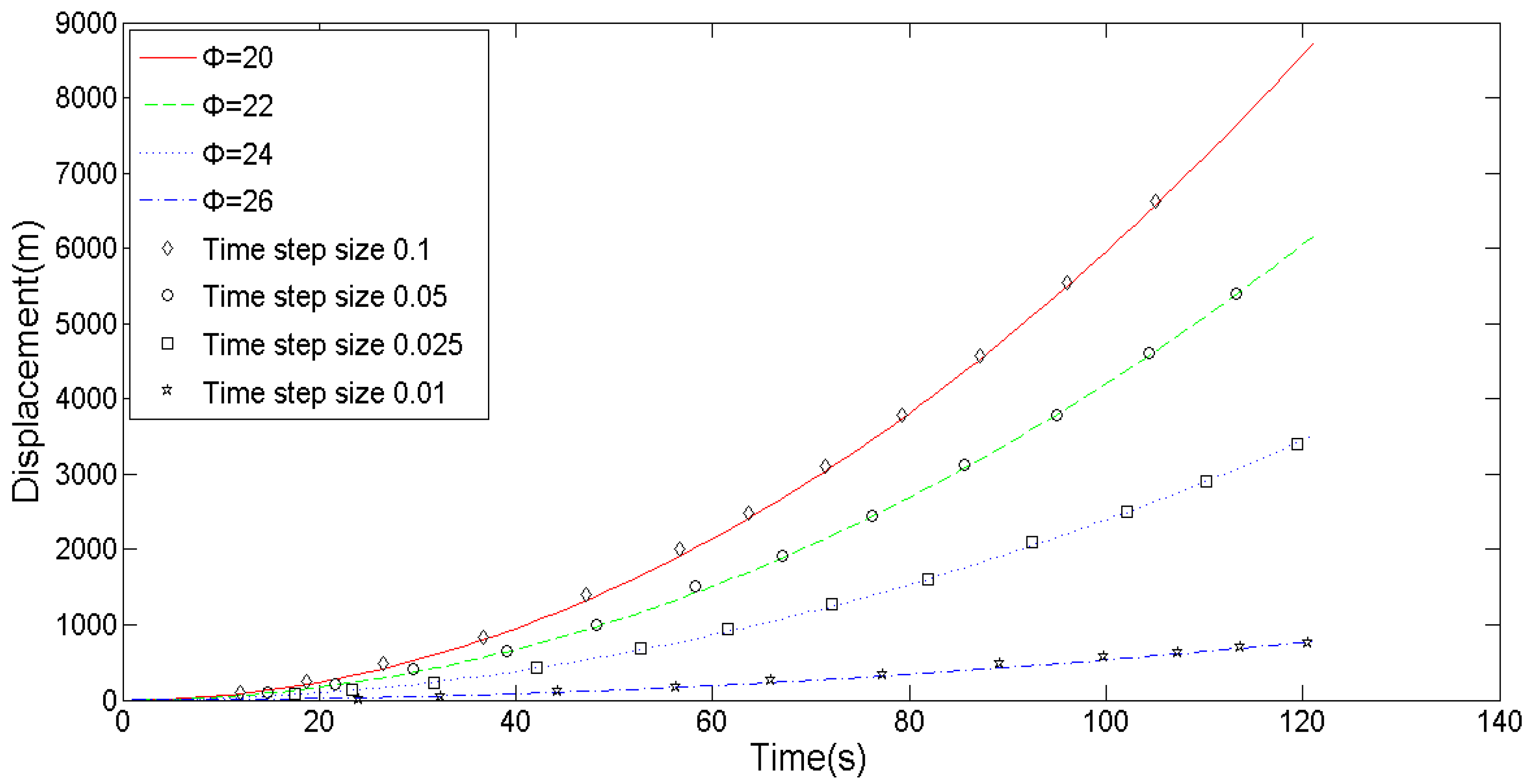
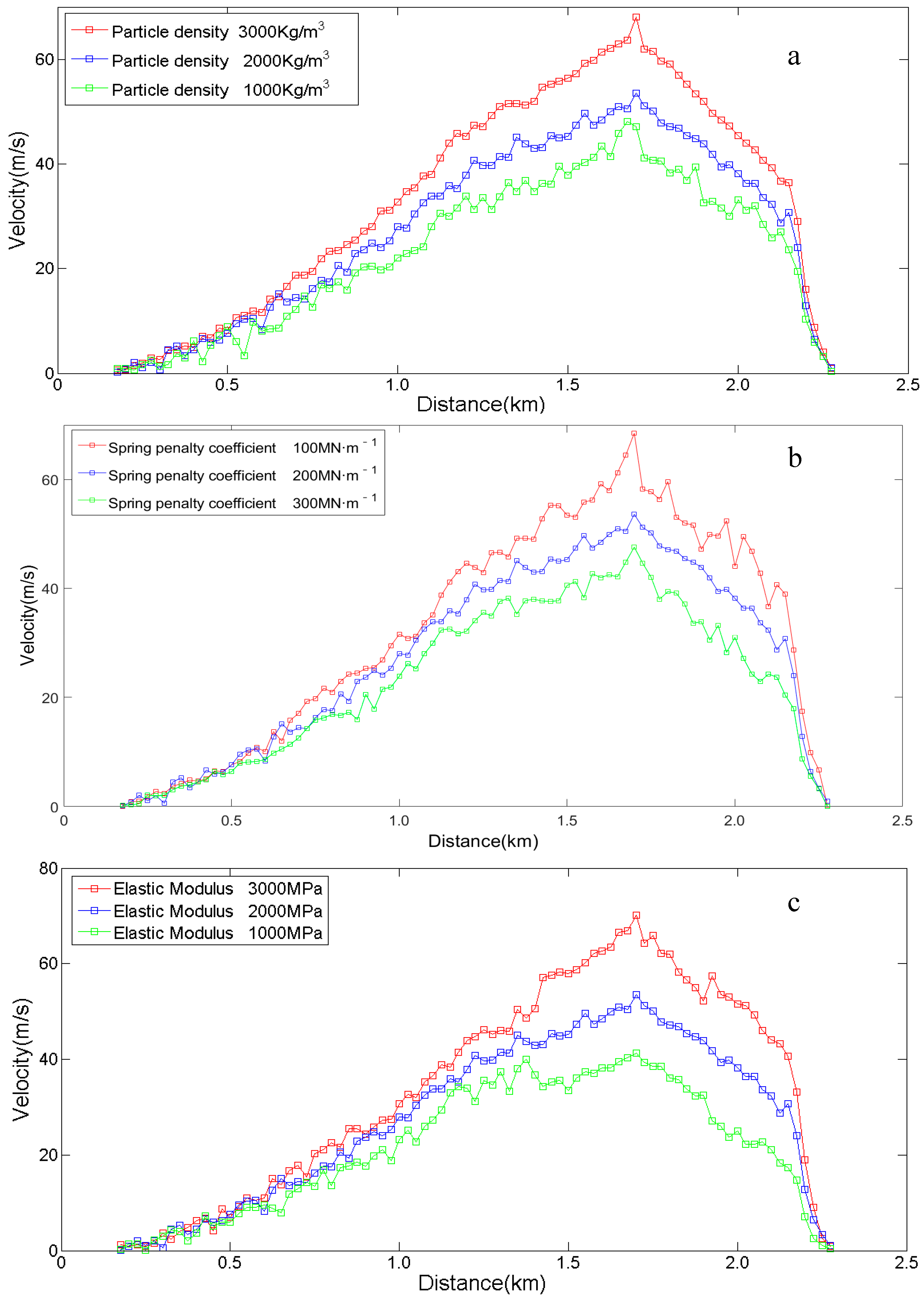
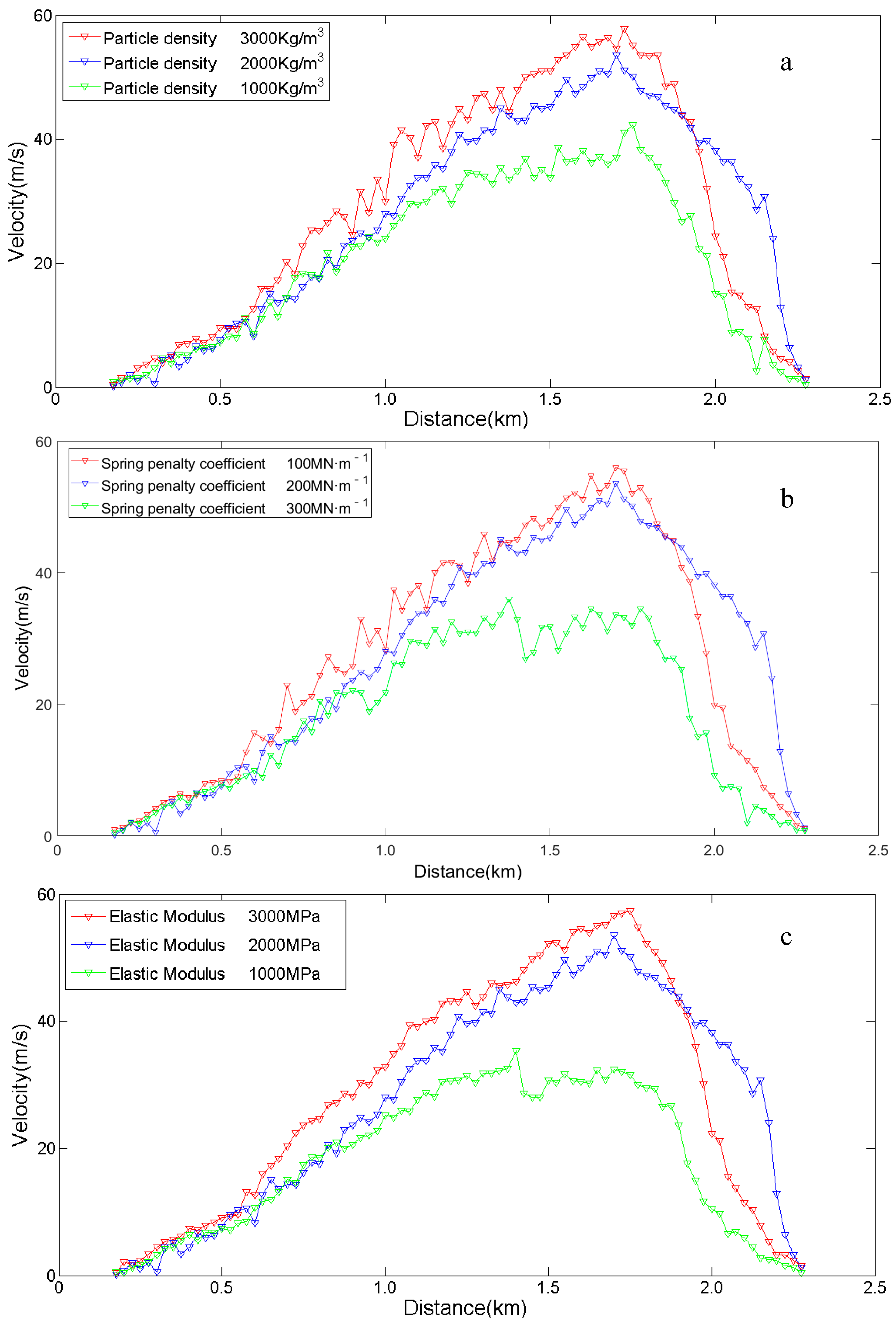
5.2. Sensitivity Analysis of Parameter
5.3. Comparison between Simulation and Measurements
5.4. Implications of Sensitivity Analysis on the Landslide Migration Mechanism
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Cruden, D.M. A simple definition of a landslide. Bull. Int. Assoc. Eng. Geol. 1991, 43, 27–29. [Google Scholar] [CrossRef]
- Revellino, P.; Guadagno, F.M.; Hungr, O. Morphological methods and dynamic modelling in landslide hazard assessment of the Campania Apennine carbonate slope. Landslides 2008, 5, 59–70. [Google Scholar] [CrossRef]
- Zhuang, J.; Peng, J.; Wang, G.; Javed, I.; Wang, Y.; Li, W. Distribution and characteristics of landslide in Loess Plateau: Acasestudy in Shaanxi province. Eng. Geol. 2018, 236, 89–96. [Google Scholar] [CrossRef]
- Xin, P.; Liu, Z.; Wu, S.-R.; Liang, C.; Lin, C. Rotational–translational landslides in the neogene basins at the northeast margin of the Tibetan Plateau. Eng. Geol. 2018, 244, 107–115. [Google Scholar] [CrossRef]
- Song, Z.-C.; Zhao, L.-H.; Li, L.; Zhang, Y.; Tang, G. Distinct Element Modelling of a Landslide Triggered by the 5.12 Wenchuan Earthquake: A Case Study. Geotech. Geol. Eng. 2018, 36, 2533–2551. [Google Scholar] [CrossRef]
- Peres, D.J.; Cancelliere, A. Modeling impacts of climate change on return period of landslide triggering. J. Hydrol. 2018, 567, 420–434. [Google Scholar] [CrossRef]
- Guo, X.; Lai, Z.; Sun, Z.; Li, X.; Yang, T. Luminescence dating of Suozi landslide in the Upper Yellow River of the Qinghai-Tibetan Plateau, China. Quat. Int. 2014, 349, 159–166. [Google Scholar] [CrossRef]
- Fan, X.; Zhan, W.; Dong, X.; van Westen, C.; Xu, Q.; Dai, L.; Yang, Q.; Huang, R.; Havenith, H.-B. Analyzing successive landslide dam formation by different triggering mechanisms: The case of the Tangjiawan landslide, Sichuan, China. Eng. Geol. 2018, 243, 128–144. [Google Scholar] [CrossRef]
- Niu, R.; Wu, X.; Yao, D.; Ling, P.; Li, A.; Peng, J. Susceptibility Assessment of Landslides Triggered by the Lushan Earthquake, April 20, 2013, China. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2017, 7, 3979–3992. [Google Scholar] [CrossRef]
- Li, X. Simulation of the sliding process of Donghekou landslide triggered by the Wenchuan earthquake using a distinct element method. Environ. Earth Sci. 2012, 65, 1049–1054. [Google Scholar] [CrossRef]
- Li, X.; Wu, Y.; He, S.; Su, L. Application of the material point method to simulate the post-failure runout processes of the Wangjiayan landslide. Eng. Geol. 2016, 212, 1–9. [Google Scholar] [CrossRef]
- Zhuang, J.; Peng, J.; Xu, C.; Li, Z.; Densmore, A.; Milledge, D.; Iqbal, J.; Cui, Y. Distribution and characteristics of loess landslides triggered by the 1920 Haiyuan Earthquake, Northwest of China. Geomorphology 2018, 314, 1–12. [Google Scholar] [CrossRef]
- Zhang, Y.S.; Yang, Z.H.; Guo, C.B.; Wang, T.; Wang, D.H.; Guo-Liang, D.U. Predicting landslide scenes under potential earthquake scenarios in the Xianshuihe fault zone, Southwest China. J. Mt. Sci. 2017, 14, 1262–1278. [Google Scholar] [CrossRef]
- Yin, Y.; Li, B.; Wang, W. Dynamic analysis of the stabilized Wangjiayan landslide in the Wenchuan Ms 8.0 earthquake and aftershocks. Landslides 2015, 12, 537–547. [Google Scholar] [CrossRef]
- Yavari-Ramshe, S.; Ataie-Ashtiani, B. Numerical modeling of subaerial and submarine landslide-generated tsunami waves—Recent advances and future challenges. Landslides 2016, 13, 1325–1368. [Google Scholar] [CrossRef]
- Wang, W.; Chen, G.; Zhang, Y.; Zheng, L.; Zhang, H. Dynamic simulation of landslide dam behavior considering kinematic characteristics using a coupled DDA-SPH method. Eng. Anal. Bound. Elements 2017, 80, 172–183. [Google Scholar] [CrossRef]
- Zhang, H.; Liu, S.-G.; Zheng, L.; Zhong, G.-H.; Lou, S.; Wu, Y.-Q.; Han, Z. Extensions of edge-to-edge contact model in three-dimensional discontinuous deformation analysis for friction analysis. Comput. Geotech. 2016, 71, 261–275. [Google Scholar] [CrossRef]
- Asteriou, P.; Saroglou, H.; Tsiambaos, G. Geotechnical and kinematic parameters affecting the coefficients of restitution for rock fall analysis. Int. J. Rock Mech. Min. Sci. 2012, 54, 103–113. [Google Scholar] [CrossRef]
- Kawanami, S.A. The effects of rockfall volume on runout distance. Eng. Geol. 2000, 58, 109–124. [Google Scholar]
- Spadari, M.; Giacomini, A.; Buzzi, O.; Fityus, S.; Giani, G.P. In situ rockfall testing in New South Wales, Australia. Int. J. Rock Mech. Min. Sci. 2012, 49, 84–93. [Google Scholar] [CrossRef]
- Chau, K.T.; Wong, R.H.C.; Wu, J.J. Coefficient of restitution and rotational motions of rockfall impacts. Int. J. Rock Mech. Min. Sci. 2002, 39, 69–77. [Google Scholar] [CrossRef]
- Manzella, I.; Labiouse, V. Flow experiments with gravel and blocks at small scale to investigate parameters and mechanisms involved in rock avalanches. Eng. Geol. 2009, 109, 146–158. [Google Scholar] [CrossRef]
- Haddad, F.; Chikouche, A.; Laour, M. Simulation of the opti-physical parameters of selectives surfaces of absorber by the FDTD method. «applied to solar water heater». Energy Procedia 2011, 6, 413–421. [Google Scholar] [CrossRef]
- Fan, H.; He, S. An Angle-Based Method Dealing with Vertex–Vertex Contact in the Two-Dimensional Discontinuous Deformation Analysis (DDA). Rock Mech. Rock Eng. 2015, 48, 2031–2043. [Google Scholar] [CrossRef]
- Thomas, A.V.; Saha, S.; Danumah, J.H.; Raveendran, S.; Prasad, M.K.; Ajin, R.S.; Kuriakose, S.L. Landslide Susceptibility Zonation of Idukki District Using GIS in the Aftermath of 2018 Kerala Floods and Landslides: A Comparison of AHP and Frequency Ratio Methods. J. Geovis. Spat. Anal. 2021, 5, 1–27. [Google Scholar] [CrossRef]
- Bickel, V.T.; Manconi, A. Decadal Surface Changes and Displacements in Switzerland. J. Geovis. Spat. Anal. 2022, 6, 1–9. [Google Scholar] [CrossRef]
- Pancholi, V.; Bhatt, N.; Singh, P.; Chopra, S. Multi-criteria approach using GIS for macro-level seismic hazard assessment of Kachchh Rift Basin, Gujarat, western India—First step towards earthquake disaster mitigation. J. Earth Syst. Sci. 2021, 131, 1–20. [Google Scholar] [CrossRef]
- Fang, H.; Shao, Y.; Xie, C.; Tian, B.; Zhu, Y.; Guo, Y.; Yang, Q.; Yang, Y. Using Persistent Scatterer Interferometry for Post-Earthquake Landslide Susceptibility Mapping in Jiuzhaigou. Appl. Sci. 2022, 12, 9228. [Google Scholar] [CrossRef]
- Desalegn, H.; Mulu, A.; Damtew, B. Landslide susceptibility evaluation in the Chemoga watershed, upper Blue Nile, Ethiopia. Nat. Hazards 2022, 113, 1391–1417. [Google Scholar] [CrossRef]
- Zhao, Z.; Liu, Z.Y.; Xu, C. Slope unit-based landslide susceptibility mapping using certainty factor (CF), support vector machine (SVM), random forest (RF), CF-SVM and CF-RF models. Front. Earth Sci. 2021, 9, 589630. [Google Scholar] [CrossRef]
- Yang, Q.; Cai, F.; Su, Z.; Ugai, K.; Xu, L.; Huang, R.; Xu, Q. Numerical Simulation of Granular Flows in a Large Flume Using Discontinuous Deformation Analysis. Rock Mech. Rock Eng. 2014, 47, 2299–2306. [Google Scholar] [CrossRef]
- Wang, L.; Jiao, Y.; Huang, G.; Zheng, F.; Zhao, Z.; Tan, F. Improvement of contact calculation in spherical discontinuous deformation analysis. Sci. China Technol. Sci. 2017, 60, 765–771. [Google Scholar] [CrossRef]
- Ning, Y.-J.; An, X.-M.; Lü, Q.; Ma, G.-W. Modeling rock failure using the numerical manifold method followed by the discontinuous deformation analysis. Acta Mech. Sin. 2012, 28, 760–773. [Google Scholar] [CrossRef]
- Liu, J.; Nan, Z.; Yi, P. Validation and application of three-dimensional discontinuous deformation analysis with tetrahedron finite element meshed block. Acta Mech. Sin. 2012, 28, 1602–1616. [Google Scholar] [CrossRef]
- Shi, G.H. Discontinuous deformation analysis: A new numerical model for the statics and dynamics of deformable block structures. Eng. Comput. 1992, 9, 157–168. [Google Scholar] [CrossRef]
- Shi, G.H. Block System Modeling by Discontinuous Deformation Analysis; Computational Mechanics Publications: Southampton, UK, 1993. [Google Scholar]
- Wu, J.H. Applying discontinuous deformation analysis to assess the constrained area of the unstable Chiu-fen-erh-shan landslide slope. Int. J. Numer. Anal. Methods Geomech. 2007, 31, 649–660. [Google Scholar] [CrossRef]
- Wu, J.H. Seismic landslide simulations in discontinuous deformation analysis. Comput. Geotech. 2010, 37, 594–601. [Google Scholar] [CrossRef]
- Ma, G.; Matsuyama, H.; Nishiyama, S.; Ohnishi, Y. Practical studies on rockfall simulation by DDA. J. Rock Mech. Geotech. Eng. 2011, 3, 57–63. [Google Scholar] [CrossRef]
- Chen, K.T.; Wu, J.H. Simulating the failure process of the Xinmo landslide using discontinuous deformation analysis. Eng. Geol. 2018, 239, 269–281. [Google Scholar] [CrossRef]
- Zhang, H.; Liu, S.G.; Han, Z.; Zheng, L.; Zhang, Y.B.; Wu, Y.Q.; Li, Y.G.; Wang, W. A new algorithm to identify contact types between arbitrarily shaped polyhedral blocks for three-dimensional discontinuous deformation analysis. Comput. Geotech. 2016, 80, 1–15. [Google Scholar] [CrossRef]
- Nie, W.; Zhao, Z.Y.; Ning, Y.J.; Sun, J.P. Development of Rock Bolt Elements in Two-Dimensional Discontinuous Deformation Analysis. Rock Mech. Rock Eng. 2014, 47, 2157–2170. [Google Scholar] [CrossRef]
- Wang, W.; Zhang, H.; Zheng, L.; Zhang, Y.-B.; Wu, Y.-Q.; Liu, S.-G. A new approach for modeling landslide movement over 3D topography using 3D discontinuous deformation analysis. Comput. Geotech. 2017, 81, 87–97. [Google Scholar] [CrossRef]
- Zhang, H.; Chen, G.; Zheng, L.; Han, Z.; Zhang, Y.; Wu, Y.; Liu, S. Detection of contacts between three-dimensional polyhedral blocks for discontinuous deformation analysis. Int. J. Rock Mech. Min. Sci. 2015, 78, 57–73. [Google Scholar] [CrossRef]
- Peng, X.; Yu, P.; Chen, G.; Xia, M.; Zhang, Y. Development of a Coupled DDA–SPH Method and its Application to Dynamic Simulation of Landslides Involving Solid–Fluid Interaction. Rock Mech. Rock Eng. 2019, 53, 113–131. [Google Scholar] [CrossRef]
- Hwang, J.Y.; Ohnishi, Y.; Wu, J. Numerical analysis of discontinuous rock masses using three-dimensional discontinuous deformation analysis (3D DDA). KSCE J. Civ. Eng. 2004, 8, 491–496. [Google Scholar] [CrossRef]
- Grayeli, R.; Hatami, K. Implementation of the finite element method in the three-dimensional discontinuous deformation analysis (3D-DDA). Int. J. Numer. Anal. Methods Géoméch. 2010, 32, 1883–1902. [Google Scholar] [CrossRef]
- Zhu, H.; Wu, W.; Chen, J.; Ma, G.; Liu, X.; Zhuang, X. Integration of three dimensional discontinuous deformation analysis (DDA) with binocular photogrammetry for stability analysis of tunnels in blocky rockmass. Tunn. Undergr. Space Technol. 2016, 51, 30–40. [Google Scholar] [CrossRef]
- Jiang, Q.H.; Yeung, M.R. A model of point-to-face contact for three-dimensional discontinuous deformation analysis. Rock Mech. Rock Eng. 2004, 37, 95–116. [Google Scholar] [CrossRef]
- Nezami, E.G.; Hashash, Y.M.A.; Zhao, D.; Ghaboussi, J. Shortest link method for contact detection in discrete element method. Int. J. Numer. Anal. Methods Geomech. 2010, 30, 783–801. [Google Scholar] [CrossRef]
- Beyabanaki, S.A.R.; Mikola, R.G.; Biabanaki, S.O.R.; Mohammadi, S. New point-to-face contact algorithm for 3-D contact problems using the augmented Lagrangian method in 3-D DDA. Geomech. Geoengin. 2009, 4, 221–236. [Google Scholar] [CrossRef]
- Ran, Q.; Hong, Y.; Li, W.; Gao, J. A modelling study of rainfall-induced shallow landslide mechanisms under different rainfall characteristics. J. Hydrol. 2018, 563, 790–801. [Google Scholar] [CrossRef]
- Yueping, Y.; Wenpei, W.; Nan, Z.; Jingkai, Y.; Yunjie, W.; Longwei, Y. Long runout geological disaster initiated by the ridge-top rockslide in a strong earthquake area: A case study of the Xinmo landslide in Maoxian County, Sichuan Province. Geol. China 2017, 44, 827–841. [Google Scholar]
- Zhang, Y.; Wang, J.; Xu, Q.; Chen, G.; Zhao, J.X.; Zheng, L.; Han, Z.; Yu, P. DDA validation of the mobility of earthquake-induced landslides. Eng. Geol. 2015, 194, 38–51. [Google Scholar] [CrossRef]
- Kamai, R.; Hatzor, Y.H. Numerical analysis of block stone displacements in ancient masonry structures: A new method to estimate historic ground motions. Int. J. Numer. Anal. Methods Géoméch. 2008, 32, 1321–1340. [Google Scholar] [CrossRef]
- Wu, J.-H. The elastic distortion problem with large rotation in discontinuous deformation analysis. Comput. Geotech. 2015, 69, 352–364. [Google Scholar] [CrossRef]
- Tao, Z.; Zhihua, Y.; Yongshuang, Z.; Liang, C.; Ruian, W. An analysis of the entrainment of the Xinmo high-position landslide in Maoxian county, Sichuan. Hydrogeol. Eng. Geol. 2019, 46, 138–145. [Google Scholar]
- Yang, B.; Yin, K.; Lacasse, S.; Liu, Z. Time series analysis and long short-term memory neural network to predict landslide displacement. Landslides 2019, 16, 677–694. [Google Scholar] [CrossRef]
- Juliev, M.; Mergili, M.; Mondal, I.; Nurtaev, B.; Pulatov, A.; Hübl, J. Comparative analysis of statistical methods for landslide susceptibility mapping in the Bostanlik District, Uzbekistan. Sci. Total Environ. 2019, 653, 801–814. [Google Scholar] [CrossRef]
- Palis, E.; Lebourg, T.; Tric, E.; Malet, J.-P.; Vidal, M. Long-term monitoring of a large deep-seated landslide (La Clapiere, South-East French Alps): Initial study. Landslides 2017, 14, 155–170. [Google Scholar] [CrossRef]
- Song, Y.; Huang, D.; Cen, D. Numerical modelling of the 2008 Wenchuan earthquake-triggered Daguangbao landslide using a velocity and displacement dependent friction law. Eng. Geol. 2016, 215, 50–68. [Google Scholar] [CrossRef]


Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wu, Z.; Zhang, H. Numerical Study on the Influence of Block Physical Characteristics on Landslide Migration Using Three-Dimensional Discontinuous Deformation Analysis. Sustainability 2023, 15, 3463. https://doi.org/10.3390/su15043463
Wu Z, Zhang H. Numerical Study on the Influence of Block Physical Characteristics on Landslide Migration Using Three-Dimensional Discontinuous Deformation Analysis. Sustainability. 2023; 15(4):3463. https://doi.org/10.3390/su15043463
Chicago/Turabian StyleWu, Zhen, and Huiwen Zhang. 2023. "Numerical Study on the Influence of Block Physical Characteristics on Landslide Migration Using Three-Dimensional Discontinuous Deformation Analysis" Sustainability 15, no. 4: 3463. https://doi.org/10.3390/su15043463
APA StyleWu, Z., & Zhang, H. (2023). Numerical Study on the Influence of Block Physical Characteristics on Landslide Migration Using Three-Dimensional Discontinuous Deformation Analysis. Sustainability, 15(4), 3463. https://doi.org/10.3390/su15043463




