State of Health Estimation of Lithium-Ion Batteries in Electric Vehicles Based on Regional Capacity and LGBM
Abstract
1. Introduction
- (1)
- A novel indicator, namely regional capacity, has been proposed in this paper as a benchmark of SOH estimation which has high flexibility and applicability.
- (2)
- Model inputs, including accumulated mileage, average charging current, average charging temperature, and start and end SOC values are easily accessible from sparse and discontinuous real-world EV operation data, leading to better feasibility.
- (3)
- The method’s effectiveness, complexity, superiority, and robustness over existing algorithms have been verified through real-world operation data collected from EVs. The proposed method can achieve accurate SOH estimation with MAPE and RMSE at only 2.049% and 1.153%, respectively.
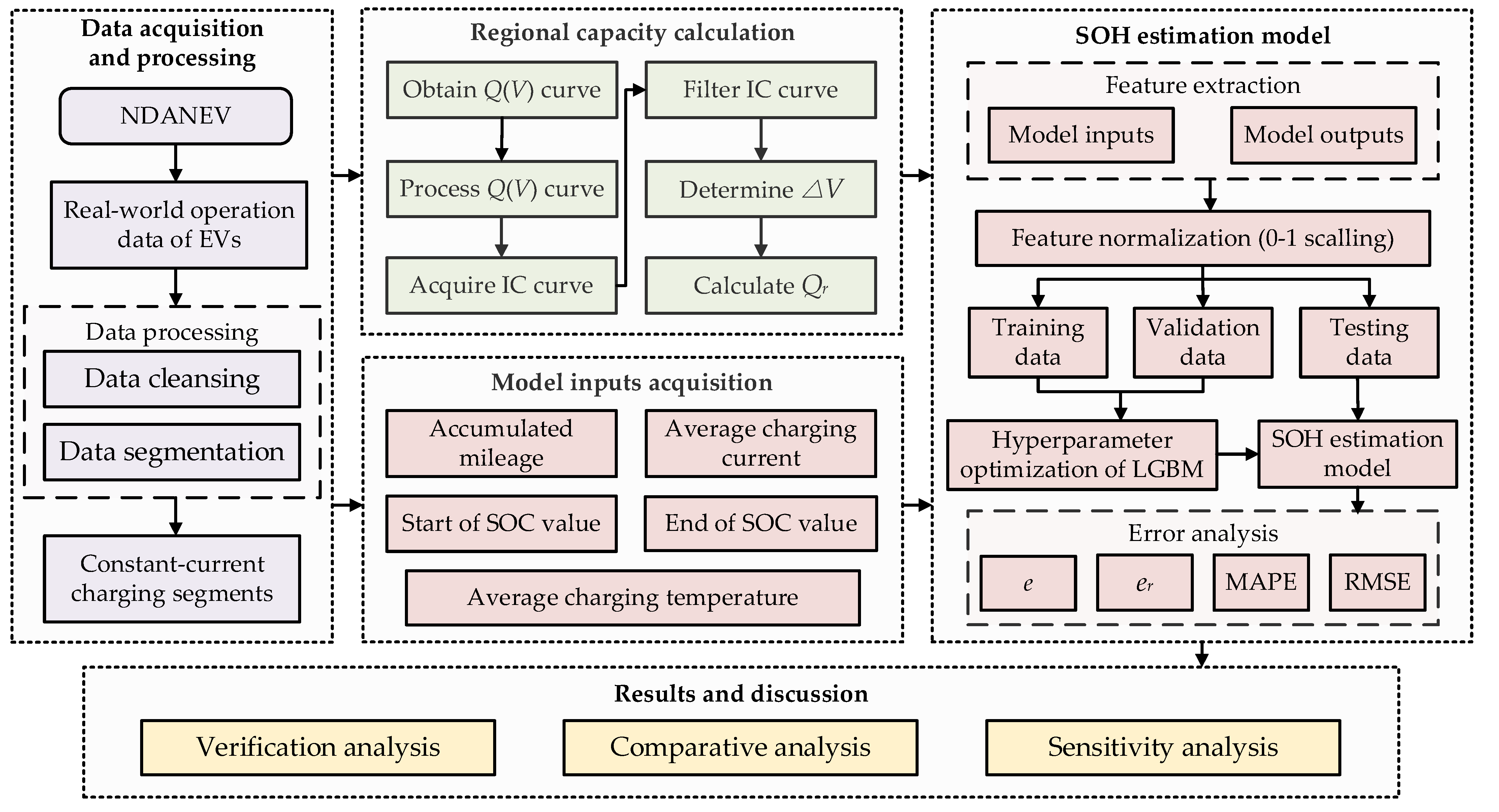
2. Framework
3. Data Acquisition and Processing
3.1. Data Acquisition
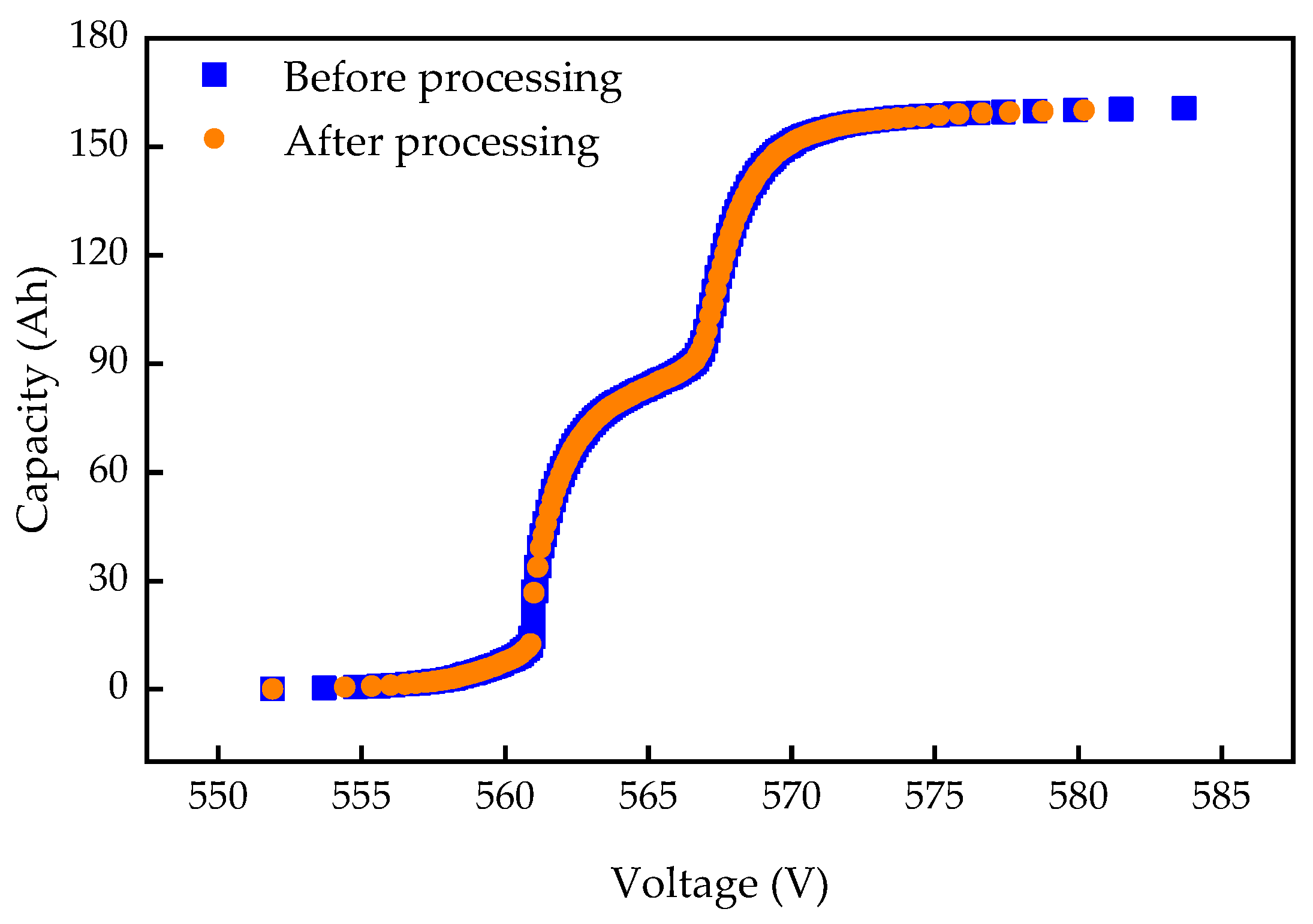
3.2. Data Processing
4. Methodology
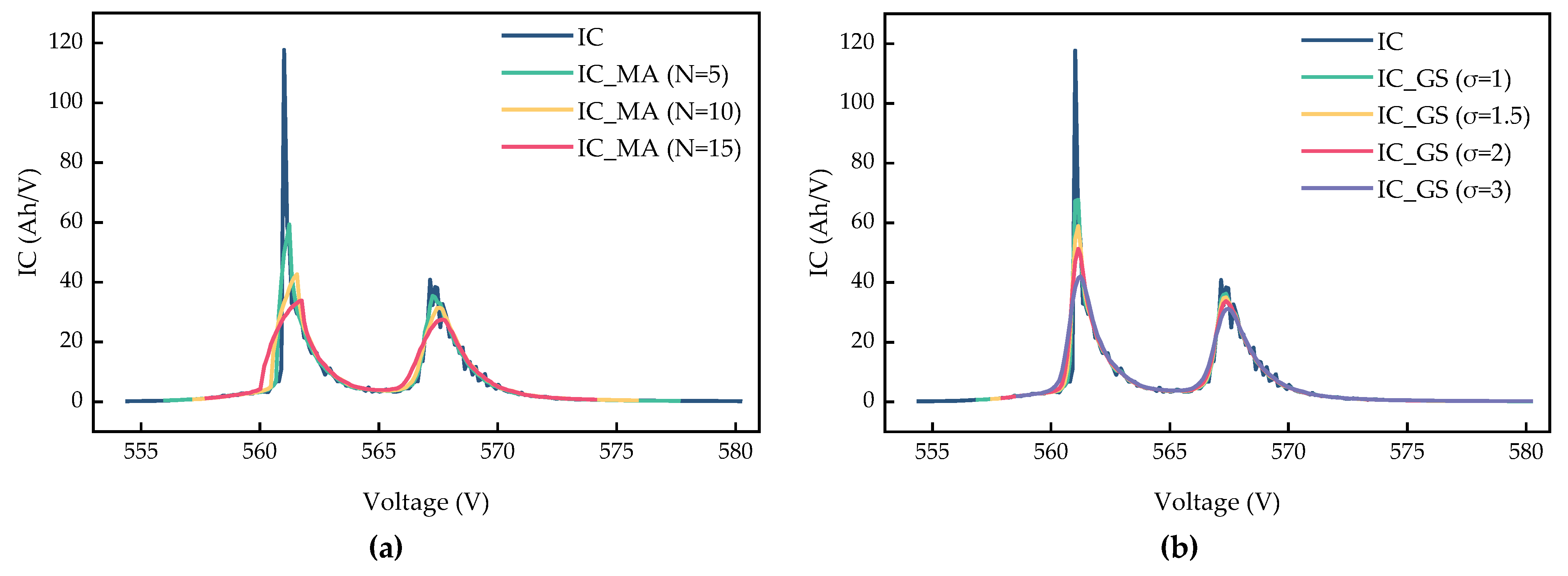
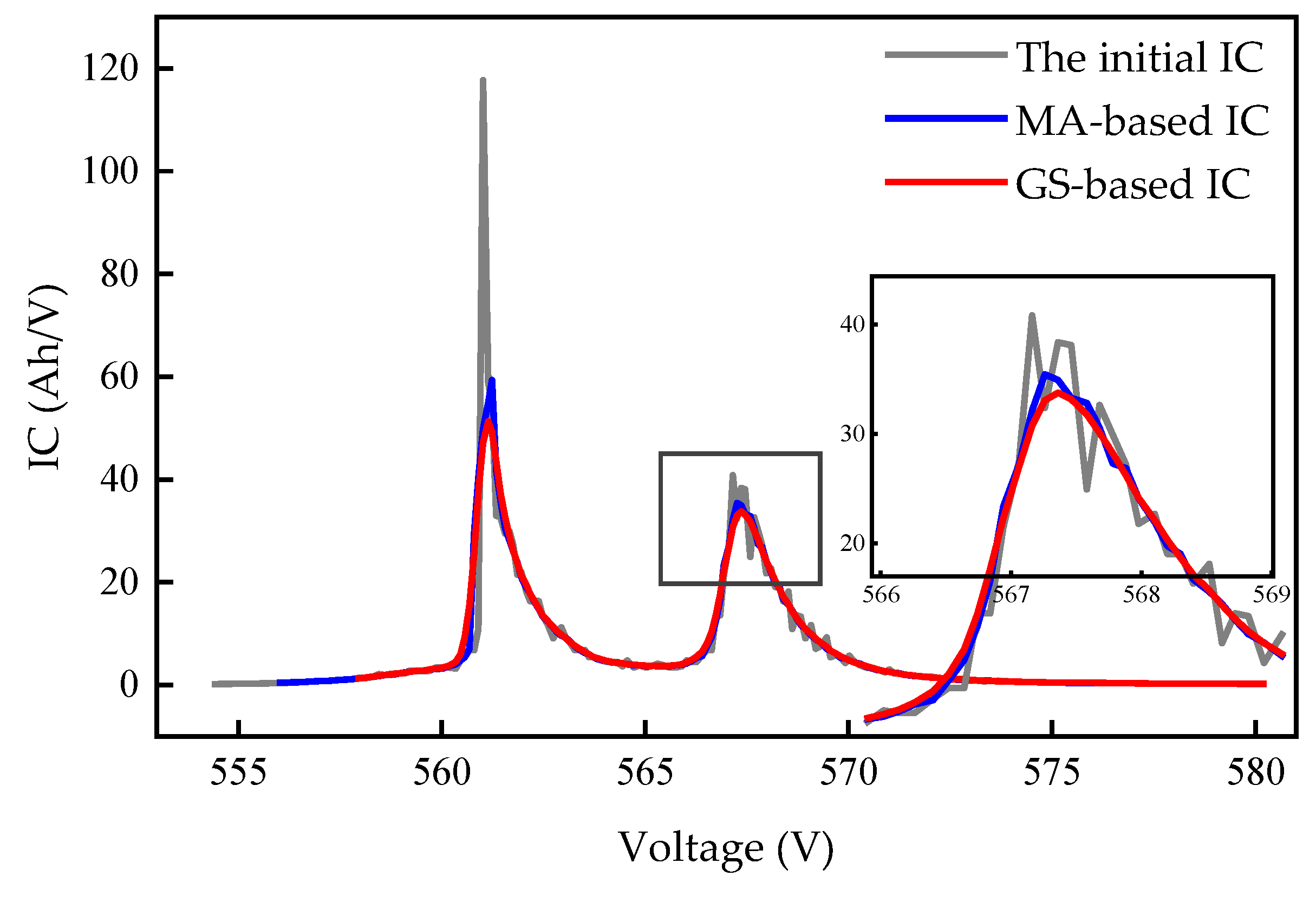
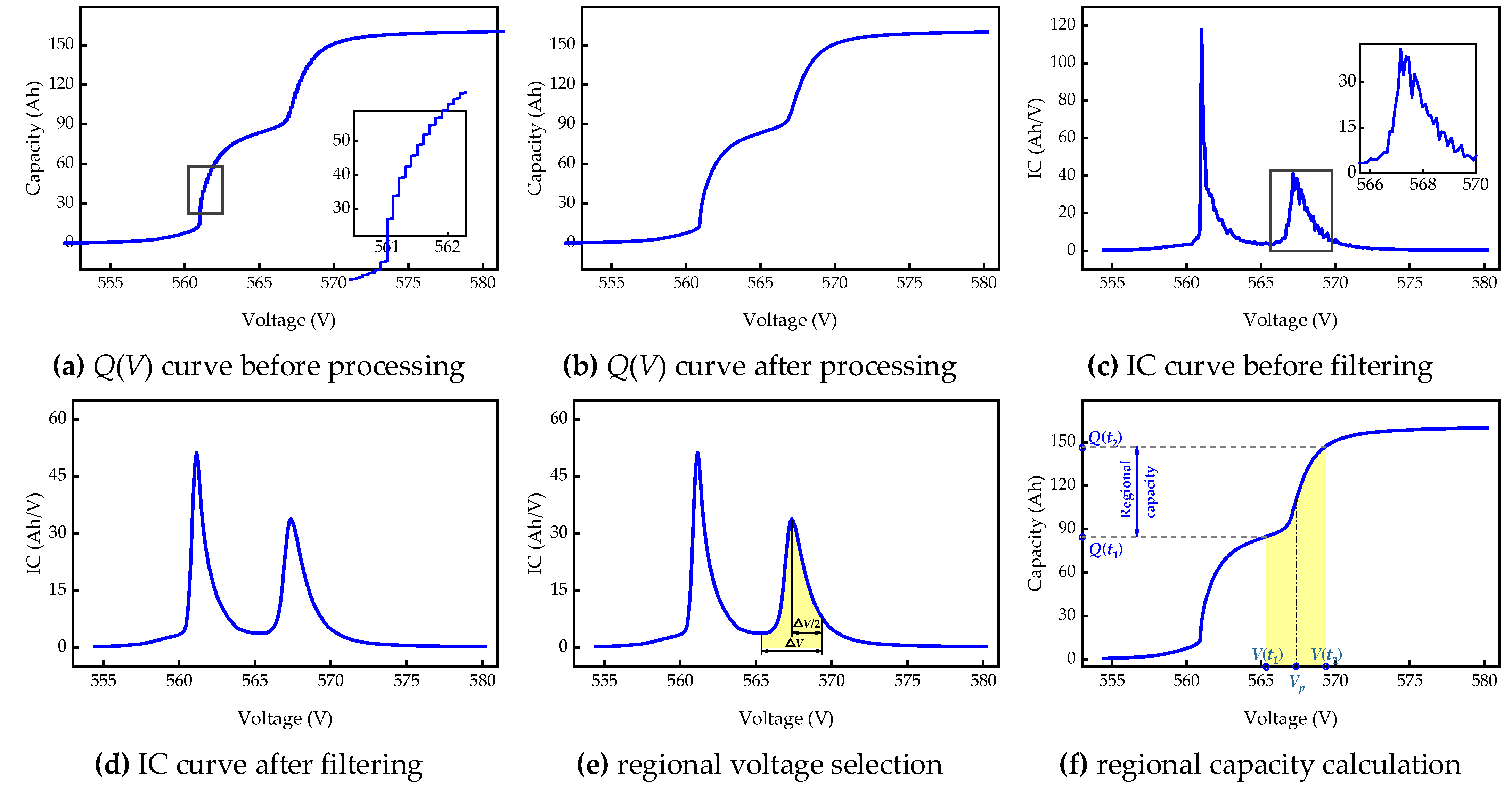
4.1. Incremental Capacity Curve Derivation Methods
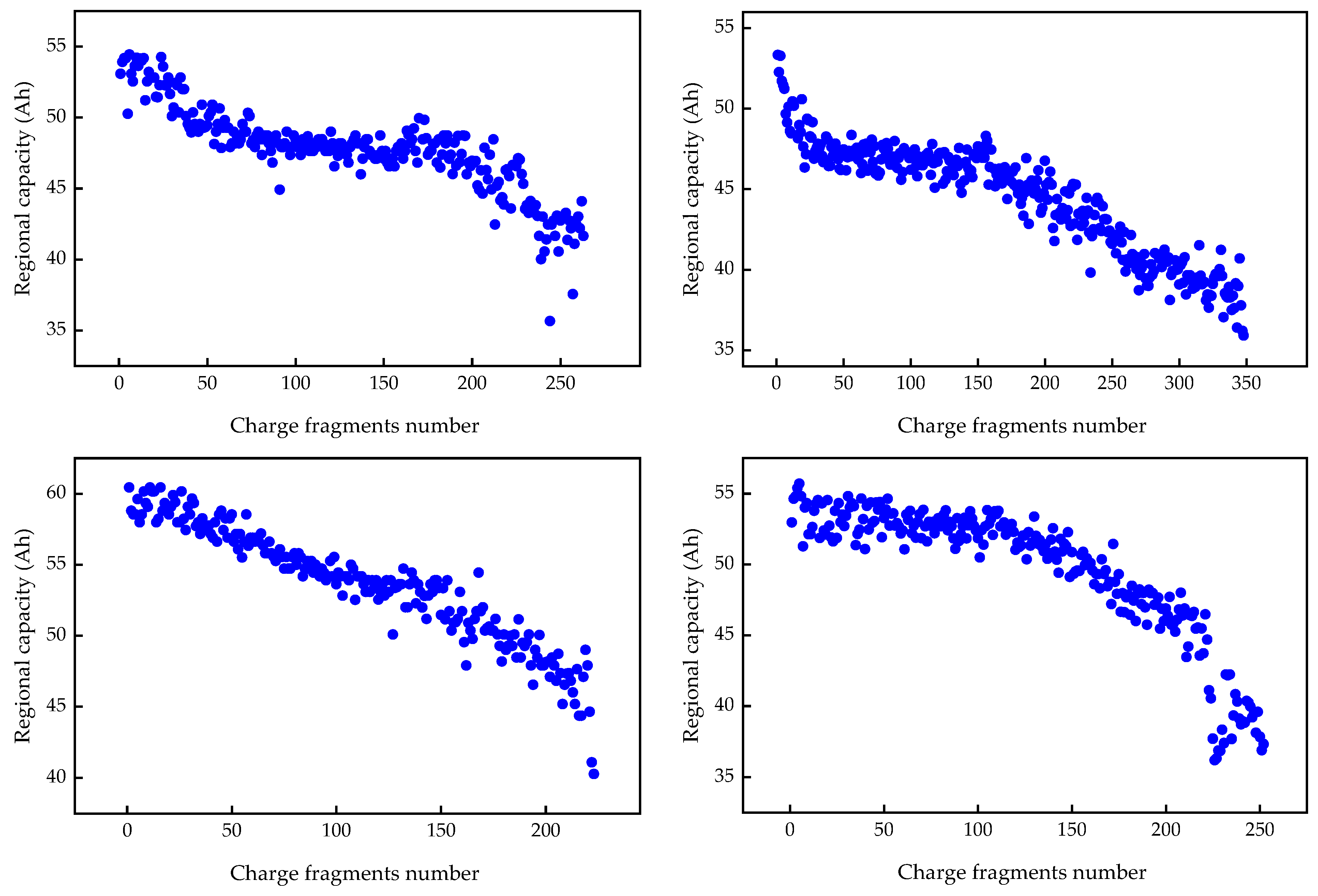
4.2. Regional Capacity Calculation
- Step 1: Obtain the charging curve Q(V). Suitable charging segments are selected based on certain constrains. Then, the charging curve Q(V) is obtained through calculation.
- Step 2: The monotonically increasing charging curve Q(V) is extracted to facilitate subsequent IC curve calculation.
- Step 3: The initial IC curve is calculated through numerical derivative methods.
- Step 4: A Gaussian smoothing filter method with a value of 2 is applied to smooth the calculated IC curve.
- Step 5: The regional voltage V is determined, whose middle point corresponds to the IC peak. In this work, we choose a regional voltage of 4 V to cover the second IC peak.
- Step 6: Calculate the regional capacity .
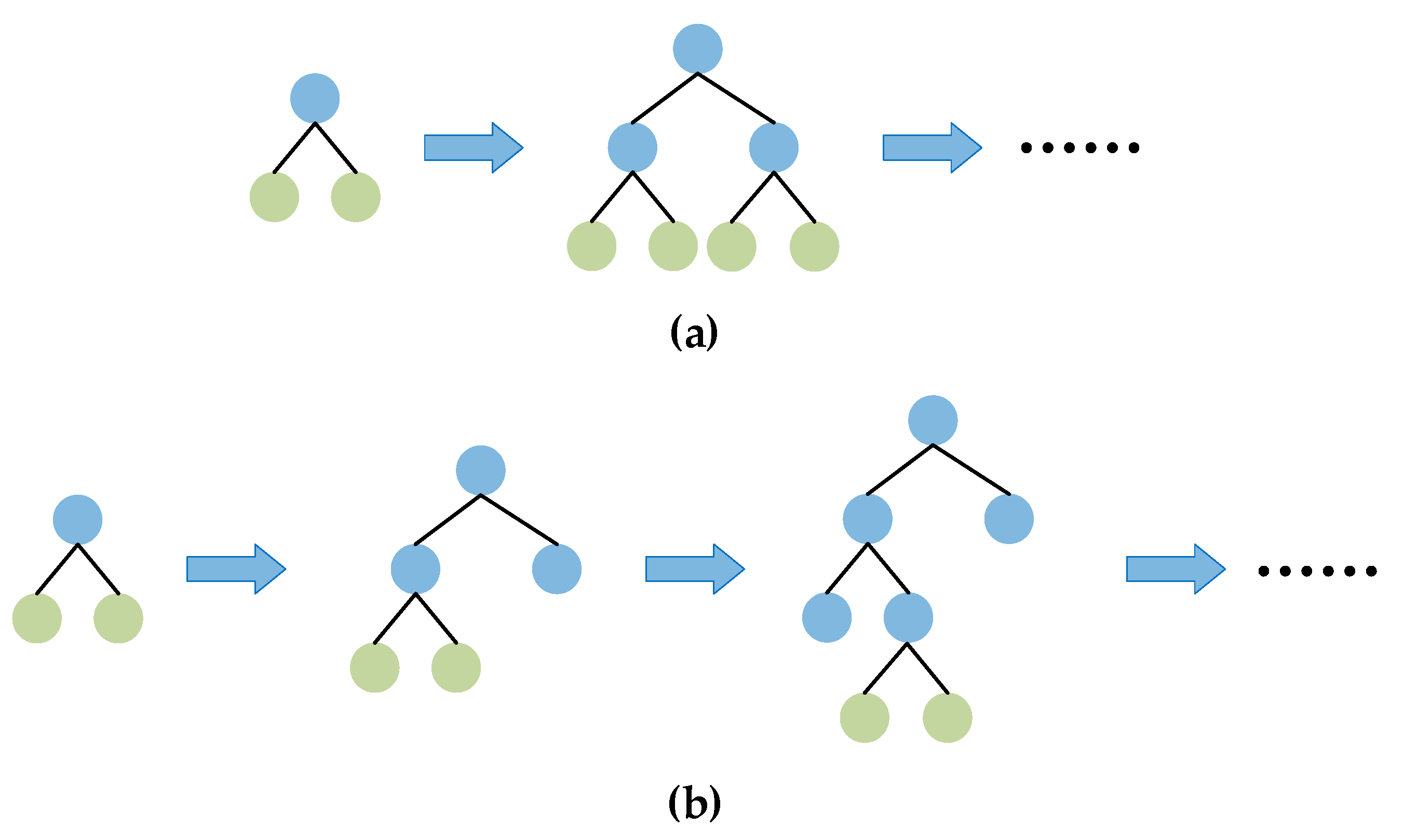
4.3. Description of the LGBM Algorithm
4.4. Construction of Battery SOH Estimation Model
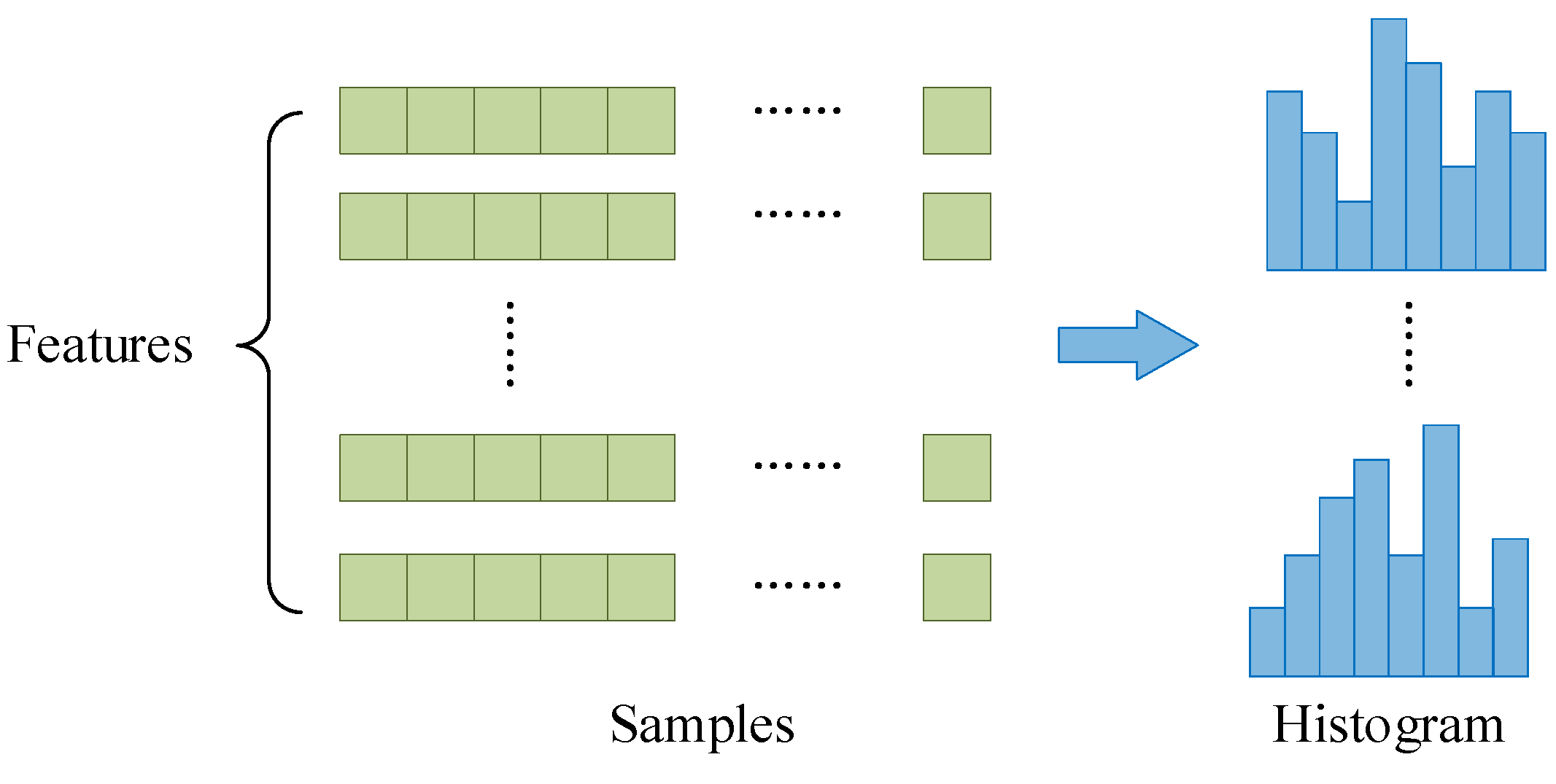
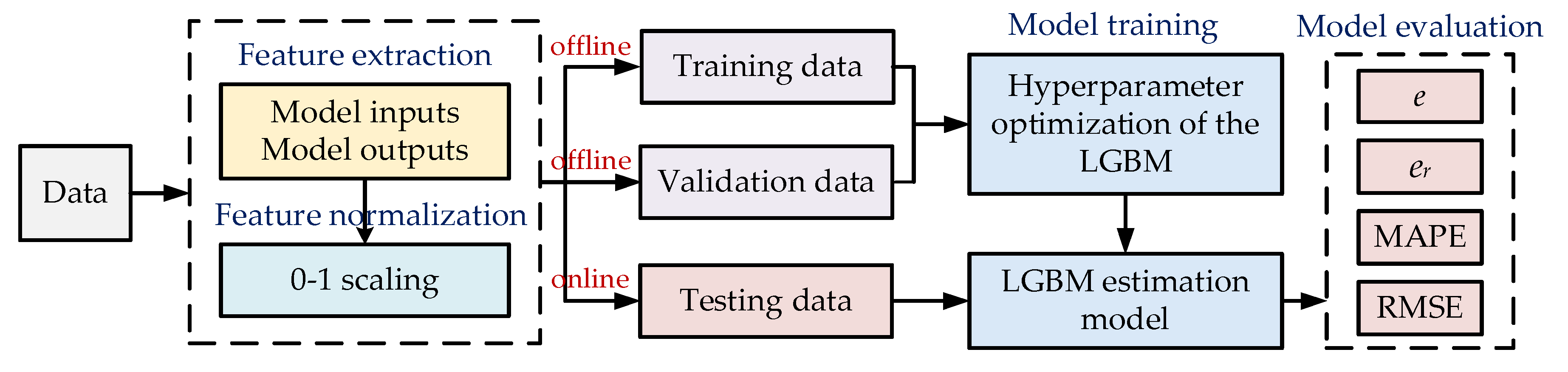
4.4.1. Feature Extraction
4.4.2. Feature Normalization
4.4.3. Model Training
4.4.4. Model Evaluation
5. Results and Discussions
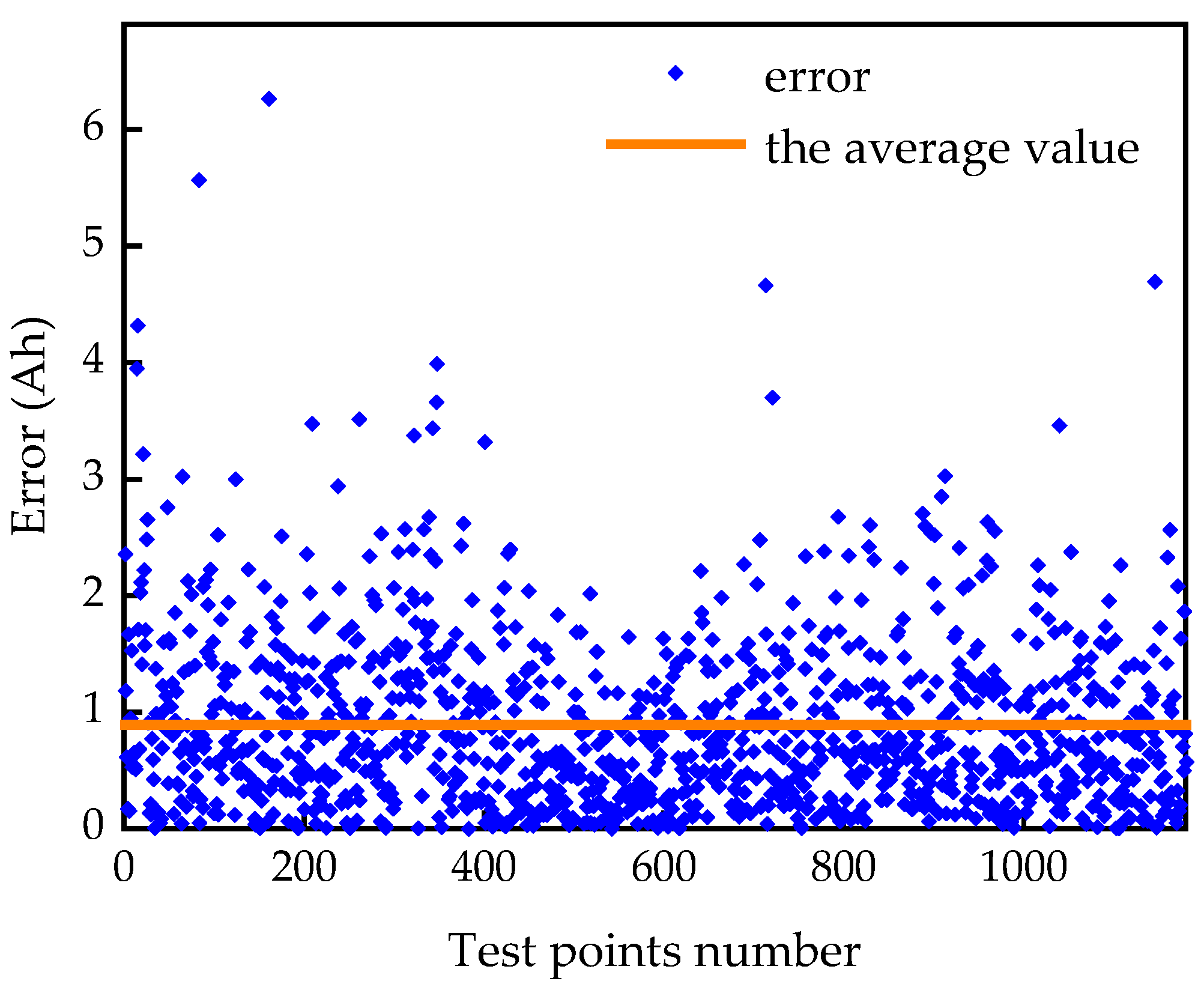
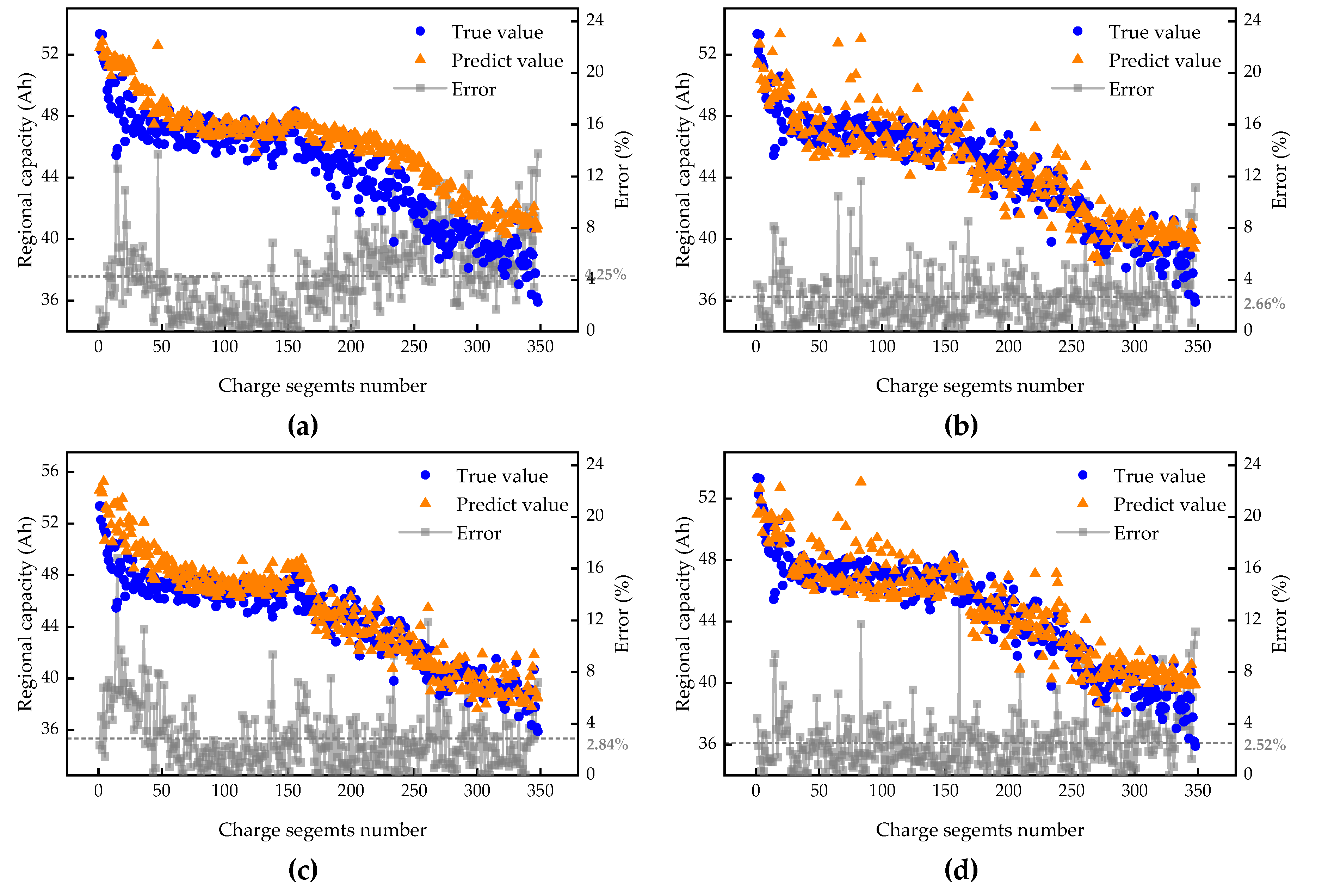
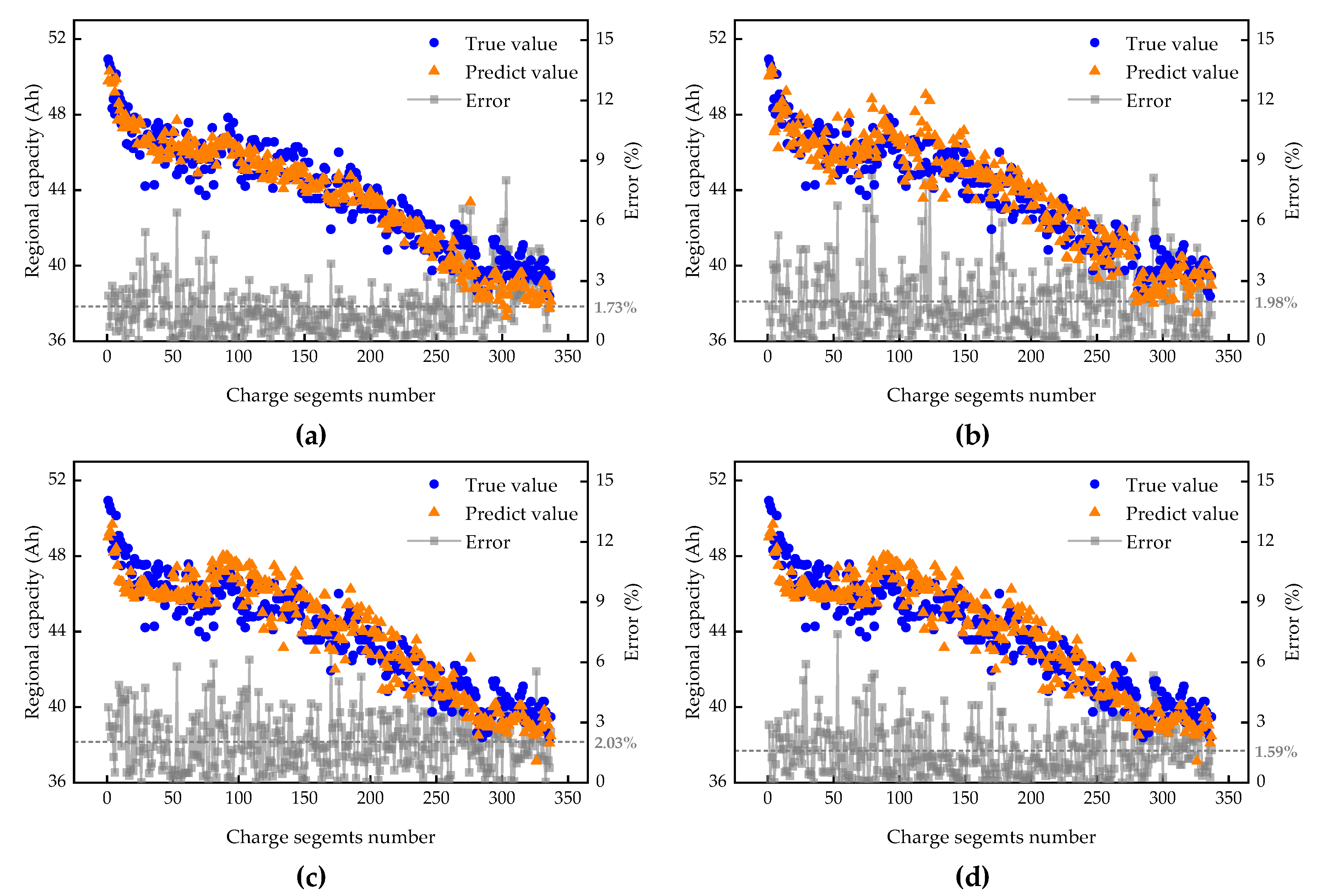
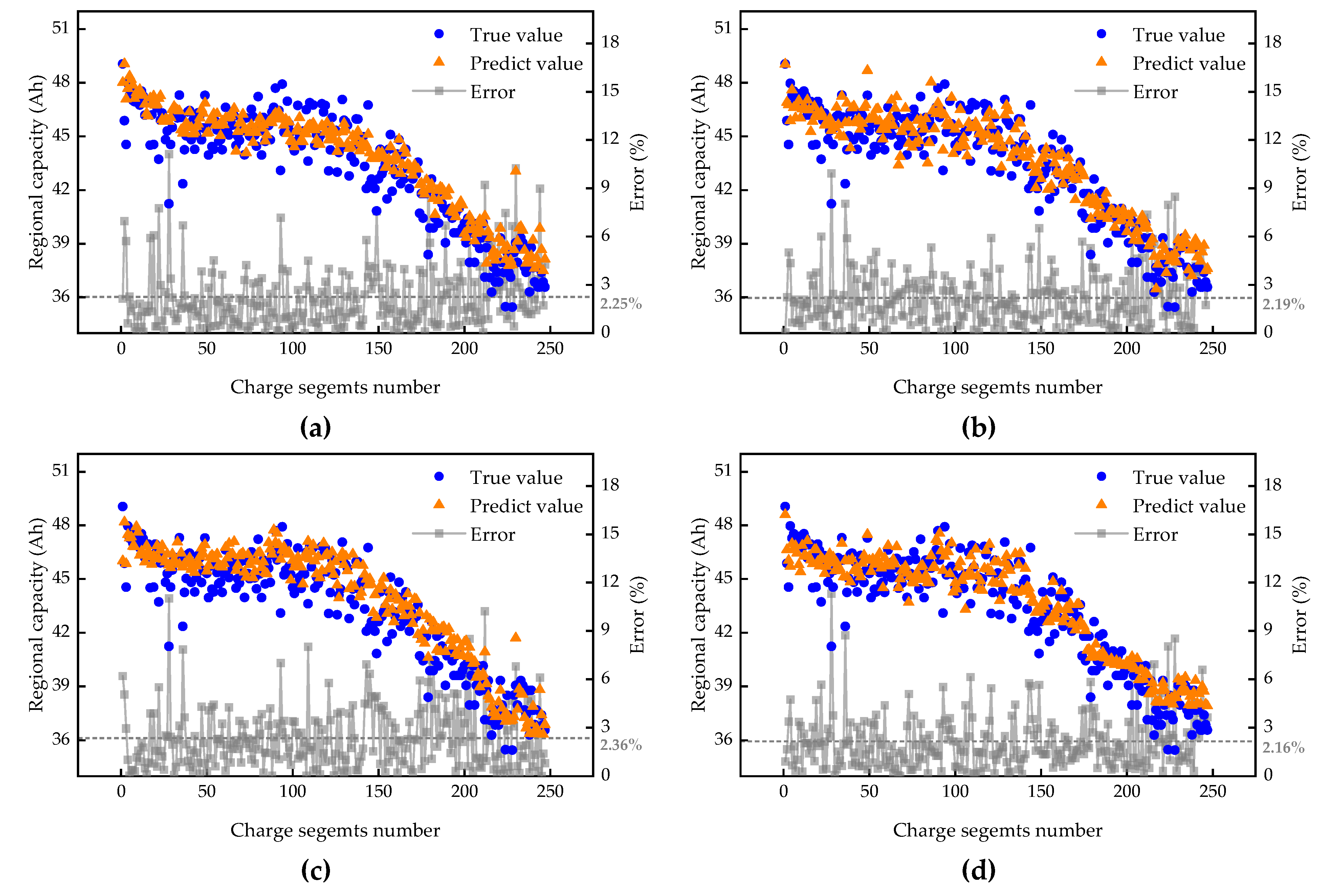
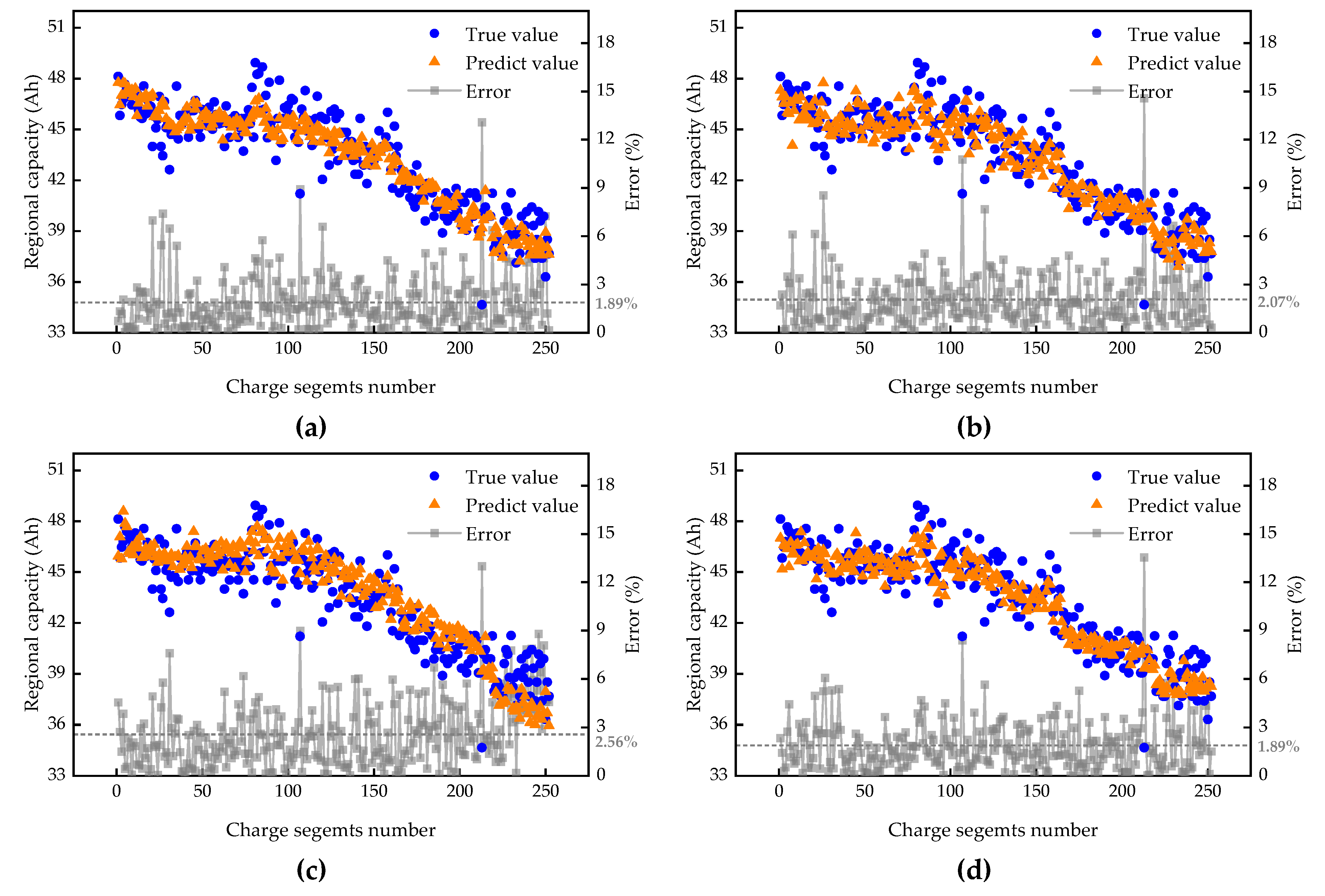
5.1. Verification in Real-World EVs
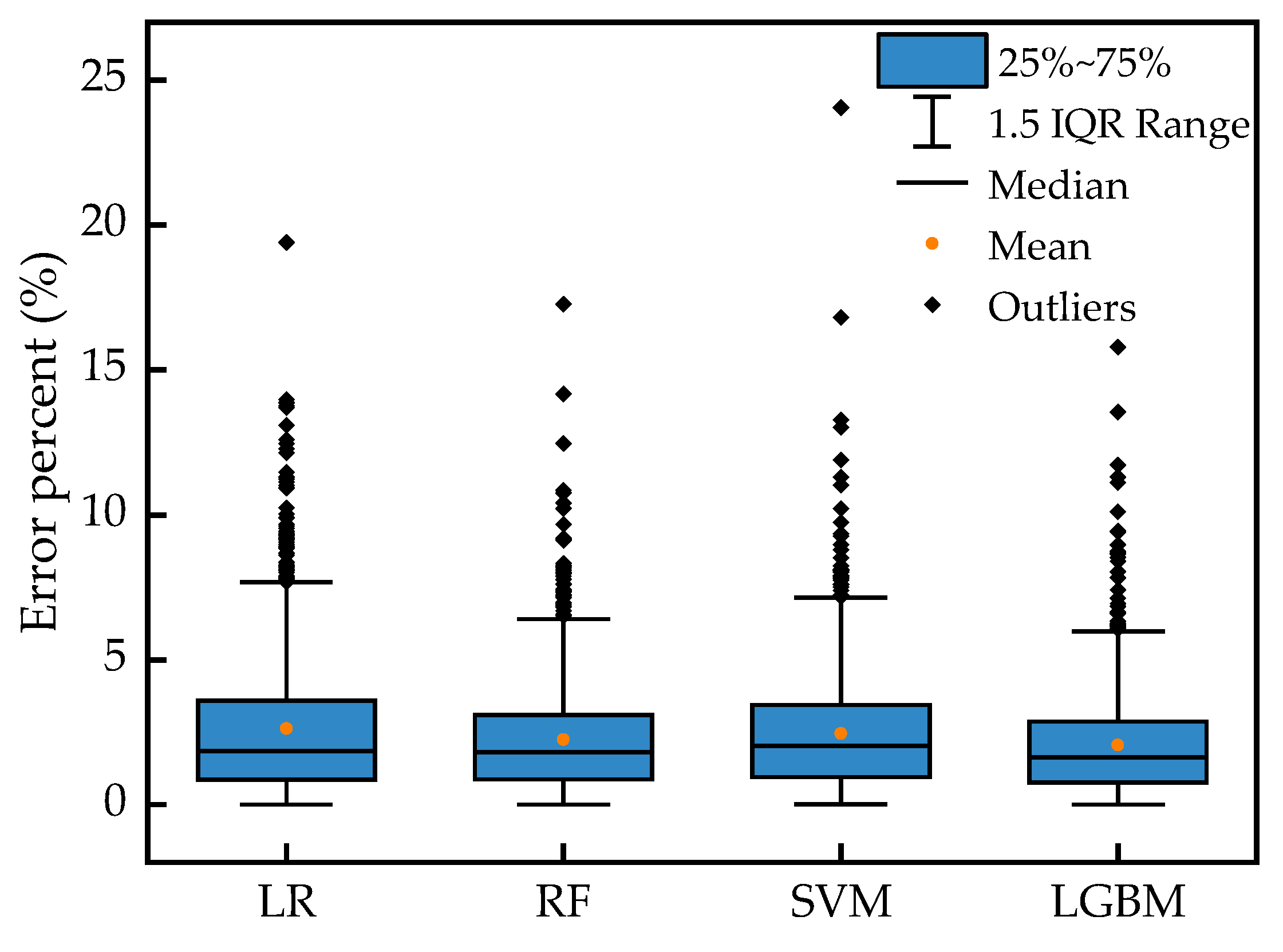
5.2. Comparative Analysis of Different Algorithms
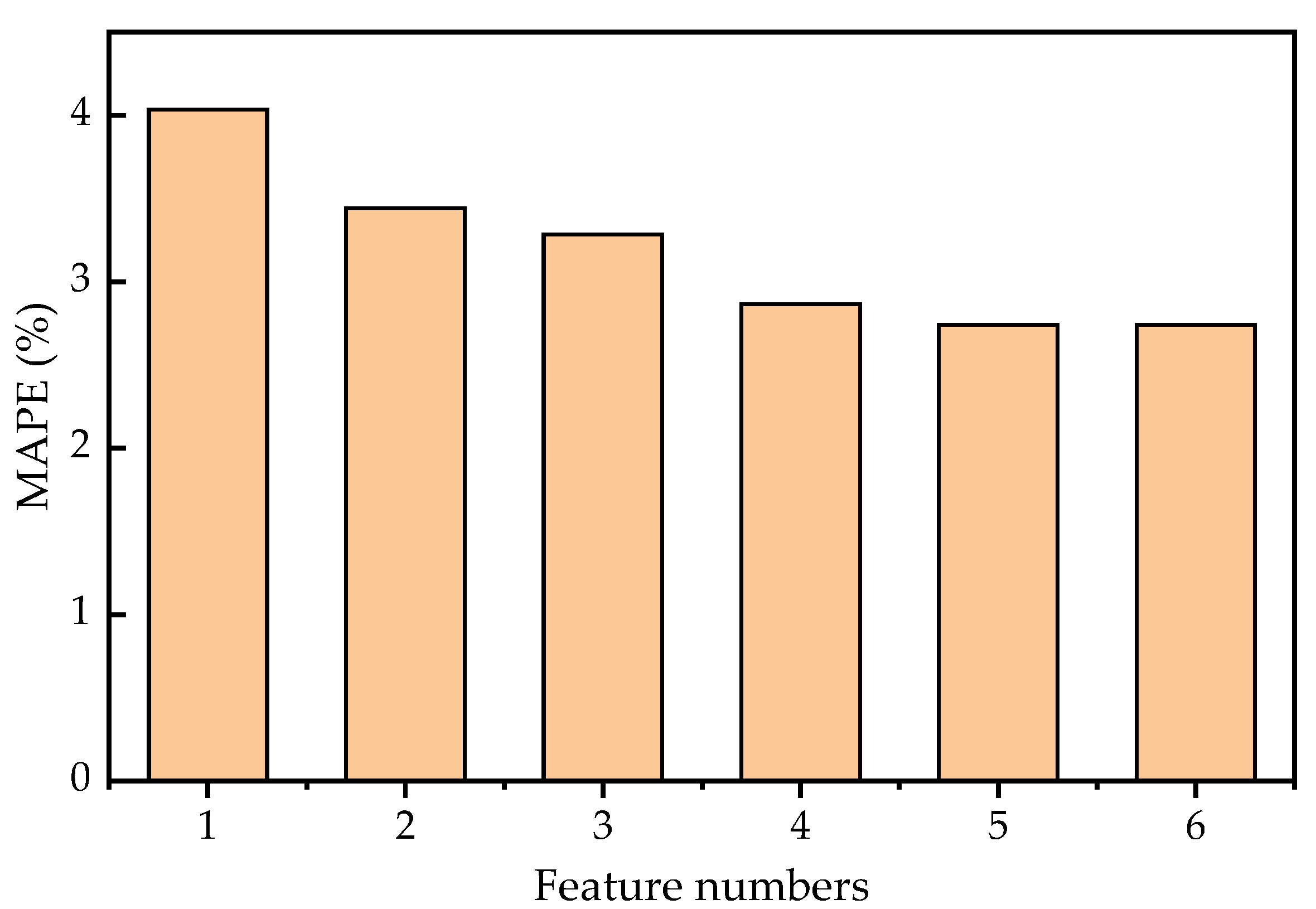
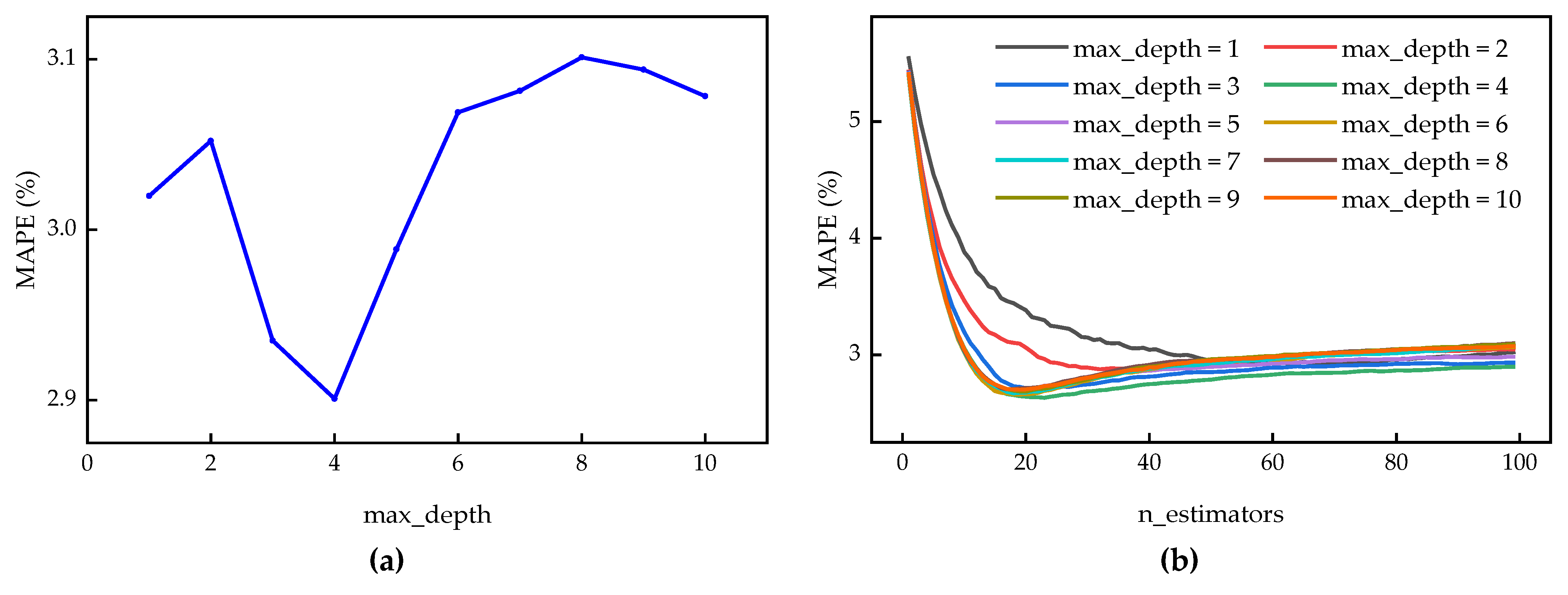
5.3. Sensitivity Analysis
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Nomenclatures
| Abbreviation | Description |
| SOH | State of health |
| EVs | Electric vehicles |
| LGBM | Light gradient boosting machine |
| ICA | Incremental capacity analysis |
| GS | Gaussian smoothing |
| BMS | Battery management system |
| EIS | Electrochemical impedance spectroscopy |
| EMs | Electrochemical models |
| ECMs | Equivalent circuit models |
| LS | Least squares |
| KF | Kalman filter |
| PF | Particle filter |
| SVM | Support vector machine |
| GPR | Gaussian process regression |
| ANN | Artificial neural network |
| NDANEV | National Big Data Alliance of New Energy Vehicles |
| MA | Moving average |
| GBDT | Gradient boosting decision tree |
| GOSS | Gradient-based one-side sampling |
| EFB | Exclusive feature bundling |
| DOD | Depth of discharge |
| MAPE | Mean absolute percentage error |
| RMSE | Root mean square error |
| LR | Linear regression |
| RF | Random forest |
References
- Ng, M.-F.; Zhao, J.; Yan, Q.; Conduit, G.J.; Seh, Z.W. Predicting the state of charge and health of batteries using data-driven machine learning. Nat. Mach. Intell. 2020, 2, 161–170. [Google Scholar] [CrossRef]
- Mitova, S.; Henao, A.; Kahsar, R.; Farmer, C.J.Q. Smart Charging for Electric Ride-Hailing Vehicles using Renewables: A San Francisco Case Study. Int. J. Sustain. Energy Environ. Res. 2022, 11, 67–85. [Google Scholar] [CrossRef]
- Dwijendra, N.K.A.; Sharma, S.; Asary, A.R.; Majdi, A.; Muda, I.; Mutlak, D.A.; Parra, R.M.R.; Hammid, A.T. Economic performance of a hybrid renewable energy system with optimal design of resources. Environ. Clim. Technol. 2022, 26, 441–453. [Google Scholar] [CrossRef]
- Harper, G.; Sommerville, R.; Kendrick, E.; Driscoll, L.; Slater, P.; Stolkin, R.; Walton, A.; Christensen, P.; Heidrich, O.; Lambert, S.; et al. Recycling lithium-ion batteries from electric vehicles. Nature 2019, 575, 75–86. [Google Scholar] [CrossRef]
- Goli, A.; Golmohammadi, A.-M.; Verdegay, J.-L. Two-echelon electric vehicle routing problem with a developed moth-flame meta-heuristic algorithm. Oper. Manag. Res. 2022, 15, 891–912. [Google Scholar] [CrossRef]
- Feng, F.; Teng, S.; Liu, K.; Xie, J.; Xie, Y.; Liu, B.; Li, K. Co-estimation of lithium-ion battery state of charge and state of temperature based on a hybrid electrochemical-thermal-neural-network model. J. Power Sources 2020, 455, 227935. [Google Scholar] [CrossRef]
- Zhou, L.; Zhao, Y.; Li, D.; Wang, Z. State-of-Health Estimation for LiFePO4 Battery System on Real-World Electric Vehicles Considering Aging Stage. IEEE Trans. Transp. Electrif. 2022, 8, 1724–1733. [Google Scholar] [CrossRef]
- Li, G.; Chen, H.; Zhang, B.; Guo, H.; Chen, S.; Chang, X.; Wu, X.; Zheng, J.; Li, X. Interfacial covalent bonding enables transition metal phosphide superior lithium storage performance. Appl. Surf. Sci. 2022, 582, 152404. [Google Scholar] [CrossRef]
- Roman, D.; Saxena, S.; Robu, V.; Pecht, M.; Flynn, D. Machine learning pipeline for battery state-of-health estimation. Nat. Mach. Intell. 2021, 3, 447–456. [Google Scholar] [CrossRef]
- Li, Y.; Liu, K.; Foley, A.M.; Zülke, A.; Berecibar, M.; Nanini-Maury, E.; Van Mierlo, J.; Hoster, H.E. Data-driven health estimation and lifetime prediction of lithium-ion batteries: A review. Renew. Sust. Energy Rev. 2019, 113, 109254. [Google Scholar] [CrossRef]
- Wang, Q.; Wang, Z.; Zhang, L.; Liu, P.; Zhang, Z. A novel consistency evaluation method for series-connected battery systems based on real-world operation data. IEEE Trans. Transp. Electrif. 2020, 7, 437–451. [Google Scholar] [CrossRef]
- She, C.; Li, Y.; Zou, C.; Wik, T.; Wang, Z.; Sun, F. Offline and Online Blended Machine Learning for Lithium-Ion Battery Health State Estimation. IEEE Trans. Transp. Electrif. 2021, 8, 1604–1618. [Google Scholar] [CrossRef]
- Li, W.; Sengupta, N.; Dechent, P.; Howey, D.; Annaswamy, A.; Sauer, D.U. Online capacity estimation of lithium-ion batteries with deep long short-term memory networks. J. Power Sources 2021, 482. [Google Scholar] [CrossRef]
- Zhang, S.; Guo, X.; Dou, X.; Zhang, X. A rapid online calculation method for state of health of lithium-ion battery based on coulomb counting method and differential voltage analysis. J. Power Sources 2020, 479, 228740. [Google Scholar] [CrossRef]
- Lyu, Z.; Gao, R.; Li, X. A partial charging curve-based data-fusion-model method for capacity estimation of Li-Ion battery. J. Power Sources 2021, 483, 229131. [Google Scholar] [CrossRef]
- Fu, Y.; Xu, J.; Shi, M.; Mei, X. A Fast Impedance Calculation-Based Battery State-of-Health Estimation Method. IEEE Trans. Ind. Electron. 2022, 69, 7019–7028. [Google Scholar] [CrossRef]
- Jiang, B.; Zhu, J.; Wang, X.; Wei, X.; Shang, W.; Dai, H. A comparative study of different features extracted from electrochemical impedance spectroscopy in state of health estimation for lithium-ion batteries. Appl. Energy 2022, 322, 119502. [Google Scholar] [CrossRef]
- Gao, Y.; Liu, K.; Zhu, C.; Zhang, X.; Zhang, D. Co-Estimation of State-of-Charge and State-of- Health for Lithium-Ion Batteries Using an Enhanced Electrochemical Model. IEEE Trans. Ind. Electronif. 2022, 69, 2684–2696. [Google Scholar] [CrossRef]
- Han, X.; Ouyang, M.; Lu, L.; Li, J. Simplification of physics-based electrochemical model for lithium ion battery on electric vehicle. Part I: Diffusion simplification and single particle model. J. Power Sources 2015, 278, 802–813. [Google Scholar] [CrossRef]
- Han, X.; Ouyang, M.; Lu, L.; Li, J. Simplification of physics-based electrochemical model for lithium ion battery on electric vehicle. Part II: Pseudo-two-dimensional model simplification and state of charge estimation. J. Power Sources 2015, 278, 814–825. [Google Scholar] [CrossRef]
- Yan, W.; Zhang, B.; Zhao, G.; Tang, S.; Niu, G.; Wang, X. A battery management system with a lebesgue-sampling-based extended kalman filter. IEEE T. Ind. Electron. 2019, 66, 3227–3236. [Google Scholar] [CrossRef]
- Yang, J.; Cai, Y.; Mi, C.C. State-of-Health Estimation for Lithium-Ion Batteries Based on Decoupled Dynamic Characteristic of Constant-Voltage Charging Current. IEEE Trans. Transp. Electrif. 2022, 8, 2070–2079. [Google Scholar] [CrossRef]
- Liang, K.; Zhang, Z.; Liu, P.; Wang, Z.; Jiang, S. Data-Driven Ohmic Resistance Estimation of Battery Packs for Electric Vehicles. Energies 2019, 12, 4772. [Google Scholar] [CrossRef]
- Wang, S.; Fernandez, C.; Yu, C.; Fan, Y.; Cao, W.; Stroe, D.-I. A novel charged state prediction method of the lithium ion battery packs based on the composite equivalent modeling and improved splice Kalman filtering algorithm. J. Power Sources 2020, 471, 228450. [Google Scholar] [CrossRef]
- Lai, X.; Wang, S.; Ma, S.; Xie, J.; Zheng, Y. Parameter sensitivity analysis and simplification of equivalent circuit model for the state of charge of lithium-ion batteries. Electrochim. Acta 2020, 330, 135239. [Google Scholar] [CrossRef]
- Tian, J.; Xiong, R.; Shen, W.; Lu, J.; Sun, F. Flexible battery state of health and state of charge estimation using partial charging data and deep learning. Energy Storage Mater. 2022, 51, 372–381. [Google Scholar] [CrossRef]
- El-kenawy, E.-S.M.; Abutarboush, H.F.; Mohamed, A.W.; Ibrahim, A. Advance artificial intelligence technique for designing double t-shaped monopole antenna. Comput. Mater. Con. 2021, 69, 2983–2995. [Google Scholar] [CrossRef]
- Wei, Z.; Ruan, H.; Li, Y.; Li, J.; Zhang, C.; He, H. Multistage State of Health Estimation of Lithium-Ion Battery With High Tolerance to Heavily Partial Charging. IEEE Trans. Power Electr. 2022, 37, 7432–7442. [Google Scholar] [CrossRef]
- Weng, C.; Cui, Y.; Sun, J.; Peng, H. On-board state of health monitoring of lithium-ion batteries using incremental capacity analysis with support vector regression. J. Power Sources 2013, 235, 36–44. [Google Scholar] [CrossRef]
- Li, X.; Yuan, C.; Li, X.; Wang, Z. State of health estimation for Li-Ion battery using incremental capacity analysis and Gaussian process regression. Energy 2020, 190, 116467. [Google Scholar] [CrossRef]
- Tian, J.; Xiong, R.; Shen, W.; Lu, J.; Yang, X.-G. Deep neural network battery charging curve prediction using 30 points collected in 10 min. Joule 2021, 5, 1521–1534. [Google Scholar] [CrossRef]
- Hsu, C.-W.; Xiong, R.; Chen, N.-Y.; Li, J.; Tsou, N.-T. Deep neural network battery life and voltage prediction by using data of one cycle only. Appl. Energy 2022, 306, 118134. [Google Scholar] [CrossRef]
- Sun, T.; Xu, B.; Cui, Y.; Feng, X.; Han, X.; Zheng, Y. A sequential capacity estimation for the lithium-ion batteries combining incremental capacity curve and discrete Arrhenius fading model. J. Power Sources 2021, 484, 229248. [Google Scholar] [CrossRef]
- Li, Y.; Abdel-Monem, M.; Gopalakrishnan, R.; Berecibar, M.; Nanini-Maury, E.; Omar, N.; van den Bossche, P.; Van Mierlo, J. A quick on-line state of health estimation method for Li-ion battery with incremental capacity curves processed by Gaussian filter. J. Power Sources 2018, 373, 40–53. [Google Scholar] [CrossRef]
- Zhang, Y.; Liu, Y.; Wang, J.; Zhang, T. State-of-health estimation for lithium-ion batteries by combining model-based incremental capacity analysis with support vector regression. Energy 2022, 239, 121986. [Google Scholar] [CrossRef]
- Ospina Agudelo, B.; Zamboni, W.; Monmasson, E. Application domain extension of incremental capacity-based battery SoH indicators. Energy 2021, 234, 121224. [Google Scholar] [CrossRef]
- Bian, X.; Wei, Z.; He, J.; Yan, F.; Liu, L. A Novel Model-Based Voltage Construction Method for Robust State-of-Health Estimation of Lithium-Ion Batteries. IEEE Trans. Ind. Electron. 2021, 68, 12173–12184. [Google Scholar] [CrossRef]
- Tang, X.; Zou, C.; Yao, K.; Chen, G.; Liu, B.; He, Z.; Gao, F. A fast estimation algorithm for lithium-ion battery state of health. J. Power Sources 2018, 396, 453–458. [Google Scholar] [CrossRef]
- Liu, P.; Wu, Y.; She, C.; Wang, Z.; Zhang, Z. Comparative Study of Incremental Capacity Curve Determination Methods for Lithium-Ion Batteries Considering the Real-World Situation. IEEE Trans. Power Electron. 2022, 37, 12563–12576. [Google Scholar] [CrossRef]
- Chakraborty, D.; Elhegazy, H.; Elzarka, H.; Gutierrez, L. A novel construction cost prediction model using hybrid natural and light gradient boosting. Adv. Eng. Inform. 2020, 46, 101201. [Google Scholar] [CrossRef]
- Ke, G.; Meng, Q.; Finley, T.; Wang, T.; Chen, W.; Ma, W.; Ye, Q.; Liu, T.-Y. Lightgbm: A highly efficient gradient boosting decision tree. Adv. Neural Inf. Process. Syst. 2017, 30, 1–9. [Google Scholar]
- Chen, C.; Zhang, Q.; Ma, Q.; Yu, B. LightGBM-PPI: Predicting protein-protein interactions through LightGBM with multi-information fusion. Chemometr. Intell. Lab. 2019, 191, 54–64. [Google Scholar] [CrossRef]
- Zhou, B.; Xu, J.; Han, F.; Yan, F.; Peng, S.; Li, Q.; Jiao, F. Pressure of different gases injected into large-scale coal matrix: Analysis of time–space dependence and prediction using light gradient boosting machine. Fuel 2020, 279, 118448. [Google Scholar] [CrossRef]
- Massaoudi, M.; Refaat, S.S.; Chihi, I.; Trabelsi, M.; Oueslati, F.S.; Abu-Rub, H. A novel stacked generalization ensemble-based hybrid LGBM-XGB-MLP model for Short-Term Load Forecasting. Energy 2021, 214, 118874. [Google Scholar] [CrossRef]
- Hu, X.; Xu, L.; Lin, X.; Pecht, M. Battery Lifetime Prognostics. Joule 2020, 4, 310–346. [Google Scholar] [CrossRef]
- Birkl, C.R.; Roberts, M.R.; McTurk, E.; Bruce, P.G.; Howey, D.A. Degradation diagnostics for lithium ion cells. J. Power Sources 2017, 341, 373–386. [Google Scholar] [CrossRef]
- Kabir, M.M.; Demirocak, D.E. Degradation mechanisms in Li-ion batteries: A state-of-the-art review. Int. J. Energy Res. 2017, 41, 1963–1986. [Google Scholar] [CrossRef]
- Han, X.; Lu, L.; Zheng, Y.; Feng, X.; Li, Z.; Li, J.; Ouyang, M. A review on the key issues of the lithium ion battery degradation among the whole life cycle. eTransportation 2019, 1, 100005. [Google Scholar] [CrossRef]
- Woody, M.; Arbabzadeh, M.; Lewis, G.M.; Keoleian, G.A.; Stefanopoulou, A. Strategies to limit degradation and maximize Li-ion battery service lifetime—Critical review and guidance for stakeholders. J. Energy Storage 2020, 28, 101231. [Google Scholar] [CrossRef]

| Parameters | Value (Units) |
|---|---|
| Curb weight | 7800 kg |
| Number of battery cells | 336 |
| Nominal voltage | 537.6 V |
| Nominal capacity | 240 Ah |
| Nominal energy | 129 kWh |
| Cathode materials | LiFePO4 |
| Time | Accumulated Mileage (km) | Velocity (km/h) | Battery System Voltage (V) | Battery System Current (A) | SOC (%) | The Highest Temperature (°C) | The Lowest Temperature (°C) |
|---|---|---|---|---|---|---|---|
| 20190612091138 | 156,334.4 | 0 | 565.3 | −192 | 86 | 31 | 28 |
| 20190612091148 | 156,334.4 | 0 | 569.5 | −192 | 86 | 31 | 28 |
| 20190612091158 | 156,334.4 | 0 | 571.5 | −192 | 86 | 31 | 28 |
| … | … | … | … | … | … | … | … |
| 20190612092158 | 156,334.4 | 0 | 573.3 | −40 | 99 | 33 | 29 |
| 20190612092208 | 156,334.4 | 0 | 573.5 | −40 | 99 | 33 | 29 |
| 20190612092218 | 156,334.4 | 0 | 573.8 | −40 | 99 | 33 | 29 |
| Time | Accumulated Mileage (km) | Velocity (km/h) | Battery System Voltage (V) | Battery System Current (A) | SOC (%) | The Highest Temperature (°C) | The Lowest Temperature (°C) |
|---|---|---|---|---|---|---|---|
| 20180105202706 | 63,545.8 | 5 | 553.1 | 16 | 62 | 30 | 23 |
| 20180105202716 | 63,545.8 | 13 | 551.9 | 33 | 62 | 30 | 23 |
| 20180105202726 | 63,545.8 | 12 | 552.9 | 17 | 62 | 30 | 23 |
| … | … | … | … | … | … | … | … |
| 20180105214356 | 63,570.8 | 3 | 550.5 | 7 | 52 | 29 | 22 |
| 20180105214406 | 63,570.8 | 6 | 550.5 | 2 | 52 | 29 | 22 |
| 20180105214416 | 63,570.9 | 5 | 550.4 | 3 | 52 | 29 | 22 |
| Vehicle | LR | RF | SVM | LGBM | ||||
|---|---|---|---|---|---|---|---|---|
| MAPE (%) | RMSE (%) | MAPE (%) | RMSE (%) | MAPE (%) | RMSE (%) | MAPE (%) | RMSE (%) | |
| 1 | 4.254 | 2.208 | 2.659 | 1.485 | 2.838 | 1.728 | 2.520 | 1.403 |
| 2 | 1.730 | 0.947 | 1.977 | 1.117 | 2.034 | 1.078 | 1.598 | 0.893 |
| 3 | 2.247 | 1.244 | 2.187 | 1.174 | 2.363 | 1.288 | 2.158 | 1.164 |
| 4 | 1.882 | 1.086 | 2.074 | 1.168 | 2.564 | 1.362 | 1.898 | 1.065 |
| Test vehicles | 2.612 | 1.504 | 2.239 | 1.258 | 2.452 | 1.396 | 2.049 | 1.153 |
| Noise | 1% | 2% | 3% | 5% |
|---|---|---|---|---|
| MAPE (%) | 2.354 | 2.442 | 2.839 | 2.881 |
| RMSE (%) | 1.401 | 1.334 | 1.569 | 1.663 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, Z.; Wang, S.; Lin, N.; Wang, Z.; Liu, P. State of Health Estimation of Lithium-Ion Batteries in Electric Vehicles Based on Regional Capacity and LGBM. Sustainability 2023, 15, 2052. https://doi.org/10.3390/su15032052
Zhang Z, Wang S, Lin N, Wang Z, Liu P. State of Health Estimation of Lithium-Ion Batteries in Electric Vehicles Based on Regional Capacity and LGBM. Sustainability. 2023; 15(3):2052. https://doi.org/10.3390/su15032052
Chicago/Turabian StyleZhang, Zhaosheng, Shuo Wang, Ni Lin, Zhenpo Wang, and Peng Liu. 2023. "State of Health Estimation of Lithium-Ion Batteries in Electric Vehicles Based on Regional Capacity and LGBM" Sustainability 15, no. 3: 2052. https://doi.org/10.3390/su15032052
APA StyleZhang, Z., Wang, S., Lin, N., Wang, Z., & Liu, P. (2023). State of Health Estimation of Lithium-Ion Batteries in Electric Vehicles Based on Regional Capacity and LGBM. Sustainability, 15(3), 2052. https://doi.org/10.3390/su15032052






