Novel Features and Neighborhood Complexity Measures for Multiclass Classification of Hybrid Data
Abstract
1. Introduction
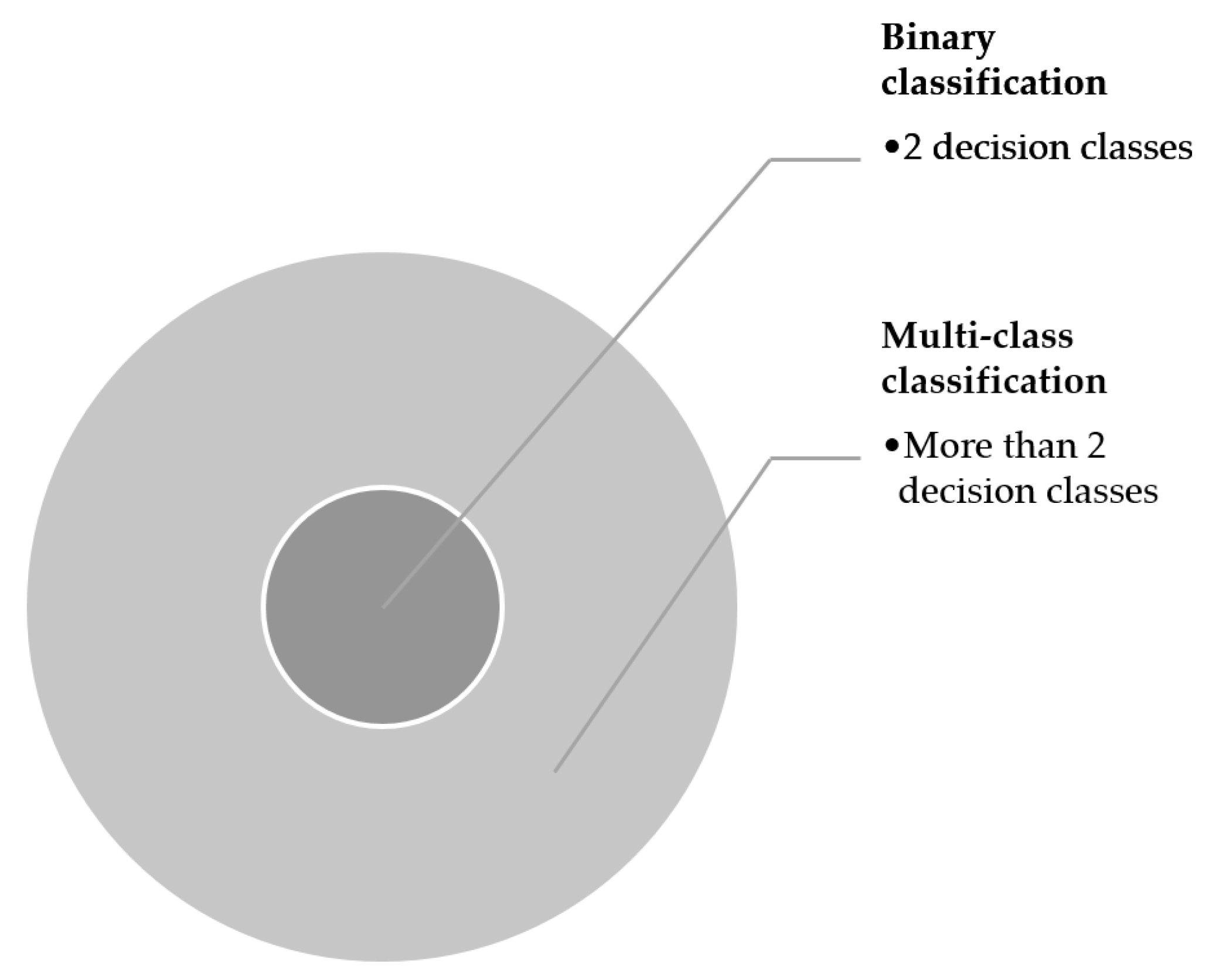
- We extend four data complexity measures for the multiclass classification scenario and for dealing with hybrid and incomplete data.
- We compute the proposed measures for publicly available multiclass hybrid and incomplete datasets.
2. Related Works
2.1. Preliminaries
- Feature-based measures describe how useful the features are to separate the classes.
- Linearity measures try to determine the extent of linear separation between the classes.
- Neighborhood measures characterize class overlapping in neighborhoods.
- Network measures focus on the structural information of the data.
- Dimensionality measures estimate data sparsity.
- Class imbalance measures consider the number of instances in the classes.
2.2. Feature-Based Measures
2.2.1. Maximum Fisher’s Discriminant Ratio (F1)
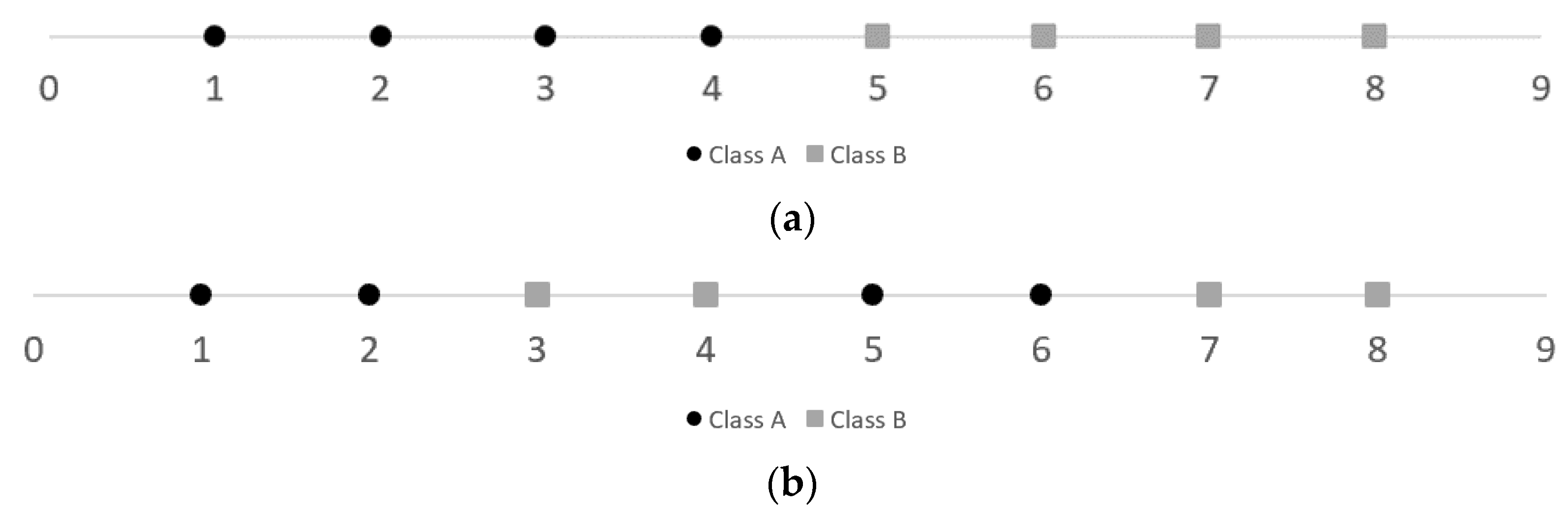
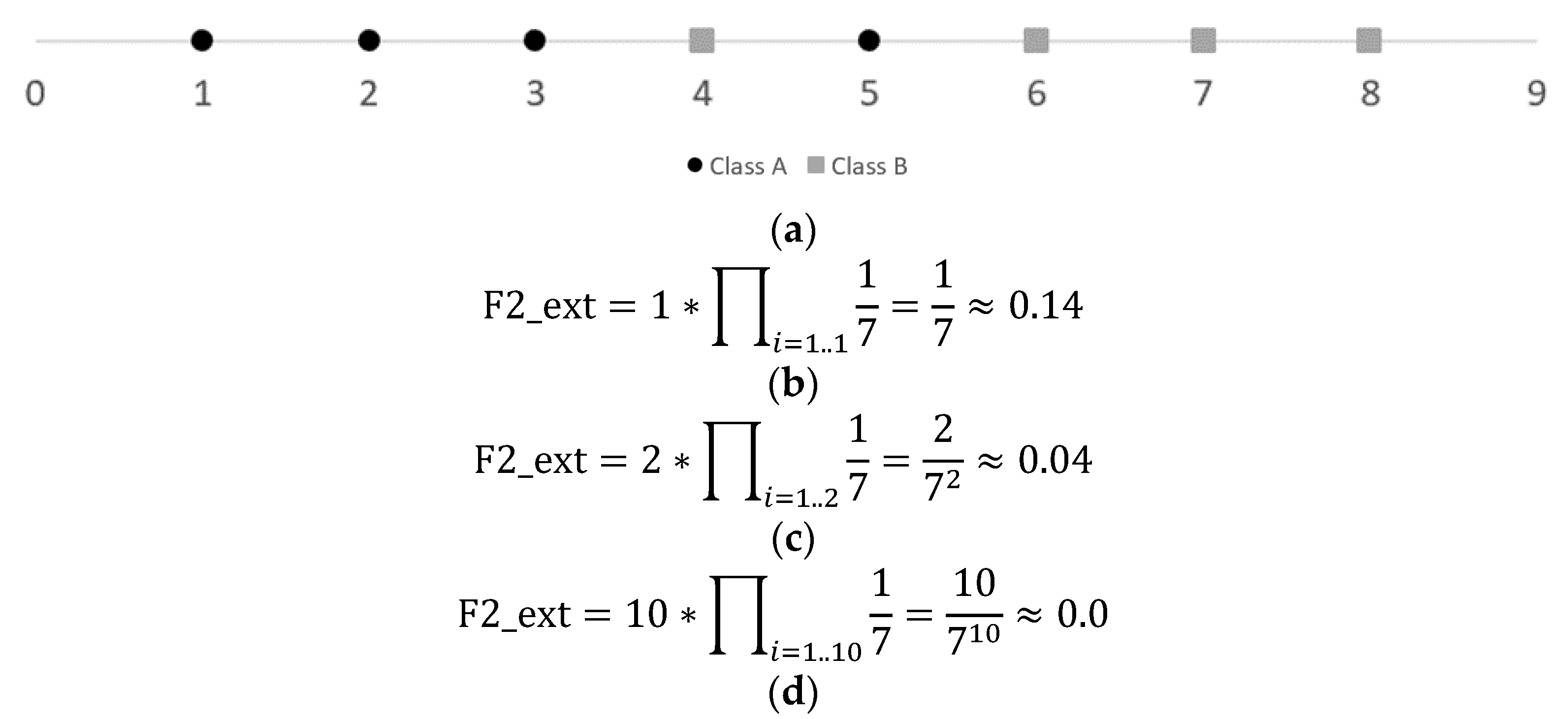
2.2.2. Volume of the Overlapping Region (F2)
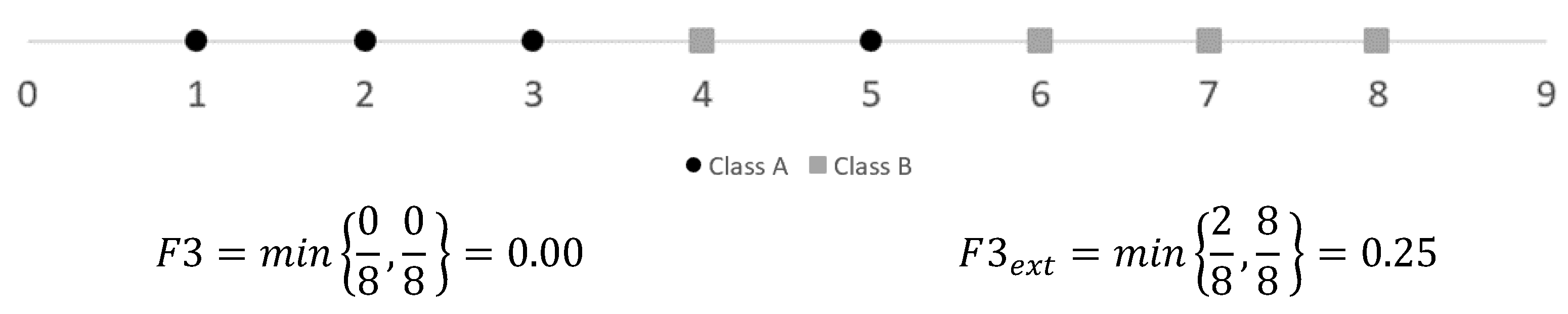
2.2.3. Maximum Individual Feature Efficiency (F3)
2.3. Linearity Measures
2.3.1. Sum of the Error Distance by Linear Programming (L1)
2.3.2. Error Rate of Linear Classifier (L2)
- It assumes two classes, as it uses an SVM;
- It assumes data is numeric and complete;
- It uses a fixed classifier (SVM) to establish the linearity of the data.
2.3.3. Non-linearity of Linear Classifier (L3)
2.4. Neighborhood Measures
2.4.1. Fraction of Borderline Points (N1)
2.4.2. Ratio of Intra/Extra Class Nearest Neighbor Distance (N2)
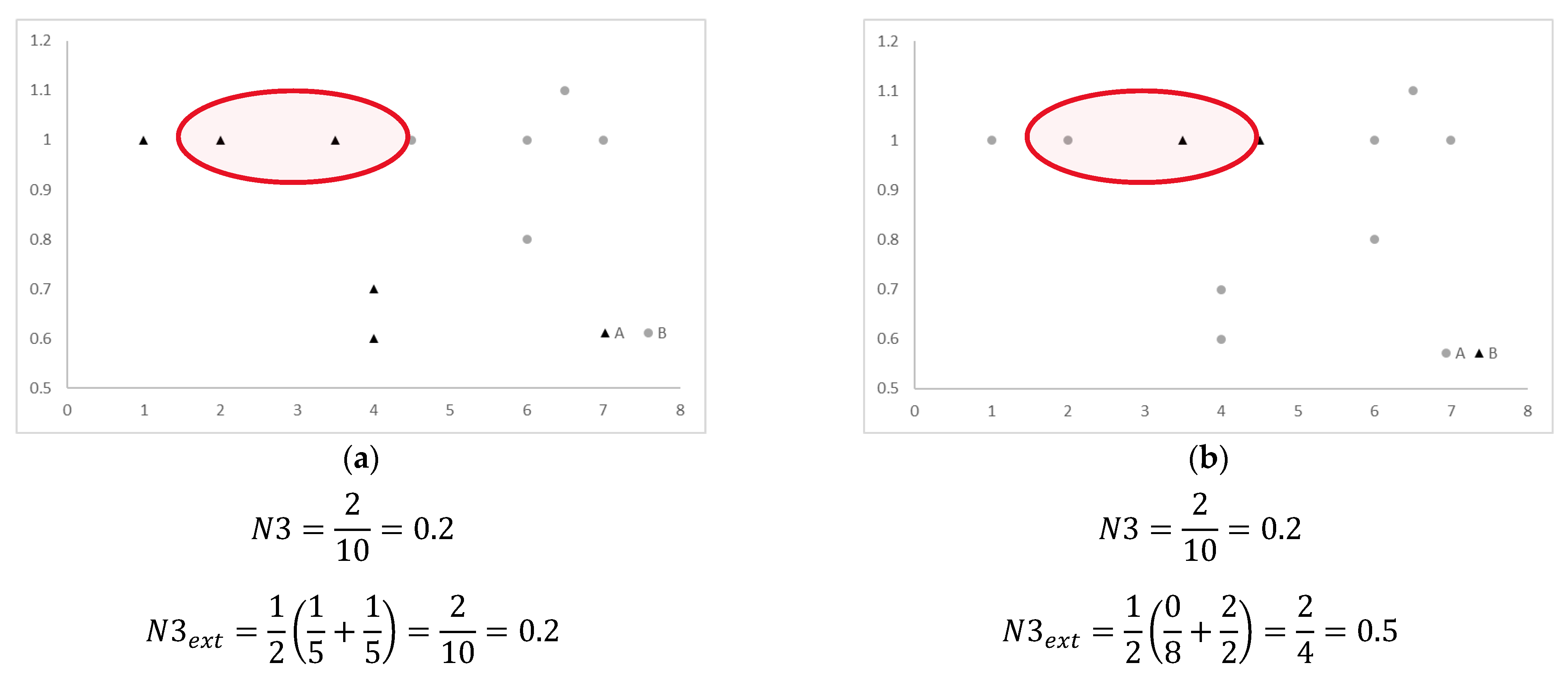
2.4.3. Error Rate of the Nearest Neighbor Classifier (N3)
2.4.4. Non-Linearity of the Nearest Neighbor Classifier (N4)
2.4.5. Fractions of Hyperspheres Covering Data (T1)
2.4.6. Local Set Average Cardinality (LSC)
3. Proposed Approach and Results
3.1. Extended Feature-Based Measures
3.1.1. Extended Maximum Fisher’s Discriminant Ratio (F1_ext)
3.1.2. Extended Volume of the Overlapping Region (F2_ext)
3.1.3. Extended Maximum Individual Feature Efficiency (F3_ext)
3.2. Linearity Measures
3.3. Neighborhood Measures
4. Discussion
4.1. Synthetic Data
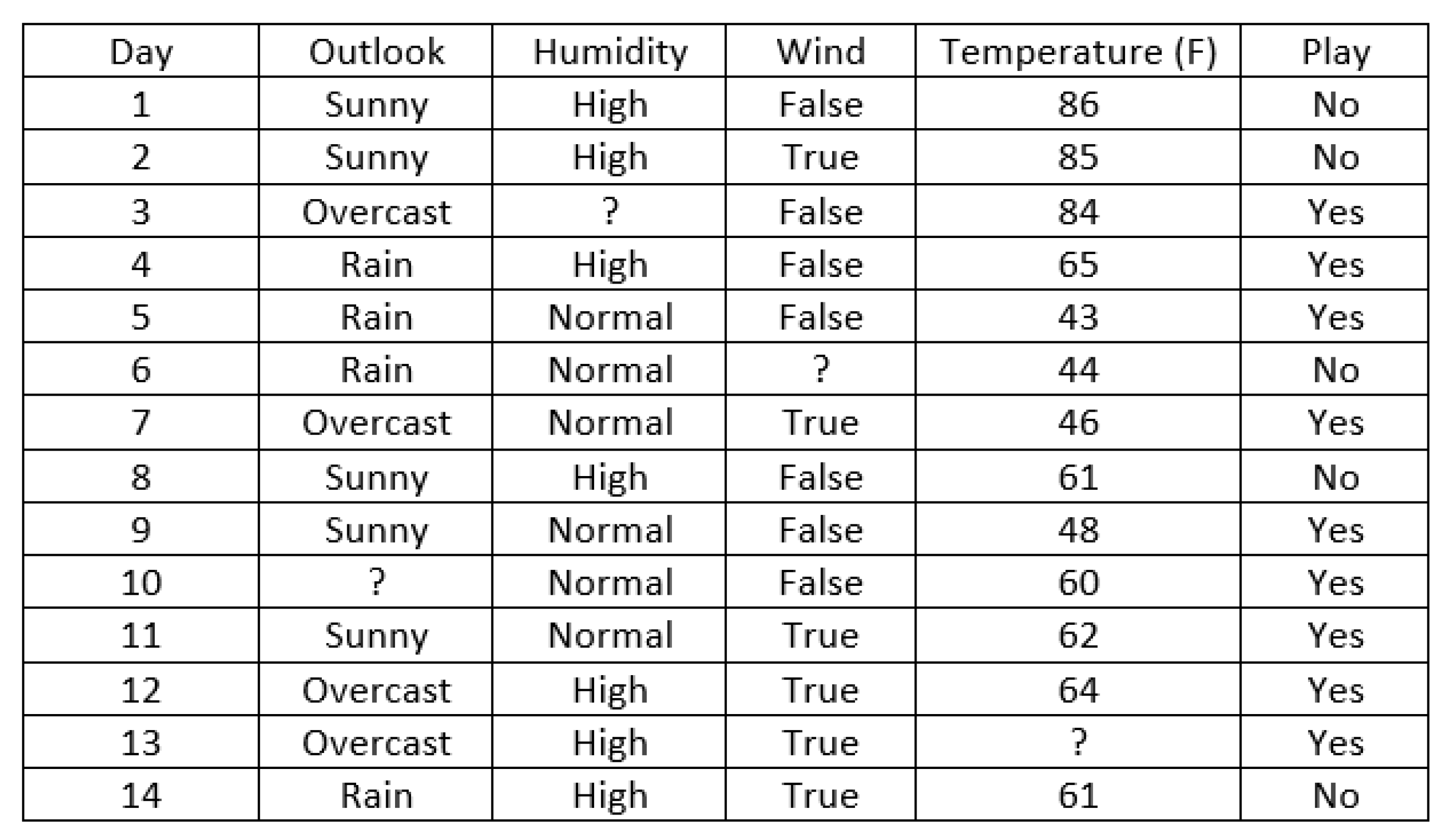
4.2. Real Data
- The F1_ext measure, as its predecessor F1, for numerical data assumes that the linear boundary is unique and perpendicular to one of the feature axes. If a feature is separable but with more than one line, it does not capture such information.
- F2_ext measure can become very small depending on the number of operands in Equation (17); that is, it is highly dependent on the number of features a dataset has.
- Neighborhood measures are bounded by . For datasets with a huge number of instances, they can be computationally expensive.
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Shetty, S.H.; Shetty, S.; Singh, C.; Rao, A. Supervised Machine Learning: Algorithms and Applications. In Fundamentals and Methods of Machine and Deep Learning: Algorithms, Tools and Applications; Singh, P., Ed.; Wiley: Hoboken, NJ, USA, 2022; pp. 1–16. [Google Scholar]
- Satinet, C.; Fouss, F. A Supervised Machine Learning Classification Framework for Clothing Products’ Sustainability. Sustainability 2022, 14, 1334. [Google Scholar] [CrossRef]
- Eastvedt, D.; Naterer, G.; Duan, X. Detection of faults in subsea pipelines by flow monitoring with regression supervised machine learning. Process Saf. Environ. Prot. 2022, 161, 409–420. [Google Scholar] [CrossRef]
- Liu, X.; Lu, D.; Zhang, A.; Liu, Q.; Jiang, G. Data-Driven Machine Learning in Environmental Pollution: Gains and Problems. Environ. Sci. Technol. 2022, 56, 2124–2133. [Google Scholar] [CrossRef] [PubMed]
- Voulgari, I.; Stouraitis, E.; Camilleri, V.; Karpouzis, K. Artificial Intelligence and Machine Learning Education and Literacy: Teacher Training for Primary and Secondary Education Teachers. In Handbook of Research on Integrating ICTs in STEAM Education; IGI Global: Hershey, PA, USA, 2022; pp. 1–21. [Google Scholar]
- Aksoğan, M.; Atici, B. Machine Learning applications in education: A literature review. In Education & Science 2022; EFE Academy: Jaipur, India, 2022; p. 27. [Google Scholar]
- Rezapour, M.; Hansen, L. A machine learning analysis of COVID-19 mental health data. Sci. Rep. 2022, 12, 14965. [Google Scholar] [CrossRef]
- Aitzaouiat, C.E.; Latif, A.; Benslimane, A.; Chin, H.-H. Machine Learning Based Prediction and Modeling in Healthcare Secured Internet of Things. Mob. Netw. Appl. 2022, 27, 84–95. [Google Scholar] [CrossRef]
- Alanazi, A. Using machine learning for healthcare challenges and opportunities. Inform. Med. Unlocked 2022, 30, 100924. [Google Scholar] [CrossRef]
- Hu, Q.; Yu, D.; Xie, Z. Neighborhood classifiers. Expert Syst. Appl. 2008, 34, 866–876. [Google Scholar] [CrossRef]
- Kotsiantis, S.B. Decision trees: A recent overview. Artif. Intell. Rev. 2013, 39, 261–283. [Google Scholar] [CrossRef]
- Abiodun, O.I.; Jantan, A.; Omolara, A.E.; Dada, K.V.; Umar, A.M.; Linus, O.U.; Arshad, H.; Kazaure, A.A.; Gana, U.; Kiru, M.U. Comprehensive review of artificial neural network applications to pattern recognition. IEEE Access 2019, 7, 158820–158846. [Google Scholar] [CrossRef]
- Cervantes, J.; Garcia-Lamont, F.; Rodríguez-Mazahua, L.; Lopez, A. A comprehensive survey on support vector machine classification: Applications, challenges and trends. Neurocomputing 2020, 408, 189–215. [Google Scholar] [CrossRef]
- Yáñez-Márquez, C.; López-Yáñez, I.; Aldape-Pérez, M.; Camacho-Nieto, O.; Argüelles-Cruz, A.J.; Villuendas-Rey, Y. Theoretical foundations for the alpha-beta associative memories: 10 years of derived extensions, models, and applications. Neural Process. Lett. 2018, 48, 811–847. [Google Scholar] [CrossRef]
- Martínez-Trinidad, J.F.; Guzmán-Arenas, A. The logical combinatorial approach to pattern recognition, an overview through selected works. Pattern Recognit. 2001, 34, 741–751. [Google Scholar] [CrossRef]
- Wolpert, D.H. The supervised learning no-free-lunch theorems. In Soft Computing and Industry; Springer: London, UK, 2002; pp. 25–42. [Google Scholar]
- Luengo, J.; Herrera, F. An automatic extraction method of the domains of competence for learning classifiers using data complexity measures. Knowl. Inf. Syst. 2015, 42, 147–180. [Google Scholar] [CrossRef]
- Ma, Y.; Zhao, S.; Wang, W.; Li, Y.; King, I. Multimodality in meta-learning: A comprehensive survey. Knowl.-Based Syst. 2022, 250, 108976. [Google Scholar] [CrossRef]
- Huisman, M.; Van Rijn, J.N.; Plaat, A. A survey of deep meta-learning. Artif. Intell. Rev. 2021, 54, 4483–4541. [Google Scholar] [CrossRef]
- Camacho-Urriolagoitia, F.J.; Villuendas-Rey, Y.; López-Yáñez, I.; Camacho-Nieto, O.; Yáñez-Márquez, C. Correlation Assessment of the Performance of Associative Classifiers on Credit Datasets Based on Data Complexity Measures. Mathematics 2022, 10, 1460. [Google Scholar] [CrossRef]
- Cano, J.-R. Analysis of data complexity measures for classification. Expert Syst. Appl. 2013, 40, 4820–4831. [Google Scholar] [CrossRef]
- Barella, V.H.; Garcia, L.P.; de Souto, M.C.; Lorena, A.C.; de Carvalho, A.C. Assessing the data complexity of imbalanced datasets. Inf. Sci. 2021, 553, 83–109. [Google Scholar] [CrossRef]
- Ho, T.K.; Basu, M. Complexity measures of supervised classification problems. IEEE Trans. Pattern Anal. Mach. Intell. 2002, 24, 289–300. [Google Scholar]
- Bello, M.; Nápoles, G.; Vanhoof, K.; Bello, R. Data quality measures based on granular computing for multi-label classification. Inf. Sci. 2021, 560, 51–67. [Google Scholar] [CrossRef]
- Hernández-Castaño, J.A.; Villuendas-Rey, Y.; Camacho-Nieto, O.; Yáñez-Márquez, C. Experimental platform for intelligent computing (EPIC). Comput. Y Sist. 2018, 22, 245–253. [Google Scholar] [CrossRef]
- Hernández-Castaño, J.A.; Villuendas-Rey, Y.; Nieto, O.C.; Rey-Benguría, C.F. A New Experimentation Module for the EPIC Software. Res. Comput. Sci. 2018, 147, 243–252. [Google Scholar] [CrossRef]
- Lorena, A.C.; Garcia, L.P.; Lehmann, J.; Souto, M.C.; Ho, T.K. How Complex is your classification problem? A survey on measuring classification complexity. ACM Comput. Surv. (CSUR) 2019, 52, 1–34. [Google Scholar] [CrossRef]
- Cummins, L. Combining and Choosing Case Base Maintenance Algorithms; University College Cork: Cork, Ireland, 2013. [Google Scholar]
- Seshia, S.A.; Sadigh, D.; Sastry, S.S. Toward verified artificial intelligence. Commun. ACM 2022, 65, 46–55. [Google Scholar] [CrossRef]
- Krichen, M.; Mihoub, A.; Alzahrani, M.Y.; Adoni, W.Y.H.; Nahhal, T. Are Formal Methods Applicable To Machine Learning And Artificial Intelligence? In Proceedings of the 2022 2nd International Conference of Smart Systems and Emerging Technologies (SMARTTECH), Riyadh, Saudi Arabia, 9–11 May 2022; pp. 48–53. [Google Scholar]
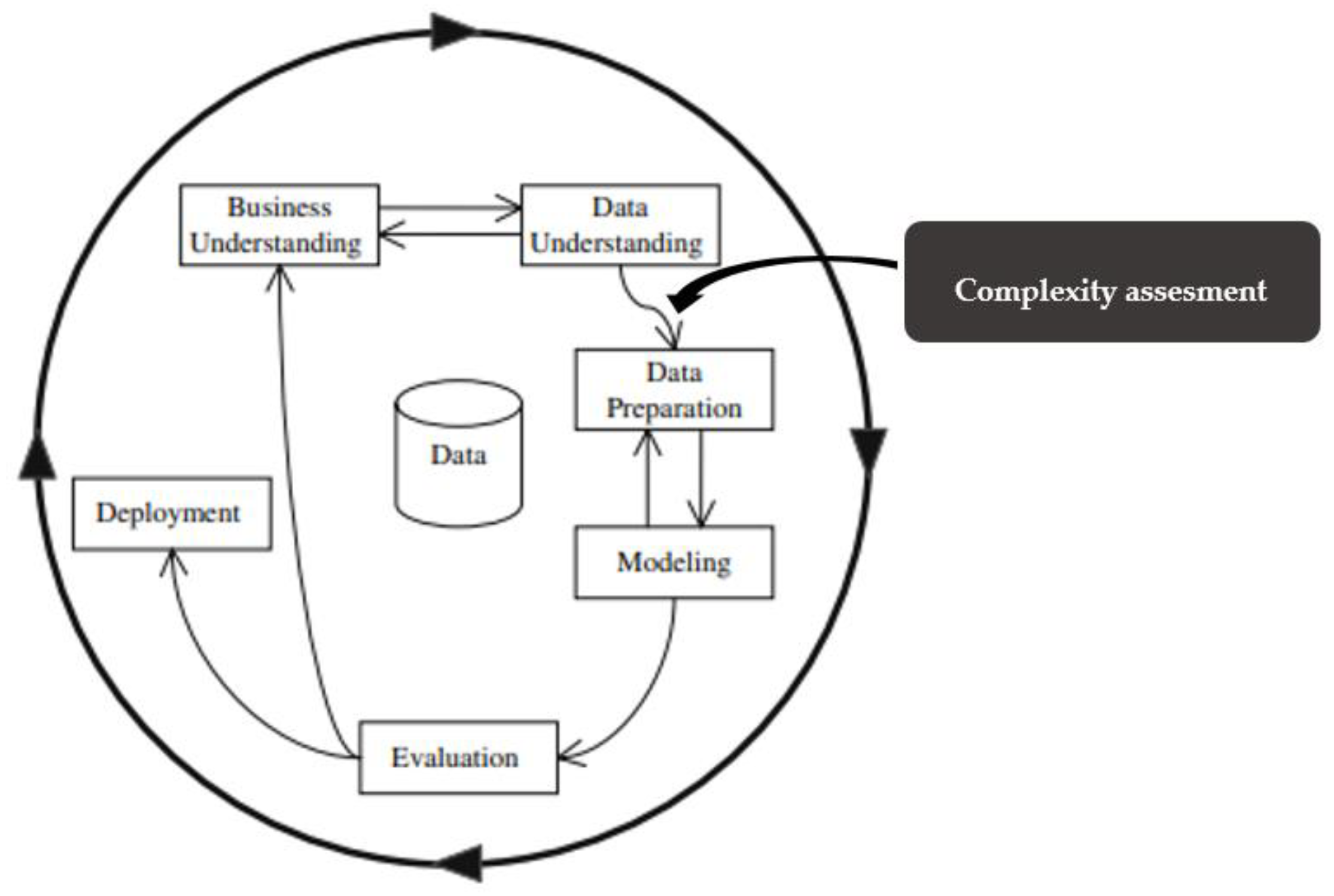
- Cios, K.J.; Swiniarski, R.W.; Pedrycz, W.; Kurgan, L.A. The knowledge discovery process. In Data Mining; Springer: Boston, MA, USA, 2007; pp. 9–24. [Google Scholar]
- Wilson, D.R.; Martinez, T.R. Improved heterogeneous distance functions. JAIR 1997, 6, 1–34. [Google Scholar] [CrossRef]
- Alcalá-Fdez, J.; Fernández, A.; Luengo, J.; Derrac, J.; García, S.; Sánchez, L.; Herrera, F. KEEL Data-Mining Software Tool: Data Set Repository, Integration of Algorithms and Experimental Analysis Framework. J. Mult.-Valued Log. Soft Comput. 2011, 17, 255–287. [Google Scholar]
- Ballabio, D.; Grisoni, F.; Todeschini, R. Multivariate comparison of classification performance measures. Chemom. Intell. Lab. Syst. 2018, 174, 33–44. [Google Scholar] [CrossRef]


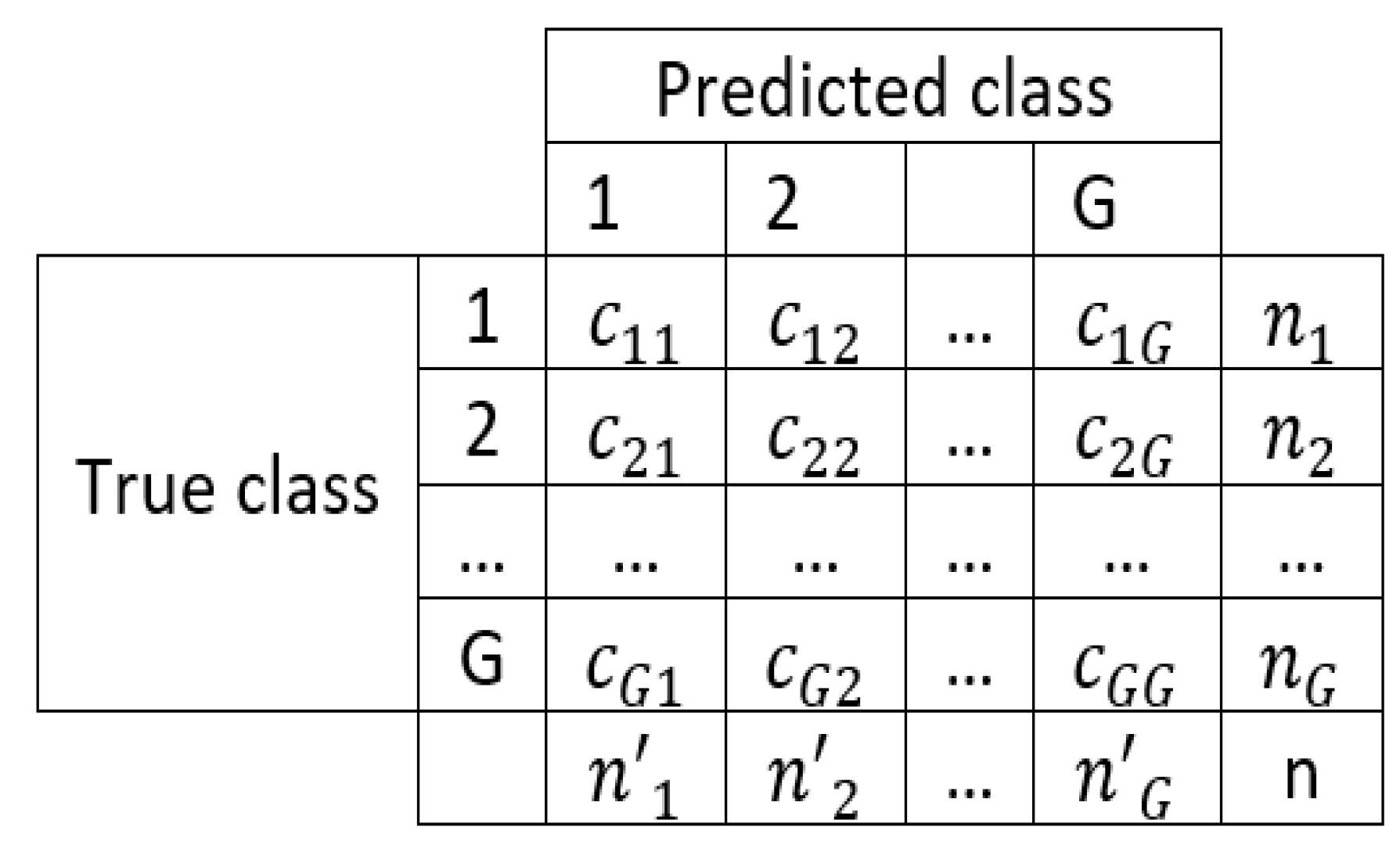
| Measure | Proportion | Boundaries | Complexity [27] | Multiclass | Hybrid | Missing Values |
|---|---|---|---|---|---|---|
| F1 | Direct | (0, 1] | Yes * | No | No | |
| F2 | Direct | (0, 1] | No | No | No | |
| F3 | Direct | [0, 1] | No | No | No | |
| L1 | Direct | [0, 1) | No | No | No | |
| L2 | Direct | [0, 1] | No | No | No | |
| L3 | Direct | [0, 1] | No | No | No | |
| N1 | Direct | [0, 1] | Yes | Yes + | Yes + | |
| N2 | Direct | [0, 1) | Yes | Yes + | Yes + | |
| N3 | Direct | [0, 1] | Yes | No | No | |
| N4 | Direct | [0, 1] | Yes | No | No | |
| T1 | Direct | [0, 1] | Yes | No | No | |
| LSC | Direct | Yes | Yes+ | Yes + |
| Measure | Iris2D | Clover | Tennis |
|---|---|---|---|
| F1_ext | 0.059 | 0.980 | 0.667 |
| F2_ext | 0.000 | 0.374 | 0.007 |
| F3_ext | 0.000 | 0.624 | 0.200 |
| N1 | 0.020 | 0.054 | 0.286 |
| N2 | 0.023 | 0.261 | 0.555 |
| N3_ext | 0.000 | 0.102 | 0.267 |
| LSC | 0.504 | 0.938 | 0.893 |
| Type | Measure | Proportion | Boundaries | Complexity | New |
|---|---|---|---|---|---|
| Feature-based | F1_ext | Direct | [0, 1] | Yes | |
| F2_ext | Direct | [0, 1] | Yes | ||
| F3_ext | Direct | [0, 1] | Yes | ||
| Neighborhood-based | N1 | Direct | [0, 1] | No | |
| N2 | Direct | [0, 1] | No | ||
| N3_ext | Direct | [0, 1] | Yes | ||
| LSC | Direct | No |
| Name | Numeric Attributes | Categorical Attributes | Instances | Classes | %Missing | Non-Error Rate |
|---|---|---|---|---|---|---|
| automobile | 15 | 10 | 205 | 6 | 26.83 | 0.44 |
| bands | 19 | 0 | 539 | 2 | 32.28 | 0.63 |
| breast | 0 | 9 | 286 | 2 | 3.15 | 0.66 |
| cleveland | 13 | 0 | 303 | 5 | 1.98 | 0.36 |
| crx | 6 | 9 | 690 | 2 | 5.36 | 0.58 |
| dermatology | 34 | 0 | 366 | 6 | 2.19 | 0.96 |
| hepatitis | 19 | 0 | 155 | 2 | 48.39 | 0.60 |
| horse-colic | 8 | 15 | 368 | 2 | 98.10 | 0.53 |
| housevotes | 0 | 16 | 435 | 2 | 46.67 | 0.93 |
| mammographic | 5 | 0 | 961 | 2 | 13.63 | 0.75 |
| marketing | 13 | 0 | 8993 | 9 | 23.54 | 0.23 |
| mushroom | 0 | 22 | 8124 | 2 | 30.53 | 1.00 |
| post-operative | 0 | 8 | 90 | 3 | 3.33 | 0.37 |
| saheart | 8 | 1 | 462 | 2 | 0.00 | 0.51 |
| wisconsin | 9 | 0 | 699 | 2 | 2.29 | 0.93 |
| Name | F1_ext | F2_ext | F3_ext | N1 | N2 | N3_ext | LSC |
|---|---|---|---|---|---|---|---|
| automobile | 0.587 | 0.000 | 0.000 | 0.546 | 0.528 | 0.520 | 0.991 |
| bands | 0.757 | 0.000 | 0.009 | 0.415 | 0.450 | 0.368 | 0.993 |
| breast | 0.490 | 0.000 | 0.009 | 0.311 | 0.464 | 0.292 | 0.991 |
| cleveland | 0.735 | 0.000 | 0.000 | 0.588 | 0.546 | 0.601 | 0.993 |
| crx | 0.525 | 0.000 | 0.004 | 0.392 | 0.396 | 0.394 | 0.994 |
| dermatology | 0.056 | 0.000 | 0.000 | 0.054 | 0.343 | 0.040 | 0.874 |
| hepatitis | 0.560 | 0.000 | 0.000 | 0.277 | 0.364 | 0.284 | 0.956 |
| horse-colic | 0.178 | 0.000 | 0.370 | 0.419 | 0.267 | 0.393 | 0.993 |
| housevotes | 0.889 | 0.000 | 0.011 | 0.088 | 0.341 | 0.072 | 0.893 |
| mammographic | 0.911 | 0.001 | 0.670 | 0.252 | 0.345 | 0.254 | 0.993 |
| marketing | 0.804 | 0.644 | 0.000 | 0.728 | 0.706 | 0.724 | 1.000 |
| mushroom | 0.733 | 0.000 | 0.000 | 0.002 | 0.269 | 0.000 | 0.876 |
| post-operative | 0.727 | 0.000 | 0.029 | 0.408 | 0.489 | 0.453 | 0.987 |
| saheart | 0.818 | 0.063 | 0.005 | 0.406 | 0.475 | 0.424 | 0.988 |
| wisconsin | 0.325 | 0.161 | 0.141 | 0.065 | 0.280 | 0.061 | 0.747 |
| Name | F1_ext | F2_ext | F3_ext | N1 | N2 | N3_ext | LSC |
|---|---|---|---|---|---|---|---|
| automobile | 2.400 | 3.600 | 2.800 | 1056.000 | 1055.400 | 949.400 | 1120.000 |
| bands | 2.200 | 0.000 | 10.200 | 4035.200 | 4407.000 | 4164.600 | 3746.800 |
| breast | 0.000 | 0.000 | 0.000 | 161.200 | 204.000 | 188.000 | 303.200 |
| cleveland | 1.200 | 0.000 | 2.000 | 1297.400 | 1374.600 | 1458.200 | 1402.200 |
| crx | 1.400 | 0.000 | 2.400 | 2836.600 | 3269.600 | 3329.400 | 3130.400 |
| dermatology | 1.200 | 0.000 | 4.600 | 1490.200 | 1491.600 | 1528.400 | 1467.600 |
| hepatitis | 0.600 | 0.000 | 5.200 | 609.400 | 526.200 | 539.400 | 631.400 |
| horse-colic | 0.800 | 0.200 | 1.600 | 1276.800 | 1249.600 | 1316.000 | 1555.400 |
| housevotes | 0.800 | 0.000 | 0.800 | 849.600 | 879.400 | 879.000 | 808.600 |
| mammographic | 1.000 | 0.000 | 2.000 | 3524.200 | 3600.600 | 3611.400 | 3371.200 |
| marketing | 35.200 | 5.600 | 67.600 | 664,776.000 | 726,545.800 | 729,344.000 | 646,769.200 |
| mushroom | 9.800 | 4.800 | 9.200 | 123,978.800 | 129,301.400 | 122,140.800 | 122,648.000 |
| post-operative | 0.000 | 0.000 | 0.000 | 27.800 | 20.400 | 27.400 | 24.800 |
| saheart | 0.600 | 0.000 | 0.800 | 547.000 | 531.400 | 550.000 | 542.600 |
| wisconsin | 1.400 | 0.000 | 2.800 | 3440.400 | 3394.000 | 3137.600 | 2905.400 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Camacho-Urriolagoitia, F.J.; Villuendas-Rey, Y.; Yáñez-Márquez, C.; Lytras, M. Novel Features and Neighborhood Complexity Measures for Multiclass Classification of Hybrid Data. Sustainability 2023, 15, 1995. https://doi.org/10.3390/su15031995
Camacho-Urriolagoitia FJ, Villuendas-Rey Y, Yáñez-Márquez C, Lytras M. Novel Features and Neighborhood Complexity Measures for Multiclass Classification of Hybrid Data. Sustainability. 2023; 15(3):1995. https://doi.org/10.3390/su15031995
Chicago/Turabian StyleCamacho-Urriolagoitia, Francisco J., Yenny Villuendas-Rey, Cornelio Yáñez-Márquez, and Miltiadis Lytras. 2023. "Novel Features and Neighborhood Complexity Measures for Multiclass Classification of Hybrid Data" Sustainability 15, no. 3: 1995. https://doi.org/10.3390/su15031995
APA StyleCamacho-Urriolagoitia, F. J., Villuendas-Rey, Y., Yáñez-Márquez, C., & Lytras, M. (2023). Novel Features and Neighborhood Complexity Measures for Multiclass Classification of Hybrid Data. Sustainability, 15(3), 1995. https://doi.org/10.3390/su15031995









