Mathematical Modeling and A Novel Heuristic Method for Flexible Job-Shop Batch Scheduling Problem with Incompatible Jobs
Abstract
1. Introduction
1.1. Job-Shop Scheduling Problem
1.2. Flexible Job-Shop Scheduling Problem
1.3. Batch Scheduling
1.4. Batch Scheduling Considering Incompatible Jobs
1.5. Contribution of This Work
2. MILP Model of the FJSPBI
2.1. Problem Description
2.2. MILP Model of the FJSPBI
3. Solution Method for the FJSPBI
3.1. Framework of the Proposed LNSIT for the FJSPBI
| Algorithm 1 LNSIT for FJSPBI |
| Input: FJSPBI instances and parameters Output: Optimal solution 1: Create initial solution let current solution initial tabu-related iteration of each operation 2: while the maximum number of iterations is not met do 3: Implement the tabu-based worst removal operator on and obtain a partial solution 4: Implement the optimal insertion-based deep greedy repair operator on and obtain a new solution 5: if do 6: 7: if do 8: 9: end if 10: else 11: Add the removed operations to tabu list with a probability of 12: 13: if do 14: Remove operation from the tabu list 15: end if 16: end if 17: Present the exponential Monte Carlo acceptance criterion 18: end while |
3.2. Initial Solution Construction
3.3. Tabu-Based Worst Removal Operator
| Algorithm 2 Tabu-based worst removal |
| Input: Current solution tabu list constant Output: Set of operations needs to be removed 1: while is in do 2: if the number of operations do 3: For all , sort by descending order 4: Remove operator = 5: end if 6: end while |
3.4. Deep Greedy Insertion Operator
| Algorithm 3 Optimal insertion-based deep greedy insertion |
| Input: Set of removed operations current solution structure , and corresponding objective Output: Solution structure with the operation inserted and corresponding objective value 1: while the number of operations and do 2: Present the optimal insertion strategy 3: for and do 4: Insert each operation to each and calculate 5: For all , sort difference of objective by ascending order 6: Choose operator 7: Insert the operator = and calculate 8: end for 9: end while |
3.4.1. Optimal Insertion Strategy
3.4.2. Search Perturbation
3.5. Objective Evaluation
4. Computational Experiments
4.1. Instances and Parameters
4.2. Numerical Results of Instances
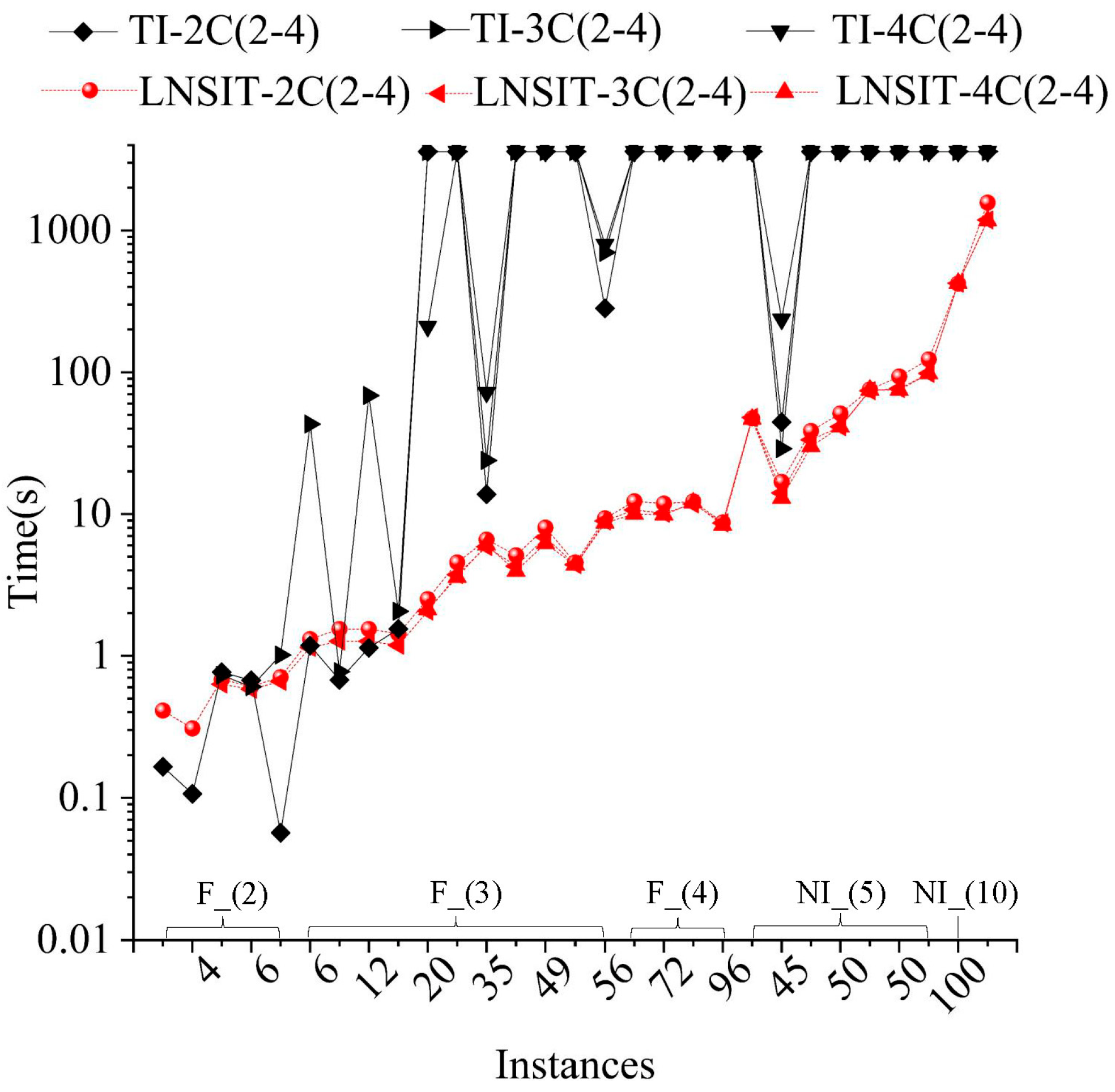
4.2.1. Results of the Exact Algorithm
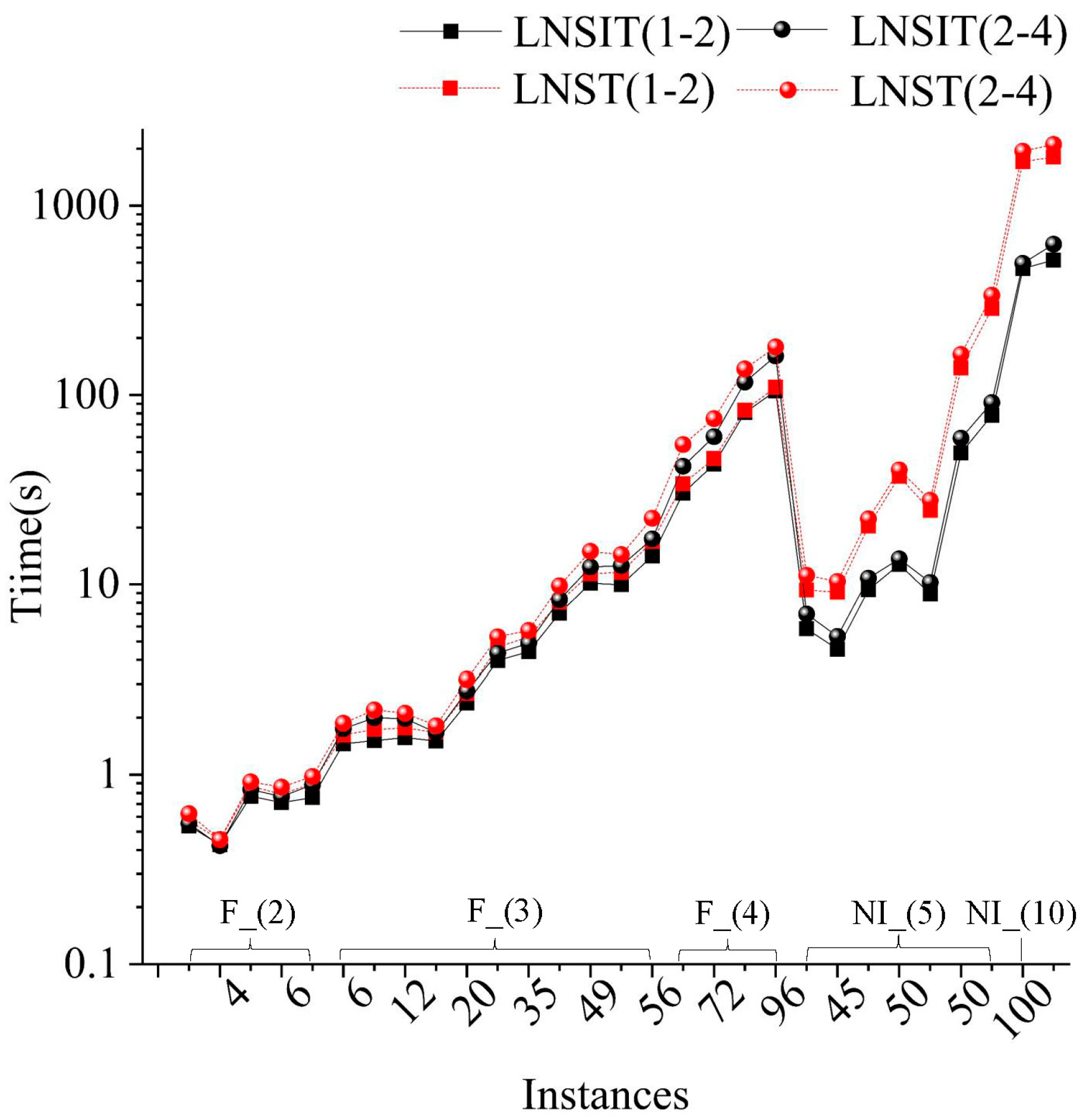
4.2.2. Results of the Proposed Heuristic Framework
4.2.3. Impacts of Batch Capacity and Incompatibility Rate
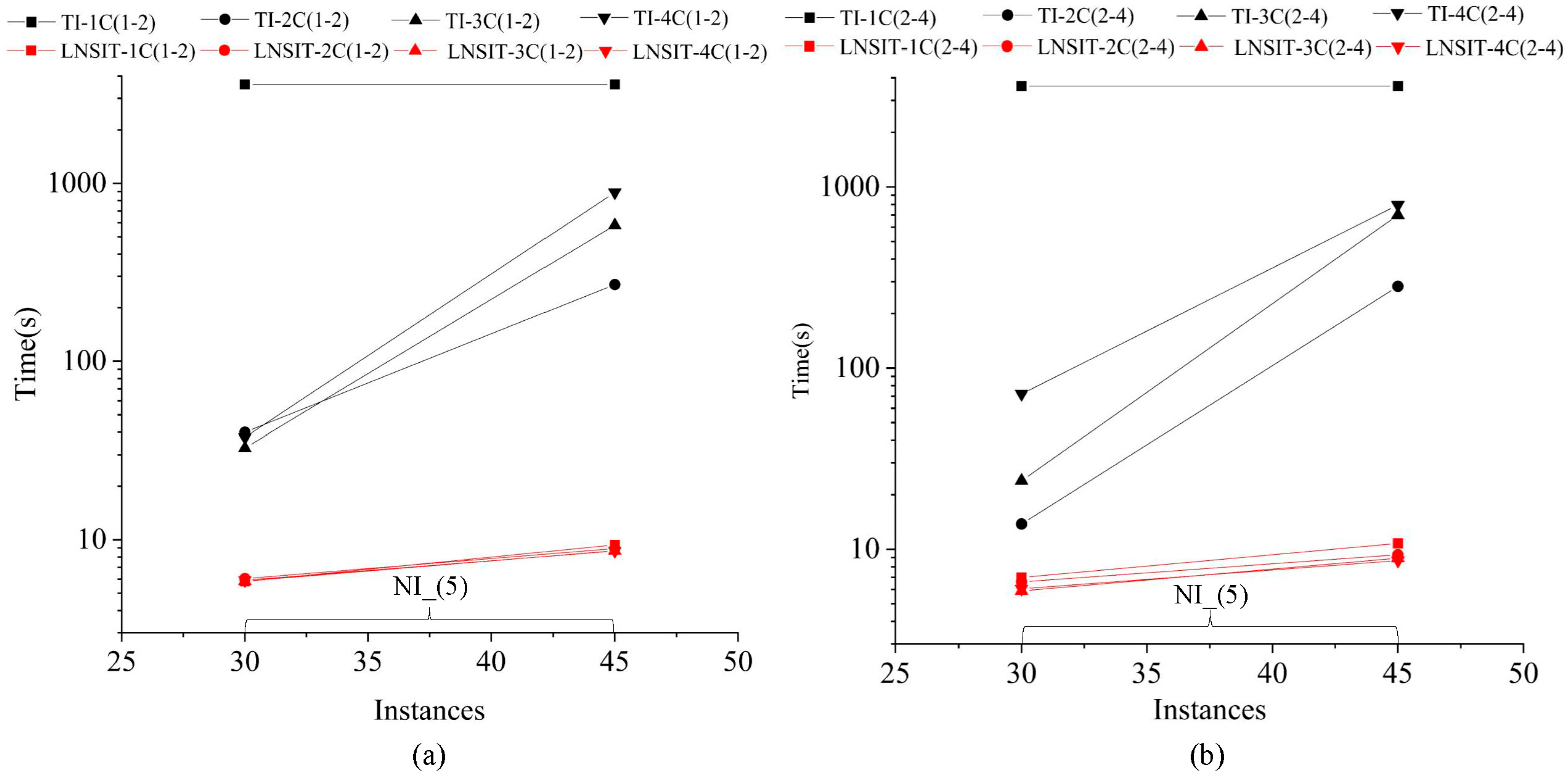
4.2.4. The Impact of Instance Scales
4.2.5. Influence of Machine Processing Rate
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Raaymakers, W.H.M.; Hoogeveen, J.A. Scheduling multipurpose batch process industries with no–wait restrictions by simulated annealing. Eur. J. Oper. Res. 2000, 126, 131–151. [Google Scholar] [CrossRef]
- Joo, B.J.; Shim, S.-O.; Chua, T.J.; Cai, T.X. Multi-level job scheduling under processing time uncertainty. Comput. Ind. Eng. 2018, 120, 480–487. [Google Scholar] [CrossRef]
- Zhang, J.; Ding, G.; Zou, Y.; Qin, S.; Fu, J. Review of job shop scheduling research and its new perspectives under Industry 4.0. J. Intell. Manuf. 2017, 30, 1809–1830. [Google Scholar] [CrossRef]
- Carlier, J.; Pinson, E. An Algorithm for Solving the Job-Shop Problem. Manag. Sci. 1989, 35, 164–176. [Google Scholar] [CrossRef]
- Fisher, H.; Thompson, G.L. Probabilistic learning combinations of local job-shop scheduling rules. In Industrial Scheduling, 1st ed.; Muth, J.F., Thompson, G.L., Eds.; Prentice-Hall: Englewood Cliffs, NJ, USA, 1963; pp. 225–251. [Google Scholar]
- Lawrence, S. Resouce constrained project scheduling: An experimental investigation of heuristic scheduling techniques. In Supplement to Resource Constrained Project Scheduling; Carnegie Mellon University, GSIA: Pittsburgh, PA, USA, 1984. [Google Scholar]
- AitZai, A.; Benmedjdoub, B.; Boudhar, M. Branch–and–bound and PSO algorithms for no–wait job shop scheduling. J. Intell. Manuf. 2016, 27, 679–688. [Google Scholar] [CrossRef]
- Ozolins, A. Bounded dynamic programming algorithm for the job shop problem with sequence dependent setup times. Oper. Res. 2020, 20, 1701–1728. [Google Scholar] [CrossRef]
- Baptiste, P.; Flamini, M.; Sourd, F. Lagrangian bounds for just–in–time job–shop scheduling. Comput. Oper. Res. 2008, 35, 906–915. [Google Scholar] [CrossRef]
- Kurdi, M. An effective new island model genetic algorithm for job shop scheduling problem. Comput. Oper. Res. 2016, 67, 132–142. [Google Scholar] [CrossRef]
- Eshim, S.E.; Hamed, M.M. Extended Hybrid Genetic Algorithm for Solving Job Shop Scheduling Problem. Int. J. Sci. Eng. Appl. 2021, 10, 017–020. [Google Scholar] [CrossRef]
- Peng, B.; Lü, Z.; Cheng, T. A tabu search/path relinking algorithm to solve the job shop scheduling problem. Comput. Oper. Res. 2015, 53, 154–164. [Google Scholar] [CrossRef]
- Vela, C.R.; Afsar, S.; Palacios, J.J.; González-Rodríguez, I.; Puente, J. Evolutionary tabu search for flexible due-date satisfaction in fuzzy job shop scheduling. Comput. Oper. Res. 2020, 119, 104931. [Google Scholar] [CrossRef]
- Huang, R.-H.; Yu, T.-H. An effective ant colony optimization algorithm for multi-objective job-shop scheduling with equal-size lot-splitting. Appl. Soft Comput. 2017, 57, 642–656. [Google Scholar] [CrossRef]
- Vinoski, J. New Research Shows Consumers Already Expect Mass Personalization. Time to Get Ready! Available online: https://www.forbes.com/sites/jimvinoski/2020/01/20/new–research–shows–consumers–already–expect–mass–personalization–time–to–get–ready/?sh=6c77e8f5223e (accessed on 20 January 2020).
- Brandimarte, P. Routing and scheduling in a flexible job shop by tabu search. Ann. Oper. Res. 1993, 41, 157–183. [Google Scholar] [CrossRef]
- Mastrolilli, M.; Gambardella L, M. Effective neighbourhood functions for the flexible job shop problem. J. Sched. 2000, 3, 3–20. [Google Scholar] [CrossRef]
- Song, H.; Liu, P. A Study on the Optimal Flexible Job-Shop Scheduling with Sequence-Dependent Setup Time Based on a Hybrid Algorithm of Improved Quantum Cat Swarm Optimization. Sustainability 2022, 14, 9547. [Google Scholar] [CrossRef]
- Zhang, S.; Hou, T.; Qu, Q.; Glowacz, A.; Alqhtani, S.M.; Irfan, M.; Królczyk, G.; Li, Z. An Improved Mayfly Method to Solve Distributed Flexible Job Shop Scheduling Problem under Dual Resource Constraints. Sustainability 2022, 14, 12120. [Google Scholar] [CrossRef]
- Fernandes, J.M.R.C.; Homayouni, S.M.; Fontes, D.B.M.M. Energy-Efficient Scheduling in Job Shop Manufacturing Systems: A Literature Review. Sustainability 2022, 14, 6264. [Google Scholar] [CrossRef]
- Fowler, J.W.; Mönch, L. A survey of scheduling with parallel batch (p-batch) processing. Eur. J. Oper. Res. 2021, 298, 1–24. [Google Scholar] [CrossRef]
- Damodaran, P.; Vélez-Gallego, M.C. A simulated annealing algorithm to minimize makespan of parallel batch processing machines with unequal job ready times. Expert Syst. Appl. 2012, 39, 1451–1458. [Google Scholar] [CrossRef]
- Muter, I. Exact algorithms to minimize makespan on single and parallel batch processing machines. Eur. J. Oper. Res. 2020, 285, 470–483. [Google Scholar] [CrossRef]
- Chang, P.-Y.; Melouk, S. Minimizing makespan on parallel batch processing machines. Int. J. Prod. Res. 2004, 42, 4211–4220. [Google Scholar] [CrossRef]
- Jia, Z.-H.; Leung, J.Y.-T. A meta-heuristic to minimize makespan for parallel batch machines with arbitrary job sizes. Eur. J. Oper. Res. 2015, 240, 649–665. [Google Scholar] [CrossRef]
- Jia, Z.-H.; Zhang, H.; Long, W.-T.; Leung, J.Y.-T.; Li, K.; Li, W. A meta-heuristic for minimizing total weighted flow time on parallel batch machines. Comput. Ind. Eng. 2018, 125, 298–308. [Google Scholar] [CrossRef]
- Shahvari, O.; Logendran, R. An Enhanced tabu search algorithm to minimize a bi-criteria objective in batching and scheduling problems on unrelated-parallel machines with desired lower bounds on batch sizes. Comput. Oper. Res. 2017, 77, 154–176. [Google Scholar] [CrossRef]
- Ham, A. Flexible job shop scheduling problem for parallel batch processing machine with compatible job families. Appl. Math. Model. 2017, 45, 551–562. [Google Scholar] [CrossRef]
- Ham, A.M.; Cakici, E. Flexible job shop scheduling problem with parallel batch processing machines: MIP and CP approaches. Comput. Ind. Eng. 2016, 102, 160–165. [Google Scholar] [CrossRef]
- Jia, Z.-H.; Wang, C.; Leung, J.Y.-T. An ACO algorithm for makespan minimization in parallel batch machines with non-identical job sizes and incompatible job families. Appl. Soft Comput. 2016, 38, 395–404. [Google Scholar] [CrossRef]
- Li, X.; Li, Y.; Huang, Y. Heuristics and lower bound for minimizing maximum lateness on a batch processing machine with incompatible job families. Comput. Oper. Res. 2019, 106, 91–101. [Google Scholar] [CrossRef]
- Gahm, C.; Wahl, S.; Tuma, A. Scheduling parallel serial-batch processing machines with incompatible job families, sequence-dependent setup times and arbitrary sizes. Int. J. Prod. Res. 2022, 60, 5131–5154. [Google Scholar] [CrossRef]
- Wu, Y.; Weise, T.; Chiong, R. Local search for the traveling salesman problem: A comparative study. In Proceedings of the 2015 IEEE 14th International Conference on Cognitive Informatics & Cognitive Computing (ICCI* CC), Beijing, China, 14 July 2015; pp. 213–220. [Google Scholar] [CrossRef]
- Tang, M.; Ji, B.; Fang, X.; Yu, S.S. Discretization-Strategy-Based Solution for Berth Allocation and Quay Crane Assignment Problem. J. Mar. Sci. Eng. 2022, 10, 495. [Google Scholar] [CrossRef]
- Ji, B.; Yuan, X.; Yuan, Y.; Lei, X.; Iu, H.H.C. An Adaptive Large Neighborhood Search for Solving Generalized Lock Scheduling Problem: Comparative Study With Exact Methods. IEEE Trans. Intell. Transp. Syst. 2019, 21, 3344–3356. [Google Scholar] [CrossRef]
- Shaw, P. A new local search algorithm providing high quality solutions to vehicle routing problems. In APES Group, Dept of Computer Science; University of Strathclyde: Glasgow, UK, 1997; p. 46. [Google Scholar]
- Schambers, A.; Eavis-O’Quinn, M.; Roberge, V.; Tarbouchi, M. Route planning for electric vehicle efficiency using the Bellman–Ford algorithm on an embedded GPU. In Proceedings of the 2018 4th International Conference on Optimization and Applications, Mohammedia, Morocco, 26–27 April; 2018; pp. 1–6. [Google Scholar]
- Ayob, M.; Kendall, G. A monte carlo hyper–heuristic to optimise component placement sequencing for multi head placement machine. In Proceedings of the international conference on intelligent technologies, Chiang Mai, Thailand, 12–15 October 2003. [Google Scholar]
- Ropke, S.; Pisinger, D. An adaptive large neighborhood search heuristic for the pickup and delivery problem with time windows. Transp. Sci. 2006, 40, 455–472. [Google Scholar] [CrossRef]
- van Laarhoven, P.J.M.; Aarts, E.H.L.; Lenstra, J.K. Job Shop Scheduling by Simulated Annealing. Oper. Res. 1992, 40, 113–125. [Google Scholar] [CrossRef]
- Fattahi, P.; Mehrabad, M.S.; Jolai, F. Mathematical modeling and heuristic approaches to flexible job shop scheduling problems. J. Intell. Manuf. 2007, 18, 331–342. [Google Scholar] [CrossRef]
- Dauzère-Pérès, S.; Paulli, J. An integrated approach for modeling and solving the general multiprocessor job-shop scheduling problem using tabu search. Ann. Oper. Res. 1997, 70, 281–306. [Google Scholar] [CrossRef]











| Sets and Parameters | Meaning |
|---|---|
| J: | Set of jobs. |
| O: | Set of operations. |
| Oj: | Set of operations of job j. |
| I: | Set of job families. |
| M: | Set of machines. |
| Mjo: | Set of machines capable of processing operation o of job j. |
| B: | Set of batches. The number of batches is defined as the number of jobs multiplied by the number of operations. |
| pjom: | Processing time of operation o of job j on machine m. |
| : | Processing capacity of machine . |
| : | Max (). |
| Variables | Meaning |
| : | Binary variable, if operation of job is processed in batch , and 0 otherwise. |
| : | Binary variable, if batch is processed on machine , and 0 otherwise. |
| : | Binary variable, if job belonging to family is processed in batch , and 0 otherwise. |
| : | Start time of operation of job . |
| : | Completion time of operation of job . |
| : | Start time of batch . |
| : | Completion time of batch . |
| : | Processing time of batch . |
| : | Makespan. |
| Instance | Instance | ||||||
|---|---|---|---|---|---|---|---|
| F_01 | 2 | 2 | 2 | F_11 | 5 | 3 | 6 |
| F_02 | 2 | 2 | 2 | F_12 | 5 | 3 | 7 |
| F_03 | 3 | 2 | 2 | F_13 | 6 | 3 | 7 |
| F_04 | 3 | 2 | 2 | F_14 | 7 | 3 | 7 |
| F_05 | 3 | 2 | 2 | F_15 | 7 | 3 | 7 |
| F_06 | 3 | 3 | 2 | F_16 | 8 | 3 | 7 |
| F_07 | 3 | 3 | 5 | F_17 | 8 | 4 | 7 |
| F_08 | 3 | 3 | 4 | F_18 | 9 | 4 | 8 |
| F_09 | 3 | 3 | 3 | F_19 | 11 | 4 | 8 |
| F_10 | 4 | 3 | 5 | F_20 | 12 | 4 | 8 |
| Instance | ||||
|---|---|---|---|---|
| NI_01–NI_06 | 5 | 5 | [1, 10] | 0.2, 0.8 |
| NI_07 | 5 | 5 | [10, 15] | 0.8 |
| NI_08 | 10 | 5 | [5, 10] | 0.8 |
| NI_09 | 10 | 10 | [10, 15] | 0.8 |
| Instance | Scale | |||
|---|---|---|---|---|
| NI_01 | 2, 3, 4 | 5/5/9 | 0.2 | 1–2, 2–4 |
| NI_02 | 2, 3, 4 | 5/5/10 | 0.2 | 1–2, 2–4 |
| NI_03 | 2, 3, 4 | 5/5/10 | 0.2 | 1–2, 2–4 |
| NI_04 | 2, 3, 4 | 5/5/9 | 0.8 | 1–2, 2–4 |
| NI_05 | 2, 3, 4 | 5/5/10 | 0.8 | 1–2, 2–4 |
| NI_06 | 2, 3, 4 | 5/5/6 | 0.8 | 1–2, 2–4 |
| NI_07 | 2, 3, 4 | 5/5/15 | 0.8 | 1–2, 2–4 |
| NI_08 | 2, 3, 4 | 10/5/10 | 0.8 | 1–2, 2–4 |
| NI_09 | 2, 3, 4 | 10/10/15 | 0.8 | 1–2, 2–4 |
| Instance | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| TI | FI [28] | TI | FI [28] | |||||||||
| F_01 | 66 | 66 | 66 | 66 | 66 | 66 | 66 | 66 | 66 | 66 | 66 | 66 |
| F_02 | 107 | 107 | 107 | 107 | 107 | 107 | 107 | 107 | 107 | 107 | 107 | 107 |
| F_03 | 208 | 208 | 208 | 208 | 208 | 208 | 208 | 208 | 208 | 208 | 208 | 208 |
| F_04 | 272 | 272 | 272 | 272 | 272 | 272 | 272 | 272 | 272 | 272 | 272 | 272 |
| F_05 | 100 | 100 | 100 | 100 | 100 | 100 | 100 | 100 | 100 | 100 | 100 | 100 |
| F_06 | 320 | 320 | 320 | 320 | 320 | 320 | 310 | 310 | 310 | 310 | 310 | 310 |
| F_07 | 397 | 397 | 397 | 397 | 397 | 397 | 397 | 397 | 397 | 397 | 397 | 397 |
| F_08 | 216 | 216 | 216 | 216 | 216 | 216 | 216 | 216 | 216 | 216 | 216 | 216 |
| F_09 | 210 | 210 | 210 | 210 | 210 | 210 | 210 | 210 | 210 | 210 | 210 | 210 |
| F_10 | 516 | 516 | 516 | 516 | 516 | 516 | 486 | 486 | 486 | 486 | 486 | 486 |
| F_11 | 410 | 410 | 410 | 419 | 410 | 410 | 403 | 403 | 403 | 403 | 403 | 403 |
| F_12 | 410 | 410 | 410 | 410 | 410 | 410 | 396 | 396 | 396 | 396 | 396 | 396 |
| F_13 | 420 | 453 | 420 | 420 | 420 | 420 | 397 | 397 | 397 | 397 | 397 | 397 |
| F_14 | 546 | 506 | 503 | 503 | 503 | 503 | 496 | 496 | 496 | 496 | 496 | 496 |
| F_15 | 488 | 488 | 488 | 488 | 488 | 488 | 426 | 426 | 426 | 426 | 426 | 426 |
| F_16 | 614 | 614 | 614 | 614 | 614 | 614 | 614 | 614 | 614 | 614 | 614 | 614 |
| F_17 | 827 | 975 | 789 | 789 | 789 | 789 | 914 | 852 | 764 | 764 | 764 | 764 |
| F_18 | 841 | 884 | 787 | 789 | 784 | 788 | – | 764 | 764 | 764 | 764 | 764 |
| F_19 | – | – | 843 | 865 | 843 | 849 | – | – | 764 | 764 | 764 | 764 |
| F_20 | – | – | 1005 | 1024 | 994 | 1001 | – | – | 944 | 954 | 944 | 947 |
| Instance | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| TI | TI | |||||||||
| NI_01 | 531 | 531 | 531 | 531 | 531 | 510 | 510 | 510 | 510 | 510 |
| NI_02 | – | 714 | 710 | 685 | 688 | – | 625 | 619 | 618 | 618 |
| NI_03 | 665 | 559 | 559 | 559 | 559 | 582 | 556 | 556 | 556 | 556 |
| NI_04 | 285 | 285 | 285 | 285 | 285 | 285 | 285 | 285 | 285 | 285 |
| NI_05 | 924 | 317 | 320 | 310 | 313 | 783 | 310 | 310 | 308 | 308 |
| NI_06 | 218 | 218 | 218 | 218 | 218 | 218 | 218 | 218 | 218 | 218 |
| NI_07 | – | 418 | 417 | 415 | 413 | – | 417 | 415 | 410 | 411 |
| NI_08 | – | 539 | 550 | 523 | 524 | – | 491 | 502 | 476 | 486 |
| NI_09 | – | 348 | 346 | 342 | 339 | – | 340 | 341 | 334 | 334 |
| Ins | Scale | 2 Job Families | 3 Job Families | 4 Job Families | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| TI | TI | TI | TI | TI | TI | ||||||||
| F_01 | 2/2/2 | 66 | 66 | 66 | 66 | ||||||||
| F_02 | 2/2/2 | 107 | 107 | 107 | 107 | ||||||||
| F_03 | 3/2/2 | 208 | 208 | 208 | 208 | 221 | 221 | 221 | 221 | ||||
| F_04 | 3/2/2 | 277 | 277 | 277 | 277 | 355 | 355 | 355 | 355 | ||||
| F_05 | 3/2/2 | 107 | 107 | 100 | 100 | 119 | 119 | 119 | 119 | ||||
| F_06 | 3/2/3 | 320 | 320 | 310 | 310 | 320 | 320 | 320 | 320 | ||||
| F_07 | 3/5/3 | 397 | 397 | 397 | 397 | 397 | 397 | 397 | 397 | ||||
| F_08 | 3/4/3 | 216 | 216 | 216 | 216 | 253 | 253 | 253 | 253 | ||||
| F_09 | 3/3/3 | 210 | 210 | 210 | 210 | 210 | 210 | 210 | 210 | ||||
| F_10 | 4/5/3 | 516 | 516 | 516 | 516 | 516 | 516 | 516 | 516 | 516 | 516 | 516 | 516 |
| F_11 | 5/6/3 | 415 | 425 | 415 | 415 | 453 | 460 | 420 | 420 | 465 | 465 | 465 | 465 |
| F_12 | 5/7/3 | 419 | 419 | 419 | 419 | 419 | 419 | 419 | 419 | 446 | 446 | 423 | 423 |
| F_13 | 6/7/3 | 460 | 460 | 446 | 454 | 457 | 457 | 413 | 420 | 459 | 466 | 468 | 459 |
| F_14 | 7/7/3 | 527 | 527 | 503 | 503 | 568 | 527 | 517 | 503 | 561 | 554 | 503 | 527 |
| F_15 | 7/7/3 | 514 | 514 | 484 | 484 | 513 | 513 | 469 | 469 | 519 | 514 | 483 | 473 |
| F_16 | 8/7/3 | 615 | 614 | 614 | 614 | 614 | 614 | 614 | 614 | 634 | 614 | 614 | 614 |
| F_17 | 8/7/4 | – | 814 | 808 | 784 | 936 | 809 | – | 789 | – | 871 | – | 809 |
| F_18 | 9/8/4 | – | 827 | 799 | 789 | – | 834 | – | 819 | – | 827 | – | 830 |
| F_19 | 11/8/4 | – | 910 | – | 822 | – | 996 | – | 991 | – | 1004 | – | 986 |
| F_20 | 12/8/4 | – | 1102 | – | 1020 | – | 1149 | – | 1072 | – | 1171 | – | 1118 |
| NI_01 | 5/5/9 | 535 | 531 | 531 | 531 | 571 | 531 | – | 531 | 531 | 531 | 531 | 531 |
| NI_02 | 5/5/10 | – | 685 | – | 660 | – | 694 | – | 650 | – | 694 | – | 694 |
| NI_03 | 5/5/10 | – | 559 | – | 556 | – | 559 | – | 559 | – | 559 | – | 556 |
| NI_04 | 5/5/9 | 285 | 285 | 285 | 285 | 285 | 285 | 285 | 285 | 285 | 285 | 285 | 285 |
| NI_05 | 5/5/10 | – | 310 | – | 315 | – | 317 | – | 311 | – | 313 | – | 313 |
| NI_06 | 5/5/6 | 218 | 218 | 218 | 218 | 218 | 218 | 218 | 218 | 218 | 218 | 218 | 218 |
| NI_07 | 5/5/15 | – | 414 | – | 413 | – | 413 | – | 415 | – | 415 | – | 414 |
| NI_08 | 10/5/10 | – | 519 | – | 513 | – | 542 | – | 524 | – | 543 | – | 538 |
| NI_09 | 10/10/15 | – | 340 | – | 333 | – | 341 | – | 339 | – | 339 | – | 337 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ji, B.; Zhang, S.; Yu, S.S.; Zhang, B. Mathematical Modeling and A Novel Heuristic Method for Flexible Job-Shop Batch Scheduling Problem with Incompatible Jobs. Sustainability 2023, 15, 1954. https://doi.org/10.3390/su15031954
Ji B, Zhang S, Yu SS, Zhang B. Mathematical Modeling and A Novel Heuristic Method for Flexible Job-Shop Batch Scheduling Problem with Incompatible Jobs. Sustainability. 2023; 15(3):1954. https://doi.org/10.3390/su15031954
Chicago/Turabian StyleJi, Bin, Shujing Zhang, Samson S. Yu, and Binqiao Zhang. 2023. "Mathematical Modeling and A Novel Heuristic Method for Flexible Job-Shop Batch Scheduling Problem with Incompatible Jobs" Sustainability 15, no. 3: 1954. https://doi.org/10.3390/su15031954
APA StyleJi, B., Zhang, S., Yu, S. S., & Zhang, B. (2023). Mathematical Modeling and A Novel Heuristic Method for Flexible Job-Shop Batch Scheduling Problem with Incompatible Jobs. Sustainability, 15(3), 1954. https://doi.org/10.3390/su15031954








