Transient Model for the Hydrodynamic Force in a Hydraulic Capsule Pipeline Transport System
Abstract
:1. Introduction
2. Transient Model for the Hydrodynamic Force
2.1. Fundamental Equation of Rigid-Body Dynamics
2.2. Far-Field Resolution of the Hydrodynamic Force
2.3. Reduced-Order Method
2.4. Transient Model for Dynamic Force
3. Experiment and Numerical Method
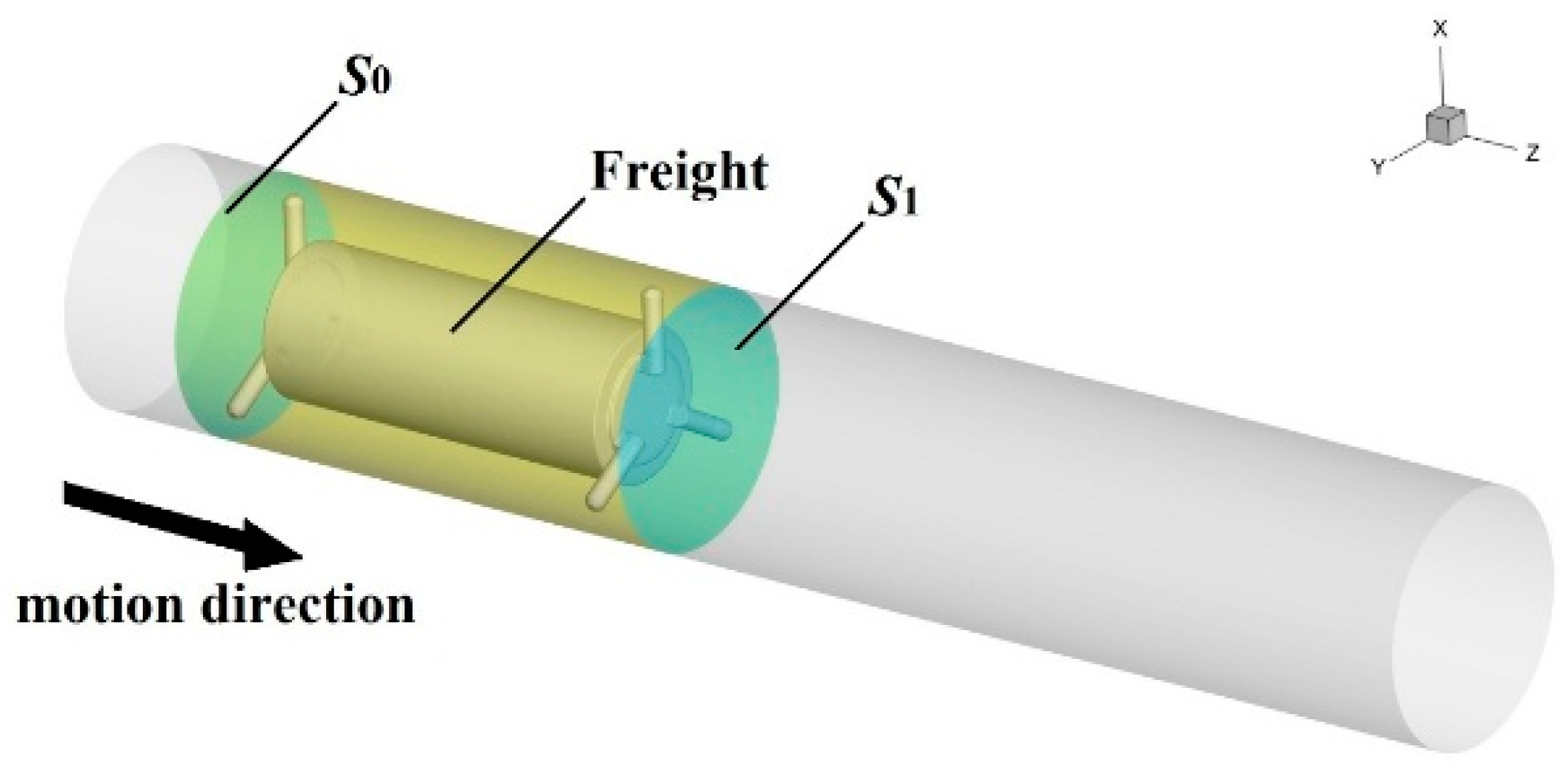
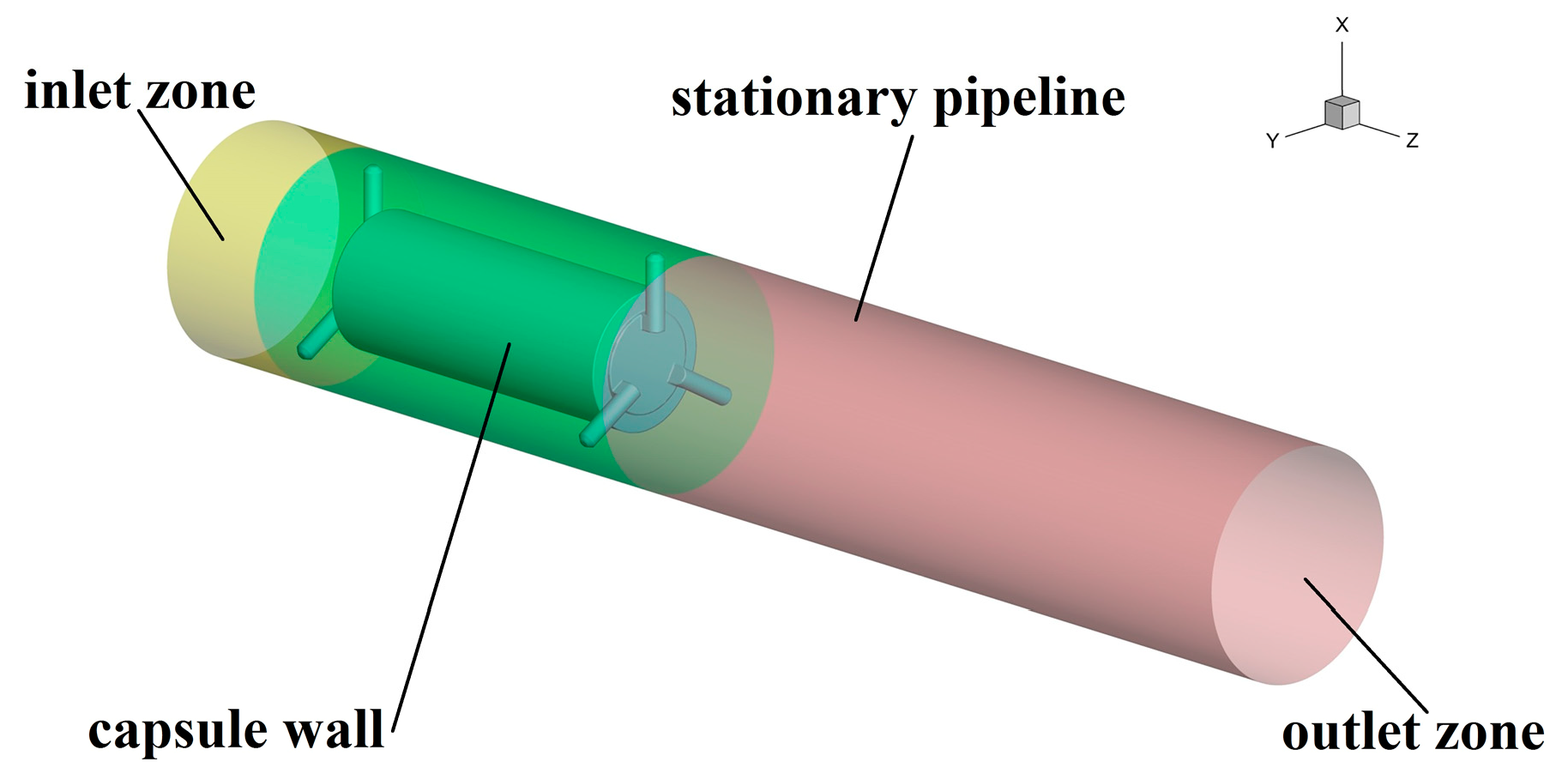
3.1. Research Conditions
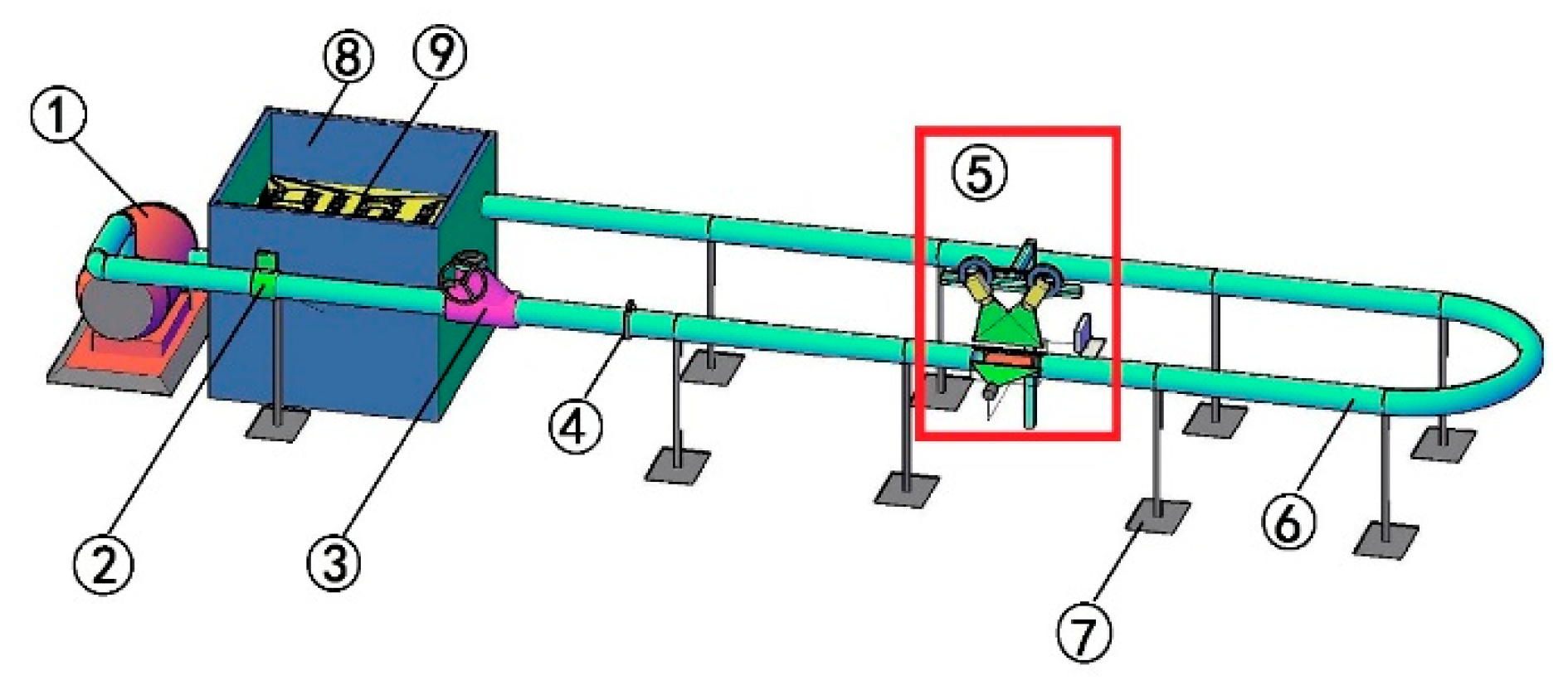
3.2. Physical Experimental System
3.3. Numerical Simulation
3.4. The Relative Error of the Simulation Results
4. Results and Discussions
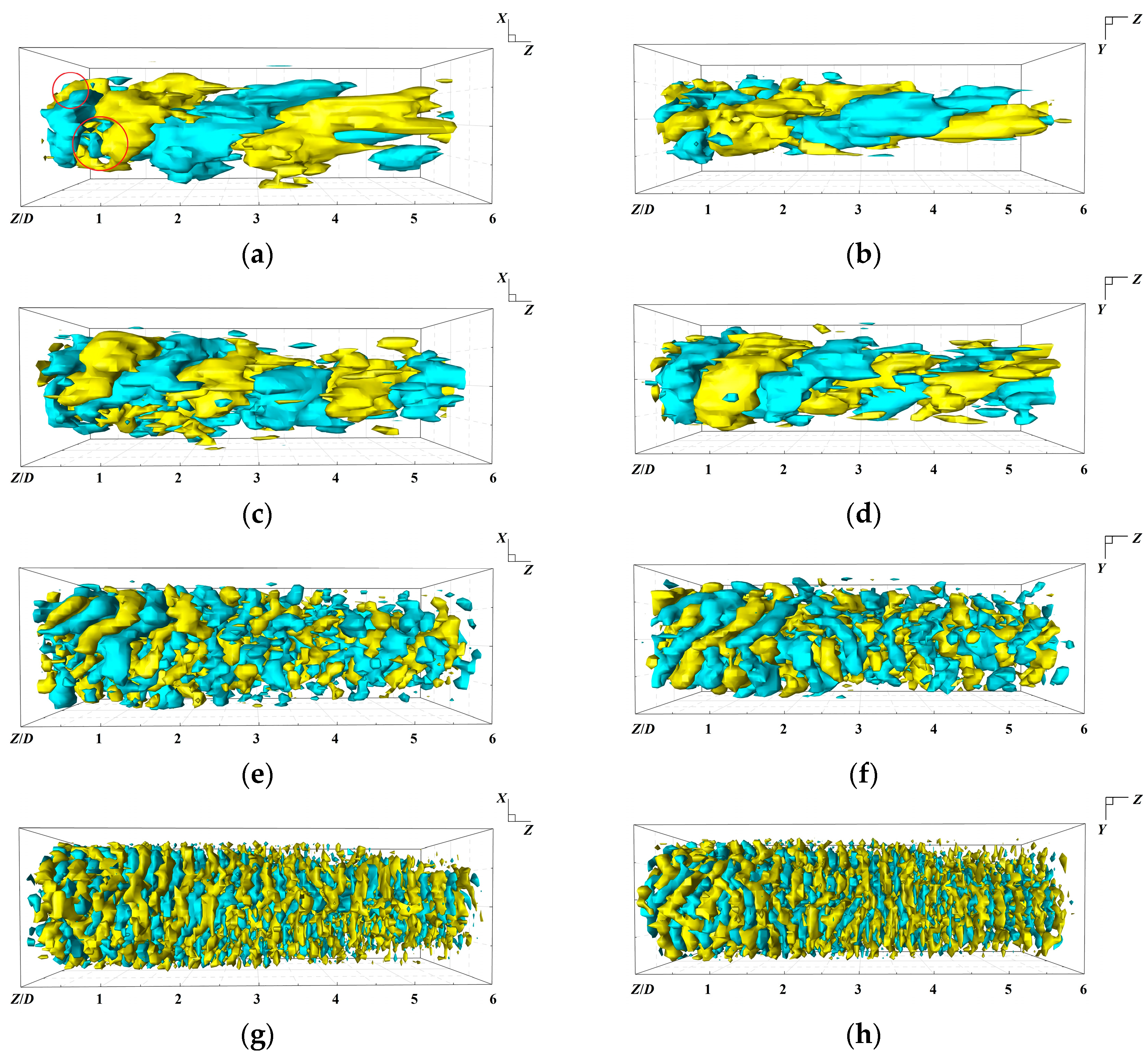
4.1. Coherent Vortex Structure of Fluctuating Modes
4.2. Hydrodynamic Force Characteristics
- (1)
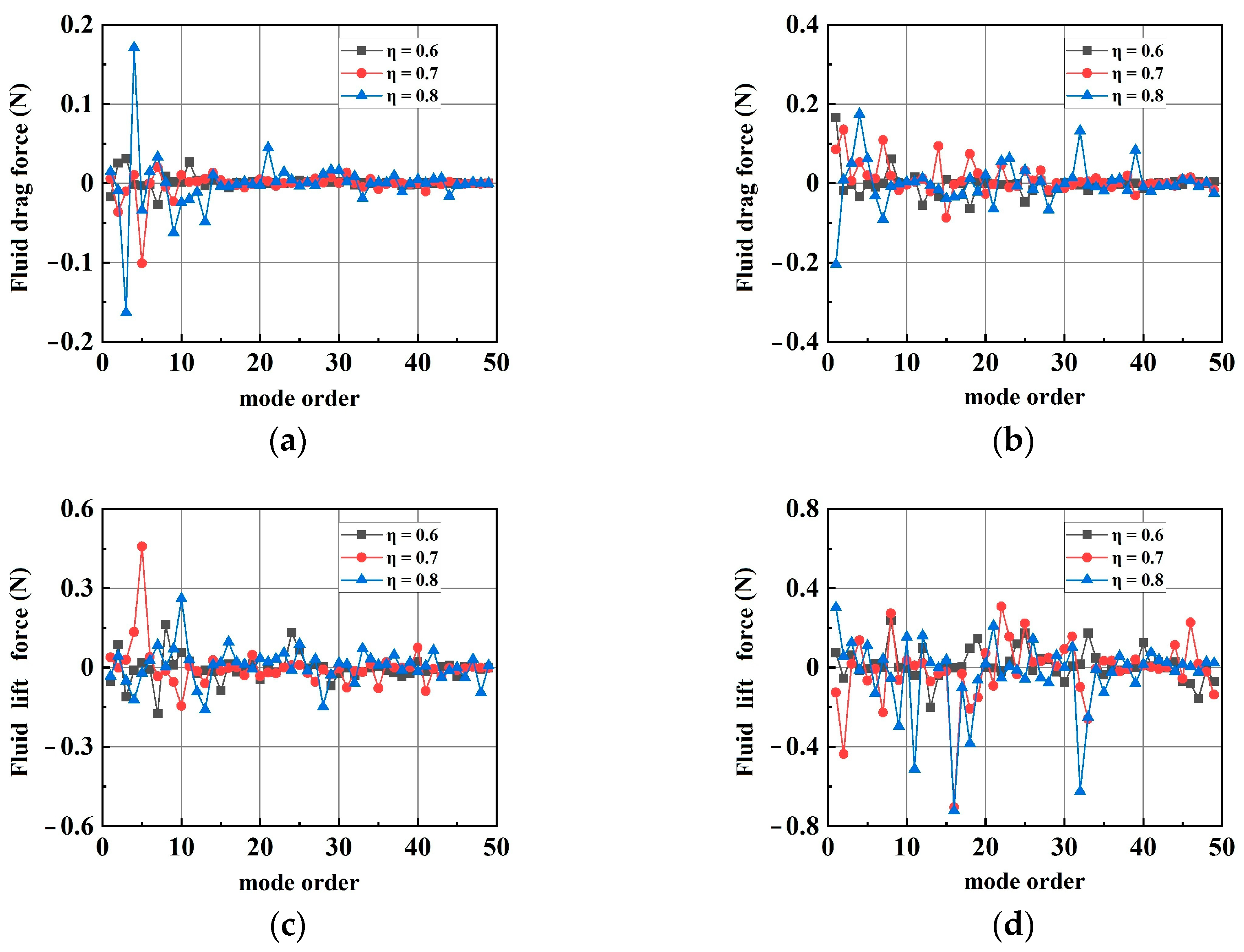
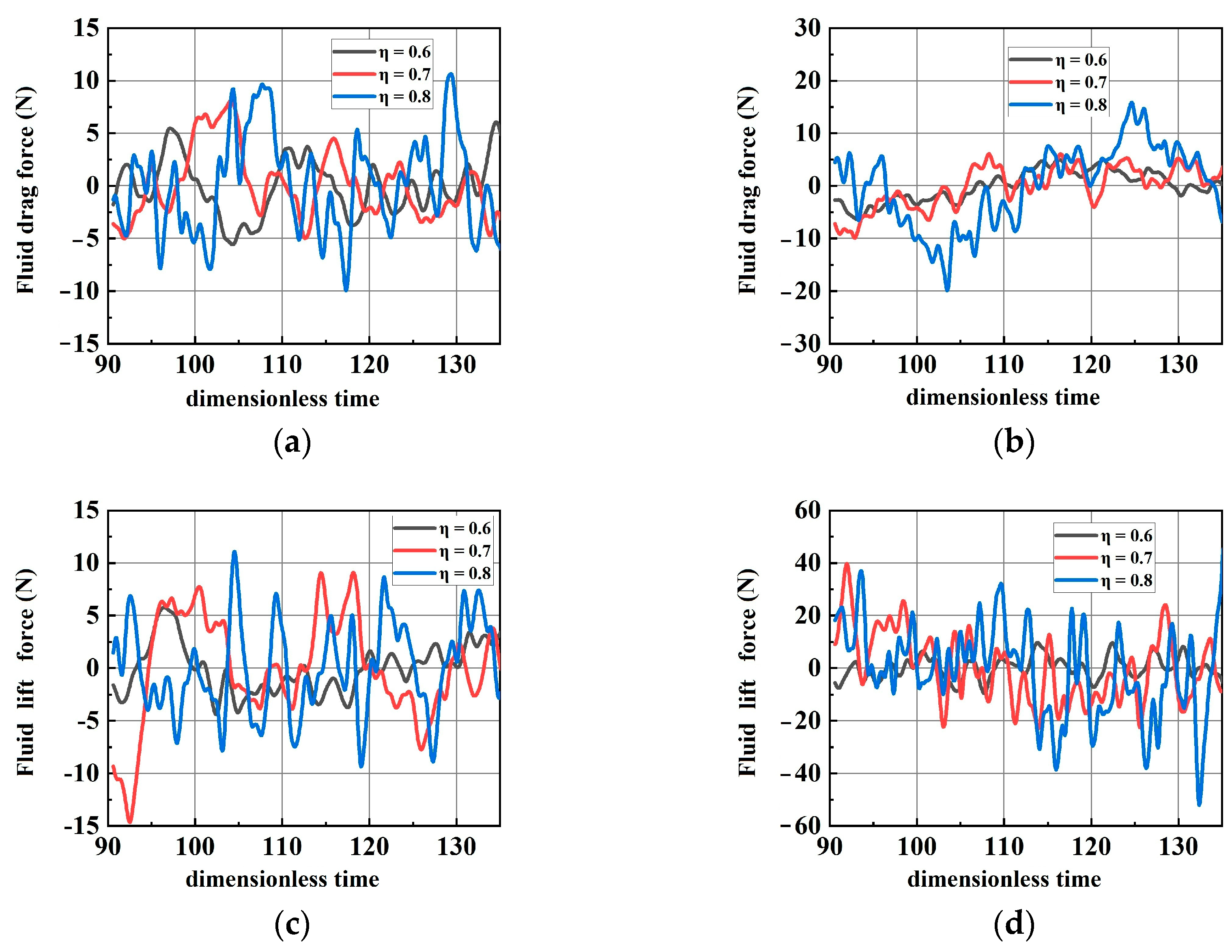
- Steady and Transient Components
- (2)
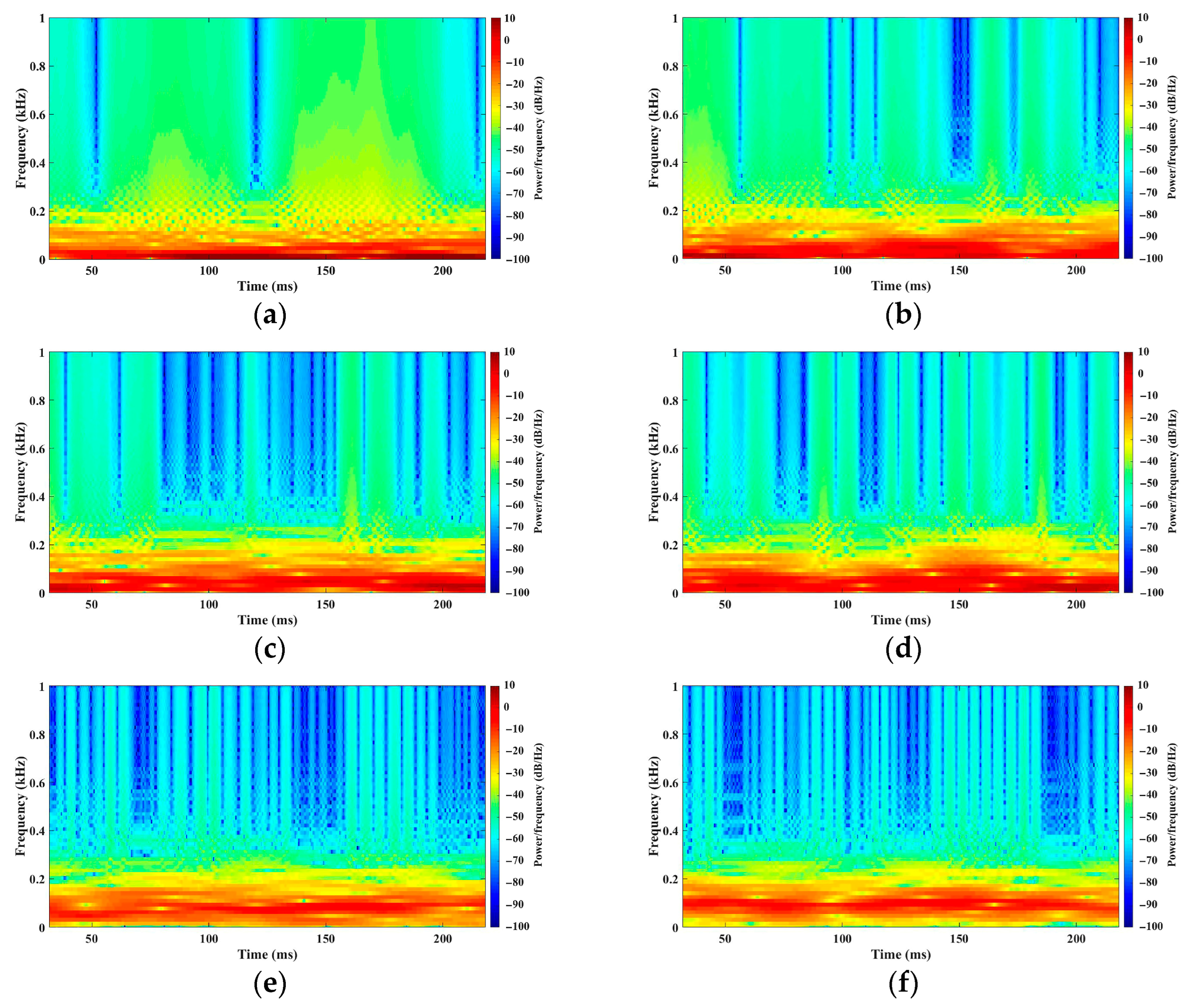
- Transient frequency characteristic
5. Conclusions
- (1)
- The transient model of the hydrodynamic force was developed using Newton’s second law of motion–force and acceleration. Then, the hydrodynamic force was resolved using the far-field resolution method and expressed by the reduced-order method as the product of time coefficients and corresponding mode functions. Finally, the time coefficients were transformed into frequency coefficients by discrete Fourier transform;
- (2)
- After carrying out the proper orthogonal decomposition, the coherent vortex structures of fluctuating modes were shown. The velocities of the iso-surfaces of the coherent vortex of the wake flow exhibited an annular trend in terms of circumferential connection. The annular structures formed by the coherent vortex gradually became more fragmented, and the number of structures increased as the mode order increased;
- (3)
- The steady component and transient component of hydrodynamic force were resolved, and the general trend seen in the forces in the transient components was that the maximum amplitude of forces reduced with the increase in mode order. The amplitude-, direction-, and time-dependent variations in the transient components constituted the transient evolution of the transient components in the hydrodynamic force. Using short-term Fourier transform, the frequency components and their variations in different terms across the whole time range can be acquired.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Nomenclature
| a(t) | time coefficient |
| A(k) | frequency coefficient |
| DC | fluid drag force |
| Faxis | result force on the capsule |
| FN | supporting force |
| k | frequency |
| LC | fluid lift force |
| lC | length of capsule |
| mc | total mass of the capsule |
| U | velocity distribution |
| P | static pressure |
| Q | flow |
| S | surface of the control volume |
| t | time |
| VC | axial speed of the capsule |
| η | diameter ratio |
| μf | frictional coefficient |
| φ | mode function |
References
- Balazadeh Meresht, N.; Moghadasi, S.; Munshi, S.; Shahbakhti, M.; McTaggart-Cowan, G. Advances in Vehicle and Powertrain Efficiency of Long-Haul Commercial Vehicles: A Review. Energies 2023, 16, 6809. [Google Scholar] [CrossRef]
- Khazini, L.; Kalajahi, M.J.; Blond, N. An Analysis of Emission Reduction Strategy for Light and Heavy-Duty Vehicles Pollutions in High Spatial-Temporal Resolution and Emission. Environ. Sci. Pollut. Res. 2022, 29, 23419–23435. [Google Scholar] [CrossRef] [PubMed]
- Achuo, E.D.; Miamo, C.W.; Nchofoung, T.N. Energy consumption and environmental sustainability: What lessons for posterity? Energy Rep. 2022, 8, 12491–12502. [Google Scholar] [CrossRef]
- Xue, P.; Liu, J.; Liu, B.; Zhu, C. Impact of Urbanisation on the Spatial and Temporal Evolution of Carbon Emissions and the Potential for Emission Reduction in a Dual-Carbon Reduction Context. Sustainability 2023, 15, 4715. [Google Scholar] [CrossRef]
- Javanmardi, E.; Hoque, M.; Tauheed, A.; Umar, M. Evaluating the Factors Affecting Electric Vehicles Adoption Considering the Sustainable Development Level. World Electr. Veh. J. 2023, 14, 120. [Google Scholar] [CrossRef]
- Okyere, S.; Yang, J.; Adams, C.A. Optimizing the Sustainable Multimodal Freight Transport and Logistics System Based on the Genetic Algorithm. Sustainability 2022, 14, 11577. [Google Scholar] [CrossRef]
- Shi, H.; Yuan, J.; Li, Y. The Impact of Swirls on Slurry Flows in Horizontal Pipelines. J. Mar. Sci. Eng. 2021, 9, 1201. [Google Scholar] [CrossRef]
- Chen, Y.; Li, G.; Duan, J.; Liu, H.; Xu, S.; Guo, Y.; Hua, W.; Jiang, J. Review of Oil–Water Flow Characteristics of Emptying by Water Displacing Oil in Mobile Pipelines. Energies 2023, 16, 2174. [Google Scholar] [CrossRef]
- Jiwa, M.Z.; Kim, Y.T.; Mustaffa, Z.; Kim, S.; Kim, D.K. A Simplified Approach for Predicting Bend Radius in HDPE Pipelines during Offshore Installation. J. Mar. Sci. Eng. 2023, 11, 2032. [Google Scholar] [CrossRef]
- Hong, X.; Huang, L.; Gong, S.; Xiao, G. Shedding Damage Detection of Metal Underwater Pipeline External Anticorrosive Coating by Ultrasonic Imaging Based on HOG + SVM. J. Mar. Sci. Eng. 2021, 9, 364. [Google Scholar] [CrossRef]
- Li, Z.; Wang, G.; Yao, S.; Yun, F.; Jia, P.; Li, C.; Wang, L. A Semi-Analytical Method for the Sealing Performance Prediction of Subsea Pipeline Compression Connector. J. Mar. Sci. Eng. 2023, 11, 854. [Google Scholar] [CrossRef]
- Paul, A.R.; Bhattacharyya, S. Analysis and Design for Hydraulic Pipeline Carrying Capsule Train. J. Pipeline Syst. Eng. Pract. 2021, 12, 04021003. [Google Scholar] [CrossRef]
- Asim, T.; Algadi, A.; Mishra, R. Effect of Capsule Shape on Hydrodynamic Characteristics and Optimal Design of Hydraulic Capsule Pipelines. J. Petrol. Sci. Eng. 2018, 161, 290–408. [Google Scholar] [CrossRef]
- Asim, T.; Mishra, R.; Abushaala, S.; Jain, A. Development of A Design Methodology for Hydraulic Pipelines Carrying Rectangular Capsules. Int. J. Pres. Pip. 2016, 146, 111–128. [Google Scholar] [CrossRef]
- Ulusarslan, D. Comparison of Experimental Pressure Gradient and Experimental Relationships for the Low Density Spherical Capsule Train with Slurry Flow Relationships. Powder Technol. 2008, 185, 170–175. [Google Scholar] [CrossRef]
- O’Connell, R.; Lenau, C.; Zhao, T. Capsule Separation by Linear Induction Motor in Pneumatic Capsule Pipeline Capsule Transport System. J. Pipeline Syst. Eng. 2010, 1, 84–90. [Google Scholar] [CrossRef]
- Chen, Y.; Guo, D.; Chen, Z.; Fan, Y.; Li, X. Using a Multi-Objective Programming Model to Validate Feasibility of an Underground Freight Transportation System for the Yangshan Port in Shanghai. Tunn. Undergr. Space Technol. 2018, 81, 463–471. [Google Scholar] [CrossRef]
- Asim, T.; Mishra, R. Computational Fluid Dynamics Based Optimal Design of Hydraulic Capsule Pipelines Transporting Cylindrical Capsules. Powder Technol. 2016, 295, 180–201. [Google Scholar] [CrossRef]
- Liu, H.; Graze, H. Lift and Drag on Stationary Capsule in Pipeline. J. Hydraul. Eng. ASCE 1983, 109, 28–47. [Google Scholar] [CrossRef]
- Asim, T.; Mishra, R. Optimal Design of Hydraulic Capsule Pipelines Transporting Spherical Capsules. Can. J. Chem. Eng. 2016, 94, 966–979. [Google Scholar] [CrossRef]
- Zhao, Y.; Li, Y.; Song, X. PIV Measurement and Proper Orthogonal Decomposition Analysis of Annular Gap Flow of a Hydraulic Machine. Machines 2022, 10, 645. [Google Scholar] [CrossRef]
- Vooren, J. The Downstream Flow of a Transonic Aircraft: A Small Disturbance, High Reynolds Number Analysis. Aerosp. Sci. Technol. 2008, 12, 457–468. [Google Scholar] [CrossRef]
- Aono, H.; Liang, F.; Liu, H. Near and Far-Field Aerodynamics in Insect Hovering Flight: An Integrated Computational Study. J. Exp. Biol. 2008, 211, 239–257. [Google Scholar] [CrossRef] [PubMed]
- Chen, Z.; Zhang, B. Drag Prediction Method Investigation Basing on the Wake Integral. Acta Aerodyn. Sin. 2009, 27, 329–334. [Google Scholar] [CrossRef]
- Paparone, L.; Tognaccini, R. Computational Fluid Dynamics-Based Drag Prediction and Decomposition. AIAA J. 2012, 41, 1647–1657. [Google Scholar] [CrossRef]
- Talezade, A.; Mojtaba, S.; Manshadi, D. Streamlined Bodies Drag Force Estimation Using Wake Integration Technique. J. Braz. Soc. Mech. Sci. 2020, 42, 293. [Google Scholar] [CrossRef]
- Lumley, J.; Blossey, P. Control of Turbulence. Annu. Rev. Fluid Mech. 1998, 30, 311–327. [Google Scholar] [CrossRef]
- D’Agostino, D.; Diez, M.; Felli, M.; Serani, A. PIV Snapshot Clustering Reveals the Dual Deterministic and Chaotic Nature of Propeller Wakes at Macro- and Micro-Scales. J. Mar. Sci. Eng. 2023, 11, 1220. [Google Scholar] [CrossRef]
- Zhao, Y.; Li, Y.; Sun, X. Modal Analysis of the Hydrodynamic Force of a Capsule in a Hydraulic Capsule Pipeline. J. Mar. Sci. Eng. 2023, 11, 1738. [Google Scholar] [CrossRef]

| Item | Parameters | ||
|---|---|---|---|
| Flow conditions | Q = 40 m3 h−1 and Q = 60 m3 h−1 | ||
| Diameter ratios | η = 0.6, η = 0.7, η = 0.8 | ||
| Other parameters | mc·g = 20 N, lC = 150 mm, μf = 0.25 | ||
| Q = 40 m3 h−1 η = 0.6 | Q = 40 m3 h−1 η = 0.7 | Q = 40 m3 h−1 η = 0.8 | |
| Q = 60 m3 h−1 η = 0.6 | Q = 60 m3 h−1 η = 0.7 | Q = 60 m3 h−1 η = 0.8 | |
| Flow | Q = 40 m3 h−1 | Q = 60 m3 h−1 | ||||
|---|---|---|---|---|---|---|
| Diameter ratio | η = 0.6 | η = 0.7 | η = 0.8 | η = 0.6 | η = 0.7 | η = 0.8 |
| Relative error | 1.06% | 2.77% | 3.02% | 2.86% | 2.61% | 2.79% |
| Hydrodynamic Force | Flow Q | Diameter Ratio η = 0.6 | Diameter Ratio η = 0.7 | Diameter Ratio η = 0.8 |
|---|---|---|---|---|
| DC | 40 m3 h−1 | 4.468 N | 4.562 N | 4.922 N |
| 60 m3 h−1 | 4.516 N | 4.850 N | 5.255 N | |
| LC | 40 m3 h−1 | 0.128 N | 0.154 N | 0.246 N |
| 60 m3 h−1 | 0.135 N | 0.201 N | 0.253 N |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhao, Y.; Li, Y.; Sun, X. Transient Model for the Hydrodynamic Force in a Hydraulic Capsule Pipeline Transport System. Sustainability 2023, 15, 15575. https://doi.org/10.3390/su152115575
Zhao Y, Li Y, Sun X. Transient Model for the Hydrodynamic Force in a Hydraulic Capsule Pipeline Transport System. Sustainability. 2023; 15(21):15575. https://doi.org/10.3390/su152115575
Chicago/Turabian StyleZhao, Yiming, Yongye Li, and Xihuan Sun. 2023. "Transient Model for the Hydrodynamic Force in a Hydraulic Capsule Pipeline Transport System" Sustainability 15, no. 21: 15575. https://doi.org/10.3390/su152115575
APA StyleZhao, Y., Li, Y., & Sun, X. (2023). Transient Model for the Hydrodynamic Force in a Hydraulic Capsule Pipeline Transport System. Sustainability, 15(21), 15575. https://doi.org/10.3390/su152115575






