A Multi-Objective Simulated Annealing Local Search Algorithm in Memetic CENSGA: Application to Vaccination Allocation for Influenza
Abstract
1. Introduction
2. Literature Review
3. Preliminaries
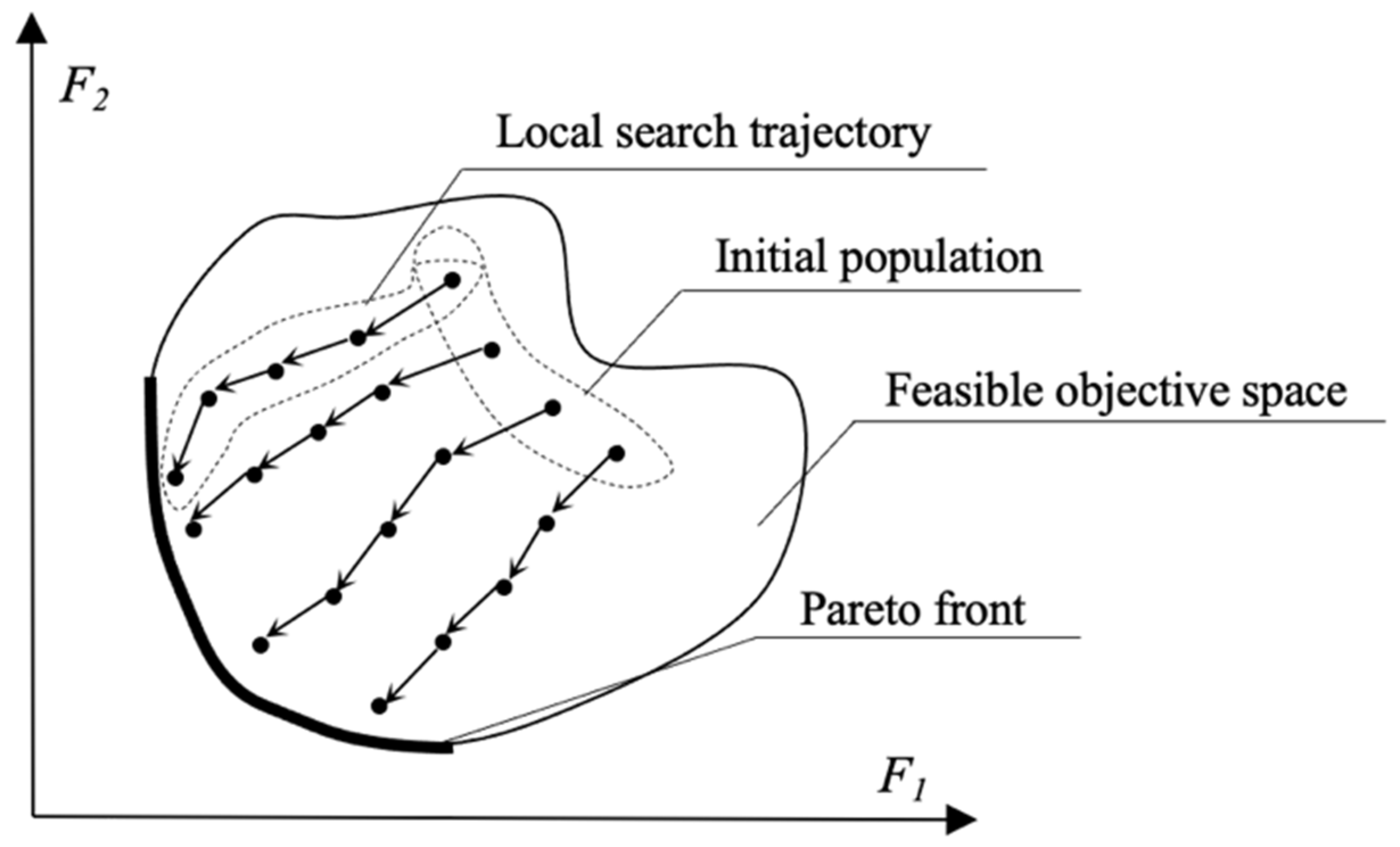
3.1. Multi-Objective Evolutionary Optimization
3.2. CENSGA
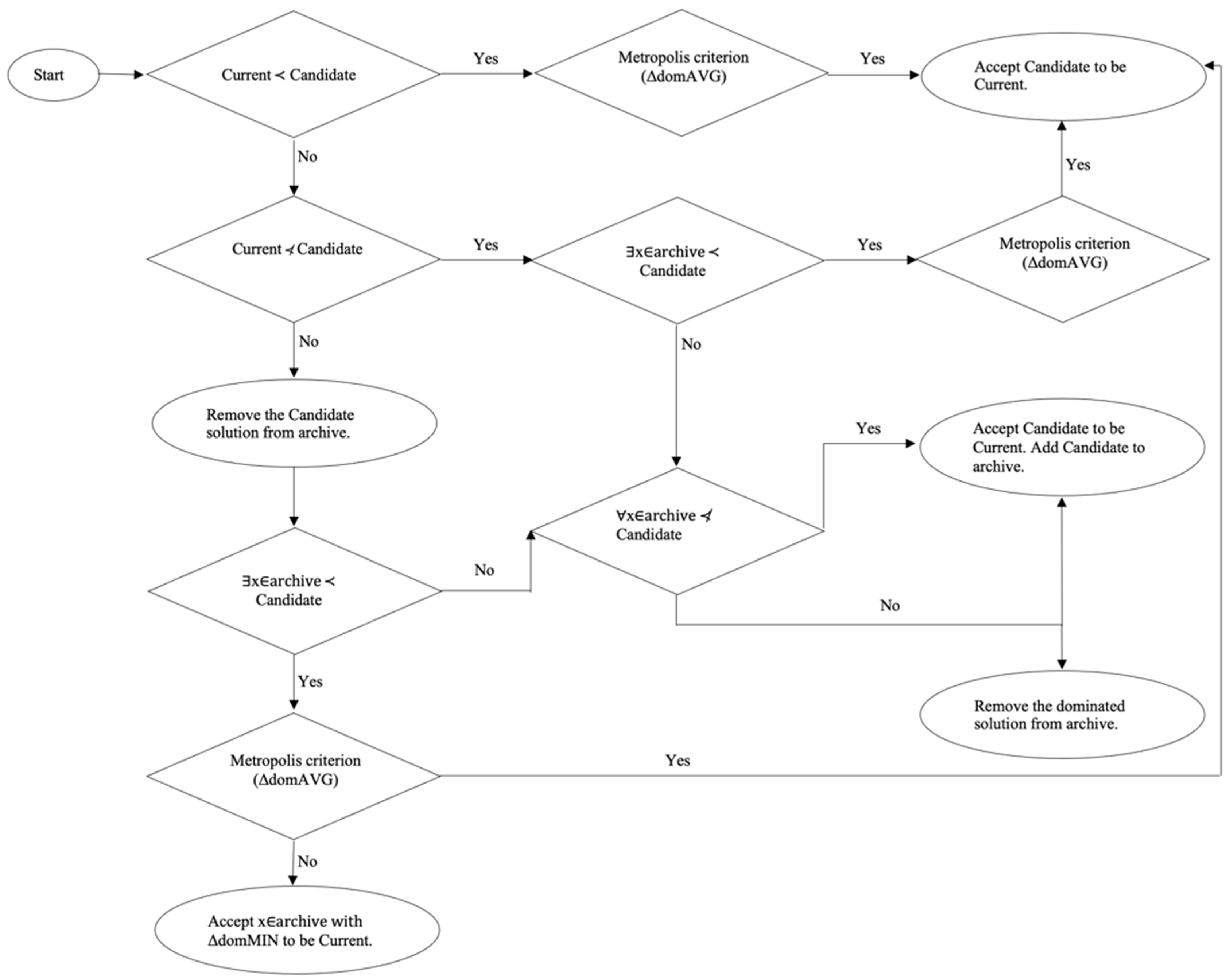
3.3. Local Search Simulated Annealing Algorithm
Simulated Annealing (SA)
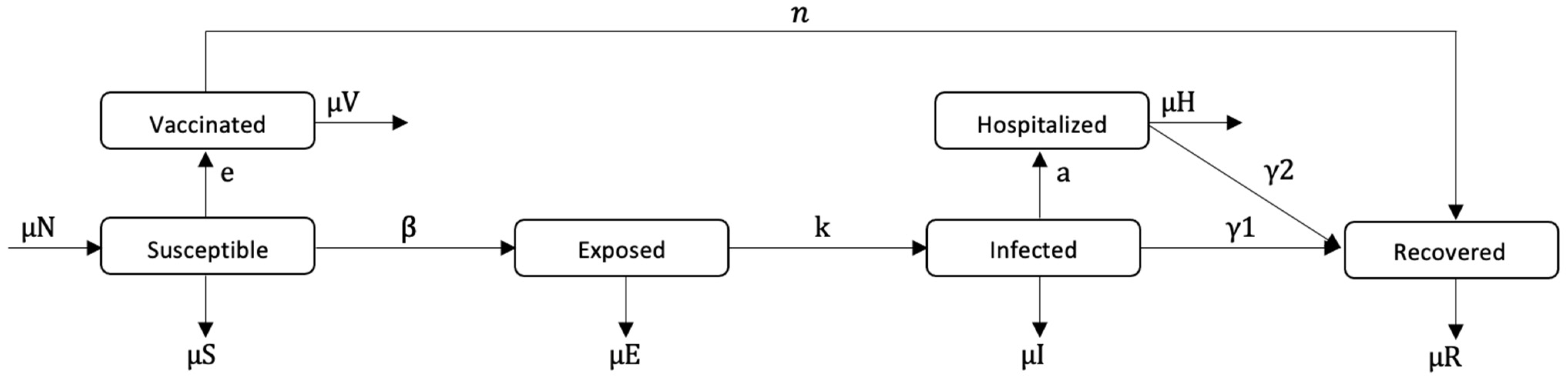
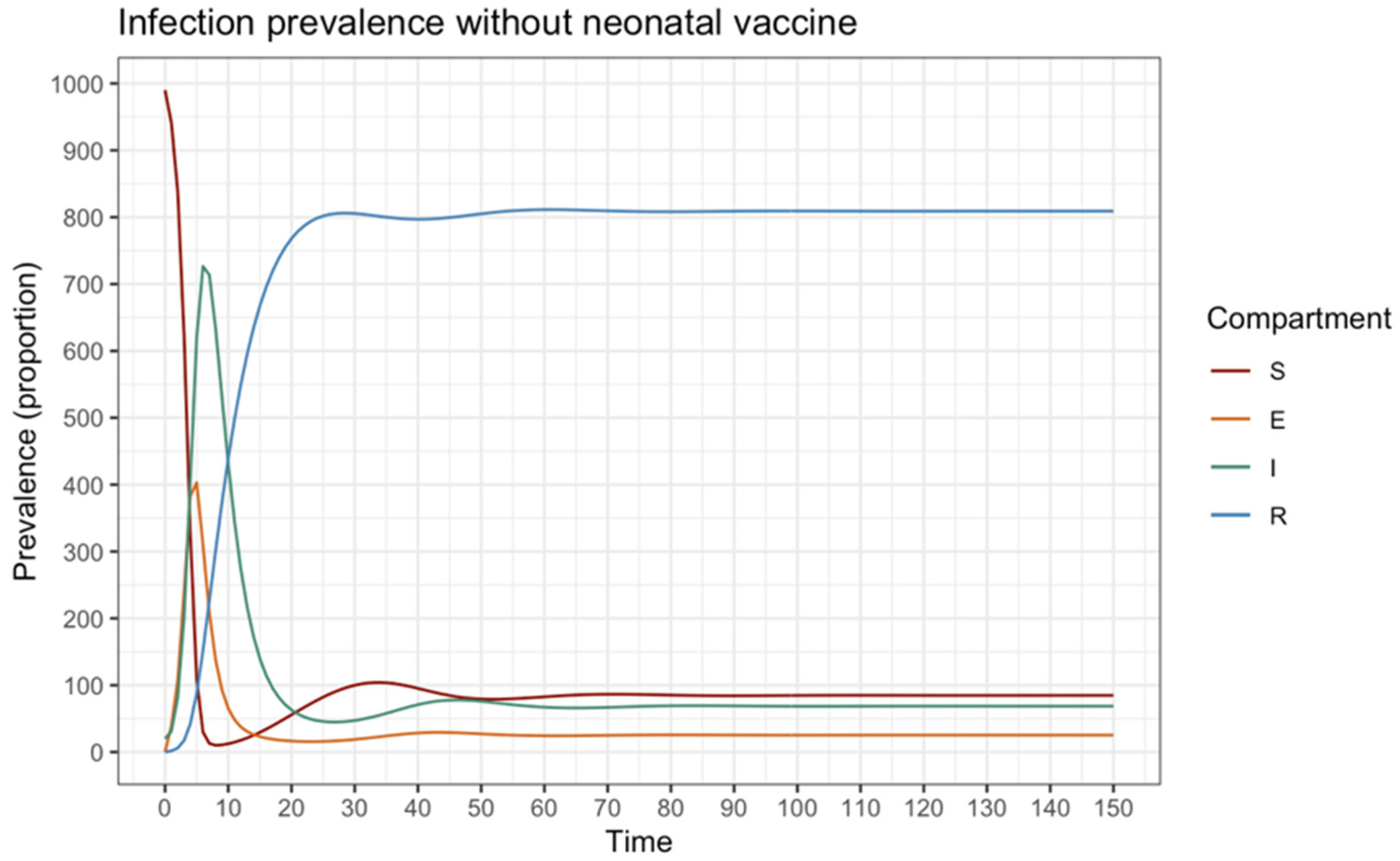
3.4. Epidemiological Model
SEIR Model
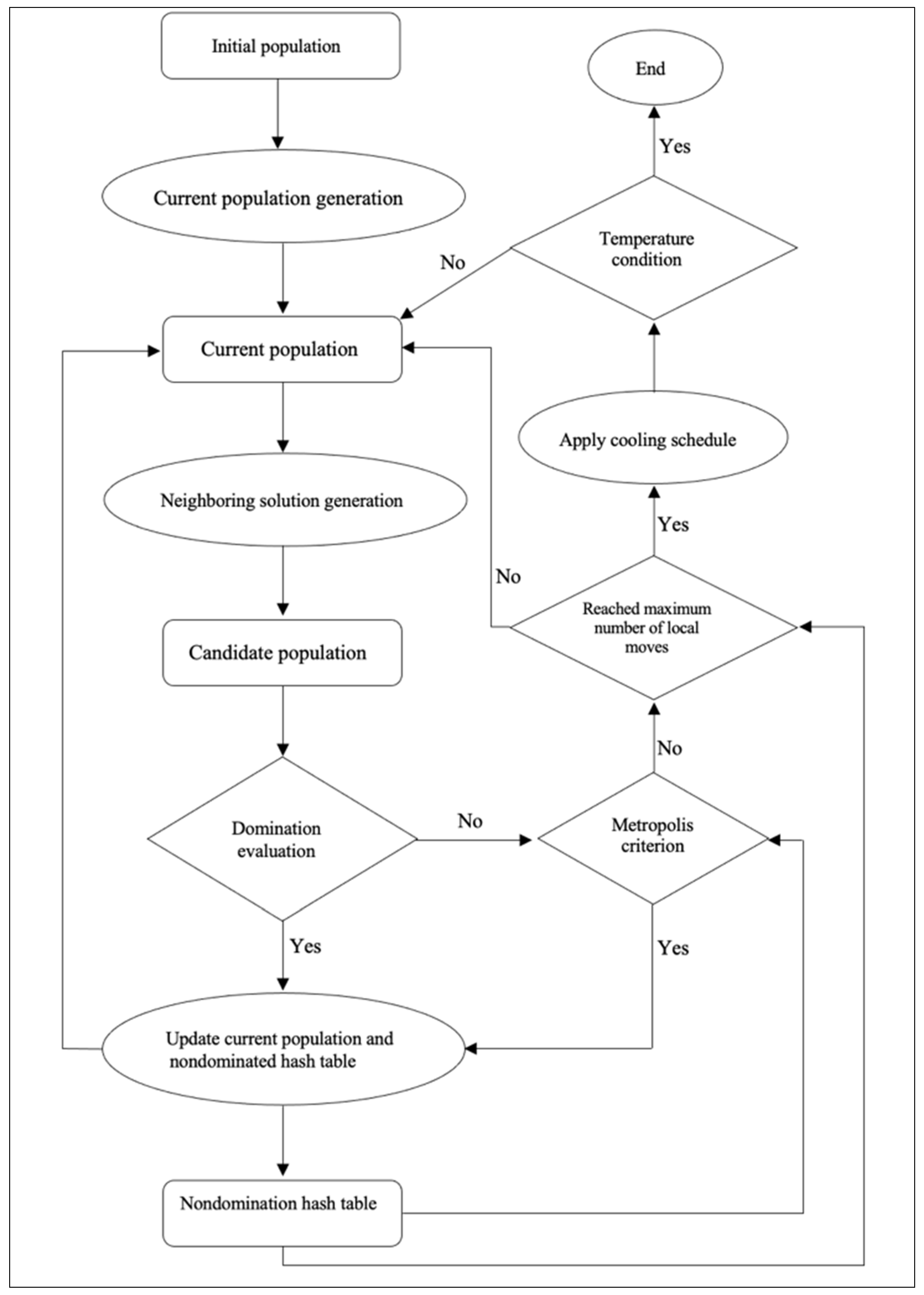
4. Evolutionary Multi-Objective Simulated Annealing (MOSA)
and ∃ i ∈ 1,2: Fi (SCandidate) < Fi (SCurrent).
5. Optimization Model
5.1. Pulse Vaccine Allocation
x(τj+) = x(τj) + u[j],
t∈ (τj+,τj+1]
j = 0, …, N − 1,
5.2. Multi-Objective Formulation
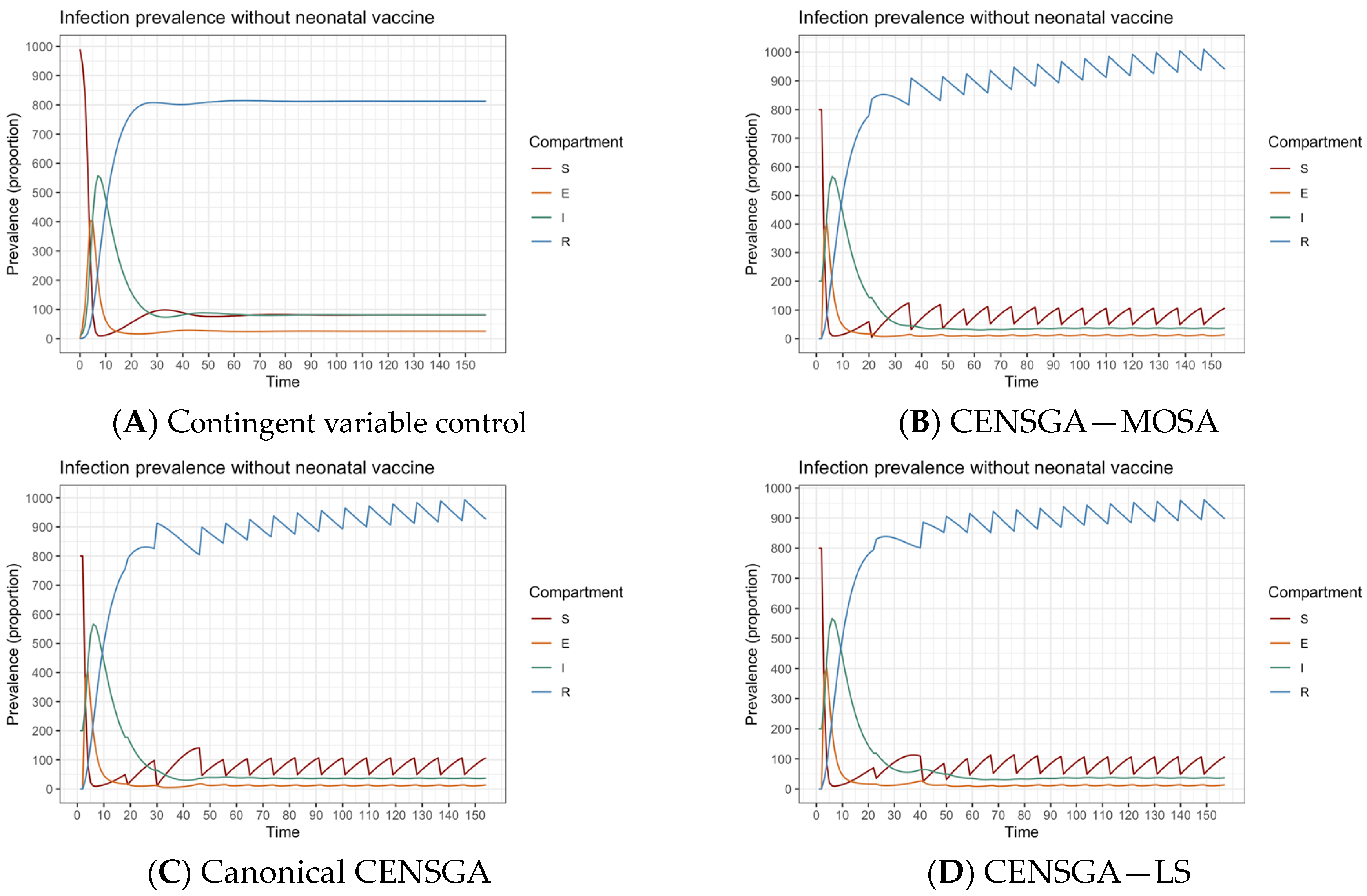
- The first Phase (I) corresponds to the contingent variable control, which considers pairs of susceptible ratios that will be vaccinated and the periods between every two consecutive policies to eradicate an ongoing outbreak;
- The second Phase (II) corresponds to the guardian static control, taking into consideration the necessity of maintaining the infection volume at an acceptable level in a finite timespan after finishing the first phase (i.e., compartment (I) ≤ tolerance ratio (itol > 0)), starting from infection-free equilibrium; see Section 3.4.
5.2.1. Formulation of the Guardian Static Control
- A fixed-time interval between two consecutive campaigns: Δτgc, for Ngc = 1, …, ;
- The fixed percentage of susceptible to-be-vaccinated people in each campaign: vgc.
- F1: integral infection volume;
- F2: vaccination cost.
- vmin ≤ vgc ≤ vmax;
- tmin ≤ Δτj ≤ tmax;
5.2.2. Formulation of the Contingent Variable Control
- The number of policies, Ncc, where Ncc can vary from ⌊Ttmp/Δtmax⌋ to ⌊Ttmp/Δtmin⌋;
- The percentages of susceptible to-be-vaccinated people in each campaign: vj, j ∈ {1, 2, …, N}, such that vj = v(τj) for each τj in Γ = {τ0, …, τN};
- The time interval between two consecutive campaigns: Δτj;
- Each vaccination ratio, vj, must follow the following rule: 0.40 ≤ vmin ≤ vmax ≤ 0.95, for the given percentage ratios, vmin and vmax.
- Each time interval between the two campaigns, Δτj, must adhere to the following rule: 1 ≤ tmin ≤ Δτj ≤ tmax ≤ 20 for the given percentage ratios vmin and vmax.
- F1: integral infection volume;
- F2: total vaccination cost.
5.3. Local Search
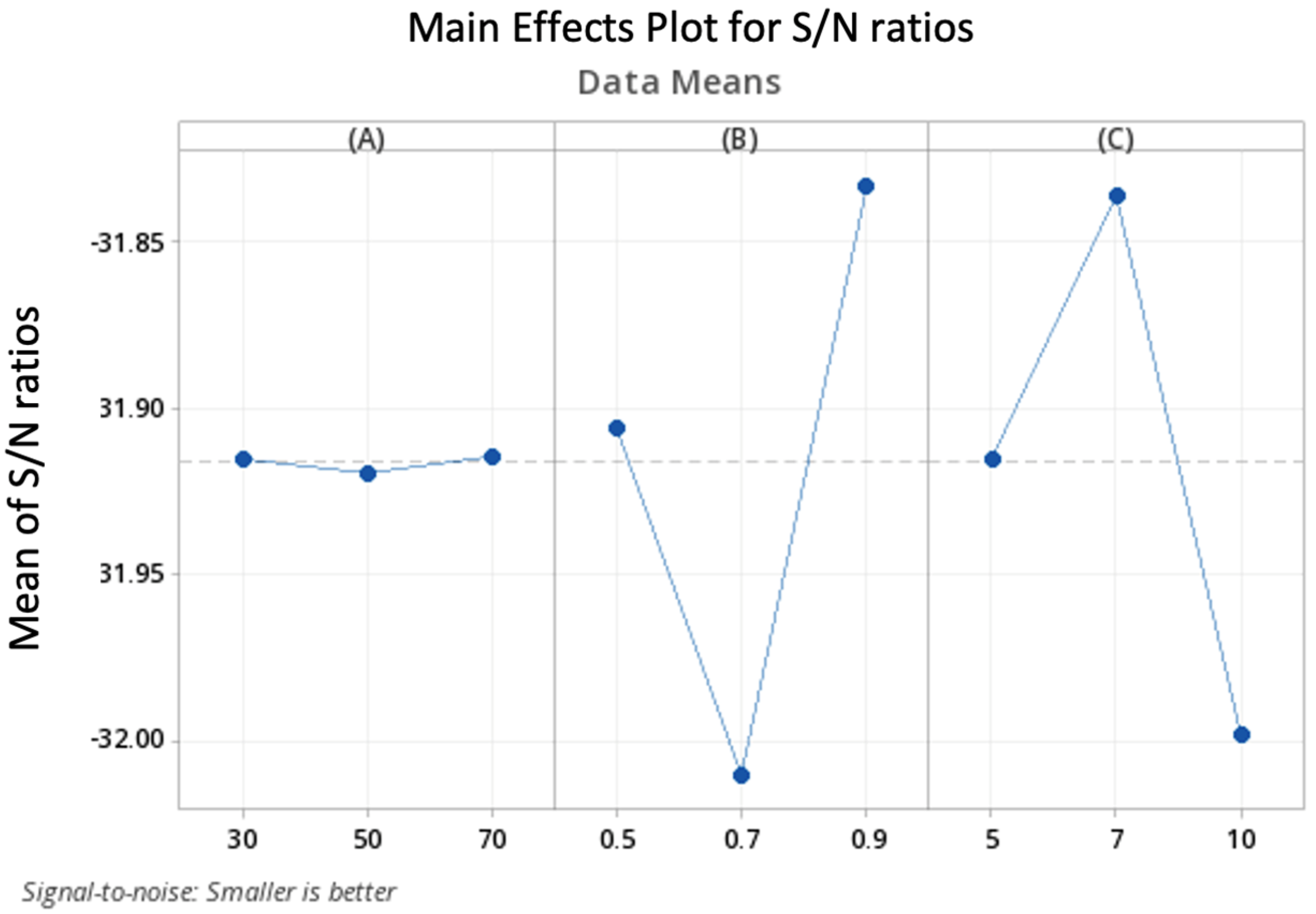
6. Parameter Tuning
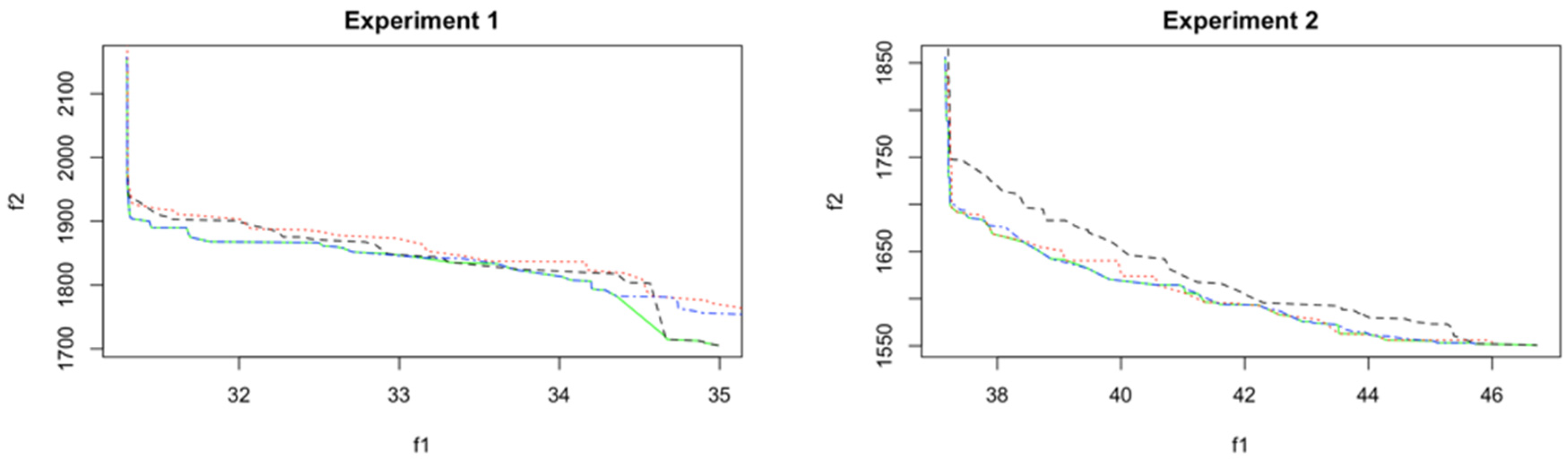
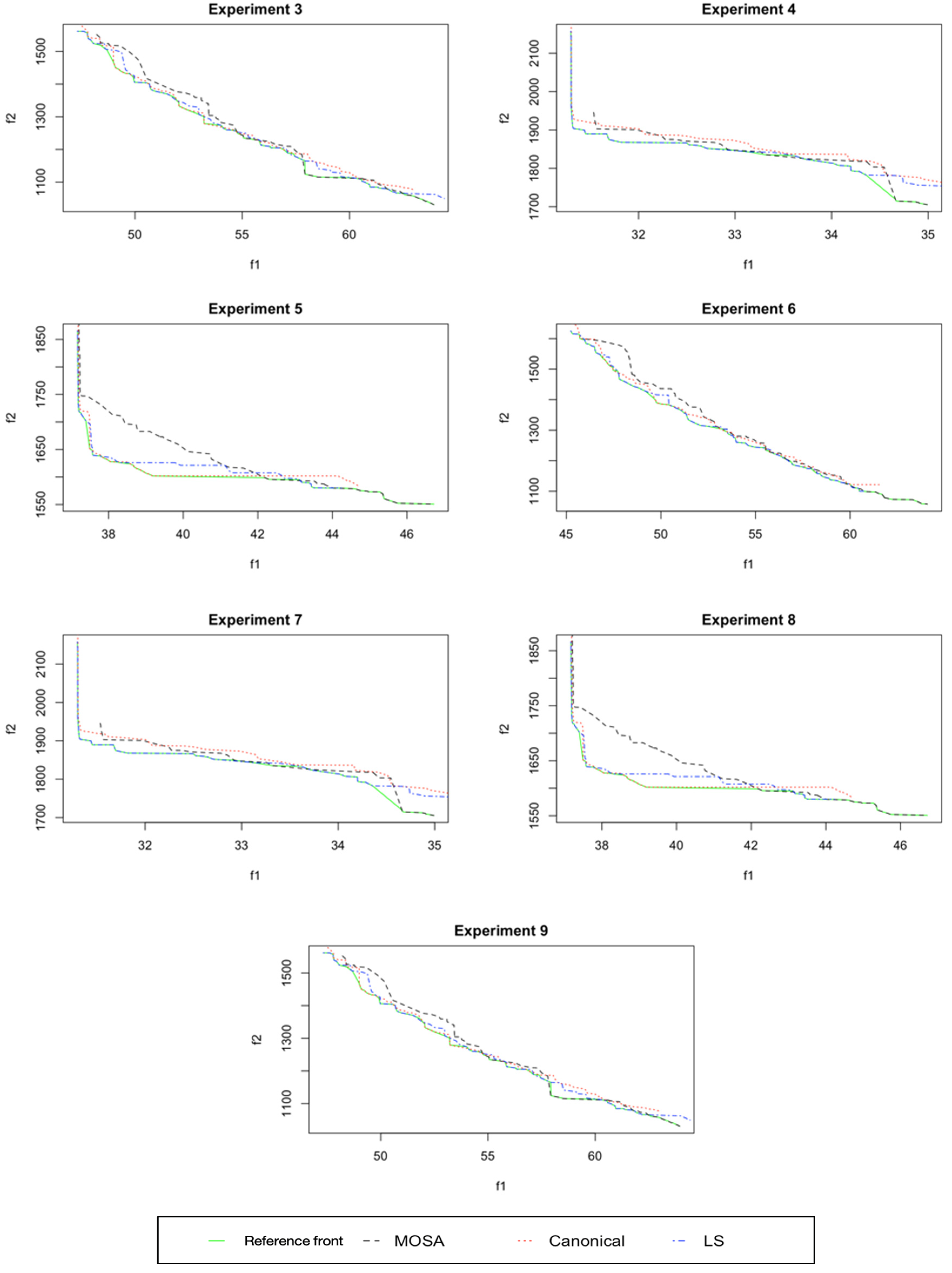
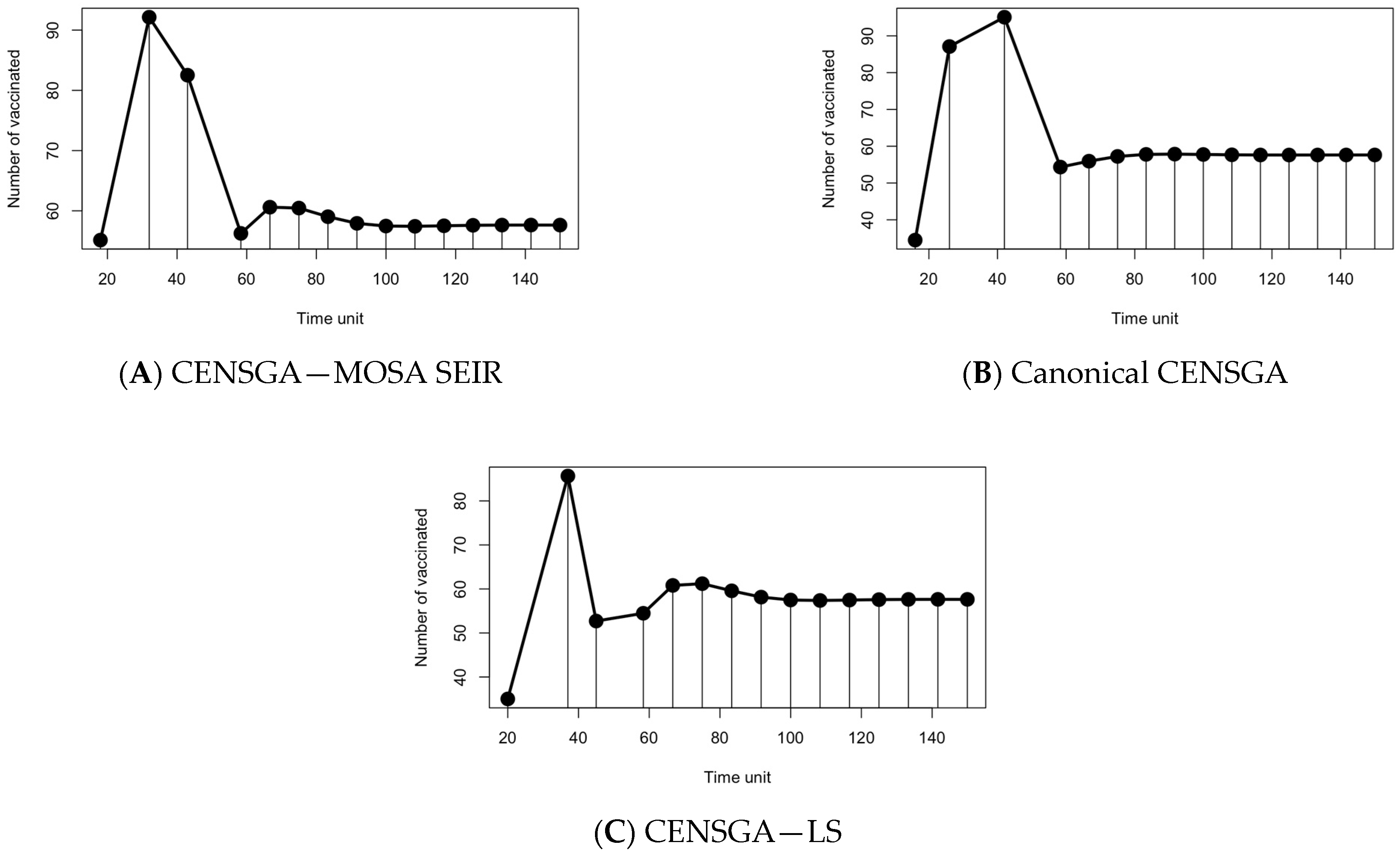
7. Results and Discussion
8. Efficiency Performance Measures
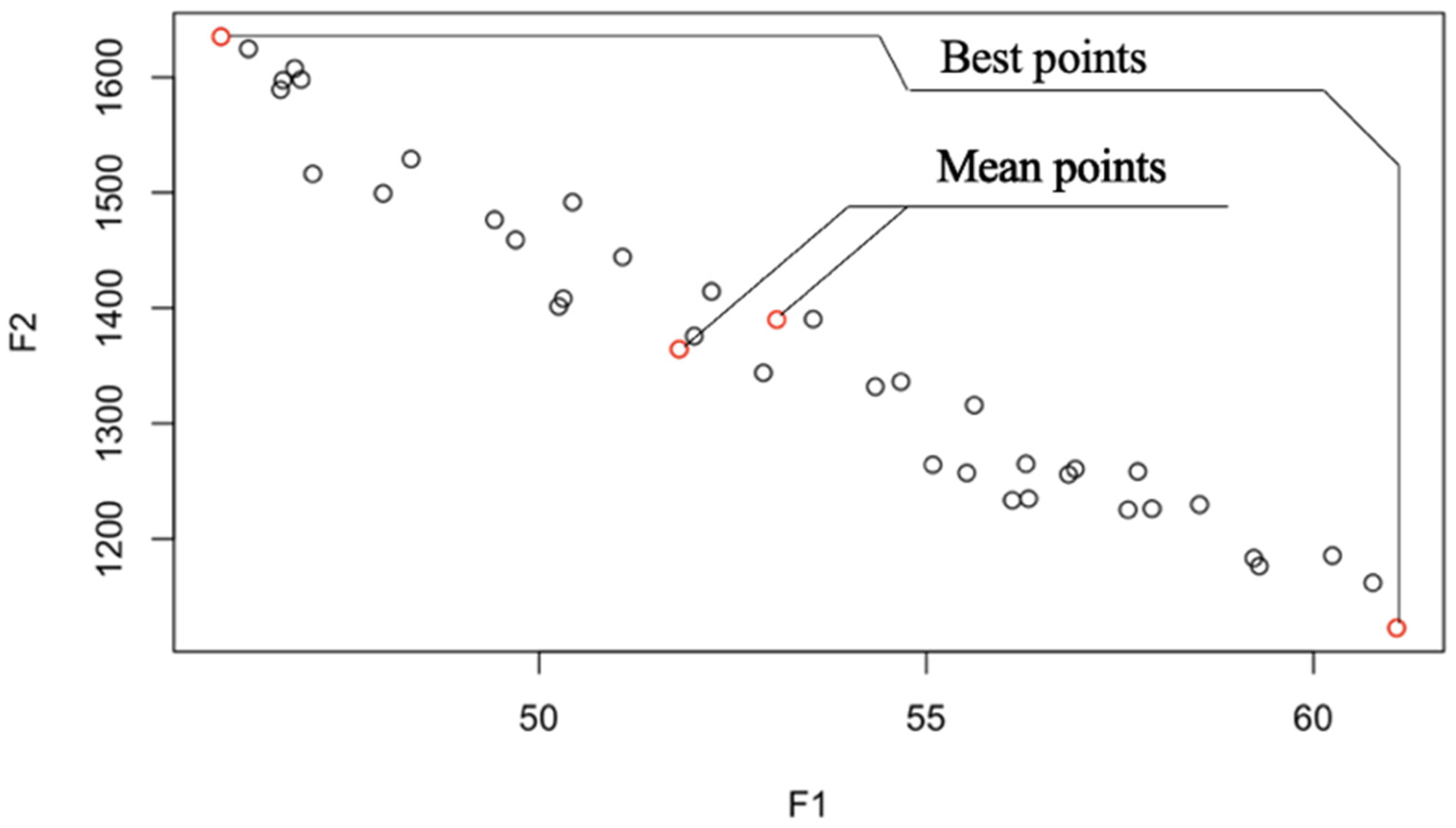
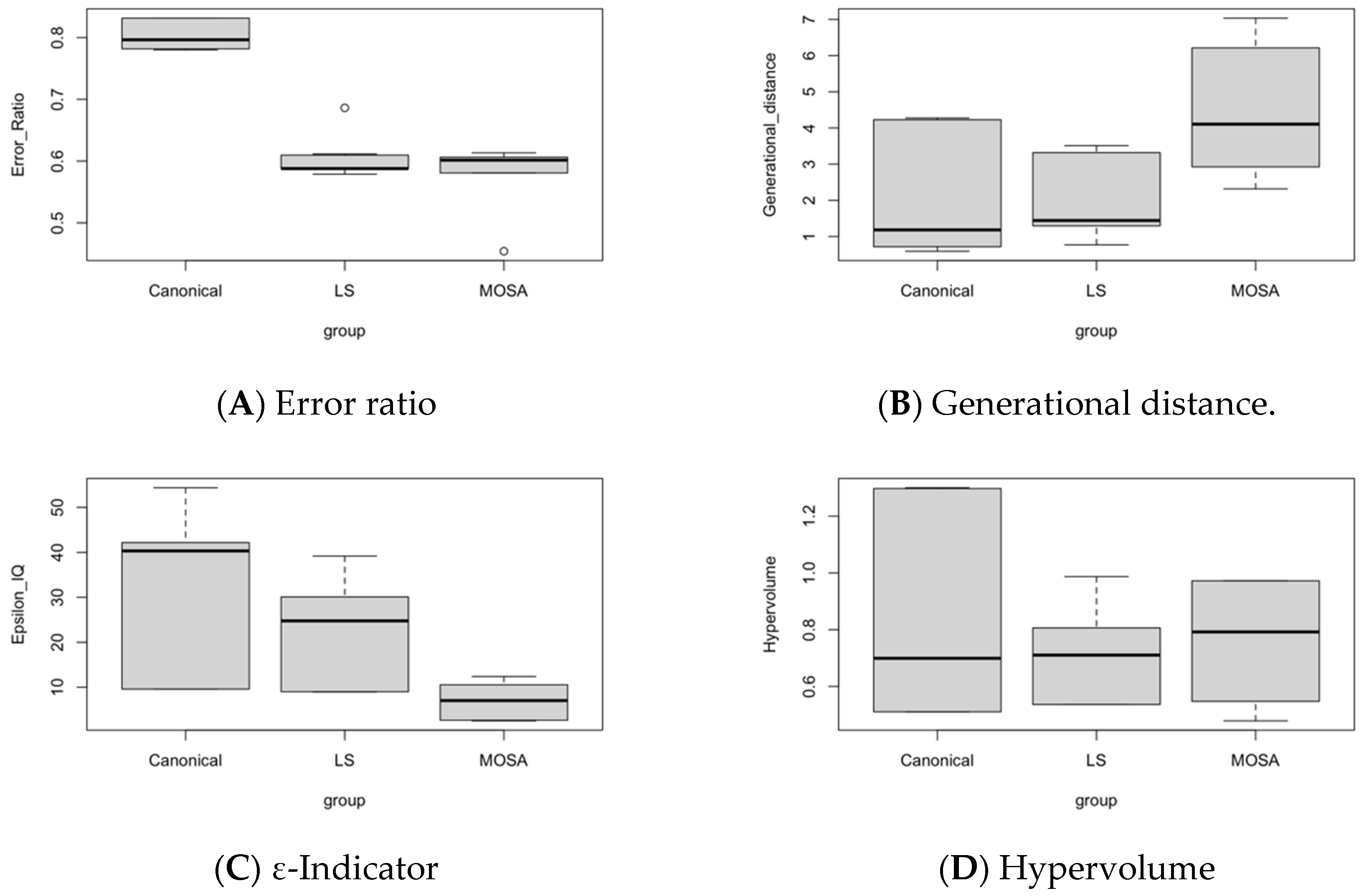
8.1. Analysis and Comparison of Results
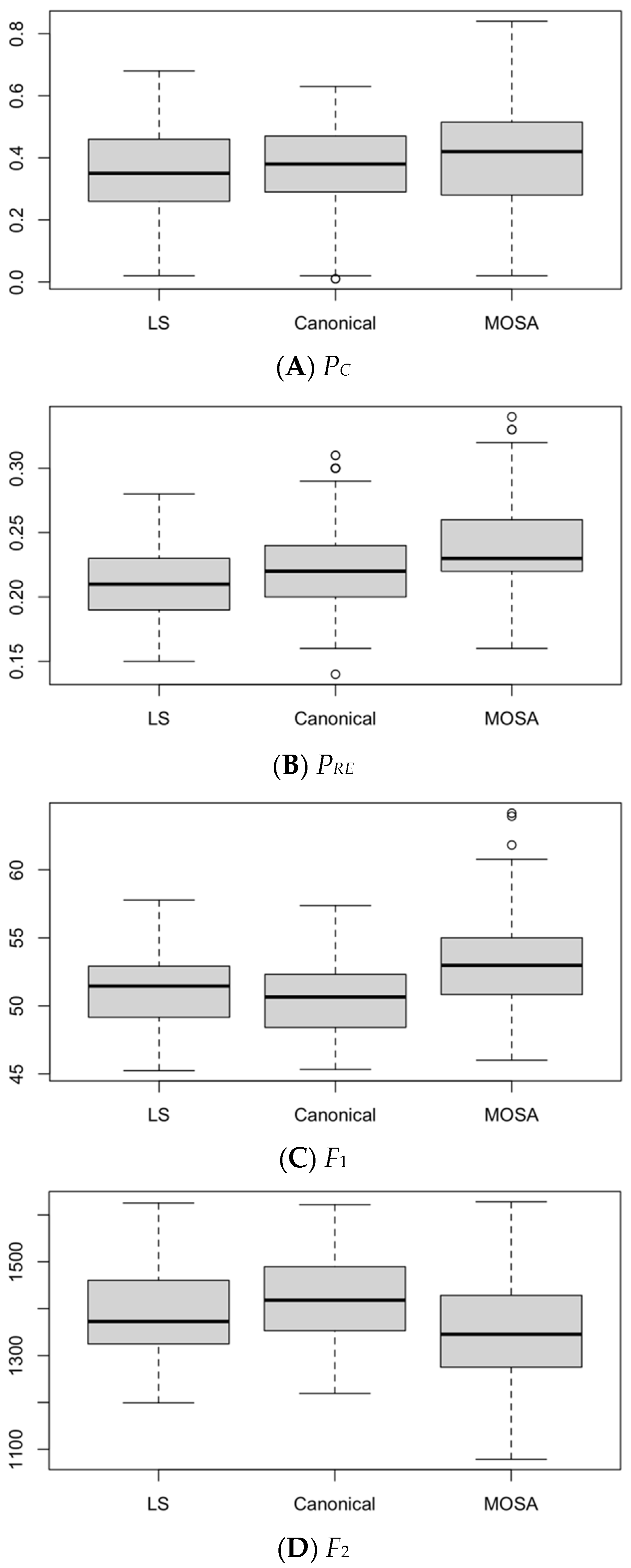
8.2. Statistical Analysis
9. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A
| PC | PRE | F1 | F2 | |
|---|---|---|---|---|
| 0.27 | 0.31 | 56.62665 | 1219.241 | |
| 0.63 | 0.18 | 45.32559 | 1621.835 | |
| 0.41 | 0.18 | 49.54934 | 1412.716 | |
| 0.43 | 0.16 | 48.04826 | 1456.893 | |
| 0.34 | 0.18 | 50.11235 | 1382.050 | |
| 0.29 | 0.29 | 54.88612 | 1273.971 | |
| 0.34 | 0.26 | 53.58605 | 1283.310 | |
| 0.44 | 0.19 | 49.11422 | 1451.460 | |
| 0.46 | 0.19 | 47.78344 | 1489.475 | |
| 0.29 | 0.21 | 51.84352 | 1341.191 | |
| 0.51 | 0.19 | 46.96687 | 1514.805 | |
| 0.38 | 0.20 | 49.50774 | 1446.645 | |
| 0.57 | 0.14 | 46.73510 | 1569.582 | |
| 0.34 | 0.20 | 51.42982 | 1349.898 | |
| 0.54 | 0.17 | 46.95162 | 1546.749 | |
| 0.58 | 0.16 | 46.39877 | 1577.155 | |
| 0.04 | 0.27 | 56.21141 | 1236.038 | |
| 0.03 | 0.25 | 55.54557 | 1247.019 | |
| 0.19 | 0.25 | 55.03263 | 1258.703 | |
| 0.60 | 0.17 | 45.81698 | 1599.144 | |
| 0.04 | 0.30 | 56.47076 | 1233.693 | |
| 0.03 | 0.26 | 55.52312 | 1247.660 | |
| 0.34 | 0.19 | 51.04084 | 1351.873 | |
| 0.20 | 0.22 | 52.74301 | 1329.603 | |
| 0.27 | 0.21 | 52.27507 | 1335.285 | |
| 0.60 | 0.17 | 46.26223 | 1596.934 | |
| 0.60 | 0.17 | 46.38803 | 1593.350 | |
| 0.34 | 0.20 | 52.76472 | 1318.208 | |
| 0.29 | 0.20 | 53.24660 | 1304.670 | |
| 0.54 | 0.16 | 46.80479 | 1552.235 | |
| 0.29 | 0.21 | 52.35913 | 1331.906 | |
| 0.34 | 0.19 | 50.44362 | 1372.778 | |
| 0.19 | 0.25 | 54.96731 | 1260.678 | |
| 0.51 | 0.17 | 47.26822 | 1492.212 | |
| 0.34 | 0.20 | 50.99551 | 1362.985 | |
| 0.34 | 0.19 | 50.56918 | 1369.225 | |
| 0.38 | 0.26 | 53.41712 | 1288.175 | |
| 0.34 | 0.20 | 52.96170 | 1312.596 | |
| 0.60 | 0.17 | 45.59469 | 1605.459 | |
| 0.20 | 0.23 | 53.40468 | 1300.726 | |
| 0.48 | 0.19 | 47.58735 | 1491.165 | |
| 0.48 | 0.18 | 47.09396 | 1506.175 | |
| 0.35 | 0.20 | 50.83495 | 1367.459 | |
| 0.61 | 0.18 | 45.53460 | 1615.811 | |
| 0.52 | 0.17 | 47.04661 | 1507.552 | |
| 0.34 | 0.20 | 52.95925 | 1312.666 | |
| 0.51 | 0.16 | 47.13045 | 1496.123 | |
| 0.44 | 0.20 | 49.35967 | 1451.188 | |
| 0.04 | 0.27 | 56.23856 | 1235.218 | |
| 0.34 | 0.26 | 53.49542 | 1285.971 | |
| 0.60 | 0.17 | 45.59091 | 1608.750 | |
| 0.12 | 0.24 | 53.40336 | 1303.785 | |
| 0.61 | 0.18 | 45.57688 | 1614.588 | |
| 0.51 | 0.16 | 47.14456 | 1495.726 | |
| 0.48 | 0.19 | 47.64557 | 1489.524 | |
| 0.34 | 0.19 | 50.45286 | 1372.555 | |
| 0.34 | 0.20 | 50.90629 | 1365.505 | |
| 0.45 | 0.21 | 49.47136 | 1449.828 | |
| 0.54 | 0.16 | 46.83629 | 1551.330 | |
| 0.41 | 0.21 | 49.45153 | 1450.786 | |
| 0.54 | 0.17 | 46.91751 | 1549.035 | |
| 0.54 | 0.17 | 46.89613 | 1549.645 | |
| 0.34 | 0.20 | 50.87697 | 1366.345 | |
| 0.61 | 0.18 | 45.53469 | 1615.808 | |
| 0.34 | 0.20 | 50.89117 | 1365.950 | |
| 0.54 | 0.17 | 46.90016 | 1549.530 | |
| Average | 0.39212121 | 0.20166667 | 50.0719612 | 1421.30529 |
| PC | PRE | F1 | F2 | |
|---|---|---|---|---|
| 0.68 | 0.17 | 45.23535 | 1625.342 | |
| 0.04 | 0.27 | 57.45398 | 1199.103 | |
| 0.46 | 0.17 | 48.18298 | 1455.939 | |
| 0.04 | 0.23 | 54.33535 | 1258.157 | |
| 0.07 | 0.27 | 56.46197 | 1229.337 | |
| 0.33 | 0.19 | 52.43802 | 1313.049 | |
| 0.07 | 0.25 | 56.97913 | 1207.264 | |
| 0.44 | 0.15 | 48.51748 | 1444.441 | |
| 0.61 | 0.18 | 45.97368 | 1595.592 | |
| 0.20 | 0.24 | 55.12622 | 1254.228 | |
| 0.38 | 0.19 | 50.42169 | 1383.349 | |
| 0.39 | 0.20 | 50.39555 | 1414.598 | |
| 0.43 | 0.17 | 49.18064 | 1427.711 | |
| 0.48 | 0.19 | 47.69939 | 1494.760 | |
| 0.42 | 0.16 | 49.70500 | 1416.870 | |
| 0.51 | 0.18 | 47.77656 | 1480.723 | |
| 0.08 | 0.24 | 53.97753 | 1260.561 | |
| 0.35 | 0.22 | 53.18574 | 1310.493 | |
| 0.64 | 0.19 | 45.70722 | 1612.027 | |
| 0.31 | 0.21 | 51.46239 | 1332.943 | |
| 0.54 | 0.16 | 47.26880 | 1539.966 | |
| 0.29 | 0.21 | 51.78511 | 1323.727 | |
| 0.42 | 0.16 | 49.74257 | 1415.811 | |
| 0.50 | 0.16 | 47.80533 | 1466.819 | |
| 0.07 | 0.25 | 57.00871 | 1206.401 | |
| 0.66 | 0.18 | 45.31438 | 1615.562 | |
| 0.14 | 0.27 | 56.27854 | 1234.734 | |
| 0.45 | 0.21 | 50.35573 | 1414.648 | |
| 0.12 | 0.26 | 55.63903 | 1252.425 | |
| 0.33 | 0.19 | 51.36229 | 1345.559 | |
| 0.50 | 0.20 | 47.53319 | 1504.106 | |
| 0.56 | 0.17 | 46.52957 | 1560.834 | |
| 0.43 | 0.17 | 49.10687 | 1429.812 | |
| 0.17 | 0.22 | 53.53970 | 1287.854 | |
| 0.60 | 0.16 | 46.19045 | 1582.079 | |
| 0.43 | 0.16 | 48.82135 | 1438.072 | |
| 0.30 | 0.21 | 51.64268 | 1327.776 | |
| 0.07 | 0.27 | 55.78742 | 1250.134 | |
| 0.58 | 0.16 | 46.48688 | 1573.861 | |
| 0.04 | 0.27 | 56.01556 | 1243.296 | |
| 0.20 | 0.24 | 55.17690 | 1252.782 | |
| 0.25 | 0.22 | 53.51076 | 1302.398 | |
| 0.53 | 0.19 | 47.31712 | 1513.110 | |
| 0.54 | 0.19 | 47.29156 | 1522.434 | |
| 0.58 | 0.15 | 46.36648 | 1575.009 | |
| 0.24 | 0.22 | 52.03842 | 1316.547 | |
| 0.36 | 0.21 | 51.11329 | 1363.213 | |
| 0.24 | 0.22 | 52.07620 | 1315.413 | |
| 0.43 | 0.16 | 48.78093 | 1439.240 | |
| 0.51 | 0.20 | 47.46645 | 1509.787 | |
| 0.55 | 0.17 | 46.77747 | 1547.786 | |
| 0.08 | 0.22 | 53.93514 | 1274.448 | |
| 0.50 | 0.16 | 47.79540 | 1467.105 | |
| 0.12 | 0.27 | 56.00962 | 1245.069 | |
| 0.38 | 0.19 | 50.57276 | 1378.985 | |
| 0.55 | 0.16 | 47.05340 | 1539.988 | |
| 0.35 | 0.21 | 53.29346 | 1303.557 | |
| 0.35 | 0.20 | 51.35117 | 1352.487 | |
| 0.36 | 0.21 | 50.73944 | 1374.238 | |
| 0.64 | 0.19 | 45.62430 | 1614.370 | |
| 0.37 | 0.20 | 51.23730 | 1355.697 | |
| 0.07 | 0.27 | 56.37726 | 1231.806 | |
| 0.56 | 0.17 | 46.56548 | 1553.677 | |
| 0.55 | 0.16 | 47.03939 | 1546.411 | |
| 0.61 | 0.16 | 46.02662 | 1584.144 | |
| 0.35 | 0.22 | 53.21447 | 1309.557 | |
| 0.60 | 0.17 | 46.01005 | 1587.142 | |
| 0.54 | 0.19 | 47.29156 | 1522.434 | |
| 0.18 | 0.21 | 53.79258 | 1282.390 | |
| 0.08 | 0.23 | 53.72129 | 1282.904 | |
| 0.36 | 0.21 | 51.03244 | 1365.847 | |
| 0.35 | 0.22 | 53.43060 | 1303.147 | |
| 0.10 | 0.24 | 53.82972 | 1276.462 | |
| 0.37 | 0.20 | 51.24867 | 1355.401 | |
| 0.55 | 0.16 | 47.04736 | 1546.219 | |
| 0.56 | 0.17 | 46.69065 | 1550.202 | |
| 0.36 | 0.21 | 50.88498 | 1370.109 | |
| 0.56 | 0.17 | 46.60819 | 1552.547 | |
| 0.10 | 0.23 | 53.62695 | 1285.639 | |
| 0.08 | 0.22 | 53.93514 | 1274.448 | |
| 0.10 | 0.24 | 53.82972 | 1276.462 | |
| 0.10 | 0.23 | 53.62686 | 1285.642 | |
| 0.56 | 0.17 | 46.66683 | 1550.891 | |
| 0.38 | 0.20 | 50.77545 | 1372.965 | |
| 0.36 | 0.21 | 50.93433 | 1368.768 | |
| 0.36 | 0.21 | 50.98178 | 1367.452 | |
| 0.38 | 0.20 | 50.82923 | 1371.429 | |
| 0.64 | 0.19 | 45.67703 | 1612.882 | |
| 0.38 | 0.19 | 50.44772 | 1382.582 | |
| 0.38 | 0.19 | 50.51767 | 1380.607 | |
| 0.60 | 0.17 | 46.01967 | 1586.891 | |
| 0.38 | 0.19 | 50.48494 | 1381.549 | |
| 0.36 | 0.21 | 50.81597 | 1372.116 | |
| 0.64 | 0.19 | 45.64040 | 1613.907 | |
| 0.36 | 0.21 | 50.95993 | 1367.982 | |
| 0.38 | 0.19 | 50.50524 | 1381.050 | |
| 0.38 | 0.19 | 50.50902 | 1380.856 | |
| 0.38 | 0.19 | 50.51456 | 1380.691 | |
| Average | 0.3705102 | 0.20071429 | 50.4904832 | 1403.15137 |
| PC | PRE | F1 | F2 | |
|---|---|---|---|---|
| 0.04 | 0.25 | 61.82448 | 1078.657 | |
| 0.84 | 0.19 | 46.00335 | 1598.634 | |
| 0.19 | 0.30 | 60.48305 | 1118.464 | |
| 0.08 | 0.33 | 59.66279 | 1147.021 | |
| 0.69 | 0.21 | 48.34750 | 1529.636 | |
| 0.66 | 0.19 | 48.46169 | 1482.997 | |
| 0.56 | 0.23 | 51.23938 | 1395.370 | |
| 0.64 | 0.21 | 49.59135 | 1450.538 | |
| 0.80 | 0.20 | 46.73227 | 1593.260 | |
| 0.79 | 0.20 | 47.14854 | 1587.460 | |
| 0.49 | 0.19 | 49.94914 | 1436.021 | |
| 0.82 | 0.20 | 47.74446 | 1579.304 | |
| 0.14 | 0.27 | 57.48562 | 1198.499 | |
| 0.51 | 0.25 | 52.26428 | 1343.450 | |
| 0.33 | 0.27 | 56.70110 | 1206.742 | |
| 0.51 | 0.24 | 51.52525 | 1375.758 | |
| 0.35 | 0.22 | 53.67868 | 1290.560 | |
| 0.57 | 0.23 | 52.08102 | 1369.949 | |
| 0.29 | 0.25 | 53.94038 | 1280.792 | |
| 0.61 | 0.18 | 48.04747 | 1572.499 | |
| 0.34 | 0.27 | 55.58911 | 1245.719 | |
| 0.50 | 0.20 | 48.96802 | 1456.712 | |
| 0.08 | 0.34 | 59.22600 | 1151.910 | |
| 0.27 | 0.30 | 57.72588 | 1184.888 | |
| 0.28 | 0.31 | 58.15882 | 1178.688 | |
| 0.08 | 0.22 | 55.71036 | 1231.114 | |
| 0.35 | 0.23 | 53.51751 | 1303.360 | |
| 0.02 | 0.31 | 58.92436 | 1161.877 | |
| 0.11 | 0.29 | 55.52485 | 1257.387 | |
| 0.63 | 0.22 | 50.81205 | 1406.255 | |
| 0.03 | 0.03 | 55.85369 | 1226.999 | |
| 0.16 | 0.16 | 55.18026 | 1258.337 | |
| 0.28 | 0.28 | 58.57443 | 1174.423 | |
| 0.28 | 0.28 | 58.87418 | 1167.199 | |
| 0.37 | 0.37 | 52.83298 | 1315.306 | |
| 0.57 | 0.57 | 48.31294 | 1538.140 | |
| 0.59 | 0.59 | 48.24304 | 1556.686 | |
| 0.58 | 0.58 | 48.14942 | 1559.639 | |
| 0.29 | 0.29 | 57.53871 | 1190.234 | |
| 0.16 | 0.16 | 54.49140 | 1279.993 | |
| 0.38 | 0.38 | 56.49555 | 1218.827 | |
| 0.49 | 0.49 | 50.54035 | 1435.585 | |
| 0.49 | 0.49 | 50.73942 | 1420.547 | |
| 0.17 | 0.17 | 56.68458 | 1214.131 | |
| 0.19 | 0.19 | 59.48303 | 1147.993 | |
| 0.39 | 0.39 | 56.30349 | 1224.317 | |
| 0.08 | 0.08 | 58.45062 | 1177.844 | |
| 0.07 | 0.07 | 54.98443 | 1265.283 | |
| 0.53 | 0.53 | 48.85818 | 1459.792 | |
| 0.59 | 0.59 | 50.58657 | 1430.856 | |
| 0.63 | 0.63 | 50.78233 | 1407.135 | |
| 0.49 | 0.49 | 50.66856 | 1422.479 | |
| 0.47 | 0.47 | 52.42334 | 1339.078 | |
| 0.65 | 0.65 | 48.64135 | 1469.225 | |
| 0.04 | 0.04 | 54.78421 | 1271.454 | |
| 0.45 | 0.45 | 51.82700 | 1375.583 | |
| 0.47 | 0.47 | 52.81972 | 1327.656 | |
| 0.66 | 0.66 | 48.62788 | 1478.788 | |
| 0.39 | 0.39 | 54.94450 | 1268.039 | |
| 0.65 | 0.65 | 48.75590 | 1466.091 | |
| 0.39 | 0.28 | 56.33183 | 1223.552 | |
| 0.35 | 0.22 | 53.00873 | 1310.315 | |
| 0.47 | 0.25 | 52.65116 | 1332.504 | |
| 0.47 | 0.25 | 52.80478 | 1328.099 | |
| 0.57 | 0.18 | 48.33079 | 1537.614 | |
| 0.46 | 0.25 | 51.95109 | 1374.904 | |
| 0.35 | 0.22 | 53.23792 | 1303.745 | |
| 0.35 | 0.22 | 53.09239 | 1307.865 | |
| 0.05 | 0.26 | 54.69342 | 1274.190 | |
| 0.45 | 0.25 | 52.62534 | 1333.093 | |
| 0.33 | 0.24 | 52.59753 | 1338.675 | |
| 0.43 | 0.18 | 50.55105 | 1434.704 | |
| 0.08 | 0.26 | 54.63971 | 1275.763 | |
| 0.21 | 0.27 | 54.53889 | 1278.453 | |
| 0.59 | 0.19 | 48.22877 | 1557.082 | |
| 0.43 | 0.28 | 54.55030 | 1275.916 | |
| 0.66 | 0.19 | 48.54107 | 1481.248 | |
| 0.33 | 0.24 | 52.59593 | 1338.721 | |
| 0.35 | 0.22 | 53.16560 | 1305.787 | |
| 0.57 | 0.23 | 52.01344 | 1371.955 | |
| 0.35 | 0.22 | 53.01436 | 1310.147 | |
| 0.65 | 0.20 | 48.71108 | 1467.348 | |
| 0.56 | 0.23 | 52.02751 | 1371.557 | |
| 0.66 | 0.19 | 48.58027 | 1480.113 | |
| 0.35 | 0.22 | 53.20860 | 1304.566 | |
| 0.65 | 0.20 | 48.71601 | 1467.209 | |
| 0.35 | 0.22 | 53.18912 | 1305.126 | |
| 0.66 | 0.19 | 48.56743 | 1480.473 | |
| 0.63 | 0.22 | 50.79620 | 1406.738 | |
| 0.35 | 0.22 | 53.23416 | 1303.845 | |
| 0.57 | 0.23 | 52.02044 | 1371.750 | |
| Average | 0.41571429 | 0.28472527 | 52.7992938 | 1346.74986 |
References
- Plotkin, S.A.; Orenstein, W.A.; Offit, P.A. (Eds.) Plotkin’s Vaccines, 7th ed.; Elsevier: Philadelphia, PA, USA, 2018. [Google Scholar]
- Cardoso, R.T.N.; Dusse, A.C.S.; Adam, K. Optimal Vaccination Campaigns Using Stochastic SIR Model and Multiobjective Impulsive Control. Trends Comput. Appl. Math. 2021, 22, 201–220. [Google Scholar] [CrossRef]
- Krammer, F.; Smith, G.J.D.; Fouchier, R.A.M.; Peiris, M.; Kedzierska, K.; Doherty, P.C.; Palese, P.; Shaw, M.L.; Treanor, J.; Webster, R.G.; et al. Influenza. Nat. Rev. Dis. Primers 2018, 4, 3. [Google Scholar] [CrossRef] [PubMed]
- Paget, J.; Spreeuwenberg, P.; Charu, V.; Taylor, R.J.; Iuliano, A.D.; Bresee, J.; Simonsen, L.; Viboud, C. Global mortality associated with seasonal influenza epidemics: New burden estimates and predictors from the GLaMOR Project. J. Glob. Health 2019, 9, 020421. [Google Scholar] [CrossRef]
- Nair, H.; Brooks, W.A.; Katz, M.; Roca, A.; Berkley, J.A.; Madhi, S.A.; Simmerman, J.M.; Gordon, A.; Sato, M.; Howie, S.; et al. Global burden of respiratory infections due to seasonal influenza in young children: A systematic review and meta-analysis. Lancet 2011, 378, 1917–1930. [Google Scholar] [CrossRef]
- Thompson, W.W.; Weintraub, E.; Dhankhar, P.; Cheng, P.Y.; Brammer, L.; Meltzer, M.I.; Bresee, J.S.; Shay, D.K. Estimates of US influenza-associated deaths made using four different methods. Influenza Resp. Viruses 2009, 3, 37–49. [Google Scholar] [CrossRef]
- Putri, W.C.W.S.; Muscatello, D.J.; Stockwell, M.S.; Newall, A.T. Economic burden of seasonal influenza in the United States. Vaccine 2018, 36, 3960–3966. [Google Scholar] [CrossRef] [PubMed]
- De Courville, C.; Cadarette, S.M.; Wissinger, E.; Alvarez, F.P. The economic burden of influenza among adults aged 18 to 64: A systematic literature review. Influenza Resp. Viruses 2022, 16, 376–385. [Google Scholar] [CrossRef]
- Gong, H.; Shen, X.; Yan, H.; Lu, W.Y.; Zhong, G.J.; Dong, K.G.; Yang, J.; Yu, H.J. Estimating the disease burden of seasonal influenza in China, 2006–2019. Zhonghua Yi Xue Za Zhi 2021, 101, 560–567. [Google Scholar] [PubMed]
- Biswas, M.H.A.; Paiva, L.T.; de Pinho, M.D.R. A SEIR model for control of infectious diseases with constraints. Math. Biosci. Eng. 2014, 11, 761–784. [Google Scholar] [CrossRef]
- Suman, B.; Kumar, P. A survey of simulated annealing as a tool for single and multiobjective optimization. J. Oper. Res. Soc. 2006, 57, 1143–1160. [Google Scholar] [CrossRef]
- Ledesma, S.; Avia, G.; Sanchez, R. Practical Considerations for Simulated Annealing Implementation. In Simulated Annealing; Ming, C., Ed.; InTech: Houston, TX, USA, 2008. [Google Scholar] [CrossRef]
- Goldberg, D.E. Genetic Algorithms in Search, Optimization, and Machine Learning; Addison-Wesley Pub. Co.: Reading, MA, USA, 1989. [Google Scholar]
- Kumar, P.; Sharath, S.; D’Souza, G.R.; Sekaran, K.C. Memetic NSGA—A multi-objective genetic algorithm for classification of microarray data. In Proceedings of the 15th International Conference on Advanced Computing and Communications (ADCOM 2007), Guwahati, India, 18–21 December 2007; IEEE: Piscataway, NJ, USA, 2007; pp. 75–80. [Google Scholar] [CrossRef]
- Bektur, G. An NSGA-II-Based Memetic Algorithm for an Energy-Efficient Unrelated Parallel Machine Scheduling Problem with Machine-Sequence Dependent Setup Times and Learning Effect. Arab. J. Sci. Eng. 2022, 47, 3773–3788. [Google Scholar] [CrossRef]
- Benlic, U.; Hao, J.-K. Memetic search for the quadratic assignment problem. Expert Syst. Appl. 2015, 42, 584–595. [Google Scholar] [CrossRef]
- Mei, Y.; Tang, K.; Yao, X. Decomposition-Based Memetic Algorithm for Multiobjective Capacitated Arc Routing Problem. IEEE Trans. Evol. Computat. 2011, 15, 151–165. [Google Scholar] [CrossRef]
- Mencía, R.; Sierra, M.R.; Mencía, C.; Varela, R. Memetic algorithms for the job shop scheduling problem with operators. Appl. Soft Comput. 2015, 34, 94–105. [Google Scholar] [CrossRef]
- Pan, Q.-K.; Ruiz, R. An estimation of distribution algorithm for lot-streaming flow shop problems with setup times. Omega 2012, 40, 166–180. [Google Scholar] [CrossRef]
- Alkhamis, A.K.; Hosny, M. A Synthesis of Pulse Influenza Vaccination Policies Using an Efficient Controlled Elitism Non-Dominated Sorting Genetic Algorithm (CENSGA). Electronics 2022, 11, 3711. [Google Scholar] [CrossRef]
- Deb, K.; Goel, T. Controlled Elitist Non-dominated Sorting Genetic Algorithms for Better Convergence. In Evolutionary Multi-Criterion Optimization; Zitzler, E., Thiele, L., Deb, K., Coello, C.A.C., Corne, D., Eds.; Springer: Berlin/Heidelberg, Germany, 2001; pp. 67–81. [Google Scholar]
- Serafini, P. Simulated Annealing for Multi Objective Optimization Problems. In Multiple Criteria Decision Making; Tzeng, G.H., Wang, H.F., Wen, U.P., Yu, P.L., Eds.; Springer: New York, NY, USA, 1994; pp. 283–292. [Google Scholar] [CrossRef]
- Czyzżak, P.; Jaszkiewicz, A. Pareto simulated annealing—A metaheuristic technique for multiple-objective combinatorial optimization. J. Multi-Crit. Decis. Anal. 1998, 7, 34–47. [Google Scholar] [CrossRef]
- Ulungu, E.L.; Teghem, J.; Fortemps, P.H.; Tuyttens, D. MOSA method: A tool for solving multiobjective combinatorial optimization problems. J. Multi-Crit. Decis. Anal. 1999, 8, 221–236. [Google Scholar] [CrossRef]
- Li, H.; Landa-Silva, D. Evolutionary Multi-objective Simulated Annealing with adaptive and competitive search direction. In Proceedings of the 2008 IEEE Congress on Evolutionary Computation (IEEE World Congress on Computational Intelligence), Hong Kong, China, 1–6 June 2008; IEEE: Piscataway, NJ, USA, 2008; pp. 3311–3318. [Google Scholar] [CrossRef]
- Suppapitnarm, A.; Seffen, K.A.; Parks, G.T.; Clarkson, P.J. A simulated annealing algorithm for multiobjective optimization. Eng. Optim. 2000, 33, 59–85. [Google Scholar] [CrossRef]
- Sankararao, B.; Yoo, C.K. Development of a Robust Multiobjective Simulated Annealing Algorithm for Solving Multiobjective Optimization Problems. Ind. Eng. Chem. Res. 2011, 50, 6728–6742. [Google Scholar] [CrossRef]
- Bandyopadhyay, S.; Saha, S.; Maulik, U.; Deb, K. A Simulated Annealing-Based Multiobjective Optimization Algorithm: AMOSA. IEEE Trans. Evol. Computat. 2008, 12, 269–283. [Google Scholar] [CrossRef]
- Suman, B. Simulated annealing-based multiobjective algorithms and their application for system reliability. Eng. Optim. 2003, 35, 391–416. [Google Scholar] [CrossRef]
- Cunha, M.; Marques, J. A New Multiobjective Simulated Annealing Algorithm—MOSA-GR: Application to the Optimal Design of Water Distribution Networks. Water Resour. Res. 2020, 56, e2019WR025852. [Google Scholar] [CrossRef]
- Zhou, A.; Qu, B.-Y.; Li, H.; Zhao, S.-Z.; Suganthan, P.N.; Zhang, Q. Multiobjective evolutionary algorithms: A survey of the state of the art. Swarm Evol. Comput. 2011, 1, 32–49. [Google Scholar] [CrossRef]
- Gunantara, N. A review of multi-objective optimization: Methods and its applications. Cogent Eng. 2018, 5, 1502242. [Google Scholar] [CrossRef]
- Hu, S.; Wu, X.; Liu, H.; Wang, Y.; Li, R.; Yin, M. Multi-Objective Neighborhood Search Algorithm Based on Decomposition for Multi-Objective Minimum Weighted Vertex Cover Problem. Sustainability 2019, 11, 3634. [Google Scholar] [CrossRef]
- Deb, K.; Pratap, A.; Agarwal, S.; Meyarivan, T. A fast and elitist multiobjective genetic algorithm: NSGA-II. IEEE Trans. Evol. Comput. 2002, 6, 182–197. [Google Scholar] [CrossRef]
- Hajipour, V.; Tavana, M.; Santos-Arteaga, F.J.; Alinezhad, A.; Di, D. An efficient controlled elitism non-dominated sorting genetic algorithm for multi-objective supplier selection under fuzziness. J. Comput. Des. Eng. 2020, 7, 469–488. [Google Scholar] [CrossRef]
- Kirkpatrick, S.; Gelatt, C.D., Jr.; Vecchi, M.P. Optimization by Simulated Annealing. Science 1983, 220, 671–680. [Google Scholar] [CrossRef] [PubMed]
- Metropolis, N.; Rosenbluth, A.W.; Rosenbluth, M.N.; Teller, A.H.; Teller, E. Equation of State Calculations by Fast Computing Machines. J. Chem. Phys. 1953, 21, 1087–1092. [Google Scholar] [CrossRef]
- Talbi, E.-G. Metaheuristics from Design to Implementation; Wiley: Hoboken, NJ, USA, 2009. [Google Scholar]
- Khan, A.; Zaman, G. Global analysis of an age-structured SEIR endemic model. Chaos Solitons Fractals 2018, 108, 154–165. [Google Scholar] [CrossRef]
- Wang, X.; Peng, H.; Shi, B.; Jiang, D.; Zhang, S.; Chen, B. Optimal vaccination strategy of a constrained time-varying SEIR epidemic model. Commun. Nonlinear Sci. Numer. Simul. 2019, 67, 37–48. [Google Scholar] [CrossRef]
- Lee, S.; Golinski, M.; Chowell, G. Modeling Optimal Age-Specific Vaccination Strategies Against Pandemic Influenza. Bull. Math. Biol. 2012, 74, 958–980. [Google Scholar] [CrossRef] [PubMed]
- Aletreby, W.T.; Alharthy, A.M.; Faqihi, F.; Mady, A.F.; Ramadan, O.E.; Huwait, B.M.; Alodat, M.A.; Lahmar, A.B.; Mahmood, N.N.; Mumtaz, S.A.; et al. Dynamics of SARS-CoV-2 outbreak in the Kingdom of Saudi Arabia: A predictive model. Saudi Crit. Care J. 2020, 4, 79. [Google Scholar] [CrossRef]
- Kim, S.; Jung, E. Prioritization of vaccine strategy using an age-dependent mathematical model for 2009 A/H1N1 influenza in the Republic of Korea. J. Theor. Biol. 2019, 479, 97–105. [Google Scholar] [CrossRef] [PubMed]
- da Cruz, A.R.; Cardoso, R.T.N.; Takahashi, R.H.C. Multiobjective synthesis of robust vaccination policies. Appl. Soft Comput. 2017, 50, 34–47. [Google Scholar] [CrossRef]
- van den Driessche, P. Reproduction numbers of infectious disease models. Infect. Dis. Model. 2017, 2, 288–303. [Google Scholar] [CrossRef]
- Shulgin, B. Pulse vaccination strategy in the SIR epidemic model. Bull. Math. Biol. 1998, 60, 1123–1148. [Google Scholar] [CrossRef]
- Hill, A.N.; Longini, I.M. The critical vaccination fraction for heterogeneous epidemic models. Math. Biosci. 2003, 181, 85–106. [Google Scholar] [CrossRef]
- Marques, J.; Cunha, M.; Savić, D. Many-objective optimization model for the flexible design of water distribution networks. J. Environ. Manag. 2018, 226, 308–319. [Google Scholar] [CrossRef]
- Amine, K. Multiobjective Simulated Annealing: Principles and Algorithm Variants. Adv. Oper. Res. 2019, 2019, 8134674. [Google Scholar] [CrossRef]
- Deb, K.; Sindhya, K.; Okabe, T. Self-adaptive simulated binary crossover for real-parameter optimization. In Proceedings of the 9th Annual Conference on Genetic and Evolutionary Computation—GECCO ’07, London, UK, 7–11 July 2007; ACM Press: New York, NY, USA, 2007; p. 1187. [Google Scholar] [CrossRef]
- Deb, K.; Deb, D. Analysing mutation schemes for real-parameter genetic algorithms. Int. J. Artif. Intell. Soft Comput. 2014, 4, 1–28. [Google Scholar] [CrossRef]
- Rao, S.; Nyquist, A.-C.; Stillwell, P.C. Influenza. In Kendig’s Disorders of the Respiratory Tract in Children; Elsevier: Amsterdam, The Netherlands, 2019; pp. 460–465.e2. [Google Scholar] [CrossRef]
- Patel, R.; Longini, I.M.; Halloran, M.E. Finding optimal vaccination strategies for pandemic influenza using genetic algorithms. J. Theor. Biol. 2005, 234, 201–212. [Google Scholar] [CrossRef]
- Cardoso, R.T.N.; Takahashi, R.H.C. Solving Impulsive Control Problems by Discrete-Time Dynamic Optimization Methods. TEMA—Tendências Em Matemática Apl. E Comput. 2008, 9, 21–30. [Google Scholar] [CrossRef][Green Version]
- Yang, T. Impulsive control. IEEE Trans. Automat. Contr. 1999, 44, 1081–1083. [Google Scholar] [CrossRef]
- Bertsekas, D.P. Dynamic Programming and Optimal Control, 2nd ed.; Athena Scientific: Belmont, MA, USA, 2000. [Google Scholar]
- Lin, Y.-K.; Yeh, C.-T. Maximal network reliability with optimal transmission line assignment for stochastic electric power networks via genetic algorithms. Appl. Soft Comput. 2011, 11, 2714–2724. [Google Scholar] [CrossRef]
- Uray, E.; Carbas, S.; Geem, Z.W.; Kim, S. Parameters Optimization of Taguchi Method Integrated Hybrid Harmony Search Algorithm for Engineering Design Problems. Mathematics 2022, 10, 327. [Google Scholar] [CrossRef]
- Sabarish, K.V.; Baskar, J.; Paul, P. Overview on L9 taguchi optimizational method. Int. J. Adv. Res. Eng. Technol. 2019, 10, 652–658. [Google Scholar] [CrossRef]
- Yazdi, M.; Nedjati, A.; Zarei, E.; Abbassi, R. Application of multi-criteria decision-making tools for a site analysis of offshore wind turbines. In Artificial Intelligence and Data Science in Environmental Sensing; Elsevier: Amsterdam, The Netherlands, 2022; pp. 109–127. [Google Scholar] [CrossRef]
- Li, M.; Yao, X. Quality Evaluation of Solution Sets in Multiobjective Optimisation: A Survey. ACM Comput. Surv. 2020, 52, 1–38. [Google Scholar] [CrossRef]
- Santos, T.; Xavier, S. A Convergence indicator for Multi-Objective Optimisation Algorithms. TEMA 2018, 19, 437–448. [Google Scholar] [CrossRef]
- Higgins, J.J. An Introduction to Modern Nonparametric Statistics; Brooks/Cole: Pacific Grove, CA, USA, 2004. [Google Scholar]
- Drake, J.H.; Kheiri, A.; Özcan, E.; Burke, E.K. Recent advances in selection hyper-heuristics. Eur. J. Oper. Res. 2020, 285, 405–428. [Google Scholar] [CrossRef]
- Dulebenets, M.A. An Adaptive Polyploid Memetic Algorithm for scheduling trucks at a cross-docking terminal. Inf. Sci. 2021, 565, 390–421. [Google Scholar] [CrossRef]
- Chuang, C.-S.; Hong, C.-C. New Self-Adaptive Algorithms and Inertial Self-Adaptive Algorithms for the Split Variational Inclusion Problems in Hilbert Space. Numer. Funct. Anal. Optim. 2022, 43, 1050–1068. [Google Scholar] [CrossRef]
- Li, J.; Gonsalves, T. Parallel Hybrid Island Metaheuristic Algorithm. IEEE Access 2022, 10, 42268–42286. [Google Scholar] [CrossRef]
- Blum, C.; Puchinger, J.; Raidl, G.R.; Roli, A. Hybrid metaheuristics in combinatorial optimization: A survey. Appl. Soft Comput. 2011, 11, 4135–4151. [Google Scholar] [CrossRef]
- Singh, P.; Pasha, J.; Moses, R.; Sobanjo, J.; Ozguven, E.E.; Dulebenets, M.A. Development of exact and heuristic optimization methods for safety improvement projects at level crossings under conflicting objectives. Reliab. Eng. Syst. Saf. 2022, 220, 108296. [Google Scholar] [CrossRef]
- Dulebenets, M.A. A Diffused Memetic Optimizer for reactive berth allocation and scheduling at marine container terminals in response to disruptions. Swarm Evol. Comput. 2023, 80, 101334. [Google Scholar] [CrossRef]
- Singh, E.; Pillay, N. A Study of Ant-Based Pheromone Spaces for Generation Perturbative Hyper-Heuristics. In Proceedings of the Genetic and Evolutionary Computation Conference, Lisbon, Portugal, 15–19 July 2023; ACM: New York, NY, USA, 2023; pp. 84–92. [Google Scholar] [CrossRef]
| Input: starting temperature value (T0), final temperature value (Tmin), temperature cooling schedule (α), and initial solution (SInitial), Initialize solution SCurrent = SInitial; Initialize temperature T = T0; Repeat Repeat Generate a random neighbor candidate solution SCandidate; ΔE = f (SCandidate) − f (SCurrent); If ΔE ≤ 0 Then SCurrent = SCandidate Else Accept SCandidate with a probability ; Until equilibrium condition T = T × α; Until stopping criteria satisfied Output: best solution found |
| Parameters | Definition | Value |
|---|---|---|
| β | Transmission rate | 4.5 (t.u.)−1 |
| γ1 | Recovery rate of infected individuals | 1/7 (t.u.)−1 |
| γ2 | Recovery rate of hospitalized individuals | 1/7 (t.u.)−1 |
| μ | Birth and mortality rate | 1/70 (t.u.)−1 |
| n | Progress to immune rate | 10 (t.u.) |
| k | Progress to infectious rate | ½ (t.u.)−1 |
| a | Rate of infectious becoming hospitalized | 0.2135 (t.u.)−1 |
| R0 | Reproduction number | 15 |
| itol | Tolerance ratio | 0.01 |
| Parameters | Parameters Levels | ||
|---|---|---|---|
| Level 1 | Level 2 | Level 3 | |
| Starting temperature (A) | 30 | 50 | 70 |
| Temperature cooling rate (B) | 0.5 | 0.7 | 0.9 |
| Number of local search moves (C) | 5 | 7 | 10 |
| Parameters | Optimal Value |
|---|---|
| Starting temperature (A) | 50 |
| Temperature cooling rate (B) | 0.7 |
| Number of local search moves (C) | 10 |
| PC | PRE | |||||
|---|---|---|---|---|---|---|
| MOSA-LS | MOSA-Canonical | LS-Canonical | MOSA-LS | MOSA-Canonical | LS-Canonical | |
| p-Value | 1.45311 × 10−7 | 0.004994938 | 0.9927282 | 5.258285 × 10−38 | 4.044913 × 10−18 | 0.9994427 |
| F1 | F2 | |||||
| MOSA-LS | MOSA-Canonical | LS-Canonical | MOSA-LS | MOSA-Canonical | LS-Canonical | |
| 1 | 1 | 0.9999513 | 5.167215 × 10−9 | 1.772605 × 10−22 | 2.568021 × 10−7 | |
| Average 10 Runs Execution Time | CENSGA—MOSA | Canonical CENSGA | CENSGA—LS |
|---|---|---|---|
| Experiment 1 | 307.4102 | 227.3253 | 256.8435 |
| Experiment 2 | 319.188 | 210.3709 | 263.9084 |
| Experiment 3 | 332.1827 | 216.6491 | 270.7399 |
| Experiment 4 | 317.2059 | 204.6829 | 266.15789 |
| Experiment 5 | 315.9615 | 214.1225 | 265.0167 |
| Experiment 6 | 318.5307 | 251.59 | 203.7231 |
| Experiment 7 | 313.8855 | 206.3925 | 270.2337 |
| Experiment 8 | 318.9852 | 205.8596 | 267.3136 |
| Experiment 9 | 336.0775 | 217.9315 | 273.2358 |
| Overall average | 319.936 | 217.214 | 259.686 |
| # | Experiments | MOSA | LS | Canonical | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| ER | GD | ε-IQ | HV | ER | GD | ε-IQ | HV | ER | GD | ε-IQ | HV | ||
| 1 | γ = 1/5, β = 1.18 | 0.613 | 2.924 | 10.55 | 0.479 | 0.607 | 3.319 | 8.988 | 0.806 | 0.781 | 4.227 | 9.594 | 1.297 |
| 2 | γ = 1/5, β = 2.36 | 0.581 | 6.213 | 7.029 | 0.972 | 0.588 | 1.442 | 30.09 | 0.536 | 0.832 | 1.182 | 40.32 | 0.511 |
| 3 | γ = 1/5, β = 4.72 | 0.602 | 2.318 | 2.521 | 0.792 | 0.579 | 1.294 | 24.76 | 0.710 | 0.819 | 0.718 | 42.17 | 0.683 |
| 4 | γ = 1/7, β = 1.18 | 0.609 | 4.105 | 12.39 | 0.516 | 0.609 | 3.450 | 8.933 | 0.811 | 0.782 | 4.272 | 9.569 | 1.299 |
| 5 | γ = 1/7, β = 2.36 | 0.581 | 6.618 | 7.029 | 0.972 | 0.588 | 1.442 | 30.09 | 0.536 | 0.832 | 1.182 | 40.32 | 0.511 |
| 6 | γ = 1/7, β = 4.72 | 0.454 | 3.446 | 2.647 | 0.746 | 0.686 | 0.770 | 39.17 | 0.680 | 0.782 | 0.593 | 54.37 | 0.729 |
| 7 | γ = 1/9, β = 1.18 | 0.606 | 4.543 | 11.69 | 0.548 | 0.611 | 3.513 | 8.933 | 0.987 | 0.782 | 4.275 | 9.569 | 1.299 |
| 8 | γ = 1/9, β = 2.36 | 0.581 | 7.035 | 7.029 | 0.972 | 0.588 | 1.442 | 30.09 | 0.536 | 0.832 | 1.182 | 40.32 | 0.511 |
| 9 | γ = 1/9, β = 4.72 | 0.602 | 2.425 | 2.521 | 0.792 | 0.579 | 1.294 | 24.76 | 0.710 | 0.797 | 0.718 | 42.17 | 0.699 |
| Average | 0.581 | 4.403 | 7.045 | 0.754 | 0.604 | 1.996 | 22.87 | 0.702 | 0.804 | 2.039 | 32.05 | 0.838 | |
| ER | GD | ||||
|---|---|---|---|---|---|
| MOSA-LS | MOSA-Canonical | LS-Canonical | MOSA-LS | MOSA-Canonical | LS-Canonical |
| 0.317 | 0.005 | 0.005 | 0.995 | 0.988 | 0.453 |
| ε-IQ | HV | ||||
| MOSA-LS | MOSA-Canonical | LS-Canonical | MOSA-LS | MOSA-Canonical | LS-Canonical |
| 0.029 | 0.029 | 0.004 | 0.317 | 0.594 | 0.829 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Alkhamis, A.K.; Hosny, M. A Multi-Objective Simulated Annealing Local Search Algorithm in Memetic CENSGA: Application to Vaccination Allocation for Influenza. Sustainability 2023, 15, 15347. https://doi.org/10.3390/su152115347
Alkhamis AK, Hosny M. A Multi-Objective Simulated Annealing Local Search Algorithm in Memetic CENSGA: Application to Vaccination Allocation for Influenza. Sustainability. 2023; 15(21):15347. https://doi.org/10.3390/su152115347
Chicago/Turabian StyleAlkhamis, Asma Khalil, and Manar Hosny. 2023. "A Multi-Objective Simulated Annealing Local Search Algorithm in Memetic CENSGA: Application to Vaccination Allocation for Influenza" Sustainability 15, no. 21: 15347. https://doi.org/10.3390/su152115347
APA StyleAlkhamis, A. K., & Hosny, M. (2023). A Multi-Objective Simulated Annealing Local Search Algorithm in Memetic CENSGA: Application to Vaccination Allocation for Influenza. Sustainability, 15(21), 15347. https://doi.org/10.3390/su152115347







