Probabilistic Approach to Transient Unsaturated Slope Stability Associated with Precipitation Event

Abstract

The massif rupture is not always reached under saturated conditions; therefore, the analysis of the unsaturated phenomenon is necessary in some cases. This study performed a probabilistic approach for unsaturated and transient conditions to understand the contribution of physical and hydraulic parameters involved in slope stability. The proposed slope stability model was based on the infinite slope method and a new unsaturated constitutive shear strength model proposed in 2021 by Cavalcante and Mascarenhas. The first-order second-moment method, which incorporated multiple stochastic variables, was used in the probabilistic analysis, allowing the incorporation of seven independent variables for the probability of failure analysis as well as for quantifying the contribution of the variables to the total variance of a factor of safety at any state of moisture. This implementation allows a more realistic estimative for the probability of failure, showing in a practical way the decrease and increase of the probability of failure during a rain event. The model provided promising results highlighting the need to migrate from deterministic analyses to more robust probabilistic analyses, considering the most significant number of stochastic variables. The proposed model helps to understand the influence of moisture content on slope stability, being a possible tool in natural disaster risk management.

1. Introduction

The considerable increase in mass movements increased the susceptibility of tropical mountainous regions to landslides owing to the high degree of soil weathering combined with long stationary periods of rain. Along with increased population and expansion to mountainous areas, these natural conditions directly affect the communities through human and economic losses [1].

During rain events, water precipitates to the surface of massifs, infiltrating the slope and negatively affecting their stability. This process often triggers superficial mass movements identified as translational or planar movements in geotechnics. The stability of a slope or embankment is quantified by the factor of safety (FS), which compares the stresses at work with the resistant strains of the massif. In this case, instability is represented when FS is less than or equal to 1.

In geotechnical engineering, FS can be quantified using several models, namely conceptual, numerical, and analytical models, that are developed according to the geometric, topographic, geotechnical, and hydraulic characteristics of the slope. However, in tropical regions, where the unsaturated state of massifs predominates, understanding mass movements due to the negative pore-water pressure response should be improved [2].

Various authors have developed or applied specific numerical solutions under adjusted conditions and simplifications for each case of stability study, highlighting the need for closed mathematical solutions for understanding the unsaturated flow that would facilitate the computational implementation, the validation of numerical models, and a better representation of the physical phenomenon [2,3,4,5,6,7,8,9].

In the context of unsaturated slope stability, the flow analysis in an unsaturated porous medium and its respective attributes, such as soil water retention curve (SWRC) and unsaturated hydraulic conductivity function of the medium (k-function), should be incorporated.

The conventional deterministic FS quantification is not a reliable indicator of the performance of a slope because the physical and mechanical properties of the soils are inherently associated with the natural uncertainties of the environment. This situation is more evident in the unsaturated state owing to the changes in the uncertainties associated with moisture and suction, which directly influence the stability response. Therefore, probabilistic models should be used to understand the transient conditions that lead to slope faults, considering the statistical dispersion of physical, mechanical, hydraulic, and unsaturated material attributes for a more realistic failure indication [10].

This study evaluated the importance of the probabilistic approach in the unsaturated and transient slope stability analysis. The evaluation methodology proposed by Rojas [11], which implemented the analytical model of infiltration defined by Cavalcante and Zornberg in 2017 [12], and analytical model of unsaturated slope stability defined by Cavalcante and Camapum de Carvalho [13], which considered the constitutive model to evaluate the unsaturated shear strength defined by Cavalcante and Mascarenhas [14], was considered in this work.

It is known that the increasing climatic variability and complex geological conditions increase the limitations inherent in deterministic methods for assessing slope stability. Traditional deterministic approaches often rely on fixed values for soil properties and environmental conditions, overlooking the inherent uncertainties and spatial-temporal variations. This study adopts a probabilistic approach to assess transient unsaturated slope stability, particularly under precipitation events. By incorporating stochastic variables and utilizing the first-order second-moment method (FOSM), our model allows for a more nuanced, risk-informed assessment of slope stability. This approach is critical for providing more realistic estimates in situations where soil properties and hydraulic conditions are not uniformly distributed and are subject to change over time. Thus, the probabilistic framework introduced here offers an improved tool for natural disaster risk management and is especially beneficial in engineering applications where uncertainties are often inevitable.

Unlike conventional geotechnical practices, the proposed methodology considered all independent variables associated with the physical stability problem as continuous random variables. Owing to the high computational cost, random variables were limited. The analyses were performed for one rainfall intensity to quantify the slope performance index and contribution of each physical parameter in the stability. The developed computational methods were implemented using Wolfram Mathematica.

2. Unsaturated Slope Stability

The behavior of materials depends directly on the interaction between the grains; thus, slope stability analysis is usually carried out in the state of effective stresses. However, as shown by Taha et al. [15] and Nishimura and Fredlund [16], the negative pore-water pressure in the unsaturated soil regime, which indicates the amount of water in the voids, directly influences the interaction of the grains, as demonstrated in the significant increases in the shear strength associated with the rise of the matrix suction in some materials. Meanwhile, the potential failure surface is not always conditioned to the saturated state of the soil, considering that the balance between the resisting and acting forces is broken under negative pore-water pressures in some situations, thereby triggering the failure in the unsaturated condition [17]. Thus, the stability of unsaturated slopes under precipitation events should be evaluated to analyze the flow phenomenon, as assessed by the Richards equation [18], and the phenomenon of stresses in the unsaturated porous medium, as validated by the principle of effective strains of Terzaghi in the unsaturated condition [19].

2.1. Unsaturated Flow in Porous Medium

Buckingham [20] incorporated the concept of negative pore pressure into the flow, thereby developing the Darcy–Buckingham law, which derives the fluid velocity in an unsaturated porous medium as follows:

$$v=-\frac{k_s\left(\psi \right)}{g}\frac{\partial \Phi }{\partial L}$$

(1)

where k_s(Ψ) is the function of the unsaturated hydraulic conductivity (LT⁻¹), $\partial \Phi /\partial L$ is the rate of change of potential energy at the extent of flow motion (L), and g is the acceleration due to gravity (LT⁻²)

Subsequently, Richards defined the continuity equation for three-dimensional flow in a porous medium, assuming an incompressible fluid without volume change in the soil mass throughout the flow process (i.e., constant ρ_w) [18]. Thus, Richards combined the continuity equation with the Darcy–Buckingham law (Equation (1)), thereby establishing a partial differential equation for three-dimensional flow in an unsaturated porous medium, as follows:

$$\frac{\partial \theta }{\partial t}=\frac{\partial }{\partial x}\left(\frac{k_x\left(\psi \right)}{g{\rho }_w}\frac{\partial \psi }{\partial x}\right)+\frac{\partial }{\partial y}\left(\frac{k_y\left(\psi \right)}{g{\rho }_w}\frac{\partial \psi }{\partial y}\right)+\frac{\partial }{\partial z}\left(k_z\left(\psi \right)\left(\frac{\partial \psi }{\partial y}\frac{1}{g{\rho }_w}-1\right)\right)$$

(2)

The solution of Equation (2) depends on two constitutive relations: (1) the SWRC, which relates the soil volumetric moisture content with the matrix suction potential, and (2) the k-function, which relates the soil hydraulic conductivity with the matrix suction potential. In practice, the most commonly used constitutive models for obtaining unsaturated soil attributes are those obtained by Brooks and Corey [21], Van Genuchten [22], and Fredlund and Xing [23]. These models established highly nonlinear relationships, resulting in the high complexity in obtaining an analytical solution to Richards’ equation under transient conditions [24].

Cavalcante and Zornberg [12,25] proposed new constitutive models to represent the SWRC and k-function, thereby obtaining four analytical solutions for the one-dimensional unsaturated flow problem represented by Richards’ partial differential equation in the vertical direction. The constitutive models of the SWRC and k-function are defined in Equations (3) and (4), respectively:

$$\psi \left(\theta \right)=\frac{1}{\delta }\ln \left(\frac{\theta -{\theta }_r}{{\theta }_s-{\theta }_r}\right)$$

(3)

$$k_z\left(\theta \right)=k_s\left(\frac{\theta -{\theta }_r}{{\theta }_s-{\theta }_r}\right)$$

(4)

where θ is the volumetric soil moisture content (L³L⁻³), θ_s is the saturated volumetric soil water content (L³L⁻³), θ_r is the residual volumetric soil water content (L³L⁻³), θ_s − θ_r is the maximum soil wetting capacity (L³L⁻³), k_s is the saturated hydraulic conductivity of the soil (LT⁻¹), and δ is the hydraulic fitting parameter of Cavalcante and Zornberg [12] (M⁻¹LT²).

In the work of Costa and Cavalcante [26], the hydraulic fitting parameter has a quantitative physical meaning related to the entry of the air pressure into the soil pore matrix. In particular, the hydraulic fitting parameter is higher for sandy soils and lower for finer soils. Subsequently, Costa and Cavalcante [27] developed a constitutive model for obtaining the SWRC and k-function of bimodal soils, represented by Equations (5) and (6), respectively:

$$\theta \left(\psi \right)={\theta }_r+\left({\theta }_s-{\theta }_r\right)\left[\lambda \exp \left(-{\delta }_1\left|\psi \right|\right)+\left(1-\lambda \right)\exp \left(-{\delta }_2\left|\psi \right|\right)\right]$$

(5)

$$k\left(\psi \right)=k_s\left[\lambda \exp \left(-{\delta }_1\left|\psi \right|\right)+\left(1-\lambda \right)\exp \left(-{\delta }_2\left|\psi \right|\right)\right]$$

(6)

where δ₁ is the hydraulic fitting parameter of the macroporous region (M⁻¹LT²), δ₂ is the hydraulic fitting parameter of the microporous region (M⁻¹LT²), and λ is the weight factor corresponding to the macroporous region.

The flow phenomenon associated with rainfall depends directly on the storage capacity of the soil on the ground surface. This region determines the amount of water available to initiate the percolation process within the massif. These characteristics are well represented by the analytical solution proposed by Cavalcante and Zornberg [12]. In particular, the authors implemented the assumptions adopted in developing the column test, considering a one-dimensional flow modeling, approximately constant soil porosity throughout the test, and a soil column with a finite compression. The initial condition of the problem was defined by a uniform moisture content throughout the domain with the assumptions of an impermeable region for the lower boundary and constant discharge velocity of the upper boundary, thereby determining the transient surface storage capacity or infiltration rate. This maximum discharge velocity is:

$$v_{i,max}=\frac{{\theta }_s{k}_s}{\left({\theta }_s-{\theta }_r\right)}$$

(7)

Thus, the analytical solution that represents the moisture fronts at any depth of the unsaturated transient flow of a slope is:

$$\theta \left(z,t\right)={\theta }_i+\left[\frac{v_i}{k_s}\left({\theta }_s-{\theta }_r\right)-{\theta }_i\right]D\left(z,t\right)$$

(8)

where v_i is the infiltration rate (LT⁻¹), θ_i is the initial volumetric soil water content (L³L⁻³), and D(z,t) is the auxiliary function of the analytical solution reported by Cavalcante and Zornberg [12], and represented as follows:

$$\begin{array}{ll}D\left(z,t\right)& =\frac{1}{2}erfc\left(Z_{-1}\right)+\sqrt{\frac{{\overline{a}}_s^{2}t}{\pi {\overline{D}}_z}}\exp \left(-\frac{{\left(z-{\overline{a}}_{s}t\right)}^2}{4{\overline{D}}_{z}t}\right)-\frac{1}{2}\left(-1+\frac{{\overline{a}}_{s}z}{{\overline{D}}_z}+\frac{{\overline{a}}_s^{2}t}{{\overline{D}}_z}\right)\\ & \times \exp \left(\frac{{\overline{a}}_{s}z}{{\overline{D}}_z}\right)erfc\left(Z_{+1}\right)+\sqrt{4\frac{{\overline{a}}_s^{2}t}{\pi {\overline{D}}_z}}\left(1+\frac{{\overline{a}}_s}{4{\overline{D}}_z}\left(2L-z+{\overline{a}}_{s}t\right)\right)\\ & \times \exp \left(\frac{{\overline{a}}_{s}L}{{\overline{D}}_z}-\frac{1}{4{\overline{D}}_{z}t}{\left(2L-z+{\overline{a}}_{s}t\right)}^2\right)\\ & -\frac{{\overline{a}}_s}{{\overline{D}}_z}\left(2L-z+\frac{3{\overline{a}}_{s}t}{2}+\frac{{\overline{a}}_s}{4{\overline{D}}_z}\left(2L-z+{\overline{a}}_{s}t\right)\right)\\ & \times \exp \left(-\frac{{\overline{a}}_{s}L}{{\overline{D}}_z}\right)erfc\left(\frac{\left(2L-z+{\overline{a}}_{s}t\right)}{2\sqrt{{\overline{D}}_{z}t}}\right)\end{array}$$

(9)

The auxiliary terms that constitute D(z,t) are given by:

$$Z_{\pm 1}=\frac{z\pm {\overline{a}}_{s}t}{2\sqrt{{\overline{D}}_z}t}$$

(10)

$${\overline{a}}_s=\frac{k_s}{\left({\theta }_s-{\theta }_r\right)}$$

(11)

$${\overline{D}}_z=\frac{k_s}{\delta \left({\theta }_s-{\theta }_r\right){\rho }_{w}g}$$

(12)

where ${\overline{a}}_s$ is the unsaturated advective seepage velocity (LT⁻¹) and ${\overline{D}}_z$ is the unsaturated water diffusivity (L²T⁻¹).

2.2. Soil-Atmosphere Interaction

In the interaction of the slope surface with the atmosphere, it is essential to highlight the function of hydrogeology, which studies the spatial and temporal dynamics of water inside the massifs to evaluate geotechnical problems. In addition, it covers a closed hydrological cycle, i.e., the phenomena of distributing water in the atmosphere, soil surface, and subsoil [28]. Thus, for surface landslides triggered by rains, the concept of the hydrological cycle is simplified to the physical phenomena of precipitation, runoff, evapotranspiration, interception and infiltration, given by:

$$i(t)=e_s(t)+v_i(t)+e_v(t)+I(t)$$

(13)

where i(t) is the precipitation intensity (LT⁻¹), v_i(t) is the infiltration rate (LT⁻¹), e_s(t) is the runoff velocity (LT⁻¹), I(t) is the interception by the vegetation (LT⁻¹), and e_v (t) is the evapotranspiration velocity (LT⁻¹).

In practice, evapotranspiration is the most challenging parameter to quantify. The increase in evapotranspiration at the slope surface produces positive effects on the stability of the surface layers, thereby requiring more significant amounts of water to reach instability [29,30]. Similarly, interception modeling is complex as it depends directly on the type of vegetation on the slope surface. Increased rainwater interception by vegetation decreases the impact of precipitation on the ground surface and reduces the water available to infiltrate the soil [31]. Thus, a more conservative analysis that disregards the action of evapotranspiration and the interception can be obtained by defining the hydro–geotechnical cycle for the study of slope stability associated with precipitation events as:

$$i(t)=e_s(t)+v_i(t)$$

(14)

In classical hydrology, the rational method determines the runoff, an accepted theoretical approach for determining runoff flows that contribute to a hydrographic basin [32]. This methodology depends on the runoff coefficient c, which is defined as a function of topography, land use, and slope surface cover, represented by:

$$Q(t)=c\cdot i(t)\cdot A$$

(15)

where Q(t) is the flow associated with runoff (L³T⁻¹), A is the area of the contribution basin (L²), and c is the runoff coefficient (dimensionless).

It is important to note that the rational method has a limitation regarding the precise mapping data of the runoff coefficient c. Considering the rational method for calculating the instantaneous flow of the runoff associated with the topography of the slope surface and maximum wetting capacity defined by Cavalcante and Zornberg [12] ($v_{i,max}$), Rojas described the runoff velocity as [11]:

$$e_s(t)=\left\{\begin{array}{ll}\mathrm{c}\cdot i(t)& \mathrm{if}{v}_i\le v_{i,max}\\ \left(i(t)-v_{i,máx}\right)+\mathrm{c}\cdot i(t)& \mathrm{if}{v}_i>v_{i,max}\end{array}\right.$$

(16)

Thus, by applying Equation (16) to Equation (14), the infiltration rate as a function of the precipitated water and amount of runoff water can be quantified as:

$$v_i(t)=i(t)-e_s(t)$$

(17)

2.3. Unsaturated Shear Strength

Determining the soil stress state is based on constitutive models and functions that correlate the variables involved in normal stresses, shear stresses, and deformations by selecting the changes in soil stress and strain. In the unsaturated state, these relationships were established as a function of the principle of effective stresses of Terzaghi [19], where the total normal stress is rewritten as the sum of the pore pressure and effective soil pressure.

The Mohr-Coulomb model was extended to the unsaturated medium to understand the mechanical behavior of soils in this state, where the effective normal stress is defined as the combination of two variables independent of the stress state of the mass incorporating the air. The most commonly used constitutive relationships in practice are those of Croney et al. [33], Bishop [34], and Fredlund et al. [35]. Among these, Bishop’s model and Fredlund’s model are the most widely used in practice and are given, respectively, by:

$$\tau =c^{\prime }+\left(\sigma -u_a\right)\tan {\varphi }^{\prime }+\chi \left(u_a-u_w\right)\tan {\varphi }^{\prime }$$

(18)

$$\tau =c^{\prime }+\left(\sigma -u_a\right)\tan {\varphi }^{\prime }+\left(u_a-u_w\right)\tan {\varphi }^b$$

(19)

where c′ is the effective cohesion of the soil (ML⁻¹T⁻²), ϕ′ is the effective friction angle of the soil (°), ϕ^b is the angle of friction of the soil relative to the matrix suction (°), σ is the normal total stress applied to the massif (ML⁻¹T⁻²), τ is the shearing stress acting on the slope (ML⁻¹T⁻²), u_w is the pore-water pressure in the soil (ML⁻¹T⁻²), and χ is the unsaturated effective stress parameter or Bishop’s parameter (non-dimensional).

Equations (18) and (19) can be essentially treated as equivalent with the assumption of the following equality [14,36]:

$$\chi \tan {\varphi }^{\prime }=\tan {\varphi }^b$$

(20)

Considering the thermodynamic arguments proposed by Lu et al. to express χ as function of the degree of saturation [37], Cavalcante and Mascarenhas [14] developed a constitutive model for the mechanical behavior of unsaturated soils, which incorporated the constitutive model of Cavalcante and Zornberg for the SWRC as showed at the Equation (3) [12]. Thus, an analytical expression as a function of a single fitting hydraulic parameter δ is defined as:

$$\chi =e^{-\delta \left|u_a-u_w\right|}$$

(21)

Replacing Equation (21) into Equation (20) and then into Equation (19), the authors defined a new constitutive model for the unsaturated shear strength as:

$$\tau =c^{\prime }+\left[(\sigma -u_a)+e^{-\delta \left|u_a-u_w\right|}\cdot (u_a-u_w)\right]\cdot \tan {\varphi }^{\prime }$$

(22)

From Equation (22), the unsaturated cohesion or total cohesion of soil is represented as:

$$c_{\mathrm{unsat}}=c^{\prime }+e^{-\delta \left|u_a-u_w\right|}\cdot (u_a-u_w)\cdot \tan {\varphi }^{\prime }$$

(23)

The infinite slope method is one of the most widely used methods in evaluating translational or planar mass movements, which generally represent the landslides associated with rainfalls [17]. This analytical method satisfies the static balance of forces involved in the massif and requires a few hypotheses for its implementation. Some of its premises are that the method considers the failure plane parallel to the surface (translational movement), and the slope length must be at least ten times greater than the soil thickness, disregarding the slope length in determining FS [38].

Thus, to represent the slope stability more realistically, Cavalcante and Camapum de Carvalho [13] rewrote the infinite slope model for the assessment of stability in the unsaturated condition by incorporating the analytical solution of Richards Equation for the one-dimensional infiltration proposed by Cavalcante and Zornberg [12]. Subsequently, the authors rewrote the constitutive model of shear strength defined by Fredlund et al. [35], assuming that the relative air pressure on the slope surface corresponds to atmospheric pressure (u_a = 0).

Following the methodology of Cavalcante and Camapum de Carvalho [13], the current work implemented the constitutive model to evaluate the unsaturated shear strength developed by Cavalcante and Mascarenhas [14]. The rationale for this choice stems from the model’s comprehensive treatment of both physical and hydraulic parameters affecting slope stability in unsaturated conditions. Moreover, this model is a recent addition to the field, incorporating state-of-the-art advancements in unsaturated soil mechanics. Its applicability and efficacy have been validated in various studies, thereby adding a layer of credibility to our analytical framework. We recognize that multiple models exist for evaluating unsaturated slope stability; however, the Cavalcante and Zornberg [12] model offers a robust and well-validated approach that aligns with the complexities and uncertainties considered in our probabilistic analysis. Thus, it serves as a suitable foundation for the methodologies and analyses presented in this manuscript. Therefore, the slope safety factor, which is the ratio between the acting forces and the resistant forces of the slope, is defined by:

$$FS(z,t)=\frac{\tan {\varphi }^{\prime }}{\tan \beta }+\frac{c^{\prime }-\left(u_a-u_w\right)\left(z,t\right)\cdot e^{-\delta \cdot \left|\left(u_w-u_w\right)\left(z,t\right)\right|}\cdot \tan {\varphi }^{\prime }}{\left({\gamma }_d+{\gamma }_w\cdot \theta (z,t)\right)\cdot \cos \left(\beta \right)\cdot \sin \left(\beta \right)\cdot z}$$

(24)

where (u_a − u_w)(z,t) is the negative pore-water pressure as a function of depth and time, which is the matric suction (ML⁻¹T⁻²), γ_d is the specific weight of the grains (MT⁻²L⁻²), γ_w is the specific weight of water (MT⁻²L⁻²), and β is the slope angle (°).

Equation (24) represents an analytical, unsaturated, and transient model with physical meaning that considers the variations in soil density, the variations in negative pore-water pressure, and the variations of the effective cohesion as a function of the degree of saturation of the porous medium for the indication of the rupture moment.

3. Failure Probability

Disregarding the uncertainties involved in the slope stability analysis is a limitation the probabilistic approach should overcome. It incorporates the systematic analysis of the geotechnical parameters’ uncertainties as continuous stochastic variables represented by a probability distribution. Consequently, the FS under specific conditions is also characterized by a probabilistic distribution instead of deterministic and constant values.

In assessing the probability of slope failure, the methods routinely applied are the Monte Carlo method, first-order second-moment method (FOSM), and point estimates method [10,13,31,39,40,41,42,43,44]. However, due to advances in technology, recent methodologies using artificial intelligence have been developed for predicting slope stability [45,46,47,48,49].

To evaluate the performance of the slope in the unsaturated condition and discover the contribution of each variable in the deterministic slope stability model (Equation (24)), the probabilistic FOSM method, which can be implemented for analytical models, was chosen by the authors. This approach requires only the statistical moments of the mean and standard deviation. Moreover, it can quantify each independent variable’s contribution to the FS’s total variance.

3.1. First-Order Second-Moment Method

FOSM is an approximate probabilistic method that uses the Taylor series to determine the moment values of the statistical distributions representing the variables involved in the analyses. To determine the dependent variable’s probability distribution function (PDF), the method requires the mean values of the independent variables and derivatives of the independent variables as a function of the dependent variable [50].

The statistical moments obtained by FOSM for the construction of PDF are the mean $\left(E\left[x\right]=\overline{x}\right)$ as a measure of the central tendency and variance $\left(V\left[x\right]={\sigma }^2\right)$ as a measure of the variation or dispersion. When there is no correlation between the independent variables, these moments are determined as follows:

$$E[f(x)]=f(\overline{x})$$

(25)

$$V[f(x)]={{\displaystyle \sum \left(\frac{\partial f(x)}{\partial x_i}\right)}}^{2}V(x_i)$$

(26)

As FOSM does not estimate the type of probability distribution of independent variables, there should be prior knowledge of the probability distribution that best represents the physical variables involved in the problem. In this case, the normal distribution, one of the most used distributions to model natural phenomena, efficiently represents the PDF of the physical and mechanical parameters of the soil involved in the slope stability analysis [51,52].

However, saturated hydraulic conductivity (k_s) is best represented by a lognormal distribution probability density function, as presented by several authors [31,39,53,54,55,56]. In this case, a simple transformation is used to represent the statistical moments of a lognormal distribution in terms of a normal distribution as:

$$\mathrm{E}{[k_s]}_{\mathrm{normal}}=\log (k_s)$$

(27)

$$\mathrm{V}{[k_s]}_{\mathrm{normal}}=\ln \left(\frac{{\mathrm{V}(\mathrm{k}}_s)}{k_s{}^2}+1\right)$$

(28)

Considering k_s = 10^log(k_s⁾, the effect of the hydraulic property on the failure probability analysis could be incorporated by rewriting Equation (8) as:

$$\theta \left(z,t\right)={\theta }_i+\left[\frac{v_i}{{10}^{\mathrm{E}{[ks]}_{\mathrm{normal}}}}\left({\theta }_s-{\theta }_r\right)-{\theta }_i\right]D\left(z,t\right)$$

(29)

3.2. Transient Failure Probability

In analyzing the stability of unsaturated slopes, the importance of obtaining the transient response of the pore water pressure should be highlighted to understand the physical and hydraulic conditions that lead to slope failure. Thus, the transient response of the probability of failure should be obtained.

In engineering practice, the application of FOSM allows the analysis of the reliability index of FS, defined by:

$$\beta \prime =\frac{E[\mathrm{FS}]-\mathrm{FSc}}{\sigma [\mathrm{FS}]}$$

(30)

where β′ is the reliability index of the FS (dimensionless) and FSc is the critical FS. The reliability index represents the number of standard deviations between FSc and FS based on the analysis. This theory was developed for a normal probability distribution, where a more significant β′ suggests a lower probability of failure (P_f).

As presented by Husein Malkawi et al. [57], the reliability index of FS is directly related to the probability of failure under a normal distribution, as follows:

$$P_f\left(\beta \prime \right)=P\left(\mathrm{FS}\le \mathrm{FSc}\right)=1-\frac{1}{2}\mathrm{erfc}\left(-\frac{\beta \prime }{\sqrt{2}}\right)$$

(31)

Knowing the analytical solution for the transient FS, presented in Equation (24), the total transient variance can be defined as:

$$V[\mathrm{FS}(z,t)]={{\displaystyle \sum \left(\frac{\partial \mathrm{FS}(z,t)}{\partial x_i}\right)}}^{2}V(x_i)$$

(32)

Replacing Equation (32) and Equation (24) into Equation (30), the slope transient reliability index is:

$$\beta \prime (t,z)=\frac{E[\mathrm{FS}(t,z)]-\mathrm{FSc}}{\sqrt{V[\mathrm{FS}(t,z)]}}$$

(33)

Consequently, the transient failure probability for the unsaturated stability problem is:

$$P_f\left(t,z\right)=P\left(\mathrm{FS}\le \mathrm{FSc}\right)=1-\frac{1}{2}\mathrm{erfc}\left(-\frac{\beta \prime (t,z)}{\sqrt{2}}\right)$$

(34)

4. Case Study

In this study, the authors used the information from Rojas [11], where the infiltration and unsaturated stability analysis was implemented in the La Arenosa basin studied by Aristizábal et al. [58]. This basin is located in the mountainous region of Colombia, where multiple landslides were recorded associated with a precipitation event on 21 September 1991.

An unconditionally unstable slope was chosen for the analysis because of its geometry, as validated by Rojas [11], which clearly exhibited rupture during the high-intensity rain event. As presented in the research by Aristizabal et al. [58], the slope failure is translational, which aligns with the model proposed in this work.

The physical, mechanical, and hydraulic parameters of the slope and coefficient of variation (CoV) of the independent variables incorporated into the probability analysis were adopted from the doctoral theses of Gitirana Jr. [39] and are presented in

Table 1. Deterministic and probabilistic parameters for analyzing an unsaturated slope’s stability and failure probability.

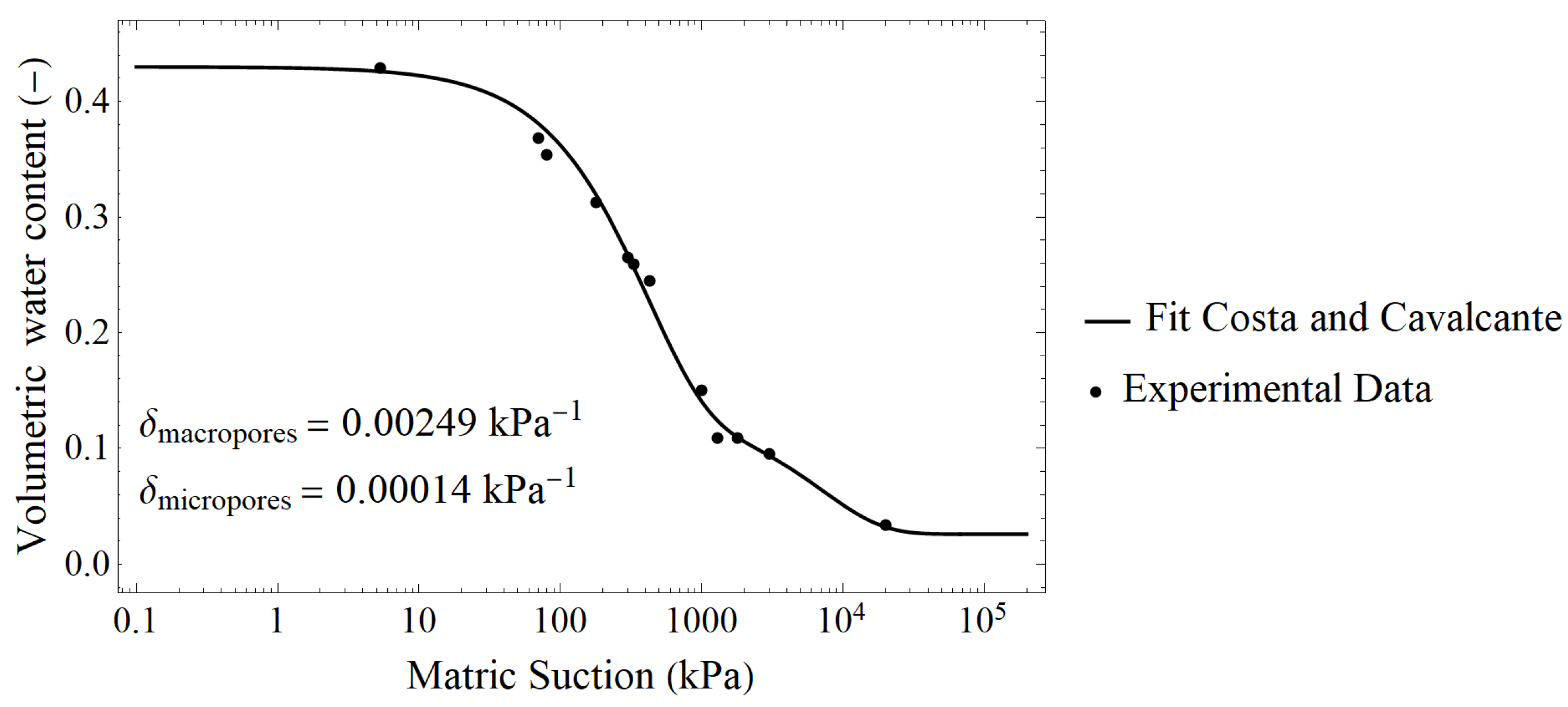
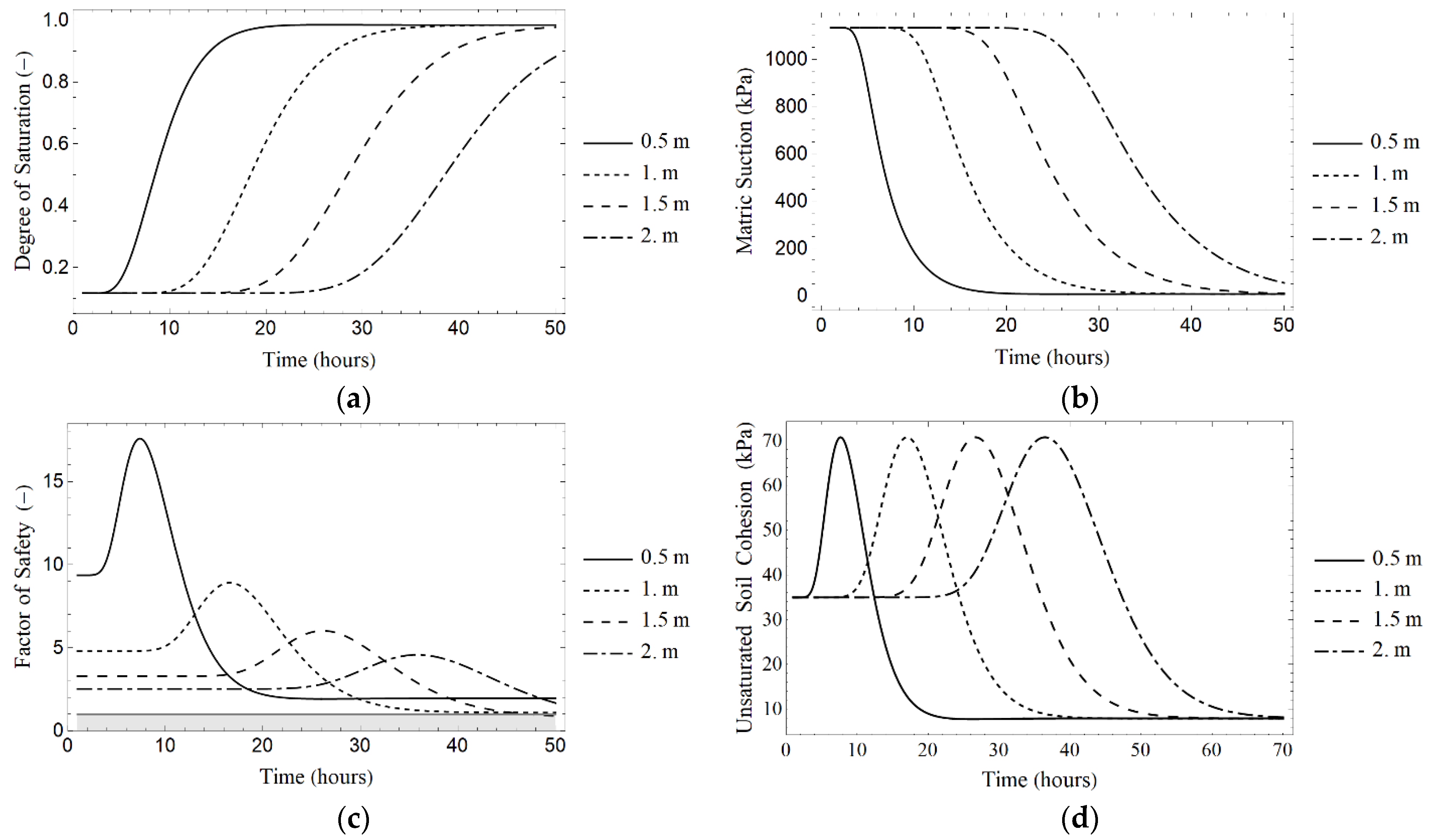
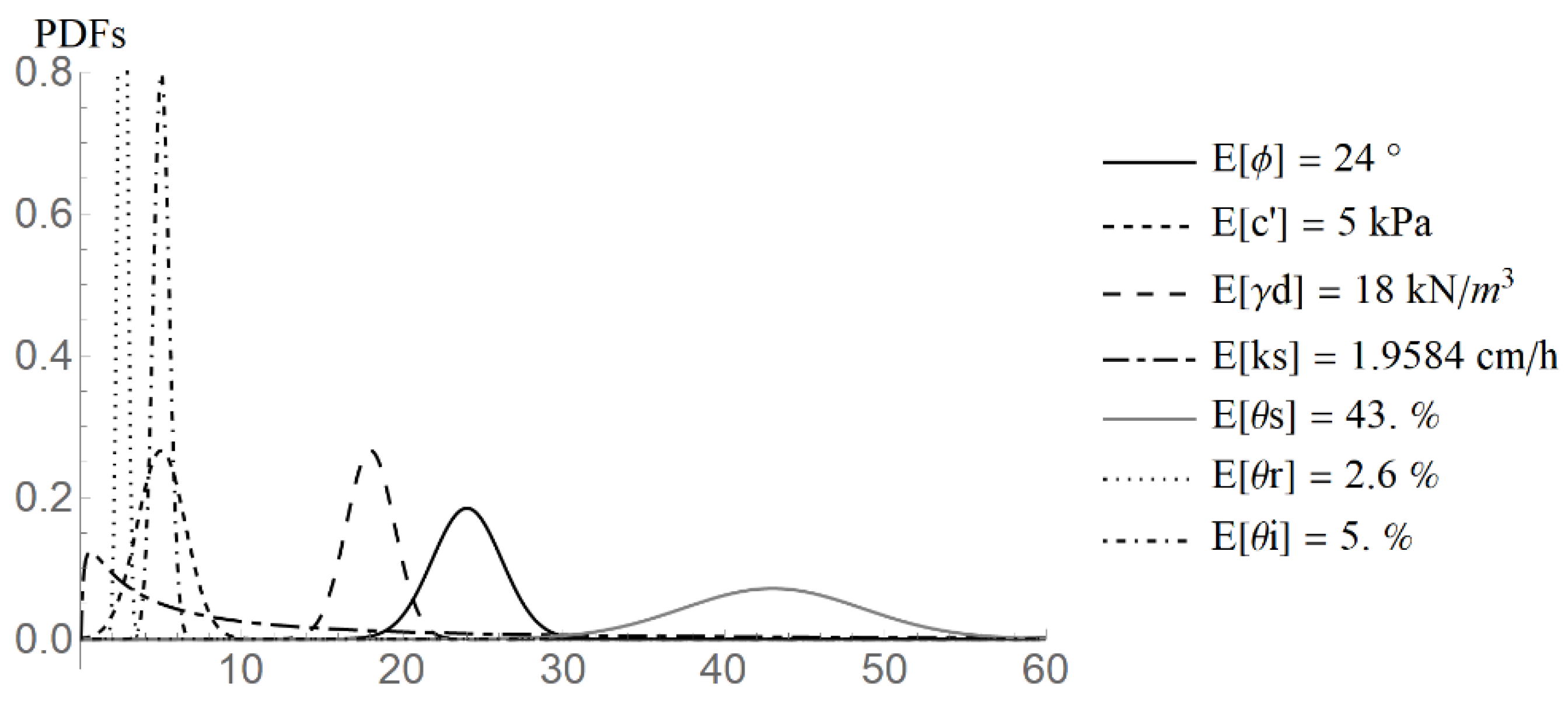
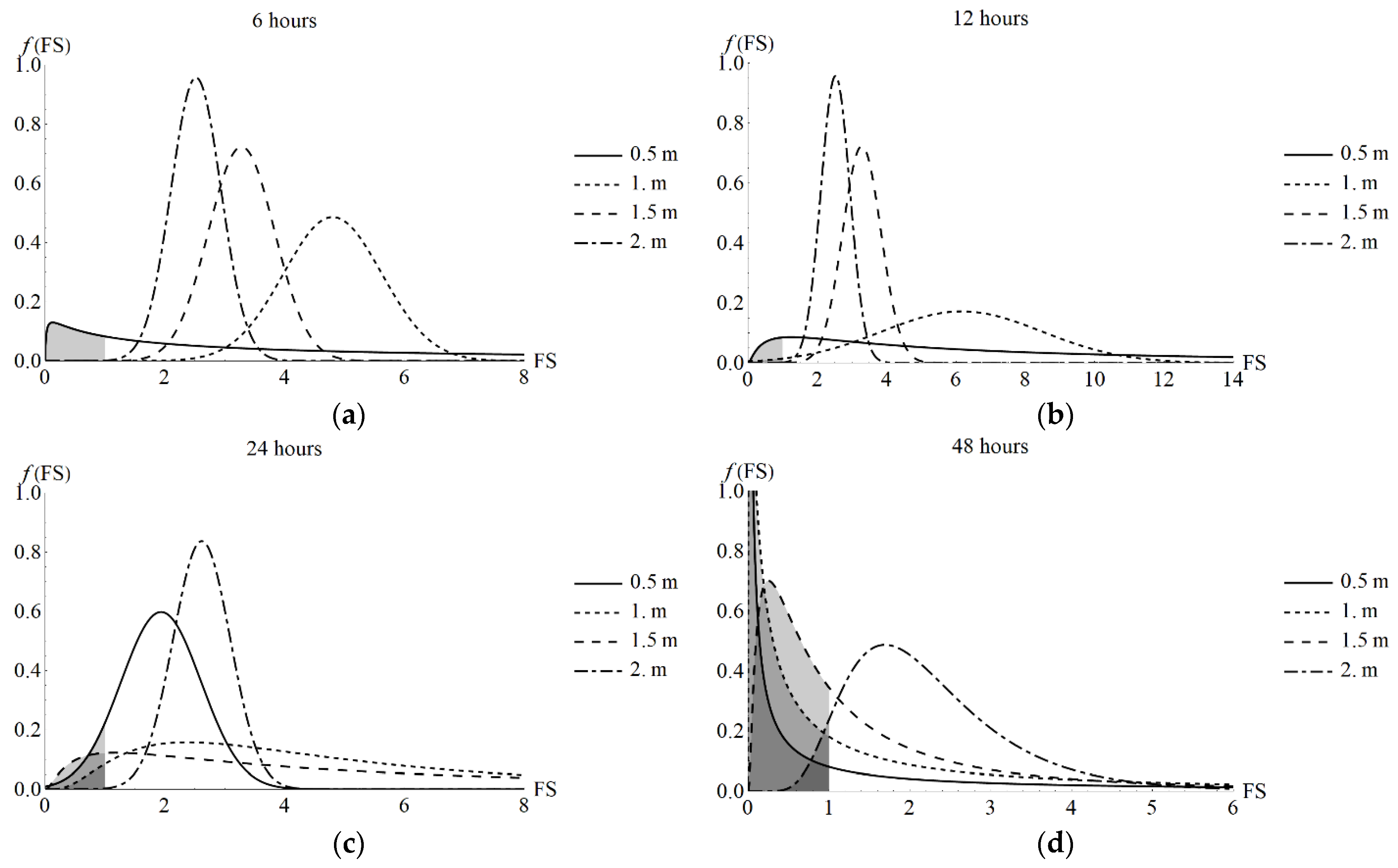
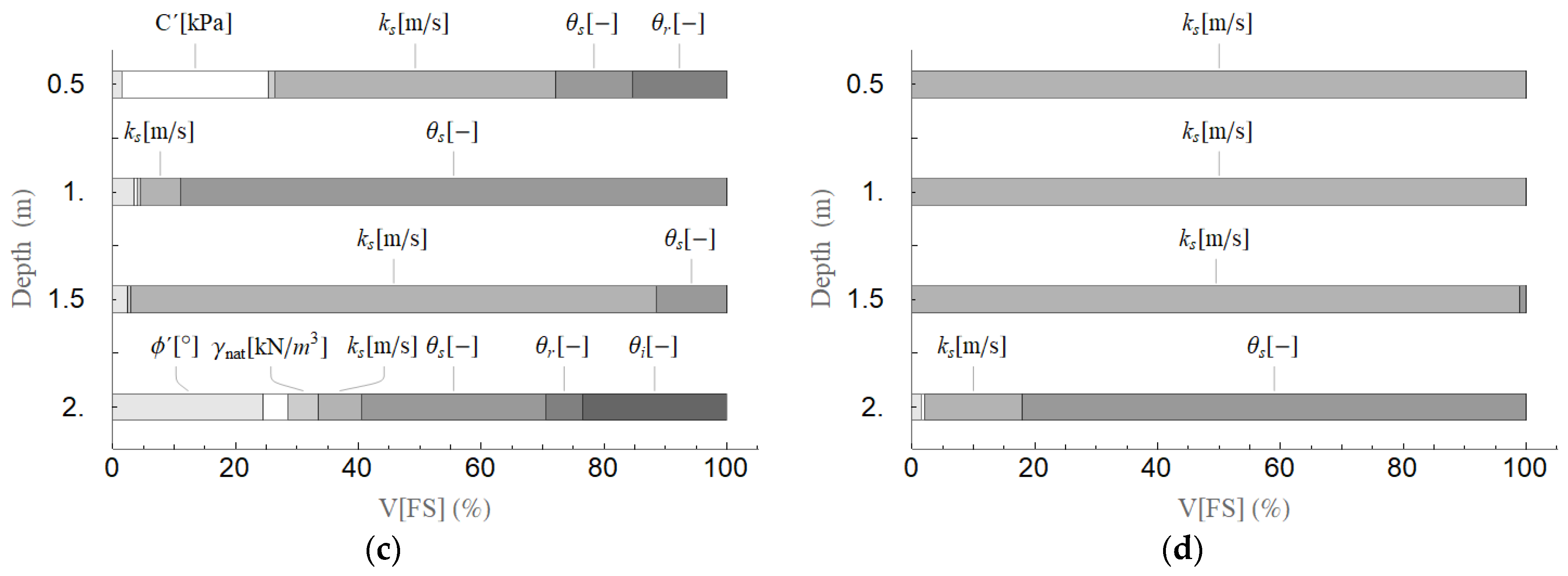
Parameter Type	Parameter	Mean	CoV
Deterministic Parameters	β (°)	62	–
	δ (kPa−1)	0.00249	–
	vi (ms−1)	5.73 × 10−6	–
	c (-)	0.375
Probabilistic Parameters	ϕ′ (°)	24	9
	C’ (kPa)	5	30
	γd (kNm−3)	18	5
	Log [ks] (ms−1)	Log [5.4 × 10−6]	80
	θr (m3m−3)	0.026	10
	θs (m3m−3)	0.43	13
	θi (m3m−3)	0.05	10

.

The unsaturated soil attributes were first obtained from the bimodal fit to the SWRC model proposed by Costa and Cavalcante [27]. As shown in Figure 1, the soil, in this case study, exhibited an SWRC with a bimodal behavior defined by two hydraulic fitting parameters δ for the micropore and macropore regions. The unsaturated attributes of the exposed soil shown in Figure 2 were obtained from the constitutive models of Cavalcante and Zornberg [12] for the macropores region.

To understand the importance of the probabilistic approach, an event with a high precipitation intensity of 20 mm/h was analyzed. The hydro-geotechnical balance analysis obtained the infiltration rate value v_i using Equation (17).

4.1. Assessment of the Transient and Unsaturated Deterministic Stability

The saturation and slope stability fronts were obtained by applying the model of Cavalcante and Zornberg [12] and Equation (24), respectively. The analyses were conducted for four depths with a distance interval of 0.5 m.

Figure 3a presents the transient saturation profile of the slope during a rainfall of 20 mm/h. This analysis shows that the rainwater percolation inside the slope can fill 90% of voids at a soil depth of 50 cm in approximately 14 h. Thus, during a 50 h analysis, only the first three control depths (0.5, 1.0, and 1.5 m) achieved saturation levels.

Figure 3b presents the transient suction behavior, where the maximum suction generated in the residual soil moisture state is 1134 kPa, and the minimum suction associated with suturing is 6 kPa. As shown in Figure 3c, when the slope stability of the soil is at the residual moisture content (5%) at maximum suction and saturation (12%), the FS performance is lower, which is the opposite of the expected behavior at higher suction values for higher FS. This behavior confirms the promoted stability owing to the water content, as shown in Figure 3c, where the highest stability performance for each depth is given in the time range corresponding to the saturation values of 13–44%. This phenomenon can be explained by the non-linear shear strength enveloping the unsaturated porous media. The increased suction generated by smaller amounts of water in the soil can create the breakage of grains or particle aggregates, thereby impairing the shear strength of soil in the dry state [59].

The transient behavior of unsaturated soil cohesion during a steady rainfall event could be determined by implementing Equation (8) into Equation (23) (Figure 3d). In the scenario with a rainfall of 20 mm/h, the unsaturated cohesion reaches 70 kPa for suction values of approximately 400 kPa and 7 kPa of cohesion for suction values of less than 6 kPa. As expected, slope rupture was inevitable under this scenario. After an analysis of 42 h, the instability, indicated by an FSc value equal to 1, is noted at a depth of 1 m. Consequently, after 2 h (analysis time of 44 h), rupture occurs at a depth of 1.5 m (Figure 3a) when the saturation value reaches 95%, thereby generating a suction of approximately 20 kPa.

4.2. Parametric Analysis of Stochastic Variables

The transient parametric analysis of the stochastic variables defined in Table 1 was performed to identify the response of the FS under different moisture states at a depth of 1 m and is presented in Figure 4.

In Figure 4a, the initial moisture content exhibited important variations for the first 18 h of the analysis, where the saturation varies between 12% and 80%. In Figure 4b, the residual moisture content greatly influences the FS in the same moisture and time range. This response indicates that the proper choice of the initial moisture condition imposed for slope modeling is critical in obtaining more realistic results. Meanwhile, the saturated hydraulic conductivity of the soil (Figure 4g) was shown to be more relevant after the first 25 h of analysis, which demonstrated safety at a lower k_s, a more impermeable soil.

The physical parameter in Figure 4d shows the effect of the specific density of the soil under an unsaturated state, which has higher FS for soils with lower densities. When the mass reaches a saturation of more than 80%, the soil density has lower interference in the FS, resulting in instability for any density and confirming the direct effect of the water in the soil matrix.

In Figure 4e,f, the effect of the soil’s effective cohesion and friction angle is directly proportional to the FS, including rupture for cohesion values below 5 kPa and a friction angle of 20° at saturation values higher than 80%. Therefore, these analyses demonstrated the ability of the deterministic analysis to predict ruptures under unsaturated conditions.

4.3. Assessment of the Probability of Transient Unsaturated Failure

The seven parameters adopted as continuous random variables among the eleven parameters required in an unsaturated stability model are presented in Table 1. The CoV of these parameters indicates the standard deviation of each variable when multiplied by the statistical mean, which is the second statistical moment needed to construct the normal and log-normal distribution of the relative frequency, as presented in Figure 5.

Similar to the deterministic analysis, four depths were fixed for the probabilistic analysis. The contribution of the statistical parameters was quantified at four different times: 6, 12, 24, and 48 h. This work considered the indexes of the United States Army Corps of Engineers-USACE (

Table 2. Permissible failure probabilities [60].

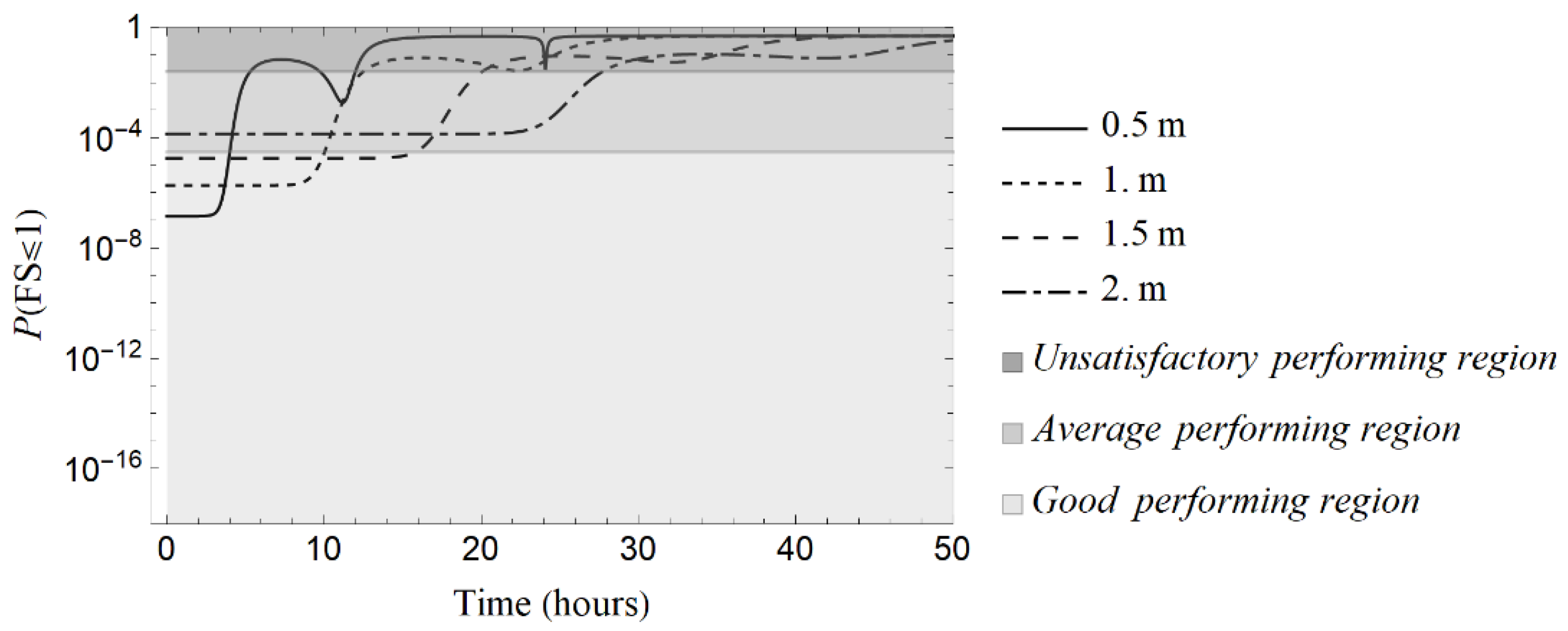
Expected Performance Level	P (FS ≤ FSc)
High	3.0 × 10−7
Good	3.0 × 10−5
Above average	3.0 × 10−3
Below average	6.0 × 10−3
Poor	2.5 × 10−2
Unsatisfactory	7.0 × 10−2
Dangerous	1.6 × 10−1

) as preliminary indications, which define the allowable slope failure probability limits considering an FSc value of 1. Thus, the failure probability should be analyzed considering the risk associated with the effects generated by a slope rupture.

The results from the probabilistic analysis implementing FOSM for rainfall of 20 mm/h are presented in Figure 6.

Table 3. Summary of the probability of failure by applying the FOSM for a rainfall of 20 mm/h.

Analysis Time (h)	z (m)	θ (m3m−3)	Sr (–)	Ψ (kPa)	FS (–)	σ [FS] (–)	p (FS ≤ 1) (%)
6	0.5	0.10	0.24	−672.56	15.74	9.03	1.06 × 100
	1.0	0.05	0.12	−1133.86	4.80	0.82	1.85 × 10−4
	1.5	0.05	0.12	−1133.86	3.28	0.55	1.81 × 10−3
	2.0	0.05	0.12	−1133.86	2.52	0.42	1.36 × 10−2
12	0.5	0.35	0.80	−94.66	8.85	4.06	1.20 × 100
	1.0	0.07	0.15	−930.23	6.16	2.32	9.12 × 10−1
	1.5	0.05	0.12	−1133.74	3.28	0.55	1.82 × 10−3
	2.0	0.05	0.12	−1133.88	2.52	0.42	1.36 × 10−2
24	0.5	0.42	0.98	−6.45	1.93	0.67	7.89 × 100
	1.0	0.35	0.81	−90.08	4.39	2.19	3.81 × 100
	1.5	0.12	0.28	−590.39	5.72	3.52	3.79 × 100
	2.0	0.05	0.12	−1103.43	2.61	0.48	3.59 × 10−2
48	0.5	0.42	0.98	−6.70	1.96	134.90	2.96 × 10−1
	1.0	0.42	0.98	−6.70	1.10	9.04	4.40 × 100
	1.5	0.42	0.97	−11.56	0.96	3.18	12.35 × 100
	2.0	0.36	0.84	−74.46	2.05	1.55	15.58 × 100

shows a summary of the statistic moments obtained for different depths concerning time and the volumetric moisture content and suction generated under each scenario.

In Figure 6a,b, the slope stability exhibits good performance at depths of 1.0, 1.5, and 2.0 m, which is analogous to the deterministic analysis results in Figure 3c. However, at a depth of 0.5 m, the probabilistic analysis revealed an average performance in the first 12 h of the study, thereby suggesting rupture at the slope surface.

In Figure 6c,d, a high probability of rupture is observed for all analyzed depths, as represented by the gray area under the curves. Unlike the deterministic analysis shown in Figure 3c, rupture in the entire slope profile after the first 24 h of study is expected in these situations with 12–80% saturation values.

To better understand the contribution of each parameter’s variance in the stability problem’s total variance, the contributions obtained by FOSM for each analysis time and depth are presented in Figure 7. Contrary to the parametric analysis presented in Figure 4g, the statistical dispersion of the FS represented by the variance (V[FS]) is influenced by the saturated hydraulic conductivity in the first hours of the analysis, as presented in Figure 7a,b. In these scenarios, when k_s accounts for at least 50% of the FS variance, there is a high probability of failure under unsaturated conditions.

The dispersion of the physical parameters (friction and cohesion) affects the total variation of the FS in the first 12 h of the analysis, confirming the importance of these parameters in the unsaturated state. The increased volume of the saturated moisture content in the infiltration process when the soil reaches high saturation values (greater than 80%), checking that this parameter determines the capacity of the soil to receive water.

Figure 8 presents the transient failure probability analysis obtained using Equation (33) to analyze the slope performance profile at different depths and times. Under a rainfall intensity of 20 mm/h, the performance indices oscillated most of the time between the average and unsatisfactory performance regions, demonstrating poor slope surface performance in the first 6 h of the steady rainfall event. Unlike the deterministic analysis, this analysis is more compatible with the field information provided by Aristizábal et al. [58], where the slope was determined to be unconditionally unstable.

5. Conclusions

In this study, a probabilistic approach for unsaturated and transient conditions was carried out to understand the contribution of physical and hydraulic parameters on the stability of slopes. The authors implemented a new stability model that implements the Cavalcante and Mascarenhas shear strength model based on the Cavalcante and Zornberg theory, where they proposed a new solution for the unsaturated flow equation as a function of the delta hydraulic adjustment parameter.

For this work, the FOSM demonstrated a satisfactory, quick, and efficient performance as the models used to evaluate the stability under unsaturated conditions were mathematically closed, thereby allowing the implementation of the method in Wolfram Mathematica software 12.0 at a low computational expense. To fully understand the slope stability during a precipitation event, this study demonstrated the importance of using models of unsaturated conditions, where the initial requirements for obtaining the FS are associated with the impact of hydraulic processes.

The probabilistic analysis confirmed its advantages in problems that involve variables with high dispersion and statistics, such as phenomena that depend on the infiltration and percolation processes. For slopes, quantifying the probability of failure becomes an essential tool for the geotechnical aspect, especially in decision-making involving the risk management associated with mass movements. The comparison of the parametric analysis with the analysis of the contribution to the total variance of the FOSM verified that the analyses of the parameter sensitivity were limited to the information of the first statistical moment (E(FS)), which limited the results on the influence of the dispersion of each parameter in the medium to the FS response.

Finally, the probabilistic analysis provided a more efficient approach under transient conditions, thereby allowing the evaluation of a slope under saturated conditions while incorporating the influence of a precipitation event and all parameters involved in the stability problem. Therefore, the probabilistic analysis can efficiently obtain the slope performance indices at any time and depth with a low computational expense. In this way, the authors suggest conducting probabilistic stability analyses, treating all variables as stochastic, to measure the effect of each parameter on the safety factor’s total variance. A minimum sample size is needed to determine the variation coefficient for each parameter.