A Signal Coordination Model for Long Arterials Considering Link Traffic Flow Characteristics
Abstract
:1. Introduction
2. Materials and Methods
2.1. Notations and Interpretations
2.2. Model Formulation
2.2.1. Objective Function
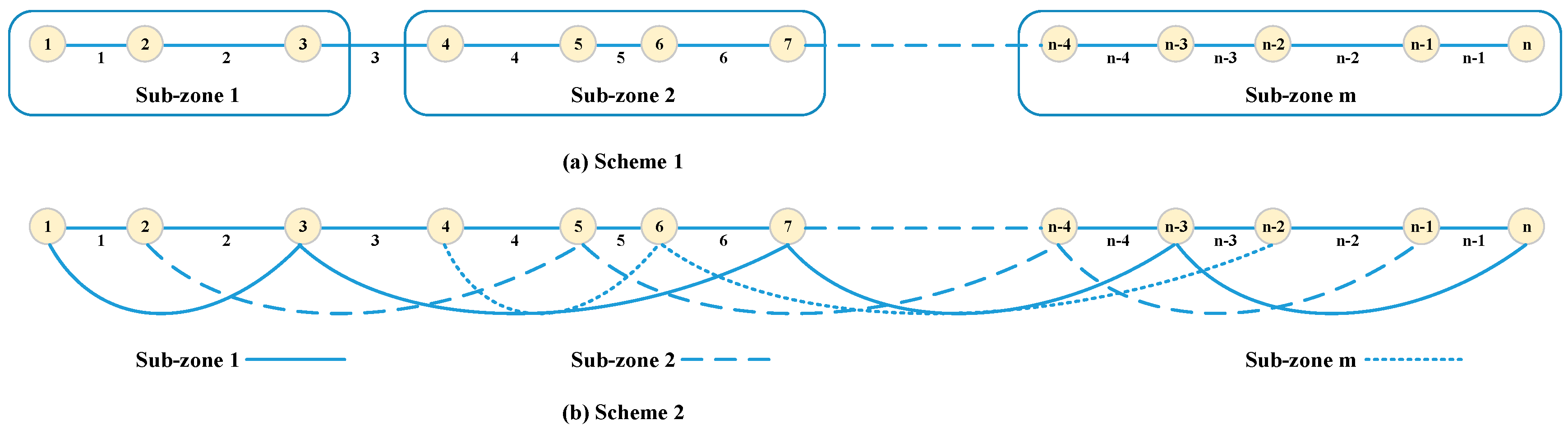
2.2.2. Partition Constraints
2.2.3. Signal Coordination Constraints for Sub-Zones
2.2.4. Link Bandwidth
3. Results
3.1. Test Setup
3.2. Test Results
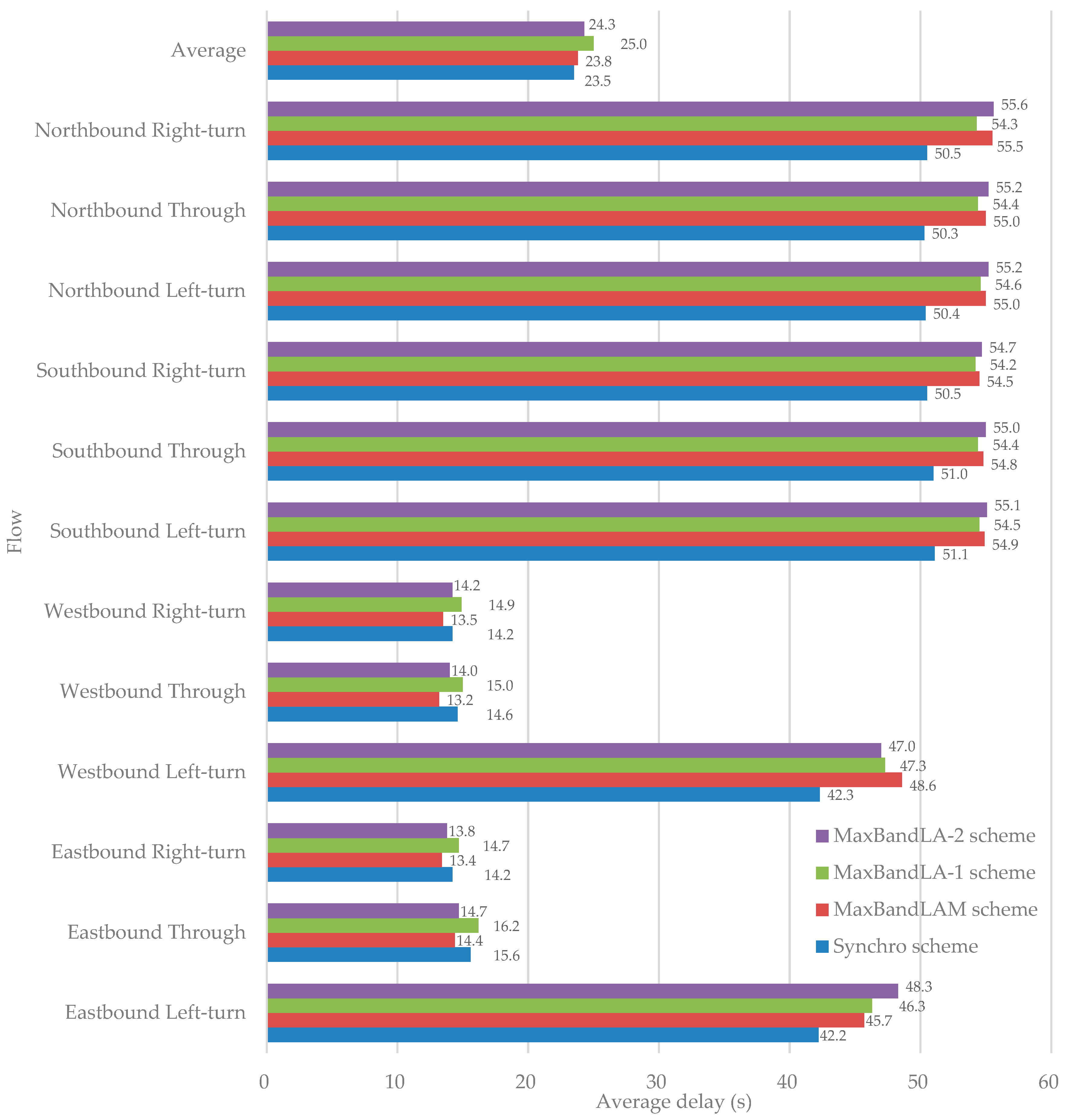
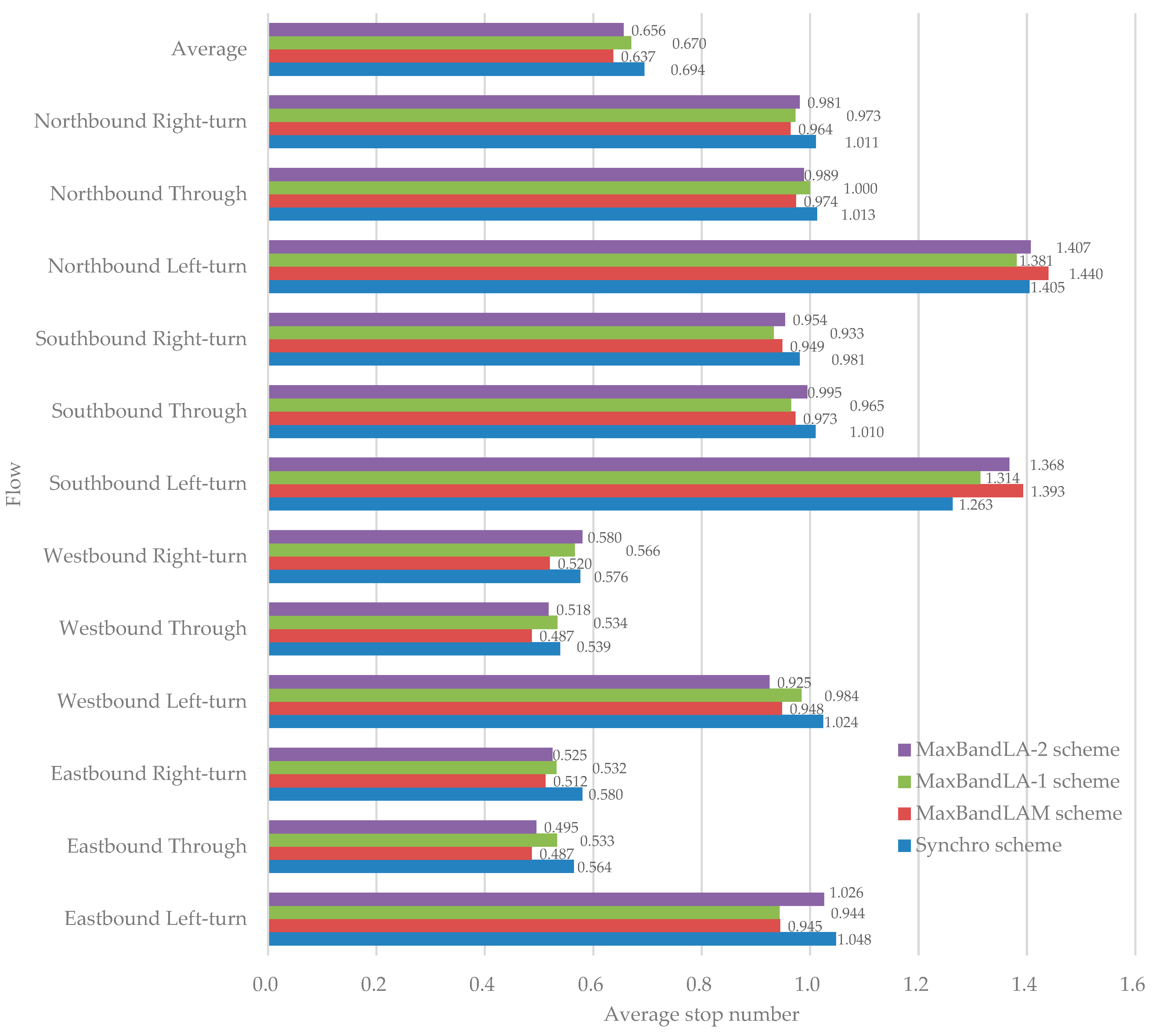
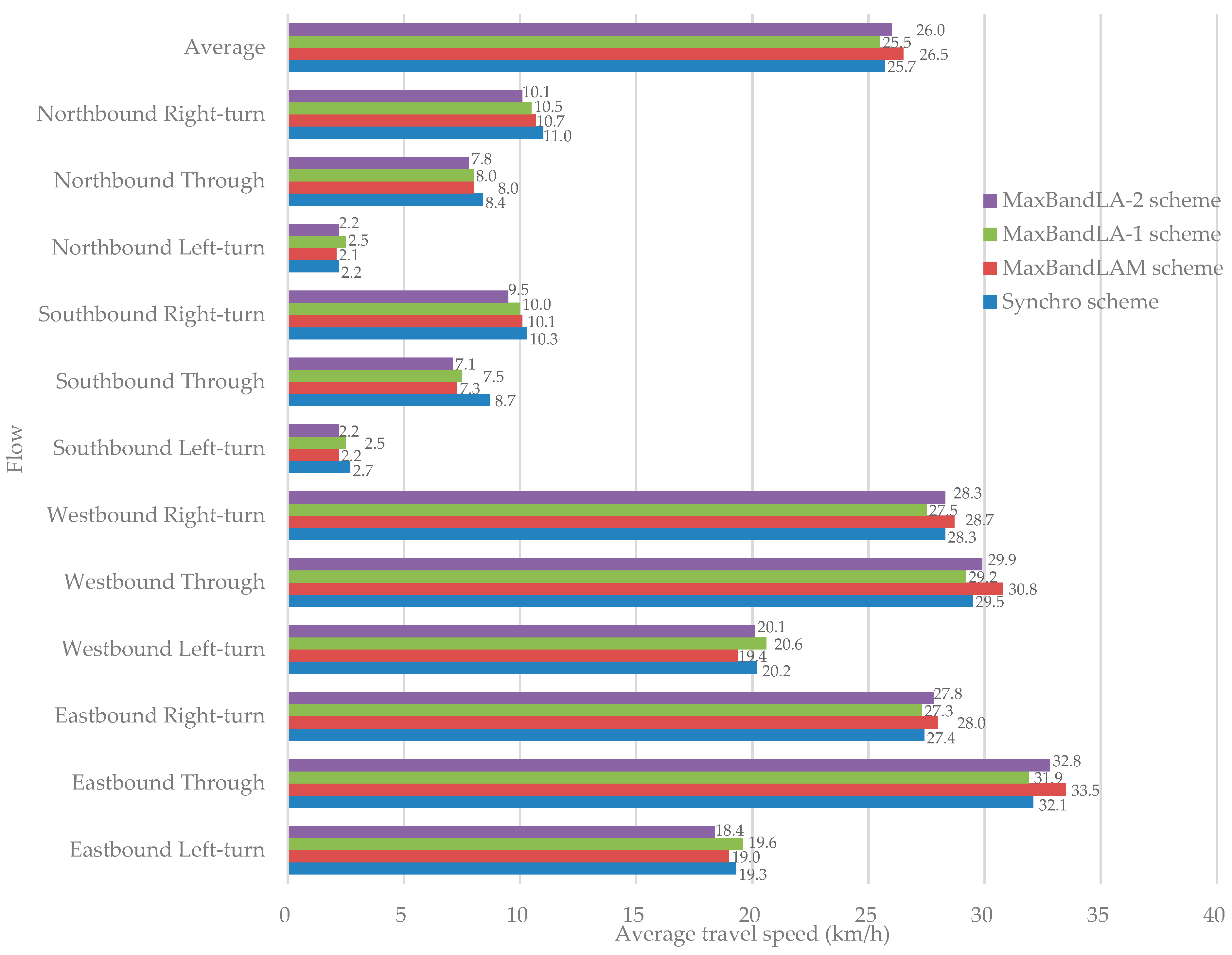
3.3. Simulation Analysis
4. Discussion
5. Conclusions
- (1)
- Frequently breaking a long arterial to partition it into more sub-zones can provide a significant two-way green bandwidth for each sub-zone. But, for traffic flows on the whole arterial, more sub-zones may deteriorate their travel efficiencies.
- (2)
- Links with light traffic flows should have greater priority than links with heavy flows to be selected as the breakpoints. This can lead to further improvement in the travel efficiencies for traffic flows on the whole arterial.
- (3)
- Compared to taking the mean two-way bandwidth of all the sub-zones as the objective to simultaneously optimize the partition scheme and signal coordination schemes for a long arterial, the objective of the weighted sum of the two-way bandwidths of links across the arterial are preferable. This can not only avoid frequently breaking an arterial but also pick out some more suitable links with light traffic flows as breakpoints.
- (4)
- Due to the numeric test performed in this paper being on a virtual arterial with a fixed traffic demand, some stochastic factors will influence the conclusion. More numeric tests on real data should be carried out in future research so that some more profound insights can be derived. Furthermore, the comparison of the combination of some partition technologies and signal coordination technologies with the MaxBandLAM model is also worth conducting in future research.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Hu, H.; Wu, X.; Liu, H.X. Managing oversaturated signalized arterials: A maximum flow based approach. Transp. Res. Part C Emer. 2013, 36, 196–211. [Google Scholar] [CrossRef]
- Zhang, L.; Yin, Y.; Lou, Y. Robust signal timing for arterials under day-to-day demand variations. Transp. Res. Rec. 2010, 2192, 156–166. [Google Scholar] [CrossRef]
- Luo, X.; Liu, B.; Jin, P.J.; Cao, Y.; Hu, W. Arterial traffic flow estimation based on vehicle-to-cloud vehicle trajectory data considering multi-intersection interaction and coordination. Transp. Res. Rec. 2019, 2673, 68–83. [Google Scholar] [CrossRef]
- Li, L.; Huang, W.; Lo, H.K. Adaptive coordinated traffic control for stochastic demand. Transp. Res. Part C Emer. 2018, 88, 31–51. [Google Scholar] [CrossRef]
- Ding, S.; Chen, X.; Yu, L.; Wang, X. Arterial offset optimization considering the delay and emission of platoon: A case study in Beijing. Sustainablity 2019, 11, 3882. [Google Scholar] [CrossRef]
- Gartner, N.H.; Assmann, S.F.; Lasaga, F.; Hou, D.L. Multiband-a variable-bandwidth arterial progression scheme. Transp. Res. Rec. 1990, 1287, 212–222. [Google Scholar]
- Yang, X. Comparison among computer packages in providing timing plans for Iowa arterial in Lawrence, Kansas. J. Transp. Eng.-ASCE 2001, 127, 311–318. [Google Scholar] [CrossRef]
- Little, J.D.C. The synchronization of traffic signals by mixed-integer linear programming. Oper. Res. 1966, 14, 568–594. [Google Scholar] [CrossRef]
- Little, J.D.C.; Kelson, M.D.; Gartner, N.H. Maxband: A program for setting signals on arteries and triangular networks. Transp. Res. Rec. 1981, 795, 40–46. [Google Scholar]
- Tian, Z.; Mangal, V.; Liu, H. Effectiveness of lead–lag phasing on progression bandwidth. Transp. Res. Rec. 2008, 2190, 22–27. [Google Scholar] [CrossRef]
- Chang, C.P.; Cohen, S.L.; Liu, C.; Chaudhary, N.A.; Messer, C. Maxband-86. program for optimizing left-turn phase sequence in multiarterial closed networks. Transp. Res. Rec. 1988, 1181, 61–67. [Google Scholar]
- Gartner, N.H.; Assman, S.F.; Lasaga, F.; Hou, D.L. A multi-band approach to arterial traffic signal optimization. Transp. Res. Part B Meth. 1991, 25, 55–74. [Google Scholar] [CrossRef]
- Zhang, C.; Xie, Y.; Gartner, N.H.; Stamatiadis, C.; Arsava, T. Am-band: An asymmetrical multi-band model for arterial traffic signal coordination. Transp. Res. Part C Emer. 2015, 58, 515–531. [Google Scholar] [CrossRef]
- Zhang, L.; Yin, Y. Robust synchronization of actuated signals on arterials. Transp. Res. Rec. 2008, 2080, 111–119. [Google Scholar] [CrossRef]
- Li, J. Bandwidth synchronization under progression time uncertainty. IEEE Trans. Intell. Transp. Syst. 2014, 15, 749–759. [Google Scholar] [CrossRef]
- Xu, L.; Jin, S.; Li, B.; Wu, J. Traffic signal coordination control for arterials with dedicated CAV lanes. J. Intell. Connect. Veh. 2022, 5, 72–87. [Google Scholar] [CrossRef]
- Ma, N.; Shao, C.; Zhao, Y. Influence factors of coordination control system in signalized intersections. J. Harbin Inst. Technol. 2011, 43, 112–117. [Google Scholar] [CrossRef]
- Yagoda, H.N.; Principle, E.H.; Vick, C.E.; Leonard, B.G. Subdivision of signal systems into control areas. Traffic Eng. 1973, 43, 42–45. [Google Scholar]
- Hook, D.; Albers, A. Comparison of alternative methodogies to determine breakpoints in signal progression. In Proceedings of the 69th Annual Meeting of Institute of Transportation Engineers, Las Vegas, NV, USA, 1–4 August 1999. [Google Scholar]
- Husch, D.; Albeck, J. Synchro Studio 7.0 User Guide, 7th ed.; Trafficware Ltd.: Sugar Land, TX, USA, 2006. [Google Scholar]
- Tian, Z.; Urbanik, T. System partition technique to improve signal coordination and traffic progression. J. Transp. Eng.-ASCE 2007, 133, 119–128. [Google Scholar] [CrossRef]
- Shen, G.; Yang, Y. A dynamic signal coordination control method for urban arterial roads and its application. Front. Inf. Technol. Electron. Eng. 2016, 17, 907–918. [Google Scholar] [CrossRef]
- Zheng, L.; Liu, H.; Ding, T. Mining method for road traffic network synchronization control area. Green Intell. Transp. Syst. 2018, 419, 949–959. [Google Scholar]
- Lan, H.H.; Wu, X.Y. Research on key technology of signal control subarea partition based on correlation degree analysis. Math. Probl. Eng. 2020, 2020, 1879503. [Google Scholar] [CrossRef]
- Zhang, L.; Song, Z.; Tang, X.; Wang, D. Signal coordination models for long arterials and grid networks. Transp. Res. Part C Emer. 2016, 71, 215–230. [Google Scholar] [CrossRef]
- Brooke, A.; Kendirck, D.; Meeraus, A. GAMS: A User’s Guide, 3rd ed.; The Scientific Press: South San Francisco, CA, USA, 1992. [Google Scholar]

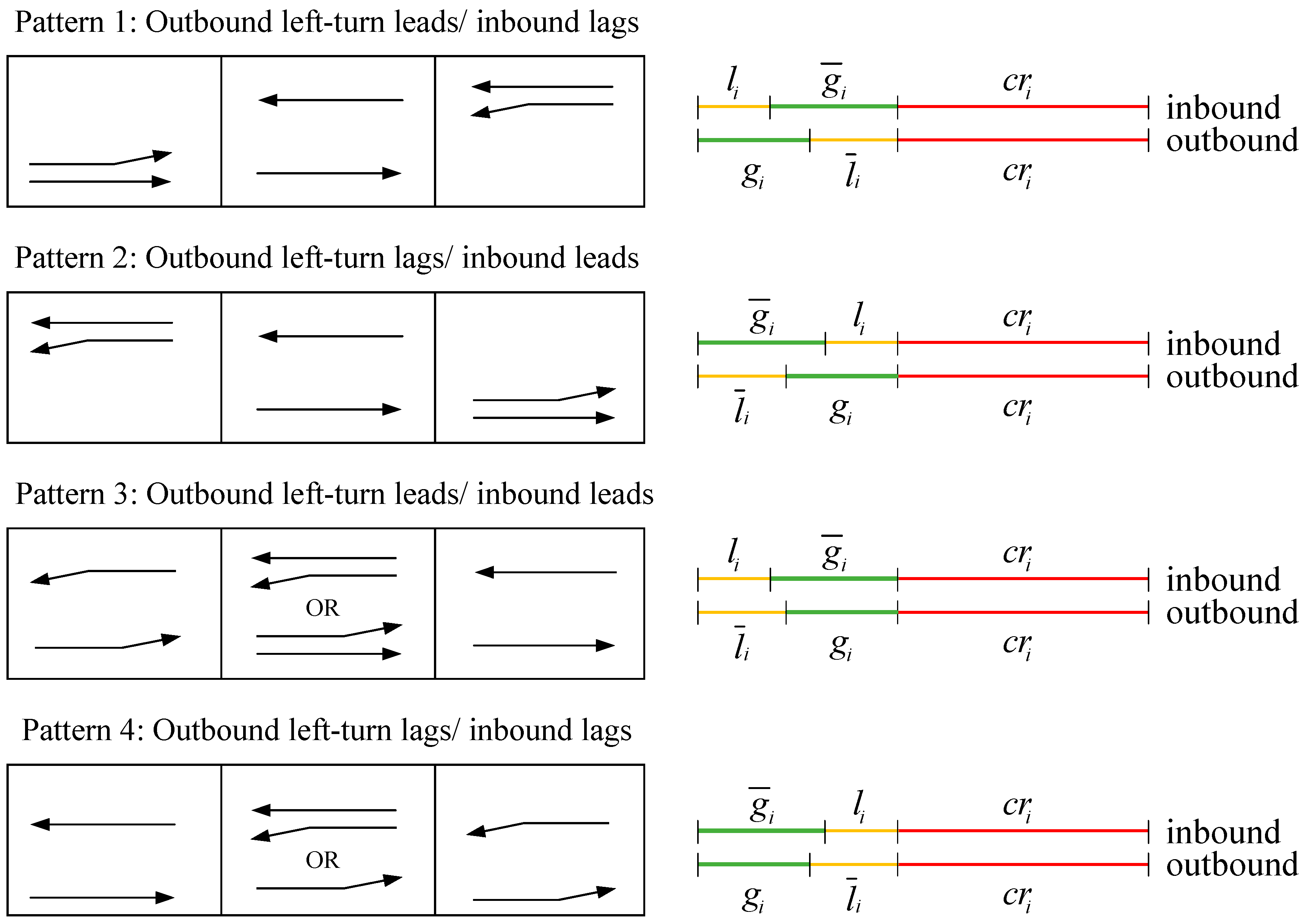
| Notation | Illustration |
|---|---|
| Intersection (Signal) set or link set. Link connects intersection and , except link , which is a virtual link; | |
| Candidate sub-zone set; | |
| Outbound (inbound) green bandwidth of sub-zone (cycles); | |
| Outbound (inbound) green bandwidth of link (cycles); | |
| Loop integer variable to reflect the relationship between outbound and inbound bandwidth on link ; | |
| integer variable; | |
| Outbound (inbound) travel time on link (cycles); | |
| Interference variable on link (cycles); | |
| Offset between signal and , measured as the time from the center of a red of signal to the next center of red of signal (cycles); | |
| Internode offset of signal and (cycles); | |
| Intranode offset of signal (cycles); | |
| Left-turn phases pattern, a binary variable; | |
| Green time for outbound (inbound) through phases of signal (cycles); | |
| Green time for outbound (inbound) left-turn phases of signal (cycles); | |
| Red time for outbound (inbound) through phases of signal (cycles); | |
| Common red time for both outbound and inbound directions to permit flow propagation on side streets (cycles); | |
| Outbound (inbound) queue clear time at intersection (cycles); | |
| The inverse of common cycle length in sub-zone (cycles/second); | |
| Distance of link (meters); | |
| Lower limit on speed of link (meters/second); | |
| Upper limit on speed of link (meters/second); | |
| Lower limit on speed variation between links and (meters/second); | |
| Upper limit on speed variation between links and (meters/second); | |
| Lower and upper limits on cycle length (seconds); | |
| Target ratios of inbound to outbound bandwidth on link ; | |
| Outbound (inbound) bandwidth weight of link ; | |
| Outbound (inbound) volume for through flow on link ; | |
| Outbound (inbound) saturation flow rate for through on link ; | |
| A binary variable to determine whether the intersection belongs to sub-zone , 1 yes, 0 no; | |
| A binary variable to determine whether the link belongs to sub-zone , 1 yes, 0 no. Note that hold for all sub-zones, representing link is a virtual link; | |
| A binary variable to determine whether sub-zone exists or not, 1 yes, 0 no. |
| Pattern | Intranode Offset | Variable | Variable | Illustration |
|---|---|---|---|---|
| 1 | 0 | 1 | Outbound left-turn leads and inbound lags | |
| 2 | 1 | 0 | Outbound left-turn lags and inbound leads | |
| 3 | 0 | 0 | Outbound left-turn leads and inbound leads | |
| 4 | 1 | 1 | Outbound left-turn lags and inbound lags |
| Signal Number | Distance (m) | East Bound (pch/h) | West Bound (pch/h) | North Bound (pch/h) | South Bound (pch/h) | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| LT | TH | RT | LT | TH | RT | LT | TH | RT | LT | TH | RT | ||
| 1 | 341 | 197 | 1439 | 53 | 188 | 1320 | 64 | 139 | 177 | 44 | 140 | 169 | 30 |
| 2 | 695 | 273 | 1217 | 60 | 260 | 1268 | 77 | 97 | 186 | 28 | 103 | 177 | 58 |
| 3 | 594 | 237 | 1412 | 105 | 227 | 1524 | 104 | 91 | 166 | 38 | 92 | 174 | 34 |
| 4 | 533 | 282 | 1188 | 73 | 263 | 1207 | 90 | 102 | 176 | 28 | 94 | 168 | 30 |
| 5 | 296 | 205 | 1456 | 101 | 206 | 1473 | 112 | 116 | 184 | 31 | 116 | 183 | 36 |
| 6 | 497 | 211 | 1566 | 110 | 208 | 1613 | 62 | 84 | 177 | 50 | 83 | 161 | 35 |
| 7 | 366 | 218 | 1491 | 87 | 236 | 1515 | 110 | 110 | 167 | 19 | 114 | 163 | 50 |
| 8 | 774 | 243 | 1523 | 95 | 251 | 1425 | 71 | 131 | 185 | 54 | 131 | 179 | 27 |
| 9 | 475 | 209 | 1412 | 95 | 206 | 1469 | 95 | 134 | 188 | 54 | 147 | 180 | 17 |
| 10 | 359 | 263 | 1400 | 100 | 270 | 1307 | 85 | 130 | 133 | 30 | 130 | 125 | 29 |
| 11 | 643 | 205 | 1387 | 92 | 203 | 1302 | 73 | 86 | 143 | 57 | 78 | 146 | 29 |
| 12 | 403 | 221 | 1453 | 74 | 211 | 1391 | 112 | 124 | 154 | 47 | 124 | 152 | 39 |
| 13 | 357 | 215 | 1644 | 53 | 198 | 1695 | 65 | 111 | 198 | 20 | 114 | 194 | 53 |
| 14 | 524 | 228 | 1297 | 87 | 212 | 1419 | 74 | 116 | 207 | 16 | 114 | 219 | 44 |
| 15 | 518 | 235 | 1273 | 88 | 218 | 1207 | 105 | 103 | 130 | 49 | 111 | 128 | 35 |
| 16 | 344 | 205 | 1398 | 96 | 218 | 1505 | 75 | 79 | 191 | 41 | 85 | 188 | 38 |
| 17 | 518 | 252 | 1473 | 105 | 254 | 1518 | 100 | 109 | 132 | 46 | 110 | 137 | 38 |
| 18 | 398 | 209 | 1540 | 53 | 197 | 1538 | 74 | 108 | 173 | 35 | 119 | 167 | 59 |
| 19 | 780 | 218 | 1577 | 72 | 227 | 1476 | 69 | 119 | 162 | 41 | 117 | 163 | 45 |
| 20 | - | 188 | 1450 | 53 | 177 | 1390 | 68 | 110 | 194 | 47 | 104 | 200 | 41 |
| Signal Number | Cycle (s) | East Bound | West Bound | Side-Street | ||||
|---|---|---|---|---|---|---|---|---|
| Split of through Phase (Cycles) | Split of Left-Turn Phase (Cycles) | Clear Time (Cycles) | Split of through Phase (Cycles) | Split of Left-Turn Phase (Cycles) | Clear Time (Cycles) | Split (Cycles) | ||
| 1 | 85 | 0.576 | 0.200 | 0.093 | 0.565 | 0.188 | 0.083 | 0.235 |
| 2 | 70 | 0.529 | 0.257 | 0.095 | 0.529 | 0.257 | 0.108 | 0.214 |
| 3 | 80 | 0.600 | 0.225 | 0.102 | 0.588 | 0.213 | 0.094 | 0.188 |
| 4 | 70 | 0.543 | 0.271 | 0.102 | 0.529 | 0.257 | 0.098 | 0.200 |
| 5 | 80 | 0.588 | 0.200 | 0.101 | 0.588 | 0.200 | 0.099 | 0.213 |
| 6 | 95 | 0.621 | 0.189 | 0.096 | 0.621 | 0.189 | 0.094 | 0.189 |
| 7 | 100 | 0.580 | 0.200 | 0.082 | 0.600 | 0.220 | 0.08 | 0.200 |
| 8 | 105 | 0.571 | 0.210 | 0.085 | 0.571 | 0.210 | 0.096 | 0.219 |
| 9 | 105 | 0.571 | 0.190 | 0.082 | 0.571 | 0.190 | 0.075 | 0.238 |
| 10 | 90 | 0.556 | 0.244 | 0.089 | 0.556 | 0.244 | 0.096 | 0.200 |
| 11 | 90 | 0.578 | 0.233 | 0.081 | 0.567 | 0.222 | 0.085 | 0.200 |
| 12 | 100 | 0.600 | 0.190 | 0.083 | 0.590 | 0.180 | 0.084 | 0.220 |
| 13 | 120 | 0.633 | 0.167 | 0.088 | 0.625 | 0.158 | 0.079 | 0.208 |
| 14 | 100 | 0.570 | 0.200 | 0.084 | 0.570 | 0.200 | 0.078 | 0.230 |
| 15 | 80 | 0.563 | 0.250 | 0.091 | 0.550 | 0.238 | 0.091 | 0.200 |
| 16 | 90 | 0.600 | 0.189 | 0.094 | 0.600 | 0.189 | 0.076 | 0.211 |
| 17 | 100 | 0.610 | 0.210 | 0.070 | 0.610 | 0.210 | 0.088 | 0.180 |
| 18 | 96 | 0.604 | 0.188 | 0.086 | 0.594 | 0.177 | 0.084 | 0.219 |
| 19 | 106 | 0.604 | 0.189 | 0.077 | 0.604 | 0.189 | 0.084 | 0.208 |
| 20 | 90 | 0.589 | 0.189 | 0.085 | 0.578 | 0.178 | 0.086 | 0.233 |
| Sub-Zone Number | Cycle (s) | Signal Number | Offset (s) | Two-Way Bandwidth | |
|---|---|---|---|---|---|
| (s) | (Cycle) | ||||
| 1 | 80 | 1 | 0 | 41 + 42 | 1.0375 |
| 2 | 24 | ||||
| 2 | 90 | 3 | 0 | 23 + 24 | 0.5222 |
| 4 | 29 | ||||
| 5 | 55 | ||||
| 6 | 63 | ||||
| 7 | 89 | ||||
| 8 | 21 | ||||
| 3 | 105 | 9 | 0 | 0 | 0 |
| 4 | 100 | 10 | 0 | 12 + 13 | 0.25 |
| 11 | 11 | ||||
| 12 | 49 | ||||
| 13 | 49 | ||||
| 14 | 12 | ||||
| 15 | 42 | ||||
| 16 | 79 | ||||
| 17 | 89 | ||||
| 18 | 20 | ||||
| 19 | 43 | ||||
| 5 | 90 | 20 | 0 | 0 | 0 |
| Sub-Zone Number | Cycle (s) | Signal Number | Offset (s) | Two-Way Bandwidth | |
|---|---|---|---|---|---|
| (s) | (Cycle) | ||||
| 1 | 120 | 1 | 0 | 63 + 63 | 1.058 |
| 2 | 31 | ||||
| 3 | 37 | ||||
| 4 | 53 | ||||
| 2 | 92 | 5 | 0 | 51 + 51 | 1.112 |
| 6 | 16 | ||||
| 7 | 47 | ||||
| 8 | 33 | ||||
| 9 | 60 | ||||
| 10 | 40 | ||||
| 3 | 120 | 11 | 0 | 68 + 66 | 1.113 |
| 12 | 58 | ||||
| 13 | 16 | ||||
| 14 | 29 | ||||
| 15 | 48 | ||||
| 4 | 114 | 16 | 0 | 67 + 66 | 1.167 |
| 17 | 19 | ||||
| 18 | 47 | ||||
| 19 | 36 | ||||
| 20 | 47 | ||||
| Sub-Zone Number | Cycle (s) | Signal Number | Offset (s) | Two-Way Bandwidth | |
|---|---|---|---|---|---|
| (s) | (Cycle) | ||||
| 1 | 120 | 1 | 0 | 63 + 63 | 1.058 |
| 2 | 29 | ||||
| 3 | 63 | ||||
| 4 | 53 | ||||
| 2 | 111 | 5 | 0 | 64 + 65 | 1.168 |
| 6 | 21 | ||||
| 7 | 45 | ||||
| 3 | 115 | 8 | 0 | 64 + 64 | 1.112 |
| 9 | 70 | ||||
| 10 | 43 | ||||
| 4 | 92 | 11 | 0 | 53 + 52 | 1.145 |
| 12 | 58 | ||||
| 13 | 36 | ||||
| 5 | 116 | 14 | 0 | 65 + 64 | 1.113 |
| 15 | 41 | ||||
| 16 | 47 | ||||
| 17 | 31 | ||||
| 6 | 92 | 18 | 0 | 54 + 53 | 1.167 |
| 19 | 36 | ||||
| 20 | 63 | ||||
| Sub-Zone Number | Cycle (s) | Signal Number | Offset (s) | Two-Way Bandwidth | |
|---|---|---|---|---|---|
| (s) | (Cycle) | ||||
| 1 | 120 | 1 | 0 | 63 + 63 | 1.058 |
| 2 | 30 | ||||
| 3 | 53 | ||||
| 4 | 54 | ||||
| 5 | 34 | ||||
| 2 | 111 | 6 | 0 | 63 + 63 | 1.142 |
| 7 | 43 | ||||
| 8 | 33 | ||||
| 9 | 59 | ||||
| 3 | 120 | 10 | 0 | 67 + 66 | 1.106 |
| 11 | 26 | ||||
| 12 | 58 | ||||
| 13 | 15 | ||||
| 14 | 29 | ||||
| 15 | 49 | ||||
| 4 | 114 | 16 | 0 | 67 + 66 | 1.167 |
| 17 | 20 | ||||
| 18 | 47 | ||||
| 19 | 36 | ||||
| 20 | 70 | ||||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wen, X.; Wang, D.; Jin, S.; Qian, G.; Zhu, Y. A Signal Coordination Model for Long Arterials Considering Link Traffic Flow Characteristics. Sustainability 2023, 15, 14874. https://doi.org/10.3390/su152014874
Wen X, Wang D, Jin S, Qian G, Zhu Y. A Signal Coordination Model for Long Arterials Considering Link Traffic Flow Characteristics. Sustainability. 2023; 15(20):14874. https://doi.org/10.3390/su152014874
Chicago/Turabian StyleWen, Xiaoyue, Dianhai Wang, Sheng Jin, Guomin Qian, and Yixuan Zhu. 2023. "A Signal Coordination Model for Long Arterials Considering Link Traffic Flow Characteristics" Sustainability 15, no. 20: 14874. https://doi.org/10.3390/su152014874
APA StyleWen, X., Wang, D., Jin, S., Qian, G., & Zhu, Y. (2023). A Signal Coordination Model for Long Arterials Considering Link Traffic Flow Characteristics. Sustainability, 15(20), 14874. https://doi.org/10.3390/su152014874









