Simulation of Rainfall Erosivity Dynamics in Romania under Climate Change Scenarios
Abstract
1. Introduction
2. Materials and Methods
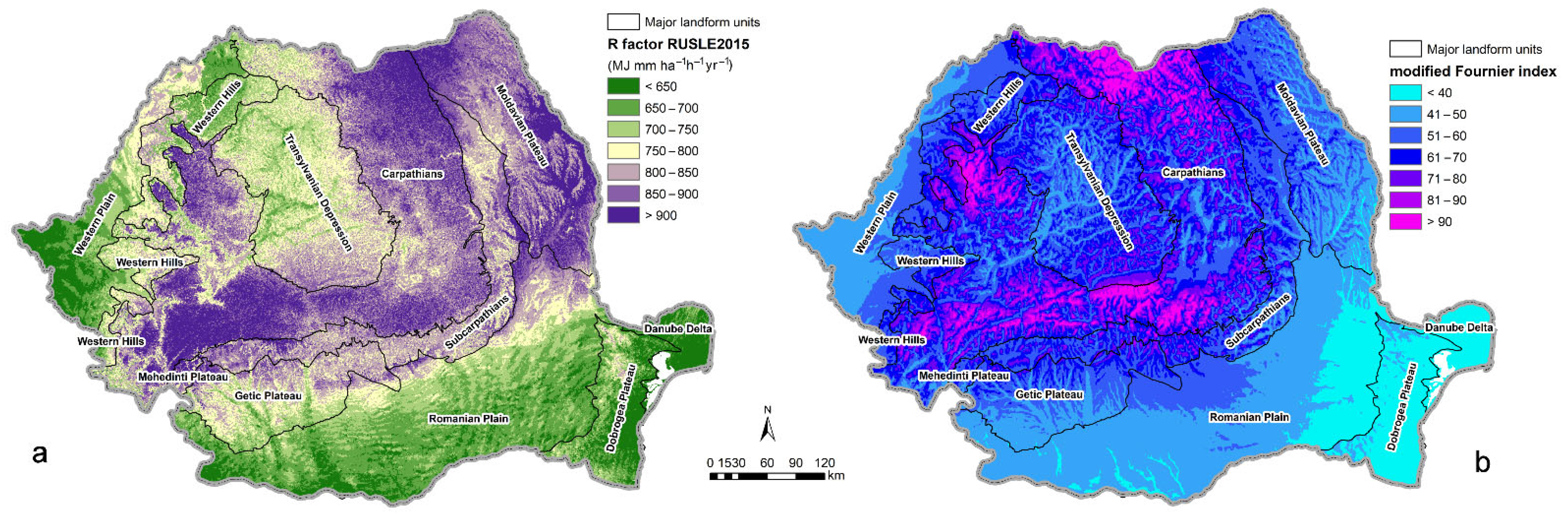
2.1. Study Region
2.2. Input Data
2.3. Methods
- e—unit rainfall energy (MJ ha−1 mm−1);
- i—rain intensity (mm h−1).
- R—annual rainfall erosivity (MJ mm ha−1 h−1 yr−1);
- Erainfall energy (MJ ha−1);
- I30—maximum rainfall intensity during a 30 min period (mm h−1).
- pi—mean monthly precipitations (mm);
- P—mean annual precipitation (mm).
3. Results
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Renard, K.G.; Freimund, J.R. Using monthly precipitation data to estimate the R factor in the revised USLE. J. Hydrol. 1994, 157, 287–306. [Google Scholar] [CrossRef]
- Panagos, P.; Ballabio, C.; Borrelli, P.; Meusburger, K.; Klik, A.; Rousseva, S.; Tadić, M.P.; Michaelides, S.; Hrabalíková, M.; Olsen, P.; et al. Rainfall erosivity in Europe. Sci. Total Environ. 2015, 511, 801–814. [Google Scholar] [CrossRef] [PubMed]
- Ballabio, C.; Borrelli, P.; Spinoni, J.; Meusburger, K.; Michaelides, S.; Beguería, S.; Klik, A.; Petan, S.; Janecek, M.; Olsen, P.; et al. Mapping monthly rainfall erosivity in Europe. Sci. Total Environ. 2017, 579, 1298–1315. [Google Scholar] [CrossRef] [PubMed]
- Bezak, N.; Ballabio, C.; Mikoš, M.; Petan, S.; Borrelli, P.; Panagos, P. Reconstruction of past rainfall erosivity and trend detection based on the REDES database and reanalysis rainfall. J. Hydrol. 2020, 590, 125372. [Google Scholar] [CrossRef]
- Panagos, P.; Ballabio, C.; Meusburger, K.; Spinoni, J.; Alewell, C.; Borrelli, P. Towards estimates of future rainfall erosivity in Europe based on REDES and WorldClim datasets. J. Hydrol. 2017, 548, 251–262. [Google Scholar] [CrossRef]
- Hijmans, R.J.; Cameron, S.E.; Parra, J.L.; Jones, P.G.; Jarvis, A. Very high resolution interpolated climate surfaces for global land areas. Int. J. Climatol. 2005, 25, 1965–1978. [Google Scholar] [CrossRef]
- Panagos, P.; Ballabio, C.; Himics, M.; Scarpa, S.; Matthews, F.; Bogonos, M.; Poesen, J.; Borrelli, P. Projections of soil loss by water erosion in Europe by 2050. Environ. Sci. Policy 2021, 124, 380–392. [Google Scholar] [CrossRef]
- Meusburger, K.; Steel, A.; Panagos, P.; Montanarella, L.; Alewell, C. Spatial and temporal variability of rainfall erosivity factor for Switzerland. Hydrol. Earth Syst. Sci. 2012, 16, 167–177. [Google Scholar] [CrossRef]
- Janeček, M.; Květoň, V.; Kubátová, E.; Kobzová, D.; Vošmerová, M.; Chlupsová, J. Values of rainfall erosivity factor for the Czech Republic. J. Hydrol. Hydromech. 2013, 61, 97–102. [Google Scholar] [CrossRef]
- Panagos, P.; Ballabio, C.; Borrelli, P.; Meusburger, K. Spatio-temporal analysis of rainfall erosivity and erosivity density in Greece. Catena 2016, 137, 161–172. [Google Scholar] [CrossRef]
- Borrelli, P.; Diodato, N.; Panagos, P. Rainfall erosivity in Italy: A national scale spatio-temporal assessment. Int. J. Digit. Earth 2016, 9, 835–850. [Google Scholar] [CrossRef]
- Grillakis, M.G.; Polykretis, C.; Alexakis, D.D. Past and projected climate change impacts on rainfall erosivity: Advancing our knowledge for the eastern Mediterranean island of Crete. Catena 2020, 193, 104625. [Google Scholar] [CrossRef]
- Routschek, A.; Schmidt, J.; Kreienkamp, F. Impact of climate change on soil erosion—A high-resolution projection on catchment scale until 2100 in Saxony/Germany. Catena 2014, 121, 99–109. [Google Scholar] [CrossRef]
- Eekhout, J.P.; De Vente, J. How soil erosion model conceptualization affects soil loss projections under climate change. Prog. Phys. Geogr. Earth Environ. 2019, 44, 212–232. [Google Scholar] [CrossRef]
- Moţoc, M.; Munteanu, S.; Băloiu, V.; Stănescu, P.; Mihai, G. Eroziunea Solului si Metodele de Combatere (Soil Erosion and the Control Methods); Ceres: Bucharest, Romania, 1975. [Google Scholar]
- Moţoc, M.; Stanescu, P.; Taloescu, I. Metode de Estimare a Eroziunii Totale și Efluente pe Bazine Hidrografice Mici (Methods for Estimating Total and Effluent Erosion on Small Hydrographic Catchments); ICPA: Bucharest, Romania, 1979. [Google Scholar]
- ICPA. Metodologia Elaborării Studiilor Pedologice. Partea a III-a—Indicatorii Ecopedologici (Methodology for Elaboration of Soil Studies. Part III—Eco-Pedological Indicators); ICPA: Bucharest, Romania, 1987. [Google Scholar]
- Stănescu, P.; Taloiescu, I.; Drăgan, L. Contribuţii la stabilirea unor indicatori de estimare a erozivităţii pluviale (Contributions to the establishment of some indicators for rainfall erosivity estimation). An. ICIFP Pedol. 1969, 2, 361–369. [Google Scholar]
- Patriche, C.V. Quantitative assessment of rill and interrill soil erosion in Romania. Soil Use Manag. 2019, 35, 257–272. [Google Scholar] [CrossRef]
- Patriche, C.V.; Roșca, B.; Pirnau, R.G.; Irimia, L.M. Evaluation of climate change impact on soil erosion in Romania. In Actes du 35ème Colloque Annuel de l’Association Internationale de Climatologie; Soubeyroux, J.M., Serça, D., Eds.; AIC: Toulouse, France, 2022; ISBN 978-2-907696-27-2. [Google Scholar]
- Ioniță, I. Gully development in the Moldavian Plateau of Romania. Catena 2006, 68, 133–140. [Google Scholar] [CrossRef]
- Panagos, P.; Borrelli, P.; Poesen, J.; Ballabio, C.; Lugato, E.; Meusburger, K.; Montanarella, L.; Alewell, C. The new assessment of soil loss by water erosion in Europe. Environ. Sci. Policy 2015, 54, 438–447. [Google Scholar] [CrossRef]
- Karger, D.N.; Conrad, O.; Böhner, J.; Kawohl, T.; Kreft, H.; Soria-Auza, R.W.; Zimmermann, N.E.; Linder, H.P.; Kessler, M. Climatologies at high resolution for the earth’s land surface areas. Sci. Data 2017, 4, 170122. [Google Scholar] [CrossRef] [PubMed]
- Sanderson, B.M.; Knutti, R.; Caldwell, P. A Representative Democracy to Reduce Interdependency in a Multimodel Ensemble. J. Clim. 2015, 28, 5171–5194. [Google Scholar] [CrossRef]
- USDA. United States Department of Agriculture. Rainfall Intensity Summarization Tool (RIST). 2014. Available online: http://www.ars.usda.gov/News/docs.htm?docid=3251 (accessed on 11 January 2023).
- Wischmeier, W.H.; Smith, D.D. Predicting Rainfall Erosion Losses: A Guide to Conservation Planning; Agriculture Handbook No. 537; USDA: Washington, DC, USA, 1978.
- Renard, R.G.; Foster, G.R.; Weesies, G.A.; McCool, D.K.; Yoder, D.C. Predicting Soil Erosion by Water: A Guide to Conservation Planning with the Revised Universal Soil Loss Equation (RUSLE); Agriculture Handbook No. 703; USDA: Washington, DC, USA; ARS: Beltsville, MA, USA, 1997.
- Brown, L.C.; Foster, G.R. Storm Erosivity Using Idealized Intensity Distributions. Trans. ASAE 1987, 30, 379–386. [Google Scholar] [CrossRef]
- Zhu, C.; Huang, Y.; Sun, J. A granular energy-controlled boundary condition for discrete element simulations of granular flows on erodible surfaces. Comput. Geotech. 2023, 154, 105115. [Google Scholar] [CrossRef]
- Arnoldus, H.M. An approximation of the rainfall factor in the universal soil loss equation. In Assessment of Erosion; De Boodt, M., Gabriels, D., Eds.; Wiley: Chichester, UK, 1980; pp. 127–132. [Google Scholar]
- Cardoso, D.P.; Avanzi, J.C.; Ferreira, D.F.; Acuña-Guzman, S.F.; Silva, M.L.N.; Pires, F.R.; Curi, N. Rainfall erosivity estimation: Comparison and statistical assessment among methods using data from Southeastern Brazil. Rev. Bras. Ciênc. Solo 2022, 46, e021012. [Google Scholar] [CrossRef]
- Addins XLSTAT Support Center. Available online: https://help.xlstat.com/ (accessed on 11 January 2023).
- Cleveland, W.S. Robust locally weighted regression and smoothing scatterplots. J. Am. Statist. Assoc. 1979, 74, 829–836. [Google Scholar] [CrossRef]
- Carvalho, N.O. Hidrossedimentologia Prática, 2nd ed.; Interciência: Rio da Janeiro, Brazil, 2008; 599p. [Google Scholar]
- Alvaro, J.B.; Gonçalves, F.N.; Fan, F.M. Spatial, seasonal, and temporal variations in rainfall aggressiveness in the south of Brazil. Eng. Agríc. 2019, 39, 466–475. [Google Scholar] [CrossRef]
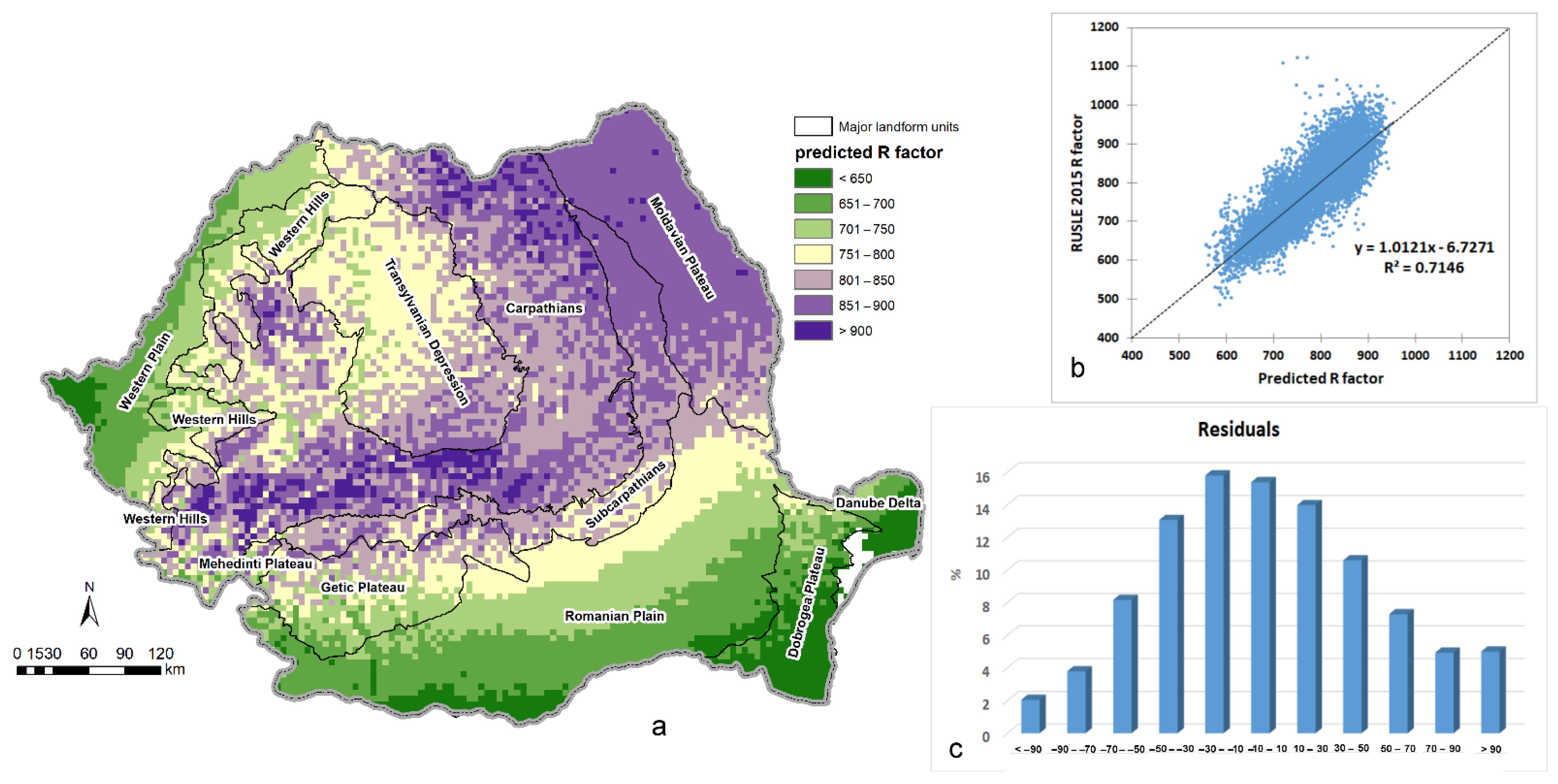
| Statistical Model | Predictors | R2 | RMSE |
|---|---|---|---|
| Linear regression |
| 0.477 | 68.880 |
| Linear regression |
| 0.522 | 65.872 |
| Non-parametric regression |
| 0.705 | 51.694 |
| Non-parametric regression |
| 0.714 | 50.965 |
| Statistics | Current | 2041–2060 | 2061–2080 | ||
|---|---|---|---|---|---|
| RCP 4.5 | RCP 8.5 | RCP 4.5 | RCP 8.5 | ||
| Average | 782.8 | 801.4 | 803.0 | 790 | 785.2 |
| Minimum | 558 | 580 | 587 | 566 | 573 |
| Maximum | 955 | 974 | 976 | 960 | 950 |
| Standard deviation | 79.6 | 74.3 | 73.9 | 75.2 | 74.4 |
| Landform Unit | Current | 2041–2060 | 2061–2080 | ||
|---|---|---|---|---|---|
| RCP4.5 | RCP8.5 | RCP4.5 | RCP8.5 | ||
| Carpathians | 842.8 | 858.9 | 860.7 | 847.9 | 841.3 |
| Subcarpathians | 834.5 | 848.0 | 847.9 | 837.0 | 831.4 |
| Transylvanian Depression | 799.1 | 810.4 | 812.2 | 800.5 | 795.9 |
| Western Hills | 765.3 | 787.7 | 793.1 | 778.6 | 771.7 |
| Mehedinti Plateau | 806.1 | 858.6 | 862.8 | 844.8 | 840.6 |
| Getic Plateau | 770.3 | 810.9 | 811.4 | 792.3 | 784.6 |
| Moldavian Plateau | 866.7 | 873.0 | 873.3 | 865.2 | 864.2 |
| Western Plain | 698.4 | 723.8 | 730.1 | 715.2 | 707.7 |
| Romanian Plain | 708.0 | 729.6 | 729.4 | 716.4 | 712.6 |
| Dobrogea Plateau | 649.5 | 671.7 | 673.8 | 658.6 | 660.8 |
| Danube Delta | 643.5 | 676.7 | 679.7 | 660.5 | 665.2 |
| Differences (MJ mm ha−1 h−1 yr−1) | 2041–2060 | 2061–2080 | ||
|---|---|---|---|---|
| RCP 4.5 | RCP 8.5 | RCP 4.5 | RCP 8.5 | |
| <0 | 0.0 | 0.0 | 39.4 | 58.5 |
| 0–10 | 27.8 | 26.3 | 30.6 | 23.6 |
| 11–20 | 37.0 | 34.2 | 18.0 | 10.7 |
| 21–30 | 19.4 | 19.1 | 7.6 | 4.0 |
| 31–40 | 8.8 | 10.7 | 2.2 | 1.8 |
| 41–50 | 3.2 | 5.4 | 1.7 | 1.0 |
| >50 | 3.7 | 4.4 | 0.6 | 0.3 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Patriche, C.V.; Roșca, B.; Pîrnău, R.G.; Vasiliniuc, I.; Irimia, L.M. Simulation of Rainfall Erosivity Dynamics in Romania under Climate Change Scenarios. Sustainability 2023, 15, 1469. https://doi.org/10.3390/su15021469
Patriche CV, Roșca B, Pîrnău RG, Vasiliniuc I, Irimia LM. Simulation of Rainfall Erosivity Dynamics in Romania under Climate Change Scenarios. Sustainability. 2023; 15(2):1469. https://doi.org/10.3390/su15021469
Chicago/Turabian StylePatriche, Cristian Valeriu, Bogdan Roșca, Radu Gabriel Pîrnău, Ionuț Vasiliniuc, and Liviu Mihai Irimia. 2023. "Simulation of Rainfall Erosivity Dynamics in Romania under Climate Change Scenarios" Sustainability 15, no. 2: 1469. https://doi.org/10.3390/su15021469
APA StylePatriche, C. V., Roșca, B., Pîrnău, R. G., Vasiliniuc, I., & Irimia, L. M. (2023). Simulation of Rainfall Erosivity Dynamics in Romania under Climate Change Scenarios. Sustainability, 15(2), 1469. https://doi.org/10.3390/su15021469







