Abstract
Overburden collapse and water inrush in mines are primarily caused by rock fractures. Mining safety can be enhanced by monitoring and identifying early signs of coal failure in the mines. This article collected acoustic emission data synchronously throughout a series of uniaxial compression (UC) experiments on natural and water-saturated coal. The influence mechanisms of water, mechanical properties, and acoustic emission signals on the stress–strain curve and the SEM results of water-saturated and dry samples are investigated. As a result, the mechanical properties of coal are not only weakened by water saturation, such as elastic modulus, strain, stress, and compressive strength but also reduced acoustic emissions. In comparison with saturated coal, natural coal has a uniaxial stress of 13.55 MPa and an elastic modulus of 1.245 GPa, while saturated coal has a stress of 8.21 MPa and an elastic modulus of 0.813 GPa. Intergranular fractures are more likely to occur in coal with a high water content, whereas transgranular fractures are less likely to occur in coal with a high water content. An innovative and unique statistical model of coal damage under uniaxial loading has been developed by analyzing the acoustic emission data. Since this technique takes into account the compaction stage, models based on this technique were found to be superior to those based on lognormal or Weibull distributions. A correlation coefficient of greater than 0.956 exists between the piecewise constitutive model and the experimental curve. Statistical damage constitutive models for coal are compatible with this model. Additionally, the model can precisely forecast the stress associated with both natural and saturated coal and can be useful in the prevention of rock-coal disasters in water conditions.
1. Introduction
In China, the mining industry is moving towards deep mining which poses additional safety concerns [1]. Deep mining coal seams can result in coal and gas outbursts, rock bursts, and gas explosions due to high stress, high pressure, and high concentration of gas [2,3,4,5]. In recent years, hydraulic flushing and water injection have been widely used to alleviate coal and gas outbursts, reduce coal dust, and prevent coal seams from spontaneous combustion [6,7,8,9,10,11]. Coal seams undergo significant changes due to hydraulic measures, resulting in significant changes in their mechanical characteristics and geophysical properties as a result [12,13,14,15]. In the application of geotechnical engineering, water relates to geological disasters, since it affects the mechanical characteristics of coal [16,17]. For example, the increase in humidity in summer leads to frequent falls of roofs and the degradation of pillars in the mine [18,19,20]. Heavy rain often leads to landslides and may lead to karst collapse. Fluid injection into a fault can trigger seismic events [21,22,23]. The injection of water to alleviate or prevent coal bursts is a common method [24,25,26]. These engineering disasters are caused by wet coal or rock mass that has been damaged and broken over different time frames, responding to external stress in an obvious manner. Consequently, knowing the saturation impact on the coal fracture behavior is very valuable in evaluating the stabilizing of rock structures and preventing damage to them.
Acoustic emission (AE), often referred to as stress wave emission, is the abrupt strain energy release in the form of an elastic wave during material deformation [27,28,29]. Researchers have extensively investigated AE waveforms and the link between AE signal performance and the mechanical process of coal failure [30]. By utilizing AE technology, significant progress has been made on the coal/rock failure process, for example, the three-dimensional rock testing and the study of the damage tensor, AE behaviors of rock and coal under uniaxial compressive test (UC), characterization of the rock cracking patterns via diametral compression, and the AE characteristics of coal during fracturing [31,32,33,34,35]. These studies demonstrate that laboratory investigations and in situ testing employing AE may accurately reflect the stress situation and rocks/coal internal fractures.
Some recent research on the AE characteristics of rocks under loading, saturated with water, has headed to the conclusion that the release of elastic energy reduces with water and weakens the AE signals [7,36,37,38,39]. For instance, Zhao et al. investigated the impact of water saturation on failure and AE features on sandstone. For this, UC tests and numerical simulations have been utilized to investigate the development of micro-cracks and sandstone failure patterns [40,41,42,43]. In simulation, using PFC2D software, the results indicated that increasing water content within the rock significantly decreased the coal strength, strain ratio (strain to peak strain), Young’s modulus, AE energy (average), and the maximum energy of a single AE event. Some researchers used strain energy density for fracture predictions [44,45,46,47]. Lin et al. studied the AE parameters during disc-cutter-induced rock fragmentation processes under various water conditions [48]. Scholars studied the evolution of microcracks in rocks under saturated conditions using AE data [49]. The results demonstrated that the varying characteristics of rock crack propagation could be characterized by the AE events frequency along with volume change [12,28,46,50].The change in P-wave velocity along with AE parameters in porous rock were studied after micro-crack closure by Fortin et al. and Liu et al. [51,52]. Zhou et al. have taken sandstone under different water contents as a research object and investigated AE characteristics along with the type I fracture mechanism [53]. The results unveiled that increasing water content decreased fracture toughness (KIc). Zhou et al. also investigated the fracture’s behavior of sandstone under quasi-static loading containing different water content. For this, notched semi-circular bending (NSCB) tests were performed. During testing, AE signals were recorded simultaneously with the cracking process [54]. During loading, Liu et al. and Zhu et al. have made the effort to investigate the AE signal frequency features with both saturated and dry coals, and the outcomes revealed that the AE signals with a high frequency were pointedly reduced by water content [55,56,57,58,59,60].
Different scholars have investigated strain energy and acoustic emission properties under loading. [27,61,62] To obtain the stress–strain interface, the scholars used the traditional stress–strain constitutive models under loading [63,64,65]. The damage constitutive model for coal under loading using AE has not yet been studied. Mechanical vibration fluctuates strain quantities on construction sites, which can result in substantial deviations from true strains. As the unique features of the acoustic emission technology are non-destructive and highly sensitive, the development of the coal constitutive model through AE will be more valuable for examining and forecasting the coal mass stability around an underground excavation. In this study, the mechanical and acoustics emission characteristics of dry and saturated coal under uniaxial loading are examined, and the quantitative relationship between strain and acoustic emission is established, to develop a statistical model for constitutive damage in saturated coal under uniaxial loading which will also consider the compaction stage. This research will contribute to developing early warning system for rock engineering disasters by monitoring acoustic emissions, such as slope collapses, tunnel damage, and coal mine collapses.
2. Materials and Methods
2.1. Sample Preparation
In order to prepare coal samples for experiments, blocks were taken from coal-mine working faces in Shanxi Province. Samples are then processed in the same direction in order to minimize the effect of anisotropy on the results. We polished the specimens with a size of 120 mm × 60 mm × 30 mm, weighed them using an electronic balance, and measured their dimensions with a Vernier caliper. A non-metallic detector (ZBL-U520) was used to measure the ultrasonic wave velocities of all experimental samples in order to verify the homogeneity of the samples. The sample selected for the experiment was one that exhibited essentially the same results as the detector. The samples were divided into two groups, natural coal and water-saturated coal. Afterwards, the samples of natural coal were placed in a container and labelled as N-1, N-2, and N-3. The samples, S-1, S-2, and S-3 were submerged in water for 72 h to ensure saturation. Samples that had been saturated (S-1, S-2, and S-3) were weighed and placed in containers that had been covered with samples in order to prevent saturation fluctuation. The properties of the samples (both natural and saturated) are summarized in Table 1.

Table 1.
Properties of natural and saturated coal samples.
2.2. Experimental Setup and Procedure
The experimental system includes a subsystem for axial compression loading and a monitoring system for acoustic emissions (Figure 1). Axial loading and control subsystem consists of an electro-hydraulic servo pressure testing machine controlled by a microcomputer (YAW4306) that is capable of performing displacement loading and stress loading, and records displacements, loads, and time during loading. This experiment uses the displacement loading method, with a loading rate of 20 N/s. Data storage and graphic display are included in AEwin Test for Express-8.0, as well as parameter setting, signal acquisition, and signal a/d conversion. The AE monitoring system was started first to measure ambient noise, but axial loading and control was not started. The threshold value should be adjusted from 0 to a value that is appropriate. If this value exceeds this threshold, AE signals cannot be detected without applying load. However, when the axial loading and control system is activated at this threshold, the AE signal can be monitored. As a result of many tests, 45 dB was selected as the threshold in these experiments [12,66]. To measure acoustic emission signals, the acoustic emission monitor, amplifier, and sensor are connected in sequence. An acoustic emission sensor is then coupled to a predetermined location on the sample surface using a viscous coupling agent. The next step involves placing the prepared coal sample on the test bench of the loading system. This is done by slowly raising the bottom of the press until the top of the coal sample is in contact with the top boundary of the loading system. It is also worth noting that the loading system and the acoustic emission monitoring system are all started simultaneously when the loading system is started.
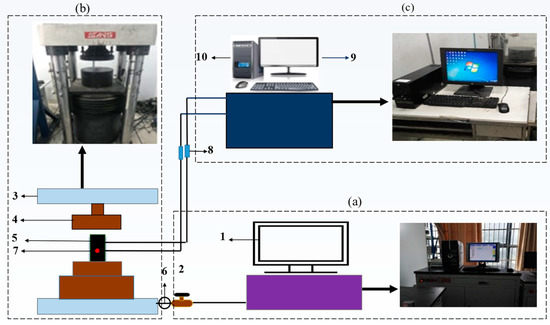
Figure 1.
Overview of the experimental system diagram for natural and saturated coal: (a) loading control system includes (1) system for loading control, and (2) valve; (b) AE and EMR signals collecting and loading system consists of (3) servo hydraulic press, (4) press head, (5) coal sample, (6) pressure gauge, (7) AE Sensor, and (8) amplifiers; (c) AE data processing and storage system comprises (9) system screen to display data, and (10) AE monitor device.
3. Results
3.1. Mechanical Behaviour and Acoustic Emission Characteristics
As shown in Figure 2, AE counts can be observed throughout the uniaxial test, but at the peak of the stress level, AE counts are at their highest levels. As soon as load progresses, “Crack closures and friction along fracture planes appear on the stress–strain curves at lower loading levels and crack propagation, penetration, friction, and slip appear at higher loading levels” [67,68,69].
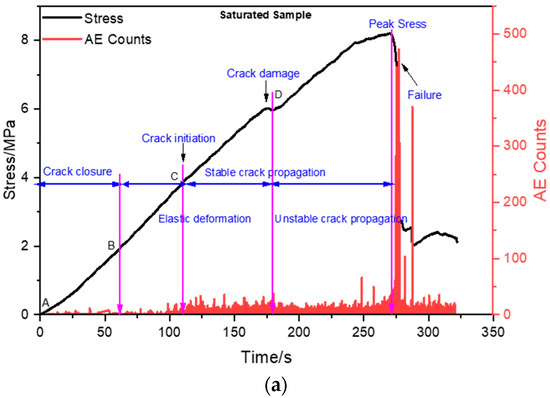
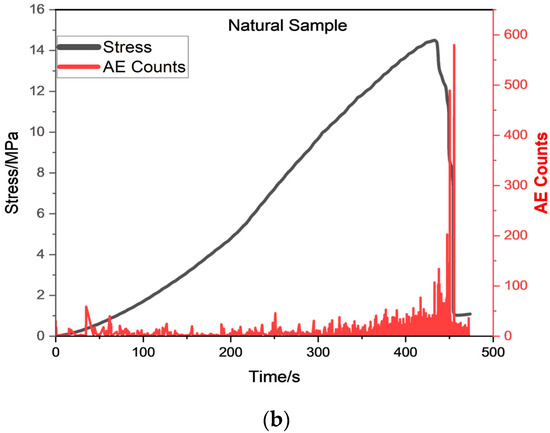
Figure 2.
Relationship of time–stress and time–AE counts of (a) saturated sample and (b) natural coal sample.
In our research, the term “crack” refers to the internal microcracks that emerge into visible macrocracks before coal samples fail because of water intrusion and loading. Several characteristics distinguish water-saturated coal samples from natural coal samples. The AE count is initially low due to fracture closure, but as the fracture closes, the count increases. Despite the microcracks that produce a limited amount of acoustic emission data, the AE system still manages to record some AE counts. In elastic deformation, the relationship between stress and strain is linear and positive, and the modulus of elasticity remains relatively constant. The AE counts increase with the progression of the stable crack propagation in coal samples, and further increase with the progression of the unstable crack propagation in coal samples. In addition, due to the water content in coal samples, the cumulative AE counts are smaller than they are for natural coal samples. It has been observed that the AE counts follow the stress–strain curve as the loading process proceeds. Based on the distribution of AE counts, it appears that crack development is reflected in the distribution of AE counts.
As shown in Figure 3a, the cumulative AE counts curve follows the stress/strain curve, so the AE approach can capture all phases of crack development. It has been noted that little, or no AE activity has been recorded in the stage called crack closure (A–B), due to the fact that existing micro- and macro-cracks are being closed. In response to an increase in uniaxial load, elastic deformation begins to occur (segment B–C), which is reflected in the increase in AE counts. The AE count increases linearly as the crack propagates toward point C, and the crack enters the stable propagation stage. An increase in the slope of the curve (C–D) indicates an increase in the strain energy released from the coal sample (i.e., more AE counts). The curve begins to deviate from a straight line at this point and cracks begin to develop until the specimen collapses (point F). A phase from D to E (D–E) prior to point F is referred to as an unstable crack propagation stage. [7,27,70].
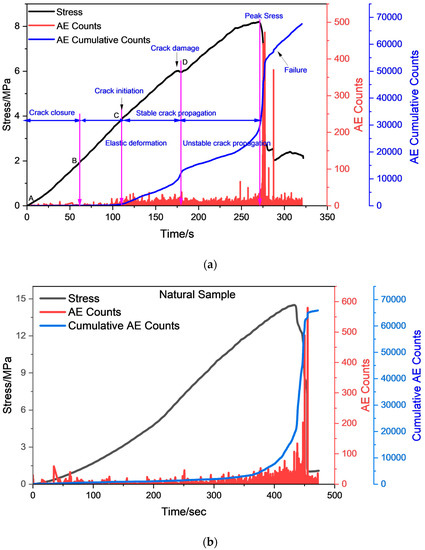
Figure 3.
Relationship of time-stress, acoustic emission counts, and AE cumulative counts of (a) saturated sample and (b) natural coal sample under uniaxial loading.
3.2. Failure Mode of Coal under Stress
It is important to consider that the coal used in this experiment is solid and fragile and is prone to failure shortly after reaching its maximum strength, resulting in audiometry. The stress–strain curve decreases rapidly following the peak stress, indicating that post peak is not readily apparent. The presence of water will affect the mechanical properties of coal. As evidenced by the failure mode of coal, water appears to have played a role in the failure mode. The failure modes of coal samples are recorded and displayed. An illustration of the failure mode and schematic diagram of dry and saturated coals following failure under uniaxial loads can be found in Figure 4.

Figure 4.
Mode of failure: (a) Natural samples; (b) Water-saturated samples.
It has been observed that many natural coal samples exhibit tensile failure. A large tension crack can be seen on the surface of the coal sample. The coal sample will not be affected immediately by the axial split, and it will retain some bearing capacity until cracks develop due to tensile collapse. For saturated coal samples, the most common failure mode is a composite failure, since tension and shear are both active factors in the failure process. This is due to the fact that the water in the coal lubricates the particles within it, thus reducing the cohesiveness and bonding force between the particles. As a result of this development stage, coal samples are more susceptible to fracture spreading and the development of new fractures (tensile fractures and shear fractures), as well as to local damage. The changes decrease the strength of the samples significantly.
4. Statistical Model
4.1. Establishing a Statistical Model to Assess Damage
In accordance with the definition of stress:
Here, stress is , F is force, and A represents cross-section area.
Based on a definition by Kachanov [71] of damage, the damage variable Dm is:
where, A° is the preliminary non-destructive sample’s cross-section area, and A* denotes the area after material damage.
A is the real area with micro cracks. Therefore, the real stress of the coal sample will be
By putting the value of Equation (3) in Equation (4), we get
By taking original area as common, we get
Put Equation (2) in Equation (6):
Substituting Equation (1) in Equation (7), we get
Lemaitre suggested, based on the hypothesis of equivalent strain, that the strain generated in the process of uniaxial compression is equal to the strain generated due to the effective stress of the undamaged sample. Therefore, effective stress will replace nominal stress as shown in Equation (9) [72].
Nominal stress = effective stress:
In the above equation, denotes the nominal stress and effective stresses in a coal subjected to uniaxial load, with the identity matrix represented by I; [M] denotes the matrix of damage variable, [L] denotes the elastic modulus matrix, and strain matrix is represented by [s].
Based on the assumption that coal damage is isotropous, coal damage can be described by the following one-dimensional constitutive equation:
with the damage variable generated under the uniaxial loading.
A coal material can have a wide variety of characteristics, and it might exhibit some imperfections, such as primary pores and microcracks. The development and growth of cracks in coal materials may be affected by such defects, and since flaws are distributed randomly, fracture damage may also occur in coal materials according to the same distribution. This may lead to a characterization of coal damage and fracture as a random variable. The statistical damage analysis of coal begins with defining a probability distribution function for its Physico-Mechanical characteristics. Previously, models of rock damage constitutive mechanisms were developed using the logarithmic normal distribution of the microelement strength of rock. In those models, the damage parameters and constitutive relationship curve of rock fractures could be described in a comprehensive manner [73]. An explanation of coal strength using the Weibull distribution is given in Equation (11), showing the function of the probability density of microelement failure [74,75].
The constants F and m explain the inhomogeneity (brittleness) of the coal sample, indicating the variation response of coal’s characteristics under load, where the random distribution function of the shape factor is represented by m; for the microelement strength, the distributed variable is F.
The range of the damage variable D2 is 0–1. It is defined as the ratio of Nf and N, where Nf represents the number of damaged microelements and N is the total number of microelements. Then, the coal-related damage variable is stated in Equation (12):
Using Equation (12) as the substitute for Equation (10), the stress–strain relationship can be determined for coal subjected to uniaxial loading.
At the peak point ) of the distribution, it is possible to calculate the M and F components of the statistical constitutive model of the Weibull distribution, on the stress–strain’s curve of natural coal and saturated coal, and the slope at the peak point of strength is 0. When , this led to the establishment of the Equation (14):
Additionally, the point of peak intensity (, ) corresponds to:
As a result of simultaneous Equations (14) and (15), we get the following results:
According to simultaneous Equations (13), (16) and (17), the coal damage constitutive model can be derived based on a Weibull distribution.
4.2. Strain Characterization by AE
The varying trend of the cumulative AE count (CAEC) with strain under coal uniaxial loading is depicted in Figure 5; CAEC and strain exhibit a linear relationship induced by uniaxial loading in coal.
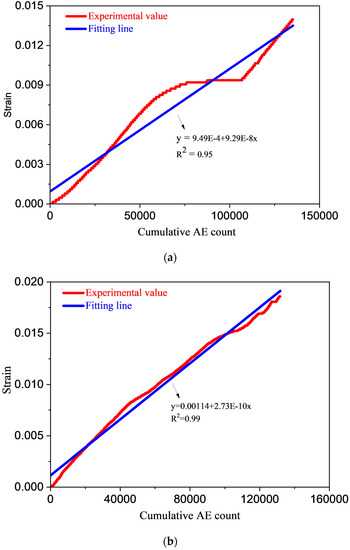
Figure 5.
Cumulative AE count () with strain of (a) saturated sample; (b) natural sample.
The correlation coefficient exceeds 0.95. The following relationship is established between CAEC and ε of coal sample N1.
ε = 0.00114 + 2.73 × 10−10*CAEC
It can be seen as follows how CAEC and water saturated sample’s relate to each other:
ε = 9.49 × 10−4 + 9.29 × 10−8*CAEC
When coal samples are loaded uniaxially, fit correlation between and CAEC satisfies the equation of first-order functions as shown below:
ε = b + a*CAEC
By substituting Equation (21) into Equation (18), the statistical damage constitutive model of coal during uniaxial load characterized by cumulative AE count can be obtained, and its expression is:
The model stress value that is calculated from the CAEC value will also be variable since the CAEC value attained during the experiment is variable. Accordingly, the CAEC data and strain fitting line (CAEC) in this study are applied instead of the CAEC value derived from the experimentation, and Equation (22) can be rewritten as follows:
The purpose of this example is to illustrate how equation (23) can be used to compute the coal’s stress value when it is subjected to uniaxial loading. The elastic modulus of S1 is 0.895 GPa. The values of a and b can be obtained from Figure 5, which are 9.29 × 10−8 and 9.49 × 10−4, respectively. The value of M is calculated by Equation (16), which is 5.40, and the value is obtained from the experimental stress–strain curve, which is 0.01103. Then, the stress value of coal under uniaxial compression is achieved by substituting the data () of the fitting line in Figure 5 into Equation (23). Figure 6 shows the experimental stress–strain curve and model stress–strain curve of coal samples N-1 and S-1. As shown in Figure 6, the model stress value of coal sample N1 is higher than the experimental stress due to the obvious compaction stage in the loading process. Because there is no compaction stage in coal sample S-1, the model stress value is in good agreement with the experimental stress. Therefore, it is necessary to establish a statistical damage constitutive model for coal, which takes into account the compaction stage of the coal.
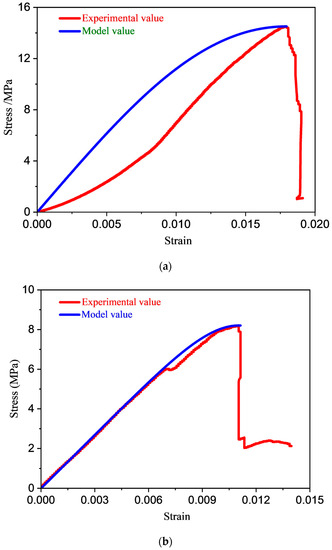
Figure 6.
Relationship of experimental and model value of (a) natural sample; (b) water-saturated sample.
4.3. Modelling the Compaction Stage from an Integrated Perspective
During the initial phase of loading a coal sample under uniaxial compression, the sample always displays an obvious stage of compaction. A closer examination of the coal sample’s stress curve shows that water increases the proportion of the compaction phase. The previous standard log-normal distribution constitutive model does not include the compaction step, resulting in large deviations in the compaction stage and an unsatisfactory match between the projected model and the actual coal stress–strain curve. It is therefore necessary to develop a constitutive model to address the compaction stage. During the compaction stage, pores and cracks in the rock are compacted without damage propagation, and subsequent damage occurs at the elastic (linear) and yield stages. According to Lu’s study, coal experiences the following strain–stress relationship during compaction [42].
When load is applied uniaxially, and represent the stress and strain, and and represent the maximum stress and strain during compaction.
To get the log-normal distribution constitutive model in the compaction stage, the Equation (24) can be substituted into Equation (18). We get
The coal damage constitutive model considered the stage of uniaxial loading and compaction, which is characterised by the number of cumulative counts, derived by substituting Equation (21) into Equation (25) and replacing the experimental CAEC value with data of CAEC and strain fitting line (). The expression is as follows:
where is the value of the fitting line at the end of the compaction phase, and is fitting line value at the peak stress point.
The model stress for the coal sample N1 is in good agreement with the experimental stress in Figure 7, suggesting that the piecewise statistical damage constitutive model, calculated by Equation (26) based on cumulative AE count established in this paper, is feasible.
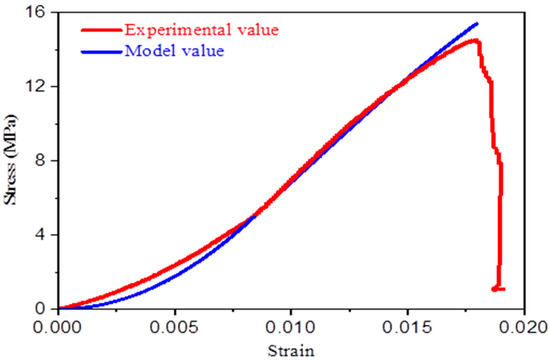
Figure 7.
Relationship of experimental and model value of N-1 sample.
5. Discussion
Water has many effects on coals, including physical, chemical, and mechanical deterioration. The swelling of water-absorbing minerals, the weakening of adhesion and friction between particles, the pore water pressure formation, and the fracture energy reduction are all considered to be the mechanisms [7,76]. Depending on the experimental settings or coal qualities, an individual one or combination of the aforementioned mechanisms may play a vital part. After failure, the failed sample sections were assessed by SEM to identify the failure mechanism of coal under water–coal interaction, and the results are given here. SEM pictures of natural and saturated samples in 2000 and 1000 are shown in Figure 8(A1,A2,B1,B2). The coal samples utilised in SEM inspection are taken from the outside of the failed samples and have an average diameter of less than 1 cm. The coal structure in the natural sample is intact and densely cemented, as illustrated in the image. Furthermore, except for a few fragments, the fracture surface is rather smooth, and the micropores are independent of one another. The adhesion between neighbouring coal particles is considerably diminished in the saturated sample due to the expansion and dissolving of certain mineral components. More unrestrained coal flakes and particles are exposed to the sample and then washed away by the free water in the sample. As a result, as illustrated in Figure 8, the pores widen, generating a variety of drainage channels, and the coal microstructure loosens or breaks. Water saturation softens the coal and considerably reduces its macro mechanical strength due to pore and microstructure changes [77].

Figure 8.
The SEM analysis of (A1,A2) natural sample with 1000× and 2000× mag. and (B1,B2) saturated sample with 1000× and 2000× mag.
Transgranular fracture is simpler to spot in natural samples, as demonstrated in Figure 8(A1,A2). (In Figure 8(A1,A2), the area is flatter and smoother). Transgranular fracture becomes less prevalent as the water content rises. The voids and crack are more dominant in saturated coal. Water-eroded cracks can also be found in water-saturated materials. As a result, the coal’s strength is reduced, deformation rises, and energy is squandered. The deterioration of coals due to water action and the uneven distribution of water within rocks can result in the creation of weak planes that are prone to crack propagation during loading on a mesoscopic level [78]. As a result, high-water-content coals have more intricate failure patterns. This mechanism is also influenced by pore water pressure.
AE counts are observed throughout the uniaxial test but is most prevalent near the peak point of the stress. Water-saturated coal samples differ from natural coal samples in a few ways. AE counts are low when loading begins because of fracture closure, which causes the AE counts to rise. Despite the present micro-fissures and small amount of acoustic emission collection level, the AE system continues to record some counts of AEs. Stress and strain are connected linearly and positively in the elastic deformation stage, and the modulus of elasticity remains virtually steady in elastic deformation. At the stable crack propagation stage, the AE counts increase. The AE signals from coal samples further increase during the crack unstable propagation stage. As a result of the presence of water content in coal samples, the cumulative AE counts are smaller than they are for the natural coal samples. It has been observed that, as the loading process goes, the AE counts follow the stress–strain curve in the entire process; hence, crack development is reflected in the distribution of AE counts. In addition, in agreement with the research results of Liu et al., the higher the water content in the sample, the more evident the AE precursor reaction prior to failure [79].
Stress-strain curves under uniaxial loading of hard and brittle coals have a downward bulging tendency during the stage of compaction but rise rapidly at the peak point of stress. The stress reduced abruptly after the peak stress, showing a vertical curve suggesting that the coal is brittle. The present study introduces a new model for estimating damage which is derived by combining the log-normal and Weibull (Lg and Wb) distribution. The experimental curve and the prediction coefficient of the new model differ significantly (>0.956). After compaction, the new model’s trend is greater than the curve of experimental. The trend of the model is, however, lower near the peak stress than that of the experimental curve, indicating that the experimental model still exhibits errors. Specifically, the theoretical curve generated from the statistical damage model indicates that the coal will harden under maximum stress, indicating plastic behavior, whereas the experimental curve does not show such behavior. Using the Lemaitre strain equivalence principle, Lg and Wb, a continuous damage phenomenological model based on acoustic emissions at the macroscopic level was constructed. In the macroscopic phenomenological model, damage is simply defined as a decrease in the stiffness of the coal, and deformation is viewed as an elastic process, disregarding the possibility that the deformation might be irreversible. A nonlinear elastic constitutive relationship is used in this constitutive model. This approximation will obscure the actual damage behavior of materials with irreversible deformation characteristics and can be used in the context of determining and explaining the mechanism of brittle material damage [80]; microcrack propagation, initiation, and nucleation cause a coal’s material failure over time due to mesolocal tensile strains [81]. We believe that this damage model will be quite useful in engineering practice if it can be applied to damage analysis.
6. Conclusions
A series of uniaxial compression tests were conducted, both on natural and water-saturated coal samples. It is significant to note that data on acoustic emissions were collected simultaneously during the tests. A detailed study of stress–strain behaviour, SEM results, and a damage analysis model is finally used to describe the effect of water on the mechanical properties of coal and acoustic emission signals. Based on the findings of this study, the following conclusions can be drawn:
- (1)
- As a result of the saturation of coal with water, the stresses, elastic modulus, strain, compressive strength, and acoustic emissions are reduced. As compared to saturated coal, natural coal has a uniaxial stress of 13.55 and an elastic modulus of 1.245, while saturated coal has a uniaxial stress of 8.21 and an elastic modulus of 0.813.
- (2)
- Intergranular fractures are more likely to occur in coal with a high water content, whereas transgranular fractures are less likely to occur in coal with a high water content. In response to water’s action, the cementitious material between coal particles will fracture, resulting in a more uniform micro-fracture pattern. The decrease in strength and the increase in deformation can be attributed to this microscopic phenomenon.
- (3)
- When rocks are saturated with water, the failure mode of the rocks might change as a result. It is evident that tensile failure is the primary mode of failure for dry coal samples, while tensile–shear composite failure is the primary mode of failure for saturated coal samples.
- (4)
- The analysis of acoustic emission data has resulted in the development of a unique statistical model of coal damage under uniaxial stress. A novel model based on this technique was established, compared to log-normal and Weibull distributions, and was found to be superior to other models due to its incorporation of the compaction stage. As compared to the experimental curve, the piecewise constitutive model presents a correlation coefficient of greater than 0.956. These models are compatible with statistical damage constitutive models for coal. Additionally, the model can precisely forecast the stress associated with both natural and saturated coal.
Author Contributions
Conceptualization, M.A.; Methodology, M.A. and Z.L; Validation, X.W. and Z.Z.; Formal analysis, E.W. and S.S.A.; Investigation, M.A.; Resources, Y.F.; Writing—original draft, M.A.; Writing—review & editing, Z.L., N.M.K. and Y.F.; Supervision, E.W; Project administration, E.W.; Funding acquisition, S.S.A. and E.W. All authors have read and agreed to the published version of the manuscript.
Funding
This research was supported by the National Natural Science Foundation of China (No. 51934007), China University of Mining and Technology, Xuzhou, Jiangsu, China; and also the Researchers Supporting Project number (RSP2022R496), King Saud University, Riyadh, Saudi Arabia.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Acknowledgments
The authors acknowledge the guidance, encouragement, and support of Xiaojun Feng, Haishan, Jia, Li Dexing, Qiming Zhang, Barkat Ullah, Jihui, and Saad S. Alarifi. Also acknowledge the Researchers Supporting Project number (RSP2022R496), King Saud University, Riyadh, Saudi Arabia.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Liu, Y.; Wang, E.; Jiang, C.; Zhang, D.; Li, M.; Yu, B.; Zhao, D. Triaxial Experimental True Study of Anisotropic Mechanical Behavior and Permeability Evolution of Initially Fractured Coal. Nat. Resour. Res. 2023. [Google Scholar] [CrossRef]
- Qiu, L.; Li, Z.; Wang, E.; Liu, Z.; Ou, J.; Li, X.; Ali, M.; Zhang, Y.; Xia, S. Characteristics and precursor information of electromagnetic signals of mining-induced coal and gas outburst. J. Loss Prev. Process Ind. 2018, 54, 206–215. [Google Scholar] [CrossRef]
- Liu, Y.; Yin, G.; Zhang, D.; Li, M.; Deng, B.; Liu, C.; Zhao, H.; Yin, S. Directional permeability evolution in intact and fractured coal subjected to true-triaxial stresses under dry and water-saturated conditions. Int. J. Rock Mech. Min. Sci. 2019, 119, 22–34. [Google Scholar] [CrossRef]
- Liu, Y.; Lebedev, M.; Zhang, Y.; Wang, E.; Li, W.; Liang, J.; Feng, R.; Ma, R. Micro-Cleat and Permeability Evolution of Anisotropic Coal During Directional CO2 Flooding: An In Situ Micro-CT Study. Nat. Resour. Res. 2022, 31, 2805–2818. [Google Scholar] [CrossRef]
- Du, F.; Wang, K.; Zhang, X.; Xin, C.; Shu, L.; Wang, G. Experimental Study of Coal–Gas Outburst: Insights from Coal–Rock Structure, Gas Pressure and Adsorptivity. Nat. Resour. Res. 2020, 29, 2481–2493. [Google Scholar] [CrossRef]
- Cheng, W.; Liu, Z.; Yang, H.; Wang, W.J. Non-linear seepage characteristics and influential factors of water injection in gassy seams. Exp. Therm. Fluid Sci. 2018, 91, 41–53. [Google Scholar] [CrossRef]
- Ali, M.; Wang, E.; Li, Z.; Jia, H.; Li, D.; Jiskani, I.M.; Ullah, B. Study on Acoustic Emission Characteristics and Mechanical Behavior of Water-Saturated Coal. Geofluids 2021, 2021, 5247988. [Google Scholar] [CrossRef]
- Shan, T.; Li, Z.; Zhang, X.; Niu, Y.; Tian, H.; Zhang, Q.; Zang, Z.; Gu, Z.; Cai, C.; Liu, C. Infrared Radiation and Acoustic Emission of Damage Evolution and Failure Precursory for Water-Bearing Coal. Rock Mech. Rock Eng. 2022, 55, 7657–7674. [Google Scholar] [CrossRef]
- Shen, R.; Chen, H.; Zhao, E.; Li, T.; Fan, W.; Yuan, Z. Electromagnetic radiation prediction of damage characteristics of water-bearing sandstone under cyclic loading and unloading. Bull. Eng. Geol. Environ. 2022, 81, 183. [Google Scholar] [CrossRef]
- Li, Z.; Zhang, X.; Wei, Y.; Ali, M. Experimental Study of Electric Potential Response Characteristics of Different Lithological Samples Subject to Uniaxial Loading. Rock Mech. Rock Eng. 2021, 54, 397–408. [Google Scholar] [CrossRef]
- Ma, D.; Duan, H.; Zhang, J.; Bai, H. A state-of-the-art review on rock seepage mechanism of water inrush disaster in coal mines. Int. J. Coal Sci. Technol. 2022, 9, 50. [Google Scholar] [CrossRef]
- Wang, X.; Wang, E.; Liu, X.; Zhou, X. Failure mechanism of fractured rock and associated acoustic behaviors under different loading rates. Eng. Fract. Mech. 2021, 247, 107674. [Google Scholar] [CrossRef]
- Wang, K.; Zhang, G.; Wang, Y.; Zhang, X.; Li, K.; Guo, W.; Du, F. A numerical investigation of hydraulic fracturing on coal seam permeability based on PFC-COMSOL coupling method. Int. J. Coal Sci. Technol. 2022, 9, 10. [Google Scholar] [CrossRef]
- Marsden, H.; Basu, S.; Striolo, A.; MacGregor, M. Advances of nanotechnologies for hydraulic fracturing of coal seam gas reservoirs: Potential applications and some limitations in Australia. Int. J. Coal Sci. Technol. 2022, 9, 27. [Google Scholar] [CrossRef]
- Chen, Y.; Zuo, J.; Liu, D.; Li, Y.; Wang, Z. Experimental and numerical study of coal-rock bimaterial composite bodies under triaxial compression. Int. J. Coal Sci. Technol. 2021, 8, 908–924. [Google Scholar] [CrossRef]
- Wong, L.N.Y.; Maruvanchery, V.; Liu, G. Water effects on rock strength and stiffness degradation. Acta Geotech. 2016, 11, 713–737. [Google Scholar] [CrossRef]
- Xie, S.; Wang, E.; Chen, D.; Li, H.; Jiang, Z.; Yang, H. Stability analysis and control technology of gob-side entry retaining with double roadways by filling with high-water material in gently inclined coal seam. Int. J. Coal Sci. Technol. 2022, 9, 52. [Google Scholar] [CrossRef]
- Chugh, Y.P.; Missavage, R.A. Effects of moisture on strata control in coal mines. Eng. Geol. 1981, 17, 241–255. [Google Scholar] [CrossRef]
- Poulsen, B.; Shen, B.; Williams, D.; Huddlestone-Holmes, C.; Erarslan, N.; Qin, J. Strength reduction on saturation of coal and coal measures rocks with implications for coal pillar strength. Int. J. Rock Mech. Min. Sci. 2014, 71, 41–52. [Google Scholar] [CrossRef]
- Liu, W.; Yang, K.; Zhang, S.; Zhang, Z.; Xu, R. Energy evolution and water immersion-induced weakening in sandstone roof of coal mines. Int. J. Coal Sci. Technol. 2022, 9, 53. [Google Scholar] [CrossRef]
- Ma, D.; Cai, X.; Li, Q.; Duan, H. In-situ and numerical investigation of groundwater inrush hazard from grouted karst collapse pillar in longwall mining. Water 2018, 10, 1187. [Google Scholar] [CrossRef]
- Ma, D.; Cai, X.; Zhou, Z.; Li, X. Experimental investigation on hydraulic properties of granular sandstone and mudstone mixtures. Geofluids 2018, 2018, 9216578. [Google Scholar] [CrossRef]
- Guglielmi, Y.; Cappa, F.; Avouac, J.-P.; Henry, P.; Elsworth, D. Seismicity triggered by fluid injection–induced aseismic slip. Science 2015, 348, 1224–1226. [Google Scholar] [CrossRef] [PubMed]
- Lu, T.; Zhao, Z.; Hu, H.J.I.J.O.R.M.; Sciences, M. Improving the gate road development rate and reducing outburst occurrences using the waterjet technique in high gas content outburst-prone soft coal seam. Int. J. Rock Mech. Min. Sci. 2011, 48, 1271–1282. [Google Scholar] [CrossRef]
- Song, D.; Wang, E.; Liu, Z.; Liu, X.; Shen, R.J. Numerical simulation of rock-burst relief and prevention by water-jet cutting. Int. J. Rock Mech. Min. Sci. 2014, 70, 318–331. [Google Scholar] [CrossRef]
- Masoumi, H.; Horne, J.; Timms, W.J. Establishing empirical relationships for the effects of water content on the mechanical behavior of Gosford sandstone. Rock Mech. Rock Eng. 2017, 50, 2235–2242. [Google Scholar] [CrossRef]
- Li, D.; Wang, E.; Kong, X.; Ali, M.; Wang, D. Mechanical behaviors and acoustic emission fractal characteristics of coal specimens with a pre-existing flaw of various inclinations under uniaxial compression. Int. J. Rock Mech. Min. Sci. 2019, 116, 38–51. [Google Scholar] [CrossRef]
- Ding, Z.; Feng, X.; Wang, E.; Wei, Q.; Zhao, X.; Hu, Q. Acoustic emission response and evolution of precracked coal in the meta-instability stage under graded loading. Eng. Geol. 2023, 312, 106930. [Google Scholar] [CrossRef]
- Feng, X.; Ding, Z.; Ju, Y.; Zhang, Q.; Ali, M. “Double Peak” of Dynamic Strengths and Acoustic Emission Responses of Coal Masses Under Dynamic Loading. Nat. Resour. Res. 2022, 31, 1705–1720. [Google Scholar] [CrossRef]
- He, S.; Qin, M.; Qiu, L.; Song, D.; Zhang, X. Early warning of coal dynamic disaster by precursor of AE and EMR “quiet period”. Int. J. Coal Sci. Technol. 2022, 9, 46. [Google Scholar] [CrossRef]
- Chang, S.H.; Lee, C.I. Estimation of cracking and damage mechanisms in rock under triaxial compression by moment tensor analysis of acoustic emission. Int. J. Rock Mech. Min. Sci. 2004, 41, 1069–1086. [Google Scholar] [CrossRef]
- Shkuratnik, V.L.; Filimonov, Y.L.; Kuchurin, S.V. Experimental investigations into acoustic emission in coal samples under uniaxial loading. J. Min. Sci. 2004, 40, 458–464. [Google Scholar] [CrossRef]
- Rodríguez, P.; Arab, P.B.; Celestino, T.B. Characterization of rock cracking patterns in diametral compression tests by acoustic emission and petrographic analysis. Int. J. Rock Mech. Min. Sci. 2016, 83, 73–85. [Google Scholar] [CrossRef]
- Li, D.; Xiao, Z.; Mu, S.; Wang, F.; Liu, Y.; Song, J.; Huang, X.; Jiang, L.; Xiao, J.; Liu, L.; et al. A Facile Space-Confined Solid-Phase Sulfurization Strategy for Growth of High-Quality Ultrathin Molybdenum Disulfide Single Crystals. Nano Lett. 2018, 18, 2021–2032. [Google Scholar] [CrossRef] [PubMed]
- Gao, R.; Kuang, T.; Zhang, Y.; Zhang, W.; Quan, C. Controlling mine pressure by subjecting high-level hard rock strata to ground fracturing. Int. J. Coal Sci. Technol. 2021, 8, 1336–1350. [Google Scholar] [CrossRef]
- Li, H.; Qiao, Y.; Shen, R.; He, M.; Cheng, T.; Xiao, Y.; Tang, J.J.E.G. Effect of water on mechanical behavior and acoustic emission response of sandstone during loading process: Phenomenon and mechanism. Eng. Geol. 2021, 294, 106386. [Google Scholar] [CrossRef]
- Chen, J.; Ye, Y.; Pu, Y.; Xu, W.; Mengli, D. Experimental study on uniaxial compression failure modes and acoustic emission characteristics of fissured sandstone under water saturation. Theor. Appl. Fract. Mech. 2022, 119, 103359. [Google Scholar] [CrossRef]
- Ma, L.; Zhang, J.; Xu, C.; Lai, X.; Luo, Q.; Liu, C.; Li, K. Comprehensive Evaluation of Blast Casting Results Based on Unascertained Measurement and Intuitionistic Fuzzy Set. Shock. Vib. 2021, 2021, 8864618. [Google Scholar] [CrossRef]
- Li, H.; Shen, R.; Qiao, Y.; He, M. Acoustic emission signal characteristics and its critical slowing down phenomenon during the loading process of water-bearing sandstone. J. Appl. Geophys. 2021, 194, 104458. [Google Scholar] [CrossRef]
- Zhao, K.; Yang, D.; Zeng, P.; Huang, Z.; Wu, W.; Li, B.; Teng, T. Effect of water content on the failure pattern and acoustic emission characteristics of red sandstone. Int. J. Rock Mech. Min. Sci. 2021, 142, 104709. [Google Scholar] [CrossRef]
- Ma, L.; Zhao, J.; Zhang, J.; Xiao, S. Slope stability analysis based on leader dolphins herd algorithm and simplified Bishop method. IEEE Access 2021, 9, 28251–28259. [Google Scholar] [CrossRef]
- Ma, L.; Liu, C.; Bi, Y.; Peng, S.; Jiang, K.; Zhang, H.; Luo, Q.; Xue, F.; Xu, T.; Li, T.; et al. Experimental Study on Impermeability Law of Aquiclude Reconstructed by Mudstone of External Dump in Arid Zone. Adv. Civ. Eng. 2021, 2021, 5561794. [Google Scholar] [CrossRef]
- Ma, L.; Lai, X.; Zhang, J.; Xiao, S.; Zhang, L.; Tu, Y. Blast-casting mechanism and parameter optimization of a benched deep-hole in an opencast coal mine. Shock. Vib. 2020, 2020, 1396483. [Google Scholar] [CrossRef]
- Seibert, P.; Susmel, L.; Berto, F.; Kästner, M.; Razavi, S.M.J. Applicability of strain energy density criterion for fracture prediction of notched PLA specimens produced via fused deposition modeling. Eng. Fract. Mech. 2021, 258, 108103. [Google Scholar] [CrossRef]
- Zhao, Y.; Chen, C.; Wu, S.; Guo, P.; Li, B. Effects of 2D&3D nonparallel flaws on failure characteristics of brittle rock-like samples under uniaxial compression: Insights from acoustic emission and DIC monitoring. Theor. Appl. Fract. Mech. 2022, 120, 103391. [Google Scholar]
- Feng, X.; Ding, Z.; Hu, Q.; Zhao, X.; Ali, M.; Banquando, J.T. Orthogonal Numerical Analysis of Deformation and Failure Characteristics of Deep Roadway in Coal Mines: A Case Study. Minerals 2022, 12, 185. [Google Scholar] [CrossRef]
- Nikolenko, P.V.; Epshtein, S.A.; Shkuratnik, V.L.; Anufrenkova, P.S. Experimental study of coal fracture dynamics under the influence of cyclic freezing–thawing using shear elastic waves. Int. J. Coal Sci. Technol. 2021, 8, 562–574. [Google Scholar] [CrossRef]
- Lin, Q.; Cao, P.; Cao, R.; Fan, X. Acoustic emission characteristics during rock fragmentation processes induced by disc cutter under different water content conditions. Appl. Sci. 2019, 9, 194. [Google Scholar] [CrossRef]
- Ayling, M.R.; Meredith, P.G.; Murrell, S.A. Microcracking during triaxial deformation of porous rocks monitored by changes in rock physical properties, I. Elastic-wave propagation measurements on dry rocks. Tectonophysics 1995, 245, 205–221. [Google Scholar] [CrossRef]
- Khan, N.; Ma, L.; Cao, K.; Spearing, A.; Liu, W.; Jie, Y.; Yousaf, M. Early violent failure precursor prediction based on infrared radiation characteristics for coal specimens under different loading rates. Rock Mech. Rock Eng. 2022, 55, 6939–6961. [Google Scholar] [CrossRef]
- Fortin, J.; Stanchits, S.; Dresen, G.; Guéguen, Y. Acoustic emission and velocities associated with the formation of compaction bands in sandstone. J. Geophys. Res. Solid Earth 2006, 111. [Google Scholar] [CrossRef]
- Liu, B.; Zhao, Y.; Zhang, C.; Zhou, J.; Li, Y.; Sun, Z. Characteristic strength and acoustic emission properties of weakly cemented sandstone at different depths under uniaxial compression. Int. J. Coal Sci. Technol. 2021, 8, 1288–1301. [Google Scholar] [CrossRef]
- Zhou, Z.; Cai, X.; Ma, D.; Du, X.; Chen, L.; Wang, H.; Zang, H. Water saturation effects on dynamic fracture behavior of sandstone. Int. J. Rock Mech. Min. Sci. 2019, 114, 46–61. [Google Scholar] [CrossRef]
- Zhou, Z.; Cai, X.; Ma, D.; Cao, W.; Chen, L.; Zhou, J. Effects of water content on fracture and mechanical behavior of sandstone with a low clay mineral content. Eng. Fract. Mech. 2018, 193, 47–65. [Google Scholar] [CrossRef]
- Guo, P.; Gu, J.; Su, Y.; Wang, J.; Ding, Z. Effect of cyclic wetting–drying on tensile mechanical behavior and microstructure of clay-bearing sandstone. Int. J. Coal Sci. Technol. 2021, 8, 956–968. [Google Scholar] [CrossRef]
- Wu, R.; Zhang, P.; Kulatilake, P.H.S.W.; Luo, H.; He, Q. Stress and deformation analysis of gob-side pre-backfill driving procedure of longwall mining: A case study. Int. J. Coal Sci. Technol. 2021, 8, 1351–1370. [Google Scholar] [CrossRef]
- Zhang, K.; Li, H.; Han, J.; Jiang, B.; Gao, J. Understanding of mineral change mechanisms in coal mine groundwater reservoir and their influences on effluent water quality: A experimental study. Int. J. Coal Sci. Technol. 2021, 8, 154–167. [Google Scholar] [CrossRef]
- Zhu, J.; Deng, J.; Chen, F.; Huang, Y.; Yu, Z. Water saturation effects on mechanical and fracture behavior of marble. Int. J. Geomech. 2020, 20, 04020191. [Google Scholar] [CrossRef]
- Liu, X.; Wu, L.; Zhang, Y.; Liang, Z.; Yao, X.; Liang, P. Frequency properties of acoustic emissions from the dry and saturated rock. Environ. Earth Sci. 2019, 78, 1–17. [Google Scholar] [CrossRef]
- Zhao, K.; Wang, X.; Wang, L.; Zeng, P.; Yang, D.; Jin, J. Investigation of the crack and acoustic emission behavior evolution of red sandstone subjected to water. Theor. Appl. Fract. Mech. 2022, 120, 103419. [Google Scholar] [CrossRef]
- Feng, X.; Zhang, Q.; Wang, E.; Ali, M.; Dong, Z.; Zhang, G. 3D modeling of the influence of a splay fault on controlling the propagation of nonlinear stress waves induced by blast loading. Soil Dyn. Earthq. Eng. 2020, 138, 106335. [Google Scholar] [CrossRef]
- Niu, Y.; Li, Z.; Wang, E.; Shen, R.; Cheng, Z.; Gao, X.; Zhang, X.; Wang, H.; Ali, M. Study on characteristics of EP responsing to coal mining. Eng. Fract. Mech. 2020, 224, 106780. [Google Scholar] [CrossRef]
- Cao, K.; Ma, L.; Wu, Y.; Spearing, A.J.S.; Khan, N.M.; Hussain, S.; Ur Rehman, F. Statistical damage model for dry and saturated rock under uniaxial loading based on infrared radiation for possible stress prediction. Eng. Fract. Mech. 2022, 260, 108134. [Google Scholar] [CrossRef]
- Yang, D.; Ning, Z.; Li, Y.; Lv, Z.; Qiao, Y. In situ stress measurement and analysis of the stress accumulation levels in coal mines in the northern Ordos Basin, China. Int. J. Coal Sci. Technol. 2021, 8, 1316–1335. [Google Scholar] [CrossRef]
- Feng, F.; Chen, S.; Zhao, X.; Li, D.; Wang, X.; Cui, J. Effects of external dynamic disturbances and structural plane on rock fracturing around deep underground cavern. Int. J. Coal Sci. Technol. 2022, 9, 15. [Google Scholar] [CrossRef]
- Wang, X.; Asem, P.; Hu, C.; Labuz, J.F. Microcracking in tensile fracture of a brittle rock. Eng. Fract. Mech. 2021, 251, 107789. [Google Scholar] [CrossRef]
- Chen, L.-H.; Chen, W.-C.; Chen, Y.-C.; Benyamin, L.; Li, A.-J. Investigation of hydraulic fracture propagation using a post-peak control system coupled with acoustic emission. Rock Mech. Rock Eng. 2015, 48, 1233–1248. [Google Scholar] [CrossRef]
- Liu, Q.; Xu, J.; Liu, X.; Jiang, J.; Liu, B. The role of flaws on crack growth in rock-like material assessed by AE technique. Int. J. Fract. 2015, 193, 99–115. [Google Scholar] [CrossRef]
- Khazaei, C.; Hazzard, J.; Chalaturnyk, R. Damage quantification of intact rocks using acoustic emission energies recorded during uniaxial compression test and discrete element modeling. Comput. Geotech. 2015, 67, 94–102. [Google Scholar] [CrossRef]
- Ranjith, P.G.; Jasinge, D.; Song, J.Y.; Choi, S.K. A study of the effect of displacement rate and moisture content on the mechanical properties of concrete: Use of acoustic emission. Mech. Mater. 2008, 40, 453–469. [Google Scholar] [CrossRef]
- Kachanov, L. Introduction to Continuum Damage Mechanics; Springer Science & Business Media: Berlin/Heidelberg, Germany, 1986; Volume 10. [Google Scholar]
- Zhang, Y.; Liu, S. Variation characteristics of thermal radiation temperature field in rock loaded process. Rock Soil Mech. 2011, 32, 1013–1017. [Google Scholar]
- Liu, X.; Zhu, Z.; Liu, A.; Tian, Y. Lognormal distribution function for describing seepage damage process of single-cracked rock. Adv. Civ. Eng. 2020, 2020, 8838670. [Google Scholar] [CrossRef]
- Sanchidrián, J.A.; Ouchterlony, F.; Segarra, P.; Moser, P. Size distribution functions for rock fragments. Int. J. Rock Mech. Min. Sci. 2014, 71, 381–394. [Google Scholar] [CrossRef]
- Shin, K.; Sugawara, K.; Okubo, S. Application of Weibull’s theory to estimating in situ maximum stress σH by hydrofracturing. Int. J. Rock Mech. Min. Sci. 2001, 38, 413–420. [Google Scholar] [CrossRef]
- Li, H.; Shen, R.; Wang, E.; Li, D.; Li, T.; Chen, T.; Hou, Z. Effect of water on the time-frequency characteristics of electromagnetic radiation during sandstone deformation and fracturing. Eng. Geol. 2020, 265, 105451. [Google Scholar] [CrossRef]
- Zhou, K.; Dou, L.; Song, S.; Ma, X.; Chen, B. Experimental Study on the Mechanical Behavior of Coal Samples during Water Saturation. ACS Omega 2021, 6, 33822–33836. [Google Scholar] [CrossRef]
- Tang, S.J. The effects of water on the strength of black sandstone in a brittle regime. Eng. Geol. 2018, 239, 167–178. [Google Scholar] [CrossRef]
- Liu, D.; Wang, Z.; Zhang, X.; Wang, Y.; Zhang, X.; Li, D.J. Experimental investigation on the mechanical and acoustic emission characteristics of shale softened by water absorption. J. Nat. Gas Sci. Eng. 2018, 50, 301–308. [Google Scholar] [CrossRef]
- Khan, N.M.; Ahmad, M.; Cao, K.; Ali, I.; Liu, W.; Rehman, H.; Hussain, S.; Rehman, F.U.; Ahmed, T. Developing a new bursting liability index based on energy evolution for coal under different loading rates. Sustainability. 2022, 14, 1572. [Google Scholar] [CrossRef]
- Peng, S.; Johnson, A. Crack growth and faulting in cylindrical specimens of Chelmsford granite. In International Journal of Rock Mechanics and Mining Sciences & Geomechanics Abstracts; Elsevier: Amsterdam, The Netherlands, 1972. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).