A Model for the Assignment of Emergency Rescuers Considering Collaborative Information

Abstract

Emergency rescue is a critical decision for emergency response, and the assignment of rescuers is crucial to the sustainable development of emergency rescue. Therefore, how to effectively assign rescuers to carry out rescue tasks, so as to achieve the best rescue effect, is a research problem with practical value. In this paper, a model for the assignment of emergency rescuers considering collaborative information is proposed. Firstly, the synergy degrees of rescuers are calculated based on the synergy effect between rescuers and the synergy ability of rescuers. Secondly, according to the evaluation values of the skill level of rescuers, the competence degrees of rescuers are calculated and the overall ability of each rescuer is obtained. Then, the satisfaction degrees of rescuers are calculated according to the subjective preferences of rescuers. Furthermore, the task fitness degrees are obtained, and the satisfaction of rescue time is calculated. Afterwards, a model for assignment of emergency rescuers is constructed with the satisfaction of rescue time and the task fitness degrees maximization as the objectives, and the optimal assignment scheme can be obtained through solving the model. Finally, an illustrative example on the rescuer assignment under public health emergencies is given to illustrate the use of the proposed model.

1. Introduction

In recent years, major emergency incidents have occurred frequently around the world, such as the super typhoon Lekima in 2019, new coronary pneumonia in 2019, and the flooding in Henan Province in July 2021, which caused a large number of casualties and property damage [1,2] and had a significant impact on economic development, social stability, and sustainability [3,4]. In order to minimize the losses caused by emergency incidents, it is necessary to actively take scientific and effective emergency response measures [5,6]. The assignment of rescuers is an important decision for emergency response. Effectively organizing and rapidly dispatching rescuers to the disaster area to complete rescue tasks is critical to the sustainability and quality of emergency response to emergencies [7,8,9]. As emergency rescue often faces complex situations, such as diverse rescue tasks and urgent rescue time [10,11], how to reasonably and effectively dispatch rescuers to the disaster area to perform rescue tasks according to the actual needs of emergency rescue tasks and rescuer’ own conditions and preferences, so as to achieve the best rescue effect, is a research issue with practical significance.

At present, some progress has been made in studies on the assignment of rescuers in emergencies [12,13,14,15,16,17,18,19,20,21,22,23,24]. For example, Falasca and Zobel [12] developed a multi-objective optimization model to help volunteers assign tasks by taking the willingness and ability of volunteers to participate in relief efforts into consideration for the problem of dispatching rescuers in humanitarian organizations. Paret et al. [13] proposed a multi-server queuing model for the spontaneous volunteer assignment problem and used a Markov decision process model to generate an optimal strategy for assigning volunteer tasks. Sperling and Schryen [14] proposed a model with a lexicon-ordered objective function for the spontaneous volunteer coordination problem and conducted computational experiments using flood disaster data to make detailed recommendations for rescue organizations. The above studies assigned personnel by considering their own ability and willingness but did not consider the rescue time constraints. Whether the rescue task can be carried out in time determines the final rescue effect to a large extent. Wex et al. [15] developed a decision support model for rescue unit scheduling and assignment aiming at the rescue scheduling problem in disaster management, which has the objective of minimizing the rescue completion time. Zhang et al. [16] proposed a multi-level allocation model for the dynamic response of rescue teams to disaster chains and developed three priority scheduling strategies based on the maximum rescue time allowed by the disaster. La et al. [17] constructed a rescue subject deployment model with the goal of optimal deployment effect based on the urgency of the rescue task and the required rescue subjects predicted by the rescue task. Shiri et al. [18] proposed the online strategies for the dispatch of search-and-rescue teams, taking into account the uncertainty of time and road conditions. Although the rescue time was considered in these studies, the competency of rescuers was not considered, which is an important factor affecting the completion of the rescue effort. Yuan et al. [19] presented a model for the assignment of rescuers by considering rescue time and the competency of rescuers. Li et al. [20] presented a two-stage multi-sided matching dispatching model based on an improved BPR function and probabilistic language term set by considering the capability of rescuers and rescue time reliability and realized the matching between rescue teams, search and rescue teams, and multiple disaster sites. Fei and Wang [21] presented a dispatching model for rescuers considering multiple disaster areas and rescue points based on Dempster–Shafer theory for the problem of rescuer allocation in an uncertain environment. These studies considered the competency of rescuers and rescue time but did not consider the subjective will of rescuers. Considering that the subjective will of rescuers can better mobilize the initiative of rescuers and improve the rescue effect. For this, Chen et al. [22] developed a method based on evidential reasoning to solve the matching problem between volunteer teams and rescue tasks by considering the uncertain preference information of rescue tasks and volunteers. Chen and Chen [23] developed a multi-person multi-task dispatch model considering the psychological perception of rescuers and rescue tasks and solved the model using an improved predator search algorithm. Chen et al. [24] proposed a rescuer dispatching method based on an improved predatory algorithm for the volunteer dispatching problem during the coronavirus disease 2019 epidemic. These studies considered the needs of rescue missions and rescuers from the perspective of bilateral matching but did not consider the collaborative information about rescuers. While collaboration has become increasingly important in emergency management [25], Chen et al. [26] proposed a collaborative framework in emergency response management. Ren et al. [27] considered the collaborative relationship between multiple groups and pointed out its necessity. Hossain and Uddin [28] proposed a design framework and the idea of collaborative modeling in a complex dynamic environment. These related studies are mainly analyzed from a qualitative perspective, and it is difficult to quantify the synergy effects. In addition to the dispatch of emergency rescuers, there are many disaster response strategies, such as the distribution of shelters and supplies after a disaster. For this, Gharib et al. [29] developed an integrated model for transporting materials to post-disaster reconstruction projects and provided disaster recovery strategies for the construction industry, so as to support the decisions about delivering construction materials to post-disaster reconstruction projects. Gharib et al. [30] proposed a model for allocating temporary shelters after large-scale disasters, which have an impact on decision makers involved in post-disaster response projects.

Based on the above studies review, it can be seen that existing studies have provided some methods and ideas for this paper, such as the measurement of rescuer capability, the representation and processing of rescue time, etc. However, it should be pointed out that there are still some limitations in the existing relevant studies: (1) In terms of the evaluation of rescuer capability, existing studies are often limited to the assessment of personal professional skills and most of them ignore the collaborative information about rescuers. In fact, rescue tasks need to be completed through the cooperation between rescuers. Therefore, in the process of assigning rescuers, not only the individual professional skills of rescuers should be considered but also the collaborative information about rescuers, so as to create a good synergy effect between rescuers dispatched to perform the same rescue task and improve the rescue effect. In addition, most of the existing synergy measurement methods are applied to the analysis and evaluation of economic systems, which are relatively complicated to calculate and difficult to apply to emergency management. (2) Most of the existing studies study the assignment of rescuers from the perspective of one-way assignment, which only considers the demands of rescue tasks and lacks consideration of subjective preferences of rescuers. Nevertheless, rescuers have different personality traits and motivations and have different preferences. Meeting their preferences is conducive to stimulating the vitality of rescuers. This can affect the enthusiasm of rescuers and rescue effects and is not suitable for solving the problem of the assignment of rescuers in social organizations. (3) In terms of the calculation of rescue time satisfaction, most of the existing studies calculate the rescue time satisfaction based on the distance between the departure place and the disaster area, without considering the time requirements of different rescue tasks, which does not conform to the actual situation of emergency rescue. Therefore, it is necessary to construct an assignment model of emergency rescuers considering collaborative information, rescue time, competence degrees, and subjective preferences of rescuers, which is the research motivation of this paper.

This study intends to propose a model to solve the problem of the assignment for rescuer considering collaborative information. Firstly, the synergy degrees of rescuers are calculated based on the collaborative information about rescuers. Secondly, according to the evaluation of the skill level of rescuers, the competence degrees of rescuers are calculated, and the overall ability of each rescuer is obtained by aggregating the synergy degree and the competence degree. Then, the satisfaction degrees of rescuers are calculated using evidential reasoning according to the subjective preferences provided by the rescuers. Further, the task fitness degrees are obtained by aggregating the satisfaction degrees and overall ability of rescuers. Afterwards, the satisfaction of rescue time is calculated based on the time for the rescuer to arrive at the disaster area to carry out the rescue task and the time requirement of each rescue task. Finally, a model for assignment of rescuers is constructed by maximizing the satisfaction of rescue time and the task fitness degrees, and the optimal assignment scheme can be obtained through solving the model.

The remainder of this paper is organized as follows: Section 2 describes the problem studied in this paper. Section 3 presents an assignment model of emergency rescuers considering collaborative information. In Section 4, the use of the proposed model is illustrated by an example and Section 5 concludes this paper.

2. Description of Emergency Rescuers Assignment Problem

To facilitate the description of the rescuer assignment problem, the notations in Table 1 are used to denote the relevant sets and quantities.

Table 1. Notations used in this paper and the corresponding explanations.

Notations	Explanations
$A=\{A_1,A_2,\dots ,A_n\}$	The set of departure places of emergency rescuers, where Ai denotes the ith departure place, $i=1,2,\dots ,n$.
$a=[a_1,a_2,\dots ,a_n]$	The vector of the number of emergency rescuers available for dispatch from the departure places, where $a_i$ denotes the number of emergency rescuers available for dispatch from the departure place Ai, $\ell ={\displaystyle \sum _{i=1}^n{a}_i}$, $i=1,2,\dots ,n$.
$P_i=\{P_{i1},P_{i2},\dots ,P_{i{a}_i}\}$	The set of emergency rescuers in the departure place Ai, where Pij denotes the jth emergency rescuer in the departure place Ai, $i=1,2,\dots ,n$, $j=1,2,\dots ,a_i$.
D	The disaster area.
$M=\{M_1,M_2,\dots ,M_m\}$	The set of rescue tasks that need to be completed in the disaster area, where Mg denotes the gth rescue task, $g=1,2,\dots ,m$.
$d=[d_1,d_2,\dots ,d_m]$	The vector of the number of emergency rescuers required for each rescue task, where dg denotes the number of emergency rescuers required for the rescue task Mg, assuming that the number of rescuers available for dispatch is sufficient, i.e., $\ell \ge {\displaystyle \sum _{g=1}^m{d}_g}$, $g=1,2,\dots ,m$.
$G=\{G_1,G_2,\dots ,G_m\}$	The set of rescue teams, where Gg denotes the rescue team responsible for completing the rescue task Mg, $g=1,2,\dots ,m$.
$S^g(P_{ij},P_{uz})$	The evaluation value of the synergy effect between Pij and Puz for the rescue task Mg, $g=1,2,\dots ,m$, $i,u=1,2,\dots ,n$, $i\ne u$, $j,z=1,2,\dots ,{\alpha }_i$, $j\ne z$. Usually, $S^g(P_{ij},P_{uz})$ can be obtained based on the collaborative cooperation in the historical rescue records of rescuers, and expressed in the form of multi granularity linguistic terms.
$C=\{C_1,C_2,\dots ,C_{\mu }\}$	The set of collaborative evaluation indicators of rescuers, where Cp denotes the pth collaborative evaluation indicator, $p=1,2,\dots ,\mu$.
$c_{ij}^p$	The evaluation value of the rescuer Pij concerning the collaborative evaluation indicator Cp, and it reflects the synergy ability of rescuers, $i=1,2,\dots ,n$, $j=1,2,\dots ,a_i$, $p=1,2,\dots ,\mu$. Usually, $c_{ij}^p$ can be obtained based on the qualifications of rescuers and the historical rescue or drill records. It is expressed in the form of scores (e.g., 1–5), and the higher the score is, the higher the synergy ability of rescuers concerning the collaborative evaluation indicator will be.
${\eta }_p^g$	The weight of the collaborative evaluation indicator Cp for the rescue task Mg, such that $0\le {\eta }_p^g\le 1$, ${\displaystyle \sum _{p=1}^{\mu }{\eta }_p^g}=1$.
$B=\{B_1,B_2,\dots ,B_q\}$	The set of evaluation indicator of skill level of rescuer required by rescue tasks, where Bk denotes the kth evaluation indicator of personal skills. It is used to describe the professional skill level of rescuer, $k=1,2,\dots ,q$.
$b_{ij}^k$	The evaluation value of rescuer Pij concerning personal skill Bk, $i=1,2,\dots ,n$, $j=1,2,\dots ,a_i$, $k=1,2,\dots ,q$. Usually, $b_{ij}^k$ can be obtained in a similar way to $c_{ij}^p$.
${\mathrm{\Gamma }}_g$	The set of evaluation indicators for personal skills of rescuers required for the rescue task Mg, where ${\mathrm{\Gamma }}_g\subset B$ and ${\mathrm{\Gamma }}_1\cup {\mathrm{\Gamma }}_2\cup \cdots \cup {\mathrm{\Gamma }}_m=B$. Due to the content of each rescue task is different, so the personal skills of rescuers required by each rescue task are also different. In addition, $H^g$ denotes the subscript set of personal skills evaluation indicators in ${\mathrm{\Gamma }}_g$, where $H^g\ne \varnothing$,$H^1\cup H^2\cup \cdots \cup H^m=\{1,2,\dots ,q\}$, $g=1,2,\dots ,m$.
${\lambda }_k^g$	The weight of evaluation indicators for personal skills Bk required by the rescue task Mg, such that $0\le {\lambda }_k^g\le 1$ and ${\displaystyle \sum _{k\in H^g}{\lambda }_k^g}=1$.
$T_g^1$	The best rescue time of the rescue task Mg.
$T_g^2$	The effective rescue time of the rescue task Mg.
$T_g^{\max }$	The failure rescue time of the rescue task Mg.
$t_i^g$	The time required by rescuers to carry out the rescue task Mg from the departure place Ai to the disaster area D. Since the emergency may cause road damage, congestion and other conditions, and different rescue tasks require different preparation times, it is difficult to determine $t_i^g$. In this paper, it is assumed that $t_i^g$ follows a uniform distribution of $[t_i^{gL},t_i^{gU}]$, where $0\le t_i^{gL}\le t_i^{gU}$.

The problem studied in this paper is how to construct an assignment model of the emergency rescuers by comprehensively considering collaborative information (i.e., the synergy effect $S^g(P_{ij},P_{uz})$ between rescuers and the synergy ability $c_{ij}^p$ of rescuers), the evaluation value $b_{ij}^k$ of personal skills of the rescuer, the subjective preference of the rescuer, and the rescue time $t_i^g$, etc., so that rescuers can be reasonably assigned to rescue teams $G_1,G_2,\dots ,G_m$ and dispatched to complete the rescue tasks $M_1,M_2,\dots ,M_m$. In addition, this paper assumes that each rescuer can only be assigned to one rescue team at most to perform corresponding rescue task and that the number of rescuers meets the needs of rescue tasks. The diagram of the rescuer assignment problem is shown in Figure 1.

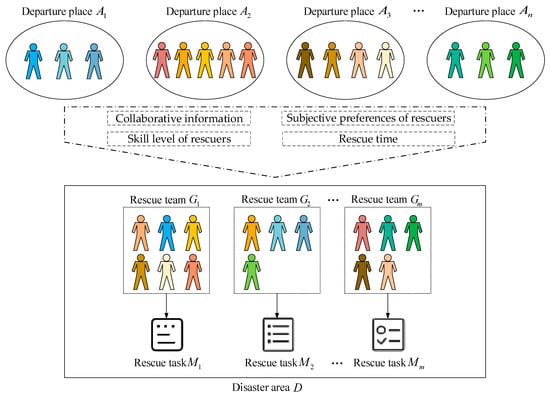
Figure 1. The problem of the emergency rescuers assignment considering collaborative information.

To solve the above problem, the resolution procedure of the emergency rescuer assignment problem considering collaborative information is given, as shown in Figure 2. Firstly, the synergy degree matrix of rescuers is constructed by aggregating the evaluation values of the synergy effect between rescuers and the synergy ability of rescuers. Secondly, according to the evaluation values of the skill level of rescuers and the weights of the skill level, the competence degree matrix is constructed. Then, the overall ability matrix of the rescuer is obtained by aggregating the synergy degree and the competence degree. Further, the satisfaction degree matrix of rescuers is constructed according to the subjective preferences of rescuers. Afterwards, the task fitness degree matrix is obtained by aggregating the satisfaction degrees and overall ability, and the time satisfaction function is used to construct the rescue time satisfaction matrix. Finally, an assignment model of emergency rescuers is constructed, and the optimal assignment scheme of rescuers can be obtained by solving the optimization model.

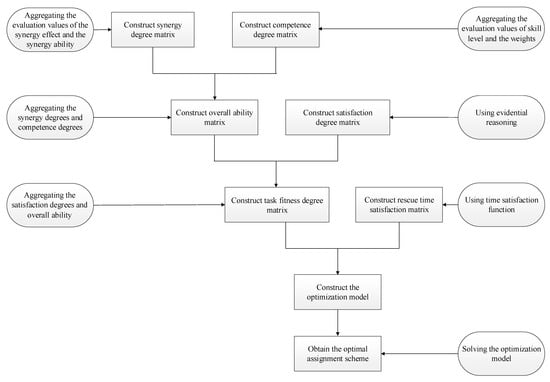
Figure 2. The resolution procedure of the emergency rescuer assignment problem considering collaborative information.

3. Construction and Solution of Emergency Rescuers Assignment Model

In this section, the assignment model of emergency rescuers is proposed based on the resolution procedure shown in Figure 2. The calculation methods of the synergy degrees of rescuers, the competence degrees of rescuers, the overall ability of rescuers, the satisfaction degrees of rescuers, the task fitness degrees, and the satisfaction of rescue time are respectively introduced. Then, the construction and solution of the assignment model are provided.

3.1. Calculation of the Synergy Degrees of the Rescuers

In the emergency rescue process, collaborative cooperation among rescuers can create greater value than individual rescuers working independently [25]. So, if the rescuers have the same goal and actively cooperate with each other in the process of carrying out the rescue task, the resulting synergy effect will have a positive impact on the completion of the rescue task [31,32]. At the same time, the synergy ability of the rescuers is also an important factor that affects the completion effect of rescue tasks. Therefore, two factors are considered in the calculation of the synergy degrees of rescuers, i.e., the synergy effect between rescuers and the synergy ability of rescuers.

3.1.1. Cooperative Performance of Rescuers

Considering the fuzziness and uncertainty of the thinking and judgement of emergency rescue experts and the complexity of rescue tasks in actual emergency rescue, it is difficult to express the synergy effect between rescuers concerning rescue tasks in the form of quantitative information. Therefore, the evaluation value $S^g(P_{ij},P_{uz})$ of the synergy effect is expressed in the form of a multi-grained linguistic term. For example, the seven-grain linguistic term set is $S$ = {s₀ = DL (definitely bad), s₁ = VL (very bad), s₂ = L (bad), s₃ = M (medium), s₄ = H (good), s₅ = VH (very good), and s₆ = DH (definitely good)}. It should be pointed that if there is no cooperation between P_ij and P_uz to complete the rescue task M_g, $S^g(P_{ij},P_{uz})$ can be supplemented based on historical cooperation between P_ij and P_uz for similar tasks of the rescue task M_g. If there is no historical cooperation between P_ij and P_uz to complete a rescue task similar to M_g, then $S^g(P_{ij},P_{uz})=null$. In addition, this paper does not consider the synergy effect between the rescuers themselves, $g=1,2,\dots ,m$, $i,u=1,2,\dots ,n$, $i\ne u$, $j,z=1,2,\dots ,{\alpha }_i$, $j\ne z$.

According to the study [33], $S^g(P_{ij},P_{uz})$ can be represented by the triangular fuzzy number ${\overline{S}}^g(P_{ij},P_{uz})$, i.e.,

$${\overline{S}}^g(P_{ij},P_{uz})=({\overline{S}}_L^g(P_{ij},P_{uz}),{\overline{S}}_M^g(P_{ij},P_{uz}),{\overline{S}}_R^g(P_{ij},P_{uz}))=(\max (\frac{v_{ij}^{uz}-1}{S_q},0),\frac{v_{ij}^{uz}}{S_q},\min (\frac{v_{ij}^{uz}+1}{S_q},1))$$

(1)

$g=1,2,\dots ,m$, $i,u=1,2,\dots ,n$, $i\ne u$, $j,z=1,2,\dots ,{\alpha }_i$, and $j\ne z$ where ${\overline{S}}_L^g(P_{ij},P_{uz})$, ${\overline{S}}_M^g(P_{ij},P_{uz})$, and ${\overline{S}}_R^g(P_{ij},P_{uz})$ are real numbers; ${\overline{S}}_R^g(P_{ij},P_{uz})$$\ge {\overline{S}}_M^g(P_{ij},P_{uz})\ge {\overline{S}}_L^g(P_{ij},P_{uz})\ge 0$; $v_{ij}^{uz}$ denotes the subscript value of the element in the linguistic term set S corresponding to $S^g(P_{ij},P_{uz})$; S_q + 1 denotes the number of elements in the linguistic term set S; and $v_{ij}^{uz}\in \{0,1,\dots ,6\}$. Here, if $S^g(P_{ij},P_{uz})=null$, then ${\overline{S}}^g(P_{ij},P_{uz})=0$, $g=1,2,\dots ,m$, $i,u=1,2,\dots ,n$, $i\ne u$, $j,z=1,2,\dots ,{\alpha }_i$, and $j\ne z$.

Then, the synergy effect evaluation value ${\overline{S}}^g(P_{ij},P_{uz})$ is aggregated and the cooperative performance ${\delta }_{ij}^g=({\delta }_{ij}^{gL},{\delta }_{ij}^{gM},{\delta }_{ij}^{gR})$ of rescuer is obtained, i.e.,

$${\delta }_{ij}^{gL}=\frac{1}{\ell }[{\displaystyle \sum _{u=1}^n{\displaystyle \sum _{z=1}^{a_n}{\overline{S}}_L^g(P_{ij},P_{uz})}}]$$

(2)

$${\delta }_{ij}^{gM}=\frac{1}{\ell }[{\displaystyle \sum _{u=1}^n{\displaystyle \sum _{z=1}^{a_n}{\overline{S}}_M^g(P_{ij},P_{uz})}}]$$

(3)

$${\delta }_{ij}^{gR}=\frac{1}{\ell }[{\displaystyle \sum _{u=1}^n{\displaystyle \sum _{z=1}^{a_n}{\overline{S}}_R^g(P_{ij},P_{uz})}}]$$

(4)

where $\ell ={\displaystyle \sum _{i=1}^n{a}_i}$, ${\delta }_{ij}^g$ denotes the cooperative performance of rescuer P_ij in cooperation with other rescuers for rescue task M_g, $g=1,2,\dots ,m$, $i,u=1,2,\dots ,n$, $i\ne u$, $j,z=1,2,\dots ,{\alpha }_i$, and $j\ne z$.

Then, the inverse fuzzy aggregation method [34] is used to transform the collaborative performance ${\delta }_{ij}^g=({\delta }_{ij}^{gL},{\delta }_{ij}^{gM},{\delta }_{ij}^{gR})$ into a crisp number $S_{ij}^g$. The aggregation method can more accurately convert triangular fuzzy numbers to crisp numbers and avoid information loss. The corresponding conversion equation is as follows:

$$S_{ij}^g=L_g+\frac{{\Delta }_g[({\delta }_{ij}^{gM}-L_g){({\Delta }_g+{\delta }_{ij}^{gR}-{\delta }_{ij}^{gM})}^2(R_g-{\delta }_{ij}^{gL})+{({\delta }_{ij}^{gR}-L_g)}^2{({\Delta }_g+{\delta }_{ij}^{gM}-{\delta }_{ij}^{gL})}^2]}{({\Delta }_g+{\delta }_{ij}^{gM}-{\delta }_{ij}^{gL}){({\Delta }_g+{\delta }_{ij}^{gR}-{\delta }_{ij}^{gM})}^2(R_g-{\delta }_{ij}^{gL})+({\delta }_{ij}^{gR}-L_g){({\Delta }_g+{\delta }_{ij}^{gM}-{\delta }_{ij}^{gL})}^2({\Delta }_g+{\delta }_{ij}^{gR}-{\delta }_{ij}^{gM})}$$

(5)

where $L_g=\min \{{\delta }_{11}^{gL},{\delta }_{12}^{gL},\dots ,{\delta }_{n{a}_n}^{gL}\}$, $R_g=\max \{{\delta }_{11}^{gR},{\delta }_{12}^{gR},\dots ,{\delta }_{n{a}_n}^{gR}\}$, ${\Delta }_g=R_g-L_g$, $g=1,2,\dots ,m$, $i,u=1,2,\dots ,n$, $i\ne u$, $j,z=1,2,\dots ,{\alpha }_i$, and $j\ne z$.

3.1.2. Comprehensive Synergy Ability and Synergy Degrees of Rescuers

The collaborative evaluation indicators $C=\{C_1,C_2,\dots ,C_{\mu }\}$ of rescuers can be divided into benefit type indicators and cost type indicators. Let C^a and C^b be the set of benefit-based indicators and the set of cost-based indicators, respectively, $C^a\cup C^b=C$ and $C^a\cap C^b=\varnothing$. Let $C{O}^a$ and $C{O}^b$ denote the subscript sets of indicators in the sets C^a and C^b, respectively, $C{O}^a\cup C{O}^b=\{1,2,\dots ,\mu \}$ and $C{O}^a\cap C{O}^b=\varnothing$.

Since the measurement standards of each indicator are different, it is necessary to normalize the evaluation value $c_{ij}^p$. The calculation formula is as follows:

$${\overline{c}}_{ij}^p=\{\begin{array}{cc}\frac{c_{ij}^p-c_{\min }^p}{c_{\max }^p-c_{\min }^p},& p\in C{O}^a\\ \frac{c_{\max }^p-c_{ij}^p}{c_{\max }^p-c_{\min }^p},& p\in C{O}^b\end{array}$$

(6)

where $c_{\min }^p=\min \left\{c_{ij}^p\right|i=1,2,\dots ,n;j=1,2,\dots ,a_i\}$, $c_{\max }^p=\max \left\{c_{ij}^p\right|i=1,2,\dots ,n;$$j=1,2,\dots ,a_i\}$, and $p=1,2,\dots ,\mu$.

According to the normalized evaluation value ${\overline{c}}_{ij}^p$ and the weight ${\eta }_p^g$, the comprehensive synergy ability of rescuer, $R_{ij}^g$, can be calculated, i.e.,

$$R_{ij}^g={\displaystyle \sum _{p=1}^{\mu }{\eta }_p^g{\overline{c}}_{ij}^p}, g=1,2,\dots ,m, i=1,2,\dots ,n, j=1,2,\dots ,{\alpha }_i$$

(7)

Then, the synergy degree of rescuer is calculated by aggregating the cooperative performance and the comprehensive synergy ability of rescuer, and the synergy degree matrix $\mathbf{S}{\mathbf{R}}_i{=[\mathrm{SR}}_{ij}^g{]}_{a_i\times m}$ of rescuer is constructed. The synergy degree ${\mathrm{SR}}_{ij}^g$ can be calculated, i.e.,

$${\mathrm{SR}}_{ij}^g=\zeta S_{ij}^g+(1-\zeta )R_{ij}^g, g=1,2,\dots ,m, i=1,2,\dots ,n, j=1,2,\dots ,{\alpha }_i$$

(8)

where ζ is the weighting factor, $\zeta \in [0,1]$. If ζ > 0.5, it indicates that the collaborative performance of rescuer is given priority in the emergency rescuer assignment. If ζ < 0.5, it indicates that the comprehensive synergy ability of rescuer is given priority in the emergency rescuer assignment. If ζ = 0.5, it indicates that the collaborative performance and the comprehensive synergy ability are equally important. The value of ζ is usually given by the emergency rescue specialists according to the actual situation.

3.2. Calculation of the Competence Degrees of Rescuers for Rescue Tasks

In the emergency rescue process, different rescue tasks require different personal skills of rescuers, so the calculation of the competence degrees of rescuers needs to consider both the requirements of rescue tasks for rescuers and the level of personal skills of rescuers.

Considering that the set $B=\{B_1,B_2,\dots ,B_q\}$ of the evaluation indicators of skill level of rescuers can be divided into two categories, i.e., benefit type indicators and cost type indicators. Let B^a and B^b be the set of benefit-based indicators of skill level and the set of cost-based indicators of skill level, respectively, $B^a\cup B^b=B$ and $B^a\cap B^b=\varnothing$. Let $B{O}^a$ and $B{O}^b$ denote the subscript sets of indicators in the sets B^a and B^b, respectively, $B{O}^a\cup B{O}^b=\{1,2,\dots ,q\}$, $B{O}^a\cap B{O}^b=\varnothing$.

The evaluation value $b_{ij}^k$ of personal skills of rescuers is normalized, and the normalized evaluation value $f_{ij}^k$ of personal skills is obtained, i.e.,

$$f_{ij}^k=\{\begin{array}{cc}\frac{b_{ij}^k-b_{\min }^k}{b_{\max }^k-b_{\min }^k},& k\in B{O}^a\\ \frac{b_{\max }^k-b_{ij}^k}{b_{\max }^k-b_{\min }^k},& k\in B{O}^b\end{array}$$

(9)

where $b_{\min }^k=\min \left\{b_{ij}^k\right|i=1,2,\dots ,n;j=1,2,\dots ,a_i\}$, $b_{\max }^k=\max \left\{b_{ij}^k\right|i=1,2,\dots ,n;$$j=1,2,\dots ,a_i\}$, and $k=1,2,\dots ,q$.

According to the normalized evaluation value $f_{ij}^k$ of personal skills and the weight ${\lambda }_k^g$, the competence degree $r_{ij}^g$ of the rescuer can be calculated, and the competence degree matrix ${\mathbf{R}}_i=[r_{ij}^g{]}_{a_i\times m}$ of rescuers can be constructed. $r_{ij}^g$ can be calculated by Equation (10), i.e.,

$$r_{ij}^g={\displaystyle \sum _{k\in H^g}{f}_{ij}^k{\lambda }_k^g}, g=1,2,\dots ,m, i=1,2,\dots ,n, j=1,2,\dots ,{\alpha }_i$$

(10)

3.3. Calculation of the Overall Ability of Rescuers

By aggregating the synergy degree and the competence degree, the overall ability $C{A}_{ij}^g$ of the rescuer can be calculated, and the overall ability matrix $\mathbf{C}{\mathbf{A}}_i=[C{A}_{ij}^g{]}_{a_i\times m}$ can be constructed. $C{A}_{ij}^g$ can be calculated, i.e.,

$$C{A}_{ij}^g=\sigma \cdot {\mathrm{SR}}_{ij}^g+(1-\sigma )r_{ij}^g, g=1,2,\dots ,m, i=1,2,\dots ,n, j=1,2,\dots ,{\alpha }_i$$

(11)

where σ is the weighting factor, $\sigma \in [0,1]$. If σ > 0.5, it indicates that the synergy degree of rescuer is given priority in the emergency rescuer assignment. If σ < 0.5, it indicates that the competence degree of rescuer is given priority in the emergency rescuer assignment. If σ = 0.5, it indicates that the synergy degree and the competence degree are equally important. The value of σ is usually given by the emergency rescue specialists according to the actual situation.

3.4. Calculation of the Satisfaction Degrees of Rescuers for Rescue Tasks

In emergency rescue, it is often accompanied by the participation of emergency rescuers in social organizations, such as volunteers. These rescuers usually have strong personal characteristics [35], such as diverse sources, complex motivations, etc. They have different preferences and expectations for rescue tasks. Therefore, the subjective preferences of rescuers for rescue tasks should be considered in the process of emergency rescuer assignment to achieve better rescue effect.

3.4.1. Establishment of Belief Structure

After the occurrence of the emergency incident, due to the complexity of the rescue task and the limitations of subjective perception, the rescue task cannot be fully understood by emergency rescuers. Rescuers often understand only part of the rescue task, especially the most desirable and least desirable parts. Therefore, rescuers cannot provide specific preference information for rescue tasks. Usually, emergency rescuer P_ij gives incomplete subjective preference evaluation information for rescue tasks by ranking, for example

$$E{M}_1^{ij}\succ E{M}_2^{ij}=E{M}_3^{ij}\succ \cdots \succ E{M}_g^{ij}\succ \cdots \succ E{M}_{E_{ij}}^{ij}$$

(12)

where $E{M}_g^{ij}$ denotes the subjective preference evaluation information of rescuer P_ij for the rescue task M_g, $E_{ij}(E_{ij}\le m)$ denotes the number of known preference evaluations of rescuers for rescue tasks, $(m-E_{ij})$ denotes the number of unknown preference evaluations of rescuers for rescue tasks, and the total number of subjective preference evaluations is $(m-1)$, $g=1,2,\dots ,m$, $i=1,2,\dots ,n$, and $j=1,2,\dots ,{\alpha }_i$.

Since the evidence reasoning method can effectively fuse several uncertain subproblems and retain the incompleteness and uncertainty of the preference evaluation information, this paper uses evidence reasoning to transform the preference evaluation information into evidence confidence. Let $H=\{H_1,H_2,H_3\}=\mathrm{\Theta }$ be the evidence identification framework, where H₁, H₂, H₃, and H denote preference evaluation relationships $\succ$, $=$, $\prec$, and $\mathrm{\Theta }$, respectively. $\mathrm{\Theta }$ denotes the unknown relationship in the preference evaluation information. Let $v_{ij}^g$ be belief structure, i.e.,

$$v_{ij}^g=\left\{\left(H_1,{\gamma }_{ij}^g(H_1)\right),\left(H_2,{\gamma }_{ij}^g(H_2)\right),\left(H_3,{\gamma }_{ij}^g(H_3)\right),\left(H,{\gamma }_{ij}^g(H)\right)\right\}$$

(13)

where ${\gamma }_{ij}^g(H_l)$$(l=1,2,3)$ denotes the belief degree of the rescuer P_ij for the rescue task M_g with respect to the preference relationship $H_l$, ${\gamma }_{ij}^g(H)$ denotes the belief degree of P_ij for M_g with respect to unknown preference relationship H, and ${\displaystyle {\sum }_{l=1}^3{\gamma }_{ij}^g(H_l)}+{\gamma }_{ij}^g(H)=1$, $g=1,2,\dots ,m$, $i=1,2,\dots ,n$, and $j=1,2,\dots ,{\alpha }_i$.

3.4.2. Satisfaction Degrees of Rescuers

Based on the established belief structure, the preference evaluation information of rescuers is converted into belief degrees, and then the belief degree of rescuers for rescue tasks can be fused using evidence reasoning to obtain the satisfaction degrees of rescuers for rescue tasks.

The belief degree of P_ij for M_g with respect to the preference evaluation relationship is transformed into basic probability masse using Equation (14), i.e.,

$$\{\begin{array}{ll}{m}_{ij}^g(H_l)=w_{ij}{\gamma }_{ij}^g(H_l),\hfill & j=1,2,\dots ,a_i;l=1,2,3\hfill \\ \begin{array}{l}{\tilde{m}}_{ij}^g(H)=w_{ij}{\gamma }_{ij}^g(H),\\ {\overline{m}}_{ij}^g(H)=1-w_{ij}\\ m_{ij}^g(H)={\tilde{m}}_{ij}^g(H)+{\overline{m}}_{ij}^g(H)\end{array}\hfill & \begin{array}{l}j=1,2,\dots ,a_i\\ j=1,2,\dots ,a_i\\ j=1,2,\dots ,a_i\\ j=1,2,\dots ,a_i\end{array}\hfill \end{array}$$

(14)

where $m_{ij}^g(H_l)$ denotes the basic probability masse of P_ij for M_g with respect to the preference evaluation relationship, ${\tilde{m}}_{ij}^g(H)$ denotes the unknown part caused by incomplete preference evaluation, ${\overline{m}}_{ij}^g(H)$ denotes the unknown part caused by relative weight, $m_{ij}^g(H)$ denotes the total unknown part caused by incomplete preference evaluation, and $w_{ij}$ denotes the relative weight of P_ij in the evaluation of rescue tasks. The relative weight can be given based on the decision-maker’s preference or can be objectively determined according to the value of each evidence. In order to achieve fairness, it is assumed that the rescuer from each departure place have the same importance in the evaluation of rescue tasks, i.e., $w_{ij}=1/a_i$, $g=1,2,\dots ,m$, $i=1,2,\dots ,n$, and $j=1,2,\dots ,{\alpha }_i$.

Then, the basic probability masse is aggregated to obtain the comprehensive evaluation evidence of rescuers at departure place A_i [36,37], and the calculation formula is as follows:

$$\{\begin{array}{ll}{\chi }_i^g(H_l)=K_i^g{\displaystyle \sum _{\begin{array}{l}{P}_{i1}\cap P_{i2}\cap \cdots \cap P_{i{\alpha }_i}=H_l\\ P_{i1},P_{i2},\cdots ,P_{i{\alpha }_i}\subseteq H\end{array}}{m}_{i1}^g(P_{i1})m_{i2}^g(P_{i2})\cdots m_{i{\alpha }_i}^g(P_{i{\alpha }_i})},\hfill & l=1,2,3\hfill \\ \begin{array}{l}{\tilde{\chi }}_i^g(H)=K_i^g\cdot \left(m_{i1}^g(H)m_{i2}^g(H)\cdots m_{i{\alpha }_i}^g(H)-{\overline{m}}_{i1}^g(H){\overline{m}}_{i2}^g(H)\cdots {\overline{m}}_{i{\alpha }_i}^g(H)\right)\\ {\overline{\chi }}_i^g(H)=K_i^g\cdot {\overline{m}}_{i1}^g(H){\overline{m}}_{i2}^g(H)\cdots {\overline{m}}_{i{\alpha }_i}^g(H)\\ K_i^g={[{\displaystyle \sum _{\begin{array}{l}{P}_{i1}\cap P_{i2}\cap \cdots \cap P_{i{\alpha }_i}\ne \varnothing \\ P_{i1},P_{i2},\cdots ,P_{i{\alpha }_i}\subseteq H\end{array}}{m}_{i1}^g(P_{i1})m_{i2}^g(P_{i2})\cdots m_{i{\alpha }_i}^g(P_{i{\alpha }_i})}]}^{-1}\end{array}\hfill & \begin{array}{l}\\ \\ \\ \end{array}\hfill \end{array}$$

(15)

According to the comprehensive evaluation evidence, the belief degree of the comprehensive evaluation evidence can be calculated, i.e.,

$$\{\begin{array}{cc}{\beta }_i^g(H_l)=\frac{{\chi }_i^g(H_l)}{1-{\overline{\chi }}_i^g(H)},& l=1,2,3\\ {\beta }_i^g(H)=\frac{{\tilde{\chi }}_{ij}^g(H)}{1-{\overline{\chi }}_i^g(H)}& \end{array}$$

(16)

Referring to the method by Chen et al. [1] for determining the utility value of preference evaluation relationship, let the utility values of preference evaluation relationship H₁, H₂, H₃, and H be as follows:

$$U(H_1)=1,\hspace{1em}U(H_2)=0.5,\hspace{1em}U(H_3)=0,\hspace{1em}U(H)=[0,1]$$

(17)

According to the decision maker’s attitude towards uncertain information, the belief degree of the comprehensive evaluation evidence is transformed into the satisfaction degree $F_i^g$ of rescuers at departure place A_i, and the satisfaction degree matrix $\mathbf{F}=[F_i^g{]}_{n\times m}$ of rescuers can be constructed. The satisfaction degree $F_i^g$ when the decision maker’s attitude is optimistic, pessimistic, and eclectic are as follows:

$$F_i^{g\max }={\displaystyle \sum _{l=1}^3{\beta }_i^g(H_l)}\cdot U(H_l)+{\beta }_i^g(H)$$

(18)

$$F_i^{g\min }={\displaystyle \sum _{l=1}^3{\beta }_i^g(H_l)}\cdot U(H_l)$$

(19)

$$F_i^{gavg}={\displaystyle \sum _{l=1}^3{\beta }_i^g(H_l)}\cdot U(H_l)+\frac{{\beta }_i^g(H)}{2}$$

(20)

where $F_i^g$ is the maximum value $F_i^{g\max }$ if the decision maker is optimistic, $F_i^g$ is the minimum value $F_i^{g\min }$ if the decision maker is pessimistic, and $F_i^g$ is the average value $F_i^{gavg}$ if the decision maker is eclectic, $g=1,2,\dots ,m$ and $i=1,2,\dots ,n$.

3.5. Calculation of the Task Fitness Degrees of Rescuers

The task fitness degrees can be calculated by aggregating the overall ability of rescuers and the satisfaction degrees of rescuers, and the task fitness degree matrix $\mathbf{F}{\mathbf{D}}_i{=[\mathrm{FD}}_{ij}^g{]}_{a_i\times m}$ of rescuers can be constructed, where ${\mathrm{FD}}_{ij}^g$ is calculated, i.e.,

$${\mathrm{FD}}_{ij}^g=\{\begin{array}{ll}\theta F_i^g+(1-\theta )C{A}_{ij}^g,\hfill & if C{A}_{ij}^g\ge \tau and F_i^g\ne 0\hfill \\ 0,\hfill & if C{A}_{ij}^g<\tau or F_i^g=0\hfill \end{array}$$

(21)

In Equation (21), θ is the weighting factor, $\theta \in [0,1]$. If θ > 0.5, it indicates that the satisfaction degree of rescuer is given priority in the emergency rescuer assignment. If θ < 0.5, it indicates that the overall ability of rescuer is given priority in the emergency rescuer assignment. If θ = 0.5, it indicates that the satisfaction degree and the overall ability are equally important. τ indicates the threshold of the overall ability of the rescuers, and $\tau \in [0,1)$. If $C{A}_{ij}^g\ge \tau$, it means that the overall capability of the rescuer P_ij can meet the requirements of the rescue task M_g. If $C{A}_{ij}^g<\tau$, it means that the overall capability of P_ij does not meet the requirements of M_g. In fact, the greater the overall capability and the number of rescuers are, the greater the threshold τ will be. The values of θ and τ are given by the emergency rescue specialists according to the actual situation, $g=1,2,\dots ,m$, $i=1,2,\dots ,n$, and $j=1,2,\dots ,{\alpha }_i$.

3.6. Calculation of the Satisfaction of Rescue Time

In emergency rescue, the time for rescuers to carry out the rescue task M_g from the departure place A_i to the disaster area D is an important factor affecting the completion effect of rescue tasks, which determines the effectiveness of rescue to a large extent. In order to effectively measure the relationship between rescue time and rescue effect, the satisfaction function $\phi (t_i^g)$ of rescue time is constructed by the researchers [19,38], i.e.,

$$\phi (t_i^g)=\{\begin{array}{ll}1,\hfill & t_i^g\le T_g^1\hfill \\ (1-z^g){(\frac{T_g^2-t_i^g}{T_g^2-T_g^1})}^{g_1}+z^g,\hfill & T_g^1<t_i^g\le T_g^2,g_1>1\hfill \\ z^g{(\frac{T_g^{\max }-t_i^g}{T_g^{\max }-T_g^2})}^{g_2},\hfill & T_g^2<t_i^g\le T_g^{\max },0<g_2<1\hfill \\ 0,\hfill & t_i^g>T_g^{\max }\hfill \end{array}$$

(22)

where $z^g$ denotes the time satisfaction of the rescuer arriving at the disaster area and carrying out the rescue task M_g at time $T_g^2$, $g_1$ indicates the efficiency satisfaction when rescuers arrive at the disaster area to carry out the rescue task less than the effective rescue time, $g_2$ indicates the efficiency satisfaction when rescuers arrive at the disaster area to carry out the rescue task greater than the effective rescue time, and the values of the parameters $T_g^1$, $T_g^2$, $T_g^{\max }$, and $z^g$ are determined by decision makers and emergency rescue experts according to different scenarios and the urgency of actual situations, $g=1,2,\dots ,m$ and $i=1,2,\dots ,n$.

The satisfaction function of rescue time is shown in Figure 3. From the Equation (22), it can be seen that the main factors affecting the satisfaction of rescue time are the time $t_i^g$ for rescuers to carry out the rescue task from the departure place to the disaster area and the requirements of each rescue task for rescue time. If the rescuer arrives at the disaster area to carry out the rescue task M_g before time $T_g^1$, the rescue effect is optimal and the value of satisfaction function of rescue time is 1. If the rescuer arrives at the disaster area to carry out the rescue task M_g between time $T_g^1$ and time $T_g^2$, the rescue is effective, but the satisfaction of rescue time decreases rapidly first and then slowly with the increase of time $t_i^g$. If the rescuer arrives at the disaster area to carry out the rescue task M_g between time $T_g^2$ and $T_g^{\max }$, although the rescue is still effective, the satisfaction of rescue time decreases slowly first and then rapidly with the increase of time $t_i^g$. If the rescuer arrives at the disaster area to carry out the rescue task M_g after time $T_g^{\max }$, the satisfaction of rescue time is 0, $g=1,2,\dots ,m$ and $i=1,2,\dots ,n$.

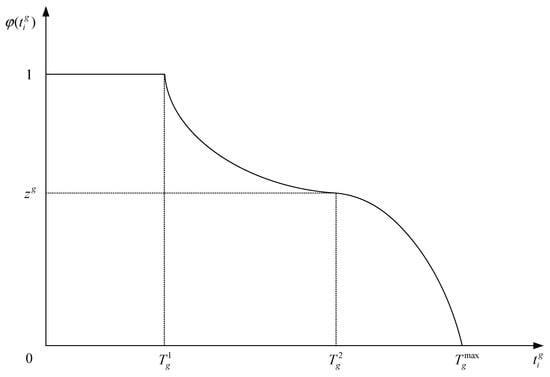
Figure 3. The satisfaction function of rescue time.

In the actual emergency rescue process, since it is often difficult to give a precise estimate of the time for the rescuer arrives at the disaster area to carry out the rescue task, the interval number is used to express the rescue time, i.e., $t_i^g=[t_i^{gL},t_i^{gU}]$. Here, it is assumed that the rescue time is uniformly distributed in the interval $[t_i^{gL},t_i^{gU}]$ [6], $0\le t_i^{gL}\le t_i^{gU}$. The satisfaction of rescue time is expressed by the expected value $S{D}_i^g$ in interval $[t_i^{gL},t_i^{gU}]$. $S{D}_i^g$ is defined as

$$S{D}_i^g=\frac{{\displaystyle {\int }_{t_i^{gL}}^{t_i^{gU}}\phi (t_i^g)d{t}_i^g}}{t_i^{gU}-t_i^{gL}}$$

(23)

To ensure the effect of the rescue, the estimate of the rescue time should be as accurate as possible. Assume that the estimated interval $[t_i^{gL},t_i^{gU}]$ of rescue time can only contain one critical turning point (i.e., $T_g^1$, $T_g^2$, and $T_g^{\max }$) at most. The critical turning points have multiple relationships, so the satisfaction of rescue time can be expressed as

$$S{D}_i^g=\{\begin{array}{ll}1,\hfill & t_i^{gL}\le t_i^{gU}\le T_g^1\hfill \\ \frac{1}{t_i^{gU}-t_i^{gL}}[(T_g^1-t_i^{gL})-\frac{1-z^g}{g_1+1}({(\frac{T_g^2-t_i^{gU}}{T_g^2-T_g^1})}^{g_1+1}-1)+z^g(t_i^{gU}-T_g^1)],\hfill & t_i^{gL}\le T_g^1<t_i^{gU}\le T_g^2\hfill \\ z^g-\frac{1-z^g}{(t_i^{gU}-t_i^{gL})(g_1+1)}({(\frac{T_g^2-t_i^{gU}}{T_g^2-T_g^1})}^{g_1+1}-{(\frac{T_g^2-t_i^{gL}}{T_g^2-T_g^1})}^{g_1+1}),\hfill & T_g^1<t_i^{gL}\le t_i^{gU}\le T_g^2\hfill \\ z^g+\frac{1}{t_i^{gU}-t_i^{gL}}[\frac{1-z^g}{g_1+1}{(\frac{T_g^2-t_i^{gL}}{T_g^2-T_g^1})}^{g_1+1}+\frac{z^g}{g_2+1}({(\frac{T_g^{\max }-t_i^{gU}}{T_g^{\max }-T_g^2})}^{g_2+1}-1)],\hfill & T_g^1<t_i^{gL}\le T_g^2<t_i^{gU}\le T_g^{\max }\hfill \\ z^g-\frac{z^g}{(t_i^{gU}-t_i^{gL})(g_2+1)}({(\frac{T_g^{\max }-t_i^{gU}}{T_g^{\max }-T_g^2})}^{g_2+1}-{(\frac{T_g^{\max }-t_i^{gL}}{T_g^{\max }-T_g^2})}^{g_2+1}),\hfill & T_g^2<t_i^{gL}\le t_i^{gU}\le T_g^{\max }\hfill \\ 0,\hfill & t_i^{gU}>T_g^{\max }\hfill \end{array}$$

(24)

On the basis of this, the rescue time satisfaction matrix $\mathbf{S}\mathbf{D}=[S{D}_i^g{]}_{n\times m}$ can be constructed, $g=1,2,\dots ,m$ and $i=1,2,\dots ,n$.

3.7. Construction and Solution of the Rescuer Assignment Model

In the assignment of emergency rescuers, two objectives need to be met: one is to maximize the task fitness degrees of rescuers as much as possible, and the other is to maximize the satisfaction of the rescue time as much as possible. In order to satisfy these two objectives simultaneously, the following multi-objective optimization model is constructed:

$$\max Z_1={\displaystyle \sum _{i=1}^n{\displaystyle \sum _{j=1}^{{\alpha }_i}{\displaystyle \sum _{g=1}^{m}F{D}_{ij}^g{x}_{ij}^g}}}$$

(25a)

$$\max Z_2={\displaystyle \sum _{i=1}^n{\displaystyle \sum _{j=1}^{{\alpha }_i}{\displaystyle \sum _{g=1}^{m}S{D}_i^g{x}_{ij}^g}}}$$

(25b)

$$s.t.\{\begin{array}{ll}{\displaystyle \sum _{g=1}^m{x}_{ij}^g\le 1,}\hfill & i=1,2,\dots ,n;j=1,2,\dots ,a_i\hfill \\ {\displaystyle \sum _{i=1}^n{\displaystyle \sum _{j=1}^{{\alpha }_i}{x}_{ij}^g=d_g,}}\hfill & g=1,2,\dots ,m\hfill \\ x_{ij}^g=0 or 1,\hfill & i=1,2,\dots ,n;j=1,2,\dots ,{\alpha }_i,g=1,2,\dots ,m\hfill \end{array}$$

(25c)

In Model (25), Equations (25a) and (25b) are objective functions, which, respectively, mean maximizing the task fitness degrees and maximizing the satisfaction of the rescue time. Equation (25c) contains three constraints, and the first constraint indicates that each rescuer can only be assigned to perform one rescue task at most. The second constraint indicates that the number of rescuers assigned to perform the rescue task is equal to the number of rescuers required for the rescue task. In the third constraint, $x_{ij}^g$ represents the 0–1 decision variable, where $x_{ij}^g=1$ means that rescuers are assigned to complete rescue tasks, otherwise $x_{ij}^g=0$.

To solve the model (25), the weight coefficients $w_1$ and $w_2$ of the objectives are introduced here. By transforming Equations (25a) and (25b) into a single objective function through a linear weighting method [39], the multi-objective optimization model (25) can be transformed into the single-objective optimization model (26), i.e.,

$$\max \mathit{Z}=w_1\cdot {\displaystyle \sum _{i=1}^n{\displaystyle \sum _{j=1}^{{\alpha }_i}{\displaystyle \sum _{g=1}^{m}F{D}_{ij}^g{x}_{ij}^g}}}+w_2\cdot {\displaystyle \sum _{i=1}^n{\displaystyle \sum _{j=1}^{{\alpha }_i}{\displaystyle \sum _{g=1}^{m}S{D}_i^g{x}_{ij}^g}}}$$

(26a)

$$s.t.\{\begin{array}{ll}{\displaystyle \sum _{g=1}^m{x}_{ij}^g\le 1,}\hfill & i=1,2,\dots ,n;j=1,2,\dots ,a_i\hfill \\ {\displaystyle \sum _{i=1}^n{\displaystyle \sum _{j=1}^{{\alpha }_i}{x}_{ij}^g=d_g,}}\hfill & g=1,2,\dots ,m\hfill \\ x_{ij}^g=0 or 1,\hfill & i=1,2,\dots ,n;j=1,2,\dots ,{\alpha }_i,g=1,2,\dots ,m\hfill \end{array}$$

(26b)

In Model (26), $w_1$ and $w_2$ represent the weight or importance of the objectives Z₁ and Z₂, respectively, $0\le w_1,w_2\le 1$ and $w_1+w_2=1$. The objective function and constraints are linear, so integer programming method can be used to solve the model. In practice, the model can be solved by optimization software packages (e.g., Lingo17.0, Cplex12.0, etc.). Thus, the result of solving the optimization model is the optimal assignment scheme of rescuers.

In summary, the specific steps for solving the emergency rescuer assignment problem are as follows:

Step 1. The synergy matrix SR_i of rescuers is constructed using Equations (1)–(8).

Step 2. The competence degree matrix R_i of rescuers is constructed using Equations (9) and (10).

Step 3. The overall ability matrix CA_i of rescuers is constructed using Equation (11).

Step 4. The satisfaction degree matrix F of rescuers is constructed using Equations (12)–(20).

Step 5. The task fitness degree matrix FD_i of rescuers is constructed using Equation (21).

Step 6. The rescue time satisfaction matrix SD of rescuers is constructed Equations (22)–(24).

Step 7. The assignment model (Model (25)) of emergency rescuers is constructed, which is transformed into the single-objective optimization model (Model (26)) and solved to determine the optimal assignment scheme of emergency rescuers.

4. Illustrative Example

In this section, the use of the proposed model is illustrated by an example in the context of the rescuer assignment problem under public health emergencies.

4.1. Example Description

In the summer of 2022, an aggregated infectious event occurred in JX District (D), WH City, China. Faced with the huge workload of the unified coordination of prevention and control efforts and distribution of supplies, it was necessary to urgently mobilize rescuers from surrounding areas to assist in rescue tasks in the disaster area D. To give full play to the role of volunteers in deploy epidemic prevention and control work, the WH Youth Volunteer Association urgently recruited 16 volunteers to participate in the rescue tasks. The recruitment requirements mainly included the following: the volunteers should be 18–40 years old, in good health, and with relevant rescue experience; in the past month, the volunteers should have had no history of fever or other diseases or been in the same area at the same time as the confirmed case and asymptomatic infected person or their close contact; and the volunteer must definitely accept the dispatching order, execute the corresponding rescue task, and always take protective measures.

These recruited volunteers as rescuers come from four departure places, i.e., HY District (A₁), JA District (A₂), HS District (A₃), and CD District (A₄). The location of the disaster area and departure places are shown in Figure 4. The number of rescuers corresponding to the departure places are $a_1=4$, $a_2=5$, $a_3=4$, and $a_4=3$. There are five rescue tasks: publicity guidance (M₁), epidemic prevention and disinfection (M₂), data entry (M₃), material distribution (M₄), and psychological counseling (M₅). The number of rescuers required by the rescue tasks are d₁ = 3, d₂ = 4, d₃ = 3, d₄ = 4, and d₅ = 2.

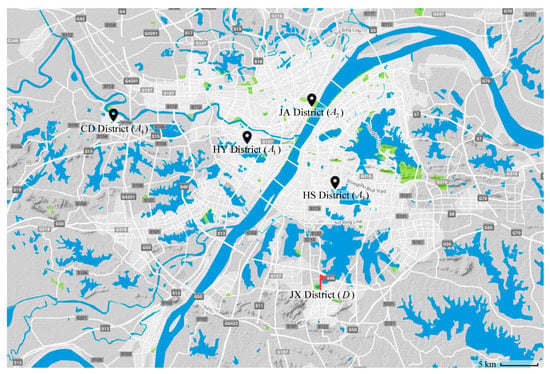
Figure 4. The location of the disaster area and departure places.

To reasonably assign rescuers, WH Youth Volunteer Association consulted emergency experts and combined with their experience, determined four evaluation indicators of personal skills: infectious disease protection ability (B₁), independent learning ability (B₂), psychological response and psychological assistance ability (B₃), and logistics service support ability (B₄). At the same time, four collaborative evaluation indicators of rescuers were determined: communication and coordination ability (C₁), team spirit (C₂), understanding ability (C₃), and emergency rescue experience (C₄). Emergency experts evaluated the performance of rescuers concerning different indicators according to a scale of 1–5 (1: worst; 5: best), and the evaluation values of personal skills and synergy ability are shown in Table 2 and Table 3, respectively. According to the historical synergistic cooperation between rescuers, the emergency experts used linguistic terms to give the evaluation values of the synergy effect between rescuers concerning rescue tasks, as shown in Table 4, Table 5, Table 6, Table 7 and Table 8. According to the actual needs of rescue tasks, the weights of personal skill evaluation indicators for each rescue task and the weights of collaborative evaluation indicators for each rescue task are given, as shown in Table 9 and Table 10.

Table 2. The evaluation values of rescuers concerning the personal skill indicators.

Pij	B1	B2	B3	B4
P11	4	3	4	4
P12	4	1	3	2
P13	3	4	5	3
P14	4	5	5	3
P21	2	4	3	4
P22	4	4	2	3
P23	3	3	4	2
P24	4	2	3	5
P25	5	5	2	3
P31	5	3	3	5
P32	2	1	4	3
P33	3	4	5	5
P34	5	2	4	5
P41	4	3	3	4
P42	2	5	5	4
P43	4	2	4	2

Table 3. The evaluation values of rescuers concerning the collaborative indicators.

Pij	C1	C2	C3	C4
P11	4	5	2	4
P12	3	1	4	5
P13	5	4	3	3
P14	3	2	5	3
P21	4	5	3	3
P22	1	4	4	3
P23	2	5	5	4
P24	4	4	3	2
P25	5	1	2	3
P31	4	2	3	5
P32	2	4	2	4
P33	4	3	1	5
P34	5	3	5	2
P41	4	3	3	5
P42	2	5	3	4
P43	3	3	4	2

Table 4. The evaluation values of the synergy effect between rescuers concerning M₁.

Pij	P11	P12	P13	P14	P21	P22	P23	P24	P25	P31	P32	P33	P34	P41	P42	P43
P11	-	VH	DH	H	DH	VL	DL	VH	H	DL	M	H	DH	VH	VL	H
P12		-	M	VL	M	DL	VL	H	L	L	DL	M	H	M	VL	null
P13			-	H	DH	VL	L	DH	H	H	VL	M	VL	VL	DL	L
P14				-	M	DL	L	VH	VL	M	VL	H	VH	VH	VL	M
P21					-	L	M	DH	VH	H	L	H	H	DH	DL	VL
P22						-	null	M	L	M	DL	L	H	M	VL	L
P23							-	M	M	VH	L	null	VH	M	null	M
P24								-	VH	M	M	L	L	VH	L	M
P25									-	H	L	M	DH	H	M	H
P31										-	M	DL	H	VH	VL	VL
P32											-	M	H	M	null	M
P33												-	DH	VH	L	L
P34													-	H	M	VH
P41														-	M	L
P42															-	M
P43																-

Table 5. The evaluation values of the synergy effect between rescuers concerning M₂.

Pij	P11	P12	P13	P14	P21	P22	P23	P24	P25	P31	P32	P33	P34	P41	P42	P43
P11	-	VH	H	VH	M	H	VH	DH	DH	VH	VL	L	M	H	DL	DH
P12		-	L	VH	VL	M	H	null	DH	H	M	M	H	VH	VL	H
P13			-	M	DL	H	L	M	H	H	DL	L	M	M	L	M
P14				-	VL	DH	VH	DH	VH	M	VL	VL	L	DH	DL	H
P21					-	null	DL	L	M	M	VL	L	H	VH	H	M
P22						-	VH	H	DH	VH	L	M	VH	H	VL	L
P23							-	M	M	H	H	VL	null	M	M	L
P24								-	DH	DH	H	M	M	DH	DH	VL
P25									-	DH	M	H	DH	DH	M	M
P31										-	VH	H	M	DH	L	H
P32											-	VL	M	L	DL	VL
P33												-	H	VH	null	H
P34													-	M	M	VH
P41														-	M	VH
P42															-	L
P43																-

Table 6. The evaluation values of the synergy effect between rescuers concerning M₃.

Pij	P11	P12	P13	P14	P21	P22	P23	P24	P25	P31	P32	P33	P34	P41	P42	P43
P11	-	VL	VH	H	VH	DH	VL	H	VH	H	L	DH	H	H	VH	M
P12		-	DL	VL	L	null	DL	H	L	M	M	H	M	H	VH	DL
P13			-	VH	H	H	L	VH	M	VH	H	M	M	L	H	L
P14				-	VH	M	M	H	M	H	M	M	H	null	M	VL
P21					-	VL	VL	VH	null	VH	M	VH	M	H	H	M
P22						-	VL	H	M	VH	H	H	M	M	H	L
P23							-	VH	M	H	H	VH	H	M	H	VL
P24								-	VH	H	M	VH	H	M	H	L
P25									-	VH	H	VH	H	H	M	DL
P31										-	M	DH	VH	VH	DH	L
P32											-	H	null	VH	M	M
P33												-	DH	H	VH	VL
P34													-	M	M	L
P41														-	H	M
P42															-	L
P43																-

Table 7. The evaluation values of the synergy effect between rescuers concerning M₄.

Pij	P11	P12	P13	P14	P21	P22	P23	P24	P25	P31	P32	P33	P34	P41	P42	P43
P11	-	L	H	VH	DH	null	H	M	VH	H	VL	M	M	H	VH	M
P12		-	VL	H	M	M	L	DL	M	VL	DL	L	DL	VL	H	DL
P13			-	DH	VH	H	M	L	M	H	VL	VH	M	VH	DH	M
P14				-	DH	DH	H	H	DH	VH	L	M	null	M	M	VL
P21					-	VH	H	L	H	H	M	M	VL	L	H	H
P22						-	VH	M	H	M	M	H	L	H	H	VL
P23							-	L	H	H	VL	M	L	H	null	M
P24								-	VH	M	DL	H	L	M	H	VL
P25									-	VH	M	M	VH	M	M	VL
P31										-	L	M	M	H	H	M
P32											-	H	null	L	M	M
P33												-	M	H	VH	M
P34													-	M	H	L
P41														-	VH	M
P42															-	H
P43																-

Table 8. The evaluation values of the synergy effect between rescuers concerning M₅.

Pij	P11	P12	P13	P14	P21	P22	P23	P24	P25	P31	P32	P33	P34	P41	P42	P43
P11	-	VH	DH	VH	VH	H	DH	VH	H	H	VH	DH	H	M	DH	H
P12		-	VH	H	H	M	H	H	M	L	M	VH	M	L	VH	VH
P13			-	VH	H	H	null	H	H	H	VH	DH	VH	M	DH	VH
P14				-	VH	M	DH	H	M	H	VH	DH	VH	null	VH	H
P21					-	L	M	H	M	L	M	null	M	L	VH	H
P22						-	M	null	VL	L	null	H	H	M	M	M
P23							-	H	H	H	VH	VH	H	M	DH	null
P24								-	M	M	M	H	M	L	VH	H
P25									-	VL	M	null	H	M	H	M
P31										-	VH	VH	H	M	VH	VH
P32											-	DH	DH	H	M	H
P33												-	VH	VH	H	M
P34													-	H	null	H
P41														-	VH	DH
P42															-	VH
P43																-

Table 9. The weights of personal skill evaluation indicators for rescue tasks.

Mg	B1	B2	B3	B4
M1	0.4	0.3	0.2	0.1
M2	0.4	0.2	-	0.4
M3	0.2	0.4	-	0.4
M4	0.4	0.1	-	0.5
M5	0.3	0.2	0.5	-

Table 10. The weights of collaborative evaluation indicators for rescue tasks.

Mg	C1	C2	C3	C4
M1	0.5	0.1	0.2	0.2
M2	0.2	0.2	0.3	0.3
M3	0.3	0.2	0.4	0.1
M4	0.3	0.3	0.2	0.2
M5	0.4	0.1	0.3	0.2

In addition, WH Youth Volunteer Association collected subjective preference evaluation information provided by rescuers by comprehensively considering the difficulty, safety factor, work cycle, and other factors of rescue tasks, as shown in Table 11. The time (unit: hour) for the rescuers to arrive at D and carry out the rescue tasks and the requirements of rescue tasks (unit: hour) for rescue time are shown in Table 12 and Table 13.

Table 11. The subjective preference evaluation information of rescuers for rescue tasks.

Pij	Ideal Preference Evaluation Relationship	Unknown Preference Evaluation Relationship	Imperfect Preference Evaluation Relationship
P11	$M_1\succ M_2=M_4$	M5	M3
P12	M3 ≻ M2	$M_4,M_5$	M1
P13	M3 ≻ M5	M1	M2 ≻ M4
P14	$M_3\succ M_2=M_5$	M4	M1
P21	M4 ≻ M1	M2	M5 ≻ M3
P22	M2 ≻ M4	$M_3,M_5$	M1
P23	M5 ≻ M3	$M_1,M_4$	M2
P24	$M_3\succ M_4=M_5$	M1	M2
P25	M1 = M3	$M_2,M_5$	M4
P31	M1 ≻ M4	$M_3$	M2 ≻ M5
P32	M2 ≻ M4	M1	M3 ≻ M5
P33	M3 = M4	$M_1,M_2$	M5
P34	M1 ≻ M3	$M_4,M_5$	M2
P41	M2 = M3	$M_1,M_5$	M4
P42	$M_5\succ M_1=M_2$	M4	M3
P43	M4 ≻ M3	$M_1,M_2$	M5

Table 12. The time for rescuers from departure places to arrive at the disaster area D and carry out the rescue tasks (unit: hour).

Ai	M1	M2	M3	M4	M5
A1	[1, 3]	[1, 2]	[2, 3]	[2, 2.5]	[1, 1.5]
A2	[1.5, 2.5]	[2, 3]	[1.5, 3]	[2, 3]	[2, 2.5]
A3	[0.5, 2]	[1.5, 2]	[0.5, 1]	[1, 2]	[1, 2]
A4	[1.5, 3]	[2, 4]	[2, 3]	[2, 3]	[1.5, 2]

Table 13. The requirements of rescue tasks for rescue time (unit: hour).

Mg	${\mathit{T}}_{\mathit{g}}^{\mathbf{1}}$	${\mathit{T}}_{\mathit{g}}^{\mathbf{2}}$	${\mathit{T}}_{\mathit{g}}^{\mathbf{max}}$	${\mathit{z}}^{\mathit{g}}$
M1	0.5	2.5	4	0.5
M2	1	3	5	0.6
M3	2	4	5	0.6
M4	1	3	4	0.7
M5	1	3	4	0.6

4.2. Resolution Process

Based on the model developed in this paper, the solution process of emergency rescuer assignment problem under public health emergencies is given below.

Firstly, the cooperative performance $S_{ij}^g$ of the rescuer P_ij concerning the rescue task M_g is calculated using Equations (1)–(5), as shown in Table 14.

Table 14. The cooperative performance of the rescuers.

Pij	M1	M2	M3	M4	M5
P11	0.5554	0.6045	0.6040	0.5340	0.7237
P12	0.3427	0.5178	0.3461	0.2884	0.5914
P13	0.4537	0.4158	0.5304	0.5611	0.6751
P14	0.4400	0.5452	0.4798	0.5889	0.6567
P21	0.5612	0.3460	0.5188	0.5710	0.5138
P22	0.2639	0.5551	0.4876	0.5244	0.4159
P23	0.3394	0.4627	0.4328	0.4677	0.5784
P24	0.5814	0.5980	0.6265	0.4033	0.5435
P25	0.5342	0.7082	0.5110	0.5818	0.4563
P31	0.4421	0.6520	0.6729	0.5352	0.5529
P32	0.3226	0.3374	0.4994	0.3048	0.6172
P33	0.4475	0.4121	0.6721	0.5349	0.6539
P34	0.6408	0.5274	0.5270	0.3515	0.6001
P41	0.5831	0.6703	0.5290	0.5157	0.5019
P42	0.2318	0.3249	0.6055	0.5930	0.6677
P43	0.3982	0.5079	0.2954	0.3730	0.6097

Secondly, the comprehensive synergy ability $R_{ij}^g$ of the rescuer P_ij is calculated using Equations (6) and (7), as shown in Table 15.

Table 15. The comprehensive synergy ability of the rescuers.

Pij	M1	M2	M3	M4	M5
P11	0.6583	0.6250	0.5917	0.7083	0.6083
P12	0.6000	0.6250	0.5500	0.5000	0.6250
P13	0.7417	0.6000	0.6833	0.6917	0.6917
P14	0.5417	0.5500	0.6333	0.4917	0.5917
P21	0.6417	0.6000	0.6583	0.6917	0.6167
P22	0.2917	0.4750	0.4833	0.4417	0.3667
P23	0.5583	0.7500	0.7417	0.7083	0.6333
P24	0.5500	0.4500	0.5750	0.5500	0.5250
P25	0.6167	0.3750	0.4333	0.4167	0.5417
P31	0.7000	0.6500	0.5750	0.6000	0.6750
P32	0.3833	0.4750	0.3917	0.4833	0.3833
P33	0.6250	0.5500	0.4250	0.5750	0.5500
P34	0.7500	0.6000	0.8000	0.6500	0.7500
P41	0.7250	0.7000	0.6250	0.6750	0.7000
P42	0.4583	0.6000	0.5417	0.6083	0.4833
P43	0.4500	0.4250	0.5500	0.4500	0.4750

Then, the synergy degree matrix SR_i of rescuers is constructed using Equation (8). Here, it is assumed that the coordination performance of rescuers and the comprehensive synergy ability of rescuers are equally important, i.e., ζ = 0.5.

$$\mathbf{S}{\mathbf{R}}_1=\left[\begin{array}{ccccc}0.6069& 0.6148& 0.5979& 0.6212& 0.6660\\ 0.4714& 0.5714& 0.4481& 0.3942& 0.6082\\ 0.5977& 0.5079& 0.6069& 0.6264& 0.6834\\ 0.4909& 0.5476& 0.5566& 0.5403& 0.6242\end{array}\right]$$

$$\mathbf{S}{\mathbf{R}}_2=\left[\begin{array}{ccccc}0.6015& 0.4730& 0.5886& 0.6314& 0.5653\\ 0.2778& 0.5151& 0.4855& 0.4831& 0.3913\\ 0.4489& 0.6064& 0.5873& 0.5880& 0.6059\\ 0.5657& 0.5240& 0.6008& 0.4767& 0.5343\\ 0.5755& 0.5416& 0.4722& 0.4993& 0.4990\end{array}\right]$$

$$\mathbf{S}{\mathbf{R}}_3=\left[\begin{array}{ccccc}0.5711& 0.6510& 0.6240& 0.5676& 0.6140\\ 0.3530& 0.4062& 0.4456& 0.3941& 0.5003\\ 0.5363& 0.4811& 0.5486& 0.5550& 0.6020\\ 0.6954& 0.5637& 0.6635& 0.5008& 0.6751\end{array}\right]$$

$$\mathbf{S}{\mathbf{R}}_4=\left[\begin{array}{ccccc}0.6541& 0.6852& 0.5770& 0.5954& 0.6010\\ 0.3451& 0.4625& 0.5736& 0.6007& 0.5755\\ 0.4241& 0.4665& 0.4227& 0.4115& 0.5424\end{array}\right]$$

Furthermore, the competence degree matrix R_i of rescuers is constructed using Equations (9) and (10), i.e.,

$${\mathbf{R}}_1=\left[\begin{array}{ccccc}0.6167& 0.6333& 0.6000& 0.6500& 0.6333\\ 0.3333& 0.2667& 0.1333& 0.2667& 0.3667\\ 0.5917& 0.4167& 0.5000& 0.3750& 0.7500\\ 0.8000& 0.6000& 0.6667& 0.5333& 0.9000\end{array}\right]$$

$${\mathbf{R}}_2=\left[\begin{array}{ccccc}0.3583& 0.4167& 0.5667& 0.4083& 0.3167\\ 0.5250& 0.5500& 0.5667& 0.5083& 0.3500\\ 0.4167& 0.2333& 0.2667& 0.1833& 0.5333\\ 0.5083& 0.7167& 0.6333& 0.7917& 0.4167\\ 0.7333& 0.7333& 0.7333& 0.6667& 0.5000\end{array}\right]$$

$${\mathbf{R}}_3=\left[\begin{array}{ccccc}0.7167& 0.9000& 0.8000& 0.9500& 0.5667\\ 0.1667& 0.1333& 0.1333& 0.1667& 0.3333\\ 0.6583& 0.6833& 0.7667& 0.7083& 0.7500\\ 0.7083& 0.8500& 0.7000& 0.9250& 0.6833\end{array}\right]$$

$${\mathbf{R}}_4=\left[\begin{array}{ccccc}0.5500& 0.6333& 0.6000& 0.6500& 0.4667\\ 0.5667& 0.4667& 0.6667& 0.4333& 0.7000\\ 0.4750& 0.3167& 0.2333& 0.2917& 0.5833\end{array}\right]$$

The overall ability matrix CA_i of rescuers is constructed using Equation (11). Here, it is assumed that the competence degrees of rescuers and the synergy degrees of rescuers are equally important, i.e., σ = 0.5.

$$\mathbf{C}{\mathbf{A}}_1=\left[\begin{array}{ccccc}0.6118& 0.6240& 0.5989& 0.6356& 0.6497\\ 0.4023& 0.4190& 0.2907& 0.3304& 0.4874\\ 0.5947& 0.4623& 0.5534& 0.5007& 0.7167\\ 0.6454& 0.5738& 0.6116& 0.5368& 0.7621\end{array}\right]$$

$$\mathbf{C}{\mathbf{A}}_2=\left[\begin{array}{ccccc}0.4799& 0.4448& 0.5776& 0.5198& 0.4410\\ 0.4014& 0.5325& 0.5261& 0.4957& 0.3707\\ 0.4328& 0.4198& 0.4270& 0.3857& 0.5696\\ 0.5370& 0.6203& 0.6170& 0.6342& 0.4755\\ 0.6544& 0.6375& 0.6027& 0.5830& 0.4995\end{array}\right]$$

$$\mathbf{C}{\mathbf{A}}_3=\left[\begin{array}{ccccc}0.6439& 0.7755& 0.7120& 0.7588& 0.5903\\ 0.2598& 0.2698& 0.2894& 0.2804& 0.4168\\ 0.5973& 0.5822& 0.6576& 0.6316& 0.6760\\ 0.7019& 0.7069& 0.6818& 0.7129& 0.6792\end{array}\right]$$

$$\mathbf{C}{\mathbf{A}}_4=\left[\begin{array}{ccccc}0.6020& 0.6592& 0.5885& 0.6227& 0.5338\\ 0.4559& 0.4646& 0.6201& 0.5170& 0.6378\\ 0.4496& 0.3916& 0.3280& 0.3516& 0.5628\end{array}\right]$$

The satisfaction degree matrix F of rescuers is obtained using Equations (12)–(20), i.e.,

$$\mathbf{F}=\left[\begin{array}{ccccc}0.3771& 0.5791& 0.8044& 0.3457& 0.5813\\ 0.5034& 0.4019& 0.6597& 0.5958& 0.5964\\ 0.8345& 0.4194& 0.6574& 0.7649& 0.0815\\ 0.5557& 0.7049& 0.5596& 0.4483& 0.5000\end{array}\right]$$

On this basis, the task fitness degree matrix FD_i of rescuers is obtained using Equation (21). Here, it is assumed that the satisfaction degrees of rescuers and the overall ability of rescuers are equally important (θ = 0.5), and the threshold value of the overall ability of rescuers is $\tau =0.3$.

$$\mathbf{F}{\mathbf{D}}_1=\left[\begin{array}{ccccc}0.4944& 0.6015& 0.7016& 0.4906& 0.6155\\ 0.3897& 0.4990& 0& 0.3381& 0.5344\\ 0.4859& 0.5207& 0.6789& 0.4232& 0.6490\\ 0.5113& 0.5764& 0.7080& 0.4412& 0.6717\end{array}\right]$$

$$\mathbf{F}{\mathbf{D}}_2=\left[\begin{array}{ccccc}0.4916& 0.4234& 0.6187& 0.5578& 0.5187\\ 0.4524& 0.4672& 0.5929& 0.5457& 0.4835\\ 0.4681& 0.4109& 0.5433& 0.4907& 0.5830\\ 0.5202& 0.5111& 0.6383& 0.6150& 0.5359\\ 0.5789& 0.5197& 0.6312& 0.5894& 0.5480\end{array}\right]$$

$$\mathbf{F}{\mathbf{D}}_3=\left[\begin{array}{ccccc}0.7392& 0.5974& 0.6847& 0.7619& 0.3359\\ 0& 0& 0& 0& 0.2491\\ 0.7159& 0.5008& 0.6575& 0.6983& 0.3787\\ 0.7682& 0.5631& 0.6696& 0.7389& 0.3803\end{array}\right]$$

$$\mathbf{F}{\mathbf{D}}_4=\left[\begin{array}{ccccc}0.5788& 0.6821& 0.5741& 0.5355& 0.5169\\ 0.5058& 0.5847& 0.5899& 0.4826& 0.5689\\ 0.5026& 0.5482& 0.4438& 0.3999& 0.5314\end{array}\right]$$

Afterwards, the time satisfaction matrix SD of rescuers is constructed using Equations (22)–(24). Here, it is assumed that the values of the parameters in the time satisfaction function are g₁ = 2 and g₂ = 0.5.

$$\mathbf{S}\mathbf{D}=\left[\begin{array}{ccccc}0.4592& 0.7167& 0.7167& 0.7219& 0.7542\\ 0.5208& 0.6167& 0.8111& 0.7125& 0.6292\\ 0.6094& 0.6792& 1& 0.7875& 0.7167\\ 0.4126& 0.4790& 0.7167& 0.7125& 0.6792\end{array}\right]$$

Based on Model (25), the model is converted into a single-objective optimization model (Model (26)) for solution. Considering that decision makers pay more attention to rescue time in the emergency rescue process of public health emergencies, the weighting coefficients of the objectives are $w_1=0.4$ and $w_2=0.6$. The assignment scheme of emergency rescuers is obtained by using Lingo 17.0 to solve the emergency rescuer assignment model is shown in Figure 5. The specific assignment scheme is as follows: the rescuers $P_{11},P_{12},P_{13},P_{14}$ in the departure place A₁ are assigned to perform the rescue task M₂; the rescuers $P_{21},P_{22},P_{24}$ in the departure place A₂ and the rescuer P₄₁ in the departure place A₄ are assigned to perform the rescue task M₄; the rescuers $P_{23},P_{25}$ in the departure place A₂ and the rescuer P₃₄ in the departure place A₃ are assigned to perform the rescue task M₁; the rescuers $P_{31},P_{32},P_{33}$ in the departure place A₃ are assigned to perform the rescue task M₃; and the rescuers $P_{42},P_{43}$ in the departure place A₄ are assigned to perform the rescue task M₅. The rescuers performing the rescue tasks $M_1,M_2,M_3,M_4,M_5$ are formed into the rescue teams $G_1,G_2,G_3,G_4,G_5$, respectively.

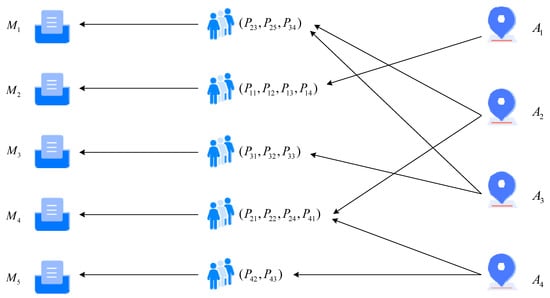
Figure 5. The rescuer assignment scheme.

4.3. Comparative Analysis

To further illustrate the advantages of the proposed model, it is compared with a similar model proposed by Li et al. [40]. Based on the background and raw data of the illustrative example in this paper, the model proposed by Li et al. [40] is used to construct the rescuer assignment model, and the assignment result obtained is shown in Table 16. As can be seen from Table 16, the rescuers $P_{11},P_{14},P_{21},P_{24},P_{34},P_{43}$ are assigned to perform the same rescue tasks in the results of the two methods. However, other rescuers were assigned different rescue tasks, and the model proposed in this paper obtained the higher objective value Z than the model proposed by Li et al. [40]. The main reasons for the differences between the two methods include three aspects:

Table 16. The rescuer assignment results of different models.

Models	M1	M2	M3	M4	M5	Z
The model proposed by Li et al. [40]	$P_{12},P_{32},P_{34}$	$P_{11},P_{14},P_{22},P_{41}$	$P_{13},P_{25},P_{42}$	$P_{21},P_{24},P_{31},P_{33}$	$P_{23},P_{43}$	10.3931
The model proposed in this paper	$P_{23},P_{25},P_{34}$	$P_{11},P_{12},P_{13},P_{14}$	$P_{31},P_{32},P_{33}$	$P_{21},P_{22},P_{24},P_{41}$	$P_{42},P_{43}$	10.5194

(1)

In terms of the evaluation of rescuer ability, Li et al. [40] obtained the rescuer ability by aggregating the evaluation values of skill indicators, while the model proposed in this paper considers not only rescuer skill level but also the synergy effect between two rescuers and synergy ability of the rescuer, making the assignment result more accurate and comprehensive.

(2)

In terms of the satisfaction degrees of rescuers, Li et al. [40] used a linear form of satisfaction function to calculate satisfaction degrees based on preference ordinal numbers, while this paper considers four preference relations with incomplete preference information, uses an evidential reasoning method to calculate the satisfaction degrees, and considers the subjective attitude of the decision maker, which is more realistic.

(3)

In terms of rescue time satisfaction, Li et al. [40] used linear time satisfaction function, ignoring the problem of disaster change over time in emergency rescue. However, this paper uses a time satisfaction function, which can better reflect the timeliness of emergency rescue.

5. Conclusions

In view of the problem of emergency decision making, a model for the assignment of emergency rescuers considering collaborative information is proposed. Firstly, the synergy degrees of rescuers are calculated based on the evaluation values of the synergy effect and the synergy ability. Secondly, the competence degrees of rescuers are calculated, and the overall ability of each rescuer is obtained. Then, the satisfaction degrees of rescuers are obtained according to the subjective preferences provided by rescuers, and the task fitness degrees are obtained. Further, the satisfaction of rescue time is obtained based on the travel time of rescuers and the time requirement of each rescue task. Afterwards, an assignment model of emergency rescuers is developed, and the optimal assignment scheme can be obtained through solving the model.

The model proposed in this paper has obvious advantages and characteristics compared with the existing models, which are mainly reflected in the following three aspects: (1) The model constructed in this paper considers the collaborative information about rescuers from the perspectives of synergy effect and synergy capability, which makes up for the limitations of the traditional rescuer assignment model that does not consider collaborative information or only considers synergy ability, helps to improve the rationality of the rescuer assignment scheme, and provides a new idea and method for solving the rescuer assignment problem. (2) The problem of emergency rescuer assignment is studied from the perspective of two-sided matching, which overcomes the shortcomings of one-way assignment (considering only the requirements of rescue tasks). This paper considers not only the requirements of rescue tasks for rescuers but also the preferences of rescuers for rescue tasks, which is conducive to improving the subjective willingness of rescuers and also helps to dispatch suitable rescuers from social organizations to perform rescue tasks and improve rescue effects. (3) The model proposed in this paper takes into account the collaborative information concerning rescuers, the competence degrees of rescuers for rescue tasks, the subjective preferences of rescuers, the time requirements of different rescue tasks, the rescue time satisfaction, and the number of rescuers required by different rescue tasks. Considering the influence of different factors on the assignment decision is not only more suitable for the actual situation of emergency rescue but can also improve the accuracy of the assignment decision. The model is suitable for guiding the emergency rescuer assignment and provides a reference for the sustainable development of emergency rescue.

In addition, this paper provides a number of managerial insights as described below. (1) Establish and improve the emergency rescue coordination mechanism. Emergency rescue work involves multiple subjects, and the rescue effect is affected by the synergy ability and synergy effect of rescuers. Therefore, it is necessary to carry out the overall layout from the aspects of coordination concept and coordination ability. The emergency management department should regularly organize cross-sector and cross-industry emergency practice drills, strengthen the training of rescuers’ rescue capabilities, enhance the synergy ability, and establish and improve the cooperative rescue system and mechanism. (2) Stimulate the enthusiasm of rescuers and make full use of their talents. Since rescuers have diverse personal characteristics, especially the rescuers from social organizations, they have different preferences for rescue tasks. Meeting the preferences of rescuers can increase their enthusiasm and promote the rescue work. Therefore, in the assignment of rescuers, not only the requirements of the rescue task on site, but also the preferences of rescuers should be considered. On this basis, the indicators required by rescue tasks for rescuers are set to make full use of their talents and maximize the actual effectiveness of rescuers. (3) Construct an emergency rescue service platform. In the era of big data, it is necessary to pool the efforts of relevant departments and industries to construct an emergency rescue service platform to better support emergency rescue work. The platform should collect the requirements of historical rescue task and the preferences of rescuers, and provide support for rescuer assignment decisions, so as to achieve resource information integration and sharing.

In future research work, the complex characteristics of rescue tasks and the diversified characteristics of rescuers can be further considered based on the application scenarios of different emergencies. In addition, other factors may also affect the results of rescuer assignment in real life [41,42]. Therefore, in order to further improve the accuracy of the assignment decisions, the proposed model can be expanded based on more factors.