Frequency Stability Enhancement Using Differential-Evolution- and Genetic-Algorithm-Optimized Intelligent Controllers in Multiple Virtual Synchronous Machine Systems
Abstract
:1. Introduction
1.1. Background and Motivation
1.2. Literature Review
1.3. Contribution
- With multiple VSIMA, frequency and grid stability is improved.
- With the proposed fuzzy proportional integral derivative (FPID) controllers optimized by DE using multiple VISMAs, the dynamic performance of the grid increases.
- The work showed better damping of grid oscillations in cases of multiple VISMAs with DE than in single VISMAs.
- Compared to the previous work in [8] using eigenvalue analysis, with the proposed method, the overshoot of change in frequency is reduced by 0.14999, and the undershoot of change in frequency is reduced by 0.1485.
2. Materials and Methods
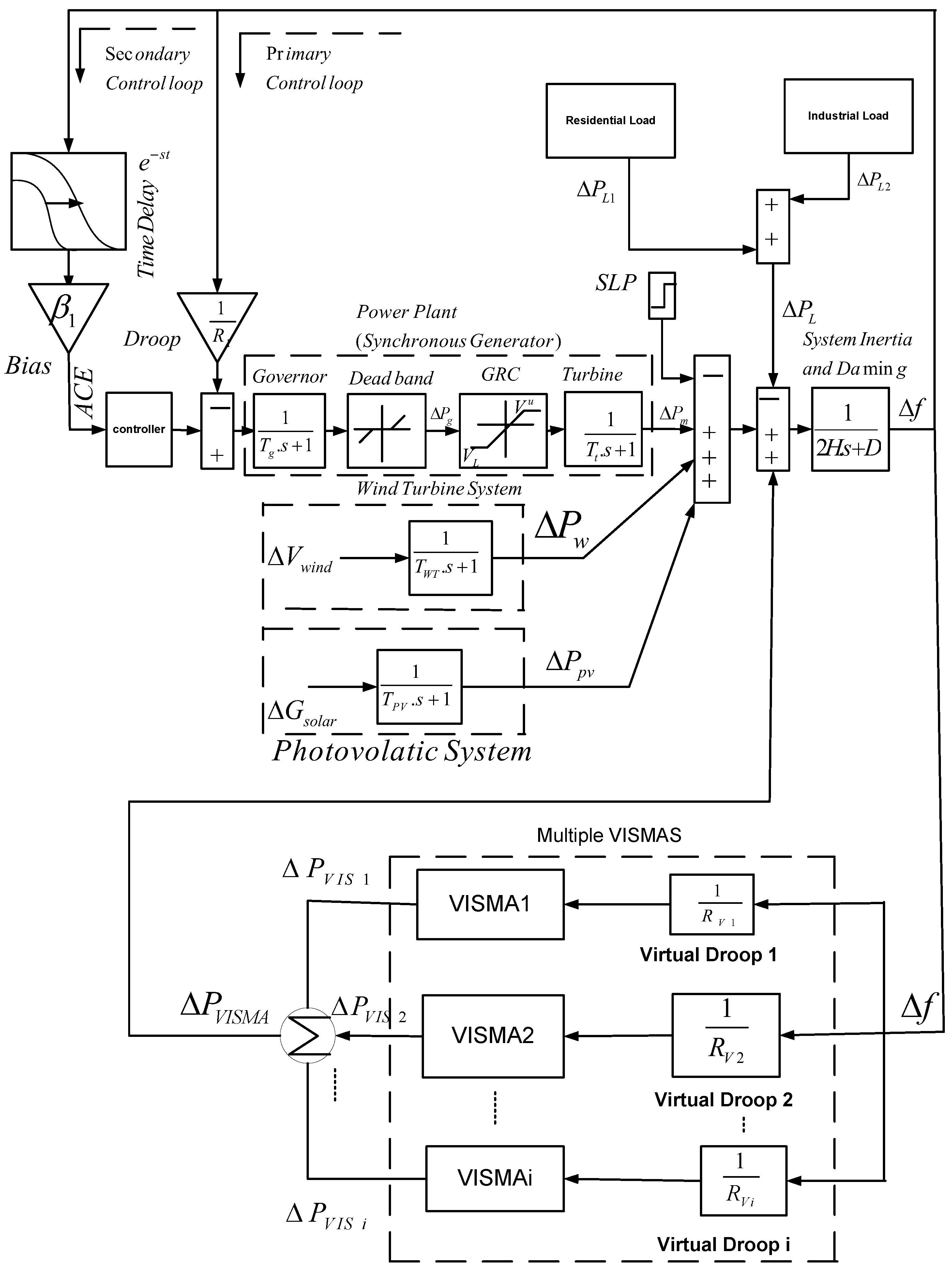
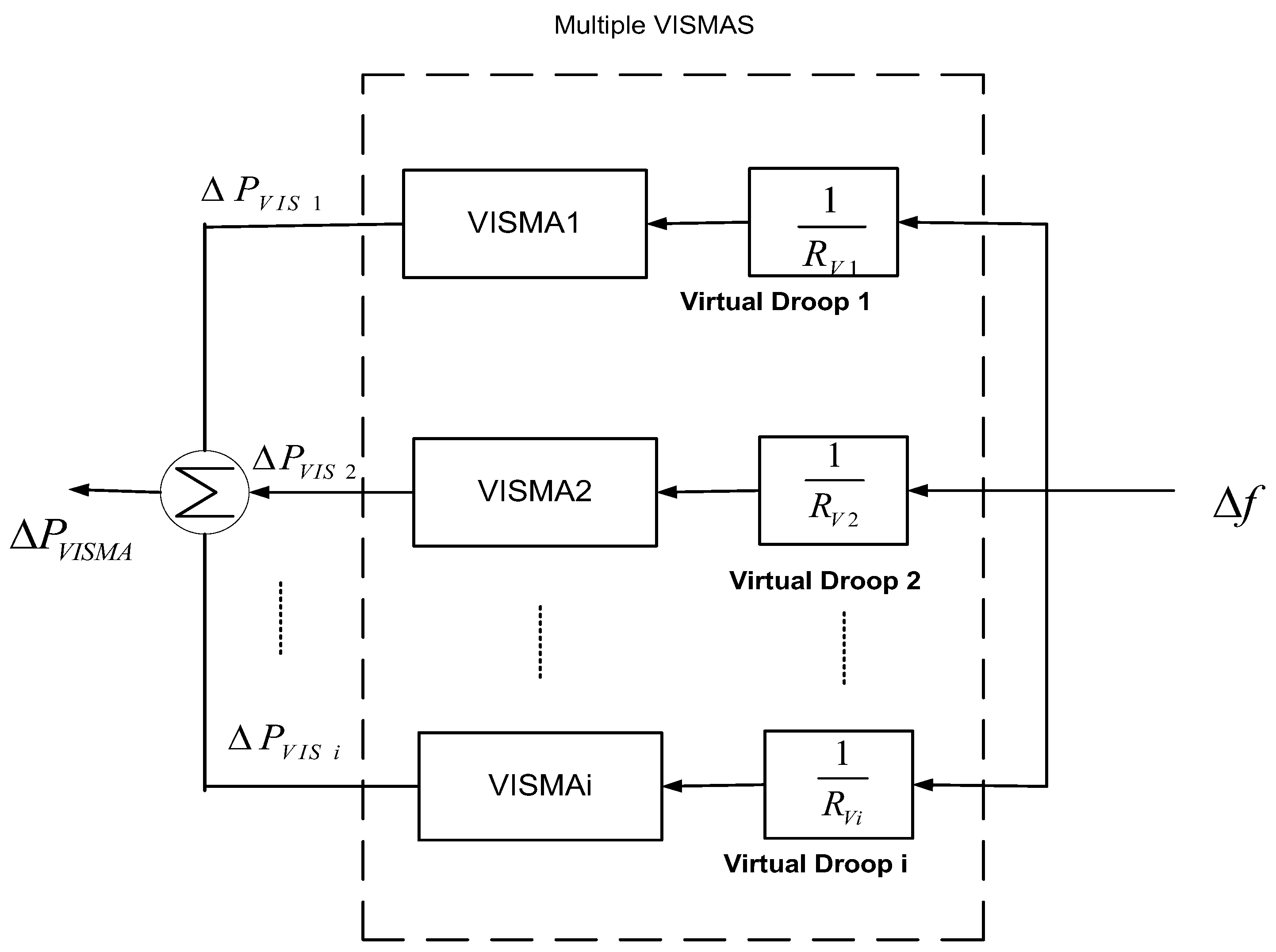
2.1. Power System Equations
2.2. Different Objective Function Analysis
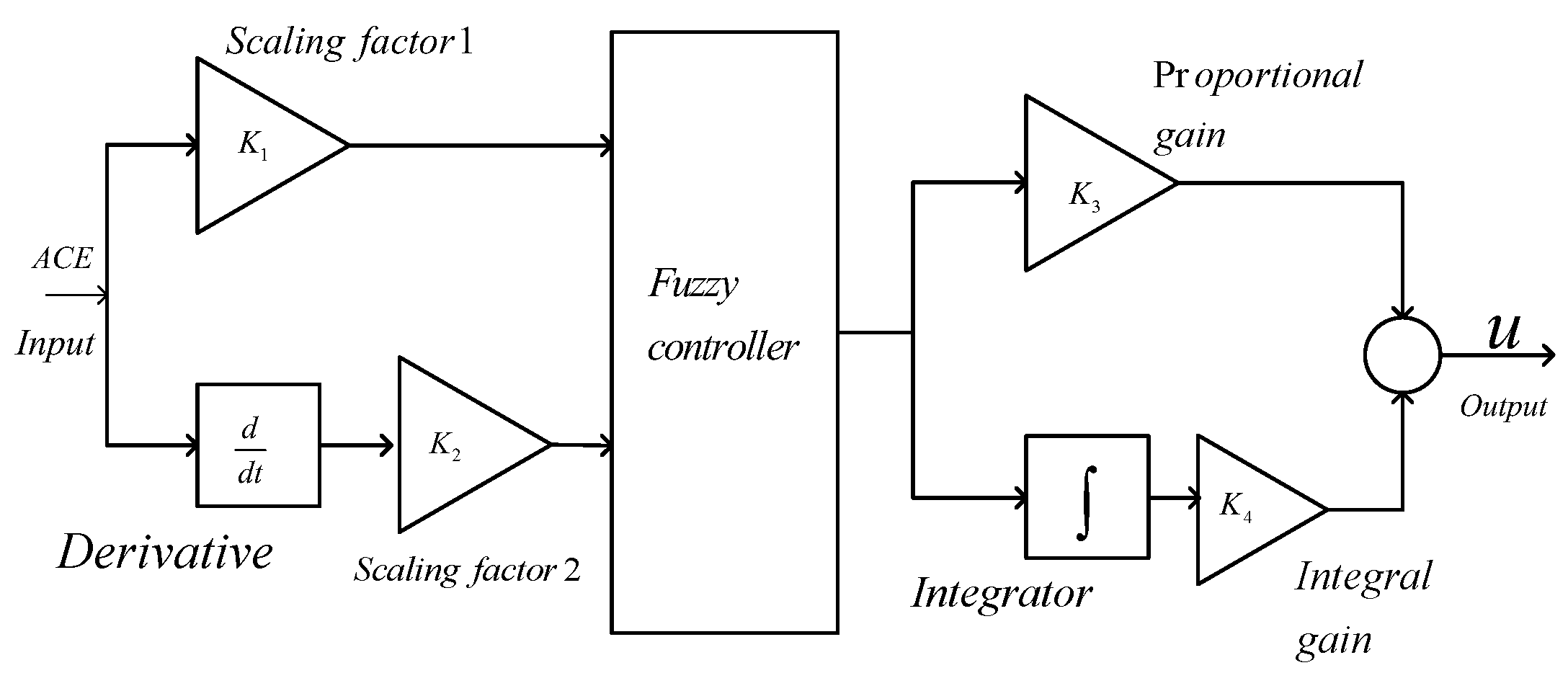
2.3. Fuzzy Logic Controller
2.4. Optimization Problem
2.4.1. Genetic Algorithm
2.4.2. Differential Evolution
Initialization
Mutation
Crossover
Selection and Stop Criteria
3. Result Analysis and Discussion
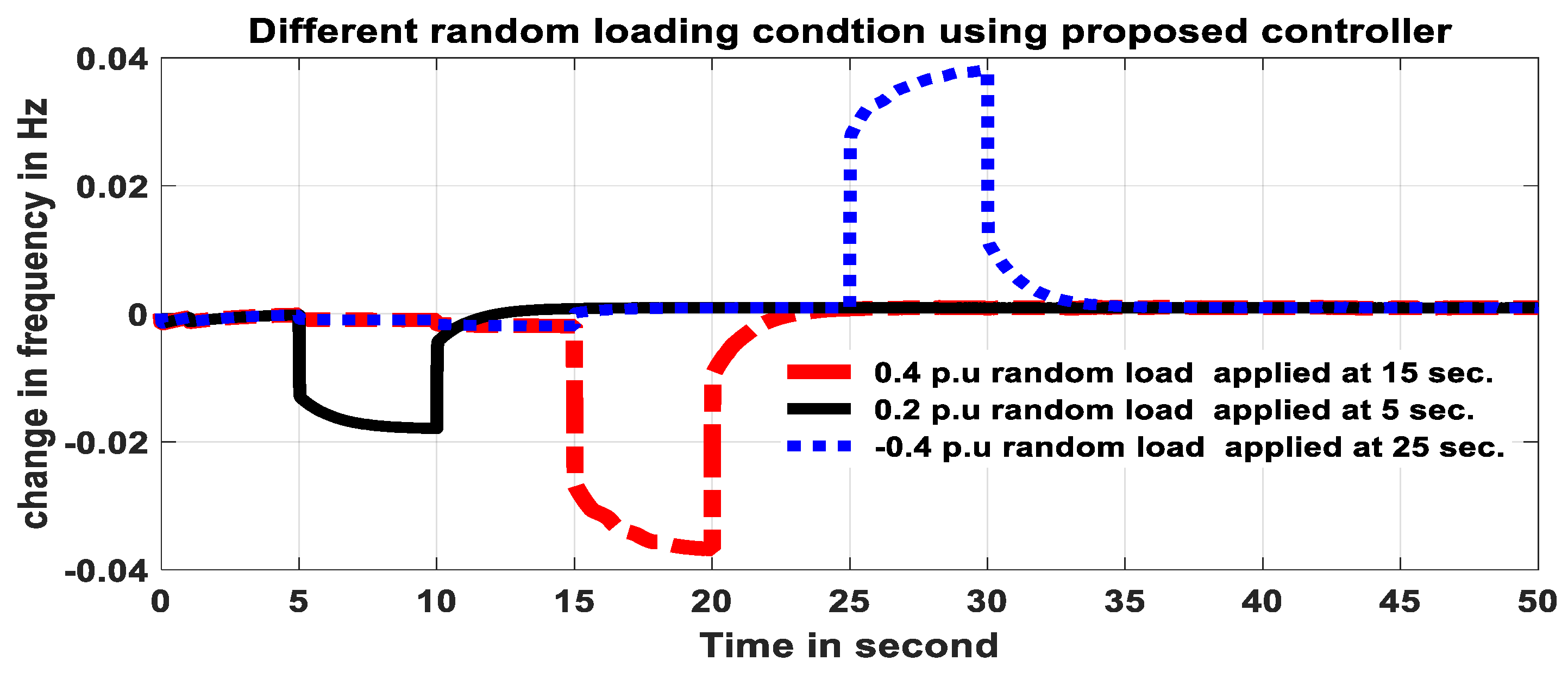
3.1. Results Analysis and Discussion on Random Load Change
3.2. Discussion on Result Comparison with Classic Control and Other Studies
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Cheema, K.M.; Chaudhary, N.I.; Tahir, M.F.; Mehmood, K.; Mudassir, M.; Kamran, M.; Milyani, A.H.; Elbarbary, Z.S. Virtual synchronous generator: Modifications, stability assessment and future applications. Energy Rep. 2022, 8, 1704–1717. [Google Scholar] [CrossRef]
- Bevrani, H.; Ise, T.; Miura, Y. Virtual synchronous generators: A survey and new perspectives. Int. J. Electr. Power Energy Syst. 2014, 54, 244–254. [Google Scholar] [CrossRef]
- Zhong, Q.C. Virtual synchronous machines: A unified interface for smart grid integration. IEEE Power Electron. Mag. 2016, 3, 18–27. [Google Scholar] [CrossRef]
- Petti, J. Virtual Synchronous Machine Phase Synchronization. Ph.D. Thesis, University of Pittsburgh, Pittsburgh, PA, USA, 2018. [Google Scholar]
- Gaur, P.; Singh, S. Investigations on issues in microgrids. J. Clean Energy Technol. 2017, 5, 47–51. [Google Scholar] [CrossRef]
- Martins, F.J.N. Virtual Synchronous Machine. TecnicoLisboa, ULisboa, 2016. Available online: https://fenix.tecnico.ulisboa.pt/downloadFile/395145918861/paper.pdf (accessed on 1 March 2020).
- Li, L.; Li, H.; Tseng, M.L.; Feng, H.; Chiu, A.S. Renewable energy system on frequency stability control strategy using virtual synchronous generator. Symmetry 2020, 12, 1697. [Google Scholar] [CrossRef]
- Kerdphol, T.; Rahman, F.S.; Watanabe, M.; Mitani, Y.; Hongesombut, K.; Phunpeng, V.; Ngamroo, I.; Turschner, D. Small-signal analysis of multiple virtual synchronous machines to enhance frequency stability of grid-connected high renewables. IET Gener. Transm. Distrib. 2021, 15, 1273–1289. [Google Scholar] [CrossRef]
- D’Arco, S.; Suul, J.A.; Fosso, O.B. A Virtual Synchronous Machine implementation for distributed control of power converters in SmartGrids. Electr. Power Syst. Res. 2015, 122, 180–197. [Google Scholar] [CrossRef]
- Yang, L.; Ma, J.; Wang, S.; Liu, T.; Wu, Z.; Wang, R.; Tang, L. The strategy of active grid frequency support for virtual synchronous generator. Electronics 2021, 10, 1131. [Google Scholar] [CrossRef]
- Chen, Y.; Hesse, R.; Turschner, D.; Beck, H.P. Dynamic properties of the virtual synchronous machine (VISMA). Proc. Icrepq 2011, 11, 755–759. [Google Scholar] [CrossRef]
- Tayyebi, A.; Groß, D.; Anta, A.; Kupzog, F.; Dörfler, F. Frequency stability of synchronous machines and grid-forming power converters. IEEE J. Emerg. Sel. Top. Power Electron. 2020, 8, 1004–1018. [Google Scholar] [CrossRef]
- Zhong, C.; Li, H.; Zhou, Y.; Lv, Y.; Chen, J.; Li, Y. Virtual synchronous generator of PV generation without energy storage for frequency support in autonomous microgrid. Int. J. Electr. Power Energy Syst. 2022, 134, 107343. [Google Scholar] [CrossRef]
- Zhang, G.; Yang, J.; Wang, H.; Cui, J. Presynchronous grid-connection strategy of virtual synchronous generator based on virtual impedance. Math. Probl. Eng. 2020, 2020, 3690564. [Google Scholar] [CrossRef]
- Miao, H.; Mei, F.; Yang, Y.; Chen, H.; Zheng, J. A comprehensive VSM control strategy designed for unbalanced grids. Energies 2019, 12, 1169. [Google Scholar] [CrossRef]
- Adefarati, T.; Bansal, R.C. Integration of renewable distributed generators into the distribution system: A review. IET Renew. Power Gener. 2016, 10, 873–884. [Google Scholar] [CrossRef]
- Tamrakar, U.; Shrestha, D.; Maharjan, M.; Bhattarai, B.P.; Hansen, T.M.; Tonkoski, R. Virtual inertia: Current trends and future directions. Appl. Sci. 2017, 7, 654. [Google Scholar] [CrossRef]
- Abuagreb, M.; Allehyani, M.F.; Johnson, B.K. Overview of Virtual Synchronous Generators: Existing Projects, Challenges, and Future Trends. Electronics 2022, 11, 2843. [Google Scholar] [CrossRef]
- Magdy, G.; Bakeer, A.; Nour, M.; Petlenkov, E. A new virtual synchronous generator design based on the SMES system for frequency stability of low-inertia power grids. Energies 2020, 13, 5641. [Google Scholar] [CrossRef]
- Sang, W.; Guo, W.; Dai, S.; Tian, C.; Yu, S.; Teng, Y. Virtual Synchronous Generator, a Comprehensive Overview. Energies 2022, 15, 6148. [Google Scholar] [CrossRef]
- Li, C.; Yang, Y.; Cao, Y.; Wang, L.; Blaabjerg, F. Frequency and voltage stability analysis of grid-forming virtual synchronous generator attached to weak grid. IEEE J. Emerg. Sel. Top. Power Electron. 2020, 10, 2662–2671. [Google Scholar] [CrossRef]
- Gunasekara, R.; Muthumuni, D.; Filizadeh, S.; Kho, D.; Marshall, B.; Ponnalagan, B.; Adeuyi, O.D. A novel virtual synchronous machine implementation and verification of its effectiveness to mitigate renewable generation connection issues at weak transmission grid locations. IET Renew. Power Gener. 2023, 17, 2436–2457. [Google Scholar] [CrossRef]
- Lu, L.; Cutululis, N.A. Virtual synchronous machine control for wind turbines: A review. In Journal of Physics: Conference Series; IOP Publishing: Bristol, UK, 2019; Volume 1356, p. 012028. [Google Scholar]
- Dewenter, T.; Heins, W.; Werther, B.; Hartmann, A.K.; Bohn, C.; Beck, H.P. Parameter Optimisation of a Virtual Synchronous Machine in a Microgrid. arXiv 2016, arXiv:1606.07357. [Google Scholar]
- Wen, T.; Zhu, D.; Zou, X.; Jiang, B.; Peng, L.; Kang, Y. Power coupling mechanism analysis and improved decoupling control for virtual synchronous generator. IEEE Trans. Power Electron. 2020, 36, 3028–3041. [Google Scholar] [CrossRef]
- Shi, R.; Zhang, X.; Hu, C.; Xu, H.; Gu, J.; Cao, W. Self-tuning virtual synchronous generator control for improving frequency stability in autonomous photovoltaic-diesel microgrids. J. Mod. Power Syst. Clean Energy 2018, 6, 482–494. [Google Scholar] [CrossRef]
- Feleke, S.; Satish, R.; Pydi, B.; Anteneh, D.; Abdelaziz, A.Y.; El-Shahat, A. Damping of Frequency and Power System Oscillations with DFIG Wind Turbine and DE Optimization. Sustainability 2023, 15, 4751. [Google Scholar] [CrossRef]
- Rahman, F.S.; Kerdphol, T.; Watanabe, M.; Mitani, Y. Optimization of virtual inertia considering system frequency protection scheme. Electr. Power Syst. Res. 2019, 170, 294–302. [Google Scholar] [CrossRef]
- Liu, D. Cluster control for EVS participating in grid frequency regulation by using virtual synchronous machine with optimized parameters. Appl. Sci. 2019, 9, 1924. [Google Scholar] [CrossRef]
- Niu, S.; Qu, L.; Lin, H.C.; Fang, W. Effective virtual inertia control using inverter optimization method in renewable energy generation. Energy Explor. Exploit. 2021, 39, 2103–2125. [Google Scholar] [CrossRef]
- Feleke, S.; Satish, R.; Tatek, W.; Abdelaziz, A.Y.; El-Shahat, A. DE-Algorithm-Optimized Fuzzy-PID Controller for AGC of Integrated Multi Area Power System with HVDC Link. Energies 2022, 15, 6174. [Google Scholar] [CrossRef]
- Feleke, S.; Pydi, B.; Satish, R.; Anteneh, D.; AboRas, K.M.; Kotb, H.; Alharbi, M.; Abuagreb, M. DE-Based Design of an Intelligent and Conventional Hybrid Control System with IPFC for AGC of Interconnected Power System. Sustainability 2023, 15, 5625. [Google Scholar] [CrossRef]
- Trillas, E.; Lotfi, A. Zadeh: On the man and his work. ScientiaIranica 2011, 18, 574–579. [Google Scholar]
- Justice, A.V.; Kathyaini, C. Controlling of nonlinear systems by using fuzzy logic controller. Int. Res. J. Eng. Technol. 2015, 2, 648–656. [Google Scholar]
- Pothiya, S.; Ngamroo, I.; Runggeratigul, S.; Tantaswadi, P. Design of optimal fuzzy logic based PI controller using multiple tabu search algorithm for load frequency control. Int. J. Control Autom. Syst. 2006, 4, 155–164. [Google Scholar]
- Storn, R.; Price, K. Differential evolution—A simple and efficient heuristic for global optimization over continuous spaces. J. Glob. Optim. 1997, 11, 341–359. [Google Scholar] [CrossRef]
- Rehman, H.U.; Yan, X.; Abdelbaky, M.A.; Jan, M.U.; Iqbal, S. An advanced virtual synchronous generator control technique for frequency regulation of grid-connected PV system. Int. J. Electr. Power Energy Syst. 2021, 125, 106440. [Google Scholar] [CrossRef]





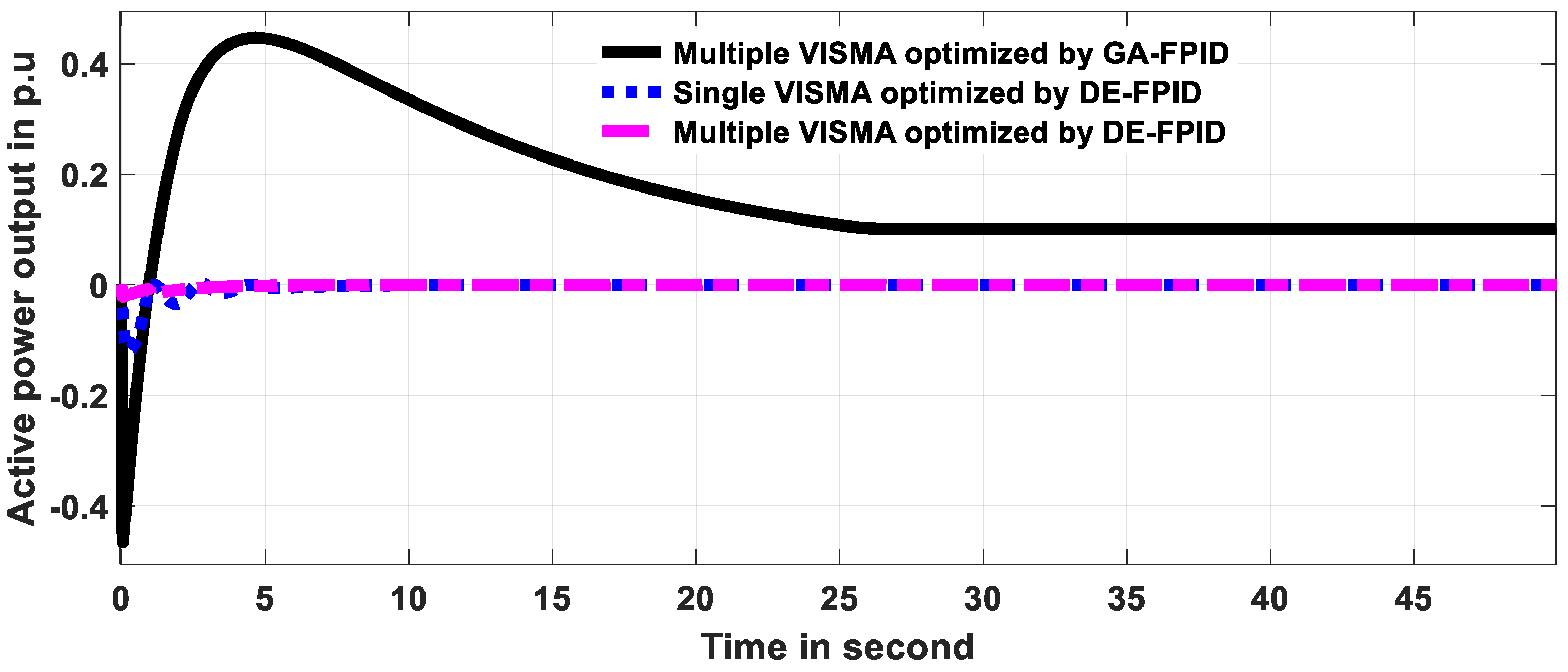
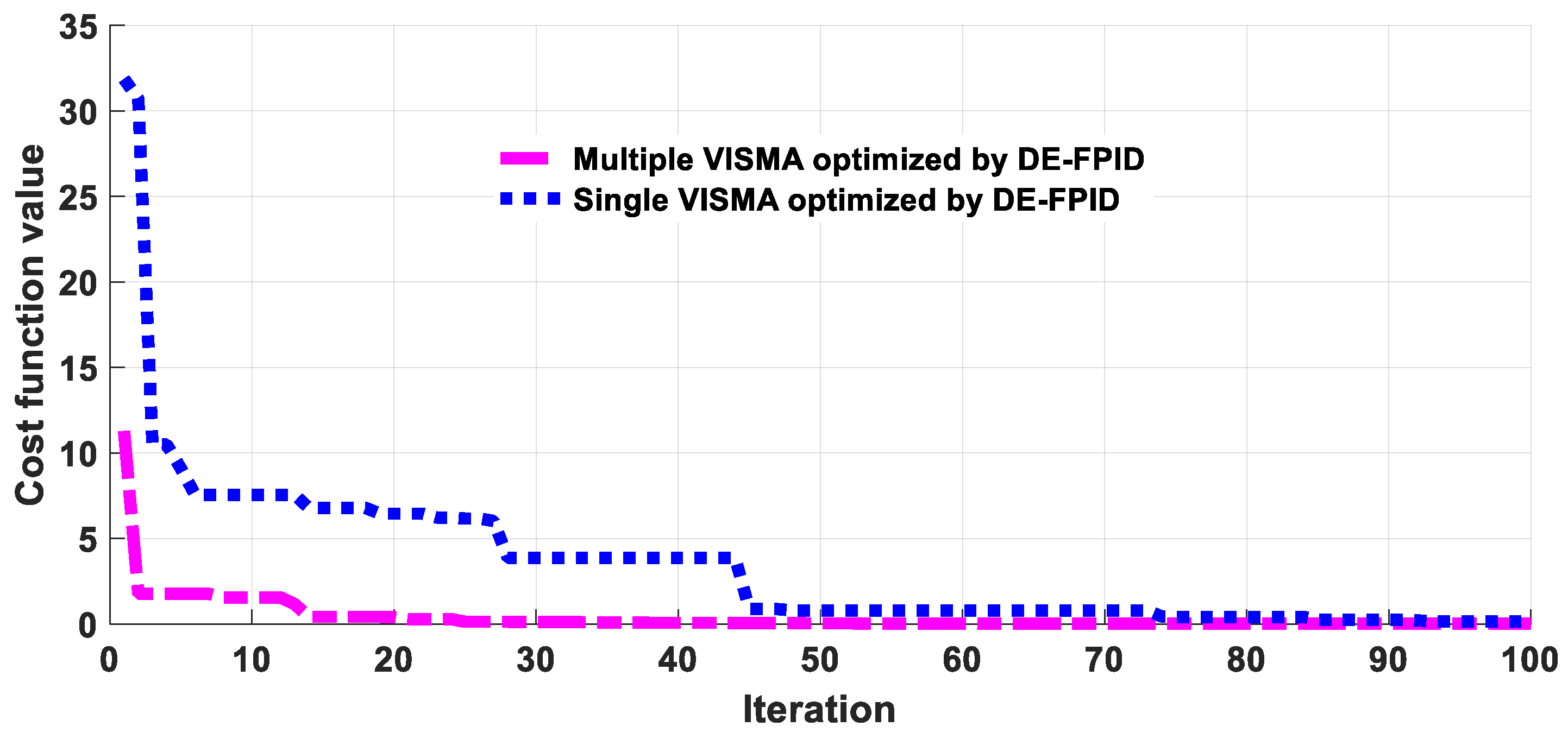

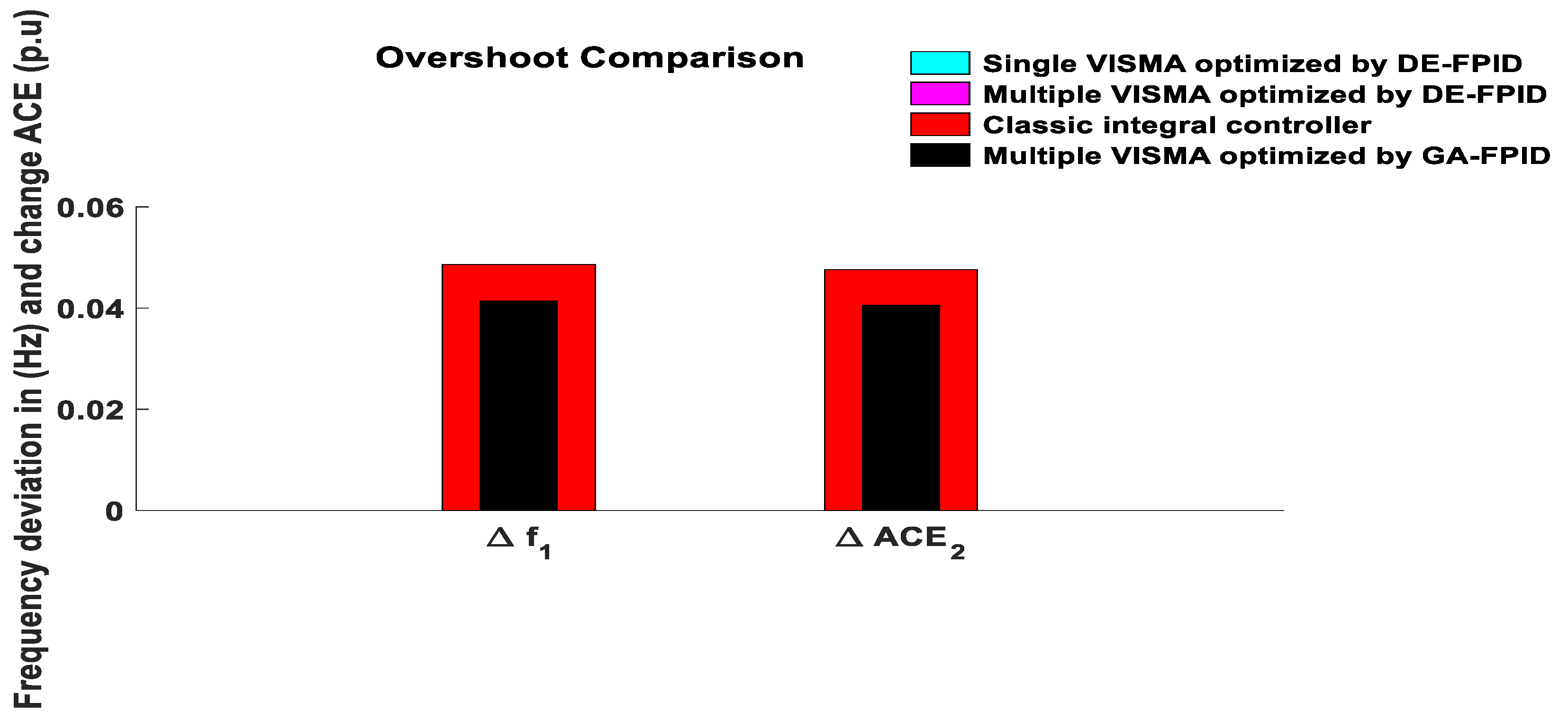
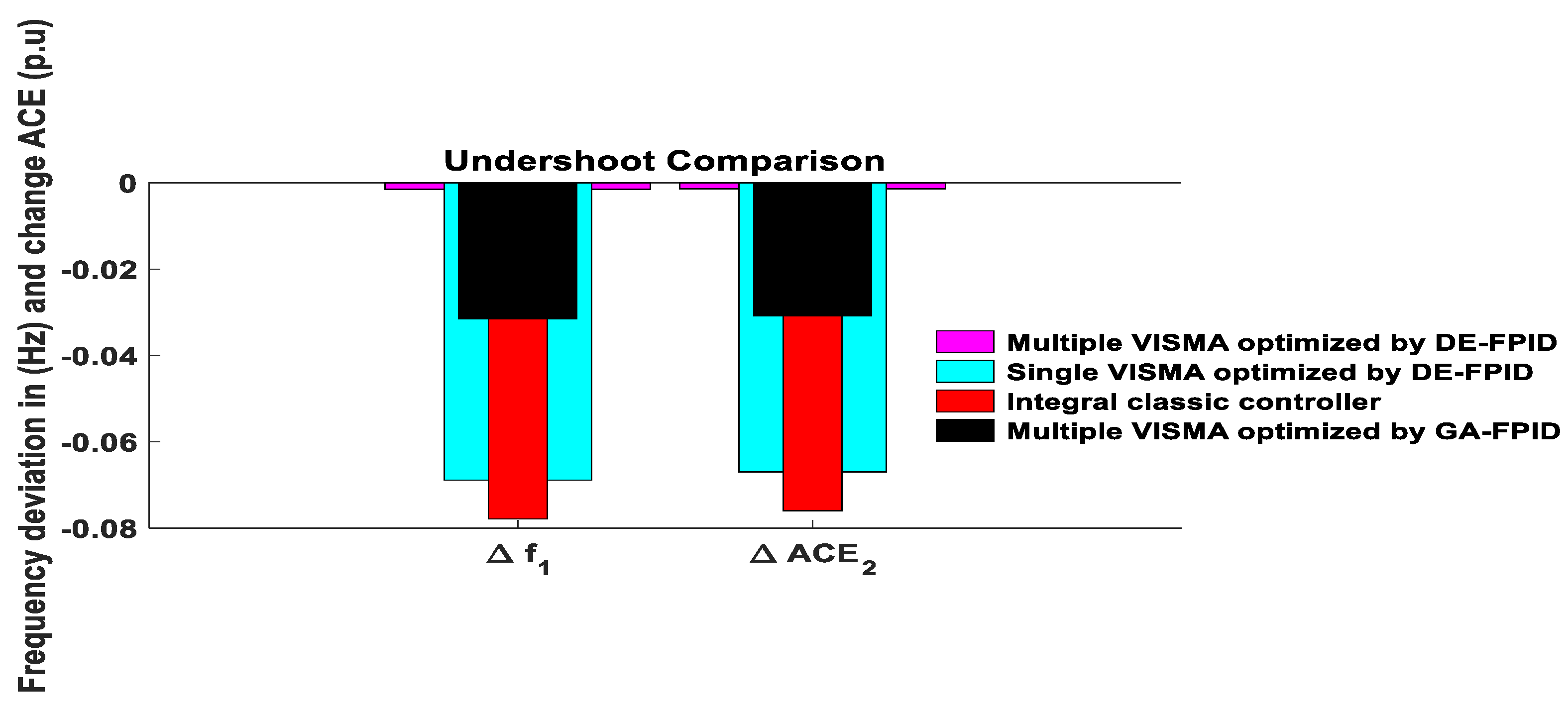

| Maeasured Variables | Rise Time | ST | Undershoot | Overshoot | |
|---|---|---|---|---|---|
| Cahnge if f1 | 5.7426 × 10−5 | 8.3205 | −0.0015 | −1.4282 × 10−6 | |
| Change if ACE | 5.0578 × 10−4 | 8.8344 | −0.0014 | −2.7761 × 10−6 | |
| Change in output P | 4.8571 × 10−5 | 7.0645 | −0.0214 | −4.0462 × 10−5 | |
| The error in cost function | 0.0219 | ||||
| Maeasured Variables | Rise Time | ST | Undershoot | Overshoot | |
|---|---|---|---|---|---|
| Cahnge if f1 | 7.9711 × 10−4 | 49.6977 | −0.0840 | 0.0154 | |
| Change if ACE | 0.0064 | 49.7039 | −0.0823 | 0.0151 | |
| Change in output P | 6.5204 × 10−4 | 48.5696 | −1.2378 | 0.1834 | |
| The error in cost function | 0.1662 | ||||
| Maeasured Variables | Rise Time | ST | Undershoot | Overshoot | |
|---|---|---|---|---|---|
| Cahnge if f1 | 1.4564 | 32.5382 | 0.0502 | 0.0739 | |
| Change if ACE | 1.5336 | 26.1729 | 0.0504 | 0.0724 | |
| Change in output P | 1.1245 | 49.7911 | 0.5393 | 0.7844 | |
| The error in cost function | 0.0979 | ||||
| Maeasured Variables | Rise Time | ST | Undershoot | Overshoot | |
|---|---|---|---|---|---|
| Cahnge if f1 | 0.3116 | 3.1474 | 0.0035 | 0.0077 | |
| Change if ACE | 0.3209 | 3.6602 | 0.0037 | 0.0075 | |
| Change in output P | 0.2473 | 23.6478 | 0.0379 | 0.0824 | |
| The error in cost function | 0.0979 | ||||
| Change in Error (e) | Derivation of Error (de) | Output (u) |
|---|---|---|
| −0.2 −0.2 −0.2 −0.1511 | −0.02 −0.02 −0.02 −0.0160 | −0.25 −0.25 −0.25 −0.1792 |
| −0.1808 −0.1191 −0.0817 | −0.0177 −0.0148 −0.0073 | −0.2248 −0.1659 −0.0902 |
| −0.1230 −0.0958 −0.0124 | −0.0101 −0.0060 −0.0029 | −0.1492 −0.1008 −0.0308 |
| −0.0461 0 0.0631 | −0.0054 0 0.0040 | −0.06960 0.0418 |
| 0.0227 0.0363 0.1322 | 0.0015 0.0053 0.0110 | 0.0176 0.0799 0.1665 |
| 0.0970 0.1656 0.1894 | 0.0077 0.0121 0.0179 | 0.1171 0.2044 0.2095 |
| 0.1341 0.2 0.2 0.2 | 0.0162 0.02 0.02 0.02 | 0.1817 0.25 0.25 0.25 |
| S. No | Description | Symbol | Value |
|---|---|---|---|
| 1 | Speed-governor time constant (s), | Tg | 0.07 |
| 2 | Dead-band rate limit (Hz) | ±0.018 | |
| 3 | Primary droop constant (Hz/p.u. MW), | R | 2.4 |
| 4 | Turbine time constant (s), | Tt | 0.36 |
| 5 | Upper valve/gate opening/closing speed (p.u.), | VU | +0.5 |
| 6 | Lower valve/gate opening/closing speed (p.u.), | VL | −0.5 |
| 7 | Frequency bias factor (p.u. MW Hz−1) | β | 0.98 |
| 8 | Time delay constant (s), | T | 0.5 |
| 9 | Virtual droop constant (s), | Rv | 2.7 |
| 10 | Virtual inertia constant (s), | Jv | 1.6 |
| 11 | Virtual damping constant (s), | Dv | 1.3 |
| 12 | Time constant of inverter-based ESS (s), | TEES | 1.0 |
| 13 | Maximum capacity of ESS (p.u. MW), | PESS_max | 0.4 |
| 14. | Minimum capacity of ESS (p.u. MW), | PESS_min | −0.4 |
| 15 | Time constant of wind turbine | TWT(s) | 1.4 |
| 16 | Time constant of solar system | TPV(s) | 1.9 |
| 17 | Inertia constant of the system (p.u. MW s), | H | 0.083 |
| 18 | Damping coefficient of the system (p.u. MW Hz−1), | D | 0.016 |
| Objective Function | Optimum Control Gains | |||||||
|---|---|---|---|---|---|---|---|---|
| ITAE | K1 | K2 | K3 | K4 | K5 | K6 | K7 | K8 |
| 0.0803 | 1.9631 | 0.1436 | 0.0100 | 0.0216 | 0.0107 | 0.0109 | 0.0115 | |
| Objective Function | Optimum Control Gains | |||||||
|---|---|---|---|---|---|---|---|---|
| ITAE | K1 | K2 | K3 | K4 | K5 | K6 | K7 | K8 |
| 1.3090 | 0.0308 | 1.2409 | 0.0355 | 0.0799 | 0.0762 | 0.0479 | 0.0983 | |
| Objective Function | Optimum Control Gains | |||||||
|---|---|---|---|---|---|---|---|---|
| ITAE | K1 | K2 | K3 | K4 | K5 | K6 | K7 | K8 |
| 0.6105 | 0.0382 | 0.0819 | 0.9189 | 0.6193 | 0.4476 | 0.1997 | 0.2960 | |
| Integral controller | Integral Ki = 0.00068 |
| Various Simulation Cases | ITAE Objective Function Value |
|---|---|
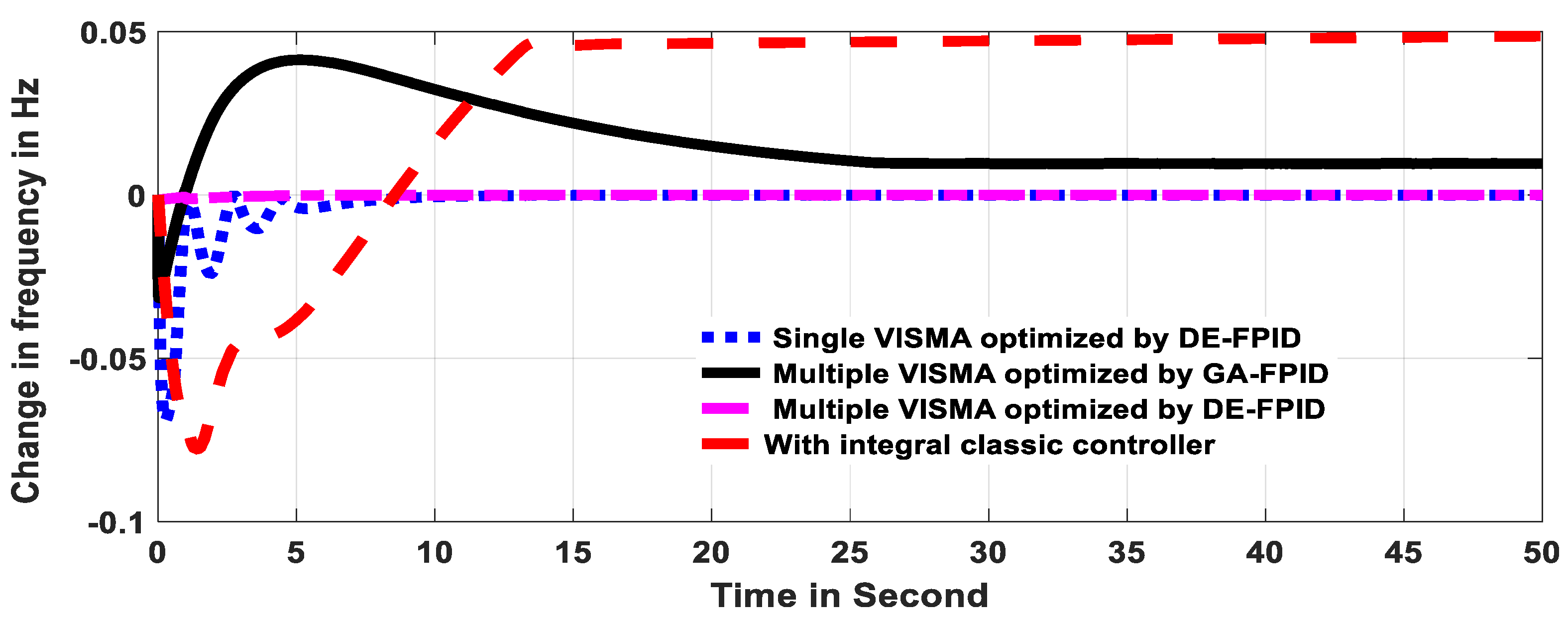
| Multiple VISMAs optimized by DE-FPID | 0.0219 |
| Single VISMAs optimized by DE-FPID | 0.3268 |
| Multiple VISMAs optimized by GA-FPID | 15.3836 |
| Classic integral controller | 55.5338 |
| Maeasured Variables | Rise Time | ST | Undershoot | Overshoot | |
|---|---|---|---|---|---|
| Cahnge if f1 | 5.7426 × 10−5 | 8.3205 | −0.0015 | −1.4282 × 10−6 | |
| Change if ACE | 5.0578 × 10−4 | 8.8344 | −0.0014 | −2.7761 × 10−6 | |
| Change in output P | 4.8571 × 10−5 | 7.0645 | −0.0214 | −4.0462 × 10−5 | |
| The error in cost function | 0.0219 | ||||
| Maeasured Variables | Rise Time | ST | Undershoot | Overshoot | |
|---|---|---|---|---|---|
| Cahnge if f1 | 6.9177 × 10−5 | 7.9905 | −0.0689 | −4.9628 × 10−6 | |
| Change if ACE | 8.5616 × 10−4 | 8.5116 | −0.0670 | −4.0813 × 10−6 | |
| Change in output P | 6.1766 × 10−5 | 7.1589 | −0.1185 | 0.0036 | |
| The error in cost function | 0.3268 | ||||
| Maeasured Variables | Rise Time | ST | Undershoot | Overshoot | |
|---|---|---|---|---|---|
| Cahnge if f1 | 0.3109 | 25.0302 | −0.0315 | 0.0414 | |
| Change if ACE | 0.3114 | 25.5142 | −0.0308 | 0.0405 | |
| Change in output P | 0.2616 | 24.4149 | −0.04653 | 0.04468 | |
| The error in cost function | 15.3836 | ||||
| Maeasured Variables | Rise Time | ST | Undershoot | Overshoot | |
|---|---|---|---|---|---|
| Cahnge if f1 | 4.0327 | 15.8646 | −0.0779 | 0.0486 | |
| Change if ACE | 4.0358 | 16.2837 | −0.0760 | 0.0476 | |
| The error in cost function | 55.5338 | ||||
| Frequency Response in (Hz) in the Previous Published Paper Using Eigenvalue Time Domain Analysis [8] | Frequency Response in (Hz) Using the Proposed FPID Optimized Using DE Technique | ||
|---|---|---|---|
| undershoot | overshoot | undershoot | overshoot |
| −0.15 | 0.15 | −0.0015 | −1.4282 × 10−6 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Feleke, S.; Pydi, B.; Satish, R.; Kotb, H.; Alenezi, M.; Shouran, M. Frequency Stability Enhancement Using Differential-Evolution- and Genetic-Algorithm-Optimized Intelligent Controllers in Multiple Virtual Synchronous Machine Systems. Sustainability 2023, 15, 13892. https://doi.org/10.3390/su151813892
Feleke S, Pydi B, Satish R, Kotb H, Alenezi M, Shouran M. Frequency Stability Enhancement Using Differential-Evolution- and Genetic-Algorithm-Optimized Intelligent Controllers in Multiple Virtual Synchronous Machine Systems. Sustainability. 2023; 15(18):13892. https://doi.org/10.3390/su151813892
Chicago/Turabian StyleFeleke, Solomon, Balamurali Pydi, Raavi Satish, Hossam Kotb, Mohammed Alenezi, and Mokhtar Shouran. 2023. "Frequency Stability Enhancement Using Differential-Evolution- and Genetic-Algorithm-Optimized Intelligent Controllers in Multiple Virtual Synchronous Machine Systems" Sustainability 15, no. 18: 13892. https://doi.org/10.3390/su151813892
APA StyleFeleke, S., Pydi, B., Satish, R., Kotb, H., Alenezi, M., & Shouran, M. (2023). Frequency Stability Enhancement Using Differential-Evolution- and Genetic-Algorithm-Optimized Intelligent Controllers in Multiple Virtual Synchronous Machine Systems. Sustainability, 15(18), 13892. https://doi.org/10.3390/su151813892








