Effects of Cornices on Wind Loads of Solar Panels Mounted on Gable Roof Building
Abstract
:1. Introduction
2. Experimental Procedure
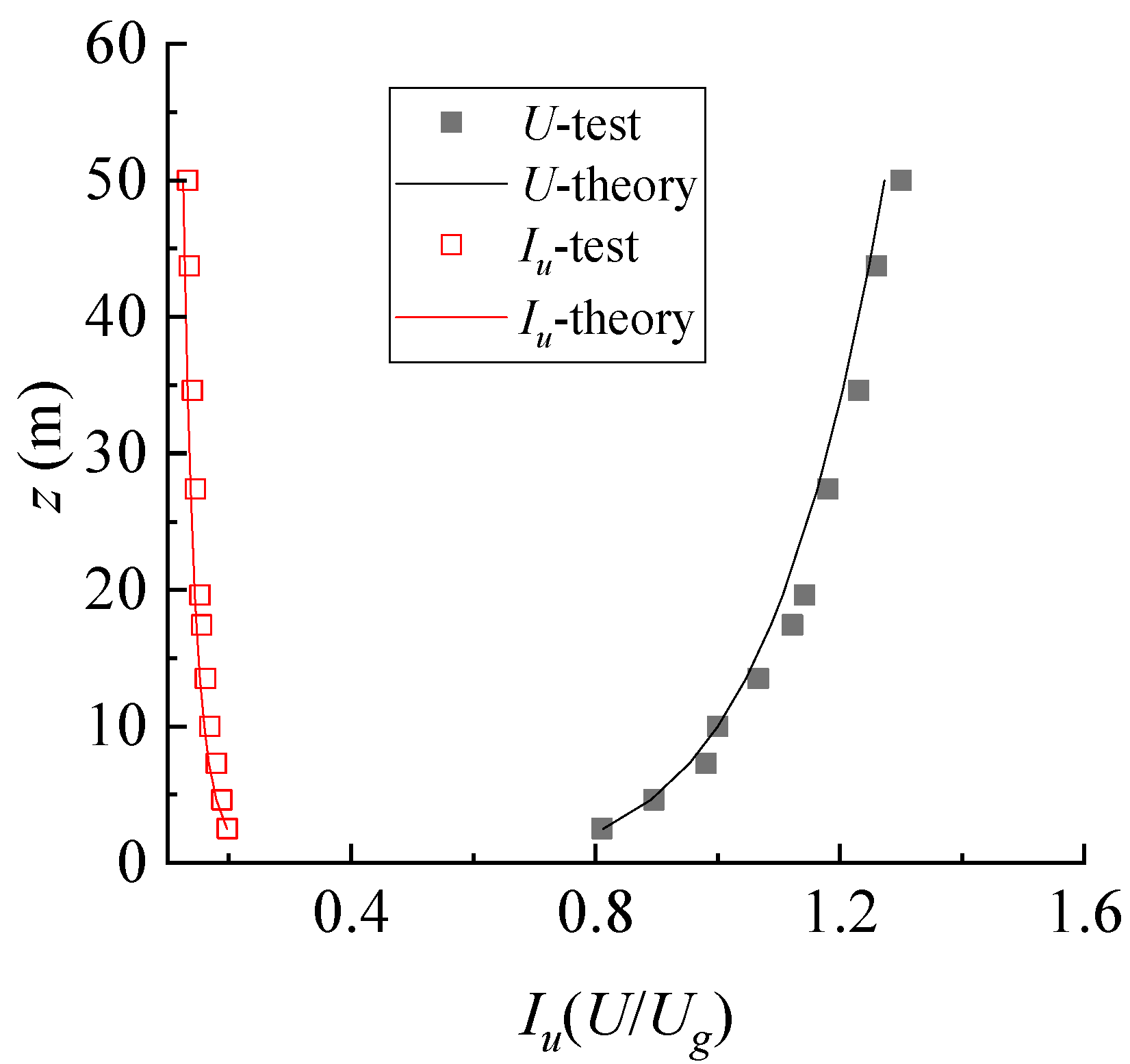
2.1. Terrain Simulation
2.2. Model Design
2.3. Data Processing
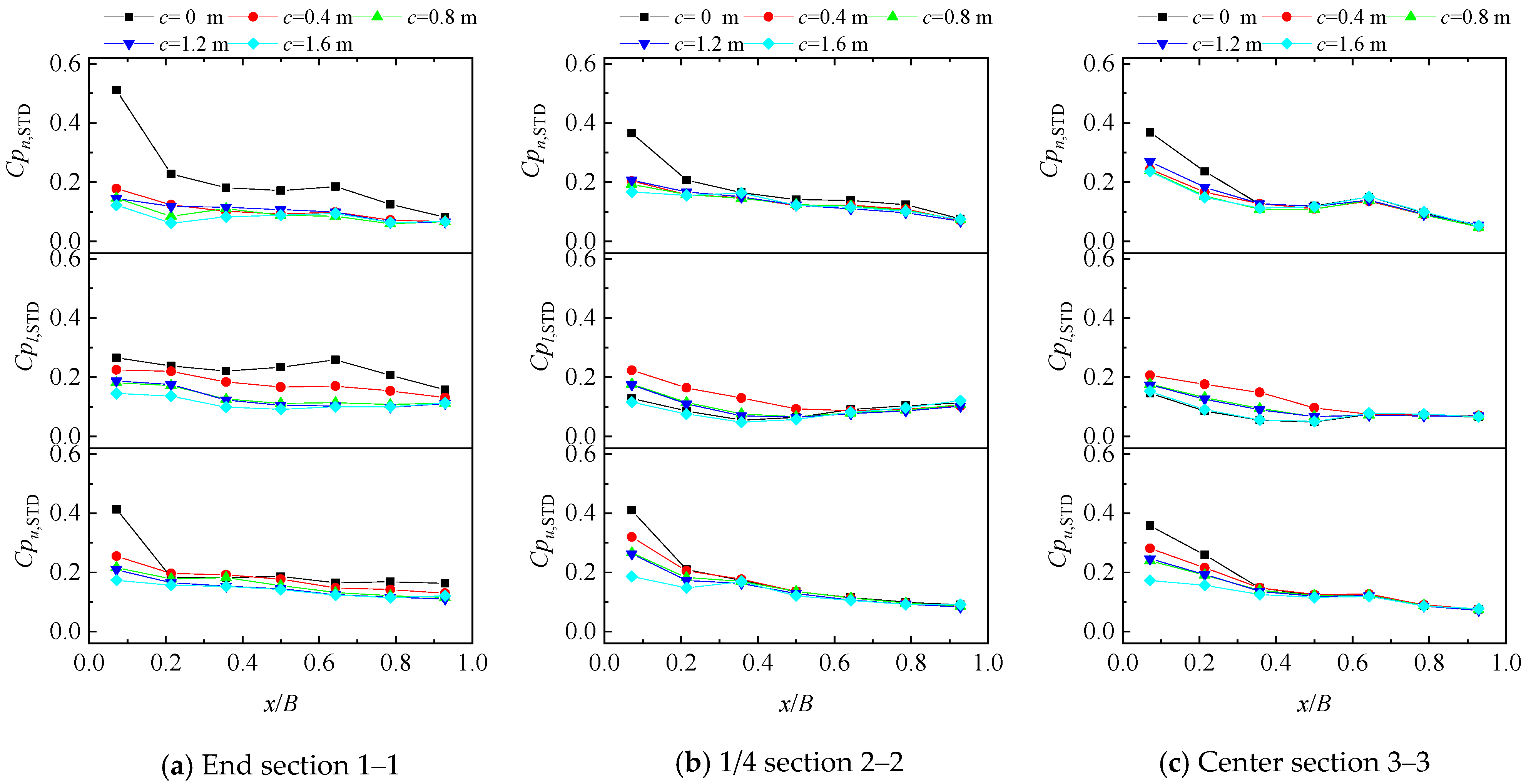
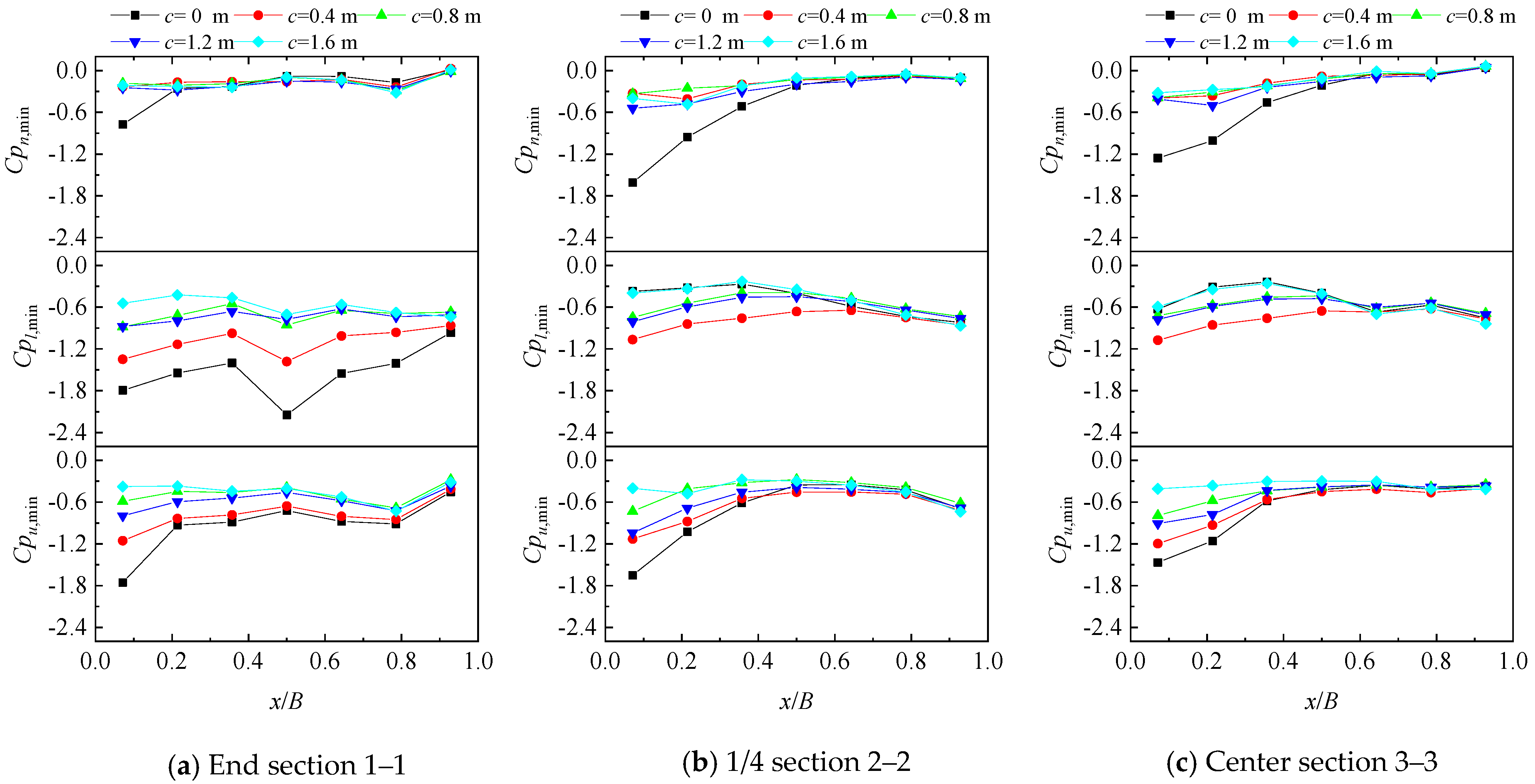
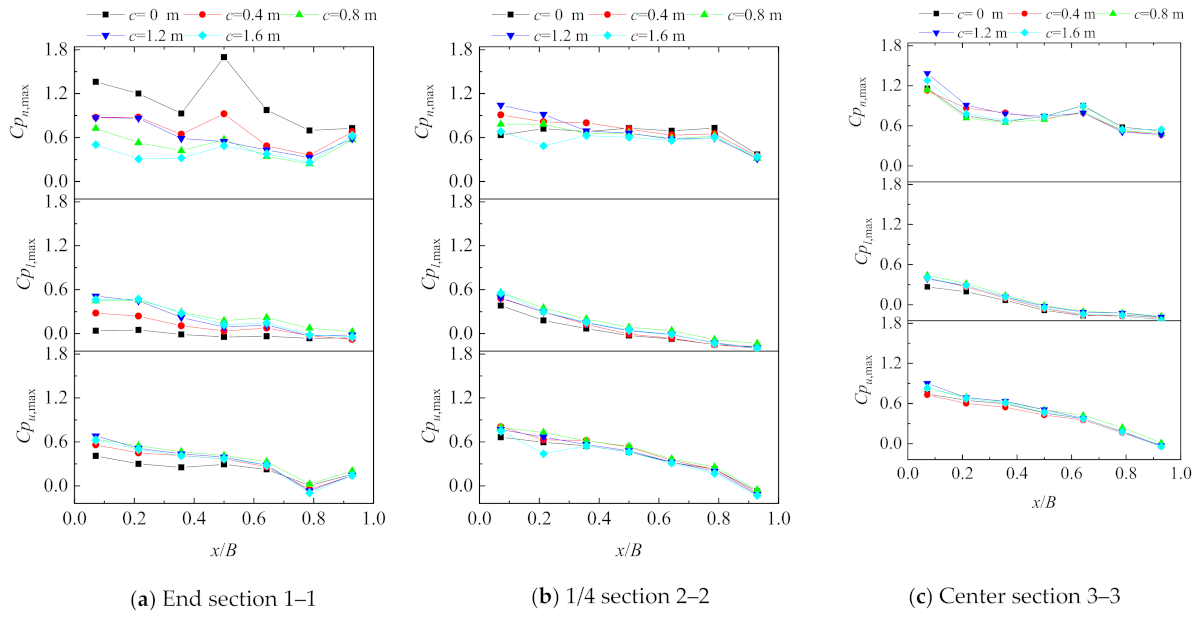
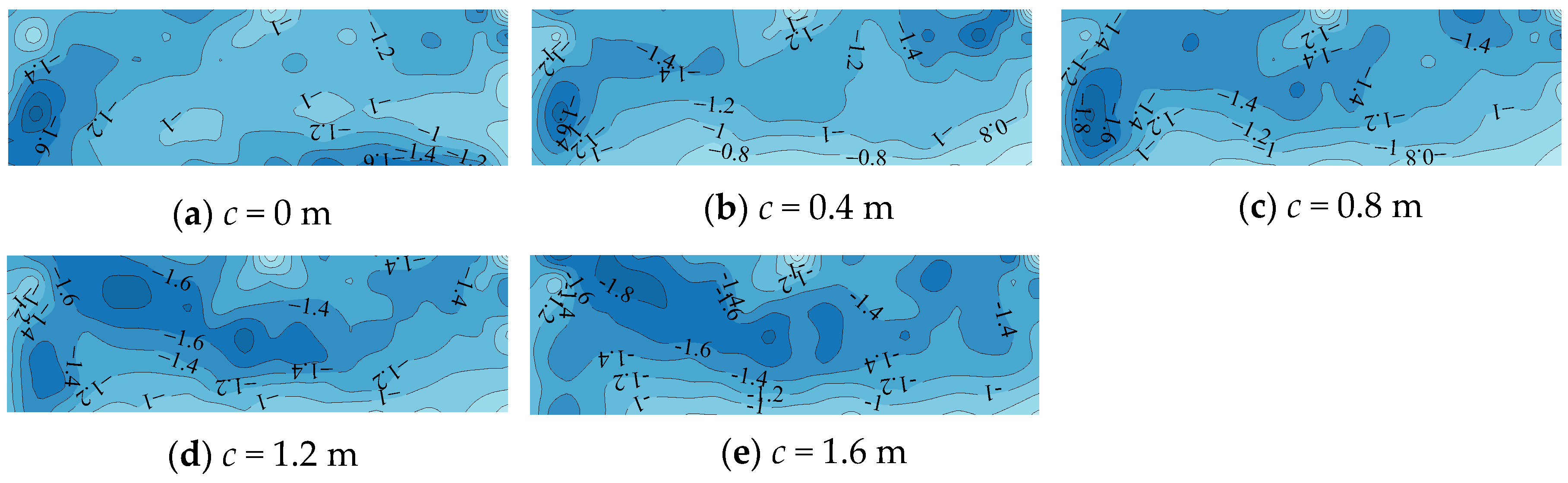
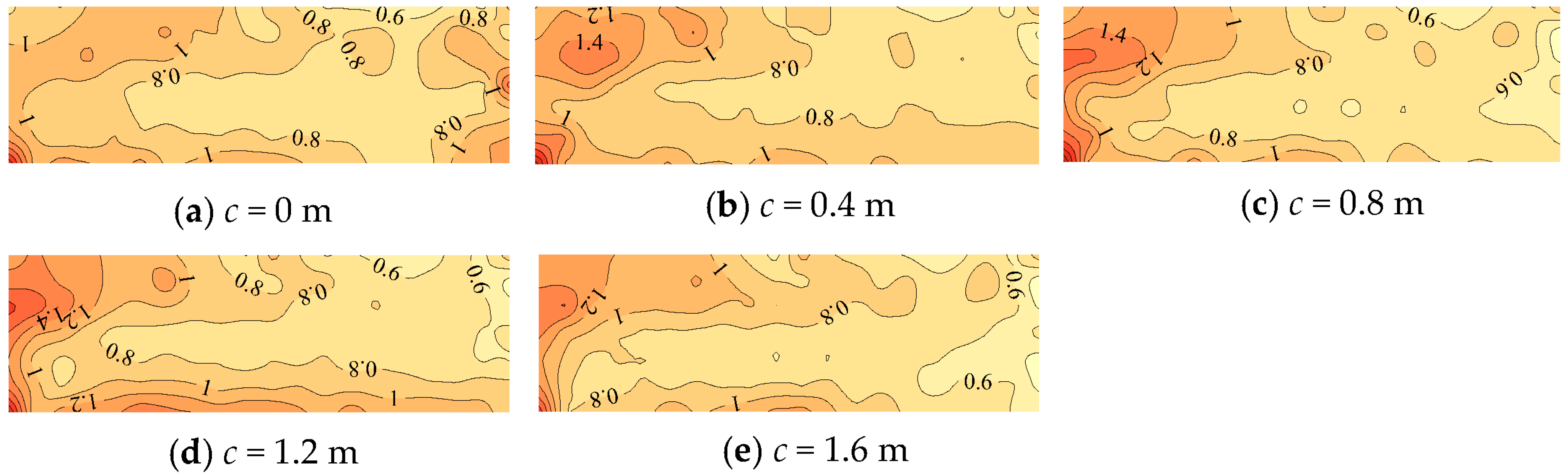
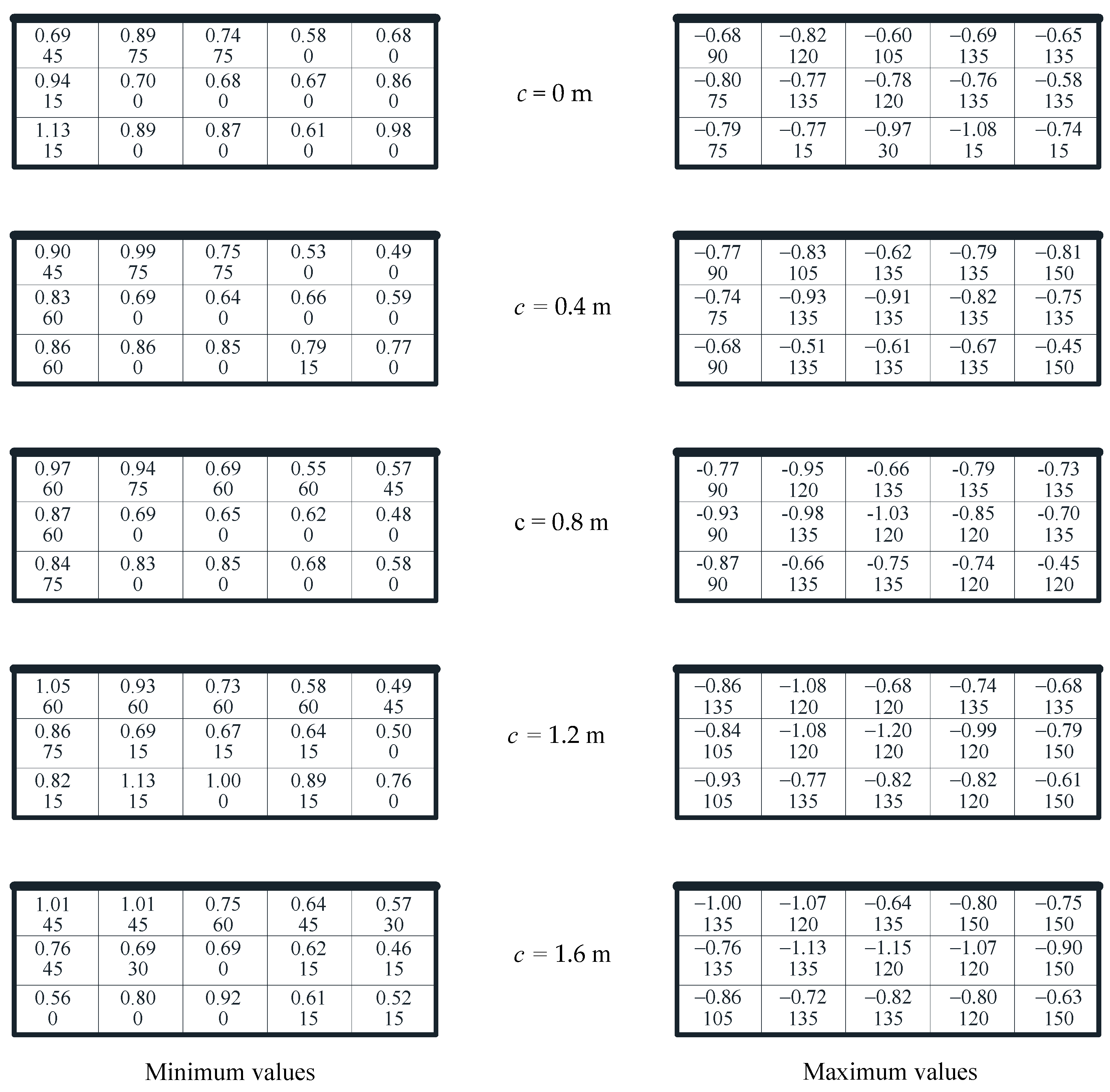
3. Results
4. Discuss
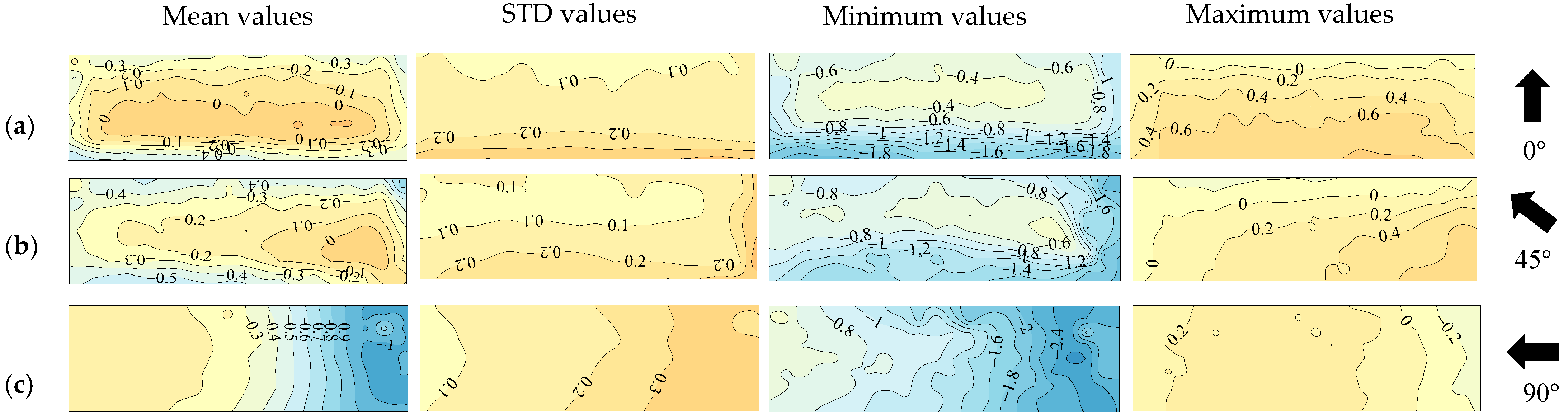
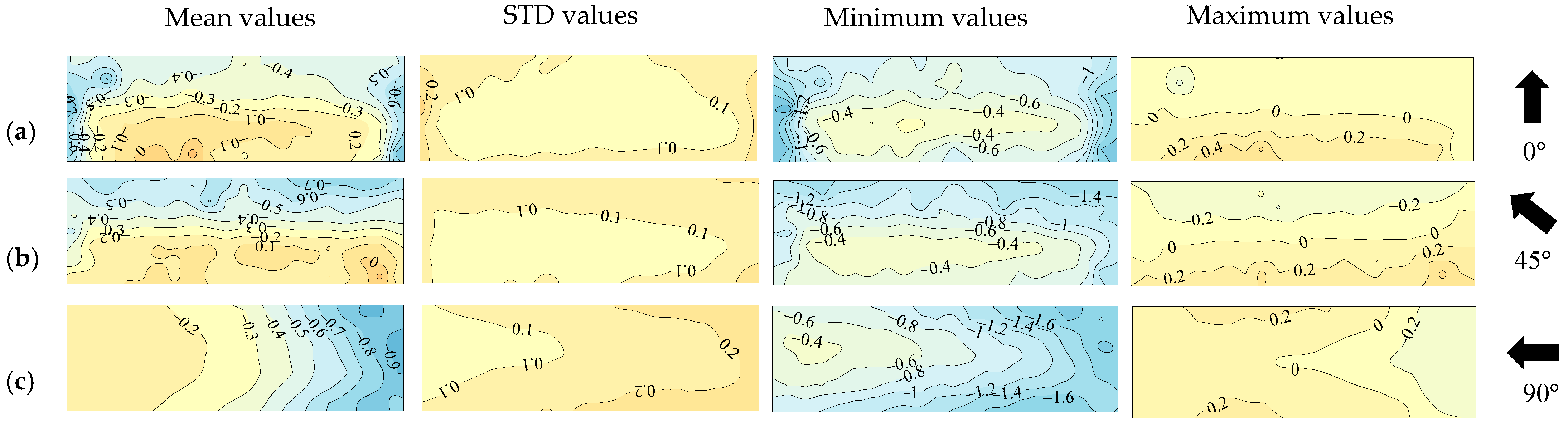
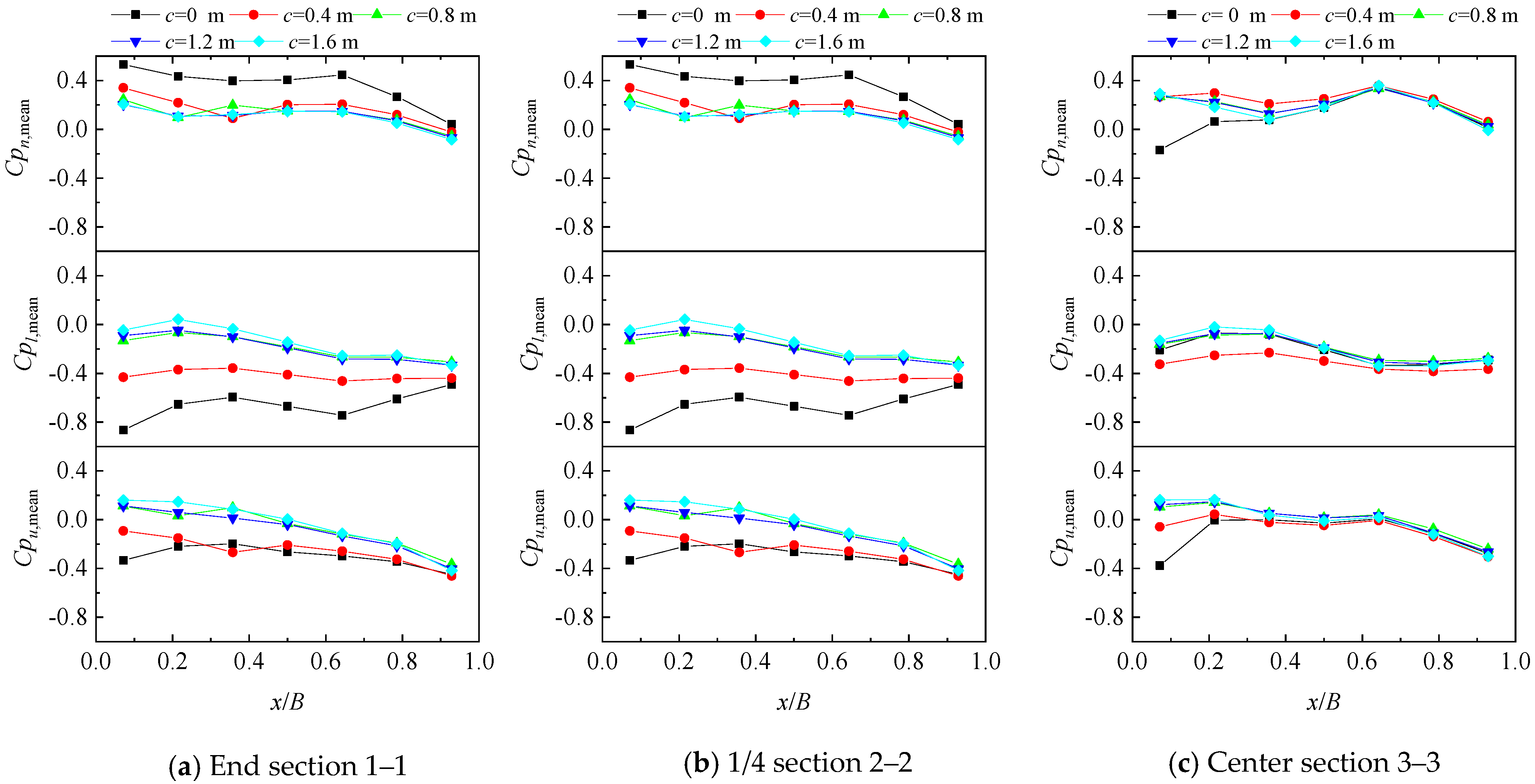
4.1. Effects of Cornice on Wind Loads of Solar Module at Wind Direction Perpendicular to Roof Ridge
4.2. Effects of Cornices on Most Unfavorable Peak Net Pressure Coefficients among All Wind Directions
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Jubayer, C.M.; Hangan, H. A numerical approach to the investigation of wind loading on an array of ground mounted solar photovoltaic (PV) panels. J. Wind Eng. Ind. Aerodyn. 2016, 153, 60–70. [Google Scholar] [CrossRef]
- Zhao, X.G.; Xie, Y.M. The economic performance of industrial and commercial rooftop photovoltaic in China. Energy 2019, 187, 115961. [Google Scholar]
- Wood, G.S.; Denoon, R.O.; Kwok, K.C.S. Wind loads on industrial solar panel arrays and supporting roof structure. Wind. Struct. 2001, 4, 481–494. [Google Scholar] [CrossRef]
- Shademan, M.; Hangan, H. Wind loading on solar panels at different inclination angles. In Proceedings of the 11th American Conference on Wind Engineering, American Association of Wind Engineering, Fort Collins, CO, USA, 22–26 June 2009. [Google Scholar]
- Dai, S.F.; Liu, H.J.; Yang, J.H.; Peng, H.Y. Wind loads on roof-mounted isolated solar panels of tall buildings through wind tunnel testing. Solar Energy 2022, 231, 607–622. [Google Scholar] [CrossRef]
- Aly, A.M.; Bitsuamlak, G. Wind-Induced Pressures on Solar Panels Mounted on Residential Homes. J. Archit. Eng. 2014, 20, 04013003. [Google Scholar] [CrossRef]
- Kopp, G.A.; Farquhar, S.; Morrison, M.J. Aerodynamic mechanisms for wind loads on tilted, roof-mounted, solar arrays. J. Wind. Eng. Ind. Aerodyn. 2012, 111, 40–52. [Google Scholar] [CrossRef]
- Pratt, R.N.; Kopp, G.A. Velocity measurements around low-profile, tilted, solar arrays mounted on large flat-roofs, for wall normal wind directions. J. Wind. Eng. Ind. Aerodyn. 2013, 123, 226–238. [Google Scholar] [CrossRef]
- Alrawashdeh, H.; Stathopoulos, T. Wind loads on solar panels mounted on flat roofs: Effect of geometric scale. J. Wind. Eng. Ind. Aerodyn. 2020, 206, 104339. [Google Scholar] [CrossRef]
- Kopp, G.A.; Banks, D. Use of the Wind Tunnel Test Method for Obtaining Design Wind Loads on Roof-Mounted Solar Arrays. J. Struct. Eng. 2013, 139, 284–287. [Google Scholar] [CrossRef]
- Stenabaugh, S.E.; Iida, Y.; Kopp, G.A.; Karava, P. Wind loads on photovoltaic arrays mounted parallel to sloped roofs on low-rise buildings. J. Wind. Eng. Ind. Aerodyn. 2015, 139, 16–26. [Google Scholar] [CrossRef]
- Naeiji, A.; Raji, F.; Zisis, I. Wind loads on residential scale rooftop photovoltaic panels. J. Wind. Eng. Ind. Aerodyn. 2017, 168, 228–246. [Google Scholar] [CrossRef]
- Geurts, C.; Blackmore, P. Wind loads on stand-off photovoltaic systems on pitched roofs. J. Wind. Eng. Ind. Aerodyn. 2013, 123, 239–249. [Google Scholar] [CrossRef]
- Wang, J.; Phuc, P.V.; Yang, Q.; Tamura, Y. LES study of wind pressure and flow characteristics of flat-roof-mounted solar arrays. J. Wind. Eng. Ind. Aerodyn. 2020, 198, 104096. [Google Scholar] [CrossRef]
- Pfahl, A.; Uhlemann, H. Wind loads on heliostats and photovoltaic trackers at various Reynolds numbers. J. Wind. Eng. Ind. Aerodyn. 2011, 99, 964–968. [Google Scholar] [CrossRef]
- Wang, J.; Yang, Q.; Hui, Y. Comparisons of design wind pressures on roof-mounted solar arrays between wind tunnel tests and codes and standards. Adv. Struct. Eng. 2021, 24, 653–666. [Google Scholar] [CrossRef]
- ASCE-7-16; Minimum Design Loads for Buildings and Other Structures. American Society of Civil Engineers: Reston, VA, USA, 2016.
- JIS C 8955-2017; Design Guide on Structures for Photovoltaic Array. Japanese Industrial Standard: Tokyo, Japan, 2017.
- NB/T 10115-2018; Code for Design of Photovoltaic Modules Support Structures. China Jihua Press: Beijing, China, 2018.
- ASCE 7-22; Minimum Design Loads for Buildings and Other Structures. American Society of Civil Engineers: Reston, VA, USA, 2022.
- GB 50009-2012; Load Code for the Design of Building Structures. China Architecture and Building Press: Beijing, China, 2012.
- Cook, N.J.; Mayne, J.R. A novel working approach to the assessment of wind loads for equivalent static design. J. Wind. Eng. Ind. Aerodyn. 1979, 4, 149–164. [Google Scholar] [CrossRef]
- Lieblein, J. Efficient Methods of Extreme Value Methodology; UK Department of Commerce, Report 74-602; National Bureau of Standards: Gaithersburg, MD, USA, 1974.





Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tu, Z.; Yao, J.; Zhou, X.; Wang, D.; Shen, G.; Yu, S. Effects of Cornices on Wind Loads of Solar Panels Mounted on Gable Roof Building. Sustainability 2023, 15, 13805. https://doi.org/10.3390/su151813805
Tu Z, Yao J, Zhou X, Wang D, Shen G, Yu S. Effects of Cornices on Wind Loads of Solar Panels Mounted on Gable Roof Building. Sustainability. 2023; 15(18):13805. https://doi.org/10.3390/su151813805
Chicago/Turabian StyleTu, Zhibin, Jianfeng Yao, Xing Zhou, Dong Wang, Guohui Shen, and Shice Yu. 2023. "Effects of Cornices on Wind Loads of Solar Panels Mounted on Gable Roof Building" Sustainability 15, no. 18: 13805. https://doi.org/10.3390/su151813805
APA StyleTu, Z., Yao, J., Zhou, X., Wang, D., Shen, G., & Yu, S. (2023). Effects of Cornices on Wind Loads of Solar Panels Mounted on Gable Roof Building. Sustainability, 15(18), 13805. https://doi.org/10.3390/su151813805






