Abstract
We present results that come from analysing students’ processes of solving tasks designed particularly for the learning of differential equations in a situational context. A teaching sequence was implemented during a semester-long course that comprised several tasks to cover the content of the course. Following a qualitative analysis, we show how a contextualised task can favour the construction of meanings associated with differential equations and how the interpretation of the terms present in those equations is developed. We also highlight some difficulties that may arise in students’ interpretations when the task involves meanings from other disciplines.
1. Introduction
In previous decades, there has been valuable and extended acceptance of ordinary differential equations as an important part of the undergraduate curriculum in several careers, including science, technology, engineering, and mathematics [1]. The incorporation of this topic in undergraduate formation has been recognized by several scientists who have justified their support from different points of view: the inclusion of differential equations enables the resolution of contextualised problems involving concepts of physics, chemistry, geometry, and biology, among other sciences [2]; differential equations are natural mathematical tools used to describe phenomena that include variation and, therefore, they allow the modelling and solving of problems from very diverse contexts [3]; and the study of differential equations provides an excellent opportunity to demonstrate the application of mathematics to real life and to engage students in the nature of contemporary research in mathematics [4]. Consequently, the relevant role of this branch of mathematics in university education has aroused the interest of researchers in the area of mathematics education, who are particularly focused on enhancing the curricular content, including recommendations for its implementation and its teaching in the classroom [5,6,7,8,9,10].
On the other hand, mathematical modelling has become one of the more relevant systemic approaches to solving mathematical problems and has also been extensively used in many different research projects arising in diverse fields [11]. It is well-known that the use of mathematical models as predictor tools in different areas of science has intensified in recent decades, this being one of the reasons why mathematical modelling has emerged as one of the fastest-growing areas in mathematics [12,13]. For instance, during the recent global spread of the COVID-19 epidemic, mathematical modelling played an essential role in the simulation of behaviour, providing, in this way, an invaluable tool for making decisions [14,15,16]. Particularly in relation to sustainability, differential equations are used as mathematical models in different areas, like the sustainable management of marine resources [17], the study of the sustainability of an urban system in the presence of haphazard development activities that affect the urban population [18], and the development of zero-carbon electric power systems [19]. The increased attention being paid to mathematical modelling is also a factor that has attracted the attention of researchers in mathematical education. Consequently, researchers and educators have supported the development of mathematical modelling skills in the training of students from elementary to higher education levels [20,21,22,23,24,25,26,27]. Based on their experience of teaching mathematical modelling, the researchers have reported several advantages of this approach for developing mathematical knowledge and improving mathematical teaching practices [28]. In this paper, mathematical modelling is conceived in two ways. The first considers mathematical modelling as the simplification of real-world phenomena to be solved using mathematics. In the second method, modelling is considered a didactic methodology that uses contextualised examples arising from validated mathematical models. In this approach, mathematical modelling also looks to motivate students by solving real-world or life problems [29]. An extensive discussion of the concepts related to mathematical modelling is developed in [29] (see also [24,30,31,32,33]).
There are several challenges in the teaching of differential equations to undergraduate students, among which at least two of the chief ones are the learning of concepts and the development of mathematical modelling skills [34]. Related to the first claim, one of the initial observations issued by mathematics education researchers is the fact that the way that differential equations have been taught does not favour the development of conceptual learning and applications of such concepts. This is due to the fact that traditional ordinary differential equations courses are centred on the teaching of algebraic solutions and algorithmic techniques, and they discard or give a very low importance to conceptual understanding. In order to overcome the limitations of traditional teaching, several proposals using contemporary didactic approaches have been considered: qualitative and numerical approaches, active learning methodologies, mathematical modelling methodologies, information and communication technology based methodologies, project-based learning, and other methodologies (see [34] and the references therein). In the case of mathematical modelling, four groups have been distinguished: the development of skills for mathematical modelling [32,35,36,37,38,39,40,41,42,43]; modelling as a pedagogical strategy to teach concepts of ordinary differential equations [33,36,44,45,46]; language games, representations, and relations of mathematics with other sciences [47,48,49,50,51]; and modelling activities using ordinary differential equations to teach other concepts [52,53,54,55,56,57,58]. As we can see, there are many approaches to the practice of modelling in education, and we can find several definitions and ways to represent the process of modelling.
In this paper, we study how model-eliciting activities can support students in th construction of their own concepts related to first-order ordinary differential equations. Thus, more specifically, our aim is
to characterise the conceptual learning of first-order differential equations developed by students when they solve a task based on a model-eliciting activity approach.
The paper is organised as follows. In Section 2, we introduce the concepts related to mathematical modelling. In particular, we consider the model-eliciting activity approach. In Section 3, we survey some results on the teaching and learning of ordinary differential equations. In Section 4, we present the methodological aspects of the research. Moreover, in Section 5, Section 6 and Section 7, the data analyses, a discussion of the findings, and the conclusions of the work are respectively presented.
2. Mathematical Modelling
In recent years, mathematical modelling in the context of mathematical education has generated the interest of several researchers who have explored new ways of teaching in different disciplines [25,27]. Particularly, a well-documented discussion on the role of modelling in education was developed by [25] (see also [59,60] for a systematic presentation).
In spite of the significant progress attained on the topic, in the current literature, a unified definition of mathematical modelling is lacking. In [61], the author defines mathematical modelling as a learning environment in which students inquire about and/or investigate through mathematics some situations that arise in other areas of reality. In [62], Blomhøj states that mathematical modelling constitutes a teaching practice that focuses the teaching and learning process regarding the relationship between the real world and mathematics. The authors of [27] define mathematical modelling as an interactive process that involves open–closed problems, real-world problems, and practical problems that make sense and allow the student to use affirmations, approximations, and multiple representations. In the opinion of Lesh & Doerr [11], modelling in mathematics education supports meaningful learning and helps the student to establish relationships between their academic training and real life. Thus, from the different interpretations of mathematical modelling, we have the outstanding characteristic that it plays a relevant role in developing skills or competencies that allow the student to relate the world of mathematics to the real world.
In this paper, we consider the notions introduced by Lesh & Doerr [11], where mathematical modelling is contextualised as a didactic approach based on activities or model-eliciting activities (MEAs) that are guided by the following principles:
- (1)
- The reality principle. This is sometimes called the “personal meaningfulness principle’. It highlights that the chosen situation for the activity must seem meaningful to the students, and it must also be connected with their previous experiences or knowledge. Some questions used to guide the construction of activities satisfying this principle are the following: Could the activity really happen in some real-life situations? Is the activity constructed to encourage the student to make sense of the situation with their own personal knowledge and experience? Is the activity such that it recognizes the ideas of the students, or are they compelled to accept the notions of the teacher as the unique and correct way to approach the situation?
- (2)
- The model construction principle. The activity should create the need for students to develop their own mathematical constructs, which should also be meaningful. It is related to the following questions: Does the activity ensure that students recognise the requirements of model construction, modification, extension, or refinement? Does the activity involve the construction, description, explanation, manipulation, prediction, or control of a system? Does it pay attention to patterns and regularity constructions rather than skin-deep information?
- (3)
- The self-evaluation principle. The situation must be such that it allows the students to evaluate their progress in the development of the activities and the interpretation of the models. The prototypical questions used to test this principle are as follows: Is the activity clear in the sense that the criteria for assessing the usefulness of alternative responses and tasks are known and clear to students? Are some parameters considered in the activities used to direct the students to judge for themselves when their responses are good enough? What are the objectives and purposes of the results?
- (4)
- The model documentation principle. This is also called the “model-externalisation principle” or the “model abstraction documentation principle”. It is related to the characteristics of activities, where the context must be such that the students express their thoughts and opinions while they develop the tasks. The activity should allow the students to leave documented records of their development. It can be validated by the following question: Is the activity constructed to require that the responses of students give explicit declarations of their thinking about the situation (given goals, possible solution paths) and which kind of knowledge (mathematical objects, relations, operations, patterns, and regularities) is used in their reports?
- (5)
- The simple prototype principle. The selected situation for the activity must be simple to meet the needs of the students’ current knowledge. The questions that address this principle are the following: Is the activity formulated in terms of a set of tasks that are as simple as possible? Does it promote the need for a significant model? Is the solution a prototype for a variety of similar situations? Is the activity capable of producing an experience that will help others make sense of similar situations?
- (6)
- The model generalisation principle. The activity should be designed with the aim of generating awareness that it is possible to generalize the model obtained or used in the activity. The questions used to test this principle are the following: Are the conceptual tools valid only for the particular situation or for a more general situation? Does the activity represent a challenge to produce improved models?
In synthesis, the characteristics of this didactic approach are as follows: (a) students begin with real-life situations presented in terms of modelling activities, which require more time, thought, and concentration compared to traditional problems; (b) the activities should be implemented in small groups in order to produce the necessary discussions; (c) the activities require the students to clearly express their ways of thinking as well as clearly define their conceptual strengths and weaknesses; (d) the development of activities requires a space for presentations and discussions, which should be considered with the purpose of clarifying the expression of their ways of thinking, promoting students’ awareness of the ways of thinking of others, allowing them to see the strengths and weaknesses of different approaches and create strategies to improve the work of others or their own work; and (e) the teacher participates in the process as a guide and with the aim of understanding the students’ ways of thinking, determining their strengths and weaknesses, and evaluating their performances. Another important aspect is that not all problems have the same context, content, and cognitive demand; in this sense, Chamberlin et al. [63] developed a way to evaluate the problems using the characteristics of the MEAs. More specifically, in [63], the authors used three taxonomies to evaluate the types of problems and suggested that the MEAs complying with the six principles can be classified in terms of their context, content, and cognitive demand.
In this research, we relied on the principles of MEAs to design the tasks that were used in our teaching experiment of ordinary differential equations. This was implemented in the classroom with the aim of determining the knowledge, skills, and creative capacity that the students show when they become involved in the activities. In this sense, another researcher [1] considered that procedural knowledge appears when the students use information only as an application of some algebraic techniques, and conceptual knowledge emerges when the students evaluate the information in depth. We focused on conceptual knowledge. In addition, Arslan [1] presented a list of the characteristics of the questions that measure conceptual and procedural knowledge. Consequently, to have elements that make identification possible and, therefore, allow us to describe and understand, how the learning of concepts and procedures is developed when students address MEAs, as a starting point, we used a list of questions proposed by Arslan [1]. For instance, the author of [1] established that a characteristic question measuring conceptual knowledge is the following: “The task given in the question has not been discussed in the class”. Then, in our MEAs we included a question related to a concept that is not taught in the class, to fix ideas, the concept of the “ordinary differential equation”. Hence, we defined “to formulate a notion of an ordinary differential equation” as a learning objective. Additionally, we constructed a group of appropriate descriptors using the verbs of Bloom’s taxonomy for the levels of understanding [64,65] (see Table 1).

Table 1.
The learning objectives of the lecture constructed according to the Bloom taxonomy [64,65].
3. Teaching and Learning of Ordinary Differential Equations
Research on the teaching and learning of differential equations has been an object of study for several years. The review developed in [34] covers a wide spectrum of works produced before 2021, and it does not include books, book collections, or conference proceedings. We recognise that, after the survey, there are also some works that have been developed within this topic, for instance [65,66,67,68,69]. It is also known that the teaching and learning of ordinary differential equations have been influenced by the different didactic approaches that are applied to the teaching and learning of mathematics, for instance, information and communication technology-based methodologies and project-based methodologies.
The traditional methodology for teaching ordinary differential equations is centred on developing algebraic or analytic methods to obtain the analytic solutions given by explicit or implicit expressions for the unknown function [8]. The main characteristics are the following: algorithmic, procedural, symbolic, and particularly related to a specific type of differential equation. More precisely, the traditional methodology used for teaching first-order ordinary differential equations is developed in three steps by the educator: (a) the introduction of the abstract forms of first-order ordinary differential equations, given by the following two equivalent forms:
where and N are given functions from to ; (b) the classification of (1) as separable, homogeneous, exact, linear, Bernoulli, and others, depending on the behaviour of the functions ; and (c) teaching the students their own algorithmic solution technique for each type of ordinary differential equation. These three steps ((a), (b) and (c)) of teaching are also applied by educators of traditional methodology to higher-order ordinary differential equations and even to first-order systems of differential equations. To summarise, the traditional approach to teaching differential equations consists of the use of a wide variety of algebraic or analytic methods for solving different types of problems [70]. Research on traditional methodologies has been conducted by several researchers [1,4,23,70,71,72,73,74,75,76,77,78,79]. In those works, the authors discuss different aspects of the traditional teaching of ordinary differential equations, such as the development of algebraic abilities, students’ difficulties in learning, the characteristics of traditional methods, characterisation of the main disadvantages, and uses of different mathematical representations, among others. In a broad sense, the authors agree that the traditional methodology has several disadvantages, specifically that it develops concept learning passively; however, they recommend that it should not be discarded entirely and should be used in combination with other active learning methodologies, since algebraic manipulation or calculus abilities are required by other methodologies [80,81,82].
Another two methodologies introduced for teaching ordinary differential equations are the well-known qualitative and numerical approaches that were studied in [5,6,8,9,49,52,73,74,81,83,84,85,86,87,88,89,90,91]. The numerical and qualitative study of differential equations appears to overcome the disadvantage that a wide class of differential equations is not solvable by analytic methods. In practical implementations, both approaches demand the incorporation of new concepts, like graphical solutions, direction fields, stability, increasing or decreasing behaviours of the solution, the interpretation of situations based on the behaviours of solutions, numerical schemes, numerical errors, and the order of approximation. However, the teaching of those concepts can be achieved by using some graphical tools to avoid tedious algebraic calculus and obtain an immediate visualisation of the solution. Thus, with the increasing incorporation of information and communication technologies in the teaching of mathematics, qualitative and numerical methods are becoming more frequently used in the classroom, and their potential characteristic is the approach to solutions of several types of ordinary differential equations [74,92].
More recently, the methodologies researched in the context of teaching ordinary differential equations are those based on well-known active learning methodologies [3,10,57,73,81,82,85,87,89,93,94,95,96,97,98,99,100,101,102,103,104,105,106,107,108,109,110,111,112,113,114,115,116,117,118,119]. Here, active learning methods are understood as student-centred teaching methodologies that provide students with the opportunity to participate in mathematical research or problem-solving groups, where they construct and share knowledge in communities while maintaining appropriate feedback on their work from experts and peers. It is also known that there are several methodologies that are grouped under the concept of active learning methodologies, and to be more precise, there are works that cover several of the standard active methodologies, for instance, inquiry-based instruction (see [10,85,89,101,102,105,106,107,108,109,110,111,117,118]), problem-based learning (see [93,100]), problem-solving methodology (see [3,57,81,95,116]), analysis of errors (see [94]), actions, processes, objects, schemas (APOS) theory (see [96]), and the competences-based methodology (see [97]). In the other works, some specific learning methodologies are developed. In this sense, the works of Raychaudhuri [112,113,114,115], where the author presents innovative active learning methodologies to teach advanced topics (for instance, existence and uniqueness theorems) associated with ordinary differential equations deserve a special mention.
On the other hand, we know that the teaching of ordinary differential equations has been influenced by mathematical modelling (see [32,33,35,36,37,38,39,40,41,42,43,44,45,46,47,48,49,50,51,52,53,54,55,56,58,83,120,121,122,123,124,125,126,127]), information and communication technologies (see [42,44,48,49,53,70,81,100,120,122,123,125,126,128]), and project-based learning (see [125,129,130,131]) approaches. The focus of those articles is diverse. For instance, in the case of mathematical modelling, we found some articles where the aim is to develop mathematical modelling abilities to solve real problem models by the application of ordinary differential equations. Other articles are dedicated to the use of mathematical modelling as a pedagogical strategy to teach some concepts of ordinary differential equations, and other articles use mathematical modelling activities with some ordinary differential equations to teach concepts of other sciences. Particularly in the present research, we consider some activities based on mathematical modelling to teach the basic concepts of first-order ordinary differential equations.
4. Methodology
4.1. Setting
The research was conducted on a course of “ordinary differential equations and numerical calculus” for pedagogy mathematics education students at a Chilean university. The students must take this course in the first semester of their fourth year. At the time of the research, the majority of the students had completed courses in algebra, differential and integral calculus, calculus of several variables, geometry, mathematical analysis, and algebraic structures. For the teaching intervention, the first unit of the subject was selected.
In order to construct the mathematical modelling activity analysed here, one of the physical problems linked to the origins of the concept of ordinary differential equations was chosen: the problem of free fall. For this problem, two solutions given by Galileo and Newton, respectively, were exposed. The students worked through the lecture and activities found in Section 4.4. The learning objectives for the mathematical modelling activity are those presented in Table 1. The activity also considered five transversal objectives: (i) the introduction of students to the notion of modelling assumptions; (ii) the use of theoretical models to identify the variables and parameters that are involved in the mathematical model; (iii) the translation of textual information into a symbolic expression with clear definitions of constants and variables; (iv) the encouragement of validation on the models with real or laboratory experiments; and (v) the proposal of generalised models that increase the approximation and are valid under new assumptions.
As the reader can see in Table 1, the learning objectives are presented in increasing order of difficulty, from identifying the physical meanings of the coefficients in a first-order ordinary differential equation to building the notion of a solution to an ordinary differential equation.
4.2. Participants
For the development of this research, an intervention was carried out during the first semester of 2018 in a course on “ordinary differential equations” for preservice teachers (mathematical education program) at a Chilean university.
Twelve students (from a total of thirty-three students in the course) voluntarily participated in the research. All students were participating in the course for the first time. At the beginning of the intervention, the students formed groups of, at most, four students. We must emphasise that the total number of students in the course was thirty-three; all of them participated in the activities, and although the written material of all the groups was collected, for the purposes of the analysis presented in this paper, only three groups (of four students each) were selected based on the following criteria: regularity of participation in the development of the activity, punctuality and class attendance, and the presence of well-documented written work.
4.3. Procedures for Data Collection
The data collection was performed during the class schedule while the students completed the mathematical modelling activities in groups. No limits were imposed on the use of sources such as printed or digital texts or numerical, symbolic, or graphic calculation software. Students worked on the activities without interaction between groups. After the students solved the task, the researchers gathered the written work from each group. Then, the teacher presented and discussed the solution with the whole class.
We must observe two facts. First, the data used in the present investigation are part of a broader investigation where ten lectures were considered to cover the teaching of other concepts of differential equations, including, for instance, stability, existence, and uniqueness, equilibrium points, and asymptomatic behaviour. The details of this complete intervention design are presented in [65]. Second, during data collection, the researcher was only an observer and did not interact with the participants.
4.4. The Mathematical Modelling Activity
We analysed the written work in which students presented their processes used to find a solution. Following the content analysis methodology, we looked for paragraphs indicating some information regarding the learning objectives shown in Table 1.
The mathematical modelling activity was compounded by two parts. In the first part, called “Lecture: The free fall problem”, the context was presented (see Section 4.4.1). The second part contained the activities for the students (see Section 4.4.2). The activities focused on the construction of their own notions of the concepts of an ordinary differential equation and the solution to an ordinary differential equation.
4.4.1. Lecture: The Free Fall Problem
The phenomenon of free fall of a body is probably the simplest example of the first context historically related to the theory of differential equations. In what follows, different aspects related to this problem are reviewed. We begin by recalling that, until the end of the 17th century, mathematicians and scientists working in astronomy thought in terms of magnitudes related to the motions of the planets. This method of analysing celestial bodies changed significantly thanks to the innovative work of Sir Isaac Newton (1642–1727). The main contribution of Newton was the incorporation of an analysis based on the forces acting on bodies instead of their motions. More specifically, Newton described the forces acting on celestial bodies, stated the laws under which motion occurs, and introduced mathematical models to describe motion. Newton’s findings opened up new avenues for looking at the universe and gave scientists a new set of tools for examining it (Newton’s laws of motion). It is also known that Newton influenced other mathematicians, such as Euler and Bernoulli, prompting them to interpret phenomena in the language of differential equations. In the lecture, this initial historical period of differential equations was contextualised with the free fall of a body.
The free fall problem is stated as follows:
Problem 1.
A body of a given mass is at rest at a certain height above the earth. Determine the velocity and distance travelled by this body if it is dropped.
The solutions of Galileo and Newton are described below.
Galileo-type solution to Problem 1. Galileo Galilei (1564–1642) was an Italian scientist who, among other problems, was interested in the movement of bodies. He is the foremost representative of what happened in scientific discovery before Newton. Curiously, the year of his death coincides with the year of Newton’s birth. Galileo was an experimentalist who developed systematic ways to build experiments, which led him to find certain relationships between several magnitudes. In particular, regarding the motion of bodies, Galileo considered the following assumption:
- (S1)
- The object moves without resistance, and the deceleration effect due to friction is discarded; that is, it is considered as if the body were falling in a vacuum.
Under the assumption (S1), using the inclined plane experiment, he empirically discovered the following laws:
- (G1)
- If an object moves at constant speed (without acceleration), the distance is proportional to the time, and the constant of proportionality is the speed.
- (G2)
- In uniformly accelerated motion, velocity is proportional to time, and the constant of proportionality is acceleration.
- (G3)
- In uniformly accelerated motion, distance is proportional to time squared, and the constant of proportionality is half the acceleration.
These laws can be expressed algebraically by the following equations:
respectively. In these equations, e denotes the distance, v is the velocity, a is the acceleration, and t is the time. Note that (2) ocurrs with . According to (G1), Galileo discovered that the solution to Problem 1 is given by
where g is the acceleration due to gravity.
Newton-type solution to Problem 1. When performing free fall experiments in environments where the assumption (S1), considered by Galileo, is not valid, it was observed that the solution (5) to the problem is not valid either. Thus, it was necessary to develop a more general theory to solve the problem under more realistic conditions. An example that came much later than Newton that clearly shows this fact was the experiment by the test parachutist Vasili Romaniuk (1910–1993). In 1945, Vasili jumped with a closed parachute and fell more than 12,000 m in these conditions. If we assume that (S1) is valid for this case, the time and velocity would be
respectively. However, Vasili reached a speed of approximately 60 m/s. Thus, the formulas deduced by Galileo led to erroneous results.
Newton observed that, to generalise Galileo’s theory, it was necessary to pay more attention to the forces involved in the movement. This is because he noticed that Galileo’s laws worked under the action of a single force, the force of gravity. Now, in the presence of air, there is another balancing force that was not taken into account by Galileo; this force is air resistance. This force is what prevented the skydiver from falling at a speed of 485 m/s and is what causes a phenomenon whose behaviour is as if it “supported” the skydiver. More specifically, Newton formulated the following three laws of motion:
- (N1)
- Every body perseveres in its state of rest or uniform and rectilinear movement unless it is forced to change its state by external forces acting on it.
- (N2)
- The change in motion is directly proportional to the external driving force and occurs according to the straight line along which that external force moves.
- (N3)
- For every action, an equal and opposite reaction always occurs, which means that the mutual actions of two bodies are always equal and directed in the opposite direction.
Note that the three laws of Newton are stated in terms of forces, and it is supposed that (S1) does not hold.
In the case of free fall movement, we suppose that the body is moving only because of two forces, gravity and air resistance, which are given by
respectively, where m is the mass and b is a proportionality constant. The negative sign in (7) means that this force is in the opposite direction to the velocity. Now, we apply (N2) and deduce the following relation:
where a is the acceleration of the body. By replacing (6) and (7) in (8), we deduce that
In (9) and for , it is possible to clear v and obtain to answer Problem 1. However, this expression is given in terms of an unknown quantity: a. Apparently, the relationship (9) is not enough to give an answer to Problem 1. This perception is wrong, since this difficulty can be overcome by incorporating the relationships among acceleration, velocity, distance, and time under the concept of the “derivative of a function”, that is,
which were defined by Newton as part of his discovery of differential calculus. Replacing (11) in (9) we have
4.4.2. Activities for the Students
After reading the lecture, the students answered the following questions:
- (I)
- Observe the relation (12) and give a justified answer to the following questions:
- (a)
- What is the physical meaning of m? What kind of mathematical object (number or scalar, vector, matrix, function, or operator) is m? Is this quantity a given data point or an unknown for the problem?
- (b)
- Answer the same questions given in item (a) for b.
- (c)
- Answer the same questions given in item (a) for g.
- (d)
- Answer the same questions given in item (a) for v.
- (II)
- In the absence of the force of air resistance, we have or, equivalently, , according to (7). In this case, from (12)–(13), the Newton-type solution to Problem 1 is given byGive a justified answer to the following questions:
- (a)
- (b)
- (c)
- From (a) and (b), deduce how Galileo’s and Newton’s solutions to Problem 1 are related in the case of the absence of air resistance.
- (III)
- It is convenient to note that Galileo gave explicit formulas for v and e. On the other hand, the solutions offered by Newton in (12) and (13) require a procedure to deduce the values of v and e. In general terms, it can be said that, to obtain Newton’s solution to Problem 1, it is necessary to “find” both v and e by some procedure. Taking into account that you have to “find” some unknown quantities and that the derivatives of these unknown expressions also participate, answer each of the following questions with justification:
- (a)
- (b)
4.4.3. Remarks of MEA Principles Used in the Lecture
The principle of reality corresponds to the interpretation of the context presented in a concrete, physical, or real situation. We understand that something can be real when it is imaginable for individuals. In this case, it is related to the historical point of view. In the free fall problem, the physical situation is connected with the previous knowledge of students, and it is clearly conceivable for them to achieve a mathematical interpretation using their own experience.
Related to the model construction principle, in the first task, the construction of a model was not precisely addressed. In this task, an introductory activity for the students to explore a model was considered. Moreover, the lecture included an introduction to some properties of modelling practices, like the modification and extension of mathematical models and a description or explanation of the phenomenon.
The third and fourth principles are satisfied as the students work in teams where they have the opportunity to express their thinking regarding the solution processes. Thus, they are able to evaluate their progress by checking out their answers, and at the same time, information in written form is collected.
The simple prototype principle is naturally present in the activity since, in the lecture, a widely studied model is presented, and its history gives rise to the construction of a model that stands out for its simplicity and clarity.
In relation to the sixth principle, the generalisation of the models presented in the lecture was addressed as the students advanced in the solution processes of the other tasks. However, with the Galileo and Newton models, it was possible to reflect on the behaviours in situations that are described by similar models.
5. Analysis of the Data and Interpretation
Information about students’ production data is displayed at the end of the article in Table A1, Table A2, Table A3 and Table A4. Moreover, a summary of the sentences is given in Table 2.

Table 2.
Summary of students’ productions for the activities given in Section 4.4.2. Here, the LO code is referred to in the second column of Table 1, and Gr refers to the group. The complete information, including the original students’ production, is shown in Table A1, Table A2, Table A3 and Table A4.
For objectives O1.T1-L1, O2.T1-L1 and O3.T1-L1, we studied the answers to items I(a), I(b), and I(c) given in rows 1, 2, and 3 of Table A1, respectively. Regarding the objective O1.T1-L1, it was deduced that the students did not present difficulties with identifying the physical meanings of and v in the first-order ordinary differential equation
which was introduced in a contextualised way in the lecture on the free fall problem as a model for describing the change in velocity of a body in free fall and under the assumptions of Newton. The three groups clearly expressed that m is the mass, b is a constant of proportionality, g is the acceleration due to gravity, and v is the velocity. For the objective O2.T1-L1, it was observed that the students from all groups identified m and b as scalar quantities, but with regard to g, two groups identified it as a scalar and one of them as a vector. The association of g as a vector probably stems from the fact that the students took courses in physics where it was emphasised that the acceleration of gravity is a vector quantity. However, in the case of the free fall problem, the direction and sense of the acceleration due to gravity remain fixed, and the notation g is a scalar. Regarding O3.T1-L1, it was observed that the students clearly recognised the parameters in the equation, since they reported m, b, and g as data. It is necessary to comment that one of the groups omitted their opinion regarding b, but taking into account that they recognised it as a constant of proportionality, it can be deduced that, for them, b also represents data.
Regarding objective O4.T1-L1, we inspected the students’ production for Item I(d), which is given in row 4 of Table A1. “What is the physical meaning of v in (16)?” “What kind of mathematical object is v?” “Is this quantity a given or an unknown for Problem 1?” It should be noted that here Problem 1 refers to the problem of free fall: “A body of given mass is at rest at a certain height above the earth. Determine the velocity and the distance travelled by this body if it is dropped.” As a response to this item, students are expected to recognise that, physically, v is the velocity of the body and, mathematically, it is a function of a real variable and that for the differential Equation (16), it is an unknown. It was observed that the three groups recognised that v is an unknown for the differential equation. Specifically, the transcription from a production standpoint: “v is the speed, is a function, is an unknown for the problem” (Group 1); “ velocity is an unknown for the problem, is a vector” (Group 2); and “ velocity, function or operator, unknown” (Group 3). However, there is no coincidence regarding the type of mathematical object, since for Group 1 it is a function, for Group 2 it is a vector, and for Group 3 it is a function or operator.
For the objective O5.T1-L1, we examined the answers to Item II(a) (see Table A2). In this case, the students were requested to determine the expressions for v and e that satisfy the following relations:
Group 2 carried out a sequence of steps without being able to determine the correct answer. None of the three groups were able to determine an algebraic expression for e. Groups 1 and 3 used properties of integration to find v, with the expressions and being reported as solutions, respectively. Group 3 realised that the expression for e could be derived via integration, but in the attempt to apply integration properties, they incorrectly interpreted the second-order derivative: the integral was interpreted as , and was interpreted as . It is important to remember that the students took courses on differential and integral calculus, where they experimented with expressions of the form and high-order derivatives, in particular, with , but here they did not recognise that can be rewritten as with In this sense, the error is related to one of the appreciations given by [79]: the student needs some time to familiarise himself with notations and terminologies until they become part of his “body of knowledge”.
Regarding objective O6.T1-L1, we analysed Item II(b) (see row 1 of Table A3). The three groups used properties of differentiation to verify that is a solution to . With regard to verifying that is a solution to , only Group 2 carried out a verification through differentiation. In this item, they were also asked to give an open opinion regarding their observations, which was not completed by any of the groups.
For objective O7.T1-L1, we reviewed the answers to item II(c) (see row 2 of Table A3). In this case, only Group 3 wrote the following: “both solutions are equal, this means that under the absence of air force, both solutions are equal” for the request to describe the relationship between the solutions proposed by Galileo and Newton to the problem of free fall. It is recalled that the expressions for the speed and the distance travelled by the body deduced by Galileo are and , and those deduced by Newton are and , respectively, with and as constants. It is observed that the students emphasised the assumption of the “absence of air force” or, to be precise, the force of air resistance; that is, they deduced that there is a relationship of equality in the solutions under this assumption.
In order to study objectives O8.T1-L1 and O9.T1-L1, we examined the answers to items III(a) and III(b) (see Table A4). In item III(a), taking advantage of the context of the Newtonian solution to the free fall problem,
students were asked to propose the notion of a differential equation. In this case, students were expected to create a text close to the formal definition of a differential equation. Faced with this activity, one group did not give any response, and the other two groups wrote the following: “unknown derivative equation, because we do not know the derivative of the values we want to find” (Group 1) and “differential equation, since it is an equation that is constituted by the differential of a function and constant values ” (Group 3). It is observed that the notion described by Group 3 is the appropriate one and that both groups agreed that there is an unknown object; Group 1 did not make it explicit, and Group 3 established that it is a function. A difference is that, in their justification, the students in Group 1 established their notion in terms of derivatives and those in Group 3 established theirs in terms of differentials. Regarding item III(b), the following responses were reported: “play the role of vectors” (Group 2) and “are the differentials of the equations” (Group 3). It is observed that the students did not understand the requested objects as functions that play the roles of solutions to the differential equations. Thus, from here, we conclude that to construct a definition or solution to an ordinary differential equation, the students did not exhibit pertinent technical writing and confused some concepts, such as v being identified as a vector being a function, and in (17), the equations are in terms of the ordinary derivatives of primer and second order and not in terms of differentials.
6. Discussion
In this article, we addressed two important issues related to the teaching and learning of differential equations: (a) we proposed a model-eliciting activity to facilitate the students’ learning of ordinary differential equation concepts and (b) we characterised the conceptual learning of first-order differential equations developed by students when they solved a task built on the basis of a model-eliciting activity approach. The first issue (a) was addressed by identifying relevant concepts associated with differential equations and creating a task to accomplish them, following the approach of model-eliciting activities. In particular, we considered the six principles to construct a specific model-eliciting activity. The activity was divided into two parts. The first part, called “Lecture: The free fall problem”, contained contextualised solution approaches given by Galileo and Newton to the free fall problem. In the second part, through different activities, we encouraged the students to construct basic concepts of first-order ordinary differential equations, such as definitions of ordinary differential equations and solutions to ordinary differential equations. Moreover, the context of the lecture allowed us to propose a way to favour interactions between the meanings related to differential equations and the meanings related to physics.
In summary, regarding the task design for teaching differential equations, we structured and developed a method of design that considered contextualised situations in different areas of the discipline and included a series of questions following the principles of MEAs. This method was also used as support for planning the content of a whole course on differential equations [65].
Regarding the characterisation of the conceptual learning of first-order differential equations (b), our findings are described in the data analysis presented in Section 5. In a broad sense, taking into account the answers of the students, we argued that the construction of concepts and the learning of procedures associated with differential equations were favourably stimulated by the proposed model-eliciting activity. Particularly, we observed that the students adequately understood the description of the texts and correctly interpreted the physical meanings of velocity, gravity, and air resistance force. Regarding the interpretation of mathematical meanings, students presented difficulties by confusing the role of mathematical objects, which were deduced through inappropriate associations with known characteristics of the object from the point of view of physics. However, this inadequate mathematical interpretation was not an obstacle for them in constructing the notion of a differential equation. Related to the use of procedures, the students did not present difficulties in carrying out analytic procedures such as differentiation and algebraic rearrangements. This favoured the students’ ability to correctly carry out an activity where they were asked to verify that a given function is a solution to a certain differential equation. However, they presented difficulties with the procedures related to integral calculus, since they did not perform the correct calculation of the integral of the form .
On the other hand, a limitation of the study is that the productions presented by the students in the course that did not belong to any of the three groups were not analysed.
7. Conclusions
In this research, a model-eliciting activity to facilitate the learning of concepts of ordinary differential equations was proposed. In this context, the conceptual learning of the students who participated in the process of solving the activities was characterised. The analysis of students’ written productions showed the presence of indicators of the learning objectives related to previously established concepts. The main findings were as follows: (i) The students recognised the physical meanings of the parameters involved in the differential equations; and (ii) The students, in spite of precise technical notations and terminologies, were able to construct their own notion of a differential equation close to the standard definition. In addition, we observed that the students were confused with the notation and some mathematical meanings that were part of their prior knowledge. For example, in the differential equation for the free fall problem, they recognised velocity as a vector, but the role it plays from the point of view of mathematics is a scalar. This is an important point to reflect on because, currently, the teaching of subjects from mathematics tends to be related to subjects from other disciplines, so it is necessary to take into account the difficulties that students may experience when working with concepts that can have different meanings in other disciplines.
Author Contributions
Conceptualisation, E.L., C.G.-O., A.C. and R.M.; methodology, E.L.; software, E.L.; validation, C.G.-O., A.C. and R.M.; formal analysis, E.L. and C.G.-O.; investigation, E.L., C.G.-O. and R.M.; resources, C.G.-O. and A.C.; data curation, E.L.; writing—original draft preparation, E.L. and A.C.; writing—review and editing, E.L., C.G.-O., A.C. and R.M.; visualisation, E.L.; supervision, E.L. and C.G.-O.; project administration, E.L.; funding acquisition, C.G.-O. and A.C. All authors have read and agreed to the published version of the manuscript.
Funding
This research was partially founded by: Agencia Nacional de Investigación y Desarrollo (ANID)-Chile through projects Fondecyt/iniciación No. 11200169, Fondecyt/Regular No. 1230560, and Fondecyt/Regular No. 1200005; EDU2017-84276-R, España; Universidad del Bío-Bío (Chile) through research project 2120436 IF/R, research project INES I+D 22–14; and the Universidad Tecnológica Metropolitana through a project supported by the Competition for Research Regular Projects, year 2020, Code LPR20-06.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Acknowledgments
The authors would like to express their sincere gratitude to anonymous reviewers of the manuscript, and to Matías Camacho (Universidad de la Laguna, España) and Francisco Cortez (Instituto Politécnico Nacional, México) for their observations on the topic of the paper when they made the review of Ph.D. thesis [65].
Conflicts of Interest
The authors declare no conflict of interest.
Appendix A. Production of Students for Activities Given on Section 4.4.2

Table A1.
Student productions for the activities of Item I given on Section 4.4.2.
Table A1.
Student productions for the activities of Item I given on Section 4.4.2.
| Item | Group | Production | Translation |
|---|---|---|---|
| I (a) | 1 |  | a) The physical meaning of m is mass. The mathematical object is a number. It is data for the problem. |
| 2 |  | (a) m = mass. It is a number or scalar. It is a datum. | |
| 3 | 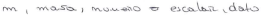 | mass, number or scalar, datum. | |
| I (b) | 1 |  | b) b is a constant of proportionality, is a number, is a datum for the problem. |
| 2 |  | (b) n = is a constant of proportionality, number or scalar. | |
| 3 | 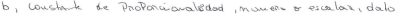 | constant of proportionality, number or scalar, datum | |
| I (c) | 1 |  | c) g is the acceleration of the gravity, is a number, is a datum for the problem. |
| 2 |  | (c) g = the acceleration of the gravity. It is a number or scalar. It is a datum. | |
| 3 | 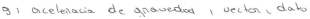 | acceleration of the gravity, vector, datum. | |
| I (d) | 1 |  | d) v is the the velocity, is a function, is an unknown for the problem |
| 2 |  | (d) v = velocity is an unknown for the problem, is a vector. | |
| 3 |  | velocity, function or vector, unknown. |

Table A2.
Students’ productions for the activities of Item II(a) given on Section 4.4.2. The “*” in the translation column corresponds to the “*” notation of the students’ production.
Table A2.
Students’ productions for the activities of Item II(a) given on Section 4.4.2. The “*” in the translation column corresponds to the “*” notation of the students’ production.
| Item | Group | Production | Translation |
|---|---|---|---|
| II (a) | 1 |  | |
| 2 |  | (a) We have the equations… using the fact that , we have that where or v is equal to * we have that the derivative of 0 with respect to t is 0. Then: if b is equal to 0. * we have that the derivative of 0 with respect to t is 0. We conclude that … . | |
| 3 | 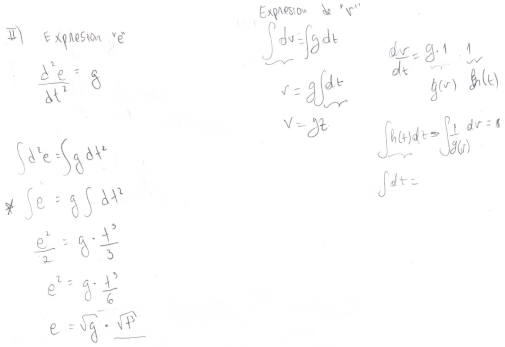 | Expression for “e” … Expression for “v” |

Table A3.
Student productions for the activities of Item II(b) and Item II(c) given on Section 4.4.2.
Table A3.
Student productions for the activities of Item II(b) and Item II(c) given on Section 4.4.2.
| Item | Group | Production | Translation |
|---|---|---|---|
| II (b) | 1 |  | |
| 2 | (b) From …,
we apply the derivative … …obtaining … …we calculate the second derivative … …we observe that, when we derivative …we obtain … | ||
| 3 | |||
| II (c) | 1 | ||
| 2 | |||
| 3 |  | Both solutions are equal, this means that under the absence of air force both solutions are equal. |

Table A4.
Student productions for the activities of Item III given on Section 4.4.2.
Table A4.
Student productions for the activities of Item III given on Section 4.4.2.
| Item | Group | Production | Transalation |
|---|---|---|---|
| III (a) | 1 |  | a) unknown derivative equation, because we do not know the derivative of the values we want to find |
| 2 | |||
| 3 |  | (a) differential equation, since it is an equation that is constituted by differentials of a function and constant values | |
| III (b) | 1 | ||
| 2 | 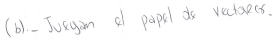 | (b) play the role of vectors. | |
| 3 |  | (b) are the differentials of the equations. |
References
- Arslan, S. Traditional instruction of differential equations and conceptual learning. Teach. Math. Appl. 2010, 29, 94–107. [Google Scholar] [CrossRef]
- Alves de Oliveira, E.; Camargo, S.B. Ensino e aprendizagem de equações diferenciais: Um levantamento preliminar da produção científica. Teia-Rev. Educ. Mat. Tecnol. Iberoam. 2013, 4, 1–24. [Google Scholar]
- Barros, A.A.; Laudares, J.B.; de Miranda, D.F. A resolução de problemas em ciências com equações diferenciais ordinárias de 1a e 2a ordem usando análise gráfica. Educ. Mat. Pesqui. 2014, 16, 323–348. [Google Scholar]
- Arslan, S. Do students really understand what an ordinary differential equation is? Int. J. Math. Educ. Sci. Technol. 2010, 41, 873–888. [Google Scholar] [CrossRef]
- Artigue, M.; Gautheron, V. Systemes Differentiels: Etude Graphique; Editions Cedic: Paris, France, 1983. [Google Scholar]
- Blanchard, P. Teaching differential equations with a dynamical systems viewpoint. Coll. Math. J. 1994, 25, 385–393. [Google Scholar] [CrossRef]
- Boyce, W.E. New Directions in Elementary Differential Equations. Coll. Math. J. 1994, 25, 364–371. [Google Scholar] [CrossRef]
- Habre, S. Investigating students’ approval of a geometrical approach to differential equations and their solutions. Int. J. Math. Educ. Sci. Technol. 2003, 34, 651–662. [Google Scholar] [CrossRef]
- Hernández, A. Obstáculos en la Articulación de los Marcos Numérico, Gráfico y Algebraico en Relación con las Ecuaciones Diferenciales Ordinarias. Ph.D. Thesis, Cinvestav, Ciudad de México, Mexico, 1995. [Google Scholar]
- Rasmussen, C.L.; King, K.D. Locating starting points in differential equations: A realistic mathematics education approach. Int. J. Math. Educ. Sci. Technol. 2000, 31, 161–172. [Google Scholar] [CrossRef]
- Lesh, R.; Doerr, H. Beyond Constructivism: A Models and Modeling Perspective on Mathematical Problem Solving, Learning, and Teaching; Lawrence Erlbaum Associates: Mahwah, NJ, USA, 2003. [Google Scholar]
- Edelstein-Keshet, L. Mathematical Models in Biology. (Classics in Applied Mathematics, 46); Society for Industrial and Applied Mathematics (SIAM): Philadelphia, PA, USA, 2005. [Google Scholar]
- Segel, L.A.; Edelstein-Keshet, L. A Primer on Mathematical Models in Biology; Society for Industrial and Applied Mathematics (SIAM): Philadelphia, PA, USA, 2013. [Google Scholar]
- Dhaoui, I.; Van Bortel, W.; Arsevska, E.; Hautefeuille, C.; Tablado Alonso, S.; Kleef, E.V. Mathematical modelling of COVID-19: A systematic review and quality assessment in the early epidemic response phase. Int. J. Infect. Dis. 2022, 116, S110. [Google Scholar] [CrossRef]
- Meehan, M.T.; Diana, P.; Rojas, D.P.; Adekunle, A.I.; Adegboye, O.A.; Caldwell, J.M.; Turek, E.; Williams, B.M.; Marais, B.J.; Trauer, J.M.; et al. Modelling insights into the COVID-19 pandemic. Paediatr. Respir. Rev. 2020, 35, 64–69. [Google Scholar] [CrossRef]
- Crokidakis, N. Modeling the early evolution of the COVID-19 in Brazil: Results from a Susceptible-Infected-Quarantined-Recovered (SIQR) model. Int. J. Modern Phys. C 2020, 31, 2050135. [Google Scholar] [CrossRef]
- Biswas, H.A.; Hossain, R.H.; Mondal, M.K. Mathematical Modeling Applied to Sustainable Management of Marine Resources. Procedia Eng. 2017, 194, 337–344. [Google Scholar] [CrossRef]
- Jyotsna, K.; Tandon, A. A nonlinear mathematical model investigating the sustainability of an urban system in the presence of haphazard urban development and excessive pollution. Nat. Resour. Model. 2018, 31, e12163. [Google Scholar] [CrossRef]
- Alabugin, A.; Osintsev, K.; Aliukov, S.; Almetova, Z.; Bolkov, Y. Mathematical foundations for modeling a zero-carbon electric power system in terms of sustainability. Mathematics 2023, 11, 2180. [Google Scholar] [CrossRef]
- Shodikin, A.; Istiandaru, A.; Purwanto, S.; Sudirman. Thinking errors of pre-service mathematics teachers in solving mathematical modelling task. J. Phys. Conf. Ser. 2019, 1188, 012004. [Google Scholar] [CrossRef]
- Anhalt, C.O.; Cortez, R. Developing Understanding of Mathematical Modeling in Secondary Teacher Preparation. J. Math. Teach. Educ. 2015, 19, 523. [Google Scholar] [CrossRef]
- English, L.D. Mathematical Modeling in the Primary School: Children’s Construction of a Consumer Guide Educ. Stud. Math. 2006, 63, 303. [Google Scholar] [CrossRef]
- Hernández, M.L.; Levy, R.; Felton-Koestler, M.D.; Zbiek, R.M. Mathematical Modeling in the High School Curriculum. Math. Teach. 2016, 110, 336. [Google Scholar] [CrossRef]
- Borromeo, R. Theoretical and empirical differentiations of phases in the modelling process. ZDM Zentralblatt Didakt. Math. 2006, 38, 86–95. [Google Scholar]
- Greefrath, G.; Vorhölter, K. Teaching and learning mathematical modelling: Approaches and developments from German speaking countries. In Teaching and Learning Mathematical Modelling (ICME-13 Topical Surveys); Kaiser, G., Ed.; Springer: Cham, Switzerland, 2016. [Google Scholar]
- Perrenet, J.; Zwaneveld, B. The many faces of the mathematical modeling cycle. J. Math. Model. Appl. 2012, 1, 3–21. [Google Scholar]
- Stohlmann, M.; De Vaul, L.; Allen, C.; Adkins, A.; Ito, T.; Lockett, D.; Wong, N. What is known about secondary grades mathematical modelling—A Review. J. Math. Res. 2016, 8, 12–28. [Google Scholar] [CrossRef]
- Kaiser, G.; Blomhøj, M.; Sriraman, B. Towards a didactical theory for mathematical modelling. ZDM. Zentralblatt Didakt. Math. 2006, 38, 82–85. [Google Scholar] [CrossRef]
- Galbraigth, P. Models of Modelling: Genres, Purposes or Perspectives. J. Math. Model. Appl. 2012, 1, 3–16. [Google Scholar]
- Leung, F.; Stillman, G.; Kaiser, G.; Won, K. (Eds.) Mathematical modelling education in east and west. In International Perspectives on the Teaching and Learning of Mathematical Modelling; Springer: Dordrecht, The Netherlands, 2021. [Google Scholar]
- Stillman, G.; Blum, W.; Kaiser, G. (Eds.) Mathematical Modelling and Applications. In ICTMA 17, International Perspectives on the Teaching and Learning of Mathematical Modelling; Springer: Dordrecht, The Netherlands, 2017. [Google Scholar]
- Czocher, J.A. Introducing modeling transition diagrams as a tool to connect mathematical modeling to mathematical thinking. Math. Think. Learn. 2016, 18, 77–106. [Google Scholar] [CrossRef]
- Czocher, J.A. How can emphasizing mathematical modeling principles benefit students in a traditionally taught differential equations course? J. Math. Behav. 2017, 45, 78–94. [Google Scholar] [CrossRef]
- Lozada, E.; Guerrero-Ortiz, C.; Coronel, A.; Medina, R. Classroom methodologies for teaching and learning ordinary differential equations: A systemic literature review and bibliometric analysis. Mathematics 2021, 9, 745. [Google Scholar] [CrossRef]
- Almeida, L.M.; Kato, L.A. Different approaches to mathematical modelling: Deduction of models and studens’ actions. Int. Electron. J. Math. Educ. 2014, 9, 3–11. [Google Scholar] [CrossRef]
- Borssoi, A.H.; de Almeida, L.M.W. Modelagem matemática e aprendizagem significativa: Uma proposta para o estudo de equações diferencias ordinárias. Educ. Mat. Pesqui. 2004, 6, 91–121. [Google Scholar]
- de Almeida, L.M.W. Considerations on the use of mathematics in modeling activities. ZDM Math. Educ. 2018, 50, 19–30. [Google Scholar] [CrossRef]
- Flegg, J.A.; Mallet, D.G.; Lupton, M. Students’ approaches to learning a new mathematical model. Teach. Math. Appl. 2013, 32, 28–37. [Google Scholar] [CrossRef]
- Klymchuk, S.; Zverkova, T.; Gruenwald, N.; Sauerbier, G. Increasing engineering students’ awareness to environment through innovative teaching of mathematical modelling. Teach. Math. Appl. 2008, 27, 123–130. [Google Scholar] [CrossRef]
- Gruenwald, N.; Sauerbier, G.; Narayanan, A.; Klymchuk, S.; Zverkova, T. Applications in unusual contexts in engineering mathematics: Students’ attitudes. Math. Teach. Res. J. Online 2010, 4, 53–67. [Google Scholar]
- Laudares, B.J.; de Miranda, D.F. Investigando a iniciação à modelagem matemática nas ciências com equações diferenciais. Educ. Mat. Pesqui. 2007, 9, 103–120. [Google Scholar]
- Molina-Mora, J.A. Mathematical modeling as a didactic strategy for calculus teaching. Uniciencia 2017, 31, 19–36. [Google Scholar] [CrossRef][Green Version]
- Rodríguez, R. Teaching and learning modelling: The case of differential equations. Rev. Latinoam. Investig. Mat. Educ. 2010, 13, 191–210. [Google Scholar]
- Liberatti, S.; da Silva, D. Mathematical modeling and analysis of mathematical models in mathematics education. Acta Sci. 2012, 14, 260–275. [Google Scholar]
- Trigueros, M. Vínculo entre la modelación y el uso de representaciones en la comprensión de los conceptos de ecuación diferencial de primer orden y de solución. Educ. Mat. 2014, 25, 207–226. [Google Scholar]
- Zang, C.M.; Fernández, G.A.; León, M.N. Reflexiones sobre la implementación de problemas de modelado para la construcción y resignificación de objetos matemáticos vinculados a las ecuaciones diferenciales. UNION Rev. Iberoam. Educ. Mat. 2015, 42, 150–165. [Google Scholar]
- Alvim, B.N.P.; de Almeida, L.M.W. Linguistic appropriation and meaning in mathematical modeling activities. BOLEMA Bol. Educ. Mat. 2019, 33, 1195–1214. [Google Scholar]
- Guerrero-Ortiz, C.; Mejía-Velasco, H.R.; Camacho-Machín, M. Representations of a mathematical model as a means of analysing growth phenomena. J. Math. Behav. 2016, 42, 109–126. [Google Scholar] [CrossRef]
- Camacho-Machín, M.; Guerrero-Ortiz, C. Identifying and exploring relationships between contextual situations and ordinary differential equations. Int. J. Math. Educ. Sci. Technol. 2015, 46, 177–195. [Google Scholar] [CrossRef]
- Chaachoua, H.; Saglam, A. Modelling by differential equations. Teach. Math. Appl. 2006, 25, 15–22. [Google Scholar] [CrossRef]
- Melendez, B.; Bowman, S.; Erickson, K.; Swim, E. An integrative learning experience within a mathematics curriculum. Teach. Math. Appl. 2009, 28, 131–144. [Google Scholar] [CrossRef]
- András, S.; Szilágyi, J. Modelling drug administration regimes for asthma: A romanian experience. Teach. Math. Appl. 2010, 29, 1–13. [Google Scholar] [CrossRef]
- Ribaric, S.; Kordas, M. Teaching cardiovascular physiology with equivalent electronic circuits in a practically oriented teaching module. Adv. Physiol. Educ. 2011, 35, 149–160. [Google Scholar] [CrossRef] [PubMed]
- Robinson, G.; Jovanoski, Z. Fighter pilot ejection study as an educational tool. Teach. Math. Appl. 2010, 29, 176–192. [Google Scholar] [CrossRef]
- Rowland, D.R.; Jovanoski, Z. Student interpretations of the terms in first-order ordinary differential equations in modelling contexts. Int. J. Math. Educ. Sci. Technol. 2004, 35, 503–516. [Google Scholar] [CrossRef]
- Rowland, D.R. Student difficulties with units in differential equations in modelling contexts. Int. J. Math. Educ. Sci. Technol. 2006, 37, 553–558. [Google Scholar] [CrossRef]
- Vajravelu, K. Innovative strategies for learning and teaching of large differential equations classes. Int. Electron. J. Math. Educ. 2018, 13, 91–95. [Google Scholar] [CrossRef][Green Version]
- Vega-Calderon, F.; Gallegos-Cazares, L.; Flores-Camachoc, F. Conceptual difficulties in understanding the bernoulli’s equation. Rev. Eureka Sobre Ensenanza Divulg. Las Ciencias 2017, 14, 339–352. [Google Scholar]
- de Loiola, J. Brazilian research on modelling in mathematics education. ZDM Math. Educ. 2010, 42, 337–348. [Google Scholar] [CrossRef]
- Kaiser, G.; Sriraman, B. A global survey of international perspectives on modelling in mathematics education. ZDM Zentralblatt Didakt. Math. 2006, 38, 302–310. [Google Scholar] [CrossRef]
- Barbosa, J. Modelagem matemática e os professores: A questão da formação. Bolema-Bol. Educ. Mat. 2001, 14, 5–23. [Google Scholar]
- Blomhøj, M. Mathematical modelling: A theory for practice. In International Perspectives on Learning and Teaching Mathematics; Clarke, B., Clarke, D.M., Göran, E., Bengt, J., Lester, D.V., Wallby, A., Wallby, K., Eds.; National Center for Mathematics Education, Göteborg University: Göteborg, Sweden, 2004; pp. 145–159. [Google Scholar]
- Chamberlin, S.; Payne, A.; Kettler, T. Mathematical modeling: A positive learning approach to facilitate student sense making in mathematics. Int. J. Math. Educ. Sci. Technol. 2020, 53, 858–871. [Google Scholar] [CrossRef]
- Bloom, B.S.; Engelhart, M.D.; Furst, E.J.; Hill, W.H.; Krathwohl, D.R. (Eds.) Handbook I. Cognitive Domain. In Taxonomy of Educational Objectives: The Classification of Educational Goals; Handbook I. Cognitive Domain; Longmans, Green & Co.: New York, NY, USA, 1956. [Google Scholar]
- Lozada, E. Study of Advanced Mathematical Thinking in Teaching and Learning in Two Courses of Ordinary Differential Equations with a Mathematical Moldeling Approach. Ph.D. Thesis, Universidad de los Lagos, Osorno, Chile, 2023. (In Spanish). [Google Scholar]
- Guo, W.; Li, W.; Tisdell, C.C. Pedagogy of Guiding Undergraduate Engineering Students Solving First-Order Ordinary Differential Equations. Mathematics 2021, 9, 1623. [Google Scholar] [CrossRef]
- Rolong, D.A. Understanding of Concepts Involved in Resolution Processes of a Differential Equation. Ph.D. Thesis, Universidad de Antioquia, Antioquia, Colombia, 2022. (In Spanish). [Google Scholar]
- Sijmkens, E.; Scheerlinck, N.; De Cock, M.; Deprez, J. Benefits of using context while teaching differential equations. Int. J. Math. Educ. Sci. Technol. 2022. [Google Scholar] [CrossRef]
- Campos, A. Advanced algebraic thinking processes in students’ modelling activities. Teach. Math. Appl. Int. J. IMA 2022. [Google Scholar] [CrossRef]
- Slavit, D.; LoFaro, T.; Cooper, K. Understandings of solutions to differential equations through contexts, web-based simulations, and student discussion. Sch. Sci. Math. 2002, 102, 380–390. [Google Scholar] [CrossRef]
- Camunga, A.; Batard, L.F. Developing skills for selecting the most appropriate method for the solution of superior order ordinary differential equations. Rev. Conrado 2017, 13, 82–88. [Google Scholar]
- Carr, M.; Prendergast, M.; Breen, C.; Faulkner, F. How well do engineering students retain core mathematical knowledge after a series of high threshold online mathematics tests? Teach. Math. Appl. 2017, 36, 136–150. [Google Scholar] [CrossRef]
- Dehesa de Gyves, N. Discursos en los registros algebraico y geométrico de las ecuaciones diferenciales ordinarias. Educ. Mat. 2006, 18, 123–148. [Google Scholar]
- Dullius, M.M.; Araujo, I.S.; Veit, E.A. Teaching and learning of differential equations with graphical, numerical and analytical approach: An experience in engineering courses. BOLEMA Bol. Educ. Mat. 2011, 24, 17–42. [Google Scholar]
- Hyland, D.; van Kampen, P.; Nolan, B.C. Outcomes of a service teaching module on odes for physics students. Int. J. Math. Educ. Sci. Technol. 2018, 49, 743–758. [Google Scholar] [CrossRef]
- Kamps, H.J.L.; Van Lint, J.H. A comparison of a classical calculus test with a similar multiple choice test. Educ. Stud. Math. 1975, 6, 259–271. [Google Scholar] [CrossRef]
- Tisdell, C.C. On mnemonic instruction and the shields acronym in the pedagogy of first-order differential equations. Teach. Math. Appl. 2019, 38, 74–84. [Google Scholar] [CrossRef]
- Wittmann, M.C.; Black, K.E. Mathematical actions as procedural resources: An example from the separation of variables. Phys. Rev. Spec. Top. Phys. Educ. Res. 2015, 11, 020114. [Google Scholar] [CrossRef]
- Villar, M.T.; Llinares, S. Análisis de errores en la conceptualización y simbolización de las ecuaciones diferenciales en alumnos de químicas. Educ. Mat. 1996, 8, 90–101. [Google Scholar]
- Czocher, J.A.; Tague, J.; Baker, G. Where does the calculus go? An investigation of how calculus ideas are used in later coursework. Int. J. Math. Sci. Technol. 2013, 44, 673–684. [Google Scholar] [CrossRef]
- Camacho, M.; Perdomo, J.; Santos, M. Newblock Conceptual and cognitive processes in the introduction of ordinary differential equations through problem solving. Ensenanza Cienc. Rev. Investig. Exp. Didact. 2012, 30, 9–32. [Google Scholar]
- Mallet, D.G.; McCue, S.W. Constructive development of the solutions of linear equations in introductory ordinary differential equations. Int. J. Math. Educ. Sci. Technol. 2009, 40, 587–595. [Google Scholar] [CrossRef]
- Bukova-Güzel, E. An examination of pre-service mathematics teachers’ approaches to construct and solve mathematical modelling problems. Teach. Math. Appl. 2011, 30, 19–36. [Google Scholar] [CrossRef]
- Habre, S. Improving understanding in ordinary differential equations through writing in a dynamical environment. Teach. Math. Appl. 2012, 31, 153–166. [Google Scholar] [CrossRef]
- Habre, S. Inquiry-oriented differential equations: A guided journey of learning. Teach. Math. Appl. 2019, 39, 201–212. [Google Scholar] [CrossRef]
- Habre, S. Exploring students’ strategies to solve ordinary differential equations in a reformed setting. J. Math. Behav. 2000, 18, 455–472. [Google Scholar] [CrossRef]
- KarimiFardinpour, Y.; Gooya, Z. Comparing three methods of geometrical approach in visualizing differential equations. Int. J. Res. Undergrad. Math. 2018, 4, 286–304. [Google Scholar] [CrossRef]
- Marrongelle, K. The function of graphs and gestures in algorithmatization. J. Math. Behav. 2007, 26, 211–229. [Google Scholar] [CrossRef]
- Rasmussen, C.; Blumenfeld, H. Reinventing solutions to systems of linear differential equations: A case of emergent models involving analytic expressions. J. Math. Behav. 2007, 26, 195–210. [Google Scholar] [CrossRef]
- Rasmussen, C.; Keene, K. Knowing solutions to differential equations with rate of change as a function: Waypoints in the journey. J. Math. Behav. 2019, 56, 100695. [Google Scholar] [CrossRef]
- Artigue, M. Une recherche d’ ingenierie didactique sur l’enseignement des equations differentielles en primer cycle universitarie. Irem Univ. Paris 1989, 107, 284–309. [Google Scholar]
- Dullius, M.M. Enseñanza y Aprendizaje en Ecuaciones Diferenciales con Abordaje Gráfico, Numérico y Analítico. Ph.D. Thesis, Universidad de Burgos, Burgos, Spain, 2009. [Google Scholar]
- Brito, L.; Farias, P.H.; Cardoso, J.V.; Ribeiro, R. Teaching of ordinary differential equations using the assumptions of the pbl method. Int. J. Eng. Pedagog. 2020, 10, 7–20. [Google Scholar]
- Barbarán, J.J.; Fernéz, J.A. The analysis of errors in the solution of ordinary differential equations. a methodology to develop mathematical competence. Ensen. Cienc. Rev. Investig. Exp. Didact. 2014, 32, 173–186. [Google Scholar]
- Blass, L.; Huguenim, A.F.; Irala, V.B.; da Silva, V. O estudo de equações diferenciais através da aplicação do perfil logarítmico do vento. Teia Rev. Educ. Mat. Tecnol. Iberoam 2019, 10, 1–18. [Google Scholar] [CrossRef]
- Cordero, F.; Miranda, E. El entendimiento de la transformada de laplace: Una epistemología como base de una descomposición genética. Rev. Latinoam. Investig. Mat. Educ. 2002, 5, 133–168. [Google Scholar]
- Curia, L.; Pérez, M.; Lavalle, A. Evaluation of the contents of differential equations through mathematical competences. Rev. Electron. Humanidades Educ. Comun. Soc. 2018, 26, 9–27. [Google Scholar]
- Gijsbers, D.; de Putter-Smits, L.; Pepin, B. Changing students’ beliefs about the relevance of mathematics in an advanced secondary mathematics class. Int. J. Math. Educ. Sci. Technol. 2020, 51, 87–102. [Google Scholar] [CrossRef]
- Goodchild, S.; Apkarian, N.; Rasmussen, C.; Katz, B. Critical stance within a community of inquiry in an advanced mathematics course for pre-service teachers. J. Math. Teach. Educ. 2020, 24, 231–252. [Google Scholar] [CrossRef]
- Hansen, D.; Cavers, W.; George, G.H. Use of a physical linear cascade to teach systems modelling. Int. J. Eng. Educ. 2003, 19, 682–695. [Google Scholar]
- Hyland, D.; Van Kampen, P.; Nolan, B.C. Introducing direction fields to students learning ordinary differential equations (odes) through guided inquiry. Int. J. Math. Educ. Sci. Technol. 2019, 52, 331–348. [Google Scholar] [CrossRef]
- Ju, M.-K.; Kwon, O.N. Ways of talking and ways of positioning: Students’ beliefs in an inquiry-oriented differential equations class. J. Math. Behav. 2007, 26, 267–280. [Google Scholar] [CrossRef]
- Kaw, A.K.; Yalcin, A. Problem-centered approach in a numerical methods course. J. Prof. Issues Eng. Pract. 2008, 134, 359–364. [Google Scholar] [CrossRef]
- Keene, K.A. A characterization of dynamic reasoning: Reasoning with time as parameter. J. Math. Behav. 2007, 26, 230–246. [Google Scholar] [CrossRef]
- Keene, K.A.; Rasmussen, C.; Stephan, M. Gestures and a chain of signification: The case of equilibrium solutions. Math. Educ. Res. J. 2012, 24, 347–369. [Google Scholar] [CrossRef]
- Kwon, O.N.; Rasmussen, C.; Allen, K. Students’ retention of mathematical knowledge and skills in differential equations. Sch. Sci. Math. 2005, 105, 227–239. [Google Scholar] [CrossRef]
- Rasmussen, C.L. New directions in differential equations: A framework for interpreting students’ understandings and difficulties. J. Math. Behav. 2001, 20, 55–87. [Google Scholar] [CrossRef]
- Rasmussen, C.; Stephan, M.; Allen, K. Classroom mathematical practices and gesturing. J. Math. Behav. 2004, 23, 301–323. [Google Scholar] [CrossRef]
- Rasmussen, C.; Zandieh, M.; King, K.; Tepo, A. Advancing mathematical activity: A practice-oriented view of advanced mathematical thinking. Math. Think. Learn. 2005, 7, 51–73. [Google Scholar] [CrossRef]
- Rasmussen, C.; Marrongelle, K. Pedagogical content tools: Integrating student reasoning and mathematics in instruction. J. Res. Math. Educ. 2006, 37, 388–420. [Google Scholar]
- Rasmussen, C.; Kwon, O.N. An inquiry-oriented approach to undergraduate mathematics. J. Math. Behav. 2007, 26, 189–194. [Google Scholar] [CrossRef]
- Raychaudhuri, D. A layer framework to investigate student understanding and application of the existence and uniqueness theorems of differential equations. Int. J. Math. Educ. Sci. Technol. 2007, 38, 367–381. [Google Scholar] [CrossRef]
- Raychaudhuri, D. Dynamics of a definition: A framework to analyse student construction of the concept of solution to a differential equation. Int. J. Math. Educ. Sci. Technol. 2008, 39, 161–177. [Google Scholar] [CrossRef]
- Raychaudhuri, D. Adaptation and extension of the framework of reducing abstraction in the case of differential equations. Int. J. Math. Educ. Sci. Technol. 2013, 45, 35–57. [Google Scholar] [CrossRef]
- Raychaudhuri, D. A framework to categorize students as learners based on their cognitive practices while learning differential equations and related concepts. Int. J. Math. Educ. Sci. Technol. 2013, 44, 139–1256. [Google Scholar] [CrossRef]
- Sabag, N. The effect of integrating lab experiments in electronic circuits into mathematic studies—A case study. Res. Sci. Technol. Educ. 2017, 35, 427–444. [Google Scholar] [CrossRef]
- Speer, N.M.; Wagner, J.F. Knowledge needed by a teacher to provide analytic scaffolding during undergraduate mathematics classroom discussions. J. Res. Math. Educ. 2009, 40, 530–562. [Google Scholar] [CrossRef]
- Stephan, M.; Rasmussen, C. Classroom mathematical practices in differential equations. J. Math. Behav. 2002, 21, 459–490. [Google Scholar] [CrossRef]
- Wittmann, M.C.; Flood, V.J.; Black, K.E. Algebraic manipulation as motion within a landscape. Educ. Stud. Math. 2013, 82, 169–181. [Google Scholar] [CrossRef]
- Andresen, M. Modeling with the software ’derive’ to support a constructivist approach to teaching. Int. Electron. J. Math. Educ. 2007, 2, 1–15. [Google Scholar] [CrossRef]
- Canu, M.; de Hosson, C.; Duque, M. Students’ understanding of equilibrium and stability: The case of dynamic systems. Int. J. Sci. Math. Educ. 2016, 14, 101–123. [Google Scholar] [CrossRef][Green Version]
- Guerrero-Ortiz, C.; Camacho-Machín, M.; Mejía-Velasco, H.R. Difficulties experienced by students in the interpretation of the solutions of ordinary differential equations that models a problem. Ensen. Cienc. Rev. Investig. Exp. Didact. 2010, 28, 341–352. [Google Scholar]
- Heck, A. Bringing reality into the classroom. Teach. Math. Appl. 2009, 28, 164–179. [Google Scholar] [CrossRef]
- Humble, S. Rolling and spinning coin: A level gyroscopic processional motion. Teach. Math. Appl. 2001, 20, 18–24. [Google Scholar] [CrossRef]
- Molina-Mora, J.-A. ICT-projects-modeling based experience for teaching of systems of differential equations. Uniciencia 2015, 29, 46–61. [Google Scholar]
- Rodríguez-Gallegos, R.; Quiroz-Rivera, S. The role of technology in the process of mathematical modeling for teaching differential equations. Rev. Latinoam. Investig. Mat. Educ. 2016, 19, 99–124. [Google Scholar]
- Vinner, S. A different test and different result analysis—An example from a calculus exam. J. Math. Didakt. 1994, 15, 311–326. [Google Scholar] [CrossRef]
- Molina, J.A. Experience in the incorporation of ict in teaching differential equations applied. Rev. Iberoam. Educ. 2015, 69, 79–96. [Google Scholar]
- Blomhøj, M.; Kjeldsen, T.H. Project organised science studies at university level: Exemplarity and interdisciplinarity. ZDM Math. Educ. 2009, 41, 183–198. [Google Scholar] [CrossRef]
- Blomhøj, M.; Kjeldsen, T.H. Teaching mathematical modelling through project work. ZDM Math. Educ. 2006, 38, 163–177. [Google Scholar] [CrossRef]
- Latulippe, C.; Latulippe, J. Student perceptions of writing projects in a university differential-equations course. Int. J. Math. Educ. Sci. Technol. 2013, 45, 1–11. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).