Abstract
Rice (Oryza sativa L.) is an important agricultural commodity in Indonesia. The combination of stability analysis on yields was considered accurate in selecting superior genotypes. The objectives of this study were as follows: identify the effects of genotypes, the environment, and their interactions (GEIs) on the yields of Fe-tolerant rice; select superior genotypes (stable and high yields) under diverse environment conditions in Indonesia; and determine the mega-environments (MEs) and representative environments for Fe-tolerant rice development. Fifteen genotypes of Fe-tolerant rice were used for this study. Field experiments were conducted at six experimental fields in Indonesia using a randomized block design with two replications. A combined analysis of variance (ANOVA) was used to determine the effect of genotypes, the environment, and their interactions on Fe-tolerant rice yields. Parametric, non-parametric, AMMI (additive main effects and multiplicative interaction), GGE biplot, and SI (sustainability index) measurements were used to determine the superior genotypes. GGE biplot was also used to determine MEs and representative environments. The measurement results showed that genotypes, the environment, and their interactions significantly affected rice yields with contributions of 13.30%, 35.78%, and 50.92%, respectively. One superior Fe-tolerant rice genotype (stable and high yield) was selected based on all measurements, namely G4 (B14316E-KA-4). In this experiment, two MEs were generated. Lampung was identified as a representative environment for the development of superior genotypes. The results of this study can be used as a consideration in the release and development of new superior varieties of Fe-tolerant rice in Indonesia.
1. Introduction
Rice (Oryza sativa L.) is one of the most important staple foods for billions of people in the world [1]. Rice is the main food source for more than 50% of the world’s population and a very important commodity for the Indonesian community [2]. In 2021–2022, rice production, reached 525 million tons, with a consumption of 53.4 kg/year per capita [3]. Furthermore, rice production in Indonesia reached 31.36 million tons in 2021 [4]. One of the problems in rice production is iron (Fe) toxicity [5]. Rice production is also influenced by various environmental factors [6,7]. Hence, it is important to develop Fe-tolerant rice, and rice that can adapt to environmental changes, in high yields.
As a staple food, rice is the greatest human energy source. Rice content is generally composed of protein, which mostly consists of glutamate and aspartic acid, carbohydrates, fiber, fat, thiamine (vitamin B1), riboflavin (vitamin B2), and niacin (vitamin B3) [8,9]. Thus, rice can be used as a nutritional source for humans.
Recently, rice with high yield potential has been widely developed. High yields are obtained via plant breeding programs. In the process of selecting superior genotypes (high and stable yields), it is obtained via multi-environmental testing. The multi-environment test is a test carried out to evaluate the performance and stability of a variety of plants in various agroecological environments [7,10]. Multi-environmental testing is important to carry out in the selection of Fe-tolerant rice with high yield and stability because it can determine genotypes by environmental interactions (GEIs). The existence of GEIs is influenced by biotic and abiotic factors. Biotic factors consist of pests and diseases [11,12], while abiotic factors are from the environment [7]. The existence of GEIs indicates that various genotypes can have different responses to environmental changes. By carrying out multi-environment tests, stable genotypes in various environments that are also adaptive to specific environments can be determined [13]. However, GEIs make the selection process difficult and inefficient under various environmental conditions [7,13,14]. Several studies have reported that GEIs complicate the selection process in sweet potatoes [7,15], durum wheat [16], soybeans [17,18,19], maize [20], Stevia [21], and turmeric [22]. Therefore, a study is needed to evaluate Fe-resistant rice genotypes under a wide range of environmental conditions to obtain superior genotypes (high and stable yields).
Iron toxicity in rice is a common problem in areas where the soil contains excessive iron. This condition adversely affects plant growth and productivity, leading to significant yield losses [23]. In order to develop rice genotypes that are resistant to iron toxicity and perform well under diverse environmental conditions, genotypes should be evaluated on various types of land. There are numerous important land types for genotypic evaluation: (1) High iron content soils. Genotypes that exhibit good growth and high yields on high iron content soils can be considered superior candidates for further development. (2) Low iron content soils. Genotypes that show good growth and high yields on low iron content soils can provide solutions for areas experiencing iron deficiency. (3) Different soil pH. Genotypes that can withstand and produce good, as well as low pH (acidic), soils can be considered genotypes that are tolerant to soil pH fluctuations and have the potential to be grown on various types of land [24,25].
Several researchers conducted multi-environmental evaluations using various stability measures. Combining stability measurements is considered to be more accurate in selecting genotypes that are stable and have a high yield [7,26]. Some of the stability analyses used are parametric estimation models, namely linear regression [27], Wricke’s equivalence [28], Shukla’s stability variance [29], coefficient of variation (CVi) [30], GE variance component (θ(i)) [31], component of mean-variance (θi) [32], and Hanson genotypic stability (Di) [33]; non-parametric estimation models, namely the Thennarasu model (NP(i)) [34], non-parametric stability (S(i)) [35], and Kang ranks (KR) [36]; as well as graphical models, i.e., AMMI [37] and GGE biplot [38]. Several researchers have also used the sustainability index (SI) to identify or select superior genotypes [39,40,41,42]. The use of the sustainability index was considered to increase selection accuracy. In addition, the concept of sustainable agriculture was also an important factor in the advancement of agricultural crops [43]. In plant breeding programs, multi-environment testing is a crucial step to increase productivity and maintain food security [44]. The use of these various methods was expected to be able to identify and evaluate genotypes in a wide range of environments.
Currently, many researchers have used the combined stability analysis model to select superior genotypes, such as in grass peas [45], barley [26], peanuts [46], maize [47], sweet potato [7], and black soybean [18]. Because the combined stability method was considered more effective and accurate in selecting stable and high-yielding genotypes compared to a single stability estimation [40]. The advantages of this model are that it is (i) suitable for data with statistical assumptions such as interaction effects and a normal distribution of errors; (ii) simple because estimation is based on genotypic performance and does not require assumptions for homogeneity of variance; and (iii) suitable for visually determining the response of a genotype to the environmental testing [26,48]. The objectives of this study were to identify the effects of genotypes, environment, and their interactions (GEIs) on the yields of Fe-tolerant rice; select superior genotypes (stable and high yields) under diverse environmental conditions in Indonesia; and determine the mega-environments (MEs) and representative environments for Fe-tolerant rice development.
2. Materials and Methods
2.1. Plant Material
The genetic materials used include 15 new Fe-tolerant rice genotypes (Table 1). The rice genotypes tested were the result of selection with varying degrees of Fe tolerance [49]. These genotypes resulted from a plant breeding program at the National Research and Innovation Agency, Indonesia. The rice genotypes tested had different genetic backgrounds and high genetic diversity.

Table 1.
Genotypes used during experiment.
2.2. Field Experiment and Data Collection
Field experiments were conducted in six environments in Indonesia, i.e., Banjar Baru (South Kalimantan), Bogor (West Java), Sorong (West Papua), Lampung (South Sumatera), Blandean (South Kalimantan), and Riau (South Sumatera). These locations were chosen because they are rice production centers in Indonesia. The experiment used a randomized completed block design that was repeated two times. Each genotype was planted at a spacing of 40 × 40 cm. The data were taken at harvest, following the standard descriptor for rice. The yield of each genotype in each experimental plot was converted in t·ha−1. Information about the experimental environment was presented in Table 2.

Table 2.
Information about the location used during the field experiment.
2.3. Data Analysis
The combined ANOVA statistical model to estimate GEIs follows the Equation (1):
where Yopqr is the value of rice genotype o in plot r and the value in environment p of each replication q; μ is the grand mean of grain yield; Go is the effect of rice genotype o; Ep is the effect of the environment p; GEop is the effect of GEIs on rice genotype o and environment p; Rq(p) is the effect of replicate q on environment p; Br(q) is the effect of replication q on plot r; and εopqr is the error effects from rice genotype o in plot r and repeat q of environment p, respectively. To calculate the combined ANOVA, we used Genstat 12th. If the data show that GEIs have a significant effect, then the yield stability analysis was carried out using parametric and non-parametric measurements, AMMI, GGE biplot, and the sustainability index (SI). Various measurements aim to improve the accuracy of the superior genotype selections.
Yopqr = μ + Go + Ep + GEop + Rq(p) + Br(q) + εopqr
Parametric and non-parametric stability measurements are used to identify stable genotypes. Linear regressions were measured following Eberhart and Russell, (1966) [27]. According to Eberhart and Russell (1966) [27], a genotype is declared stable if it has a regression deviation = 1 and a variance deviation value (S2di) = 0. To estimate the mean-variance component (θi), following Plaisted and Peterson, (1959) [32], we used the following formula:
The GE variance component (θ(i)) was calculated according to [31] as
Wricke’s ecovalence (Wi2) was calculated according to [50] as
Shukla’s stability variance was calculated according to [29] as
and the coefficient of variance (CVi) was calculated according to [30] as
Hanson’s genotype stability measure (Di) was calculated [33] with the following formula:
For all measurements used, the variables were defined as follows: xij: grand yield from the rice genotype i across all environments; : mean of yield from rice genotype i; : mean of yield in environment j; : overall average yield; p and q: the numbers of rice genotypes and environments; SDg: the standard deviation of all GEIs.
Stability non-parametric (S(i)) components were applied according to [35,51] with the following formulas:
where rij: rank of stability from rice genotype i in the environment j; : mean rank across all environments for each rice genotype; and N: number of environments. Parametric stability (NP(i)) were measured following Thennarasu (1995) [34] with the following formulas:
where : stability rank in environment j from rice genotype i based on adjusted data; : median rank for adjusted data (yield); Mdi: original data from the same parameters; N: number of environments. Kang rank’s (KR) non-parametric stability model following Kang (1988) was used [36]. In this method, yield performance and stability variance are used to identify high yielding and stable genotypes given a weighting of 1. We identified stable genotypes based on non-parametric and parametric stability measurements using STABILITYSOFT (online software) [52]. The results of parametric and non-parametric measurements were grouped using cluster analysis (dendrogram) based on the stability rank of each measurement. Cluster analysis was estimated using SPSS v19 software [53].
AMMI is used to estimate the stability of Fe-tolerant rice yields, following [37]:
where Yef is the yield performance of the genotype eth in the year fth; is the average of all yield performances from genotypes used; Ge is the genotype eth mean deviation; Ef is the year fth mean deviation; λk is the square root of the eigenvalue of the PCA axis g; αeg and γfg were the PC score for PCA axis g of the genotype ith and the year fth, respectively; ef is the residual. According to AMMI measurement, genotypes were considered stable if they were within the radius of the circle and close to the axis (0.0). In contrast, the adaptive genotypes are far from the axis and close to the environment line vector. AMMI was analyzed used PBStat online [54].
AMMI stability value (ASV) was used to estimate the stability of Fe-tolerant rice yields, applying the following formula [55]:
where ss IPCA 1 and ss IPCA 2 were the weight given to the IPCA 1 and IPCA 2 scores by divided the ss IPCA 1 and ss IPCA 2. IPCA 1 score and IPCA 2 score were the first and second from the IPCA scores for each genotype from the AMMI analysis. Genotypes that were stable across the years were indicated by a small ASV value and vice versa.
The genotype stability index (GSI) for Fe-tolerant rice genotypes was calculated based on the ASV Rank (RASV) from the genotypes tested in three environments (years) and the yield performance ranks (RGM) of genotypes tested in three years with Equation (18). Genotypes that were stable across the years were indicated by a small GSI value and vice versa.
GSI = RASV + RAY
The model for GGE biplot following [56] uses the formula below:
where, Yij is the average yield of somaclone i in season j; is the average yield over all somaclone in season j; and are the singular values for PC1 and PC2, respectively; and are the PC1 and PC2 scores, respectively, for somaclone i; and are the PC1 and PC2 scores, respectively, for season j; is the residual of the model associated with the somaclone i in season j.
The sustainability index (SI) was estimated by the following formula used by [57]:
where Y is the mean yield performance of a rice genotype, σn is the standard deviation, and YM is the best yield performance of a rice genotype in any environment. The SI values were classified arbitrarily into five groups, i.e., very low (up to 20%), low (21% to 40%), moderate (41% to 60%), high (61% to 80%), and very high (above 80%) [58]. SI was calculated using ms. Excel 2013. The best rice genotypes were obtained based on the slices of all measurements. The selected rice genotypes were considered to have stable and high yields in all growing environments.
3. Results
3.1. Combined Analysis of Variance (ANOVA) on Fe-Tolerant Rice Yields in Six Environments
The results of the combined ANOVA of Fe-tolerant rice in six environments are presented in Table 3. The genotypes, environments, and their interactions showed a significant effect on yield variation with contributions of 13.30%, 35.78%, and 50.92%, respectively. The large influence of the environment and the interactions indicated a very large effect of the environment on the variation in yields. Yields were in the range of 0.27–14.52 t·ha−1, where the average yields were highest in Riau and lowest in West Papua. The resulting CV value is also high, namely 27.28% (Table 3), which indicates that external factors, including the environment, highly influence the resulting data. Therefore, further analysis was needed to express GEIs in selecting superior genotypes.

Table 3.
Combined ANOVA of new promising Fe-tolerant rice genotypes in six environments.
3.2. Parametric and Non-Parametric Stability Measurements on Rice Yields
The average yields and parametric stability measurements of the rice genotypes are shown in Table 4. The average yields of the rice genotypes were in the range of 3.62–6.05 t/ha. Eight genotypes were identified that had higher yields than the overall average value (>4.18 t·ha−1), with G7 being the highest. Seven other genotypes were identified as having below-average yields, with G2 being the lowest. Genotype stability based on regression measurements by Eberhart and Russell (1996) [27] was determined by the regression coefficient, (bi) = 1, and the deviation of variance (S2di) being low (close to zero). Genotypes G11, G1, and G3 had bi values close to 1, but all three had lower yields than the average overall yield. Therefore, these three are less adapted to a range of environments. The genotypes G5, G12, G13, and G15 (bi > 1) had a low level of stability, indicating that they were adapted specifically to certain environments and produced high yields in certain environments. Genotype G2 has a value of bi < 1, and the average yield is lower than the overall average yield. This indicates that the genotype has a low and unstable yield in all test environments. Based on S2di measurements, genotype G11 had the lowest score, followed by genotypes G2 and G4; therefore, these three genotypes were considered the most stable according to this measurement. However, only G4 had an average yield higher than the overall average, so G4 was considered the most ideal genotype according to this measurement. Based on the stability variant parametric model of Francis and Kannenberg (CVi), the genotypes G6, G2, and G4 were classified as highly stable genotypes. Plaisted and Peterson’s mean variance component (θi) defined G7, G12, and G8 as the most stable genotypes. Three other parametric stability models (Wricke ecovalence (Wi2), Shukla stability variant (σ2i), and GE Plaisted component variant (θ(i)) showed that G11, G2, and G4 were the most stable genotypes. The Di measurement showed that G12 is the most stable, followed by G2 and G5. ASV measurements chose G2 as the most stable, followed by G11 and G4. While the GSI measurement chose G4 as the most stable, followed by G14 and G5.

Table 4.
The stability analysis of 15 Fe-tolerant rice genotypes in Indonesia using parametric and non-parametric measurements.
The estimation of stability using non-parametric measurements was also presented in Table 4. Almost all non-parametric stability measurements chose G4 as the most stable genotype, except for NP(2), which chose G14 as the most stable. On the other hand, S(1), S(2), S(3), and NP(1) measurements identified G12 as the most unstable genotype. S(6), NP(2), and NP(3) measurements identified G10 as the most unstable genotype, while NP(4) and KR measurements identified G1 as the most unstable genotype. Table 5 provides information on the sum of ranks (SR), the average rank (AR), and the standard deviation of the stability ranks (SD) for each genotype based on all parametric and non-parametric measurements. Based on Table 5, the G4 genotype has the smallest average rank (AR); hence, it is the most stable genotype. Meanwhile, G10 has the largest AR value; it is the most unstable, or the least adaptable, genotype in certain environments.

Table 5.
Rank of stability for 15 Fe-tolerant rice genotypes in Indonesia based on parametric and non-parametric measurements.
To classify superior rice genotypes, cluster analysis (dendrogram) was used based on the stability rank of each measurement. The dendrogram in this analysis divided the rice genotypes into two main groups (Figure 1). The first group is the stable genotype group and is divided into two sub-clusters: (1) the sub-cluster that has a high average yield (above the overall average yield) and a low average stability rank, consisting of genotypes G4, G5, G14, and G15; (2) a sub-cluster that has a yield lower than the overall average but has a low average stability rank (stable low grain yield), consisting of genotypes G2 and G11. The second group is the unstable group and is also divided into two sub-clusters: (1) the sub-cluster that has yields above the overall average and high average stability rank (unstable high grain yield), which consists of genotypes G7, G8, G9, and G12; (2) sub-clusters with yields below the overall average and relatively high average rankings (unstable low grain yield), consisting of genotypes G1, G3, G6, G10, and G13.
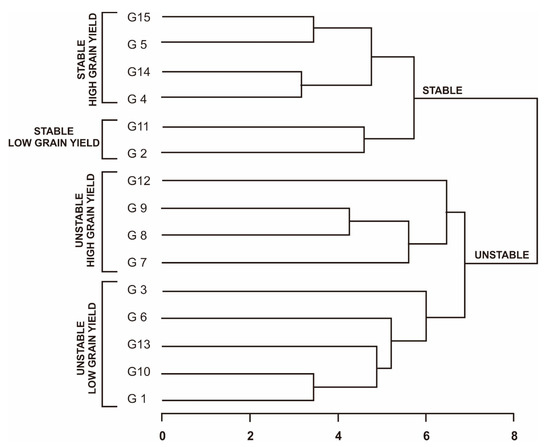
Figure 1.
Grouping of 15 Fe-tolerant rice genotypes in six planting environments based on parametric and non-parametric measurements.
3.3. The Relationship between Parametric and Non-Parametric Stability Measurements with Rice Yields
The relationship between yield and stability measurements, as well as between each stability measurement was indicated by the value marked in bold (Table 6). The coefficient of Spearman’s correlation rank revealed that the average yield has a positive and significant correlation with NP(4) and θi and that it is significantly and negatively correlated with Wi2, σ2i, s2di, θ(i), and ASV (Table 6). In addition, Table 6 also presents information regarding the relationship between each stability measurement. Measures that have a positive and significant correlation indicate that they have equal power in selecting stable genotypes. However, if they have a significant and negative correlation coefficient, then they have the opposite power when choosing a stable genotype.

Table 6.
Spearman correlation rank of parametric and non-parametric stability measurements.
The relationship between the various stability measurements was determined using principal component analysis (PCA), which also combined them into distinct groups. The first three PCs with an eigenvalue > 1 produce a cumulative value of 85.783% of the total variation between parametric and non-parametric measurements (Table 7). The first two components are used to visualize the PCA biplot because they have the highest variability values (PC1 = 55.20% and PC2 = 23.71%), as shown in Figure 2. Parametric and non-parametric measurements are grouped into five main groups, namely the first group consists of Di, NP(2), NP(3), NP(4), S(3), S(6), KR, and GSI; the second group consists of S(1), S(2), NP(1), CVi, and bi; the third group consists of s2di, θ(i), Wi2, σ2i, and ASV measurements; the fourth group consists of yield (Y); and the fifth group consists of θi.

Table 7.
Eigenvalue, percent, and cumulative value of stability measurements.
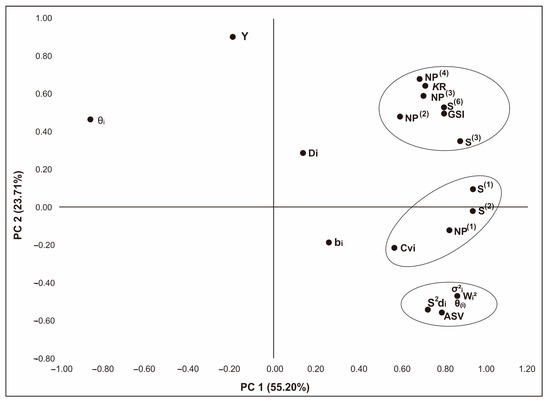
Figure 2.
Principal component analysis (PCA) of parametric and non-parametric stability measurements on Fe-tolerant rice in Indonesia.
3.4. Fe-Tolerant Rice Yield Stability Based on AMMI Analysis
A visualization of rice yield stability using AMMI analysis was presented in Figure 3. PC1 and PC2 show a total contribution of 80.7% to the variation in yield. This number is high enough to represent the yield variance across all genotypes examined. This means that the level of accuracy of the resulting data is good enough to assess the genotypes tested in six environments. Based on Figure 3, Lampung has the longest environment vector. This shows that Lampung is a representative environment in selecting superior genotypes and has a large influence on GEIs. Meanwhile, Banjarbaru and West Papua have the shortest environmental vectors, indicating that they have a small effect on GEIs and do not represent the actual yield. In the AMMI biplot, five rice genotypes were identified that were close to the axis (0.0) and within the radius of the circle. They were G2, G3, G4, G11, and G15. This shows that the five of them have stable yields in the six test environments. Other genotypes identified as adaptive to specific environments, namely G7 and G10 in Lampung; G5, G12, and G13 in Blandean; G14 in Riau; G8 and G9 in West Papua; and G1 and G6 in Bogor.
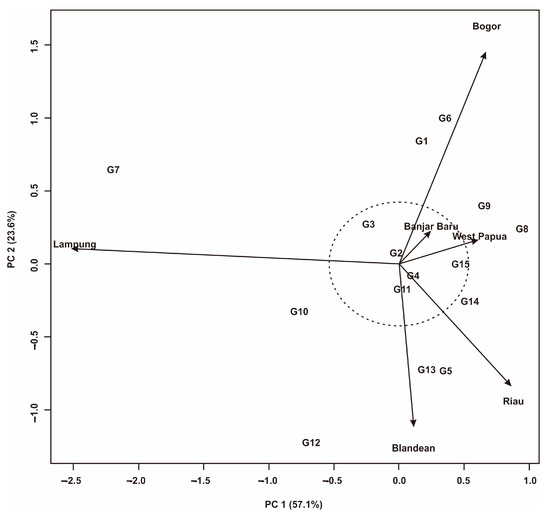
Figure 3.
AMMI biplot for 15 Fe-tolerant rice genotypes in six planting environments.
3.5. Mega-Environments, Representative Location, and Yield Stability Based on GGE Biplot
The results of GGE biplot analysis on 15 genotypes of Fe-tolerant rice showed that PC1 and PC2 contributed 54.2% and 19.1% of the total yield variation, respectively (Figure 4, Figure 5 and Figure 6). According to the ‘representative versus discriminative’ display of the GGE biplot (Figure 4), the test environments can be classified into three types, namely the type I environment has a short vector and provides little information about the genotype being tested, so it should not be used as a test environment. The type II environment has a long and small angle vector with an average abscissa, making it ideal for selecting superior genotypes. Type III environments have long and large angle vectors with abscissa mean environments, so they cannot be used to select ideal genotypes but are useful for selecting unstable genotypes (adapt-specific) [59,60].
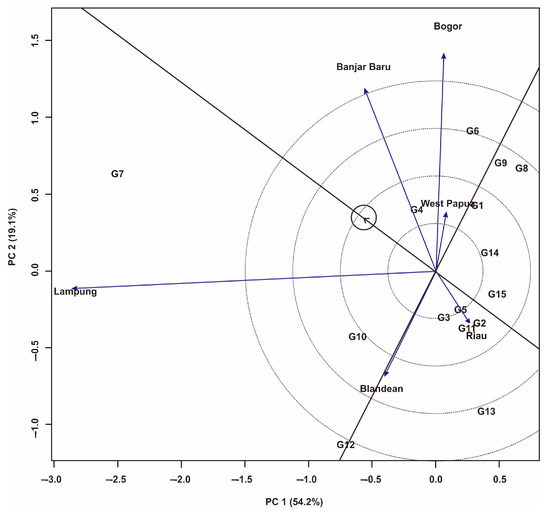
Figure 4.
GGE biplot pattern of “representative vs. discriminative” against 15 Fe-tolerant rice genotypes in six planting environments.
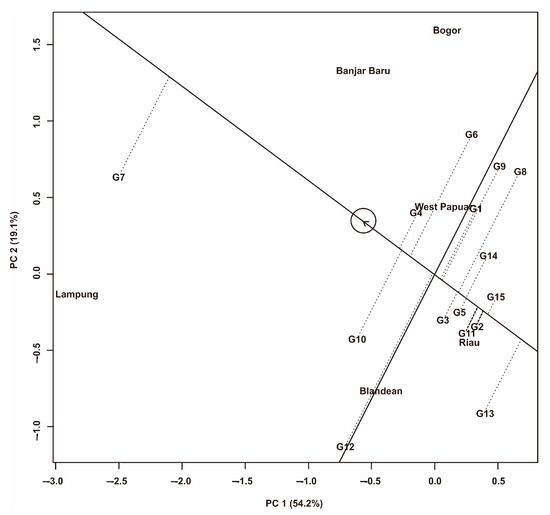
Figure 5.
GGE biplot pattern of ‘mean vs. stability’ of 15 Fe-tolerant rice genotypes in six planting environments.
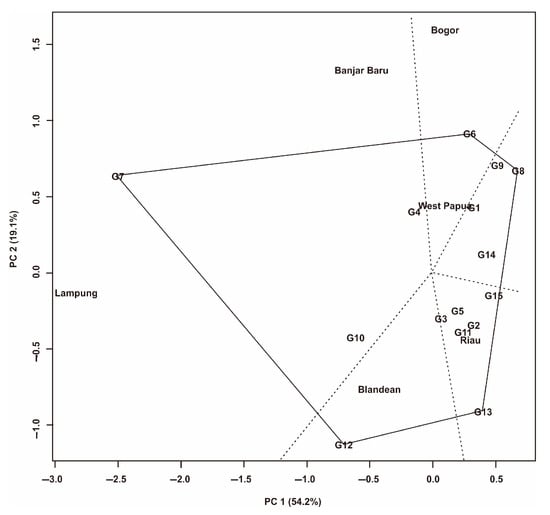
Figure 6.
GGE biplot pattern of ‘which won where’ for 15 Fe-tolerant rice genotypes in six planting environments.
The results of research on rice populations are presented in Figure 4, indicating that the West Papua, Riau, and Blandean environments were Type I environments and should not be used as test environments. Lampung is an ideal environment (Type II) to select superior genotypes because of its high discriminatory and representativeness and has a small angle with the abscissa. The Banjarbaru and Bogor environments were Type III environments and could not be used to select superior genotypes but could be used to determine adaptive or region-specific genotypes.
The ‘mean vs. stability” biplot is presented in Figure 5. The Y-axis shows the average yield of each genotype, and the X-axis shows the yield stability for each genotype tested. In this study, the genotypes to the left of the Y-axis had higher yields than the average overall yield. In contrast, the genotypes to the right of the Y-axis had lower yields than the average overall yield. If the genotype is close to the X-axis, then the genotype is stable and vice versa [56]. The measurement results showed that five genotypes had yields above the overall average yield: G4, G6, G7, G10, and G12. In contrast, the other ten genotypes had yields below the overall average yield. G4 tends to be stable and has high yields because it is close to the X-axis and is to the left of the Y-axis. G7 has the highest average yield (6.05 t·ha−1), which was indicated by its farthest position from the Y-axis. G13 is the genotype that has the worst yields in all environments.
The ‘which wins where’ pattern shows that the six environments have five sectors with different peak genotypes (Figure 6). There are two sectors that consist of more than one environment to form a mega-environment. The first mega-environment is in Sector I, consisting of Lampung and Banjar Baru environments, with G7 as the peak genotype. The second mega-environment is in the second sector, which consists of the Bogor and West Papua environments, with G6 as the peak genotype. In the third sector, G8 is the peak genotype, but there is no environment in this sector. In sector four, there is the Riau environment with G13 as the peak genotype. Sector Five has a Blandean environment with G12 as the peak genotype. In this study, G1, G3, G4, G5, and G14 tend to be close to the central axis, which indicates that they have a small (stable) GEI effect.
3.6. Yield Stability Based on Sustainability Index (SI)
An evaluation of the Fe-tolerant rice yield stability based on the sustainability index (SI) was presented in Table 8. In this study, the SI criteria obtained were divided into three groups, namely low, medium, and high (Table 8). SI estimates for rice yields range from 27.78% (low) to 66.11% (high). SI in the high category was indicated by G2, G4, and G6, but only G4 and G6 had yields above the overall average yield (4.18 t·ha−1), so these two genotypes are included in the selected category. There are nine rice genotypes that have a medium SI (40–60%) (Table 8). They were G1, G3, G5, G8, G9, G10, G11, G14, and G15; however, only three genotypes had yields above the overall average yield (>4.18 t·ha−1), namely G5, G8, and G14 (Table 8). They belong to the ideal group because they have high yields and are stable in six different environments. The SI with a low category (20–40%) is shown by G7, G12, and G13 (Table 8). Low SI values indicate unstable yields for the three genotypes, whereas G7 and G12 have average yields above the overall average yield, which indicates that both are adapted to a representative environment.

Table 8.
The result of the sustainability index (SI) analysis on 15 Fe-tolerant rice genotypes in Indonesia.
To select superior (stable and high yielding) rice genotypes, slices were taken from all measurements used. Information on selected genotypes is presented in Table 9. AMMI, GGE biplot, and the SI each succeeded in selecting stable genotypes by 33.33%, while combined stability (parametric and non-parametric) succeeded in selecting 26.67%. However, only one genotype was selected based on all measurements (6.67%), namely G4. Thus, G4 is highly recommended to be used as a new superior rice variety that is stable and has a high yield.

Table 9.
Selected superior rice genotypes based on stability measurements.
4. Discussion
Genotype, environmental, and GEI factors showed a significant effect on Fe-tolerant rice yields. GEIs (50.92%) contributed more, followed by environment (35.78%) and genotype (13.30%). This indicates that the variation in rice yields tested in six different environments was dominantly influenced by external effects, in this case, the environment. The emergence of GEIs in multi-location testing makes plant breeding programs difficult, especially in selecting ideal genotypes [7]. Several studies have reported that GEIs significantly affect rice yields [6,61,62]. In other studies, GEIs also have a significant effect on crop yields, such as maize [13,40,41], sweet potatoes [7], butterfly pea [42], and soybean [18,19]. The large contribution of GEIs also indicates a high environmental effect, where the six test environments have different conditions. Environmental differences can be seen in the type of agro-climate and altitude (Table 2). In addition, the resulting CV also shows a value of 27.28%. This value was included in the high criteria (>20%). The high CV value was caused by various factors, one of which is the environment [14]. Therefore, highly significant GEIs for rice yields justify using parametric, non-parametric, AMMI, GGE biplot, and sustainability index (SI) stability measures to represent GEIs against tested genotypes and estimate the yield stability of rice genotypes that are evaluated.
In plant breeding programs, the presence of GEIs complicates the plant selection process. This situation indicates that the selection of rice genotypes based on yields must be carried out in certain environments, resulting in inefficient breeding programs [13]. In addition, the appearance of GEIs indicates that the tested rice genotypes have different potential when planted in different locations [7], so the development program must be adjusted based on a representative environment. The influence of GEIs also causes sub-optimal genotypic potential under different environmental conditions [47]. However, the presence of GEIs can also provide an opportunity to select rice genotypes that have high yields in certain environments (adapt-specific). These conditions indicate that the selection of appropriate rice genotypes must be carried out in each environment. This is very interesting because Indonesia has very varied land requirements, so the use of specific (adaptive) genotypes will greatly assist the development of certain areas in terms of rice production. Therefore, plant breeding activities must be directed according to the appropriate environmental conditions so that the plant varieties developed are able to adapt well to various environments.
In the process of selecting high yielding varieties that are stable in a wide range of environments, various methods have been proposed. The use of a single stability measure is still considered difficult for determining stable and high yielding genotypes [7,13,26], so another selection model was needed to obtain the ideal genotype. Several studies have reported the selection of stable genotypes and high yields by applying a combination of stability models, including grass peas [45], barley [26], soybeans [18,19], turmeric [22], and maize hybrid [13,40]. In this study, parametric and non-parametric stability models, AMMI, GGE biplot, and the sustainability index (SI) were applied to identify stable and high-yielding Fe-tolerant rice genotypes in six different environments. The average rank (AR) values of all stability models (parametric and non-parametric) were used to select high-yielding and stable rice genotypes (with low AR values). This was also expressed by Vaezi et al. (2019) [26]. Genotypes G4 and G14 had the lowest AR values, indicating a high level of stability and production (above the average overall yield), as shown in Table 5.
A grouping of Fe-tolerant rice genotypes using a dendrogram based on stability rating was used to confirm these results. The dendrogram was developed based on ranking the average yield of all parametric and non-parametric measurements. The resulting dendrogram divides the Fe-tolerant rice genotypes into two main clusters (Figure 1): stable and unstable. Each main cluster was divided into two sub-clusters. The stable high-grain-yield sub-cluster consists of genotypes G4, G5, G14, and G15. This group is an ideal group because the genotypes are able to adapt to a wide range of environments and have high yields. This is followed by the stable low-grain-yield sub-cluster, which consists of genotypes G2 and G11. The next sub-cluster is the unstable high grain yield, which contains the genotypes G7, G8, G9, and G12. This group is a group that can be recommended as a genotype with a specific adaptation because the genotypes in this group will have high production in a representative environment [7]. Finally, the unstable low grain yield group consists of genotypes G1, G3, G6, G10, and G13. This group is the worst and is not recommended for development on a large scale. This was also conveyed by Ruswandi et al. (2022) [47], where genotypes that were in the stable high-grain-yield group were more desirable, and, conversely, genotypes that were in the unstable low-grain-yield group were not expected and were not used for the development of superior varieties.
The results of Spearman’s rank correlation analysis revealed that the stability measures NP(4) and θi were clearly related to the average yield (Y), indicating that these two were included in the category of dynamic stability measures. Stability measures that are positively correlated with yields can be used to recommend genotypes in a specific environment (adapt) [63]. Both of these measurements are useful for selecting Fe-tolerant rice genotypes with high average yields in an environment with good growing conditions (representative). In contrast, stability measures were significantly and negatively correlated with crop yields, indicating them to be a static stability term that can be used to select genotypes in unfavorable environments [26]. Wi2 with σ2i, s2di, θ(i), and ASV measurements have a negative and significant correlation with yield (Table 6), so they are included in the concept of static stability. Stability measurements that have positive and significant correlations indicate that they have a strong strength in selecting stable genotypes [7]. However, if they have significant and negative correlation coefficients, then they have the opposite power in choosing a stable genotype. For example, in this study, S(1) has almost the same power as S(2), S(3), S(6), NP(1), NP(2), NP(3), NP(4), KR, Wi2, σ2i, s2di, θ(i), ASV, and GSI. In addition, there is also a measure of stability that has the same power in selecting stable genotypes (correlation coefficient = 1.00), namely Wi2 with σ2i and θ(i). In a graphical visualization based on the PCA biplot, the three are also in the same group (Figure 2), so one can use one of them to select a stable genotype [13,19]. The PCA’s visualization of stability measurements divides them into five groups. The first group consists of Di, NP(2), NP(3), NP(4), S(3), S(6), KR, and GSI; the second group consists of S(1), S(2), NP(1), CVi, and bi; the third group consists of s2di, θ(i), Wi2, σ2i, and ASV measurements; the fourth group consists of yield (Y); and the fifth group consists of θi. The first three groups and the fifth group represent the concept of static stability. According to Vaezi et al. 2019 [26], the concept of stability is divided into two, i.e., the concept of static and dynamic stability. The concept of static stability can be used to select genotypes under unfavorable environmental conditions. Conversely, the concept of dynamic stability can be used to recommend genotypes in favorable environments [40]. Thus, both parametric and non-parametric measurements provide recommendations for selecting rice in unfavorable environments.
To select stable and high yielding genotypes, graphical visualization is essential. In this study, two graphical measurements were used, namely AMMI and GGE biplots. The AMMI biplot presented in Figure 3 shows that PC1 contributed 57.1% to diversity and 23.6% to PC2. The large contribution of PC1 to yield diversity implies that the interaction of rice genotypes with the six growing environments in Indonesia was predicted by the first PC from genotype and environment. Several researchers also revealed the same thing, where the PC1 value plays an important role in the diversity of yields in the AMMI biplot [21,42,64]. In the AMMI biplot, genotypes that are close to the biplot axis are stable and have low GEIs [37]. In this study, five Fe-tolerant rice genotypes were identified that were close to the axis (0.0) and within the radius of the circle. They were G2, G3, G4, G11, and G15. This shows that the five of them have stable yields in the six test environments. Other genotypes identified as adaptive to specific environments, namely G7 and G10 in Lampung; G5, G12, and G13 in Blandean; G14 in Riau; G8 and G9 in West Papua; and G1 and G6 in Bogor. Thus, the identified genotypes can be developed according to their position in relation to their environment. Based on Figure 3, Lampung has the longest environmental vector. This shows that Lampung is a representative environment in selecting superior genotypes and has a large influence on GEIs. This is in line with the results of the GGE biplot analysis, where Lampung is included in environmental type II, which means it is very representative for testing [13]. Meanwhile, Banjar Baru and West Papua have the shortest environmental vectors in the AMMI and GGE biplots and were included as a Type I environment, which indicates that both have a small effect on GEIs and do not represent the actual yields.
In the GGE biplot, the ‘representative versus discriminative’ display (Figure 4) shows that the West Papua, Riau, and Blandean environments are Type I environments, so they should not be used as test environments. Among the six test environments, Lampung is a Type II environment that has selective influence and high representativeness; hence, Lampung is an ideal location to select superior genotypes (Figure 4) [7]. The Banjar Baru and Bogor environments are Type III environments and should not be used to select superior genotypes but can be used to select adaptive or region-specific genotypes [60]. The ‘mean vs. stability’ biplot display shows that five genotypes have yields above the overall average, including G4, G6, G7, G10, and G12 (Figure 5), while the other ten genotypes had yields below the overall average yield. G4 tends to be stable and has high yields because it is close to the X-axis and to the left of the Y-axis [60]. G7 has the highest average yield (6.05 t·ha−1), which is indicated by its farthest position from the Y-axis. On the other hand, G13 is the genotype that has the worst yield in all environments, so this genotype is not recommended for large-scale development.
The ‘which won where’ display shows that the six environments have five sectors with different peak genotypes (Figure 6). Several researchers revealed that this biplot could indicate the existence of a mega-environment [7,40,48]. There are two sectors that consist of more than one environment so as to form a mega-environment. The first mega-environment is in sector I, which consists of Lampung and Banjar Baru, with G7 as the peak genotype. The second mega-environment is in the second sector, consisting of Bogor and West Papua, with G6 as the peak genotype. These results indicate that there were various environmental groupings during the trials. The first PC explained 54.2% of the total variation due to environmental effects (E) and GEIs during the experiment (Figure 4, Figure 5 and Figure 6). The grouping of environments and mega-environments in various regions in Indonesia with different peak genotypes indicates a genotype-specific adaptation to the mega-environment and the positive utilization of GEIs [7,10,19]. Our findings reveal that several Fe-tolerant rice genotypes have adapted to different environments in Indonesia. This will facilitate the selection process for wider development. In the third sector, G8 is the peak genotype but there is no environment. In sector four, there is the Riau environment with G13 as the peak genotype. Sector five has a Blandean environment with G12 as the peak genotype. Genotypes that are at the top of each sector indicate that these genotypes have high yields in the environment in that sector [20,21]. Genotypes that are in a sector containing more than one environment or mega-environment show the ideal genotype [19,40,65]. Conversely, genotypes at the top of the sector but that do not have an environment show low yields [7]. Therefore, the genotypes in this sector are not recommended for further development.
The evaluation of the yield stability of Fe-tolerant rice based on the sustainability index (SI) divided the genotypes into three groups, namely low, medium, and high (Table 8). SI estimates for rice yields range from 27.78% (low) to 66.11% (high). Genotypes with high and very high SI categories are expected [39,41,42]. Our results show that the genotypes with the highest SI category were shown by G2, G4, and G6, but only G4 and G6 had yields above the overall average yield (4.18 t·ha−1), so these two genotypes are included in the selected category. In addition, in another study, Filio et al. (2023) revealed that genotypes with medium SI criteria and that had high average yields were included in the ideal category. Nine rice genotypes were in the medium SI category (40–60%) (Table 8), including G1, G3, G5, G8, G9, G10, G11, G14, and G15; however, only genotypes G5, G8, and G14 have a yield above the average overall yield (>4.18 t·ha−1). Genotypes with low SI values indicate unstable yields for these three genotypes, so they are not recommended for further development [41,42].
To select superior (stable and high-yielding) rice genotypes, slices were taken from all measurements used. This has also been carried out by several researchers, including grass peas [45], sweet potatoes [7,66], soybeans [17,18], and maize [13,40,41]. The information on selected genotypes presented in Table 9 shows that AMMI, GGE biplot, and the SI each selected stable genotypes by 33.33%. In comparison, the combined stability (parametric and non-parametric) succeeded in selecting 26.67%. However, only one genotype was determined based on all measurements (6.67%), namely G4. Therefore, G4 is highly recommended to be used as a new superior, stable rice variety with a high yield.
5. Conclusions
The measurement results showed that the genotypes, environments, and GEIs significantly influenced Fe-tolerant rice yields with contributions of 13.30%, 35.78%, and 50.92%, respectively. Based on all measurements, G4 (B14316E-KA-4) was selected as a superior (stable and high yield) Fe-tolerant rice genotype. In this experiment, two mega-environments (MEs) were generated, i.e., Lampung and Banjar Baru and Bogor and West Papua. Lampung was identified as a representative environment for the development of superior genotypes based on AMMI and GGE biplots. The results of this study can be used as a consideration in the release and development of new superior varieties of Fe-tolerant rice in Indonesia.
Author Contributions
Conceptualization, D.W.U. and A.K.; methodology, D.W.U. and A.K.; software, H.M.; validation, A.K. and D.W.U.; formal analysis, H.M.; investigation, A.M., P.H.S. and S.B.; resources, D.W.U.; data curation, A.M.; writing—original draft preparation, H.M. and D.W.U.; writing—review and editing, P.H.S., S.B., A.M. and A.K.; visualization, H.M.; supervision, D.W.U. and A.K.; project administration, D.W.U. and A.K.; funding acquisition, D.W.U. and A.K. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the National Research and Innovation Agency, and the APC was funded by Universitas Padjadjaran (UNPAD).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Acknowledgments
Appreciation is also given to the Rector of Universitas Padjadjaran (UNPAD) for providing research facilities. Some of the data used were part of Ajang Maruapey’s dissertation research at Universitas Padjadjaran. High appreciation is also dedicated to the National Research and Innovation Agency for the post-doctoral grant with the number 151/II/HK/2022.
Conflicts of Interest
The authors declare no conflict of interest.
Abbreviations
| GEIs | Genotype by environmental interactions |
| MEs | Mega-environments |
| ANOVA | Analysis of variance |
| SI | Sustainability index |
| AMMI | Additive main effects and multiplicative interactions |
| GGE | Genotype plus genotype by environmental interactions |
| m asl | Meters above sea level |
| mm | Millimeter |
| ASV | AMMI stability value |
| RASV | Rank of ASV |
| RAY | Rank of average yield |
| GSI | Genotype stability index |
| RGSI | Rank of GSI |
| YM | The best yield performance |
| IPCA | Interaction principal component axis |
| CV | Coefficient of variation |
References
- Purugganan, M.D. An evolutionary genomic tale of two rice species. Nat. Genet. 2014, 46, 931–932. [Google Scholar] [CrossRef] [PubMed]
- Mahender, A.; Swamy, B.P.M.; Anandan, A.; Ali, J. Tolerance of Iron-Deficient and -toxic soil conditions in Rice. Plants 2019, 8, 31. [Google Scholar] [CrossRef] [PubMed]
- FAO. Food Outlook—Biannual Report on Global Food Market. Available online: http://www.fao.org/docrep/013/Al969e/Al969e00Pdf2022 (accessed on 27 November 2022).
- Central Bureau of Statistics. Luas Panen dan Produksi Padi di Indonesia 2021. Available online: https://www.bps.go.id/publication/2022/07/12/C52d5cebe530c363d0ea4198/Luas-Panen-Dan-Produksi-Padi-Di-Indonesia-2021.html.2022 (accessed on 10 October 2022).
- Kar, S.; Panda, S.K. Iron homeostasis in rice: Deficit and excess. Proc. Natl. Acad. Sci. India Sect. B Biol. Sci. 2018, 90, 227–235. [Google Scholar] [CrossRef]
- Inabangan-Asilo, M.A.; Swamy, B.P.M.; Amparado, A.F.; Descalsota-Empleo, G.I.L.; Arocena, E.C.; Reinke, R. Stability and G × E analysis of zinc-biofortified rice genotypes evaluated in diverse environments. Euphytica 2019, 215, 61. [Google Scholar] [CrossRef]
- Maulana, H.; Nafi’ah, H.H.; Solihin, E.; Ruswandi, D.; Arifin, M.; Amien, S.; Karuniawan, A. Combined stability analysis to select stable and high yielding sweet potato genotypes in multi-environmental trials in West Java, Indonesia. Agric. Nat. Resour. 2022, 56, 761–772. [Google Scholar] [CrossRef]
- Deepa, G.; Singh, V.; Naidu, K.A. Nutrient composition and physicochemical properties of Indian medicinal rice—Njavara. Food Chem. 2008, 106, 165–171. [Google Scholar] [CrossRef]
- Rohman, A.; Helmiyati, S.; Hapsari, M.; Setyaningrum, D.L. Rice in health and nutrition. Int. Food Res. J. 2014, 21, 13–24. [Google Scholar]
- Yan, W.; Mitchell-Fetch, J.; Beattie, A.; Nilsen, K.T.; Pageau, D.; DeHaan, B.; Hayes, M.; Mountain, N.; Cummiskey, A.; MacEachern, D. Oat mega-environments in Canada. Crop Sci. 2021, 61, 1141–1153. [Google Scholar] [CrossRef]
- Maharani, Y.; Puspitaningrum, D.; Istifadah, N.; Hidayat, S.; Ismail, A. Biology and life table of fall armyworm, Spodoptera frugiperda (J.E. Smith) (Lepidoptera: Noctuidae) on maize and rice. Serangga 2021, 26, 161–174. [Google Scholar]
- Dewayani, S.; Maulana, H.; Wicaksana, N.; Suganda, T.; Concibido, V.; Karuniawan, A. Distribution and prevalence of scurf (Monilochaetes infuscans) on sweet potato (Ipomea batatas) in West Java, Indonesia. Biodiversitas 2021, 22, 2876–2883. [Google Scholar] [CrossRef]
- Li, T.; Zhang, X.; Liu, Q.; Yan, P.; Liu, J.; Chen, Y.; Sui, P. Yield and yield stability of single cropping maize under different sowing dates and the corresponding changing trends of climatic variables. Field Crops Res. 2022, 285, 108589. [Google Scholar] [CrossRef]
- Andrade, M.I.; Naico, A.; Ricardo, J.; Eyzaguirre, R.; Makunde, G.S.; Ortiz, R.; Grüneberg, W.J. Genotype x environment interaction and selection for drought adaptation in sweetpotato (Ipomoea batatas [L.] Lam.) in Mozambique. Euphytica 2016, 209, 61–80. [Google Scholar] [CrossRef]
- Ngailo, S.; Shimelis, H.; Sibiya, J.; Mtunda, K.; Mashilo, J. Genotype-by-environment interaction of newly-developed sweet potato genotypes for storage root yield, yield-related traits and resistance to sweet potato virus disease. Heliyon 2019, 5, e01448. [Google Scholar] [CrossRef]
- Kendal, E. Comparing durum wheat cultivars by genotype × yield × trait and genotype × trait biplot method. Chil. J. Agric. Res. 2019, 79, 512–522. [Google Scholar] [CrossRef]
- Goksoy, A.T.; Sincik, M.; Erdogmus, M.; Ergin, M.; Aytac, S.; Gumuscu, G.; Gunduz, O.; Keles, R.; Bayram, G.; Senyigit, E. The parametric and non-parametric stability analyses for interpreting genotype by environment interaction of some soybean genotypes. Turk. J. Field Crops 2019, 24, 28–38. [Google Scholar] [CrossRef]
- Wijaya, A.A.; Maulana, H.; Susanto, G.W.A.; Sumardi, D.; Suseno, A.; Ruswandi, D.; Karuniawan, A. Grain yield stability of black soybean lines across three agroecosystems in West Java, Indonesia. Open Agric. 2022, 7, 749–763. [Google Scholar] [CrossRef]
- Hebtegebriel, M.H. Adaptability and stability for soybean yield by AMMI and GGE models in Ethiopia. Front. Plant Sci. 2022, 13, 950992. [Google Scholar] [CrossRef]
- Dosho, B.M.; Ifie, B.E.; Asante, I.K.; Danquah, E.Y.; Zeleke, H. Genotype-by-environment interaction and yield stability for grain yield of quality protein maize hybrids under low and optimum soil nitrogen environments. J. Crop Sci. Biotech. 2022, 25, 437–450. [Google Scholar] [CrossRef]
- Amien, S.; Maulana, H.; Ruswandi, D.; Nurjanah, S. Stevia (Stevia rebaudiana B.) genotypes assessment for leaf yield stability through genotype by environment interactions, AMMI, and GGE biplot analysis. Sabrao J. Breed. Genet. 2022, 54, 767–779. [Google Scholar] [CrossRef]
- Tavares, K.; Kirk, E.; Motomura-Wages, S.; Calpito, J.; Bingham, J.P.; Ahmad, A.A.; Flanagan, K.; Uyeda, J.; Kantar, M.B.; Radovich, T.J.K. Genotypic and Environmental Influence on Fresh Rhizome Yield of Turmeric (Curcuma longa L.). Agronomy 2022, 12, 2703. [Google Scholar] [CrossRef]
- Alloway, B.J. Soil factors associated with zinc deficiency in crops and humans. Environ. Geochem. Health 2009, 31, 537–548. [Google Scholar] [CrossRef] [PubMed]
- Qian, Q.; Guo, L.; Smith, S.M.; Li, J. Breeding high-yield superior quality hybrid super rice by rational design. Natl. Sci. Rev. 2016, 3, 283–294. [Google Scholar] [CrossRef]
- Tandzi, L.N.; Mutengwa, C.S.; Ngonkeu, E.L.M.; Gracen, V. Breeding maize for tolerance to acidic soils: A review. Agronomy 2018, 8, 84. [Google Scholar] [CrossRef]
- Vaezi, B.; Pour-Aboughadareh, A.; Mohammadi, R.; Mehraban, A.; Pour-Hossein, T.; Koohkan, E.; Ghasemi, S.; Moradkhani, H.; Siddique, K.H. Integrating different stability models to investigate genotype x environment interactions and identify stable and high-yielding barley genotypes. Euphytica 2019, 215, 63. [Google Scholar] [CrossRef]
- Eberhart, S.A.; Russell, W.A. Stability parameters for comparing varieties. Crop Sci. 1966, 6, 36–40. [Google Scholar] [CrossRef]
- Wricke, G.; Weber, W.E. Erweiterte Analyse von Wechselwirkungen in Versuchsserien; Springer: Berlin/Heidelberg, Germany, 1980; pp. 87–95. [Google Scholar] [CrossRef]
- Shukla, G.K. Some statistical aspects of partitioning genotype-environmental components of variability. Heredity 1972, 29, 237–245. [Google Scholar] [CrossRef]
- Francis, T.R.; Kannenberg, L.W. Yield stability studies in short-season maize: I. A descriptive method for grouping genotypes. Can. J. Plant Sci. 1978, 5, 1029–1034. [Google Scholar] [CrossRef]
- Plaisted, R.L. A shorter method for evaluating the ability of selections to yield consistently over locations. Am. Potato J. 1960, 37, 166–172. [Google Scholar] [CrossRef]
- Plaisted, R.L.; Peterson, L.C. A technique for evaluating the ability of selection to yield consistently in different locations or seasons. Am. Potato J. 1959, 36, 381–385. [Google Scholar] [CrossRef]
- Hanson, W.D. Genotypic stability. Theor. Appl. Genet. 1970, 40, 226–231. [Google Scholar] [CrossRef]
- Thennarasu, K. On Certain non-Parametric Procedures for Studying Genotype-Environment Interactions and Yield Stability. Ph.D. Thesis, PJ School, IARI, New Delhi, India, 1995. [Google Scholar]
- Nassar, R.; Huhn, M. Studies on Estimation of Phenotypic Stability: Tests of Significance for Nonparametric Measures of Phenotypic Stability. Biometrics 1987, 43, 45–53. [Google Scholar] [CrossRef]
- Kang, M.S. A rank-sum method for selecting high-yielding, stable corn genotypes. Cereal Res. Commun. 1988, 16, 113–115. [Google Scholar]
- Gauch, H.G. A Simple Protocol for AMMI Analysis of Yield Trials. Crop Sci. 2013, 53, 1860–1869. [Google Scholar] [CrossRef]
- Yan, W.; Rajcan, I. Biplot analysis of test sites and trait relations of soybean in Ontario. Crop Sci. 2002, 42, 11–20. [Google Scholar] [CrossRef]
- Verma, S.K.; Tuteja, O.P.; Monga, D. Studies on stability parameters and sustainability index for selecting stable genotypes in Asiatic cotton (Gossypium arboreum). Indian J. Agric. Sci. 2013, 83, 1377–1380. [Google Scholar]
- Wicaksana, N.; Maulana, H.; Yuwariah, Y.; Ismail, A.; Ruswandi, Y.A.R.; Ruswandi, D. Selection of high yield and stable maize hybrids in mega-environments of Java island, Indonesia. Agronomy 2022, 12, 2923. [Google Scholar] [CrossRef]
- Maulana, H.; Maxiselly, Y.; Yuwariah, Y.; Dedi, R. Heritability and selection using GGE biplots and the Sustainability Index (SI) of maize mutants under different cropping systems in upland. Sustainability 2023, 15, 6824. [Google Scholar] [CrossRef]
- Filio, Y.L.; Maulana, H.; Aulia, R.; Suganda, T.; Ulimaz, T.A.; Aziza, V.; Concibido, V.; Karuniawan, A. Evaluation of Indonesian butterfly pea (Clitoria ternatea L.) using stability analysis and sustainability index. Sustainability 2023, 15, 2459. [Google Scholar] [CrossRef]
- Maxiselly, Y.; Chiarawipa, R.; Somnuk, K.; Hamchara, P.; Cherdthong, A.; Suntara, C.; Prachumchai, R.; Chanjula, P. Digestibility, blood parameters, rumen fermentation, hematology, and nitrogen balance of goats after receiving supplemental coffee cherry pulp as a source of phytochemical nutrients. Vet. Sci. 2022, 9, 532. [Google Scholar] [CrossRef]
- Olivoto, T.; Lúcio, A.D.C. metan: An R package for multi-environment trial analysis. Methods Ecol. Evol. 2020, 11, 783–789. [Google Scholar] [CrossRef]
- Ahmadi, J.; Vaezi, B.; Shaabani, A.; Khademi, K.; Ourang, S.F. Non-parametric measures for yield stability in grass pea (Lathyrus sativus L.) advanced lines in semi warm regions. J. Agric. Sci. Technol. 2015, 17, 1825–1838. [Google Scholar]
- Ajay, B.C.; Bera, S.K.; Singh, A.L.; Kumar, N.; Gangadhar, K.; Kona, P. Evaluation of genotype x environment interaction and yield stability analysis in peanut under phosphorus stress condition using stability parameters of AMMI model. Agric. Res. 2020, 9, 477–486. [Google Scholar] [CrossRef]
- Ruswandi, D.; Azizah, E.; Maulana, H.; Ariyanti, M.; Nuraini, A. Selection of high—Yield maize hybrid under different cropping systems based on stability and adaptability parameters. Open Agric. 2022, 7, 161–170. [Google Scholar] [CrossRef]
- Yan, W. Mega-environment analysis and test location evaluation based on unbalanced multiyear data. Crop Sci. 2015, 55, 113–122. [Google Scholar] [CrossRef]
- Maruapey, A.; Wicaksana, N.; Karuniawan, A.; Windarsih, G.; Utami, D.W.U. Swampy rice lines for iron toxicity tolerance and yield components performance under inland swamp at Sorong, West Papua, Indonesia. Biodiversitas 2020, 21, 5394–5402. [Google Scholar] [CrossRef]
- Wricke, G. Übereine Methode zur Erfassung der ökologischen Streubreite in Feldversuchen. Z. Pflanz. 1962, 47, 92–96. [Google Scholar]
- Huehn, M. Nonparametric measures of phenotypic stability. Part 1: Theory. Euphytica 1990, 47, 189–194. [Google Scholar] [CrossRef]
- Pour-Aboughadareh, A.; Yousefian, M.; Moradkhani, H.; Poczai, P.; Siddique, K.H.M. STABILITYSOFT: A new online program to calculate parametric and non-parametric stability statistics for crop traits. Appl. Plant Sci. 2019, 7, e01211. [Google Scholar] [CrossRef]
- Yim, O.; Ramdeen, K.T. Hierarchical Cluster Analysis: Comparison of Three Linkage Measures and Application to Psychological Data. Quant. Methods Psychol. 2015, 11, 8–21. [Google Scholar] [CrossRef]
- Suwarno, W.B.; Sobir; Aswidinnoor, H.; Syukur, M. PBSTAT: A web-based statistical analysis software for participatory plant breeding. In Proceedings of the 3rd International Conference on Mathematics and Statistics, Bogor, Indonesia, 5–6 August 2008; pp. 852–858. [Google Scholar]
- Purchase, J.L.; Hatting, H.; van Deventer, C.S. Genotype × environment interaction of winter wheat (Triticum aestivum L.) in South Africa: II. Stability analysis of yield performance. S. Afr. J. Plant Soil 2000, 17, 101–107. [Google Scholar] [CrossRef]
- Yan, W.; Tinker, N.A. Biplot analysis of multi-environment trial data: Principles and applications. Can. J. Plant Sci. 2006, 86, 623–645. [Google Scholar] [CrossRef]
- Tuteja, O.P. Comparative studies on stability parameters and sustainability index for selecting stable genotypes in upland cotton (Gossypium hirsutum L.). Indian J. Genet. Plant Breed. 2006, 66, 221–224. [Google Scholar]
- Atta, B.M.; Shah, T.M.; Abbas, G.; Haq, M.A. Genotype x environment interaction for seed yield in kabuli chickpea (Cicer arietinum L.) genotypes developed through mutation breeding. Pak. J. Bot. 2009, 41, 1883–1890. [Google Scholar]
- Yan, W.; Hunt, L.A.; Sheng, Q.; Szlavnics, Z. Cultivar Evaluation and Mega-Environment Investigation Based on the GGE Biplot. Crop Sci. 2000, 40, 597–605. [Google Scholar] [CrossRef]
- Yan, W.; Kang, M.S.; Ma, B.; Woods, S.; Cornelius, P.L. GGE Biplot vs. AMMI Analysis of Genotype-by-Environment Data. Crop Sci. 2007, 47, 641–653. [Google Scholar] [CrossRef]
- Senguttuvel, P.; Sravanraju, N.; Jaldhani, V.; Divya, B.; Beulah, P.; Nagaraju, P.; Manasa, Y.; Prasad, A.H.; Brajendra, P.; Gireesh, C.; et al. Evaluation of genotype by environment interaction and adaptability in lowland irrigated rice hybrids for grain yield under high temperature. Sci. Rep. 2021, 11, 15825. [Google Scholar] [CrossRef]
- Poli, Y.; Balakrishnan, D.; Desiraju, S.; Panigrahy, M.; Voleti, S.R.; Mangrauthia, S.K.; Neelamraju, S. Genotype × environment interactions of Nagina 22 rice mutants for yield traits under low phosphorus, water limited and normal irrigated conditions. Sci. Rep. 2018, 8, 15530. [Google Scholar] [CrossRef]
- Mohammadi, R.; Amri, A. Comparison of parametric and non-parametric methods for selecting stable and adapted durum wheat genotypes in variable environments. Euphytica 2008, 159, 419–432. [Google Scholar] [CrossRef]
- Tolorunse, K.D.; Gana, A.S.; Bala, A.; Sangodele, E.A. Yield stability studies of soybean (Glycine max (L.) Merrill) under rhizobia inoculation in the savanna region of Nigeria. Plant Breed. 2018, 137, 262–270. [Google Scholar] [CrossRef]
- Erdemci, I. Investigation of genotype × environment interaction in chickpea genotypes using AMMI and GGE biplot analysis. Turk. J. Field Crops 2018, 23, 20–26. [Google Scholar] [CrossRef]
- Maulana, H.; Dewayani, S.; Solihin, M.A.; Arifin, M.; Amien, S.; Karuniawan, A. Yield stability dataset of new orange fleshed genotypes in West Java, Indonesia. Data Brief 2020, 32, 106297. [Google Scholar] [CrossRef] [PubMed]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).