Elasto-Plastic Solution for a Circular Lined Tunnel Considering Yield Criteria for Surrounding Rock and Functionally Graded Lining in Cold-Region Tunnels
Abstract
:1. Introduction
2. Basic Assumptions
- (1)
- The plane strain condition was applied for any tunnel cross-section because the tunnel length in the longitudinal direction was much larger than that in the horizontal direction.
- (2)
- The rock surrounding the tunnel was simplified as a homogeneous and elasto-plastic medium, while the lining was considered as an inhomogeneous and elastic medium.
- (3)
- The frost-heaving process of the surrounding rock, the tunnel construction stages, and the lining installation were neglected.
- (4)
- The displacement of the frozen surrounding rock induced by the frost heave force varied linearly in the radial direction.
- (5)
- The cross-sections of the lining, the tunnel, and the frozen surrounding rock were approximately equivalent to a circular shape.
- (6)
- The far-field pressures acting on the tunnel in the vertical and horizontal directions were identical.
- (7)
- The analysis was based on the axisymmetric problem because the tunnel’s cross-section geometrical configuration and the far-field pressures acting on the tunnel were axisymmetric.
- (8)
- The body forces of the rock and the lining were neglected.
3. Mechanical Model
4. Analytical Solution of Mechanical Model
4.1. Solution for Unfrozen Elastic Zone III
4.2. Solution for Frozen Elastic Zone II-2
4.3. Solution for Frozen Plastic Zone II-1
4.4. Solution for Lining Zone I
4.5. Continuity Conditions
5. Verification
5.1. Comparison with Existing Mechanical Model
5.2. Comparison with a Model Experiment
6. Parametric Analysis
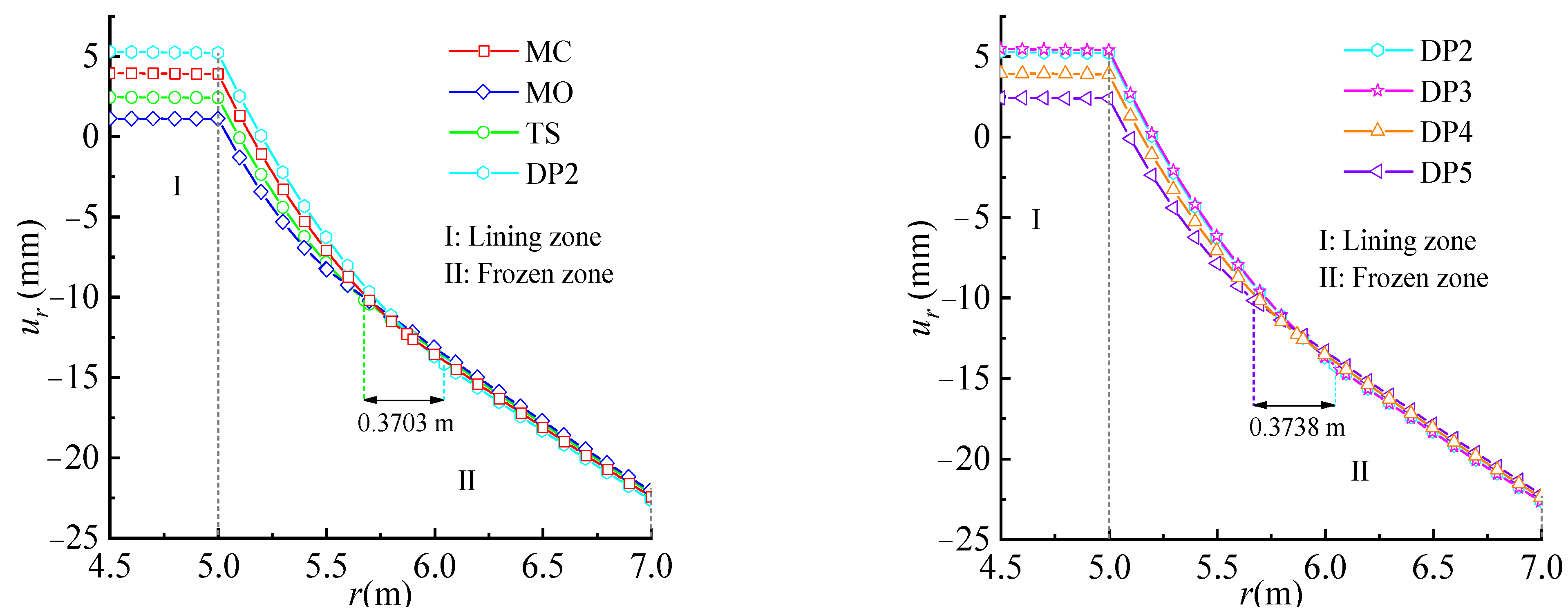
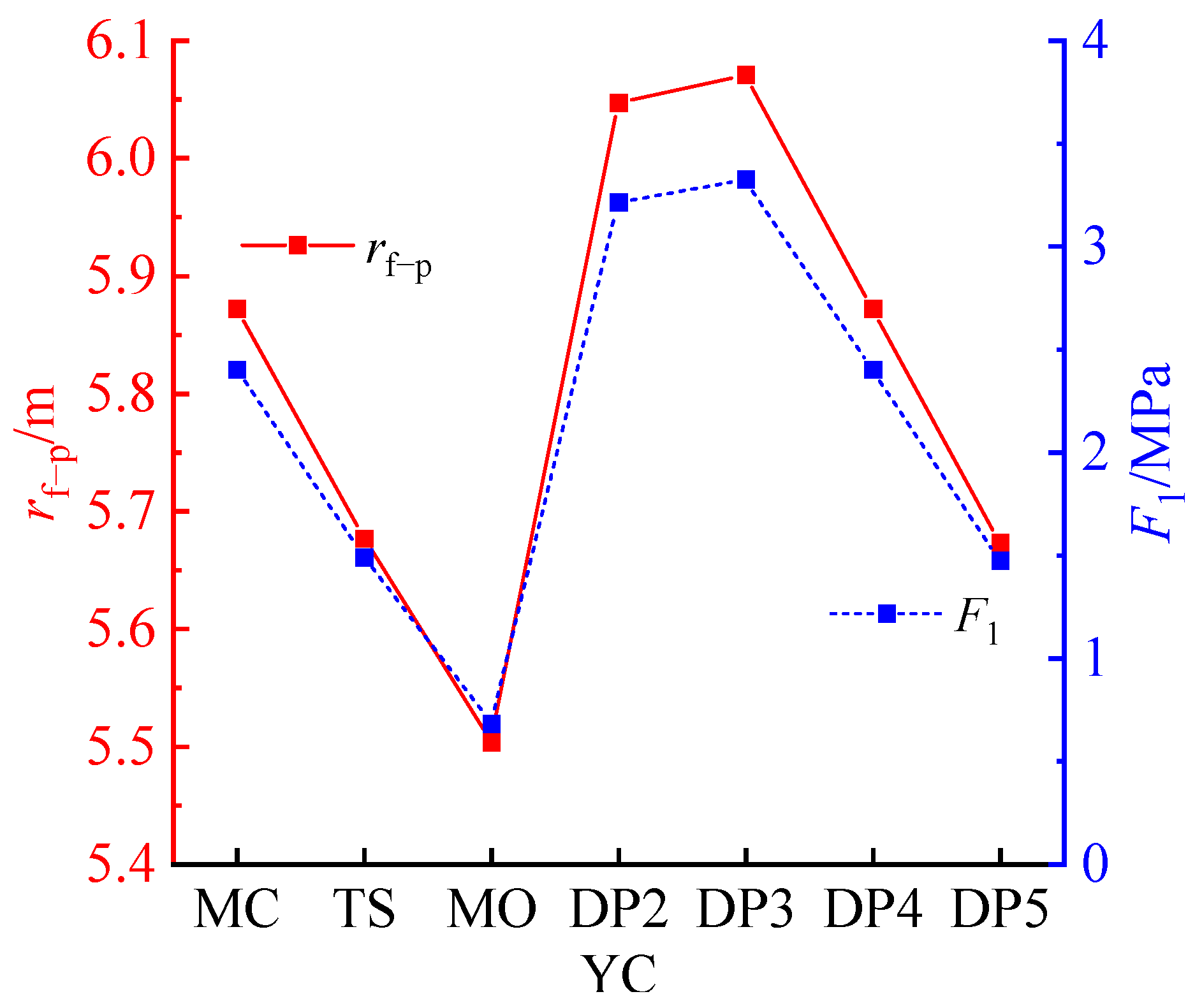
6.1. Yield Criterion of Surrounding Rock
6.2. Inhomogeneity of Lining
6.3. Radial Pressure Acting on Inner Surface of Lining
7. Conclusions
- (1)
- The uniform distribution of the displacement fields in lining zone I is not affected by the yield criterion. The influence of the yield criterion on the displacement fields in frozen zone II decreases with the increase in the distance far from the tunnel. The influences of the yield criterion on the plastic-zone radius rf−p and radial pressure F1 acting on interface I are significant. The maximum difference between MO criterion and DP3 criterion for rf−p and F1 reach 0.567 m and 2.64 MPa, respectively.
- (2)
- The influences of the inhomogeneous coefficient α < 0 on the stress and displacement fields of the lined tunnel are significantly greater than those of α > 0. The influences of the inhomogeneous coefficient α on the stress and displacement fields decrease with the increase in the value of α. As the inhomogeneous coefficient α increases, the plastic-zone radius rf−p decreases, and the radial pressure F1 acting on interface I increases as well.
- (3)
- The circumferential stresses and radial displacements in lining zone I and frozen zone II increase with the increases in the radial pressure acting on the inner surface of lining F0. As F0 increases, the plastic-zone radius rf−p linearly decreases, and the radial pressure F1 acting on interface I linearly increases as well.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Xu, X.Z.; Wang, J.C.; Zhang, L.X. Frozen Soil Physics; Science Press: Beijing, China, 2001; pp. 1–3. [Google Scholar]
- Feng, Q.; Fu, S.G.; Wang, C.X.; Liu, W.W.; Qiao, W.G. Analytical elasto-plastic solution for frost force of cold-region tunnels considering anisotropic frost heave in the surrounding rock. KSCE J. Civ. Eng. 2019, 23, 3831–3842. [Google Scholar] [CrossRef]
- Lai, Y.M.; Wu, H.; Wu, Z.W.; Liu, S.Y.; Den, X.J. Analytical viscoelastic solution for frost force in cold-region tunnels. Cold Reg. Sci. Technol. 2000, 31, 227–234. [Google Scholar] [CrossRef]
- Yasanthi, R.G.N.; Mehran, B. Application of different data analytics for evaluation of heavy vehicle vulnerability in cold-region rural highways. Transp. Res. Rec. J. Transp. Res. Board 2023, 2677, 282–298. [Google Scholar] [CrossRef]
- Lai, Y.M.; Wu, Z.W.; Zhu, Y.L.; Zhu, L.N. Elastic visco-plastic analysis for earthquake response of tunnels in cold regions. Cold Reg. Sci. Technol. 2000, 31, 175–188. [Google Scholar] [CrossRef]
- Feng, Q.; Jiang, B.S.; Zhang, Q.; Wang, L.P. Analytical elasto-plastic solution for stress and deformation of surrounding rock in cold region tunnels. Cold Reg. Sci. Technol. 2014, 108, 59–68. [Google Scholar] [CrossRef]
- Feng, Q.; Liu, W.W.; Jiang, B.S. Analytical solution for the stress and deformation of rock surrounding a cold-regional tunnel under unequal compression. Cold Reg. Sci. Technol. 2017, 139, 1–10. [Google Scholar] [CrossRef]
- Du, J.M.; Fang, Q.; Wang, G.; Wang, J. Analytical solution of a circular lined tunnel with alterable mechanical property under hydrostatic stress and internal pressure. J. Cent. South Univ. 2022, 29, 2757–2770. [Google Scholar] [CrossRef]
- Lai, Y.M.; Wu, Z.W.; Zhu, Y.L.; Zhu, L.N. Nonlinear analysis for the coupled problem of temperature, seepage and stress fields in cold-region tunnels. Tunn. Undergr. Space Technol. 1998, 13, 435–440. [Google Scholar] [CrossRef]
- Lai, Y.M.; Zhang, X.F.; Yu, W.B.; Zhang, S.J.; Liu, Z.Q.; Xiao, J.Z. Three-dimensional nonlinear analysis for the coupled problem of the heat transfer of the surrounding rock and the heat convection between the air and the surrounding rock in cold-region tunnel. Tunn. Undergr. Space Technol. 2005, 20, 323–332. [Google Scholar] [CrossRef]
- Gao, G.Y.; Chen, Q.S.; Zhang, Q.S.; Chen, G.Q. Analytical elasto-plastic solution for stress and plastic zone of surrounding rock in cold region tunnels. Cold Reg. Sci. Technol. 2012, 72, 50–57. [Google Scholar] [CrossRef]
- Zhao, X.; Yang, X.H.; Zhang, H.W.; Lai, H.P.; Wang, X.Y. An analytical solution for frost heave force by the multifactor of coupled heat and moisture transfer in cold-region tunnels. Cold Reg. Sci. Technol. 2020, 175, 103077. [Google Scholar] [CrossRef]
- Zheng, H.; Kanie, S.J. Combined thermal-hydraulic-mechanical frost heave model based on Takashi’s equation. J. Cold Reg. Eng. 2014, 29, 04014019. [Google Scholar] [CrossRef]
- Feng, Q.; Yang, Z.D.; Liu, W.W.; Zhao, W.S. Experimental study of the anisotropic frost heave characteristics of rock surrounding tunnels in cold regions. J. Cold Reg. Eng. 2021, 35, 04021014. [Google Scholar] [CrossRef]
- Zheng, H.; Kanie, S.J.; Niu, F.J.; Li, A.Y. Three-dimensional frost heave evaluation based on practical Takashi’s equation. Cold Reg. Sci. Technol. 2015, 118, 30–37. [Google Scholar] [CrossRef]
- Huang, J.H.; Xia, C.C.; Han, C.L. Analytical solution of frost heave force acting on cold-region tunnel liner considering anisotropy frost heave of surrounding rock. Chin. J. Rock Mech. Eng. 2015, 34, 3666–3774. [Google Scholar] [CrossRef]
- Xia, C.C.; Lv, Z.T.; Li, Q.; Huang, J.H.; Bai, X.Y. Transversely isotropic frost heave of saturated rock under unidirectional freezing condition and induced frost heaving force in cold region tunnels. Cold Reg. Sci. Technol. 2018, 152, 48–58. [Google Scholar] [CrossRef]
- Liu, W.W.; Feng, Q.; Fu, S.G.; Wang, C.X. Elasto-plastic solution for cold-regional tunnels considering the compound effect of non-uniform frost heave, supporting strength and supporting time. Tunn. Undergr. Space Technol. 2018, 82, 293–302. [Google Scholar] [CrossRef]
- Lv, Z.T.; Xia, C.C.; Wang, Y.S.; Luo, J. Analytical elasto-plastic solution of frost heaving force in cold region tunnels considering transversely isotropic frost heave of surrounding rock. Cold Reg. Sci. Technol. 2019, 163, 87–97. [Google Scholar] [CrossRef]
- Koizumi, M. FGM activities in Japan. Compos. Part B Eng. 1997, 28, 1–4. [Google Scholar] [CrossRef]
- Batra, R.C. Optimal design of functionally graded incompressible linear elastic cylinders and spheres. AIAA J. 2008, 46, 2050–2057. [Google Scholar] [CrossRef] [Green Version]
- Xiang, H.J.; Shi, Z.F.; Zhang, T.T. Elastic analyses of heterogeneous hollow cylinders. Mechanics Research Communications 2006, 33, 681–691. [Google Scholar] [CrossRef]
- Tutuncu, N. Stresses in thick-walled FGM cylinders with exponentially-varying properties. Eng. Struct. 2007, 29, 2032–2035. [Google Scholar] [CrossRef]
- Stampouloglou, I.H.; Theotokoglou, E.E. The radially nonhomogeneous thermoelastic axisymmetric problem. Int. J. Mech. Sci. 2017, 120, 311–321. [Google Scholar] [CrossRef]
- Shi, Z.F.; Zhang, T.T.; Xiang, H.J. Exact solutions of heterogeneous elastic hollow cylinders. Compos. Struct. 2007, 79, 140–147. [Google Scholar] [CrossRef]
- Yang, Y.Y. Time-dependent stress analysis in functionally graded materials. Int. J. Solids Struct. 2000, 37, 7593–7608. [Google Scholar] [CrossRef]
- Tutuncua, N.; Ozturk, M. Exact solutions for stresses in functionally graded pressure vessels. Compos. Part B Eng. 2001, 32, 683–686. [Google Scholar] [CrossRef]
- Çallıoğlu, H.; Sayer, M.; Demir, E. Elastic–plastic stress analysis of rotating functionally graded discs. Thin-Walled Struct. 2015, 94, 38–44. [Google Scholar] [CrossRef]
- Zhang, N.; Lu, A.Z.; Li, C.C.; Zhou, J.; Wang, S.; Chen, X. Support performance of functionally graded concrete lining. Constr. Build. Mater. 2017, 147, 35–47. [Google Scholar] [CrossRef]
- Zhang, T.T.; Cui, Z.D.; Wang, S.Y. Deformation properties of functionally graded lining in deeply buried subway tunnel. J. Tianjin Univ. (Sci. Technol.) 2019, 52, 135–140. [Google Scholar]
- Sun, B. Model test study of frost heaving pressures in tunnels excavated in fractured rock mass in cold regions. Sci. Cold Arid Reg. 2010, 2, 405–410. [Google Scholar]
- Du, J.M.; Fang, Q.; Wang, G.; Zhang, D.L.; Chen, T.L. Fatigue damage and residual life of secondary lining of high-speed railway tunnel under aerodynamic pressure wave. Tunn. Undergr. Space Technol. 2021, 111, 103851. [Google Scholar] [CrossRef]
- Du, J.M.; Fang, Q.; Wang, J.; Wang, G. Influences of high-speed train speed on tunnel aerodynamic pressures. Appl. Sci. 2022, 12, 303. [Google Scholar] [CrossRef]
- Sadd, M.H. Elasticity Theory: Applications, and Numerics; Academic Press: Cambridge, MA, USA, 2005. [Google Scholar] [CrossRef]
- Levin, V.A.; Podladchikov, Y.Y.; Zingerman, K.M. An exact solution to the Lame problem for a hollow sphere for new types of nonlinear elastic materials in the case of large deformations. Eur. J. Mech. A/Solids 2021, 90, 104345. [Google Scholar] [CrossRef]
- Huang, X.J.; Zhang, J.X.; Yang, L.; Yang, S.K.; Wang, X.L. Elasto-plastic analysis of the surrounding rock mass in circular tunnel based on the generalized nonlinear unified strength theory. Int. J. Min. Sci. Technol. 2016, 26, 819–823. [Google Scholar] [CrossRef]
- Al-Ajmi, A.M.; Zimmerman, R.W. Relation between the Mogi and the Coulomb failure criteria. Int. J. Rock. Mech. Min. Sci. 2005, 42, 431–439. [Google Scholar] [CrossRef]

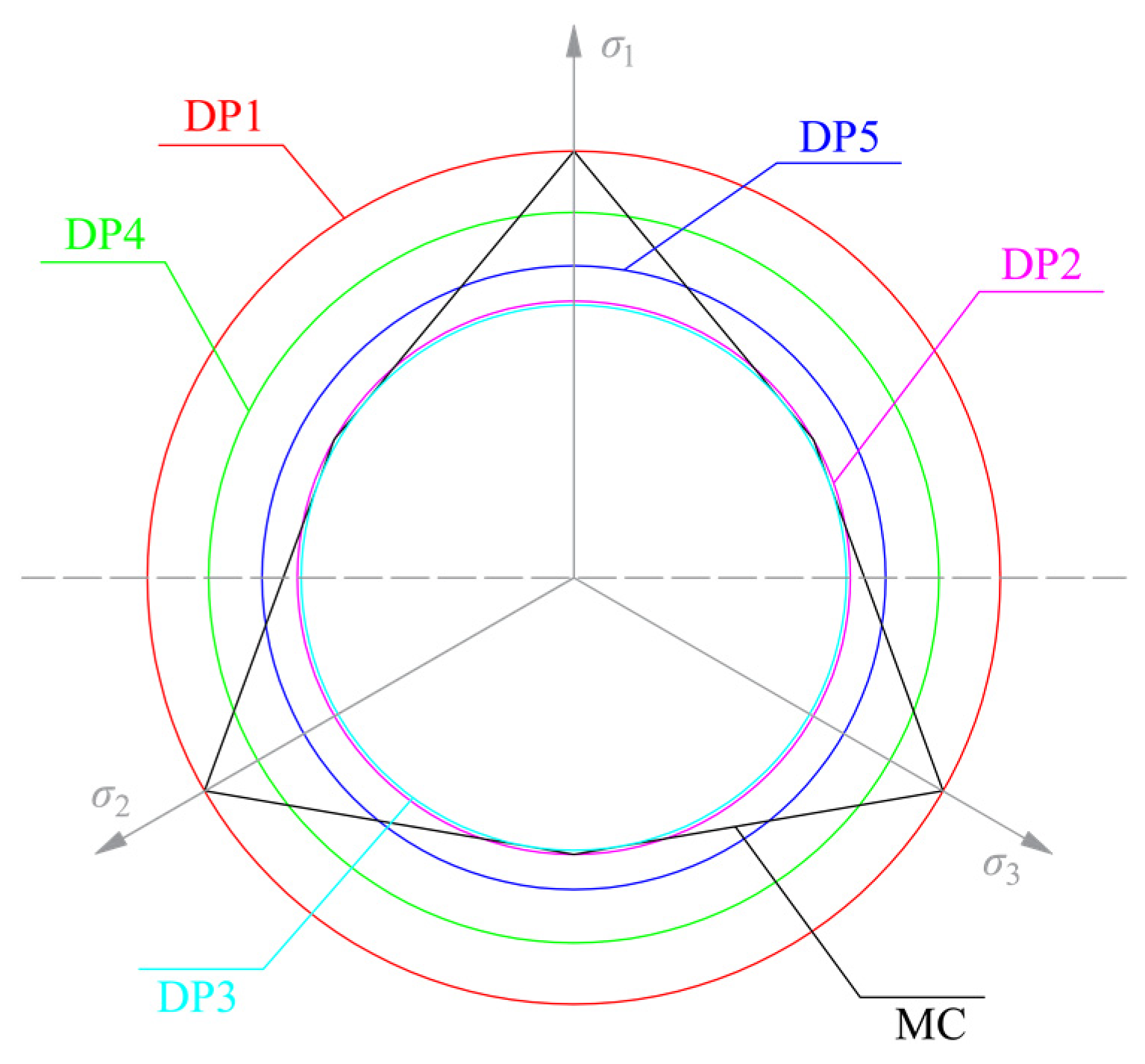








| Yield Criterion | A1 | A2 | |
|---|---|---|---|
| Mohr–Coulomb (MC) | |||
| Unified Strength Theory (UST) | |||
| Mogi-Coulomb (MO) [37] | |||
| Drucker–Prager (DP) | DP1 | ||
| DP2 | |||
| DP3 | |||
| DP4 | |||
| DP5 | |||
| Parameter | Unit | Value |
|---|---|---|
| rL−i | m | 4.5 |
| rL−o = rf−i | m | 5.0 |
| EL | GPa | 28.0 |
| uL | - | 0.16 |
| Ef | GPa | 7.8 |
| uf | - | 0.35 |
| ηv | - | 0.0165 |
| kf | - | 1.0 |
| c | MPa | 1.7 |
| φ | ° | 45 |
| hf | - | 3.0 |
| rf−o = ruf−i | m | 7.0 |
| Euf | GPa | 4.6 |
| uuf | - | 0.33 |
| P0 | MPa | 2.5 |
| δ | - | 0.0 |
| Parameter | Unit | Value |
|---|---|---|
| rL−i | m | 0.08 |
| rL−o = rf-i | m | 0.095 |
| EL | GPa | 615.0 |
| uL | - | 0.205 |
| Ef | GPa | 48.5 |
| uf | - | 0.42 |
| ηv | - | 0.0203 |
| c | kPa | 5.0 |
| φ | ° | 38 |
| hf | - | 2.37 |
| rf−o = ruf−i | m | 0.10 |
| Euf | GPa | 37.0 |
| uuf | - | 0.41 |
| P0 | kPa | 5.639 |
| δ | - | 0.0 |
| Anisotropic frost heave coefficient kf | 1.0 | 1.5 | 2.0 | 2.5 | 3.0 | ||
| b | 0.0 | Proposed model (kPa) | 51.64 | 53.09 | 53.73 | 54.46 | 54.96 |
| Model-test average value (kPa) | 47.4 | 47.4 | 47.4 | 47.4 | 47.7 | ||
| Difference (%) | 8.95 | 12.00 | 13.35 | 14.89 | 15.22 | ||
| b | 0.25 | Proposed model (kPa) | 47.45 | 48.43 | 4944 | 50.08 | 50.43 |
| Model-test average value (kPa) | 47.4 | 47.4 | 47.4 | 47.4 | 47.7 | ||
| Difference (%) | 0.11 | 2.17 | 4.30 | 5.65 | 5.72 | ||
| b | 0.50 | Proposed model (kPa) | 44.24 | 45.54 | 46.45 | 46.91 | 47.39 |
| Model-test average value (kPa) | 47.4 | 47.4 | 47.4 | 47.4 | 47.7 | ||
| Difference (%) | 6.67 | 3.92 | 2.00 | 1.03 | 0.65 | ||
| b | 0.75 | Proposed model (kPa) | 41.96 | 43.17 | 43.88 | 44.45 | 45.03 |
| Model-test average value (kPa) | 47.4 | 47.4 | 47.4 | 47.4 | 47.7 | ||
| Difference (%) | 11.48 | 8.92 | 7.42 | 6.22 | 5.60 | ||
| b | 1.00 | Proposed model (kPa) | 40.27 | 41.64 | 42.15 | 42.81 | 43.09 |
| Model-test average value (kPa) | 47.4 | 47.4 | 47.4 | 47.4 | 47.7 | ||
| Difference (%) | 15.04 | 12.15 | 11.08 | 9.68 | 9.66 | ||
| Yield Criteria | MC | TS | MO | DP2 | DP3 | DP4 | DP5 | ||
|---|---|---|---|---|---|---|---|---|---|
| r (m) | 4.5 | σr (MPa) | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 |
| σq (MPa) | 10.11 | 6.28 | 2.88 | 13.53 | 13.99 | 10.11 | 6.21 | ||
| r (m) | 5.0 | σr (MPa) | 0.96 | 0.60 | 0.27 | 1.29 | 1.33 | 0.96 | 0.59 |
| σq (MPa) | 9.15 | 5.68 | 2.61 | 12.24 | 12.67 | 9.15 | 5.62 | ||
| r (m) | 6.0 | σr (MPa) | 3.25 | 3.19 | 3.14 | 3.44 | 3.52 | 3.25 | 3.18 |
| σq (MPa) | 19.74 | 19.84 | 19.92 | 19.50 | 19.42 | 19.74 | 19.85 | ||
| r (m) | 7.0 | σr (MPa) | 5.43 | 5.40 | 5.37 | 5.48 | 5.49 | 5.44 | 5.40 |
| σq (MPa) | 17.55 | 17.63 | 17.69 | 17.46 | 17.46 | 17.55 | 17.63 | ||
| r (m) | 8.0 | σr (MPa) | 4.39 | 4.37 | 4.34 | 4.30 | 4034 | 4.40 | 4.36 |
| σq (MPa) | −2.40 | −2.37 | −2.34 | −2.43 | −2.43 | −2.40 | −2.36 | ||
| r (m) | 10.0 | σr (MPa) | 3.17 | 3.15 | 3.14 | 3.19 | 3.20 | 3.17 | 3.15 |
| σq (MPa) | −1.17 | −1.53 | −1.14 | −1.19 | 1.20 | −1.17 | −1.15 | ||
| Inhomogeneous Coefficients (α) | −2.0 | −1.0 | −0.5 | 0.0 | 1.0 | 2.0 | 4.0 | ||
| r/rL−i (m) | 4.5 | σr (MPa) | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 |
| σq (MPa) | 2.47 | 5.23 | 6.58 | 7.59 | 8.37 | 8.27 | 7.48 | ||
| r/rL−i (m) | 5.0 | σr (MPa) | 0.21 | 0.47 | 0.61 | 0.72 | 0.84 | 0.87 | 0.88 |
| σq (MPa) | 1.81 | 4.27 | 5.65 | 6.87 | 8.41 | 9.21 | 10.27 | ||
| r/rL−i (m) | 6.0 | σr (MPa) | 2.42 | 2.63 | 2.97 | 3.21 | 3.43 | 3.49 | 3.51 |
| σq (MPa) | 20.38 | 20.77 | 20.21 | 19.81 | 19.44 | 19.34 | 19.32 | ||
| r/rL−i (m) | 7.0 | σr (MPa) | 4.48 | 5.04 | 5.26 | 5.41 | 5.55 | 5.59 | 5.60 |
| σq (MPa) | 19.50 | 18.37 | 17.92 | 17.61 | 17.32 | 17.24 | 17.22 | ||
| r/rL−i (m) | 8.0 | σr (MPa) | 3.66 | 4.09 | 4.26 | 4.38 | 4.48 | 4.51 | 4.45 |
| σq (MPa) | −1.66 | −2.09 | −2.26 | −2.38 | −2.49 | −2.51 | −2.52 | ||
| r/rL−i (m) | 10.0 | σr (MPa) | 2.71 | 2.98 | 3.09 | 3.16 | 3.23 | 3.25 | 3.25 |
| σq (MPa) | −0.71 | −0.98 | −1.08 | −1.16 | −1.23 | −1.25 | −1.25 | ||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Du, J.; Zhang, X.; Wang, H. Elasto-Plastic Solution for a Circular Lined Tunnel Considering Yield Criteria for Surrounding Rock and Functionally Graded Lining in Cold-Region Tunnels. Sustainability 2023, 15, 11577. https://doi.org/10.3390/su151511577
Du J, Zhang X, Wang H. Elasto-Plastic Solution for a Circular Lined Tunnel Considering Yield Criteria for Surrounding Rock and Functionally Graded Lining in Cold-Region Tunnels. Sustainability. 2023; 15(15):11577. https://doi.org/10.3390/su151511577
Chicago/Turabian StyleDu, Jianming, Xuan Zhang, and Hualao Wang. 2023. "Elasto-Plastic Solution for a Circular Lined Tunnel Considering Yield Criteria for Surrounding Rock and Functionally Graded Lining in Cold-Region Tunnels" Sustainability 15, no. 15: 11577. https://doi.org/10.3390/su151511577
APA StyleDu, J., Zhang, X., & Wang, H. (2023). Elasto-Plastic Solution for a Circular Lined Tunnel Considering Yield Criteria for Surrounding Rock and Functionally Graded Lining in Cold-Region Tunnels. Sustainability, 15(15), 11577. https://doi.org/10.3390/su151511577





