Seismic Stability Analysis of Tunnel Faces in Heterogeneous and Anisotropic Soils Using Modified Pseudodynamic Method
Abstract
1. Introduction
2. Methodology
2.1. Modified Pseudodynamic Method
2.2. Heterogeneity and Anisotropy Materials
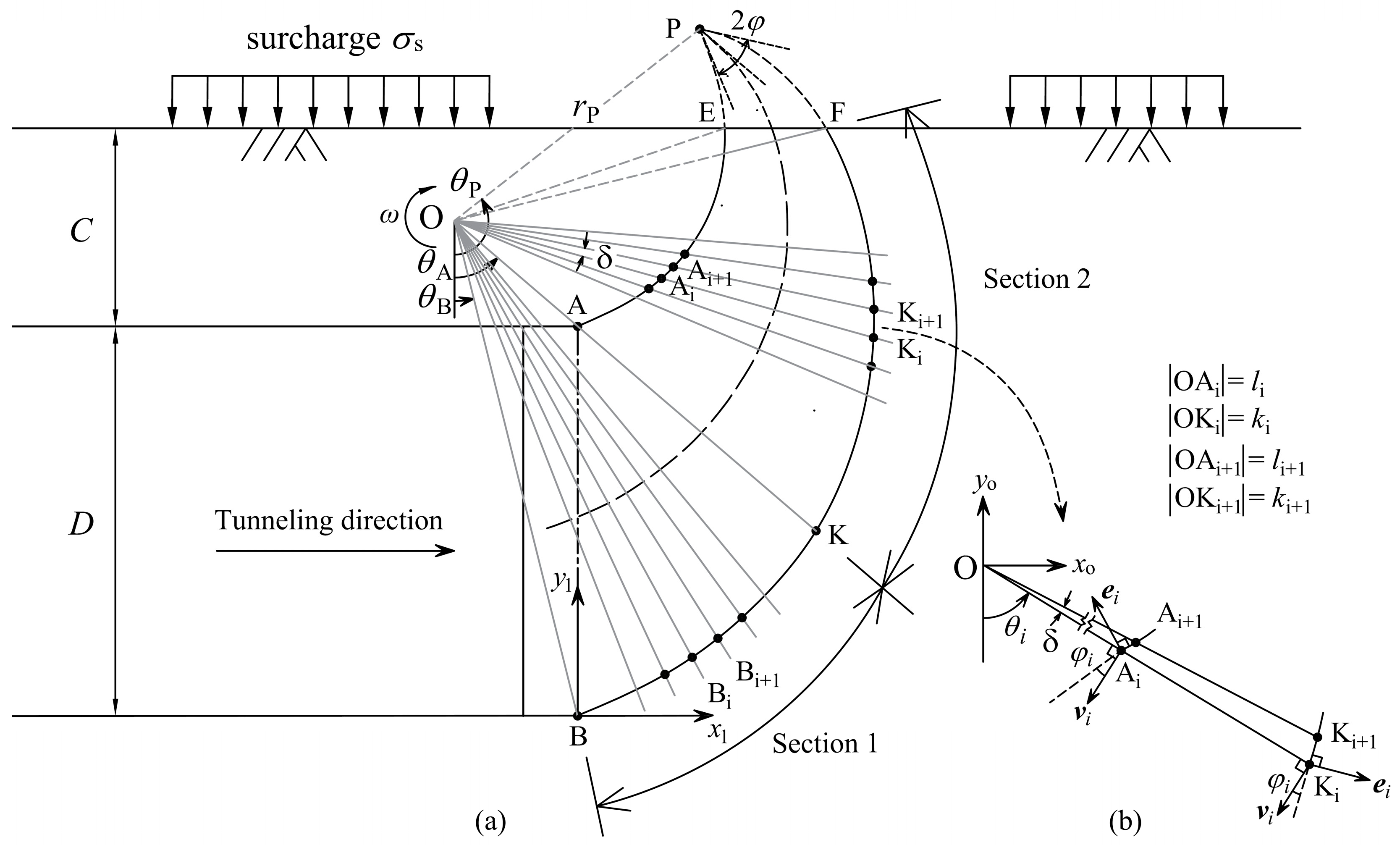
3. Determination of the Discretized Mechanism
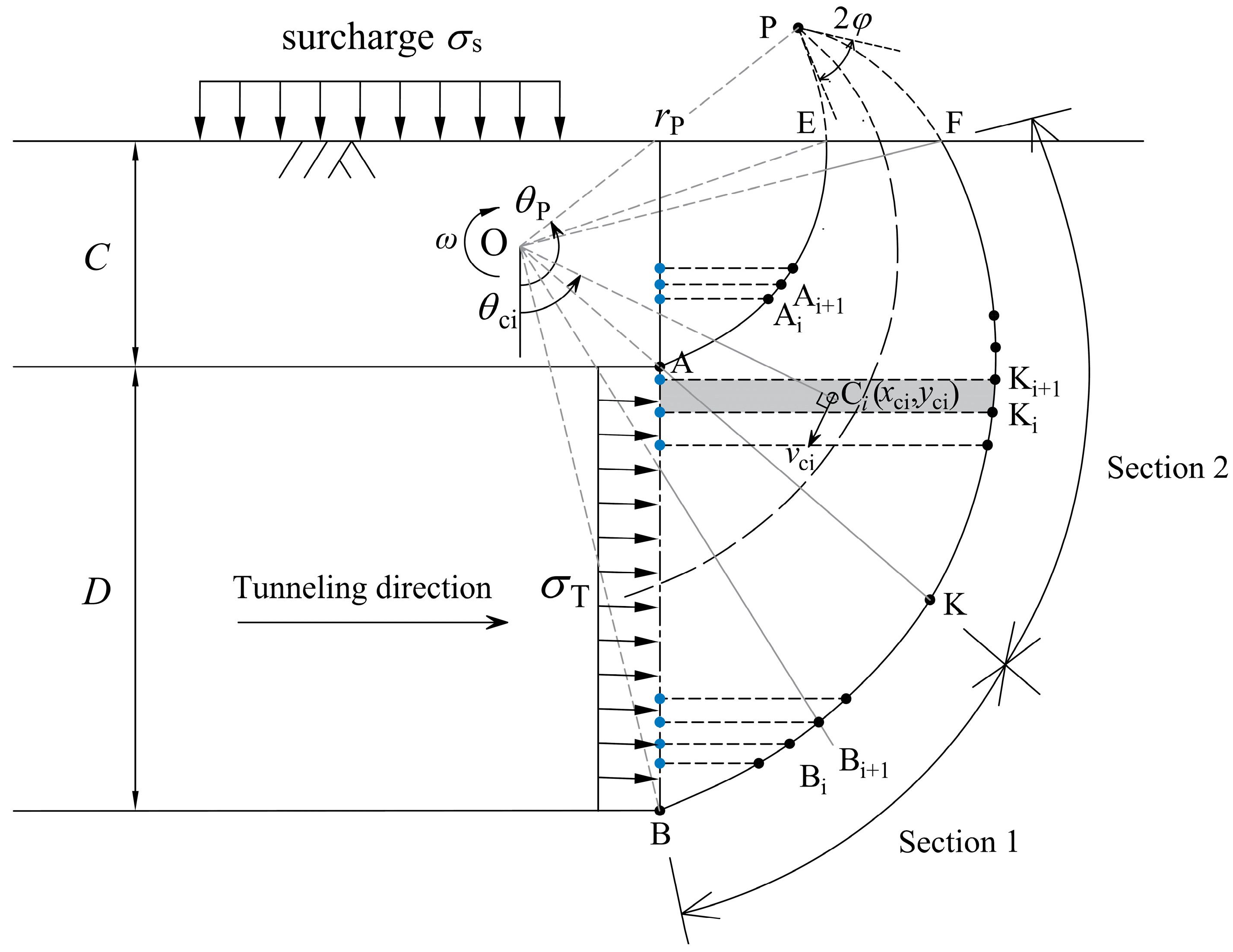
4. Face Stability Analysis by Kinematic Theorem
5. Results and Discussion
5.1. Comparison
5.2. Parametric Studies
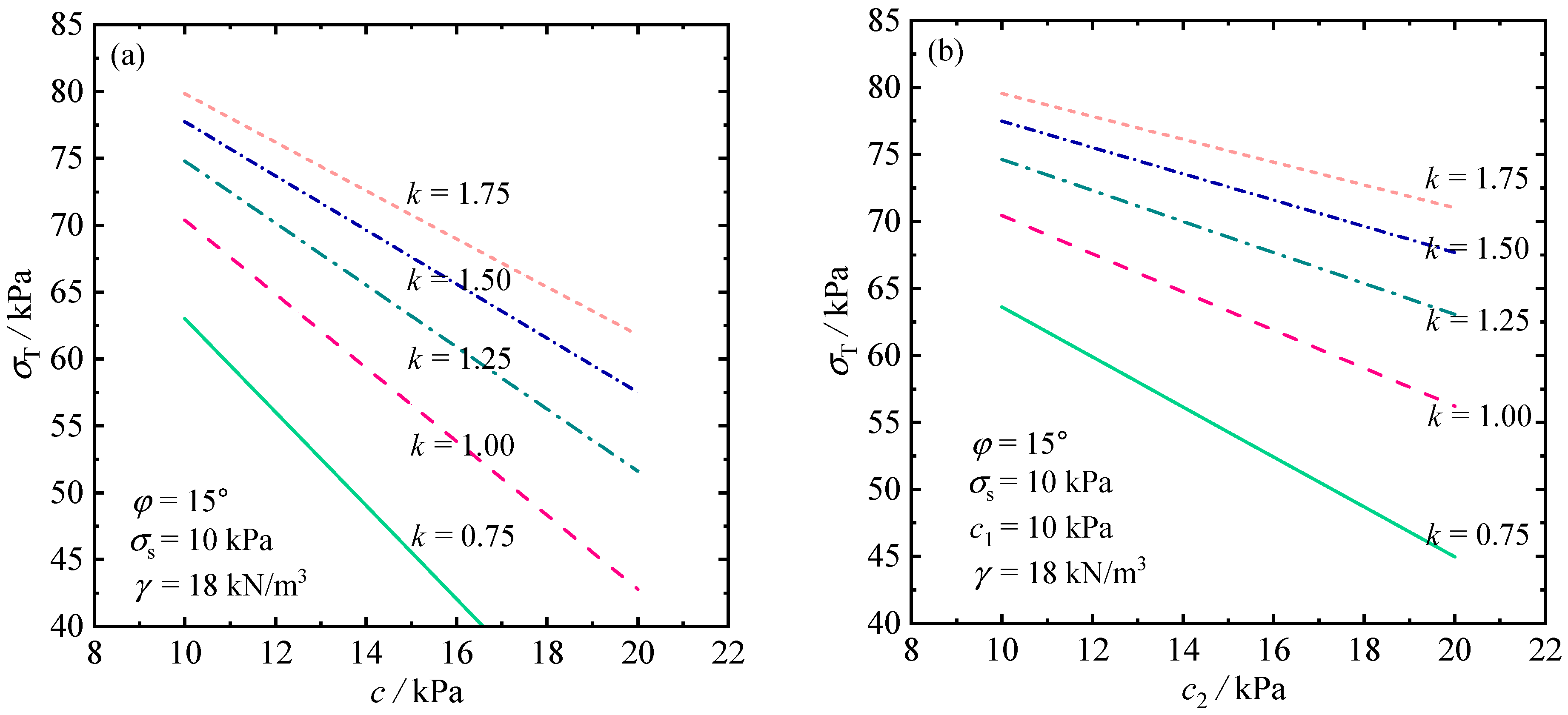
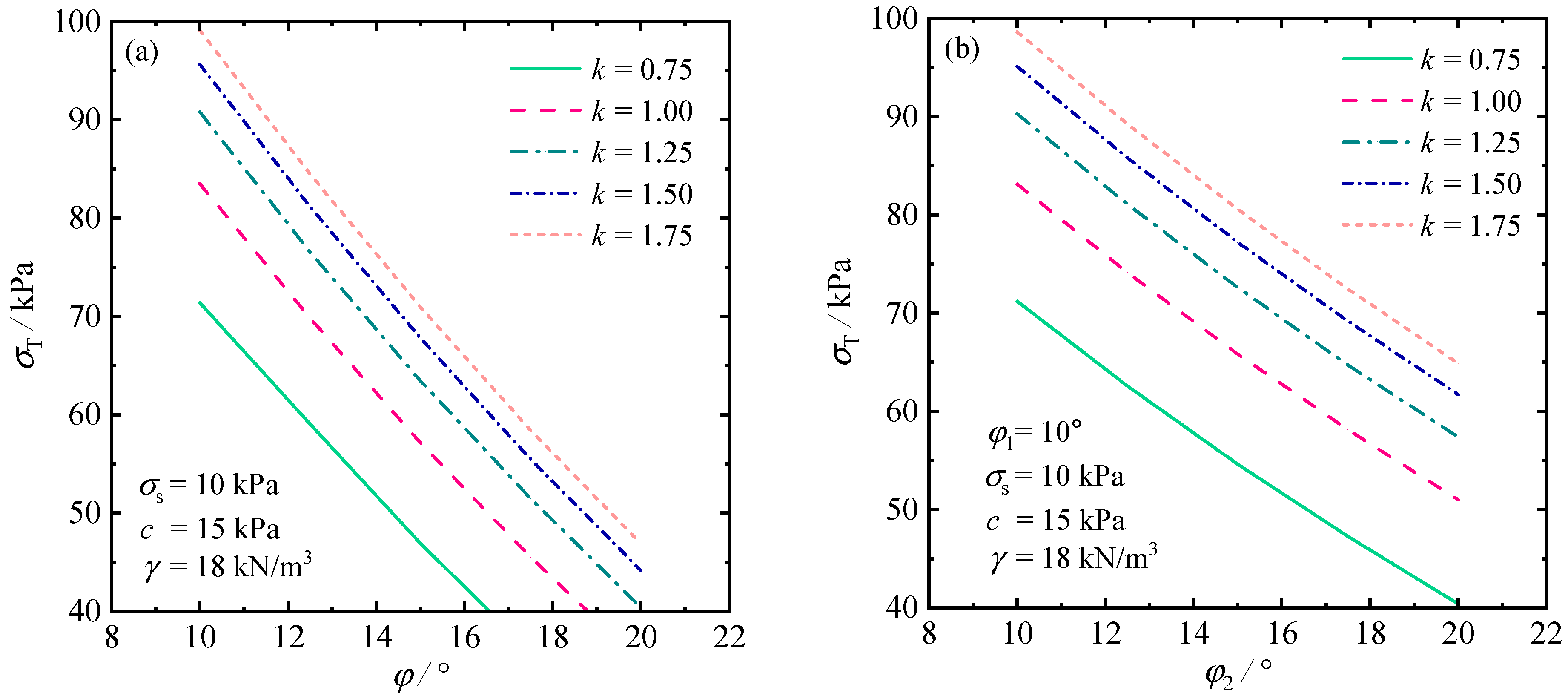
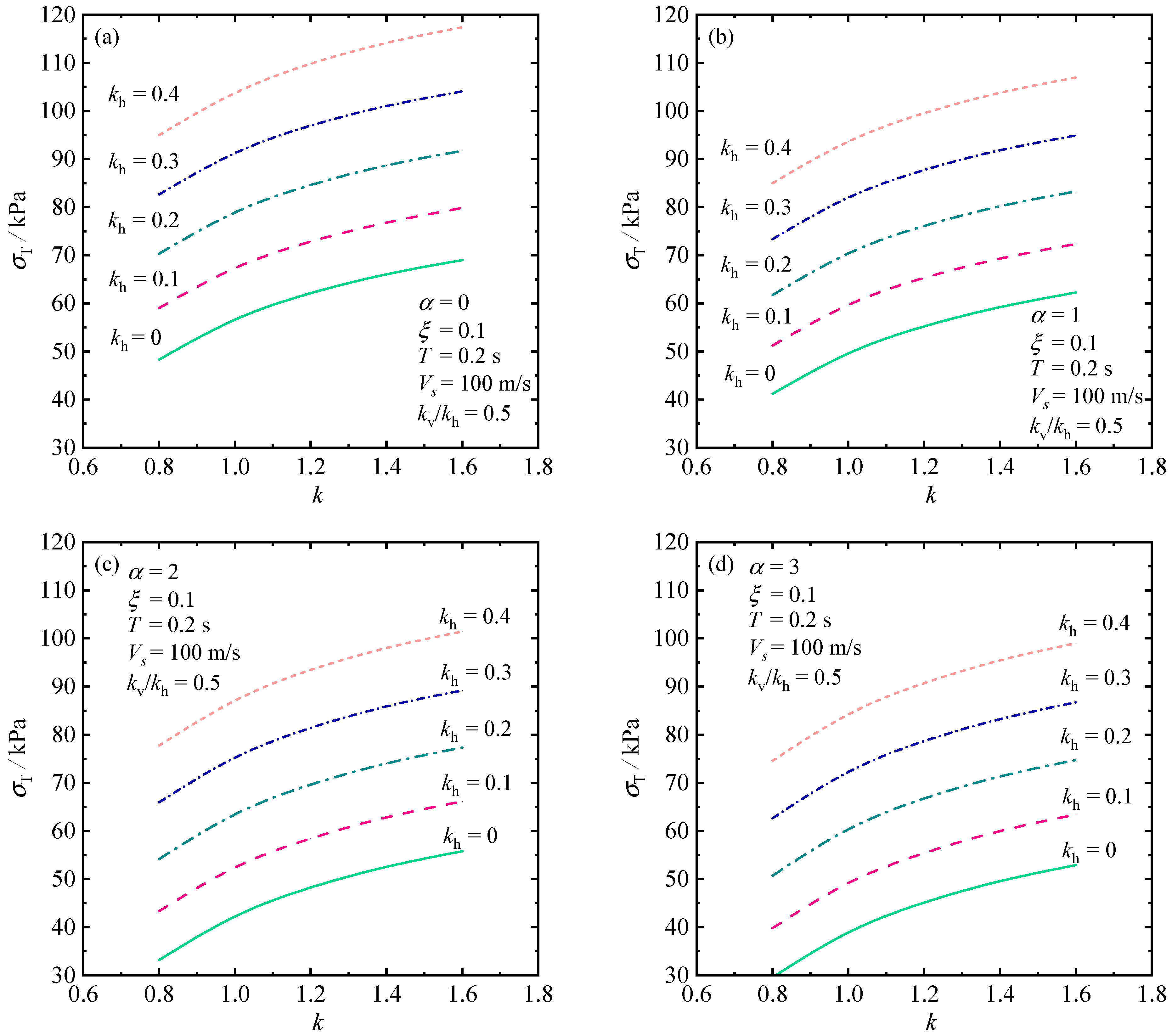
5.2.1. Influence of Heterogeneity and Anisotropy
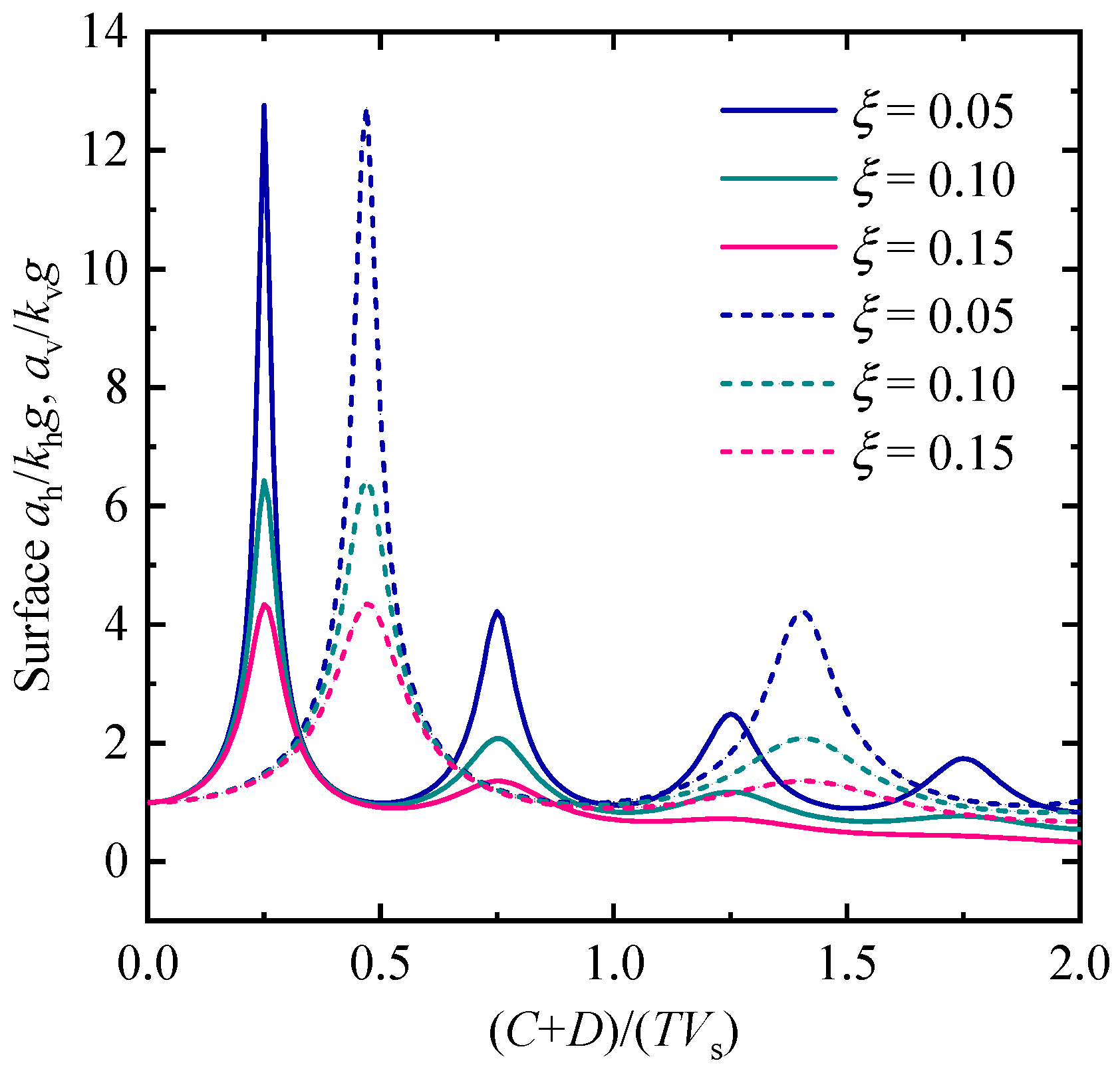
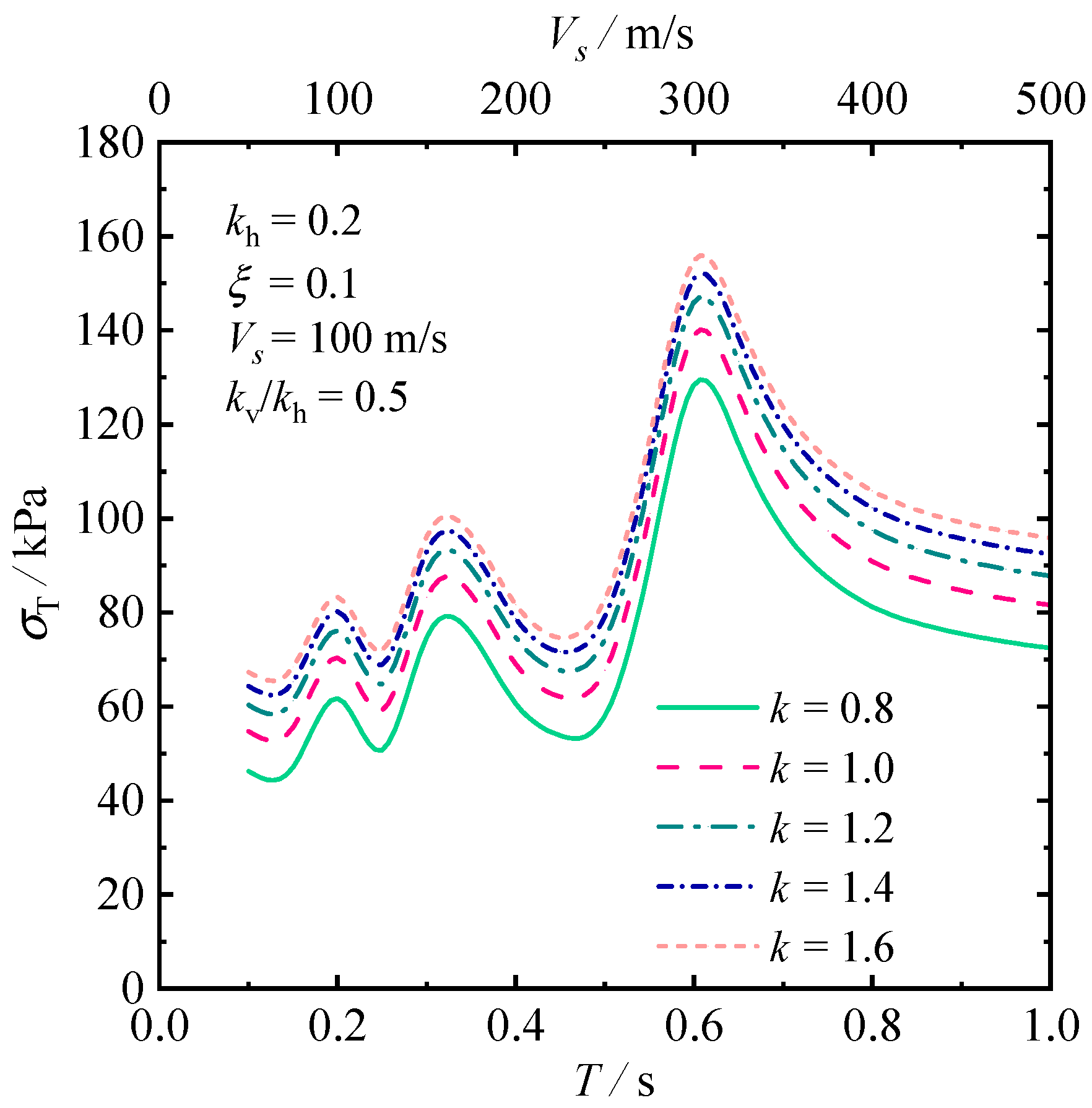
5.2.2. Influence of the Earthquake
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Zhou, Z.; Ling, T.; Huang, F.; Zhang, M. The Face Stability Analysis of Shield Tunnels Subjected to Seepage Based on the Variational Principle. Sustainability 2022, 14, 16538. [Google Scholar] [CrossRef]
- Jiang, B.; Ding, M.; Li, W.; Gu, S.; Ji, H. Investigation on Characteristics and Prevention of Rockburst in a Deep Hard and Soft Compound Stratum Tunnel Excavated Using TBM. Sustainability 2022, 14, 3190. [Google Scholar] [CrossRef]
- Perazzelli, P.; Leone, T.; Anagnostou, G. Tunnel face stability under seepage flow conditions. Tunn. Undergr. Space Technol. 2014, 43, 459–469. [Google Scholar] [CrossRef]
- Chen, R.P.; Tang, L.J.; Yin, X.S.; Chen, Y.M.; Bian, X.C. An improved 3d wedge-prism model for the face stability analysis of the shield tunnel in cohesionless soils. Acta Geotech. 2015, 10, 683–692. [Google Scholar] [CrossRef]
- Zhang, X.; Wang, M.N.; Wang, Z.L.; Li, J.W.; Tong, J.J.; Liu, D.G. A limit equilibrium model for the reinforced face stability analysis of a shallow tunnel in cohesive-frictional soils. Tunn. Undergr. Space Technol. 2020, 105, 103562. [Google Scholar] [CrossRef]
- Wu, L.; Liang, Z.; Chen, M.; Zhou, J. Experiments and Fluent–Engineering Discrete Element Method-Based Numerical Analysis 550of Block Motion in Underwater Rock-Plug Blasting. Appl. Sci. 2023, 13, 348. [Google Scholar] [CrossRef]
- Yi, C.; Senent, S.; Jimenez, R. Effect of advance drainage on tunnel face stability using limit analysis and numerical simulations. Tunn. Undergr. Space Technol. 2019, 93, 103105. [Google Scholar] [CrossRef]
- Li, C.; Wang, Z.; Liu, Q. Numerical Simulation of Mudstone Shield Tunnel Excavation with ABAQUS Seepage–Stress Coupling: A Case Study. Sustainability 2023, 15, 667. [Google Scholar] [CrossRef]
- Niu, Y.; Ren, T.; Zhou, Q.; Jiao, X.; Shi, J.; Xiang, K.; Tao, J.; Zhai, Q.; Satyanaga, A. Analysis of Excavation Parameters on Face Stability in Small Curvature Shield Tunnels. Sustainability 2023, 15, 6797. [Google Scholar] [CrossRef]
- Hou, C.; Zhong, J.; Yang, X. Three-dimensional stability assessments of a non-circular tunnel face reinforced by bolts under seepage flow conditions. Tunn. Undergr. Space Technol. 2023, 131, 104831. [Google Scholar] [CrossRef]
- Zhong, J.; Hou, C.; Yang, X. Three-dimensional face stability analysis of rock tunnels excavated in Hoek-Brown media with a novel multi-cone mechanism. Comput. Geotech. 2023, 154, 105158. [Google Scholar] [CrossRef]
- Zhong, J.; Zhao, S.; Wang, P.; Hou, C. Tunnel Face Stability Considering the Influence of Excess Slurry Pressure. Sustainability 2023, 15, 8230. [Google Scholar] [CrossRef]
- Hou, C.; Yang, X. Three-dimensional face stability of tunnels in unsaturated soils with nonlinear soil strength. Int. J. Geomech. 2021, 21, 06021006. [Google Scholar] [CrossRef]
- Li, Z.W.; Yang, X.L. Active earth pressure for soils with tension cracks under steady unsaturated flow conditions. Can. Geotech. J. 2018, 55, 1850–1859. [Google Scholar] [CrossRef]
- Li, Z.W.; Yang, X.L.; Li, T.Z. Static and seismic stability assessment of 3D slopes with cracks. Eng. Geol. 2020, 265, 105450. [Google Scholar] [CrossRef]
- Zhang, Z.L.; Yang, X.L. Pseudo-dynamic analysis of three-dimensional fissured slopes reinforced with piles. Int. J. Geomech. 2023, 23, 04022315. [Google Scholar] [CrossRef]
- Li, T.Z.; Gong, W.P.; Tang, H.M.; Zhang, L.M. A meshed kinematical approach for 3D slope stability analysis. Int. J. Numer. Anal. Methods. 2022, 46, 2913–2930. [Google Scholar] [CrossRef]
- Zhang, Z.L.; Zhu, J.Q.; Yang, X.L. Three-Dimensional Active Earth Pressures for Unsaturated Backfills with Cracks Considering Steady Seepage. Int. J. Geomech. 2023, 23, 04022270. [Google Scholar] [CrossRef]
- Leca, E.; Dormieux, L. Upper and lower bound solutions for the face stability of shallow circular tunnels in frictional material. Géotechnique 1990, 40, 581–606. [Google Scholar] [CrossRef]
- Mollon, G.; Dias, D.; Soubra, A.H. Face stability analysis of circular tunnels driven by a pressurized shield. J. Geotech. Geoenviron. 2009, 136, 215–229. [Google Scholar] [CrossRef]
- Subrin, D.; Wong, H. Tunnel face stability in frictional material: A new 3D failure mechanism. Comptes Rendus Mec. 2002, 330, 513–519. [Google Scholar] [CrossRef]
- Mollon, G.; Dias, D.; Soubra, A.H. Rotational failure mechanisms for the face stability analysis of tunnels driven by a pressurized shield. Int. J. Numer. Anal. Methods. 2011, 35, 1363–1388. [Google Scholar] [CrossRef]
- Chakraborty, D.; Kumar, J. Stability of a long unsupported circular tunnel in soils with seismic forces. Nat. Hazards. 2013, 68, 419–431. [Google Scholar] [CrossRef]
- Saada, Z.; Maghous, S.; Garnier, D. Pseudo-static analysis of tunnel face stability using the generalized hoek-brown strength criterion. Int. J. Numer. Anal. Methods. 2013, 37, 3194–3212. [Google Scholar] [CrossRef]
- Sahoo, J.P.; Kumar, J. Stability of a circular tunnel in presence of pseudostatic seismic body forces. Tunn. Undergr. Space Technol. 2014, 42, 264–276. [Google Scholar] [CrossRef]
- Pan, Q.J.; Dias, D. The effect of pore water pressure on tunnel face stability. Int. J. Numer. Anal. Methods. 2016, 40, 2123–2136. [Google Scholar] [CrossRef]
- Pan, Q.J.; Dias, D. Three dimensional face stability of a tunnel in weak rock masses subjected to seepage forces. Tunn. Undergr. Space Technol. 2018, 71, 555–566. [Google Scholar] [CrossRef]
- Gong, W.; Juang, C.H.; Wasowski, J. Geohazards and human settlements: Lessons learned from multiple relocation events in Badong, China–Engineering geologist’s perspective. Eng. Geol. 2021, 285, 106051. [Google Scholar] [CrossRef]
- Li, T.Z.; Pan, Q.; Dias, D. Active learning relevant vector machine for reliability analysis. Appl. Math. Model. 2021, 89, 381–399. [Google Scholar] [CrossRef]
- Chen, G.H.; Zou, J.F.; Chen, J.Q. Shallow tunnel face stability considering pore water pressure in non-homogeneous and anisotropic soils. Comput. Geotech. 2019, 116, 103205. [Google Scholar] [CrossRef]
- Qin, C.B.; Chian, S.C. Seismic bearing capacity of non-uniform soil slopes using discretization-based kinematic analysis considering rayleigh waves. Soil. Dyn. Earthq. Eng 2018, 109, 23–32. [Google Scholar] [CrossRef]
- Zhong, J.H.; Yang, X.L. Kinematic stability of tunnel face in non-uniform soils. KSCE J. Civ. Eng. 2019, 24, 670–681. [Google Scholar] [CrossRef]
- Zhong, J.H.; Yang, X.L. Kinematic analysis of the three-dimensional stability for tunnel faces by pseudodynamic approach. Comput. Geotech. 2020, 128, 103802. [Google Scholar] [CrossRef]
- Kramer, S.L. Geotechnical Earthquake Engineering; Pearson Education: Cranbury, NJ, USA, 1996. [Google Scholar]
- Bellezza, I. A new pseudo-dynamic approach for seismic active soil thrust. Geotech. Geol. Eng. 2014, 32, 561–576. [Google Scholar] [CrossRef]
- Casagrande, A.; Carillo, N. Shear failure of anisotropic materials. J. Boston Soc. Civ. Eng. 1944, 31, 122–135. [Google Scholar]


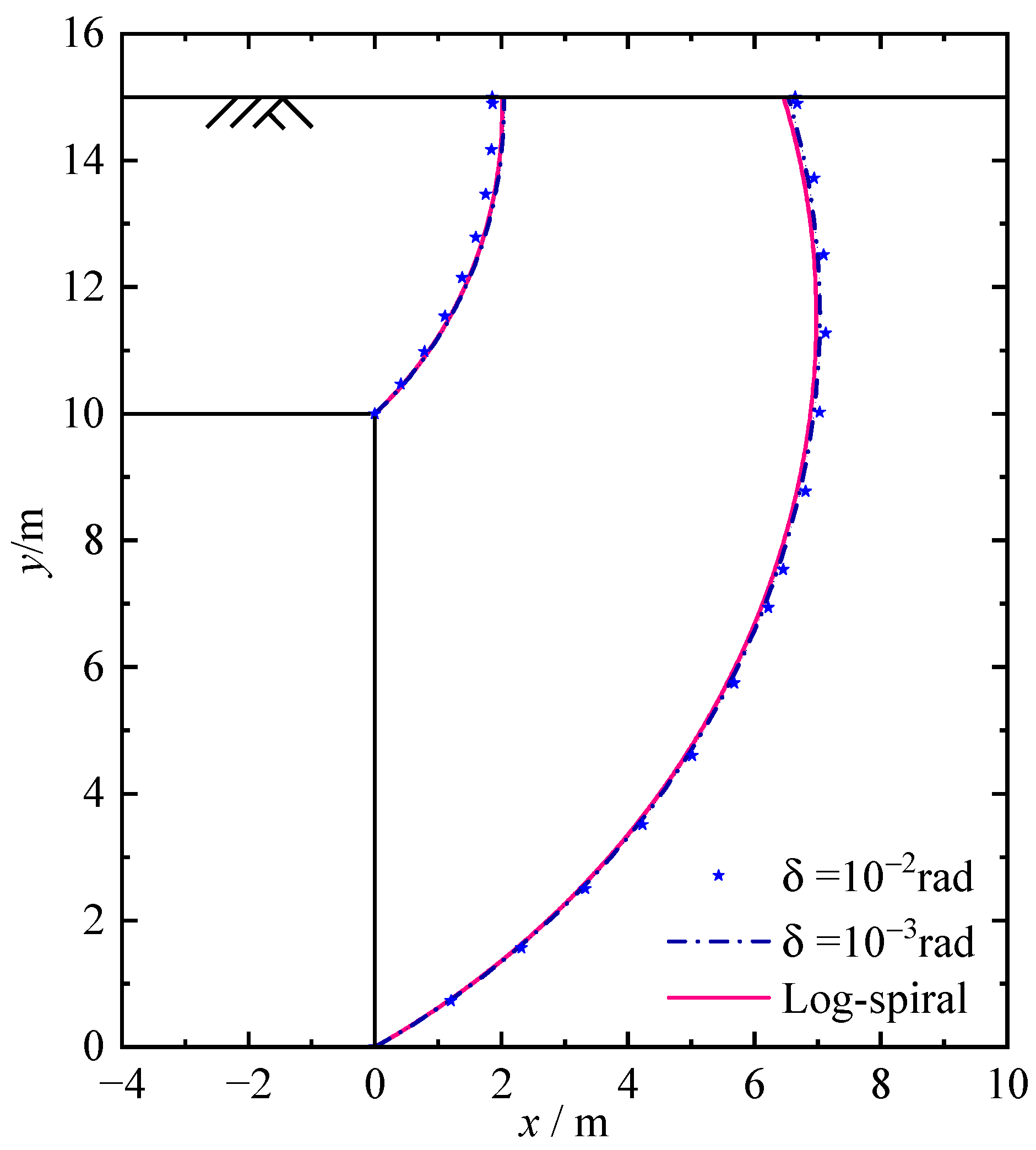





| Discretized Mechanism | Log-Spiral Mechanism | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| = 0.01 rad | = 0.001 rad | ||||||||
| c = 5 | c = 10 | c = 15 | c = 5 | c = 10 | c = 15 | c = 5 | c = 10 | c = 15 | |
| 5 | 137.86 | 121.01 | 104.41 | 136.39 | 119.64 | 103.12 | 136.23 | 119.49 | 102.98 |
| 10 | 109.89 | 94.66 | 79.57 | 108.56 | 93.41 | 78.40 | 108.41 | 93.27 | 78.27 |
| 15 | 82.67 | 68.81 | 55.00 | 81.59 | 67.80 | 54.06 | 81.47 | 67.69 | 53.96 |
| 20 | 59.65 | 47.00 | 34.40 | 58.80 | 46.21 | 33.67 | 58.70 | 46.12 | 33.58 |
| 25 | 41.51 | 30.65 | 19.80 | 40.92 | 30.19 | 19.45 | 40.86 | 30.13 | 19.41 |
| C/D | Discretized Mechanism | Log-Spiral Mechanism | |||||
|---|---|---|---|---|---|---|---|
| Homogeneity and Isotropy | Heterogeneity and Anisotropy | Homogeneity and Isotropy | Heterogeneity and Anisotropy | ||||
| 0.20 | 72.04 | 78.95 | 68.75 | 69.59 | 71.94 | 78.84 | 69.48 |
| 0.40 | 86.82 | 94.51 | 83.00 | 84.31 | 86.69 | 94.38 | 84.18 |
| 0.60 | 99.42 | 107.72 | 94.77 | 97.11 | 99.27 | 107.56 | 96.95 |
| 0.80 | 109.47 | 118.29 | 103.89 | 107.55 | 109.30 | 118.11 | 107.37 |
| 1.00 | 116.65 | 126.03 | 110.26 | 115.29 | 116.45 | 125.83 | 115.08 |
| 1.20 | 120.69 | 130.75 | 113.68 | 120.07 | 120.48 | 130.53 | 119.84 |
| This Study | Zhong and Yang [32] | |||||
|---|---|---|---|---|---|---|
| Pseudostatic Method | Results by MPD | Results by CPD | ||||
| kh = 0.1 | kh = 0.3 | kh = 0.1 | kh = 0.3 | kh = 0.1 | kh = 0.3 | |
| 5 | 140.34 | 194.84 | 130.72 | 160.02 | 130.62 | 154.19 |
| 10 | 108.79 | 144.01 | 106.13 | 134.54 | 103.94 | 124.48 |
| 15 | 80.51 | 107.45 | 80.22 | 107.49 | 77.12 | 95.72 |
| 20 | 56.54 | 77.82 | 57.01 | 80.71 | 53.97 | 69.31 |
| 25 | 38.35 | 55.32 | 39.10 | 58.91 | 36.25 | 48.48 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, X.; Zhang, K.; Wang, W. Seismic Stability Analysis of Tunnel Faces in Heterogeneous and Anisotropic Soils Using Modified Pseudodynamic Method. Sustainability 2023, 15, 11083. https://doi.org/10.3390/su151411083
Chen X, Zhang K, Wang W. Seismic Stability Analysis of Tunnel Faces in Heterogeneous and Anisotropic Soils Using Modified Pseudodynamic Method. Sustainability. 2023; 15(14):11083. https://doi.org/10.3390/su151411083
Chicago/Turabian StyleChen, Xi, Kun Zhang, and Wei Wang. 2023. "Seismic Stability Analysis of Tunnel Faces in Heterogeneous and Anisotropic Soils Using Modified Pseudodynamic Method" Sustainability 15, no. 14: 11083. https://doi.org/10.3390/su151411083
APA StyleChen, X., Zhang, K., & Wang, W. (2023). Seismic Stability Analysis of Tunnel Faces in Heterogeneous and Anisotropic Soils Using Modified Pseudodynamic Method. Sustainability, 15(14), 11083. https://doi.org/10.3390/su151411083




