Sizing of Hybrid PV/Battery/Wind/Diesel Microgrid System Using an Improved Decomposition Multi-Objective Evolutionary Algorithm Considering Uncertainties and Battery Degradation
Abstract
1. Introduction
- The paper uses the multi-objective approach of problem formulation because it has the unique Pareto Front (PF) property of presenting the set of solutions of a multi-objective problem in a single shot. Using their expertise, the design requirements, and constraints, the design engineers can choose from any available solution.
- To address the issue of developing HMSs, a novel multi-objective strategy based on an enhanced Decomposition-Based Multi-Objective Evolutionary Algorithm (MOEA/D) is developed in this study. The results obtained from several decomposition methods are combined into a single set of solutions using the proposed novel approach.
- To assess its impact on the completed design, this article models and examines two crucial features: load variability (uncertainty) and battery deterioration.
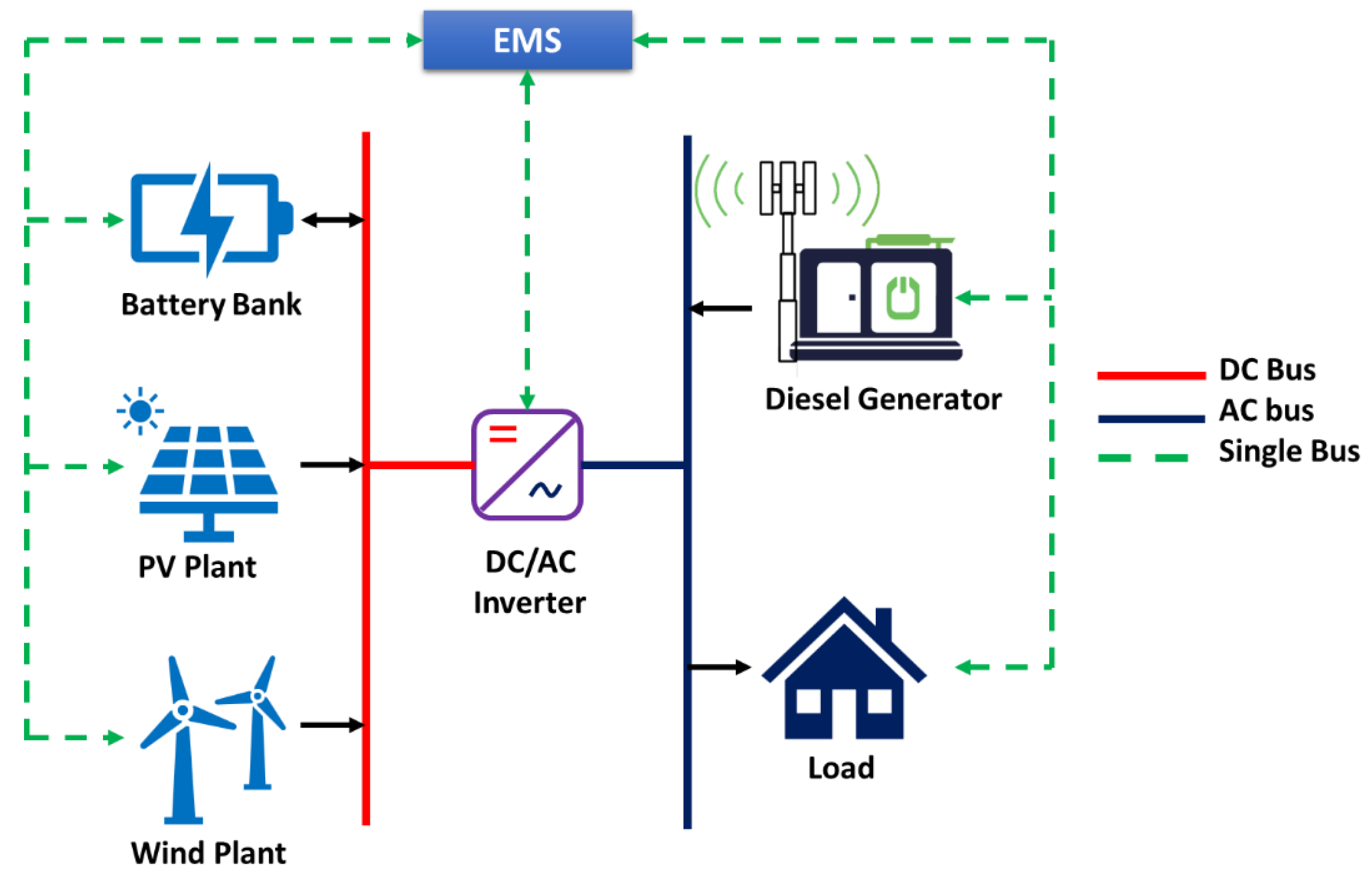
2. Hybrid Microgrid System Configuration
2.1. Mathematical Model of the HMS
2.1.1. PV Plant
2.1.2. Wind Plant
2.1.3. Battery
2.1.4. Diesel Generator
2.1.5. Inverter
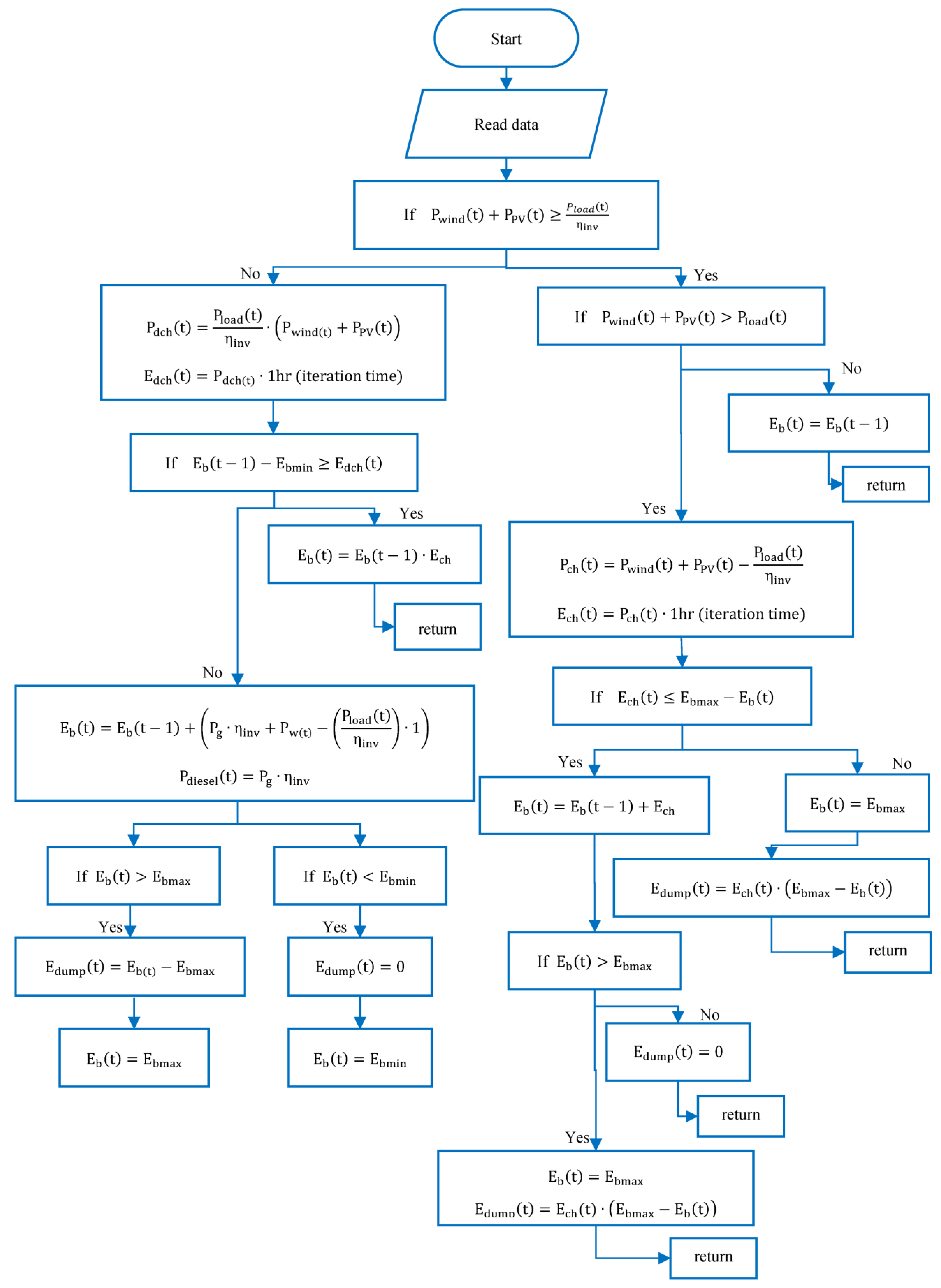
2.1.6. Management Strategy of EMS
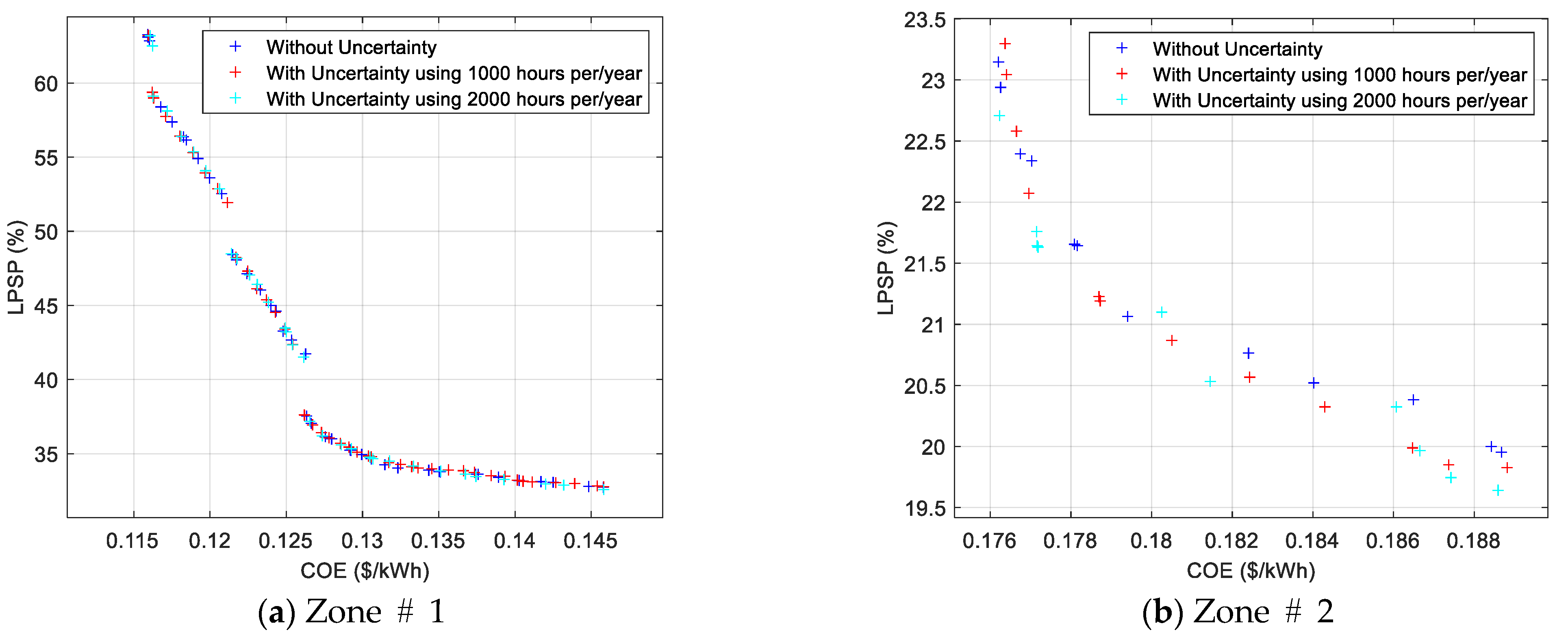
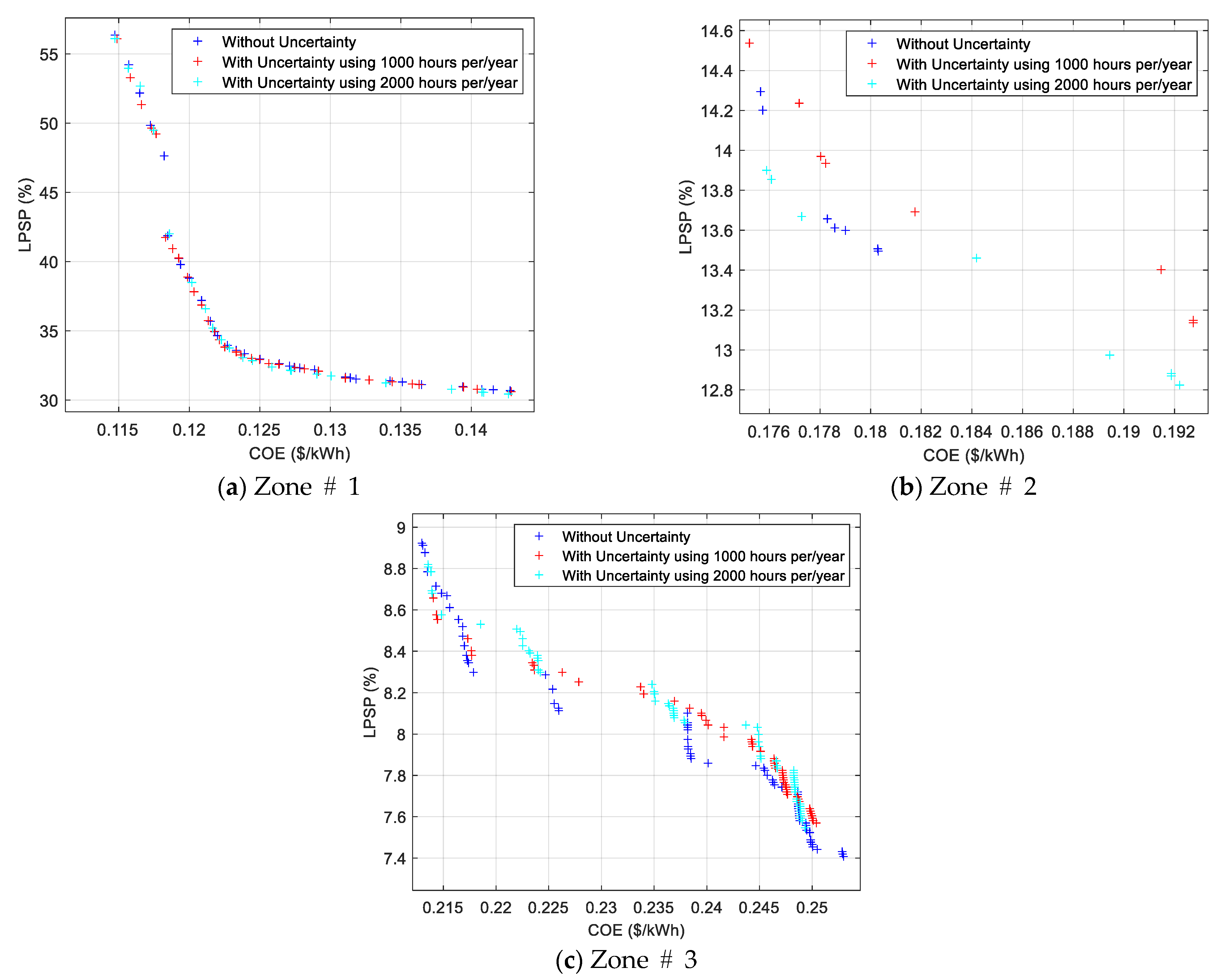
2.2. Uncertainty
2.2.1. Uncertainty in Microgrids
2.2.2. Stochastic and Deterministic Models
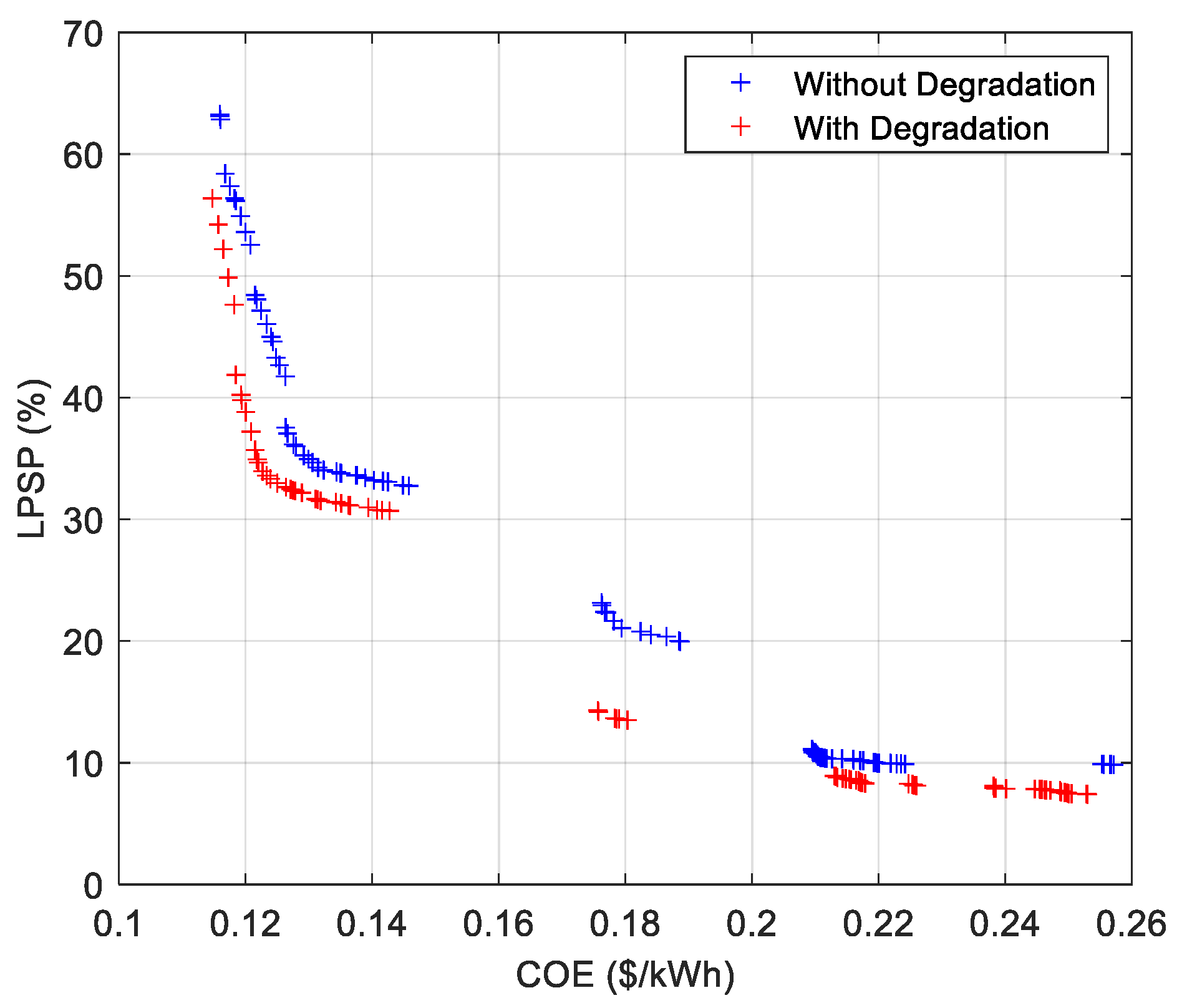
2.3. Battery Degradation
3. Optimization Process
3.1. Problem Formulation
3.2. Objective Functions
3.2.1. Cost of Electricity (COE)
3.2.2. Loss of Power Supply Probability (LPSP)
3.3. The Constraints for Optimization
3.4. Design Variables
3.5. Formulating the Uncertainty
3.6. Degradation Formulation
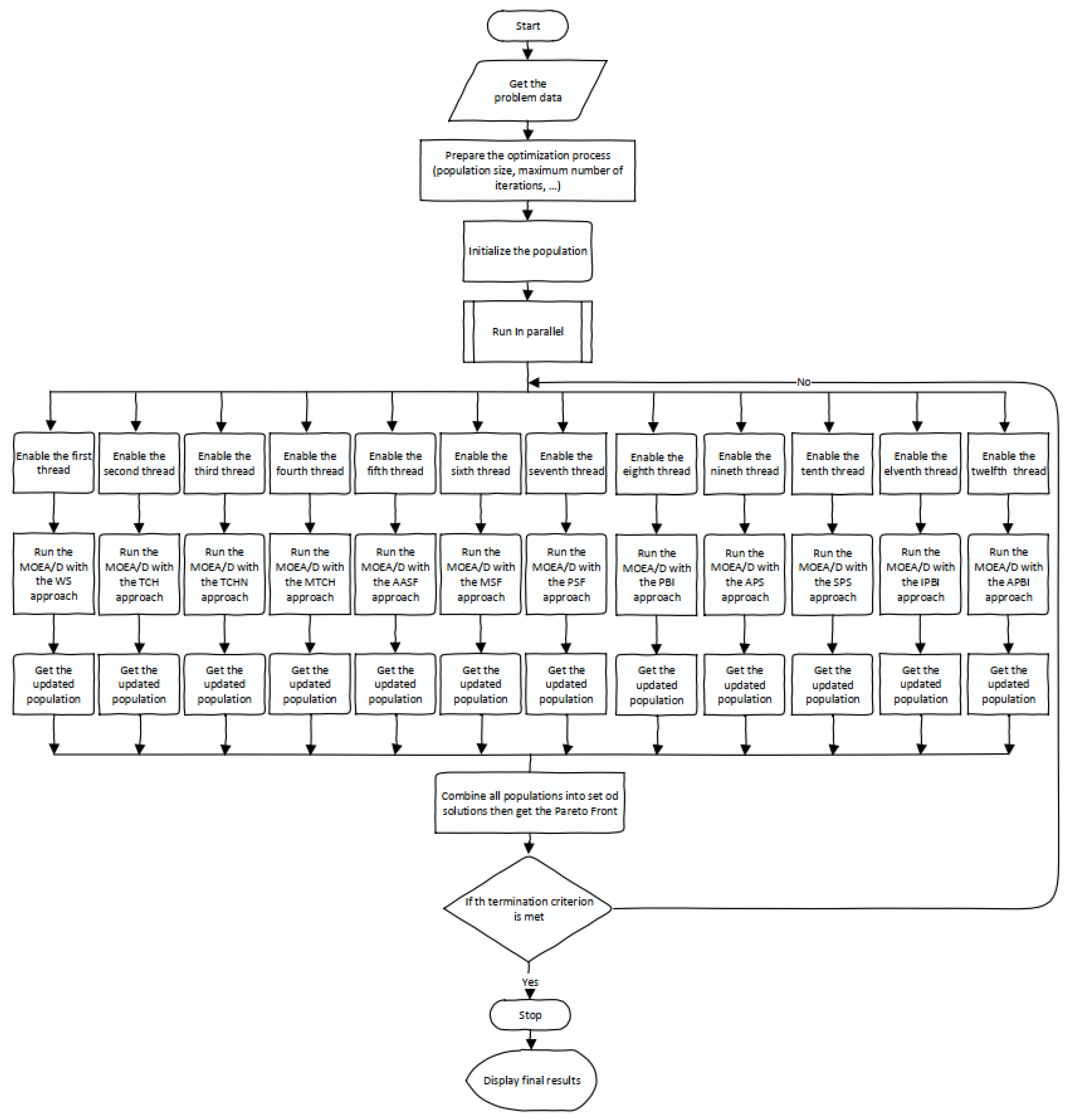
3.7. Problem Solution Using Decomposition-Based Multi-Objective Evolutionary Algorithm (MOEA/D)
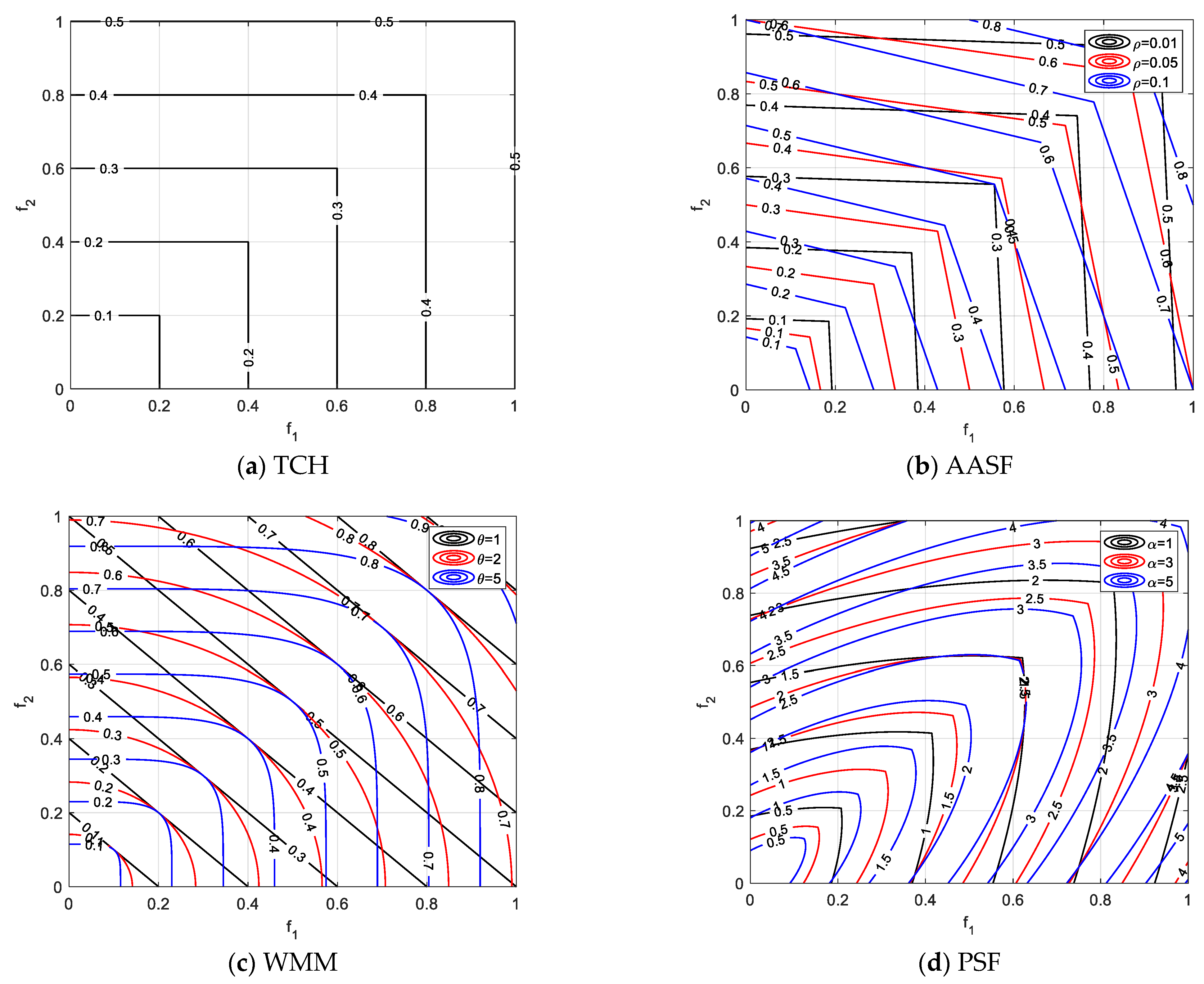
3.7.1. The Weighted Sum Approach
3.7.2. The Weighted Tchebycheff (TCH) Approach
3.7.3. The Normalized TCH Version (NTCH)
3.7.4. The Modified TCH Version (MTCH)
3.7.5. Variants of the TCH Approach
Augmented Achievement Scalarizing Function (AASF)
Weighted-Metrics-Based (WMM) Methods
Multiplicative Scalarizing Function (MSF)
Penalty-Based Scalarizing Function (PSF)
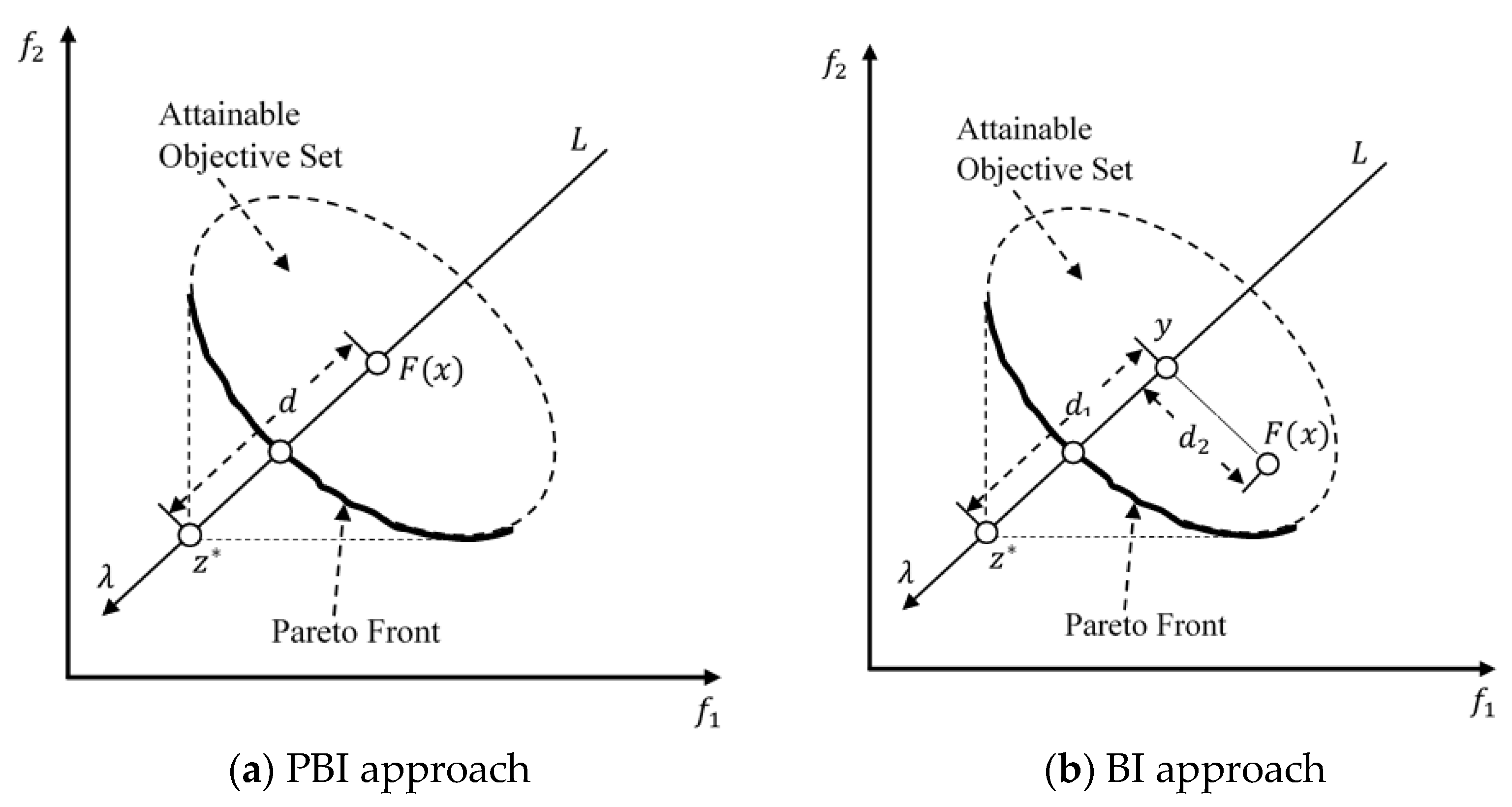
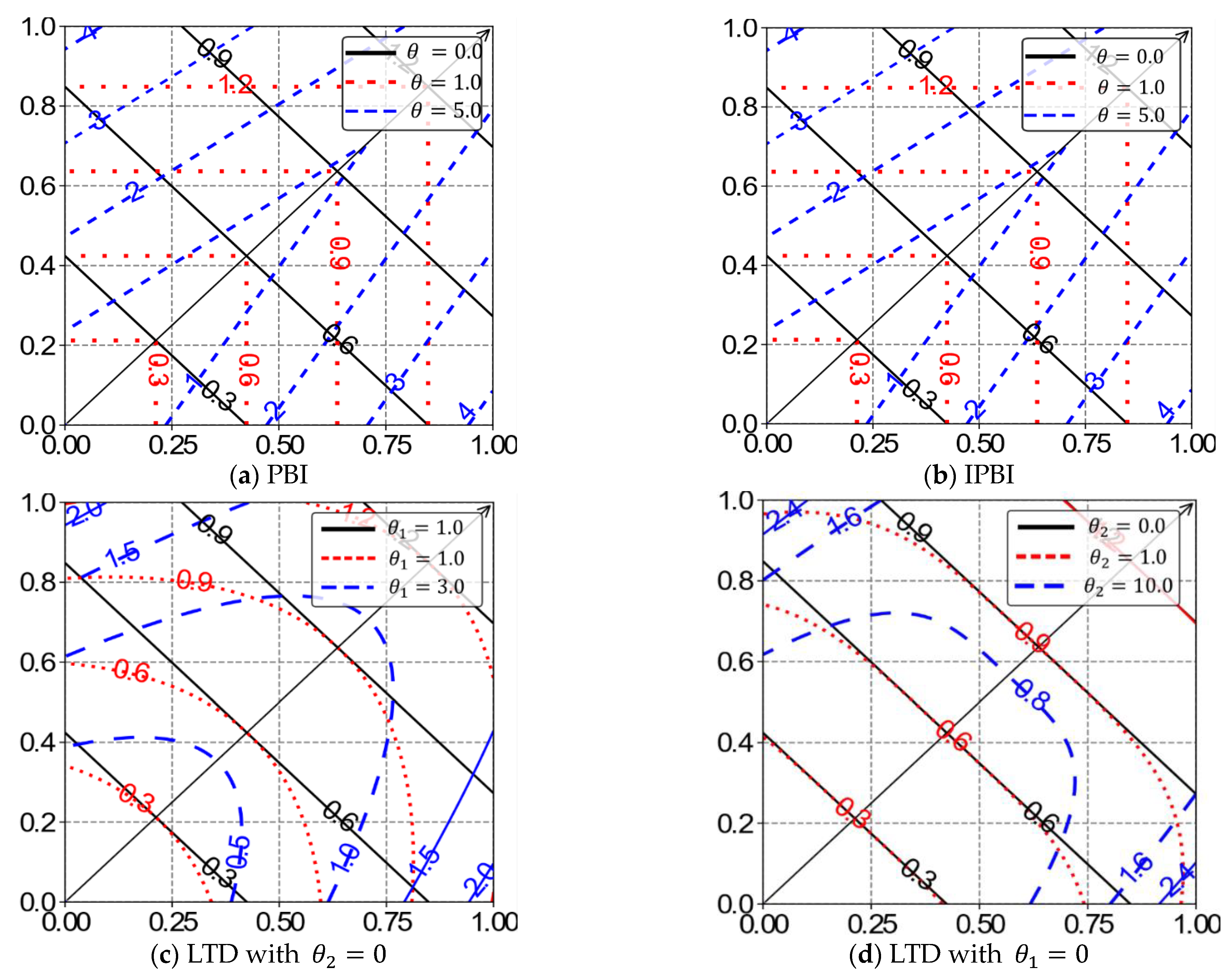
3.7.6. The Penalty-Based Boundary Intersection (PBI) Approach
3.7.7. Variants of the PBI Approach
Adaptive Penalty Scheme (APS)
Subproblem-Based Penalty Scheme (SPS)
Inverted PBI (IPBI)
The Augmented PBI (APBI)
3.7.8. The General Framework for MOEA/D
- 1.
- The population of the most recent solution to the N subproblems, .
- 2.
- The F values of these recent solutions, .
- 3.
- The set of optimal values for the objectives discovered so far, .
- 4.
- An external population, comprising solutions that are nondominated.
- 5.
- Refer to Algorithm 1 for the details of the MOEA/D algorithm [44].
| Algorithm 1: MOEA/D | |
| Input: (1) MOP (11); (2) Stopping criteria ; (3) N: Number of MOEA/D subproblems ; (4) N uniform spread of weight vectors (5) T: no. of weight vectors in the neighborhood of each weight vector Output: | |
| 1 | Initialization: |
| 2 | Compute the Euclidean distance between any two weight vectors and find the T closest weight |
| vectors to each weight vector. | |
| 3 | for do |
| 4 | – the T closest weight vectors to . |
| 5 | end for |
| 6 | Generate initial population randomly or by the problem-specific method. |
| 7 | Set . |
| 8 | Initialize by a problem-specific method |
| 9 | while the stopping criteria is not met do |
| 10 | Update: |
| 11 | for do |
| 12 | Reproduction: |
| 13 | Randomly select two indexes from , and generate a new solution |
| from and by using genetic operators | |
| 14 | Improvement: |
| 15 | Apply a problem-specific repair/improvement heuristic on to produce |
| 16 | Update |
| 17 | for to do |
| 18 | if then |
| 19 | |
| 20 | end if |
| 21 | end for |
| 22 | Update Neighboring Solutions: |
| 23 | for do |
| 24 | if |
| 25 | set and |
| 26 | end if |
| 27 | end for |
| 28 | Update EP: |
| 29 | Remove from EP all the vectors dominated by |
| 30 | Add to EP if no vectors in EP dominate |
| 31 | end for |
| 32 | end while |
4. The Proposed IMOEAD Approach: Description and Implementation
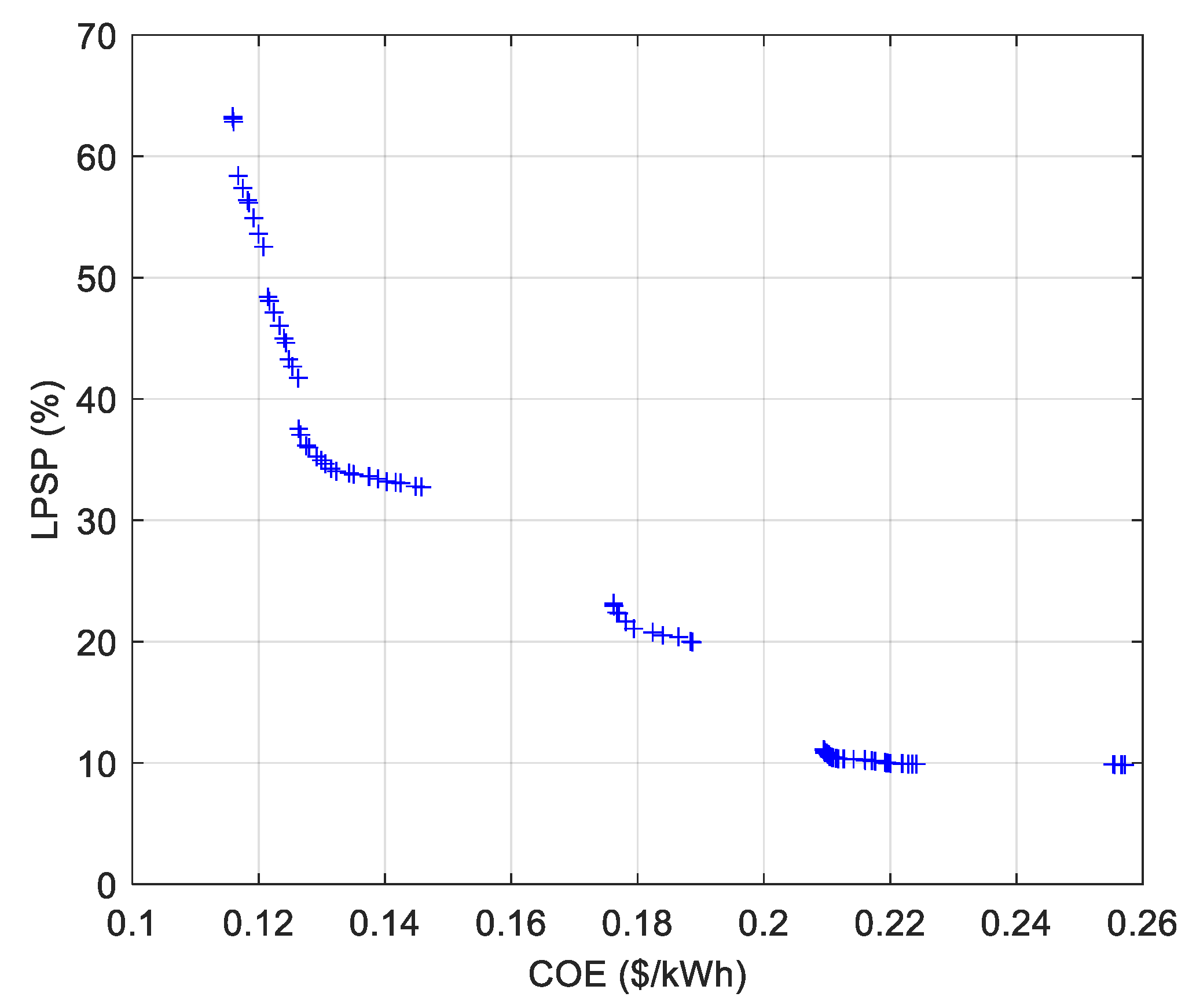
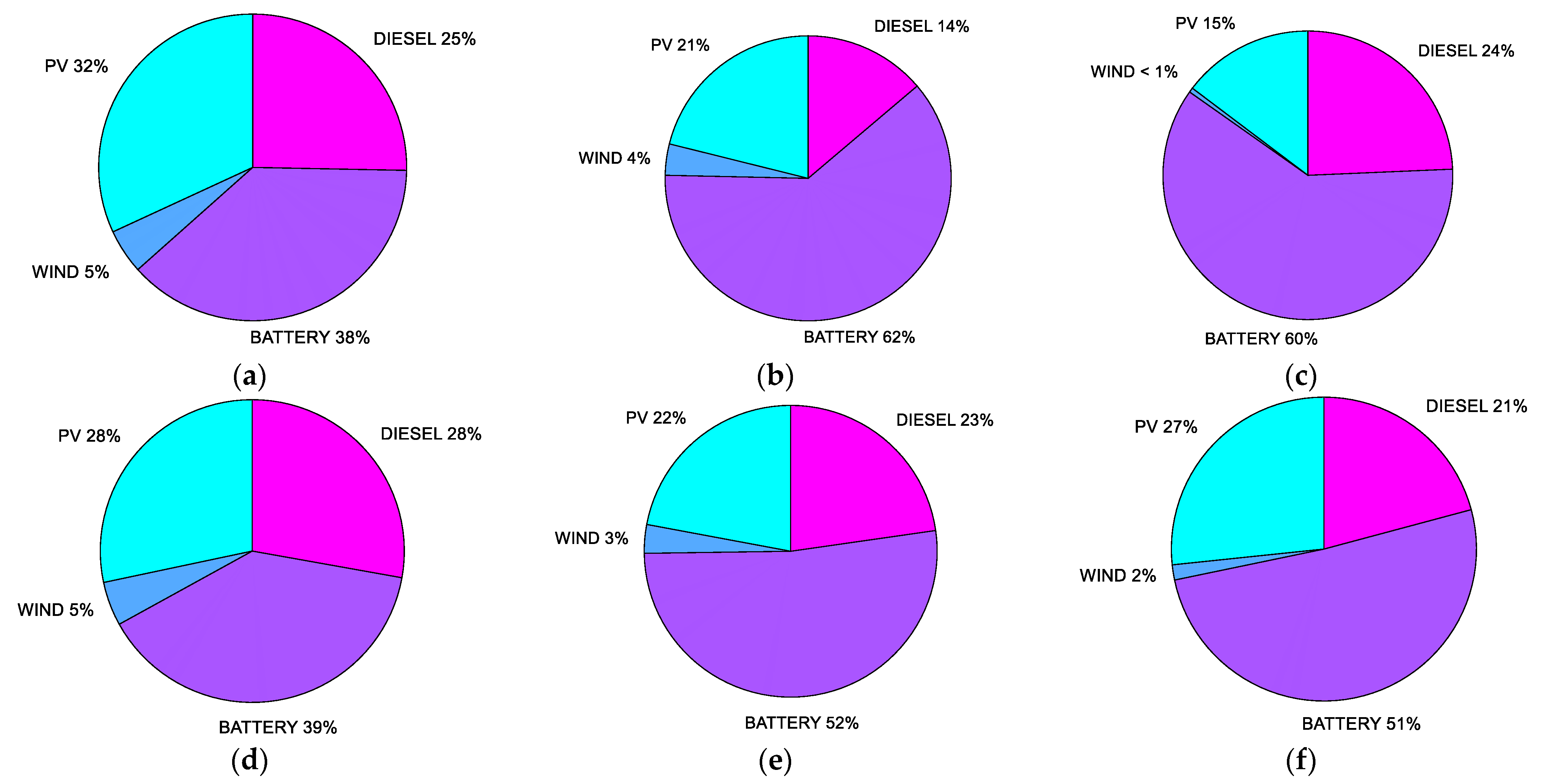
5. Application Results and Discussion
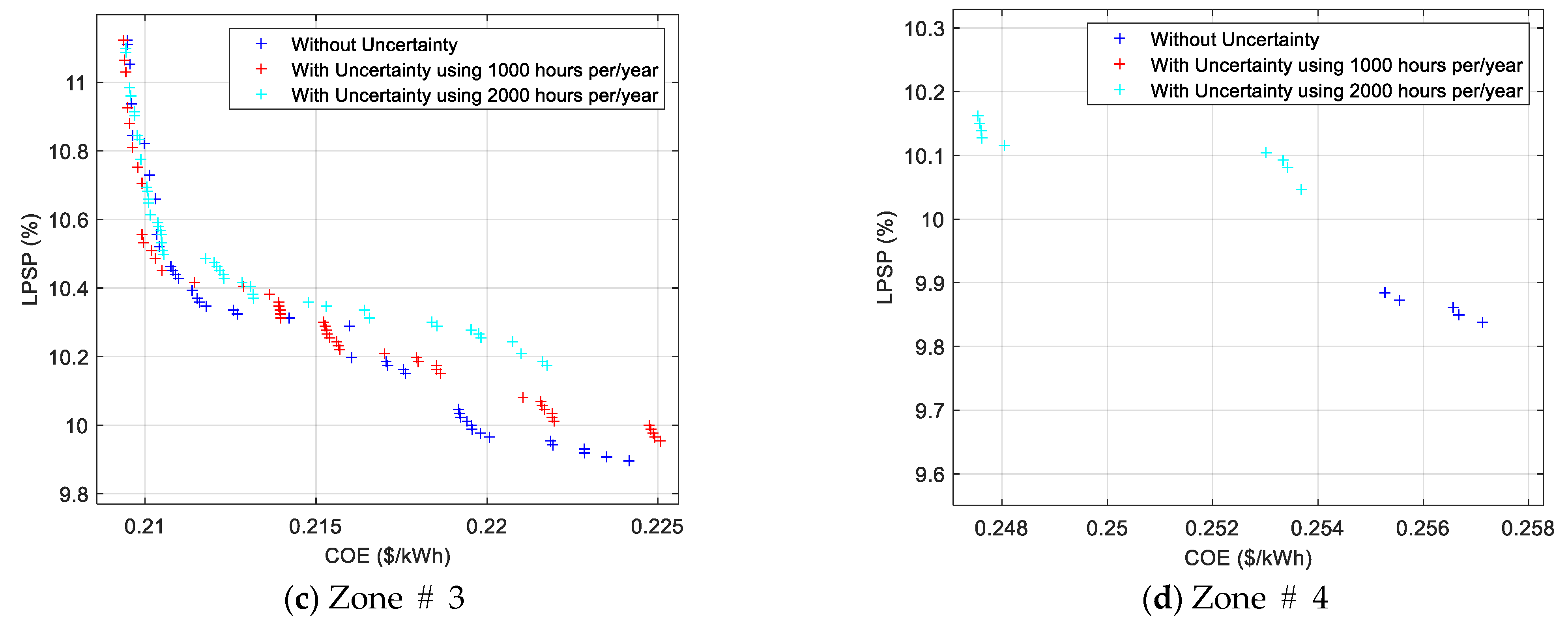
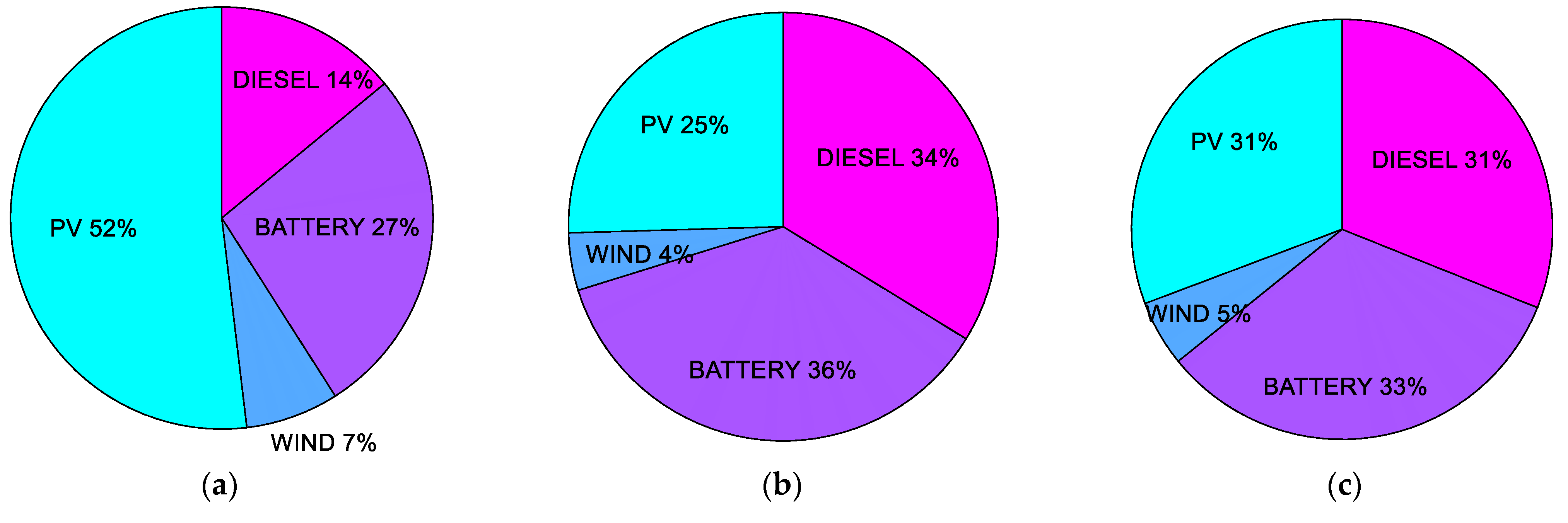
5.1. Investigated Cases
5.2. Five Houses’ Cases
5.3. Ten Houses’ Cases
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| AASF | Augmented Achieving Scalarizing Function |
| AC | Alternating Current |
| AD | Autonomy Days |
| AIS | Artificial Immune System |
| APBI | Augmented-Penalty-based Boundary Intersection |
| APS | Adaptive Penalty Scheme |
| BI | Boundary Intersection |
| COE | Cost of Electricity |
| CRF | Capital Recovery Factor |
| CSA | Cuckoo Search Algorithm |
| DC | Direct Current |
| DE | Differential Evolution |
| DOD | Depth of Discharge |
| EMS | Energy Management System |
| GA | Genetic Algorithm |
| GOA | Grasshopper Optimization System |
| GWO | Grey Wolf Optimization |
| HMS | Hybrid Microgrid System |
| IEC | International Electrotechnical Commission |
| IGBT | Insulated-gate Bipolar Transistor |
| IMOEAD | Improved Decomposition Multi-Objective Evolutionary Algorithm |
| IPBI | Inverted-Penalty-based Boundary Intersection |
| LPSP | Loss of Power Supply Probability |
| LTD | Learning to Decompose |
| MILP | Mixed Integer Linear Programming |
| MIP | Mixed Integer Programming |
| MOEA | Multi-objective Evolutionary Algorithm |
| MOEA/D | Multi-objective Evolutionary Algorithm by Decomposition |
| MOEA/D-LTD | Multi-objective Evolutionary Algorithm by Decomposition using Learning to Decompose Paradigm |
| MOEA/D-PaP | Multi-objective Evolutionary Algorithm by Decomposition using Pareto Adaptive PBI |
| MOEA/D-Par | Multi-objective Evolutionary Algorithm by Decomposition using Pareto adaptive scalarizing functions |
| MOEA/D-Pas | Multi-objective Evolutionary Algorithm by Decomposition using Pareto Adaptive Scalarizing methods |
| MSF | Multiplicative Scalarizing Function |
| MTCH | Modified Tchebycheff |
| NAD | Number of Autonomy Days |
| NDiesel | Number of Diesel Generators |
| NPC | Net Profit Cost |
| NSGA | Non-dominated Sorting Genetic Algorithm |
| NSGA-III-AASF | Non-dominated Sorting Genetic Algorithm III using Augmented achievement scalarizing function |
| NSGA-III-EPBI | Non-dominated Sorting Genetic Algorithm III using Penalty-based Boundary Intersection |
| NTCH | Normalized Tchebycheff |
| NWT | Number of Wind Turbines |
| O&M | Operation and Maintenance |
| PBI | Penalty-based Boundary Intersection |
| PF | Pareto Front |
| PSF | Penalty-based Scalarizing Function |
| PSO | Particle Swarm Optimization |
| PV | Photovoltaic |
| RES | Renewable Energy Source |
| RF | Renewable Factor |
| SA | Simulated Annealing |
| SDE | Self-Adaptive Differential Evolution |
| SPS | Subproblem-based Penalty Scheme |
| STC | Standard Test Conditions |
| TCH | Tchebycheff |
| TLBO | Teaching-Learning-Based Optimization |
| TLBO | Teaching-Learning-Based Optimization |
| TS | Tabu Search |
| TS | Tabu Search |
| WS | Weighted Sum |
| WT | Wind Turbine |
| WWM | Weighted-Metrics-based Methods |
References
- Das, B.K.; Alotaibi, M.A.; Das, P.; Islam, M.S.; Das, S.K.; Hossain, M.A. Feasibility and Techno-Economic Analysis of Stand-Alone and Grid-Connected PV/Wind/Diesel/Batt Hybrid Energy System: A Case Study. Energy Strateg. Rev. 2021, 37, 100673. [Google Scholar] [CrossRef]
- Ellabban, O.; Abu-Rub, H.; Blaabjerg, F. Renewable Energy Resources: Current Status, Future Prospects and Their Enabling Technology. Renew. Sustain. Energy Rev. 2014, 39, 748–764. [Google Scholar] [CrossRef]
- Moghaddam, A.A.; Seifi, A.; Niknam, T.; Alizadeh Pahlavani, M.R. Multi-Objective Operation Management of a Renewable MG (Micro-Grid) with Back-up Micro-Turbine/Fuel Cell/Battery Hybrid Power Source. Energy 2011, 36, 6490–6507. [Google Scholar] [CrossRef]
- Hepbasli, A.; Alsuhaibani, Z. A Key Review on Present Status and Future Directions of Solar Energy Studies and Applications in Saudi Arabia. Renew. Sustain. Energy Rev. 2011, 15, 5021–5050. [Google Scholar] [CrossRef]
- Al-Abbadi, N.M. Wind Energy Resource Assessment for Five Locations in Saudi Arabia. Renew. Energy 2005, 30, 1489–1499. [Google Scholar] [CrossRef]
- Rehman, S.; Al-Abbadi, N.M. Wind Shear Coefficients and Energy Yield for Dhahran, Saudi Arabia. Renew. Energy 2007, 32, 738–749. [Google Scholar] [CrossRef]
- Bouchekara, H.R.A.-H.; Shahriar, M.S.; Javaid, M.S.; Sha’aban, Y.A.; Ramli, M.A.M. Multi-Objective Optimization of a Hybrid Nanogrid/Microgrid: Application to Desert Camps in Hafr Al-Batin. Energies 2021, 14, 1245. [Google Scholar] [CrossRef]
- Bouchekara, H.R.E.H.; Shahriar, M.S.; Irshad, U.B.; Sha’aban, Y.A.; Mahmud, M.A.P.; Javaid, M.S.; Ramli, M.A.M.; Farjana, S.H. Optimal Sizing of Hybrid Photovoltaic/Diesel/Battery Nanogrid Using a Parallel Multiobjective PSO-Based Approach: Application to Desert Camping in Hafr Al-Batin City in Saudi Arabia. Energy Rep. 2021, 7, 4360–4375. [Google Scholar] [CrossRef]
- Sultan, H.M.; Kuznetsov, O.N.; Diab, A.A.Z. Site Selection of Large-Scale Grid-Connected Solar PV System in Egypt. In Proceedings of the 2018 IEEE Conference of Russian Young Researchers in Electrical and Electronic Engineering, ElConRus 2018, St. Petersburg, Russia, 29 January–1 February 2018; Institute of Electrical and Electronics Engineers Inc.: New York, NY, USA, 2018; Volume 2018, pp. 813–818. [Google Scholar]
- Al-Ghussain, L.; Ahmed, H.; Haneef, F. Optimization of Hybrid PV-Wind System: Case Study Al-Tafilah Cement Factory, Jordan. Sustain. Energy Technol. Assess. 2018, 30, 24–36. [Google Scholar] [CrossRef]
- Diab, A.A.Z.; Sultan, H.M.; Mohamed, I.S.; Kuznetsov, O.N.; Do, T.D. Application of Different Optimization Algorithms for Optimal Sizing of PV/Wind/Diesel/Battery Storage Stand-Alone Hybrid Microgrid. IEEE Access 2019, 7, 119223–119245. [Google Scholar] [CrossRef]
- Himri, Y.; Malik, A.S.; Boudghene Stambouli, A.; Himri, S.; Draoui, B. Review and Use of the Algerian Renewable Energy for Sustainable Development. Renew. Sustain. Energy Rev. 2009, 13, 1584–1591. [Google Scholar] [CrossRef]
- Malik, A.Q. Assessment of the Potential of Renewables for Brunei Darussalam. Renew. Sustain. Energy Rev. 2011, 15, 427–437. [Google Scholar] [CrossRef]
- Mazzeo, D.; Matera, N.; De Luca, P.; Baglivo, C.; Maria Congedo, P.; Oliveti, G. Worldwide Geographical Mapping and Optimization of Stand-Alone and Grid-Connected Hybrid Renewable System Techno-Economic Performance across Köppen-Geiger Climates. Appl. Energy 2020, 276, 115507. [Google Scholar] [CrossRef]
- Dalton, G.J.; Lockington, D.A.; Baldock, T.E. Feasibility Analysis of Renewable Energy Supply Options for a Grid-Connected Large Hotel. Renew. Energy 2009, 34, 955–964. [Google Scholar] [CrossRef]
- Dalton, G.J.; Lockington, D.A.; Baldock, T.E. Case Study Feasibility Analysis of Renewable Energy Supply Options for Small to Medium-Sized Tourist Accommodations. Renew. Energy 2009, 34, 1134–1144. [Google Scholar] [CrossRef]
- Phuangpornpitak, N.; Kumar, S. User Acceptance of Diesel/PV Hybrid System in an Island Community. Renew. Energy 2011, 36, 125–131. [Google Scholar] [CrossRef]
- Phuangpornpitak, N.; Kumar, S. PV Hybrid Systems for Rural Electrification in Thailand. Renew. Sustain. Energy Rev. 2007, 11, 1530–1543. [Google Scholar] [CrossRef]
- Ma, T.; Yang, H.; Lu, L. A Feasibility Study of a Stand-Alone Hybrid Solar-Wind-Battery System for a Remote Island. Appl. Energy 2014, 121, 149–158. [Google Scholar] [CrossRef]
- Acuña, L.G.; Padilla, R.V.; Mercado, A.S. Measuring Reliability of Hybrid Photovoltaic-Wind Energy Systems: A New Indicator. Renew. Energy 2017, 106, 68–77. [Google Scholar] [CrossRef]
- Kaabeche, A.; Belhamel, M.; Ibtiouen, R. Techno-Economic Valuation and Optimization of Integrated Photovoltaic/Wind Energy Conversion System. Sol. Energy 2011, 85, 2407–2420. [Google Scholar] [CrossRef]
- Dali, M.; Belhadj, J.; Roboam, X. Hybrid Solar-Wind System with Battery Storage Operating in Grid-Connected and Standalone Mode: Control and Energy Management—Experimental Investigation. Energy 2010, 35, 2587–2595. [Google Scholar] [CrossRef]
- Agbossou, K.; Kolhe, M.; Hamelin, J.; Bose, T.K. Performance of a Stand-Alone Renewable Energy System Based on Energy Storage as Hydrogen. IEEE Trans. Energy Convers. 2004, 19, 633–640. [Google Scholar] [CrossRef]
- Wang, C.; Nehrir, M.H. Power Management of a Stand-Alone Wind/Photovoltaic/Fuel Cell Energy System. IEEE Trans. Energy Convers. 2008, 23, 957–967. [Google Scholar] [CrossRef]
- Bukar, A.L.; Tan, C.W.; Lau, K.Y. Optimal Sizing of an Autonomous Photovoltaic/Wind/Battery/Diesel Generator Microgrid Using Grasshopper Optimization Algorithm. Sol. Energy 2019, 188, 685–696. [Google Scholar] [CrossRef]
- HOMER. Available online: https://www.homerenergy.com/dynamic-content/press_releases/pr_doe012810.html (accessed on 15 June 2020).
- Erdinc, O.; Uzunoglu, M. Optimum Design of Hybrid Renewable Energy Systems: Overview of Different Approaches. Renew. Sustain. Energy Rev. 2012, 16, 1412–1425. [Google Scholar] [CrossRef]
- Mohammadi, M.; Hosseinian, S.H.; Gharehpetian, G.B. GA-Based Optimal Sizing of Microgrid and DG Units under Pool and Hybrid Electricity Markets. Int. J. Electr. Power Energy Syst. 2012, 35, 83–92. [Google Scholar] [CrossRef]
- Luna-Rubio, R.; Trejo-Perea, M.; Vargas-Vázquez, D.; Ríos-Moreno, G.J. Optimal Sizing of Renewable Hybrids Energy Systems: A Review of Methodologies. Sol. Energy 2012, 86, 1077–1088. [Google Scholar] [CrossRef]
- Borhanazad, H.; Mekhilef, S.; Gounder Ganapathy, V.; Modiri-Delshad, M.; Mirtaheri, A. Optimization of Micro-Grid System Using MOPSO. Renew. Energy 2014, 71, 295–306. [Google Scholar] [CrossRef]
- Ramli, M.A.M.; Bouchekara, H.R.E.H.; Alghamdi, A.S. Optimal Sizing of PV/Wind/Diesel Hybrid Microgrid System Using Multi-Objective Self-Adaptive Differential Evolution Algorithm. Renew. Energy 2018, 121, 400–411. [Google Scholar] [CrossRef]
- Bouchekara, H.R.E.H.; Javaid, M.S.; Shaaban, Y.A.; Shahriar, M.S.; Ramli, M.A.M.; Latreche, Y. Decomposition Based Multiobjective Evolutionary Algorithm for PV/Wind/Diesel Hybrid Microgrid System Design Considering Load Uncertainty. Energy Rep. 2021, 7, 52–69. [Google Scholar] [CrossRef]
- Rouhani, A.; Jabbari, M.; Honarmand, S. A Teaching Learning Based Optimization for Optimal Design of a Hybrid Energy System. Int. J. Electr. Comput. Energ. Electron. Commun. Eng. 2015, 9, 737–744. [Google Scholar]
- Katsigiannis, Y.A.; Georgilakis, P.S. Optimal Sizing of Small Isolated Hybrid Power Systems Using Tabu Search. J. Optoelectron. Adv. Mater. 2008, 10, 1241. [Google Scholar]
- Ekren, O.; Ekren, B.Y. Size Optimization of a PV/Wind Hybrid Energy Conversion System with Battery Storage Using Simulated Annealing. Appl. Energy 2010, 87, 592–598. [Google Scholar] [CrossRef]
- Sanajaoba, S.; Fernandez, E. Maiden Application of Cuckoo Search Algorithm for Optimal Sizing of a Remote Hybrid Renewable Energy System. Renew. Energy 2016, 96, 1–10. [Google Scholar] [CrossRef]
- Hatata, A.Y.; Osman, G.; Aladl, M.M. An Optimization Method for Sizing a Solar/Wind/Battery Hybrid Power System Based on the Artificial Immune System. Sustain. Energy Technol. Assess. 2018, 27, 83–93. [Google Scholar] [CrossRef]
- Gaabour, A.; Metatla, A.; Kelaiaia, R.; Bourennani, F.; Kerboua, A.; Kerboua Akerboua, A. Recent Bibliography on the Optimization of Multi-Source Energy Systems. Arch. Comput. Methods Eng. 2019, 26, 809–830. [Google Scholar] [CrossRef]
- Sinha, S.; Chandel, S.S. Review of Software Tools for Hybrid Renewable Energy Systems. Renew. Sustain. Energy Rev. 2014, 32, 192–205. [Google Scholar] [CrossRef]
- Emad, D.; El-Hameed, M.A.; Yousef, M.T.; El-Fergany, A.A. Computational Methods for Optimal Planning of Hybrid Renewable Microgrids: A Comprehensive Review and Challenges. Arch. Comput. Methods Eng. 2019, 27, 1297–1319. [Google Scholar] [CrossRef]
- Wang, R.; Li, G.; Ming, M.; Wu, G.; Wang, L. An Efficient Multi-Objective Model and Algorithm for Sizing a Stand-Alone Hybrid Renewable Energy System. Energy 2017, 141, 2288–2299. [Google Scholar] [CrossRef]
- Zhao, F.; Zhao, L.; Wang, L.; Song, H. A Collaborative LSHADE Algorithm with Comprehensive Learning Mechanism. Appl. Soft Comput. J. 2020, 96, 106609. [Google Scholar] [CrossRef]
- Saha, S.; Saini, G.; Chauhan, A.; Upadhyay, S.; Madurai Elavarasan, R.; Hossain Lipu, M.S. Optimum Design and Techno-Socio-Economic Analysis of a PV/Biomass Based Hybrid Energy System for a Remote Hilly Area Using Discrete Grey Wolf Optimization Algorithm. Sustain. Energy Technol. Assess. 2023, 57, 103213. [Google Scholar] [CrossRef]
- Zhang, Q.; Li, H. MOEA/D: A Multiobjective Evolutionary Algorithm Based on Decomposition. IEEE Trans. Evol. Comput. 2007, 11, 712–731. [Google Scholar] [CrossRef]
- Li, K. Decomposition Multi-Objective Evolutionary Optimization: From State-of-the-Art to Future Opportunities. arXiv 2021, arXiv:2108.09588. [Google Scholar] [CrossRef]
- Giagkiozis, I.; Fleming, P.J. Methods for Multi-Objective Optimization: An Analysis. Inf. Sci. 2015, 293, 338–350. [Google Scholar] [CrossRef]
- Wang, R.; Zhang, Q.; Zhang, T. Decomposition-Based Algorithms Using Pareto Adaptive Scalarizing Methods. IEEE Trans. Evol. Comput. 2016, 20, 821–837. [Google Scholar] [CrossRef]
- Wang, R.; Zhang, Q.; Zhang, T. Pareto Adaptive Scalarising Functions for Decomposition Based Algorithms. In Proceedings of the Evolutionary Multi-Criterion Optimization: 8th International Conference, Guimarães, Portugal, 29 March–1 April 2015; pp. 248–262. [Google Scholar]
- Jiang, S.; Yang, S.; Wang, Y.; Liu, X. Scalarizing Functions in Decomposition-Based Multiobjective Evolutionary Algorithms. IEEE Trans. Evol. Comput. 2018, 22, 296–313. [Google Scholar] [CrossRef]
- Yang, S.; Jiang, S.; Jiang, Y. Improving the Multiobjective Evolutionary Algorithm Based on Decomposition with New Penalty Schemes. Soft Comput. 2017, 21, 4677–4691. [Google Scholar] [CrossRef]
- Sato, H. Analysis of Inverted PBI and Comparison with Other Scalarizing Functions in Decomposition Based MOEAs. J. Heuristics 2015, 21, 819–849. [Google Scholar] [CrossRef]
- Sato, H. Inverted PBI in MOEA/D and Its Impact on the Search Performance on Multi and Many-Objective Optimization. In Proceedings of the 2014 Annual Conference on Genetic and Evolutionary Computation, Vancouver, BC, Canada, 12–16 July 2014; ACM: New York, NY, USA, 2014; pp. 645–652. [Google Scholar]
- Wu, M.; Li, K.; Kwong, S.; Zhang, Q.; Zhang, J. Learning to Decompose: A Paradigm for Decomposition-Based Multiobjective Optimization. IEEE Trans. Evol. Comput. 2019, 23, 376–390. [Google Scholar] [CrossRef]
- Bernal-Agustín, J.L.; Dufo-López, R.; Rivas-Ascaso, D.M. Design of Isolated Hybrid Systems Minimizing Costs and Pollutant Emissions. Renew. Energy 2006, 31, 2227–2244. [Google Scholar] [CrossRef]
- Justus, C.G. Wind Energy Statistics for Large Arrays of Wind Turbines (New England and Central U.S. Regions). Sol. Energy 1978, 20, 379–386. [Google Scholar] [CrossRef]
- Farrugia, R.N. The Wind Shear Exponent in a Mediterranean Island Climate. Renew. Energy 2003, 28, 647–653. [Google Scholar] [CrossRef]
- Jaramillo, O.A.; Borja, M.A. Wind Speed Analysis in La Ventosa, Mexico: A Bimodal Probability Distribution Case. Renew. Energy 2004, 29, 1613–1630. [Google Scholar] [CrossRef]
- Bañuelos-Ruedas, F.; Angeles-Camacho, C.; Rios-Marcuello, S. Analysis and Validation of the Methodology Used in the Extrapolation of Wind Speed Data at Different Heights. Renew. Sustain. Energy Rev. 2010, 14, 2383–2391. [Google Scholar] [CrossRef]
- Bechrakis, D.A.; Sparis, P.D. Simulation of the Wind Speed at Different Heights Using Artificial Neural Networks. Wind Eng. 2000, 24, 127–136. [Google Scholar] [CrossRef]
- Patel, M.R. Wind and Solar Power Systems: Design, Analysis, and Operation; Taylor & Francis: Oxfordshire, UK, 2006; ISBN 9780849315701. [Google Scholar]
- IEC International Standard 61400-1; Wind Turbines—Part 1: Design Requirements. IEC International Standard: Geneva, Switzerland, 2005.
- IEC International Standard. Wind Energy Generation Systems-Part 3-1: Design Requirements for Fixed Offshore Wind Turbines; International Electrotechnical Commission: Geneva, Switzerland, 2019; ISBN 978-2-8322-6600-7. [Google Scholar]
- Yue, X.; Zhang, J.; Dong, Y.; Chen, Y.; Shi, Z.; Xu, X.; Li, X.; Liang, Z. Reversible Li Plating on Graphite Anodes through Electrolyte Engineering for Fast-Charging Batteries. Angew. Chem. Int. 2023, 62, e202302285. [Google Scholar] [CrossRef] [PubMed]
- Hossain Lipu, M.S.; Ansari, S.; Miah, M.S.; Hasan, K.; Meraj, S.T.; Faisal, M.; Jamal, T.; Ali, S.H.M.; Hussain, A.; Muttaqi, K.M.; et al. A Review of Controllers and Optimizations Based Scheduling Operation for Battery Energy Storage System towards Decarbonization in Microgrid: Challenges and Future Directions. J. Clean. Prod. 2022, 360, 132188. [Google Scholar] [CrossRef]
- Wang, L.; Singh, C. PSO-Based Multi-Criteria Optimum Design of a Grid-Connected Hybrid Power System with Multiple Renewable Sources of Energy. In Proceedings of the 2007 IEEE Swarm Intelligence Symposium, SIS 2007, Honolulu, HI, USA, 1–5 April 2007; pp. 250–257. [Google Scholar]
- Korpaas, M.; Holen, A.T.; Hildrum, R. Operation and Sizing of Energy Storage for Wind Power Plants in a Market System. Int. J. Electr. Power Energy Syst. 2003, 25, 599–606. [Google Scholar] [CrossRef]
- El-Hefnawi, S.H. Photovoltaic Diesel-Generator Hybrid Power System Sizing. Renew. Energy 1998, 13, 33–40. [Google Scholar] [CrossRef]
- Ashari, M.; Nayar, C.V. An Optimum Dispatch Strategy Using Set Points for a Photovoltaic (PV)-Diesel-Battery Hybrid Power System. Sol. Energy 1999, 66, 1–9. [Google Scholar] [CrossRef]
- Skarstein, Ø.; Uhlen, K. Design Considerations with Respect to Long-Term Diesel Saving in Wind/Diesel Plants. Wind Eng. 1989, 13, 72–87. [Google Scholar]
- Azoumah, Y.; Yamegueu, D.; Ginies, P.; Coulibaly, Y.; Girard, P. Sustainable Electricity Generation for Rural and Peri-Urban Populations of Sub-Saharan Africa: The “Flexy-Energy” Concept. Energy Policy 2011, 39, 131–141. [Google Scholar] [CrossRef]
- Deshmukh, M.K.; Deshmukh, S.S. Modeling of Hybrid Renewable Energy Systems. Renew. Sustain. Energy Rev. 2008, 12, 235–249. [Google Scholar] [CrossRef]
- Diaf, S.; Diaf, D.; Belhamel, M.; Haddadi, M.; Louche, A. A Methodology for Optimal Sizing of Autonomous Hybrid PV/Wind System. Energy Policy 2007, 35, 5708–5718. [Google Scholar] [CrossRef]
- Darras, C.; Sailler, S.; Thibault, C.; Muselli, M.; Poggi, P.; Hoguet, J.C.; Melscoet, S.; Pinton, E.; Grehant, S.; Gailly, F.; et al. Sizing of Photovoltaic System Coupled with Hydrogen/Oxygen Storage Based on the ORIENTE Model. Int. J. Hydrogen Energy 2010, 35, 3322–3332. [Google Scholar] [CrossRef]
- Paniagua Sánchez-Mateos, J. Reliability-Constrained Microgrid Design. Master’s Thesis, KTH School of Electrical Engineering and Computer Science, Stockholm, Sweden, 2016. [Google Scholar]
- Alsaidan, I.; Alanazi, A.; Gao, W.; Wu, H.; Khodaei, A. State-of-the-Art in Microgrid-Integrated Distributed Energy Storage Sizing. Energies 2017, 10, 1421. [Google Scholar] [CrossRef]
- Alsaidan, I.; Khodaei, A.; Gao, W. Determination of Optimal Size and Depth of Discharge for Battery Energy Storage in Standalone Microgrids. In Proceedings of the 2016 North American Power Symposium (NAPS), Denver, CO, USA, 18–20 September 2016. [Google Scholar] [CrossRef]
- Moradzadeh, M.; Abdelaziz, M.M.A. A New MILP Formulation for Renewables and Energy Storage Integration in Fast Charging Stations. IEEE Trans. Transp. Electrif. 2020, 6, 181–198. [Google Scholar] [CrossRef]
- Amini, M.; Khorsandi, A.; Vahidi, B.; Hosseinian, S.H.; Malakmahmoudi, A. Optimal Sizing of Battery Energy Storage in a Microgrid Considering Capacity Degradation and Replacement Year. Electr. Power Syst. Res. 2021, 195, 107170. [Google Scholar] [CrossRef]
- ur Rehman, W.; Bo, R.; Mehdipourpicha, H.; Kimball, J.W. Sizing Battery Energy Storage and PV System in an Extreme Fast Charging Station Considering Uncertainties and Battery Degradation. Appl. Energy 2022, 313, 118745. [Google Scholar] [CrossRef]
- Kaabeche, A.; Belhamel, M.; Ibtiouen, R. Sizing Optimization of Grid-Independent Hybrid Photovoltaic/Wind Power Generation System. Energy 2011, 36, 1214–1222. [Google Scholar] [CrossRef]
- Yang, H.; Zhou, W.; Lu, L.; Fang, Z. Optimal Sizing Method for Stand-Alone Hybrid Solar-Wind System with LPSP Technology by Using Genetic Algorithm. Sol. Energy 2008, 82, 354–367. [Google Scholar] [CrossRef]
- Rajkumar, R.K.; Ramachandaramurthy, V.K.; Yong, B.L.; Chia, D.B. Techno-Economical Optimization of Hybrid Pv/Wind/Battery System Using Neuro-Fuzzy. Energy 2011, 36, 5148–5153. [Google Scholar] [CrossRef]
- Wu, M.; Li, K.; Kwong, S.; Zhang, Q. Evolutionary Many-Objective Optimization Based on Adversarial Decomposition. IEEE Trans. Cybern. 2020, 50, 753–764. [Google Scholar] [CrossRef]
- Ming, M.; Wang, R.; Zha, Y.; Zhang, T. Pareto Adaptive Penalty-Based Boundary Intersection Method for Multi-Objective Optimization. Inf. Sci. 2017, 414, 158–174. [Google Scholar] [CrossRef]
- Singh, H.K.; Deb, K. Investigating the Equivalence between PBI and AASF Scalarization for Multi-Objective Optimization. Swarm Evol. Comput. 2020, 53, 100630. [Google Scholar] [CrossRef]
- Rehman, S. Prospects of Wind Farm Development in Saudi Arabia. Renew. Energy 2005, 30, 447–463. [Google Scholar] [CrossRef]
- Rehman, S.; Ahmad, A. Assessment of Wind Energy Potential for Coastal Locations of the Kingdom of Saudi Arabia. Energy 2004, 29, 1105–1115. [Google Scholar] [CrossRef]
- Ramli, M.A.M.; Hiendro, A.; Al-Turki, Y.A. Techno-Economic Energy Analysis of Wind/Solar Hybrid System: Case Study for Western Coastal Area of Saudi Arabia. Renew. Energy 2016, 91, 374–385. [Google Scholar] [CrossRef]
- Alaidroos, A.; He, L.; Krarti, M. Feasibility of Renewable Energy Based Distributed Generations in Yanbu, Saudi Arabia. In Proceedings of the World Renewable Energy Forum, WREF 2012, Including World Renewable Energy Congress XII and Colorado Renewable Energy Society (CRES) Annual Conference, Denver, CO, USA, 13–17 May 2012; Volume 5, pp. 3826–3833. [Google Scholar]

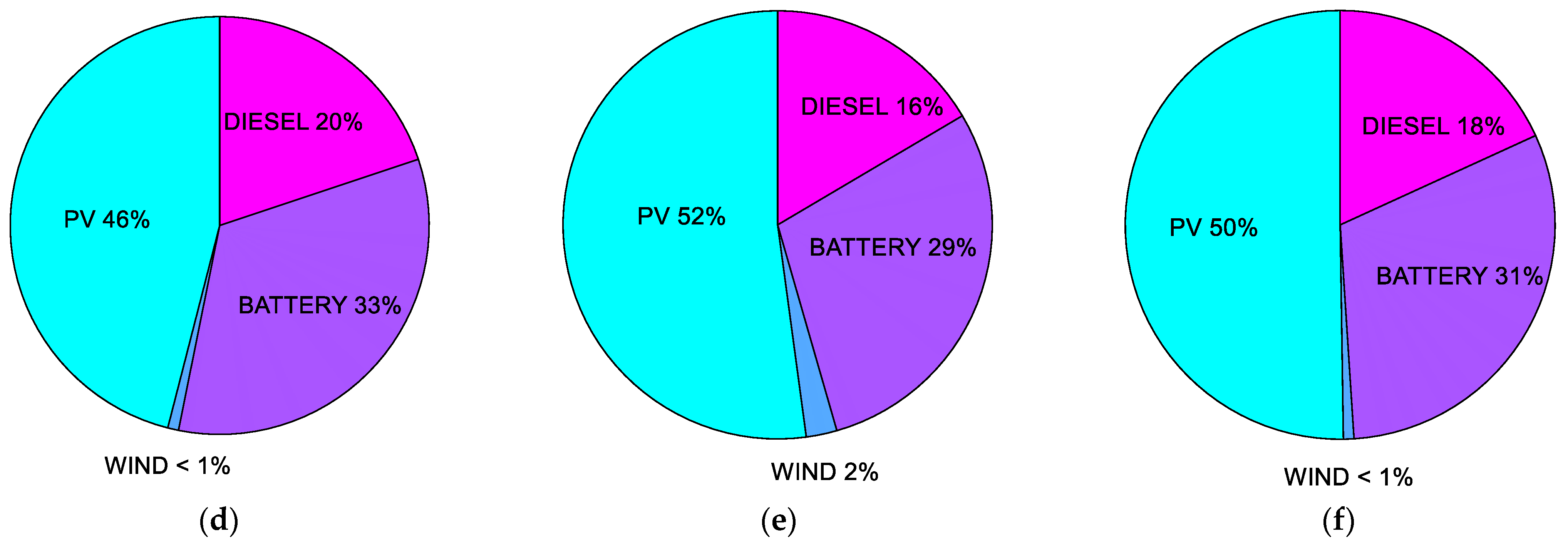
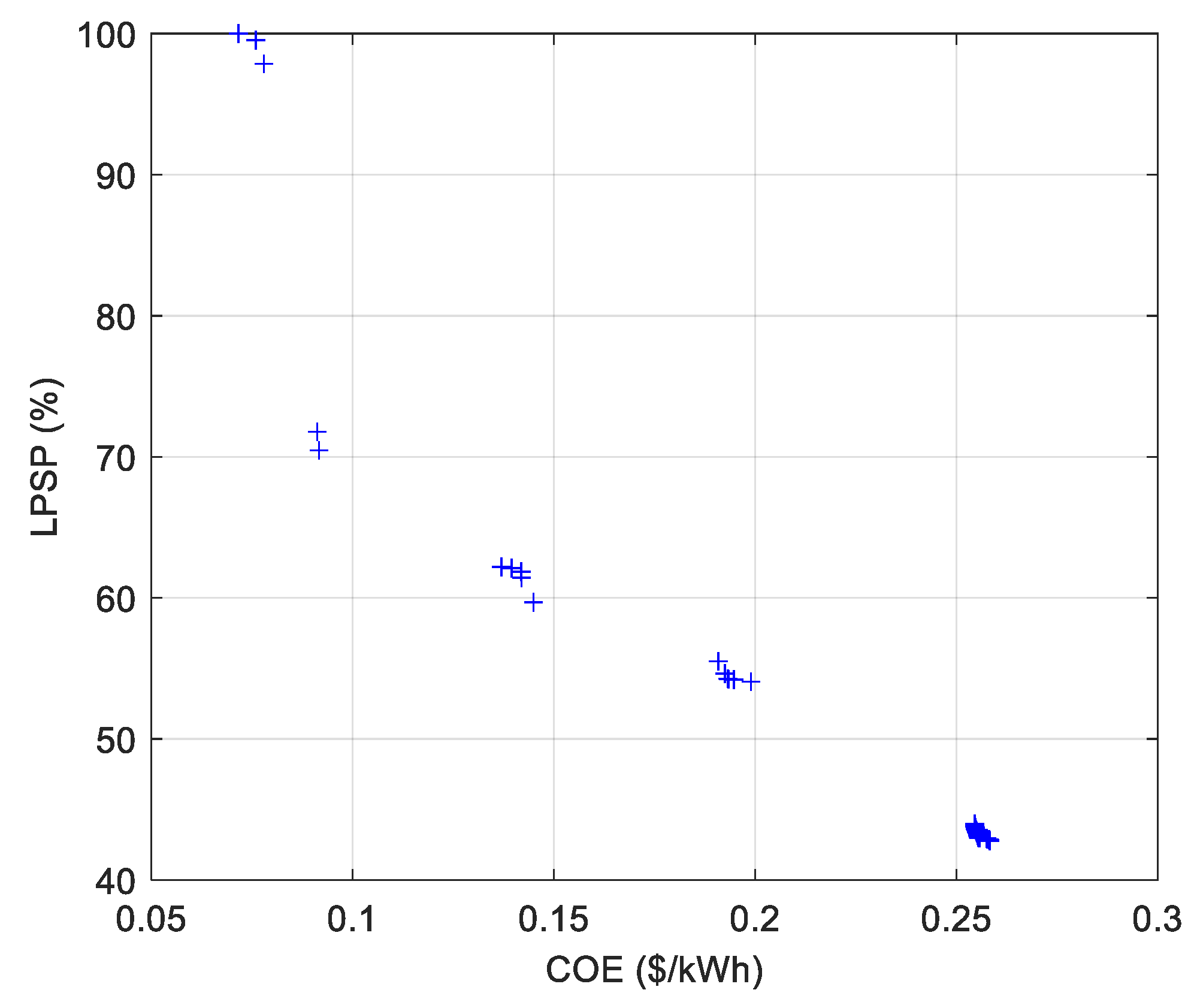
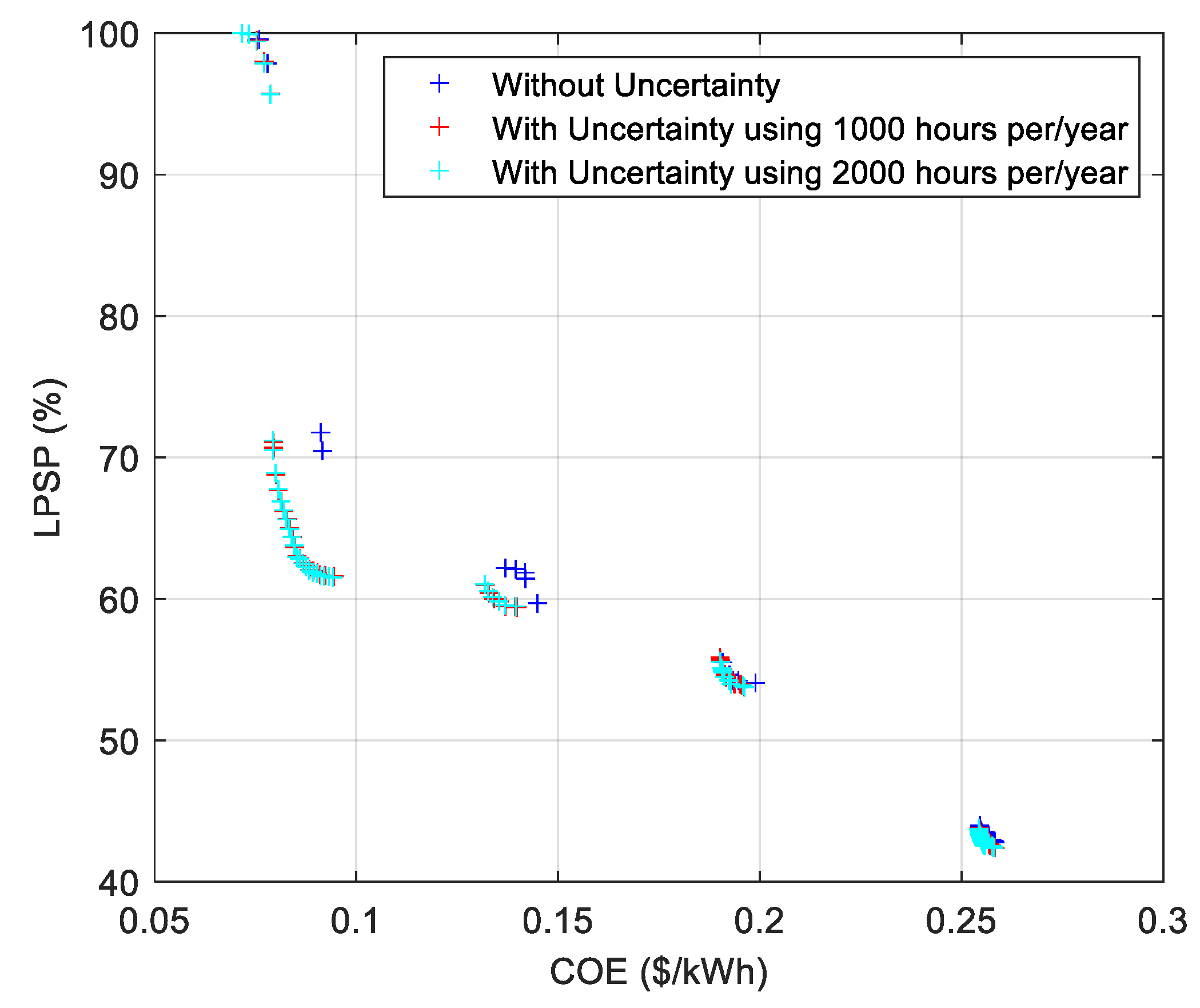
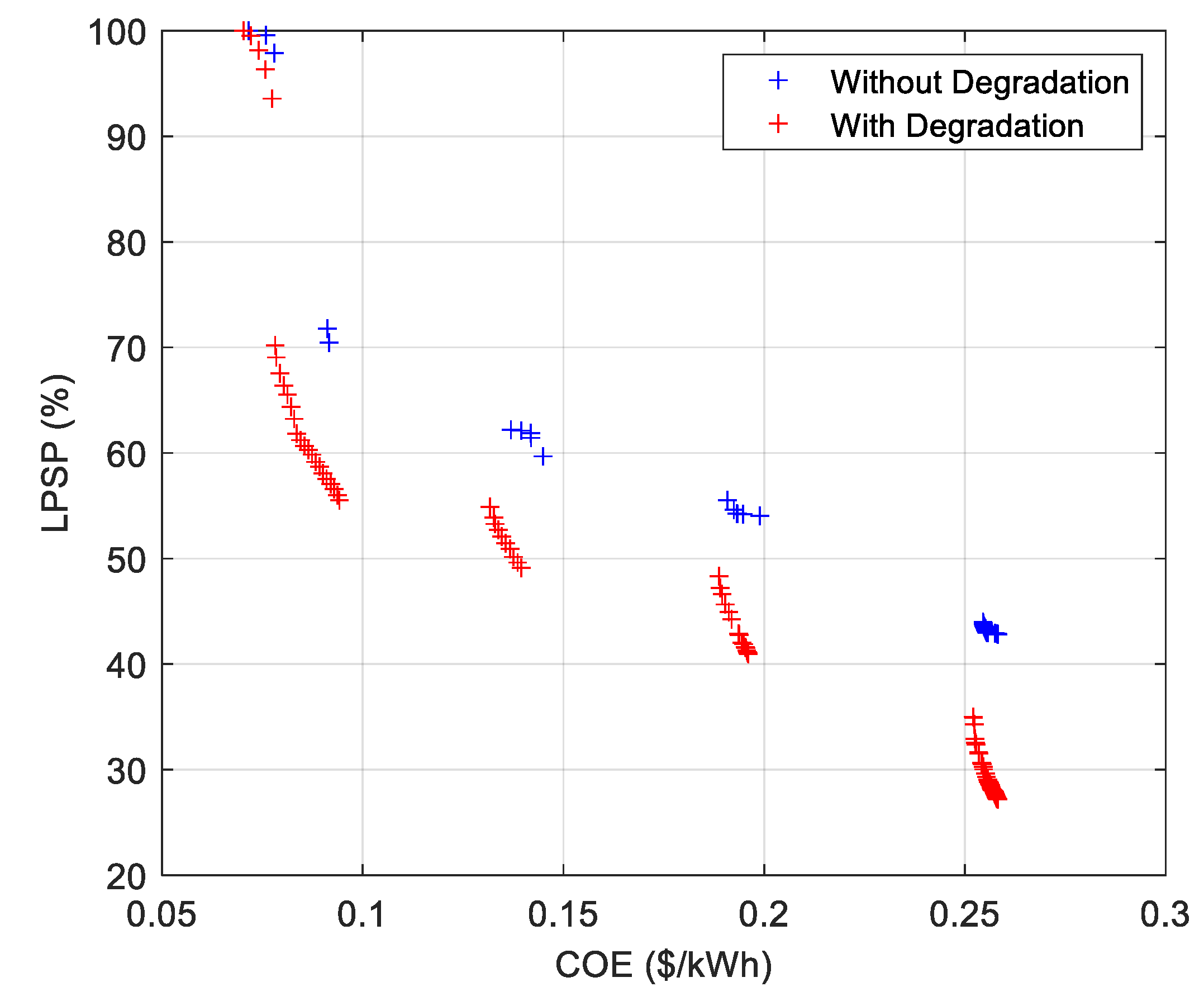

| CASE # | 5 Houses | CASE # | 10 Houses |
|---|---|---|---|
| CASE 1.0 |  Uncertainty Uncertainty Degradation Degradation | CASE 2.0 |  Uncertainty Uncertainty Degradation Degradation |
| CASE 1.1 |  10% of load uncertainty on 1000 h per year 10% of load uncertainty on 1000 h per year Degradation Degradation | CASE 2.1 |  Uncertainty (Same as CASE 1.1) Uncertainty (Same as CASE 1.1) Degradation Degradation |
| CASE 1.2 |  10% of load uncertainty on 2000 h per year 10% of load uncertainty on 2000 h per year Degradation Degradation | CASE 2.2 |  Uncertainty (Same as CASE 1.2) Uncertainty (Same as CASE 1.2) Degradation Degradation |
| CASE 1.3 |  Uncertainty Uncertainty Degradation Degradation | CASE 2.3 |  Uncertainty Uncertainty Degradation Degradation |
| CASE 1.4 |  Uncertainty (Same as CASE 1.1) Uncertainty (Same as CASE 1.1) Degradation Degradation | CASE 2.4 |  Uncertainty (Same as CASE 1.1) Uncertainty (Same as CASE 1.1) Degradation Degradation |
| CASE 1.5 |  Uncertainty (Same as CASE 2.1) Uncertainty (Same as CASE 2.1) Degradation Degradation | CASE 2.5 |  Uncertainty (Same as CASE 1.2) Uncertainty (Same as CASE 1.2) Degradation Degradation |
| Parameter | HMS Component | ||||
|---|---|---|---|---|---|
| PV | Wind | Diesel Generator | Inverter | Battery | |
| Efficiency (%) | 95 (regulator) | 95 (regulator) | 92 | 85 | |
| Lifetime (years) | 24 | 24 | 3 | 24 | 12 |
| Initial cost (USD/kW) | 3400 | 2000 | 1000 | 2500 | 280 (USD/kWh) |
| Rated power (kW) | 7.3 | 5 | 4 | 40 (kWh) | |
| Regulator cost (USD) | 1500 | 1000 | |||
| Model | ZEYU FD-2KW | ||||
| Cut in (m/s) | 2.5 | ||||
| Cut out (m/s) | 40 | ||||
| Rated speed (m/s) | 9.5 | ||||
| Economic parameters | |||||
| Discount rate (%) | Real interest (%) | Fuel inflation rate (%) | O&M running cost (%) | Project lifetime (%) | |
| 8 | 13 | 5 | 20 | 24 | |
| Solution # | PV (kW) | NAD | NWT | NDiesel | COE (USD/kWh) | LPSP (%) | RF (%) | PV (kWh) | Wind (kWh) | Battery (kWh) | Diesel (kWh) |
|---|---|---|---|---|---|---|---|---|---|---|---|
| Solution # 1 | 43.43 | 4.99 | 9 | 3 | 0.1159 | 63.10 | 83.71 | 88,645.97 | 12,180.59 | 46,068.49 | 23,923.68 |
| Solution # 2 | 33.36 | 4.99 | 10 | 3 | 0.1175 | 57.37 | 80.35 | 68,098.57 | 13,533.99 | 46,810.32 | 25,237.44 |
| Solution # 3 | 33.06 | 5.00 | 10 | 3 | 0.1184 | 56.16 | 80.19 | 67,471.12 | 13,533.99 | 46,870.40 | 25,336.80 |
| Solution # 4 | 43.98 | 4.96 | 9 | 3 | 0.1192 | 54.91 | 83.74 | 89,767.21 | 12,180.59 | 45,997.24 | 24,056.16 |
| Solution # 5 | 20.76 | 4.26 | 9 | 4 | 0.1200 | 53.60 | 58.38 | 42,371.06 | 12,180.59 | 51,788.15 | 44,263.04 |
| Solution # 6 | 44.19 | 4.64 | 1 | 3 | 0.1208 | 52.53 | 77.67 | 90,207.82 | 1353.40 | 52,627.11 | 32,192.64 |
| Solution # 7 | 34.23 | 4.99 | 10 | 3 | 0.1217 | 48.07 | 80.80 | 69,863.69 | 13,533.99 | 46,646.39 | 24,972.48 |
| Solution # 8 | 43.08 | 5.00 | 9 | 3 | 0.1224 | 47.14 | 83.62 | 87,931.77 | 12,180.59 | 46,114.35 | 23,945.76 |
| Solution # 9 | 44.39 | 4.95 | 9 | 3 | 0.1233 | 46.04 | 83.85 | 90,615.16 | 12,180.59 | 45,944.16 | 24,023.04 |
| Solution # 10 | 33.06 | 5.00 | 10 | 3 | 0.1243 | 44.62 | 80.19 | 67,484.73 | 13,533.99 | 46,869.09 | 25,336.80 |
| Solution # 11 | 43.98 | 4.96 | 9 | 3 | 0.1253 | 42.66 | 83.74 | 89,767.21 | 12,180.59 | 45,997.24 | 24,056.16 |
| Solution # 12 | 20.76 | 4.26 | 9 | 4 | 0.1263 | 41.72 | 58.38 | 42,371.06 | 12,180.59 | 51,788.15 | 44,263.04 |
| Solution # 13 | 44.19 | 4.64 | 1 | 3 | 0.1263 | 37.53 | 77.67 | 90,207.82 | 1353.40 | 52,627.11 | 32,192.64 |
| Solution # 14 | 44.49 | 5.00 | 9 | 3 | 0.1280 | 36.00 | 84.00 | 90,807.09 | 12,180.59 | 45,932.16 | 23,824.32 |
| Solution # 15 | 33.06 | 5.00 | 10 | 3 | 0.1299 | 34.94 | 80.19 | 67,484.73 | 13,533.99 | 46,869.09 | 25,336.80 |
| Solution # 16 | 43.43 | 4.99 | 9 | 3 | 0.1376 | 33.61 | 83.71 | 88,655.69 | 12,180.59 | 46,067.86 | 23,934.72 |
| Solution # 17 | 44.82 | 5.00 | 10 | 3 | 0.1763 | 22.94 | 84.74 | 91,494.15 | 13,533.99 | 45,072.29 | 22,908.00 |
| Solution # 18 | 43.43 | 4.99 | 9 | 3 | 0.1781 | 21.66 | 83.71 | 88,655.69 | 12,180.59 | 46,067.86 | 23,934.72 |
| Solution # 19 | 33.06 | 5.00 | 10 | 3 | 0.1865 | 20.38 | 80.19 | 67,471.12 | 13,533.99 | 46,870.40 | 25,336.80 |
| Solution # 20 | 20.76 | 4.26 | 9 | 4 | 0.2160 | 10.29 | 58.38 | 42,371.06 | 12,180.59 | 51,788.15 | 44,263.04 |
| Solution # | PV (kW) | NAD | NWT | NDiesel | COE (USD/kWh) | LPSP (%) | RF (%) | PV (kWh) | Wind (kWh) | Battery (kWh) | Diesel (kWh) |
|---|---|---|---|---|---|---|---|---|---|---|---|
| Solution # 1 | 44.66 | 4.99 | 9 | 3 | 0.1160 | 63.21 | 84.03 | 91,149.54 | 12,180.59 | 45,956.12 | 23,846.40 |
| Solution # 2 | 42.69 | 5.00 | 9 | 3 | 0.1163 | 58.99 | 83.45 | 87,133.04 | 12,180.59 | 46,214.81 | 24,078.24 |
| Solution # 3 | 44.55 | 4.94 | 10 | 3 | 0.1171 | 57.74 | 84.41 | 90,924.96 | 13,533.99 | 45,150.16 | 23,327.52 |
| Solution # 4 | 45.00 | 4.98 | 9 | 3 | 0.1180 | 56.41 | 84.11 | 91,851.93 | 12,180.59 | 45,912.36 | 23,824.32 |
| Solution # 5 | 45.00 | 5.00 | 10 | 3 | 0.1189 | 55.31 | 84.77 | 91,851.63 | 13,533.99 | 45,094.66 | 22,919.04 |
| Solution # 6 | 45.00 | 5.00 | 10 | 3 | 0.1197 | 53.94 | 84.77 | 91,851.93 | 13,533.99 | 45,094.64 | 22,919.04 |
| Solution # 7 | 44.53 | 4.99 | 9 | 3 | 0.1211 | 51.93 | 84.01 | 90,901.78 | 12,180.59 | 45,971.70 | 23,835.36 |
| Solution # 8 | 32.93 | 5.00 | 10 | 3 | 0.1225 | 47.31 | 80.11 | 67,215.92 | 13,533.99 | 46,950.62 | 25,403.04 |
| Solution # 9 | 17.65 | 2.21 | 5 | 4 | 0.1237 | 45.37 | 44.60 | 36,029.35 | 6766.99 | 58,415.20 | 56,068.48 |
| Solution # 10 | 44.55 | 4.94 | 10 | 3 | 0.1243 | 44.54 | 84.41 | 90,924.96 | 13,533.99 | 45,150.16 | 23,327.52 |
| Solution # 11 | 45.00 | 4.98 | 9 | 3 | 0.1249 | 43.41 | 84.11 | 91,851.93 | 12,180.59 | 45,912.36 | 23,824.32 |
| Solution # 12 | 45.00 | 5.00 | 10 | 3 | 0.1254 | 42.37 | 84.77 | 91,851.63 | 13,533.99 | 45,094.66 | 22,919.04 |
| Solution # 13 | 42.69 | 5.00 | 9 | 3 | 0.1262 | 37.59 | 83.45 | 87,133.04 | 12,180.59 | 46,214.81 | 24,078.24 |
| Solution # 14 | 32.93 | 5.00 | 10 | 3 | 0.1278 | 36.06 | 80.11 | 67,215.92 | 13,533.99 | 46,950.62 | 25,403.04 |
| Solution # 15 | 44.55 | 4.94 | 10 | 3 | 0.1296 | 35.10 | 84.41 | 90,924.96 | 13,533.99 | 45,150.16 | 23,327.52 |
| Solution # 16 | 45.00 | 4.98 | 9 | 3 | 0.1384 | 33.52 | 84.11 | 91,851.93 | 12,180.59 | 45,912.36 | 23,824.32 |
| Solution # 17 | 45.00 | 4.77 | 10 | 3 | 0.1766 | 22.58 | 84.01 | 91,851.56 | 13,533.99 | 45,094.66 | 24,056.16 |
| Solution # 18 | 44.53 | 4.99 | 9 | 3 | 0.1787 | 21.19 | 84.01 | 90,901.78 | 12,180.59 | 45,971.70 | 23,835.36 |
| Solution # 19 | 19.45 | 2.21 | 5 | 4 | 0.1865 | 19.99 | 49.01 | 39,698.93 | 6766.99 | 56,797.48 | 52,653.44 |
| Solution # 20 | 44.45 | 5.00 | 10 | 3 | 0.2139 | 10.35 | 84.57 | 90,728.97 | 13,533.99 | 45,162.18 | 23,051.52 |
| Solution # | PV (kW) | NAD | NWT | NDiesel | COE (USD/kWh) | LPSP (%) | RF (%) | PV (kWh) | Wind (kWh) | Battery (kWh) | Diesel (kWh) |
|---|---|---|---|---|---|---|---|---|---|---|---|
| Solution # 1 | 44.18 | 4.76 | 1 | 3 | 0.1161 | 63.18 | 78.06 | 90,187.91 | 1353.40 | 52,601.02 | 31,618.56 |
| Solution # 2 | 24.14 | 1.25 | 6 | 4 | 0.1163 | 59.11 | 54.91 | 49,275.02 | 8120.39 | 53,074.37 | 49,812.48 |
| Solution # 3 | 44.19 | 4.76 | 1 | 3 | 0.1172 | 58.11 | 78.07 | 90,205.25 | 1353.40 | 52,599.74 | 31,618.56 |
| Solution # 4 | 44.18 | 4.76 | 1 | 3 | 0.1181 | 56.40 | 78.06 | 90,187.91 | 1353.40 | 52,601.02 | 31,618.56 |
| Solution # 5 | 41.39 | 5.00 | 10 | 3 | 0.1189 | 55.36 | 83.76 | 84,479.67 | 13,533.99 | 45,497.33 | 23,305.44 |
| Solution # 6 | 44.72 | 4.98 | 9 | 3 | 0.1197 | 54.09 | 84.03 | 91,272.70 | 12,180.59 | 45,886.23 | 23,846.40 |
| Solution # 7 | 44.27 | 4.97 | 9 | 3 | 0.1206 | 52.86 | 83.84 | 90,356.41 | 12,180.59 | 45,943.00 | 23,989.92 |
| Solution # 8 | 33.38 | 5.00 | 10 | 3 | 0.1218 | 48.17 | 80.39 | 68,129.68 | 13,533.99 | 46,783.90 | 25,182.24 |
| Solution # 9 | 33.38 | 5.00 | 10 | 3 | 0.1226 | 47.06 | 80.40 | 68,132.39 | 13,533.99 | 46,783.64 | 25,182.24 |
| Solution # 10 | 24.14 | 1.25 | 6 | 4 | 0.1238 | 45.21 | 54.91 | 49,275.02 | 8120.39 | 53,074.37 | 49,812.48 |
| Solution # 11 | 44.18 | 4.76 | 1 | 3 | 0.1250 | 43.22 | 78.06 | 90,187.91 | 1353.40 | 52,601.02 | 31,618.56 |
| Solution # 12 | 44.36 | 4.98 | 9 | 3 | 0.1261 | 41.50 | 83.91 | 90,549.90 | 12,180.59 | 45,930.98 | 23,923.68 |
| Solution # 13 | 44.27 | 4.97 | 9 | 3 | 0.1265 | 37.19 | 83.84 | 90,356.41 | 12,180.59 | 45,943.00 | 23,989.92 |
| Solution # 14 | 33.38 | 5.00 | 10 | 3 | 0.1286 | 35.59 | 80.39 | 68,129.68 | 13,533.99 | 46,783.90 | 25,182.24 |
| Solution # 15 | 44.19 | 4.76 | 1 | 3 | 0.1318 | 34.50 | 78.07 | 90,205.25 | 1353.40 | 52,599.74 | 31,618.56 |
| Solution # 16 | 34.92 | 4.97 | 4 | 3 | 0.1393 | 33.25 | 76.54 | 71,271.76 | 5413.59 | 51,648.75 | 30,106.08 |
| Solution # 17 | 24.14 | 1.25 | 6 | 4 | 0.1762 | 22.71 | 54.91 | 49,275.02 | 8120.39 | 53,074.37 | 49,812.48 |
| Solution # 18 | 43.96 | 4.93 | 10 | 3 | 0.1772 | 21.63 | 84.25 | 89,720.80 | 13,533.99 | 45,164.60 | 23,371.68 |
| Solution # 19 | 34.92 | 4.97 | 4 | 3 | 0.1867 | 19.97 | 76.54 | 71,271.76 | 5413.59 | 51,648.75 | 30,106.08 |
| Solution # 20 | 43.06 | 5.00 | 10 | 3 | 0.2121 | 10.46 | 84.29 | 87,894.04 | 13,533.99 | 45,278.26 | 23,051.52 |
| Solution # | PV (kW) | NAD | NWT | NDiesel | COE (USD/kWh) | LPSP (%) | RF (%) | PV (kWh) | Wind (kWh) | Battery (kWh) | Diesel (kWh) |
|---|---|---|---|---|---|---|---|---|---|---|---|
| Solution # 1 | 39.28 | 5.00 | 1 | 3 | 0.1147 | 56.37 | 76.64 | 80,184.76 | 1353.40 | 53,423.34 | 31,530.24 |
| Solution # 2 | 36.74 | 4.99 | 4 | 3 | 0.1157 | 54.21 | 77.65 | 75,000.73 | 5413.59 | 51,306.67 | 29,443.68 |
| Solution # 3 | 35.13 | 5.00 | 1 | 2 | 0.1165 | 52.18 | 79.46 | 71,702.13 | 1353.40 | 54,249.22 | 26,150.08 |
| Solution # 4 | 39.26 | 5.00 | 1 | 3 | 0.1172 | 49.85 | 76.63 | 80,140.24 | 1353.40 | 53,427.22 | 31,530.24 |
| Solution # 5 | 36.54 | 5.00 | 1 | 3 | 0.1182 | 47.64 | 75.20 | 74,576.48 | 1353.40 | 53,948.12 | 32,203.68 |
| Solution # 6 | 32.43 | 5.00 | 10 | 3 | 0.1185 | 41.86 | 79.76 | 66,185.89 | 13,533.99 | 46,996.42 | 25,645.92 |
| Solution # 7 | 32.38 | 5.00 | 10 | 3 | 0.1193 | 40.23 | 79.72 | 66,082.49 | 13,533.99 | 47,006.77 | 25,679.04 |
| Solution # 8 | 19.17 | 1.91 | 2 | 3 | 0.1200 | 38.81 | 45.51 | 39,125.47 | 2706.80 | 60,209.30 | 55,597.44 |
| Solution # 9 | 36.95 | 4.97 | 1 | 3 | 0.1209 | 37.20 | 75.37 | 75,416.35 | 1353.40 | 53,864.27 | 32,181.60 |
| Solution # 10 | 39.35 | 4.99 | 1 | 3 | 0.1215 | 35.69 | 76.66 | 80,319.01 | 1353.40 | 53,411.69 | 31,530.24 |
| Solution # 11 | 33.21 | 4.92 | 3 | 3 | 0.1218 | 34.93 | 74.31 | 67,794.01 | 4060.20 | 52,921.45 | 32,060.16 |
| Solution # 12 | 37.32 | 4.99 | 10 | 3 | 0.1233 | 33.60 | 82.17 | 76,176.16 | 13,533.99 | 46,116.81 | 24,221.76 |
| Solution # 13 | 32.38 | 5.00 | 10 | 3 | 0.1250 | 32.96 | 79.72 | 66,082.49 | 13,533.99 | 47,006.77 | 25,679.04 |
| Solution # 14 | 36.95 | 4.97 | 1 | 3 | 0.1275 | 32.37 | 75.37 | 75,416.35 | 1353.40 | 53,864.27 | 32,181.60 |
| Solution # 15 | 37.32 | 4.99 | 10 | 3 | 0.1318 | 31.52 | 82.17 | 76,176.16 | 13,533.99 | 46,116.81 | 24,221.76 |
| Solution # 16 | 36.95 | 4.97 | 1 | 3 | 0.1394 | 30.97 | 75.37 | 75,416.35 | 1353.40 | 53,864.27 | 32,181.60 |
| Solution # 17 | 36.54 | 5.00 | 1 | 3 | 0.1757 | 14.29 | 75.21 | 74,581.65 | 1353.40 | 53,947.60 | 32,203.68 |
| Solution # 18 | 32.38 | 5.00 | 10 | 3 | 0.1790 | 13.60 | 79.72 | 66,084.30 | 13,533.99 | 47,006.59 | 25,679.04 |
| Solution # 19 | 35.13 | 4.99 | 1 | 3 | 0.2170 | 8.43 | 74.26 | 71,702.13 | 1353.40 | 54,249.22 | 32,766.72 |
| Solution # 20 | 39.16 | 5.00 | 1 | 3 | 0.2487 | 7.67 | 76.59 | 79,936.44 | 1353.40 | 53,445.00 | 31,541.28 |
| Solution # | PV (kW) | NAD | NWT | NDiesel | COE (USD/kWh) | LPSP (%) | RF (%) | PV (kWh) | Wind (kWh) | Battery (kWh) | Diesel (kWh) |
|---|---|---|---|---|---|---|---|---|---|---|---|
| Solution # 1 | 36.29 | 4.67 | 0 | 3 | 0.1149 | 56.09 | 73.38 | 74,081.23 | 0.00 | 54,904.47 | 34,334.40 |
| Solution # 2 | 36.56 | 4.97 | 0 | 3 | 0.1158 | 53.29 | 74.62 | 74,630.22 | 0.00 | 54,847.39 | 32,866.08 |
| Solution # 3 | 41.27 | 4.98 | 1 | 3 | 0.1166 | 51.33 | 77.51 | 84,243.13 | 1353.40 | 53,108.81 | 31,199.04 |
| Solution # 4 | 44.68 | 4.98 | 3 | 3 | 0.1176 | 49.22 | 80.26 | 91,204.87 | 4060.20 | 50,903.19 | 28,858.56 |
| Solution # 5 | 33.02 | 5.00 | 10 | 3 | 0.1183 | 41.75 | 80.10 | 67,394.63 | 13,533.99 | 46,908.34 | 25,436.16 |
| Solution # 6 | 33.02 | 5.00 | 10 | 3 | 0.1188 | 40.94 | 80.10 | 67,409.06 | 13,533.99 | 46,906.93 | 25,436.16 |
| Solution # 7 | 44.45 | 4.98 | 3 | 3 | 0.1193 | 40.25 | 80.19 | 90,731.53 | 4060.20 | 50,936.41 | 28,869.60 |
| Solution # 8 | 18.81 | 1.03 | 5 | 4 | 0.1199 | 38.88 | 45.62 | 38,386.16 | 6766.99 | 57,280.86 | 55,700.48 |
| Solution # 9 | 34.59 | 4.99 | 0 | 3 | 0.1203 | 37.82 | 73.27 | 70,602.75 | 0.00 | 55,287.48 | 33,649.92 |
| Solution # 10 | 44.73 | 4.97 | 3 | 3 | 0.1209 | 36.86 | 80.25 | 91,302.70 | 4060.20 | 50,896.33 | 28,880.64 |
| Solution # 11 | 36.21 | 4.91 | 0 | 3 | 0.1213 | 35.74 | 74.23 | 73,910.87 | 0.00 | 54,922.35 | 33,197.28 |
| Solution # 12 | 40.85 | 4.99 | 1 | 3 | 0.1218 | 34.95 | 77.38 | 83,381.78 | 1353.40 | 53,178.84 | 31,199.04 |
| Solution # 13 | 44.66 | 4.98 | 3 | 3 | 0.1221 | 34.35 | 80.24 | 91,160.81 | 4060.20 | 50,906.28 | 28,869.60 |
| Solution # 14 | 33.02 | 5.00 | 10 | 3 | 0.1233 | 33.47 | 80.10 | 67,394.63 | 13,533.99 | 46,908.34 | 25,436.16 |
| Solution # 15 | 18.81 | 1.03 | 5 | 4 | 0.1250 | 32.93 | 45.62 | 38,386.16 | 6766.99 | 57,280.86 | 55,700.48 |
| Solution # 16 | 40.12 | 4.99 | 1 | 3 | 0.1282 | 32.26 | 77.03 | 81,899.81 | 1353.40 | 53,302.55 | 31,364.64 |
| Solution # 17 | 34.59 | 4.99 | 0 | 3 | 0.1363 | 31.12 | 73.27 | 70,602.75 | 0.00 | 55,287.48 | 33,649.92 |
| Solution # 18 | 33.02 | 5.00 | 10 | 3 | 0.1780 | 13.97 | 80.10 | 67,394.63 | 13,533.99 | 46,908.34 | 25,436.16 |
| Solution # 19 | 34.59 | 4.99 | 0 | 3 | 0.1927 | 13.15 | 73.27 | 70,602.75 | 0.00 | 55,287.48 | 33,649.92 |
| Solution # 20 | 34.59 | 4.99 | 0 | 3 | 0.2443 | 7.95 | 73.27 | 70,602.75 | 0.00 | 55,287.48 | 33,649.92 |
| Solution # | PV (kW) | AD | nWT | nDiesel | COE (USD/kWh) | LPSP (%) | RF (%) | PV (kWh) | Wind (kWh) | Battery (kWh) | Diesel (kWh) |
|---|---|---|---|---|---|---|---|---|---|---|---|
| Solution # 1 | 35.12 | 5.00 | 1 | 3 | 0.1147 | 56.10 | 74.42 | 71,685.37 | 1353.40 | 54,206.89 | 32,545.92 |
| Solution # 2 | 26.93 | 1.94 | 10 | 3 | 0.1157 | 53.96 | 65.27 | 54,976.20 | 13,533.99 | 48,281.56 | 40,560.96 |
| Solution # 3 | 44.27 | 4.97 | 7 | 3 | 0.1165 | 52.67 | 82.70 | 90,359.14 | 9473.79 | 47,553.35 | 25,491.36 |
| Solution # 4 | 44.29 | 4.97 | 7 | 3 | 0.1175 | 49.49 | 82.70 | 90,399.16 | 9473.79 | 47,550.75 | 25,502.40 |
| Solution # 5 | 37.19 | 4.99 | 1 | 3 | 0.1186 | 42.00 | 75.65 | 75,916.60 | 1353.40 | 53,771.17 | 31,905.60 |
| Solution # 6 | 44.84 | 4.86 | 4 | 3 | 0.1202 | 38.50 | 80.62 | 91,529.58 | 5413.59 | 49,963.63 | 28,472.16 |
| Solution # 7 | 35.42 | 4.99 | 1 | 3 | 0.1211 | 36.60 | 74.67 | 72,296.69 | 1353.40 | 54,140.81 | 32,369.28 |
| Solution # 8 | 35.48 | 4.99 | 1 | 3 | 0.1217 | 35.20 | 74.69 | 72,421.06 | 1353.40 | 54,127.47 | 32,369.28 |
| Solution # 9 | 32.64 | 5.00 | 10 | 3 | 0.1223 | 34.35 | 79.98 | 66,626.69 | 13,533.99 | 46,904.86 | 25,436.16 |
| Solution # 10 | 32.64 | 5.00 | 10 | 3 | 0.1228 | 33.76 | 79.98 | 66,628.05 | 13,533.99 | 46,904.73 | 25,436.16 |
| Solution # 11 | 26.93 | 1.94 | 10 | 3 | 0.1245 | 32.85 | 65.27 | 54,976.20 | 13,533.99 | 48,281.56 | 40,560.96 |
| Solution # 12 | 44.29 | 4.97 | 7 | 3 | 0.1272 | 32.15 | 82.70 | 90,399.16 | 9473.79 | 47,550.75 | 25,502.40 |
| Solution # 13 | 35.42 | 4.99 | 1 | 3 | 0.1301 | 31.75 | 74.67 | 72,296.69 | 1353.40 | 54,140.81 | 32,369.28 |
| Solution # 14 | 34.49 | 5.00 | 10 | 3 | 0.1339 | 31.24 | 81.00 | 70,392.98 | 13,533.99 | 46,552.64 | 24,784.80 |
| Solution # 15 | 32.64 | 5.00 | 10 | 3 | 0.1408 | 30.58 | 79.98 | 66,628.05 | 13,533.99 | 46,904.73 | 25,436.16 |
| Solution # 16 | 44.29 | 4.97 | 7 | 3 | 0.1773 | 13.67 | 82.70 | 90,399.16 | 9473.79 | 47,550.75 | 25,502.40 |
| Solution # 17 | 44.74 | 4.95 | 5 | 3 | 0.1919 | 12.88 | 81.55 | 91,326.32 | 6766.99 | 49,145.43 | 27,169.44 |
| Solution # 18 | 31.39 | 5.00 | 10 | 2 | 0.2138 | 8.78 | 82.07 | 64,080.30 | 13,533.99 | 47,163.58 | 22,367.04 |
| Solution # 19 | 32.64 | 5.00 | 10 | 3 | 0.2348 | 8.24 | 79.98 | 66,628.05 | 13,533.99 | 46,904.73 | 25,436.16 |
| Solution # 20 | 42.24 | 4.94 | 1 | 3 | 0.2484 | 7.73 | 77.81 | 86,212.76 | 1353.40 | 52,879.45 | 31,165.92 |
| Solution # | PV (kW) | NAD | NWT | NDiesel | COE (USD/kWh) | LPSP (%) | RF (%) | PV (kWh) | Wind (kWh) | Battery (kWh) | Diesel (kWh) |
|---|---|---|---|---|---|---|---|---|---|---|---|
| Solution # 1 | 45.00 | 3.70 | 10 | 4 | 0.0716 | 99.99 | 66.12 | 91,851.87 | 13,533.99 | 109,654.81 | 72,849.28 |
| Solution # 2 | 45.00 | 3.69 | 10 | 4 | 0.0759 | 99.55 | 66.12 | 91,848.30 | 13,533.99 | 109,655.68 | 72,864.00 |
| Solution # 3 | 45.00 | 3.68 | 10 | 4 | 0.0780 | 97.86 | 66.12 | 91,849.12 | 13,533.99 | 109,655.48 | 72,864.00 |
| Solution # 4 | 45.00 | 3.69 | 10 | 4 | 0.0912 | 71.77 | 66.12 | 91,848.13 | 13,533.99 | 109,655.72 | 72,864.00 |
| Solution # 5 | 21.50 | 3.07 | 4 | 2 | 0.0916 | 70.46 | 68.13 | 43,874.87 | 5413.59 | 148,289.70 | 62,972.16 |
| Solution # 6 | 15.00 | 1.00 | 0 | 1 | 0.1395 | 62.12 | 83.91 | 30,617.31 | 0.00 | 166,960.85 | 31,791.52 |
| Solution # 7 | 45.00 | 3.57 | 10 | 4 | 0.1418 | 61.86 | 66.12 | 91,848.30 | 13,533.99 | 109,655.68 | 72,864.00 |
| Solution # 8 | 45.00 | 3.43 | 10 | 4 | 0.1419 | 61.42 | 66.11 | 91,848.38 | 13,533.99 | 109,655.66 | 72,878.72 |
| Solution # 9 | 17.72 | 3.04 | 4 | 2 | 0.1449 | 59.69 | 67.83 | 36,164.91 | 5413.59 | 155,999.66 | 63,560.96 |
| Solution # 10 | 44.98 | 2.77 | 9 | 4 | 0.1908 | 55.51 | 65.50 | 91,818.51 | 12,180.59 | 110,650.67 | 74,056.32 |
| Solution # 11 | 44.99 | 3.63 | 10 | 4 | 0.1925 | 54.63 | 66.11 | 91,823.48 | 13,533.99 | 109,661.76 | 72,878.72 |
| Solution # 12 | 45.00 | 3.69 | 10 | 4 | 0.1934 | 54.24 | 66.12 | 91,848.38 | 13,533.99 | 109,655.66 | 72,864.00 |
| Solution # 13 | 15.00 | 1.00 | 0 | 1 | 0.1989 | 54.05 | 83.91 | 30,617.31 | 0.00 | 166,960.85 | 31,791.52 |
| Solution # 14 | 45.00 | 3.69 | 10 | 4 | 0.2545 | 43.97 | 66.12 | 91,851.90 | 13,533.99 | 109,654.80 | 72,864.00 |
| Solution # 15 | 45.00 | 2.33 | 10 | 4 | 0.2546 | 43.80 | 65.51 | 91,851.93 | 13,533.99 | 109,654.80 | 74,159.36 |
| Solution # 16 | 21.50 | 3.07 | 4 | 2 | 0.2547 | 43.61 | 68.13 | 43,874.87 | 5413.59 | 148,289.70 | 62,972.16 |
| Solution # 17 | 44.97 | 1.44 | 10 | 4 | 0.2549 | 43.46 | 63.92 | 91,789.48 | 13,533.99 | 109,670.09 | 77,574.40 |
| Solution # 18 | 15.00 | 1.00 | 0 | 1 | 0.2551 | 43.31 | 83.91 | 30,617.31 | 0.00 | 166,960.85 | 31,791.52 |
| Solution # 19 | 45.00 | 3.69 | 10 | 4 | 0.2553 | 43.14 | 66.12 | 91,848.38 | 13,533.99 | 109,655.66 | 72,864.00 |
| Solution # 20 | 45.00 | 3.70 | 10 | 4 | 0.2576 | 42.93 | 66.12 | 91,851.87 | 13,533.99 | 109,654.81 | 72,849.28 |
| Solution # | PV (kW) | NAD | NWT | NDiesel | COE (USD/kWh) | LPSP (%) | RF (%) | PV (kWh) | Wind (kWh) | Battery (kWh) | Diesel (kWh) |
|---|---|---|---|---|---|---|---|---|---|---|---|
| Solution # 1 | 45.00 | 3.69 | 10 | 4 | 0.0734 | 99.93 | 66.14 | 91,850.48 | 13,533.99 | 109,593.94 | 72,790.40 |
| Solution # 2 | 44.91 | 3.70 | 10 | 4 | 0.0772 | 97.99 | 66.08 | 91,673.65 | 13,533.99 | 109,637.81 | 72,878.72 |
| Solution # 3 | 44.89 | 3.72 | 10 | 4 | 0.0788 | 95.71 | 66.06 | 91,635.26 | 13,533.99 | 109,647.37 | 72,908.16 |
| Solution # 4 | 45.00 | 3.84 | 10 | 4 | 0.0795 | 70.68 | 66.19 | 91,851.93 | 13,533.99 | 109,593.58 | 72,687.36 |
| Solution # 5 | 45.00 | 3.72 | 10 | 4 | 0.0800 | 68.78 | 66.15 | 91,849.70 | 13,533.99 | 109,594.13 | 72,775.68 |
| Solution # 6 | 45.00 | 3.72 | 10 | 4 | 0.0807 | 67.69 | 66.15 | 91,849.84 | 13,533.99 | 109,594.10 | 72,775.68 |
| Solution # 7 | 45.00 | 2.38 | 10 | 4 | 0.0814 | 66.90 | 65.59 | 91,843.75 | 13,533.99 | 109,595.61 | 73,982.72 |
| Solution # 8 | 45.00 | 3.69 | 10 | 4 | 0.0828 | 65.65 | 66.14 | 91,850.48 | 13,533.99 | 109,593.94 | 72,790.40 |
| Solution # 9 | 22.42 | 2.39 | 4 | 2 | 0.0835 | 65.01 | 68.31 | 45,769.58 | 5413.59 | 146,325.07 | 62,596.80 |
| Solution # 10 | 45.00 | 3.69 | 10 | 4 | 0.0842 | 64.39 | 66.14 | 91,849.82 | 13,533.99 | 109,594.11 | 72,790.40 |
| Solution # 11 | 45.00 | 3.72 | 10 | 4 | 0.0848 | 63.67 | 66.15 | 91,850.36 | 13,533.99 | 109,593.97 | 72,775.68 |
| Solution # 12 | 45.00 | 3.72 | 10 | 4 | 0.0868 | 62.51 | 66.15 | 91,849.70 | 13,533.99 | 109,594.13 | 72,775.68 |
| Solution # 13 | 45.00 | 3.69 | 10 | 4 | 0.0904 | 61.84 | 66.14 | 91,850.48 | 13,533.99 | 109,593.94 | 72,790.40 |
| Solution # 14 | 45.00 | 3.51 | 9 | 4 | 0.1329 | 60.41 | 65.74 | 91,851.93 | 12,180.59 | 110,583.09 | 73,526.40 |
| Solution # 15 | 45.00 | 2.38 | 10 | 4 | 0.1369 | 59.48 | 65.59 | 91,843.75 | 13,533.99 | 109,595.61 | 73,982.72 |
| Solution # 16 | 45.00 | 3.69 | 10 | 4 | 0.1903 | 55.68 | 66.14 | 91,849.82 | 13,533.99 | 109,594.11 | 72,790.40 |
| Solution # 17 | 45.00 | 2.38 | 10 | 4 | 0.1910 | 54.80 | 65.59 | 91,843.75 | 13,533.99 | 109,595.61 | 73,982.72 |
| Solution # 18 | 42.75 | 4.14 | 10 | 4 | 0.1936 | 54.02 | 64.18 | 87,264.25 | 13,533.99 | 110,813.31 | 75,793.28 |
| Solution # 19 | 45.00 | 3.72 | 10 | 4 | 0.2546 | 43.41 | 66.15 | 91,849.70 | 13,533.99 | 109,594.13 | 72,775.68 |
| Solution # 20 | 23.69 | 2.37 | 6 | 1 | 0.2556 | 42.69 | 84.01 | 48,358.58 | 8120.39 | 141,032.02 | 31,578.08 |
| Solution # | PV (kW) | NAD | NWT | NDiesel | COE (USD/kWh) | LPSP (%) | RF (%) | PV (kWh) | Wind (kWh) | Battery (kWh) | Diesel (kWh) |
|---|---|---|---|---|---|---|---|---|---|---|---|
| Solution # 1 | 44.99 | 2.45 | 10 | 4 | 0.0734 | 99.92 | 65.60 | 91,839.91 | 13,533.99 | 109,804.46 | 74,012.16 |
| Solution # 2 | 44.88 | 3.60 | 10 | 4 | 0.0771 | 97.87 | 66.01 | 91,600.77 | 13,533.99 | 109,864.39 | 73,084.80 |
| Solution # 3 | 44.88 | 3.60 | 10 | 4 | 0.0787 | 95.67 | 66.01 | 91,600.77 | 13,533.99 | 109,864.39 | 73,084.80 |
| Solution # 4 | 44.97 | 2.32 | 10 | 4 | 0.0794 | 71.19 | 65.53 | 91,795.77 | 13,533.99 | 109,815.48 | 74,159.36 |
| Solution # 5 | 45.00 | 2.32 | 10 | 4 | 0.0795 | 70.51 | 65.54 | 91,848.42 | 13,533.99 | 109,802.34 | 74,144.64 |
| Solution # 6 | 44.88 | 3.55 | 10 | 4 | 0.0800 | 68.89 | 66.00 | 91,600.60 | 13,533.99 | 109,864.43 | 73,099.52 |
| Solution # 7 | 18.80 | 4.12 | 1 | 2 | 0.0807 | 67.77 | 67.86 | 38,366.18 | 1353.40 | 157,996.50 | 63,538.88 |
| Solution # 8 | 44.88 | 3.55 | 10 | 4 | 0.0813 | 66.89 | 66.00 | 91,597.04 | 13,533.99 | 109,865.33 | 73,099.52 |
| Solution # 9 | 44.88 | 3.55 | 10 | 4 | 0.0820 | 66.26 | 66.00 | 91,596.90 | 13,533.99 | 109,865.36 | 73,099.52 |
| Solution # 10 | 44.99 | 3.01 | 10 | 4 | 0.0827 | 65.61 | 65.99 | 91,833.09 | 13,533.99 | 109,806.16 | 73,187.84 |
| Solution # 11 | 44.91 | 3.45 | 10 | 4 | 0.0834 | 64.97 | 66.04 | 91,674.10 | 13,533.99 | 109,845.96 | 73,040.64 |
| Solution # 12 | 44.88 | 3.60 | 10 | 4 | 0.0846 | 63.77 | 66.01 | 91,600.77 | 13,533.99 | 109,864.39 | 73,084.80 |
| Solution # 13 | 44.88 | 3.55 | 10 | 4 | 0.0867 | 62.50 | 66.00 | 91,600.60 | 13,533.99 | 109,864.43 | 73,099.52 |
| Solution # 14 | 43.28 | 3.70 | 10 | 4 | 0.0911 | 61.63 | 64.62 | 88,334.07 | 13,533.99 | 110,723.73 | 75,204.48 |
| Solution # 15 | 44.88 | 3.55 | 10 | 4 | 0.1327 | 60.54 | 66.00 | 91,600.60 | 13,533.99 | 109,864.43 | 73,099.52 |
| Solution # 16 | 44.88 | 3.55 | 10 | 4 | 0.1353 | 59.83 | 66.00 | 91,597.04 | 13,533.99 | 109,865.33 | 73,099.52 |
| Solution # 17 | 44.88 | 3.60 | 10 | 4 | 0.1906 | 55.10 | 66.01 | 91,600.77 | 13,533.99 | 109,864.39 | 73,084.80 |
| Solution # 18 | 44.97 | 2.32 | 10 | 4 | 0.1928 | 53.99 | 65.53 | 91,795.77 | 13,533.99 | 109,815.48 | 74,159.36 |
| Solution # 19 | 18.80 | 4.12 | 1 | 2 | 0.2544 | 43.56 | 67.86 | 38,365.81 | 1353.40 | 157,996.87 | 63,538.88 |
| Solution # 20 | 44.88 | 3.60 | 10 | 4 | 0.2554 | 42.70 | 66.01 | 91,600.60 | 13,533.99 | 109,864.43 | 73,084.80 |
| Solution # | PV (kW) | NAD | NWT | NDiesel | COE (USD/kWh) | LPSP (%) | RF (%) | PV (kWh) | Wind (kWh) | Battery (kWh) | Diesel (kWh) |
|---|---|---|---|---|---|---|---|---|---|---|---|
| Solution # 1 | 44.99 | 4.99 | 10 | 4 | 0.0722 | 99.51 | 66.17 | 91,832.55 | 13,533.99 | 109,659.54 | 72,746.24 |
| Solution # 2 | 44.99 | 4.97 | 10 | 4 | 0.0741 | 98.14 | 66.16 | 91,827.91 | 13,533.99 | 109,660.67 | 72,760.96 |
| Solution # 3 | 39.95 | 4.86 | 10 | 4 | 0.0758 | 96.32 | 61.45 | 81,543.00 | 13,533.99 | 112,657.55 | 80,076.80 |
| Solution # 4 | 44.83 | 5.00 | 10 | 4 | 0.0774 | 93.56 | 66.04 | 91,508.64 | 13,533.99 | 109,739.33 | 72,937.60 |
| Solution # 5 | 44.99 | 4.99 | 10 | 4 | 0.0785 | 69.05 | 66.16 | 91,827.84 | 13,533.99 | 109,660.69 | 72,760.96 |
| Solution # 6 | 45.00 | 2.84 | 10 | 4 | 0.0804 | 66.38 | 65.84 | 91,851.62 | 13,533.99 | 109,654.87 | 73,467.52 |
| Solution # 7 | 44.94 | 5.00 | 10 | 4 | 0.0829 | 63.23 | 66.13 | 91,724.46 | 13,533.99 | 109,686.06 | 72,805.12 |
| Solution # 8 | 44.99 | 4.47 | 10 | 4 | 0.0855 | 60.67 | 66.17 | 91,834.96 | 13,533.99 | 109,658.95 | 72,746.24 |
| Solution # 9 | 45.00 | 2.84 | 10 | 4 | 0.0893 | 58.69 | 65.84 | 91,851.62 | 13,533.99 | 109,654.87 | 73,467.52 |
| Solution # 10 | 44.52 | 4.86 | 10 | 4 | 0.0937 | 56.02 | 65.83 | 90,876.48 | 13,533.99 | 109,896.81 | 73,232.00 |
| Solution # 11 | 45.00 | 4.30 | 10 | 4 | 0.1330 | 53.28 | 66.16 | 91,850.33 | 13,533.99 | 109,655.19 | 72,760.96 |
| Solution # 12 | 21.17 | 1.39 | 7 | 3 | 0.1356 | 51.44 | 53.78 | 43,213.00 | 9473.79 | 144,891.37 | 91,311.84 |
| Solution # 13 | 44.05 | 4.74 | 10 | 4 | 0.1395 | 49.13 | 65.35 | 89,905.59 | 13,533.99 | 110,143.77 | 73,997.44 |
| Solution # 14 | 45.00 | 4.23 | 10 | 4 | 0.1895 | 46.63 | 66.16 | 91,850.63 | 13,533.99 | 109,655.11 | 72,760.96 |
| Solution # 15 | 44.99 | 4.99 | 10 | 4 | 0.1912 | 44.92 | 66.16 | 91,827.95 | 13,533.99 | 109,660.66 | 72,760.96 |
| Solution # 16 | 45.00 | 4.70 | 10 | 4 | 0.1953 | 41.59 | 66.17 | 91,849.99 | 13,533.99 | 109,655.27 | 72,746.24 |
| Solution # 17 | 44.99 | 4.99 | 10 | 4 | 0.2521 | 34.92 | 66.16 | 91,827.82 | 13,533.99 | 109,660.70 | 72,760.96 |
| Solution # 18 | 44.99 | 4.95 | 10 | 4 | 0.2527 | 32.41 | 66.16 | 91,827.95 | 13,533.99 | 109,660.66 | 72,760.96 |
| Solution # 19 | 44.99 | 4.99 | 10 | 4 | 0.2546 | 30.28 | 66.16 | 91,827.91 | 13,533.99 | 109,660.67 | 72,760.96 |
| Solution # 20 | 45.00 | 2.84 | 10 | 4 | 0.2574 | 27.82 | 65.84 | 91,851.62 | 13,533.99 | 109,654.87 | 73,467.52 |
| Solution # | PV (kW) | NAD | NWT | NDiesel | COE (USD/kWh) | LPSP (%) | RF (%) | PV (kWh) | Wind (kWh) | Battery (kWh) | Diesel (kWh) |
|---|---|---|---|---|---|---|---|---|---|---|---|
| Solution # 1 | 44.99 | 4.97 | 10 | 4 | 0.0722 | 99.46 | 66.17 | 91,840.97 | 13,533.99 | 109,725.41 | 72,775.68 |
| Solution # 2 | 44.99 | 4.44 | 10 | 4 | 0.0741 | 97.99 | 66.17 | 91,839.72 | 13,533.99 | 109,725.71 | 72,775.68 |
| Solution # 3 | 45.00 | 4.88 | 10 | 4 | 0.0758 | 96.06 | 66.17 | 91,851.89 | 13,533.99 | 109,722.71 | 72,775.68 |
| Solution # 4 | 44.99 | 4.99 | 10 | 4 | 0.0774 | 93.29 | 66.17 | 91,839.72 | 13,533.99 | 109,725.71 | 72,775.68 |
| Solution # 5 | 45.00 | 4.51 | 10 | 4 | 0.0785 | 69.05 | 66.17 | 91,847.06 | 13,533.99 | 109,723.90 | 72,775.68 |
| Solution # 6 | 44.99 | 2.73 | 10 | 4 | 0.0794 | 67.44 | 65.80 | 91,834.75 | 13,533.99 | 109,726.94 | 73,555.84 |
| Solution # 7 | 45.00 | 4.99 | 10 | 4 | 0.0823 | 64.29 | 66.17 | 91,850.76 | 13,533.99 | 109,722.99 | 72,775.68 |
| Solution # 8 | 44.99 | 4.99 | 10 | 4 | 0.0857 | 60.60 | 66.17 | 91,839.72 | 13,533.99 | 109,725.71 | 72,775.68 |
| Solution # 9 | 27.66 | 2.58 | 6 | 2 | 0.0903 | 58.01 | 70.59 | 56,453.84 | 8120.39 | 133,213.65 | 58,173.44 |
| Solution # 10 | 44.99 | 4.99 | 10 | 4 | 0.0942 | 55.69 | 66.17 | 91,839.72 | 13,533.99 | 109,725.71 | 72,775.68 |
| Solution # 11 | 45.00 | 4.99 | 10 | 4 | 0.1341 | 52.57 | 66.17 | 91,845.38 | 13,533.99 | 109,724.32 | 72,775.68 |
| Solution # 12 | 45.00 | 5.00 | 10 | 4 | 0.1390 | 49.42 | 66.17 | 91,851.93 | 13,533.99 | 109,722.70 | 72,775.68 |
| Solution # 13 | 44.99 | 3.20 | 10 | 4 | 0.1892 | 47.16 | 66.06 | 91,834.77 | 13,533.99 | 109,726.94 | 72,996.48 |
| Solution # 14 | 27.66 | 2.58 | 6 | 2 | 0.1903 | 45.49 | 70.59 | 56,453.84 | 8120.39 | 133,213.65 | 58,173.44 |
| Solution # 15 | 44.99 | 4.99 | 10 | 4 | 0.1920 | 44.04 | 66.17 | 91,840.28 | 13,533.99 | 109,725.58 | 72,775.68 |
| Solution # 16 | 44.99 | 4.99 | 10 | 4 | 0.1960 | 40.97 | 66.17 | 91,839.72 | 13,533.99 | 109,725.71 | 72,775.68 |
| Solution # 17 | 45.00 | 5.00 | 10 | 4 | 0.2521 | 35.31 | 66.17 | 91,843.83 | 13,533.99 | 109,724.70 | 72,775.68 |
| Solution # 18 | 44.99 | 4.99 | 10 | 4 | 0.2526 | 32.84 | 66.17 | 91,839.72 | 13,533.99 | 109,725.71 | 72,775.68 |
| Solution # 19 | 45.00 | 4.54 | 10 | 4 | 0.2551 | 29.88 | 66.17 | 91,850.66 | 13,533.99 | 109,723.01 | 72,775.68 |
| Solution # 20 | 27.66 | 2.58 | 6 | 2 | 0.2577 | 27.64 | 70.59 | 56,453.84 | 8120.39 | 133,213.65 | 58,173.44 |
| Solution # | PV (kW) | NAD | NWT | NDiesel | COE (USD/kWh) | LPSP (%) | RF (%) | PV (kWh) | Wind (kWh) | Battery (kWh) | Diesel (kWh) |
|---|---|---|---|---|---|---|---|---|---|---|---|
| Solution # 1 | 44.95 | 2.98 | 10 | 3 | 0.0705 | 99.90 | 73.34 | 91,751.51 | 13,533.99 | 109,688.05 | 57,319.68 |
| Solution # 2 | 45.00 | 4.99 | 10 | 4 | 0.0740 | 97.97 | 66.16 | 91,845.21 | 13,533.99 | 109,664.72 | 72,775.68 |
| Solution # 3 | 43.71 | 4.39 | 10 | 4 | 0.0758 | 95.94 | 65.06 | 89,228.45 | 13,533.99 | 110,340.95 | 74,468.48 |
| Solution # 4 | 44.99 | 4.77 | 10 | 4 | 0.0775 | 93.33 | 66.15 | 91,839.05 | 13,533.99 | 109,666.25 | 72,790.40 |
| Solution # 5 | 44.96 | 4.99 | 10 | 4 | 0.0785 | 69.16 | 66.14 | 91,772.80 | 13,533.99 | 109,682.74 | 72,805.12 |
| Solution # 6 | 45.00 | 2.65 | 10 | 4 | 0.0804 | 66.42 | 65.75 | 91,848.21 | 13,533.99 | 109,663.98 | 73,644.16 |
| Solution # 7 | 45.00 | 4.99 | 10 | 4 | 0.0813 | 65.21 | 66.16 | 91,845.24 | 13,533.99 | 109,664.71 | 72,775.68 |
| Solution # 8 | 44.98 | 5.00 | 10 | 4 | 0.0832 | 63.13 | 66.14 | 91,808.27 | 13,533.99 | 109,673.91 | 72,805.12 |
| Solution # 9 | 44.69 | 5.00 | 10 | 4 | 0.0856 | 60.53 | 65.90 | 91,211.39 | 13,533.99 | 109,824.38 | 73,158.40 |
| Solution # 10 | 45.00 | 4.99 | 10 | 4 | 0.0902 | 57.79 | 66.16 | 91,845.14 | 13,533.99 | 109,664.74 | 72,775.68 |
| Solution # 11 | 40.84 | 4.84 | 9 | 4 | 0.0938 | 55.71 | 61.97 | 83,358.93 | 12,180.59 | 113,124.68 | 79,355.52 |
| Solution # 12 | 45.00 | 4.33 | 10 | 4 | 0.1331 | 53.09 | 66.15 | 91,847.40 | 13,533.99 | 109,664.18 | 72,790.40 |
| Solution # 13 | 32.89 | 3.14 | 3 | 2 | 0.1370 | 50.57 | 73.70 | 67,123.61 | 4060.20 | 128,175.19 | 52,432.64 |
| Solution # 14 | 44.97 | 4.99 | 10 | 4 | 0.1893 | 46.72 | 66.14 | 91,781.83 | 13,533.99 | 109,680.49 | 72,805.12 |
| Solution # 15 | 44.96 | 4.99 | 10 | 4 | 0.1913 | 44.51 | 66.14 | 91,772.80 | 13,533.99 | 109,682.74 | 72,805.12 |
| Solution # 16 | 32.89 | 3.14 | 3 | 2 | 0.1954 | 41.44 | 73.70 | 67,123.61 | 4060.20 | 128,175.19 | 52,432.64 |
| Solution # 17 | 45.00 | 4.99 | 10 | 4 | 0.2522 | 35.43 | 66.16 | 91,845.18 | 13,533.99 | 109,664.73 | 72,775.68 |
| Solution # 18 | 45.00 | 4.80 | 10 | 4 | 0.2531 | 31.48 | 66.16 | 91,846.38 | 13,533.99 | 109,664.43 | 72,775.68 |
| Solution # 19 | 44.96 | 4.99 | 10 | 4 | 0.2549 | 29.44 | 66.14 | 91,772.80 | 13,533.99 | 109,682.74 | 72,805.12 |
| Solution # 20 | 45.00 | 4.58 | 10 | 4 | 0.2577 | 27.18 | 66.16 | 91,847.51 | 13,533.99 | 109,664.15 | 72,775.68 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bouchekara, H.R.E.H.; Sha’aban, Y.A.; Shahriar, M.S.; Abdullah, S.M.; Ramli, M.A. Sizing of Hybrid PV/Battery/Wind/Diesel Microgrid System Using an Improved Decomposition Multi-Objective Evolutionary Algorithm Considering Uncertainties and Battery Degradation. Sustainability 2023, 15, 11073. https://doi.org/10.3390/su151411073
Bouchekara HREH, Sha’aban YA, Shahriar MS, Abdullah SM, Ramli MA. Sizing of Hybrid PV/Battery/Wind/Diesel Microgrid System Using an Improved Decomposition Multi-Objective Evolutionary Algorithm Considering Uncertainties and Battery Degradation. Sustainability. 2023; 15(14):11073. https://doi.org/10.3390/su151411073
Chicago/Turabian StyleBouchekara, Houssem R. E. H., Yusuf A. Sha’aban, Mohammad S. Shahriar, Saad M. Abdullah, and Makbul A. Ramli. 2023. "Sizing of Hybrid PV/Battery/Wind/Diesel Microgrid System Using an Improved Decomposition Multi-Objective Evolutionary Algorithm Considering Uncertainties and Battery Degradation" Sustainability 15, no. 14: 11073. https://doi.org/10.3390/su151411073
APA StyleBouchekara, H. R. E. H., Sha’aban, Y. A., Shahriar, M. S., Abdullah, S. M., & Ramli, M. A. (2023). Sizing of Hybrid PV/Battery/Wind/Diesel Microgrid System Using an Improved Decomposition Multi-Objective Evolutionary Algorithm Considering Uncertainties and Battery Degradation. Sustainability, 15(14), 11073. https://doi.org/10.3390/su151411073







