Optimal Operation of Sustainable Virtual Power Plant Considering the Amount of Emission in the Presence of Renewable Energy Sources and Demand Response
Abstract
1. Introduction
1.1. Background
1.2. Literature Review
- (1)
- Considering a new stochastic multi-objective system for SVPP management to minimize the operational costs and emissions.
- (2)
- Proposing a multi-energy SVPP that includes electrical, natural gas, heating, and cooling sectors to meet the type of user demand and balance supply and demand at all times.
- (3)
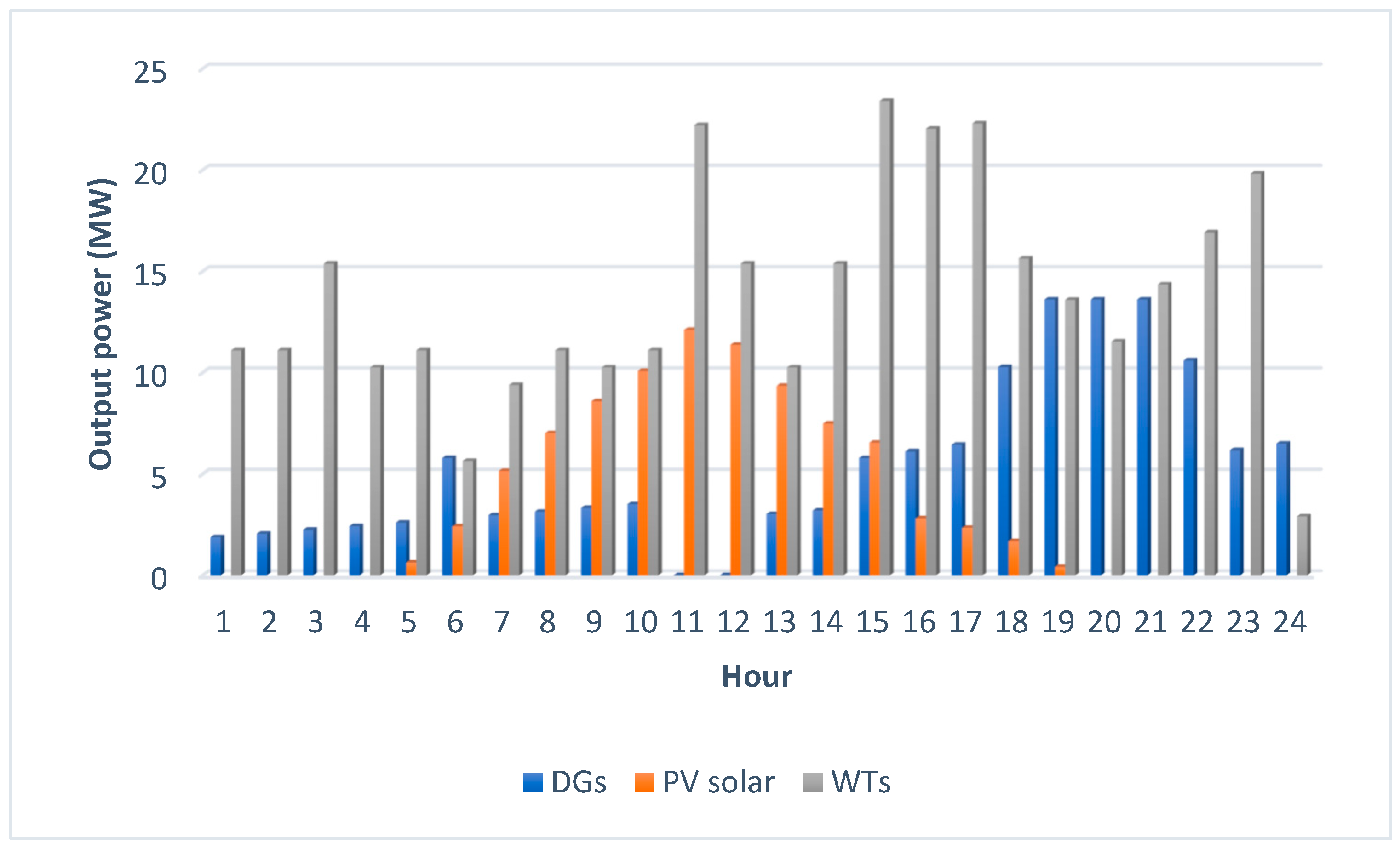
- Investigating the effect of cost-effective and environment-friendly sources such as PVs, WTs, and ESS on the operation and scheduling of an SVPP.
2. System Model
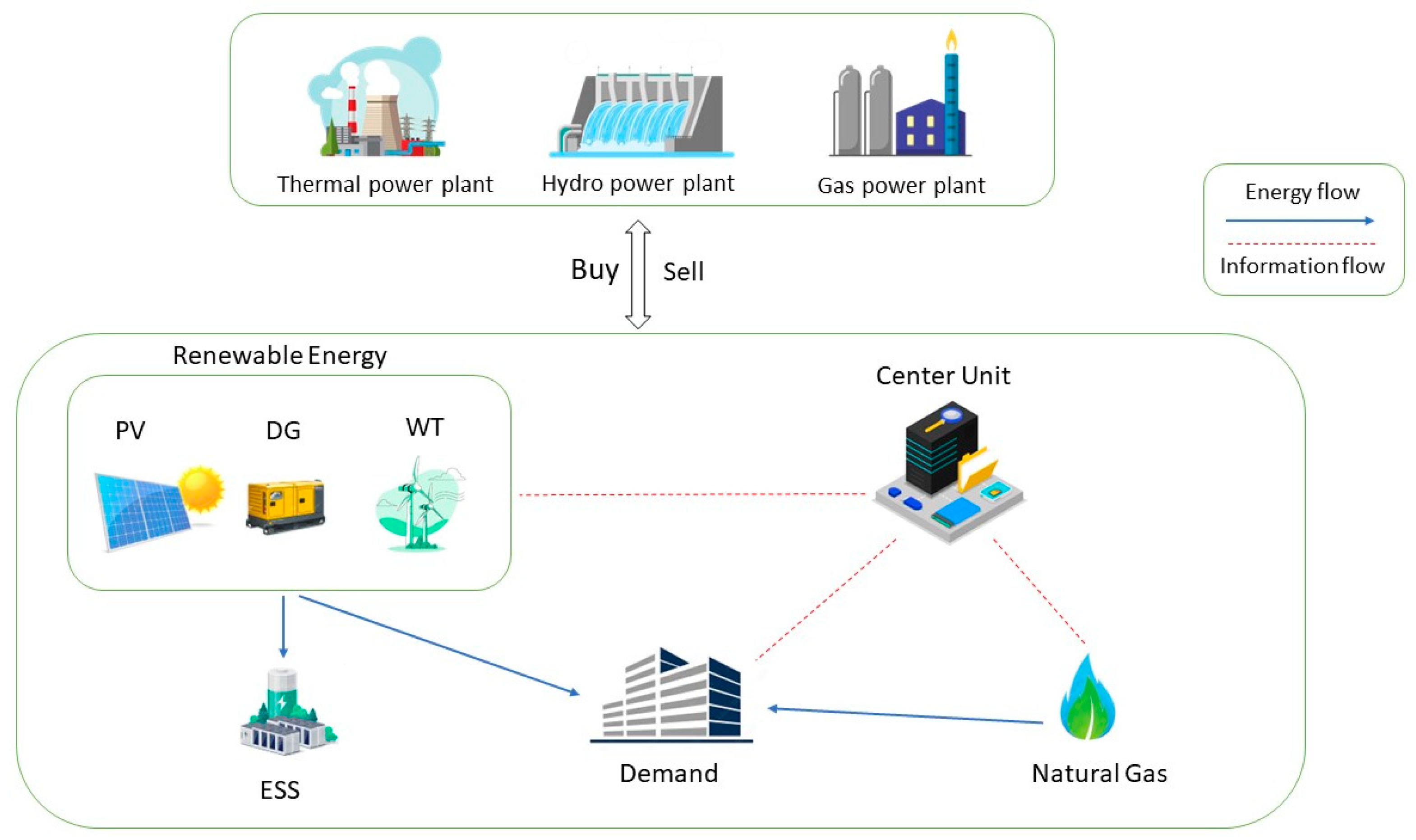
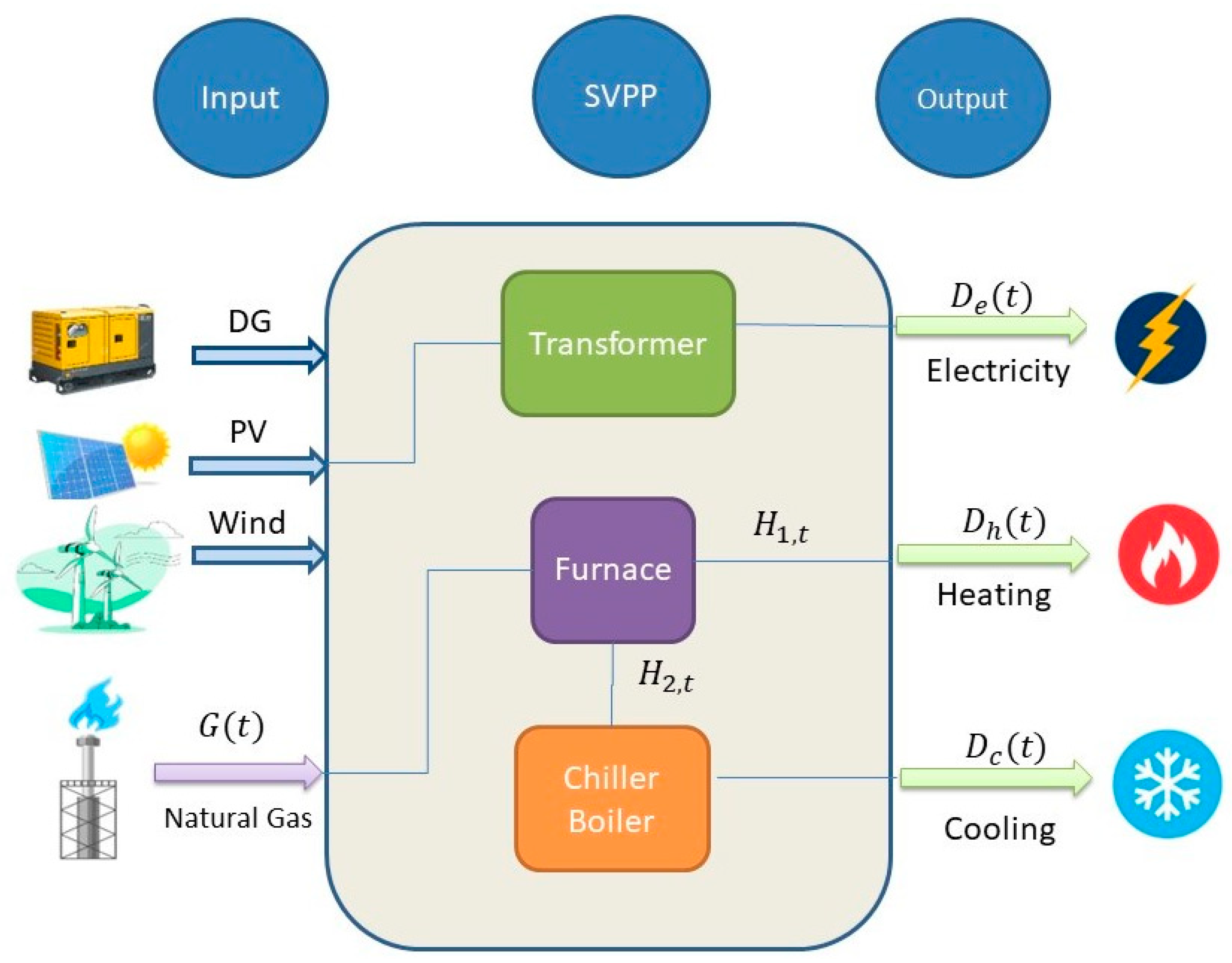
2.1. Multi-Energy Sustainable Virtual Power Plant (SVPP) Architecture
2.2. SVPP Operation Model
3. The Mathematical Model
3.1. Wind Turbine (WT)
3.2. Photovoltaic (PV)
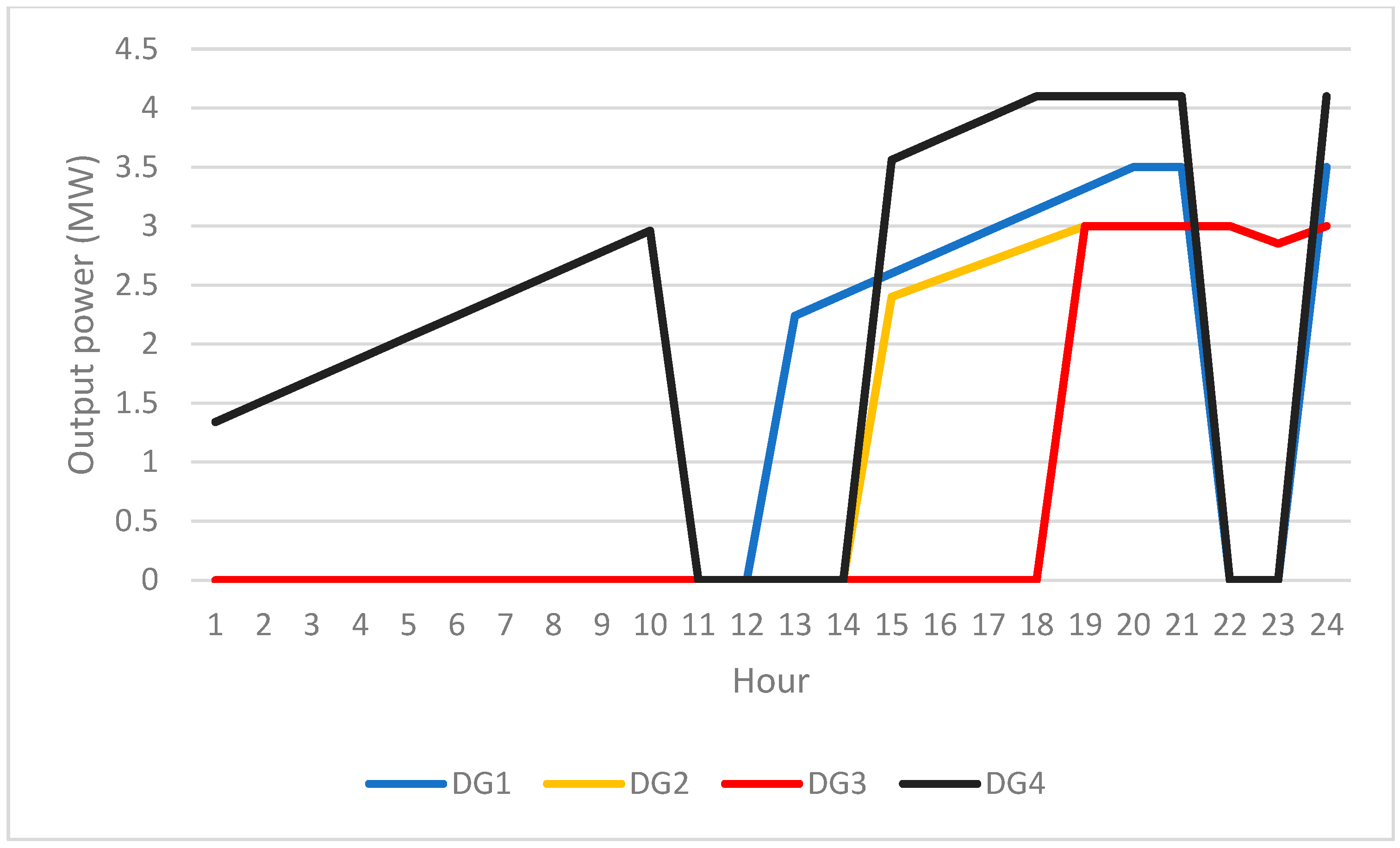
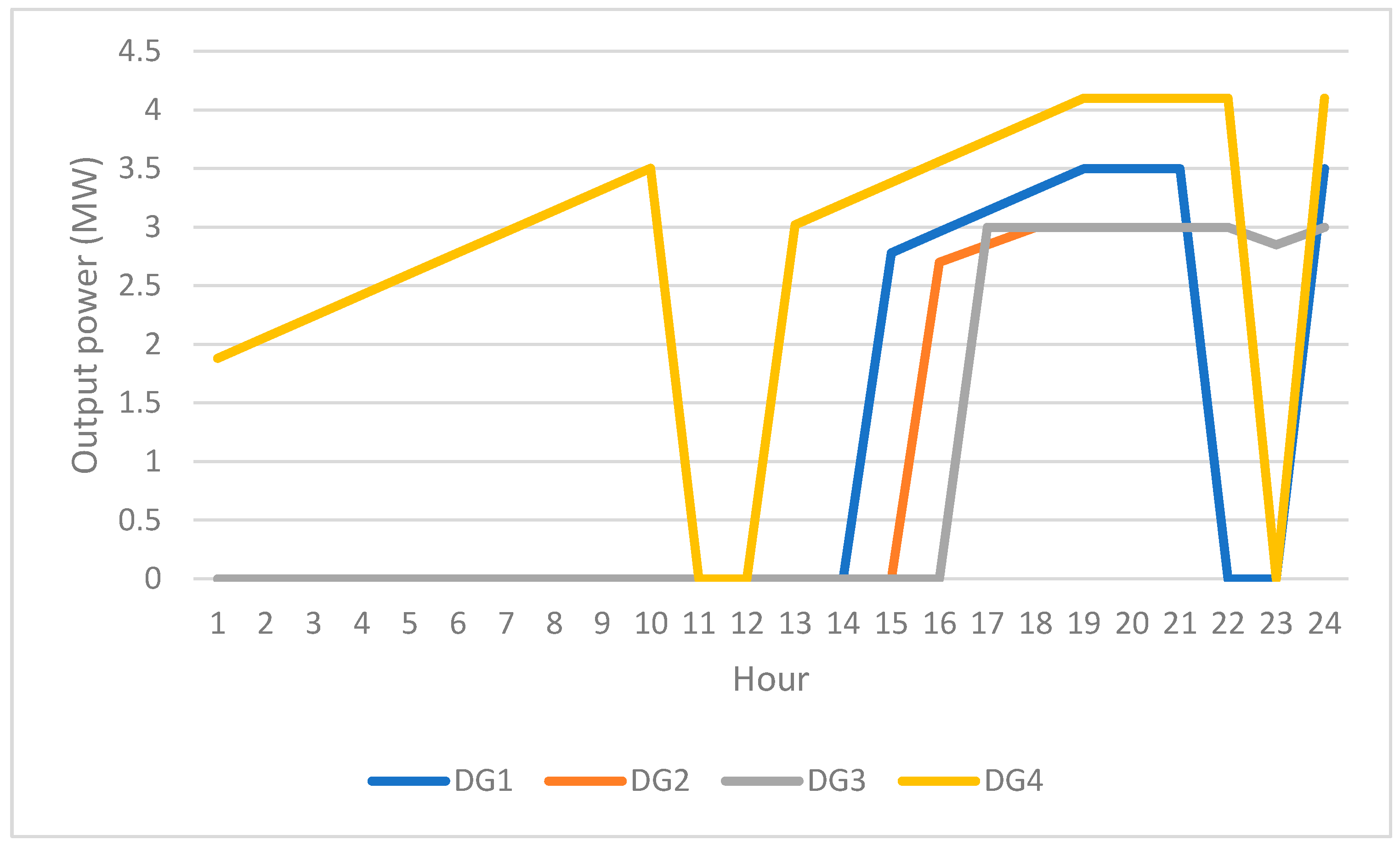
3.3. Diesel Generator (DG)
3.3.1. Costs of DG
3.3.2. DG Generation Constraints
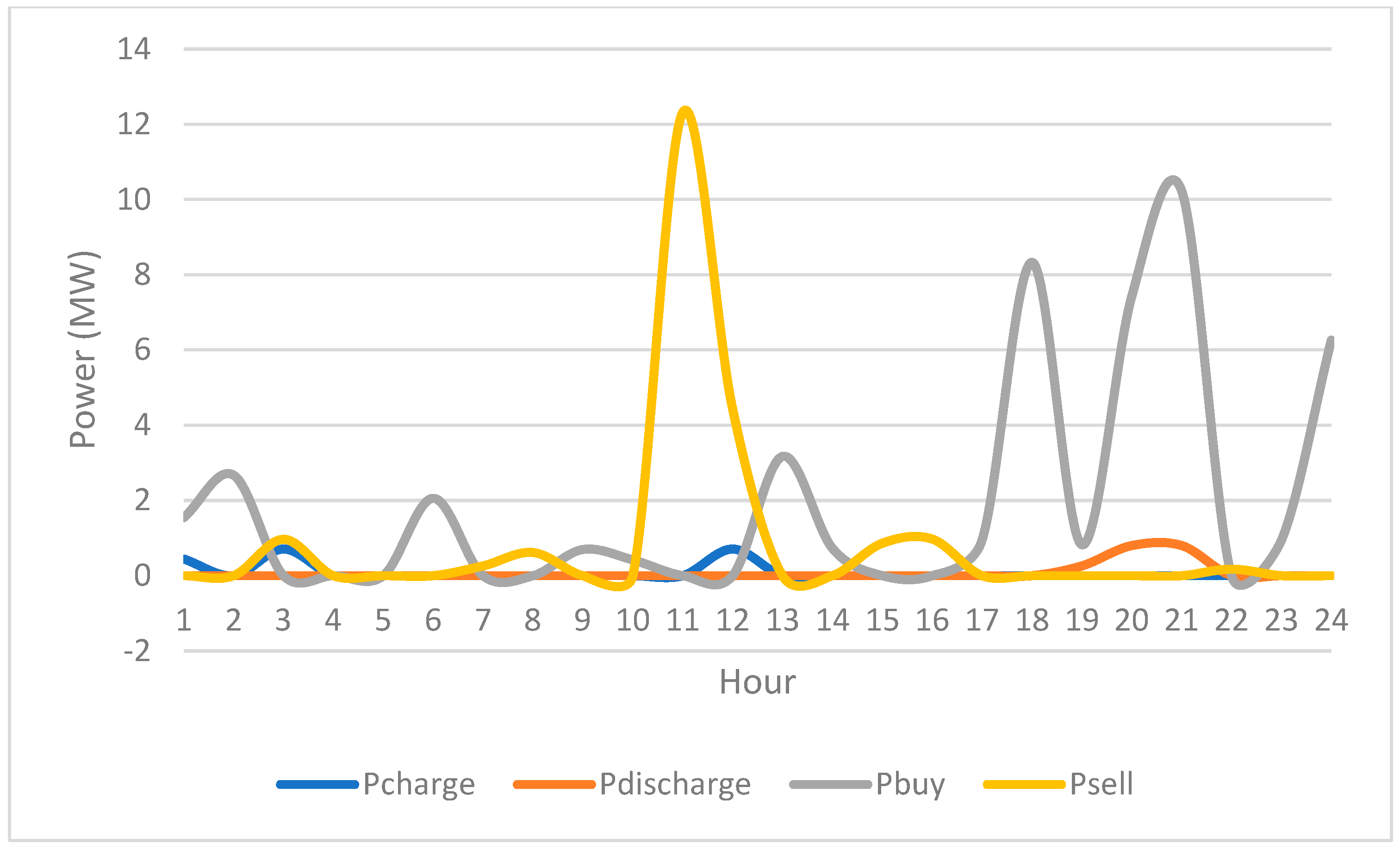
3.4. Energy Storage System (ESS)
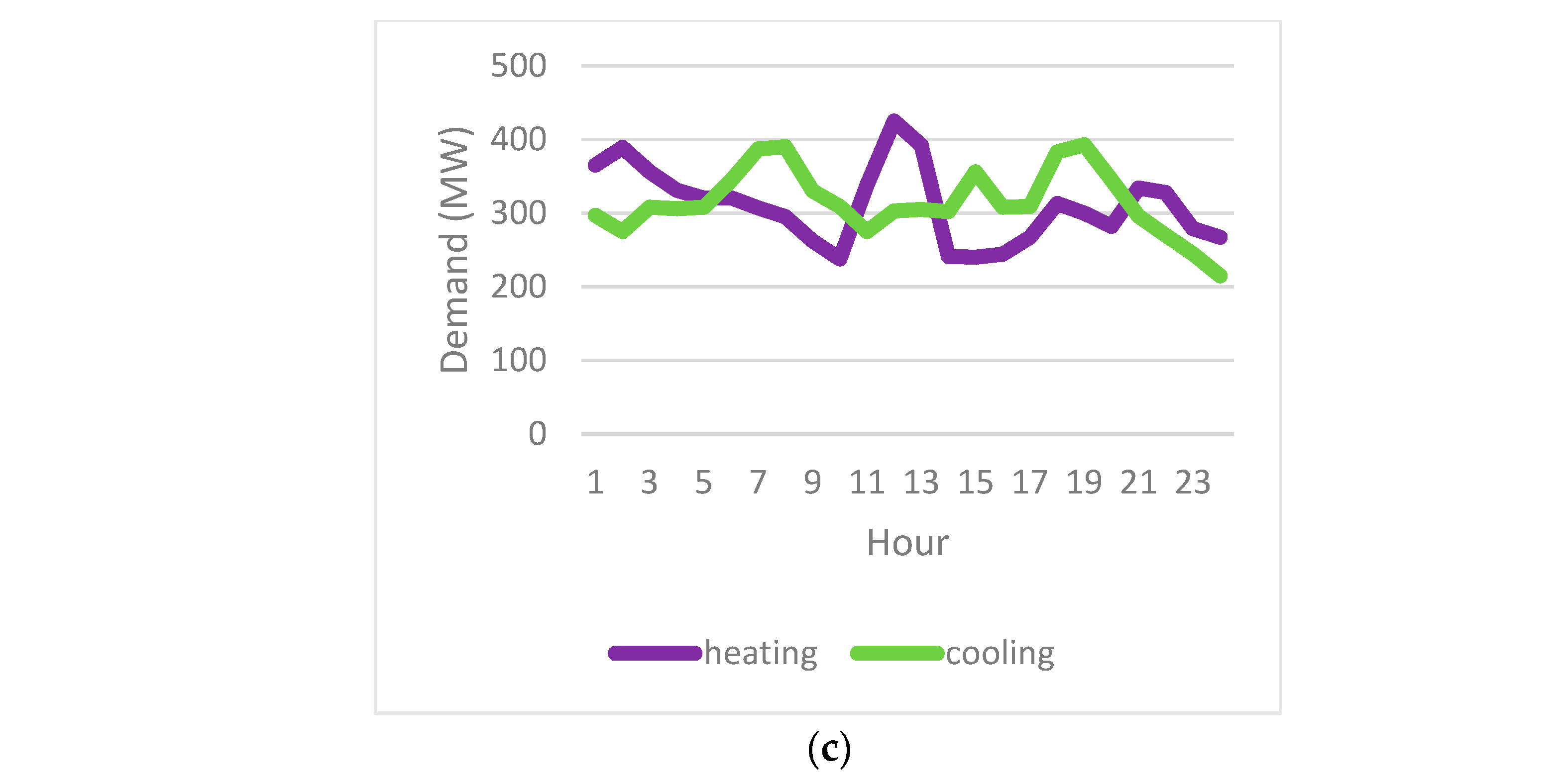
3.5. Heating and Cooling Loads
3.6. Objective Function
3.6.1. Costs of SVPP’s Operator
3.6.2. Emission
3.7. Problem Constraints
3.8. Modeling of Demand Response Program (DRP)
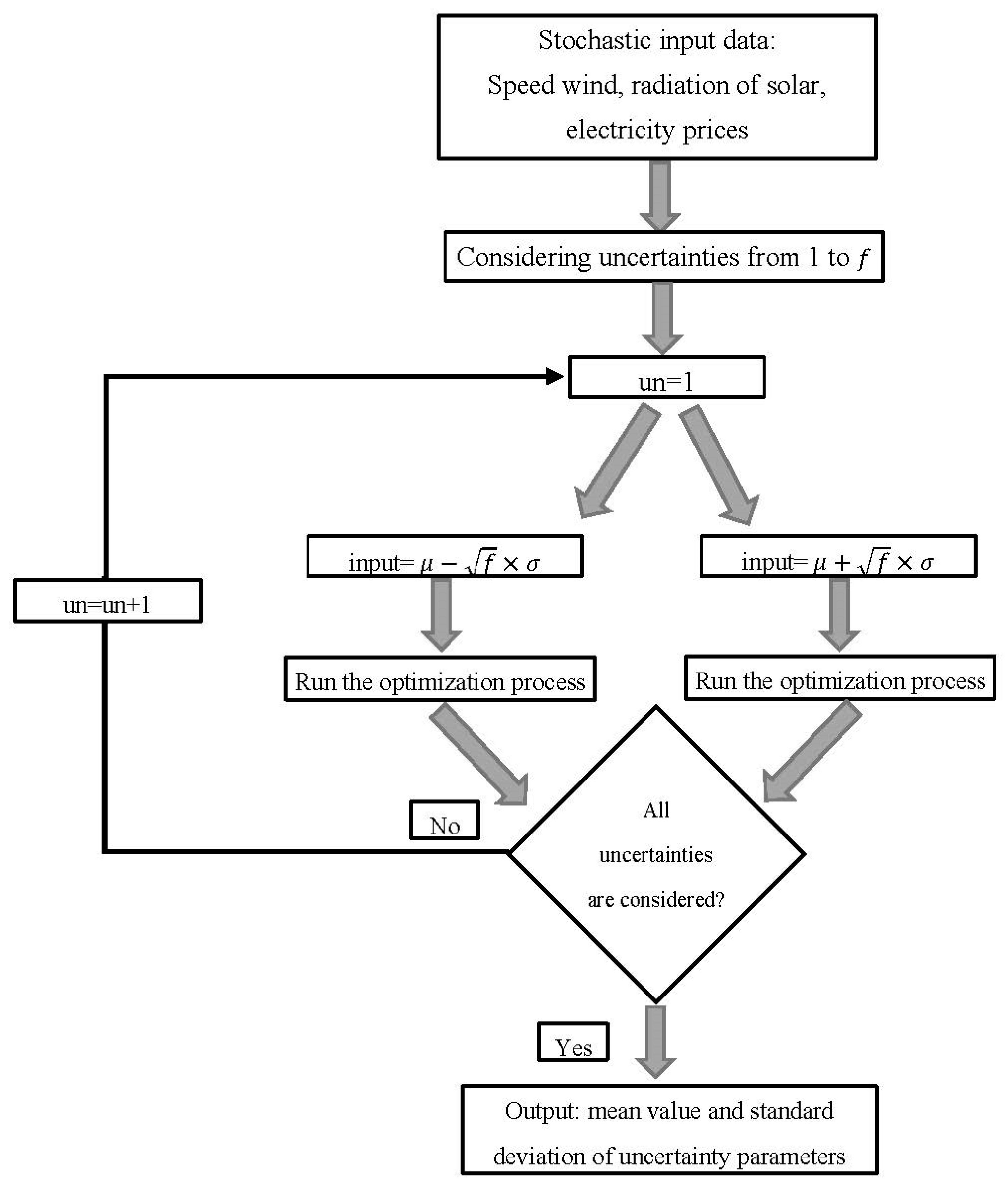
3.9. Uncertainty Modeling
4. Simulations and Discussion
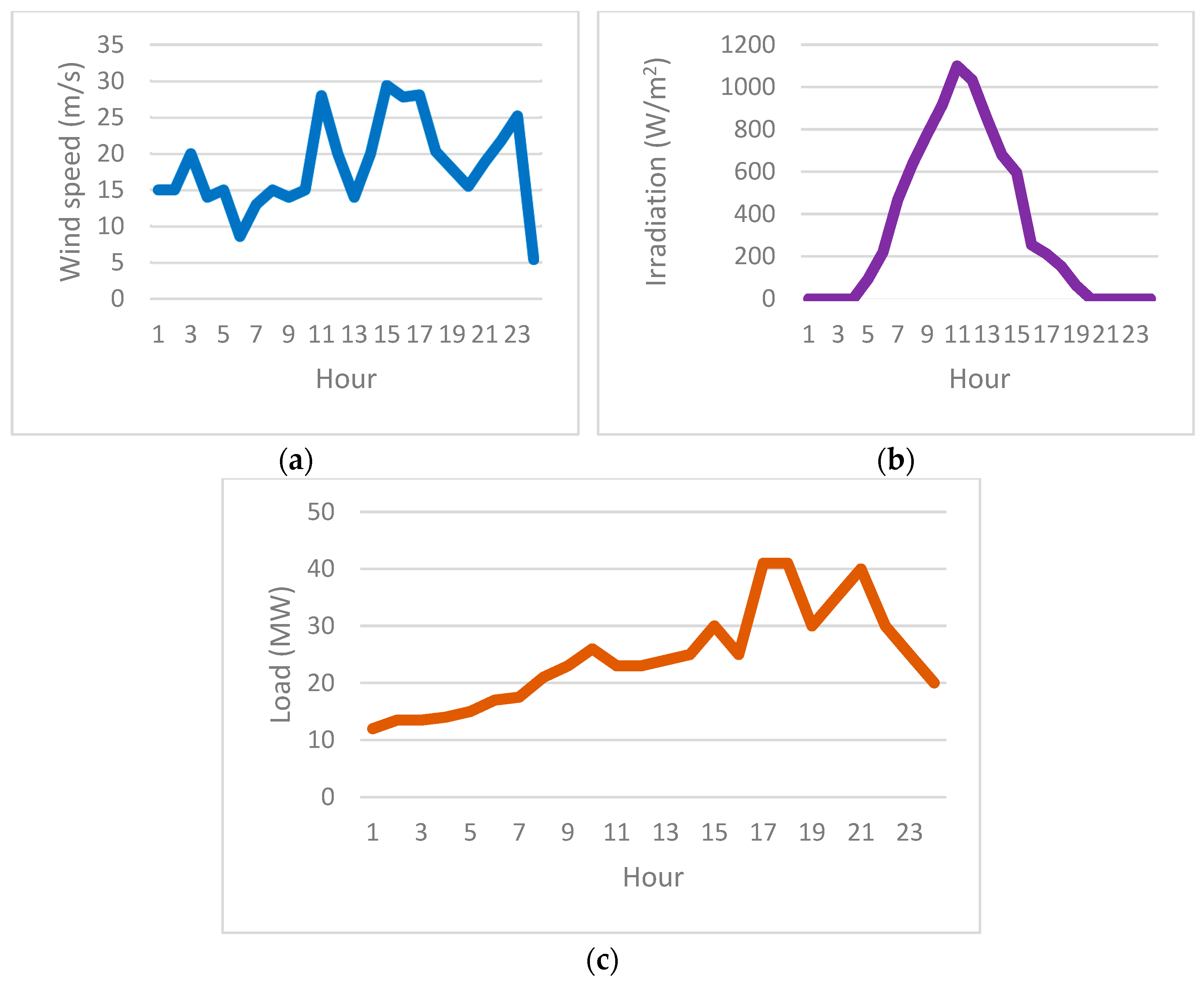
4.1. Basic Data
4.2. Case Studies (CSs)
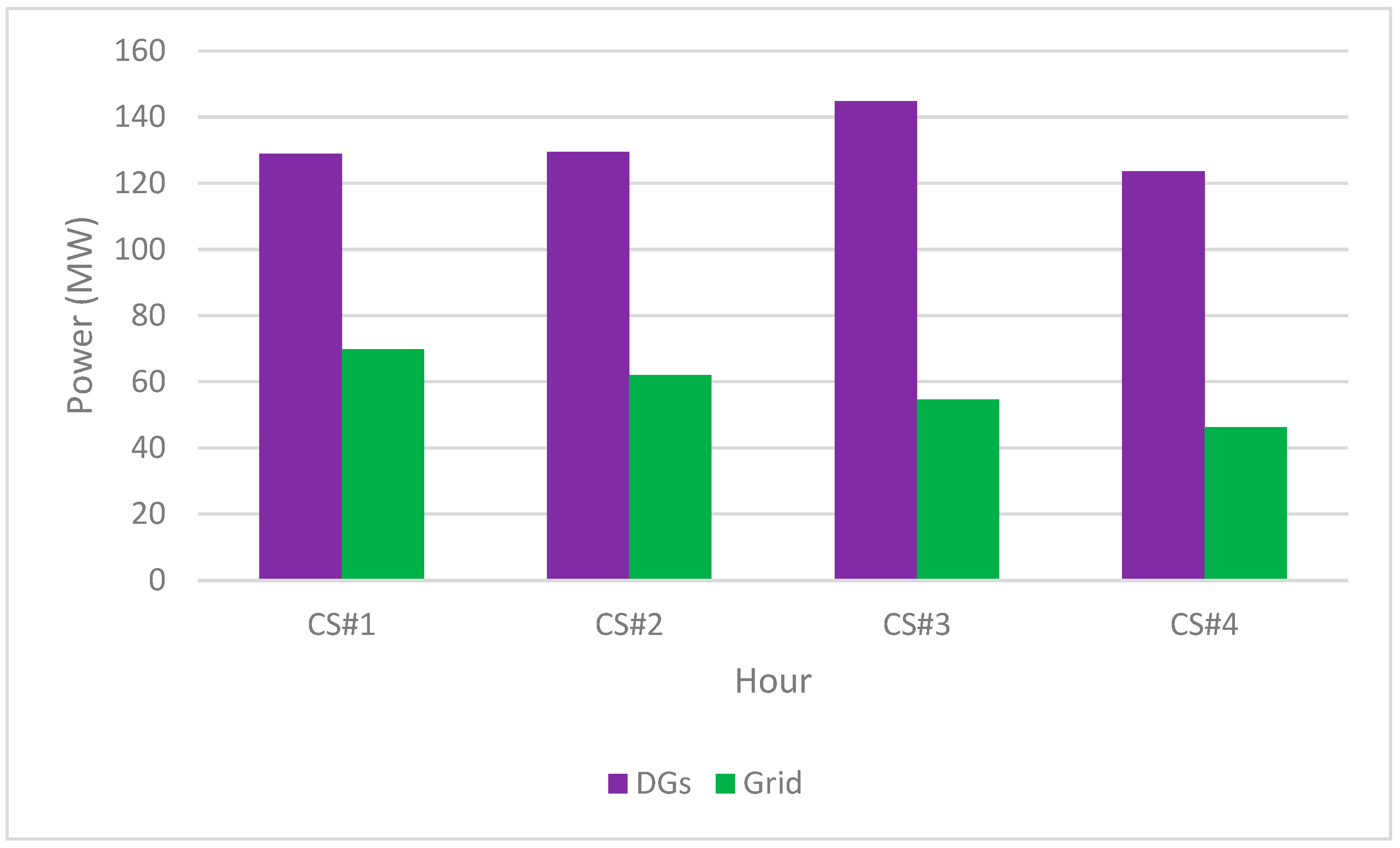
4.3. Simulation Results and Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| List of acronyms. | |
| Symbol | Meaning |
| 2PEM | Two-Point Estimate Method |
| CHP | Combined Heat and Power |
| DER | Distributed Energy Resource |
| DG | Diesel Generator |
| DRP DSO | Demand Response Program Distributed System Operator |
| EMS | Energy Management System |
| ESS | Energy Storage System |
| GA | Genetic Algorithm |
| ISO MINLP | Independent System Operator Mixed-Integer Non-linear Programming |
| PSO | Particle Swarm Optimization |
| PV | Photovoltaic |
| RES | Renewable Energy Source |
| SVPP | Sustainable Virtual Power Plant |
| TOU | Time of Use |
| VPP | Virtual Power Plant |
| WT | Wind Turbine |
| List of symbols. | |
| Abbreviation | Meaning |
| Index for WT | |
| Index for PV | |
| Index for DG | |
| Index for ESS | |
| Index for time (hour) | |
| Index for uncertainty parameters | |
| Coefficients of DG cost function | |
| Operational ($/MWh) and maintenance costs of ESS ($) | |
| Operational ($/MWh) and constant costs of PV ($) | |
| Operational ($/MWh) and constant costs of WT ($) | |
| Total ($) and operational costs of natural gas ($/MWh) | |
| Emission factor of DG (kg/MWh) | |
| Emission factor of main grid (kg/MWh) | |
| Cost of emission main grid and DG ($/kg) | |
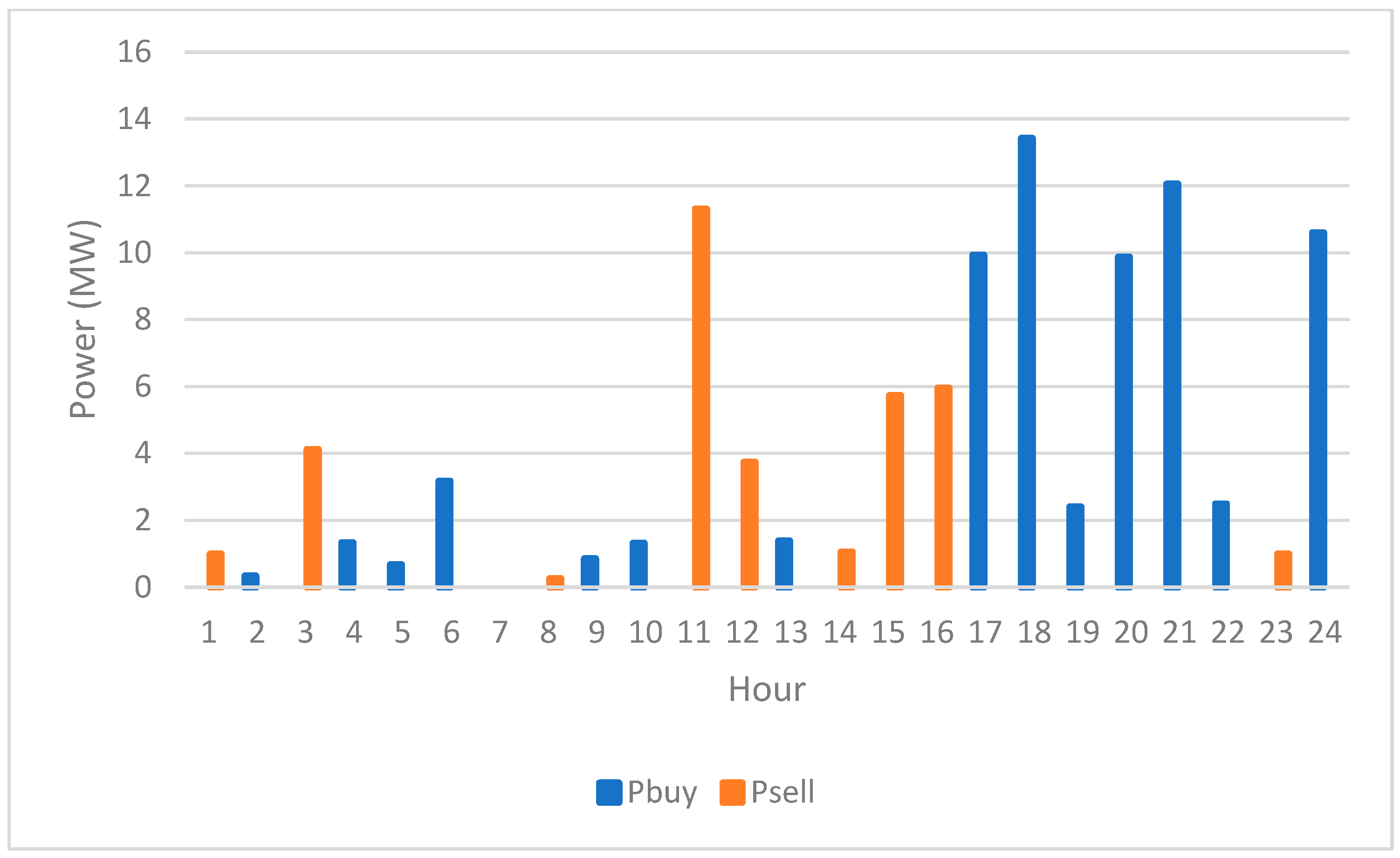
| Cost of buying/selling power from/to the main grid ($/MWh) | |
| Heating and cooling loads (MW) | |
| The minimum up/minimum down-time of DG (hour) | |
| Initial state of charge of ESS (MWh) | |
| Minimum and maximum energy of ESS (MWh) | |
| Solar radiation in standard test condition (W/m2) | |
| Solar radiation for normal operating cell temperature (W/m2) | |
| Amount of load (MW) | |
| Maximum capacity of transmission line (MW) | |
| Maximum charge and discharge rates of ESS (MW) | |
| Rated power of WT (MW) | |
| Rated power of PV (MW) | |
| Minimum and maximum power in operating of DG (MW) | |
| Certain radiation point for PV (W/m2) | |
| Minimum and maximum wind speed (m/s) | |
| Rated wind speed (m/s) | |
| Wind speed (m/s) | |
| Elasticity | |
| Efficiency of chiller boiler and furnace (%) | |
| Efficiency of charge and discharge (%) | |
| Efficiency of the transformer (%) | |
| , | Electricity prices before and after DRP |
| Interval of operation | |
| Cost function of DG ($) | |
| Cost of all DGs ($) | |
| Cost of all ESSs ($) | |
| Cost of all PVs ($) | |
| Cost of all WTs ($) | |
| Cost of buying energy ($) | |
| Total emissions (kg) | |
| Energy of ESS | |
| Amount of energy for cooling and heating sector (MW) | |
| Amount of produced natural gas (MW) | |
| Binary variable for on/off state DG | |
| Binary variable for start-up state DG | |
| Binary variable for shut-down state DG | |
| Amount produced power of DG (MW) | |
| Amount produced power of PV (MW) | |
| Amount produced power of WT (MW) | |
| Total costs of sold energy ($) | |
| Binary variable of charge and discharge modes | |
| Total costs of SVPP ($) | |
| Power demand after implementation DRP (MW) | |
| Power of WT, PV, and DG considering efficiency transformer (MW) | |
| Objective Function | |
| Total costs of emissions ($) | |
References
- Bahramara, S.; Sheikhahmadi, P.; Golpîra, H. Co-optimization of energy and reserve in standalone micro-grid considering uncertainties. Energy 2019, 176, 792–804. [Google Scholar] [CrossRef]
- Hadayeghparast, S.; Farsangi, A.S.; Shayanfar, H. Day-ahead stochastic multi-objective economic/emission operational scheduling of a large scale virtual power plant. Energy 2019, 172, 630–646. [Google Scholar] [CrossRef]
- Guo, W.; Liu, P.; Shu, X. Optimal dispatching of electric-thermal interconnected virtual power plant considering market trading mechanism. J. Clean. Prod. 2021, 279, 123446. [Google Scholar] [CrossRef]
- Tan, Z.; Wang, G.; Ju, L.; Tan, Q.; Yang, W. Application of CVaR risk aversion approach in the dynamical scheduling optimization model for virtual power plant connected with wind-photovoltaic-energy storage system with uncertainties and demand response. Energy 2017, 124, 198–213. [Google Scholar] [CrossRef]
- Zhang, L.; Liu, D.; Cai, G.; Lyu, L.; Koh, L.H.; Wang, T. An optimal dispatch model for virtual power plant that incorporates carbon trading and green certificate trading. Int. J. Electr. Power Energy Syst. 2023, 144, 108558. [Google Scholar] [CrossRef]
- Naval, N.; Yusta, J.M. Virtual power plant models and electricity markets-A review. Renew. Sustain. Energy Rev. 2021, 149, 111393. [Google Scholar] [CrossRef]
- Babaei, S.; Zhao, C.; Fan, L. A data-driven model of virtual power plants in day-ahead unit commitment. IEEE Trans. Power Syst. 2019, 34, 5125–5135. [Google Scholar] [CrossRef]
- Lucchi, E. Renewable Energies and Architectural Heritage: Advanced Solutions and Future Perspectives. Buildings 2023, 13, 631. [Google Scholar] [CrossRef]
- Corinaldesi, C.; Schwabeneder, D.; Lettner, G.; Auer, H. A rolling horizon approach for real-time trading and portfolio optimization of end-user flexibilities. Sustain. Energy Grids Netw. 2020, 24, 100392. [Google Scholar] [CrossRef]
- Kardakos, E.G.; Simoglou, C.K.; Bakirtzis, A.G. Optimal offering strategy of a virtual power plant: A stochastic bi-level approach. IEEE Trans. Smart Grid 2015, 7, 794–806. [Google Scholar] [CrossRef]
- Gougheri, S.S.; Jahangir, H.; Golkar, M.A.; Ahmadian, A.; Golkar, M.A. Optimal participation of a virtual power plant in electricity market considering renewable energy: A deep learning-based approach. Sustain. Energy Grids Netw. 2021, 26, 100448. [Google Scholar] [CrossRef]
- Baringo, A.; Baringo, L.; Arroyo, J.M. Holistic planning of a virtual power plant with a nonconvex operational model: A risk-constrained stochastic approach. Int. J. Electr. Power Energy Syst. 2021, 132, 107081. [Google Scholar] [CrossRef]
- Liu, B.; Lund, J.R.; Liao, S.; Jin, X.; Liu, L.; Cheng, C. Optimal power peak shaving using hydropower to complement wind and solar power uncertainty. Energy Convers. Manag. 2020, 209, 112628. [Google Scholar] [CrossRef]
- Naval, N.; Sánchez, R.; Yusta, J.M. A virtual power plant optimal dispatch model with large and small-scale distributed renewable generation. Renew. Energy 2020, 151, 57–69. [Google Scholar] [CrossRef]
- Taheri, S.I.; Salles, M.B.; Costa, E.C. Optimal cost management of distributed generation units and microgrids for virtual power plant scheduling. IEEE Access 2020, 8, 208449–208461. [Google Scholar] [CrossRef]
- Tahmasebi, M.; Pasupuleti, J.; Mohamadian, F.; Shakeri, M.; Guerrero, J.M.; Basir Khan, M.R.; Nazir, M.S.; Safari, A.; Bazmohammadi, N. Optimal Operation of Stand-Alone Microgrid Considering Emission Issues and Demand Response Program Using Whale Optimization Algorithm. Sustainability 2021, 13, 7710. [Google Scholar] [CrossRef]
- Kang, W.; Chen, M.; Lai, W.; Luo, Y. Distributed real-time power management for virtual energy storage systems using dynamic price. Energy 2021, 216, 119069. [Google Scholar] [CrossRef]
- Sadeghian, O.; Oshnoei, A.; Khezri, R.; Muyeen, S. Risk-constrained stochastic optimal allocation of energy storage system in virtual power plants. J. Energy Storage 2020, 31, 101732. [Google Scholar] [CrossRef]
- Corinaldesi, C.; Fleischhacker, A.; Lang, L.; Radl, J.; Schwabeneder, D.; Lettner, G. European case studies for impact of market-driven flexibility management in distribution systems. In Proceedings of the 2019 IEEE International Conference on Communications, Control, and Computing Technologies for Smart Grids (SmartGridComm), Beijing, China, 21–23 October 2019; pp. 1–6. [Google Scholar]
- Ryu, J.; Kim, J. Virtual Power Plant Operation Strategy Under Uncertainty with Demand Response Resources in Electricity Markets. IEEE Access 2022, 10, 62763–62771. [Google Scholar] [CrossRef]
- Sheidaei, F.; Ahmarinejad, A. Multi-stage stochastic framework for energy management of virtual power plants considering electric vehicles and demand response programs. Int. J. Electr. Power Energy Syst. 2020, 120, 106047. [Google Scholar] [CrossRef]
- Sakr, W.S.; Abd el-Ghany, H.A.; EL-Sehiemy, R.A.; Azmy, A.M. Techno-economic assessment of consumers’ participation in the demand response program for optimal day-ahead scheduling of virtual power plants. Alex. Eng. J. 2020, 59, 399–415. [Google Scholar] [CrossRef]
- Wang, Y.; Gao, W.; Qian, F.; Li, Y. Evaluation of economic benefits of virtual power plant between demand and plant sides based on cooperative game theory. Energy Convers. Manag. 2021, 238, 114180. [Google Scholar] [CrossRef]
- Azimi, Z.; Hooshmand, R.-A.; Soleymani, S. Optimal integration of demand response programs and electric vehicles in coordinated energy management of industrial virtual power plants. J. Energy Storage 2021, 41, 102951. [Google Scholar] [CrossRef]
- Yan, Q.; Zhang, M.; Lin, H.; Li, W. Two-stage adjustable robust optimal dispatching model for multi-energy virtual power plant considering multiple uncertainties and carbon trading. J. Clean. Prod. 2022, 336, 130400. [Google Scholar] [CrossRef]
- Kong, X.; Xiao, J.; Liu, D.; Wu, J.; Wang, C.; Shen, Y. Robust stochastic optimal dispatching method of multi-energy virtual power plant considering multiple uncertainties. Appl. Energy 2020, 279, 115707. [Google Scholar] [CrossRef]
- Rahimi, M.; Ardakani, F.J.; Ardakani, A.J. Optimal stochastic scheduling of electrical and thermal renewable and non-renewable resources in virtual power plant. Int. J. Electr. Power Energy Syst. 2021, 127, 106658. [Google Scholar] [CrossRef]
- Ju, L.; Zhao, R.; Tan, Q.; Lu, Y.; Tan, Q.; Wang, W. A multi-objective robust scheduling model and solution algorithm for a novel virtual power plant connected with power-to-gas and gas storage tank considering uncertainty and demand response. Appl. Energy 2019, 250, 1336–1355. [Google Scholar] [CrossRef]
- Ju, L.; Yin, Z.; Zhou, Q.; Li, Q.; Wang, P.; Tian, W.; Li, P.; Tan, Z. Nearly-zero carbon optimal operation model and benefit allocation strategy for a novel virtual power plant using carbon capture, power-to-gas, and waste incineration power in rural areas. Appl. Energy 2022, 310, 118618. [Google Scholar] [CrossRef]
- Alahyari, A.; Ehsan, M.; Mousavizadeh, M. A hybrid storage-wind virtual power plant (VPP) participation in the electricity markets: A self-scheduling optimization considering price, renewable generation, and electric vehicles uncertainties. J. Energy Storage 2019, 25, 100812. [Google Scholar] [CrossRef]
- Shafiekhani, M.; Ahmadi, A.; Homaee, O.; Shafie-khah, M.; Catalao, J.P. Optimal bidding strategy of a renewable-based virtual power plant including wind and solar units and dispatchable loads. Energy 2022, 239, 122379. [Google Scholar] [CrossRef]
- Yuan, H.; Feng, K.; Li, W.; Sun, X. Multi-objective optimization of virtual energy hub plant integrated with data center and plug-in electric vehicles under a mixed robust-stochastic model. J. Clean. Prod. 2022, 363, 132365. [Google Scholar] [CrossRef]
- Pandey, A.K.; Jadoun, V.K. Real-time and day-ahead risk averse multi-objective operational scheduling of virtual power plant using modified Harris Hawk’s optimization. Electr. Power Syst. Res. 2023, 220, 109285. [Google Scholar] [CrossRef]
- Ullah, Z.; Hassanin, H. Modeling, optimization, and analysis of a virtual power plant demand response mechanism for the internal electricity market considering the uncertainty of renewable energy sources. Energies 2022, 15, 5296. [Google Scholar] [CrossRef]
- Soroudi, A. Power System Optimization Modeling in GAMS; Springer: Berlin/Heidelberg, Germany, 2017; Volume 78. [Google Scholar]
- Bornapour, M.; Hooshmand, R.-A.; Khodabakhshian, A.; Parastegari, M. Optimal coordinated scheduling of combined heat and power fuel cell, wind, and photovoltaic units in micro grids considering uncertainties. Energy 2016, 117, 176–189. [Google Scholar] [CrossRef]
- Mainali, B.; Dhital, R. Isolated and mini-grid solar PV systems: An alternative solution for providing electricity access in remote areas (case study from Nepal). In Solar Energy Storage; Elsevier: Amsterdam, The Netherlands, 2015; pp. 359–374. [Google Scholar]
- Sadati, S.M.B.; Moshtagh, J.; Shafie-khah, M.; Rastgou, A.; Catalão, J.P. Operational scheduling of a smart distribution system considering electric vehicles parking lot: A bi-level approach. Int. J. Electr. Power Energy Syst. 2019, 105, 159–178. [Google Scholar] [CrossRef]
- Su, C.-L.; Lu, C.-N. Two-point estimate method for quantifying transfer capability uncertainty. IEEE Trans. Power Syst. 2005, 20, 573–579. [Google Scholar] [CrossRef]
- Morales, J.M.; Perez-Ruiz, J. Point estimate schemes to solve the probabilistic power flow. IEEE Trans. Power Syst. 2007, 22, 1594–1601. [Google Scholar] [CrossRef]
- Shokouhmand, E.; Ghasemi, A. Stochastic optimal scheduling of electric vehicles charge/discharge modes of operation with the aim of microgrid flexibility and efficiency enhancement. Sustain. Energy Grids Netw. 2022, 32, 100929. [Google Scholar] [CrossRef]
- Ghahramani, M.; Nazari-Heris, M.; Zare, K.; Mohammadi-Ivatloo, B. Energy and reserve management of a smart distribution system by incorporating responsive-loads/battery/wind turbines considering uncertain parameters. Energy 2019, 183, 205–219. [Google Scholar] [CrossRef]
- Jafari, A.; Khalili, T.; Ganjehlou, H.G.; Bidram, A. Optimal integration of renewable energy sources, diesel generators, and demand response program from pollution, financial, and reliability viewpoints: A multi-objective approach. J. Clean. Prod. 2020, 247, 119100. [Google Scholar] [CrossRef]
- Das, S.; Basu, M. Day-ahead optimal bidding strategy of microgrid with demand response program considering uncertainties and outages of renewable energy resources. Energy 2020, 190, 116441. [Google Scholar] [CrossRef]
- Farham, H.; Mohammadian, L.; Alipour, H.; Pouladi, J. Robust performance of photovoltaic/wind/grid based large electricity consumer. Sol. Energy 2018, 174, 923–932. [Google Scholar] [CrossRef]
- Askarzadeh, A. Distribution generation by photovoltaic and diesel generator systems: Energy management and size optimization by a new approach for a stand-alone application. Energy 2017, 122, 542–551. [Google Scholar] [CrossRef]
- Cui, H.; Xia, W.; Yang, S.; Wang, X. Real-time emergency demand response strategy for optimal load dispatch of heat and power micro-grids. Int. J. Electr. Power Energy Syst. 2020, 121, 106127. [Google Scholar] [CrossRef]





| DGs | Start-Up Cost ($) | Minimum-Up/Down Time (h) | Maximum Ramp-Up/Down Rate (MW/h) | ||
|---|---|---|---|---|---|
| DG1 | 15 | 2 | 1.8 | 3.5 | 1 |
| DG2 | 25 | 1 | 1.5 | 3 | 0.75 |
| DG3 | 28 | 1 | 1.5 | 3 | 0.75 |
| DG4 | 26 | 2 | 1.5 | 4.1 | 1 |
| DGs | |||
|---|---|---|---|
| DG 1 | 0.0025 | 87 | 27 |
| DG 2 | 0.0035 | 87 | 25 |
| DG 3 | 0.0035 | 92 | 28 |
| DG 4 | 0.184 | 81 | 26 |
| Wind Turbine [45] | PV [36] | ||||
|---|---|---|---|---|---|
| Parameters | Amount | Unit | Parameters | Amount | Unit |
| 2.05 | MW | 1.1 | MW | ||
| 2 | m/s | 1000 | W/m2 | ||
| 14 | m/s | 150 | W/m2 | ||
| 25 | m/s | ||||
| Parameters | Amount | Unit |
|---|---|---|
| 0.2 | MW | |
| 2 | MW | |
| 0.5 | MW | |
| 0.5 | MW | |
| 0.2 | MW | |
| 90 | % | |
| 80 | % | |
| 0.001 | $/h | |
| 15 | $/MWh |
| Emission Factor | DG [46] | Main-Grid [47] |
|---|---|---|
| 73.98 | 921.25 | |
| 1.02 | 3.583 | |
| 0.09 | 2.295 |
| CS | Cost | Variation * (%) | Emission | Variation * (%) |
|---|---|---|---|---|
| CS#1 | 238,077.95 $ | - | 74,580.2 kg | - |
| CS#2 | 236,937.56 $ | 0.47 | 67,359.99 kg | 9.68 |
| CS#3 | 237,801.2 $ | 0.11 | 61,717.98 kg | 17.24 |
| CS#4 | 235,473.46 $ | 1.10 | 52,354.95 kg | 29.80 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Darvishi, M.; Tahmasebi, M.; Shokouhmand, E.; Pasupuleti, J.; Bokoro, P.; Raafat, J.S. Optimal Operation of Sustainable Virtual Power Plant Considering the Amount of Emission in the Presence of Renewable Energy Sources and Demand Response. Sustainability 2023, 15, 11012. https://doi.org/10.3390/su151411012
Darvishi M, Tahmasebi M, Shokouhmand E, Pasupuleti J, Bokoro P, Raafat JS. Optimal Operation of Sustainable Virtual Power Plant Considering the Amount of Emission in the Presence of Renewable Energy Sources and Demand Response. Sustainability. 2023; 15(14):11012. https://doi.org/10.3390/su151411012
Chicago/Turabian StyleDarvishi, Mostafa, Mehrdad Tahmasebi, Ehsan Shokouhmand, Jagadeesh Pasupuleti, Pitshou Bokoro, and Jwan Satei Raafat. 2023. "Optimal Operation of Sustainable Virtual Power Plant Considering the Amount of Emission in the Presence of Renewable Energy Sources and Demand Response" Sustainability 15, no. 14: 11012. https://doi.org/10.3390/su151411012
APA StyleDarvishi, M., Tahmasebi, M., Shokouhmand, E., Pasupuleti, J., Bokoro, P., & Raafat, J. S. (2023). Optimal Operation of Sustainable Virtual Power Plant Considering the Amount of Emission in the Presence of Renewable Energy Sources and Demand Response. Sustainability, 15(14), 11012. https://doi.org/10.3390/su151411012






