A Robust Stochastic Programming Model for the Well Location Problem: The Case of The Brazilian Northeast Region
Abstract
1. Introduction
2. Literature Review
2.1. Facility Location Problem
2.2. Robust Optimization
2.3. Research Gaps and Innovations
3. Model Formulation
3.1. Problem Statement
3.2. Deterministic Model
3.3. Robust Model
3.4. Solution Approach
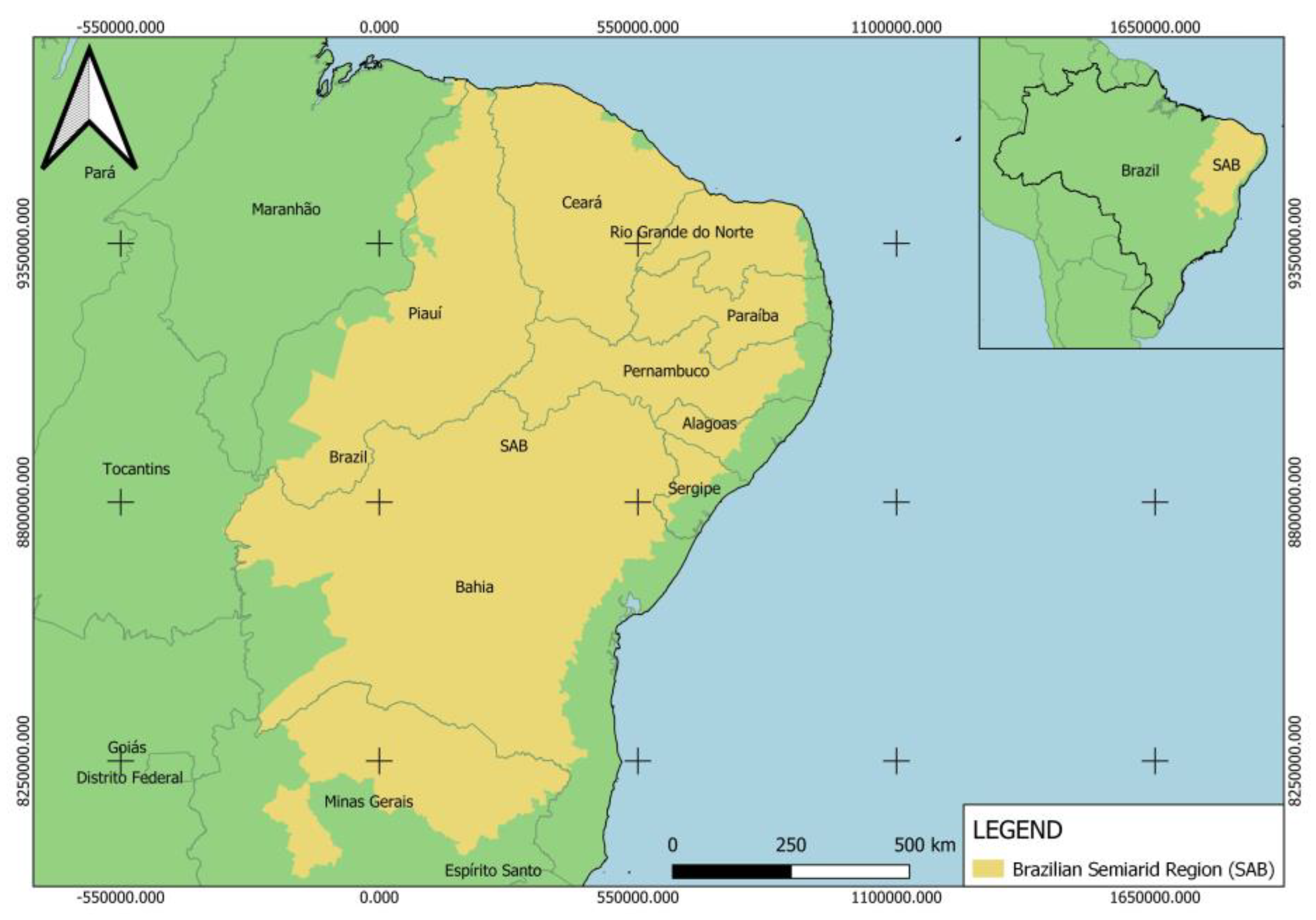
4. Case Study: The Brazilian Northeast Region
4.1. Data Collection
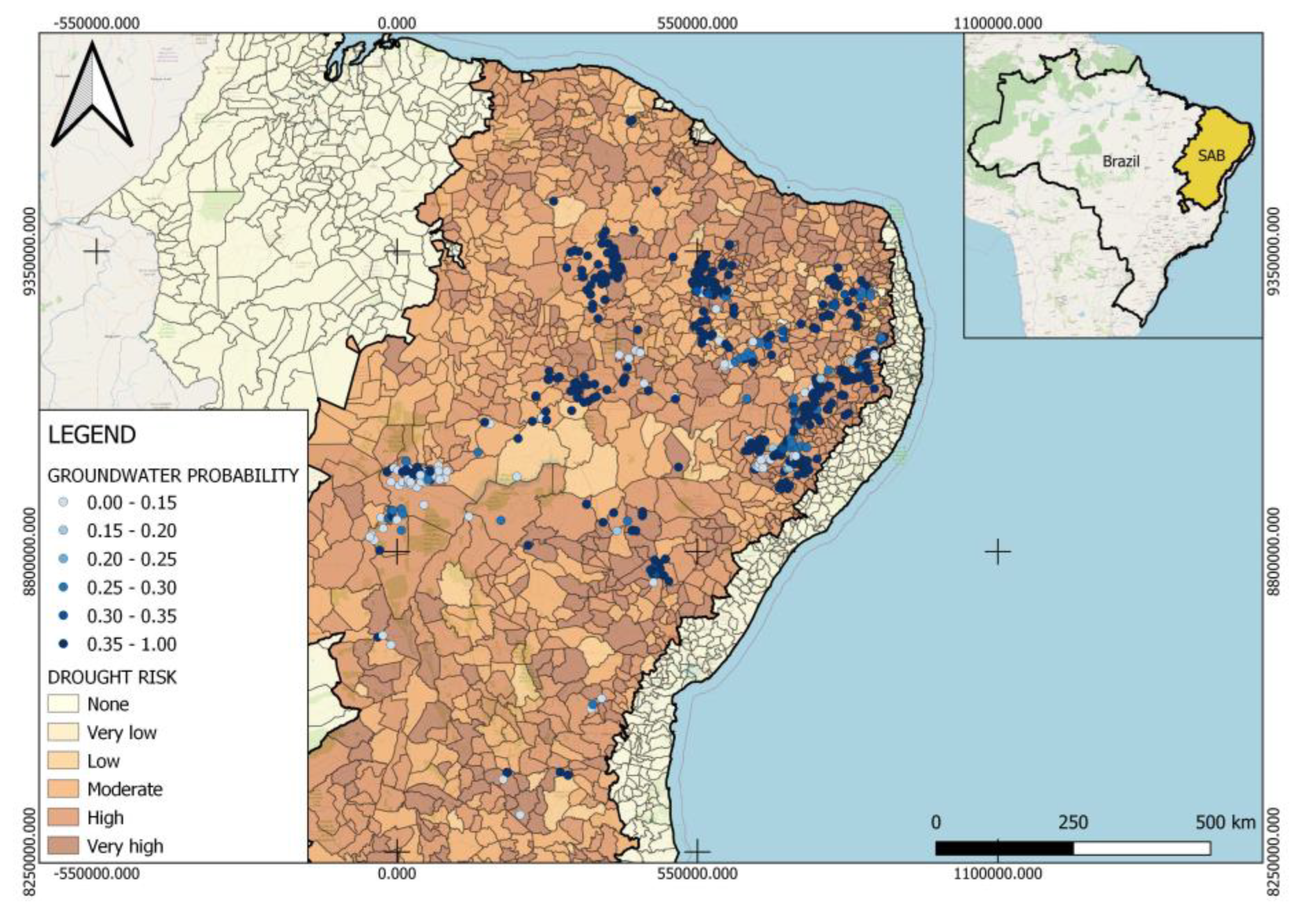
4.2. Results
- Experiment 1 (equiprobable scenarios):
- Experiment 2 (Scenario 1 most likely):
- Experiment 3 (Scenario 2 most likely):
- Experiment 4 (Scenario 3 most likely):
4.3. Discussion and Managerial Insights
5. Conclusions and Recommendations
- A Multi-Criteria Decision Making (MCDM) method, such as AHP (Analytic Hierarchy Process), could be applied to set weights for the multiple objectives. Then, instead of considering transportation and setup costs as constraints, one could use them to compose the objective function;
- To deepen the present study, it would be relevant to consider other uncertain parameters in the robust model, such as precipitation indices and well’s flow rate;
- It would be interesting to improve the estimate of the probabilities concerning real scenarios once the robust approach highly depends on it.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Ortega-Gaucin, D.; Pérez, M.L.; Cortés, F.A. Drought risk management in Mexico: Progress and challenges. Int. J. Saf. Secur. Eng. 2016, 6, 161–170. [Google Scholar] [CrossRef]
- Cunha, A.P.M.; do, A.; Marchezini, V.; Lindoso, D.P.; Saito, S.M.; Alvalá, R.C.; dos, S. The challenges of Consolidation of a Drought-Related Disaster Risk Warning System to Brazil. Sustain. Debate 2019, 10, 43–76. [Google Scholar] [CrossRef]
- Van Wassenhove, L. Blackett memorial lecturet humanitarian aid logistics: Supply chain. J. Oper. Res. Soc. 2006, 57, 475–489. [Google Scholar] [CrossRef]
- Pelling, M.; Özerdem, A.; Barakat, S. The macro-economic impact of disasters. Prog. Dev. Stud. 2002, 2, 283–305. [Google Scholar] [CrossRef]
- Hao, Z.; Hao, F.; Singh, V.P.; Ouyang, W.; Cheng, H. An integrated package for drought monitoring, prediction and analysis to aid drought modeling and assessment. Environ. Model. Softw. 2017, 91, 199–209. [Google Scholar] [CrossRef]
- CEPED UFSC (Centro Universitário de Estudos e Pesquisas sobre Desastres—Universidade Federal de Santa Catarina). Atlas Brasileiro de Desastres Naturais 1991 a 2010. Volume Brasil, Volume Pará, Volume Amapá, Florianópolis, 2012. Available online: https://www.ceped.ufsc.br/wp-content/uploads/2012/01/AMAZONAS_mioloWEB.pdf (accessed on 8 September 2022).
- Sena, A.; Barcellos, C.; Freitas, C.; Corvalan, C. Managing the health impacts of drought in Brazil. Int. J. Environ. Res. Public Health 2014, 11, 10737–10751. [Google Scholar] [CrossRef]
- Água Para Todos. Available online: https://antigo.mdr.gov.br/dadosabertos/317-secretaria-nacional-de-programas-urbanos/agua-para-todos/6076-agua-para-todos (accessed on 8 September 2022).
- Brito, S.S.B.; Cunha, A.P.M.; Cunningham, C.C.; Alvalá, R.C.; Marengo, J.A.; Carvalho, M.A. Frequency, duration and severity of drought in the Semiarid Northeast Brazil region. Int. J. Climatol. 2018, 38, 517–529. [Google Scholar] [CrossRef]
- Gutiérrez, A.P.A.; Engle, N.L.; De Nys, E.; Molejón, C.; Martins, E.S. Drought preparedness in Brazil. Weather and Clim. Extrem. 2014, 3, 95–106. [Google Scholar] [CrossRef]
- Nam, W.H.; Hayes, M.J.; Svoboda, M.D.; Tadesse, T.; Wilhite, D.A. Drought hazard assessment in the context of climate change for South Korea. Agric. Water Manag. 2015, 160, 106–117. [Google Scholar] [CrossRef]
- Akgün, İ.; Gümüşbuğa, F.; Tansel, B. Risk based facility location by using fault tree analysis in disaster management. Omega 2015, 52, 168–179. [Google Scholar] [CrossRef]
- Coppola, D.P. Introduction to International Disaster Management; Elsevier: Amsterdam, The Netherlands, 2007. [Google Scholar]
- Boonmee, C.; Arimura, M.; Asada, T. Facility location optimization model for emergency humanitarian logistics. Int. J. Disaster Risk Reduct. 2017, 24, 485–498. [Google Scholar] [CrossRef]
- Owen, S.H.; Daskin, M.S. Strategic facility location: A review. Eur. J. Oper. Res. 1998, 111, 423–447. [Google Scholar] [CrossRef]
- Machado, T.T.V.; Dias, J.T.; Silva, T.C.D. Evolução e avaliação das políticas públicas para a atenuação dos efeitos da seca no semiárido brasileiro. Gaia Sci. 2017, 11, 84–103. [Google Scholar] [CrossRef]
- Nag, S.K.; Kundu, A. Delineation of groundwater potential zones in hard rock terrain in Kashipur block, Purulia district, West Bengal, using geospatial techniques. Int. J. Waste Resour. 2016, 6, 1000201. [Google Scholar] [CrossRef]
- Limaye, S.D. Groundwater Development in Hard Rocks. Groundwater 2002, 2. Available online: http://www.eolss.net/Sample-Chapters/C07/E2-09-05-05.pdf (accessed on 8 September 2022).
- Singh, K.K.K.; Bharti, A.K.; Pal, S.K.; Prakash, A.; Kumar, R.; Singh, P.K. Delineation of fracture zone for groundwater using combined inversion technique. Environ. Earth Sci. 2019, 78, 1–12. [Google Scholar] [CrossRef]
- Zhang, D.D.; Yan, D.H.; Lu, F.; Wang, Y.C.; Feng, J. Copula-based risk assessment of drought in Yunnan province, China. Nat. Hazards 2015, 75, 2199–2220. [Google Scholar] [CrossRef]
- Wilhite, D.A. Drought as a natural hazard: Concepts and definitions. In Drought: A Global Assessment; Routledge: London, UK, 2000; Volume 1, pp. 3–18. [Google Scholar]
- González Tánago, I.; Urquijo, J.; Blauhut, V.; Villarroya, F.; De Stefano, L. Learning from experience: A systematic review of assessments of vulnerability to drought. Nat. Hazards 2016, 80, 951–973. [Google Scholar] [CrossRef]
- Bravo, R.Z.B. Monitoramento e alerta de secas no Brasil: Nova abordagem baseada em um índice de risco. Doctoral Thesis, Pontifícia Universidade Católica do Rio de Janeiro, Rio de Janeiro, Brazil, 2021. [Google Scholar]
- Habib, M.S.; Lee, Y.H.; Memon, M.S. Mathematical models in humanitarian supply chain management: A systematic literature review. Math. Probl. Eng. 2016, 2016, 3212095. [Google Scholar] [CrossRef]
- Zokaee, S.; Bozorgi-Amiri, A.; Sadjadi, S.J. A robust optimization model for humanitarian relief chain design under uncertainty. Appl. Math. Model. 2016, 40, 7996–8016. [Google Scholar] [CrossRef]
- Yu, C.S.; Li, H.L. A robust optimization model for stochastic logistic problems. Int. J. Prod. Econ. 2000, 64, 385–397. [Google Scholar] [CrossRef]
- Vieira, Y.E.M.; Bandeira, R.A.M.; da Silva Junior, O.S. Application of a Logit Model for Water well site location in fractured-bedrock aquifers in northeastern Brazil. Int. J. Innov. Educ. Res. 2022, 10, 33–52. [Google Scholar] [CrossRef]
- Laporte, G.; Nickel, S.; Saldanha-da-Gama, F. Introduction to location science. In Location Science; Springer: Berlin/Heidelberg, Germany, 2019; pp. 1–21. [Google Scholar]
- Hakimi, S.L. Optimum locations of switching centers and the absolute centers and medians of a graph. Oper. Res. 1964, 12, 450–459. [Google Scholar] [CrossRef]
- Hakimi, S.L. Optimum distribution of switching centers in a communication network and some related graph theoretic problems. Oper. Res. 1965, 13, 462–475. [Google Scholar] [CrossRef]
- Toregas, C.; Swain, R.; ReVelle, C.; Bergman, L. The location of emergency service facilities. Oper. Res. 1971, 19, 1363–1373. [Google Scholar] [CrossRef]
- Church, R.; ReVelle, C. The maximal covering location problem. Pap. Reg. Sci. Assoc. 1974, 32, 101–118. [Google Scholar] [CrossRef]
- Cornuejols, G.; Fisher, M.; Nemhauser, G.L. On the uncapacitated location problem. Ann. Discret. Math. 1977, 1, 163–177. [Google Scholar]
- Current, J.R.; Storbeck, J.E. Capacitated covering models. Environ. Plan. B Plan. Des. 1988, 15, 153–163. [Google Scholar] [CrossRef]
- Sankaran, J.K.; Raghavan, N.S. Locating and sizing plants for bottling propane in south India. Interfaces 1997, 27, 1–15. [Google Scholar] [CrossRef]
- Alp, O.; Erkut, E.; Drezner, Z. An efficient genetic algorithm for the p-median problem. Ann. Oper. Res. 2003, 122, 21–42. [Google Scholar] [CrossRef]
- Mladenović, N.; Labbé, M.; Hansen, P. Solving the p-center problem with tabu search and variable neighborhood search. Netw. Int. J. 2003, 42, 48–64. [Google Scholar] [CrossRef]
- Daskin, M.S. SITATION Facility Location Software; Department of Industrial Engineering and Management Sciences, Northwestern University: Evanston, IL, USA, 2002. [Google Scholar]
- Muñoz-Márquez, M. Orloca: Operations Research LOCational Analysis Models; Departamento de Matematicas, Departamento de Estadistica e Investigacion Operativa, Universidad de Cadiz: Cadiz, Spain, 2008. [Google Scholar]
- Kalcsics, J.; Butsch, A.; Jürgens, R. Library of Location Algorithms (LoLA); Institute of Operations Research, Karlsruhe Institute of Technology: Karlsruhe, Germany, 2011. [Google Scholar]
- Erdoğan, G.; Stylianou, N.; Vasilakis, C. An open source decision support system for facility location analysis. Decis. Support Syst. 2019, 125, 113116. [Google Scholar] [CrossRef]
- Lin, Y.; Jia, H.; Yang, Y.; Tian, G.; Tao, F.; Ling, L. An improved artificial bee colony for facility location allocation problem of end-of-life vehicles recovery network. J. Clean. Prod. 2018, 205, 134–144. [Google Scholar] [CrossRef]
- Aras, N.; Bilge, Ü. Robust supply chain network design with multi-products for a company in the food sector. Appl. Math. Model. 2018, 60, 526–539. [Google Scholar] [CrossRef]
- Jabbarzadeh, A.; Haughton, M.; Khosrojerdi, A. Closed-loop supply chain network design under disruption risks: A robust approach with real world application. Comput. Ind. Eng. 2018, 116, 178–191. [Google Scholar] [CrossRef]
- Ghahremani-Nahr, J.; Kian, R.; Sabet, E. A robust fuzzy mathematical programming model for the closed-loop supply chain network design and a whale optimization solution algorithm. Expert Syst. Appl. 2019, 116, 454–471. [Google Scholar] [CrossRef]
- Saedinia, R.; Vahdani, B.; Etebari, F.; Nadjafi, B.A. Robust gasoline closed loop supply chain design with redistricting, service sharing and intra-district service transfer. Transp. Res. Part E Logist. Transp. Rev. 2019, 123, 121–141. [Google Scholar] [CrossRef]
- Yu, H.; Sun, X.; Solvang, W.D.; Laporte, G.; Lee, C.K.M. A stochastic network design problem for hazardous waste management. J. Clean. Prod. 2020, 277, 123566. [Google Scholar] [CrossRef]
- Mohammed, A.; Wang, Q. Multi-criteria optimization for a cost-effective design of an RFID-based meat supply chain. Br. Food J. 2017, 119, 676–689. [Google Scholar] [CrossRef]
- Mohammed, A.; Wang, Q.; Li, X. A cost-effective decision-making algorithm for an RFID-enabled HMSC network design: A multi-objective approach. Ind. Manag. Data Syst. 2017, 117, 1782–1799. [Google Scholar] [CrossRef]
- Mogale, D.G.; Kumar, M.; Kumar, S.K.; Tiwari, M.K. Grain silo location-allocation problem with dwell time for optimization of food grain supply chain network. Transp. Res. Part E Logist. Transp. Rev. 2018, 111, 40–69. [Google Scholar] [CrossRef]
- Wang, L.; Shi, H.; Gan, L. Healthcare facility location-allocation optimization for China’s developing cities utilizing a multi-objective decision support approach. Sustainability 2018, 10, 4580. [Google Scholar] [CrossRef]
- Chen, Y.; Lai, Z. A Multi-Objective Optimization Approach for Emergency Medical Service Facilities Location-Allocation in Rural Areas. Risk Manag. Healthc. Policy 2022, 15, 473. [Google Scholar] [CrossRef] [PubMed]
- Ni, W.; Shu, J.; Song, M. Location and emergency inventory pre-positioning for disaster response operations: Min-max robust model and a case study of Yushu earthquake. Prod. Oper. Manag. 2018, 27, 160–183. [Google Scholar] [CrossRef]
- Paul, J.A.; Wang, X.J. Robust location-allocation network design for earthquake preparedness. Transp. Res. Part B: Methodol. 2019, 119, 139–155. [Google Scholar] [CrossRef]
- Yahyaei, M.; Bozorgi-Amiri, A. Robust reliable humanitarian relief network design: An integration of shelter and supply facility location. Ann. Oper. Res. 2019, 283, 897–916. [Google Scholar] [CrossRef]
- Maharjan, R.; Hanaoka, S. A credibility-based multi-objective temporary logistics hub location-allocation model for relief supply and distribution under uncertainty. Socio-Econ. Plan. Sci. 2020, 70, 100727. [Google Scholar] [CrossRef]
- Mohammadi, S.; Darestani, S.A.; Vahdani, B.; Alinezhad, A. A robust neutrosophic fuzzy-based approach to integrate reliable facility location and routing decisions for disaster relief under fairness and aftershocks concerns. Comput. Ind. Eng. 2020, 148, 106734. [Google Scholar] [CrossRef]
- Ribas, G.P. Modelo de programação estocástica para o planejamento estratégico da cadeia integrada de petróleo. Master’s Thesis, Pontifícia Universidade Católica do Rio de Janeiro, Rio de Janeiro, Brazil, 2008. [Google Scholar]
- Mulvey, J.M.; Vanderbei, R.J.; Zenios, S.A. Robust optimization of large-scale systems. Oper. Res. 1995, 43, 264–281. [Google Scholar] [CrossRef]
- Bozorgi-Amiri, A.; Jabalameli, M.S.; Mirzapour Al-e-Hashem, S.M.J. A multi-objective robust stochastic programming model for disaster relief logistics under uncertainty. OR Spectr. 2013, 35, 905–933. [Google Scholar] [CrossRef]
- Jabbarzadeh, A.; Fahimnia, B.; Seuring, S. Dynamic supply chain network design for the supply of blood in disasters: A robust model with real world application. Transp. Res. Part E Logist. Transp. Rev. 2014, 70, 225–244. [Google Scholar] [CrossRef]
- Cunha, M.D.C.; Antunes, A.P. On the efficient location of pumping facilities in an aquifer system. Int. Trans. Oper. Res. 1997, 4, 175–184. [Google Scholar] [CrossRef]
- Ferreira, J.; Cunha, M.C.; Vieira, J.; Monteiro, J.P. Optimized exploitation of aquifers: Application to the Querença-Silves aquifer system. Water Resour. Manag. 2009, 125, 3. [Google Scholar]
- Ng, T.L. Expanding Neighborhood Tabu Search for facility location problems in water infrastructure planning. In Proceedings of the 2014 IEEE International Conference on Systems, Man, and Cybernetics (SMC), San Diego, CA, USA, 5–8 October 2014; pp. 3851–3854. [Google Scholar]
- Roman, O.; Hoque, S.F.; Ford, L.; Salehin, M.; Alam, M.M.; Hope, R.; Hall, J.W. Optimizing rural drinking water supply infrastructure to account for spatial variations in groundwater quality and household welfare in coastal Bangladesh. Water Resour. Res. 2021, 57, e2021WR029621. [Google Scholar] [CrossRef]
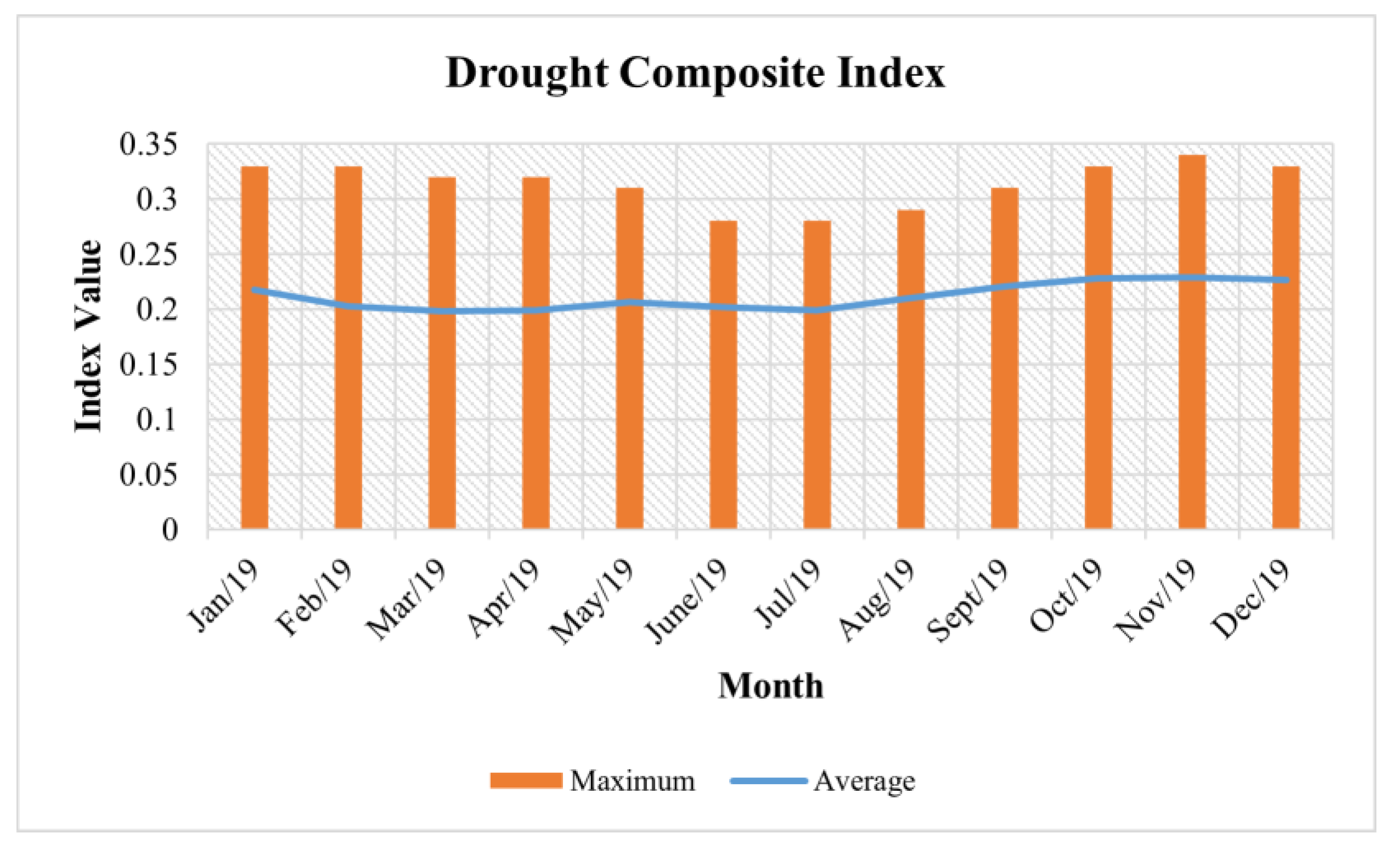
- Bravo, R.Z.B.; Cunha, A.P.M.D.A.; Leiras, A.; Cyrino Oliveira, F.L. A new approach for a drought composite index. Nat. Hazards 2021, 108, 755–773. [Google Scholar] [CrossRef]
- Alvalá, R.; Cunha, A.P.; Brito, S.S.; Seluchi, M.E.; Marengo, J.A.; Moraes, O.L.; Carvalho, M.A. Drought monitoring in the Brazilian Semiarid region. An. Da Acad. Bras. De Ciências 2017, 91. [Google Scholar] [CrossRef]
- Silva, J.M.C.D.; Barbosa, L.C.F.; Leal, I.R.; Tabarelli, M. The Caatinga: Understanding the challenges. In Caatinga: The Largest Tropical Dry Forest Region in South America; Springer: Berlin/Heidelberg, Germany, 2017; pp. 3–19. [Google Scholar]
- Marengo, J.A. Vulnerabilidade, impactos e adaptação à mudança do clima no semiárido do Brasil. Parcer. Estratégicas 2008, 27, 149–175. [Google Scholar]
- Brasil, Inteministerial Ordinance n.1. Provides for the mutual technical and financial cooperation between the Ministries of National Integration and Defense to carry out complementary actions to support the distribution of drinking water to the populations affected by drought and drought in the semi-arid region of the Northeast and the night region of the States of Minas Gerais and Espírito Santo, called Operação Carro Pipa. Diário Oficial da União, 25 July 2012.
- Portal da Operação Carro Pipa. Available online: http://sedec.5cta.eb.mil.br/ (accessed on 8 September 2022).
- Defesanet. Available online: https://www.defesanet.com.br/aciso/noticia/34215/exercito-brasileiro-finaliza-a-entrega-de-mais-de-300-pocos-artesianos-no-semiarido-nordestino/#:~:text=O%20Ex%C3%A9rcito%20Brasileiro%20encerrou%2C%20no,Regi%C3%A3o%20Nordeste%20do%20nosso%20pa%C3%ADs (accessed on 8 September 2022).
- Vieira, Y.E.M.; Bandeira, R.A.M.; da Silva Junior, O.S. Multi-depot vehicle routing problem for large scale disaster relief in drought scenarios: The case of the brazilian northeast region. Int. J. Disaster Risk Reduct. 2021, 58, 102193. [Google Scholar] [CrossRef]
- CMNE (Comando Militar Do Nordeste). Ordem de Serviço Nr 008 de 17 de agosto de 2015. Regula a Participação do Comando Militar do Nordeste no Programa Emergencial de Distribuição de Água Potável no Semiárido Brasileiro—Operação Carro-Pipa. Available online: https://6rm.eb.mil.br/images/servicos/operacao_pipa/pdf/Anexo_G-Criterios_para_Calculo_dos_Valores.pdf (accessed on 8 September 2022).
- IBGE. Available online: https://www.ibge.gov.br/estatisticas/sociais/populacao/9109-projecao-da-populacao.html?=&t=resultados (accessed on 8 September 2022).
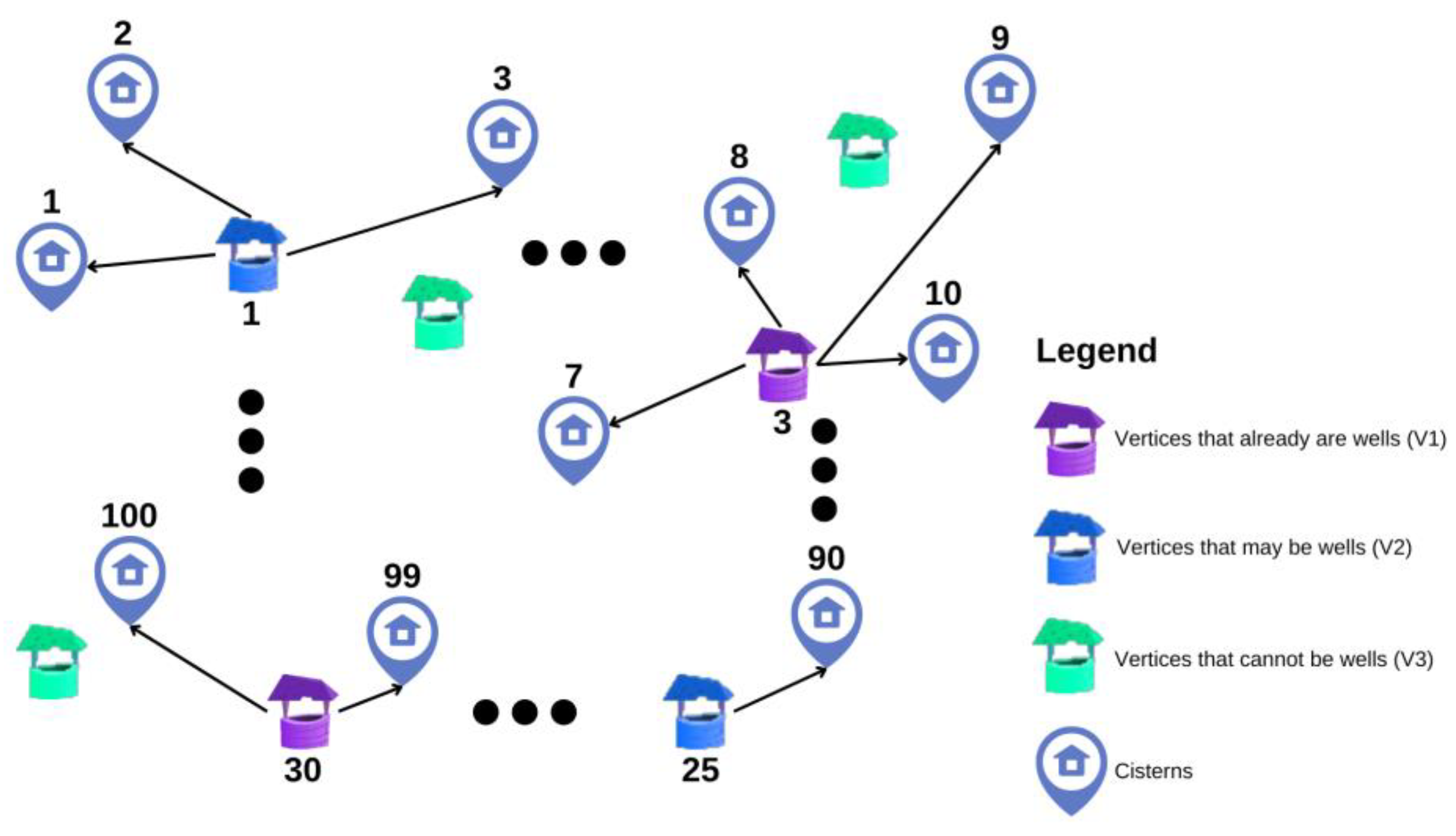

| Notation | Description |
|---|---|
| The complete digraph to represent the distribution network | |
| The set of all nodes (indexed by i and j) | |
| The subset of V with the nodes that already are wells | |
| The subset of V with the nodes that can be wells | |
| The subset of V with the nodes that cannot be wells | |
| The probability of occurrence of groundwater of node j | |
| The water demand of node i | |
| The drought composite index of node i | |
| The cost of installing a well in j | |
| The estimated capacity of a well located in j | |
| δ | The maximum service distance |
| The distance between the nodes i and j | |
| c | The average cost of transportation |
| The budget limit for well drilling | |
| The budget limit for water distribution | |
| Equals 1 if node i is served by a facility in j, and 0 otherwise | |
| Equals 1 if vertex j is going to locate a well, and 0 otherwise |
| Notation | Description |
|---|---|
| S | The set of demand scenarios (indexed by s and s’) |
| The probability of occurrence of scenario s | |
| The water demand of node i in the scenario s | |
| Λ | The weight assigned to the variance of the solution |
| Equals 1 if vertex i is served by a facility in j in scenario s, and 0 otherwise. | |
| The scenario-dependent auxiliary variable for the linearization of the model |
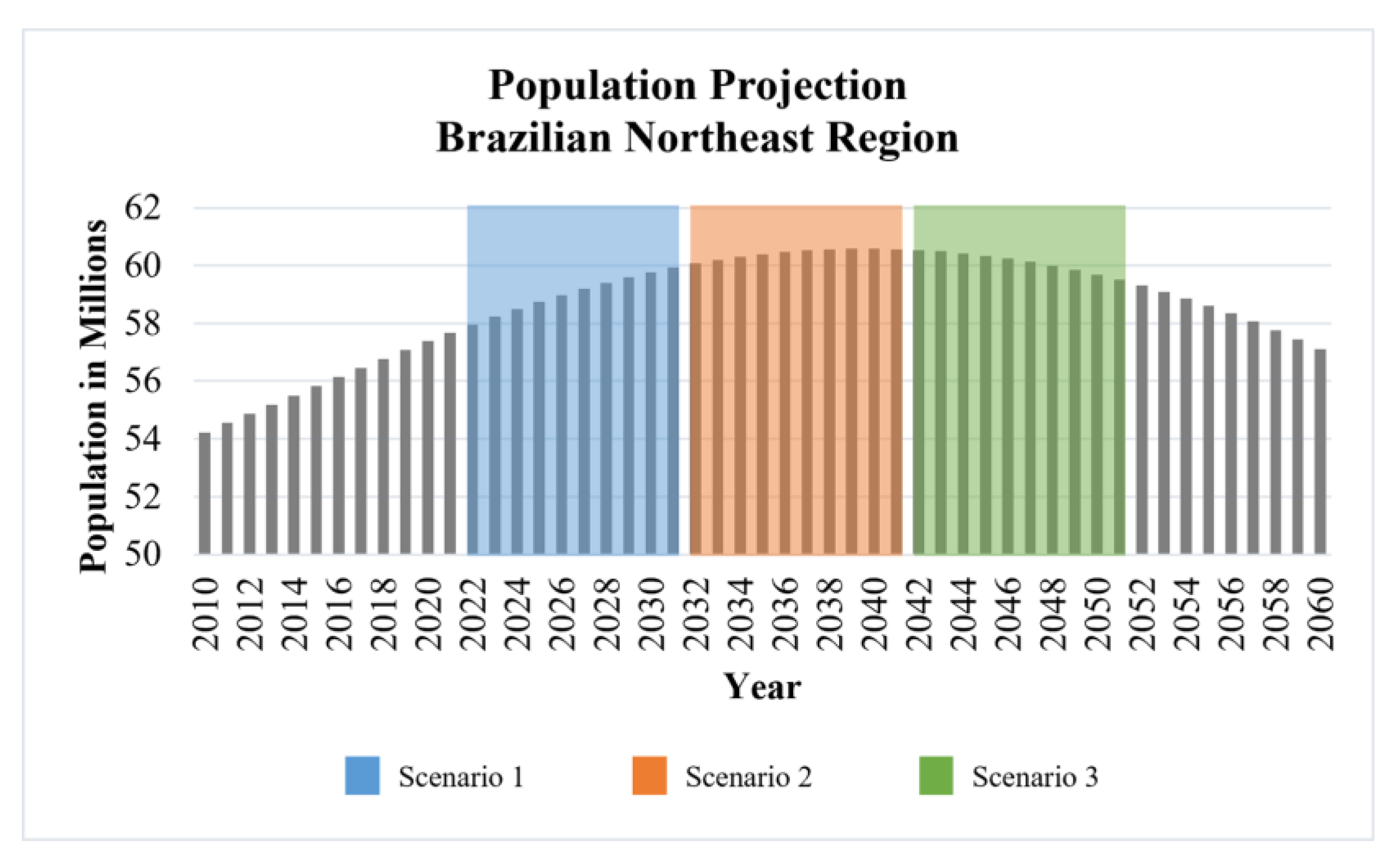
| Period | Scenario | Growth Rate |
|---|---|---|
| 2022–2031 | 1 | 3.40% |
| 2032–2041 | 2 | 0.84% |
| 2042–2051 | 3 | −1.71% |
| Demand | Objective Function Value | Number of Wells Located | Number of Points Covered | Demand Covered | Transportation Cost (US $) |
|---|---|---|---|---|---|
| Current | 270,263.64 | 184 | 739 | 1,149,830.30 | 12,906,850.50 |
| Scenario 1 | 279,333.51 | 192 | 739 | 1,188,919.86 | 12,512,629.46 |
| Scenario 2 | 272,500.21 | 168 | 739 | 1,159,475.62 | 12,904,931.08 |
| Scenario 3 | 265,687.72 | 168 | 739 | 1,130,119.55 | 12,907,292.52 |
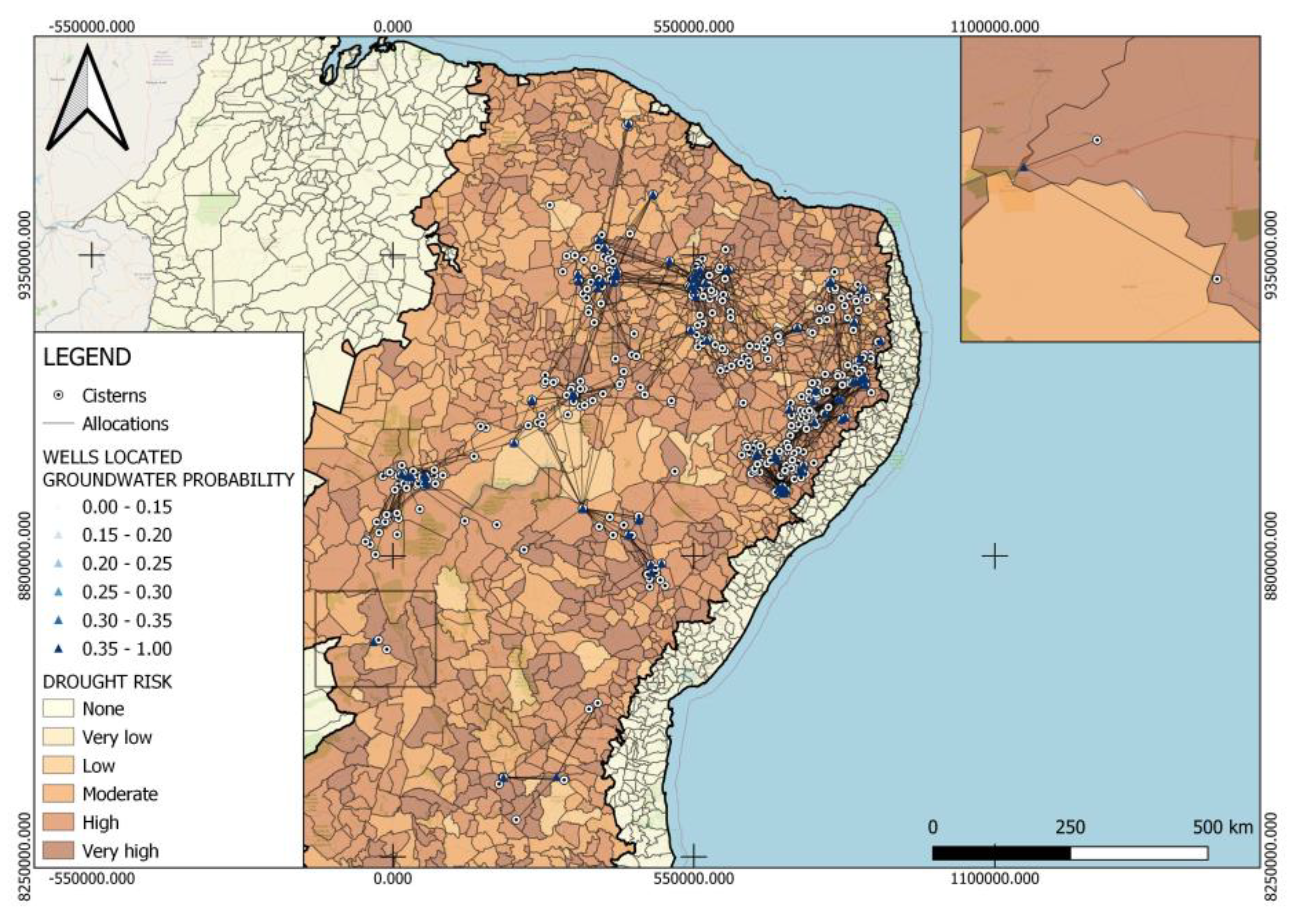
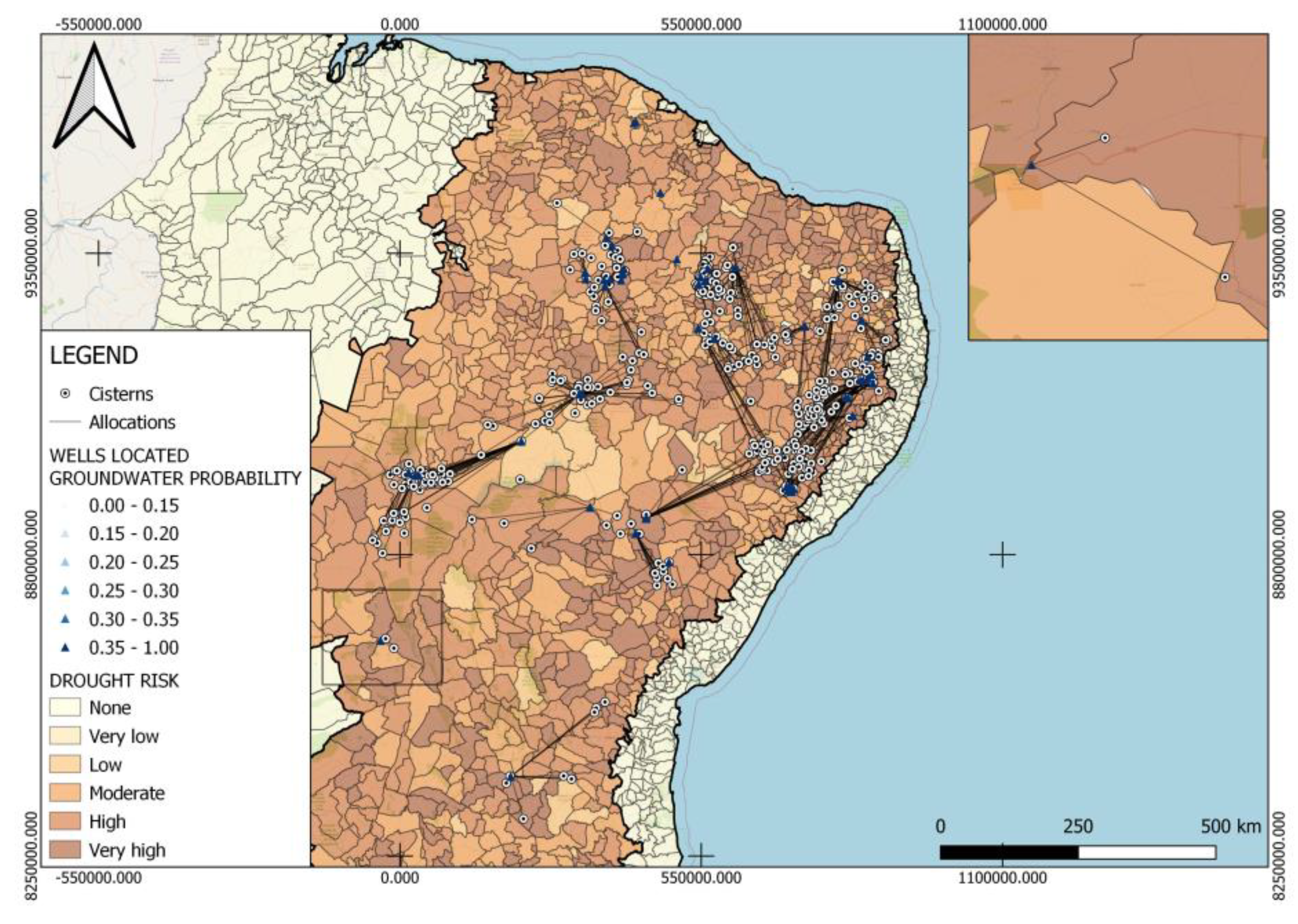
| Risk | Average Probability of Water Occurrence | |
|---|---|---|
| Optimization with Drought Risk Index | Optimization without Drought Risk Index | |
| High | 0.995565344 | 0.981914234 |
| Moderate | 0.983896345 | 0.983896345 |
| Low | 0.978024654 | 0.979950119 |
| Very low | 0.963007283 | 0.983068566 |
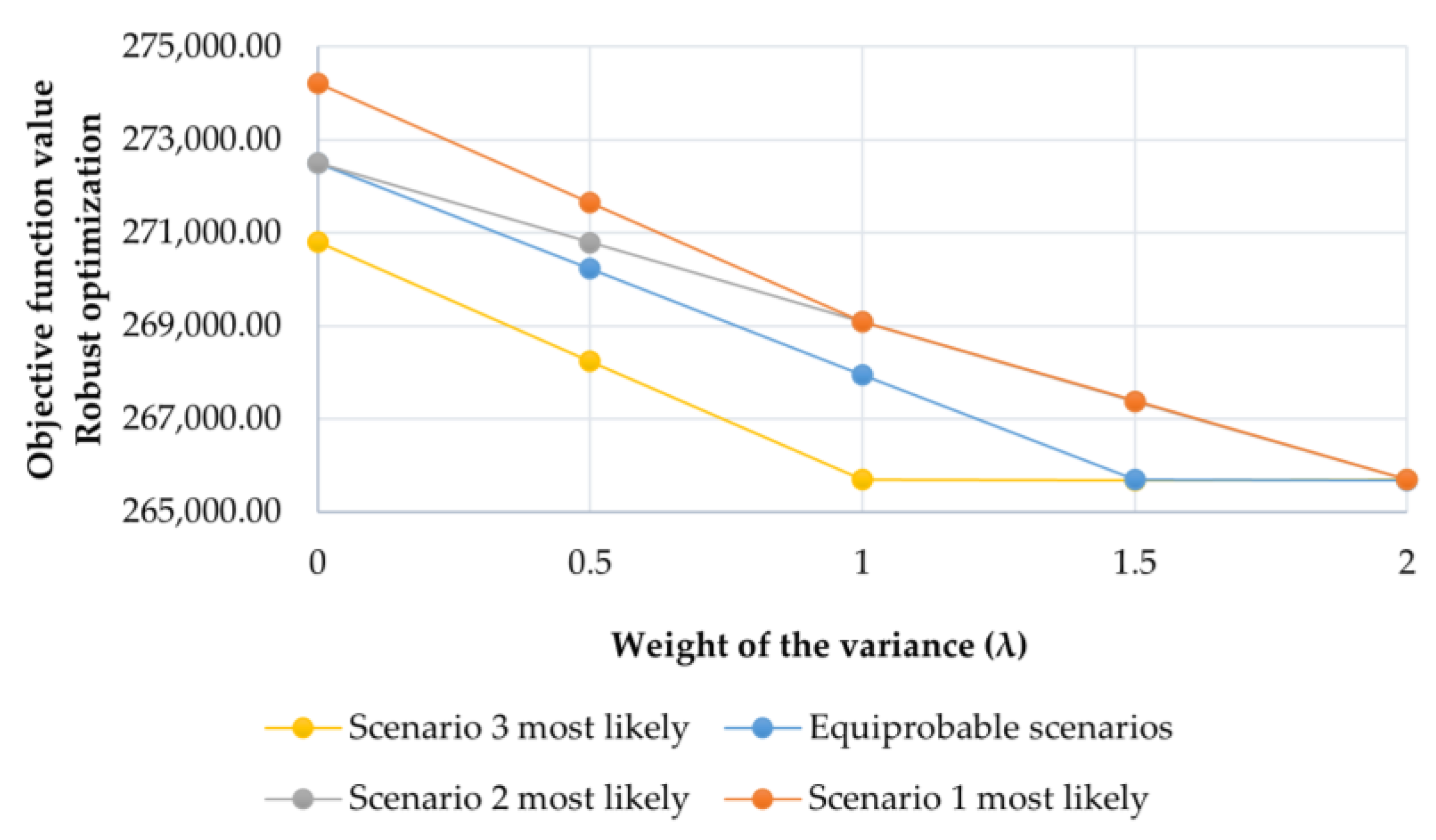
| Lambda | Objective Function | Variance | ||
|---|---|---|---|---|
| Scenario 1 | Scenario 2 | Scenario 3 | ||
| 0.0 | 279,333.19 | 272,499.91 | 0.0 | 279,333.19 |
| 0.5 | 279,329.29 | 272,495.61 | 0.5 | 279,329.29 |
| 1.0 | 279,293.16 | 272,487.36 | 1.0 | 279,293.16 |
| 1.5 | 267,229.18 | 268,764.41 | 1.5 | 267,229.18 |
| 2.0 | 265,684.02 | 265,683.99 | 2.0 | 265,684.02 |
| Lambda | Number of Points Covered | ||
|---|---|---|---|
| Scenario 1 | Scenario 2 | Scenario 3 | |
| 0 | 739 | 739 | 739 |
| 0.5 | 739 | 739 | 739 |
| 1.0 | 739 | 739 | 739 |
| 1.5 | 716 | 734 | 739 |
| 2.0 | 711 | 734 | 739 |
| Experiment | Results | Difference | |
|---|---|---|---|
| Deterministic (Worst Scenario) | Robust | ||
| Experiment 1 (Equiprobable scenarios) | 268,847.64 | 272,506.45 | −1.36% |
| Experiment 2 (Scenario 1 most likely) | 268,787.90 | 274,211.82 | −2.02% |
| Experiment 3 (Scenario 2 most likely) | 269,739.64 | 272,505.03 | −1.03% |
| Experiment 4 (Scenario 3 most likely) | 268,015.36 | 270,798.85 | −1.04% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
da Cunha Nunes, D.R.; da Silva Júnior, O.S.; de Mello Bandeira, R.A.; Vieira, Y.E.M. A Robust Stochastic Programming Model for the Well Location Problem: The Case of The Brazilian Northeast Region. Sustainability 2023, 15, 10916. https://doi.org/10.3390/su151410916
da Cunha Nunes DR, da Silva Júnior OS, de Mello Bandeira RA, Vieira YEM. A Robust Stochastic Programming Model for the Well Location Problem: The Case of The Brazilian Northeast Region. Sustainability. 2023; 15(14):10916. https://doi.org/10.3390/su151410916
Chicago/Turabian Styleda Cunha Nunes, Dayanna Rodrigues, Orivalde Soares da Silva Júnior, Renata Albergaria de Mello Bandeira, and Yesus Emmanuel Medeiros Vieira. 2023. "A Robust Stochastic Programming Model for the Well Location Problem: The Case of The Brazilian Northeast Region" Sustainability 15, no. 14: 10916. https://doi.org/10.3390/su151410916
APA Styleda Cunha Nunes, D. R., da Silva Júnior, O. S., de Mello Bandeira, R. A., & Vieira, Y. E. M. (2023). A Robust Stochastic Programming Model for the Well Location Problem: The Case of The Brazilian Northeast Region. Sustainability, 15(14), 10916. https://doi.org/10.3390/su151410916







