Numerical Simulation of Hydrogen Diffusion in Cement Sheath of Wells Used for Underground Hydrogen Storage
Abstract
1. Introduction
2. Mathematical Model
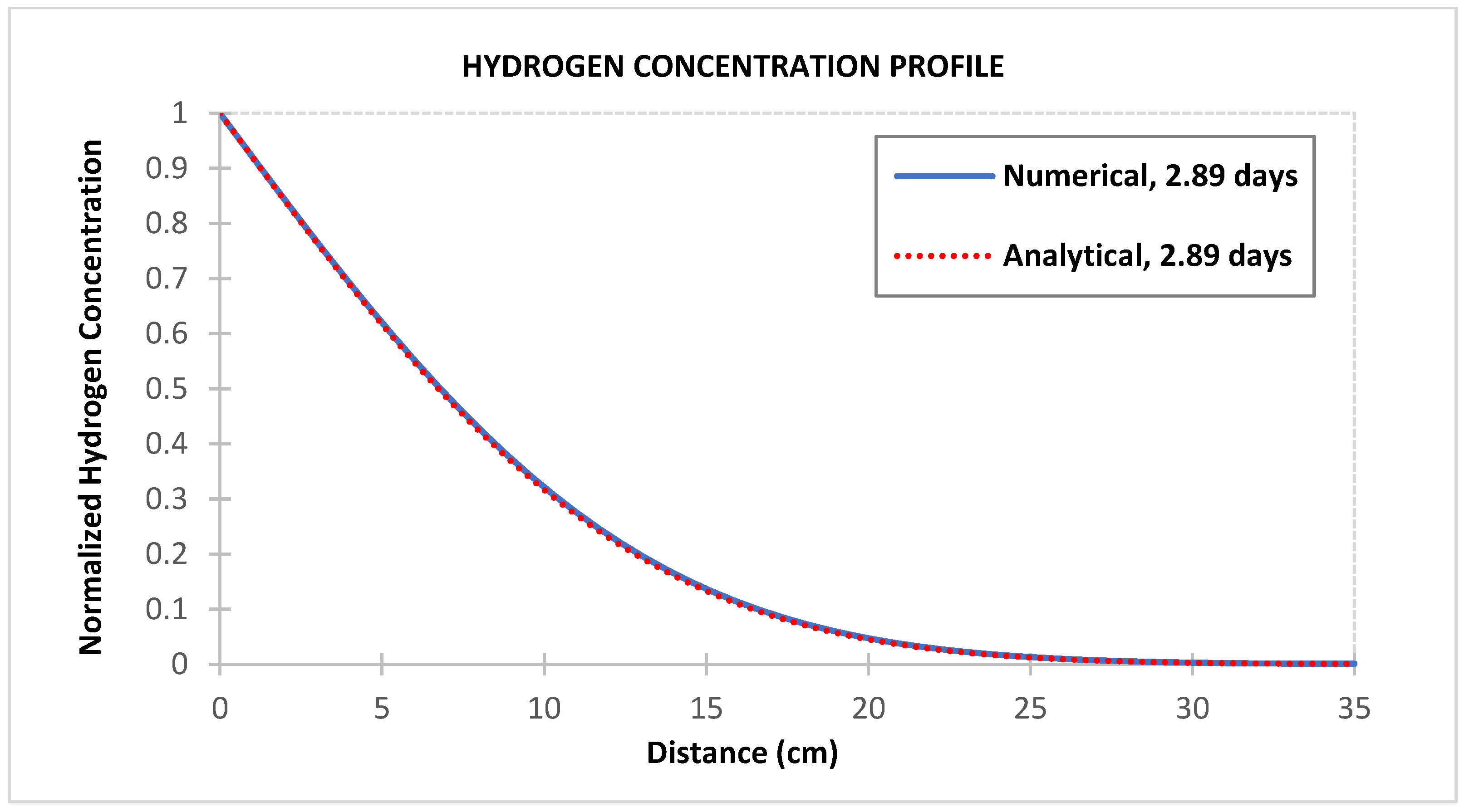
3. Model Validation
4. Numerical Experiments and Analysis of Results
5. Conclusions
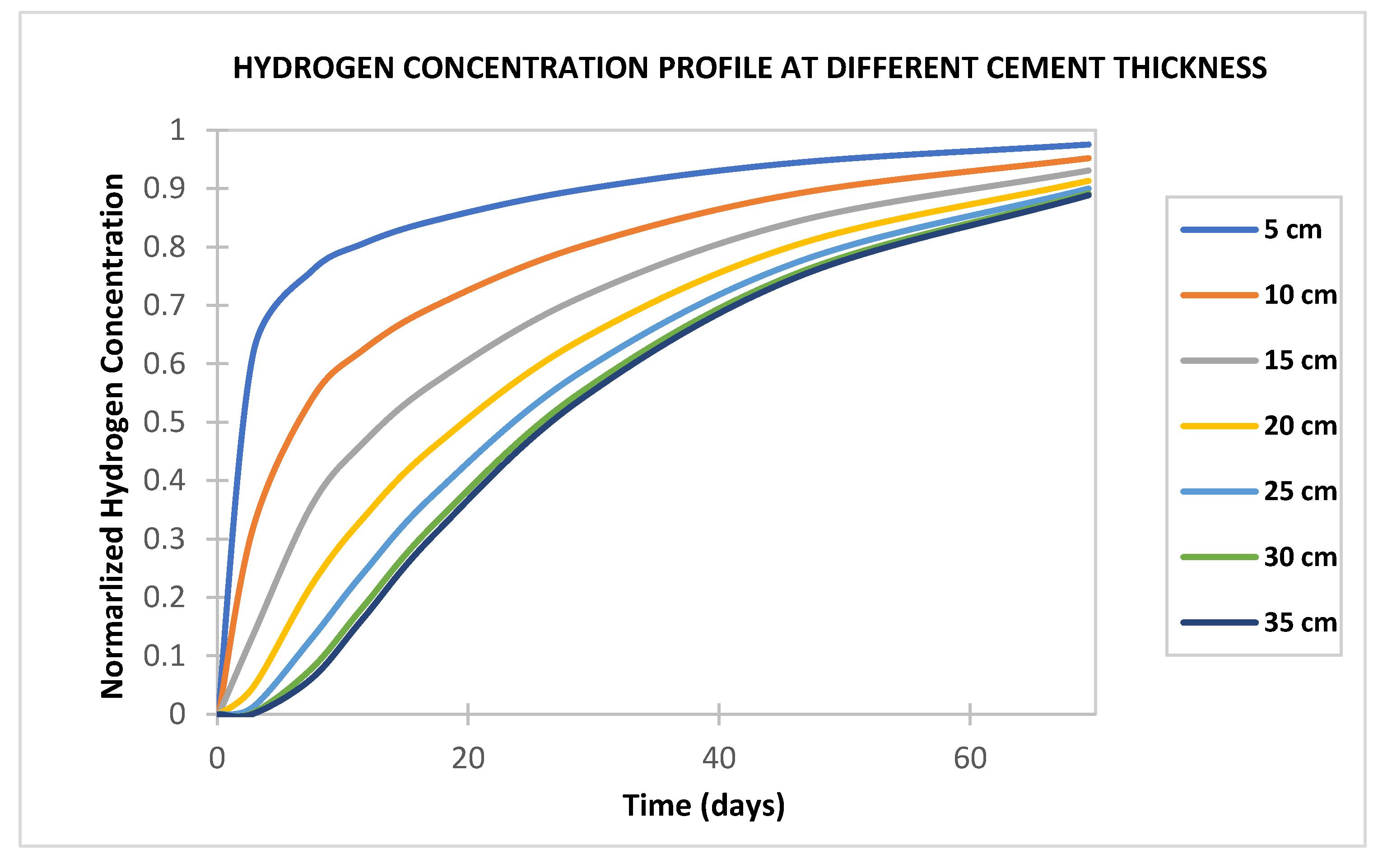
- Hydrogen should take about 7.5 days to fully penetrate a 35 cm cement sheath under the condition in Table 1. The relatively short duration for hydrogen breakthrough in the cement sheath is mainly due to the small molecule size and high hydrogen diffusivity. If the hydrogen reaches a vertical channel behind the casing, a hydrogen leak from the well is soon expected. Therefore, the well cement integrity is paramount to ensuring any successful UHS project.
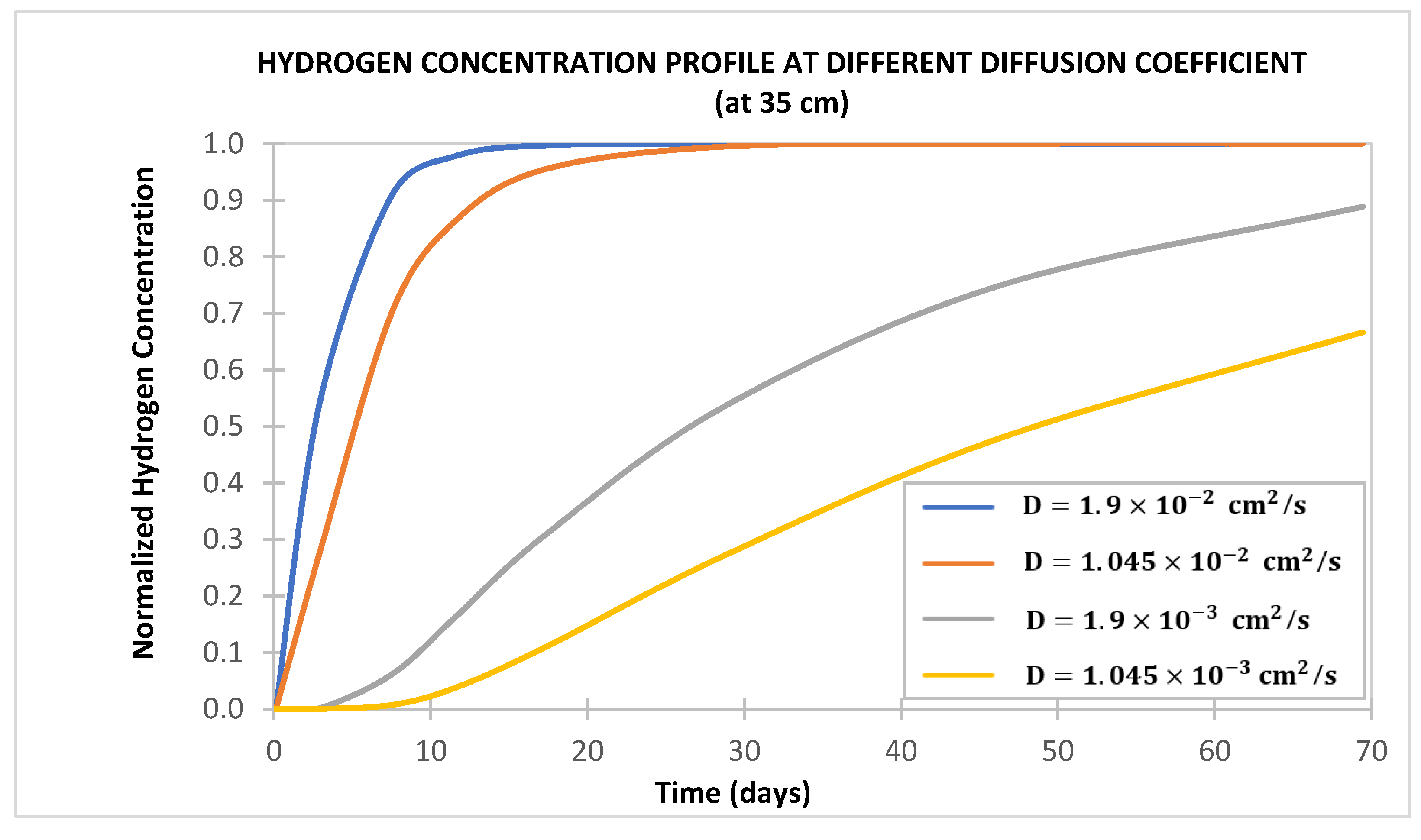
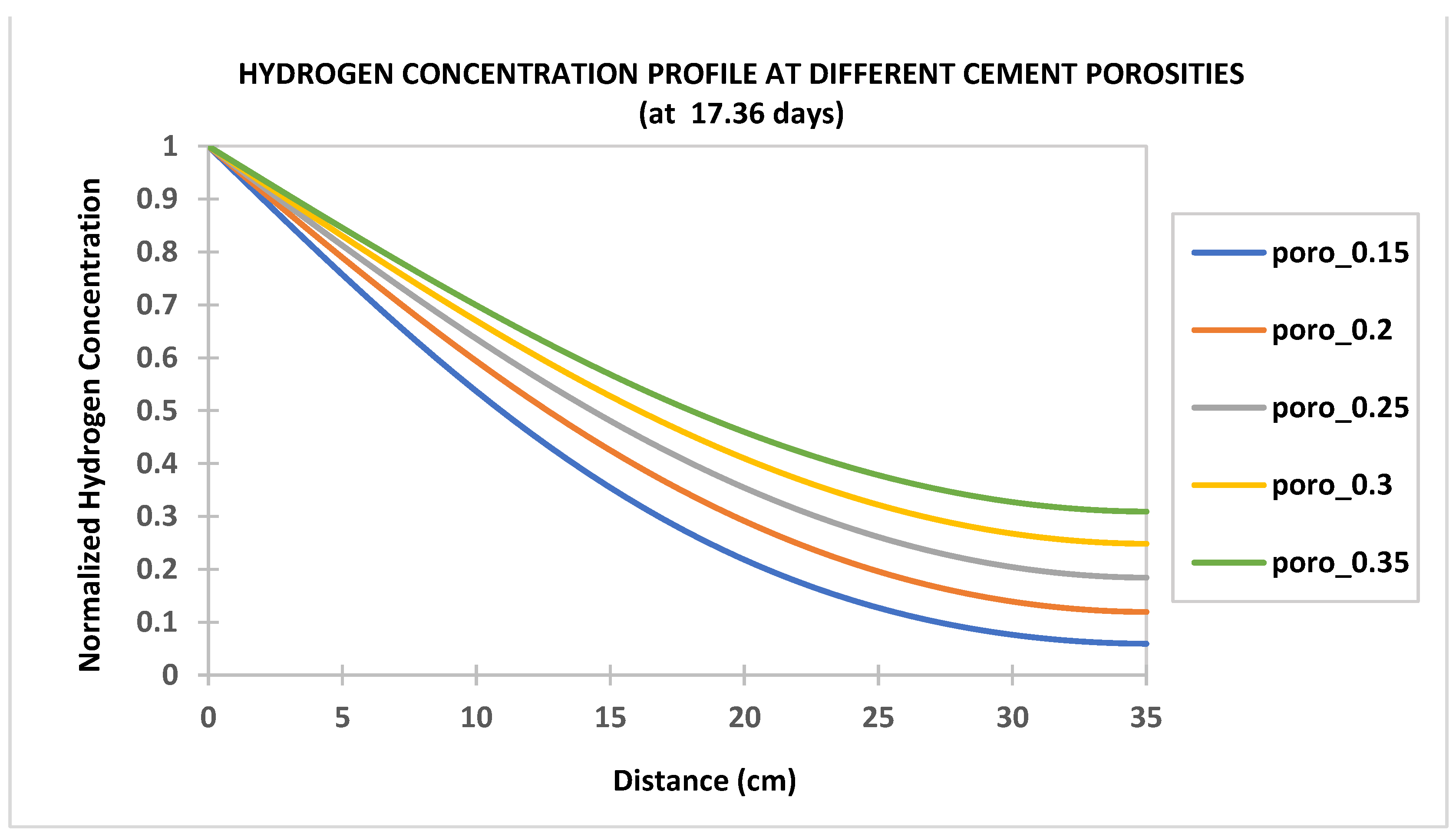
- Hydrogen diffusion into cement sheaths increases with increased cement porosity and diffusion coefficient and decreases with water saturation (increases with hydrogen saturation). Hence, cement with a low water-to-cement ratio to reduce water content and low cement porosity is desirable for wells used in UHS.
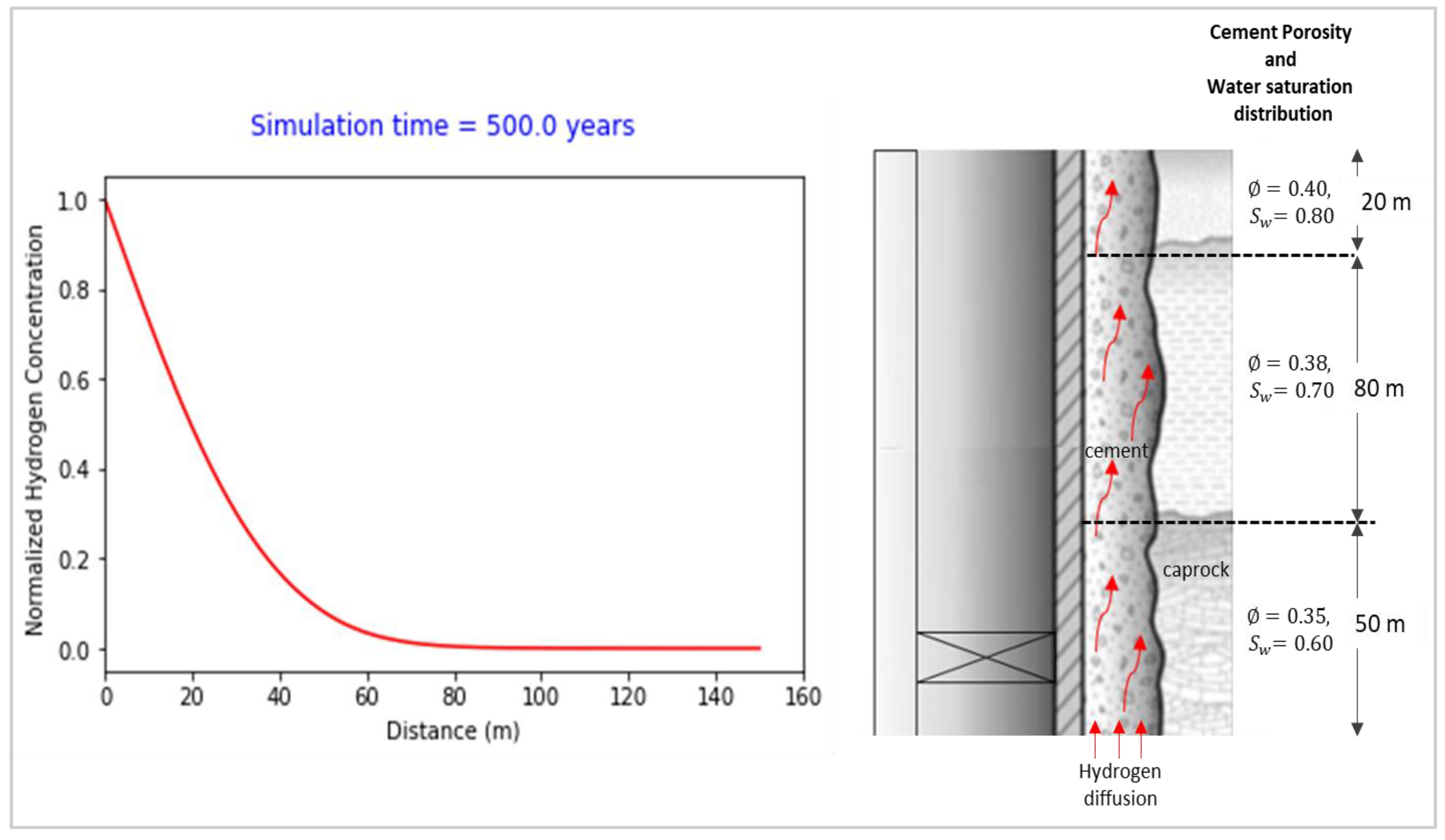
- The simulation result implies that the time taken for hydrogen migration along the axial direction of a 50m cement column across the caprock and above the storage zone is estimated to be about 500 years. Hence, provided the cement sheath is crack-free, hydrogen leaks to the surrounding formations may likely happen along the traverse direction of the cement sheath during the operating life of the UHS sites.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
References
- Heinemann, N.; Alcalde, J.; Miocic, J.M.; Hangx, S.J.; Kallmeyer, J.; Ostertag-Henning, C.; Rudloff, A. Enabling large-scale hydrogen storage in porous media–the scientific challenges. Energy Environ. Sci. 2021, 14, 853–864. [Google Scholar] [CrossRef]
- Cracolici, F.; Iorio, V.S.; Parrozza, F.; Sabatino, L.M.F.; Previde Massara, E.; Consonni, A.; Poloni, R. Experimental Investigation of Cement Compatibility in Underground Hydrogen Storage in Depleted Reservoir. In Proceedings of the International Petroleum Technology Conference, Bangkok, Thailand, 1–3 March 2023. [Google Scholar]
- Lord, A.S.; Kobos, P.H.; Borns, D.J. Geologic Storage of Hydrogen: Scaling up to meet city transportation demands. Int. J. Hydrog. Energy 2014, 39, 15570–15582. [Google Scholar] [CrossRef]
- Agartan, E.; Gaddipati, M.; Yip, Y.; Savage, B.; Ozgen, C. CO2 storage in depleted oil and gas fields in the Gulf of Mexico. Int. J. Greenh. Gas Control 2018, 72, 38–48. [Google Scholar] [CrossRef]
- Michanowicz, D.R.; Buonocore, J.J.; Rowland, S.T.; Konschnik, K.E.; Goho, S.A.; Bernstein, A.S. A national assessment of underground natural gas storage: Identifying wells with designs likely vulnerable to a single-point-of-failure. Environ. Res. Lett. 2017, 12, 064004. [Google Scholar] [CrossRef]
- Goodman, H.A.; Kutchko, B.; Lackey, G.; Gulliver, D.; Strazisar, B.R.; Tinker, K.A.; Wright, R.; Haeri, F.; Huerta, N.; Baek, S. Subsurface Hydrogen and Natural Gas Storage: State of Knowledge and Research Recommendations Report; DOE/NETL-2022/3236; U.S. Department of Energy: Washington, DC, USA, 2022. [Google Scholar]
- Boersheim, E.C.; Reitenbach, V.; Albrecht, D.; Pudlo, D.; Ganzer, L. Experimental investigation of integrity issues of UGS containing hydrogen. In Proceedings of the SPE Europe Featured at 81st EAGE Conference and Exhibition, London, UK, 3–6 June 2019. [Google Scholar]
- Yang, Z.; Zhang, X.; Deng, D. Underground gas storage injection-production well completion process. Well Test. 2008, 2, 63–68. [Google Scholar]
- Bai, M.; Song, K.; Sun, Y.; He, M.; Li, Y.; Sun, J. An overview of Hydrogen underground storage technology and prospects in China. J. Pet. Sci. Eng. 2014, 124, 132–136. [Google Scholar] [CrossRef]
- Zhao, K. Injection Wells. The Formation Underground Gas Storage in the Process of the Usability Research. Ph.D. Thesis, Chinese Academy of Sciences, Beijing, China, 2009. [Google Scholar]
- Barrera, O.; Bombac, D.; Chen, Y.; Daff, T.D.; Galindo-Nava, E.; Gong, P.; Sweeney, F. Understanding, and mitigating hydrogen embrittlement of steels: A review of experimental, modeling and design progress from atomistic to continuum. J. Mater. Sci. 2018, 53, 6251–6290. [Google Scholar] [CrossRef]
- Djukic, M.B.; Zeravcic, V.S.; Bakic, G.; Sedmak, A.; Rajicic, B. Hydrogen embrittlement of low carbon structural steel. Procedia Mater. Sci. 2014, 3, 1167–1172. [Google Scholar] [CrossRef]
- Findley, K.O.; Lawrence, S.K.; O’Brien, M.K. Engineering challenges associated with hydrogen embrittlement in steels. In Encyclopedia of Materials: Metals and Alloys; Elsevier: Amsterdam, The Netherlands, 2022; pp. 235–249. [Google Scholar]
- Ramjaun, T.I.; Ooi, S.W.; Morana, R.; Bhadeshia, H.K.D.H. Designing steel to resist hydrogen embrittlement: Part 1—Trapping capacity. Mater. Sci. Technol. 2018, 34, 1737–1746. [Google Scholar] [CrossRef]
- Ugarte, E.R.; Salehi, S. A review on well integrity issues for underground hydrogen storage. J. Energy Resour. Technol. 2022, 144, 042001. [Google Scholar] [CrossRef]
- Brownell, M.; Frischknecht, A.L.; Wilson, M.A. Subdiffusive high-pressure hydrogen gas dynamics in elastomers. Macromolecules 2022, 55, 3788–3800. [Google Scholar] [CrossRef]
- Patel, H.; Salehi, S.; Ahmed, R.; Teodoriu, C. Review of elastomer seal assemblies in oil & gas wells: Performance evaluation, failure mechanisms, and gaps in industry standards. J. Pet. Sci. Eng. 2019, 179, 1046–1062. [Google Scholar]
- Simmons, K.L.; Kuang, W.; Burton, S.D.; Arey, B.W.; Shin, Y.; Menon, N.C.; Smith, D.B. H-Mat hydrogen compatibility of polymers and elastomers. Int. J. Hydrog. Energy 2021, 46, 12300–12310. [Google Scholar] [CrossRef]
- Simmons, K.; Bhamidipaty, K.; Menon, N.; Smith, B.; Naskar, A.; Veenstra, M. Compatibility of Polymeric Materials Used in the Hydrogen Infrastructure; DOE Annual Merit Review; Pacific Northwest National Laboratory: Richland, WA, USA, 2017. [Google Scholar]
- Kulkarni, S.S.; Choi, K.S.; Kuang, W.; Menon, N.; Mills, B.; Soulami, A.; Simmons, K. Damage evolution in polymer due to exposure to high-pressure hydrogen gas. Int. J. Hydrog. Energy 2021, 46, 19001–19022. [Google Scholar] [CrossRef]
- Arbad, N.; Teodoriu, C. A review of recent research on contamination of oil well Cement with oil-based drilling fluid and the need for new and accurate correlations. ChemEngineering 2020, 4, 28. [Google Scholar] [CrossRef]
- Hussain, A.; Al-Hadrami, H.; Emadi, H.; Altawati, F.; Thiyagarajan, S.R.; Watson, M. Experimental Investigation of Wellbore Integrity of Depleted Oil and Gas Reservoirs for Underground Hydrogen Storage. In Proceedings of the Offshore Technology Conference, Houston, TX, USA, 2–5 May 2022. [Google Scholar]
- Yang, H.; Bu, Y.; Guo, S.; Liu, H.; Du, J.; Cao, X. Effects of in-situ stress and elastic parameters of cement sheath in salt rock formation of underground gas storage on seal integrity of cement sheath. Eng. Fail. Anal. 2021, 123, 105258. [Google Scholar] [CrossRef]
- Zhang, P.; Guo, B.; Liu, N. Numerical simulation of CO2 migration into cement sheath of oil/gas wells. J. Nat. Gas Sci. Eng. 2021, 94, 104085. [Google Scholar] [CrossRef]
- McElroy, P.D.; Emadi, H.; Watson, M.C. Optimization of wellbore cement sheath resilience using nano and microscale reinforcement: A statistical approach using design of experiments. J. Pet. Sci. Eng. 2021, 200, 108324. [Google Scholar] [CrossRef]
- Bugrayev, A.; Nafikova, S.; Taoutaou, S.; Timonin, A.; Gurbanov, G.; Burkenya, A.; Hegab, M. Case Studies of Expanding Cement to Improve Wellbore Sealing. In Proceedings of the SPE Gas & Oil Technology Showcase and Conference, Dubai, United Arab Emirates, 21–23 October 2019. [Google Scholar]
- Bai, M.; Reinicke, K.M. Numerical Simulation of CO2 Leakage through Abandoned Wells during CO2 Underground Storage. In Clean Energy Systems in the Subsurface: Production, Storage and Conversion: Proceedings of the 3rd Sino-German Conference Underground Storage of CO2 and Energy, Goslar, Germany, 21–23 May 2013; Springer: Berlin/Heidelberg, Germany; pp. 197–210.
- Iorio, V.S.; Cracolici, F.; Parrozza, F.; Sabatino, L.M.; Massara, E.P.; Consonni, A.; De Simoni, M. Cement to Safeguard the Wells Integrity in Underground Hydrogen Storage: An Experimental Investigation. Chem. Eng. Trans. 2022, 96, 307–312. [Google Scholar]
- Jacquemet, N.; Chiquet, P.; Grauls, A. Hydrogen reactivity with (1) a well cement-PHREEQC geochemical thermodynamics calculations. In Proceedings of the 1st Geoscience & Engineering in Energy Transition Conference, Strasbourg, France, 16–18 November 2020; Volume 2020, pp. 1–5. [Google Scholar]
- Sercombe, J.; Vidal, R.; Gallé, C.; Adenot, F. Experimental study of gas diffusion in cement paste. Cem. Concr. Res. 2007, 37, 579–588. [Google Scholar] [CrossRef]
- Teodoriu, C.; Asamba, P.; Ichim, A. Well integrity estimation of salt cements with application to long term underground storage systems. In Proceedings of the SPE Europec Featured at 78th EAGE Conference and Exhibition, Vienna, Austria, 30 May–2 June 2016. [Google Scholar]
- Ghaedi, M.; Andersen, P.Ø.; Gholami, R. Hydrogen diffusion into caprock: A semi-analytical solution and a hydrogen loss criterion. J. Energy Storage 2023, 64, 107134. [Google Scholar] [CrossRef]
- Wolfrum, C.; Lang, H.; Moser, H.; Jordan, W. Determination of diffusion coefficients based on Ficks second law for various boundary conditions. Radiochim. Acta 1988, 44, 245–250. [Google Scholar] [CrossRef]
- Fick, A.V. On liquid diffusion. Lond. Edinb. Dublin Philos. Mag. J. Sci. 1855, 10, 30–39. [Google Scholar] [CrossRef]
- Jacops, E.; Aertsens, M.; Maes, N.; Bruggeman, C.; Swennen, R.; Krooss, B.; Littke, R. The dependency of diffusion coefficients and geometric factor on the size of the diffusing molecule: Observations for different clay-based materials. Geofluids 2017, 2017, 8652560. [Google Scholar] [CrossRef]
- Mejlbro, L. The complete solution of Fick’s second law of diffusion with time-dependent diffusion coefficient and surface concentration. In Durability of Concrete in Saline Environment; Cementa AB: Lund, Sweden, 1996; pp. 127–158. [Google Scholar]
- Kolsi, L.; Abbasi, A.; Al-Khaled, K.; Farooq, W.; Ghachem, K.; Gul, M.; Khan, S.U. Stagnation point flow of chemically reactive nanofluid due to the curved stretching surface with modified Fourier and Fick theories. Waves Random Complex Media 2023, 33, 841–859. [Google Scholar] [CrossRef]
- Crank, J. The Mathematics of Diffusion, (Revised); Clarendon Press: Oxford, UK, 1970. [Google Scholar]
- Podgorsek, R.P.; Franke, H. Optical determination of molecule diffusion coefficients in polymer films. Appl. Phys. Lett. 1998, 73, 2887–2889. [Google Scholar] [CrossRef]
- Pálsson, G.K.; Bliersbach, A.; Wolff, M.; Zamani, A.; Hjörvarsson, B. Using light transmission to watch hydrogen diffuse. Nat. Commun. 2012, 3, 892. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions, and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions, or products referred to in the content. |



| Properties | Value | Darcy Units |
|---|---|---|
| Cement sheath thickness, L | 35 | cm |
| Cement porosity, Ø | 0.35 | |
| Diffusion coefficient of hydrogen, | ||
| Saturation water in cement pores, | 0.7 | |
| Initial normalized concentration of hydrogen, | 1 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dudun, A.; Feng, Y.; Guo, B. Numerical Simulation of Hydrogen Diffusion in Cement Sheath of Wells Used for Underground Hydrogen Storage. Sustainability 2023, 15, 10844. https://doi.org/10.3390/su151410844
Dudun A, Feng Y, Guo B. Numerical Simulation of Hydrogen Diffusion in Cement Sheath of Wells Used for Underground Hydrogen Storage. Sustainability. 2023; 15(14):10844. https://doi.org/10.3390/su151410844
Chicago/Turabian StyleDudun, Anireju, Yin Feng, and Boyun Guo. 2023. "Numerical Simulation of Hydrogen Diffusion in Cement Sheath of Wells Used for Underground Hydrogen Storage" Sustainability 15, no. 14: 10844. https://doi.org/10.3390/su151410844
APA StyleDudun, A., Feng, Y., & Guo, B. (2023). Numerical Simulation of Hydrogen Diffusion in Cement Sheath of Wells Used for Underground Hydrogen Storage. Sustainability, 15(14), 10844. https://doi.org/10.3390/su151410844







