Surrogate Model Development for Slope Stability Analysis Using Machine Learning
Abstract
1. Introduction
2. Dataset
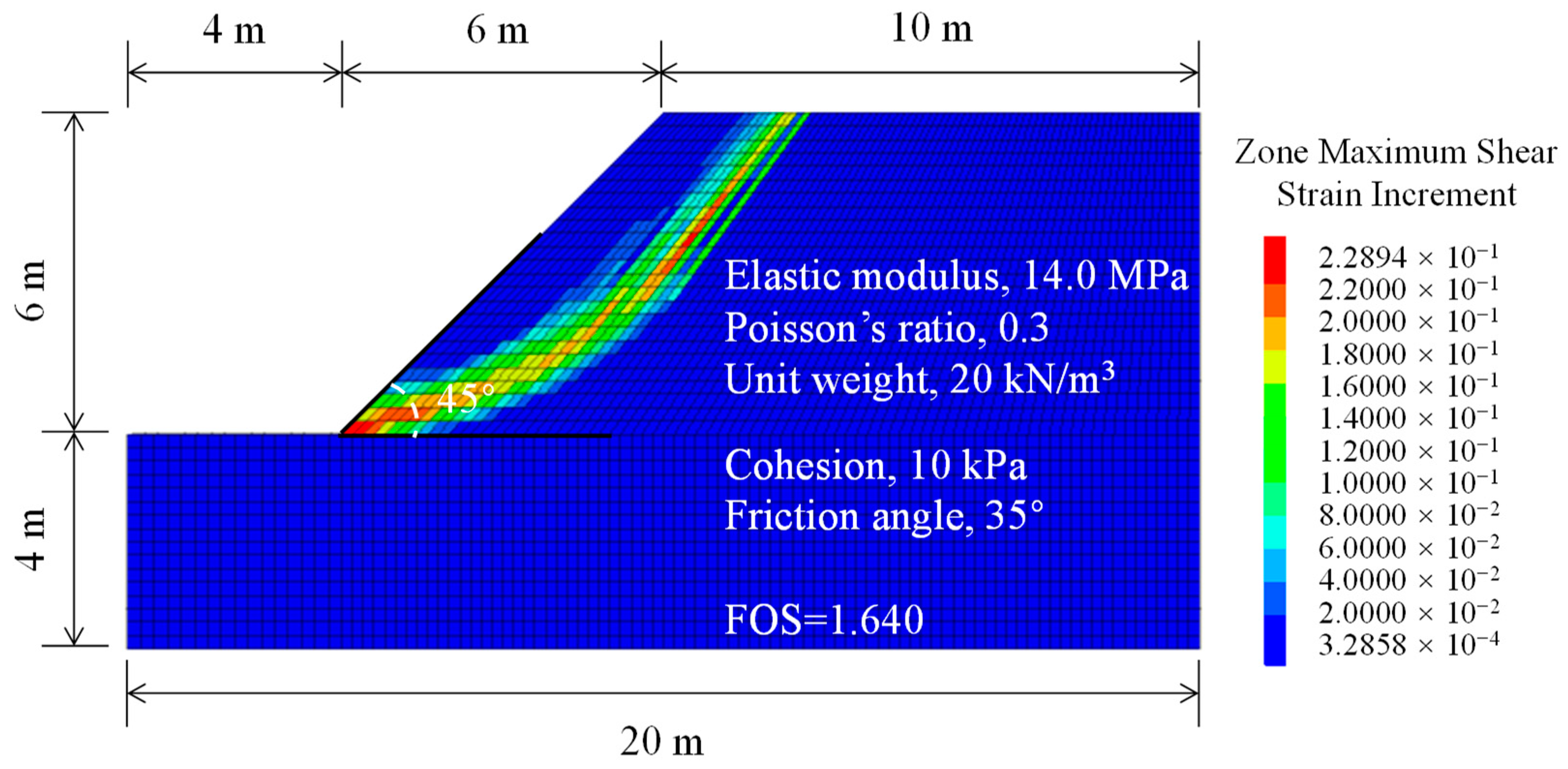
2.1. Modeling: A Simple and Homogeneous Soil Slope
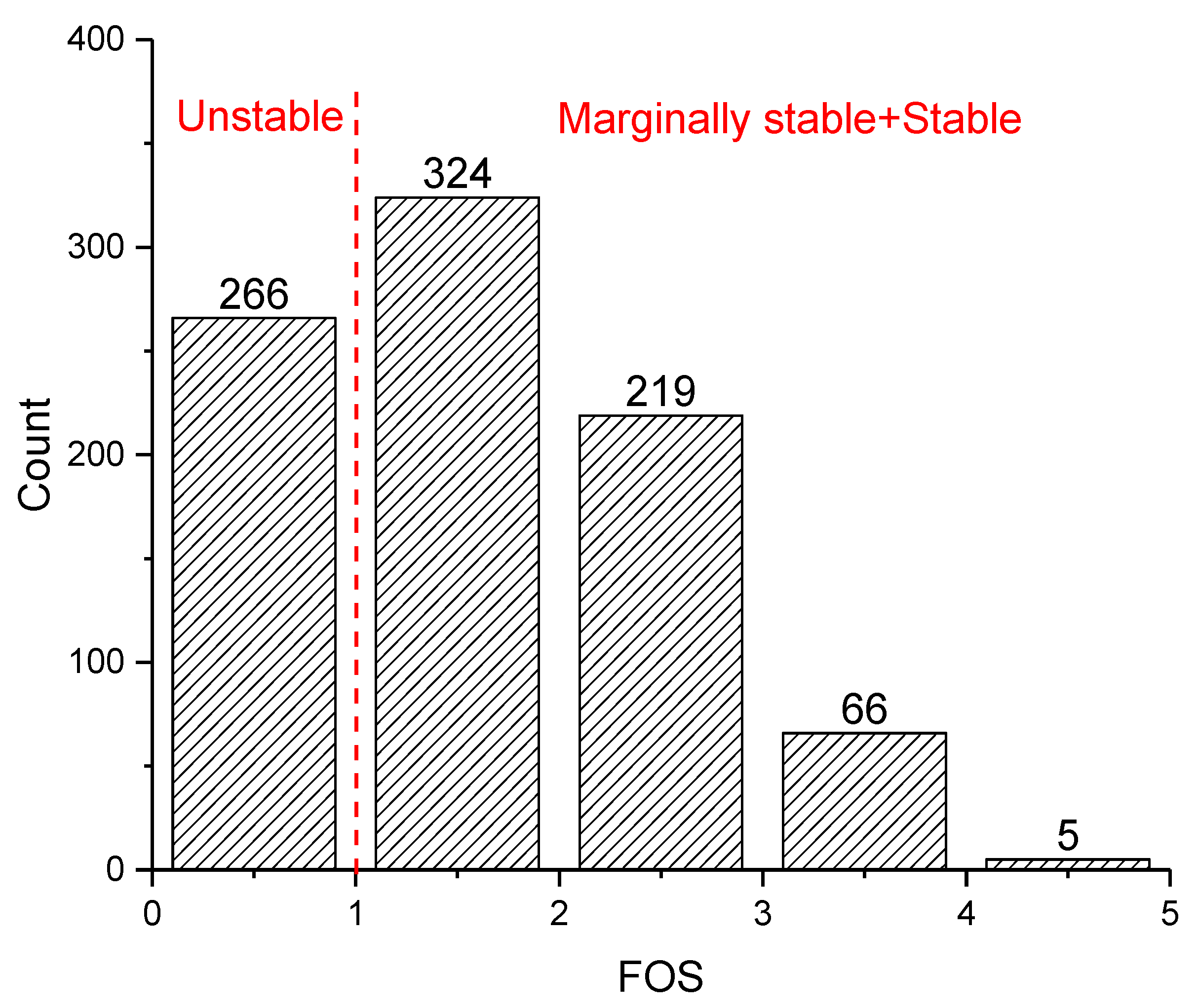
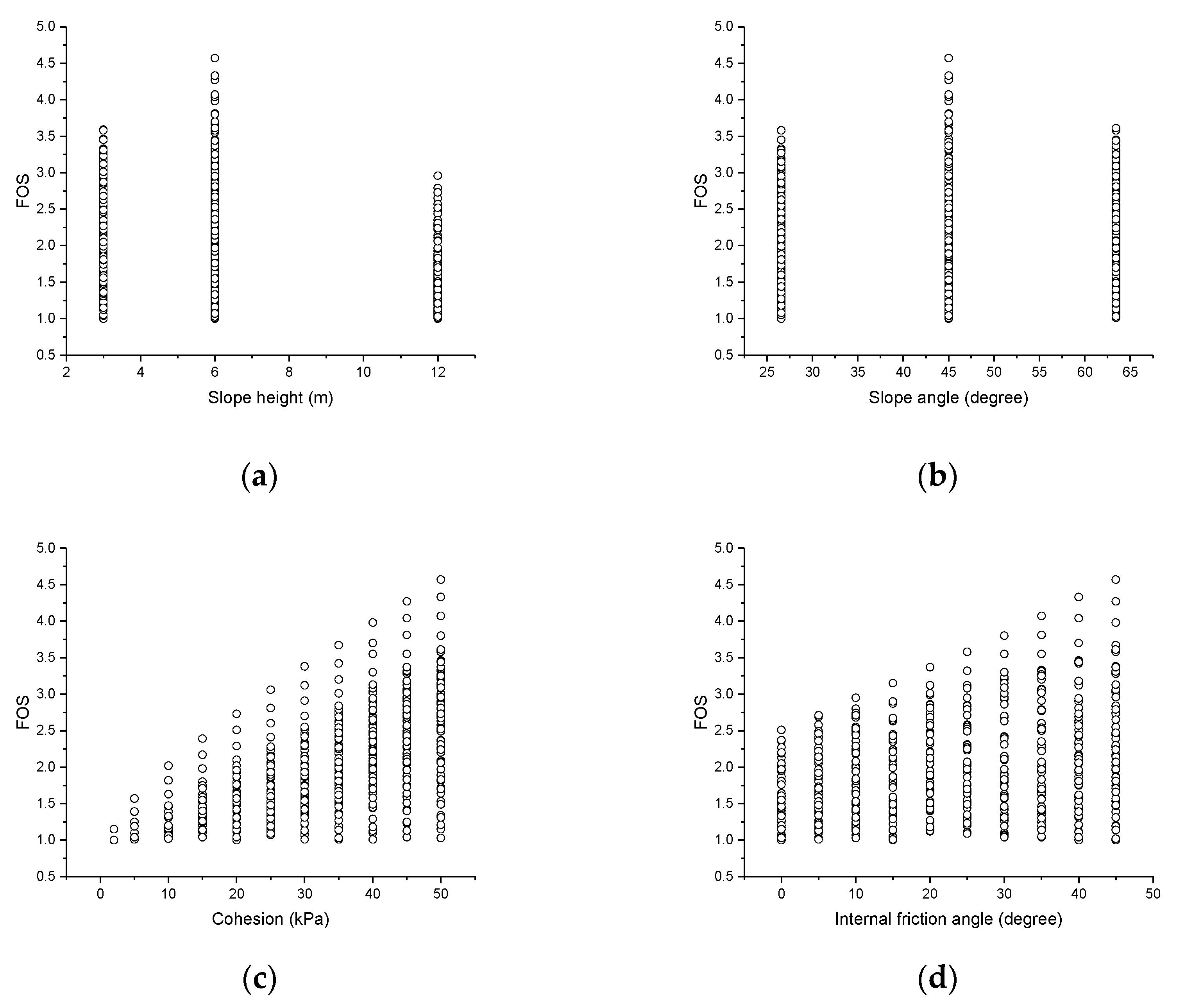
2.2. An Established Dataset
3. Model Development
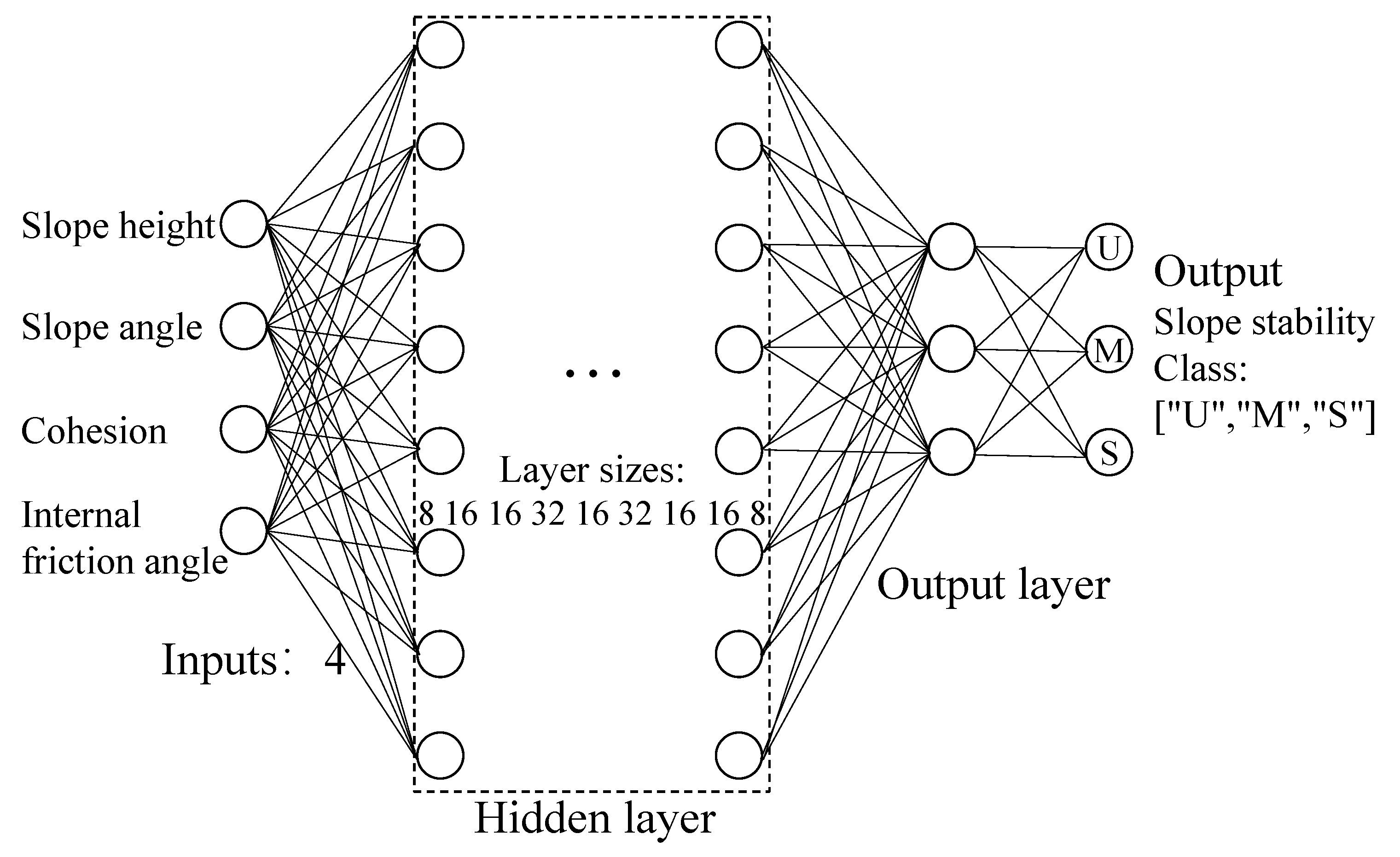
3.1. A Deep Neural Network Model for Slope Classification
- (a)
- Data preprocessing: The first step is to prepare the input data and target labels used to train the network. This typically involves dividing the data into training and test sets.
- (b)
- Network construction and training: The next step is to train the network using the training data. A DNN model is trained on the input data, which requires specifying the input data, target labels, and the type of network to be trained.
- (c)
- Prediction: Once the network is trained, the model can be used to predict the test set.
- (d)
- Performance evaluation: The performance of the network can be evaluated using a confusion matrix.
3.2. A Deep Neural Network Model for the Factor of Safety Regression
- (a)
- Data preprocessing: The dataset is divided into training and test sets, and necessary preprocessing steps such as feature normalization and the handling of missing values are performed.
- (b)
- Network construction and training: A DNN consisting of input, hidden, and output layers is constructed, with the architecture of the network determined by factors such as the number of hidden layers and nodes. The network is trained using a training set.
- (c)
- Prediction: The trained model is utilized to generate predicted values for new input data.
- (d)
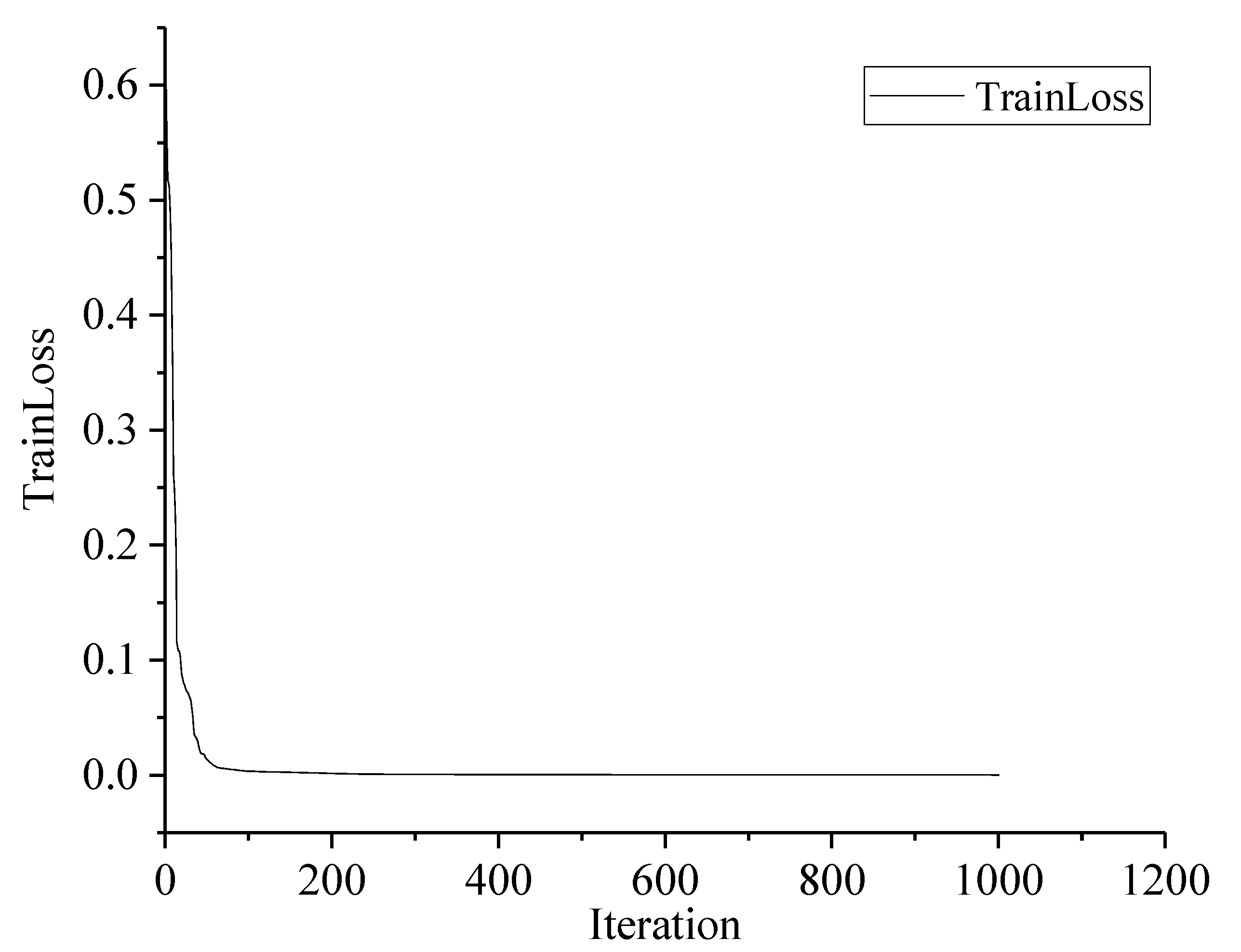
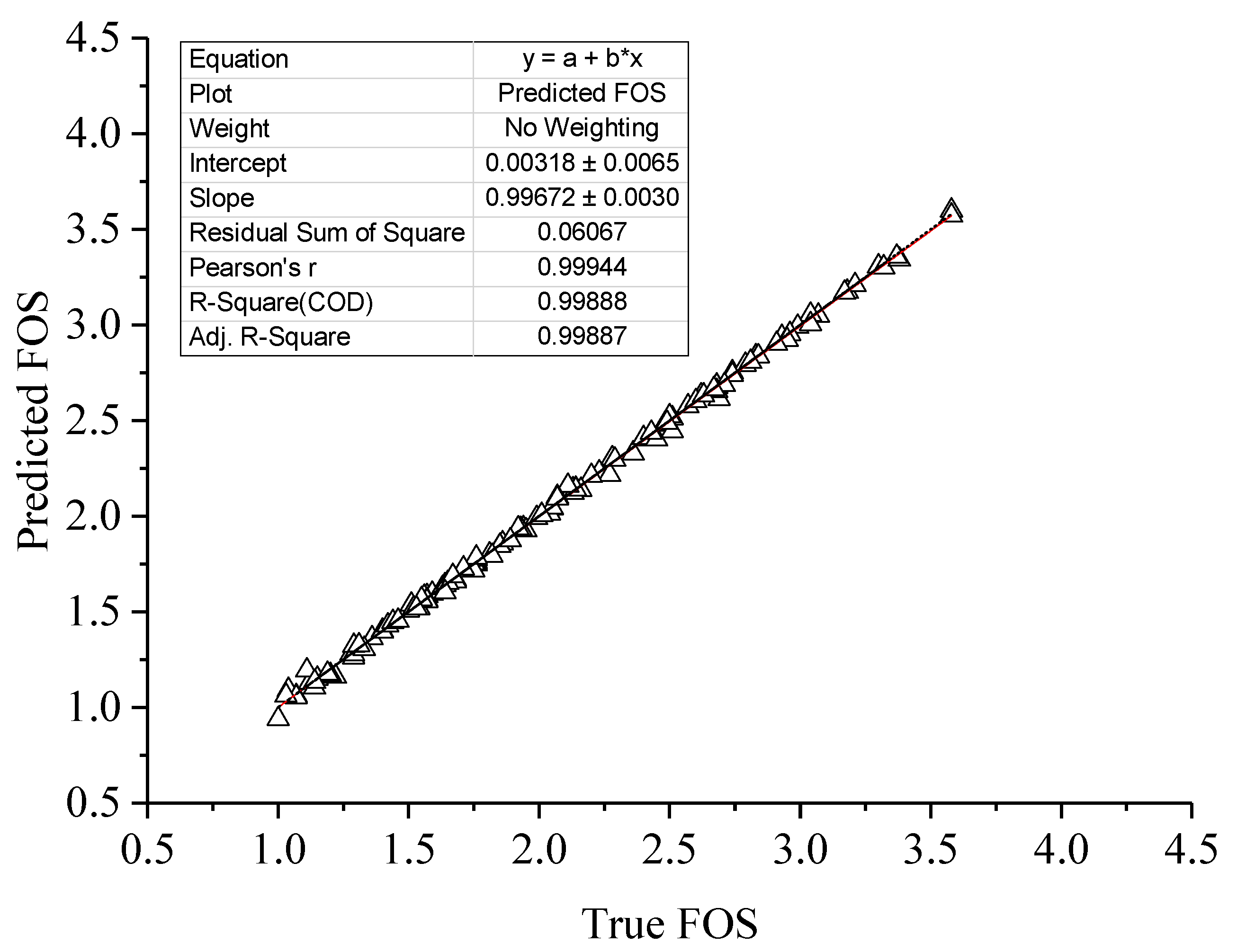
- Performance evaluation: The performance of the model was evaluated using metrics such as the mean squared error (MSE) and correlation coefficient R-square value.
4. Results and Discussion
4.1. Slope Classification
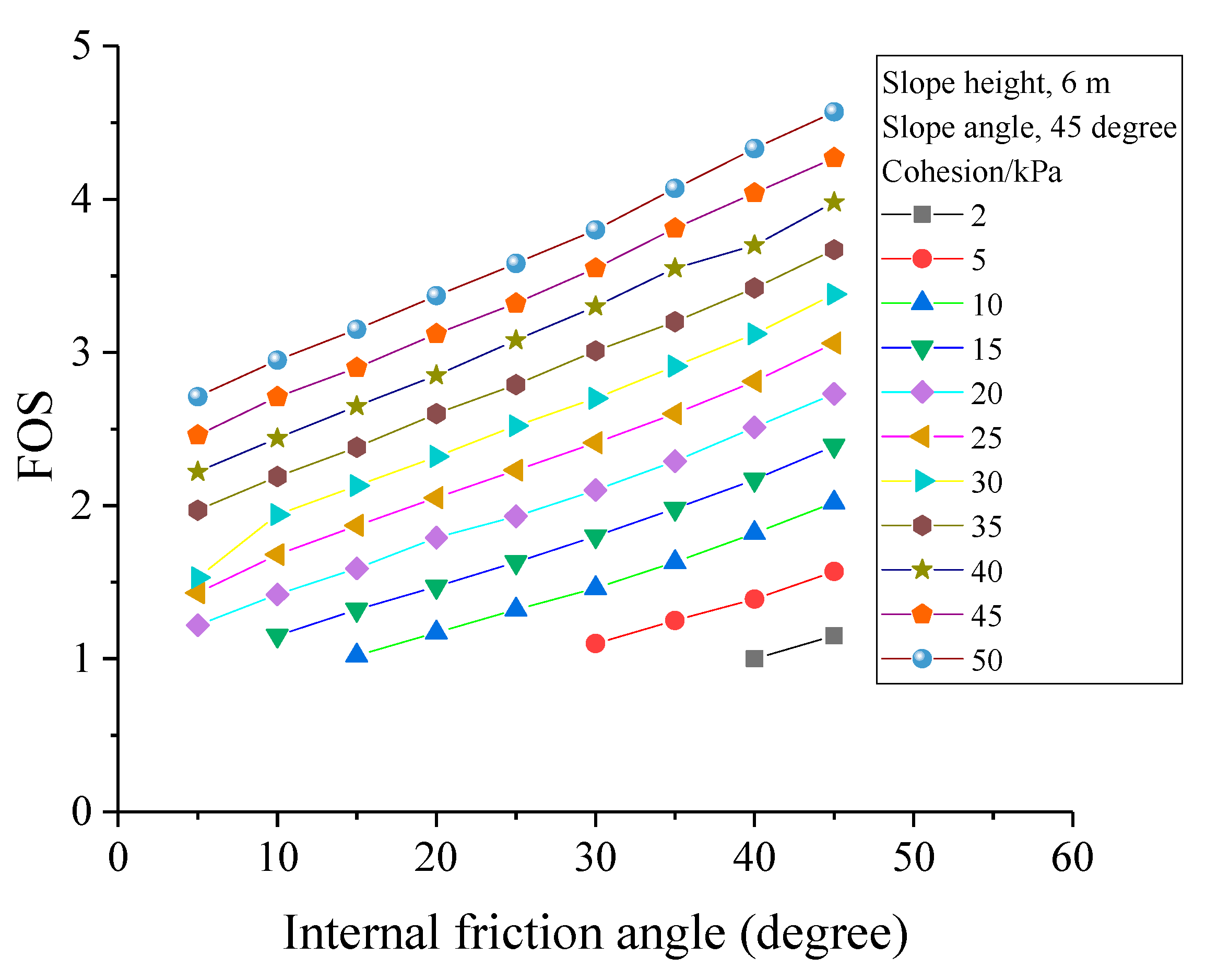
4.2. Slope FOS Prediction
4.3. Time Consumption
4.4. Discussion
4.5. Contributions, Limitations, and Further Research
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
| Case No. | Slope Height/m | Slope Angle/° | Cohesion/kPa | Friction Angle/° | FOS | Labels |
|---|---|---|---|---|---|---|
| 1 | 3 | 26.57 | 2 | 5 | - | U |
| 2 | 3 | 26.57 | 2 | 10 | - | U |
| 3 | 3 | 26.57 | 2 | 15 | - | U |
| 4 | 3 | 26.57 | 2 | 20 | - | U |
| 5 | 3 | 26.57 | 2 | 25 | - | U |
| 6 | 3 | 26.57 | 2 | 30 | - | U |
| 7 | 3 | 26.57 | 2 | 35 | - | U |
| 8 | 3 | 26.57 | 2 | 40 | - | U |
| 9 | 3 | 26.57 | 2 | 45 | - | U |
| 10 | 3 | 26.57 | 5 | 5 | - | U |
| 11 | 3 | 26.57 | 5 | 10 | - | U |
| 12 | 3 | 26.57 | 5 | 15 | - | U |
| 13 | 3 | 26.57 | 5 | 20 | - | U |
| 14 | 3 | 26.57 | 5 | 25 | - | U |
| 15 | 3 | 26.57 | 5 | 30 | - | U |
| 16 | 3 | 26.57 | 5 | 35 | - | U |
| 17 | 3 | 26.57 | 5 | 40 | - | U |
| 18 | 3 | 26.57 | 5 | 45 | - | U |
| 19 | 3 | 26.57 | 10 | 5 | - | U |
| 20 | 3 | 26.57 | 10 | 10 | - | U |
| 21 | 3 | 26.57 | 10 | 15 | - | U |
| 22 | 3 | 26.57 | 10 | 20 | - | U |
| 23 | 3 | 26.57 | 10 | 25 | - | U |
| 24 | 3 | 26.57 | 10 | 30 | - | U |
| 25 | 3 | 26.57 | 10 | 35 | 1.04 | M |
| 26 | 3 | 26.57 | 10 | 40 | 1.12 | M |
| 27 | 3 | 26.57 | 10 | 45 | 1.2 | M |
| 28 | 3 | 26.57 | 15 | 5 | - | U |
| 29 | 3 | 26.57 | 15 | 10 | - | U |
| 30 | 3 | 26.57 | 15 | 15 | 1.04 | M |
| 31 | 3 | 26.57 | 15 | 20 | 1.12 | M |
| 32 | 3 | 26.57 | 15 | 25 | 1.2 | M |
| 33 | 3 | 26.57 | 15 | 30 | 1.28 | S |
| 34 | 3 | 26.57 | 15 | 35 | 1.36 | S |
| 35 | 3 | 26.57 | 15 | 40 | 1.46 | S |
| 36 | 3 | 26.57 | 15 | 45 | 1.54 | S |
| 37 | 3 | 26.57 | 20 | 5 | 1.14 | M |
| 38 | 3 | 26.57 | 20 | 10 | 1.23 | S |
| 39 | 3 | 26.57 | 20 | 15 | 1.31 | S |
| 40 | 3 | 26.57 | 20 | 20 | 1.4 | S |
| 41 | 3 | 26.57 | 20 | 25 | 1.49 | S |
| 42 | 3 | 26.57 | 20 | 30 | 1.57 | S |
| 43 | 3 | 26.57 | 20 | 35 | 1.67 | S |
| 44 | 3 | 26.57 | 20 | 40 | 1.76 | S |
| 45 | 3 | 26.57 | 20 | 45 | 1.86 | S |
| 46 | 3 | 26.57 | 25 | 5 | 1.4 | S |
| 47 | 3 | 26.57 | 25 | 10 | 1.49 | S |
| 48 | 3 | 26.57 | 25 | 15 | 1.58 | S |
| 49 | 3 | 26.57 | 25 | 20 | 1.68 | S |
| 50 | 3 | 26.57 | 25 | 25 | 1.76 | S |
| 51 | 3 | 26.57 | 25 | 30 | 1.85 | S |
| 52 | 3 | 26.57 | 25 | 35 | 1.95 | S |
| 53 | 3 | 26.57 | 25 | 40 | 2.05 | S |
| 54 | 3 | 26.57 | 25 | 45 | 2.17 | S |
| 55 | 3 | 26.57 | 30 | 5 | 1.67 | S |
| 56 | 3 | 26.57 | 30 | 10 | 1.76 | S |
| 57 | 3 | 26.57 | 30 | 15 | 1.85 | S |
| 58 | 3 | 26.57 | 30 | 20 | 1.93 | S |
| 59 | 3 | 26.57 | 30 | 25 | 2.04 | S |
| 60 | 3 | 26.57 | 30 | 30 | 2.13 | S |
| 61 | 3 | 26.57 | 30 | 35 | 2.23 | S |
| 62 | 3 | 26.57 | 30 | 40 | 2.34 | S |
| 63 | 3 | 26.57 | 30 | 45 | 2.46 | S |
| 64 | 3 | 26.57 | 35 | 5 | 1.91 | S |
| 65 | 3 | 26.57 | 35 | 10 | 2.02 | S |
| 66 | 3 | 26.57 | 35 | 15 | 2.12 | S |
| 67 | 3 | 26.57 | 35 | 20 | 2.21 | S |
| 68 | 3 | 26.57 | 35 | 25 | 2.3 | S |
| 69 | 3 | 26.57 | 35 | 30 | 2.4 | S |
| 70 | 3 | 26.57 | 35 | 35 | 2.51 | S |
| 71 | 3 | 26.57 | 35 | 40 | 2.62 | S |
| 72 | 3 | 26.57 | 35 | 45 | 2.74 | S |
| 73 | 3 | 26.57 | 40 | 5 | 2.16 | S |
| 74 | 3 | 26.57 | 40 | 10 | 2.29 | S |
| 75 | 3 | 26.57 | 40 | 15 | 2.38 | S |
| 76 | 3 | 26.57 | 40 | 20 | 2.48 | S |
| 77 | 3 | 26.57 | 40 | 25 | 2.57 | S |
| 78 | 3 | 26.57 | 40 | 30 | 2.68 | S |
| 79 | 3 | 26.57 | 40 | 35 | 2.79 | S |
| 80 | 3 | 26.57 | 40 | 40 | 2.9 | S |
| 81 | 3 | 26.57 | 40 | 45 | 3.02 | S |
| 82 | 3 | 26.57 | 45 | 5 | 2.41 | S |
| 83 | 3 | 26.57 | 45 | 10 | 2.55 | S |
| 84 | 3 | 26.57 | 45 | 15 | 2.64 | S |
| 85 | 3 | 26.57 | 45 | 20 | 2.74 | S |
| 86 | 3 | 26.57 | 45 | 25 | 2.83 | S |
| 87 | 3 | 26.57 | 45 | 30 | 2.93 | S |
| 88 | 3 | 26.57 | 45 | 35 | 3.07 | S |
| 89 | 3 | 26.57 | 45 | 40 | 3.18 | S |
| 90 | 3 | 26.57 | 45 | 45 | 3.3 | S |
| 91 | 3 | 26.57 | 50 | 5 | 2.69 | S |
| 92 | 3 | 26.57 | 50 | 10 | 2.8 | S |
| 93 | 3 | 26.57 | 50 | 15 | 2.9 | S |
| 94 | 3 | 26.57 | 50 | 20 | 3 | S |
| 95 | 3 | 26.57 | 50 | 25 | 3.1 | S |
| 96 | 3 | 26.57 | 50 | 30 | 3.2 | S |
| 97 | 3 | 26.57 | 50 | 35 | 3.33 | S |
| 98 | 3 | 26.57 | 50 | 40 | 3.45 | S |
| 99 | 3 | 26.57 | 50 | 45 | 3.58 | S |
| 100 | 3 | 26.57 | 2 | 0 | - | U |
| 101 | 3 | 26.57 | 5 | 0 | - | U |
| 102 | 3 | 26.57 | 10 | 0 | - | U |
| 103 | 3 | 26.57 | 15 | 0 | - | U |
| 104 | 3 | 26.57 | 20 | 0 | 1 | M |
| 105 | 3 | 26.57 | 25 | 0 | 1.25 | S |
| 106 | 3 | 26.57 | 30 | 0 | 1.5 | S |
| 107 | 3 | 26.57 | 35 | 0 | 1.76 | S |
| 108 | 3 | 26.57 | 40 | 0 | 2.02 | S |
| 109 | 3 | 26.57 | 45 | 0 | 2.27 | S |
| 110 | 3 | 26.57 | 50 | 0 | 2.51 | S |
| 111 | 3 | 45 | 2 | 5 | - | U |
| 112 | 3 | 45 | 2 | 10 | - | U |
| 113 | 3 | 45 | 2 | 15 | - | U |
| 114 | 3 | 45 | 2 | 20 | - | U |
| 115 | 3 | 45 | 2 | 25 | - | U |
| 116 | 3 | 45 | 2 | 30 | - | U |
| 117 | 3 | 45 | 2 | 35 | - | U |
| 118 | 3 | 45 | 2 | 40 | - | U |
| 119 | 3 | 45 | 2 | 45 | - | U |
| 120 | 3 | 45 | 5 | 5 | - | U |
| 121 | 3 | 45 | 5 | 10 | - | U |
| 122 | 3 | 45 | 5 | 15 | - | U |
| 123 | 3 | 45 | 5 | 20 | - | U |
| 124 | 3 | 45 | 5 | 25 | - | U |
| 125 | 3 | 45 | 5 | 30 | - | U |
| 126 | 3 | 45 | 5 | 35 | - | U |
| 127 | 3 | 45 | 5 | 40 | - | U |
| 128 | 3 | 45 | 5 | 45 | - | U |
| 129 | 3 | 45 | 10 | 5 | - | U |
| 130 | 3 | 45 | 10 | 10 | - | U |
| 131 | 3 | 45 | 10 | 15 | - | U |
| 132 | 3 | 45 | 10 | 20 | - | U |
| 133 | 3 | 45 | 10 | 25 | - | U |
| 134 | 3 | 45 | 10 | 30 | - | U |
| 135 | 3 | 45 | 10 | 35 | 1.04 | M |
| 136 | 3 | 45 | 10 | 40 | 1.12 | M |
| 137 | 3 | 45 | 10 | 45 | 1.2 | M |
| 138 | 3 | 45 | 15 | 5 | - | U |
| 139 | 3 | 45 | 15 | 10 | - | U |
| 140 | 3 | 45 | 15 | 15 | 1.04 | M |
| 141 | 3 | 45 | 15 | 20 | 1.13 | M |
| 142 | 3 | 45 | 15 | 25 | 1.21 | S |
| 143 | 3 | 45 | 15 | 30 | 1.28 | S |
| 144 | 3 | 45 | 15 | 35 | 1.36 | S |
| 145 | 3 | 45 | 15 | 40 | 1.44 | S |
| 146 | 3 | 45 | 15 | 45 | 1.54 | S |
| 147 | 3 | 45 | 20 | 5 | 1.13 | M |
| 148 | 3 | 45 | 20 | 10 | 1.23 | S |
| 149 | 3 | 45 | 20 | 15 | 1.31 | S |
| 150 | 3 | 45 | 20 | 20 | 1.41 | S |
| 151 | 3 | 45 | 20 | 25 | 1.49 | S |
| 152 | 3 | 45 | 20 | 30 | 1.57 | S |
| 153 | 3 | 45 | 20 | 35 | 1.67 | S |
| 154 | 3 | 45 | 20 | 40 | 1.76 | S |
| 155 | 3 | 45 | 20 | 45 | 1.87 | S |
| 156 | 3 | 45 | 25 | 5 | 1.38 | S |
| 157 | 3 | 45 | 25 | 10 | 1.49 | S |
| 158 | 3 | 45 | 25 | 15 | 1.59 | S |
| 159 | 3 | 45 | 25 | 20 | 1.68 | S |
| 160 | 3 | 45 | 25 | 25 | 1.76 | S |
| 161 | 3 | 45 | 25 | 30 | 1.85 | S |
| 162 | 3 | 45 | 25 | 35 | 1.95 | S |
| 163 | 3 | 45 | 25 | 40 | 2.06 | S |
| 164 | 3 | 45 | 25 | 45 | 2.16 | S |
| 165 | 3 | 45 | 30 | 5 | 1.63 | S |
| 166 | 3 | 45 | 30 | 10 | 1.75 | S |
| 167 | 3 | 45 | 30 | 15 | 1.85 | S |
| 168 | 3 | 45 | 30 | 20 | 1.94 | S |
| 169 | 3 | 45 | 30 | 25 | 2.04 | S |
| 170 | 3 | 45 | 30 | 30 | 2.14 | S |
| 171 | 3 | 45 | 30 | 35 | 2.23 | S |
| 172 | 3 | 45 | 30 | 40 | 2.34 | S |
| 173 | 3 | 45 | 30 | 45 | 2.46 | S |
| 174 | 3 | 45 | 35 | 5 | 1.85 | S |
| 175 | 3 | 45 | 35 | 10 | 2.01 | S |
| 176 | 3 | 45 | 35 | 15 | 2.12 | S |
| 177 | 3 | 45 | 35 | 20 | 2.2 | S |
| 178 | 3 | 45 | 35 | 25 | 2.31 | S |
| 179 | 3 | 45 | 35 | 30 | 2.42 | S |
| 180 | 3 | 45 | 35 | 35 | 2.5 | S |
| 181 | 3 | 45 | 35 | 40 | 2.61 | S |
| 182 | 3 | 45 | 35 | 45 | 2.74 | S |
| 183 | 3 | 45 | 40 | 5 | 2.12 | S |
| 184 | 3 | 45 | 40 | 10 | 2.25 | S |
| 185 | 3 | 45 | 40 | 15 | 2.39 | S |
| 186 | 3 | 45 | 40 | 20 | 2.47 | S |
| 187 | 3 | 45 | 40 | 25 | 2.58 | S |
| 188 | 3 | 45 | 40 | 30 | 2.69 | S |
| 189 | 3 | 45 | 40 | 35 | 2.77 | S |
| 190 | 3 | 45 | 40 | 40 | 2.91 | S |
| 191 | 3 | 45 | 40 | 45 | 3.02 | S |
| 192 | 3 | 45 | 45 | 5 | 2.36 | S |
| 193 | 3 | 45 | 45 | 10 | 2.5 | S |
| 194 | 3 | 45 | 45 | 15 | 2.63 | S |
| 195 | 3 | 45 | 45 | 20 | 2.74 | S |
| 196 | 3 | 45 | 45 | 25 | 2.85 | S |
| 197 | 3 | 45 | 45 | 30 | 2.94 | S |
| 198 | 3 | 45 | 45 | 35 | 3.04 | S |
| 199 | 3 | 45 | 45 | 40 | 3.18 | S |
| 200 | 3 | 45 | 45 | 45 | 3.32 | S |
| 201 | 3 | 45 | 50 | 5 | 2.58 | S |
| 202 | 3 | 45 | 50 | 10 | 2.74 | S |
| 203 | 3 | 45 | 50 | 15 | 2.88 | S |
| 204 | 3 | 45 | 50 | 20 | 2.99 | S |
| 205 | 3 | 45 | 50 | 25 | 3.1 | S |
| 206 | 3 | 45 | 50 | 30 | 3.21 | S |
| 207 | 3 | 45 | 50 | 35 | 3.32 | S |
| 208 | 3 | 45 | 50 | 40 | 3.46 | S |
| 209 | 3 | 45 | 50 | 45 | 3.59 | S |
| 210 | 3 | 45 | 2 | 0 | - | U |
| 211 | 3 | 45 | 5 | 0 | - | U |
| 212 | 3 | 45 | 10 | 0 | - | U |
| 213 | 3 | 45 | 15 | 0 | - | U |
| 214 | 3 | 45 | 20 | 0 | - | U |
| 215 | 3 | 45 | 25 | 0 | 1.17 | M |
| 216 | 3 | 45 | 30 | 0 | 1.4 | S |
| 217 | 3 | 45 | 35 | 0 | 1.64 | S |
| 218 | 3 | 45 | 40 | 0 | 1.87 | S |
| 219 | 3 | 45 | 45 | 0 | 2.13 | S |
| 220 | 3 | 45 | 50 | 0 | 2.36 | S |
| 221 | 3 | 63.43 | 2 | 5 | - | U |
| 222 | 3 | 63.43 | 2 | 10 | - | U |
| 223 | 3 | 63.43 | 2 | 15 | - | U |
| 224 | 3 | 63.43 | 2 | 20 | - | U |
| 225 | 3 | 63.43 | 2 | 25 | - | U |
| 226 | 3 | 63.43 | 2 | 30 | - | U |
| 227 | 3 | 63.43 | 2 | 35 | - | U |
| 228 | 3 | 63.43 | 2 | 40 | - | U |
| 229 | 3 | 63.43 | 2 | 45 | - | U |
| 230 | 3 | 63.43 | 5 | 5 | - | U |
| 231 | 3 | 63.43 | 5 | 10 | - | U |
| 232 | 3 | 63.43 | 5 | 15 | - | U |
| 233 | 3 | 63.43 | 5 | 20 | - | U |
| 234 | 3 | 63.43 | 5 | 25 | - | U |
| 235 | 3 | 63.43 | 5 | 30 | - | U |
| 236 | 3 | 63.43 | 5 | 35 | - | U |
| 237 | 3 | 63.43 | 5 | 40 | - | U |
| 238 | 3 | 63.43 | 5 | 45 | - | U |
| 239 | 3 | 63.43 | 10 | 5 | - | U |
| 240 | 3 | 63.43 | 10 | 10 | - | U |
| 241 | 3 | 63.43 | 10 | 15 | - | U |
| 242 | 3 | 63.43 | 10 | 20 | - | U |
| 243 | 3 | 63.43 | 10 | 25 | - | U |
| 244 | 3 | 63.43 | 10 | 30 | - | U |
| 245 | 3 | 63.43 | 10 | 35 | 1.04 | M |
| 246 | 3 | 63.43 | 10 | 40 | 1.12 | M |
| 247 | 3 | 63.43 | 10 | 45 | 1.2 | M |
| 248 | 3 | 63.43 | 15 | 5 | - | U |
| 249 | 3 | 63.43 | 15 | 10 | - | U |
| 250 | 3 | 63.43 | 15 | 15 | 1.05 | M |
| 251 | 3 | 63.43 | 15 | 20 | 1.12 | M |
| 252 | 3 | 63.43 | 15 | 25 | 1.21 | S |
| 253 | 3 | 63.43 | 15 | 30 | 1.29 | S |
| 254 | 3 | 63.43 | 15 | 35 | 1.36 | S |
| 255 | 3 | 63.43 | 15 | 40 | 1.45 | S |
| 256 | 3 | 63.43 | 15 | 45 | 1.53 | S |
| 257 | 3 | 63.43 | 20 | 5 | 1.12 | M |
| 258 | 3 | 63.43 | 20 | 10 | 1.23 | S |
| 259 | 3 | 63.43 | 20 | 15 | 1.31 | S |
| 260 | 3 | 63.43 | 20 | 20 | 1.4 | S |
| 261 | 3 | 63.43 | 20 | 25 | 1.48 | S |
| 262 | 3 | 63.43 | 20 | 30 | 1.57 | S |
| 263 | 3 | 63.43 | 20 | 35 | 1.67 | S |
| 264 | 3 | 63.43 | 20 | 40 | 1.75 | S |
| 265 | 3 | 63.43 | 20 | 45 | 1.86 | S |
| 266 | 3 | 63.43 | 25 | 5 | 1.34 | S |
| 267 | 3 | 63.43 | 25 | 10 | 1.5 | S |
| 268 | 3 | 63.43 | 25 | 15 | 1.59 | S |
| 269 | 3 | 63.43 | 25 | 20 | 1.68 | S |
| 270 | 3 | 63.43 | 25 | 25 | 1.75 | S |
| 271 | 3 | 63.43 | 25 | 30 | 1.85 | S |
| 272 | 3 | 63.43 | 25 | 35 | 1.94 | S |
| 273 | 3 | 63.43 | 25 | 40 | 2.05 | S |
| 274 | 3 | 63.43 | 25 | 45 | 2.16 | S |
| 275 | 3 | 63.43 | 30 | 5 | 1.59 | S |
| 276 | 3 | 63.43 | 30 | 10 | 1.74 | S |
| 277 | 3 | 63.43 | 30 | 15 | 1.85 | S |
| 278 | 3 | 63.43 | 30 | 20 | 1.95 | S |
| 279 | 3 | 63.43 | 30 | 25 | 2.04 | S |
| 280 | 3 | 63.43 | 30 | 30 | 2.13 | S |
| 281 | 3 | 63.43 | 30 | 35 | 2.23 | S |
| 282 | 3 | 63.43 | 30 | 40 | 2.32 | S |
| 283 | 3 | 63.43 | 30 | 45 | 2.44 | S |
| 284 | 3 | 63.43 | 35 | 5 | 1.8 | S |
| 285 | 3 | 63.43 | 35 | 10 | 1.99 | S |
| 286 | 3 | 63.43 | 35 | 15 | 2.1 | S |
| 287 | 3 | 63.43 | 35 | 20 | 2.2 | S |
| 288 | 3 | 63.43 | 35 | 25 | 2.3 | S |
| 289 | 3 | 63.43 | 35 | 30 | 2.4 | S |
| 290 | 3 | 63.43 | 35 | 35 | 2.51 | S |
| 291 | 3 | 63.43 | 35 | 40 | 2.63 | S |
| 292 | 3 | 63.43 | 35 | 45 | 2.75 | S |
| 293 | 3 | 63.43 | 40 | 5 | 2.05 | S |
| 294 | 3 | 63.43 | 40 | 10 | 2.22 | S |
| 295 | 3 | 63.43 | 40 | 15 | 2.35 | S |
| 296 | 3 | 63.43 | 40 | 20 | 2.46 | S |
| 297 | 3 | 63.43 | 40 | 25 | 2.57 | S |
| 298 | 3 | 63.43 | 40 | 30 | 2.68 | S |
| 299 | 3 | 63.43 | 40 | 35 | 2.79 | S |
| 300 | 3 | 63.43 | 40 | 40 | 2.9 | S |
| 301 | 3 | 63.43 | 40 | 45 | 3.04 | S |
| 302 | 3 | 63.43 | 45 | 5 | 2.27 | S |
| 303 | 3 | 63.43 | 45 | 10 | 2.46 | S |
| 304 | 3 | 63.43 | 45 | 15 | 2.63 | S |
| 305 | 3 | 63.43 | 45 | 20 | 2.74 | S |
| 306 | 3 | 63.43 | 45 | 25 | 2.85 | S |
| 307 | 3 | 63.43 | 45 | 30 | 2.96 | S |
| 308 | 3 | 63.43 | 45 | 35 | 3.06 | S |
| 309 | 3 | 63.43 | 45 | 40 | 3.17 | S |
| 310 | 3 | 63.43 | 45 | 45 | 3.28 | S |
| 311 | 3 | 63.43 | 50 | 5 | 2.49 | S |
| 312 | 3 | 63.43 | 50 | 10 | 2.68 | S |
| 313 | 3 | 63.43 | 50 | 15 | 2.87 | S |
| 314 | 3 | 63.43 | 50 | 20 | 3.01 | S |
| 315 | 3 | 63.43 | 50 | 25 | 3.12 | S |
| 316 | 3 | 63.43 | 50 | 30 | 3.23 | S |
| 317 | 3 | 63.43 | 50 | 35 | 3.31 | S |
| 318 | 3 | 63.43 | 50 | 40 | 3.45 | S |
| 319 | 3 | 63.43 | 50 | 45 | 3.58 | S |
| 320 | 3 | 63.43 | 2 | 0 | - | U |
| 321 | 3 | 63.43 | 5 | 0 | - | U |
| 322 | 3 | 63.43 | 10 | 0 | - | U |
| 323 | 3 | 63.43 | 15 | 0 | - | U |
| 324 | 3 | 63.43 | 20 | 0 | - | U |
| 325 | 3 | 63.43 | 25 | 0 | 1.15 | M |
| 326 | 3 | 63.43 | 30 | 0 | 1.36 | S |
| 327 | 3 | 63.43 | 35 | 0 | 1.56 | S |
| 328 | 3 | 63.43 | 40 | 0 | 1.81 | S |
| 329 | 3 | 63.43 | 45 | 0 | 2.05 | S |
| 330 | 3 | 63.43 | 50 | 0 | 2.27 | S |
| 331 | 6 | 26.57 | 2 | 5 | - | U |
| 332 | 6 | 26.57 | 2 | 10 | - | U |
| 333 | 6 | 26.57 | 2 | 15 | - | U |
| 334 | 6 | 26.57 | 2 | 20 | - | U |
| 335 | 6 | 26.57 | 2 | 25 | - | U |
| 336 | 6 | 26.57 | 2 | 30 | - | U |
| 337 | 6 | 26.57 | 2 | 35 | - | U |
| 338 | 6 | 26.57 | 2 | 40 | - | U |
| 339 | 6 | 26.57 | 2 | 45 | - | U |
| 340 | 6 | 26.57 | 5 | 5 | - | U |
| 341 | 6 | 26.57 | 5 | 10 | - | U |
| 342 | 6 | 26.57 | 5 | 15 | - | U |
| 343 | 6 | 26.57 | 5 | 20 | - | U |
| 344 | 6 | 26.57 | 5 | 25 | - | U |
| 345 | 6 | 26.57 | 5 | 30 | - | U |
| 346 | 6 | 26.57 | 5 | 35 | - | U |
| 347 | 6 | 26.57 | 5 | 40 | - | U |
| 348 | 6 | 26.57 | 5 | 45 | - | U |
| 349 | 6 | 26.57 | 10 | 5 | - | U |
| 350 | 6 | 26.57 | 10 | 10 | - | U |
| 351 | 6 | 26.57 | 10 | 15 | - | U |
| 352 | 6 | 26.57 | 10 | 20 | - | U |
| 353 | 6 | 26.57 | 10 | 25 | - | U |
| 354 | 6 | 26.57 | 10 | 30 | - | U |
| 355 | 6 | 26.57 | 10 | 35 | 1.05 | M |
| 356 | 6 | 26.57 | 10 | 40 | 1.11 | M |
| 357 | 6 | 26.57 | 10 | 45 | 1.2 | M |
| 358 | 6 | 26.57 | 15 | 5 | - | U |
| 359 | 6 | 26.57 | 15 | 10 | - | U |
| 360 | 6 | 26.57 | 15 | 15 | 1.05 | M |
| 361 | 6 | 26.57 | 15 | 20 | 1.13 | M |
| 362 | 6 | 26.57 | 15 | 25 | 1.2 | M |
| 363 | 6 | 26.57 | 15 | 30 | 1.29 | S |
| 364 | 6 | 26.57 | 15 | 35 | 1.36 | S |
| 365 | 6 | 26.57 | 15 | 40 | 1.46 | S |
| 366 | 6 | 26.57 | 15 | 45 | 1.54 | S |
| 367 | 6 | 26.57 | 20 | 5 | - | U |
| 368 | 6 | 26.57 | 20 | 10 | 1.21 | S |
| 369 | 6 | 26.57 | 20 | 15 | 1.32 | S |
| 370 | 6 | 26.57 | 20 | 20 | 1.4 | S |
| 371 | 6 | 26.57 | 20 | 25 | 1.49 | S |
| 372 | 6 | 26.57 | 20 | 30 | 1.57 | S |
| 373 | 6 | 26.57 | 20 | 35 | 1.66 | S |
| 374 | 6 | 26.57 | 20 | 40 | 1.75 | S |
| 375 | 6 | 26.57 | 20 | 45 | 1.86 | S |
| 376 | 6 | 26.57 | 25 | 5 | 1.18 | M |
| 377 | 6 | 26.57 | 25 | 10 | 1.43 | S |
| 378 | 6 | 26.57 | 25 | 15 | 1.58 | S |
| 379 | 6 | 26.57 | 25 | 20 | 1.67 | S |
| 380 | 6 | 26.57 | 25 | 25 | 1.76 | S |
| 381 | 6 | 26.57 | 25 | 30 | 1.85 | S |
| 382 | 6 | 26.57 | 25 | 35 | 1.94 | S |
| 383 | 6 | 26.57 | 25 | 40 | 2.05 | S |
| 384 | 6 | 26.57 | 25 | 45 | 2.17 | S |
| 385 | 6 | 26.57 | 30 | 5 | 1.36 | S |
| 386 | 6 | 26.57 | 30 | 10 | 1.64 | S |
| 387 | 6 | 26.57 | 30 | 15 | 1.81 | S |
| 388 | 6 | 26.57 | 30 | 20 | 1.87 | S |
| 389 | 6 | 26.57 | 30 | 25 | 2.01 | S |
| 390 | 6 | 26.57 | 30 | 30 | 2.13 | S |
| 391 | 6 | 26.57 | 30 | 35 | 2.23 | S |
| 392 | 6 | 26.57 | 30 | 40 | 2.34 | S |
| 393 | 6 | 26.57 | 30 | 45 | 2.46 | S |
| 394 | 6 | 26.57 | 35 | 5 | 1.51 | S |
| 395 | 6 | 26.57 | 35 | 10 | 1.81 | S |
| 396 | 6 | 26.57 | 35 | 15 | 2.03 | S |
| 397 | 6 | 26.57 | 35 | 20 | 2.2 | S |
| 398 | 6 | 26.57 | 35 | 25 | 2.27 | S |
| 399 | 6 | 26.57 | 35 | 30 | 2.41 | S |
| 400 | 6 | 26.57 | 35 | 35 | 2.5 | S |
| 401 | 6 | 26.57 | 35 | 40 | 2.62 | S |
| 402 | 6 | 26.57 | 35 | 45 | 2.74 | S |
| 403 | 6 | 26.57 | 40 | 5 | 1.73 | S |
| 404 | 6 | 26.57 | 40 | 10 | 1.99 | S |
| 405 | 6 | 26.57 | 40 | 15 | 2.24 | S |
| 406 | 6 | 26.57 | 40 | 20 | 2.45 | S |
| 407 | 6 | 26.57 | 40 | 25 | 2.55 | S |
| 408 | 6 | 26.57 | 40 | 30 | 2.68 | S |
| 409 | 6 | 26.57 | 40 | 35 | 2.77 | S |
| 410 | 6 | 26.57 | 40 | 40 | 2.9 | S |
| 411 | 6 | 26.57 | 40 | 45 | 3.02 | S |
| 412 | 6 | 26.57 | 45 | 5 | 1.88 | S |
| 413 | 6 | 26.57 | 45 | 10 | 2.18 | S |
| 414 | 6 | 26.57 | 45 | 15 | 2.45 | S |
| 415 | 6 | 26.57 | 45 | 20 | 2.68 | S |
| 416 | 6 | 26.57 | 45 | 25 | 2.84 | S |
| 417 | 6 | 26.57 | 45 | 30 | 2.95 | S |
| 418 | 6 | 26.57 | 45 | 35 | 3.06 | S |
| 419 | 6 | 26.57 | 45 | 40 | 3.17 | S |
| 420 | 6 | 26.57 | 45 | 45 | 3.31 | S |
| 421 | 6 | 26.57 | 50 | 5 | 2.09 | S |
| 422 | 6 | 26.57 | 50 | 10 | 2.36 | S |
| 423 | 6 | 26.57 | 50 | 15 | 2.63 | S |
| 424 | 6 | 26.57 | 50 | 20 | 2.86 | S |
| 425 | 6 | 26.57 | 50 | 25 | 3.08 | S |
| 426 | 6 | 26.57 | 50 | 30 | 3.15 | S |
| 427 | 6 | 26.57 | 50 | 35 | 3.27 | S |
| 428 | 6 | 26.57 | 50 | 40 | 3.45 | S |
| 429 | 6 | 26.57 | 50 | 45 | 3.58 | S |
| 430 | 6 | 26.57 | 2 | 0 | - | U |
| 431 | 6 | 26.57 | 5 | 0 | - | U |
| 432 | 6 | 26.57 | 10 | 0 | - | U |
| 433 | 6 | 26.57 | 15 | 0 | - | U |
| 434 | 6 | 26.57 | 20 | 0 | - | U |
| 435 | 6 | 26.57 | 25 | 0 | - | U |
| 436 | 6 | 26.57 | 30 | 0 | 1.08 | M |
| 437 | 6 | 26.57 | 35 | 0 | 1.27 | S |
| 438 | 6 | 26.57 | 40 | 0 | 1.44 | S |
| 439 | 6 | 26.57 | 45 | 0 | 1.6 | S |
| 440 | 6 | 26.57 | 50 | 0 | 1.81 | S |
| 441 | 6 | 45 | 2 | 5 | - | U |
| 442 | 6 | 45 | 2 | 10 | - | U |
| 443 | 6 | 45 | 2 | 15 | - | U |
| 444 | 6 | 45 | 2 | 20 | - | U |
| 445 | 6 | 45 | 2 | 25 | - | U |
| 446 | 6 | 45 | 2 | 30 | - | U |
| 447 | 6 | 45 | 2 | 35 | - | U |
| 448 | 6 | 45 | 2 | 40 | 1 | M |
| 449 | 6 | 45 | 2 | 45 | 1.15 | M |
| 450 | 6 | 45 | 5 | 5 | - | U |
| 451 | 6 | 45 | 5 | 10 | - | U |
| 452 | 6 | 45 | 5 | 15 | - | U |
| 453 | 6 | 45 | 5 | 20 | - | U |
| 454 | 6 | 45 | 5 | 25 | - | U |
| 455 | 6 | 45 | 5 | 30 | 1.1 | M |
| 456 | 6 | 45 | 5 | 35 | 1.25 | S |
| 457 | 6 | 45 | 5 | 40 | 1.39 | S |
| 458 | 6 | 45 | 5 | 45 | 1.57 | S |
| 459 | 6 | 45 | 10 | 5 | - | U |
| 460 | 6 | 45 | 10 | 10 | - | U |
| 461 | 6 | 45 | 10 | 15 | 1.02 | M |
| 462 | 6 | 45 | 10 | 20 | 1.17 | M |
| 463 | 6 | 45 | 10 | 25 | 1.32 | S |
| 464 | 6 | 45 | 10 | 30 | 1.46 | S |
| 465 | 6 | 45 | 10 | 35 | 1.63 | S |
| 466 | 6 | 45 | 10 | 40 | 1.82 | S |
| 467 | 6 | 45 | 10 | 45 | 2.02 | S |
| 468 | 6 | 45 | 15 | 5 | - | U |
| 469 | 6 | 45 | 15 | 10 | 1.15 | M |
| 470 | 6 | 45 | 15 | 15 | 1.32 | S |
| 471 | 6 | 45 | 15 | 20 | 1.47 | S |
| 472 | 6 | 45 | 15 | 25 | 1.63 | S |
| 473 | 6 | 45 | 15 | 30 | 1.8 | S |
| 474 | 6 | 45 | 15 | 35 | 1.98 | S |
| 475 | 6 | 45 | 15 | 40 | 2.17 | S |
| 476 | 6 | 45 | 15 | 45 | 2.39 | S |
| 477 | 6 | 45 | 20 | 5 | 1.22 | S |
| 478 | 6 | 45 | 20 | 10 | 1.42 | S |
| 479 | 6 | 45 | 20 | 15 | 1.59 | S |
| 480 | 6 | 45 | 20 | 20 | 1.79 | S |
| 481 | 6 | 45 | 20 | 25 | 1.93 | S |
| 482 | 6 | 45 | 20 | 30 | 2.1 | S |
| 483 | 6 | 45 | 20 | 35 | 2.29 | S |
| 484 | 6 | 45 | 20 | 40 | 2.51 | S |
| 485 | 6 | 45 | 20 | 45 | 2.73 | S |
| 486 | 6 | 45 | 25 | 5 | 1.43 | S |
| 487 | 6 | 45 | 25 | 10 | 1.68 | S |
| 488 | 6 | 45 | 25 | 15 | 1.87 | S |
| 489 | 6 | 45 | 25 | 20 | 2.05 | S |
| 490 | 6 | 45 | 25 | 25 | 2.23 | S |
| 491 | 6 | 45 | 25 | 30 | 2.41 | S |
| 492 | 6 | 45 | 25 | 35 | 2.6 | S |
| 493 | 6 | 45 | 25 | 40 | 2.81 | S |
| 494 | 6 | 45 | 25 | 45 | 3.06 | S |
| 495 | 6 | 45 | 30 | 5 | 1.53 | S |
| 496 | 6 | 45 | 30 | 10 | 1.94 | S |
| 497 | 6 | 45 | 30 | 15 | 2.13 | S |
| 498 | 6 | 45 | 30 | 20 | 2.32 | S |
| 499 | 6 | 45 | 30 | 25 | 2.52 | S |
| 500 | 6 | 45 | 30 | 30 | 2.7 | S |
| 501 | 6 | 45 | 30 | 35 | 2.91 | S |
| 502 | 6 | 45 | 30 | 40 | 3.12 | S |
| 503 | 6 | 45 | 30 | 45 | 3.38 | S |
| 504 | 6 | 45 | 35 | 5 | 1.97 | S |
| 505 | 6 | 45 | 35 | 10 | 2.19 | S |
| 506 | 6 | 45 | 35 | 15 | 2.38 | S |
| 507 | 6 | 45 | 35 | 20 | 2.6 | S |
| 508 | 6 | 45 | 35 | 25 | 2.79 | S |
| 509 | 6 | 45 | 35 | 30 | 3.01 | S |
| 510 | 6 | 45 | 35 | 35 | 3.2 | S |
| 511 | 6 | 45 | 35 | 40 | 3.42 | S |
| 512 | 6 | 45 | 35 | 45 | 3.67 | S |
| 513 | 6 | 45 | 40 | 5 | 2.22 | S |
| 514 | 6 | 45 | 40 | 10 | 2.44 | S |
| 515 | 6 | 45 | 40 | 15 | 2.65 | S |
| 516 | 6 | 45 | 40 | 20 | 2.85 | S |
| 517 | 6 | 45 | 40 | 25 | 3.08 | S |
| 518 | 6 | 45 | 40 | 30 | 3.3 | S |
| 519 | 6 | 45 | 40 | 35 | 3.55 | S |
| 520 | 6 | 45 | 40 | 40 | 3.7 | S |
| 521 | 6 | 45 | 40 | 45 | 3.98 | S |
| 522 | 6 | 45 | 45 | 5 | 2.46 | S |
| 523 | 6 | 45 | 45 | 10 | 2.71 | S |
| 524 | 6 | 45 | 45 | 15 | 2.9 | S |
| 525 | 6 | 45 | 45 | 20 | 3.12 | S |
| 526 | 6 | 45 | 45 | 25 | 3.32 | S |
| 527 | 6 | 45 | 45 | 30 | 3.55 | S |
| 528 | 6 | 45 | 45 | 35 | 3.81 | S |
| 529 | 6 | 45 | 45 | 40 | 4.04 | S |
| 530 | 6 | 45 | 45 | 45 | 4.27 | S |
| 531 | 6 | 45 | 50 | 5 | 2.71 | S |
| 532 | 6 | 45 | 50 | 10 | 2.95 | S |
| 533 | 6 | 45 | 50 | 15 | 3.15 | S |
| 534 | 6 | 45 | 50 | 20 | 3.37 | S |
| 535 | 6 | 45 | 50 | 25 | 3.58 | S |
| 536 | 6 | 45 | 50 | 30 | 3.8 | S |
| 537 | 6 | 45 | 50 | 35 | 4.07 | S |
| 538 | 6 | 45 | 50 | 40 | 4.33 | S |
| 539 | 6 | 45 | 50 | 45 | 4.57 | S |
| 540 | 6 | 45 | 2 | 0 | - | U |
| 541 | 6 | 45 | 5 | 0 | - | U |
| 542 | 6 | 45 | 10 | 0 | - | U |
| 543 | 6 | 45 | 15 | 0 | - | U |
| 544 | 6 | 45 | 20 | 0 | 1 | M |
| 545 | 6 | 45 | 25 | 0 | 1.2 | M |
| 546 | 6 | 45 | 30 | 0 | 1.46 | S |
| 547 | 6 | 45 | 35 | 0 | 1.61 | S |
| 548 | 6 | 45 | 40 | 0 | 1.95 | S |
| 549 | 6 | 45 | 45 | 0 | 2.19 | S |
| 550 | 6 | 45 | 50 | 0 | 2.37 | S |
| 551 | 6 | 63.43 | 2 | 5 | - | U |
| 552 | 6 | 63.43 | 2 | 10 | - | U |
| 553 | 6 | 63.43 | 2 | 15 | - | U |
| 554 | 6 | 63.43 | 2 | 20 | - | U |
| 555 | 6 | 63.43 | 2 | 25 | - | U |
| 556 | 6 | 63.43 | 2 | 30 | - | U |
| 557 | 6 | 63.43 | 2 | 35 | - | U |
| 558 | 6 | 63.43 | 2 | 40 | - | U |
| 559 | 6 | 63.43 | 2 | 45 | - | U |
| 560 | 6 | 63.43 | 5 | 5 | - | U |
| 561 | 6 | 63.43 | 5 | 10 | - | U |
| 562 | 6 | 63.43 | 5 | 15 | - | U |
| 563 | 6 | 63.43 | 5 | 20 | - | U |
| 564 | 6 | 63.43 | 5 | 25 | - | U |
| 565 | 6 | 63.43 | 5 | 30 | - | U |
| 566 | 6 | 63.43 | 5 | 35 | - | U |
| 567 | 6 | 63.43 | 5 | 40 | - | U |
| 568 | 6 | 63.43 | 5 | 45 | 1.01 | M |
| 569 | 6 | 63.43 | 10 | 5 | - | U |
| 570 | 6 | 63.43 | 10 | 10 | - | U |
| 571 | 6 | 63.43 | 10 | 15 | - | U |
| 572 | 6 | 63.43 | 10 | 20 | - | U |
| 573 | 6 | 63.43 | 10 | 25 | - | U |
| 574 | 6 | 63.43 | 10 | 30 | 1.07 | M |
| 575 | 6 | 63.43 | 10 | 35 | 1.16 | M |
| 576 | 6 | 63.43 | 10 | 40 | 1.31 | S |
| 577 | 6 | 63.43 | 10 | 45 | 1.39 | S |
| 578 | 6 | 63.43 | 15 | 5 | - | U |
| 579 | 6 | 63.43 | 15 | 10 | - | U |
| 580 | 6 | 63.43 | 15 | 15 | 1.04 | M |
| 581 | 6 | 63.43 | 15 | 20 | 1.14 | M |
| 582 | 6 | 63.43 | 15 | 25 | 1.25 | S |
| 583 | 6 | 63.43 | 15 | 30 | 1.35 | S |
| 584 | 6 | 63.43 | 15 | 35 | 1.46 | S |
| 585 | 6 | 63.43 | 15 | 40 | 1.59 | S |
| 586 | 6 | 63.43 | 15 | 45 | 1.75 | S |
| 587 | 6 | 63.43 | 20 | 5 | 1.03 | M |
| 588 | 6 | 63.43 | 20 | 10 | 1.16 | M |
| 589 | 6 | 63.43 | 20 | 15 | 1.29 | S |
| 590 | 6 | 63.43 | 20 | 20 | 1.41 | S |
| 591 | 6 | 63.43 | 20 | 25 | 1.52 | S |
| 592 | 6 | 63.43 | 20 | 30 | 1.63 | S |
| 593 | 6 | 63.43 | 20 | 35 | 1.74 | S |
| 594 | 6 | 63.43 | 20 | 40 | 1.87 | S |
| 595 | 6 | 63.43 | 20 | 45 | 2.02 | S |
| 596 | 6 | 63.43 | 25 | 5 | 1.26 | S |
| 597 | 6 | 63.43 | 25 | 10 | 1.39 | S |
| 598 | 6 | 63.43 | 25 | 15 | 1.53 | S |
| 599 | 6 | 63.43 | 25 | 20 | 1.65 | S |
| 600 | 6 | 63.43 | 25 | 25 | 1.77 | S |
| 601 | 6 | 63.43 | 25 | 30 | 1.9 | S |
| 602 | 6 | 63.43 | 25 | 35 | 2.02 | S |
| 603 | 6 | 63.43 | 25 | 40 | 2.15 | S |
| 604 | 6 | 63.43 | 25 | 45 | 2.28 | S |
| 605 | 6 | 63.43 | 30 | 5 | 1.48 | S |
| 606 | 6 | 63.43 | 30 | 10 | 1.63 | S |
| 607 | 6 | 63.43 | 30 | 15 | 1.75 | S |
| 608 | 6 | 63.43 | 30 | 20 | 1.88 | S |
| 609 | 6 | 63.43 | 30 | 25 | 2.01 | S |
| 610 | 6 | 63.43 | 30 | 30 | 2.15 | S |
| 611 | 6 | 63.43 | 30 | 35 | 2.29 | S |
| 612 | 6 | 63.43 | 30 | 40 | 2.42 | S |
| 613 | 6 | 63.43 | 30 | 45 | 2.55 | S |
| 614 | 6 | 63.43 | 35 | 5 | 1.71 | S |
| 615 | 6 | 63.43 | 35 | 10 | 1.84 | S |
| 616 | 6 | 63.43 | 35 | 15 | 1.99 | S |
| 617 | 6 | 63.43 | 35 | 20 | 2.12 | S |
| 618 | 6 | 63.43 | 35 | 25 | 2.25 | S |
| 619 | 6 | 63.43 | 35 | 30 | 2.39 | S |
| 620 | 6 | 63.43 | 35 | 35 | 2.54 | S |
| 621 | 6 | 63.43 | 35 | 40 | 2.69 | S |
| 622 | 6 | 63.43 | 35 | 45 | 2.84 | S |
| 623 | 6 | 63.43 | 40 | 5 | 1.92 | S |
| 624 | 6 | 63.43 | 40 | 10 | 2.08 | S |
| 625 | 6 | 63.43 | 40 | 15 | 2.21 | S |
| 626 | 6 | 63.43 | 40 | 20 | 2.35 | S |
| 627 | 6 | 63.43 | 40 | 25 | 2.49 | S |
| 628 | 6 | 63.43 | 40 | 30 | 2.63 | S |
| 629 | 6 | 63.43 | 40 | 35 | 2.78 | S |
| 630 | 6 | 63.43 | 40 | 40 | 2.94 | S |
| 631 | 6 | 63.43 | 40 | 45 | 3.13 | S |
| 632 | 6 | 63.43 | 45 | 5 | 2.14 | S |
| 633 | 6 | 63.43 | 45 | 10 | 2.29 | S |
| 634 | 6 | 63.43 | 45 | 15 | 2.43 | S |
| 635 | 6 | 63.43 | 45 | 20 | 2.57 | S |
| 636 | 6 | 63.43 | 45 | 25 | 2.71 | S |
| 637 | 6 | 63.43 | 45 | 30 | 2.86 | S |
| 638 | 6 | 63.43 | 45 | 35 | 3.02 | S |
| 639 | 6 | 63.43 | 45 | 40 | 3.18 | S |
| 640 | 6 | 63.43 | 45 | 45 | 3.37 | S |
| 641 | 6 | 63.43 | 50 | 5 | 2.36 | S |
| 642 | 6 | 63.43 | 50 | 10 | 2.53 | S |
| 643 | 6 | 63.43 | 50 | 15 | 2.67 | S |
| 644 | 6 | 63.43 | 50 | 20 | 2.81 | S |
| 645 | 6 | 63.43 | 50 | 25 | 2.95 | S |
| 646 | 6 | 63.43 | 50 | 30 | 3.09 | S |
| 647 | 6 | 63.43 | 50 | 35 | 3.25 | S |
| 648 | 6 | 63.43 | 50 | 40 | 3.44 | S |
| 649 | 6 | 63.43 | 50 | 45 | 3.61 | S |
| 650 | 6 | 63.43 | 2 | 0 | - | U |
| 651 | 6 | 63.43 | 5 | 0 | - | U |
| 652 | 6 | 63.43 | 10 | 0 | - | U |
| 653 | 6 | 63.43 | 15 | 0 | - | U |
| 654 | 6 | 63.43 | 20 | 0 | - | U |
| 655 | 6 | 63.43 | 25 | 0 | 1.07 | M |
| 656 | 6 | 63.43 | 30 | 0 | 1.33 | S |
| 657 | 6 | 63.43 | 35 | 0 | 1.55 | S |
| 658 | 6 | 63.43 | 40 | 0 | 1.76 | S |
| 659 | 6 | 63.43 | 45 | 0 | 1.97 | S |
| 660 | 6 | 63.43 | 50 | 0 | 2.2 | S |
| 661 | 12 | 45 | 2 | 5 | - | U |
| 662 | 12 | 45 | 2 | 10 | - | U |
| 663 | 12 | 45 | 2 | 15 | - | U |
| 664 | 12 | 45 | 2 | 20 | - | U |
| 665 | 12 | 45 | 2 | 25 | - | U |
| 666 | 12 | 45 | 2 | 30 | - | U |
| 667 | 12 | 45 | 2 | 35 | - | U |
| 668 | 12 | 45 | 2 | 40 | - | U |
| 669 | 12 | 45 | 2 | 45 | 1 | M |
| 670 | 12 | 45 | 5 | 5 | - | U |
| 671 | 12 | 45 | 5 | 10 | - | U |
| 672 | 12 | 45 | 5 | 15 | - | U |
| 673 | 12 | 45 | 5 | 20 | - | U |
| 674 | 12 | 45 | 5 | 25 | - | U |
| 675 | 12 | 45 | 5 | 30 | - | U |
| 676 | 12 | 45 | 5 | 35 | - | U |
| 677 | 12 | 45 | 5 | 40 | 1.04 | M |
| 678 | 12 | 45 | 5 | 45 | 1.19 | M |
| 679 | 12 | 45 | 10 | 5 | - | U |
| 680 | 12 | 45 | 10 | 10 | - | U |
| 681 | 12 | 45 | 10 | 15 | - | U |
| 682 | 12 | 45 | 10 | 20 | - | U |
| 683 | 12 | 45 | 10 | 25 | - | U |
| 684 | 12 | 45 | 10 | 30 | 1.06 | M |
| 685 | 12 | 45 | 10 | 35 | 1.2 | M |
| 686 | 12 | 45 | 10 | 40 | 1.33 | S |
| 687 | 12 | 45 | 10 | 45 | 1.47 | S |
| 688 | 12 | 45 | 15 | 5 | - | U |
| 689 | 12 | 45 | 15 | 10 | - | U |
| 690 | 12 | 45 | 15 | 15 | - | U |
| 691 | 12 | 45 | 15 | 20 | - | U |
| 692 | 12 | 45 | 15 | 25 | 1.11 | M |
| 693 | 12 | 45 | 15 | 30 | 1.26 | S |
| 694 | 12 | 45 | 15 | 35 | 1.4 | S |
| 695 | 12 | 45 | 15 | 40 | 1.55 | S |
| 696 | 12 | 45 | 15 | 45 | 1.71 | S |
| 697 | 12 | 45 | 20 | 5 | - | U |
| 698 | 12 | 45 | 20 | 10 | - | U |
| 699 | 12 | 45 | 20 | 15 | 1 | M |
| 700 | 12 | 45 | 20 | 20 | 1.12 | M |
| 701 | 12 | 45 | 20 | 25 | 1.29 | S |
| 702 | 12 | 45 | 20 | 30 | 1.42 | S |
| 703 | 12 | 45 | 20 | 35 | 1.57 | S |
| 704 | 12 | 45 | 20 | 40 | 1.76 | S |
| 705 | 12 | 45 | 20 | 45 | 1.96 | S |
| 706 | 12 | 45 | 25 | 5 | - | U |
| 707 | 12 | 45 | 25 | 10 | - | U |
| 708 | 12 | 45 | 25 | 15 | 1.13 | M |
| 709 | 12 | 45 | 25 | 20 | 1.26 | S |
| 710 | 12 | 45 | 25 | 25 | 1.44 | S |
| 711 | 12 | 45 | 25 | 30 | 1.6 | S |
| 712 | 12 | 45 | 25 | 35 | 1.75 | S |
| 713 | 12 | 45 | 25 | 40 | 1.93 | S |
| 714 | 12 | 45 | 25 | 45 | 2.14 | S |
| 715 | 12 | 45 | 30 | 5 | - | U |
| 716 | 12 | 45 | 30 | 10 | 1.07 | M |
| 717 | 12 | 45 | 30 | 15 | 1.22 | S |
| 718 | 12 | 45 | 30 | 20 | 1.43 | S |
| 719 | 12 | 45 | 30 | 25 | 1.55 | S |
| 720 | 12 | 45 | 30 | 30 | 1.74 | S |
| 721 | 12 | 45 | 30 | 35 | 1.93 | S |
| 722 | 12 | 45 | 30 | 40 | 2.11 | S |
| 723 | 12 | 45 | 30 | 45 | 2.3 | S |
| 724 | 12 | 45 | 35 | 5 | 1.01 | M |
| 725 | 12 | 45 | 35 | 10 | 1.19 | M |
| 726 | 12 | 45 | 35 | 15 | 1.37 | S |
| 727 | 12 | 45 | 35 | 20 | 1.53 | S |
| 728 | 12 | 45 | 35 | 25 | 1.67 | S |
| 729 | 12 | 45 | 35 | 30 | 1.89 | S |
| 730 | 12 | 45 | 35 | 35 | 2.07 | S |
| 731 | 12 | 45 | 35 | 40 | 2.27 | S |
| 732 | 12 | 45 | 35 | 45 | 2.47 | S |
| 733 | 12 | 45 | 40 | 5 | 1.1 | M |
| 734 | 12 | 45 | 40 | 10 | 1.29 | S |
| 735 | 12 | 45 | 40 | 15 | 1.45 | S |
| 736 | 12 | 45 | 40 | 20 | 1.64 | S |
| 737 | 12 | 45 | 40 | 25 | 1.86 | S |
| 738 | 12 | 45 | 40 | 30 | 1.97 | S |
| 739 | 12 | 45 | 40 | 35 | 2.22 | S |
| 740 | 12 | 45 | 40 | 40 | 2.44 | S |
| 741 | 12 | 45 | 40 | 45 | 2.65 | S |
| 742 | 12 | 45 | 45 | 5 | 1.23 | S |
| 743 | 12 | 45 | 45 | 10 | 1.42 | S |
| 744 | 12 | 45 | 45 | 15 | 1.59 | S |
| 745 | 12 | 45 | 45 | 20 | 1.75 | S |
| 746 | 12 | 45 | 45 | 25 | 1.97 | S |
| 747 | 12 | 45 | 45 | 30 | 2.11 | S |
| 748 | 12 | 45 | 45 | 35 | 2.35 | S |
| 749 | 12 | 45 | 45 | 40 | 2.57 | S |
| 750 | 12 | 45 | 45 | 45 | 2.79 | S |
| 751 | 12 | 45 | 50 | 5 | 1.34 | S |
| 752 | 12 | 45 | 50 | 10 | 1.53 | S |
| 753 | 12 | 45 | 50 | 15 | 1.72 | S |
| 754 | 12 | 45 | 50 | 20 | 1.89 | S |
| 755 | 12 | 45 | 50 | 25 | 2.07 | S |
| 756 | 12 | 45 | 50 | 30 | 2.31 | S |
| 757 | 12 | 45 | 50 | 35 | 2.52 | S |
| 758 | 12 | 45 | 50 | 40 | 2.73 | S |
| 759 | 12 | 45 | 50 | 45 | 2.96 | S |
| 760 | 12 | 45 | 2 | 0 | - | U |
| 761 | 12 | 45 | 5 | 0 | - | U |
| 762 | 12 | 45 | 10 | 0 | - | U |
| 763 | 12 | 45 | 15 | 0 | - | U |
| 764 | 12 | 45 | 20 | 0 | - | U |
| 765 | 12 | 45 | 25 | 0 | - | U |
| 766 | 12 | 45 | 30 | 0 | - | U |
| 767 | 12 | 45 | 35 | 0 | - | U |
| 768 | 12 | 45 | 40 | 0 | - | U |
| 769 | 12 | 45 | 45 | 0 | 1.04 | M |
| 770 | 12 | 45 | 50 | 0 | 1.15 | M |
| 771 | 12 | 63.43 | 2 | 5 | - | U |
| 772 | 12 | 63.43 | 2 | 10 | - | U |
| 773 | 12 | 63.43 | 2 | 15 | - | U |
| 774 | 12 | 63.43 | 2 | 20 | - | U |
| 775 | 12 | 63.43 | 2 | 25 | - | U |
| 776 | 12 | 63.43 | 2 | 30 | - | U |
| 777 | 12 | 63.43 | 2 | 35 | - | U |
| 778 | 12 | 63.43 | 2 | 40 | - | U |
| 779 | 12 | 63.43 | 2 | 45 | - | U |
| 780 | 12 | 63.43 | 5 | 5 | - | U |
| 781 | 12 | 63.43 | 5 | 10 | - | U |
| 782 | 12 | 63.43 | 5 | 15 | - | U |
| 783 | 12 | 63.43 | 5 | 20 | - | U |
| 784 | 12 | 63.43 | 5 | 25 | - | U |
| 785 | 12 | 63.43 | 5 | 30 | - | U |
| 786 | 12 | 63.43 | 5 | 35 | - | U |
| 787 | 12 | 63.43 | 5 | 40 | - | U |
| 788 | 12 | 63.43 | 5 | 45 | - | U |
| 789 | 12 | 63.43 | 10 | 5 | - | U |
| 790 | 12 | 63.43 | 10 | 10 | - | U |
| 791 | 12 | 63.43 | 10 | 15 | - | U |
| 792 | 12 | 63.43 | 10 | 20 | - | U |
| 793 | 12 | 63.43 | 10 | 25 | - | U |
| 794 | 12 | 63.43 | 10 | 30 | - | U |
| 795 | 12 | 63.43 | 10 | 35 | - | U |
| 796 | 12 | 63.43 | 10 | 40 | - | U |
| 797 | 12 | 63.43 | 10 | 45 | 1.02 | M |
| 798 | 12 | 63.43 | 15 | 5 | - | U |
| 799 | 12 | 63.43 | 15 | 10 | - | U |
| 800 | 12 | 63.43 | 15 | 15 | - | U |
| 801 | 12 | 63.43 | 15 | 20 | - | U |
| 802 | 12 | 63.43 | 15 | 25 | - | U |
| 803 | 12 | 63.43 | 15 | 30 | - | U |
| 804 | 12 | 63.43 | 15 | 35 | - | U |
| 805 | 12 | 63.43 | 15 | 40 | 1.04 | M |
| 806 | 12 | 63.43 | 15 | 45 | 1.14 | M |
| 807 | 12 | 63.43 | 20 | 5 | - | U |
| 808 | 12 | 63.43 | 20 | 10 | - | U |
| 809 | 12 | 63.43 | 20 | 15 | - | U |
| 810 | 12 | 63.43 | 20 | 20 | - | U |
| 811 | 12 | 63.43 | 20 | 25 | - | U |
| 812 | 12 | 63.43 | 20 | 30 | 1.04 | M |
| 813 | 12 | 63.43 | 20 | 35 | 1.14 | M |
| 814 | 12 | 63.43 | 20 | 40 | 1.21 | S |
| 815 | 12 | 63.43 | 20 | 45 | 1.31 | S |
| 816 | 12 | 63.43 | 25 | 5 | - | U |
| 817 | 12 | 63.43 | 25 | 10 | - | U |
| 818 | 12 | 63.43 | 25 | 15 | - | U |
| 819 | 12 | 63.43 | 25 | 20 | - | U |
| 820 | 12 | 63.43 | 25 | 25 | 1.09 | M |
| 821 | 12 | 63.43 | 25 | 30 | 1.19 | M |
| 822 | 12 | 63.43 | 25 | 35 | 1.3 | S |
| 823 | 12 | 63.43 | 25 | 40 | 1.39 | S |
| 824 | 12 | 63.43 | 25 | 45 | 1.48 | S |
| 825 | 12 | 63.43 | 30 | 5 | - | U |
| 826 | 12 | 63.43 | 30 | 10 | - | U |
| 827 | 12 | 63.43 | 30 | 15 | 1.01 | M |
| 828 | 12 | 63.43 | 30 | 20 | 1.13 | M |
| 829 | 12 | 63.43 | 30 | 25 | 1.23 | S |
| 830 | 12 | 63.43 | 30 | 30 | 1.31 | S |
| 831 | 12 | 63.43 | 30 | 35 | 1.42 | S |
| 832 | 12 | 63.43 | 30 | 40 | 1.54 | S |
| 833 | 12 | 63.43 | 30 | 45 | 1.66 | S |
| 834 | 12 | 63.43 | 35 | 5 | - | U |
| 835 | 12 | 63.43 | 35 | 10 | 1.03 | M |
| 836 | 12 | 63.43 | 35 | 15 | 1.14 | M |
| 837 | 12 | 63.43 | 35 | 20 | 1.27 | S |
| 838 | 12 | 63.43 | 35 | 25 | 1.35 | S |
| 839 | 12 | 63.43 | 35 | 30 | 1.46 | S |
| 840 | 12 | 63.43 | 35 | 35 | 1.56 | S |
| 841 | 12 | 63.43 | 35 | 40 | 1.62 | S |
| 842 | 12 | 63.43 | 35 | 45 | 1.81 | S |
| 843 | 12 | 63.43 | 40 | 5 | 1.01 | M |
| 844 | 12 | 63.43 | 40 | 10 | 1.13 | M |
| 845 | 12 | 63.43 | 40 | 15 | 1.29 | S |
| 846 | 12 | 63.43 | 40 | 20 | 1.24 | S |
| 847 | 12 | 63.43 | 40 | 25 | 1.49 | S |
| 848 | 12 | 63.43 | 40 | 30 | 1.58 | S |
| 849 | 12 | 63.43 | 40 | 35 | 1.7 | S |
| 850 | 12 | 63.43 | 40 | 40 | 1.81 | S |
| 851 | 12 | 63.43 | 40 | 45 | 1.97 | S |
| 852 | 12 | 63.43 | 45 | 5 | 1.13 | M |
| 853 | 12 | 63.43 | 45 | 10 | 1.25 | S |
| 854 | 12 | 63.43 | 45 | 15 | 1.4 | S |
| 855 | 12 | 63.43 | 45 | 20 | 1.51 | S |
| 856 | 12 | 63.43 | 45 | 25 | 1.64 | S |
| 857 | 12 | 63.43 | 45 | 30 | 1.73 | S |
| 858 | 12 | 63.43 | 45 | 35 | 1.83 | S |
| 859 | 12 | 63.43 | 45 | 40 | 1.96 | S |
| 860 | 12 | 63.43 | 45 | 45 | 2.07 | S |
| 861 | 12 | 63.43 | 50 | 5 | 1.21 | S |
| 862 | 12 | 63.43 | 50 | 10 | 1.31 | S |
| 863 | 12 | 63.43 | 50 | 15 | 1.49 | S |
| 864 | 12 | 63.43 | 50 | 20 | 1.64 | S |
| 865 | 12 | 63.43 | 50 | 25 | 1.7 | S |
| 866 | 12 | 63.43 | 50 | 30 | 1.83 | S |
| 867 | 12 | 63.43 | 50 | 35 | 1.97 | S |
| 868 | 12 | 63.43 | 50 | 40 | 2.06 | S |
| 869 | 12 | 63.43 | 50 | 45 | 2.24 | S |
| 870 | 12 | 63.43 | 2 | 0 | - | U |
| 871 | 12 | 63.43 | 5 | 0 | - | U |
| 872 | 12 | 63.43 | 10 | 0 | - | U |
| 873 | 12 | 63.43 | 15 | 0 | - | U |
| 874 | 12 | 63.43 | 20 | 0 | - | U |
| 875 | 12 | 63.43 | 25 | 0 | - | U |
| 876 | 12 | 63.43 | 30 | 0 | - | U |
| 877 | 12 | 63.43 | 35 | 0 | - | U |
| 878 | 12 | 63.43 | 40 | 0 | - | U |
| 879 | 12 | 63.43 | 45 | 0 | - | U |
| 880 | 12 | 63.43 | 50 | 0 | 1.03 | M |
References
- Massey, C.; Della Pasqua, F.; Holden, C.; Kaiser, A.; Richards, L.; Wartman, J.; McSaveney, M.J.; Archibald, G.; Yetton, M.; Janku, L. Rock slope response to strong earthquake shaking. Landslides 2017, 14, 249–268. [Google Scholar] [CrossRef]
- Li, Q.; Wang, Y.M.; Zhang, K.B.; Yu, H.; Tao, Z.Y. Field investigation and numerical study of a siltstone slope instability induced by excavation and rainfall. Landslides 2020, 17, 1485–1499. [Google Scholar] [CrossRef]
- Nagatani, K.; Abe, M.; Osuka, K.; Chun, P.-j.; Okatani, T.; Nishio, M.; Chikushi, S.; Matsubara, T.; Ikemoto, Y.; Asama, H. Innovative technologies for infrastructure construction and maintenance through collaborative robots based on an open design approach. Adv. Robot. 2021, 2021, 715–722. [Google Scholar] [CrossRef]
- Das, S.K.; Biswal, R.K.; Sivakugan, N.; Das, B. Classification of slopes and prediction of factor of safety using differential evolution neural networks. Environ. Earth Sci. 2011, 64, 201–210. [Google Scholar] [CrossRef]
- Sloan, S.W. Geotechnical stability analysis. Geotechnique 2013, 63, 531–572. [Google Scholar] [CrossRef]
- Cheng, Y.M.; Lansivaara, T.; Wei, W.B. Two-dimensional slope stability analysis by limit equilibrium and strength reduction methods. Comput. Geotech. 2007, 34, 137–150. [Google Scholar] [CrossRef]
- Reale, C.; Xue, J.; Gavin, K. System reliability of slopes using multimodal optimisation. Geotechnique 2016, 66, 413–423. [Google Scholar] [CrossRef]
- Tschuchnigg, F.; Schweiger, H.F.; Sloan, S.W.; Lyamin, A.V.; Raissakis, I. Comparison of finite-element limit analysis and strength reduction techniques. Geotechnique 2015, 65, 249–257. [Google Scholar] [CrossRef]
- Song, D.; Chen, Z.; Chao, H.; Ke, Y.; Nie, W. Numerical study on seismic response of a rock slope with discontinuities based on the time-frequency joint analysis method. Soil Dyn. Earthq. Eng. 2020, 133, 106112. [Google Scholar] [CrossRef]
- Sakellariou, M.G.; Ferentinou, M.D. A study of slope stability prediction using neural networks. Geotech. Geol. Eng. 2005, 23, 419–445. [Google Scholar] [CrossRef]
- Samui, P. Slope stability analysis: A support vector machine approach. Environ. Geol. 2008, 56, 255–267. [Google Scholar] [CrossRef]
- Zhou, J.; Li, E.; Yang, S.; Wang, M.; Shi, X.; Yao, S.; Mitri, H.S. Slope stability prediction for circular mode failure using gradient boosting machine approach based on an updated database of case histories. Saf. Sci. 2019, 118, 505–518. [Google Scholar] [CrossRef]
- Mahmoodzadeh, A.; Mohammadi, M.; Farid Hama Ali, H.; Hashim Ibrahim, H.; Nariman Abdulhamid, S.; Nejati, H.R. Prediction of safety factors for slope stability: Comparison of machine learning techniques. Nat. Hazards 2022, 111, 1771–1799. [Google Scholar] [CrossRef]
- Shi, N.; Xu, J.; Wurster, S.W.; Guo, H.; Woodring, J.; Van Roekel, L.P.; Shen, H.W. GNN-Surrogate: A Hierarchical and Adaptive Graph Neural Network for Parameter Space Exploration of Unstructured-Mesh Ocean Simulations. IEEE Trans. Vis. Comput. Graph. 2022, 28, 2301–2313. [Google Scholar] [CrossRef] [PubMed]
- Jain, A.K.; Mao, J.; Mohiuddin, K.M. Artificial neural networks: A tutorial. Computer 1996, 29, 31–44. [Google Scholar] [CrossRef]
- Dreiseitl, S.; Ohno-Machado, L. Logistic regression and artificial neural network classification models: A methodology review. J. Biomed. Inform. 2002, 35, 352–359. [Google Scholar] [CrossRef]
- Georgevici, A.I.; Terblanche, M. Neural networks and deep learning: A brief introduction. Intensive Care Med. 2019, 45, 712–714. [Google Scholar] [CrossRef]
- Dahiya, N.; Saini, B.; Chalak, H.D. Deep neural network-based storey drift modelling of precast concrete structures using RStudio. J. Soft Comput. Civ. Eng. 2021, 5, 88–100. [Google Scholar] [CrossRef]
- Yamane, T.; Chun, P.-J. Crack detection from a concrete surface image based on semantic segmentation using deep learning. J. Adv. Concr. Technol. 2020, 18, 493–504. [Google Scholar] [CrossRef]
- Chun, P.-j.; Yamane, T.; Tsuzuki, Y. Automatic detection of cracks in asphalt pavement using deep learning to overcome weaknesses in images and gis visualization. Appl. Sci. 2021, 11, 892. [Google Scholar] [CrossRef]
- Chun, P.-j.; Yamane, T.; Maemura, Y. A deep learning-based image captioning method to automatically generate comprehensive explanations of bridge damage. Comput. Civ. Infrastruct. Eng. 2022, 37, 1387–1401. [Google Scholar] [CrossRef]
- Yamane, T.; Chun, P.-j.; Dang, J.; Honda, R. Recording of bridge damage areas by 3D integration of multiple images and reduction of the variability in detected results. Comput. Civ. Infrastruct. Eng. 2023, 1–17. [Google Scholar] [CrossRef]
- Xu, J.J.; Zhang, H.; Tang, C.S.; Cheng, Q.; Liu, B.; Shi, B. Automatic soil desiccation crack recognition using deep learning. Geotechnique 2022, 72, 337–349. [Google Scholar] [CrossRef]
- Lozano-Diez, A.; Zazo, R.; Toledano, D.T.; Gonzalez-Rodriguez, J. An analysis of the influence of deep neural network (DNN) topology in bottleneck feature based language recognition. PLoS ONE 2017, 12, e0182580. [Google Scholar] [CrossRef]
- Xu, Y.; Du, J.; Dai, L.R.; Lee, C.H. A regression approach to speech enhancement based on deep neural networks. IEEE/ACM Trans. Audio Speech Lang. Process. 2015, 23, 7–19. [Google Scholar] [CrossRef]
- Liu, S.Y.; Shao, L.T.; Li, H.J. Slope stability analysis using the limit equilibrium method and two finite element methods. Comput. Geotech. 2015, 63, 291–298. [Google Scholar] [CrossRef]


| No. | Cohesion /kPa | Friction Angle /° | FOS * | FOS_LEM [6] | FOS Difference | Relative Error /% |
|---|---|---|---|---|---|---|
| 1 | 2 | 5 | - | 0.25 | - | - |
| 2 | 2 | 15 | - | 0.50 | - | - |
| 3 | 2 | 25 | - | 0.74 | - | - |
| 4 | 2 | 45 | 1.15 | 1.35 | 0.20 | 14.81 |
| 5 | 5 | 5 | - | 0.41 | - | - |
| 6 | 5 | 15 | - | 0.70 | - | - |
| 7 | 5 | 25 | - | 0.98 | - | - |
| 8 | 5 | 35 | 1.25 | 1.28 | 0.03 | 2.34 |
| 9 | 5 | 45 | 1.57 | 1.65 | 0.08 | 4.85 |
| 10 | 10 | 5 | - | 0.65 | - | - |
| 11 | 10 | 15 | 1.02 | 0.98 | 0.04 | 4.08 |
| 12 | 10 | 25 | 1.32 | 1.30 | 0.02 | 1.54 |
| 13 | 10 | 35 | 1.64 | 1.63 | 0.01 | 0.61 |
| 14 | 10 | 45 | 2.02 | 2.04 | 0.02 | 0.98 |
| 15 | 20 | 5 | 1.22 | 1.06 | 0.16 | 15.09 |
| 16 | 20 | 15 | 1.59 | 1.48 | 0.11 | 7.43 |
| 17 | 20 | 25 | 1.93 | 1.85 | 0.08 | 4.32 |
| 18 | 20 | 35 | 2.29 | 2.24 | 0.05 | 2.23 |
| 19 | 20 | 45 | 2.73 | 2.69 | 0.04 | 1.49 |
| 20 | 5 | 0 | - | 0.20 | - | - |
| 21 | 10 | 0 | - | 0.40 | - | - |
| 22 | 20 | 0 | 1.00 | 0.80 | 0.20 | 25.00 |
| Output | Training | Cross-Validation Training | Test | |
|---|---|---|---|---|
| Three classes | Error | 0.0081 | 0.1104 | 0.0778 |
| Accuracy | 0.9919 | 0.8896 | 0.9222 | |
| Two classes | Error | 0.0308 | 0.0908 | 0.0685 |
| Accuracy | 0.9692 | 0.9092 | 0.9315 | |
| Methods | Numerical Simulation | Classification (Three Classes) | Regression | ||
|---|---|---|---|---|---|
| Set | - | Training | Test | Training | Test |
| Case No. | 1 | 616 (70%) | 264 (30%) | 704 (80%) | 176 (20%) |
| Time/s | 125 | 1.549320 | 0.001513 | 0.045756 | 0.003117 |
| No. | Cohesion /kPa | Friction Angle /° | FOS_LEM [6] | FOS by Surrogate Model | The Difference | Relative Error /% |
|---|---|---|---|---|---|---|
| 4 | 2 | 45 | 1.35 | 1.16 | −0.19 | −14.37 |
| 8 | 5 | 35 | 1.28 | 1.24 | −0.04 | −3.41 |
| 9 | 5 | 45 | 1.65 | 1.54 | −0.11 | −6.72 |
| 12 | 10 | 25 | 1.30 | 1.33 | 0.03 | 1.97 |
| 13 | 10 | 35 | 1.63 | 1.63 | 0.00 | 0.04 |
| 14 | 10 | 45 | 2.04 | 2.02 | −0.02 | −1.05 |
| 15 | 20 | 5 | 1.06 | 1.16 | 0.10 | 9.58 |
| 16 | 20 | 15 | 1.48 | 1.60 | 0.12 | 8.11 |
| 17 | 20 | 25 | 1.85 | 1.93 | 0.08 | 4.56 |
| 18 | 20 | 35 | 2.24 | 2.29 | 0.05 | 2.40 |
| 19 | 20 | 45 | 2.69 | 2.75 | 0.06 | 2.21 |
| Slope Classification | FOS | Countermeasures |
|---|---|---|
| U | <1.0 | Prompt treatment |
| M | 1.0 ≤ FOS ≤ 1.2 | Monitoring and early warning |
| S | >1.2 | Regular monitoring and maintenance |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, X.; Nishio, M.; Sugawara, K.; Iwanaga, S.; Chun, P.-j. Surrogate Model Development for Slope Stability Analysis Using Machine Learning. Sustainability 2023, 15, 10793. https://doi.org/10.3390/su151410793
Li X, Nishio M, Sugawara K, Iwanaga S, Chun P-j. Surrogate Model Development for Slope Stability Analysis Using Machine Learning. Sustainability. 2023; 15(14):10793. https://doi.org/10.3390/su151410793
Chicago/Turabian StyleLi, Xianfeng, Mayuko Nishio, Kentaro Sugawara, Shoji Iwanaga, and Pang-jo Chun. 2023. "Surrogate Model Development for Slope Stability Analysis Using Machine Learning" Sustainability 15, no. 14: 10793. https://doi.org/10.3390/su151410793
APA StyleLi, X., Nishio, M., Sugawara, K., Iwanaga, S., & Chun, P.-j. (2023). Surrogate Model Development for Slope Stability Analysis Using Machine Learning. Sustainability, 15(14), 10793. https://doi.org/10.3390/su151410793








