Water Hammer Protection Characteristics and Hydraulic Performance of a Novel Air Chamber with an Adjustable Central Standpipe in a Pressurized Water Supply System

Abstract

Water scarcity is an urgent issue for social and economic development in arid and semi-arid areas. Constructing long-distance pressurized water supply projects is a commonly used measure to solve water scarcity problems in these areas. With the increasing complexity of long-distance pressurized water supply projects, the issue of water hammer protection has become more and more prominent. Air chambers have been widely used to solve the issue of water hammer accidents. In this paper, we propose a novel air chamber with an adjustable central standpipe, and then analyze the hydraulic performance, as well as the water hammer protection characteristics, of the proposed novel air chamber using numerical simulations. The influences of the inner length, the diameter of the central standpipe, and the diameter of the bottom connecting pipe on the hydraulic performance of the air chamber are also studied. Then, the optimization of the relevant parameters of the central standpipe for the proposed air chamber is conducted. In addition, the volumes of the proposed air chamber and conventional air chambers are compared.

1. Introduction

Water resources play an irreplaceable role in social and economic development. In China, humid and semi-humid areas that are appropriate for social and economic development are merely 47% of the total land mass; the other 53% are arid and semi-arid areas. Hydraulic engineering projects, such as water supply projects, play important roles in sustainable water resource management, particularly in scenarios affected by climate change and extreme aridity, for the purpose of solving the uneven distribution of water resources and promoting global sustainable development. Water scarcity is an urgent issue for water resource management, especially in arid and semi-arid areas. Long-distance pressurized water supply systems provide a solution for solving water scarcity problems due to their high flow rate and long pipelines. Issues such as water hammer accidents occur during the operation of water supply projects, which greatly affect the safety operation of the projects. Therefore, it is essential to pay attention to the physical and numerical modeling of hydraulic characteristics in water supply projects so as to reveal the underlying mechanisms of these problems.

Water hammer accidents are caused by the rapid closing or opening of valves or the sudden starting or stopping of pumps, and occasionally by pump power failure. In the case of the pressure in the pipeline rising (several- or ten-fold higher than normal pressure) in an instant, pipe bursting and other accidents may occur. In addition, when the pressure in the pipeline is insufficient, collapse and other accidents may occur [1]. At present, with the water supply system becoming more and more complex, the issue of water hammer protection becomes more and more important. Thus, numbers of researchers have given insights to this topic, and provided solutions for water hammer protection [2,3].

Water hammer protection measures commonly used in pressurized water supply systems include one-way surge tanks [4], double-chamber surge tanks [5,6], air vessels [7,8], air valves [9], over-pressure relief valves [10], air chambers [11], etc. Among these, surge tanks are commonly used for long-distance water supply systems with low head and large flow. For high head water supply systems, the cost of using surge tanks is high. Air vessels and air valves can control the generation of liquid column separation, but their water hammer protection performance is affected by multiple factors and the reliability is not sufficient. Other measures, such as over-pressure relief valves, are generally used in combination with other measures and serve as auxiliary measures. Compared to other water hammer protection measures, air chambers not only have the advantage of high reliably, but also can effectively reduce the positive and negative water hammer in pipelines. Specifically, air chambers have excellent performance on water hammer protection in high lift and low flow rate water supply systems. A substantial amount of research concerning hydraulic performance and water hammer protection characteristics has been conducted in previous studies. Li et al. performed a transient analysis for a conventional air chamber using the characteristic line method [11]. Zhao et al. compared several different formulations and water hammer protection schemes and found that air chambers with different friction head loss formulas have effective performance in water hammer protection [12]. On the basis of the principal mathematical model of air chambers, a novel mathematical model based on the water hammer protection of air chambers with air valves was proposed [13,14].

Conventional air chambers can be classified into three types: water-filled air chambers, inflatable air chambers, and diaphragm air chambers [15]. Conventional air chambers need to be equipped with air compressors for regular automatic water replenishment, which increases the project investment and the difficulty of maintenance. Due to the high costs, conventional air chambers with air compressors are usually used in small-scale flow regulation projects. Proposing innovative air chambers which have are low cost and easily maintained is of great significance for water supply systems. In recent years, a novel air-valve-regulating chamber was proposed, whereby a short pipe is set in the water pipeline with the top of the short pipe sealed, and an air valve is installed on the top of the chamber, which significantly reduces the project investment [13]. An air chamber based on the air valve pressure chamber was proposed, whereby a central riser is placed on the upper center of the air chamber to ensure that the air in the chamber will not be emptied, which improves the water hammer protection performance and can operate without an air compressor [16]. Comparing the schemes of air chambers at different positions of the water transmission pipeline, setting air chambers at the head and tail of the pipeline can effectively reduce the total volume of air chambers without reducing the performance of water hammer protection [17,18]. In long-distance water supply systems, installing air chambers can effectively prevent water hammer accidents. However, when the water flow rate is large and unsteady, the volume required by the air chamber is often large, which also increases the project cost indirectly. Thus, certain measures, such as air valves, outlet overflow tanks, and pressure-regulating towers have been combined to make water hammer protection more economical and reliable [19]. It is important to determine the type and position of the air valve and the size of the air chamber to adjust the pressure and minimize the total cost [20,21].

For the optimization of an air chamber, the main parameters include the volume of the air chamber and the diameter of the connecting pipe. Under normal working conditions, the pre-stored pressure of the air chamber is about 90% of the pump pressure [22]. The larger the initial air volume in the chamber, the better the performance of the water hammer protection. Water flow into and flow out of the air chamber are the same, and the head loss caused by water flow into the air chamber is 2.5 times higher than that caused by water flow out of the air chamber [23]. Reducing the diameter of the bypass pipe or throttle opening is conducive to optimizing the volume of the air chamber [24]. In recent years, methods that combining physical model experiments and numerical simulation have been widely used to quantify the influence of air chamber volume under different working conditions on the water hammer protection performance [25]. Researchers found that when the air–water ratio ranges between 20% and 30%, increasing the proportion of air can effectively control the rise of pressure in the pipe: that is, the air chamber has a good performance in water hammer protection, and the volume of the air chamber need not increase.

To optimize the conventional air chamber in a long-distance pressurized water supply system, we propose a novel air chamber with an adjustable central standpipe and analyze the hydraulic performance, as well as the water hammer protection characteristics, of the proposed air chamber. With the support of the central standpipe, the proposed air chamber replenishes the air in the chamber relying on the air valve system, which is different from conventional air chambers which need to be equipped with air compressors. The risk of water hammer accidents varies with the requirements of the water supply system. As the water requirements change with the development of the society and economy, the flow rate of the water supply project may increase or decrease compared to the designed flow rate from when the project was put into operation. Thus, adjusting the characteristics of water hammer protection according to the requirements of the water supply project is of great importance. As the parameters of the central standpipe are adjustable, the proposed air chamber could adjust the water hammer protection performance of the air chamber by varying the parameters of the central standpipe. We then investigate the effect of the inner length and the diameter of the central standpipe on the water hammer protection performance. As the volume of chamber is also a factor influencing the cost, the volume of the proposed air chamber is also compared with conventional air chambers.

This paper is organized as follows: the working principle is presented in Section 2. The mathematical model is illustrated in Section 3. A case study is analyzed in Section 4. Concluding remarks are presented in Section 5.

2. Working Principle

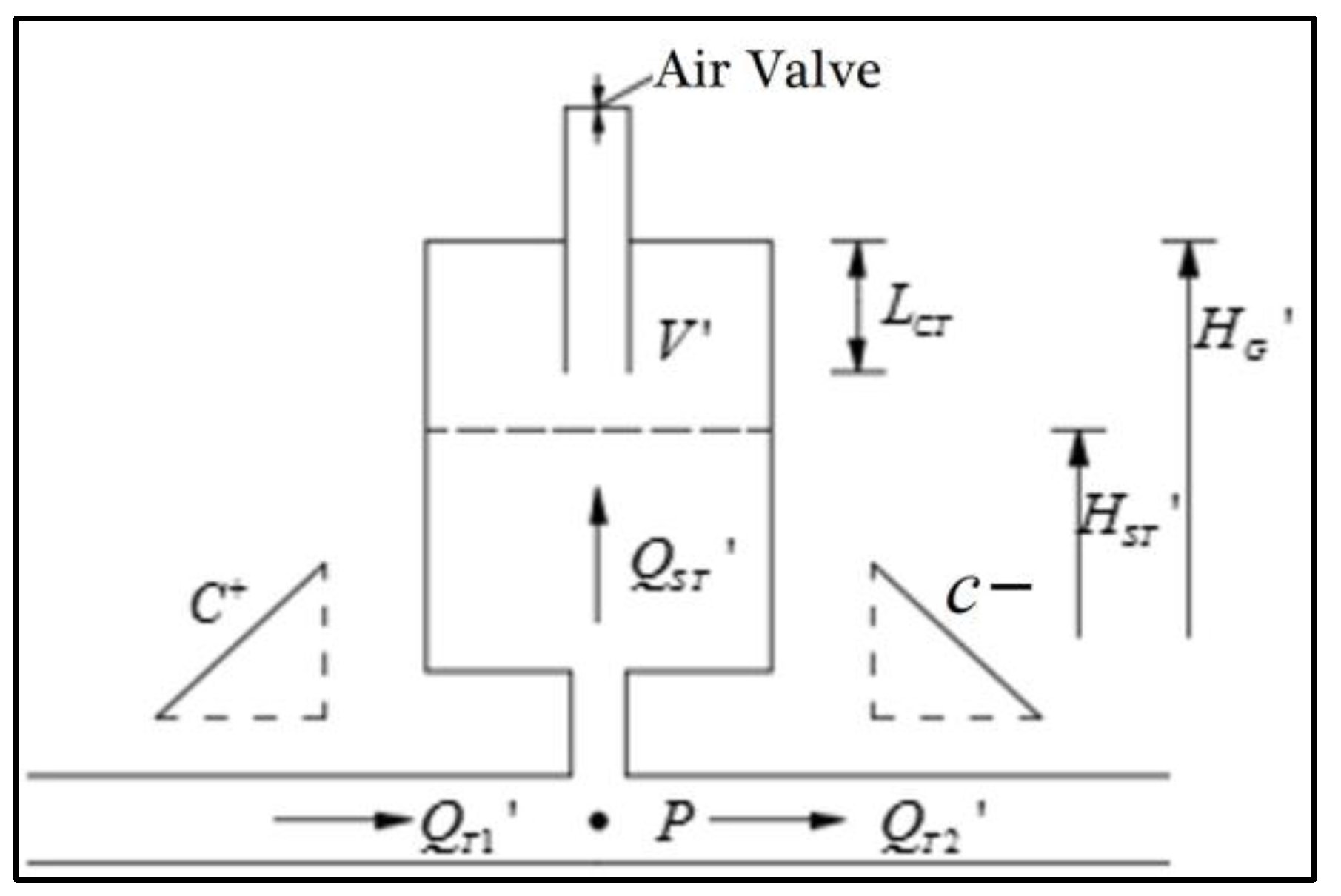
Figure 1 shows the working principle of the air chamber with an adjustable central standpipe, which has an air valve on the top of the chamber to replenish air. At the top center of the air chamber, a flexible vertical pipe that can move up and down is installed, which connects the air valve and the chamber. The air valve system supplements the air chamber with an adjustable central standpipe.

As shown in Figure 1a, when the water pump loses transmission capacity or the pump is stopped, the air in the chamber begins to expand, and the chamber sends liquid to the main pipeline to avoid negative pressure in the pipeline. At this stage, the proposed novel air chamber works in the same way as conventional air chambers, and the water level in the chamber varies with the variation of pressure. When the water level drops and the pressure drops to the opening pressure of the air valve system, the air valve system opens, allowing a large amount of air flow into the standpipe to avoid negative pressure in the chamber. The volume of air in the chamber increases through the air valve system to balance the liquid flowing out from the chamber, which stabilizes the pressure head of the chamber.

As shown in Figure 1b, when the liquid in the pipeline flows back, the pressure in the pipeline rises and the water in the pipeline flows into the chamber. The water level in the chamber increases with the increase in the water pressure. Then, the air in the chamber is compressed. As the air valve system controls the flow of air, the air valve can be slowly discharged to prevent the pressure rising unexpectedly. When the water level reaches the lower end of the center standpipe, air near the lowest point of the central standpipe is compressed and passes through the standpipe. The air valve is drained, and the liquid enters the central standpipe. When the water level reaches the top of the central standpipe, the air valve system closes, and the remaining air in the chamber is compressed by the back flow of water. When the hydraulic transient decays and the pipe pressure stabilizes, the adjustable central standpipe gradually returns to a resting state, and then, at the end of the hydraulic transient, the central standpipe is filled with water.

In order to ensure that the proposed air chamber keeps working during the pump shutdown process, the water level of the transient pressure gauge should drop and the piping system configuration should be suitable. In this case, the air chamber provides water hammer protection when the pump is stopped and relies on the air valve system to replenish air into the chamber, which is different from conventional air chambers which need to be equipped with air compressors. As the air chamber with an adjustable central standpipe does not rely on either an air compressor, nor any power source, it can be installed at any indicated location along the main pipeline of the water supply system. At the connecting position to the main pipe, the throttling control of the flow into the chamber needs to be considered. In addition, the volume of the proposed novel air chamber should be determined based on the actual engineering demands, to ensure that the chamber contains enough air.

3. Mathematical Model

This section presents the mathematical expressions of the proposed air chamber. A sketch of the proposed air chamber is shown in Figure 2.

1.

Case: $H_{ST}{}^{`}\ge H_G{}^{`}-L_{CT}$

${\mathrm{H}}_{\mathrm{ST}}{}^{`}$ is the height of the water level in the chamber; ${\mathrm{H}}_{\mathrm{G}}{}^{`}$ is the height of the chamber; ${\mathrm{L}}_{\mathrm{CT}}$ is the length of the central standpipe. When the intake and exhaust port at the bottom of the central vertical pipe are below the water surface, the intake and exhaust function is lost, and the air is sealed in the chamber to form a closed air chamber.

When the water pump works under normal operational conditions, the pressure head inside and outside of the proposed air chamber remains balanced, as shown below:

$$H_A{}^{`}\ge H_P{}^{`}-H_{ST}{}^{`}$$

(1)

where ${\mathrm{H}}_{\mathrm{A}}{}^{`}$ is the initial pressure in the chamber and ${\mathrm{H}}_{\mathrm{P}}{}^{`}$ is the piezometric head at node P at the bottom of the chamber.

Assuming the air pressure in the chamber is evenly distributed at any time, regardless of the inertia of air and the friction of the chamber wall, we can assume that the air follows a reversible variable relationship:

$$p^{`}{V}^{`k}=C^{`}$$

(2)

where $p^{`}$ is the absolute pressure of air, $V^{`}$ is the volume of air in the chamber, $C^{`}$ is a constant, and $k$ is a polytropic index which relates to the thermodynamics of air. Here, the multi-party exponent $k$ refers to the value of the conventional air chamber and is taken as a single constant of 1.2.

The continuous equation of the fluid at point P at the bottom of the proposed air chamber is as follows:

$$Q_{T1}{}^{`}=Q_{ST}{}^{`}+Q_{T2}{}^{`}$$

(3)

where $Q_{T1}{}^{`}$ is the upstream flow at the P node; $Q_{ST}{}^{`}$ is the fluid flow into and flow out of the chamber, taking the inflow as a positive value; and $Q_{T2}{}^{`}$ is the downstream flow at the P node. The effective cross-sectional area of the proposed air chamber $A_{ST}{}^{``}$ is:

$$A_{ST}{}^{``}=A_{ST}{}^{`}-A_{CT}$$

(4)

where $A_{ST}{}^{``}$ is the effective cross-sectional area of the air chamber, $A_{ST}{}^{`}$ is the cross-sectional area of the air chamber, and $A_{CT}$ is the cross-sectional area of the central standpipe.

The equation for the liquid level, air volume, and flow into the adjustable central riser air chamber is as follows:

$$A_{ST}{}^{``}\frac{d{H}_{st}{}^{`}}{dt}=-\frac{d{V}^{`}}{dt}=Q_{ST}{}^{`}$$

(5)

Integrating $P{V}_a=M{R}^{`}T$ and selecting a second-order approximation, we can obtain the expressions of the height of the water level in the chamber $H_{ST}{}^{`}$ and the volume of air in the chamber $V^{`}$:

$$H_{ST}{}^{`}=H_{ST0}{}^{`}+0.5\mathsf{\Delta }t\frac{Q_{ST}{}^{`}+Q_{ST0}{}^{`}}{A_{ST}{}^{``}}$$

(6)

$$V^{`}=V_0{}^{`}-0.5\mathsf{\Delta }t\left(Q_{ST}{}^{`}+Q_{ST0}{}^{`}\right)$$

(7)

The relationship among the piezometric pipe head at node P $H_P{}^{`}$, the absolute pressure of the air in the chamber $p^{`}$, and the height of the water level $H_{st}{}^{`}$ in the proposed air chamber can be expressed as follows:

$$H_P{}^{`}=\left(\frac{p^{`}}{{\rho }_{w}g}-\overline{H}\right)+H_{st}{}^{`}+{\sigma }^{`}\frac{\left|Q_{ST}{}^{`}\right|Q_{ST}{}^{`}}{2g{A}_{\omega }{}^{`2}}$$

(8)

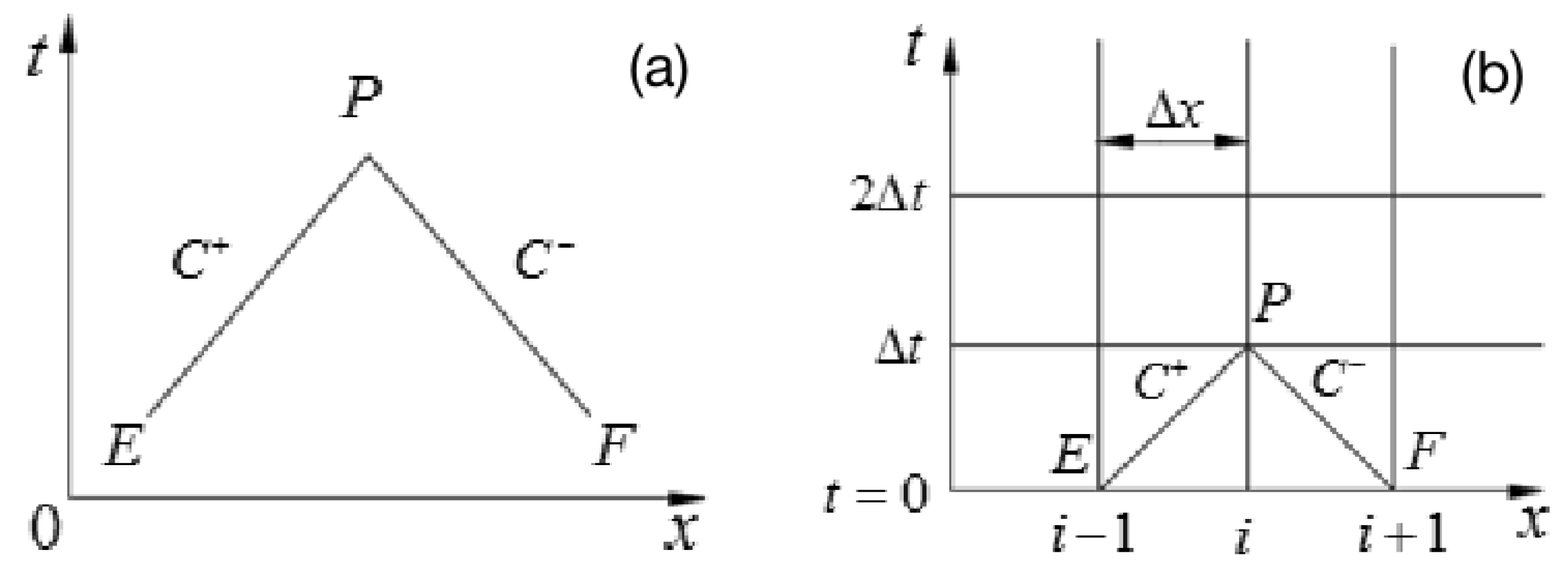
where $\overline{H}$ is the local atmospheric pressure, ${\sigma }^{`}$ is the impedance orifice coefficient, $A_{\omega }{}^{`}$ is the cross-sectional area of the connecting pipe, ${\rho }_w$ is the water density, and $g$ is the gravity acceleration. The characteristic line method is a commonly used method for solving water hammer problems, with the advantages of high accuracy and easy computation. For a given pipe on an x-t plane, the positive characteristic line $C^{+}$ and negative characteristic line $C^{-}$ depend on the rate of the grade of the pipe as shown in Figure 3.

The simplified functions of the positive characteristic line $C^{+}$ and negative characteristic line $C^{-}$ are as follows:

$$C^{+}:H_{Pi}{}^{`}=C_P-B_P{Q}_{Pi}{}^{`}$$

(9)

$$C^{-}:H_{Pi}{}^{`}=C_M+B_M{Q}_{Pi}{}^{`}$$

(10)

where $C_P$, $C_M$, $B_P$, and $B_M$ are known parameters. The upstream flow at the P node $Q_{T1}{}^{`}$ and the downstream flow at the P node $Q_{T2}{}^{`}$ can be obtained from Equations (9) and (10):

$$Q_{T1}{}^{`}=\frac{C_P-H_P}{B_P}$$

(11)

$$Q_{T2}{}^{`}=\frac{H_P-C_M}{B_M}$$

(12)

Combining Equations (3), (11) and (12), we can obtain:

$$H_P{}^{`}=\left[\left(\frac{C_P}{B_P}+\frac{C_M}{B_M}-Q_{ST}{}^{`}\right)\right]/\left(\frac{1}{B_P}+\frac{1}{B_M}\right)$$

(13)

Substituting Equations (6) and (13) into Equation (8), we can obtain:

$$\frac{p^{`}}{{\rho }_{w}g}=\left[\left(\frac{C_P}{B_P}+\frac{C_M}{B_M}-Q_{ST}{}^{`}\right)\right]/\left(\frac{1}{B_P}+\frac{1}{B_M}\right)+\overline{H}-H_{ST0}{}^{`}-0.5\mathsf{\Delta }t\frac{Q_{ST}{}^{`}+Q_{ST0}{}^{`}}{A_{ST}{}^{``}}-{\sigma }^{`}\frac{\left|Q_{ST}{}^{`}\right|Q_{ST}{}^{`}}{2g{A}_{\omega }{}^{`2}}$$

(14)

Equations (7) and (14) can be simultaneously solved by the Newton–Levson method, and the required variables $H_{ST}$, $V^{`},Q_{T1}{}^{`},Q_{T2}{}^{`},\mathrm{and} p^{`}$ can be obtained.

2.

Case: $H_{ST}{}^{`}<H_G{}^{`}-L_{CT}$

When the air intake and exhaust port at the bottom of the central standpipe are located above the water surface, the air intake and exhaust function can be exerted, and the air can be circulated. Then, the function of the proposed air chamber is equivalent to an air valve.

The boundary conditions can be divided into the following four cases depending on the velocity of air that flows into and flows out of the air chamber:

(1)

Air flows in at a subsonic speed:

$${\dot{M}}_{in}{}^{`}=C_{in}{}^{`}{A}_{in}{}^{`}\sqrt{7p_{abs}{\rho }_0{\left(\frac{p^{`}}{p_{abs}}\right)}^{1.4286}-{\left(\frac{p^{`}}{p_{abs}}\right)}^{1.714}},0.53p_{abs}<p^{`}<p_{abs}$$

(15)

(2)

Air flows in at a critical flow rate:

$${\dot{M}}_{in}{}^{`}=C_{in}{}^{`}{A}_{in}{}^{`}\frac{0.686}{\sqrt{R^{`}{T}_{abs}}}{p}_{abs},\hspace{1em}{p}^{`}\le 0.53p_{abs}$$

(16)

(3)

Air flows out at a subsonic speed:

$${\dot{M}}_{out}{}^{`}=-C_{out}{}^{`}{A}_{out}{}^{`}\sqrt{\frac{7}{R^{`}{T}^{`}}\left({\left(\frac{p^{`}}{p_{abs}}\right)}^{-1.4286}-{\left(\frac{p^{`}}{p_{abs}}\right)}^{-1.714}\right)},p_{abs}<p^{`}<\frac{p_{abs}}{0.53}$$

(17)

(4)

Air flows out at a critical flow rate:

$${\dot{M}}_{out}{}^{`}=-C_{out}{}^{`}{A}_{out}{}^{`}\frac{0.686p^{`}}{\sqrt{R^{`}{T}^{`}}},p^{`}\ge \frac{p_{abs}}{0.53}$$

(18)

where ${\dot{M}}_{in}{}^{`}$ and ${\dot{M}}_{out}{}^{`}$ are the mass flow rate of the air inflow and outflow, respectively; $C_{in}{}^{`}$ and $C_{out}{}^{`}$ are the flow coefficient of the valve during the entering and exiting of air, respectively; $A_{in}{}^{`}$ and $A_{out}{}^{`}$ are the flow area of the valve when the air is entering and exiting, respectively; and $T^{`}$ is the absolute temperature in the pipe.

When there is no air in the pipeline and the water pressure is higher than the atmospheric pressure, the inner section solution of the node at the air valve is the boundary condition. When the water head is lower than the height of the pipeline, the air valve opens and air flows in. When the air is not exhausted, the air satisfies the constant temperature air law, which can be expressed as:

$$p^{`}{V}_a=M^{`}{R}^{`}{T}^{`}$$

(19)

where $V_a$ is the void volume. At time $t$, the following equation can be approximately obtained:

$$p^{`}\left[V_{t_0}{}^{`}+0.5\mathsf{\Delta }t\left(Q_i{}^{`}-Q_{P{X}_i}{}^{`}-Q_{P{P}_i}{}^{`}+Q_{P_i}{}^{`}\right)\right]=M_{t_0}{}^{`}+0.5\mathsf{\Delta }t\left({\dot{M}}_{t_0}{}^{`}+{\dot{M}}^{`}\right)R^{`}{T}^{`}$$

(20)

where $V_{t_0}{}^{`}$ is the cavity volume at $t_0$, $Q_i{}^{`}$ is the outflow of section $i$ at $t_0$, $Q_{P_i}{}^{`}$ is the outflow of section $i$ at $t_{}$, $Q_{P{X}_i}{}^{`}$ is the inflow of section $i$ at $t_0$, $Q_{P{P}_i}{}^{`}$ is the inflow of section $i$ at $t_{}$, $M_{t_0}{}^{`}$ is the time–space, $t_0$ is the air mass in the chamber, ${\dot{M}}_{t_0}{}^{`}$ is the mass flow of air flowing into or out of the chamber at $t_0$, and ${\dot{M}}^{`}$ is the mass flow of air flowing into or out of the chamber at $t$. The relation between $H_P{}^{`}$ and $p^{`}$ is as follows:

$$H_P{}^{`}=\frac{p^{`}}{{\gamma }_w}-H_a+Z_a{}^{`}$$

(21)

where ${\mathrm{Z}}_{\mathrm{a}}{}^{`}$ is the elevation of of the air valve. Substituting Equations (9)–(11) into Equation (20) obtains the following expression:

$$p^{`}\left\{V_{t_0}{}^{`}+0.5\mathsf{\Delta }t\left[Q_i{}^{`}-Q_{P{X}_i}{}^{`}-\left(\frac{C_P}{B_P}+\frac{C_M}{B_M}\right)+\left(\frac{1}{B_P}+\frac{1}{B_M}\right)\left(\frac{p^{`}}{{\gamma }_w}-H_a+Z_a{}^{`}\right)\right]\right\}=\left[M_{t_0}{}^{`}+0.5\mathsf{\Delta }t\left({\dot{M}}_{t_0}{}^{`}+{\dot{M}}^{`}\right)\right]R^{`}{T}^{`}$$

(22)

4. Case Analysis and Discussion

4.1. Project Overview

The water supply project is composed of an inlet pool, a water intake pump station, a water supply pipeline, and a high-level pool. The total length of the water transmission pipeline is 1.67 km, using a 1 × DN1600 mm cast-iron pipe, and the elevation of the pipe’s central line ranges between 1955 and 2070 m. The designed water level of the inlet pool is 1971.40 m. A high-level pool is built at the pump station outlet with a volume of 15,000 m³. The penstock enters the high-level pool, which is submerged by the outflow. The water level of the high-level pool is 2069.00 m. The designed flow rate of the pump station is 12,492 m³/h, and the characteristic head (the designed geometric head) is 97.6 m. Horizontal single-stage double-suction centrifugal pumps are used in the project. The geometric parameters of the pump are shown in

Table 1. Geometric parameters of the water pump.

Parameters	Values
Design flow	4167 m3/h
Design head	102.6 m
Design point efficiency	85%
Dimensionless specific speed	0.44
Rated speed	990 r/min
GD2	384 kg·m2

. The dimensionless specific speed is given by $\mathrm{K}=\frac{2{\mathsf{\pi }\mathrm{nQ}}^{0.5}}{60{\mathrm{g}}^{0.75}{\mathrm{H}}^{0.75}}$, where K is the dimensionless specific speed, n is the rotating speed, Q is the flow rate, H is the pump head, and g is the gravity acceleration. Four pumps are installed, and one of them is reserved as a backup. The pumps are equipped with an asynchronous motor (in an air-cooling mode) with a power of 1600 kW and a voltage of 10 kV, and the water pump GD2 is 384 kg·m².

4.2. Calculation of the Hydraulic Performance of the Proposed Air Chamber

Since the proposed air chamber does not need to be equipped with an air compressor, it does not rely on any power supply and can be installed at any appropriate position along the pipeline of the water supply system. We now calculate the hydraulic performance for the air chambers which are installed at different positions. The water hammer protection scheme is as follows:

(1) Three air chambers with central adjustable standpipes are settled at 740 m, 860 m, and 1380 m from the starting point of the water conveyance pipeline. The related parameters are shown in

Table 2. Parameters of the air chambers with adjustable central standpipe.

Numbering	Chamber Diameter (m)	Chamber Cross-Sectional Area (m2)	Inner Length of the Central Standpipe Chamber (m)	Central Standpipe Diameter (m)	Total Chamber Height (m)	Connecting Pipe Diameter (m)	Total Volume (m3)
#1	2.26	4.0	3.5	0.2	4.0	0.3	16
#2	2.26	4.0	3.5	0.2	4.0	0.3	16
#3	2.26	4.0	4.4	0.2	5.0	0.3	20

.

(2) The configuration of the pump outlet valve is the same as that of a conventional air chamber. A swash-plate-type butterfly buffer check valve is used, and the two-section broken line closing rule is adopted: the valve is quickly closed for 2 s, from being fully opened to a 20% opening, and then slowly closed for 18 s to a 0% opening, with a total closing time of 20 s. The calculation results of the hydraulic performance are shown in Figure 4, Figure 5, Figure 6 and Figure 7.

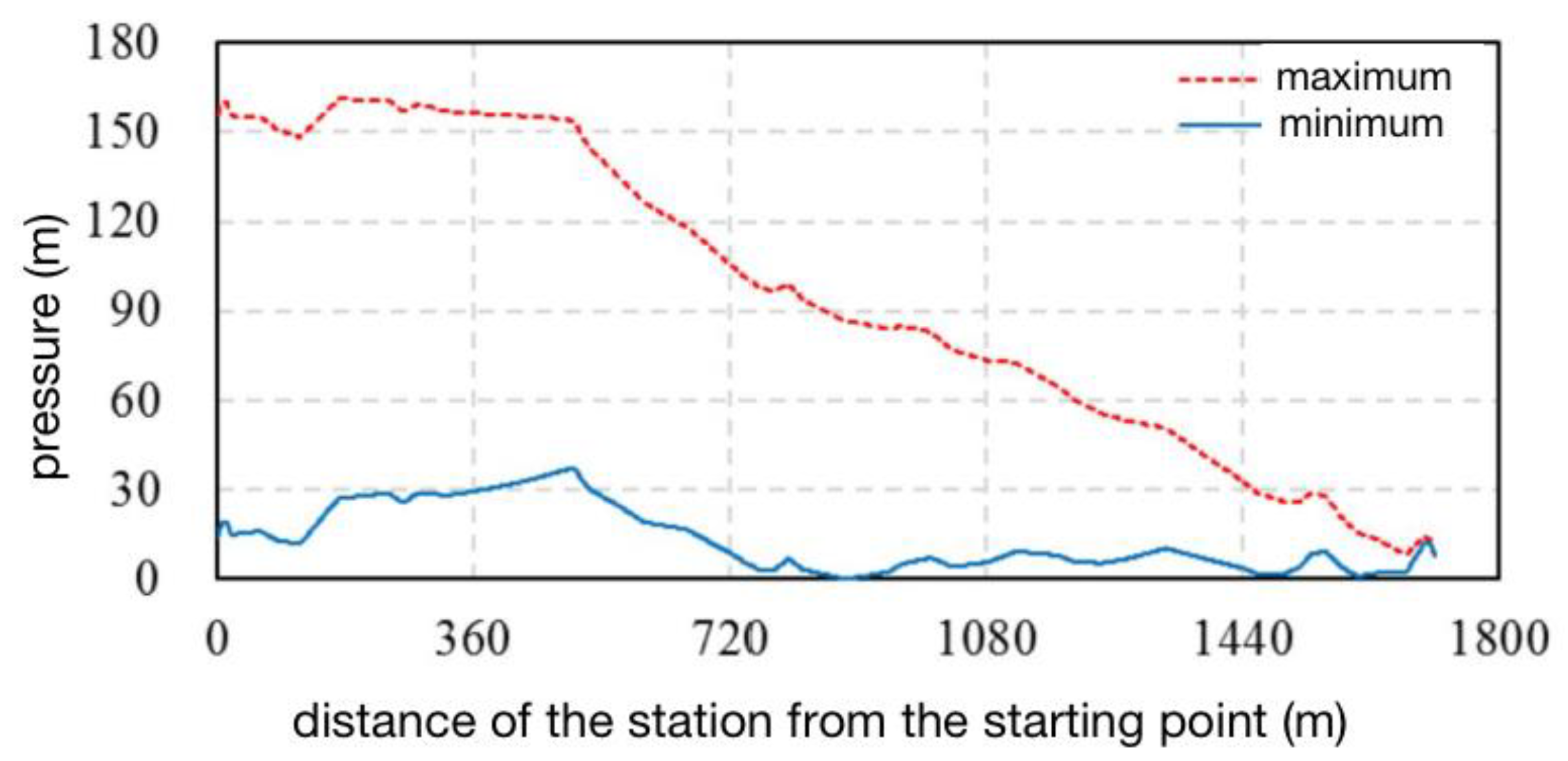
It can be seen from Figure 4 and Figure 5 that using the proposed air chamber for water hammer protection, the maximum reverse speed of the three pumps is 624.89 r/min, which is 63.12% of the rated speed, and the reverse duration is less than 2 min under the condition of a simultaneous accidental shutdown of the pumps. The maximum internal water pressure along the line appears at 161.18 m from the starting point of the water conveyance pipeline, and the pressure is under the upper limit of 166 m. The minimum internal water pressure along the line appears at 881 m from the starting point of the water conveyance pipeline.

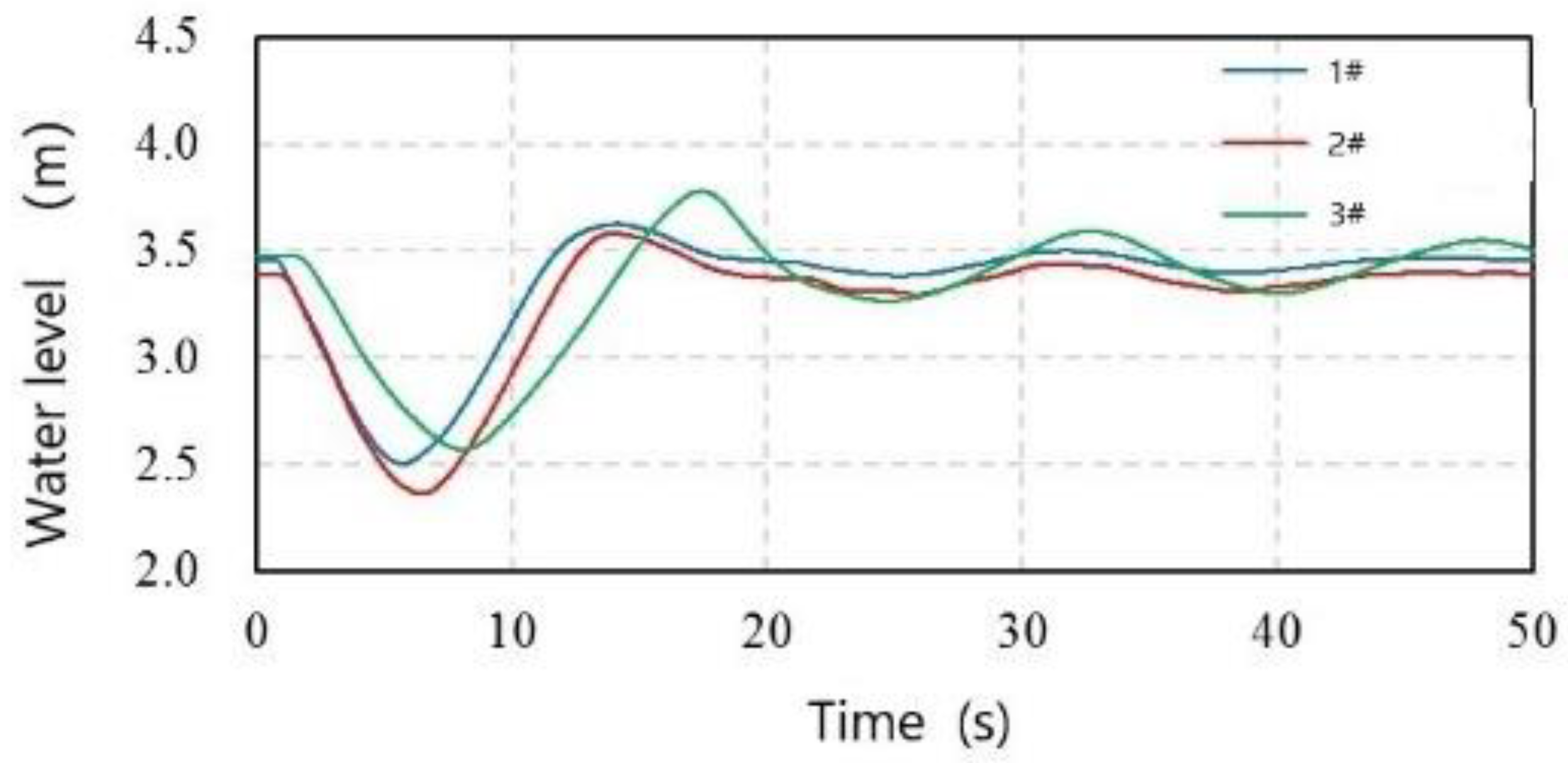
Figure 6 shows the time variation of the water level in the proposed air chamber. Once the pump is stopped, the proposed air chamber quickly fills the water line. At 5.71 s, the water level in the air chamber at station #1 reaches its minimum of 2.50 m. For a water hammer of positive pressure, when the wave arrives, the water in the pipe is pressurized and enters the air chamber. At 14.16 s, the water level in the chamber reaches its highest point of 3.62 m. After that, the water level in the chamber exhibits fluctuations, and the fluctuation gradually decreases. At 6.47 s, the water level in the air chamber at station #2 reaches its lowest point of 2.36 m. At 13.97 s, the water level in the chamber reaches its highest point of 3.58 m, and then the water level in the chamber fluctuates greatly, and the fluctuation range is gradually reduced. The water level in the air chamber at station #3 reaches its lowest point of 2.57 m at 8.09 s, and the water level in the air chamber reaches its highest point of 3.78 m at 17.47 s.

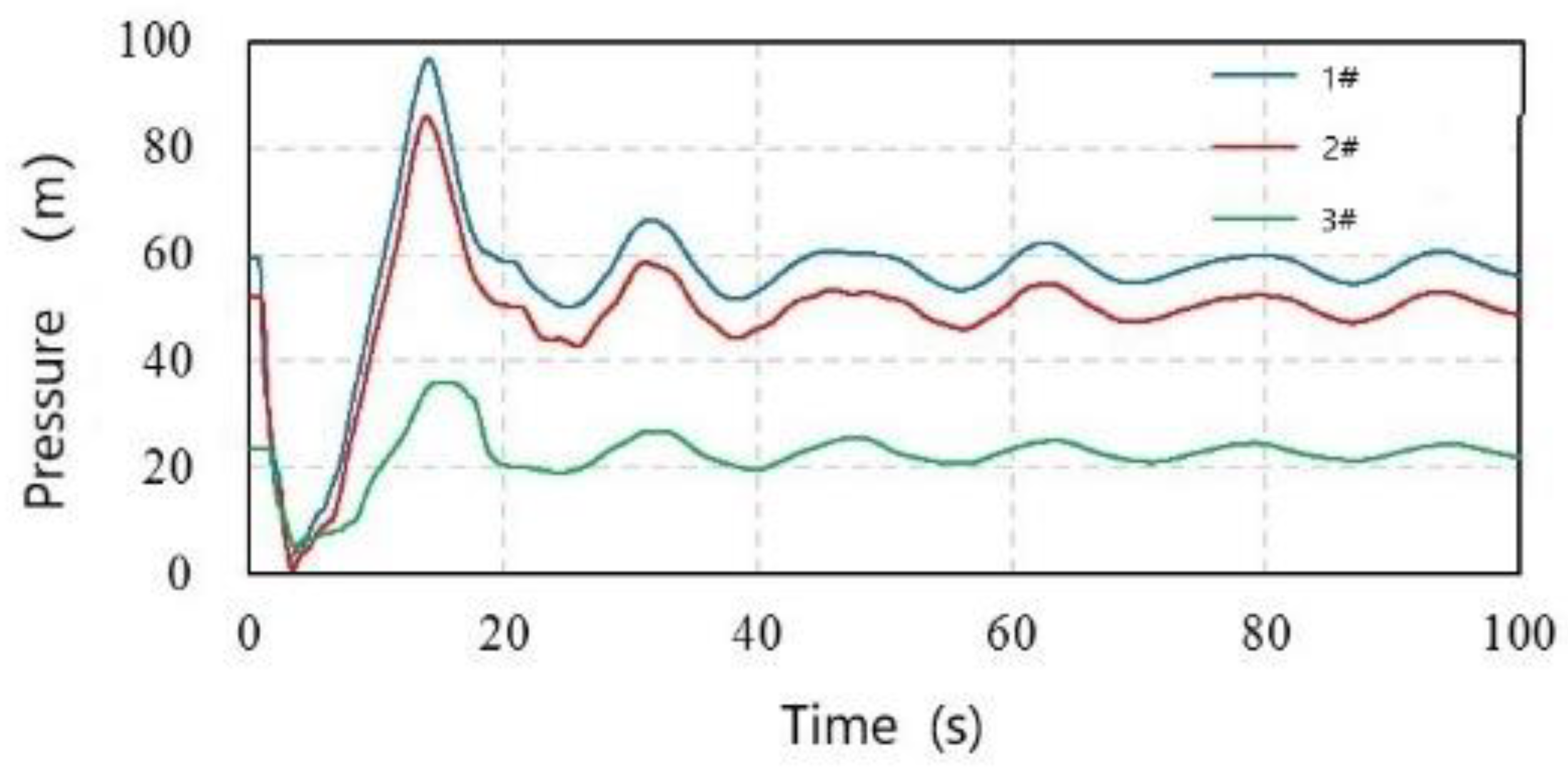
Figure 7 shows the variation of pressure at the bottom of the proposed air chamber. At 3.27 s, the pressure in the air chamber at station #1 surpasses 3.27 s reaches its lowest value of 3.29 m. The maximum pressure is 96.87 m at 14.16 s. The air chamber at station #2 has a minimum pressure of 0.78 m at 3.50 s, and has a maximum pressure of 85.95 m at 13.97 s. The air chamber at station #3 has a minimum pressure of 4.90 m at 3.57 s, and has a maximum pressure of 36.06 m at 15.35 s. The pressure did not exceed the control requirements. The parameters of the above water pump, pipeline, and air chamber are also analyzed. In addition, under the same conditions of the pump outlet valve and the closing rule, the required chamber volume of a conventional air chamber is 50.24 m³; however, the required chamber volume of an air chamber with an adjustable central standpipe is 52 m³. The volume of the air chamber is given by the minimum volume necessary to ensure that the chamber cannot be empty. The required chamber volumes are similar.

4.3. Dominating Factors of the Proposed Air Chamber

The air chamber with an adjustable central standpipe adds a central standpipe onto the basis of the conventional air chamber, and its water hammer protection effect depends on the parameters of the central standpipe. To optimize the proposed air chamber with an adjustable central standpipe, we then studied the structural parameters, including the inner length of the standpipe, diameter of the standpipe, and diameter of the bottom connecting pipe. The parameters to represent water hammer protection performance characteristics are selected based on the Chinese standards for pumping station design (GB50265-2022), which includes the ratio of the reverse pump speed, the maximum and minimum pressure along the way, and the minimum water level in the chamber.

4.3.1. Effect of the Inner Length and Diameter of the Central Standpipe

Using a fixed variables method, we first analyze the effect of the length of the central standpipe on the water hammer protection. The air chamber at station #1 is taken as a case study. The inner length and diameter of the central standpipe is adjusted using a thread structure device. For this case study, the inner length is varied from 0 m to 3.5 m, and the diameter is varied from 0.1 m to 0.6 m. The initial parameters are as follows: the cross-sectional area of the air chamber is 4 m², the diameter of the central standpipe is 0.2 m, the total height of the chamber is 4 m, the diameter of the connecting pipe is 0.3 m, and the total volume of the chamber is 16 m³. The calculated inner lengths are 1.0 m, 1.5 m, 2.0 m, 2.5 m, 3.0 m, and 3.5 m.

Table 3. The water hammer protection characteristics with different inner lengths of central standpipes.

Inner Length of the Central Standpipe (m)	Maximum Reverse Pump Speed/Rated Speed (%)	Maximum Pressure along the Way (m)	Minimum Pressure along the Way (m)	Lowest Water Level in the Chamber (m)
0	66.32	141.24	−0.56	3.81
1.0	65.80	146.12	−0.41	3.33
1.5	65.59	150.01	−0.34	3.12
2.0	65.24	153.31	−0.24	2.95
2.5	64.47	156.25	−0.13	2.79
3.0	63.82	159.15	0.01	2.64
3.5	63.12	161.18	0.14	2.50

shows the results of the water hammer protection characteristics with different inner lengths of the central standpipe. It is noted that with the cross-sectional area, chamber height, central standpipe diameter, and bottom connecting pipe diameter being tested under the same conditions, with the increase in the inner length of the central standpipe in the air chamber, the maximum reverse pump speed/rated speed decreases gradually, and the ability to control the negative pressure along the way increases. The greater the maximum pressure, the greater the fluctuation amplitude of the water hammer pressure, and the lower the minimum water level in the chamber. This means that with the increase in the inner length of the central standpipe, the air volume enclosed in the upper part of the air chamber above the lower end of the central standpipe and the water level in the chamber do not reach the central standpipe. When the air valve at the top of the central standpipe is not opened, the air volume in the chamber increases based on the ideal gas equation. Thus, the absolute pressure is weakened by the influence of air volume, and the negative water hammer effect increases. When the pipeline water flows backwards and the pipeline pressure rises, the compressed water enters the chamber. Before the water level in the chamber reaches the central standpipe, the air in the chamber is compressed and the air valve is opened to discharge air. With the increase in the inner length of the central standpipe, the water level in the chamber submerging the bottom of the central standpipe takes less time, and the positive water hammer effect increases.

We then analyzed the effect of the diameter of the central standpipe on the characteristics of water hammer protection. The initial parameters of the calculation model are as follows: the cross-sectional area of the air chamber is 4 m², the inner length of the central standpipe chamber is 3.5 m, the total height of the chamber is 4 m, the diameter of the connecting pipe is 0.3 m, and the total volume of the chamber 16 m³. The diameters of the central standpipe are 0.1 m, 0.2 m, 0.3 m, 0.4 m, 0.5 m, and 0.6 m. The calculation results are shown in

Table 4. The water hammer protection characteristics with different diameters of central standpipes.

Central Standpipe Diameter (m)	Maximum Reverse Pump Speed/Rated Speed (%)	Maximum Pressure along the Way (m)	Minimum Pressure along the Way (m)	Lowest Water Level in the Chamber (m)
0.1	63.09	161.25	0.15	2.51
0.2	63.12	161.18	0.14	2.50
0.3	63.16	161.07	0.13	2.50
0.4	63.23	160.90	0.11	2.49
0.5	63.32	160.66	0.09	2.48
0.6	63.43	160.35	0.07	2.47

.

It can be seen from Table 4 that with the chamber height, inner length of the central standpipe, and the diameter of the bottom connecting pipe under the same conditions, with the increase in the diameter of central standpipe, the ratio between maximum pump reversal speed and rated speed is almost unchanged, the maximum and minimum pressure along the process increase on the whole (the variation is small), and the minimum water level in the chamber is basically unchanged. This means that with the same shape of air chamber, the diameter of the central standpipe has a small effect on the water hammer protection ability. The ratio of the maximum reversal speed to the rated speed is reasonable, and the maximum pressure along the way does not exceed the standard. Additionally, there is no negative pressure along the line.

4.3.2. Effect of the Diameter of the Bottom Connecting Pipe

This section analyzes the effect of the diameter of the bottom connecting pipe on the water hammer protection characteristics. The initial parameters of the calculation model are as follows: the cross-sectional area is 4 m², the inner length of the central standpipe chamber is 3.5 m, the diameter of the central standpipe is 0.2 m, the total height of the chamber is 4 m, and the total chamber height is 4 m. The volume of the chamber is 16 m³, and the diameters of the bottom connecting pipe are 0.3 m, 0.4 m, 0.5 m, and 0.6 m. The calculation results are shown in

Table 5. The water hammer protection characteristics with different diameters of bottom connecting pipes.

Diameter of the Bottom Connecting Pipes (m)	Maximum Reverse Pump Speed/Rated Speed (%)	Maximum Pressure along the Way (m)	Minimum Pressure along the Way (m)	Lowest Water Level in the Chamber (m)
0.3	63.12	161.18	0.14	2.50
0.4	64.09	161.02	0.80	2.24
0.5	64.70	159.90	0.70	2.07
0.6	65.03	160.61	0.59	1.97
0.7	65.20	160.77	0.52	1.92
0.8	65.29	160.84	0.48	1.90

.

Table 5 shows that with the chamber height, inner length of the central standpipe, and diameter of the central standpipe under the same conditions, with the increase in the diameter of the bottom connecting pipe, the ratio of the maximum reversal speed to the rated speed gradually increases. The maximum pressure decreases at the initial stage and then starts to increase gradually. The minimum pressure increases at the initial stage and then starts to decrease gradually. The effect of the diameter of the bottom connecting pipe on the water hammer protection characteristics first increases and then gradually weakens, and the minimum water level in the chamber continues to decrease. This shows that under the same shape of air chamber, with the increase in the diameter of the bottom connecting pipe, the hydraulic loss during the outflow and inflow of water in the chamber decreases, water flow into the main pipeline increases, and the water hammer protection is increased. The capacity is enhanced. However, when the diameter of the bottom connecting pipe reaches a certain value, the reversal speed of the pump increases due to water flowing into the pipe, and the water hammer pressure caused by closing the pump outlet valve is affected by the reverse flow and the pressure.

Therefore, if the ratio of the maximum reversal speed to the rated speed is reasonable, the maximum pressure along the way does not exceed the control standard, there is no negative pressure along the line, and the water in the chamber is not emptied, the test can be passed and the optimal bottom connecting pipe diameter can be obtained.

4.4. Optimization of the Air Chamber with an Adjustable Central Standpipe

The above results show that, with a given shape of air chamber, adjusting the inner length of the central standpipe can affect the characteristics of water hammer protection. The diameter of the central standpipe has little effect on the water hammer protection characteristics. In addition, there is an optimal value of the diameter of the bottom connecting pipe, which can be obtained by trial calculations. The water hammer protection characteristics of the proposed air chamber are optimized. The optimized scheme is as follows:

(1) Three air chambers with adjustable central standpipes are set at station #1, station #2, and station #3. The specific parameters are shown in

Table 6. Optimal parameters of the air chamber with an adjustable central standpipe.

Number of Station	Chamber Diameter (m)	Chamber Cross-Sectional Area (m2)	The Inner Length of the Central Standpipe (m)	Central Standpipe Diameter (m)	Total Chamber Height (m)	Connecting Pipe Diameter (m)	Total Volume (m3)
#1	2.11	3.5	2.8	0.1	2.3	0.50	8.05
#2	2.11	3.5	3.2	0.1	3.7	0.30	12.95
#3	2.11	3.5	3.9	0.1	4.4	0.35	15.40

.

(2) The configuration of the pump outlet valve is the same as that before the optimization, and a swash-plate-type butterfly buffer check valve is used. The total closing time is 20 s.

Table 6 shows the optimal parameters of the air chamber with an adjustable central standpipe. In practical engineering, water hammer protection considers the following influencing factors: the maximum pressure along the way should be controlled, the water level in the air chamber should be ensured, negative pressure in the pipeline should be avoided, and the ratio of the maximum reverse pump speed to the rated speed should be limited. The optimization of these parameters considers the suitable range of the above influencing factors. As indicated in Section 4.3.1, the diameter of the central standpipe has a negligible effect on the performance of water hammer protection; therefore, the diameter of the central standpipe is fixed to 0.1 in the optimization scheme. The inner length of the central standpipe is mainly restricted by the limitations of the maximum reverse pump speed and negative pressure along the way.

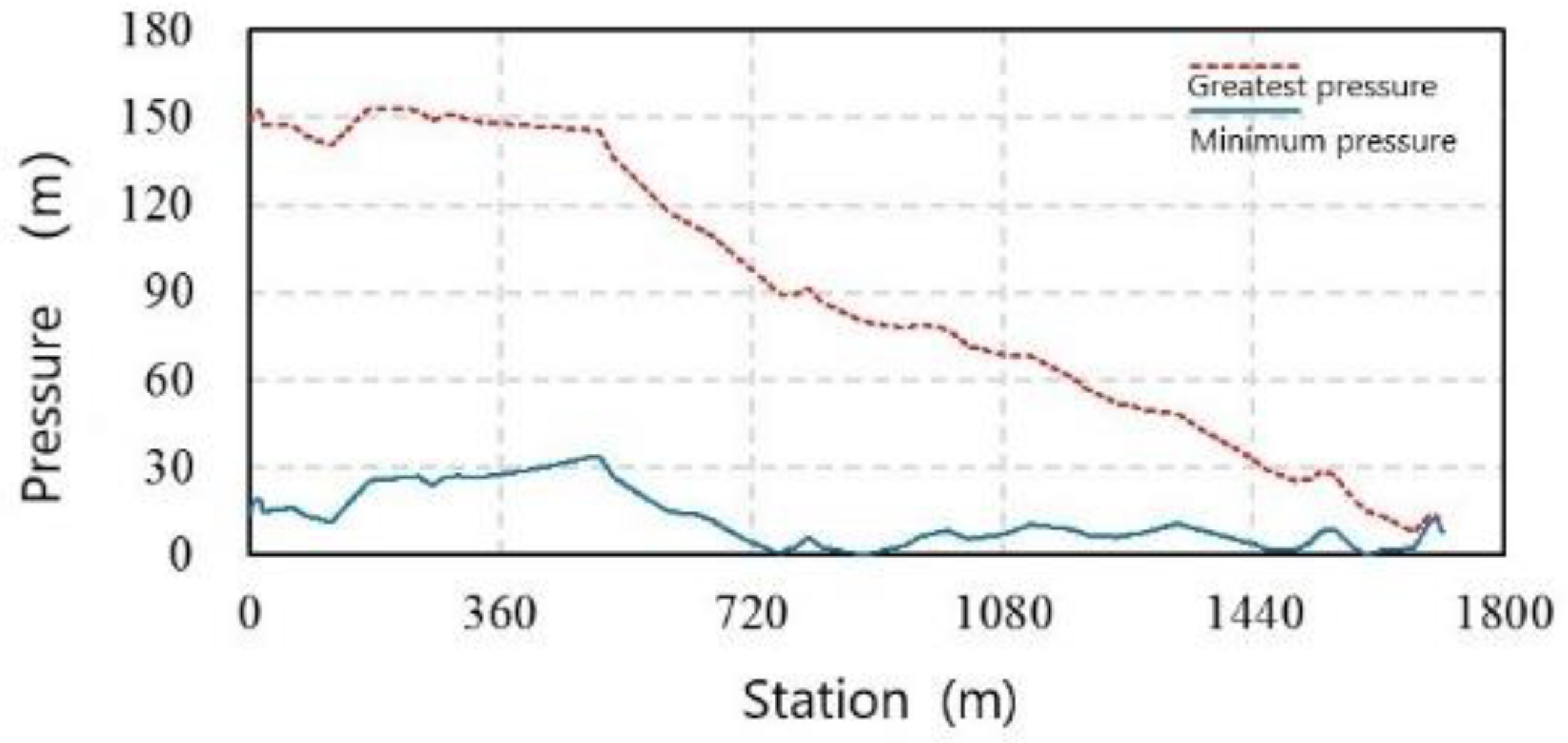
Figure 8 and Figure 9 show that, after optimizing the water hammer protection scheme of the proposed air chambers, under the condition of accidental shutdown of the pumps, the maximum reverse rotation speed of the pumps is 651.42 r/min, which is 65.80% of the rated speed. The rotation duration is less than 2 min. The maximum water pressure along the way appears at pile number 0 + 171 and is 153.32 m, which is less than the maximum pressure control standard of 166 m. The minimum water pressure along the way is 0.06 m, appearing at pile number 0 + 881, which meets the pipeline operation requirements (no negative pressure).

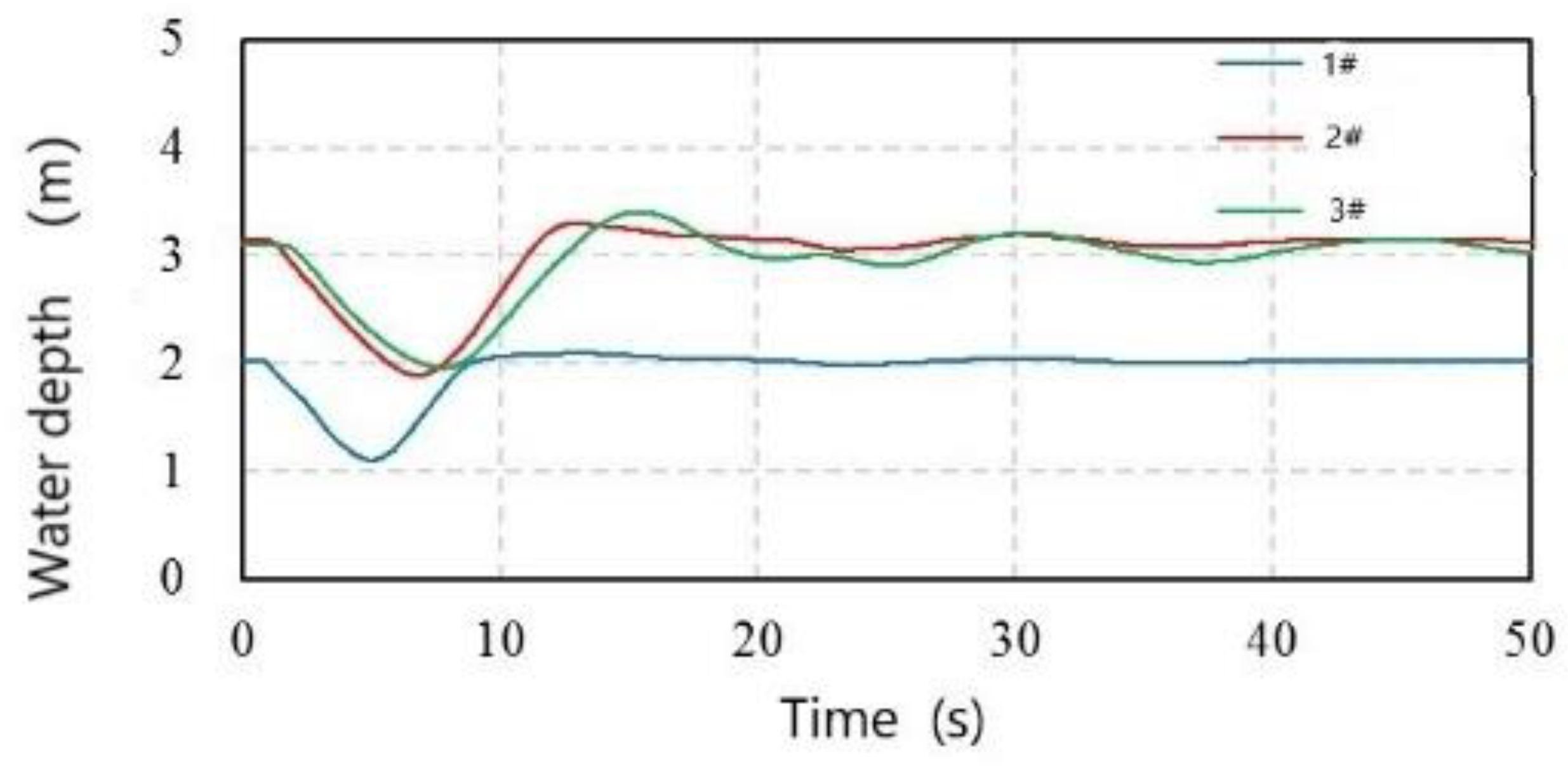
Figure 10 shows the time evolution of the water level in the proposed air chamber after optimization. Once the pump is stopped, the air chamber replenishes the water to the line quickly. For the air chamber at station #1 at 5.02 s, the water level in the air chamber reaches its lowest point of 1.10 m. With positive water hammer pressure, when the wave arrives, the water in the pipeline is pressurized and enters the air chamber. The water level in the chamber reaches its highest point of 2.10 m at 13.07 s, and the fluctuation of the water level in the chamber is relatively small. The water level in the air chamber at station #2 reaches its lowest point of 1.89 m at 6.80 s, and the water level in the chamber reaches its highest point of 3.30 m at 12.94 s. The water level in the air chamber at station 3 reaches its lowest point of 1.95 m at 7.79 s. The water level in the chamber reaches its highest point of 3.40 m at 15.42 s, and then the water level in the chamber fluctuates, with a gradually reducing fluctuation range. In addition, the air in these three air chambers does not enter the water delivery line.

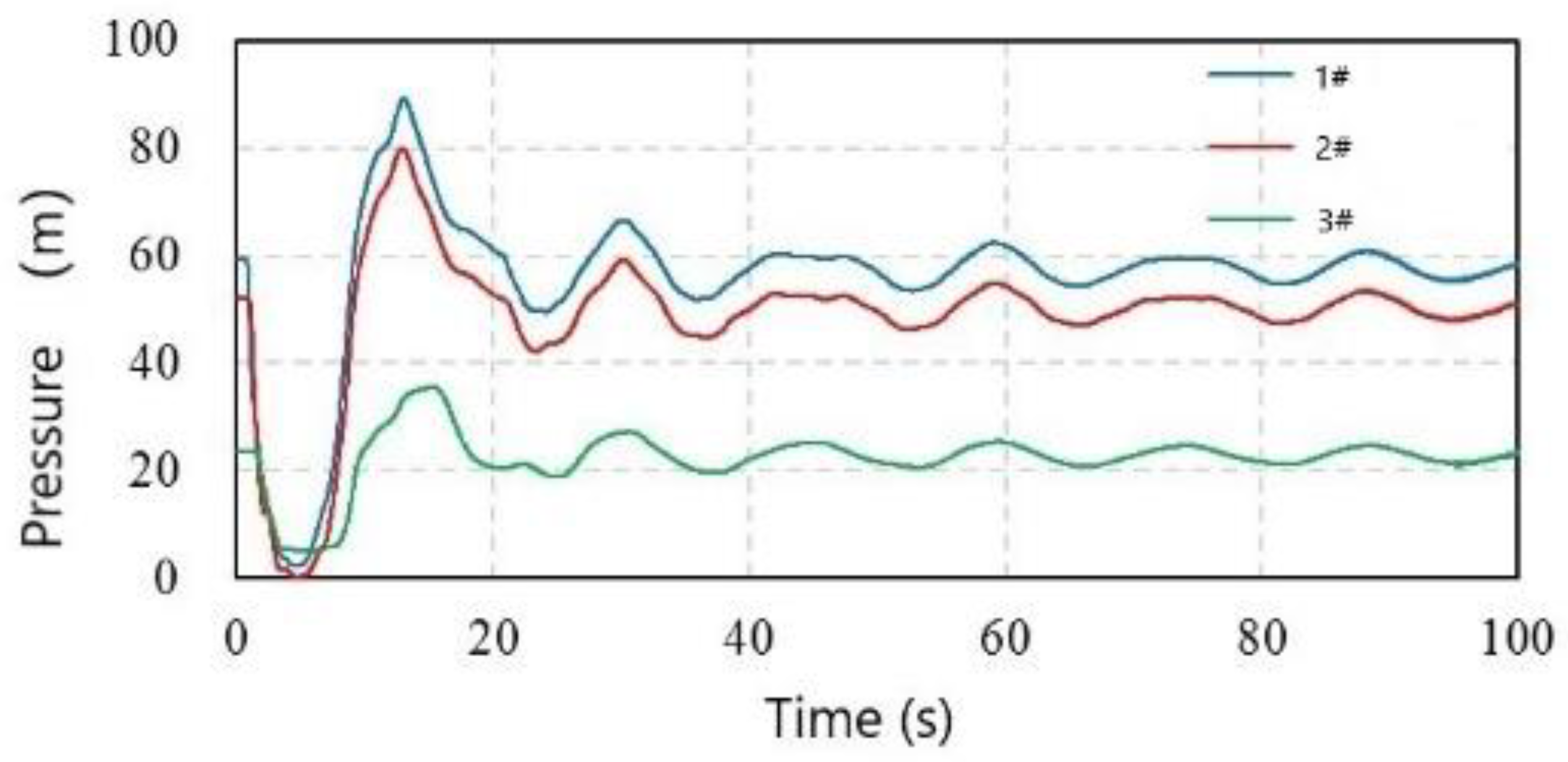
Figure 11 shows the time variation of the pressure at the bottom of the three air chambers after optimization. The pressure fluctuates and gradually decays. For the air chamber at station #1, the minimum pressure is 2.30 m at 4.72 s. The maximum pressure value is 89.16 m at 13.07 s. For the air chamber at station #2, the minimum pressure is 0.78 m at 4.42 s, and the maximum pressure value is 80.01 m at 12.94 s. For the air chamber at station #3, the minimum pressure is 4.95 m at 5.81 s, and the maximum pressure value is 35.64 m at 15.42 s. The pressure does not exceed the control requirements.

Comparing the optimized calculation results of the conventional air chamber and the proposed air chamber, under the conditions of the same pump outlet valve and closing rule, when the conventional air chamber is used for water hammer protection, the required chamber volume is 50.24 m³, and when the proposed air chamber is used for water hammer protection, the total chamber volume required is 36.40 m³. The difference of the chamber volume required by these two schemes is 13.84 m³.

4.5. Advantages of the Proposed Air Chamber

Firstly, as presented in Section 2, compared to a conventional air chamber which replenishes air into the air chamber using an air compressor, the proposed air chamber replenishes air into the air chamber relying on an air valve. The operation of an air compressor in a conventional air chamber relies on electric power, which limits the positions available for installing the air chamber. As the running of the air chamber with an adjustable central standpipe does not rely on an air compressor, it does not need any power source, and thus it can be installed at any indicated location along the principal pipeline. The air chamber with an adjustable central standpipe can not only save the cost of a power source, but also save the cost of an air compressor.

Secondly, the parameters of the central standpipe are adjustable. As presented in Section 4.3, the inner length of the central standpipe and the diameter of the bottom connecting pipe affect the performance of water hammer protection. As the hydraulic characteristics such as flow rate vary depending on water requirements, the demands of water hammer protection change depending on the engineering demands of the water supply system. The advantage of the air chamber with an adjustable central standpipe is that it can provide different levels of water hammer protection depending on the demands of the water supply system by adjusting the inner length of the central standpipe.

Thirdly, as the volume of the chamber is also an important factor influencing the construction budget, the volume of the proposed air chamber is also compared with conventional air chamber. When the pump outlet valve closing law is the same, the conventional air chamber requires a total volume of 50.24 m³, while the air chamber with an adjustable central standpipe requires a total volume of 52 m³. The chamber volumes required by the two schemes are similar.

5. Conclusions

This study proposed a novel air chamber with an adjustable central standpipe. It not only can flexibly adjust the parameters depending on the water hammer protection demands of the project, but also has the advantage of no required power supply. The working principle of the air chamber is explained in detail, and the hydraulic performance of the proposed air chamber is analyzed under different conditions, which enriches the theoretical analysis of the water hammer protection by the air chamber. We also compared and analyzed the water hammer protection performance of the conventional air chamber and the proposed air chamber. Results indicated that when the pump outlet valve closing law is the same, the conventional air chamber requires a total volume of 50.24 m³ while the air chamber with an adjustable central standpipe requires a total volume of 52 m³. The chamber volumes required by the two schemes are similar. As the air chamber with an adjustable central standpipe does not require an air compressor, its layout position is more flexible compared to the conventional air chamber. In addition, the rated speed decreases with an increase in the inner length of the central standpipe and with a decrease in the diameter of the central standpipe. If the diameter of the bottom connecting pipe is within a certain range, the water hammer protection performance of the proposed air chamber can be better than a conventional air chamber.