Next Article in Journal
Spatial Disequilibrium and Dynamic Evolution of Eco-Efficiency in China’s Tea Industry
Previous Article in Journal
A Study of the Effects of a Diet with Functional Foods on the Adaptogenicity of First-Year Students to the Student Lifestyle
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Sustainability
Volume 15
Issue 12
10.3390/su15129596
sustainability-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles thumb_up
...
Endorse textsms
...
Comment
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

A Systemic Approach to Simulate the Construction Process of Self-Supporting Masonry Structures

by
Vittorio Paris
1,*,
Giuseppe Ruscica
1,*,
Carlo Olivieri
2 and
Giulio Mirabella Roberti
1
1
Department of Engineering and Applied Sciences, Università degli Studi di Bergamo, Via G. Marconi 5, 24044 Dalmine, Italy
2
Department of Civil Engineering, University of Salerno, Via Giovanni Paolo II, 132, 84084 Fisciano, Italy
*
Authors to whom correspondence should be addressed.
Sustainability 2023, 15(12), 9596; https://doi.org/10.3390/su15129596
Submission received: 5 May 2023 / Revised: 31 May 2023 / Accepted: 12 June 2023 / Published: 15 June 2023
(This article belongs to the Special Issue Computational and Technological Advancements for Low-Carbon Structures)
Browse Figures
Review Reports Versions Notes

Abstract

:
The building sector has a significant impact on the environment due to its unproductive and technologically outdated practices. Although digital tools have emerged as potential solutions, current building practices often lack automation and efficiency. Throughout history, several self-supporting techniques, i.e., construction methods dedicated to the building of shells that do not need support during the construction works, have been developed. These techniques allow for reducing waste and minimizing construction costs. Combining self-supporting techniques and digital tools could aid the development of contemporary, highly sustainable, and efficient building practices that permit the use of alternative and sustainable materials. Building on this, the research conducted defines an approach for evaluating the balanced state of masonry structures during construction works and built using robotic technologies. The approach considers the factors that govern the stability under construction derived through studying self-supporting building techniques. The proposed approach assesses the structural state under construction, evaluating the need for temporary supports. An example of a masonry arch is provided to emphasize the importance of construction factors in sustainable building practices. Then the method is applied to a real case study. Overall, integrating self-supporting techniques with digital tools has the potential to revolutionize the building sector, and create highly sustainable and efficient practices.

1. Introduction

Over the last few decades, masonry has received growing interest from the scientific community, as proven by several investigations and avant-garde architectures [1,2]. Despite these efforts, masonry structures are barely adopted in practical applications, especially vaults and domes that find limited use within contemporary building practice. The longevity of the numerous historical masonry architectures suggests that their scarce adoption is not due to their lack of structural efficiency or sustainability.
Current investigations mainly aim to explore the potential of digital fabrication tools and innovative design approaches for the renewed application of masonry [3,4,5]. Since the beginning of the twentieth century, attempts at on-site automated bricklaying have been carried out [6]. However, only in the last two decades has the attention on automation grown in the field of architecture, engineering, and construction (AEC) [7,8]. Nowadays, researchers are focusing on the adoption of various digital tools, for assembly, as in the case of robotic arms [9,10,11] (see Figure 1), or drones [3,12,13], and for fabrication within the context of additive manufacturing [14,15,16]. The development of innovative building technologies using these tools leads to new challenges, e.g., the need to re-think the shape of construction elements in the case of drones [12] or the necessity of exploring unusual wall stratigraphy for additive manufacturing [15]. Few researchers are exploring the construction systems dedicated to horizontal structural elements suitable for covering spaces [17]. Even fewer explorations consider historical masonry construction techniques to develop innovative ones [12]. Amongst these, relevant studies are dedicated to self-supporting methods, i.e., building practices that allow the construction of vaults, domes, or shells without any temporary support. Indeed, throughout history, several cultures have sought these construction methods primarily based on principles of efficiency, economy, and sustainability [18].
Within this domain, the authors are investigating the possibility of developing contemporary self-supporting techniques for constructing horizontal structural elements; the explorations are pursued by integrating modern assembly tools, e.g., robotic arms, and historical self-supporting techniques. The development of these practices could drastically increase the efficiency of the building sector [19,20], reduce the waste material production associated with the need for temporary supports, and provide an essential element for defining an alternative to the typical frame structural typology established on concrete and steel. The paper presents a systematic approach adopted to assess the equilibrium of masonry structures, particularly for arches, vaults, shells, and domes, built by applying self-supporting techniques and using robotic arms during their construction process. The approach, based on the individuation of factors whose function influences the construction process, permits evaluating the state of the structure at every stage of construction. The research background, hypotheses, and primary research goal are discussed in Section 2, while Section 3 focuses on the primary research’s aim. Section 4 describes the factors that govern the structural state during construction. The systematic approach is discussed in Section 5. In Section 6, the approach is applied to evaluating the state of a masonry arch during its construction using three robotic arms. In the end, Section 7 reports a critical evaluation and future steps.

2. Robotic Assistance in Masonry Structures: Combating Tensile Stress through Compression-Focused Design

The concept of masonry is broad, not strictly related to the material itself; rather, it refers to how the material is used; it can be associated with a wide range of materials, e.g., concrete and raw earth. In fact, the stability of a masonry structure primarily relies on features derived from the material’s compressive capacity and the geometry of structural elements [21,22]. Such aspects were already established in ancient building practices, where the construction rules were expressed through geometrical ratios and highlighted in modern structural analysis methods [23,24]. Indeed, historically, masonry structures have been characterized by their unique construction mechanism, one that largely harnesses the form rather than the material’s inherent strength. Distinct from modern framed structures, these masonry units underscore the effective usage of structural forms to absorb and distribute loads, aligning more closely with principles of compression than tension [25].
Inherent in masonry is its minimal tensile strength, a trait that might initially seem detrimental. However, this property is overshadowed by its commendable compression resistance, a characteristic that defines the strategy for designing these structures. Unlike many modern construction materials which can effectively handle both tension and compression, masonry’s resistance to compression far outweighs its tensile resistance. In comparison to the tensile strength, many materials display high compressive strength, especially recycled ones. Despite that, the current design approach leans on flexural behaviour, such as frame typology structures, mainly built using steel and reinforced concrete, significantly impacting sustainability [26]. Therefore, the development of contemporary vaulting techniques could open up the possibility of adopting low mechanical strength but more environmentally friendly materials, including recycled or organic ones.
Nowadays, the building sector is one of the fields most responsible for producing waste and pollution; it is one of the most technologically backward and is amongst the least productive industrial sectors [20]. Recent studies have revealed how automation, robotization, and digitalization could aid in drastically improving the sector’s performance [20]. Drones and robotic arms are highly suitable for constructing structures made of elements with modest dimensions like bricks or small rigid elements. The structures built with these innovative tools can be composed of elementary units and behave as discrete elements with interfaces. In this sense, they could have behaviour similar to masonry buildings. Furthermore, by integrating innovative technologies with historical self-supporting construction techniques, the need for temporary support during construction could be avoided and this could open up a new range of geometries that can be built. Therefore, combining historical self-supporting techniques with robotic assembly technologies can lead to the definition of sustainable and efficient contemporary self-supporting construction techniques. This could increase the construction sector’s productivity, mitigate its environmental impact, and enable a widespread application of masonry shells.
Furthermore, the incorporation of robotics into the construction of masonry structures offers an innovative approach to maintain this crucial compression. More than simply laying blocks, robotics can actively contribute to the design philosophy of these structures. Through a well-calibrated response, a robotic arm can manipulate the blocks in such a way as to keep the structure consistently compressed, thereby preventing the formation of tension-induced cracks or block slippage.
Robotic technology, therefore, extends far beyond the mere automated assembly of masonry; it serves as an active participant in the construction strategy, fostering a sustained state of compression within the structure. This not only enhances the efficiency of the construction process but also significantly improves the durability and resilience of the completed structure.
By integrating the traditional principles of masonry design with advanced robotic technology, we can preserve the integrity of these structures, effectively addressing the inherent limitations of masonry materials and leveraging their strengths for more resilient and efficient construction processes.

3. Aim of the Paper

The advancement of modern self-supporting vaulting techniques, adaptable for robotic arms or drones, necessitates a dedicated approach to studying and simulating the attributes of historical self-supporting methods. The proposed simulation process gathers essential information for describing the construction of masonry structural elements, with a primary focus on arches, vaults, domes, and shells. It identifies the key features of self-supporting structures, emphasizing their strengths and weaknesses, and evaluates their impact on the structural state during construction.
The development of contemporary self-supporting vaulting techniques can also contribute to the preservation of historical methods, which depend on the examination and analysis of historic buildings, along with workers’ skills and knowledge. However, labour costs must also be considered, as the risk of losing expertise in ancient construction techniques increases without appropriate intervention. Robotic assembly technologies offer a promising solution for reviving traditional techniques in a modernized context, while also utilizing eco-friendly building materials subjected primarily to compressive forces. This approach bridges the gap between historical and contemporary practices, fostering innovation towards sustainable construction.

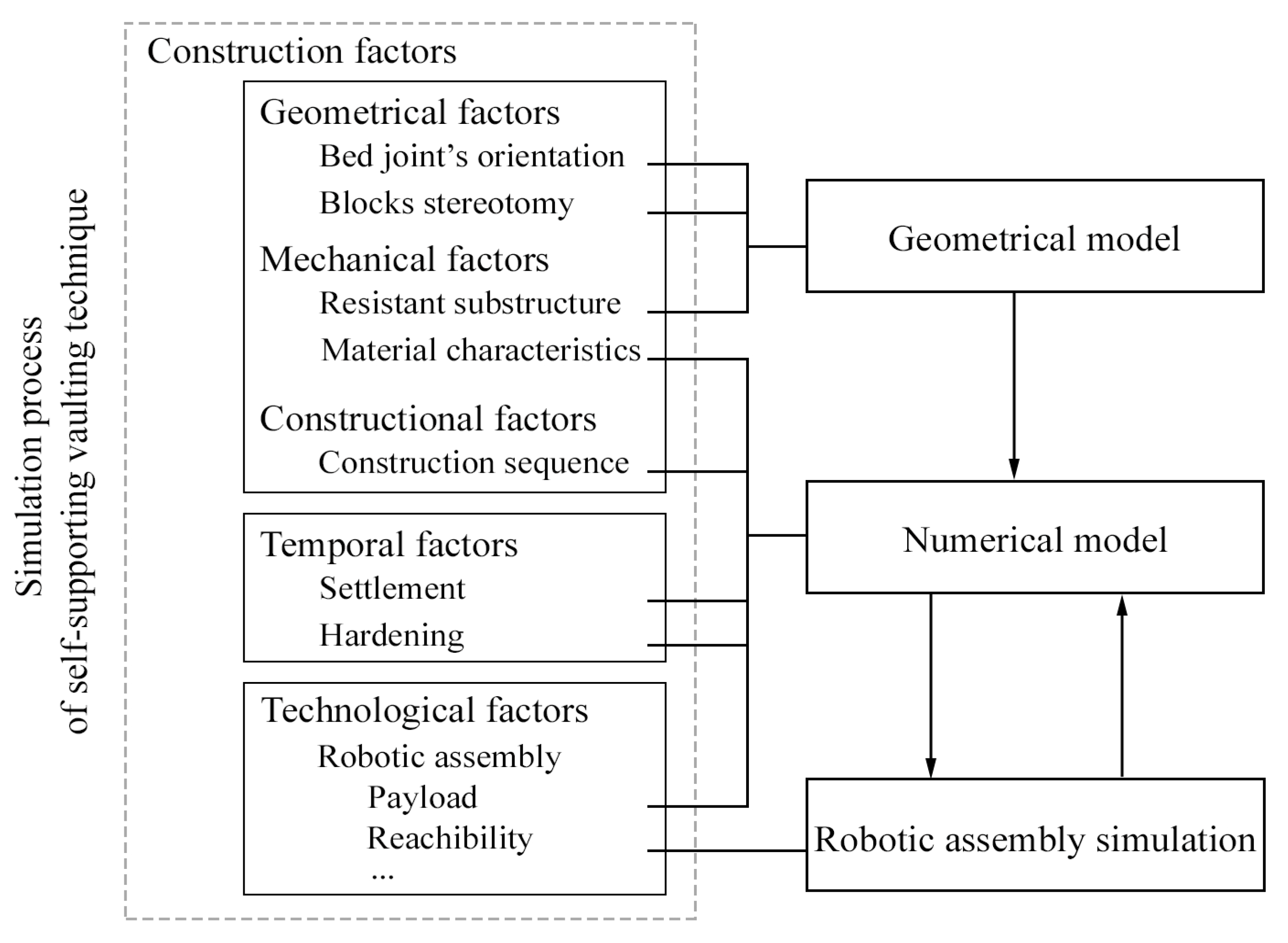
4. Construction Factors

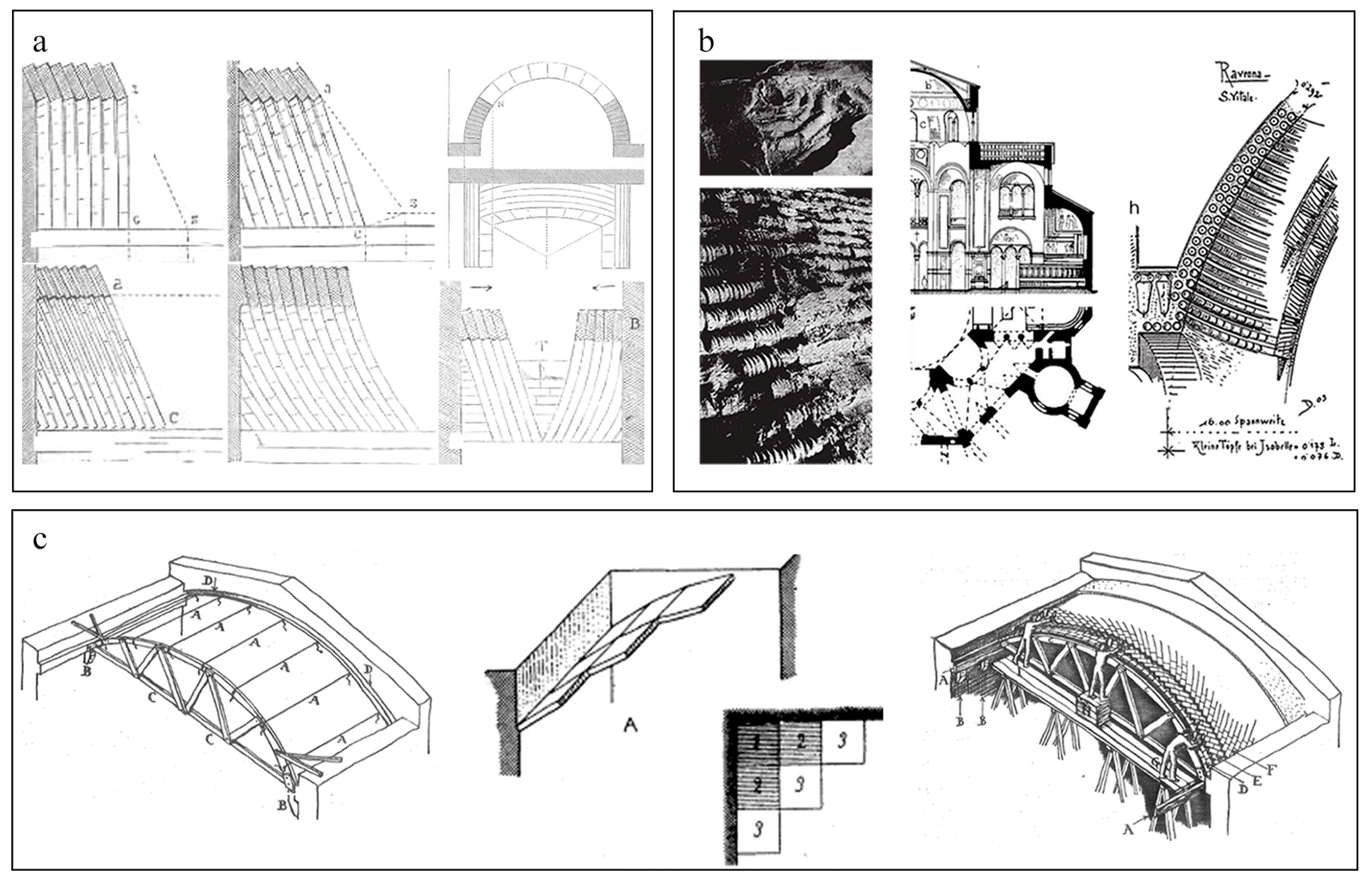
4.1. Construction Factors in Historical Self-Supporting Vaulting Technologies

Examining historical self-supporting construction techniques is essential for understanding the characteristics responsible for their self-supporting ability. Throughout history, domes, vaults, and arches have been applied in different cultural contexts, leading to the development of various self-supporting techniques, see Figure 2. Presumably, the corbelling vaulting technique is among the earliest developed, and its application can be found in almost all cultures and was adopted to create openings and cover spaces by stacking cantilevered blocks [27]. Amongst all techniques developed throughout history, four self-supporting vaulting techniques were considered based on their representativity and popularity. The pitched vaulting technique (PVT) [28] dates back to the 21st century BCE. Shells built with PVT are characterized by peculiar masonry tessellation, see Figure 2a): the bricks are laid radially to form arches placed in inclined planes and laid one next to another with the new arch resting over the previous one. The second technique explored is the clay tube vaulting technique (CTVT), developed around the 4th century BCE [29]. It was mainly applied in Africa Proconsularis (today Tunisia, Libya, Algeria, and Morocco) and throughout Europe [30], today used in India to build shells. Completely different from the CTVT, the tile vaulting technique (TVT) developed in Spain around the 13th–14th CE and is still applied in regions like Mexico, India, and some areas of Africa [31]. Tile technology is based on the use of fast-setting mortar and thin tiles but, as in Figure 2c, even the building sequence plays a relevant role in achieving stability during construction. The last vaulting technique observed is the herringbone vaulting technique (HVT), adopted by Brunelleschi and Sangallo architects during the Italian Renaissance. The origins of this construction technique can be traced back to the civilizations of ancient Persia. The technique confers a self-supporting capacity, largely dependent on the precise order of laying bricks and the presence of resistant substructures: the plate-bande [32].
The mentioned self-supporting techniques (PVT, CTVT, TVT, HVT) provide the information needed to understand the self-balanced state of masonry structures under construction. All self-supporting techniques have peculiar characteristics conferred by factors relevant during construction, but they do not strongly impact the structural stability upon completion. For this reason, these factors are denoted by the term construction factors (CF). They can be categorized as either geometric, mechanical, or constructional and impact the effectiveness of the self-supporting techniques. Indeed, each CF plays a role concerning the technology adopted, assuming different relevance in different self-supporting vaulting techniques. For example, the existence of resistant substructures is fundamental in the construction process of HVT, while it does not have any relevance if TVT is adopted. The following non-exhaustive collection of relevant CFs has been derived from examining historical documents, current practices [33,34], and full-scale tests [17,18].

4.1.1. Geometrical Factors

As testified by a broad literature [12,35,36], geometry affects the behaviour of a completed structure as well as during construction works [18]. In historical self-supporting techniques, two geometrical CFs assume a prominent role: the stereotomy and the bed joint’s orientation, both of which affect the state during construction works. The bed joint’s orientation is an essential CF in PVT; the wrong orientation of the mortar joint could lead to the overturning or sliding of bricks during their placement. During the placing operation, block stereotomy significantly influences sliding, as witnessed by CTVT or corbelled vaulting technique [18,30].

4.1.2. Mechanical Factors

The structural state under construction could be affected by mechanical CFs, particularly by the presence of resistant substructures and by the material characteristics. Some masonry patterns allow the occurrence of resistant substructures even during the placing operations. For example, in the scenario of HVT, the plate-bande built during the initial stages of construction is meant to acquire the necessary resources for establishing a stable state at an advanced level of construction. The presence of substructures throughout the construction process also holds significance in PVT and CTVT. The material properties are always significant. During construction, they preeminently influence technologies such as TVT, where the cohesive and fast-setting mortar characteristics coupled with the lightness of tiles are necessary for reaching a balanced state.

4.1.3. Construction Factors

The construction sequence, i.e., a precise order to place masonry elements, is a factor that affects all self-supporting technologies. A wrong adoption of a construction sequence can lead to the sliding phenomenon or preclude the stability of the structure.

4.2. Technological Factors

The CFs mentioned above and examined in the context of historical self-supporting techniques are still pertinent for determining contemporary self-supporting vaulting techniques. In this sense, they can easily be coupled with drones or robotic assembly technologies. Technological CFs are related to the technology adopted and must be considered to verify the buildability, e.g., the possible interferences and collisions in the case of multiple robotic arms. These factors are strictly related to the technology selected and impact the entire construction process; for example, in the case of drone technology, blocks with tetrahedral-based shapes called droxels [12] have been developed to overcome tolerance issues during assembly, while reachability and manoeuvrability on the construction site are significant limitations for robotic arms.

4.3. Temporal Factors

Due to building operations, the geometry of structures, similar to the loads, changes during the construction works. Consequently, to assess the state of the structure, it is necessary to examine the temporal evolution of the structure itself. Here, time assumes an unconventional role. Such a concept is easily recognizable considering the mortar’s setting and hardening process or the time in which settlements occur. Furthermore, during the construction of a voussoir arch, the load carried by the centering changes at every step. For each block laid, the structural state is slightly altered and the structural behaviour changes instantaneously once the centering has been removed [18]. Therefore, analyses should refer to a specific time or construction stage even if the loads are static. This phenomenon is traditionally neglected but has an essential relevance in self-balanced technologies, where the absence of temporary supports permits displacements and settlements to occur even in the early stages of construction. The alteration of structural behaviour concerning the variation of the structure’s geometry is of greater relevance even in double-curved structures, e.g., for hemispherical domes, the hoop forces cannot act until the brick course is completed. However, when the hoop forces appear, the structural state changes and a membrane behaviour activates after the completion of several brick courses [37]. Through these examples, it is evident that time plays a crucial role in assessing the state of the structure during construction works and it should be considered as a factor to ensure a proper evaluation of the construction technique.

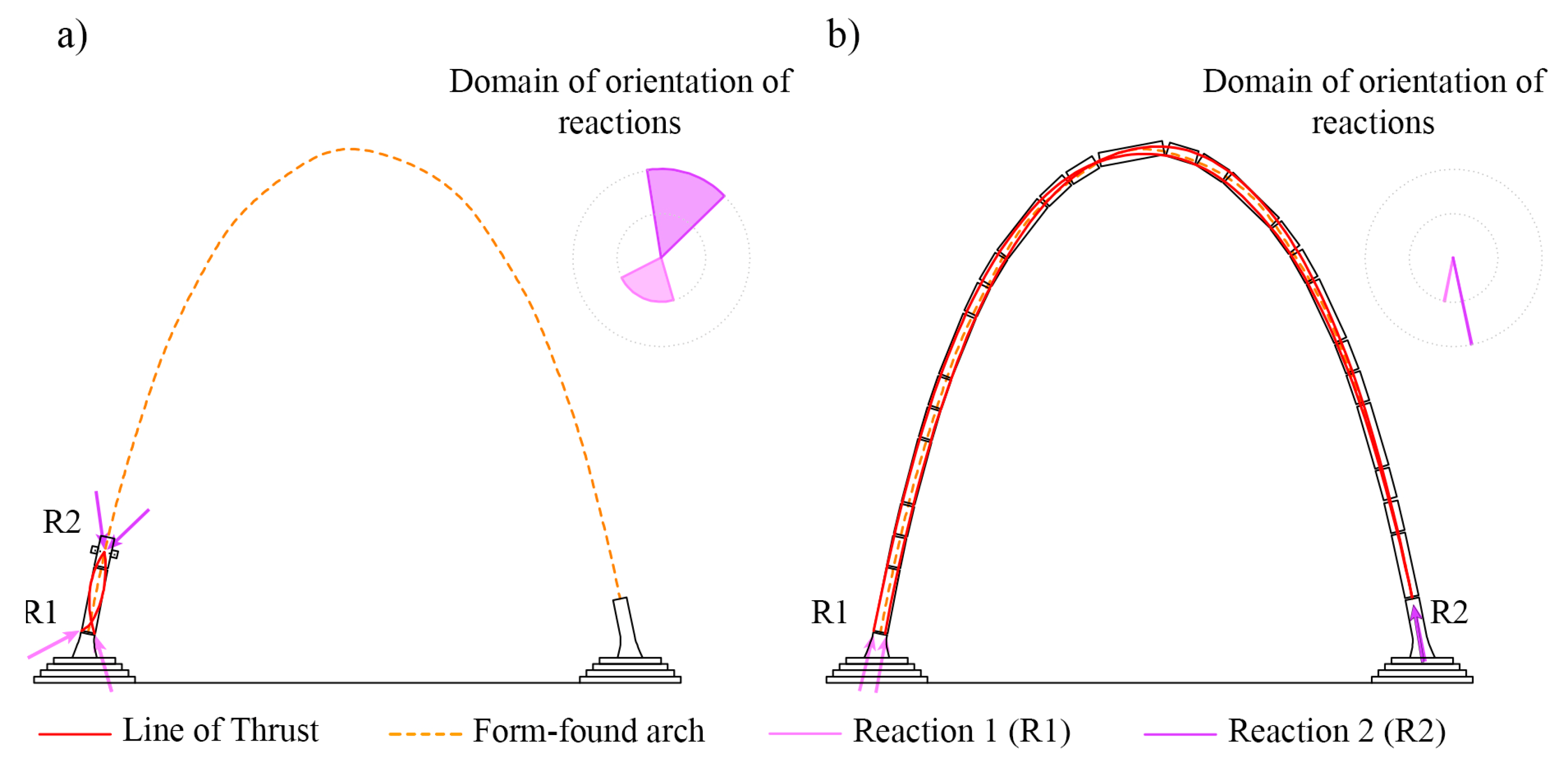
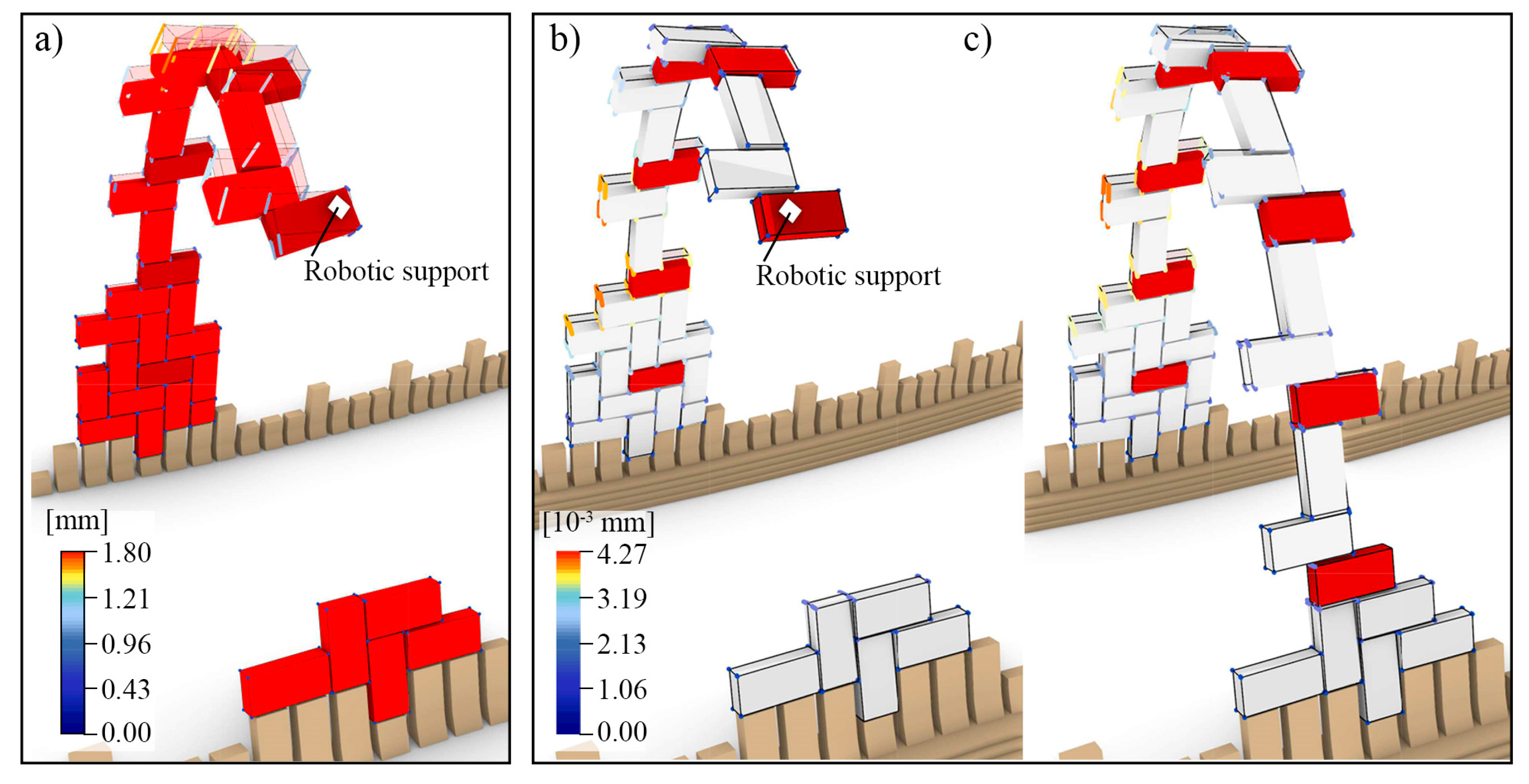
5. Simulation of the Construction Process

The influence of the CFs mentioned in the previous section, see Section 4, is considered within three models: a geometrical model, a numerical model, and a simulation of robotic assembly, see Figure 3. These three models are interconnected and provide detailed information needed to evaluate the state of a structure during its construction. They constitute the simulation of the construction process for assessing the state of the structure during construction works.
The geometrical model is composed of an exact copy of the actual structure. It describes the structure and the building site. It also collects geometrical information about masonry units, i.e., the stereotomy of bricks or blocks as their position, spatial organization, and details about the mortar joints. The geometrical model contains all information that could affect the structural state during the construction works or influence the construction process, e.g., the robotic workspace. The significance of a detailed model has to be stressed; an incorrect or non-detailed geometric description of the structure could preclude the functionality of the numerical and assembly simulations.
The numerical model is composed of a set of consequential analyses linked by a cause-and-effect relationship: each numerical analysis evaluates the structural state for a given construction stage and provides information configuration for assessing the following construction stage. For example, the simulation of the construction process of a hemispherical dome built using HVT can be carried out by estimating the structural state for each time a plate-bande is placed and when a horizontal brick course is completed. Each evaluation associated with a new construction stage is assessed by recognizing the effect of the actual structural configuration of the portion already built [38]. Material characteristics’ alteration is acknowledged in the numerical model, e.g., the change in the stiffness and strength of the mortar due to hardening. In this manner, through the intermediate configurations, the effect of the temporal factor is assumed within the numerical model.
A model dedicated to the assembly simulation completes the construction process simulation. This model is strictly related to the technology and enables the assembly process step by step by showing the robot path planning. In this manner, such a model informs the other two of the technology’s possible limitations.

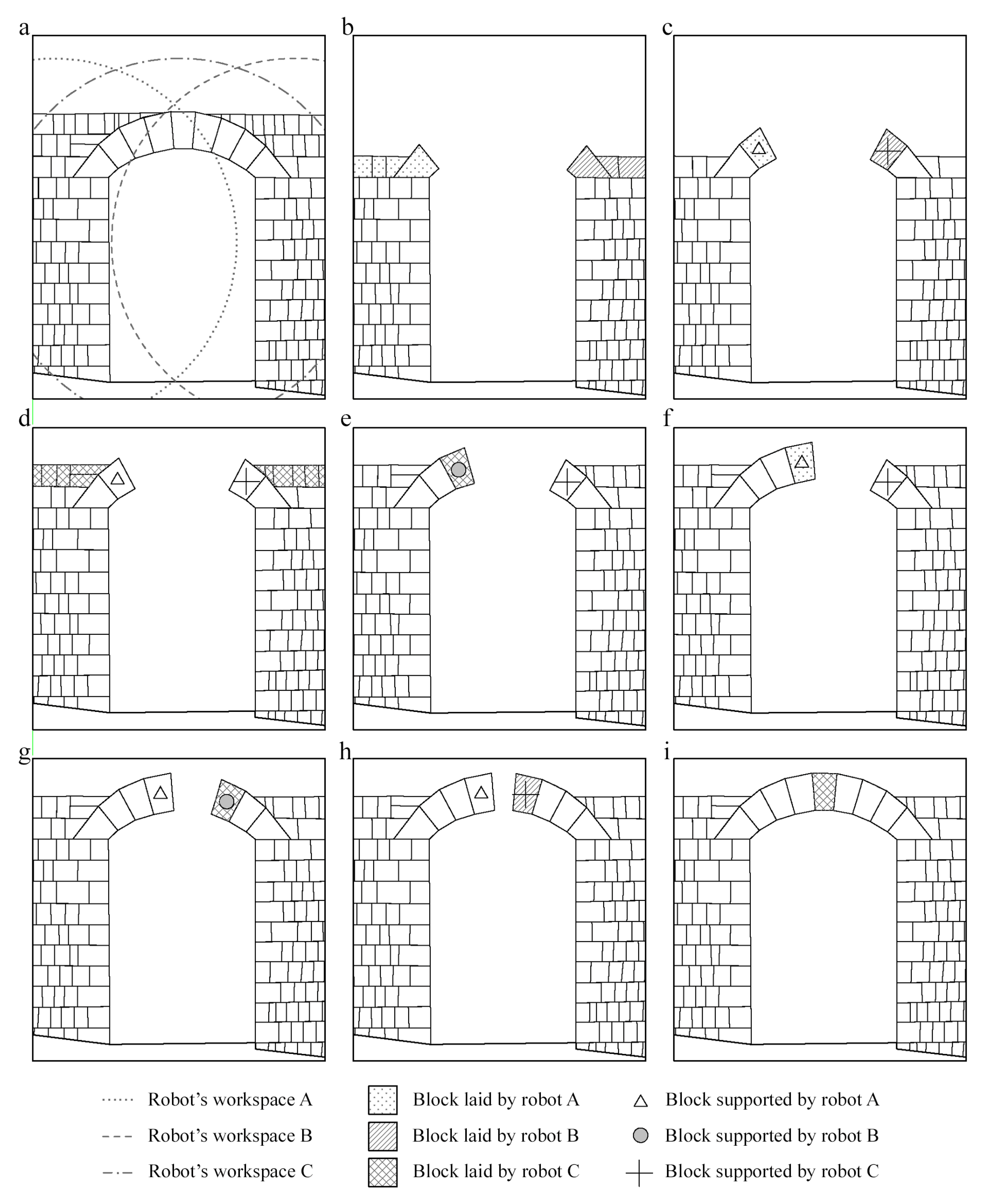
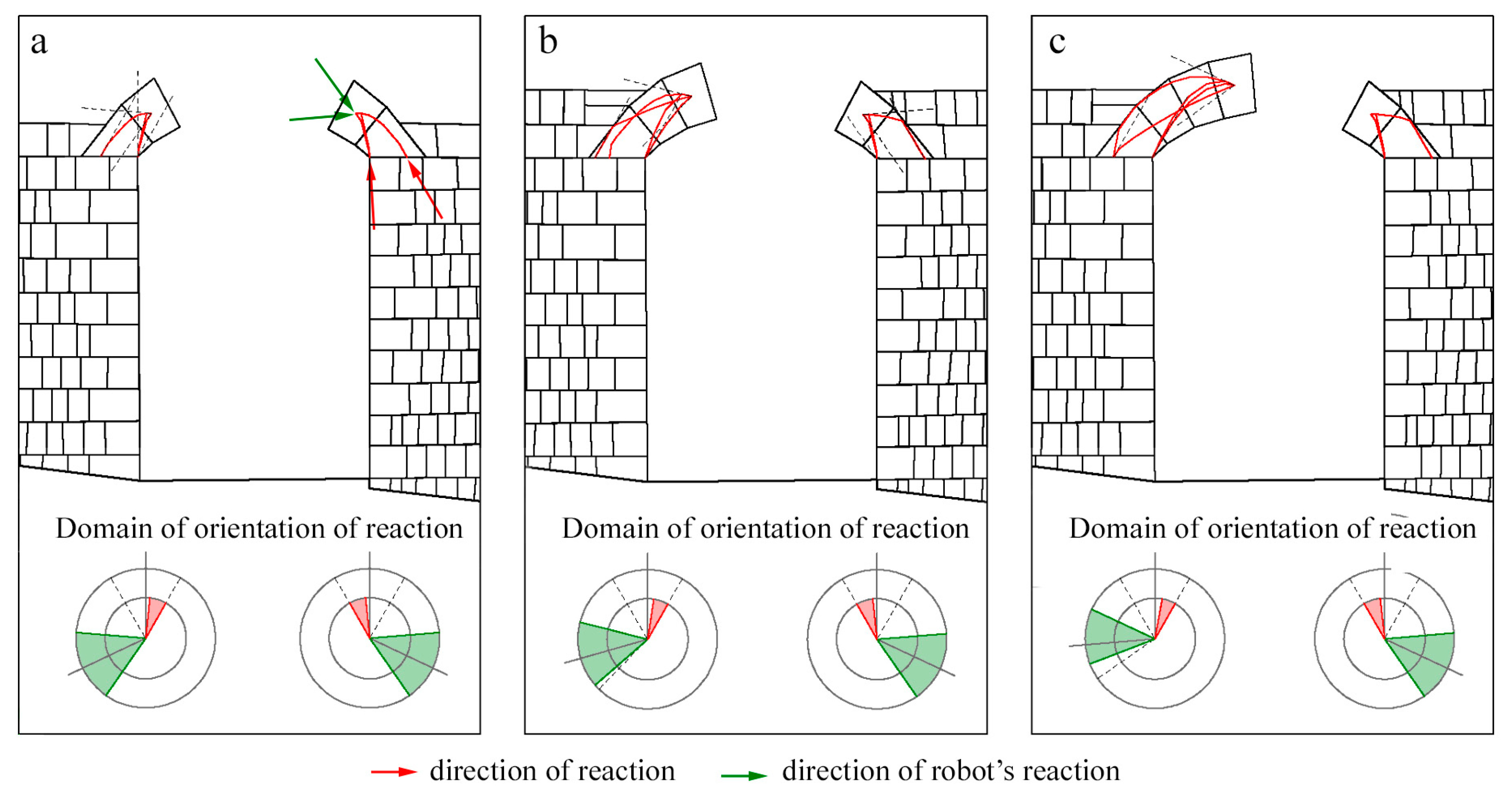
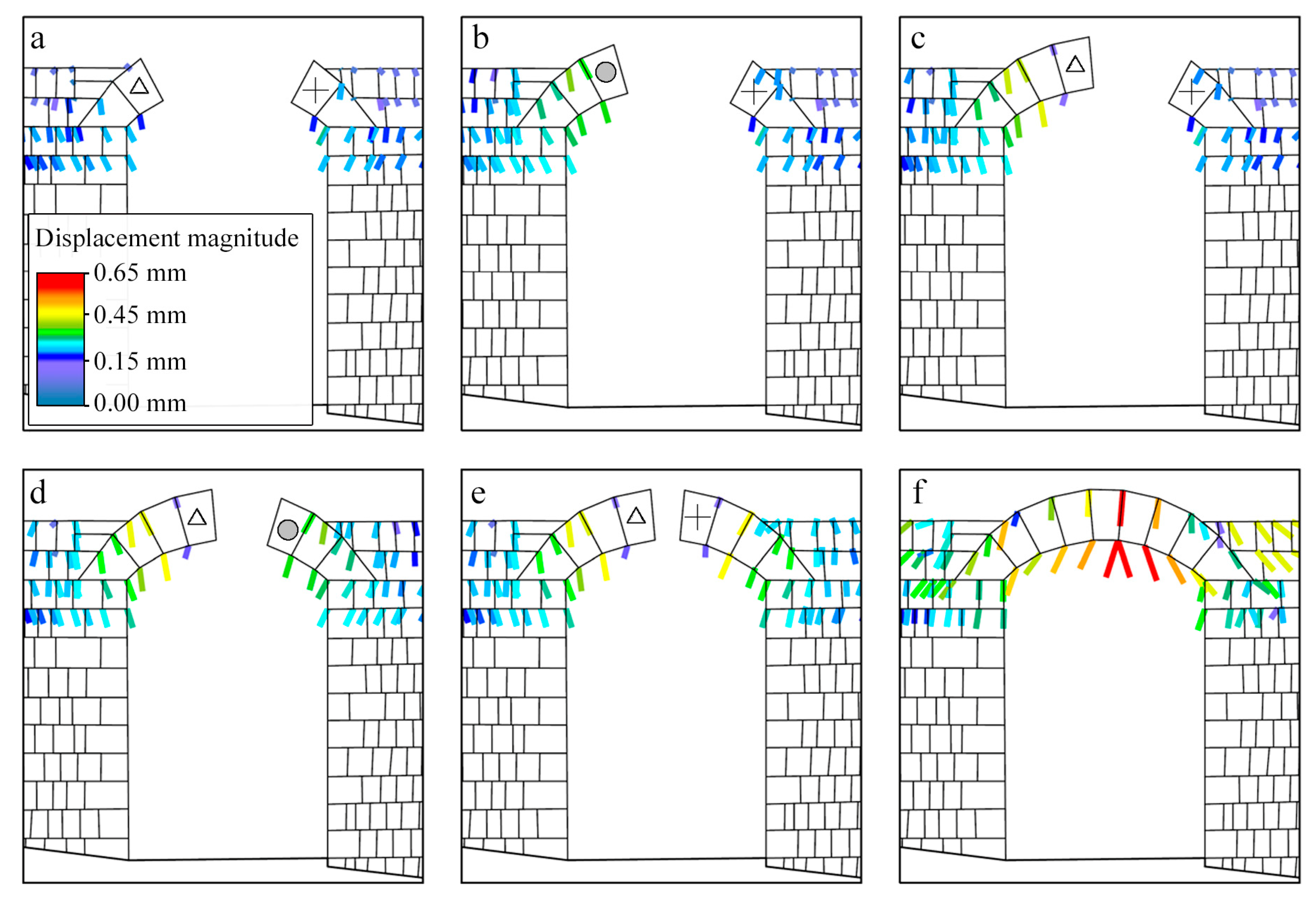
6. The Construction of the Voussoir Arch

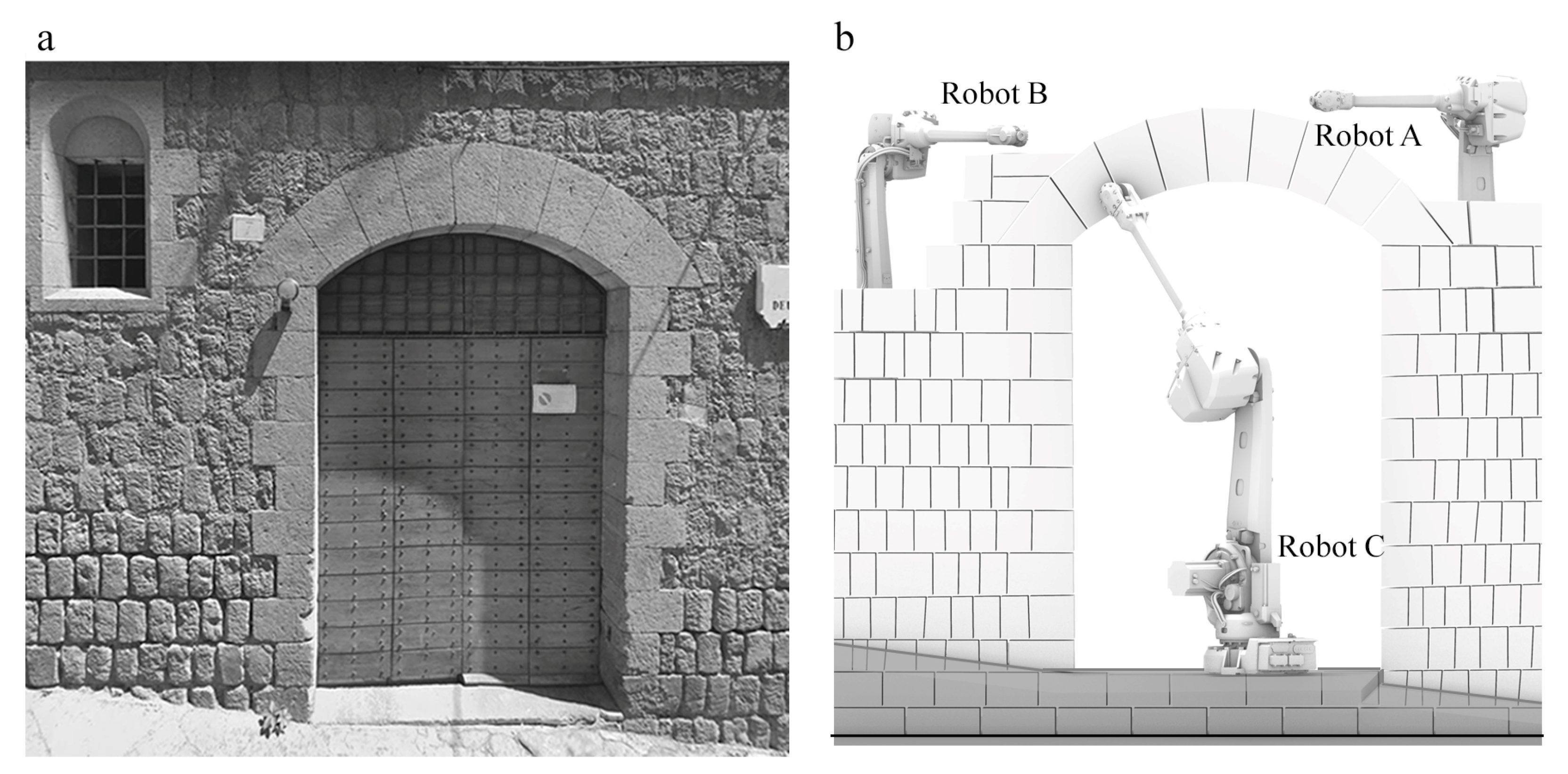
6.1. Case Study: Masonry Historical Arch

This section delivers a simple but meaningful application of the construction process simulation presented in Section 5. The example, shown in Figure 4, refers to a masonry structure constituted of a stone arch built with the aid of three collaborative robotic arms, denoted by the letters A, B, and C [17], and without the centering support. The example is chosen to highlight the relevance of the simulation of the construction process presented in Section 3 and the role of the CFs described in Section 4.
The construction process simulation was carried out based on a detailed geometrical model representative of the actual structure, see Figure 4b. Although the case study adopted refers to an arch, the generalization of the simulation of the construction process to spatial structures such as vaults, domes, or shells could be accomplished with some additional computational costs. The arch’s span is about 2.07 m, and its stone blocks are about 35 cm wide, 50 cm high, and 40 cm deep, with an estimated density of 2300 kg/m3. The blocks placed on the abutments are arranged on a horizontal bed joint, as illustrated in Figure 4.
After the geometries were established, the robotic arms were positioned based on the workspace and reachability. Then, several numerical models were implemented, each considering a different construction sequence; amongst all these, Figure 5 depicts the one in which the smallest displacements are recorded. According to this construction sequence, arms A and B place blocks at both arch springs, see Figure 5b; then, they place the two voussoirs in the higher course and hold the two portions of the structure, see Figure 5c. Subsequently, arm C lays the second course of blocks, see Figure 5d, and the voussoir at the next course. At this point, arm B releases the voussoir of the second course; meanwhile, arm C supplies the resources to support the portion of the arch under construction, see Figure 5e. Then, similar to the previous step, the robotic arms cooperate in pairs, first B and C, and then C and A. The last simulated construction stage consists of the keystone placing; see Figure 5i. In the simulation of the process of construction, all blocks laid by the robotic arms are held in a manner that the resultant force can be considered applied to the centroid of the block and to avoid any overturning [17]. Therefore, robots act to place the blocks and support portions of the structures during construction, allowing for the development of resistant substructures.
For each construction stage, analyses were carried out to estimate the structural state. Two different methods were applied to estimate this state of the arch: the line of thrust analysis to establish the forces required to reach an equilibrium state [21] and discrete-element analysis to estimate the block displacements [39,40]. Discrete-element methods allow the motion of a system of rigid elements to be detected but are generally time-consuming and require high computational costs compared to finite-element methods. Together these two methods provide an overall description of the state of the structure.
The first set of consequential analyses has been conducted within the framework of limit analysis estimating the line of thrust [21]. The minimum and maximum horizontal thrusts were also evaluated considering sliding, i.e., assuming a friction angle of 30°. In fact, as Figure 6a shows, the peculiar bed joint orientation of the first voussoir favours slippage. This phenomenon is contrasted by the mass provided by the blocks already placed at the second course; see Figure 6b. At this construction stage, the position of the line of thrust can shift toward the extrados. As shown in Figure 6, the line of thrust changes during construction; thus, to assess the possibility of building the arch without centering is necessary to estimate the state for all construction stages. Here the domains of the orientation of reactions of three different construction stages are also seen. This domain describes the limit of the orientation of forces that the robotic arm should be able to provide to reach an equilibrated state; the wider the domain, the easier it is to reach an equilibrated state. In the case analyzed, with the progress of the construction work, the domain of orientation of reactions narrows; see the left side of Figure 6. The set of consequential analyses shows that the minimum and maximum horizontal thrust increase along the construction, respectively, from 0.9 kN to 1.8 kN and from 1.1 kN to 14.0 kN, while the domain of orientation of reactions drastically narrows down from 60° to 46.1° for robotic support and for reaction at the spring of the arch; the variation of the domain is 23.1° to 16.2°.
Numerical analyses were performed within 3DEC software version 5. 20 (3DEC|US Minneapolis-Itasca Consulting Group), considering stone blocks as rigid bodies. The failure Mohr–Coulomb model with zero tensile capacity and zero cohesion was adopted in this study. Therefore, the interfaces between blocks are characterized only by joint stiffness parameters: kN, kS, and the coefficient of Coulomb friction [41]. As described in [42], kN and kS are related, respectively, to the difficulty of pressing and slipping of the blocks with respect to each other. The values assumed within the simulation are kN = 3.7 × 109 N/m and kS = 3.7 × 108 N/m, with a friction angle of about 30°. The displacement recorded during the simulations of the construction sequence is illustrated in Figure 7 where vector displacements of each block along the construction process are illustrated. The set of sequential analyses was executed as described in Section 5, i.e., estimating the deformation and settlements considering the actual configurations of the previous building stages.
According to the illustrated construction sequence, the maximum displacement recorded is about 0.65 mm and occurs when the keystone has been placed. The knowledge of this value is meaningful to check the compatibility with the assembly technology chosen. In this case, it should be compared with the accuracy of robotic arms; values greater than technological accuracy could preclude the possibility of building and demand adjustment in the simulation approach. The use of robot arms as temporary support and not only for placing allows resistant substructures to materialize at each construction stage.
The specific geometry of the case study adopted, characterized by the unusual stereotomy of the spring’s stones that facilitates sliding phenomena, allows an understanding of the role of CFs. Sliding is enabled by adopting a friction angle of about 20°, see Figure 8a. Despite that, the slippage does not occur if the stereotomy of the first voussoir is altered, as seen in Figure 8b, even if the friction angle decreases to 15°.
As mentioned in Section 4, the construction sequence is another CF that affects the state of the arch. Its relevance is illustrated in Figure 8c,d, where two construction stages of two alternative construction sequences are shown. In particular, the collapse of the structure illustrated in Figure 8c is due to the absence of the stone blocks positioned at the side of the arch. In this case horizontal thrust of the arch is not balanced and sliding occurs.
The second alternative construction sequence implicates the use of only two collaborative robots, see Figure 8d,e. The construction of the structure is pursued starting only from the arch’s right side and placing a voussoir one after another until it has reached the opposite side of the arch. Here, the load supported by robotic arms is about 75% more than the previous cases, see Figure 5. Thus, the robot’s payload assumes a discriminating criterion. In this case, the maximum displacement recorded increased up to about 0.95 mm at the completed structure, i.e., expressed by the ratio between displacement and the arch’s span, equal to 4.6 × 10−4. Further, a comparison is made with the traditional construction process, i.e., the stone arch is built using centering, as illustrated in Figure 8f. Here the maximum displacement recorded is about 0.45 mm, i.e., about 31% lower than the previous simulations. As expected, the construction sequence variation affects the structure’s state. The role of CFs is visible in the structural analysis and affects the state preeminently during the construction works, while they could be irrelevant once the structure is completed. The various examples presented with alterations applied to the CFs identify the significance of the CFs in the structural analysis and affect the state during construction.

6.2. Case Study: Anatomy of Structure Masonry Historical Arch

The case study described here is an actual application of the proposed approach. The analyses were applied to estimate the structural state during construction of a glass masonry vault, see Figure 1c. The structure has been built with the aid of two industrial robotic arms (ABB-IRB 6400) at the “Anatomy of Structure” exhibit hosted at the Ambika P3 Gallery in London (for a detailed description of the project see [43,44]). The two robotic arms position bricks in complex orientations and temporarily support the unfinished structure.
The vault’s design was inspired by historical self-supporting techniques (PVT, HVT, and CTVT) [1,28]. The vault’s shape resembles a saddle with a catenary profile. It spans 2.7 m, with a length of 4.4 m. The outer edges have a maximum rise of about 2.2 m, while the central arch rises approximately 1.9 m. Glass bricks were adopted, and epoxy was used to fill the joints allowing a quick setting and giving enough strength to hold the bricks in place.
Regarding the construction process, two distinct phases were individuated: the first phase is the most critical. Here robot arms built the central arch providing support. The commencement of the construction process occurred on one extremity of the vault, whereby the sequential laying of bricks was executed up to the opposite extremity. Throughout this phase, the two robots alternately provide support and lay completion of the central arch. The second phase starts when the robots work independently to build outward from the central arch, completing the remaining vault portion.
Numerical analyses were conducted for both phases, focusing on the most critical one: the construction of the central arch. For this phase, the thrust line, the domain of orientation of reaction, and DE analyses were performed. The structural evaluations were determined based on a digital copy of the structures, i.e., for each glass brick a block was modeled (geometrical CFs); the actual assembly sequences were also considered (temporal CF). Unlike the previous example, illustrated in Section 6.1, here, the domain of orientation of the reactions drastically changes during construction work. As depicted in Figure 9a), during the initial phase of construction, a state of equilibrium is achieved when the horizontal thrust falls within the range of 0.00–0.001 kN with a wide range of domain of orientation of reaction, spanning approximately 79.5° and around 54.0° for the two reactions. As construction progresses, as illustrated in Figure 9b, both the minimum and maximum horizontal thrust increase to 0.09–0.10 kN, while the domain of reaction orientations undergoes a significant reduction, narrowing down to 1.1° and 0.8°, denoting critical construction stages.
The arch was modeled as a system of rigid blocks with interfaces ruled by the Mohr–Coulomb model, assuming finite tensile strength and cohesion. These parameters were estimated and verified through experiment tests, incorporating a safety coefficient (mechanical CFs). From a numerical perspective, the interaction between the robotic arm and the structure was considered as CF and evaluated as a yielding constraint. Indeed, laboratory tests have indicated that the gripping points of the robotic arms enable movements when the forces meet specific conditions, such as a predefined shear limit (mechanical and technological CFs).
As displayed in Figure 10a, the numerical simulations revealed that the equilibrium state is sensitive to the placement of the robotic gripping point. This emphasizes that an improperly positioned grip may lead to out-of-plane displacements. To avoid overturning phenomena a particular robotic sequencing construction method was developed in order to avoid out-of-plane twisting displacement [11,17]. The simulation of the construction stages conducted with DEM confirms the results obtained by TLA: the central arch reaches an equilibrium state, with the robotic arm as support, in each construction stage of the central arch; the maximum displacement estimated is of 4.27 × 10−3 mm.
Once the central arch has been completed, the simulations show displacements smaller than the previous phase.

7. Conclusions

This study centers around identifying an approach for simulating the structural state of curved structures assembled with robotics technologies and composed of discrete elements. These constructions are primarily subject to compressive forces and, in this sense, resemble historic masonry structures. Within this context, the study aims to integrate self-supporting techniques with robotic arms to develop contemporary, sustainable, and efficient building practices. This approach is explored by evaluating the state of a structure built without centering and with the aid of robotic arms, establishing a correlation between the building technique and the construction state.
Studying construction factors governing historic self-supporting techniques offers valuable insights. Indeed, although not exhaustive, the example provided in Section 6.1 critically examines the variations in construction factors (CFs) and demonstrates their influence on the structural state during construction. The example critically examines construction factor (CF) variations and demonstrates their influence on the structural state during construction. When combined with modern technologies such as robotic arms, these CFs can drive innovation in vaulting techniques, enable the wider application of spatial structures (such as vaults and domes), and create opportunities to use eco-friendly materials, including recycled or organic options. The approach has been applied to simulate the construction of a glass structure and to assess the state of an arch indicating the most critical phase.
The approach outlined in this research could serve as a foundation for developing a framework dedicated to evaluating the cost and sustainability of contemporary self-supporting techniques, thus enhancing the efficiency of the building sector. Numerical simulations of construction works based on consequential analyses could pave the way for innovative research topics, such as cost optimization, structural stability during construction, and sustainability. However, it should be noted that a critical assessment of efficiency or sustainability has not yet been addressed in this study. Future studies could incorporate these evaluations into the proposed approach, ultimately providing a comprehensive workflow for simulating stability, efficiency, and sustainability to develop innovative building techniques.

Author Contributions

Conceptualization, V.P., G.R. and G.M.R.; Methodology, V.P., G.R. and G.M.R.; Software, V.P.; Validation, C.O.; Investigation, V.P. and C.O.; Writing—original draft, V.P. and C.O.; Writing—review & editing, G.R. and G.M.R.; Supervision, G.R. and G.M.R. All authors have read and agreed to the published version of the manuscript.

Funding

This research received no external funding.

Institutional Review Board Statement

Not applicable.

Informed Consent Statement

Not applicable.

Data Availability Statement

Not applicable.

Acknowledgments

The authors would like to thank Rima Ghazal, Nicola Lepore, and Nandini Priya Thatikonda for the support provided during the study. The Software 3DEC was provided by Itasca C.G. under the Education Partnership Program for which the authors also express their gratitude.

Conflicts of Interest

The authors declare no conflict of interest.

Abbreviations

The following abbreviations are used in this manuscript:
CFConstruction Factor
AECArchitecture, Engineering, and Construction
PVTPitched Vaulting Technique
CTVTClay Tube Vaulting Technique
TVTTile Vaulting Technique
HVTHerringbone Vaulting Technique

References

  1. Parascho, S.; Han, I.X.; Walker, S.; Beghini, A.; Bruun, E.P.G.; Adriaenssens, S. Robotic vault: A cooperative robotic assembly method for brick vault construction. Constr. Robot. 2020, 4, 117–126. [Google Scholar] [CrossRef]
  2. Adriaenssens, S.; Gramazio, F.; Kohler, M.; Menges, A.; Pauly, M. Advances in Architectural Geometry 2016; VDF Hochschulverlag AG: Zürich, Switzerland, 2016. [Google Scholar]
  3. Latteur, P.; Goessens, S.; Mueller, C. Masonry construction with drones. In Proceedings of the IASS Annual Symposium: Spatial Structures in the 21st Century, Tokyo, Japan, 26–30 September 2016; Volume 2016. [Google Scholar]
  4. Bruckmann, T.; Boumann, R. Simulation and optimization of automated masonry construction using cable robots. Adv. Eng. Inform. 2021, 50, 101388. [Google Scholar] [CrossRef]
  5. Wu, K.; Kilian, A. Designing Compression-Only Arch Structures Using Robotic Equilibrium Assembly. In Impact: Design with All Senses; Gengnagel, A., Baverel, O., Burry, J., Ramsgaard Thomsen, M., Weinzierl, S., Eds.; Springer International Publishing: Cham, Switzerland, 2020; pp. 608–622. [Google Scholar]
  6. Thomson, J. Brick-Laying Machine. U.S. Patent 772191A, 11 October 1904. [Google Scholar]
  7. Willmann, J.; Block, P.; Hutter, M.; Byrne, K.; Schork, T. Robotic Fabrication in Architecture, Art and Design 2018: Foreword by Sigrid Brell-Cokcan and Johannes Braumann, Association for Robots in Architecture; Springer: Berlin/Heidelberg, Germany, 2018. [Google Scholar]
  8. Bock, T.; Linner, T. Robot-Oriented Design: Design and Management Tools for the Deployment of Automation and Robotics in Construction; Cambridge University Press: Cambridge, UK, 2015. [Google Scholar]
  9. Thoma, A.; Adel, A.; Helmreich, M.; Wehrle, T.; Gramazio, F.; Kohler, M. Robotic Fabrication of Bespoke Timber Frame Modules. In Robotic Fabrication in Architecture, Art and Design 2018; Springer International Publishing: Zurich, Switzerland, 2018; pp. 447–458. [Google Scholar]
  10. Dörfler, K.; Sandy, T.; Giftthaler, M.; Gramazio, F.; Kohler, M.; Buchli, J. Mobile Robotic Brickwork. In Robotic Fabrication in Architecture, Art and Design 2016; Reinhardt, D., Saunders, R., Burry, J., Eds.; Springer International Publishing: Cham, Switzerland, 2016; pp. 204–217. [Google Scholar]
  11. Parascho, S.; Han, I.X.; Beghini, A.; Mike, M.; Bruun, E.P.G.; Adriaenssens, S.A. Design and Robotic Fabrication Method for Complex Masonry Structures. Adv. Archit. Geom. 2021, 25, 350–375. [Google Scholar]
  12. Goessens, S.; Mueller, C.; Latteur, P. Feasibility study for drone-based masonry construction of real-scale structures. Autom. Constr. 2018, 94, 458–480. [Google Scholar] [CrossRef]
  13. Nwaogu, J.M.; Yang, Y.; Chan, A.P.C.; Chi, H. Application of drones in the architecture, engineering, and construction (AEC) industry. Autom. Constr. 2023, 150, 104827. [Google Scholar] [CrossRef]
  14. Paoletti, I. Mass customization with additive manufacturing: New perspectives for multi performative building components in architecture. Procedia Eng. 2017, 180, 1150–1159. [Google Scholar] [CrossRef]
  15. Paolini, A.; Kollmannsberger, S.; Rank, E. Additive manufacturing in construction: A review on processes, applications, and digital planning methods. Addit. Manuf. 2019, 30, 100894. [Google Scholar] [CrossRef]
  16. Bonswetch, T.; Hobel, D.; Gramazio, F.; Kohler, M. The Informed Wall: Applying additive digital fabrication techniques on architecture. In Proceedings of the 25th Annual Conference of the Association for Computer-Aided Design in Architecture: Synthetic, Louisville, KY, USA, 12–15 October 2006; pp. 489–495. [Google Scholar]
  17. Paris, V.; Lepore, N.; Brunn, E.P.G.; Ruscica, G.; Piccioni, M.D.; Beghini, A.; Parascho, S.; Adriaenssens, S. Robotic Construction of a Self-Balancing glass masonry vault: DEM study of stability during the construction stages. In Proceedings of the IASS Annual Symposia, Surrey, UK, 23–27 August 2021. [Google Scholar]
  18. Paris, V. Equilibrium of Self-Balanced Shells. Cross-Herringbone Technology; Collana Della Scuola di Alta Formazione Dottorale; University of Bergamo: Bergamo, Italy, 2021. [Google Scholar]
  19. Chaturvedi, S.; Ochsendorf, J. Global environmental impacts due to cement and steel. Struct. Eng. Int. 2004, 14, 198–200. [Google Scholar] [CrossRef]
  20. Barbosa, F.; Woetzel, J.; Mischke, J. Reinventing Construction: A Route of Higher Productivity; Technical Report; McKinsey Global Institute: New York, NY, USA, 2017. [Google Scholar]
  21. Heyman, J. The stone skeleton. Int. J. Solids Struct. 1966, 2, 249–279. [Google Scholar] [CrossRef]
  22. Montanino, A.; De Gregorio, D.; Olivieri, C.; Iannuzzo, A. The continuous Airy-based for stress-singularities (CASS) method: An energy-based numerical formulation for unilateral materials. Int. J. Solids Struct. 2022, 256, 111954. [Google Scholar] [CrossRef]
  23. Marmo, F. ArchLab: A MATLAB tool for the Thrust Line Analysis of masonry arches. Curved Layer. Struct. 2021, 8, 26–35. [Google Scholar] [CrossRef]
  24. Marmo, F.; Rosati, L. Reformulation and extension of the thrust network analysis. Comput. Struct. 2017, 182, 104–118. [Google Scholar] [CrossRef]
  25. Angelillo, M.; Lourenço, P.B.; Milani, G. Masonry behaviour and modelling. In Mechanics of Masonry Structures; Angelillo, M., Ed.; In CISM International Centre for Mechanical Sciences; Springer: Vienna, Austria, 2014; pp. 1–26. [Google Scholar]
  26. United Nations Environment Programme. Global Status Report for Buildings and Construction: Towards a Zero-Emission. In Efficient and Resilient Buildings and Construction Sector; Global Alliance for Building and Construction: Nairobi, Kenya, 2021. [Google Scholar]
  27. Mirabella Roberti, G.; Lombardini, N.; Falter, H. Late Roman domes in clay tubes: Historical and numerical study of San Vitale in Ravenna. In Spatial Structures: Heritage, Present and Future; International Association of Shell and Space Structures: Milan, Italy, 1995; Volume 2, pp. 1237–1244. [Google Scholar]
  28. Huerta Fernández, S. The Geometry and Construction of Byzantine Vaults: The Fundamental Contribution of Auguste Choisy; Instituto Juan de Herrera: Madrid, Spain, 2009. [Google Scholar]
  29. Moya Blanco, L. Bóvedas Tabicadas; Dirección General de Arquitectura: Madrid, Spain, 1947. [Google Scholar]
  30. Lancaster, L.C. Innovative Vaulting in the Architecture of the Roman Empire: 1st to 4th Centuries CE.; Cambridge University Press: Cambridge, UK, 2015. [Google Scholar]
  31. Huerta Fernández, S. La construcción tabicada y la teoría cohesiva de Rafael Guastavino; Instituto Juan de Herrera: Madrid, Spain, 2006. [Google Scholar]
  32. Huerta Fernández, S. Wedges and plate-bandes: Mechanical theories after De la Hire. In L’architrave, le Plancher, la Plate-Forme. Nouvelle Histoire de la Construction. Architecture Essais; Gargiano, R., Ed.; Presses polytechniques et Universitaires Romandes: Lausanne, Switzerland, 2012; pp. 405–435. [Google Scholar]
  33. Block, P.; DeJong, M.; Davis, L.; Ochsendorf, J. Tile vaulted systems for low-cost construction in Africa. ATDF J. 2010, 7, 4–13. [Google Scholar]
  34. Davis, L.; Rippmann, M.; Pawlofsky, T. Innovative funicular tile vaulting: A prototype vault in Switzerland. Struct. Eng. 2012, 90, 46–56. [Google Scholar]
  35. Olivieri, C.; Iannuzzo, A.; Fortunato, A.; DeJong, M.J. The effect of concentrated loads on open-well masonry spiral stairs. Eng. Struct. 2022, 272, 114952. [Google Scholar] [CrossRef]
  36. Olivieri, C.; Adriaenssens, S.; Cennamo, C. A novel graphical assessment approach for compressed curved structures under vertical loading. Int. J. Space Struct. 2023, 38, 09560599231161424. [Google Scholar] [CrossRef]
  37. Paris, V.; Ruscica, G.; Mirabella Roberti, G. Graphical modelling of hoop force distribution for equilibrium analysis of masonry domes. Nexus Netw. J. 2021, 23, 855–878. [Google Scholar] [CrossRef]
  38. Paris, V.; Pizzigoni, P.; Adriaenssens, S. Statics of self-balancing masonry domes constructed with a cross-herringbone spiraling pattern. Eng. Struct. 2020, 215, 110440. [Google Scholar] [CrossRef]
  39. Cundall, P.A. Formulation of a three-dimensional distinct element model—Part I. A scheme to detect and represent contacts in a system composed of many polyhedral blocks. Int. J. Rock Mech. Min. Sci. Geomech. Abstr. 1988, 25, 107–116. [Google Scholar] [CrossRef]
  40. Hart, R.; Cundall, P.A.; Lemos, J. Formulation of a three-dimensional distinct element model—Part II. Mechanical calculations for motion and interaction of a system composed of many polyhedral blocks. Int. J. Rock Mech. Min. Sci. Geomech. Abstr. 1988, 25, 117–125. [Google Scholar] [CrossRef]
  41. Lemos, J.V. Discrete Element Modeling of Masonry Structures. Int. J. Archit. Herit. 2007, 1, 190–213. [Google Scholar] [CrossRef]
  42. Simon, J.; Bagi, K. Discrete Element Analysis of the Minimum Thickness of Oval Masonry Domes. Int. J. Archit. Herit. 2016, 10, 457–475. [Google Scholar] [CrossRef]
  43. Han, I.X.; Bruun, E.P.G.; Marsh, S.; Tavano, M.; Adriaenssens, S.; Parascho, S. From Concept to Construction: A Transferable Design and Robotic Fabrication Method for a Building-Scale Vault. In Proceedings of the 40th Annual Conference of the Association for Computer Aided Design in Architecture, Online, 24–30 October 2020. [Google Scholar]
  44. Bruun, E.P.G.; Pastrana, R.; Paris, V.; Beghini, A.; Pizzigoni, A.; Parascho, S.; Adriaenssens, S. Three cooperative robotic fabrication methods for the scaffold-free construction of a masonry arch. Autom. Constr. 2021, 129, 103803. [Google Scholar] [CrossRef]
Sustainability 15 09596 g001 550
Figure 1. Masonry glass shell under construction using robotic arms. Reprinted with permission from Ref. [17].
Figure 1. Masonry glass shell under construction using robotic arms. Reprinted with permission from Ref. [17].
Sustainability 15 09596 g001
Sustainability 15 09596 g002 550
Figure 2. Self-supporting vaulting techniques. (a) Pitched vaults, different schemes to lay bricks. Drawing of A. Choisy [28]. (b) Clay tube vault, detail of a section of the San Vitale dome (Ravenna, Italy), horizontal and vertical orientation of the tubes [27]. (c) Process of construction of tile vault. From left to right: light-centering, construction sequence, and layering of the vault [29].
Figure 2. Self-supporting vaulting techniques. (a) Pitched vaults, different schemes to lay bricks. Drawing of A. Choisy [28]. (b) Clay tube vault, detail of a section of the San Vitale dome (Ravenna, Italy), horizontal and vertical orientation of the tubes [27]. (c) Process of construction of tile vault. From left to right: light-centering, construction sequence, and layering of the vault [29].
Sustainability 15 09596 g002
Sustainability 15 09596 g003 550
Figure 3. Simulation scheme of self-supporting vaulting techniques.
Figure 3. Simulation scheme of self-supporting vaulting techniques.
Sustainability 15 09596 g003
Sustainability 15 09596 g004 550
Figure 4. (a) Masonry arch (Viterbo, Italy). (b) Geometrical model of masonry arch construction analyzed. The structure rests on a horizontal foundation even though the street level is sloping, so all analyses were conducted considering a horizontal plane as the foundation (black line).
Figure 4. (a) Masonry arch (Viterbo, Italy). (b) Geometrical model of masonry arch construction analyzed. The structure rests on a horizontal foundation even though the street level is sloping, so all analyses were conducted considering a horizontal plane as the foundation (black line).
Sustainability 15 09596 g004
Sustainability 15 09596 g005 550
Figure 5. (a) Workspaces of robots A, B, and C. (b–i) Construction stages. The three robots cooperate for the construction. During the different stages each robot works alternatively providing support or placing blocks. For example, in (d) robots A and B support the arch and C places blocks, while in (e) robots C and B support and A positions the stone.
Figure 5. (a) Workspaces of robots A, B, and C. (b–i) Construction stages. The three robots cooperate for the construction. During the different stages each robot works alternatively providing support or placing blocks. For example, in (d) robots A and B support the arch and C places blocks, while in (e) robots C and B support and A positions the stone.
Sustainability 15 09596 g005
Sustainability 15 09596 g006 550
Figure 6. (a–c) Lines of thrusts and domains of orientation of reactions of three different construction stages (a–c). Dashed lines represent the limit direction defined by friction angle. Domains change during construction due to the advancement of the lay of new blocks.
Figure 6. (a–c) Lines of thrusts and domains of orientation of reactions of three different construction stages (a–c). Dashed lines represent the limit direction defined by friction angle. Domains change during construction due to the advancement of the lay of new blocks.
Sustainability 15 09596 g006
Sustainability 15 09596 g007 550
Figure 7. (a–f) Displacement for six construction stages. Displacements are shown by colored lines.
Figure 7. (a–f) Displacement for six construction stages. Displacements are shown by colored lines.
Sustainability 15 09596 g007
Sustainability 15 09596 g008 550
Figure 8. (a) CF: friction angle. Failure mode due to slippage. (b) CF: stereotomy, the variation of the shape of the two blocks at the arch spring leads to a different displacement field; see Figure 7c. (c) Failure mode due to the absence of the lateral stone courses that aid in the contrast of the horizontal thrusts. (d,e) Alternative assembly sequence using only two robots. (f) The construction of the arch that adopts the centering leads to different (smaller) displacements than that obtained in Figure 7f.
Figure 8. (a) CF: friction angle. Failure mode due to slippage. (b) CF: stereotomy, the variation of the shape of the two blocks at the arch spring leads to a different displacement field; see Figure 7c. (c) Failure mode due to the absence of the lateral stone courses that aid in the contrast of the horizontal thrusts. (d,e) Alternative assembly sequence using only two robots. (f) The construction of the arch that adopts the centering leads to different (smaller) displacements than that obtained in Figure 7f.
Sustainability 15 09596 g008
Sustainability 15 09596 g009 550
Figure 9. Domain of orientation of reactions. (a) First construction stage of Phase I. (b) Last construction stage of Phase I. The size of domains decreases with the advancement of construction, suggesting the identification of the most critical construction phases. Reprinted with permission from Ref. [17].
Figure 9. Domain of orientation of reactions. (a) First construction stage of Phase I. (b) Last construction stage of Phase I. The size of domains decreases with the advancement of construction, suggesting the identification of the most critical construction phases. Reprinted with permission from Ref. [17].
Sustainability 15 09596 g009
Sustainability 15 09596 g010 550
Figure 10. Construction stages of the central arch. (a) Incomplete arch showing the position of the robotic support. Out-of-plane overturning phenomena occur leading to a displacement of about 1.80 mm. (b,c) Simulation of construction of the central arch. The robot arm gripping point lies in the plane of the arch. The color scale is associated with the displacement vectors of each node.
Figure 10. Construction stages of the central arch. (a) Incomplete arch showing the position of the robotic support. Out-of-plane overturning phenomena occur leading to a displacement of about 1.80 mm. (b,c) Simulation of construction of the central arch. The robot arm gripping point lies in the plane of the arch. The color scale is associated with the displacement vectors of each node.
Sustainability 15 09596 g010
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

Share and Cite

MDPI and ACS Style

Paris, V.; Ruscica, G.; Olivieri, C.; Mirabella Roberti, G. A Systemic Approach to Simulate the Construction Process of Self-Supporting Masonry Structures. Sustainability 2023, 15, 9596. https://doi.org/10.3390/su15129596

AMA Style

Paris V, Ruscica G, Olivieri C, Mirabella Roberti G. A Systemic Approach to Simulate the Construction Process of Self-Supporting Masonry Structures. Sustainability. 2023; 15(12):9596. https://doi.org/10.3390/su15129596

Chicago/Turabian Style

Paris, Vittorio, Giuseppe Ruscica, Carlo Olivieri, and Giulio Mirabella Roberti. 2023. "A Systemic Approach to Simulate the Construction Process of Self-Supporting Masonry Structures" Sustainability 15, no. 12: 9596. https://doi.org/10.3390/su15129596

Note that from the first issue of 2016, this journal uses article numbers instead of page numbers. See further details here.

Article Metrics

Back to TopTop