Designing, Modeling, and Fabrication of a Novel Solar-Concentrating Spittoon against COVID-19 for Antibacterial Sustainable Atmosphere
Abstract
1. Introduction
2. Mathematical Modelling
- Properties of protein molecules are neglected.
- Saliva is assumed to be water and of uniform composition.
- Variation of specific heat at constant temperature is neglected.
- Initial temperature of saliva is assumed to be the body temperature of a healthy person.
2.1. The Energy Requirement to Evaporate and Burn Saliva
2.2. Power Required to Burn out Saliva in 1 min
2.3. Aperture Area Required
3. Materials and Methods
- It should not lose heat to the surroundings.
- Receiver temperature should be maintained at more than 373 K.
- It should generate heat when the sun falls from a different angle.
- It should be compact and lightweight.
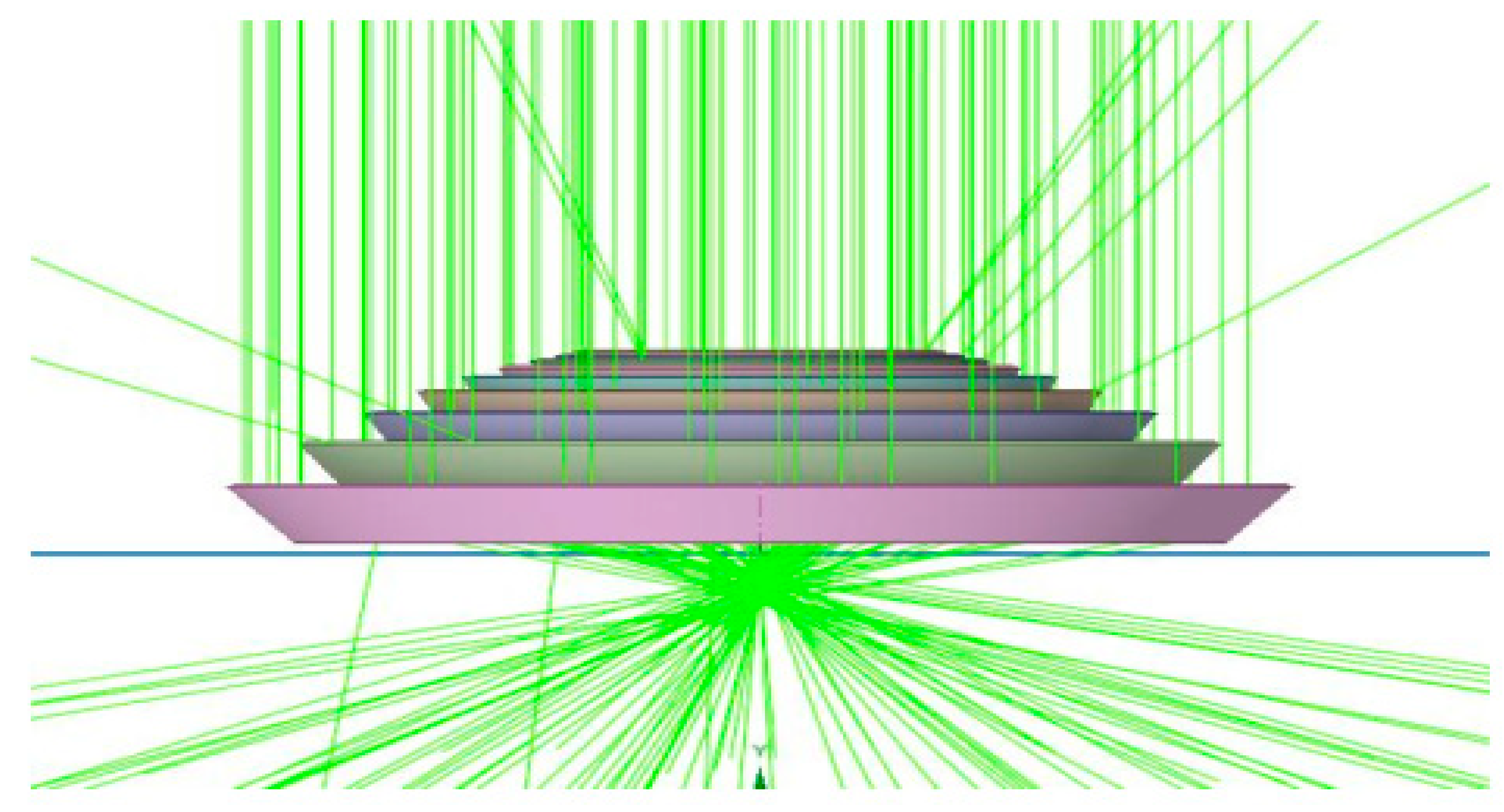
4. Fabrication and Designing of Solar-Concentrating Spittoon
4.1. Design of Concentrator
4.2. Focal Length
4.3. Focal Length to Diameter Ratio
4.4. Rim Angle
4.5. Aperture Area
4.6. Absorber Area or Concentrating Area
4.7. Geometric Concentration Ratio
4.8. Design Calculation
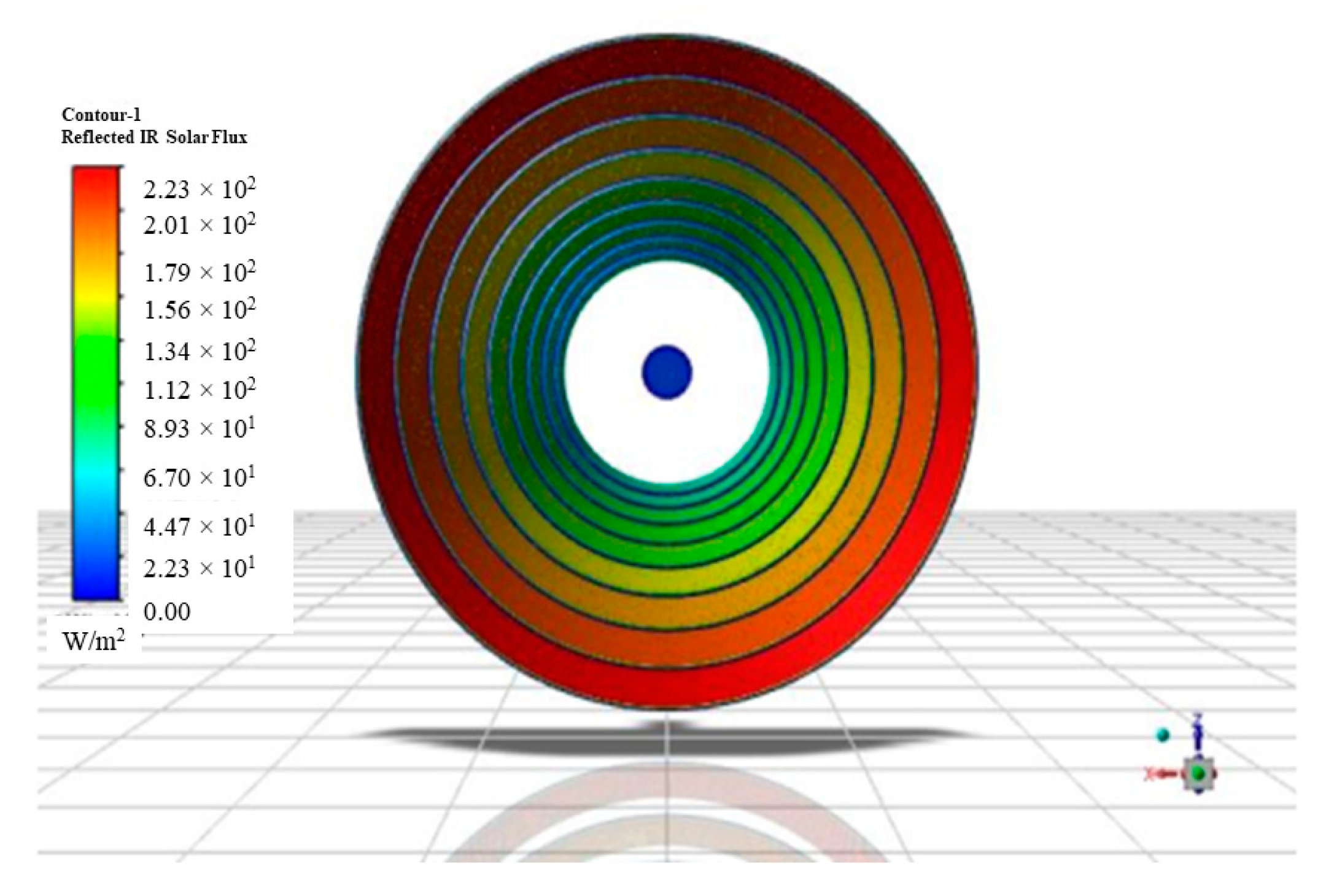
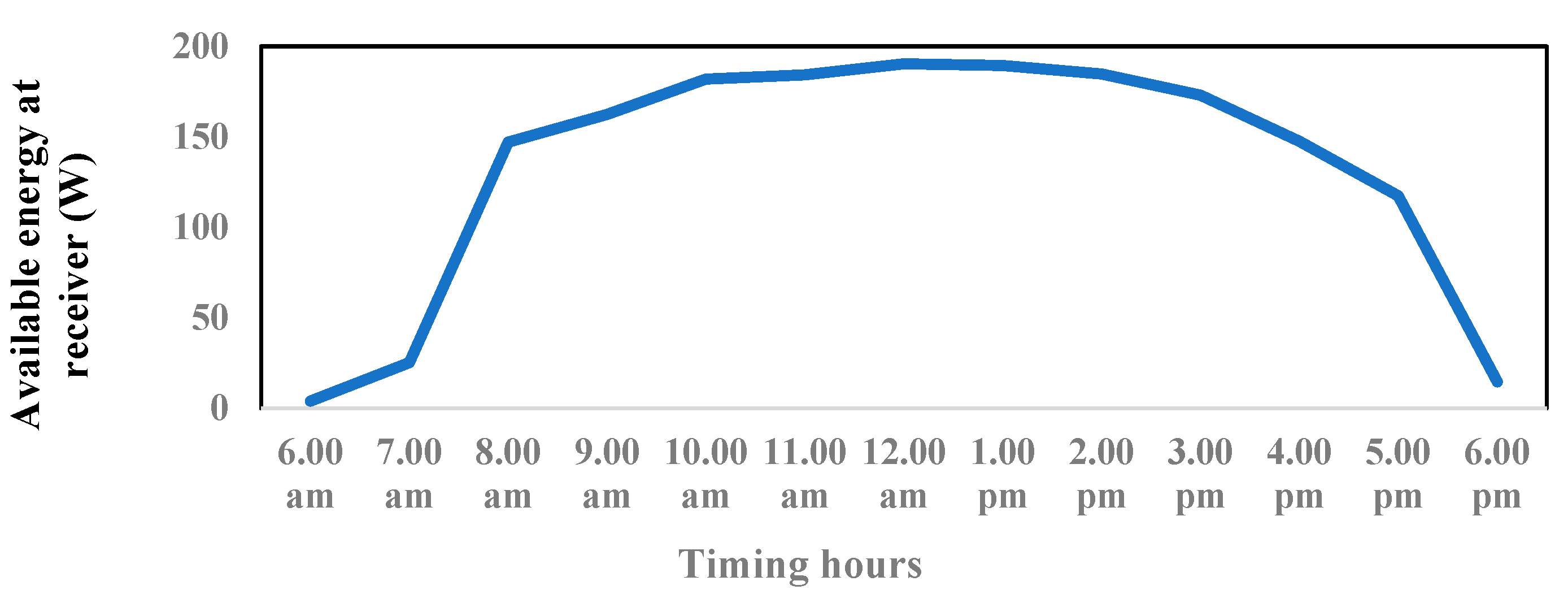
4.8.1. Rate of Thermal Energy Available at the Receiver
× [10.45 × (383 K − 313 K) + 5.67 × 10−8 × 0.25 × (383 K4 − 313 K4)]
4.8.2. Time Taken for Burning out Spitted Saliva
5. Results
5.1. Simulation Results
5.2. Performance Analysis
5.2.1. Optical or Concentrator Efficiency
5.2.2. Receiver Thermal Efficiency
5.2.3. Overall Efficiency
6. Discussion
Limitations of Solar-Concentrating Spittoon
7. Conclusions
8. Future Scope
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Nomenclature
| Q | Energy required to evaporate saliva (J). |
| m | Average amount of saliva spit by a person (kg). |
| Cpw | Specific heat of saliva (kJ/kg K). |
| Tb | Evaporation temperature of saliva at atmospheric pressure (k). |
| Te | Body temperature of a person (K). |
| Lt | Latent heat of vaporization of water (KJ/Kg). |
| P | Power (W). |
| Τ | Time (sec). |
| A | Aperture area of solar concentrator reflector in (m2). |
| IS | Radiant energy received by earth surface from the sun in India (W/m2). |
| qloss | Heat loss by receiver to surrounding by convection (W). |
| X | Aperture plane coordinate in x-axis. |
| Y | Aperture plane coordinate in y-axis. |
| Z | Distance from the vertex of concentrator parallel to the symmetry axis of the reflector (m). |
| f | Focal length of concentrator (m). |
| d | Diameter of concentrator (m). |
| φrm | Rim angle. |
| r | Normal area of reflector that is exposed to sun (m2). |
| n | Number of wooden frames. |
| af | Area of frame that is exposed to sunlight (m2). |
| d0 | Diameter of outer ring of reflector (m). |
| di | Diameter of inner most ring of reflectors (m). |
| t | Thickness of frame (m). |
| l | Length of frame (m). |
| Aab | Absorber area (m2). |
| dr | Diameter of receiver (m). |
| lr | Effective length of receiver area where flux of heat collected (m). |
| CRg | Geometric concentration ratio. |
| Arecn | Area of receiver normal to incident radiation (m2). |
| ηrec | Receiver efficiency. |
| ηop | Optical efficiency. |
| ηo | Overall efficiency. |
| Isn | Normal Solar irradiation (W/m2). |
| U | Overall heat transfer coefficient (W/m2K). |
| σ | Stefan Boltzmann constant. |
| F | Radiative conductance. |
| e | Fraction of area exposer to sun. |
| α | Absorptance. |
| τ | Transmittance. |
| i | Fraction of intercept. |
| r | Reflectivity of reflectors. |
References
- Kamyab, H.; Naderipour, A.; Jahannoush, M.; Abdullah, A.; Marzbali, M.H. Potential effect of SARS-CoV-2 on solar energy generation: Environmental dynamics and implications. Sustain. Energy Technol. Assess. 2022, 52, 102027. [Google Scholar] [CrossRef]
- Van Doremalen, N.; Bushmaker, T.; Morris, D.H.; Holbrook, M.G.; Gamble, A.; Williamson, B.N.; Tamin, A.; Harcourt, J.L.; Thornburg, N.J.; Gerber, S.I.; et al. Aerosol and surface stability of SARS-CoV-2 as compared with SARS-CoV-1. New Engl. J. Med. 2020, 382, 1564–1567. [Google Scholar] [CrossRef] [PubMed]
- Raeiszadeh, M.; Adeli, B. A critical review on ultraviolet disinfection systems against COVID-19 outbreak: Applicability, validation, and safety considerations. Acs Photonics 2020, 7, 2941–2951. [Google Scholar] [CrossRef]
- Chin, A.W.; Poon, L.L. Stability of SARS-CoV-2 in different environmental conditions–Authors’ reply. Lancet Microbe 2020, 1, e10. [Google Scholar] [CrossRef]
- John, R.M.; Sinha, P.; Munish, V.G.; Tullu, F.T. Economic costs of diseases and deaths attributable to tobacco use in India, 2017–2018. Nicotine Tob. Res. 2021, 23, 294–301. [Google Scholar] [CrossRef]
- Kumar, D.; Mitra, R.K.; Chouhan, T.; Farrukh, M.; Faisal, N. Effect of Moisture Absorption on Interfacial Shear Properties of the Bio-Composites. In Aging Effects on Natural Fiber-Reinforced Polymer Composites: Durability and Life Prediction; Springer Nature Singapore: Singapore, 2022; pp. 237–256. [Google Scholar]
- Coomber, R.; Moyle, L.; Pavlidis, A. Public spitting in “developing” nations of the global south: Harmless embedded practice or disgusting. Harmful and deviant? In The Palgrave Handbook of Criminology and the Global South; Springer International Publishing AG: Singapore, 2018; pp. 493–520. [Google Scholar]
- Pal, S.; Verma, A.; Raikwar, S.; Prajapati, Y.K.; Saini, J.P. Detection of DNA hybridization using graphene-coated black phosphorus surface plasmon resonance sensor. Appl. Phys. A 2018, 124, 1. [Google Scholar] [CrossRef]
- Huang, W.; Zhu, J.; Wang, M.; Hu, L.; Tang, Y.; Shu, Y.; Xie, Z.; Zhang, H. Emerging mono-elemental bismuth nanostructures: Controlled synthesis and their versatile applications. Adv. Funct. Mater. 2021, 31, 2007584. [Google Scholar] [CrossRef]
- Abraham, J.P.; Plourde, B.D.; Cheng, L. Using heat to kill SARS-CoV-2. Rev. Med. Virol. 2020, 30, e2115. [Google Scholar] [CrossRef]
- Gautret, P.; Colson, P.; Lagier, J.C.; Parola, P.; Raoult, D. Does spitting in public play a role in transmitting SARS-CoV-2? Travel Med. Infect. Dis. 2020, 36, 101759. [Google Scholar] [CrossRef]
- Kholaif, M.M.N.H.K.; Xiao, M.; Tang, X. COVID-19’s fear-uncertainty effect on renewable energy supply chain management and ecological sustainability performance; the moderate effect of big-data analytics. Sustain. Energy Technol. Assess. 2022, 53, 102622. [Google Scholar]
- Marr, L.C.; Tang, J.W.; Van Mullekom, J.; Lakdawala, S.S. Mechanistic insights into the effect of humidity on airborne influenza virus survival, transmission and incidence. J. R. Soc. Interface 2019, 16, 20180298. [Google Scholar] [CrossRef]
- Chan, K.H.; Peiris, J.M.; Lam, S.Y.; Poon, L.L.M.; Yuen, K.Y.; Seto, W.H. The Effects of Temperature and Relative Humidity on the Viability of the SARS Coronavirus. Adv. Virol. 2011, 2011, 734690. [Google Scholar] [CrossRef]
- Kumara, D.; Faisalb, N.; Layekc, A.; Kumard, N.; Kumare, R. Performance Improvement of a Solar Desalination System Assisted with Solar Air Heater: An Experimental Approach. J. Indian Chem. Soc. 2020, 97, 1967–1972. [Google Scholar]
- Chen, Z.; Li, J.; Li, T.; Fan, T.; Meng, C.; Li, C.; Huang, Y.; Wang, Y.; Zhang, H. A CRISPR/Cas12a-Empowered Surface Plasmon Resonance Platform for Rapid and Specific Diagnosis of the Omicron Variant of SARS-CoV-2. Nat. Sci. Rev. 2022, 9, nwac104. [Google Scholar] [CrossRef] [PubMed]
- Ou, G.; Tang, Y.; Niu, S.; Wu, L.; Li, S.; Yang, Y.; Ma, X.; Peng, L.; Liu, Y. Wastewater Surveillance and an Automated Robot: Effectively Tracking SARS-CoV-2 Transmission in the Post-Epidemic Era. Nat. Sci. Rev. 2023, 10, nwad089. [Google Scholar] [CrossRef]
- Razab, M.K.A.A.; Nawi, N.M.; Hadzuan, F.H.M.; Abdullah, N.H.; Muhamad, M.; Sunaiwi, R.; Ibrahim, F.; Zin, F.A.M.; Noor, A.M. Fluorine-18 Fluorodeoxyglucose Isolation Using Graphene Oxide for Alternative Radiopharmaceutical Spillage Decontamination in PET Scan. Sustainability 2022, 14, 4492. [Google Scholar] [CrossRef]
- Al-Rawi, M.; Farid, M.M.; Jones, R.J.; Louie, K. Evaluation of a Polyester Filter and UV Light (PFUV) Dehumidifier to Improve Indoor Environmental Quality: Preliminary Results. Sustainability 2022, 14, 4504. [Google Scholar] [CrossRef]
- Hu, Y.; Xu, Z.; Hu, Y.; Hu, L.; Zi, Y.; Wang, M.; Feng, X.; Huang, W. Bismuth Quantum Dot (Bi QD)/Polydimethylsiloxane (PDMS) Nanocomposites with Self-Cleaning and Antibacterial Activity for Dental Applications. Nanomaterials 2022, 12, 3911. [Google Scholar] [CrossRef]
- Chen, H.; Wang, M.; Huang, W. Two-Dimensional Selenium Nanosheet-Based Sponges with Superior Hydrophobicity and Excellent Photothermal Performance. Nanomaterials 2022, 12, 3756. [Google Scholar] [CrossRef]
- Yan, J.; Grantham, M.; Pantelic, J.; De Mesquita, P.J.B.; Albert, B.; Liu, F.; Ehrman, S.; Milton, D.K.; Consortium, E. Infectious virus in exhaled breath of symptomatic seasonal influenza cases from a college community. Proc. Natl. Acad. Sci. USA 2018, 115, 1081–1086. [Google Scholar] [CrossRef] [PubMed]
- Ma, Y.; Zhao, Y.; Liu, J.; He, X.; Wang, B.; Fu, S.; Yan, J.; Niu, J.; Zhou, J.; Luo, B. Effects of temperature variation and humidity on the death of COVID-19 in Wuhan, China. Sci. Total Environ. 2020, 724, 138226. [Google Scholar] [CrossRef]
- Morris, D.H.; Yinda, K.C.H.; Gamble, A.; Rossine, F.W.; Huang, Q.; Bushmaker, T.; Fischer, R.J.; Matson, M.J.; Van Doremalen, N.; Vikesland, P.J.; et al. The effect of temperature and humidity on the stability of SARS-CoV-2 and other enveloped viruses. BioRxiv 2020. [Google Scholar] [CrossRef]
- Vellingiri, B.; Jayaramayya, K.; Iyer, M.; Narayanasamy, A.; Govindasamy, V.; Giridharan, B.; Ganesan, S.; Venugopal, A.; Venkatesan, D.; Ganesan, H.; et al. COVID-19: A promising cure for the global panic. Sci. Total Environ. 2020, 725, 138277. [Google Scholar] [CrossRef] [PubMed]
- Duttaluru, G.; Singh, P.; Ansu, A.K.; Sharma, R.K.; Mishra, S. Methods to enhance the thermal properties of organic phase change materials: A review. Mater. Today Proc. 2022, 63, 685–691. [Google Scholar] [CrossRef]
- Zhao, H.J.; Liu, X.Y.; Liu, Z.H.; Zhang, H.T.; Yan, J.H. Experimental Investigation of the Specific Heat Capacity of Nanofluids. Appl. Therm. Eng. 2016, 99, 393–398. [Google Scholar]
- Scannapieco, A.; Genco, R. Impact of Oral Health on Systemic Health in Older Adults. Oral Dis. 2019, 25, 14–19. [Google Scholar]
- Kalogirou, S.A. A review on the performance of solar collectors. Renew. Sustain. Energy Rev. 2004, 11, 403–427. [Google Scholar]
- Li, Y.; Li, J.; Li, H.; Li, Y.; Wang, J.; Wu, H.; Li, J. Numerical investigation of a high-temperature solar receiver for a solar tower power plant. Energy Convers. Manag. 2020, 213, 112813. [Google Scholar]
- Jones, P.D.; Hulme, M. Calculating Regional Climatic Time Series for Temperature and Precipitation: Methods and Illustrations. Int. J. Climatol. 1997, 17, 141–157. [Google Scholar] [CrossRef]
- Huang, J.; You, Q.; Yang, K.; Ren, G. Estimation of Air Temperature Lapse Rates in the Tibetan Plateau: A Case Study over the Tuotuohe Basin. J. Geophys. Res. Atmos. 2011, 116, D04102. [Google Scholar]
- Santamouris, M.; Papanikolaou, N.; Livada, I.; Koronakis, I.; Georgakis, C.; Argiriou, A.; Assimakopoulos, D.N. On the impact of urban climate on the energy consumption of buildings. Sol. Energy 2001, 70, 201–216. [Google Scholar] [CrossRef]
- Kasten, F.; Czeplak, G. Solar and terrestrial radiation dependent on the amount and type of cloud. Sol. Energy 1980, 24, 177–189. [Google Scholar] [CrossRef]
- Loferski, J.J. Theoretical Limits to the Conversion of Solar Radiation into Electricity. J. Appl. Phys. 1956, 27, 777–788. [Google Scholar] [CrossRef]
- Rezaei, M.; Farzaneh-Gord, M. Experimental Investigation of Convective Heat Transfer and Thermal Radiation Heat Transfer from a Heated Horizontal Cylinder. Int. J. Heat Mass Transf. 2019, 135, 928–940. [Google Scholar]
- Kumar, A.; Kumar, R. Solar Collector Efficiency Enhancement: A Comprehensive Review. Renew. Sustain. Energy Rev. 2017, 73, 149–168. [Google Scholar]









Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sharma, A.; Kumar, D.; Kumar, A.; Faisal, N.; Kumar, N.; Pandey, S.; Hasnain, S.M.M.; Al-Hazani, T.M.; AlKahtane, A.A.; Alkahtani, S.; et al. Designing, Modeling, and Fabrication of a Novel Solar-Concentrating Spittoon against COVID-19 for Antibacterial Sustainable Atmosphere. Sustainability 2023, 15, 9286. https://doi.org/10.3390/su15129286
Sharma A, Kumar D, Kumar A, Faisal N, Kumar N, Pandey S, Hasnain SMM, Al-Hazani TM, AlKahtane AA, Alkahtani S, et al. Designing, Modeling, and Fabrication of a Novel Solar-Concentrating Spittoon against COVID-19 for Antibacterial Sustainable Atmosphere. Sustainability. 2023; 15(12):9286. https://doi.org/10.3390/su15129286
Chicago/Turabian StyleSharma, Abhimannyu, Dheeraj Kumar, Amit Kumar, Nadeem Faisal, Naresh Kumar, Shatrudhan Pandey, S. M. Mozammil Hasnain, Tahani Mohamed Al-Hazani, Abdullah A. AlKahtane, Saad Alkahtani, and et al. 2023. "Designing, Modeling, and Fabrication of a Novel Solar-Concentrating Spittoon against COVID-19 for Antibacterial Sustainable Atmosphere" Sustainability 15, no. 12: 9286. https://doi.org/10.3390/su15129286
APA StyleSharma, A., Kumar, D., Kumar, A., Faisal, N., Kumar, N., Pandey, S., Hasnain, S. M. M., Al-Hazani, T. M., AlKahtane, A. A., Alkahtani, S., & Chatterjee, R. (2023). Designing, Modeling, and Fabrication of a Novel Solar-Concentrating Spittoon against COVID-19 for Antibacterial Sustainable Atmosphere. Sustainability, 15(12), 9286. https://doi.org/10.3390/su15129286






