Rapid Urbanization Increased the Risk of Agricultural Waterlogging in the Huaibei Plain, China
Abstract
1. Introduction
2. Materials and Methods
2.1. Study Area and Data
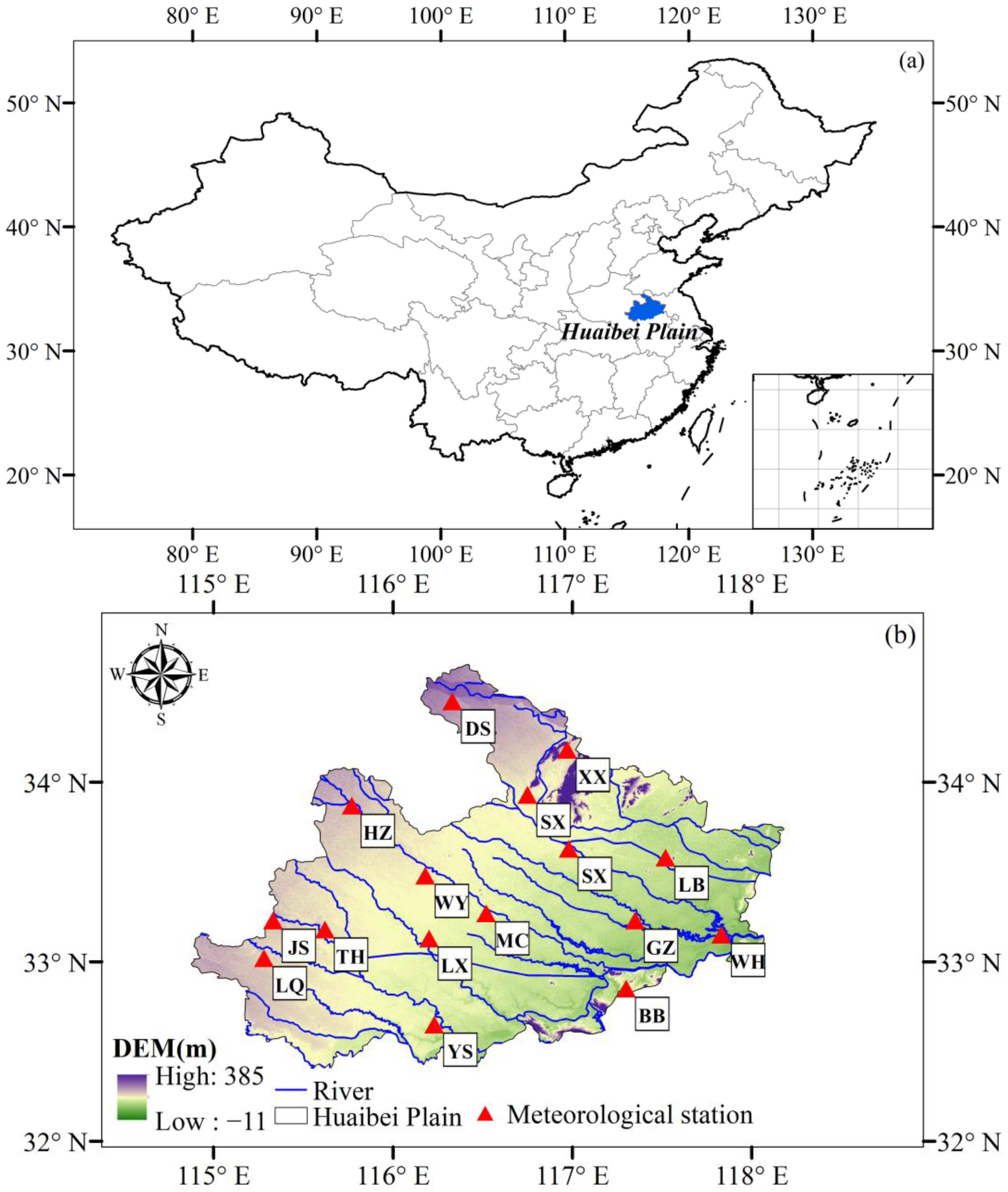
2.1.1. Study Area
2.1.2. Datasets
2.2. Methods
2.2.1. Calculation of Drainage Modulus
2.2.2. Mann–Kendall Test
2.2.3. Sen’s Slope Estimator
2.2.4. Wavelet Analysis
2.2.5. Sensitivity Analysis
2.2.6. Contribution Rate Analysis
3. Results
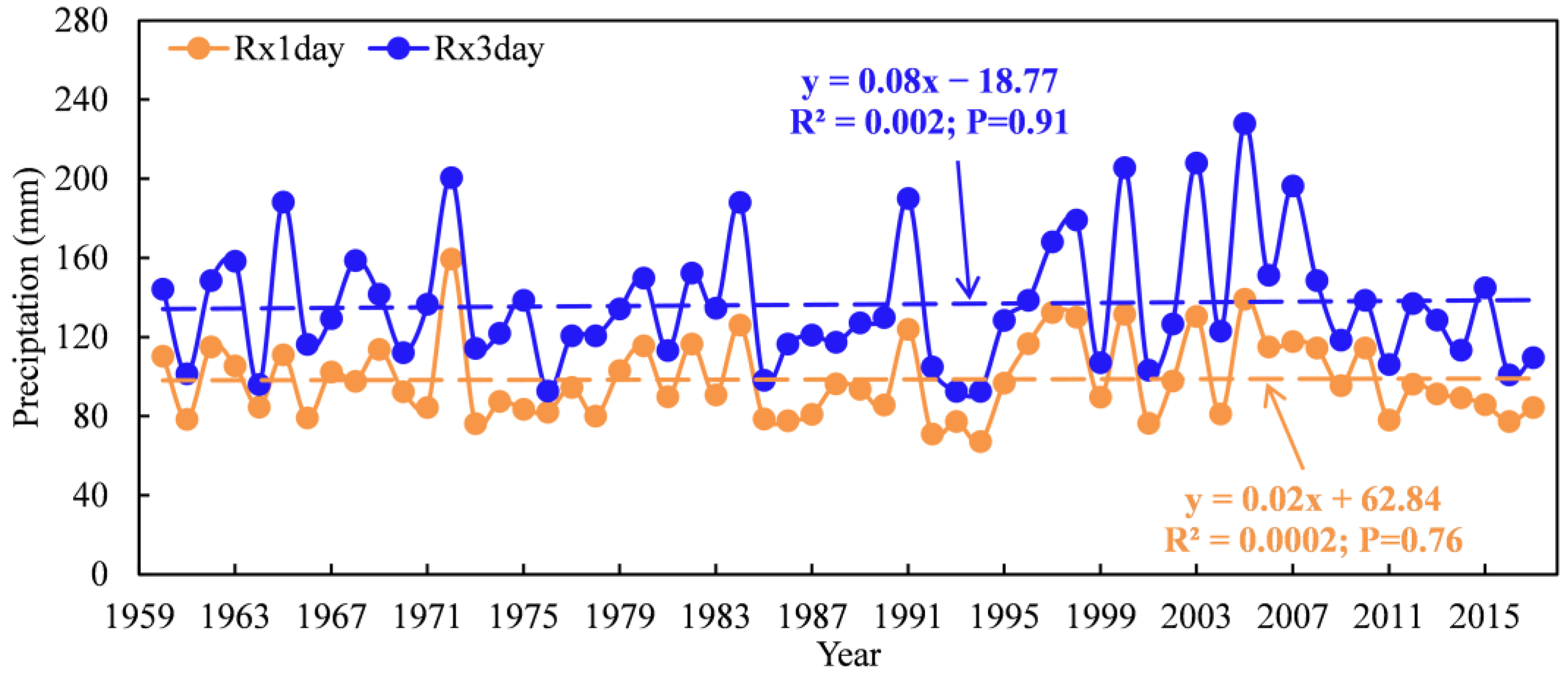
3.1. Temporal Variation in Annual Maximum 1-Day and 3-Day Precipitation Amounts
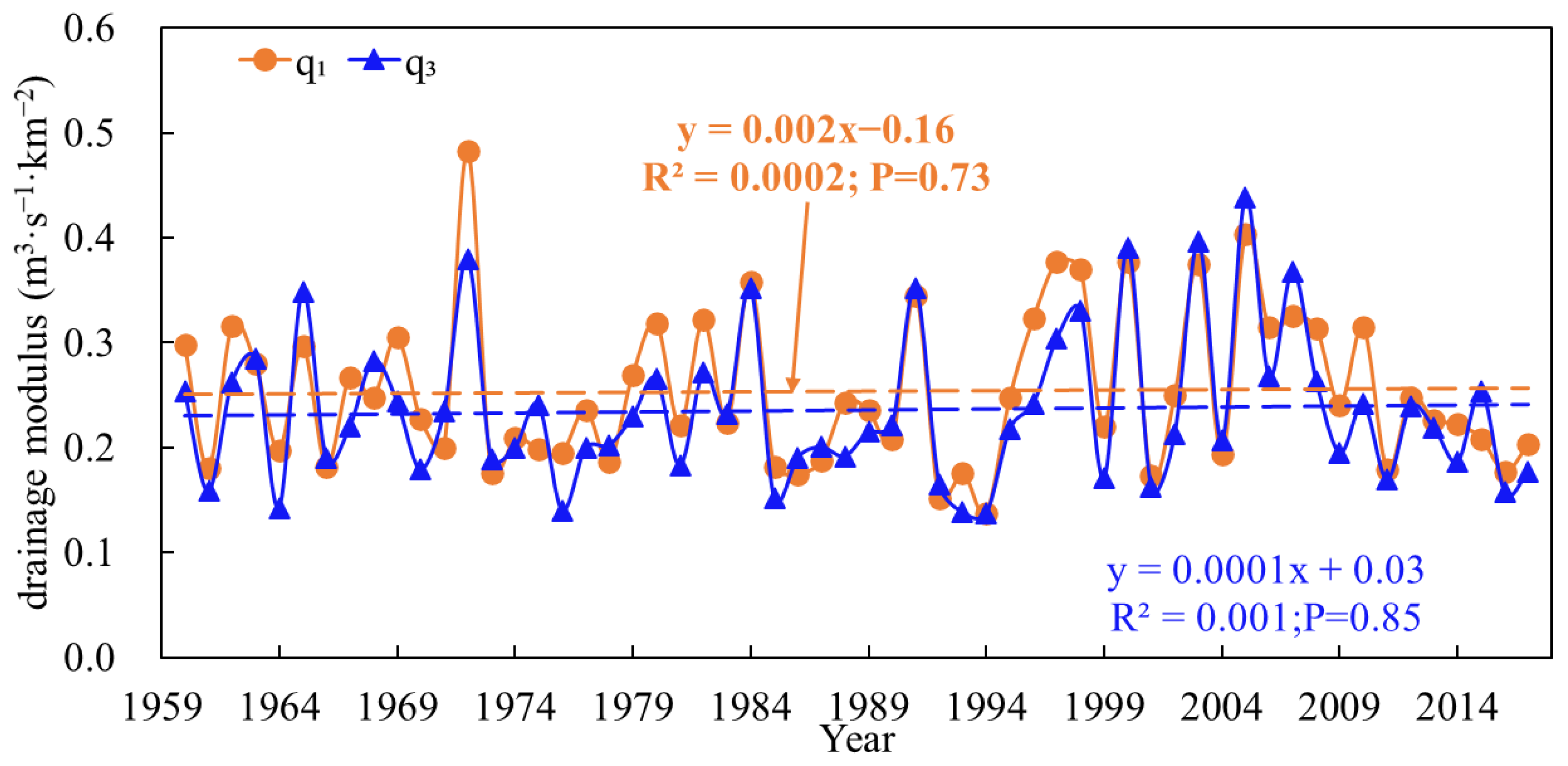
3.2. Temporal Variability of Drainage Modulus
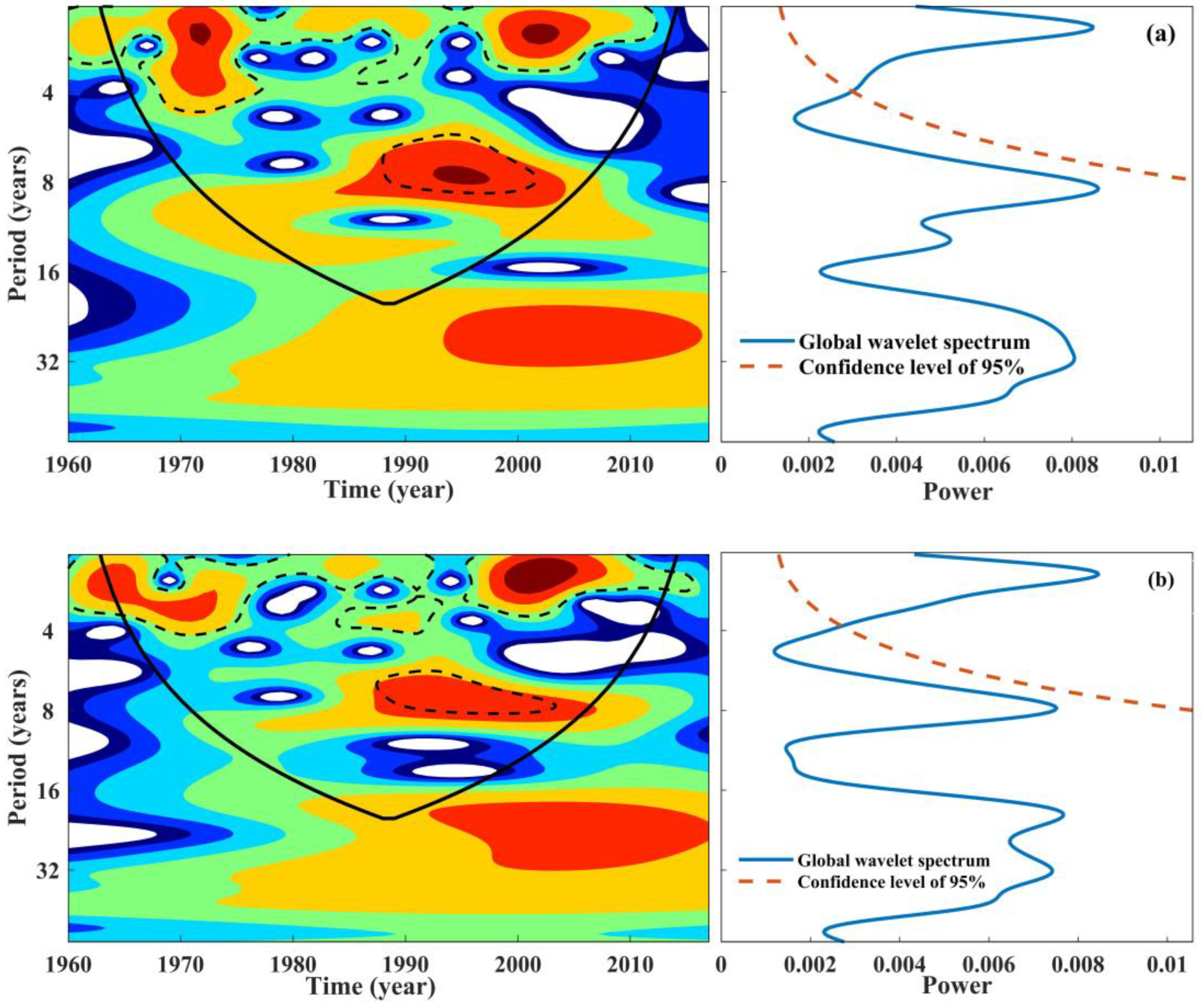
3.3. Periodic Variation in the Drainage Modulus
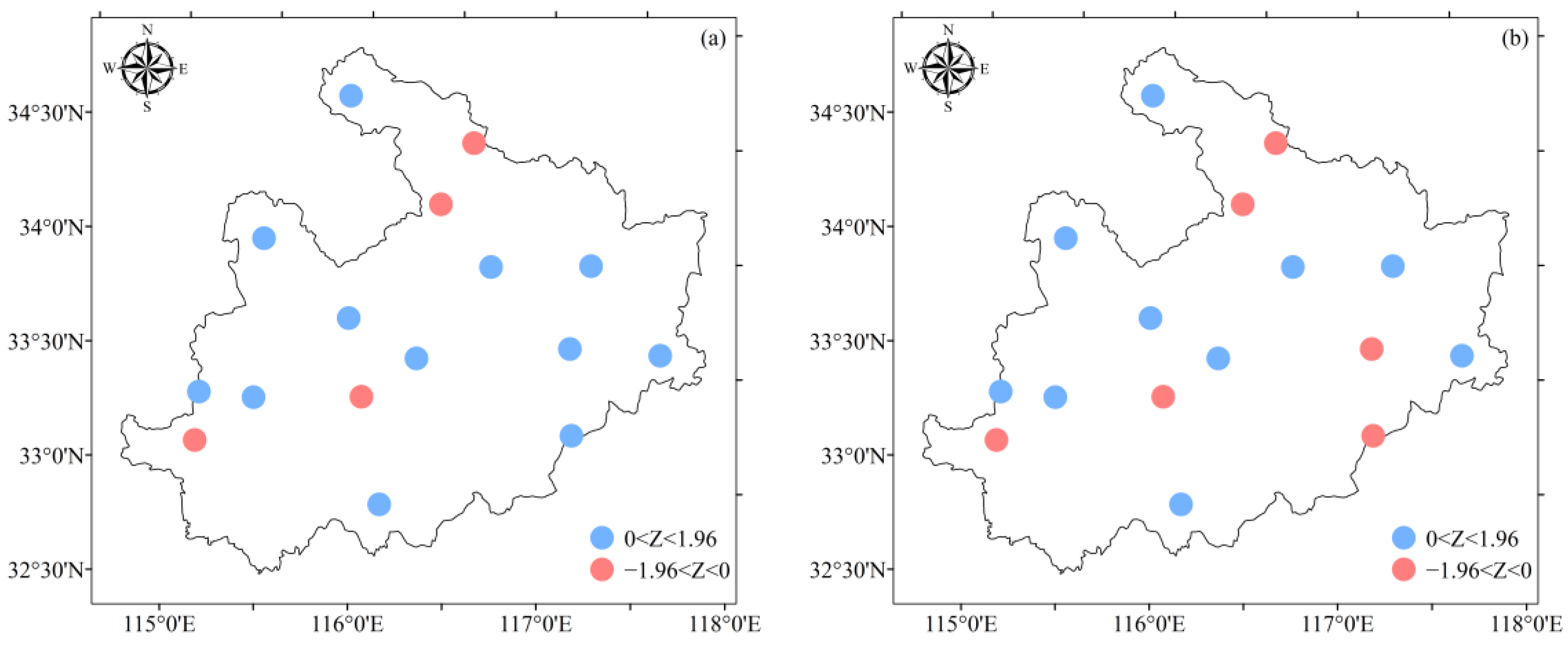
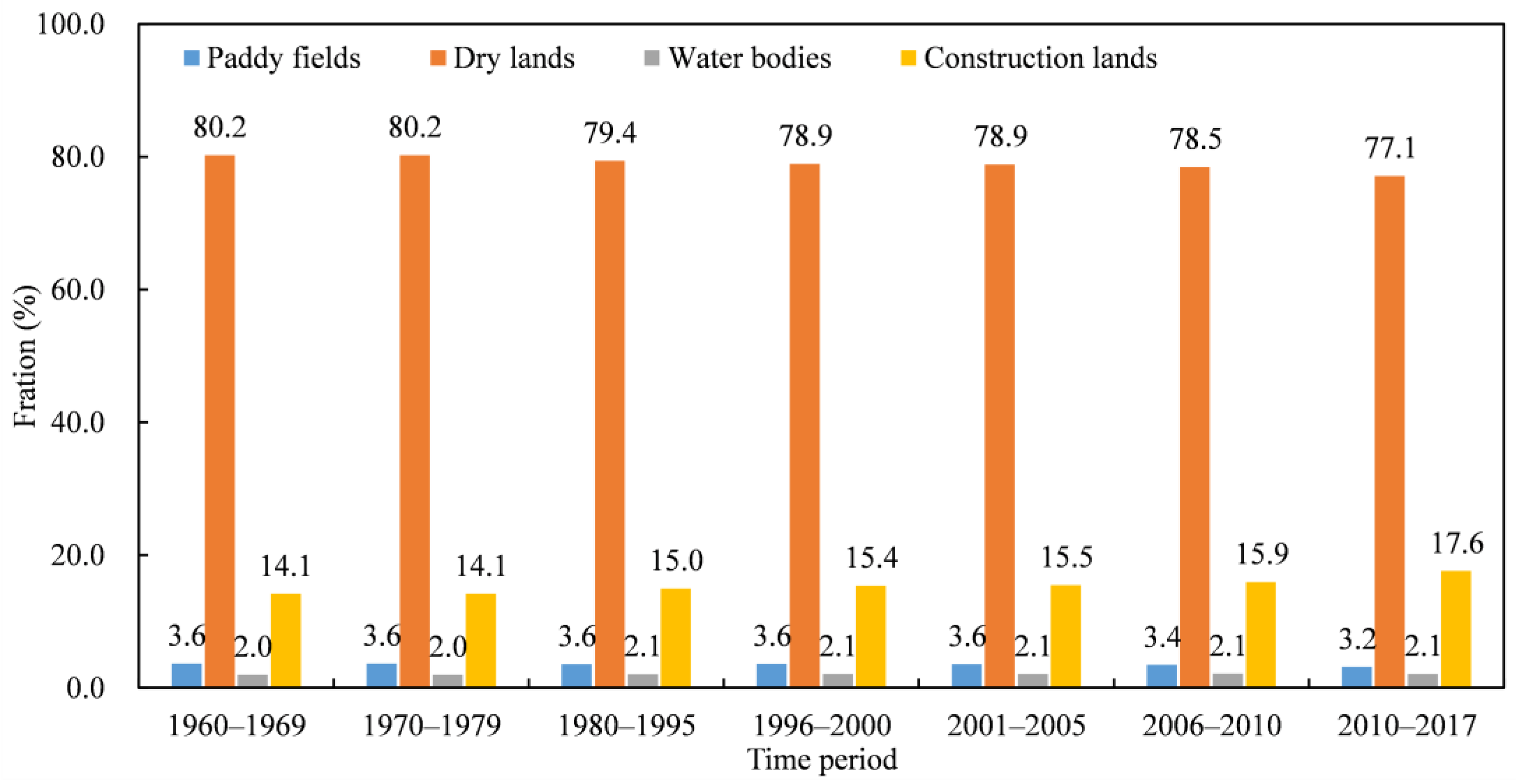
3.4. Environmental Factors That Affect Drainage Modulus Variability
4. Discussion
4.1. Drainage Modulus and Farmland Water Management
4.2. Environmental Factors That Affect the Drainage Modulus
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Kaur, G.; Vikal, Y.; Kaur, L.; Kalia, A.; Mittal, A.; Kaur, D.; Yadav, I. Elucidating the morpho-physiological adaptations and molecular responses under long-term waterlogging stress in maize through gene expression analysis. Plant Sci. 2021, 304, 110823. [Google Scholar] [CrossRef]
- Liu, C.; Li, K.; Zhang, J.; Guga, S.; Wang, R.; Liu, X.; Tong, Z. Dynamic risk assessment of waterlogging disaster to spring peanut (Arachis hypogaea L.) in Henan Province, China. Agric. Water Manag. 2023, 277, 108094. [Google Scholar] [CrossRef]
- Liu, K.; Harrison, M.; Yan, H.; Meinke, H.; Wang, B.; Peng, B.; Guan, K.; Jägermeyr, J.; Wang, E.; Zhang, F.; et al. Silver lining to a climate crisis in multiple prospects for alleviating crop waterlogging under future climates. Nat. Commun. 2023, 14, 765. [Google Scholar] [CrossRef] [PubMed]
- Yan, H.; Harrison, M.; Liu, K.; Wang, B.; Feng, P.; Fahad, S.; Meinke, H.; Yang, R.; Archontoulis, S.; Huber, I.; et al. Crop traits enabling yield gains under more frequent extreme climatic events. Sci. Total Environ. 2021, 808, 152170. [Google Scholar] [CrossRef] [PubMed]
- Setter, T.L.; Waters, I. Review of prospects for germplasm improvement for waterlogging tolerance in wheat, barley and oats. Plant Soil 2003, 253, 1–34. [Google Scholar] [CrossRef]
- Feng, G. Irrigation and Drainage in China; China WaterPower Press: Beijing, China, 2005. [Google Scholar]
- Wang, S.; Xu, D.; Chen, H.; Han, S.; Jiao, P. Review on research of farmland drainage technology. J. Drain. Irrig. Mach. Eng. 2014, 32, 7. [Google Scholar]
- Jin, H.; Chen, X.; Zhong, R.; Duan, K. Frequency analysis of extreme precipitation in different regions of the Huaihe River Basin. Int. J. Climatol. 2021, 42, 3517–3536. [Google Scholar] [CrossRef]
- Wu, H.; Wang, X.; Xu, M.; Zhang, J. The Effect of Water Deficit and Waterlogging on the Yield Components of Cotton. Crop. Sci. 2018, 58, 1751–1761. [Google Scholar] [CrossRef]
- Singh, A. Soil salinization and waterlogging: A threat to environment and agricultural sustainability. Ecol. Indic. 2015, 57, 128–130. [Google Scholar] [CrossRef]
- Jin, M.; Lancia, M.; Tian, Y.; Viaroli, S.; Andrews, C.; Liu, J.; Zheng, C. Hydrogeological Criteria to Improve the Sponge City Strategy of China. Front. Environ. Sci. 2021, 9, 700463. [Google Scholar] [CrossRef]
- Luo, W.; Wang, X.; Luo, Q. Comparison of methods for calculating farmland drainage modulus. Trans. Chin. Soc. Agric. Eng. 2013, 29, 7. [Google Scholar]
- Luo, W.; Wang, X.; Luo, Q.; Zhang, X. Effects of underlying surface changes on drainage modulus in Four-lake Watershed. Adv. Water Sci. 2014, 25, 7. [Google Scholar] [CrossRef]
- El-Sadek, A.; Feyen, J.; Berlamont, J. Comparison of Models for Computing Drainage Discharge. Irrig. Drain. Eng. 2001, 127, 363–369. [Google Scholar] [CrossRef]
- Arnold, J.; Williams, J.; Maidment, D. A Continuous Time Water and Sediment Routing Model for Large Basins. J. Hydraul. Eng. -Asce 1995, 121, 171–183. [Google Scholar] [CrossRef]
- You, L.; Wang, S.; Tao, Y.; Liu, Y. Appropriate Method to Estimate Farmland Drainage Coefficient in the Wanyan River Surface Waterlogged Area in Suibin County of the Sanjiang Plain, China. Appl. Sci. 2023, 13, 2769. [Google Scholar] [CrossRef]
- Chen, X.; Guo, L.; Guan, G.; Zhang, Y.; Jia, B. Research and Improvement of the Theoretical Model of Drainage Modulus in the Plain Mixed Area. China Rural. Water Hydropower 2018, 12, 8–12. [Google Scholar]
- Ding, J.Y. A measure of watershed nonlinearity: Interpreting a variable instantaneous unit hydrograph model on two vastly different sized watersheds. Hydrol. Earth Syst. Sci. 2011, 15, 405–423. [Google Scholar] [CrossRef]
- Tao, Y.; Wang, S.; Xu, D.; Yuan, H.; Chen, H. Field and numerical experiment of an improved subsurface drainage system in Huaibei plain. Agric. Water Manag. 2017, 194, 24–32. [Google Scholar] [CrossRef]
- Gou, Q.; Zhu, Y.; Horton, R.; Lü, H.; Wang, Z.; Su, J.; Cui, C.; Zhang, H.; Wang, X.; Zheng, J.; et al. Effect of climate change on the contribution of groundwater to the root zone of winter wheat in the Huaibei Plain of China. Agric. Water Manag. 2020, 240, 106292. [Google Scholar] [CrossRef]
- Yuan, X.; Zhang, X.-C.; Wang, X.-G.; Zhang, Y. Flood disaster monitoring based on Sentinel-1 data: A case study of Sihu Basin and Huaibei Plain, China. Water Sci. Eng. 2021, 14, 87–96. [Google Scholar] [CrossRef]
- Wang, Y. Controling of Waterlogging in Huaihe River Basin; Science Press: Beijing, China, 2015. [Google Scholar]
- Cheng, X.; Zhao, J.; Zhang, H.; Wang, K.; Xu, M. Numerical Simulation of Land Surface Hydrological Process Over Huaihe River Basin. Procedia Eng. 2016, 154, 1064–1070. [Google Scholar] [CrossRef]
- Ju, Q.; Hu, Y.; Liu, Q.; Liu, Y.; Hu, T. Key hydrological process of a multiple aquifer flow system in the mining area of Huaibei plain, Eastern China. Appl. Geochem. 2022, 140, 105270. [Google Scholar] [CrossRef]
- Li, D.; Qi, H.; Ma, X. The Climate Index and Assessment about Drought and Flood in Maize’s Key Growth Stage in Huaibei Plain in Anhui Province. Chin. Agric. Sci. Bull. 2013, 29, 9. [Google Scholar]
- Wu, H.; Wang, X.; Wang, Y.; Xu, Y.; Han, X. Temporal variations in reference evapotranspiration in Hubei Province, China, from 1960 to 2014. Theor. Appl. Climatol. 2018, 135, 433–448. [Google Scholar] [CrossRef]
- Kousari, M.R.; Asadi Zarch, M.A.; Ahani, H.; Hakimelahi, H. A survey of temporal and spatial reference crop evapotranspiration trends in Iran from 1960 to 2005. Clim. Chang. 2013, 120, 277–298. [Google Scholar] [CrossRef]
- Wang, Y.; Peng, Z.; Wu, H.; Wang, P. Spatiotemporal Variability in Precipitation Extremes in the Jianghuai Region of China and the Analysis of Its Circulation Features. Sustainability 2022, 14, 6680. [Google Scholar] [CrossRef]
- Li, X.; Wang, X.; Babovic, V. Analysis of variability and trends of precipitation extremes in Singapore during 1980–2013. Int. J. Climatol. 2018, 38, 125–141. [Google Scholar] [CrossRef]
- Xu, M.; Kang, S.; Wu, H.; Yuan, X. Detection of spatio-temporal variability of air temperature and precipitation based on long-term meteorological station observations over Tianshan Mountains, Central Asia. Atmos. Res. 2018, 203, 141–163. [Google Scholar] [CrossRef]
- Liu, T.; Li, L.; Lai, J.; Liu, C.; Zhuang, W. Reference evapotranspiration change and its sensitivity to climate variables in southwest China. Theor. Appl. Climatol. 2015, 125, 499–508. [Google Scholar] [CrossRef]
- Li, C.; Wu, P.T.; Li, X.L.; Zhou, T.W.; Sun, S.K.; Wang, Y.B.; Luan, X.B.; Yu, X. Spatial and temporal evolution of climatic factors and its impacts on potential evapotranspiration in Loess Plateau of Northern Shaanxi, China. Sci. Total Environ. 2017, 589, 165–172. [Google Scholar] [CrossRef]
- Yin, Y.; Wu, S.; Chen, G.; Dai, E. Attribution analyses of potential evapotranspiration changes in China since the 1960s. Theor. Appl. Climatol. 2010, 101, 19–28. [Google Scholar] [CrossRef]
- Ling, H.; Xu, H.; Fu, J. High- and low-flow variations in annual runoff and their response to climate change in the headstreams of the Tarim River, Xinjiang, China. Hydrol. Process. 2013, 27, 975–988. [Google Scholar] [CrossRef]
- Li, N.; Wang, X.; Luo, Q.; Wang, S.; Ke, Z. Using SWAT and CLUE-S Models to Evaluate the Effect of Land Use on Drainage Modules. J. Irrig. Drain. 2019, 38, 8. [Google Scholar] [CrossRef]
- Xiao, J.; Luo, Q.; Wang, X.; Luo, W.; Zhang, C. Impact of urbanization on drainage modulus in tidal river networks. Trans. Chin. Soc. Agric. Eng. Ransactions CSAE 2014, 30, 9. [Google Scholar] [CrossRef]
- Zhao, J.; Zhang, J.; Hu, Y.; Li, Y.; Tang, P.; Gusarov, A.V.; Yu, Y. Effects of land uses and rainfall regimes on surface runoff and sediment yield in a nested watershed of the Loess Plateau, China. J. Hydrol. Reg. Stud. 2022, 44, 101277. [Google Scholar] [CrossRef]
- Mfwango, L.H.; Kisiki, C.P.; Ayenew, T.; Mahoo, H.F. The impact of land use/cover change on surface runoff at Kibungo sub-catchment of Upper Ruvu catchment in Tanzania. Environ. Chall. 2022, 7, 100466. [Google Scholar] [CrossRef]
- Ma, K.; Huang, X.; Liang, C.; Zhao, H.; Zhou, X.; Wei, X. Effect of land use/cover changes on runoff in the Min River watershed. River Res. Appl. 2020, 36, 749–759. [Google Scholar] [CrossRef]
- Wang, H.; Stephenson, S.R. Quantifying the impacts of climate change and land use/cover change on runoff in the lower Connecticut River Basin. Hydrol. Process. 2018, 32, 1301–1312. [Google Scholar] [CrossRef]
- He, X.; Liang, J.; Zeng, G.; Yuan, Y.; Li, X. The Effects of Interaction between Climate Change and Land-Use/Cover Change on Biodiversity-Related Ecosystem Services. Glob. Chall. 2019, 3, 1800095. [Google Scholar] [CrossRef]
- Wang, F.; Duan, K.; Fu, S.; Gou, F.; Liang, W.; Yan, J.; Zhang, W. Partitioning climate and human contributions to changes in mean annual streamflow based on the Budyko complementary relationship in the Loess Plateau, China. Sci. Total Environ. 2019, 665, 579–590. [Google Scholar] [CrossRef]
- Ramezani, M.R.; Helfer, F.; Yu, B. Individual and combined impacts of urbanization and climate change on catchment runoff in Southeast Queensland, Australia. Sci. Total Environ. 2023, 861, 160528. [Google Scholar] [CrossRef] [PubMed]
- Huq, E.; Abdul-Aziz, O.I. Climate and land cover change impacts on stormwater runoff in large-scale coastal-urban environments. Sci. Total Environ. 2021, 778, 146017. [Google Scholar] [CrossRef] [PubMed]


| Drainage Modulus | Design Rainstorm (Day) | Design Drainage Day (Day) |
|---|---|---|
| q1 | 1 | 3 |
| q3 | 3 | 5 |
| Sensitivity Coefficient | Sensitivity Level |
|---|---|
| 0.00 ≤ |Svi| < 0.05 | Negligible |
| 0.05 ≤ |Svi| < 0.20 | Moderate |
| 0.20 ≤ |Svi| < 1.00 | High |
| 1.00 ≤ |Svi| | Very high |
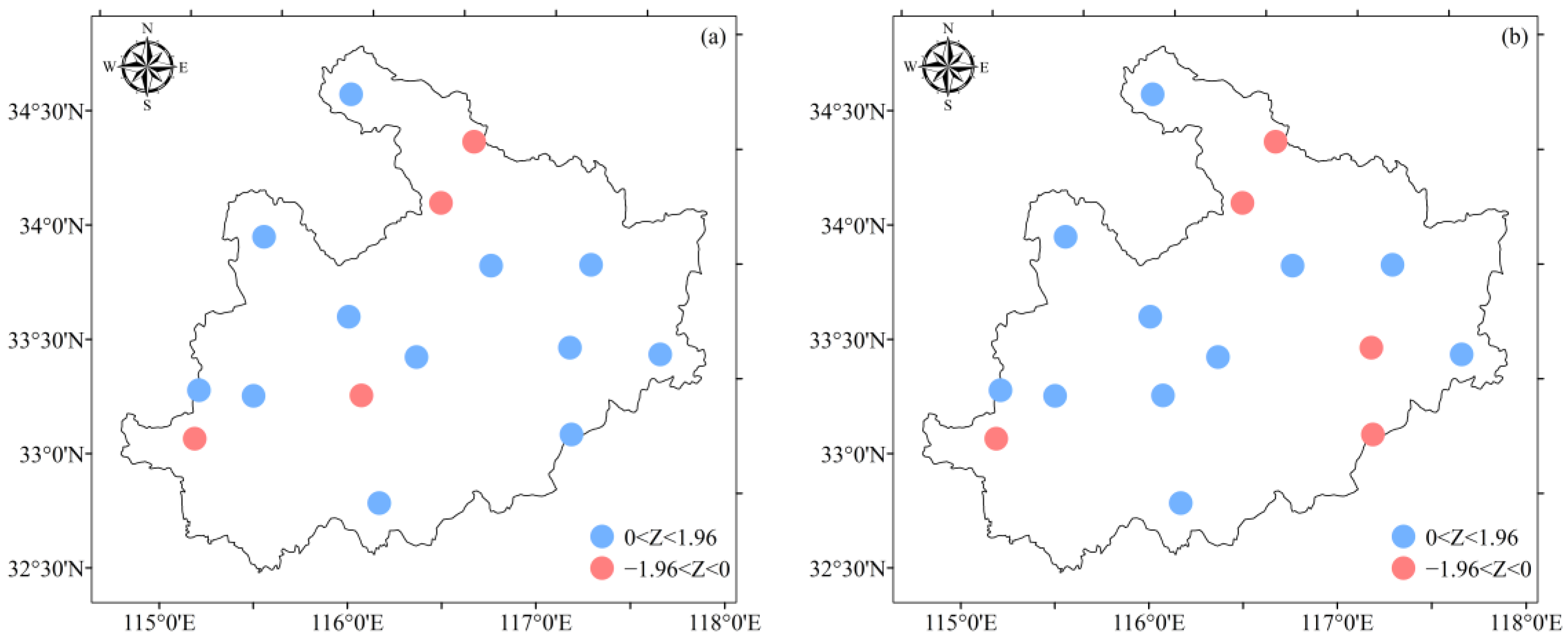
| Station | Z | β (mm·10 a−1) | ||
|---|---|---|---|---|
| Rx1day | Rx3day | Rx1day | Rx3day | |
| DS | 0.71 | 0.42 | 1.00 | 0.56 |
| XX | −1.29 | −0.79 | −4.27 | −3.18 |
| HZ | 0.54 | 0.94 | 1.06 | 3.07 |
| LQ | −1.23 | −1.14 | −4.62 | −5.08 |
| JS | 0.21 | 0.25 | 0.71 | 0.38 |
| TH | 0.36 | 0.68 | 1.21 | 1.47 |
| SX | −0.94 | −1.60 | −3.11 | −6.50 |
| WY | 0.81 | 0.53 | 1.62 | 1.76 |
| LX | −0.34 | −0.06 | −0.74 | −0.68 |
| MC | 0.79 | 1.01 | 2.67 | 3.70 |
| SX | 0.52 | 0.46 | 1.11 | 2.79 |
| LB | 1.41 | 1.22 | 2.11 | 4.65 |
| GZ | 0.28 | −0.28 | 0.83 | −0.27 |
| WH | 1.23 | 0.98 | 3.43 | 3.57 |
| YS | 0.75 | 0.60 | 2.74 | 1.22 |
| BB | 0.82 | −0.41 | 2.58 | −0.31 |
| Station | Z | β (mm·day−1·10 a−1) | ||
|---|---|---|---|---|
| q1 | q3 | q1 | q3 | |
| DS | 0.85 | 0.54 | 3.72 | 1.30 |
| XX | −1.20 | −0.75 | −13.22 | −5.88 |
| HZ | 0.70 | 1.03 | 5.01 | 6.13 |
| LQ | −1.18 | −1.12 | −14.77 | −9.76 |
| JS | 0.25 | 0.30 | −2.25 | 0.78 |
| TH | 0.45 | 0.74 | 4.67 | 3.37 |
| SX | −0.86 | −1.56 | −9.16 | −12.18 |
| WY | 0.90 | 0.57 | 5.18 | 3.63 |
| LX | −0.27 | 0.06 | −2.16 | 1.30 |
| MC | 0.81 | 1.03 | 8.81 | 7.60 |
| SX | 0.67 | 0.50 | 3.97 | 5.62 |
| LB | 1.42 | 1.23 | 7.26 | 9.33 |
| GZ | 0.28 | −0.28 | 2.68 | −0.17 |
| WH | 1.31 | 1.00 | 10.37 | 5.70 |
| YS | 0.75 | 0.53 | 7.78 | 2.16 |
| BB | 1.25 | −0.08 | 9.76 | −0.95 |
| Factors | q1 | q3 |
|---|---|---|
| Rx1day, Rx3day | 1.81 | 1.71 |
| Spf | 0.01 | 0.02 |
| Sdl | 0.68 | 0.74 |
| Swb | 0.00 | 0.00 |
| Sbl | 0.30 | 0.23 |
| Factors | q1 | q3 |
|---|---|---|
| Rx1day, Rx3day | 1.91 | 4.38 |
| Spf | −0.10 | −0.20 |
| Sdl | −2.48 | −2.70 |
| Swb | 0.00 | 0.00 |
| Sbl | 5.81 | 5.45 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tao, Y.; Wu, H.; Wang, Y. Rapid Urbanization Increased the Risk of Agricultural Waterlogging in the Huaibei Plain, China. Sustainability 2023, 15, 9144. https://doi.org/10.3390/su15129144
Tao Y, Wu H, Wang Y. Rapid Urbanization Increased the Risk of Agricultural Waterlogging in the Huaibei Plain, China. Sustainability. 2023; 15(12):9144. https://doi.org/10.3390/su15129144
Chicago/Turabian StyleTao, Yuxin, Hao Wu, and Yitong Wang. 2023. "Rapid Urbanization Increased the Risk of Agricultural Waterlogging in the Huaibei Plain, China" Sustainability 15, no. 12: 9144. https://doi.org/10.3390/su15129144
APA StyleTao, Y., Wu, H., & Wang, Y. (2023). Rapid Urbanization Increased the Risk of Agricultural Waterlogging in the Huaibei Plain, China. Sustainability, 15(12), 9144. https://doi.org/10.3390/su15129144







