A Backstepping Control Strategy for Power System Stability Enhancement
Abstract
1. Introduction
1.1. Research Background
1.2. Related Works
1.3. Main Contributions
1.4. Paper Organization
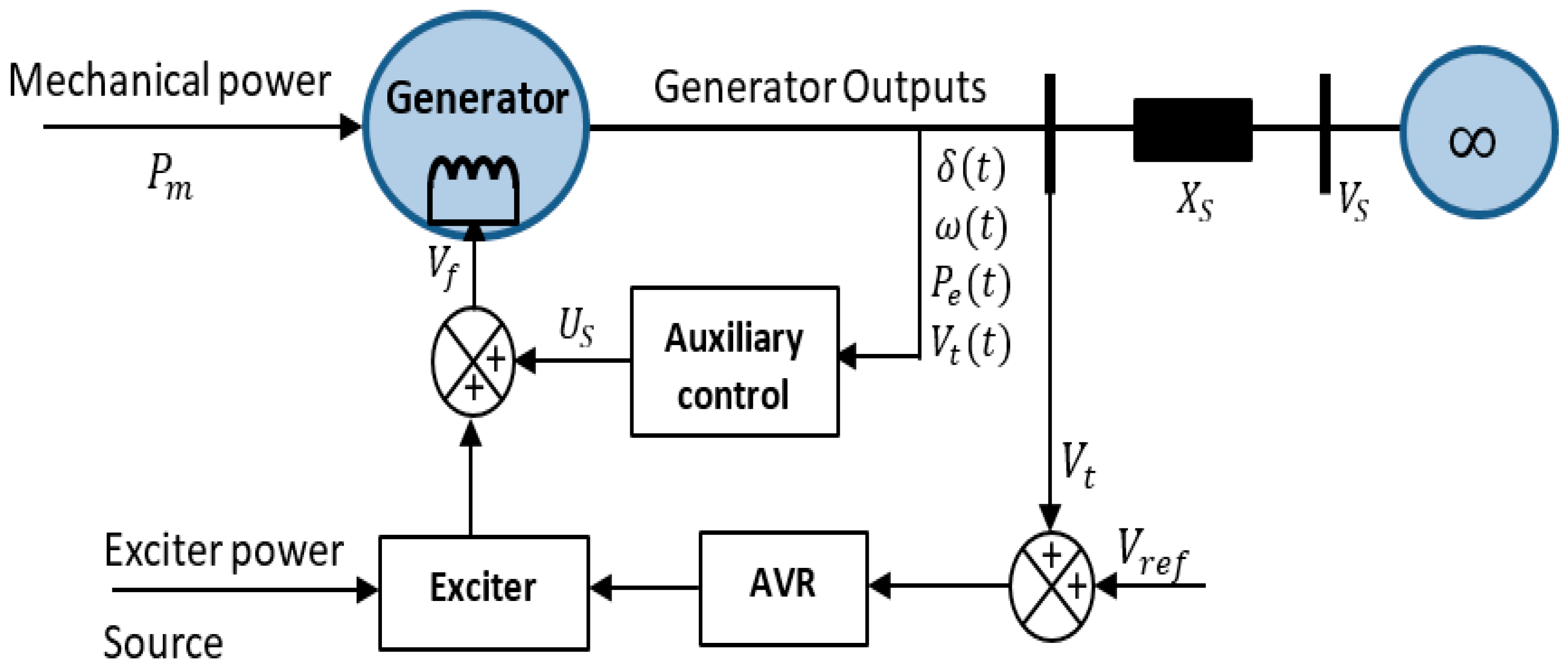
2. System Dynamic Modeling
3. Design of a Backstepping Controller Fit for an SMIB System
3.1. Controller Design
- Step 1:
- The derivative of can be drawn from the system Equation (7) on a differentiation basis:
- Step 2:
- This step involves the backstepping methodology, which consists in calculating the second error variable corresponding derivative using Equations (7), (11), and (17), such as:
- Step 3:
- This step involves calculating the derivative of the next error variable regarding the state and error variables. Using Equations (7), (12) and (21), the derivative of is expressed by:
- Step 4:
- The ultimate step of the Lyapunov methodology involves calculating the derivative of the last error variable, , in relation to the state variables, prior to representing the system dynamics model by means of the new error variables:
3.2. Development of Stability Analysis and Control Law Design for System Optimization
4. Design Controller Optimization
4.1. Problem Formulation
4.2. Optimization Techniques
4.2.1. The Jaya Algorithm
- Step 1:
- Select the number m of the design variables (c), the population size (), the minimum and maximum limits of the design variables and the maximum number of iterations ().
- Step 2:
- Generate the initial solution as random values within a range of design parameters’ min and max values. The equation of this initial solution is designed by:
- Step 3:
- Simulate the SMIB system with the proposed excitation controller and calculate the objective functions for each member of the population under different types of possible faults considered at separate time intervals throughout the simulation time ().
- Step 4:
- Identify the best and worst solutions in the population corresponding, respectively, to the minimum and the maximum of the objective functions for each member of the population , and update the population using Equation (35).
- Step 5:
- For each candidate of the new population, re-simulate the SMIB system with the proposed excitation controller and compute the new objective functions .
- Step 6:
- Compare the objective function vectors and retain the candidate that displays the best optimal objective function to form a new population.
- Step 7:
- Reiterate steps 3 to 6 successively until the stopping criteria are verified. In this study, the optimization algorithm ends when the maximum number of iterations is reached or the objective function cannot be improved, as described by inequality (39).
- Step 8:
- Report this solution as the best global one for the design variables: .
4.2.2. Genetic Algorithm (GA)
- Step 1:
- Specify the population size , mutation probability , crossover probability , limits of the controller parameters, selection operator (tournament selection), and the maximum number of generations ().
- Step 2:
- As the JA, the initial population is generated, while the power system time–domain simulation is fixed (), and various types of fault scenarios are considered at different simulation times.
- Step 3:
- Simulate the SMIB with the selected excitation controller (backstepping or PSS) for each individual of the current population with the last condition and compute the corresponding fitness function.
- Step 4:
- Check the stopping condition of the algorithm. The same termination criteria as those for JA are adopted.
- Step 5:
- If the stopping criterion is not verified, apply GA operators: selection, crossover and mutation to obtain a new population. Then, return to step three with the updated parameters of the new population.
- Step 6:
- If the stopping criterion is satisfied, retain the best solution of the controller parameters corresponding to the minimum of in the last population.
5. Simulation Studies and Results
- Case 1: The system is subjected to a three-phase short-circuit fault appearing at t = 1 s with a duration of ∆t = 50 ms. Once the fault is resolved, the system resumes its original configuration.
- Case 2: A 20% step change in the input power of the machine (mechanical power) is applied.
- Case 3: A three-phase fault with a duration of ∆t = 150 ms occurs at t = 1 s. The fault location is in one of the parallel lines and close to the terminal bus. The fault is cleared by opening the faulty line.
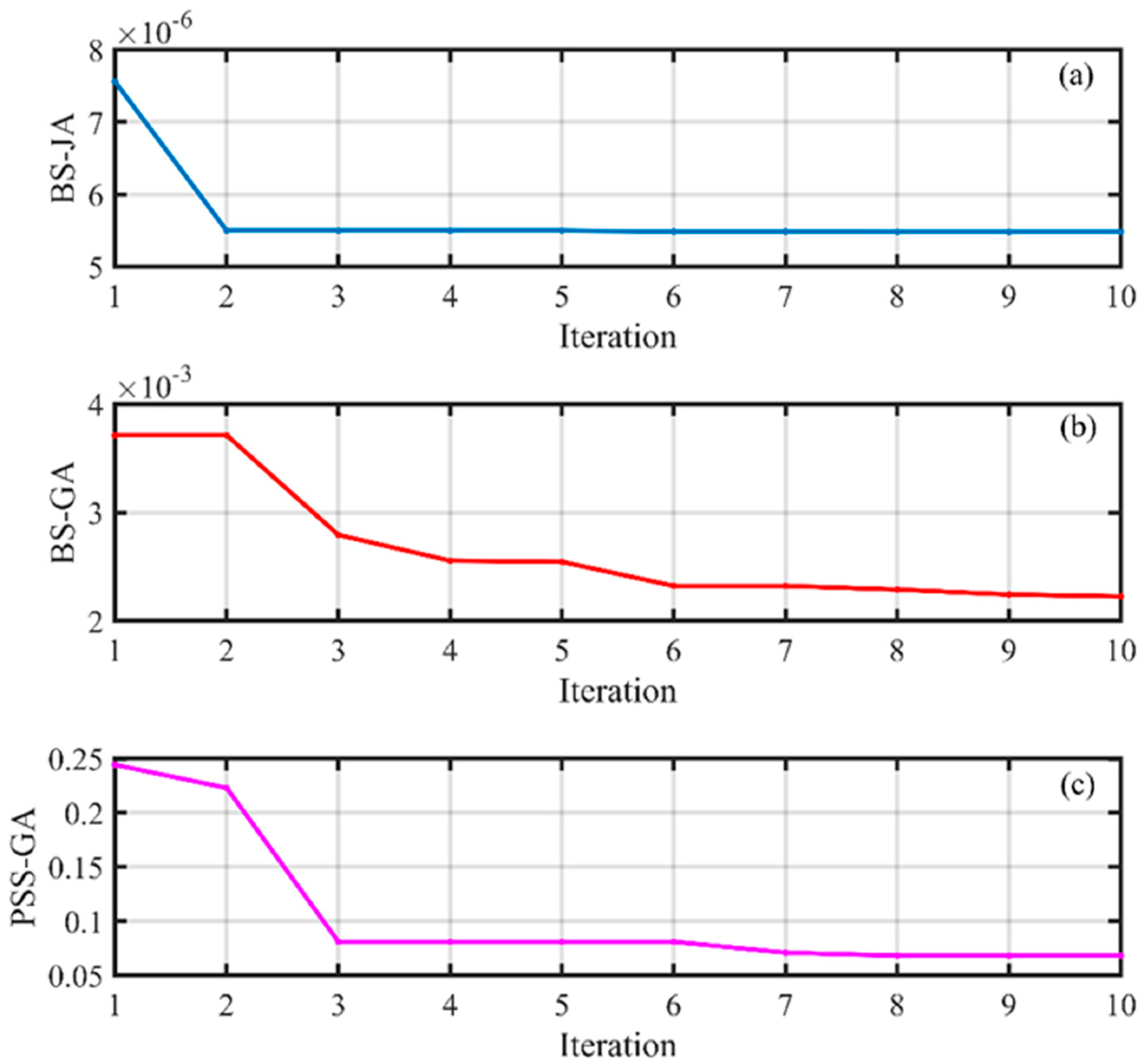
5.1. Identification of JA and GA Parameters
5.2. Faults Simulation Results
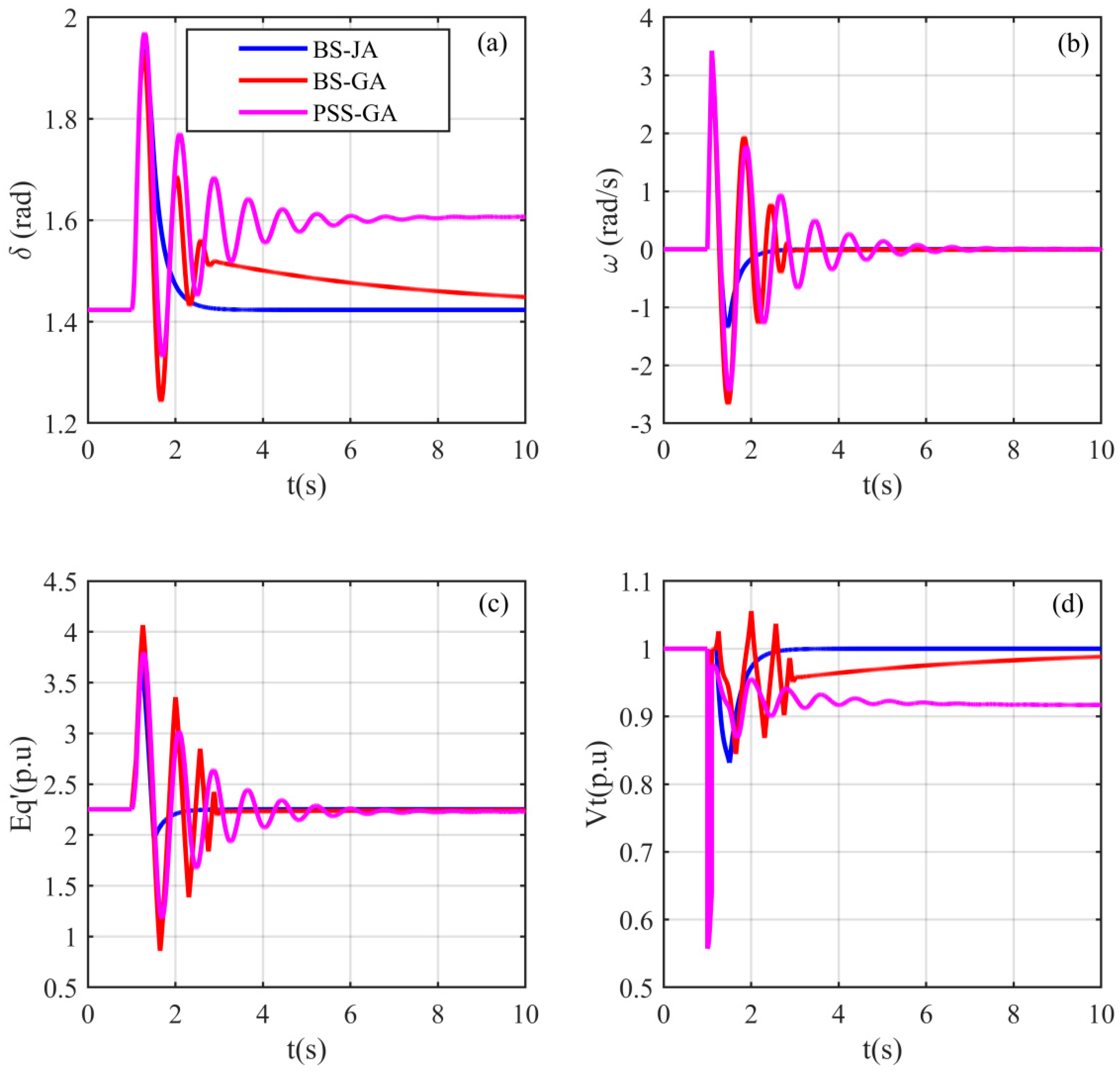
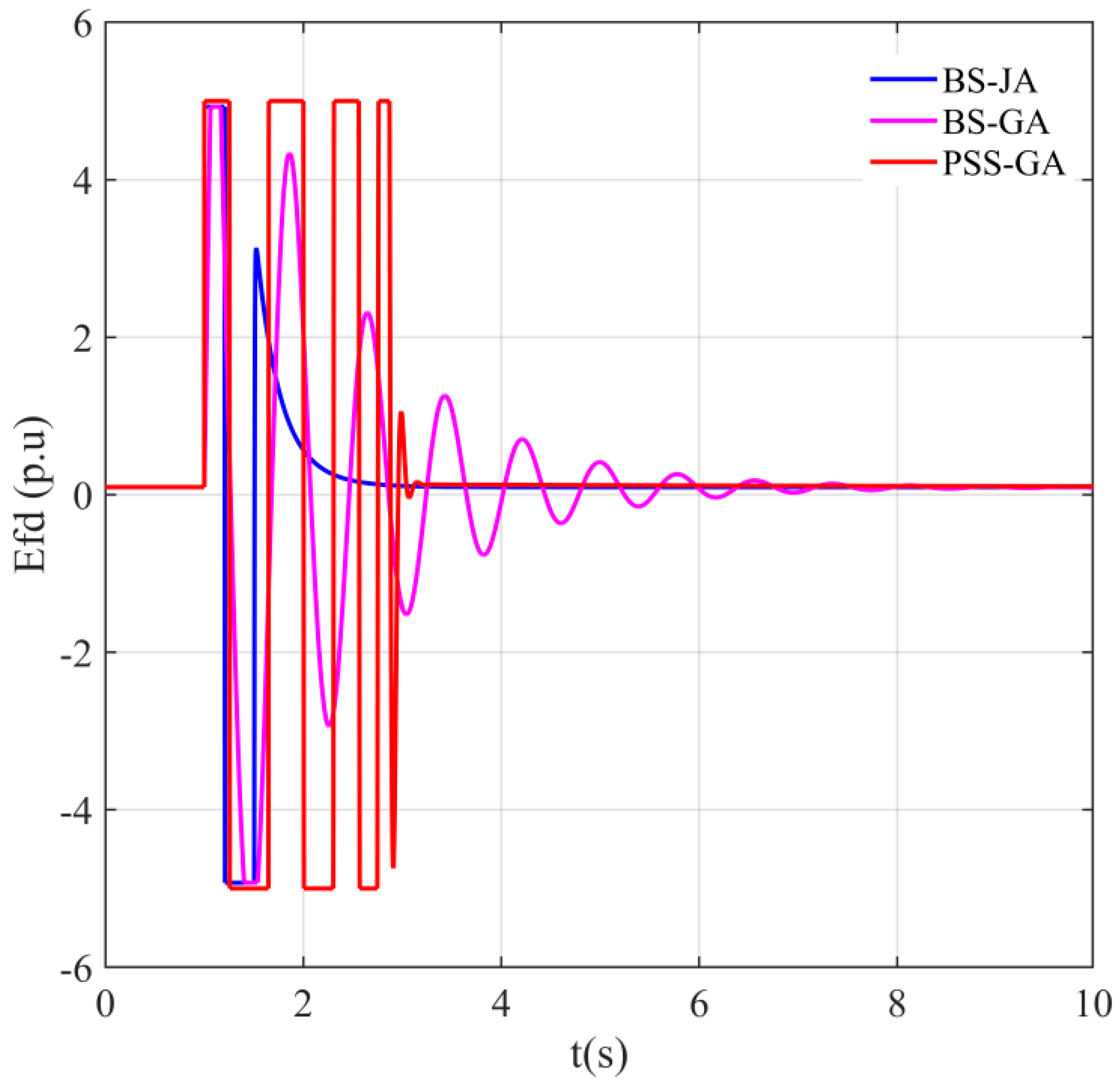
5.2.1. Case 1
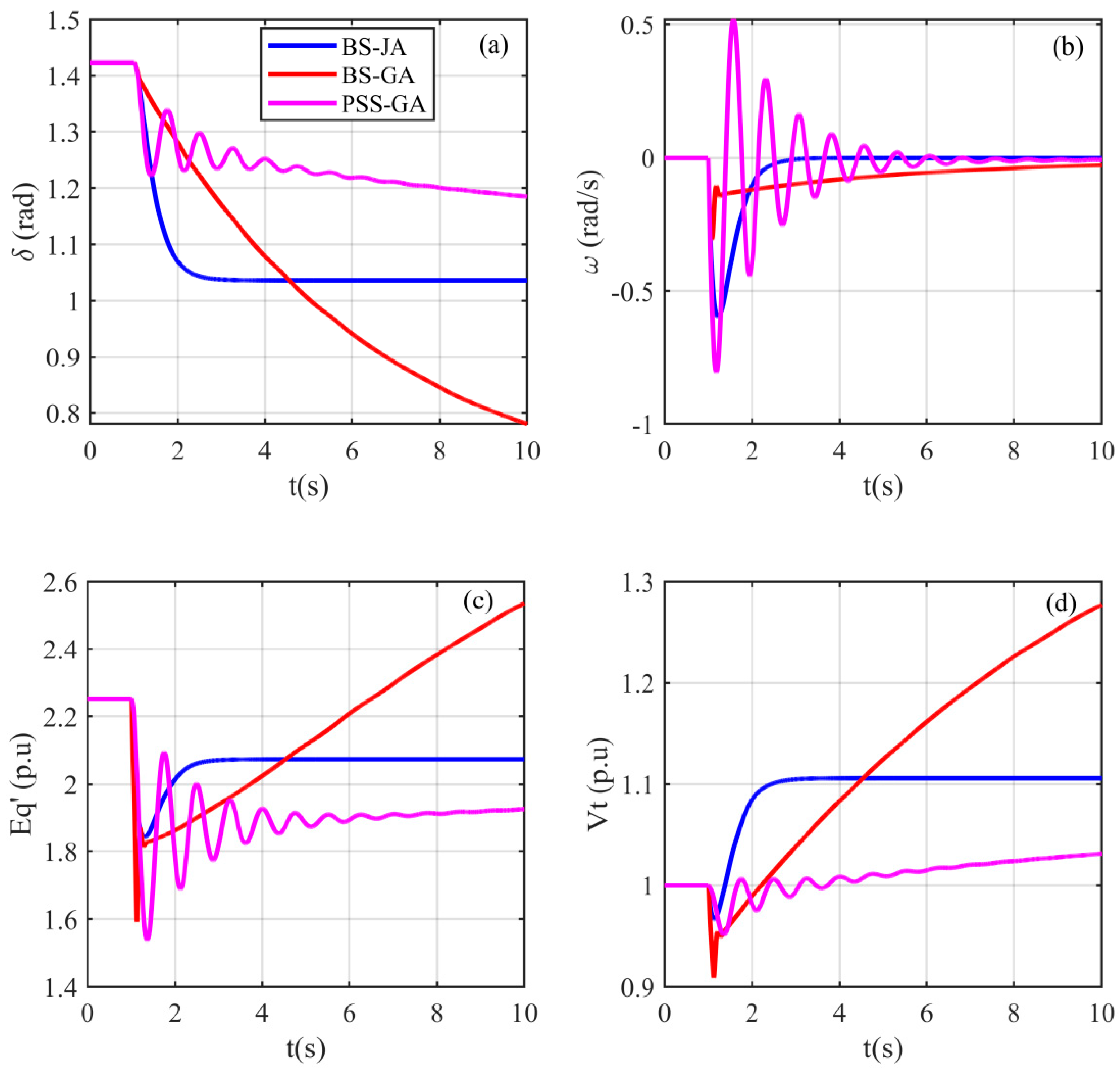
5.2.2. Case 2
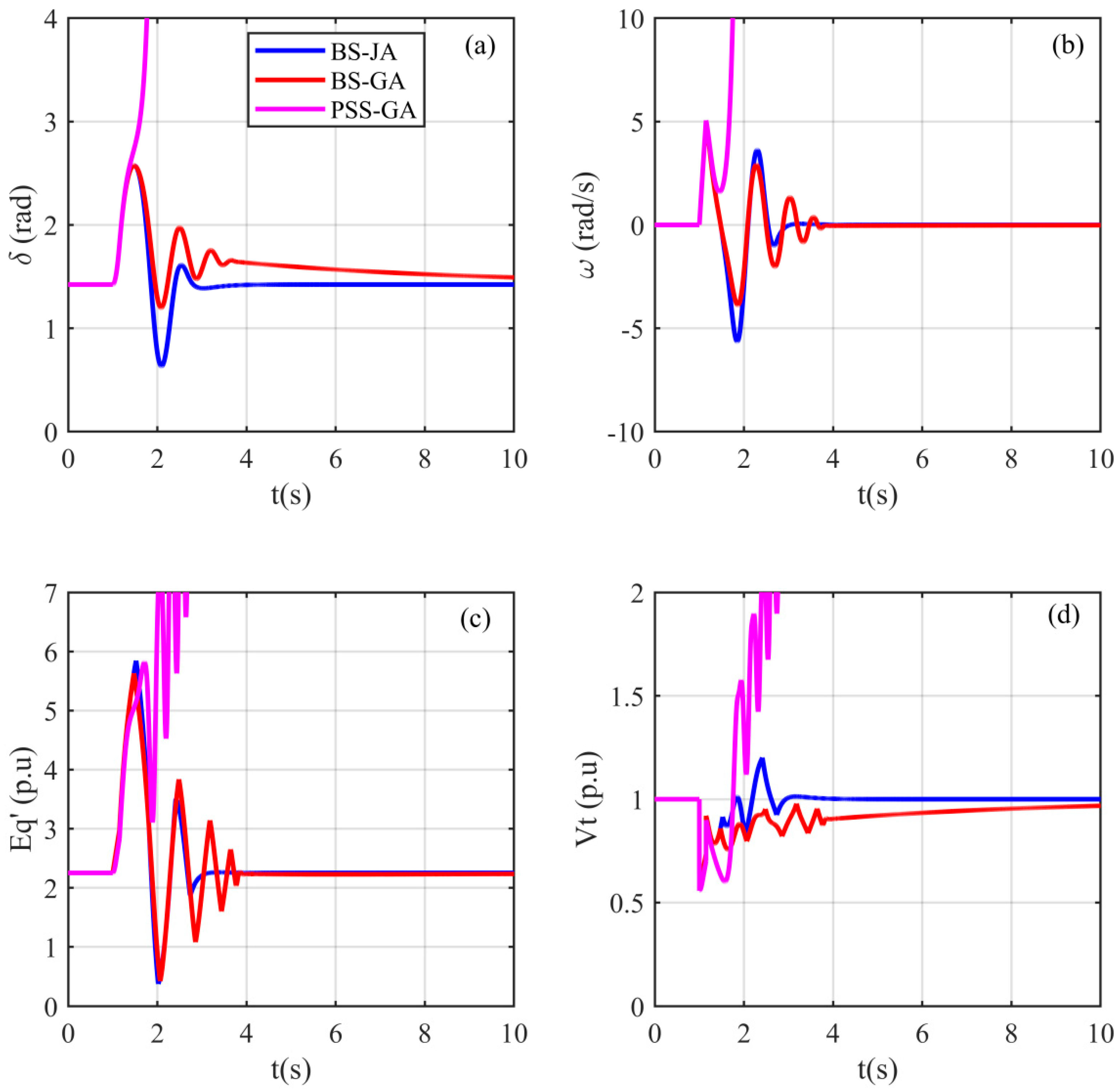
5.2.3. Case 3
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Anderson, P.M.; Fouad, A.A. Power System Control and Stability, 2nd ed.; Wiley-IEEE Press: Danvers, MA, USA, 2002. [Google Scholar]
- Kundur, P. Power System Stability and Control, 3rd ed.; McGraw-Hill Education: New York, NY, USA, 1994. [Google Scholar]
- IEEE Std 421.5™; IEEE Recommended Practice for Excitation System Models for Power System Stability Studies. IEEE: Piscataway, NJ, USA, 2005.
- Ekinci, S.; Demiroren, A.; Hekimoglu, B. Parameter optimization of power system stabilizers via kidney-inspired algorithm. Trans. Inst. Meas. Control 2018, 41, 1405–1417. [Google Scholar] [CrossRef]
- Jebali, M.; Kahouli, O.; Hadj Abdallah, H. Optimizing PSS parameters for a multi-machine power system using genetic algorithm and neural network techniques. Int. J. Adv. Manuf. Technol. 2016, 90, 2669–2688. [Google Scholar] [CrossRef]
- Ranjan Sahu, P.; Kumar Lenka, R.; Kumar Khadanga, R.; Kumar Hota, P.; Panda, S.; Selim Ustun, T. Power System Stability Improvement of FACTS Controller and PSS Design: A Time-Delay Approach. Sustainability 2022, 14, 14649. [Google Scholar] [CrossRef]
- Dasu, B.; Mangipudi, S.; Rayapudi, S. Mall signal stability enhancement of a large scale power system using a bio-inspired whale optimization algorithm. Prot. Control Mod. Power Syst. 2021, 6, 35. [Google Scholar] [CrossRef]
- Farah, A.; Guesmi, T.; Hadj Abdallah, H.; Ouali, A. A novel chaotic teaching–learning-based optimization algorithm for multi-machine power system stabilizers design problem. Electr. Power Energy Syst. 2016, 77, 197–209. [Google Scholar] [CrossRef]
- Farah, A.; Belazi, A.; Alqunun, K.; Almalaq, A.; Alshammari, B.M.; Ben Hamida, M.B.; Abbassi, R. A New Design Method for Optimal Parameters Setting of PSSs and SVC Damping Controllers to Alleviate Power System Stability Problem. Energies 2021, 14, 7312. [Google Scholar] [CrossRef]
- Keskes, S.; Bouchiba, N.; Sallem, S.; Chrifi-Alaoui, L.; Kammoun, M.B.A. Modified direct feedback linearization Excitation Controller for transient stability and voltage regulation of SMIB power system. In Proceedings of the 7th International Conference on Systems and Control, Valencia, Spain, 24–26 October 2018. [Google Scholar]
- Mahmud, M.A.; Pota, H.R.; Hossain, M.J. Full-order nonlinear observer-based excitation controller design for interconnected power systems via exact linearization approach. Electr. Power Energy Syst. 2012, 41, 54–62. [Google Scholar] [CrossRef]
- Kanti Roy, T.; Apel Mahmu, M.d.; Shen, W.; Maung Than Oo, A. Non-linear adaptive excitation control scheme for feedback linearized synchronous generations in multimachine power systems. IET Gener. Transm. Distrib. 2021, 15, 1501–1520. [Google Scholar]
- Chaudhary, R.; Kumar Singh, A. Transient Stability Improvement of Power System Using Non-Linear Controllers. Energy Power Eng. 2014, 6, 10–16. [Google Scholar] [CrossRef]
- Kumar, A. On the Rotor Angle and Voltage Dynamics Decoupling in Synchronous Generators with Nonlinear AVR. Electr. Power Compon. Syst. 2019, 47, 1514–1523. [Google Scholar] [CrossRef]
- Zhao, T.; Wang, J.; Lu, X.; Du, Y. Neural Lyapunov Control for Power System Transient Stability: A Deep Learning-Based Approach. IEEE Trans. Power Systems 2022, 37, 955–966. [Google Scholar] [CrossRef]
- Tacchi, M.; Marinescu, B.; Anghel, M.; Kundu, S.; Benahmed, S.; Cardozo, C. Power System Transient Stability Analysis Using Sum of Squares Programming. In Proceedings of the 2018 Power Systems Computation Conference (PSCC), Dublin, Ireland, 11–15 June 2018. [Google Scholar]
- Thanh Long, T.V.; Konstantin, T. Lyapunov Functions Family Approach to Transient Stability Assessment. IEEE Trans. Power Syst. 2016, 31, 1269–1277. [Google Scholar]
- Pai, M.A.; Sauer, P.W. Stability Analysis of Power Systems by Lyapunov’s Direct Method. IEEE Control. Syst. Mag. 1989, 9, 23–27. [Google Scholar] [CrossRef]
- Wang, S.; Wang, Z. Sliding Mode Dynamic Surface Control for MultiMachine Power Systems with Time Delays and Dead-Zones. Cybern. Syst. 2020, 52, 58–72. [Google Scholar] [CrossRef]
- Fadil, H.E.; Oulcaid, M.; Yahya, A.; Ammeh, L.; Giri, F. Adaptive Sliding Mode Control of Power System with Photovoltaic Generator. In Proceedings of the 16th International Multi-Conference on Systems, Signals & Devices, Istanbul, Turkey, 21–24 March 2019. [Google Scholar]
- Yang, B.; Yu, T.; Shu, H.C.; Yao, W.; Jiang, L. Sliding-mode perturbation observer-based sliding-mode control design for stability enhancement of multi-machine power systems. Trans. Inst. Meas. Control. 2018, 41, 1418–1434. [Google Scholar] [CrossRef]
- Benayache, R.; Bahloul, W.; Chrifi-Alaoui, L.; Bussy, P.; Kamoun, M.B.A. Transient stability of power systems using robust nonlinear second order sliding mode controller. In Proceedings of the 2010 American Control Conference, Baltimore, MD, USA, 30 June–2 July 2010. [Google Scholar]
- Liu, H.; Su, J.; Qi, J. Decentralized Voltage and Power Control of Multi-Machine Power Systems with Global Asymptotic Stability. IEEE Access 2019, 7, 14273–14282. [Google Scholar] [CrossRef]
- Saad, H.; Ramadan, M.; Becherif, M. Dynamic Performance Enhancement of Synchronous Generator Excitation via Nonlinear Backstepping Control. Int. J. Emerg. Electr. Power Syst. 2016, 18, 20160290. [Google Scholar]
- Bahloul, W.; Benayache, R.; Chrifi-Alaoui, L.; Kamoun, M.B.A. Combined Nonlinear Excitation Controller Dedicated to a Grid-Connected Alternator Transient Stability and Voltage Regulation Enhancement. Trans. Syst. Signals Devices 2010, 5, 1–18. [Google Scholar]
- Keskes, S.; Bouchiba, N.; Sallem, S.; Kammoun, S.; Chrifi-Alaoui, L.; Kammoun, M.B.A. An improved Backstepping technique using sliding mode control for transient stability enhancement and voltage regulation of SMIB power system. Int. J. Syst. Sci. 2018, 49, 1964–1973. [Google Scholar] [CrossRef]
- Roy, T.K.; Mahmud, M.A.; Shen, W.; Oo, A.M.T.; Haque, M.E. Robust nonlinear adaptive backstepping excitation controller design for rejecting external disturbances in multimachine power systems. Int. J. Elect. Power Energy Syst. 2017, 84, 76–86. [Google Scholar] [CrossRef]
- Yan, R.; Yang Dong, Z.; Saha, T.K.; Majumder, R. A power system nonlinear adaptive decentralized controller design. Automatica 2010, 46, 330–336. [Google Scholar] [CrossRef]
- Ge, J.; Wang, M.; Hong, H.; Zhao, J.; Cai, G.; Zhang, X.; Lu, P. Discrete-Time Adaptive Decentralized Control for Interconnected Multi-Machine Power Systems with Input Quantization. Machines 2022, 10, 878. [Google Scholar] [CrossRef]
- Karimi, A.; Feliachi, A. Decentralized adaptive backstepping control of electric power systems. Electr. Power Syst. Res. 2008, 78, 484–493. [Google Scholar] [CrossRef]
- Akyol, S.; Alatas, B. Plant intelligence based metaheuristic optimization algorithms. Artif. Intell. Rev. 2017, 47, 417–462. [Google Scholar] [CrossRef]
- Alatas, B.; Bingol, H. Comparative assessment of light-based intelligent search and optimization algorithms. Light Eng. 2020, 28, 51–59. [Google Scholar] [CrossRef]
- Schmitt, L.M. Fundamental Study Theory of genetic algorithms. Theor. Comput. Sci. 2001, 259, 1–61. [Google Scholar] [CrossRef]
- Deb, K.; Pratap, A.; Agarwal, S.; Meyarivan, T. A fast and elitist multiobjective genetic algorithm: Nsga-II. Trans. Evol. Comp. 2002, 6, 182–197. [Google Scholar] [CrossRef]
- Ahmad, M.F.; Isa, N.A.M.; Lim, W.H.; Ang, K.M. Differential evolution: A recent review based on state-of-the-art works Author links open overlay panel. Alex. Eng. J. 2022, 61, 3831–3872. [Google Scholar] [CrossRef]
- Kennedy, J.; Eberhart, R. Particle Swarm Optimization. Int. Conf. Neural Netw. 1995, 4, 1942–1948. [Google Scholar]
- Mirjalili, S.; Mirjalili, S.M.; Lewis, A. Grey Wolf Optimizer. Adv. Eng. Softw. 2014, 69, 46–56. [Google Scholar] [CrossRef]
- Karaboga, D.; Basturk, B. A powerful and efficient algorithm for numerical function optimization: Artificial bee colony (ABC) algorithm. J. Glob. Optim. Vol. 2007, 39, 459–471. [Google Scholar] [CrossRef]
- Hassanat, A.; Almohammadi, K.; Alkafaween, E.; Abunawas, E.; Hammouri, A.; Surya Prasath, V.B. Choosing Mutation and Crossover Ratios for Genetic Algorithms. A Rev. A New Dyn. Approach Inf. 2019, 10, 390. [Google Scholar]
- Rao, R.V.; Savsani, V.J.; Vakharia, D.P. Teaching–Learning-Based Optimization: An optimization method for continuous non-linear large scale problems. Inf. Sci. 2012, 183, 1–15. [Google Scholar] [CrossRef]
- Rao, R.V. Jaya: A simple and new optimization algorithm for solving constrained and unconstrained optimization problems. Int. J. Ind. Eng. Comput. 2016, 7, 19–34. [Google Scholar]
- Krstic, M.; Kanellakopoulos, I.; Kokotovic, P.V. Nonlinear and Adaptive Control Design; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 1995. [Google Scholar]
- Zargarzadeh, H.; Dierks, T.; Jagannathan, S. Adaptive neural network-based optimal control of nonlinear continuous-time systems in strict-feedback form. Int. J. Adapt. Control. Signal Process 2013, 28, 305–324. [Google Scholar] [CrossRef]
- Khalil, K. Nonlinear Systems, 2nd ed.; Prentice-Hall: New-York, NY, USA, 1996. [Google Scholar]
- Lal, D.K.; Barisal, A.K. Combined load frequency and terminal voltage control of power systems using moth flame optimization algorithm. J. Electr. Syst. Inf. Technol. 2019, 6, 8. [Google Scholar] [CrossRef]
- Ramjug-Ballgobin, R.; Fowdar, R. Application of metaheuristic control strategies to voltage regulation. SN Appl. Sci. 2019, 1, 1731. [Google Scholar] [CrossRef]
- Plevris, V.; Solorzano, G.A. Collection of 30 Multidimensional Functions for Global Optimization Benchmarking. Data 2022, 7, 46. [Google Scholar] [CrossRef]
- Mills, K.L.; Filliben, J.J.; Haines, A.L. Determining Relative Importance and Effective Settings for Genetic Algorithm Control Parameters. Evol. Comput. 2015, 23, 309–342. [Google Scholar] [CrossRef]
- Ben Ammar, M.; Bahloul, W.; Zdiri, M.A.; Haj Abdallah, H. New decentralized control based on T-S fuzzy logic approach of an electrical wind-source integrating grid. Int. J. Model. Identif. Control. 2022, 41, 256–276. [Google Scholar] [CrossRef]


| Machine | Transformer | Transmission Line | AVR | |||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Parameter | ||||||||||
| Value | 1.863 | 0.257 | 1.49 | 6.9 | 4 | 6 | 0.127 | 0.242 | 200 | 0.05 |
| Unit | (p.u) | (p.u) | (p.u) | (s) | MJ/MVA | (p.u) | (p.u) | (p.u) | (s) | |
| Std | ||||||||
|---|---|---|---|---|---|---|---|---|
| 0.90 | 0.01 | 0.2172 | 3.50 × 10−6 | 0.95 | 0.01 | 0.2594 | 1.12 × 10−6 | |
| 0.02 | 0.2751 | 3.56 × 10−5 | 0.02 | 0.2455 | 1.62 × 10−4 | |||
| 0.03 | 0.6444 | 5.90 × 10−6 | 0.03 | 0.2662 | 1.16 × 10−3 | |||
| 0.04 | 0.2332 | 6.11 × 10−5 | 0.04 | 0.2715 | 9.50 × 10−4 | |||
| 0.05 | 0.2219 | 6.80 × 10−6 | 0.05 | 0.3903 | 9.51 × 10−4 | |||
| 0.91 | 0.01 | 0.3007 | 2.41 × 10−4 | 0.96 | 0.01 | 0.2407 | 9.22 × 10−5 | |
| 0.02 | 0.2326 | 2.48 × 10−4 | 0.02 | 0.2479 | 3.28 × 10−5 | |||
| 0.03 | 0.2298 | 2.75 × 10−4 | 0.03 | 0.2745 | 1.19 × 10−4 | |||
| 0.04 | 0.3020 | 2.34 × 10−4 | 0.04 | 0.2343 | 1.51 × 10−4 | |||
| 0.05 | 0.2330 | 4.4 × 10−5 | 0.05 | 0.4364 | 4.96 × 10−5 | |||
| 0.92 | 0.01 | 0.2340 | 2.93 × 10−4 | 0.97 | 0.01 | 0.2931 | 7.14 × 10−5 | |
| 0.02 | 0.3452 | 3.12 × 10−4 | 0.02 | 0.3123 | 8.42 × 10−5 | |||
| 0.03 | 0.3452 | 2.30 × 10−4 | 0.03 | 0.2301 | 9.00 × 10−6 | |||
| 0.04 | 0.3224 | 2.44 × 10−4 | 0.04 | 0.2440 | 2.70 × 10−5 | |||
| 0.05 | 0.3271 | 2.18 × 10−4 | 0.05 | 0.2288 | 1.40 × 10−5 | |||
| 0.93 | 0.01 | 0.3002 | 2.19 × 10−4 | 0.98 | 0.01 | 0.2188 | 1.40 × 10−4 | |
| 0.02 | 0.2367 | 2.50 × 10−4 | 0.02 | 0.2501 | 7.12 × 10−6 | |||
| 0.03 | 0.2313 | 2.47 × 10−4 | 0.03 | 0.2467 | 1.50 × 10−6 | |||
| 0.04 | 0.2484 | 2.22 × 10−4 | 0.04 | 0.2223 | 1.25 × 10−5 | |||
| 0.05 | 0.2477 | 2.31 × 10−4 | 0.05 | 0.2306 | 8.70 × 10−6 | |||
| 0.94 | 0.01 | 0.3452 | 2.50 × 10−4 | 0.99 | 0.01 | 0.2501 | 6.32 × 10−6 | |
| 0.02 | 0.2297 | 2.50 × 10−4 | 0.02 | 0.2501 | 3.89 × 10−5 | |||
| 0.03 | 0.2308 | 2.50 × 10−4 | 0.03 | 0.2501 | 9.11 × 10−5 | |||
| 0.04 | 0.2572 | 2.36 × 10−4 | 0.04 | 0.2356 | 6.50 × 10−6 | |||
| 0.05 | 0.23554 | 2.50 × 10−4 | 0.05 | 0.2501 | 7.58 × 10−6 |
| Parameters/Method | JA | GA |
|---|---|---|
| 4 | ||
| 40 | 40 | |
| 30 | 30 | |
| - | ||
| - | ||
| NFE | 1200 | 1200 |
| Controllers/Performances | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| BS-JA | 38.3 | 1.8 | 54 | 18 | 1 | 0 | 0 | 0 | 0 |
| BS-GA | 39.2 | 2 | 74 | 35 | 2 | 5.7 | 0 | 0 | 0.01 |
| PSS-GA | 40.4 | 2.1 | 70 | 42 | 4.5 | 10.3 | 0 | 0 | 0.09 |
| Controllers/Performances | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| BS-JA | 0 | 0.2 | 19 | 2 | 1 | 0 | 0 | 0 | 0.10 |
| BS-GA | 0 | 0.13 | 29.5 | 5 | 10 | 5.7 | 0 | 0 | 0.30 |
| PSS-GA | 14 | 0.5 | 31 | 9 | 5 | 10.3 | 0 | 0 | 0.03 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bahloul, W.; Zdiri, M.A.; Marouani, I.; Alqunun, K.; Alshammari, B.M.; Alturki, M.; Guesmi, T.; Hadj Abdallah, H.; Tlijani, K. A Backstepping Control Strategy for Power System Stability Enhancement. Sustainability 2023, 15, 9022. https://doi.org/10.3390/su15119022
Bahloul W, Zdiri MA, Marouani I, Alqunun K, Alshammari BM, Alturki M, Guesmi T, Hadj Abdallah H, Tlijani K. A Backstepping Control Strategy for Power System Stability Enhancement. Sustainability. 2023; 15(11):9022. https://doi.org/10.3390/su15119022
Chicago/Turabian StyleBahloul, Wissem, Mohamed Ali Zdiri, Ismail Marouani, Khalid Alqunun, Badr M. Alshammari, Mansoor Alturki, Tawfik Guesmi, Hsan Hadj Abdallah, and Kamel Tlijani. 2023. "A Backstepping Control Strategy for Power System Stability Enhancement" Sustainability 15, no. 11: 9022. https://doi.org/10.3390/su15119022
APA StyleBahloul, W., Zdiri, M. A., Marouani, I., Alqunun, K., Alshammari, B. M., Alturki, M., Guesmi, T., Hadj Abdallah, H., & Tlijani, K. (2023). A Backstepping Control Strategy for Power System Stability Enhancement. Sustainability, 15(11), 9022. https://doi.org/10.3390/su15119022








