Adaptive Stability Control Based on Sliding Model Control for BEVs Driven by In-Wheel Motors
Abstract
1. Introduction
2. Vehicle Modeling
2.1. Vehicle Dynamic Model
2.2. Driver Model
2.3. In-Wheel Motor Model
2.4. Battery Model
2.5. Tire Model
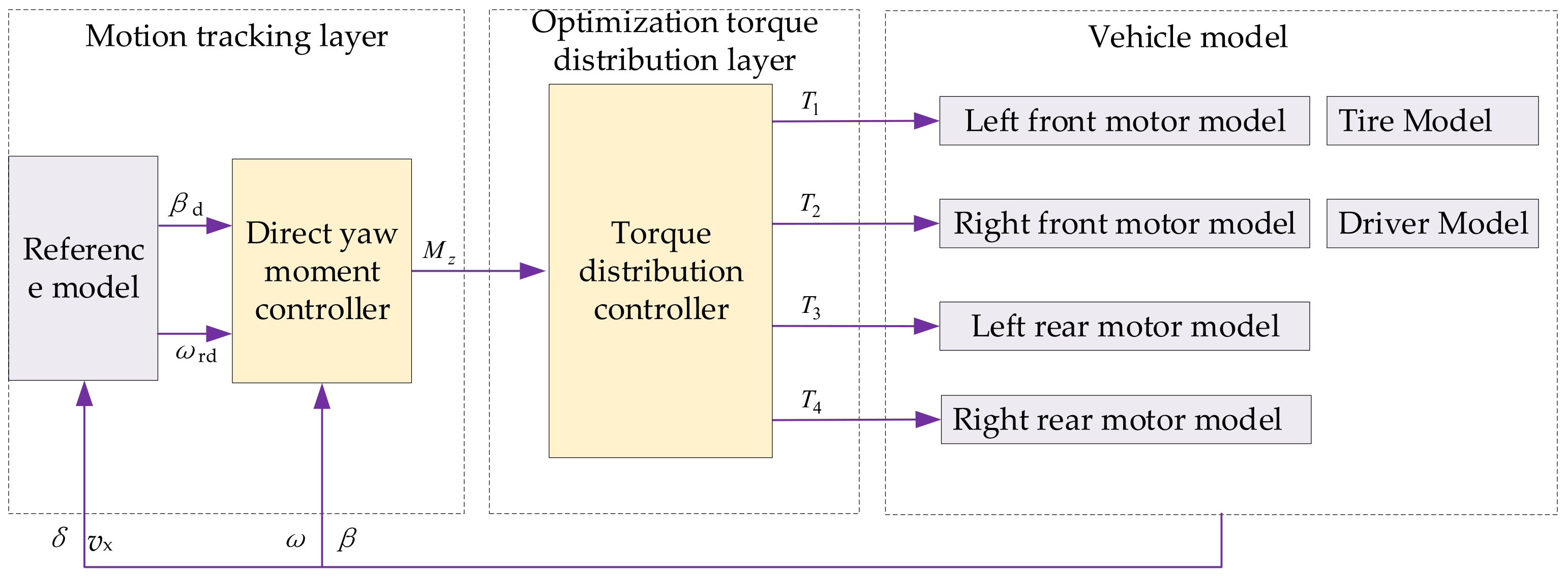
3. Adaptive Stability Control
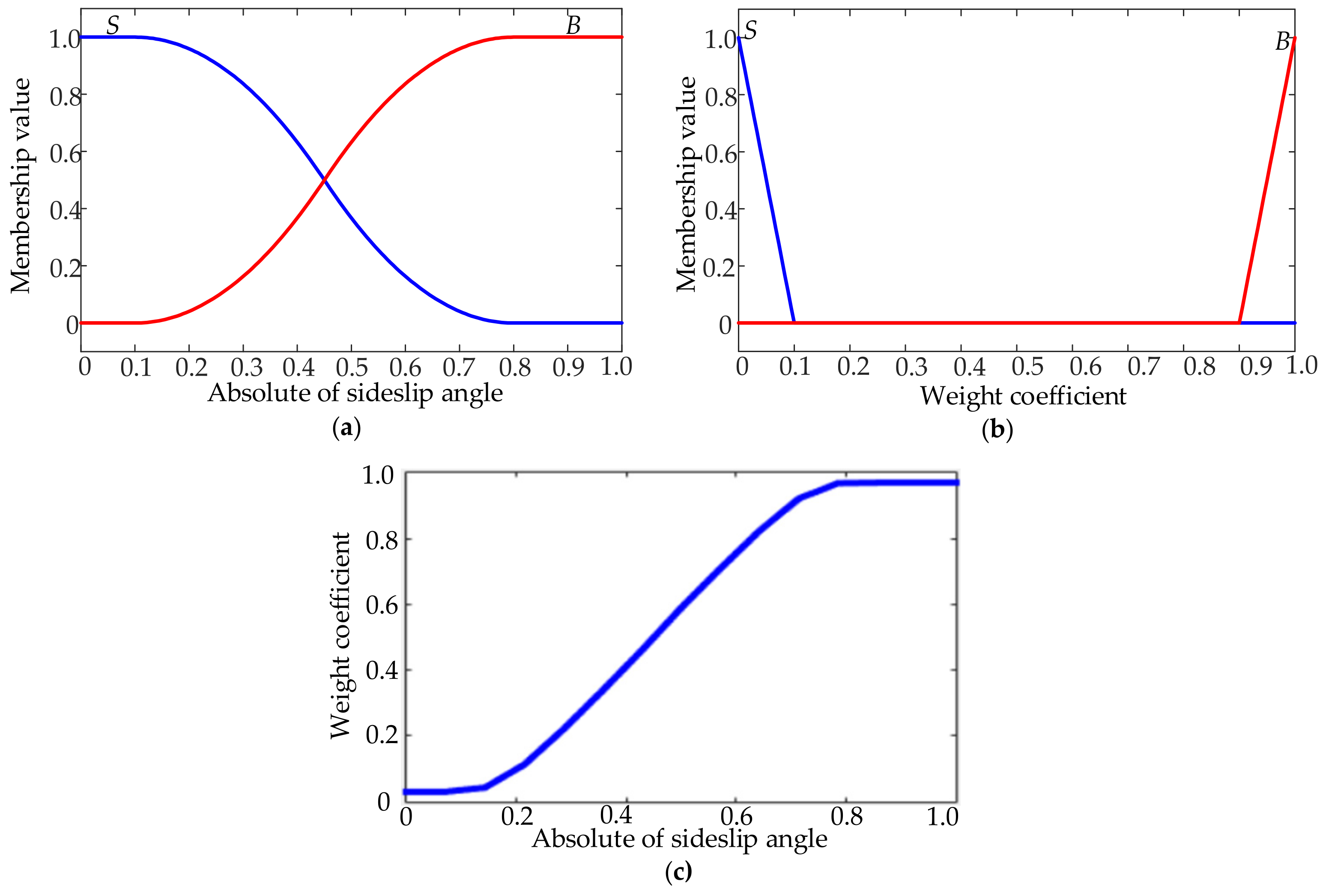
3.1. Stability Analysis and Judgement
3.2. Direct Yaw Moment Controller Based on Adaptive Sliding Mode
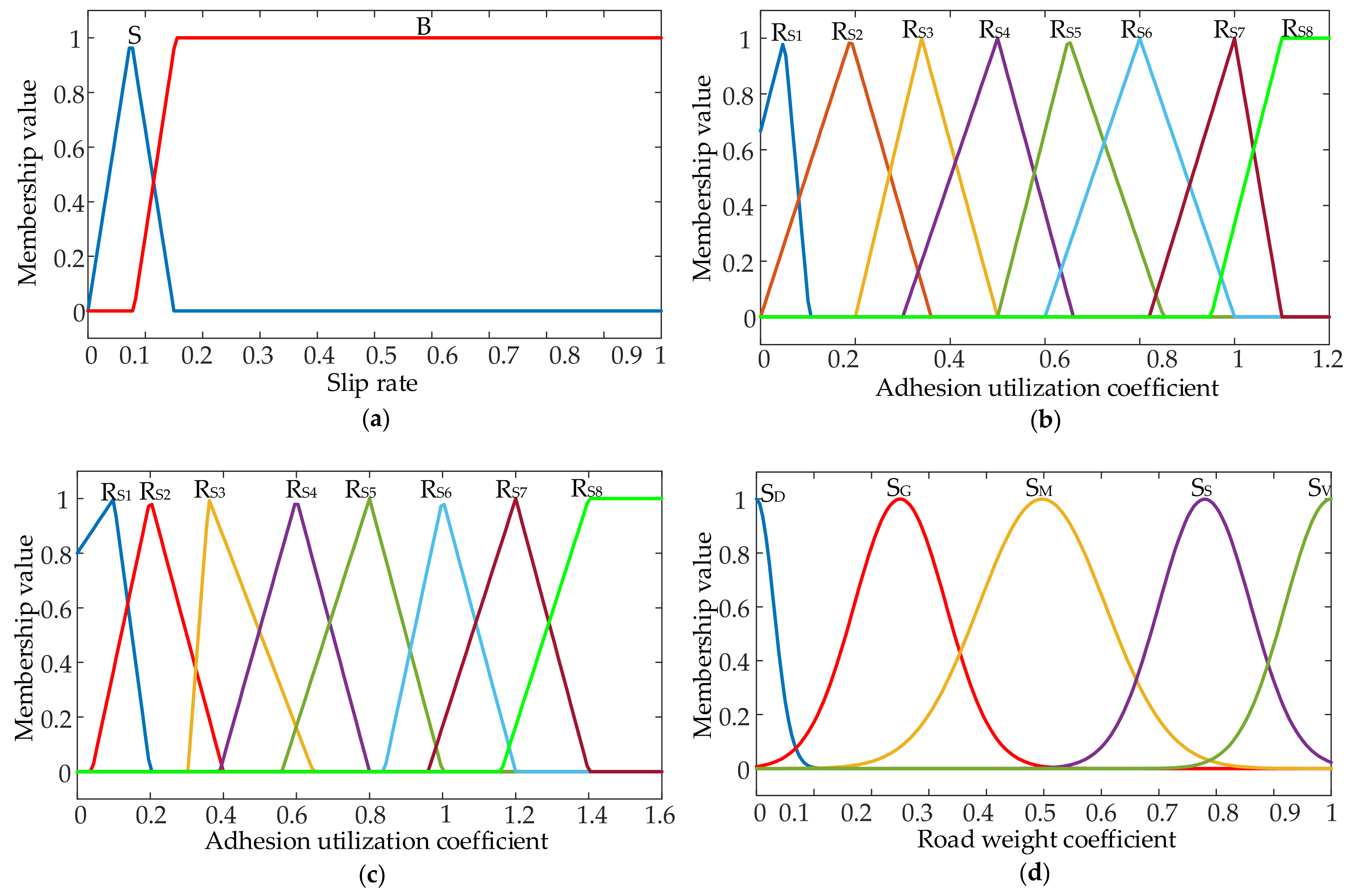
3.3. Torque Distribution Controller Based on Road Adhesion Coefficient Recognition
4. Simulation Verification
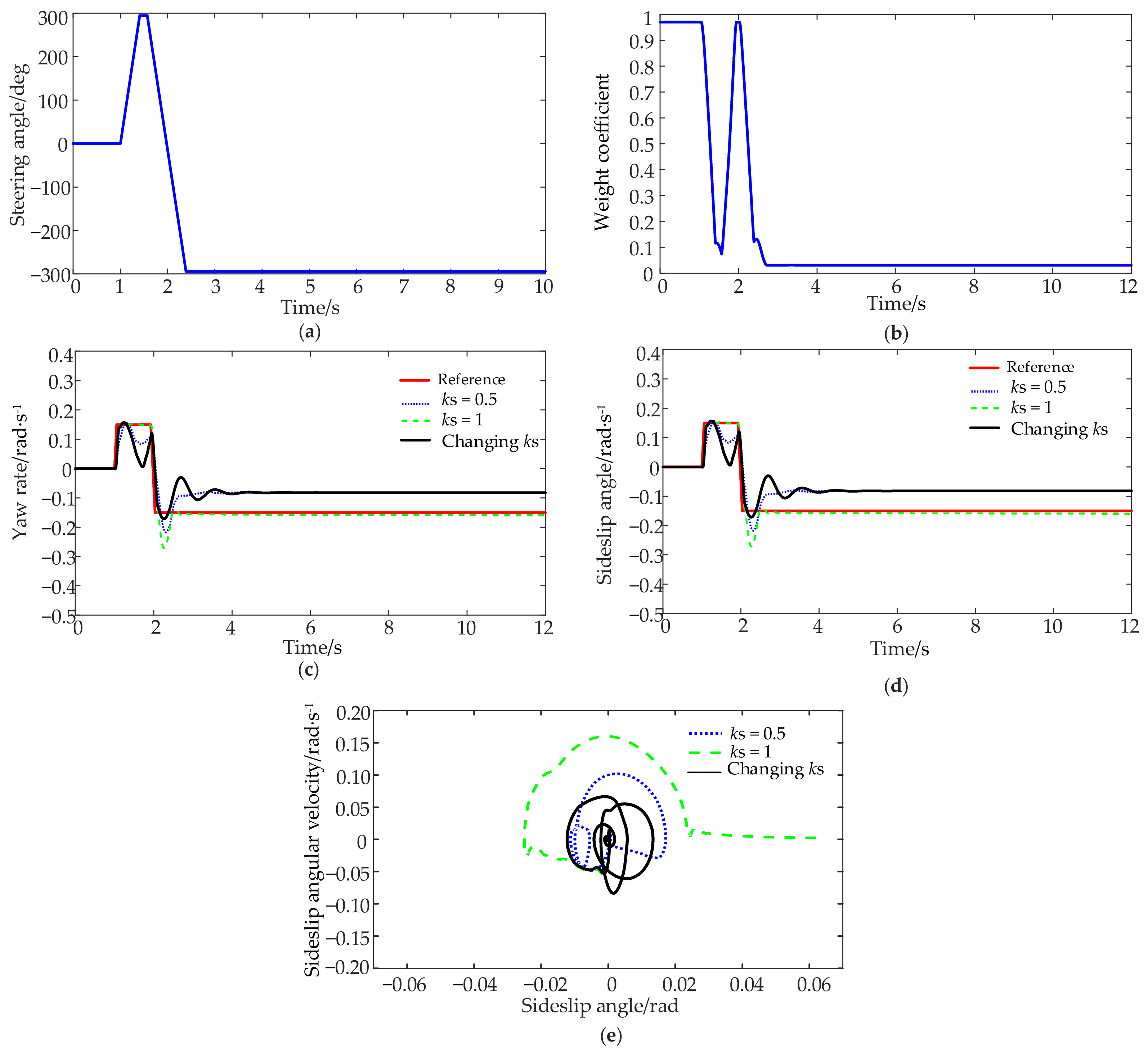
4.1. Verification of Direct Yaw Moment Controller
4.2. Verification of Torque Distribution Controller
5. Discussion and Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| EV | Battery Electric Vehicle |
| DYC | Direct Yaw Moment Control |
| GNL | General Nonlinear Model |
| MPC | Model Predictive Control |
| PID | Proportional Integral Differential |
| PNGV | Partnership for a New Generation of Vehicle Battery Model |
| SMC | Sliding Mode Control |
References
- He, S.W.; Fan, X.B.; Wang, Q.W.; Chen, X.B.; Zhu, S.W. Review on torque distribution scheme of four-wheel in-wheel motor electric vehicle. Machines 2022, 10, 619. [Google Scholar] [CrossRef]
- Joa, E.; Yi, K.; Hyun, Y. Estimation of the tire slip angle under various road conditions without tire-road information for vehicle stability control. Control Eng. Pract. 2019, 86, 129–143. [Google Scholar] [CrossRef]
- Liu, W.; Quijano, K.; Crawford, M.M. YOLOv5-tassel: Detecting tassels in RGB UAV imagery with improved YOLOv5 based on transfer learning. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2022, 15, 8085–8094. [Google Scholar] [CrossRef]
- Zhai, L.; Wang, C.P.; Zhang, X.Y.; Hou, R.F.; Mok, Y.M.; Hou, Y.H. Handling stability control strategy for four-wheel hub motor-driven vehicle based on adaptive control for road adhesion. IET Intell. Transp. Syst. 2022, 16, 586–601. [Google Scholar] [CrossRef]
- Zhou, C.; Liu, X.H.; Xu, F.X. Intervention criterion and control strategy of active front steering system for emergency rescue vehicle. Mech. Syst. Signal Process. 2021, 148, 107160. [Google Scholar] [CrossRef]
- Zhang, H.; Wang, J.M. Vehicle lateral dynamics control through AFS/DYC and robust gain-scheduling approach. IEEE Trans. Veh. Technol. 2016, 65, 489–494. [Google Scholar] [CrossRef]
- Wang, H.B.; Zhou, J.T.; Hu, C.L.; Chen, W.W. Vehicle lateral stability control based on stability category recognition with improved brain emotional learning network. IEEE Trans. Veh. Technol. 2022, 71, 5930–5943. [Google Scholar] [CrossRef]
- Wu, W.; Lu, S.; Li, C. Adaptive coordinated stability control of vehicle considering stability margin. In Proceedings of the 2021 33rd Chinese Control and Decision Conference, Kunming, China, 22–24 May 2021; pp. 5191–5196. [Google Scholar]
- Hu, C.; Wang, Z.; Taghavifar, H.; Na, J.; Qin, Y.; Guo, J.; Wei, C. MME-EKF-based path-tracking control of autonomous vehicles considering input saturation. IEEE Trans. Veh. Technol. 2019, 68, 5246–5259. [Google Scholar] [CrossRef]
- Dong, J.; Li, J.; Gao, Q.; Hu, J.; Liu, Z. Optimal coordinated control of active steering and direct yaw moment for distributed-driven electric vehicles. Control Eng. Pract. 2023, 134, 105486. [Google Scholar] [CrossRef]
- Ahmed, A.A.; Ahmed, A.A.; Alarga, A.S.D.; Alsharif, A. Simulation research on vehicle handling and stability enhancement based on PID control technology. In Proceedings of the IEEE International Conference on Power, Electrical, Electronic and Industrial Applications, Dhaka, Bangladesh, 3–4 December 2021; pp. 10–15. [Google Scholar]
- Jung, H.; Jung, D.; Choi, S.B. LQR control of an all-wheel drive vehicle considering variable input constraint. IEEE Trans. Control Syst. Technol. 2022, 30, 85–96. [Google Scholar] [CrossRef]
- Majidi, M.; Asiabar, A.N. Stability enhancement of in-wheel motor drive electric vehicle using adaptive sliding mode control. Int. J. Adv. Manuf. Technol. 2022, 15, 23–33. [Google Scholar]
- Liu, C.; Liu, H.; Han, L.; Wang, W.; Guo, C. Multi-level coordinated yaw stability control based on sliding mode predictive control for distributed drive electric vehicles under extreme conditions. IEEE Trans. Veh. Technol. 2022, 72, 280–296. [Google Scholar] [CrossRef]
- Li, P.; Li, P.; Zhang, B.; Zhao, J.; Du, B. Velocity-based lateral stability control for four-wheel independently actuated electric vehicles with homogeneous polynomial approach. Int. J. Control Autom. Syst. 2021, 19, 255–266. [Google Scholar] [CrossRef]
- Liu, Z.; Qiao, Y.; Chen, X. A novel control strategy of straight-line driving stability for 4WID electric vehicles based on sliding mode control. In Proceedings of the 2021 5th CAA International Conference on Vehicular Control and Intelligence, Tianjin, China, 29–31 October 2021. [Google Scholar]
- Qin, Y.; Li, C.; Jing, H.; Cui, R.; Lei, Y. Lateral stability control of four-wheel-drive vehicle based on coordinated control of torque distribution and vehicle dynamics. In Proceedings of the 2022 Global Conference on Robotics, Artificial Intelligence and Information Technology, Chicago, IL, USA, 30–31 July 2022. [Google Scholar]
- Asiabar, A.N.; Kazemi, R. A direct yaw moment controller for a four in-wheel motor drive electric vehicle using adaptive sliding mode control. Proc. Inst. Mech. Eng. Part K-J. Multi-Body Dyn. 2019, 233, 549–567. [Google Scholar] [CrossRef]
- Yang, K.; Dong, D.X.; Ma, C.; Tian, Z.X.; Chang, Y.L.; Wang, G. Stability control for electric vehicles with four in-wheel-motors based on sideslip angle. World Electr. Veh. J. 2021, 12, 42. [Google Scholar] [CrossRef]
- Liu, W.; Xiong, L.; Xia, X.; Lu, Y.; Gao, L.; Song, S. Vision-aided intelligent vehicle sideslip angle estimation based on a dynamic model. IET Intell. Transp. Syst. 2020, 14, 1183–1189. [Google Scholar] [CrossRef]
- Ma, Y.; Chen, J.; Zhu, X.; Xu, Y. Lateral stability integrated with energy efficiency control for electric vehicles. Mech. Syst. Signal Process. 2019, 127, 1–15. [Google Scholar] [CrossRef]
- Wang, Y.; Zhao, Y.; Zhou, S.; Yan, Q.; Zhan, H.; Cheng, Y.; Yin, W. Impact of individual cell parameter difference on the performance of series–parallel battery packs. ACS Omega 2023, 8, 10512–10524. [Google Scholar] [CrossRef]
- Fukada, Y. Slip-angle estimation for vehicle stability control. Veh. Syst. Dyn. 1999, 32, 375–388. [Google Scholar] [CrossRef]
- Boada, B.L.; Boada, M.J.L.; Diaz, V. Vehicle sideslip angle measurement based on sensor data fusion using an integrated ANFIS and an Unscented Kalman Filter algorithm. Mech. Syst. Signal Process. 2016, 72–73, 832–845. [Google Scholar] [CrossRef]
- Mirzaeinejad, H.; Mirzaei, M.; Rafatnia, S. A novel technique for optimal integration of active steering and differential braking with estimation to improve vehicle directional stability. ISA Trans. 2018, 80, 513–527. [Google Scholar] [CrossRef] [PubMed]
- Najjari, B.; Mirzaei, M.; Tahouni, A. Decentralized integration of constrained active steering and torque vectoring systems to energy-efficient stability control of electric vehicles. J. Frankl. Inst. 2022, 359, 8713–8741. [Google Scholar] [CrossRef]
- Xiang, C.L.; Peng, H.N.; Wang, W.D.; Li, L.; An, Q.; Cheng, S. Path tracking coordinated control strategy for autonomous four in-wheel-motor independent-drive vehicles with consideration of lateral stability. Proc. Inst. Mech. Eng. Part D-J. Automob. Eng. 2021, 235, 1023–1036. [Google Scholar] [CrossRef]
- Leng, B.; Jin, D.; Xiong, L.; Yang, X.; Yu, Z.P. Estimation of tire-road peak adhesion coefficient for intelligent electric vehicles based on camera and tire dynamics information fusion. Mech. Syst. Signal Process. 2021, 150, 107275. [Google Scholar] [CrossRef]
- Burckhardt, M. Fahrwerktechnik: Radschlupfregel Systeme; Vogel-Verlag: Wurzburg, Germany, 1993; pp. 62–70. [Google Scholar]
- Vieira, D.; Orjuela, R.; Spisser, M.; Basset, M. An adapted Burckhardt tire model for off-road vehicle applications. J. Terramech. 2022, 104, 15–24. [Google Scholar] [CrossRef]
- Crocetti, F.; Costante, G.; Fravolini, M.L.; Valigi, P. Tire-road friction estimation and uncertainty assessment to improve electric aircraft braking system. In Proceedings of the 29th Mediterranean Conference on Control and Automation, Puglia, Italy, 22–25 June 2021; pp. 330–335. [Google Scholar] [CrossRef]
- Guo, L.; Ge, P.S.; Sun, D.C. Torque distribution algorithm for stability control of electric vehicle driven by four in-wheel motors under emergency conditions. IEEE Access 2019, 7, 104737–104748. [Google Scholar] [CrossRef]
- Kamidi, V.R.; Kim, J.; Fawcett, R.T.; Ames, A.D.; Hamed, K.A. Distributed quadratic programming-based nonlinear controllers for periodic gaits on legged robots. IEEE Control Syst. Lett. 2022, 6, 2509–2514. [Google Scholar] [CrossRef]
- Hu, L.; Tian, Q.; Zou, C.; Huang, J.; Ye, Y.; Wu, X. A study on energy distribution strategy of electric vehicle hybrid energy storage system considering driving style based on real urban driving data. Renew. Sustain. Energy Rev. 2022, 162, 112416. [Google Scholar] [CrossRef]



| Parameter | Value |
|---|---|
| Capacity | 5.00 Ah |
| Rated working voltage | 3.60 V |
| Maximum voltage limit | 3.65 V |
| Minimum voltage limit | 2.50 V |
| Parameter | Symbol | Value |
|---|---|---|
| Mass | m | 1416 kg |
| Moment of inertia about Z axis | IZ | 1523 kg·m2 |
| Distance from front axis to the center of gravity | a | 1.016 m |
| Distance from rear axis to the center of gravity | b | 1.562 m |
| Wheelbase | L | 2.578 m |
| Tire radius | R | 0.357 m |
| Front tire cornering stiffness | kf | −65,520 N/rad |
| Rear tire cornering stiffness | kr | −57,200 N/rad |
| Type | Peak Adhesion Coefficient |
|---|---|
| Ice | 0.05 |
| Snow | 0.19 |
| Wet pebble | 0.34 |
| Road 1 | 0.50 |
| Road 2 | 0.65 |
| Wet asphalt | 0.80 |
| Dry cement | 1.09 |
| Road 3 | 1.25 |
| Slip Rate | Adhesion Coefficient | RS1 | RS2 | RS3 | RS4 | RS5 | RS6 | RS7 | RS8 |
|---|---|---|---|---|---|---|---|---|---|
| S | RS1 | SV | SG | SD | SD | SD | SD | SD | SD |
| RS2 | SM | SV | SD | SD | SD | SD | SD | SD | |
| RS3 | SG | SS | SV | SM | SG | SD | SD | SD | |
| RS4 | SD | SD | SM | SV | SM | SG | SD | SD | |
| RS5 | SD | SD | SD | SM | SV | SS | SD | SD | |
| RS6 | SD | SD | SG | SM | SS | SV | SS | SM | |
| RS7 | SD | SD | SD | SD | SD | SS | SV | SM | |
| RS8 | SD | SD | SD | SD | SD | SM | SS | SV | |
| B | RS1 | SV | SG | SD | SD | SD | SD | SD | SD |
| RS2 | SM | SV | SG | SD | SD | SD | SD | SD | |
| RS3 | SG | SS | SV | SS | SG | SD | SD | SD | |
| RS4 | SD | SD | SM | SV | SS | SD | SD | SD | |
| RS5 | SD | SD | SD | SM | SV | SS | SM | SS | |
| RS6 | SD | SD | SG | SM | SS | SV | SS | SM | |
| RS7 | SD | SD | SD | SD | SD | SS | SV | SM | |
| RS8 | SD | SD | SD | SD | SD | SM | SM | SV |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ge, P.; Guo, L.; Feng, J.; Zhou, X. Adaptive Stability Control Based on Sliding Model Control for BEVs Driven by In-Wheel Motors. Sustainability 2023, 15, 8660. https://doi.org/10.3390/su15118660
Ge P, Guo L, Feng J, Zhou X. Adaptive Stability Control Based on Sliding Model Control for BEVs Driven by In-Wheel Motors. Sustainability. 2023; 15(11):8660. https://doi.org/10.3390/su15118660
Chicago/Turabian StyleGe, Pingshu, Lie Guo, Jindun Feng, and Xiaoyue Zhou. 2023. "Adaptive Stability Control Based on Sliding Model Control for BEVs Driven by In-Wheel Motors" Sustainability 15, no. 11: 8660. https://doi.org/10.3390/su15118660
APA StyleGe, P., Guo, L., Feng, J., & Zhou, X. (2023). Adaptive Stability Control Based on Sliding Model Control for BEVs Driven by In-Wheel Motors. Sustainability, 15(11), 8660. https://doi.org/10.3390/su15118660








