Predictive Churn Modeling for Sustainable Business in the Telecommunication Industry: Optimized Weighted Ensemble Machine Learning
Abstract
1. Introduction
2. Related Work
3. System Design
4. System Implementation
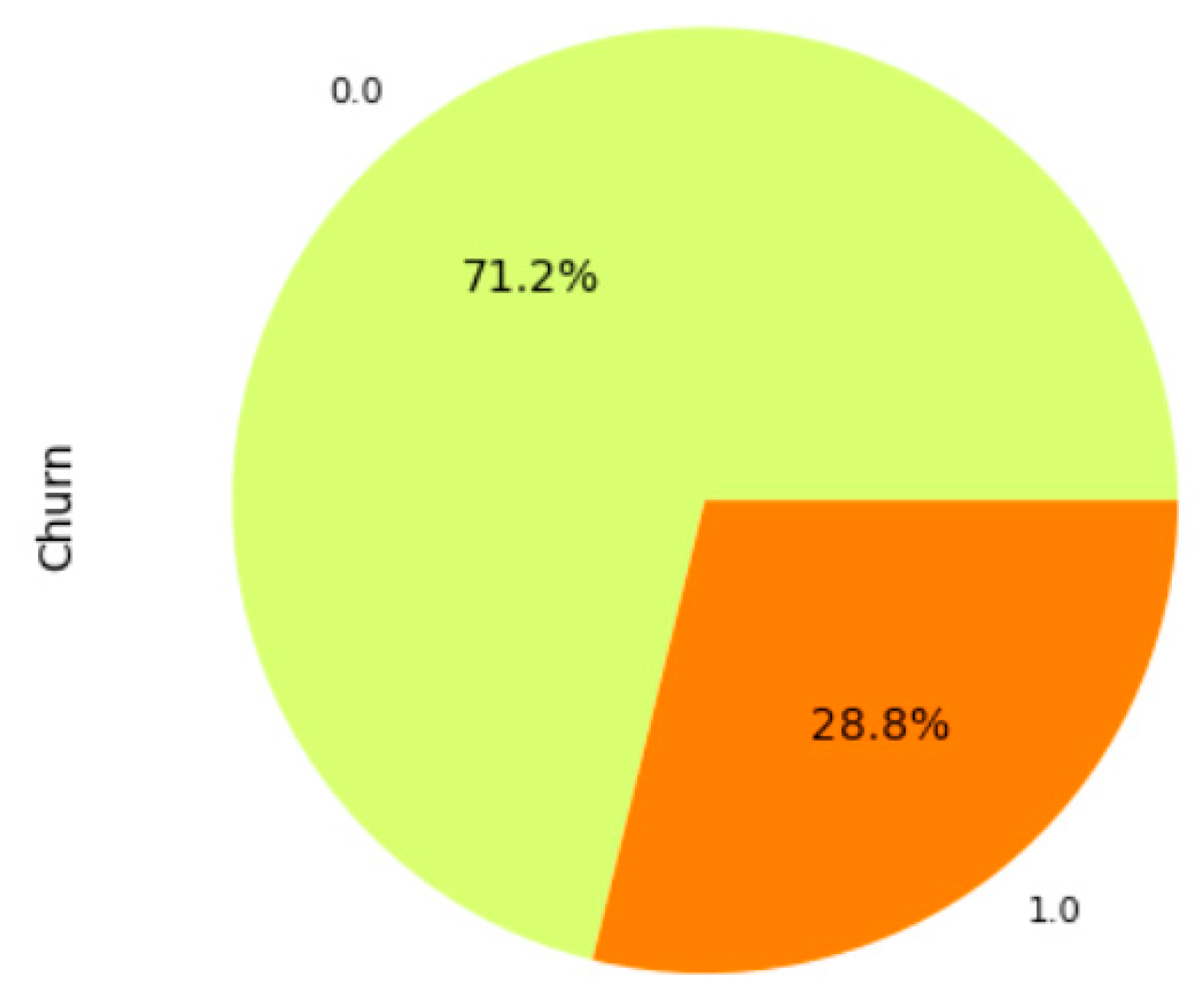
4.1. Dataset
- Customer demographics and personal data;
- Customer care service data;
- Customer credit scores;
- Billing and payment data;
- Customer usage patterns;
- Value-adding services.
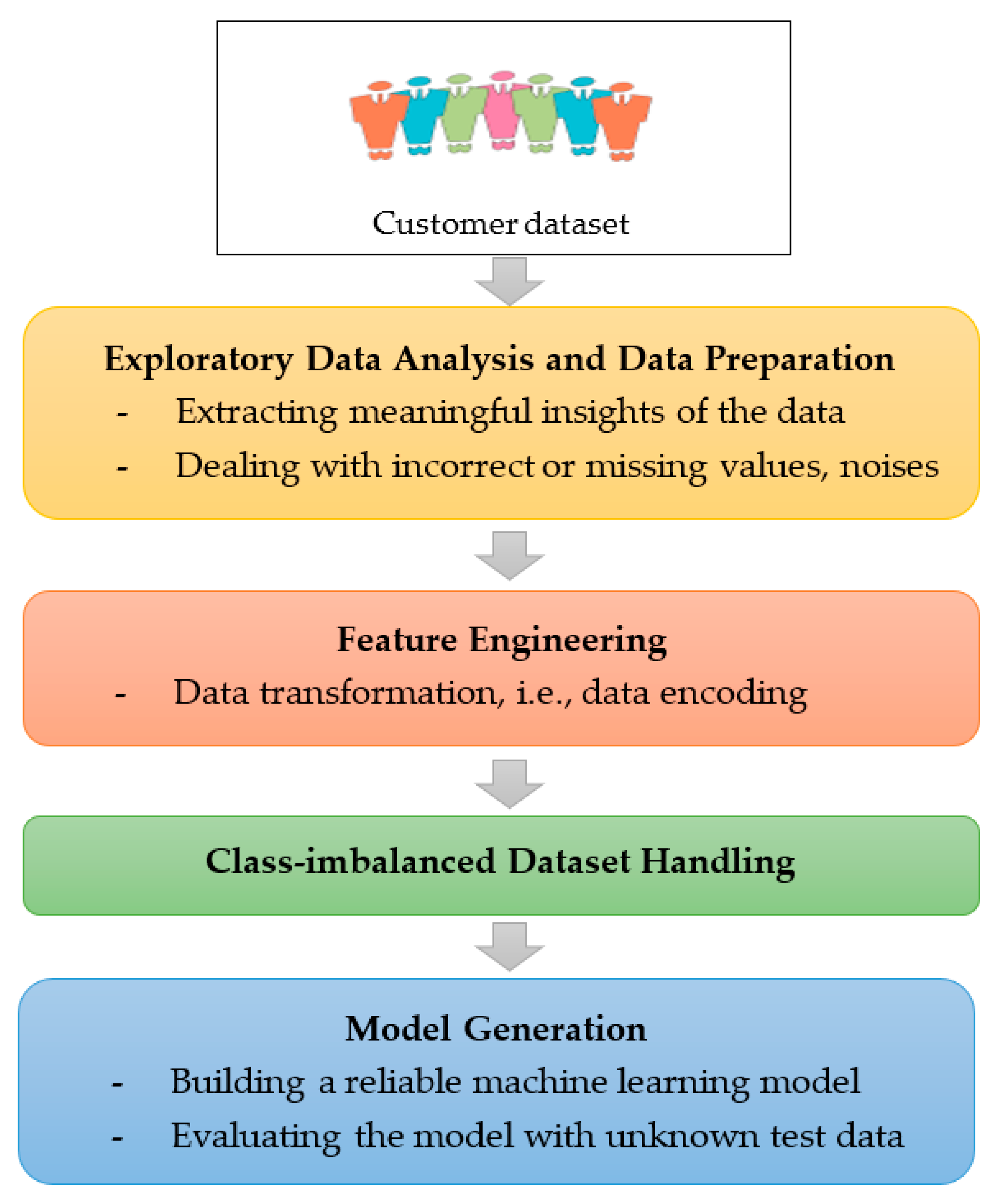
4.2. Exploratory Data Analysis and Data Preprocessing
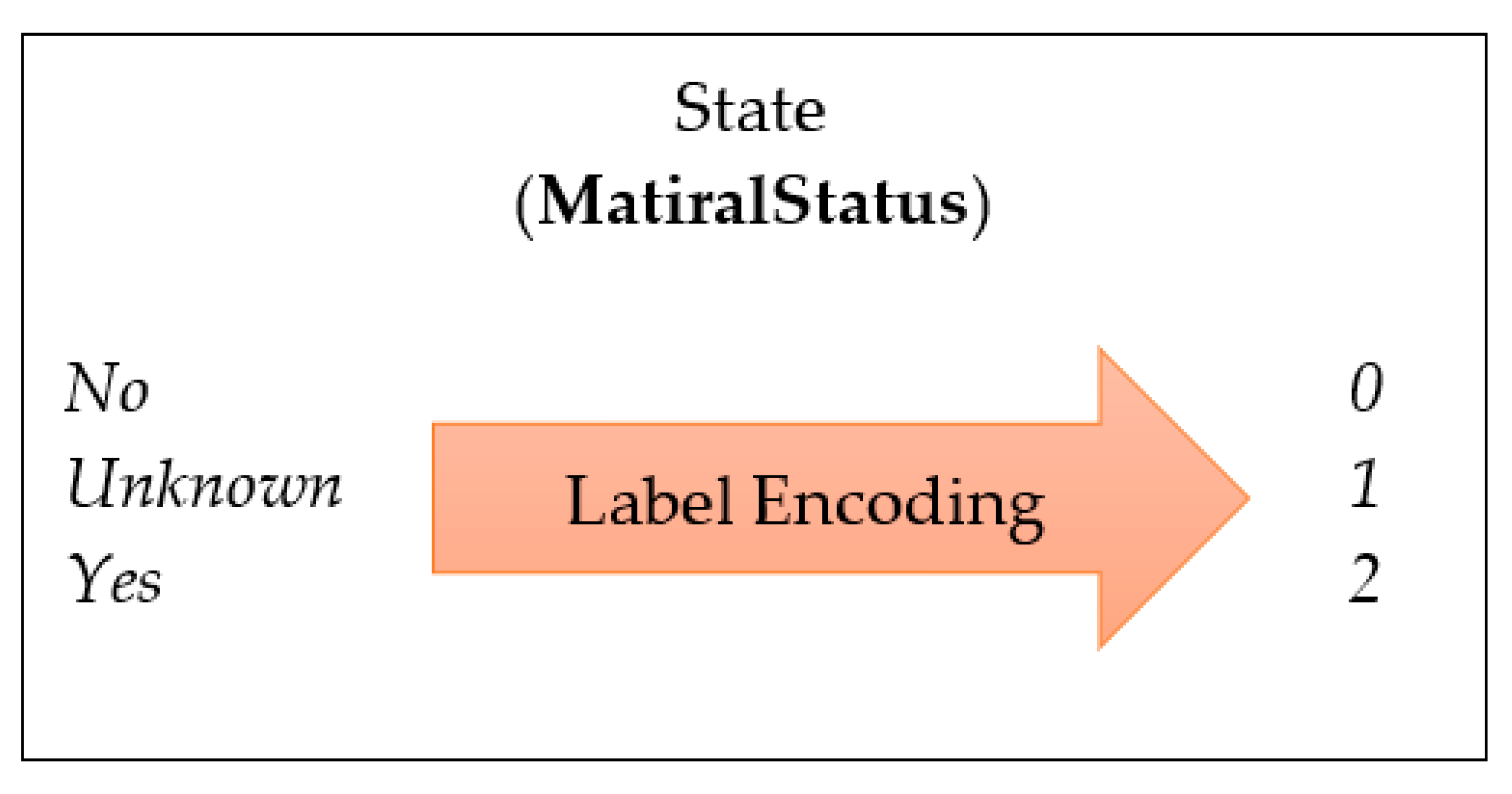
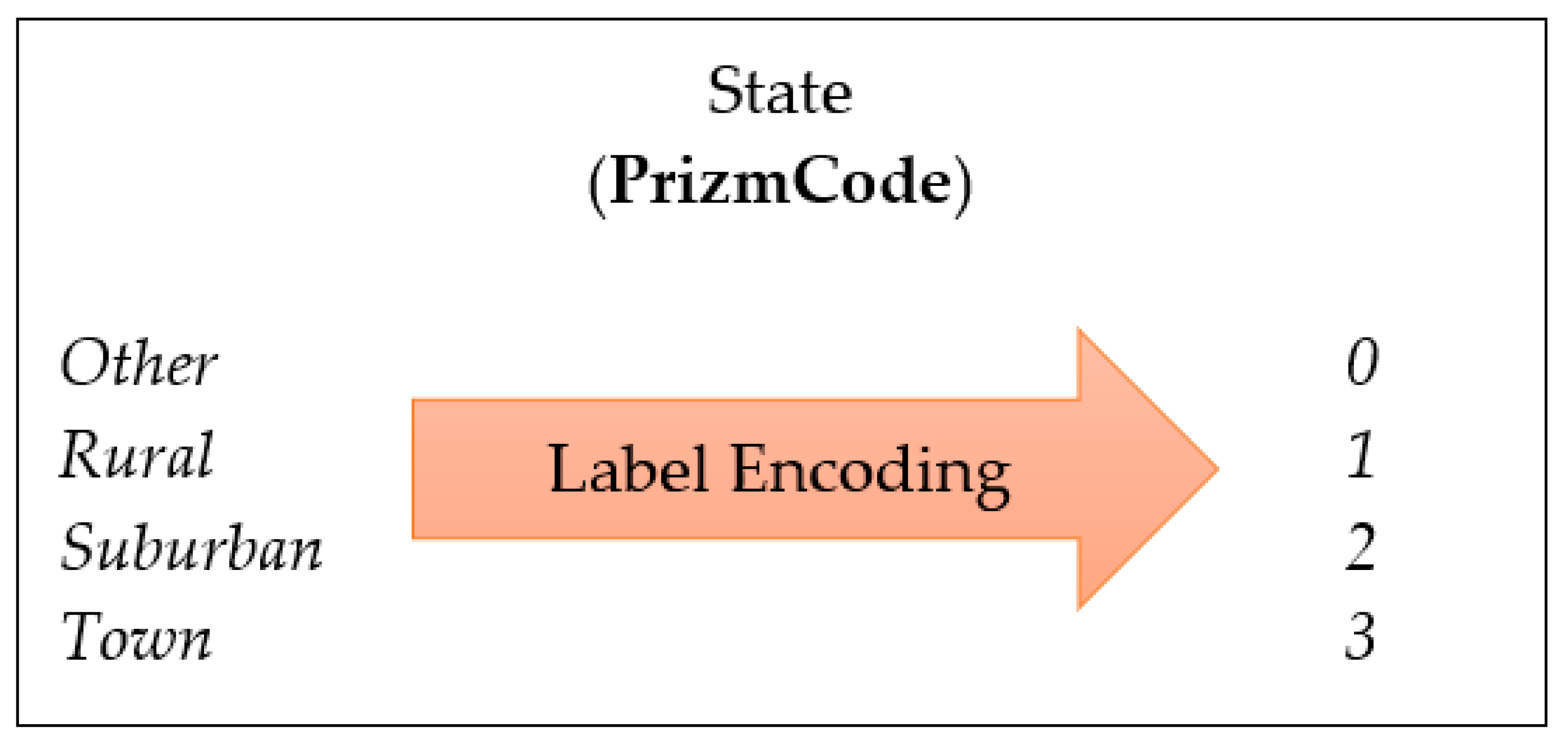
4.3. Feature Engineering
4.4. Class-Imbalanced Dataset Handling
- Do nothing (dealing with the original imbalanced dataset);
- Classification with the undersampling technique (deleting observations from the majority class to balance the data);
- Classification with the oversampling method (creating synthetic samples of the minority class by employing the synthetic minority over-sampling technique (SMOTE).
4.5. Model Generation: Optimally Weighted Ensemble Learner
4.5.1. K-Nearest Neighbors (KNN)
4.5.2. CatBoost
- -
- Optimal split selection: The algorithm in CatBoost is designed to choose the best-split point for each node in a decision tree by minimizing the loss function concerning the split ends. This is accomplished by constructing a function that approximates the loss function as a function of the split point. Then, a Newton–Raphson solver is applied to seek the minimum of the procedure. This optimal split selection algorithm allows faster convergence during training and improved accuracy.
- -
- Reduced overfitting feature: Overfitting is a common issue in gradient boosting, especially when the dataset is small or noisy. CatBoost incorporates several features for preventing overfitting. One of them is ordered boosting, a novel gradient-based regularization technique that penalizes complex models that overfit the data. Furthermore, using a per-iteration learning rate enables the model to adapt to the problem’s complexity at each iteration, preventing overfitting.
4.5.3. Random Forest
| Algorithm 1: The algorithm of random forest |
| Let be a training dataset,
Let , an ensemble of weak classifiers Each is a decision tree and the parameters of the tree are defined as Each decision tree i leads to a classifier (X|) Final Prediction = high voted predicted target based on b |
4.5.4. Weighted Soft Voting Ensemble Learner with Optimized Ensemble Weights Using Powell’s Optimization Algorithm
| Algorithm 2: Powell’s optimization algorithm |
| Initialize the starting point , independent vectors , the tolerance for stopping criteria , set while (stopping criterion is not met, i.e. ) do for i = 1 to D do if ( >= 2) then endif , is determined by minimizing endfor , , = k+1, , endwhile |
5. Experimental Results and Discussion
5.1. Experimental Setup and Performance Metrics
5.2. Results and Discussion
5.2.1. Performance Analysis of the Base Classifiers



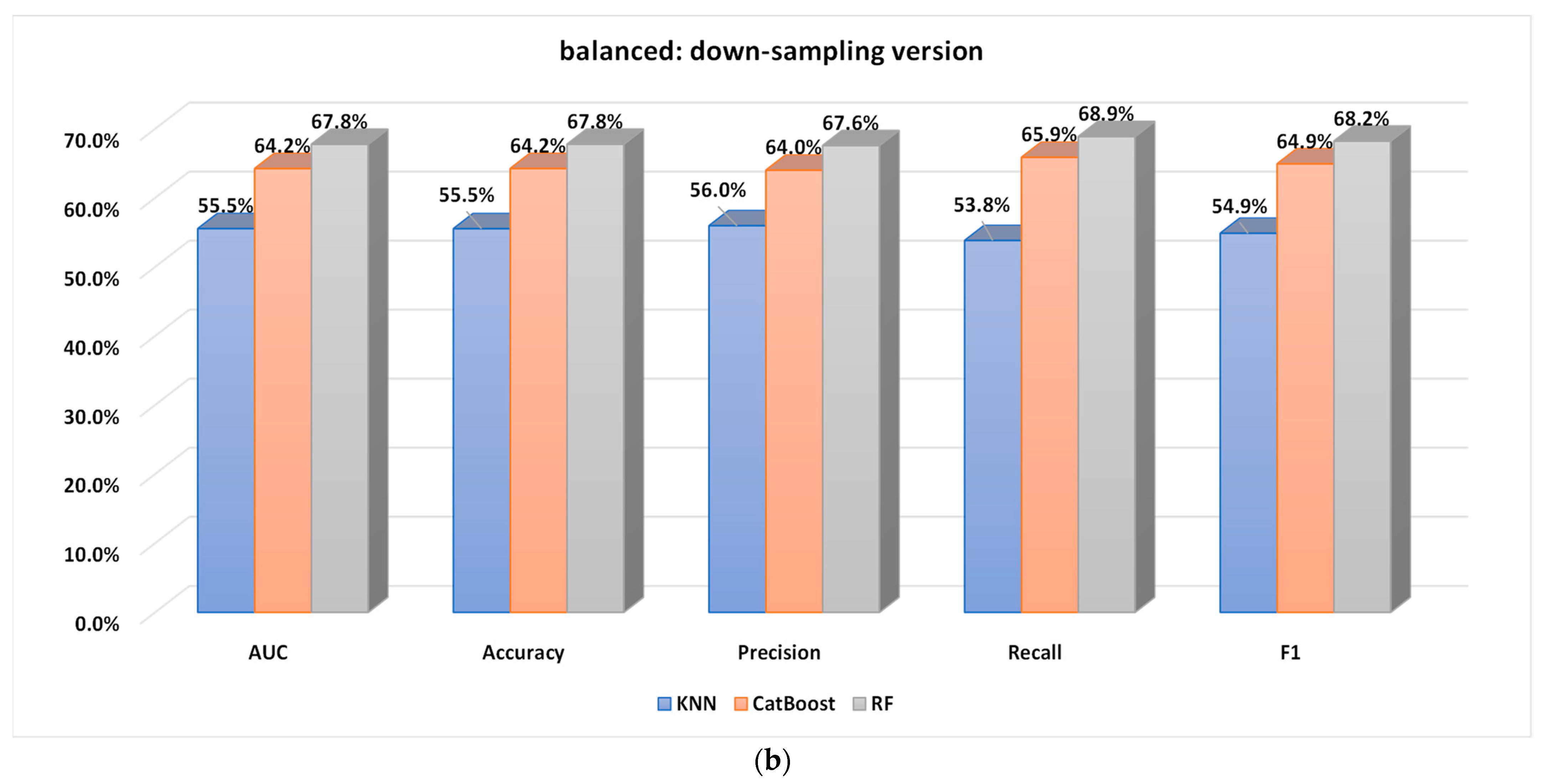
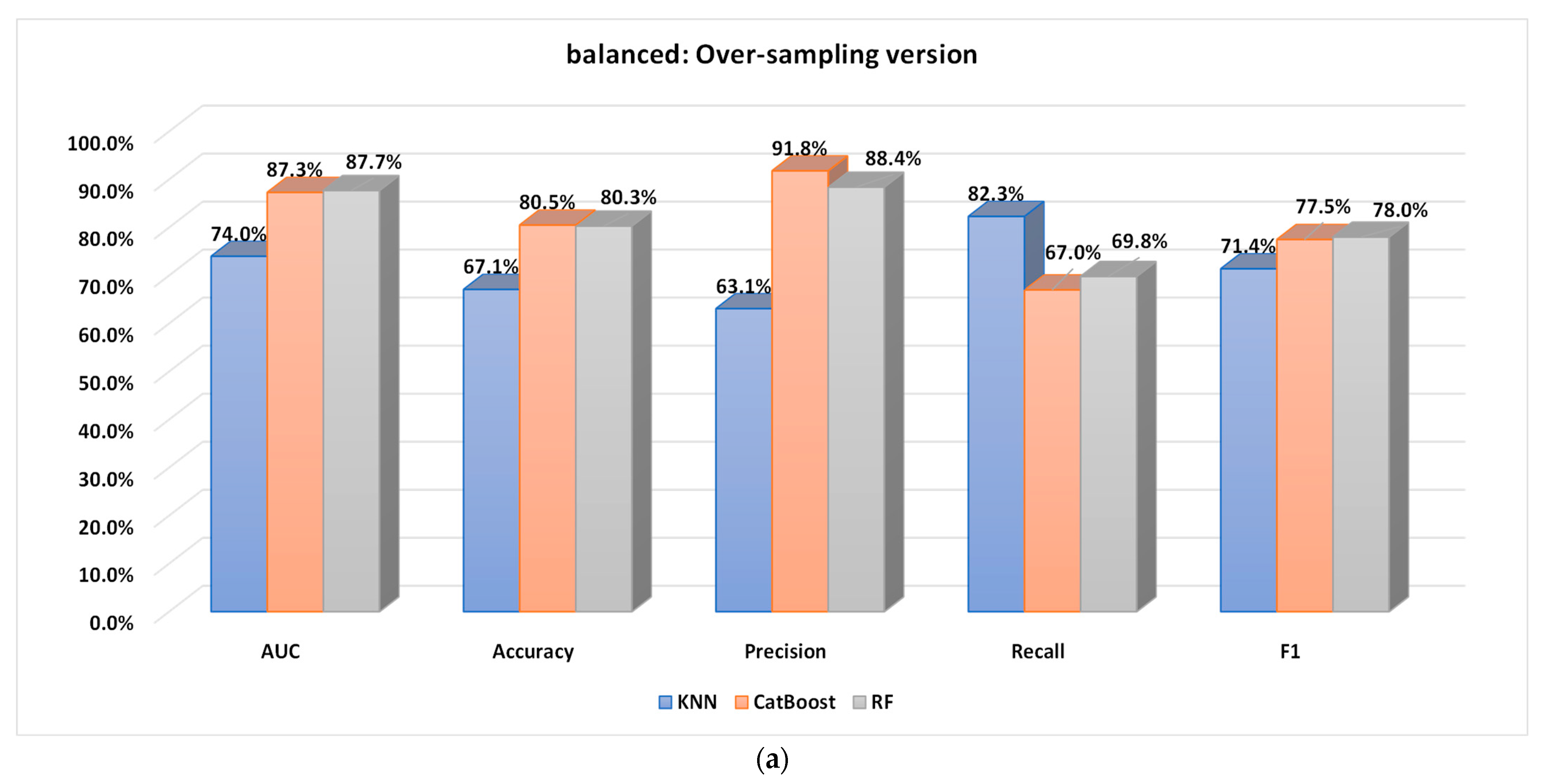
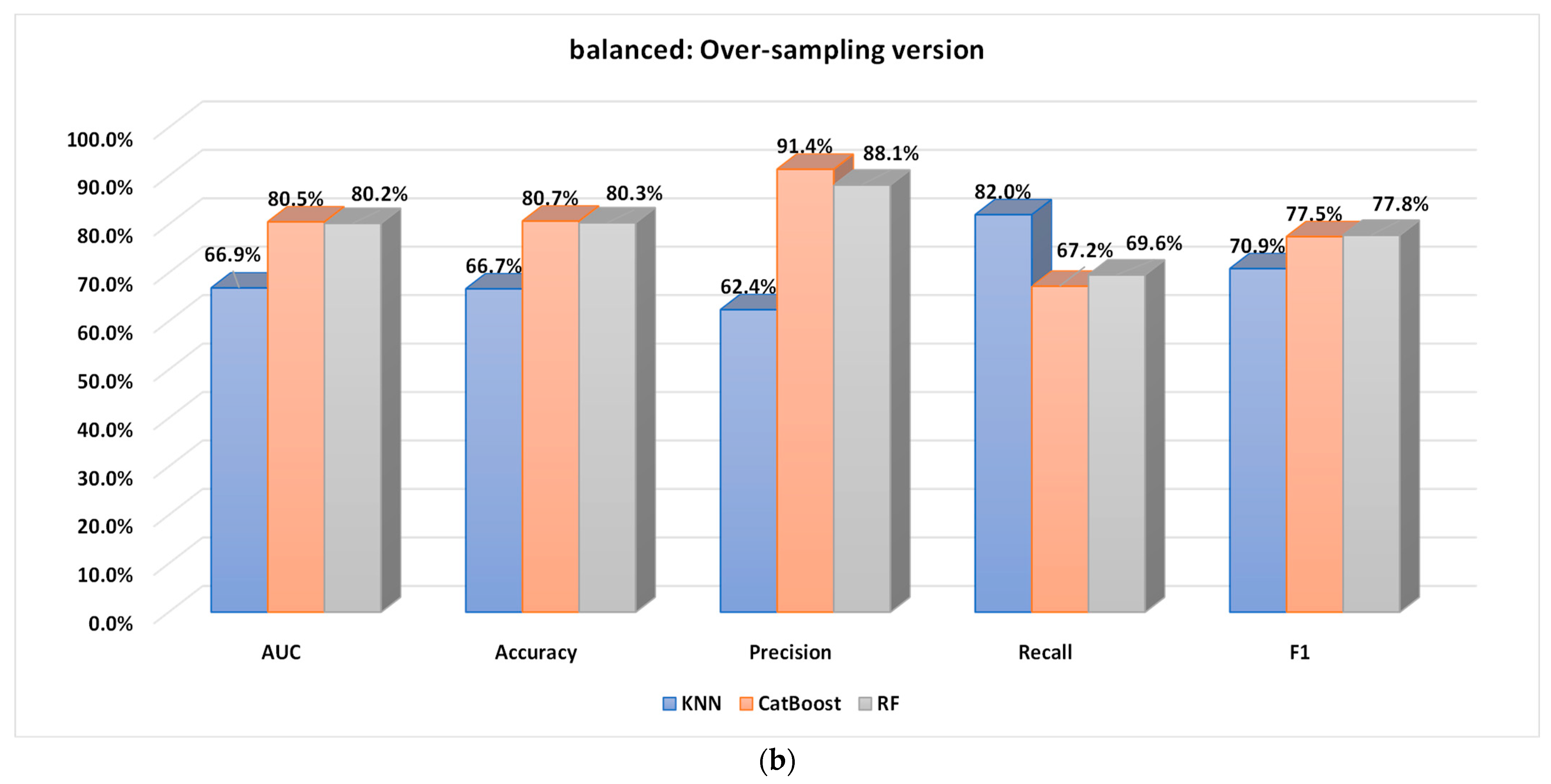
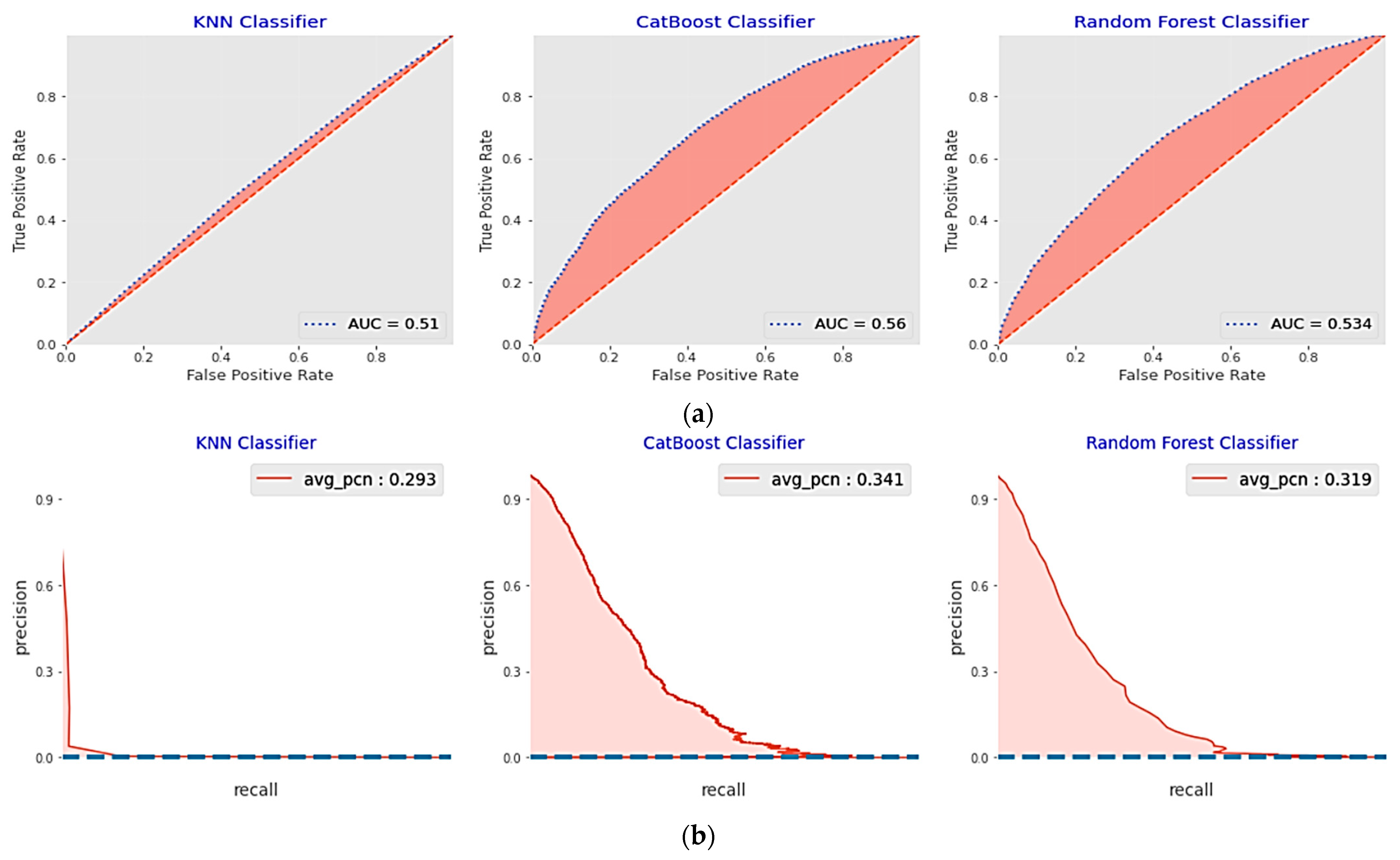


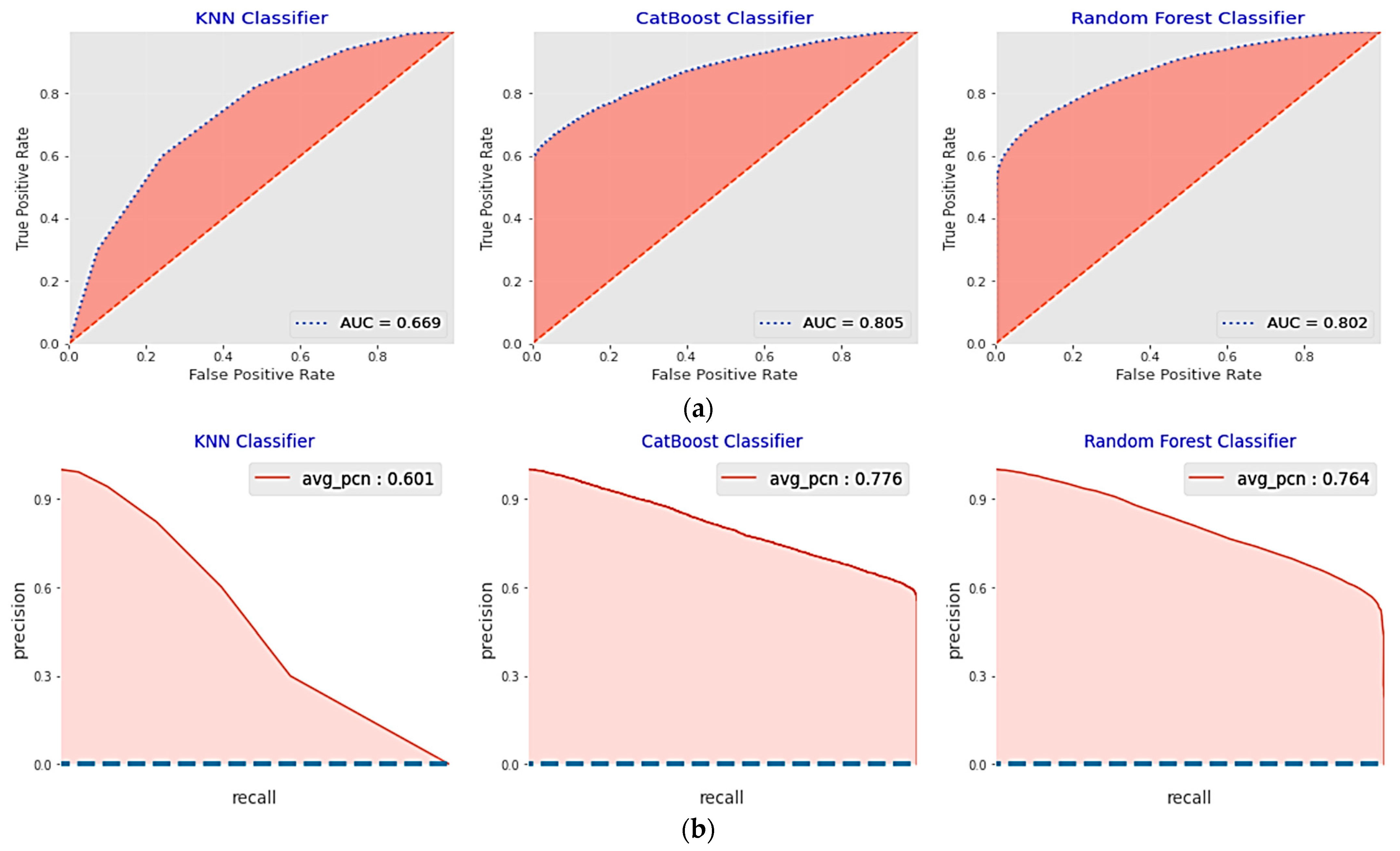
5.2.2. Performance of the Proposed Optimized Weighted Ensemble Learner and Comparison with the Other Ensemble Learning Methods
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Matuszelański, K.; Kopczewska, K. Customer Churn in Retail E-Commerce Business: Spatial and Machine Learning Approach. J. Theor. Appl. Electron. Commer. Res. 2022, 17, 9. [Google Scholar] [CrossRef]
- Ullah, I.; Raza, B.; Malik, A.K.; Imran, M.; Islam, S.U.; Kim, S.W. A Churn Prediction Model Using Random Forest: Analysis of Machine Learning Techniques for Churn Prediction and Factor Identification in Telecom Sector. IEEE Access 2019, 7, 60134–60149. [Google Scholar] [CrossRef]
- Verbeke, W.; Martens, D.; Mues, C.; Baesens, B. Building comprehensible customer churn prediction models with advanced rule induction techniques. Expert Syst. Appl. 2011, 38, 2354–2364. [Google Scholar] [CrossRef]
- Jessica Tracking Churn To Measure Customer Loyalty and Satisfaction in the Telecommunications Industry | Open World Learning. Available online: https://www.openworldlearning.org/tracking-churn-to-measure-customer-loyalty-and-satisfaction-in-the-telecommunications-industry/ (accessed on 2 February 2023).
- Sharma, A.; Shukla, P.; Gourisaria, M.K.; Sharma, B.; Dhaou, I.B. Telecom Churn Analysis using Machine Learning in Smart Cities. In Proceedings of the 2023 1st International Conference on Advanced Innovations in Smart Cities (ICAISC), Jeddah, Saudi Arabia, 23–25 January 2023; pp. 1–5. [Google Scholar] [CrossRef]
- Sharma, A.; Gupta, D.; Nayak, N.; Singh, D.; Verma, A. Prediction of Customer Retention Rate Employing Machine Learning Techniques. In Proceedings of the 2022 1st International Conference on Informatics, Noida, India, 14–16 April 2022; Institute of Electrical and Electronics Engineers Inc.: Piscataway, NJ, USA, 2022; pp. 103–107. [Google Scholar]
- Huang, B.; Kechadi, M.T.; Buckley, B. Customer churn prediction in telecommunications. Expert Syst. Appl. 2012, 39, 1414–1425. [Google Scholar] [CrossRef]
- Kimura, T. Customer churn prediction with hybrid resampling and ensemble learning. J. Manag. Inf. Decis. Sci. 2022, 25, 1–23. [Google Scholar]
- Kim, S.; Lee, H. Customer Churn Prediction in Influencer Commerce: An Application of Decision Trees. Procedia Comput. Sci. 2022, 199, 1332–1339. [Google Scholar] [CrossRef]
- ÜNLÜ, K.D. Predicting credit card customer churn using support vector machine based on Bayesian optimization. Commun. Fac. Sci. Univ. Ankara Ser. A1 Math. Stat. 2021, 70, 827–836. [Google Scholar] [CrossRef]
- Thorat, A.S.; Sonawane, V.R. Customer Churn Prediction in the Telecom Industry Using Machine Learning Algorithms. Comput. Integr. Manuf. Syst. 2023, 29, 1–11. [Google Scholar]
- Bose, A.; Thomas, K.T. A Comparative Study of Machine Learning Techniques for Credit Card Customer Churn Prediction. In Lecture Notes on Data Engineering and Communications Technologies; Springer Science and Business Media Deutschland GmbH: Berlin/Heidelberg, Germany, 2023; Volume 141, pp. 295–307. [Google Scholar]
- Coussement, K.; De Bock, K.W. Customer churn prediction in the online gambling industry: The beneficial effect of ensemble learning. J. Bus. Res. 2013, 66, 1629–1636. [Google Scholar] [CrossRef]
- Jain, H.; Khunteta, A.; Srivastava, S. Churn Prediction in Telecommunication using Logistic Regression and Logit Boost. Procedia Comput. Sci. 2020, 167, 101–112. [Google Scholar] [CrossRef]
- Lalwani, P.; Mishra, M.K.; Chadha, J.S.; Sethi, P. Customer churn prediction system: A machine learning approach. Computing 2022, 104, 271–294. [Google Scholar] [CrossRef]
- Elgohary, E.M.; Galal, M.; Mosa, A.; Elshabrawy, G.A. Smart evaluation for deep learning model: Churn prediction as a product case study. Bull. Electr. Eng. Inform. 2023, 12, 1219–1225. [Google Scholar] [CrossRef]
- Xu, S.; Tang, Q.; Jin, L.; Pan, Z. A cascade ensemble learning model for human activity recognition with smartphones. Sensors 2019, 19, 2307. [Google Scholar] [CrossRef]
- Tariq, M.U.; Babar, M.; Poulin, M.; Khattak, A.S. Distributed model for customer churn prediction using convolutional neural network. J. Model. Manag. 2022, 17, 853–863. [Google Scholar] [CrossRef]
- Gabhane, M.D.; Suriya, A.; Kishor, S.B. Churn Prediction in Telecommunication Business using CNN and ANN. J. Posit. Sch. Psychol. 2022, 2022, 4672–4680. [Google Scholar]
- Sudharsan, R.; Ganesh, E.N. A Swish RNN based customer churn prediction for the telecom industry with a novel feature selection strategy. Connect. Sci. 2022, 34, 1855–1876. [Google Scholar] [CrossRef]
- Mishra, A.; Reddy, U.S. A Novel Approach for Churn Prediction Using Deep Learning. In Proceedings of the 2017 IEEE International Conference on Computational Intelligence and Computing Research (ICCIC), Coimbatore, India, 14–16 December 2017. [Google Scholar] [CrossRef]
- Umayaparvathi, V.; Iyakutti, K. Automated Feature Selection and Churn Prediction using Deep Learning Models. Int. Res. J. Eng. Technol. (IRJET) 2017, 4, 1846–1854. [Google Scholar]
- Ahmed, U.; Khan, A.; Khan, S.H.; Basit, A.; Haq, I.U.; Lee, Y.S. Transfer Learning and Meta Classification Based Deep Churn Prediction System for Telecom Industry. arXiv 2019, arXiv:1901.06091. [Google Scholar] [CrossRef]
- Wael Fujo, S.; Subramanian, S.; Ahmad Khder, M.; Fujo, W.; Khder, A. Customer Churn Prediction in Telecommunication Industry Using Deep Learning. Inf. Sci. Lett. 2022, 11, 185–198. [Google Scholar] [CrossRef]
- Dorogush, A.V.; Ershov, V.; Yandex, A.G. CatBoost: Gradient Boosting with Categorical Features Support. arXiv 2018, arXiv:1810.11363. [Google Scholar]
- Zhu, M.; Liu, J. Telecom Customer Churn Prediction Based on Classification Algorithm. In Proceedings of the 2021 International Conference on Aviation Safety and Information Technology, Changsha China, 18–20 December 2021; ACM: New York, NY, USA, 2021; pp. 268–273. [Google Scholar]
- Sagala, N.T.M.; Permai, S.D. Enhanced Churn Prediction Model with Boosted Trees Algorithms in the Banking Sector. In Proceedings of the 2021 International Conference on Data Science and Its Applications, ICoDSA 2021, Bandung, Indonesia, 6–7 October 2021; Institute of Electrical and Electronics Engineers Inc.: Piscataway, NJ, USA, 2021; pp. 240–245. [Google Scholar]
- Ibrahim, A.A.; Ridwan, R.L.; Muhammed, M.M.; Abdulaziz, R.O.; Saheed, G.A. Comparison of the CatBoost Classifier with other Machine Learning Methods. Int. J. Adv. Comput. Sci. Appl. 2020, 11, 738–748. [Google Scholar] [CrossRef]
- Friedman, J.H. Greedy Function Approximation: A Gradient Boosting Machine. Ann. Statistics. 2001, 29, 1189–1232. [Google Scholar] [CrossRef]
- Prokhorenkova, L.; Gusev, G.; Vorobev, A.; Dorogush, A.V.; Gulin, A. CatBoost: Unbiased boosting with categorical features. In Proceedings of the 32nd Conference on Neural Information Processing Systems (NeurIPS 2018): Advances in neural Information Processing Systems, Montréal, QC, Canada, 2–6 December 2018; pp. 6638–6648. [Google Scholar]
- Zhou, Z.H. Ensemble Methods: Foundations and Algorithms; Chapman and Hall/CRC: Boca Raton, FL, USA, 2012. [Google Scholar]
- Taha, A. Intelligent Ensemble Learning Approach for Phishing Website Detection Based on Weighted Soft Voting. Mathematics 2021, 9, 2799. [Google Scholar] [CrossRef]
- Mathews, J.H. Module for Powell Search Method for a Minimum; Fullerton Retrieved 16 June 2017; California State University: Northridge, CA, USA, 2017. [Google Scholar]
- Zhang, S.; Zhou, Y. Grey Wolf Optimizer Based on Powell Local Optimization Method for Clustering Analysis. Discret. Dyn. Nat. Soc. 2015, 2015, 4813360. [Google Scholar] [CrossRef]
- Gu, Q.; Zhu, L.; Cai, Z. Evaluation measures of the classification performance of imbalanced data sets. In ISICA 2009: Computational Intelligence and Intelligent Systems; Springer: Berlin/Heidelberg, Germany, 2009; Volume 51, pp. 461–471. [Google Scholar]
- Goel, G.; Maguire, L.; Li, Y.; McLoone, S. Evaluation of sampling methods for learning from imbalanced data. In ICIC 2013: Intelligent Computing Theories; Lecture Notes in Computer Science Book Series; Springer: Berlin/Heidelberg, Germany, 2013; pp. 392–401. [Google Scholar] [CrossRef]
- Branco, P.; Torgo, L.; Ribeiro, R.P. A Survey of Predictive Modelling under Imbalanced Distributions. arXiv 2015, arXiv:1505.01658. [Google Scholar]

| Numerical Feature | Data Format | Categorical Feature | Data Format |
|---|---|---|---|
| CustomerID | Int | Churn | (Yes/No) |
| MonthlyRevenue | float | ServiceArea | string |
| MonthlyMinutes | float | ChildrenInHH | (Yes/No) |
| TotalRecurringCharge | float | HandsetRefurbished | (Yes/No) |
| DirectorAssistedCalls | float | HandsetWebCapable | (Yes/No) |
| OverageMinutes | float | TruckOwner | (Yes/No) |
| RoamingCalls | float | RVOwner | (Yes/No) |
| PercChangeMinutes | float | Homeownership | (Known/Unknown) |
| PercChangeRevenues | float | BuysViaMailOrder | (Yes/No) |
| DroppedCalls | float | RespondsToMailOffers | (Yes/No) |
| BlockedCalls | float | OptOutMailings | (Yes/No) |
| UnansweredCalls | float | NonUSTravel | (Yes/No) |
| CustomerCareCalls | float | OwnsComputer | (Yes/No) |
| ThreewayCalls | float | HasCreditCard | (Yes/No) |
| ReceivedCalls | float | NewCellphoneUser | (Yes/No) |
| OutboundCalls | float | NotNewCellphoneUser | (Yes/No) |
| InboundCalls | float | OwnsMotorcycle | (Yes/No) |
| PeakCallsInOut | float | HandsetPrice | string |
| OffPeakCallsInOut | float | MadeCallToRetentionTeam | (Yes/No) |
| DroppedBlockedCalls | float | CreditRating | string |
| CallForwardingCalls | float | PrizmCode | (Other/Suburban/ Town/Rural) |
| CallWaitingCalls | float | Occupation | (Other/Professional/ Crafts/Clerical/Self/ Retired/Student/ Homemaker) |
| MonthsInService | int | MaritalStatus | (Unknown/Yes/No) |
| UniqueSubs | int | ||
| ActiveSubs | int | ||
| Handsets | float | ||
| HandsetModels | float | ||
| CurrentEquipmentDays | float | ||
| AgeHH1 | float | ||
| AgeHH2 | float | ||
| RetentionCalls | int | ||
| RetentionOffersAccepted | int | ||
| ReferralsMadeBySubscriber | int | ||
| IncomeGroup | int | ||
| AdjustmentsToCreditRating | int |
| Feature Variable | Number of Missing Values |
|---|---|
| MonthlyRevenue | 156 |
| MonthlyMinutes | 156 |
| TotalRecurringCharge | 156 |
| DirectorAssistedCalls | 156 |
| OverageMinutes | 156 |
| RoamingCalls | 156 |
| PercChangeMinutes | 367 |
| PercChangeRevenues | 367 |
| ServiceArea | 24 |
| Handsets | 1 |
| HandsetModels | 1 |
| CurrentEquipmentDays | 1 |
| AgeHH1 | 909 |
| AgeHH2 | 909 |
| Classifier | Accuracy | Precision | Recall | F1 Score |
|---|---|---|---|---|
| Majority/hard voting | 0.81975 | 0.89528 | 0.71922 | 0.79765 |
| Soft voting (uniform weight) | 0.80826 | 0.81691 | 0.78858 | 0.80250 |
| Stacking classifier with meta learner = logistic regression | 0.83674 | 0.86290 | 0.79596 | 0.82808 |
| Weighted soft voting by Nelder–Mead | 0.82876 | 0.91772 | 0.71769 | 0.80547 |
| Large feedforward neural network * [22] | 0.7166 | - | - | - |
| Convolutional neural network * [22] | 0.7166 | - | - | - |
| TL-DeepE * [23] | 0.682 | - | - | - |
| Deep-BP-ANN * [24] | 0.7938 | 0.7450 | 0.8932 | 0.8124 |
| The proposed weighted ensemble learner with Powell’s optimization | 0.84114 | 0.86108 | 0.80891 | 0.83418 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Khoh, W.H.; Pang, Y.H.; Ooi, S.Y.; Wang, L.-Y.-K.; Poh, Q.W. Predictive Churn Modeling for Sustainable Business in the Telecommunication Industry: Optimized Weighted Ensemble Machine Learning. Sustainability 2023, 15, 8631. https://doi.org/10.3390/su15118631
Khoh WH, Pang YH, Ooi SY, Wang L-Y-K, Poh QW. Predictive Churn Modeling for Sustainable Business in the Telecommunication Industry: Optimized Weighted Ensemble Machine Learning. Sustainability. 2023; 15(11):8631. https://doi.org/10.3390/su15118631
Chicago/Turabian StyleKhoh, Wee How, Ying Han Pang, Shih Yin Ooi, Lillian-Yee-Kiaw Wang, and Quan Wei Poh. 2023. "Predictive Churn Modeling for Sustainable Business in the Telecommunication Industry: Optimized Weighted Ensemble Machine Learning" Sustainability 15, no. 11: 8631. https://doi.org/10.3390/su15118631
APA StyleKhoh, W. H., Pang, Y. H., Ooi, S. Y., Wang, L.-Y.-K., & Poh, Q. W. (2023). Predictive Churn Modeling for Sustainable Business in the Telecommunication Industry: Optimized Weighted Ensemble Machine Learning. Sustainability, 15(11), 8631. https://doi.org/10.3390/su15118631








