Abstract
Along with global climate change and industrialization, domino effects caused by Natech events occurred frequently in chemical industrial parks over the past decades. Previous research has not yet proposed a reliable method to obtain all possible paths of Natech domino effects, and moreover, a risk assessment and mitigation system has not been established. The present work aims to develop a quantitative framework for propagation paths of Natech domino effects, which can effectively safeguard the sustainable development of chemical industrial parks. The presentation of this work is divided into two parts: Part I (current paper) proposes a path probability calculation method that can simultaneously consider multiple primary accident scenarios and multi-level domino effects triggered by natural disasters. The proposed method transforms the propagation paths of domino effects into the paths of directed graph by constructing the equipment failure state transition matrix and the equipment failure state transition probability matrix. The depth-first traversal algorithm is used to obtain all possible propagation paths and their propagation probabilities, providing data support for the quantitative risk assessment and prevention and control measures presented in the accompanying paper (Part II). The case study shows that the probability of equipment failure caused by multi-level domino effects triggered by Natech accidents is higher than that of conventional accidents. However, the present work only considers the spatial propagation of domino effects, while their spatio-temporal propagation remains as a further direction for this area of inquiry.
1. Introduction
Chemical industrial parks usually have a large number of flammable and explosive hazardous substances, and large chemical installations are densely distributed in these locations [1,2]. Once a major accident occurs, it is likely to destroy adjacent plants or enterprises, leading to the occurrence of domino effects [3], which may have a serious negative impact on the sustainable development of chemical industrial parks [4]. Due to worldwide climate change and industrialization, technological accidents triggered by natural events have occurred frequently in recent years, which are commonly called Natech events (an abbreviation for natural disaster-induced technological accidents) [5,6,7,8]. Natural disasters can lead to the simultaneous destruction of multiple dangerous installations in chemical industrial parks, damage or destroy safety barriers, and block the lifelines required for emergency rescue [9,10,11]. A series of major accidents show that once a Natech event occurs, it will lead to more serious consequences than conventional accidents and is more likely to result in domino effects. For example, the 2011 Great East Japan earthquake caused serious damage to oil and gas storage tanks and other hazardous chemical facilities in some chemical industrial parks [12]. According to the investigation of the Fire and Disaster Management Agency (FDMA), a total of 3324 hazardous chemical facilities were damaged, and 42 fire accidents and 122 leakage accidents happened after the earthquake [13].
In recent decades, the increasing risk of domino effects and Natech events have attracted extensive attention from scholars, and the academic community has carried out a series of studies on domino effects and Natech events. In the field of domino effects, the current research mainly focuses on the following four aspects: statistical analysis of historical accidents [14,15,16], equipment vulnerability assessment model [17,18,19,20], risk assessment [21,22,23,24,25,26,27], and accident prevention and control [28,29,30,31]. For example, Darbra et al. analyzed 225 domino accidents and found that about 33% of domino accidents were caused by fire, explosion, lightning, flood, earthquake, and other external disasters [16]. Similarly with domino effects, the research on Natech events mainly focuses on the statistical analysis of historical accidents [32,33], equipment vulnerability assessment model for natural disasters [34,35,36], risk assessment [37,38,39], and risk mitigation [40,41]. Previous studies of accident statistics reported that floods and lightning have the highest frequency, while earthquake-related Natech events caused the most serious consequences of accidents among Natech accidents [42]. However, the above studies considered domino effects and Natech events separately and did not comprehensively study domino effects caused by natural disasters, which should be taken into account for a more realistic and comprehensive estimation.
Recently, some scholars have paid more attention to possible domino effects triggered by Natech events. Using a Bayesian Network, Yang et al. proposed a prediction method to evaluate the probability of domino effects triggered by lightning [43], while Misuri et al. carried out a quantitative risk assessment method for domino effects triggered by lightning [44]. However, the assessment method for lighting only considers a single primary accident scenario, but it is not suitable for assessing how earthquakes, floods, and other disasters may lead to multiple primary accident scenarios. Huang et al. developed a usable probabilistic analysis methodology for earthquake-induced domino effects based on a Monte Carlo simulation [45], while Zeng et al. proposed a novel methodology for quantitative risk analysis of domino effects triggered by floods [46]. Lan et al. used a network-based approach to carry out a Natech-related domino effects simulation involving a case study on a coastal oil storage base with respect to hurricanes and secondary flooding [47]. Khakzad developed a fire-spread model to obtain spread probabilities showing the most probable path of wildfire in wildland-industrial interfaces based on a dynamic Bayesian network [48]. The above research efforts have put forward solid ideas and have laid a strong foundation for the domino effects caused by natural disasters. However, these studies could not accurately identify the accident propagation paths of Natech-related domino effects, and quantitative risk assessment research has not been carried out, even though it plays an important role in effective accident prevention and control.
In order to solve the above shortcomings, Men et al. proposed an event-driven probabilistic methodology to simulate the spatial-temporal evolution of domino chains triggered by natural hazards, and the proposed method can quickly identify the critical system units and temporal intervals [49]. Chen et al. developed a three-dimensional visualization system for domino effects triggered by Natech events in oil-gas depots, which can be used to calculate the probability and evolution path of the accident chain [50]. However, these methods could not identify all the possible propagation paths and did not carry out quantitative risk assessment, which would thus lead to underestimated results. Yang et al. proposed a method for assessing all the propagation paths and probabilities of domino effects triggered by Natech events [51], but this method is only applicable to vapor cloud explosions, and not to fires or other scenarios.
The present work focuses on two research topics to fill the gap mentioned in the current research, which is divided into two parts. Part I (current paper) develops a probability calculation method to obtain all possible propagation paths and their probabilities and to identify the most dangerous equipment units and propagation paths of domino effects triggered by Natech events, which provides data support for the quantitative risk assessment and prevention and control methods presented in Part II of this work. Part II (accompanying paper) proposes an individual risk and social risk assessment model for domino effects triggered by Natech events, and a full-life cycle prevention and control system is studied considering the influence of natural disasters and multi-level domino effects simultaneously. The individual risks and social risks of natural disasters and multi-level domino effects are compared and analyzed through a case study, to reveal the propagation principles of natural disasters and domino effects for increased risk in chemical industrial parks, and to quantify the effects of accident prevention and control with the proposed risk assessment models, so as to provide a theoretical basis for optimizing prevention and control strategies. Therefore, the current work can not only improve the safety level of chemical industrial parks and protect the safety of humans and property, but also simultaneously improve the sustainable production of chemical industrial parks, producing a double benefit [4,52]. The rest of the current paper is organized as follows: The propagation rules of domino effects triggered by Natech events are stated in Section 2. The methodology procedures and corresponding equations and algorithms are demonstrated in Section 3. The application of the proposed methodology to a case study is illustrated in Section 4. Finally, the conclusions drawn from the present work are formulated in Section 5. This work includes additional Supplementary Materials. Some models proposed by other authors, alongside tables of some calculations. are available in the Supplementary Materials.
2. Propagation Rules of Domino Effects Triggered by Natech Events
Natural disasters have a wide range of impacts and are highly destructive, usually destroying multiple equipment units [6]. In addition to the direct damage caused by natural disasters, other infrastructure such as communication and power grids, pipelines, and road transport infrastructure are oftentimes also damaged, which hinders emergency response actions, thus aggravating the severity of the consequences and resulting in domino effects [38]. According to the type of equipment and stored hazardous substances, damaged equipment may potentially lead to fires or explosions, which are escalation vectors resulting in domino effects. When a primary equipment unit is damaged by a natural disaster, the fire or explosion generated by the primary unit may lead to the destruction of adjacent target equipment units, thus triggering an accident chain of domino effects.
The domino effects triggered by natural disasters are essentially propagated by taking the dangerous equipment units as the carrier, and the domino effects escalation vectors as the medium, such as fires and explosions generated by the damaged equipment units. The propagation rules are mainly divided into two parts: the interaction relationship between equipment units and the synergistic effects between escalation vectors [3]. For illustrative purposes, the accidental chains of domino effects among four tanks affected by natural disasters are illustrated in Figure 1.
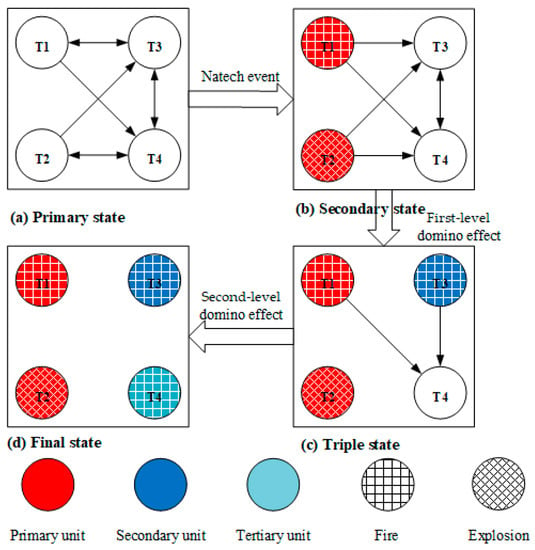
Figure 1.
An example of the evolution process of the accidental chains of domino effects triggered by natural disasters.
2.1. Interaction between Equipment Units
The primary accident scenarios caused by natural disasters are uncertain. When the primary equipment unit is undetermined, there are three possible interaction relationships between the two dangerous equipment units:
- (i)
- Bidirectional-acting relationship. The intensity of the escalation vector generated by an equipment unit is larger than the escalation threshold of the target equipment unit, as is shown by T1 and T3 in Figure 1a. When T1 first occurs in an accident, it may damage T3, and when T3 first occurs in an accident, it may cause T1 to be damaged.
- (ii)
- Single-acting relationship. The intensity of the escalation vector generated by one equipment unit is larger than the escalation threshold of the target equipment unit, while the intensity of the escalation vector generated by the other equipment unit is less than the escalation threshold of the target equipment unit, as is shown by T1 and T4 in Figure 1a. When T1 occurs first in an accident, it may damage T4, while when T4 occurs first in an accident, it will not lead to the destruction of T1.
- (iii)
- No interaction relationship. The intensity of the escalation vector generated by the two equipment units is less than the escalation threshold of the target equipment unit. For example, T1 and T2 in Figure 1a cannot damage each other in the case of an accident.
In the propagation process, the first damaged equipment unit will affect the target equipment unit as the primary equipment unit, and the later damaged equipment unit will not affect the already damaged equipment unit. For example, as shown in Figure 1b, if T1 and T2 are assumed to be the primary equipment units that are damaged by natural disasters, then T1 may affect T3 after T1 is damaged, but T3 cannot have an impact on T1.
From the above analysis, it can be seen that due to the uncertainty in accident propagation, the propagation process of domino effects has many possible propagation paths. For example, as shown in Figure 1b, both T3 and T4 have the possibility of failure. However, when the first-level domino effect is propagated to Figure 1c, only T3 has a fire accident after becoming damaged, and T4 is still not damaged. Therefore, for the analysis of accident propagation process, in addition to the most possible propagation paths, all other possible propagation paths should also be considered.
2.2. Synergistic Effects
During the propagation process of domino effects, the thermal radiation of fires may have synergistic effects, which may strengthen the resulting impacts on the target equipment. For example, a fire usually lasts for a long time (usually lasting for hours or even days). If multiple equipment units are subject to fire accidents simultaneously, the generated thermal radiation will act on the same target equipment unit at the same time, resulting in an increase in the damage probability of the target equipment unit. For example, as shown in Figure 1c, both T1 and T3 are subject to fire accidents, and the generated thermal radiation acts together on T4. At this time, the thermal radiation effects of T1 and T3 need to be considered simultaneously; that is, the thermal radiation intensity of T4 is the superposition of thermal radiation intensity from T1 and T3.
3. Methodology
3.1. Failure State Combination of Primary Equipment Units Caused by Natural Disasters
Once a natural disaster occurs, it is very likely to cause multiple primary equipment units to be destroyed simultaneously. If there are n key equipment units in a chemical industrial park, assuming that each equipment unit is independent from the impact of natural disasters, the failure probability of any equipment unit affected by natural disasters is independent from the failure probability of other n − 1 equipment units. Therefore, when n key equipment units are affected by natural disasters or fires and explosions, there are Ns different failure state combinations, and Ns can be calculated by Equation (1) [53,54].
where k is the number of damaged equipment units in different failure state combinations (1 ≤ k ≤ n).
If a numerical index (1 − n) is assigned to each of the n equipment units that may be triggered by natural disasters, a single overall Natech scenario may thus be identified as a Boolean matrix , which represents the i-th failure state combination (), is the j-th element of (j = 1, 2, ···, n), which represents the failure state of the j-th equipment unit in the i-th failure state combination. If the j-th equipment unit is in the undamaged state in , ; if the j-th equipment unit is in the damaged state, then .
If represents the failure probability of the j-th equipment unit due to the influence of a given natural disaster (which can be obtained by the vulnerability assessment model in the previous studies [34,36,55]), the probability of the i-th failure state combination suffering from natural disasters can be expressed by Equation (2) [53,54].
where represents the frequency of natural disasters; is the combination index, which represents the failure state of the j-th equipment in the i-th failure state combination, and its judgment rule is shown in Equation (3):
Assuming that each failure state combination is fixed, this combination may be the failure state combination of the primary equipment unit caused by natural disasters or domino effects caused by fires or explosions. If equipment unit j will not be affected by natural disasters, but may be affected by domino effects triggered by natural disasters, then , it can be seen from Equation (2) that even if the j-th equipment unit in the failure state combination is in a damaged state, the probability of failure state combination as the primary accident scenario is , indicating that the failure state combination will not be used as the primary failure state combination, and it can only be used as a combination of subsequent domino effect failure states.
3.2. Propagation Path Probabilities of Domino Effects Triggered by Natural Disasters
3.2.1. Equipment Escalation Matrix and Escalation Probability Matrix
When an equipment unit is damaged, a variety of accident scenarios may occur according to the leaked material and the ignition time, and the occurrence conditions of each accident scenario have great uncertainty. This paper assumes that only a single accident scenario will occur after each equipment unit is damaged, and the probability of each scenario can be obtained by referring to the event tree analysis [56]. If there is at least one accident scenario in the event tree of equipment unit i that can cause the target equipment unit j to be damaged, it indicates that the primary equipment unit i can damage the target equipment unit j. If the equipment unit i is damaged, there may be accident scenario, and the probability of the k-th accident scenario is , and the probability of the k-th accident scenario after the equipment unit i is damaged resulting in the failure of the equipment unit j is (can be calculated by the probit model [22,54], which is widely used to cope with the uncertainties in the escalation process and to express the damage potential with a set of those related variables in domino effects [57], as shown in the Supplementary Material S1), then the failure probability of the equipment unit j after the equipment unit i damaged can be calculated by Equation (4):
The interaction relationship between the damaged equipment units is represented by the equipment escalation matrix . If there is at least one accident scenario that can damage the target equipment unit j after the damage of the equipment unit i, it means that the damaged equipment unit i can damage the target equipment unit j, then EQij = 1, otherwise EQij = 0.
After the equipment escalation matrix is obtained, the escalation probability between each damaged equipment unit can be expressed by the equipment escalation probability matrix , as shown in Equation (5).
where the element in the matrix can be obtained by Equation (4).
3.2.2. Failure State Transition Probability Matrix
When multiple primary equipment units are damaged by natural disasters, the remaining undamaged equipment units may be damaged by the impact of fire heat radiation and explosion shock wave generated by the primary equipment units, which may lead to domino effects. As time goes on, the fire thermal radiation, explosion shock wave, and other escalation vectors generated after the destruction of the secondary equipment unit may damage the tertiary equipment unit, and then the high-level domino effect will happen successively, leading to more serious consequences. In the multi-level propagation process of domino effects induced by natural disasters, there is the possibility that one primary equipment unit can act on multiple target equipment units, or multiple primary equipment units can act on the same target equipment unit simultaneously. Each escalation event may only produce one or more damaged equipment units simultaneously. The possible combination of newly damaged equipment units is related to the combination of failure states before the escalation, which increases the uncertainty and complexity in the propagation process of domino effects.
According to the analysis in Section 3.1, there are failure state combinations in n key equipment units, and each failure state combination can be expressed by a Boolean matrix representing the safety (0) and failure (1) states of the equipment unit. For illustrative purposes, Figure 2 displays the failure states and possible propagation paths of three equipment units in a certain area, and each equipment unit can affect each other; that is, if any equipment unit is damaged, the other two undamaged equipment units can be used as potential target equipment units. According to Equation (1), there are seven failure state combinations.
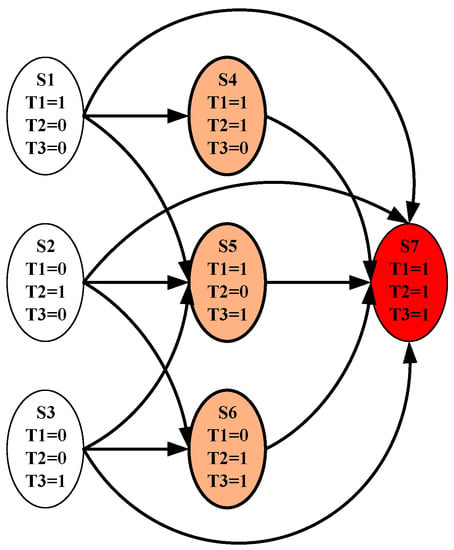
Figure 2.
Schematic diagram of propagation paths of domino effects caused by natural disasters for three key equipment units.
The multi-level propagation process of domino effects can be simplified as a series of events that escalate and transform between different failure state combinations. In order to evaluate the possibility of a specific failure state combination occurring in the propagation process of domino effects, the escalation probability from other failure state combinations to that specific failure state combination must be evaluated first. Assuming that only the first level of domino effects is considered, it can be reasonably considered that the failure of each secondary equipment unit is an independent event. However, in the case of multi-level domino effects, the escalation of failure states is mutually restricted. The probability of each failure state depends on the occurrence or non-occurrence of other failure states, and the subsequent failure states are related to the previous failure states. The escalation relationship between failure states can be expressed by the failure state transition matrix . which means that the failure state combination can be escalated to the failure state combination or otherwise to .
The escalation of failure states caused by natural disasters have the following rules:
- (i)
- The primary failure state combination caused by natural disasters is uncertain, as shown in Figure 2, and all seven failure state combinations have the possibility to be the primary failure state.
- (ii)
- Only undamaged equipment units can be escalated to damaged equipment units, but damaged equipment units cannot be escalated to undamaged equipment units; that is, they are non-maintainable equipment units in the propagation process. For example, as shown in Figure 2, T2 is not damaged in S1 failure state, and can be damaged when escalating to S4, but S4 cannot be converted to S1.
- (iii)
- The failure state with a large number of damaged equipment units cannot be converted into a failure state with a smaller number of damaged equipment units. For example, S7 cannot be converted to S5, and S5 cannot be converted to S2.
- (iv)
- The failure states of the same number of damaged equipment units cannot be mutually converted, such as S4, S5, and S6.
- (v)
- The state combination with a small number of damaged equipment units will escalate to the state combination with a larger number of damaged equipment units, and the state combination with a larger number of damaged equipment units may escalate directly from the primary state combination (such as S1 → S7), or from the intermediate state combination with a smaller number of damaged equipment units (such as S1 → S4 → S7). The specific possible evolution path is shown in Figure 2 (a total of 18 possible paths, as listed in Supplementary Material S2).
In order to analyze the propagation process and causal relationship of each failure state combination, the escalation transformation between different failure state combinations can be intuitively expressed in the form of a directed acyclic graph. In the directed graph, each node represents different failure state combinations, the directed arc between nodes represents the escalation relationship between two nodes, the node from the directed arc is the parent node, and the node from the directed graph is the child node, which indicates that the failure state combination of the parent node may be escalated to the failure state combination of the child node. Assuming that a damaged equipment unit in a certain failure state combination may affect multiple undamaged target equipment units at the same time, the failure state combination node will serve as the parent node and point to all the failure state child nodes that may lead to escalation. The transition relationship of each node in the directed graph can be expressed by the failure state transition matrix ST, also known as the adjacency matrix of the directed graph. According to the propagation rules, the state transition matrix in Figure 2 is shown in Equation (6):
When the failure state transition matrix and the equipment escalation probability matrix are obtained, the transition probability between each failure state combination can be evaluated; that is, the failure state transition probability matrix . indicates the possibility of directly leading to the failure state combination when the failure state combination occurs. If and represent the k-th equipment unit in the failure status combination and failure state combination , respectively, then the value of the k-th element in the new comparison vector CRij(k) depends on the comparison result of the failure state of the k-th equipment unit in the two failure state combinations and , as shown in Table 1.

Table 1.
The possible results of the comparison of the k-th units of the Boolean vectors and .
In Table 1, is the probability that the damaged equipment unit in failure state combination damages the k-th equipment unit, which can be expressed by Equation (7):
where represents the set of all damaged equipment units in failure state combination , as shown in Equation (8):
The failure state transition probability represents the probability that failure state combination will directly escalate to failure state combination due to domino effects, which is actually a conditional probability, because they are dependent on the occurrence of their parent node, and it can be calculated by Equation (9).
According to the failure state transition matrix and the failure state transition probability calculated in Equation (9), the failure state transition probability matrix can be obtained, as shown in Equation (10).
3.2.3. Propagation Path Probabilities of Domino Effects Based on Directed Graph
When the state transition matrix and the state transition probability matrix are obtained, all possible propagation paths of domino effects can be solved by searching all paths in the directed graph, and the path search of the directed graph can be solved based on the depth-first traversal algorithm in Figure 3, which is developed by a Matlab program.
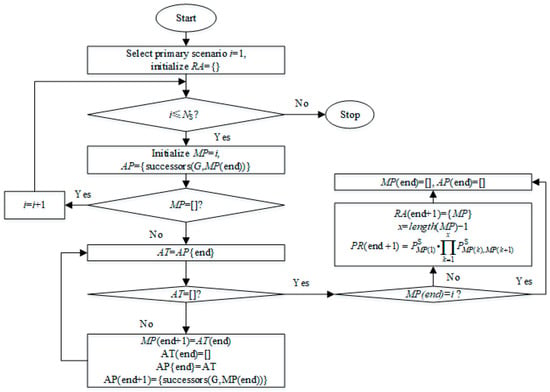
Figure 3.
Algorithm program to obtain all the possible paths and probabilities.
- The failure state combination S(i), i = 1, is set as the primary scenario, and the path sets are stored in the path cell array RA, which is initialized to a null set.
- The main path matrix MP is used to store the ID of primary failure state combination i, and its adjacent node set matrix is obtained by the function successors (ST, MP(end)), which is stored in the cell array AP.
- If the main path matrix MP is not a null set, the last item of MP will be pushed onto the top of matrix AT, which indicates the un-accessed adjacency failure states, while the primary failure state will otherwise be reset to S(i + 1).
- If AT is a null set, whereby namely there is no adjacent failure states or all the adjacent failure states have been visited, such that the path cell array RA will be used to store the new path in main path MP, and its corresponding path probability will be obtained and put in PR, then the last items of MP and AP will be deleted, and the algorithm program will continue.
- If AT is a null set, the last item of AT will be the top item of MP, and other items of AT will be put in AP, then the adjacent failure states of the new items in MP will be put in the top item of AP.
- If all the primary failure states have been visited, the algorithm program will be terminated, and all the possible paths and their probabilities can be obtained from the cell arrays RA and PR.
After all possible paths are obtained, if MP is the ID number set of failure state combinations, the probability of each propagation path PR can be expressed as follows:
where x is the number of propagation level for path MP, ; k is the level of failure state; represents the probability of the primary failure state combination induced by natural disasters in this path; represents the probability that the k-level failure state combination escalates to the (k + 1)-level failure state combination in this path.
4. Case Study
4.1. Overview of the Case Study
The proposed method is demonstrated by a case study with a tank farm located in a coastal area of China, and the layout of the tank farm is shown in Figure 4. Since the filling coefficient of the storage liquid in the tank constantly varied during the operation stage, the filling coefficient of the storage liquid in this case is a randomly assumed parameter in accordance with standard specifications. The characteristic parameters and storage liquid parameters of each tank are shown in Table 2. According to the predominant meteorological conditions in the chemical industrial park, the wind speed is selected as 5 m/s with stability class B from the northwest, while the ambient temperature is 22 °C, and relative humidity is 0.67. The chemical industrial park is located in a flood-prone area; thus the catastrophic flood scenario with a return period of 200 years (i.e., the flood frequency is 0.005 times/year), having last occurred in 1915, is selected as the referenced natural disaster event. The maximum flood submergence depth is about 3.5 m, and the flood velocity is about 0.5 m/s. In the case study, the vulnerability assessment model for flooding proposed by the author is adopted (See Supplementary Material S3 for detailed model) [34], and the failure probability of each tank due to flooding is shown in Table 2.

Figure 4.
The layout of tank farm in the case study.

Table 2.
Characteristic parameters and failure probabilities of tanks.
4.2. Accident Consequence Analysis and Accident Escalation Probability
Due to the great uncertainty of equipment damage and leakage intensity caused by natural and technical disasters, on the premise of ensuring safety, this paper adopts the worst-case accident scenario, assuming that the equipment failure caused by natural and technical disasters is catastrophic failure, and the leakage scenario is instantaneous leakage.
Gasoline and naphtha are volatile and flammable liquids, according to the event tree analysis, which may result in pool fire or vapor cloud explosion. Crude oil is a non-volatile flammable liquid, which may cause pool fire. The accident consequence can be calculated by the PHAST 8.21 software, which is one of the most famous and widely used software tools available in the field of risk analysis [58], and the intensities of thermal radiation and overpressure received by the target tank from the primary tank are listed in Supplementary Material S4.
The equipment escalation probability of a single accident scenario can be calculated by the probit model in Supplementary Material S1. The escalation probability of the target equipment unit after the primary equipment unit is damaged can be calculated by Equation (4), and the equipment escalation probability matrix is shown in Equation (12), which takes into account the tank failure probabilities due to overpressure and thermal radiation in the subsequent calculations based on the probit model in Supplementary Material S1 and accident consequences in Supplementary Material S4.
4.3. Primary Failure State Assessment
Natural disasters may destroy multiple primary equipment units simultaneously. For the tank farm of eight tanks in this case study, there are 255 different failure state combinations. The failure state combinations and their identifications are shown in Supplementary Material S5. The probability of each primary failure state combination can be calculated by Equation (2). Since a failure state combination with a probability of less than 10−10 is considered almost impossible and its impact on risk can be neglected [38], this paper only considers the failure state combinations with primary failure probabilities larger than 10−10. There are thirty-five primary accident scenarios with probabilities larger than 10−10, and the top ten most likely primary failure state combinations are shown in Table 3. It can be seen from Table 3 that the most likely primary failure state combination is S24. In this combination, T3 and T6 have the highest probability of being damaged by flood, so T3 and T6 being simultaneously damaged has the highest probability, which is . Among the top ten most likely primary accident scenarios, the probability ranges from 10−3 to 10−7, and most of the combinations have T3 or T6 tanks, indicating that these two tanks have a large impact on the primary failure scenario, which can be considered as the most likely primary equipment unit.

Table 3.
The most likely combinations of primary failure states.
4.4. Propagation Path Analysis
4.4.1. Most Likely Propagation Path
Analyzing the propagation path probability of domino effects caused by natural disasters can identify the most likely propagation path and probability and provide a data basis for quantitative risk assessment and mitigation. Table 4 lists the top ten most likely propagation paths with probability ranges from to . The primary failure state combination of these ten propagation paths is S24 or S6, indicating that a primary failure state combination with high occurrence probability is most likely to trigger domino effects.

Table 4.
The most likely propagation paths and their probabilities.
4.4.2. Propagation Paths at All Levels
Table 5 lists the number and probability of propagation paths at each level to analyze the impact of domino effects at different levels.

Table 5.
The number and probability distribution of propagation paths at each level.
It can be seen from Table 5 that the number of paths with single-level domino effects is the smallest, and the number of domino effect paths at 3–6th levels is up to the tens of thousands, but their cumulative probabilities are less than that of the first and second levels. The maximum path probability at each level decreases gradually from to with the increase of levels, indicating that the occurrence probability of the high-level domino effect cannot be ignored. The minimum path probability of each level gradually decreases from to , and these path probabilities are less than the cutoff value of 10−10.
4.4.3. Failure Probability Distribution of Tanks at All Levels
Figure 5 shows the total failure probability and cumulative failure probability of tanks at different levels, and the total failure probability of T7 and T5 is the highest due to how they are adjacent to the T3 and T6 tanks that are susceptible to natural disasters, followed by T1, T4, T8, and T2. However, the failure probability of the above tanks is similar, at about 89–90% of the failure probability of T7. The total failure probability of T3 and T6 is the lowest, which is 28% and 2.8% of the failure probability of T7, respectively, because these two tanks are served as primary equipment units and are less affected by the domino effects of other tanks. The failure probability of the T2, T3, T6, and T7 tanks at the first level of domino effects is larger than that of other levels, because these four tanks are adjacent to the most likely primary equipment unit T3 or T6. Therefore, those tanks are susceptible to the influence of T3 or T6. However, the T1, T4, T5, and T8 tanks are susceptible to the domino effects of the T2, T3, T6, and T7 tanks, resulting in a high probability of a second level of domino effects. The proportion of domino effects occurring at or above three levels in these tanks is less than 20%, and the impact on the overall domino effect is relatively small compared to accidents at other levels.
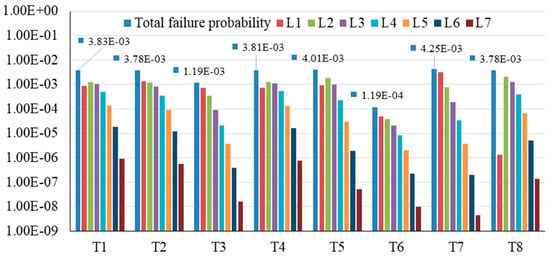
Figure 5.
Cumulative failure frequency distribution at different levels of each tank.
4.5. Accident Scenario Analysis
In order to analyze the impact of different scenarios on the failure probability of each tank, four situations are analyzed: (a) Natech events and conventional accident scenarios; (b) multi-level domino effects triggered by Natech events and conventional accident scenarios; (c) single-level domino effects triggered by Natech events and conventional accident scenarios; (d) only conventional accident scenarios. Table 6 lists the combination of different accident scenarios, and Figure 6 shows the failure probability of each tank under different accident scenarios.

Table 6.
Combination of different accident scenarios.
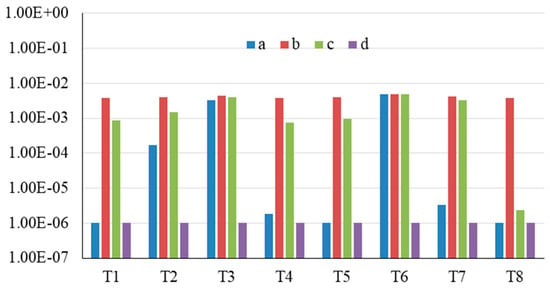
Figure 6.
Tank failure probability under different accident scenarios.
- Impact of Natech events
By the comparative analysis of failure probability of A and D accident scenarios, it is shown that when considering the Natech scenario, the failure probability of T2, T3, and T6 is significantly increased compared with the conventional accident scenario, by about two to three orders of magnitude, and the increased risk for other tanks is less than one order of magnitude. It shows that natural disasters can significantly increase the failure probability of some tanks, such as T2, T3, and T6 in this case, and ignoring the impact of natural disasters will cause the risk to be underestimated.
- 2.
- Impact of domino effects
Comparing the failure probability of accident scenarios A and B, it can be seen that the failure probability of the T1, T2, T4, T5, T7, and T8 tanks increases by about three orders of magnitude when considering multi-level domino effects, which indicates that the occurrence of domino effects have a great impact on the failure probability of these tanks. Due to the impact of natural disasters, the other tanks are mostly served as primary equipment units and are relatively less affected by domino effects. It shows that domino effects will also lead to the destruction of tanks that are less affected by natural disasters, significantly increasing the risk for the chemical industrial park.
- 3.
- Impact of multi-level domino effects
In order to compare and analyze the impact of multi-level domino effects and single-level domino effects, the failure probabilities of B and C accident scenarios are shown in Figure 6. It can be seen that multi-level domino effects will lead to the most significant increase in the failure probability of T8, at about three orders of magnitude. The failure probability of T1, T2, T4, and T5 also increased significantly, with an increase range of about one to three times. It shows that considering multi-level domino effects can have a larger impact on the failure probability of some tanks and ignoring multi-level domino effects will cause the risk of some tanks to be underestimated.
5. Conclusions
This paper presents a probability analysis method for predicting all the possible propagation paths of Natech domino effects, which considers multiple primary equipment units and multi-level domino effects simultaneously. A chemical tank farm located in a flood prone area of China is selected as a case study to demonstrate the application of the proposed method, and the case application shows that this method can effectively identify all possible propagation paths and calculate their probabilities.
In the case study, the probability analysis of primary failure state combinations shows that the probability of the top ten most likely primary accident scenarios decreases from 10−3 to 10−7, and most of the top ten primary failure state combinations contain T3 or T6 tanks, indicating that these two tanks can be considered as the most likely primary equipment unit. The probability analysis of the propagation path of the domino effects induced by natural disasters in the case study shows that the primary failure state has the greatest impact on the propagation probability of domino effects, and the cumulative failure probability of each tank is greatly affected by the primary failure state. The number of propagation paths of the single-level domino effect is the least, but the cumulative failure probability is the largest, and the influence of the multi-level domino effect cannot be ignored. The failure probability analysis of each tank in different scenarios shows that Natech events and multi-level domino effects have a significant impact on the failure probability of tanks, even resulting in the failure probability of some tanks increasing by several orders of magnitude. Ignoring the impacts both of natural disasters and the multi-level domino effect will lead the failure probability of tanks to be underestimated.
The equipment failure probability calculated in this paper can be used for quantitative risk assessment, and the most dangerous propagation path and equipment unit identified can provide a reference for the optimizing risk mitigation measures proposed in Part II of the present work. It can be concluded that the results and mitigation measures proposed in this work play a critical role in safety production in chemical industrial parks, and improving safety performance will produce two-pronged benefits: reducing the safety risks of chemical industrial parks and simultaneously improving sustainability performance.
Nonetheless, it should be remarked that this paper only considers the possibility of the spatial propagation of domino effects and does not focus on the temporal evolution of domino effects. However, equipment failure caused by fire may take some time, and safety barriers and fire rescue actions have a delayed or even eliminative effect on the evolution of domino effects. Therefore, the accuracy of results may increase by considering the temporal factor of domino effects caused by fire, and future research should comprehensively consider the spatio-temporal evolution law of accident propagation and dynamic risk assessment method.
Supplementary Materials
The following supporting information can be downloaded at: https://www.mdpi.com/article/10.3390/su15108362/s1, Some models proposed by other authors alongside tables of some calculations, S1: probit model; S2: 18 possible paths in Figure 2; S3: Vulnerability assessment model for flood; S4: Accident consequence calculation; S5: Failure state combinations.
Author Contributions
Y.Y. developed the methodology and its application, analyzed the results, drafted the manuscript, and finalized it; G.C. and Y.Z. administrated and supervised this study, ac-quired funding and data, and provided suggestions on the manuscript. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported by the Science and Technology Planning Project of Guangdong Province (Number: 2019B020208012) and the National Natural Science Foundation of China (22078109).
Data Availability Statement
While not publicly available due to confidentiality, the data presented in this study are available on request from the corresponding author.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Zeng, T.; Chen, G.; Yang, Y.; Reniers, G.; Zhao, Y.; Liu, X. A Systematic Literature Review on Safety Research Related to Chemical Industrial Parks. Sustainability 2020, 12, 5753. [Google Scholar] [CrossRef]
- Yang, Y.; Chen, G.; Reniers, G.; Goerlandt, F. A bibliometric analysis of process safety research in China: Understanding safety research progress as a basis for making China’s chemical industry more sustainable. J. Clean. Prod. 2020, 263, 121433. [Google Scholar] [CrossRef]
- Chen, C.; Reniers, G.; Khakzad, N. A thorough classification and discussion of approaches for modeling and managing domino effects in the process industries. Saf. Sci. 2020, 125, 104618. [Google Scholar] [CrossRef]
- Syaifullah, D.H.; Tjahjono, B.; McIlhatton, D.; Zagloel, T.Y.M. The impacts of safety on sustainable production performance in the chemical industry: A systematic review of literature and conceptual framework. J. Clean. Prod. 2022, 366, 132876. [Google Scholar] [CrossRef]
- Pilone, E.; Casson Moreno, V.; Cozzani, V.; Demichela, M. Climate change and NaTech events: A step towards local-scale awareness and preparedness. Saf. Sci. 2021, 139, 105264. [Google Scholar] [CrossRef]
- Mesa-Gómez, A.; Casal, J.; Muñoz, F. Risk analysis in Natech events: State of the art. J. Loss Prev. Process Ind. 2020, 64, 104071. [Google Scholar] [CrossRef]
- Luo, X.; Cruz, A.M.; Tzioutzios, D. Climate change and temporal-spatial variation of tropical storm-related Natechs in the United States from 1990 to 2017: Is there a link? Int. J. Disaster Risk Reduct. 2021, 62, 102366. [Google Scholar] [CrossRef]
- Chen, X.; Chen, G.; Yang, Q.; Li, J.; Yuan, Z.; Jiang, S. A Periodic Assessment System for Urban Safety and Security Considering Multiple Hazards Based on WebGIS. Sustainability 2021, 13, 13993. [Google Scholar] [CrossRef]
- Misuri, A.; Casson Moreno, V.; Quddus, N.; Cozzani, V. Lessons learnt from the impact of hurricane Harvey on the chemical and process industry. Reliab. Eng. Syst. Saf. 2019, 190, 106521. [Google Scholar] [CrossRef]
- Kumasaki, M.; King, M. Three cases in Japan occurred by natural hazards and lessons for Natech disaster management. Int. J. Disaster Risk Reduct. 2020, 51, 101855. [Google Scholar] [CrossRef]
- Ma, J.; Chen, G.; Zeng, T.; Zhou, L.; Zhao, J.; Zhao, Y. Methodology for Resilience Assessment of Oil Pipeline Network System Exposed to Earthquake. Sustainability 2023, 15, 972. [Google Scholar] [CrossRef]
- Yu, J.; Cruz, A.M.; Piatyszek, E.; Lesbats, M.; Tardy, A.; Hokugo, A.; Tatano, H. A survey of impact on industrial parks caused by the 2011 Great East Japan earthquake and tsunami. J. Loss Prev. Process Ind. 2017, 50, 317–324. [Google Scholar] [CrossRef]
- Chakraborty, A.; Ibrahim, A.; Cruz, A.M. A study of accident investigation methodologies applied to the Natech events during the 2011 Great East Japan earthquake. J. Loss Prev. Process Ind. 2018, 51, 208–222. [Google Scholar] [CrossRef]
- Kourniotis, S.P.; Kiranoudis, C.T.; Markatos, N.C. Statistical analysis of domino chemical accidents. J. Hazard. Mater. 2000, 71, 239–252. [Google Scholar] [CrossRef]
- Abdolhamidzadeh, B.; Abbasi, T.; Rashtchian, D.; Abbasi, S.A. Domino effect in process-industry accidents–An inventory of past events and identification of some patterns. J. Loss Prev. Process Ind. 2011, 24, 575–593. [Google Scholar] [CrossRef]
- Darbra, R.M.; Palacios, A.; Casal, J. Domino effect in chemical accidents: Main features and accident sequences. J. Hazard. Mater. 2010, 183, 565–573. [Google Scholar] [CrossRef]
- Alileche, N.; Cozzani, V.; Reniers, G.; Estel, L. Thresholds for domino effects and safety distances in the process industry: A review of approaches and regulations. Reliab. Eng. Syst. Saf. 2015, 143, 74–84. [Google Scholar] [CrossRef]
- Cozzani, V.; Salzano, E. Threshold values for domino effects caused by blast wave interaction with process equipment. J. Loss Prev. Process Ind. 2004, 17, 437–447. [Google Scholar] [CrossRef]
- Landucci, G.; Gubinelli, G.; Antonioni, G.; Cozzani, V. The assessment of the damage probability of storage tanks in domino events triggered by fire. Accid. Anal. Prev. 2009, 41, 1206–1215. [Google Scholar] [CrossRef]
- Cozzani, V.; Salzano, E. The quantitative assessment of domino effects caused by overpressure: Part I. Probit models. J. Hazard. Mater. 2004, 107, 67–80. [Google Scholar] [CrossRef] [PubMed]
- Cozzani, V.; Gubinelli, G.; Antonioni, G.; Spadoni, G.; Zanelli, S. The assessment of risk caused by domino effect in quantitative area risk analysis. J. Hazard. Mater. 2005, 127, 14–30. [Google Scholar] [CrossRef] [PubMed]
- Cozzani, V.; Antonioni, G.; Spadoni, G. Quantitative assessment of domino scenarios by a GIS-based software tool. J. Loss Prev. Process Ind. 2006, 19, 463–477. [Google Scholar] [CrossRef]
- Rad, A.; Abdolhamidzadeh, B.; Abbasi, T.; Rashtchian, D. Freedom II: An improved methodology to assess domino effect frequency using simulation techniques. Process Saf. Environ. Prot. 2014, 92, 714–722. [Google Scholar] [CrossRef]
- Khakzad, N. Application of dynamic Bayesian network to risk analysis of domino effects in chemical infrastructures. Reliab. Eng. Syst. Saf. 2015, 138, 263–272. [Google Scholar] [CrossRef]
- Chen, G.; Yang, Q.; Chen, X.; Huang, K.; Zeng, T.; Yuan, Z. Methodology of Urban Safety and Security Assessment Based on the Overall Risk Management Perspective. Sustainability 2021, 13, 6560. [Google Scholar] [CrossRef]
- Huang, K.; Chen, G.; Khan, F.; Yang, Y. Dynamic analysis for fire-induced domino effects in chemical process industries. Process Saf. Environ. Prot. 2021, 148, 686–697. [Google Scholar] [CrossRef]
- Zeng, T.; Chen, G.; Yang, Y.; Chen, P.; Reniers, G. Developing an advanced dynamic risk analysis method for fire-related domino effects. Process Saf. Environ. Prot. 2020, 134, 149–160. [Google Scholar] [CrossRef]
- Cozzani, V.; Tugnoli, A.; Salzano, E. Prevention of domino effect: From active and passive strategies to inherently safer design. J. Hazard. Mater. 2007, 139, 209–219. [Google Scholar] [CrossRef]
- Landucci, G.; Argenti, F.; Tugnoli, A.; Cozzani, V. Quantitative assessment of safety barrier performance in the prevention of domino scenarios triggered by fire. Reliab. Eng. Syst. Saf. 2015, 143, 30–43. [Google Scholar] [CrossRef]
- Ghasemi, A.M.; Nourai, F. A framework for minimizing domino effect through optimum spacing of storage tanks to serve in land use planning risk assessments. Saf. Sci. 2017, 97, 20–26. [Google Scholar] [CrossRef]
- Khakzad, N.; Landucci, G.; Reniers, G. Application of dynamic Bayesian network to performance assessment of fire protection systems during domino effects. Reliab. Eng. Syst. Saf. 2017, 167, 232–247. [Google Scholar] [CrossRef]
- Renni, E.; Krausmann, E.; Cozzani, V. Industrial accidents triggered by lightning. J. Hazard. Mater. 2010, 184, 42–48. [Google Scholar] [CrossRef]
- Cozzani, V.; Campedel, M.; Renni, E.; Krausmann, E. Industrial accidents triggered by flood events: Analysis of past accidents. J. Hazard. Mater. 2010, 175, 501–509. [Google Scholar] [CrossRef] [PubMed]
- Yang, Y.; Chen, G.; Reniers, G. Vulnerability assessment of atmospheric storage tanks to floods based on logistic regression. Reliab. Eng. Syst. Saf. 2020, 196, 106721. [Google Scholar] [CrossRef]
- Necci, A.; Antonioni, G.; Cozzani, V.; Krausmann, E.; Borghetti, A.; Nucci, C.A. A model for process equipment damage probability assessment due to lightning. Reliab. Eng. Syst. Saf. 2013, 115, 91–99. [Google Scholar] [CrossRef]
- Salzano, E.; Iervolino, I.; Fabbrocino, G. Seismic risk of atmospheric storage tanks in the framework of quantitative risk analysis. J. Loss Prev. Process Ind. 2003, 16, 403–409. [Google Scholar] [CrossRef]
- Fabbrocino, G.; Iervolino, I.; Orlando, F.; Salzano, E. Quantitative risk analysis of oil storage facilities in seismic areas. J. Hazard. Mater. 2005, 123, 61–69. [Google Scholar] [CrossRef]
- Antonioni, G.; Bonvicini, S.; Spadoni, G.; Cozzani, V. Development of a framework for the risk assessment of Na-Tech accidental events. Reliab. Eng. Syst. Saf. 2009, 94, 1442–1450. [Google Scholar] [CrossRef]
- Girgin, S.; Krausmann, E. RAPID-N: Rapid natech risk assessment and mapping framework. J. Loss Prev. Process Ind. 2013, 26, 949–960. [Google Scholar] [CrossRef]
- Paolacci, F.; Giannini, R.; De Angelis, M. Seismic response mitigation of chemical plant components by passive control techniques. J. Loss Prev. Process Ind. 2013, 26, 924–935. [Google Scholar] [CrossRef]
- Misuri, A.; Landucci, G.; Cozzani, V. Assessment of safety barrier performance in Natech scenarios. Reliab. Eng. Syst. Saf. 2020, 193, 106597. [Google Scholar] [CrossRef]
- Suarez-Paba, M.C.; Perreur, M.; Munoz, F.; Cruz, A.M. Systematic literature review and qualitative meta-analysis of Natech research in the past four decades. Saf. Sci. 2019, 116, 58–77. [Google Scholar] [CrossRef]
- Yang, Y.; Chen, G.; Chen, P. The probability prediction method of domino effect triggered by lightning in chemical tank farm. Process Saf. Environ. Prot. 2018, 116, 106–114. [Google Scholar] [CrossRef]
- Misuri, A.; Antonioni, G.; Cozzani, V. Quantitative risk assessment of domino effect in Natech scenarios triggered by lightning. J. Loss Prev. Process Ind. 2020, 64, 104095. [Google Scholar] [CrossRef]
- Huang, K.; Chen, G.; Yang, Y.; Chen, P. An innovative quantitative analysis methodology for Natech events triggered by earthquakes in chemical tank farms. Saf. Sci. 2020, 128, 104744. [Google Scholar] [CrossRef]
- Zeng, T.; Chen, G.; Reniers, G.; Yang, Y. Methodology for quantitative risk analysis of domino effects triggered by flood. Process Saf. Environ. Prot. 2021, 147, 866–877. [Google Scholar] [CrossRef]
- Lan, M.; Gardoni, P.; Qin, R.; Zhang, X.; Zhu, J.; Lo, S. Modeling NaTech-related domino effects in process clusters: A network-based approach. Reliab. Eng. Syst. Saf. 2022, 221, 108329. [Google Scholar] [CrossRef]
- Khakzad, N. Modeling wildfire spread in wildland-industrial interfaces using dynamic Bayesian network. Reliab. Eng. Syst. Saf. 2019, 189, 165–176. [Google Scholar] [CrossRef]
- Men, J.; Chen, G.; Yang, Y.; Reniers, G. An event-driven probabilistic methodology for modeling the spatial-temporal evolution of natural hazard-induced domino chain in chemical industrial parks. Reliab. Eng. Syst. Saf. 2022, 226, 108723. [Google Scholar] [CrossRef]
- Chen, G.; Luo, C.; Zhou, L.; Rao, X. Research on three-dimensional visualization system of Natech events triggered domino accidents in oil-gas depots. J. Loss Prev. Process Ind. 2023, 81, 104953. [Google Scholar] [CrossRef]
- Yang, Y.; Chen, G.; Reniers, G. A method for assessing propagation paths and probabilities of domino effects triggered by natech events. Chem. Eng. Prog. 2020, 82, 67–72. [Google Scholar]
- Nawaz, W.; Linke, P.; Koç, M. Safety and sustainability nexus: A review and appraisal. J. Clean. Prod. 2019, 216, 74–87. [Google Scholar] [CrossRef]
- Antonioni, G.; Landucci, G.; Necci, A.; Gheorghiu, D.; Cozzani, V. Quantitative assessment of risk due to NaTech scenarios caused by floods. Reliab. Eng. Syst. Saf. 2015, 142, 334–345. [Google Scholar] [CrossRef]
- Cozzani, V.; Antonioni, G.; Landucci, G.; Tugnoli, A.; Bonvicini, S.; Spadoni, G. Quantitative assessment of domino and NaTech scenarios in complex industrial areas. J. Loss Prev. Process Ind. 2014, 28, 10–22. [Google Scholar] [CrossRef]
- Kameshwar, S.; Padgett, J.E. Fragility and resilience indicators for portfolio of oil storage tanks subjected to hurricanes. J. Infrastruct. Syst. 2018, 24, 04018003. [Google Scholar] [CrossRef]
- Vílchez, J.A.; Espejo, V.; Casal, J. Generic event trees and probabilities for the release of different types of hazardous materials. J. Loss Prev. Process Ind. 2011, 24, 281–287. [Google Scholar] [CrossRef]
- Xu, Y.; Reniers, G.; Yang, M.; Yuan, S.; Chen, C. Uncertainties and their treatment in the quantitative risk assessment of domino effects: Classification and review. Process Saf. Environ. Prot. 2023, 172, 971–985. [Google Scholar] [CrossRef]
- Pouyakian, M.; Ashouri, M.; Eidani, S.; Madvari, R.F.; Laal, F. A systematic review of consequence modeling studies of the process accidents in Iran from 2006 to 2022. Heliyon 2023, 9, e13550. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).