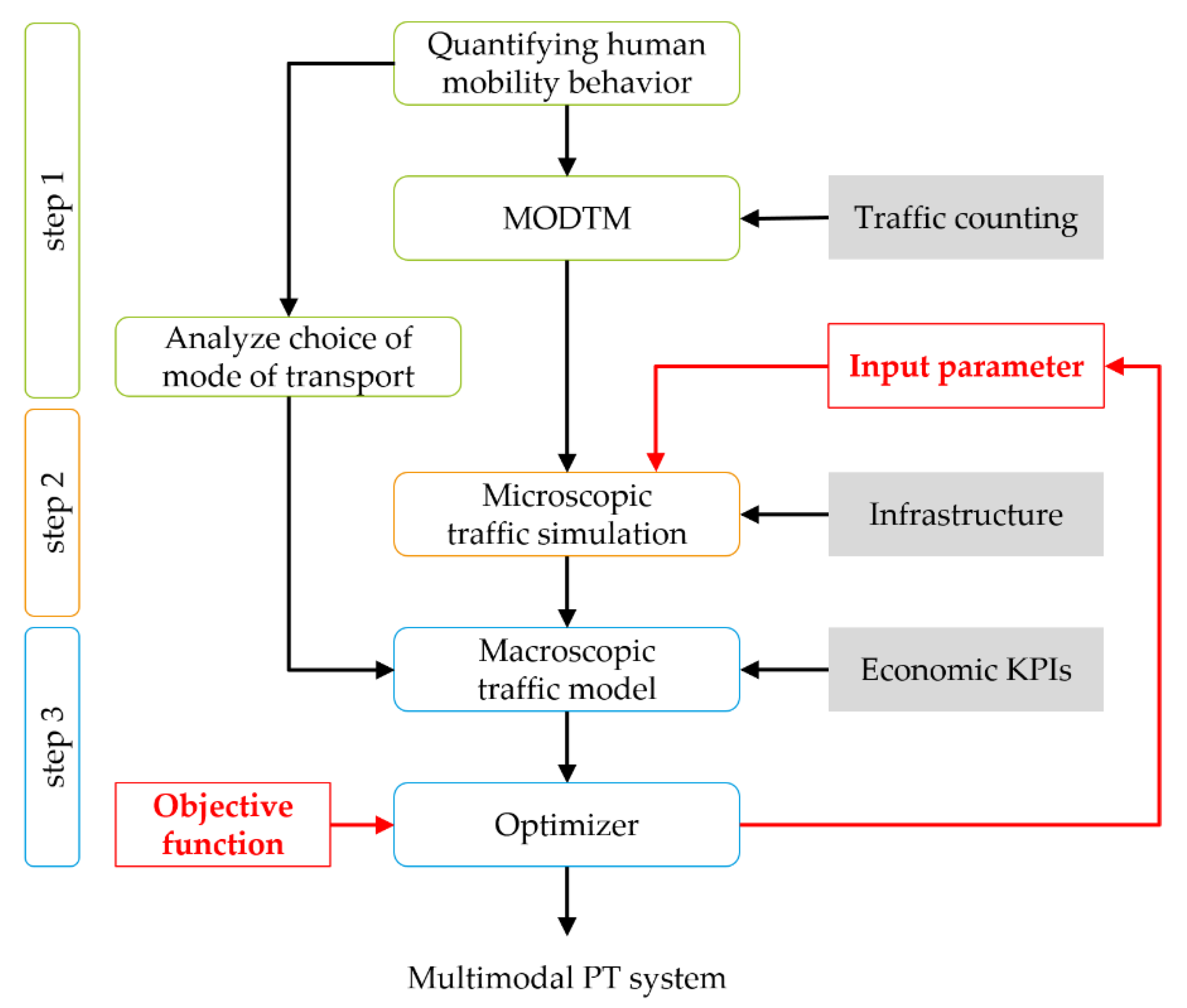
From Modeling to Optimizing Sustainable Public Transport: A New Methodological Approach
Abstract
1. Introduction
2. Quantifying Human-Mobility Behavior
2.1. Accessing Mobility Behavior
2.2. Data-Collection Methods for Mobility Behavior
2.3. Using and Enhancing Mobility Data
3. Microscopic Traffic Simulation
4. Macroscopic Multimodal Public-Transport Model
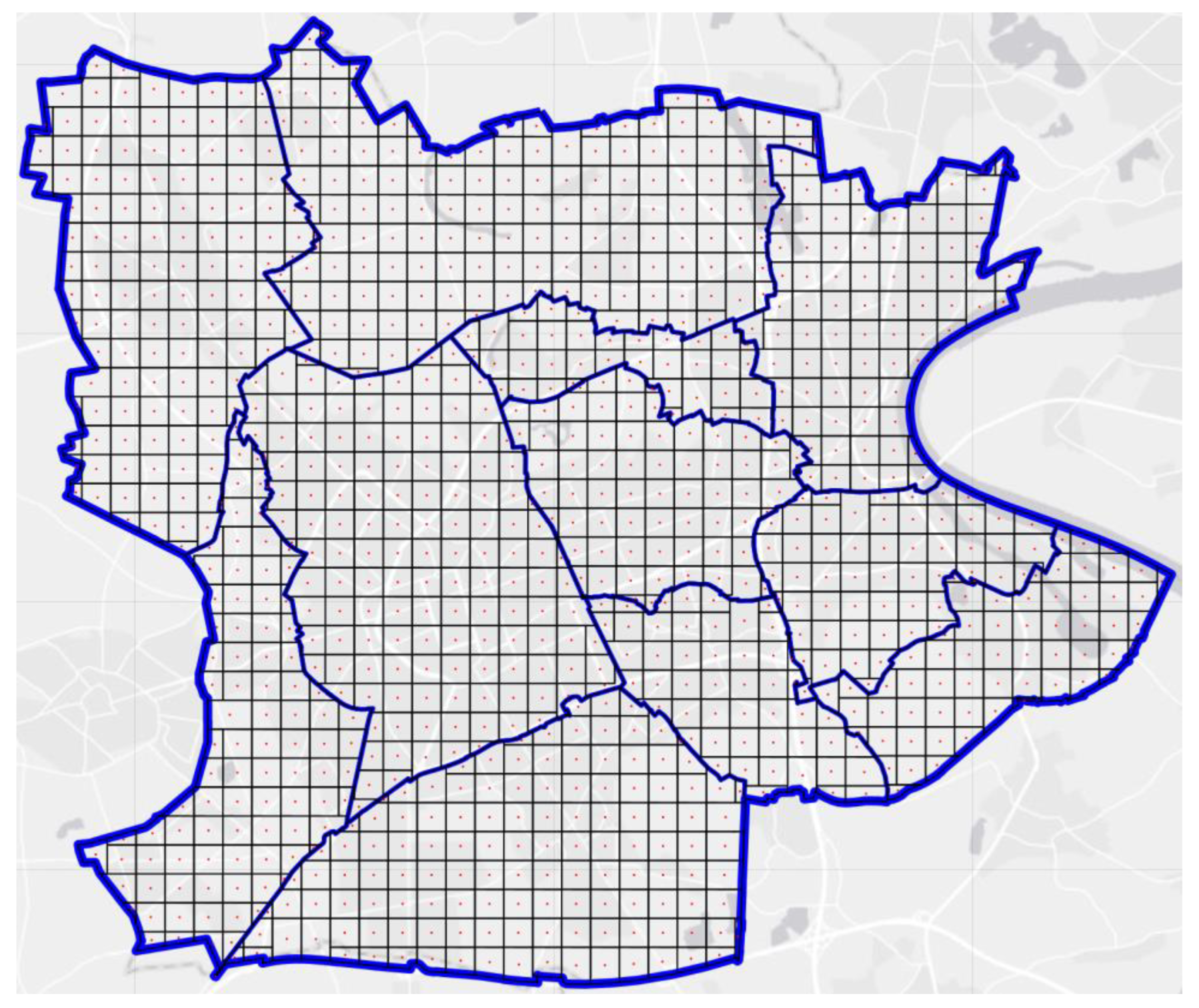
4.1. Discretization of the Area under Investigation
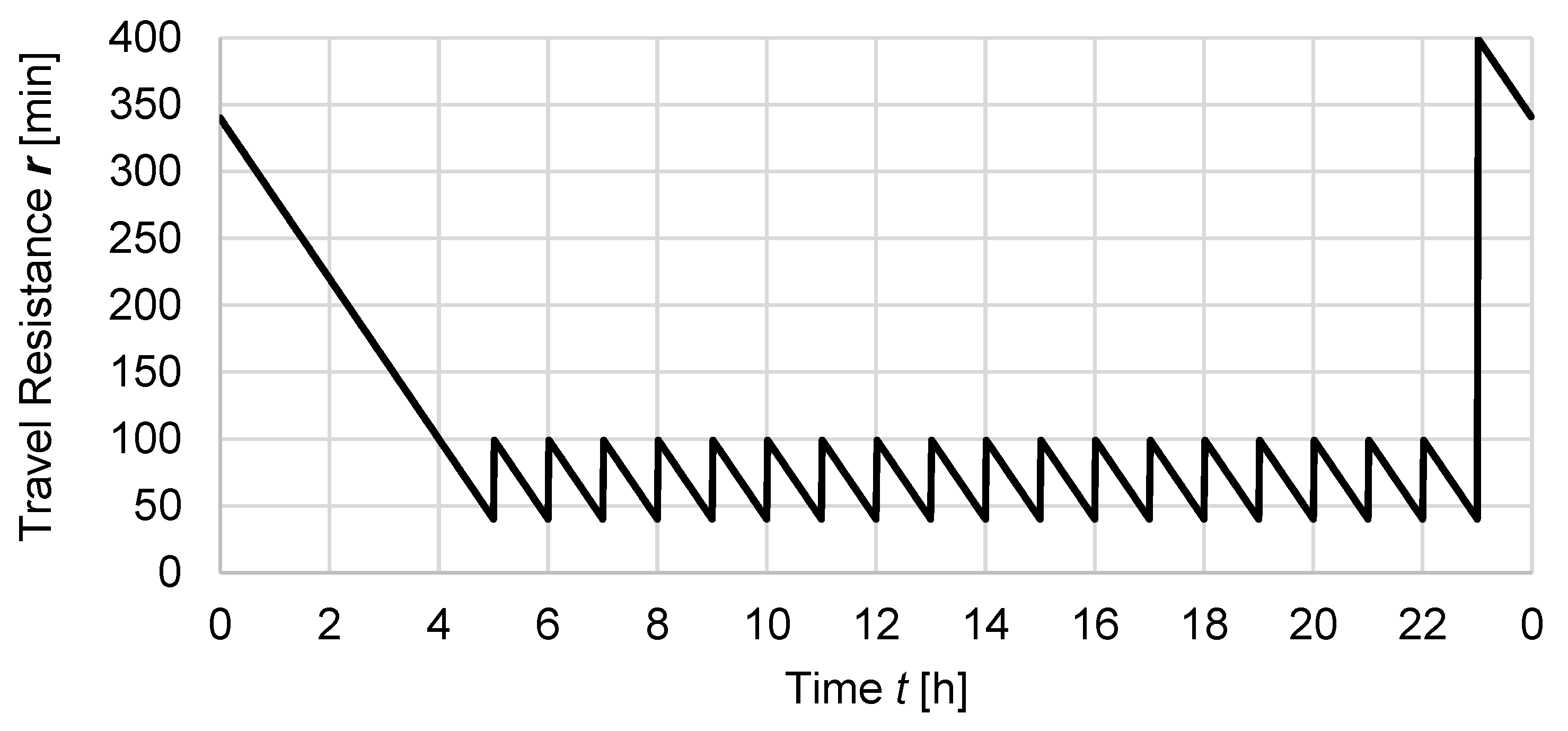
4.2. Public-Transport Travel Resistances
- : travel resistance of relation from origin i to destination j with PT;
- : travel resistance of approaching or departing PT;
- : additional resistance of station due to insufficient amenities;
- : rated travel time of part of the path;
- : part (section) of the whole path;
- : rated travel time of the footpath between stations;
- : travel-time equivalent for waiting times while changing mode of transport;
- : travel-time equivalent for additional inconveniences of changing mode of transport (except waiting times).
- : time to approach PT in minutes.
4.3. Time-Dependent-Directed Graph
4.4. Time-Dependent Shortest-Path Algorithm with Multidimensional Edge Weights
4.5. Constant Travel Resistances of Transfers in Graph Theory
4.6. Travel Resistances of Motorized Private Transport, Cycling, and Footpaths
4.7. Macroscopic Modeling of Mobility on Demand
4.8. Economic Point of View
4.9. Optimization Problem
- Minimize average public-transport travel resistance of all relations or maximize the modal shift with today’s investments as the maximum budget.
- Minimize cost or maximize revenue with today’s travel resistances.
- Minimize government subsidies to get a modal split of 30%, 40%, …, or 60% PT.
- Minimize CO2 emissions with a certain amount of government subsidies.
5. Summary of Results
6. Discussion
7. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- United States Department of Transportation. Transportation Statistics Annual Report 2021; United States Department of Transportation: Washington, DC, USA, 2020.
- United Nations. The Paris Agreement: United Nations Framework Convention on Climate Change; United Nations: New York, NY, USA, 2015.
- Crawford, J.H.; Verner, A. Carfree Cities; International Books: Dublin, Ireland, 2000. [Google Scholar]
- Eckersley, R.; Dixon, J.; Douglas, R.M.; Douglas, B. The Social Origins of Health and Well-Being; Cambridge University Press: Cambridge, UK, 2001. [Google Scholar]
- Oviedo, D.; Sabogal, O.; Villamizar Duarte, N.; Chong, A.Z.W. Perceived liveability, transport, and mental health: A story of overlying inequalities. J. Transp. Health 2022, 27, 101513. [Google Scholar] [CrossRef]
- Statista. Wieso nutzen Sie die öffentlichen Nahverkehrsmittel nicht öfter? Statista: Hamburg, Germany, 2019. [Google Scholar]
- Yap, M.D.; Correia, G.; van Arem, B. Preferences of travellers for using automated vehicles as last mile public transport of multimodal train trips. Transp. Res. Part A Policy Pract. 2016, 94, 1–16. [Google Scholar] [CrossRef]
- Verkehrsbetriebe Hamburg-Holstein GmbH. Ein On-Demand-Angebot als Teil des hvv. Available online: https://vhhbus.de/hop/ (accessed on 28 March 2023).
- AöR, V.R.-R. Ausbildungsverkehr-Richtlinie AusbV-RL. 2019. Available online: https://zvis.vrr.de/bi/vo0050.asp?__kvonr=6064 (accessed on 23 March 2023).
- Bank, W. Urbanisierungsgrad: Anteil der Stadtbewohner an der Gesamtbevölkerung in Deutschland in den Kahren von 2000 bis 2021; Statista: Hamburg, Germany, 2022. [Google Scholar]
- Bundesamt, S. Bevölkerungsstand: Amtliche Einwohnerzahl Deutschlands 2022. Available online: https://www.destatis.de/DE/Themen/Gesellschaft-Umwelt/Bevoelkerung/Bevoelkerungsstand/_inhalt.html (accessed on 23 March 2023).
- Statista. Einwohnerzahl der größten Städte in Deutschland am 31 Dezember 2021. Available online: https://de.statista.com/statistik/daten/studie/1353/umfrage/einwohnerzahlen-der-grossstaedte-deutschlands/ (accessed on 23 March 2023).
- Makse, H.A.; Havlin, S.; Stanley, H.E. Modelling urban growth patterns. Nature 1995, 377, 608–612. [Google Scholar] [CrossRef]
- Xu, F.; Li, Y.; Jin, D.; Lu, J.; Song, C. Emergence of urban growth patterns from human mobility behavior. Nat. Comput. Sci. 2021, 1, 791–800. [Google Scholar] [CrossRef]
- Benita, F. Human mobility behavior in COVID-19: A systematic literature review and bibliometric analysis. Sustain. Cities Soc. 2021, 70, 102916. [Google Scholar] [CrossRef] [PubMed]
- Han, S.Y.; Tsou, M.-H.; Knaap, E.; Rey, S.; Cao, G. How do cities flow in an emergency? Tracing human mobility patterns during a natural disaster with big data and geospatial data science. Urban Sci. 2019, 3, 51. [Google Scholar] [CrossRef]
- Gonzalez, M.C.; Hidalgo, C.A.; Barabasi, A.-L. Understanding individual human mobility patterns. Nature 2008, 453, 779–782. [Google Scholar] [CrossRef]
- Do, T.M.T.; Gatica-Perez, D. Contextual conditional models for smartphone-based human mobility prediction. In Proceedings of the 2012 ACM Conference on Ubiquitous Computing, Pittsburgh, PA, USA, 5–8 September 2012; pp. 163–172. [Google Scholar]
- Song, C.; Koren, T.; Wang, P.; Barabási, A.-L. Modelling the scaling properties of human mobility. Nat. Phys. 2010, 6, 818–823. [Google Scholar] [CrossRef]
- Vazquez-Prokopec, G.M.; Bisanzio, D.; Stoddard, S.T.; Paz-Soldan, V.; Morrison, A.C.; Elder, J.P.; Ramirez-Paredes, J.; Halsey, E.S.; Kochel, T.J.; Scott, T.W. Using GPS technology to quantify human mobility, dynamic contacts and infectious disease dynamics in a resource-poor urban environment. PLoS ONE 2013, 8, e58802. [Google Scholar] [CrossRef]
- Hadjidemetriou, G.M.; Sasidharan, M.; Kouyialis, G.; Parlikad, A.K. The impact of government measures and human mobility trend on COVID-19 related deaths in the UK. Transp. Res. Interdiscip. Perspect. 2020, 6, 100167. [Google Scholar] [CrossRef]
- Du, B.; Zhao, Z.; Zhao, J.; Yu, L.; Sun, L.; Lv, W. Modelling the epidemic dynamics of COVID-19 with consideration of human mobility. Int. J. Data Sci. Anal. 2021, 12, 369–382. [Google Scholar] [CrossRef]
- Andrade, T.; Cancela, B.; Gama, J. Discovering locations and habits from human mobility data. Ann. Telecommun. 2020, 75, 505–521. [Google Scholar] [CrossRef]
- Archer, C.L.; Cervone, G.; Golbazi, M.; Al Fahel, N.; Hultquist, C. Changes in air quality and human mobility in the USA during the COVID-19 pandemic. Bull. Atmos. Sci. Technol. 2020, 1, 491–514. [Google Scholar] [CrossRef]
- Schaefer, A.; Jacoby, H.D.; Heywood, J.B.; Waitz, I.A. The Other Climate Threat: Transportation: A global travel surge is inevitable, but runaway growth of mobility-related CO2 emissions is not. Am. Sci. 2009, 97, 476–483. [Google Scholar] [CrossRef]
- Lin, M.; Hsu, W.-J. Mining GPS data for mobility patterns: A survey. Pervasive Mob. Comput. 2014, 12, 1–16. [Google Scholar] [CrossRef]
- Jin, L.; Xue, Y.; Li, Q.; Feng, L. Integrating human mobility and social media for adolescent psychological stress detection. In Proceedings of the International Conference on Database Systems for Advanced Applications, Dallas, TX, USA, 16–19 April 2016; pp. 367–382. [Google Scholar]
- DeMasi, O.; Feygin, S.; Dembo, A.; Aguilera, A.; Recht, B. Well-being tracking via smartphone-measured activity and sleep: Cohort study. JMIR Mhealth Uhealth 2017, 5, e7820. [Google Scholar] [CrossRef]
- Anagnostopoulou, E.; Urbančič, J.; Bothos, E.; Magoutas, B.; Bradesko, L.; Schrammel, J.; Mentzas, G. From mobility patterns to behavioural change: Leveraging travel behaviour and personality profiles to nudge for sustainable transportation. J. Intell. Inf. Syst. 2020, 54, 157–178. [Google Scholar] [CrossRef]
- Ampt, E.S.; de Dios Ortúzar, J.; Richardson, A.J. Large-scale ongoing mobility surveys: The state of practice. In Transport Survey Methods: Keeping Up with a Changing World; Emerald Group Publishing Limited: Bentley, UK, 2009. [Google Scholar]
- Ampt, E.S.; Ortúzar, J.D.D. On best practice in continuous large-scale mobility surveys. Transp. Rev. 2004, 24, 337–363. [Google Scholar] [CrossRef]
- Zumkeller, D.; Ottmann, P. Moving from cross-sectional to continuous surveying: Synthesis of a workshop. In Transport Survey Methods: Keeping Up with a Changing World; Emerald Group Publishing Limited: Bentley, UK, 2009. [Google Scholar]
- Ortúzar, J.D.D.; Armoogum, J.; Madre, J.L.; Potier, F. Continuous mobility surveys: The state of practice. Transp. Rev. 2011, 31, 293–312. [Google Scholar] [CrossRef]
- Bliemer, M.C.J.; Rose, J.M. Experimental design influences on stated choice outputs An empirical study in air travel choice. Transp. Res. A-Pol. 2011, 45, 63–79. [Google Scholar] [CrossRef]
- Roddis, S.; Winter, S.; Zhao, F.; Kutadinata, R. Respondent preferences in travel survey design: An initial comparison of narrative, structured and technology-based travel survey instruments. Travel Behav. Soc. 2019, 16, 1–12. [Google Scholar] [CrossRef]
- McCool, D.; Lugtig, P.; Mussmann, O.; Schouten, B. An App-Assisted Travel Survey in Official Statistics: Possibilities and Challenges. J. Off. Stat. 2021, 37, 149–170. [Google Scholar] [CrossRef]
- Richardson, A.J. Survey Methods for Transport Planning; Richardson, A.J., Ampt, E.S., Meyburg, A.H., Eds.; Eucalyptus: Parkville, VIC, Australia, 1995. [Google Scholar]
- Thomas, N.; Jana, A.; Bandyopadhyay, S. Physical distancing on public transport in Mumbai, India: Policy and planning implications for unlock and post-pandemic period. Transp. Policy 2022, 116, 217–236. [Google Scholar] [CrossRef]
- Talpur, M.A.H.; Napiah, M.B.; Chandio, I.A.; Khahro, S.H. Transportation Planning Survey Methodologies for the Proposed Study of Physical and Socio-economic Development of Deprived Rural Regions: A Review. Math. Model. Methods Appl. Sci. 2012, 6, 1. [Google Scholar] [CrossRef]
- Aschauer, F.; Hossinger, R.; Jara-Diaz, S.; Schmid, B.; Axhausen, K.; Gerike, R. Comprehensive data validation of a combined weekly time use and travel survey. Transp. Res. A-Pol. 2021, 153, 66–82. [Google Scholar] [CrossRef]
- Eisenmann, C.; Chlond, B.; Minster, C.; Jödden, C.; Vortisch, P. Mixed mode survey design and panel repetition—Findings from the German Mobility Panel. Transp. Res. Procedia 2018, 32, 319–328. [Google Scholar] [CrossRef]
- Eriksson, J.; Lindborg, E.; Adell, E.; Holmström, A.; Silvano, A.; Nilsson, A.; Henriksson, P.; Wiklund, M.; Dahlberg, L. New Ways of Collecting Individual Travel Information Evaluation of Data Collection and Recruitment Methods; Swedish National Road and Transport Research Institute: Stockholm, Sweden, 2018. [Google Scholar]
- Quiroga, C.; Henk, R.; Jacobson, M. Innovative data collection techniques for roadside origin-destination surveys. Transp. Res Rec. 2000, 1719, 140–146. [Google Scholar] [CrossRef]
- Stephan, K.; Köhler, K.; Heinrichs, M.; Berger, M.; Platzer, M.; Selz, E. Das Elektronische Wegetagebuch—Chancen und Herausforderungen einer Automatisierten Wegeerfassung Intermodaler Wege; Springer Vieweg: Wiesbaden, Germany, 2014. [Google Scholar]
- Assemi, B.; Jafarzadeh, H.; Mesbah, M.; Hickman, M. Participants’ perceptions of smartphone travel surveys. Transp. Res. Part F Traffic Psychol. Behav. 2018, 54, 338–348. [Google Scholar] [CrossRef]
- Hunecke, M.; Haustein, S.; Grischkat, S.; Bohler, S. Psychological, sociodemographic, and infrastructural factors as determinants of ecological impact caused by mobility behavior. J Environ. Psychol 2007, 27, 277–292. [Google Scholar] [CrossRef]
- MATsim Website. Available online: https://www.matsim.org/ (accessed on 4 April 2023).
- PTV Vissim Website. Available online: https://www.myptv.com/en-us/mobility-software/ptv-vissim (accessed on 4 April 2023).
- TransModeler Website. Available online: https://www.caliper.com/transmodeler/requirements.html (accessed on 4 April 2023).
- Aimsun Website. Available online: https://www.aimsun.com/ (accessed on 4 April 2023).
- SUMO Website. Available online: https://www.eclipse.org/sumo/about/ (accessed on 4 April 2023).
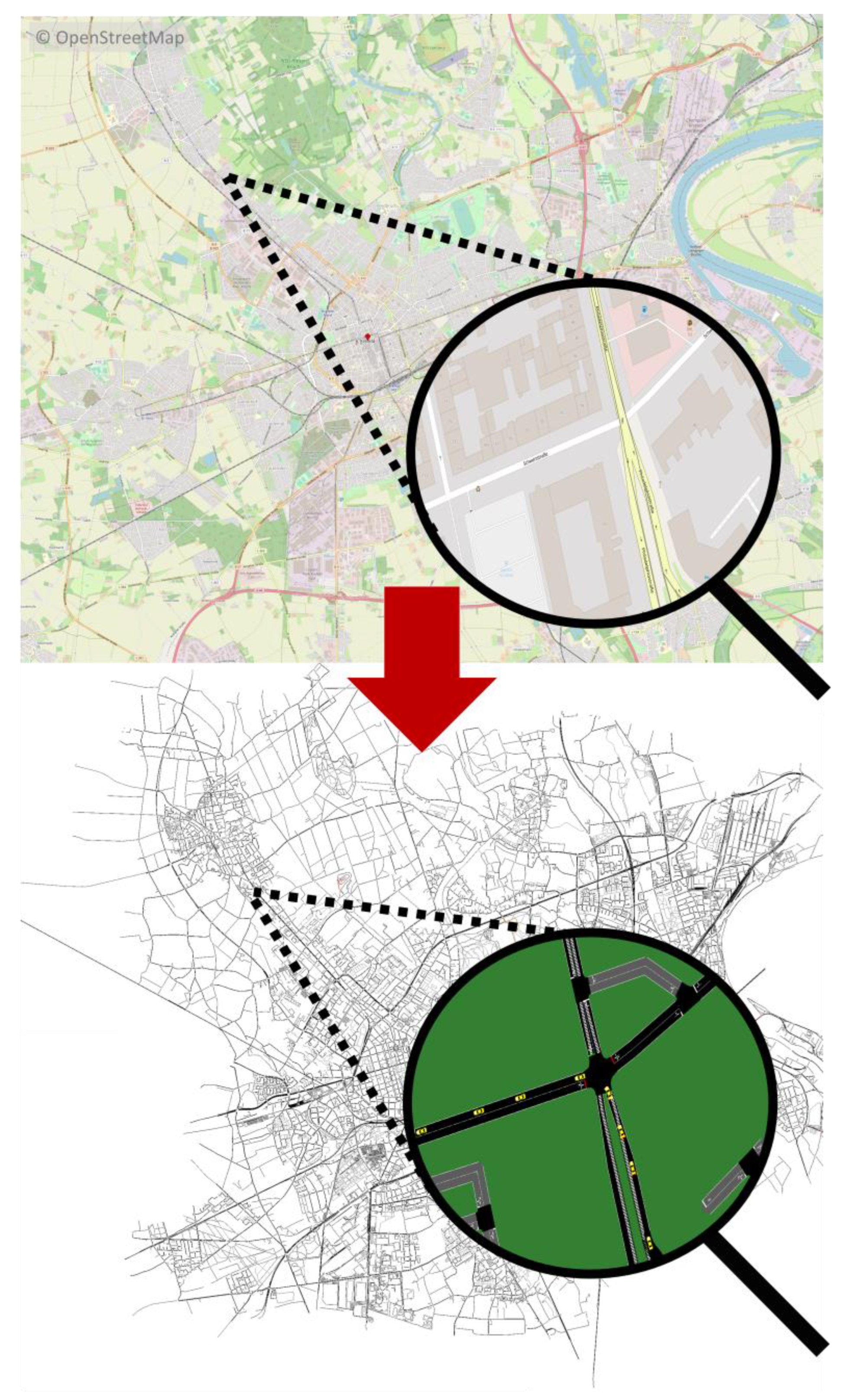
- OpenStreetMap Website. Available online: https://www.openstreetmap.org/ (accessed on 4 April 2023).
- GmbH, S.M. Mobilitätskonzept Krefeld—Potentialbestimmung für Autonome Fahrzeuge im ÖPNV und Aufbau eines multimodalen Verkehrsangebots. 2020. Available online: https://www.zukunft-nachhaltige-mobilitaet.de/projekt-mobilitaetskonzept-krefeld-potentialbestimmung-fuer-autonome-fahrzeuge-im-oepnv-und-aufbau-eines-multimodalen-verkehrsangebots/ (accessed on 7 March 2023).
- Madsen, M.; Gennat, M. Reisewiderstandsbestimmung mit automatisierter Umsteigeerkennung. In Making Connected Mobility Work: Technische und Betriebswirtschaftliche Aspekte; Proff, H., Ed.; Springer Fachmedien Wiesbaden: Wiesbaden, Germany, 2021; pp. 855–870. [Google Scholar]
- Madsen, M.; Spengler, L.; Gennat, M. Entwicklung einer Kennzahl zur Identifikation von Verbesserungspotenzial in der Verkehrsinfrastruktur. In Transforming Mobility—What Next? Technische und Betriebswirtschaftliche Aspekte; Proff, H., Ed.; Springer Fachmedien Wiesbaden: Wiesbaden, Germany, 2022; pp. 355–365. [Google Scholar]
- Spengler, L.; Gennat, M. Fahrzeitermittlung im städtischen Raum mittels Google API. In Making Connected Mobility Work: Technische und Betriebswirtschaftliche Aspekte; Proff, H., Ed.; Springer Fachmedien Wiesbaden: Wiesbaden, Germany, 2021; pp. 839–853. [Google Scholar]
- Malandraki, C.; Daskin, M.S. Time Dependent Vehicle Routing Problems: Formulations, Properties and Heuristic Algorithms. Transp. Sci. 1992, 26, 185–200. [Google Scholar] [CrossRef]
- Dabia, S.; Ropke, S.; van Woensel, T.; De Kok, T. Branch and Price for the Time-Dependent Vehicle Routing Problem with Time Windows. Transp. Sci. 2013, 47, 380–396. [Google Scholar] [CrossRef]
- Montero, A.; Méndez-Díaz, I.; Miranda-Bront, J.J. An integer programming approach for the time-dependent traveling salesman problem with time windows. Comput. Oper. Res. 2017, 88, 280–289. [Google Scholar] [CrossRef]
- Andres Figliozzi, M. The time dependent vehicle routing problem with time windows: Benchmark problems, an efficient solution algorithm, and solution characteristics. Transp. Res. Part E Logist. Transp. Rev. 2012, 48, 616–636. [Google Scholar] [CrossRef]
- Taş, D.; Dellaert, N.; van Woensel, T.; de Kok, T. The time-dependent vehicle routing problem with soft time windows and stochastic travel times. Transp. Res. Part C Emerg. Technol. 2014, 48, 66–83. [Google Scholar] [CrossRef]
- Zhang, T.; Chaovalitwongse, W.A.; Zhang, Y. Integrated Ant Colony and Tabu Search approach for time dependent vehicle routing problems with simultaneous pickup and delivery. J. Comb. Optim. 2014, 28, 288–309. [Google Scholar] [CrossRef]
- Hashimoto, H.; Yagiura, M.; Ibaraki, T. An iterated local search algorithm for the time-dependent vehicle routing problem with time windows. Discret. Optim. 2008, 5, 434–456. [Google Scholar] [CrossRef]
- Friedman, M. A mathematical programming model for optimal scheduling of buses’ departures under deterministic conditions. Transp. Res. 1976, 10, 83–90. [Google Scholar] [CrossRef]
- Gerdts, M.; Lempio, F. Mathematische Optimierungsverfahren des Operations Research; De Gruyter: Berlin, Germany, 2011. [Google Scholar]
- Helmert, I. Modal-Split-Erhebung—Mobilitätsbefragung 2017. 2017. Available online: https://www.krefeld.de/C1257CBD001F275F/files/mobilitaetsbefragung2017_170830.pdf/$file/mobilitaetsbefragung2017_170830.pdf?OpenElement (accessed on 24 February 2023).
- Intraplan Consult GmbH. Standardisierte Bewertung von Verkehrswegeinvestitionen im Öffentlichen Personennahverkehr; Intraplan Consult GmbH: München, Germany, 2023. [Google Scholar]
- Dijkstra, E.W. A note on two problems in connexion with graphs. Numer. Math. 1959, 1, 269–271. [Google Scholar] [CrossRef]
- Bellman, R. On a routing problem. Q. Appl. Math. 1958, 16, 87–90. [Google Scholar] [CrossRef]
- Ford, L.R.J. Network Flow Theory; RAND Corporation: Santa Monica, CA, USA, 1956. [Google Scholar]
- Hart, P.E.; Nilsson, N.J.; Raphael, B. A Formal Basis for the Heuristic Determination of Minimum Cost Paths. IEEE Trans. Syst. Sci. Cybern. 1968, 4, 100–107. [Google Scholar] [CrossRef]
- Caicedo, F.; Blazquez, C.; Miranda, P. Prediction of parking space availability in real time. Expert Syst. Appl. 2012, 39, 7281–7290. [Google Scholar] [CrossRef]
- Awan, F.M.; Saleem, Y.; Minerva, R.; Crespi, N. A Comparative Analysis of Machine/Deep Learning Models for Parking Space Availability Prediction. Sensors 2020, 20, 322. [Google Scholar] [CrossRef] [PubMed]
- Bock, F.; Martino, S.D.; Origlia, A. Smart Parking: Using a Crowd of Taxis to Sense On-Street Parking Space Availability. IEEE Trans. Intell. Transp. Syst. 2020, 21, 496–508. [Google Scholar] [CrossRef]
- Compostella, J.; Fulton, L.M.; De Kleine, R.; Kim, H.C.; Wallington, T.J. Near- (2020) and long-term (2030–2035) costs of automated, electrified, and shared mobility in the United States. Transp. Policy 2020, 85, 54–66. [Google Scholar] [CrossRef]
- Haustein, S. Changes in Mobility Behavior through Changes in the Sociocultural and Physical Environment: A Psychological Perspective; De Gruyter: Berlin, Germany, 2022; pp. 71–81. [Google Scholar]
- Richter, I.; Gabe-Thomas, E.; Queirós, A.M.; Sheppard, S.R.J.; Pahl, S. Advancing the potential impact of future scenarios by integrating psychological principles. Environ. Sci. Policy 2023, 140, 68–79. [Google Scholar] [CrossRef]
- Schubert, M. Verkehrsverflechtungsprognose 2030; Intraplan Consult GmbH: München, Germany, 2014. [Google Scholar]
- Umweltbundesamt. Klimaschutz im Verkehr. Available online: https://www.umweltbundesamt.de/themen/verkehr-laerm/klimaschutz-im-verkehr (accessed on 4 April 2023).
- Hernández, D.F. Public transport, well-being and inequality: Coverage and affordability in the city of Montevideo. Cepal Rev. 2018, 2017, 151–169. [Google Scholar] [CrossRef]
- Scheiner, J. Mobility Biographies and Mobility Socialisation—New Approaches to an Old Research Field. In Life-Oriented Behavioral Research for Urban Policy; Zhang, J., Ed.; Springer: Tokyo, Japan, 2017; pp. 385–401. [Google Scholar]
- Meyer, J.; Becker, H.; Bösch, P.M.; Axhausen, K.W. Autonomous vehicles: The next jump in accessibilities? Res. Transp. Econ. 2017, 62, 80–91. [Google Scholar] [CrossRef]


| Per Operating Hour | Per Year | Per Kilometer |
|---|---|---|
| Driver’s wage | Insurance | Energy |
| Employee training | Inspection | Tires |
| Monitoring | Overhead | Maintenance |
| Additional services |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Spengler, L.; Gößwein, E.; Kranefeld, I.; Liebherr, M.; Kracht, F.E.; Schramm, D.; Gennat, M. From Modeling to Optimizing Sustainable Public Transport: A New Methodological Approach. Sustainability 2023, 15, 8171. https://doi.org/10.3390/su15108171
Spengler L, Gößwein E, Kranefeld I, Liebherr M, Kracht FE, Schramm D, Gennat M. From Modeling to Optimizing Sustainable Public Transport: A New Methodological Approach. Sustainability. 2023; 15(10):8171. https://doi.org/10.3390/su15108171
Chicago/Turabian StyleSpengler, Lukas, Eva Gößwein, Ingmar Kranefeld, Magnus Liebherr, Frédéric Etienne Kracht, Dieter Schramm, and Marc Gennat. 2023. "From Modeling to Optimizing Sustainable Public Transport: A New Methodological Approach" Sustainability 15, no. 10: 8171. https://doi.org/10.3390/su15108171
APA StyleSpengler, L., Gößwein, E., Kranefeld, I., Liebherr, M., Kracht, F. E., Schramm, D., & Gennat, M. (2023). From Modeling to Optimizing Sustainable Public Transport: A New Methodological Approach. Sustainability, 15(10), 8171. https://doi.org/10.3390/su15108171













