A Comparison of Deep Transfer Learning Methods for Land Use and Land Cover Classification
Abstract
1. Introduction
2. Materials and Methods
2.1. Dataset
2.1.1. EuroSAT Dataset
2.1.2. Data Augmentation
2.1.3. Train, Validation and Test Sets
2.2. Methods
2.2.1. A Brief Review of Used Deep Learning Models for Transfer Learning
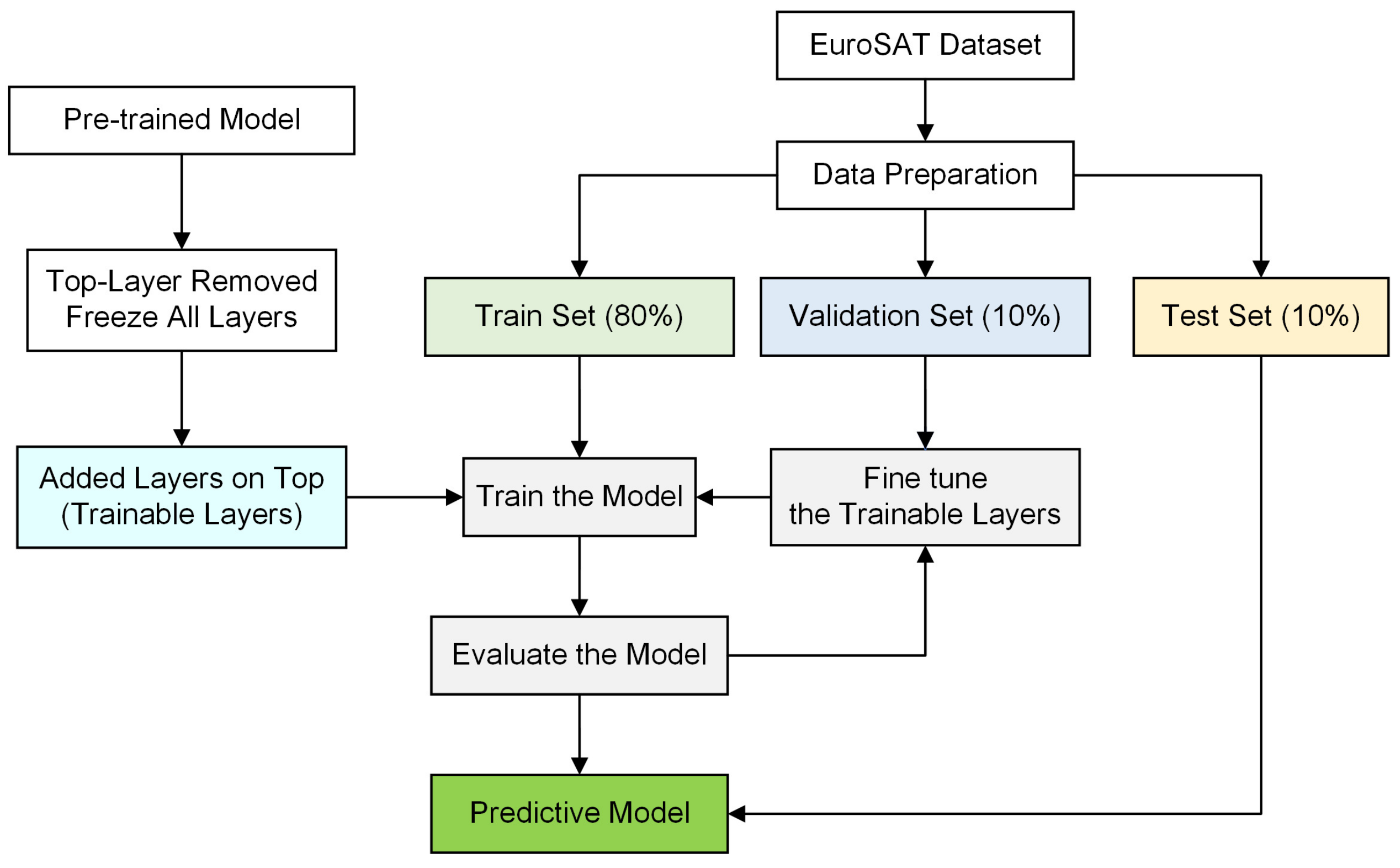
2.2.2. Deep Transfer Learning Methods
- DenseNet121, DenseNet169, and DenseNet201 [40];
- EfficientNetB0–EfficientNetB7 [41];
- EfficientNetV2B0–EfficientNetV2B3 [42];
- InceptionV3 [30];
- NASNetMobile [54];
- RegNetX002, RegNetX004, RegNetX006, RegNetX008, and RegNetX032 [45];
- ResNet50, ResNet101, and ResNet152 [29];
- ResNetRS50, ResNetRS101, ResNetRS152, ResNetRS200, ResNetRS270, ResNetRS350, and ResNetRS420 [50];
- ResNet50V2, ResNet101V2, and ResNet152V2 [55];
- VGG16 and VGG19 [28].
2.2.3. Modifications in Network Architecture
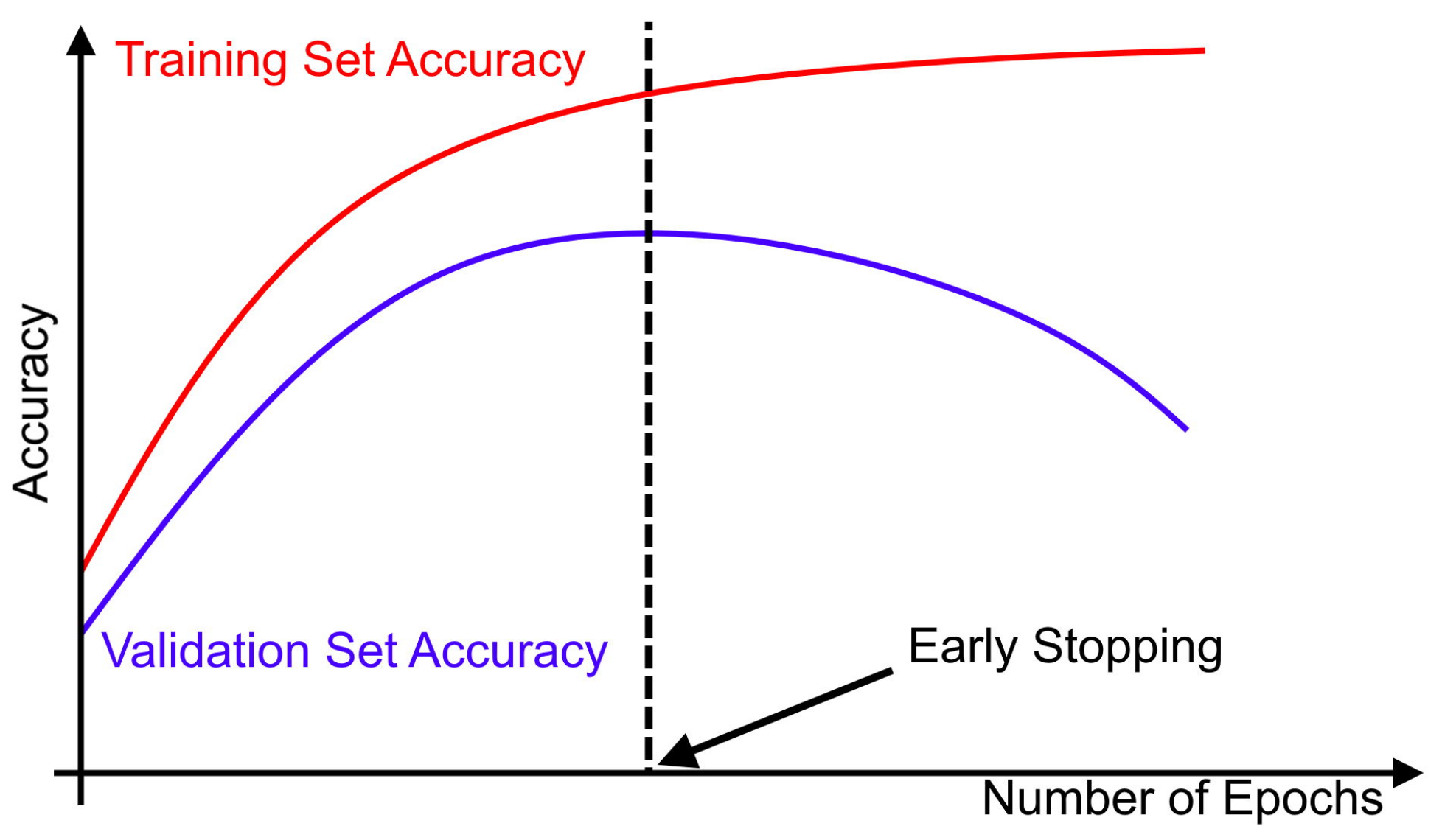
2.2.4. Early Stopping
2.2.5. Categorical Cross-Entropy Loss Function
2.2.6. Optimizations and Learning Rate
2.2.7. Accuracy Metrics
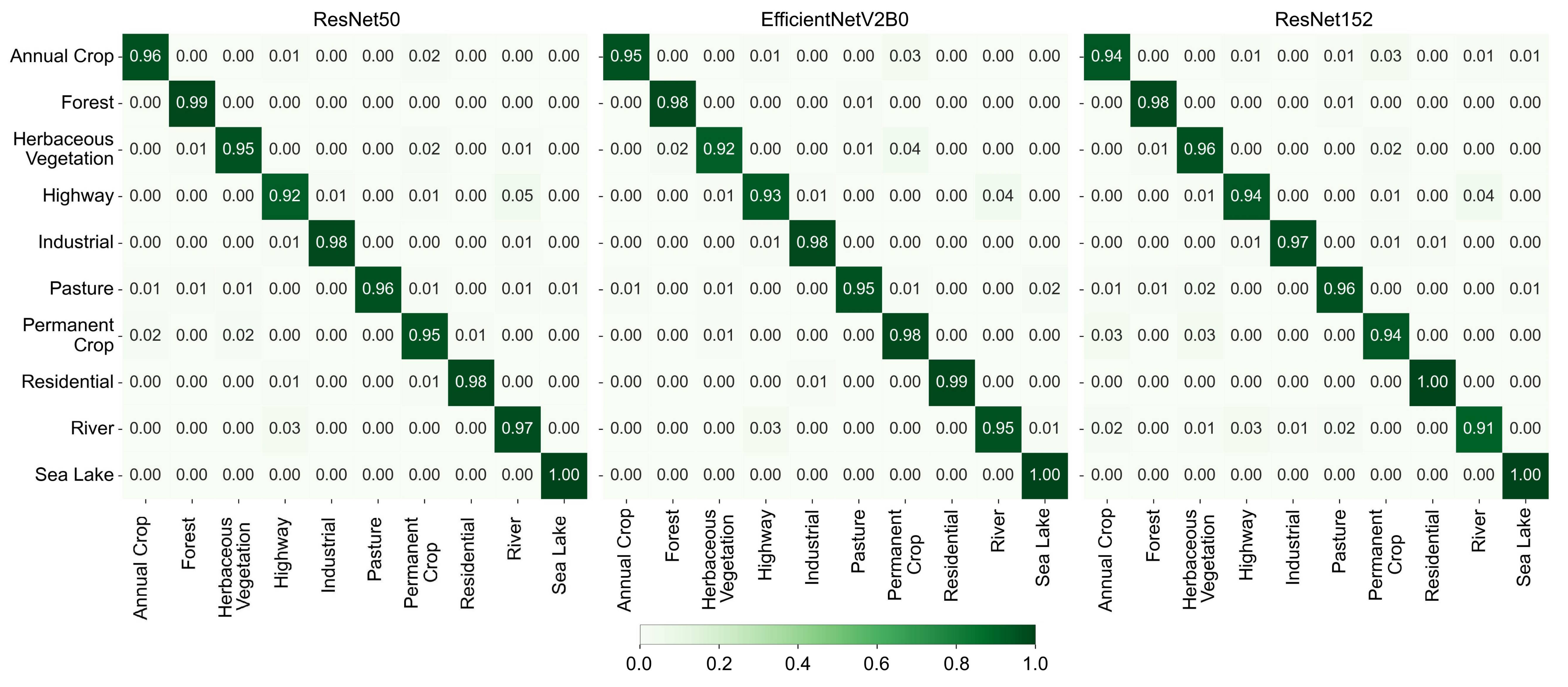
3. Results
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Dastour, H.; Ghaderpour, E.; Zaghloul, M.S.; Farjad, B.; Gupta, A.; Eum, H.; Achari, G.; Hassan, Q.K. Wavelet-based spatiotemporal analyses of climate and vegetation for the Athabasca river basin in Canada. Int. J. Appl. Earth Obs. Geoinf. 2022, 114, 103044. [Google Scholar] [CrossRef]
- Afrin, S.; Gupta, A.; Farjad, B.; Ahmed, M.R.; Achari, G.; Hassan, Q.K. Development of land-use/land-cover maps using Landsat-8 and MODIS data, and their integration for hydro-ecological applications. Sensors 2019, 19, 4891. [Google Scholar] [CrossRef] [PubMed]
- Akbar, T.A.; Hassan, Q.K.; Achari, G. Clusterization of Surface Water Quality and Its Relation to Climate and Land Use/Cover. J. Environ. Prot. 2013, 4, 333–343. [Google Scholar] [CrossRef]
- Abdullah, A.Y.M.; Masrur, A.; Adnan, M.S.G.; Baky, M.; Al, A.; Hassan, Q.K.; Dewan, A. Spatio-temporal patterns of land use/land cover change in the heterogeneous coastal region of Bangladesh between 1990 and 2017. Remote Sens. 2019, 11, 790. [Google Scholar] [CrossRef]
- Liu, X.; He, J.; Yao, Y.; Zhang, J.; Liang, H.; Wang, H.; Hong, Y. Classifying urban land use by integrating remote sensing and social media data. Int. J. Geogr. Inf. Sci. 2017, 31, 1675–1696. [Google Scholar] [CrossRef]
- Huang, Z.; Dumitru, C.O.; Pan, Z.; Lei, B.; Datcu, M. Classification of large-scale high-resolution SAR images with deep transfer learning. IEEE Geosci. Remote Sens. Lett. 2020, 18, 107–111. [Google Scholar] [CrossRef]
- Mc Cutchan, M.; Comber, A.J.; Giannopoulos, I.; Canestrini, M. Semantic boosting: Enhancing deep learning based LULC classification. Remote Sens. 2021, 13, 3197. [Google Scholar] [CrossRef]
- Phan, T.N.; Kuch, V.; Lehnert, L.W. Land cover classification using Google Earth Engine and random forest classifier—The role of image composition. Remote Sens. 2020, 12, 2411. [Google Scholar] [CrossRef]
- Moharram, M.A.; Sundaram, D.M. Land Use and Land Cover Classification with Hyperspectral Data: A comprehensive review of methods, challenges and future directions. Neurocomputing 2023, 536, 90–113. [Google Scholar] [CrossRef]
- Zhang, J.; Wang, H.; Wang, Y.; Zhou, Q.; Li, Y. Deep network based on up and down blocks using wavelet transform and successive multi-scale spatial attention for cloud detection. Remote Sens. Environ. 2021, 261, 112483. [Google Scholar] [CrossRef]
- Gómez, P.; Meoni, G. MSMatch: Semisupervised Multispectral Scene Classification With Few Labels. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2021, 14, 11643–11654. [Google Scholar] [CrossRef]
- Naushad, R.; Kaur, T.; Ghaderpour, E. Deep transfer learning for land use and land cover classification: A comparative study. Sensors 2021, 21, 8083. [Google Scholar] [CrossRef]
- Günen, M.A. Performance comparison of deep learning and machine learning methods in determining wetland water areas using EuroSAT dataset. Environ. Sci. Pollut. Res. 2022, 29, 21092–21106. [Google Scholar] [CrossRef]
- Qi, K.; Wu, H.; Shen, C.; Gong, J. Land-use scene classification in high-resolution remote sensing images using improved correlatons. IEEE Geosci. Remote Sens. Lett. 2015, 12, 2403–2407. [Google Scholar]
- Marmanis, D.; Datcu, M.; Esch, T.; Stilla, U. Deep learning earth observation classification using ImageNet pretrained networks. IEEE Geosci. Remote Sens. Lett. 2015, 13, 105–109. [Google Scholar] [CrossRef]
- Das, A.; Giri, R.; Chourasia, G.; Bala, A.A. Classification of retinal diseases using transfer learning approach. In Proceedings of the 2019 International Conference on Communication and Electronics Systems (ICCES), Coimbatore, India, 17–19 July 2019; pp. 2080–2084. [Google Scholar]
- Pan, S.J.; Yang, Q. A survey on transfer learning. IEEE Trans. Knowl. Data Eng. 2009, 22, 1345–1359. [Google Scholar] [CrossRef]
- Tan, C.; Sun, F.; Kong, T.; Zhang, W.; Yang, C.; Liu, C. A survey on deep transfer learning. In Proceedings of the International Conference on Artificial Neural Networks, Rhodes, Greece, 4–7 October 2018; pp. 270–279. [Google Scholar]
- Zhuang, F.; Qi, Z.; Duan, K.; Xi, D.; Zhu, Y.; Zhu, H.; Xiong, H.; He, Q. A comprehensive survey on transfer learning. Proc. IEEE 2020, 109, 43–76. [Google Scholar] [CrossRef]
- Alem, A.; Kumar, S. Transfer learning models for land cover and land use classification in remote sensing image. Appl. Artif. Intell. 2022, 36, 2014192. [Google Scholar] [CrossRef]
- Tseng, H.H.; Yang, M.D.; Saminathan, R.; Hsu, Y.C.; Yang, C.Y.; Wu, D.H. Rice Seedling Detection in UAV Images Using Transfer Learning and Machine Learning. Remote Sens. 2022, 14, 2837. [Google Scholar] [CrossRef]
- Chen, J.; Sun, J.; Li, Y.; Hou, C. Object detection in remote sensing images based on deep transfer learning. Multimed. Tools Appl. 2022, 81, 12093–12109. [Google Scholar]
- Hilal, A.M.; Al-Wesabi, F.N.; Alzahrani, K.J.; Al Duhayyim, M.; Ahmed Hamza, M.; Rizwanullah, M.; García Díaz, V. Deep transfer learning based fusion model for environmental remote sensing image classification model. Eur. J. Remote Sens. 2022, 55, 12–23. [Google Scholar] [CrossRef]
- Song, H.; Yang, W. GSCCTL: A general semi-supervised scene classification method for remote sensing images based on clustering and transfer learning. Int. J. Remote Sens. 2022, 43, 5976–6000. [Google Scholar] [CrossRef]
- Dumitru, C.O.; Schwarz, G.; Datcu, M. Land cover semantic annotation derived from high-resolution SAR images. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2016, 9, 2215–2232. [Google Scholar] [CrossRef]
- Li, W.; Wang, Z.; Wang, Y.; Wu, J.; Wang, J.; Jia, Y.; Gui, G. Classification of high-spatial-resolution remote sensing scenes method using transfer learning and deep convolutional neural network. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2020, 13, 1986–1995. [Google Scholar] [CrossRef]
- Zhong, Y.; Han, X.; Zhang, L. Multi-class geospatial object detection based on a position-sensitive balancing framework for high spatial resolution remote sensing imagery. ISPRS J. Photogramm. Remote Sens. 2018, 138, 281–294. [Google Scholar] [CrossRef]
- Simonyan, K.; Zisserman, A. Very deep convolutional networks for large-scale image recognition. arXiv 2014, arXiv:1409.1556. [Google Scholar]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Deep residual learning for image recognition. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 27–30 June 2016; pp. 770–778. [Google Scholar]
- Szegedy, C.; Vanhoucke, V.; Ioffe, S.; Shlens, J.; Wojna, Z. Rethinking the inception architecture for computer vision. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 27–30 June 2016; pp. 2818–2826. [Google Scholar]
- Helber, P.; Bischke, B.; Dengel, A.; Borth, D. EuroSAT: A novel dataset and deep learning benchmark for land use and land cover classification. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2019, 12, 2217–2226. [Google Scholar] [CrossRef]
- Helber, P. EuroSAT: Land Use and Land Cover Classification with Sentinel-2. 2019. Available online: https://github.com/phelber/EuroSAT (accessed on 1 October 2022).
- Helber, P.; Bischke, B.; Dengel, A.; Borth, D. Introducing EuroSAT: A Novel Dataset and Deep Learning Benchmark for Land Use and Land Cover Classification. In Proceedings of the IGARSS 2018-2018 IEEE International Geoscience and Remote Sensing Symposium, Valencia, Spain, 22–27 July 2018; pp. 204–207. [Google Scholar]
- Al-Qizwini, M.; Barjasteh, I.; Al-Qassab, H.; Radha, H. Deep learning algorithm for autonomous driving using GoogLeNet. In Proceedings of the 2017 IEEE Intelligent Vehicles Symposium (IV), Los Angeles, CA, USA, 11–14 June 2017; pp. 89–96. [Google Scholar]
- Li, J.; Lin, D.; Wang, Y.; Xu, G.; Zhang, Y.; Ding, C.; Zhou, Y. Deep discriminative representation learning with attention map for scene classification. Remote Sens. 2020, 12, 1366. [Google Scholar] [CrossRef]
- Yassine, H.; Tout, K.; Jaber, M. Improving LULC Classification from Satellite Imagery Using Deep Learning–EuroSAT Dataset. ISPRS-Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2021, 43, 369–376. [Google Scholar] [CrossRef]
- Mikołajczyk, A.; Grochowski, M. Data augmentation for improving deep learning in image classification problem. In Proceedings of the 2018 International Interdisciplinary PhD Workshop (IIPhDW), Swinoujscie, Poland, 9–12 May 2018; pp. 117–122. [Google Scholar]
- Shorten, C.; Khoshgoftaar, T.M. A survey on image data augmentation for deep learning. J. Big Data 2019, 6, 1–48. [Google Scholar]
- Eelbode, T.; Sinonquel, P.; Maes, F.; Bisschops, R. Pitfalls in training and validation of deep learning systems. Best Pract. Res. Clin. Gastroenterol. 2021, 52, 101712. [Google Scholar] [CrossRef]
- Huang, G.; Liu, Z.; Van Der Maaten, L.; Weinberger, K.Q. Densely connected convolutional networks. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Honolulu, HI, USA, 21–26 July 2017; pp. 4700–4708. [Google Scholar]
- Tan, M.; Le, Q. EfficientNet: Rethinking model scaling for convolutional neural networks. In Proceedings of the International Conference on Machine Learning, PMLR, Long Beach, CA, USA, 9–15 June 2019; pp. 6105–6114. [Google Scholar]
- Tan, M.; Le, Q. EfficientNetV2: Smaller models and faster training. In Proceedings of the 38th International Conference on Machine Learning, Virtual, 18–24 July 2021; pp. 10096–10106. [Google Scholar]
- Howard, A.G.; Zhu, M.; Chen, B.; Kalenichenko, D.; Wang, W.; Weyand, T.; Andreetto, M.; Adam, H. MobileNets: Efficient convolutional neural networks for mobile vision applications. arXiv 2017, arXiv:1704.04861. [Google Scholar]
- Sandler, M.; Howard, A.; Zhu, M.; Zhmoginov, A.; Chen, L.C. MobileNetV2: Inverted residuals and linear bottlenecks. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–22 June 2018; pp. 4510–4520. [Google Scholar]
- Radosavovic, I.; Kosaraju, R.P.; Girshick, R.; He, K.; Dollár, P. Designing network design spaces. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Seattle, WA, USA, 14–19 June 2020; pp. 10428–10436. [Google Scholar]
- Krizhevsky, A.; Sutskever, I.; Hinton, G.E. ImageNet classification with deep convolutional neural networks. Commun. ACM 2017, 60, 84–90. [Google Scholar] [CrossRef]
- Shaha, M.; Pawar, M. Transfer learning for image classification. In Proceedings of the 2018 Second International Conference on Electronics, Communication and Aerospace Technology (ICECA), Coimbatore, India, 29–31 March 2018; pp. 656–660. [Google Scholar]
- Russakovsky, O.; Deng, J.; Su, H.; Krause, J.; Satheesh, S.; Ma, S.; Huang, Z.; Karpathy, A.; Khosla, A.; Bernstein, M.; et al. ImageNet Large Scale Visual Recognition Challenge. Int. J. Comput. Vis. (IJCV) 2015, 115, 211–252. [Google Scholar] [CrossRef]
- Deng, J.; Dong, W.; Socher, R.; Li, L.J.; Li, K.; Fei-Fei, L. ImageNet: A large-scale hierarchical image database. In Proceedings of the 2009 IEEE Conference on Computer Vision and Pattern Recognition, Miami, FL, USA, 20–25 June 2009; pp. 248–255. [Google Scholar]
- Bello, I.; Fedus, W.; Du, X.; Cubuk, E.D.; Srinivas, A.; Lin, T.Y.; Shlens, J.; Zoph, B. Revisiting ResNets: Improved training and scaling strategies. Adv. Neural Inf. Process. Syst. 2021, 34, 22614–22627. [Google Scholar]
- Gong, Z.; Zhong, P.; Yu, Y.; Hu, W. Diversity-promoting deep structural metric learning for remote sensing scene classification. IEEE Trans. Geosci. Remote Sens. 2017, 56, 371–390. [Google Scholar] [CrossRef]
- Agarwal, A.; Vatsa, M.; Singh, R.; Ratha, N. Intelligent and adaptive mixup technique for adversarial robustness. In Proceedings of the 2021 IEEE International Conference on Image Processing (ICIP), Anchorage, AK, USA, 19–22 September 2021; pp. 824–828. [Google Scholar]
- Weiss, K.; Khoshgoftaar, T.M.; Wang, D. A survey of transfer learning. J. Big Data 2016, 3, 1–40. [Google Scholar] [CrossRef]
- Zoph, B.; Vasudevan, V.; Shlens, J.; Le, Q.V. Learning transferable architectures for scalable image recognition. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–22 June 2018; pp. 8697–8710. [Google Scholar]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Identity mappings in deep residual networks. In Proceedings of the European Conference on Computer Vision, Amsterdam, The Netherlands, 11–14 October 2016; pp. 630–645. [Google Scholar]
- Abadi, M.; Barham, P.; Chen, J.; Chen, Z.; Davis, A.; Dean, J.; Devin, M.; Ghemawat, S.; Irving, G.; Isard, M.; et al. TensorFlow: A system for Large-Scale machine learning. In Proceedings of the 12th USENIX Symposium on Operating Systems Design and Implementation (OSDI 16), Savannah, GA, USA, 2–4 November 2016; pp. 265–283. [Google Scholar]
- Hsiao, T.Y.; Chang, Y.C.; Chou, H.H.; Chiu, C.T. Filter-based deep-compression with global average pooling for convolutional networks. J. Syst. Archit. 2019, 95, 9–18. [Google Scholar]
- Li, Y.; Yuan, Y. Convergence analysis of two-layer neural networks with ReLU activation. In Proceedings of the 31st Conference on Neural Information Processing Systems (NIPS 2017), Long Beach, CA, USA, 4–9 December 2017. [Google Scholar]
- Dunne, R.A.; Campbell, N.A. On the pairing of the softmax activation and cross-entropy penalty functions and the derivation of the softmax activation function. In Proceedings of the 8th Australasian Conference on Neural Networks, Melbourne, Australia, 3–4 April 1997; Volume 181, p. 185. [Google Scholar]
- Sattarifar, A.; Nestorović, T. Damage localization and characterization using one-dimensional convolutional neural network and a sparse network of transducers. Eng. Appl. Artif. Intell. 2022, 115, 105273. [Google Scholar] [CrossRef]
- Milanova, I.; Sarvanoska, K.; Srbinoski, V.; Gjoreski, H. Automatic text generation in Macedonian using recurrent neural networks. In Proceedings of the International Conference on ICT Innovations, Ohrid, North Macedonia, 17–19 October 2019; pp. 1–12. [Google Scholar]
- Kingma, D.P.; Ba, J. Adam: A method for stochastic optimization. arXiv 2014, arXiv:1412.6980. [Google Scholar]
- Yu, X.H.; Chen, G.A.; Cheng, S.X. Dynamic learning rate optimization of the backpropagation algorithm. IEEE Trans. Neural Netw. 1995, 6, 669–677. [Google Scholar] [PubMed]
- Zaheer, M.; Reddi, S.; Sachan, D.; Kale, S.; Kumar, S. Adaptive methods for nonconvex optimization. In Proceedings of the 32nd Conference on Neural Information Processing Systems (NeurIPS 2018), Montréal, QC, Canada, 3–8 December 2018. [Google Scholar]
- Cohen, J. A coefficient of agreement for nominal scales. Educ. Psychol. Meas. 1960, 20, 37–46. [Google Scholar] [CrossRef]
- Artstein, R.; Poesio, M. Inter-coder agreement for computational linguistics. Comput. Linguist. 2008, 34, 555–596. [Google Scholar] [CrossRef]
- Buitinck, L.; Louppe, G.; Blondel, M.; Pedregosa, F.; Mueller, A.; Grisel, O.; Niculae, V.; Prettenhofer, P.; Gramfort, A.; Grobler, J.; et al. API design for machine learning software: Experiences from the scikit-learn project. In Proceedings of the ECML PKDD Workshop: Languages for Data Mining and Machine Learning, Prague, Czech Republic, 23–27 September 2013; pp. 108–122. [Google Scholar]
- Warrens, M.J. Cohen’s kappa is a weighted average. Stat. Methodol. 2011, 8, 473–484. [Google Scholar] [CrossRef]
- Powers, D. Evaluation: From Precision, Recall and F-Measure to ROC, Informedness, Markedness & Correlation. J. Mach. Learn. Technol. 2011, 2, 37–63. [Google Scholar]
- Zou, Q.; Xie, S.; Lin, Z.; Wu, M.; Ju, Y. Finding the best classification threshold in imbalanced classification. Big Data Res. 2016, 5, 2–8. [Google Scholar] [CrossRef]


| Layer Name | Layer Type | Size of Feature Map | Activation Function |
|---|---|---|---|
| Global Avg Pooling 2D | Global Average Pooling 2D | Varies for all models | N/A |
| Flatten | Flatten | Varies for all models | N/A |
| Dense | Dense | Varies for all models | relu |
| Dense_output | Dense | 10 | softmax |
| Rank | Model Name | Epoch | Train Time (s) | Loss | Accuracy | Rank | Model Name | Epoch | Train Time (s) | Loss | Accuracy |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | ResNet50 | 20 | 644.5 | 0.091 | 0.975 | 21 | RegNetX004 | 26 | 390.1 | 0.138 | 0.954 |
| 2 | EfficientNetV2B0 | 20 | 367.5 | 0.087 | 0.972 | 22 | RegNetX006 | 17 | 249.2 | 0.138 | 0.954 |
| 3 | ResNet152 | 17 | 1265.2 | 0.087 | 0.971 | 23 | DenseNet169 | 11 | 454.3 | 0.138 | 0.953 |
| 4 | ResNetRS50 | 19 | 742.9 | 0.094 | 0.969 | 24 | EfficientNetB4 | 15 | 784.9 | 0.139 | 0.953 |
| 5 | ResNetRS152 | 17 | 1419.3 | 0.106 | 0.968 | 25 | ResNetRS350 | 15 | 3049.3 | 0.150 | 0.951 |
| 6 | ResNet101 | 16 | 858.7 | 0.103 | 0.967 | 26 | MobileNet | 12 | 152.7 | 0.146 | 0.950 |
| 7 | RegNetX008 | 23 | 423.7 | 0.120 | 0.966 | 27 | VGG19 | 14 | 658.6 | 0.156 | 0.949 |
| 8 | ResNetRS200 | 16 | 1988.2 | 0.106 | 0.964 | 28 | ResNet101V2 | 12 | 650.6 | 0.156 | 0.948 |
| 9 | ResNetRS270 | 18 | 2991.4 | 0.109 | 0.964 | 29 | ResNetRS420 | 14 | 3430.0 | 0.163 | 0.946 |
| 10 | EfficientNetV2B1 | 15 | 340.2 | 0.116 | 0.963 | 30 | VGG16 | 12 | 463.1 | 0.165 | 0.945 |
| 11 | ResNetRS101 | 12 | 728.2 | 0.121 | 0.960 | 31 | MobileNetV2 | 15 | 229.2 | 0.169 | 0.944 |
| 12 | EfficientNetV2B2 | 12 | 308.6 | 0.132 | 0.957 | 32 | EfficientNetB5 | 14 | 979.9 | 0.168 | 0.944 |
| 13 | RegNetX032 | 13 | 534.7 | 0.125 | 0.957 | 33 | EfficientNetB7 | 17 | 2106.8 | 0.167 | 0.943 |
| 14 | EfficientNetV2B3 | 13 | 416.3 | 0.124 | 0.957 | 34 | RegNetX002 | 19 | 194.4 | 0.165 | 0.943 |
| 15 | EfficientNetB2 | 14 | 441.2 | 0.128 | 0.957 | 35 | ResNet50V2 | 11 | 332.1 | 0.179 | 0.942 |
| 16 | DenseNet201 | 11 | 558.2 | 0.128 | 0.956 | 36 | EfficientNetB6 | 22 | 2054.6 | 0.172 | 0.942 |
| 17 | EfficientNetB0 | 12 | 264.6 | 0.133 | 0.956 | 37 | ResNet152V2 | 11 | 812.1 | 0.187 | 0.937 |
| 18 | DenseNet121 | 13 | 419.4 | 0.133 | 0.955 | 38 | NASNetMobile | 13 | 324.0 | 0.224 | 0.925 |
| 19 | EfficientNetB1 | 14 | 438.6 | 0.133 | 0.955 | 39 | InceptionV3 | 14 | 278.4 | 0.256 | 0.918 |
| 20 | EfficientNetB3 | 13 | 526.0 | 0.136 | 0.955 |
| Model Name | Set | Kappa | Loss | Accuracy |
|---|---|---|---|---|
| ResNet50 | Train | 0.9900 | 0.0304 | 0.9910 |
| Validation | 0.9629 | 0.1226 | 0.9667 | |
| Test | 0.9641 | 0.1189 | 0.9678 | |
| EfficientNetV2B0 | Train | 0.9789 | 0.0572 | 0.9811 |
| Validation | 0.9662 | 0.0969 | 0.9696 | |
| Test | 0.9600 | 0.1064 | 0.9641 | |
| ResNet152 | Train | 0.9864 | 0.0395 | 0.9878 |
| Validation | 0.9613 | 0.1063 | 0.9652 | |
| Test | 0.9559 | 0.1153 | 0.9604 |
| (a) ResNet50 | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| Train | Validation | Test | |||||||
| Class | Precision | Recall | F1-Score | Precision | Recall | F1-Score | Precision | Recall | F1-Score |
| Annual Crop | 0.996 | 0.989 | 0.992 | 0.987 | 0.954 | 0.970 | 0.967 | 0.964 | 0.966 |
| Forest | 0.995 | 0.997 | 0.996 | 0.990 | 0.983 | 0.986 | 0.986 | 0.993 | 0.989 |
| Herbaceous Vegetation | 0.990 | 0.983 | 0.986 | 0.980 | 0.964 | 0.972 | 0.975 | 0.954 | 0.964 |
| Highway | 0.986 | 0.982 | 0.984 | 0.933 | 0.925 | 0.929 | 0.948 | 0.916 | 0.932 |
| Industrial | 0.996 | 0.993 | 0.995 | 0.992 | 0.964 | 0.978 | 0.988 | 0.981 | 0.984 |
| Pasture | 0.981 | 0.989 | 0.985 | 0.951 | 0.947 | 0.949 | 0.974 | 0.964 | 0.969 |
| Permanent Crop | 0.983 | 0.989 | 0.986 | 0.920 | 0.982 | 0.950 | 0.933 | 0.950 | 0.941 |
| Residential | 0.996 | 1.000 | 0.998 | 0.980 | 0.997 | 0.988 | 0.987 | 0.984 | 0.986 |
| River | 0.980 | 0.988 | 0.984 | 0.929 | 0.943 | 0.936 | 0.918 | 0.966 | 0.941 |
| Sea Lake | 0.999 | 0.998 | 0.999 | 0.987 | 0.997 | 0.992 | 0.990 | 1.000 | 0.995 |
| Accuracy | 0.991 | 0.991 | 0.991 | 0.967 | 0.967 | 0.967 | 0.968 | 0.968 | 0.968 |
| Macro avg | 0.990 | 0.991 | 0.991 | 0.965 | 0.966 | 0.965 | 0.967 | 0.967 | 0.967 |
| Weighted avg | 0.991 | 0.991 | 0.991 | 0.967 | 0.967 | 0.967 | 0.968 | 0.968 | 0.968 |
| (b) EfficientNetV2B0 | |||||||||
| Train | Validation | Test | |||||||
| Class | Precision | Recall | F1-Score | Precision | Recall | F1-Score | Precision | Recall | F1-Score |
| Annual Crop | 0.981 | 0.988 | 0.984 | 0.973 | 0.980 | 0.976 | 0.989 | 0.951 | 0.970 |
| Forest | 0.983 | 0.991 | 0.987 | 0.983 | 0.986 | 0.984 | 0.976 | 0.976 | 0.976 |
| Herbaceous Vegetation | 0.989 | 0.939 | 0.964 | 0.984 | 0.940 | 0.961 | 0.975 | 0.920 | 0.946 |
| Highway | 0.975 | 0.972 | 0.973 | 0.944 | 0.944 | 0.944 | 0.944 | 0.933 | 0.939 |
| Industrial | 0.992 | 0.995 | 0.993 | 0.975 | 0.988 | 0.981 | 0.977 | 0.984 | 0.980 |
| Pasture | 0.965 | 0.968 | 0.967 | 0.966 | 0.952 | 0.959 | 0.948 | 0.948 | 0.948 |
| Permanent Crop | 0.953 | 0.983 | 0.968 | 0.932 | 0.982 | 0.957 | 0.903 | 0.984 | 0.941 |
| Residential | 0.992 | 0.997 | 0.995 | 0.993 | 0.993 | 0.993 | 0.990 | 0.990 | 0.990 |
| River | 0.977 | 0.981 | 0.979 | 0.936 | 0.933 | 0.934 | 0.947 | 0.955 | 0.951 |
| Sea Lake | 0.994 | 0.996 | 0.995 | 0.993 | 0.993 | 0.993 | 0.977 | 1.000 | 0.988 |
| Accuracy | 0.981 | 0.981 | 0.981 | 0.970 | 0.970 | 0.970 | 0.964 | 0.964 | 0.964 |
| Macro avg | 0.980 | 0.981 | 0.980 | 0.968 | 0.969 | 0.968 | 0.962 | 0.964 | 0.963 |
| Weighted avg | 0.981 | 0.981 | 0.981 | 0.970 | 0.970 | 0.970 | 0.965 | 0.964 | 0.964 |
| (c) ResNet152 | |||||||||
| Train | Validation | Test | |||||||
| Class | Precision | Recall | F1-Score | Precision | Recall | F1-Score | Precision | Recall | F1-Score |
| Annual Crop | 0.989 | 0.987 | 0.988 | 0.956 | 0.966 | 0.961 | 0.953 | 0.943 | 0.948 |
| Forest | 0.994 | 0.996 | 0.995 | 0.976 | 0.989 | 0.983 | 0.990 | 0.979 | 0.984 |
| Herbaceous Vegetation | 0.981 | 0.984 | 0.983 | 0.967 | 0.964 | 0.966 | 0.950 | 0.962 | 0.956 |
| Highway | 0.978 | 0.981 | 0.979 | 0.937 | 0.915 | 0.925 | 0.933 | 0.940 | 0.936 |
| Industrial | 0.997 | 0.984 | 0.990 | 0.992 | 0.972 | 0.982 | 0.988 | 0.966 | 0.977 |
| Pasture | 0.991 | 0.983 | 0.987 | 0.956 | 0.952 | 0.954 | 0.932 | 0.962 | 0.947 |
| Permanent Crop | 0.979 | 0.977 | 0.978 | 0.958 | 0.958 | 0.958 | 0.929 | 0.939 | 0.934 |
| Residential | 0.988 | 0.999 | 0.993 | 0.983 | 0.997 | 0.990 | 0.987 | 0.997 | 0.992 |
| River | 0.986 | 0.981 | 0.984 | 0.936 | 0.936 | 0.936 | 0.943 | 0.906 | 0.924 |
| Sea Lake | 0.994 | 0.999 | 0.996 | 0.984 | 0.990 | 0.987 | 0.983 | 0.997 | 0.990 |
| Accuracy | 0.988 | 0.988 | 0.988 | 0.965 | 0.965 | 0.965 | 0.960 | 0.960 | 0.960 |
| Macro avg | 0.988 | 0.987 | 0.987 | 0.964 | 0.964 | 0.964 | 0.959 | 0.959 | 0.959 |
| Weighted avg | 0.988 | 0.988 | 0.988 | 0.965 | 0.965 | 0.965 | 0.960 | 0.960 | 0.960 |
| Predicted Probability | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Actual Class | Annual Crop | Forest | Herbaceous Vegetation | Highway | Industrial | Pasture | Permanent Crop | Residential | River | Sea Lake |
| Annual Crop | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| Highway | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 |
| Residential | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 |
| Sea Lake | 0 | 0 | 0 | 0 | 0 | 0.0633 | 0 | 0 | 0 | 0.9367 |
| Highway | 0.0050 | 0 | 0 | 0.9709 | 0.0140 | 0 | 0 | 0 | 0.0101 | 0 |
| Sea Lake | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 |
| Sea Lake | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 |
| Permanent Crop | 0 | 0 | 0 | 0.0411 | 0 | 0 | 0.9589 | 0 | 0 | 0 |
| Pasture | 0 | 0.0036 | 0.0026 | 0.0001 | 0 | 0.9914 | 0 | 0 | 0.0022 | 0 |
| Highway | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 |
| Sea Lake | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 |
| River | 0 | 0 | 0 | 0.0035 | 0 | 0 | 0 | 0 | 0.9965 | 0 |
| Highway | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 |
| Forest | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| Sea Lake | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 |
| Annual Crop | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| Industrial | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 |
| Sea Lake | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 |
| Annual Crop | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| Residential | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 |
| Forest | 0 | 0.9988 | 0.0004 | 0.0003 | 0 | 0.0005 | 0 | 0 | 0 | 0 |
| Herbaceous Vegetation | 0 | 0 | 0.9998 | 0 | 0 | 0 | 0.0002 | 0 | 0 | 0 |
| Pasture | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 |
| Herbaceous Vegetation | 0 | 0 | 0.9998 | 0 | 0 | 0.0001 | 0.0001 | 0 | 0 | 0 |
| Permanent Crop | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 |
| Permanent Crop | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 |
| Industrial | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 |
| Annual Crop | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| Forest | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| Residential | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 |
| Highway | 0 | 0 | 0 | 0.9996 | 0 | 0 | 0 | 0 | 0.0004 | 0 |
| Permanent Crop | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 |
| Highway | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 |
| Residential | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 |
| Sea Lake | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 |
| Pasture | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 |
| Forest | 0 | 0.9934 | 0.0066 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| Herbaceous Vegetation | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| Pasture | 0 | 0 | 0.0143 | 0.9465 | 0.0008 | 0.0247 | 0.0047 | 0.0090 | 0 | 0 |
| Permanent Crop | 0.0120 | 0 | 0.0196 | 0.0002 | 0.0001 | 0.0039 | 0.9642 | 0 | 0 | 0 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dastour, H.; Hassan, Q.K. A Comparison of Deep Transfer Learning Methods for Land Use and Land Cover Classification. Sustainability 2023, 15, 7854. https://doi.org/10.3390/su15107854
Dastour H, Hassan QK. A Comparison of Deep Transfer Learning Methods for Land Use and Land Cover Classification. Sustainability. 2023; 15(10):7854. https://doi.org/10.3390/su15107854
Chicago/Turabian StyleDastour, Hatef, and Quazi K. Hassan. 2023. "A Comparison of Deep Transfer Learning Methods for Land Use and Land Cover Classification" Sustainability 15, no. 10: 7854. https://doi.org/10.3390/su15107854
APA StyleDastour, H., & Hassan, Q. K. (2023). A Comparison of Deep Transfer Learning Methods for Land Use and Land Cover Classification. Sustainability, 15(10), 7854. https://doi.org/10.3390/su15107854







