A Hybrid Forecasting Model to Simulate the Runoff of the Upper Heihe River
Abstract
1. Introduction
2. Materials and Methods
2.1. Study Area and Data
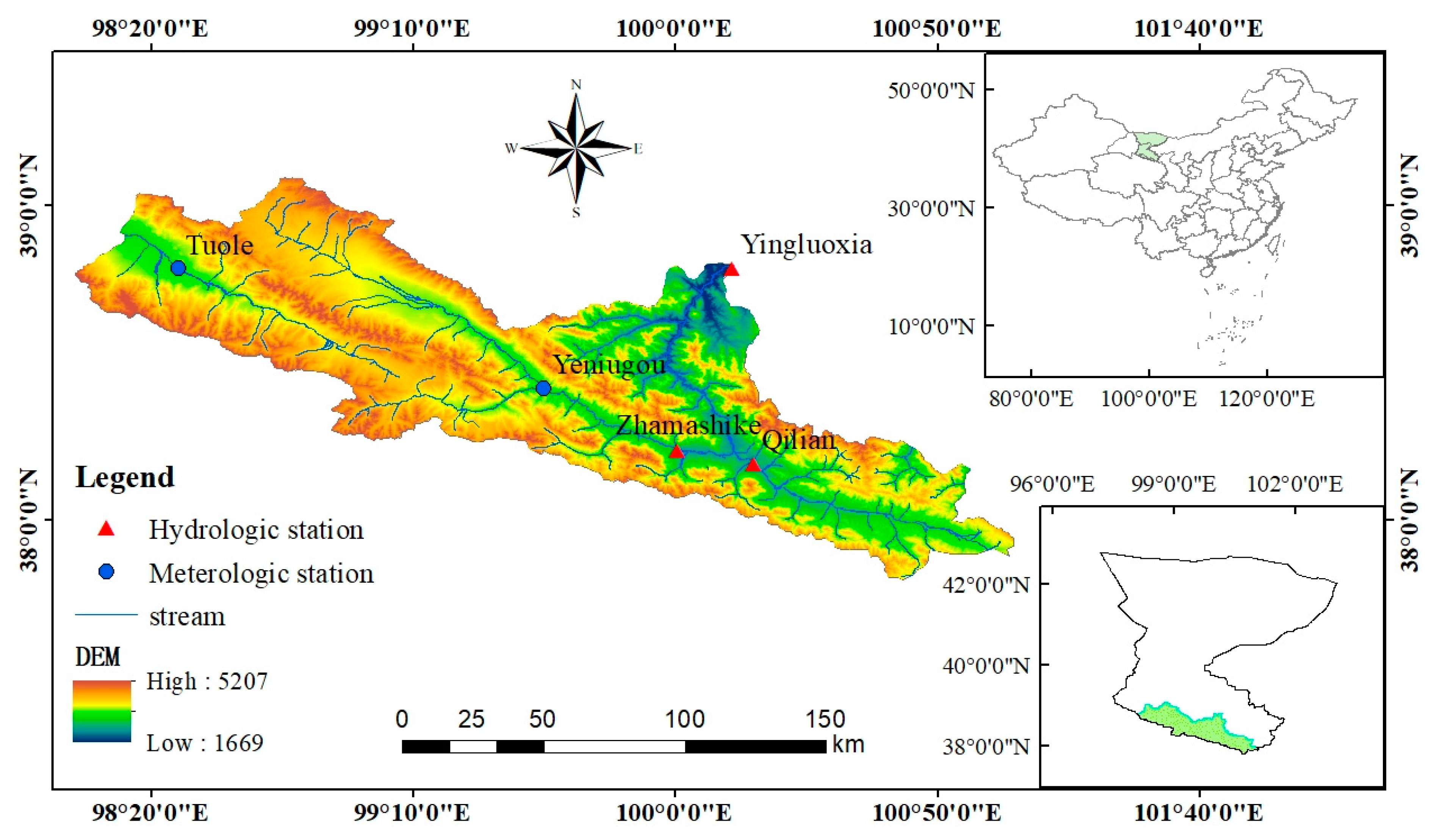
2.1.1. Study Area
2.1.2. Data
2.2. Methodology
2.2.1. Variational Mode Decomposition
2.2.2. Mutual Information
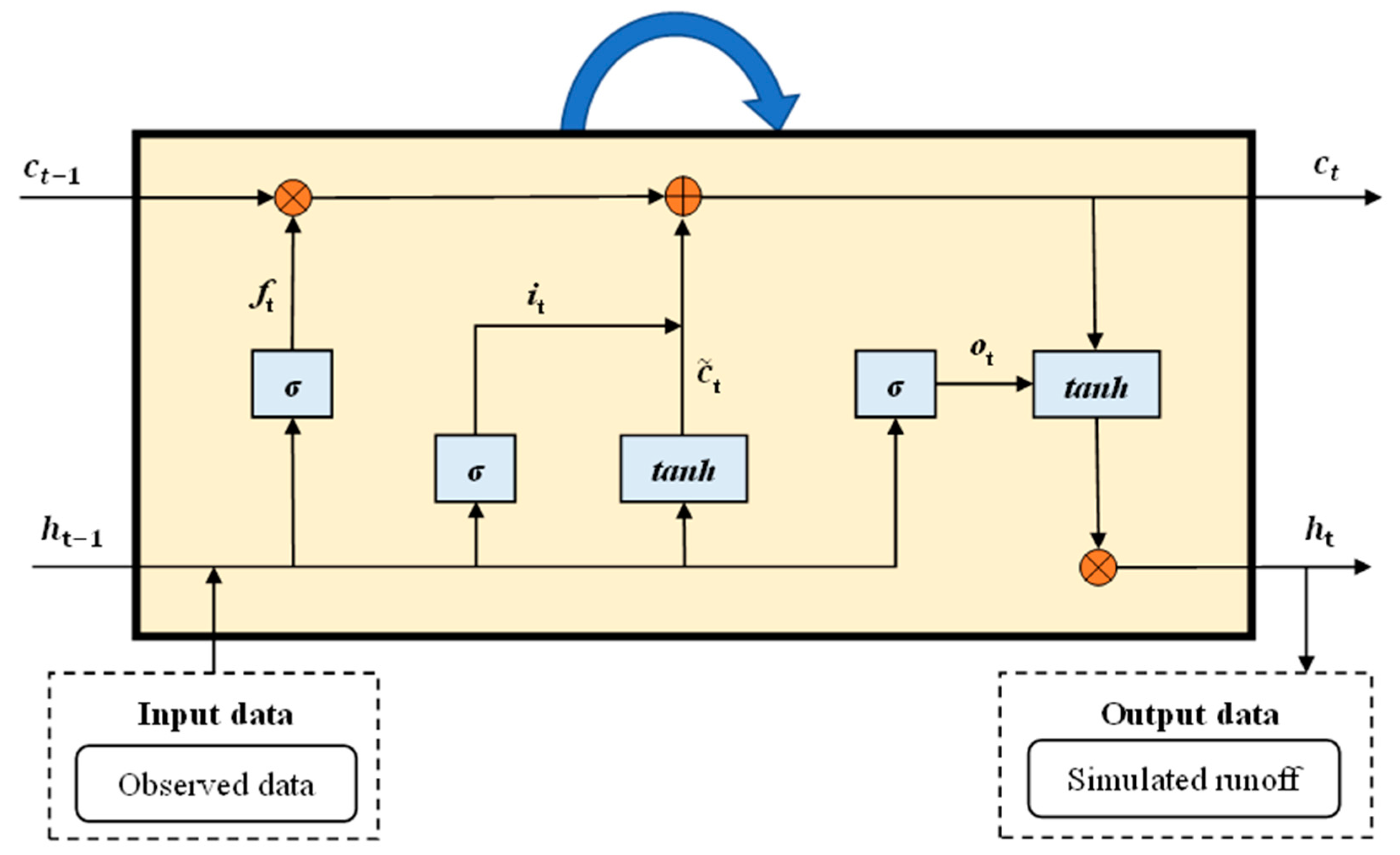
2.2.3. LSTM
2.2.4. Nonparametric Kernel Density Estimation
2.2.5. Evaluation of the Model’s Performance
2.3. Model Implementation
2.3.1. Determining Network Parameters
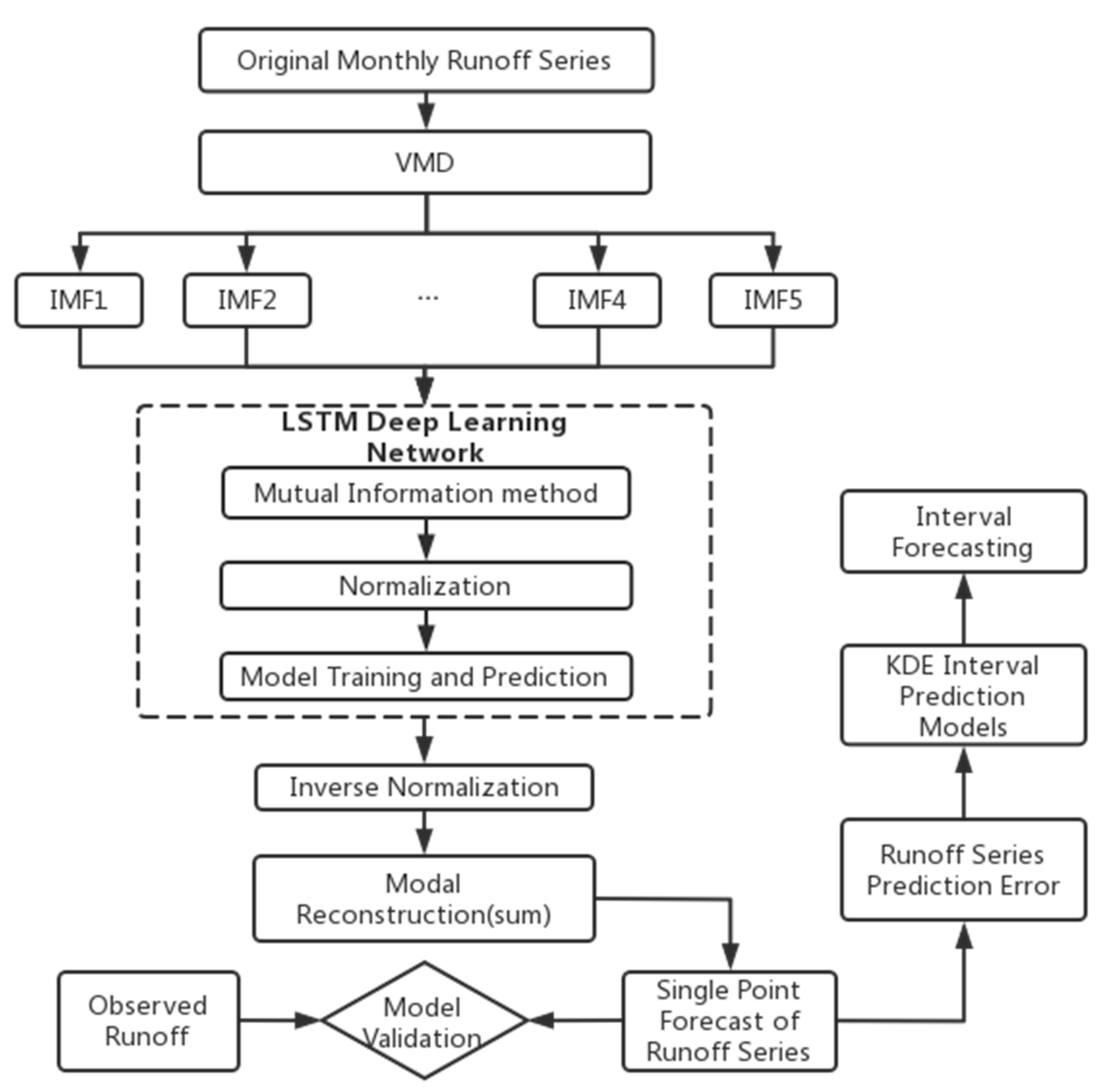
2.3.2. Process of Training the VMD-LSTM Model
- (1)
- The required monthly runoff sample data are selected, and a model training set and a test set are established.
- (2)
- The VMD method is used to decompose the original runoff sequence to obtain several components, and each component and the original runoff sequence are normalized.
- (3)
- The MI method is used to determine the model input delay (in this paper, the time step), and each component is input into the LSTM model for prediction.
- (4)
- After the forecast is completed, the data are denormalized, and the prediction results for each mode component are combined to obtain the final runoff forecast sequence.
- (5)
- The runoff series forecasting error is calculated, the nonparametric KDE method is applied to estimate the runoff series interval, and the accuracy of prediction results is evaluated.
3. Results
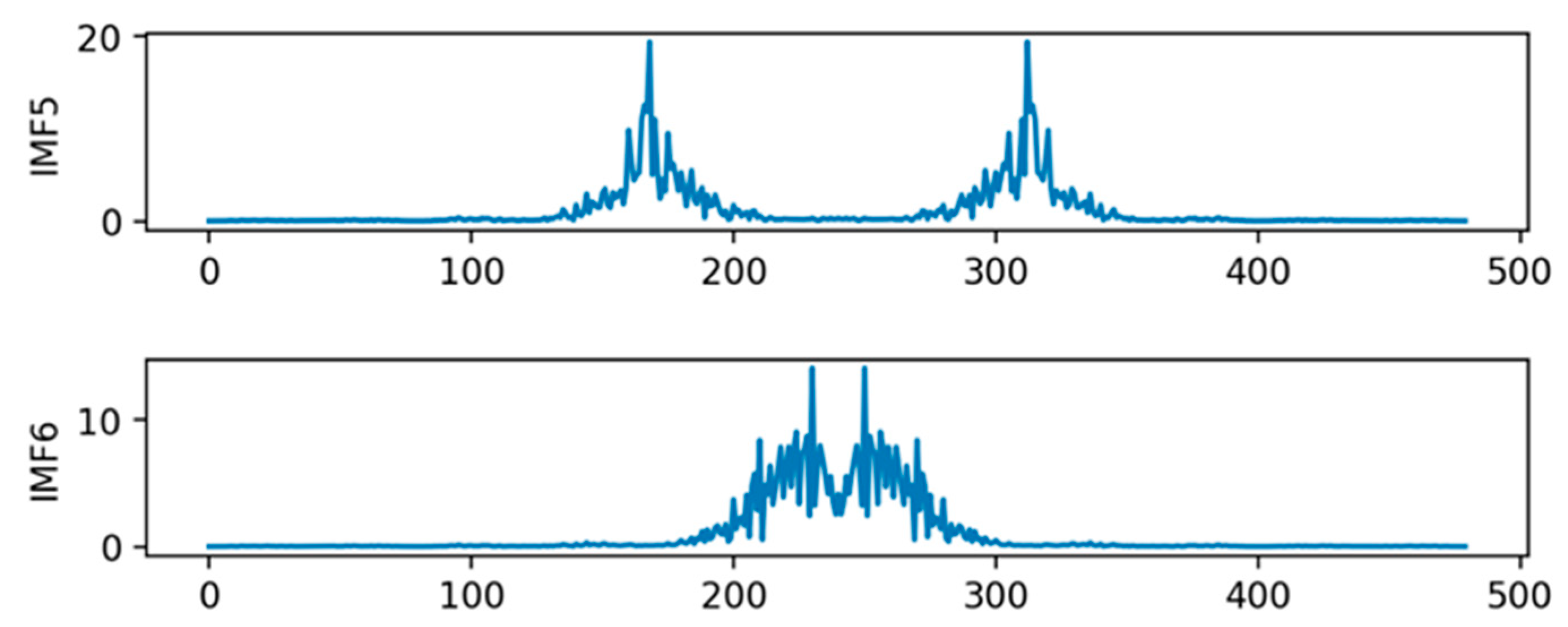
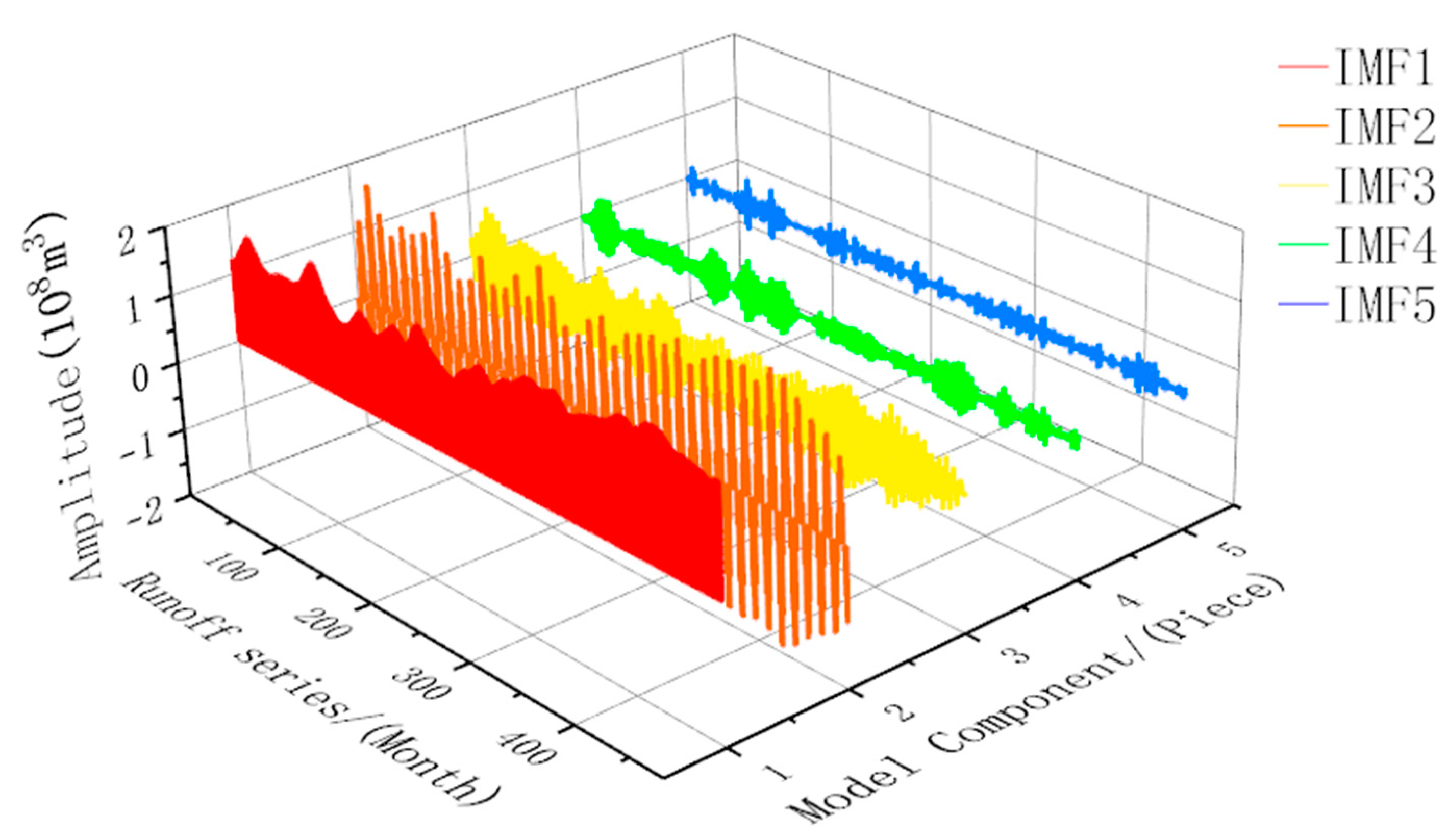
3.1. Determination of the Number of VMD Components
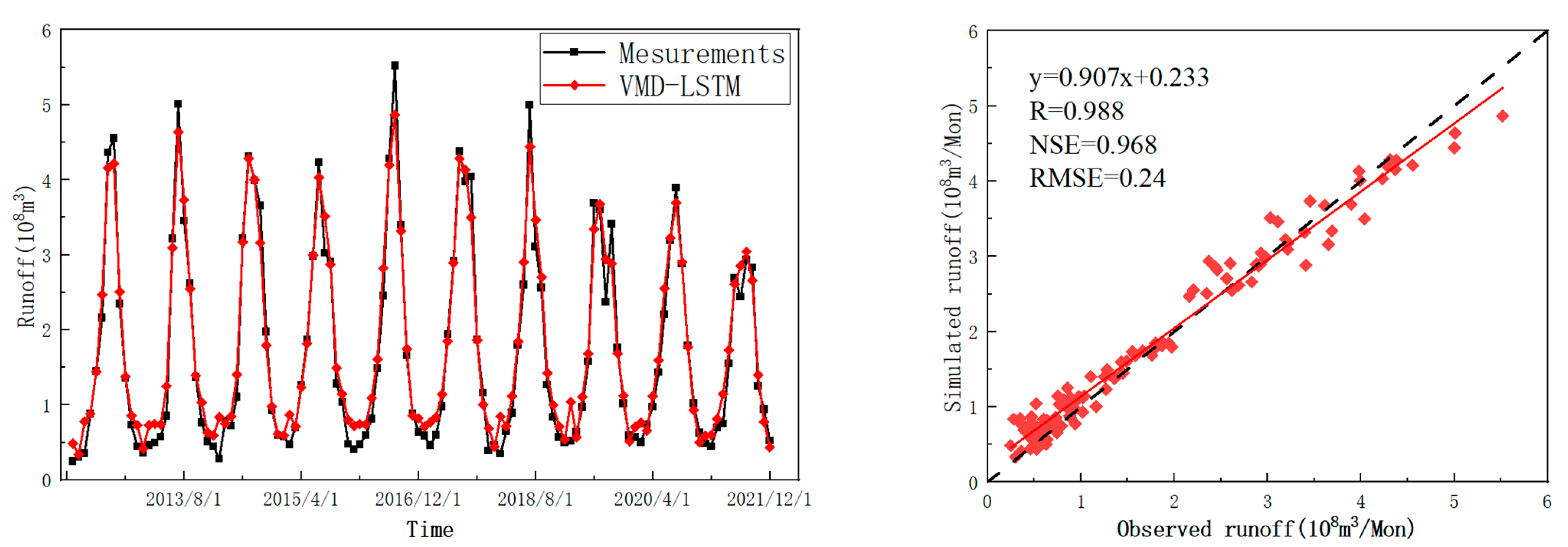
3.2. Runoff Estimation
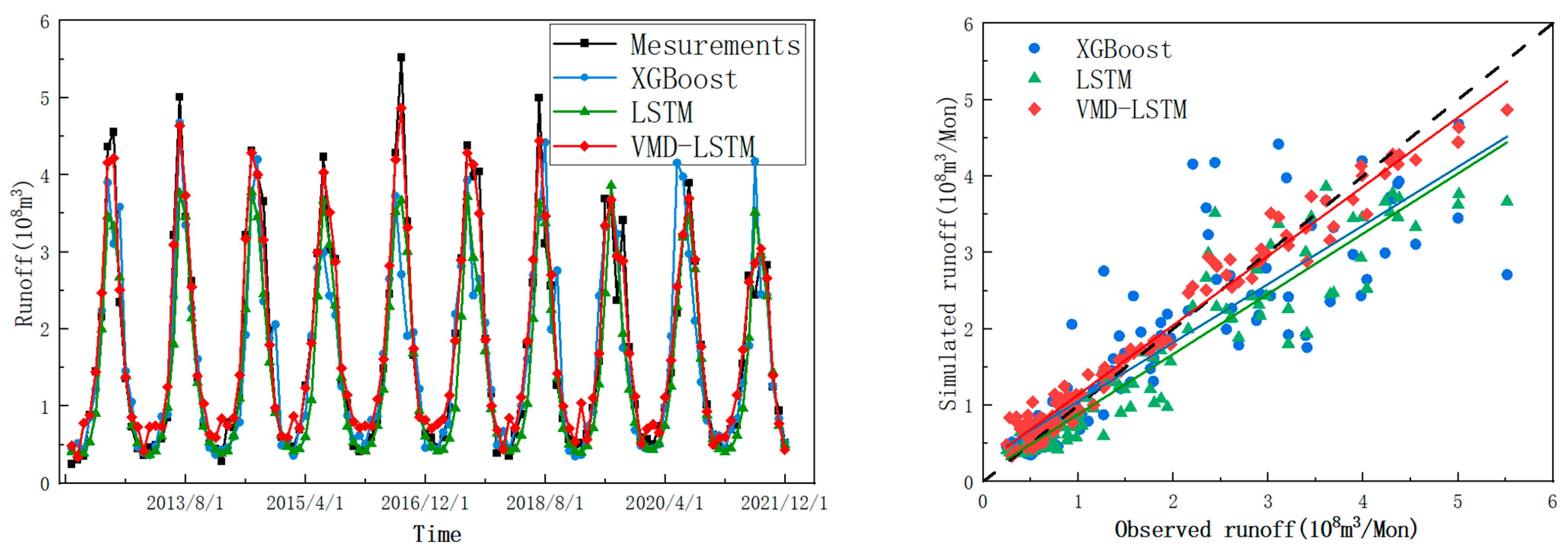
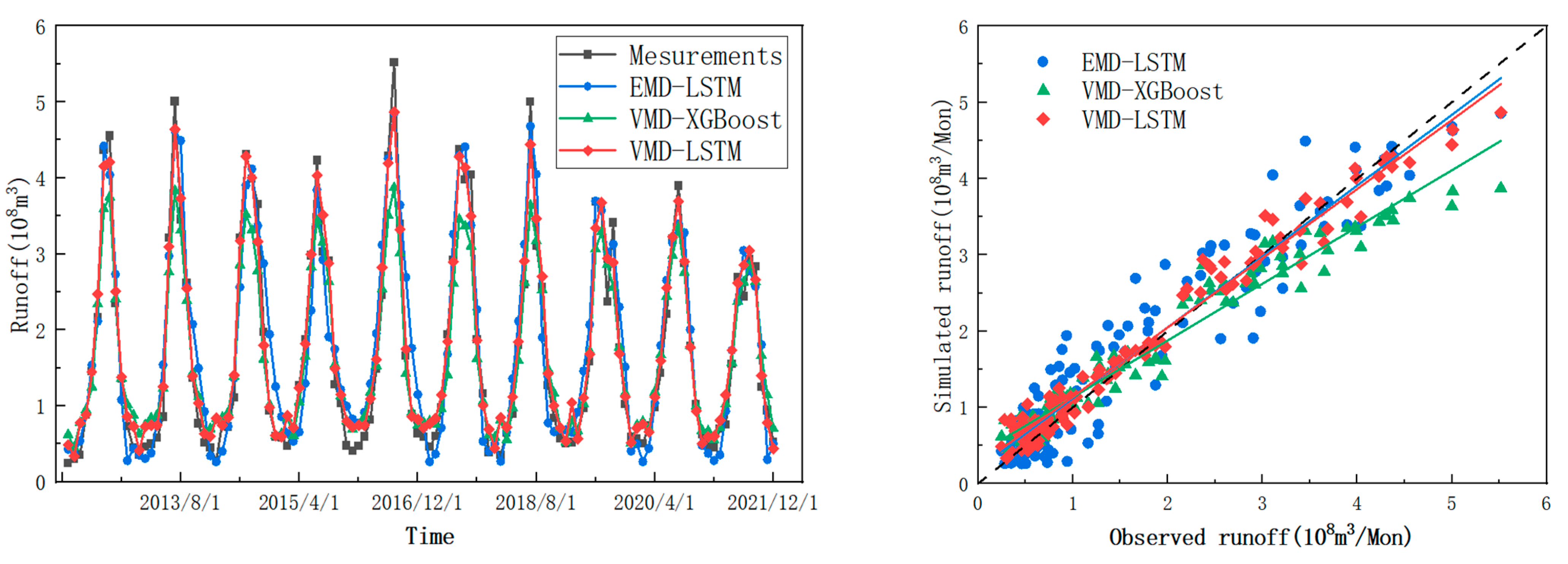
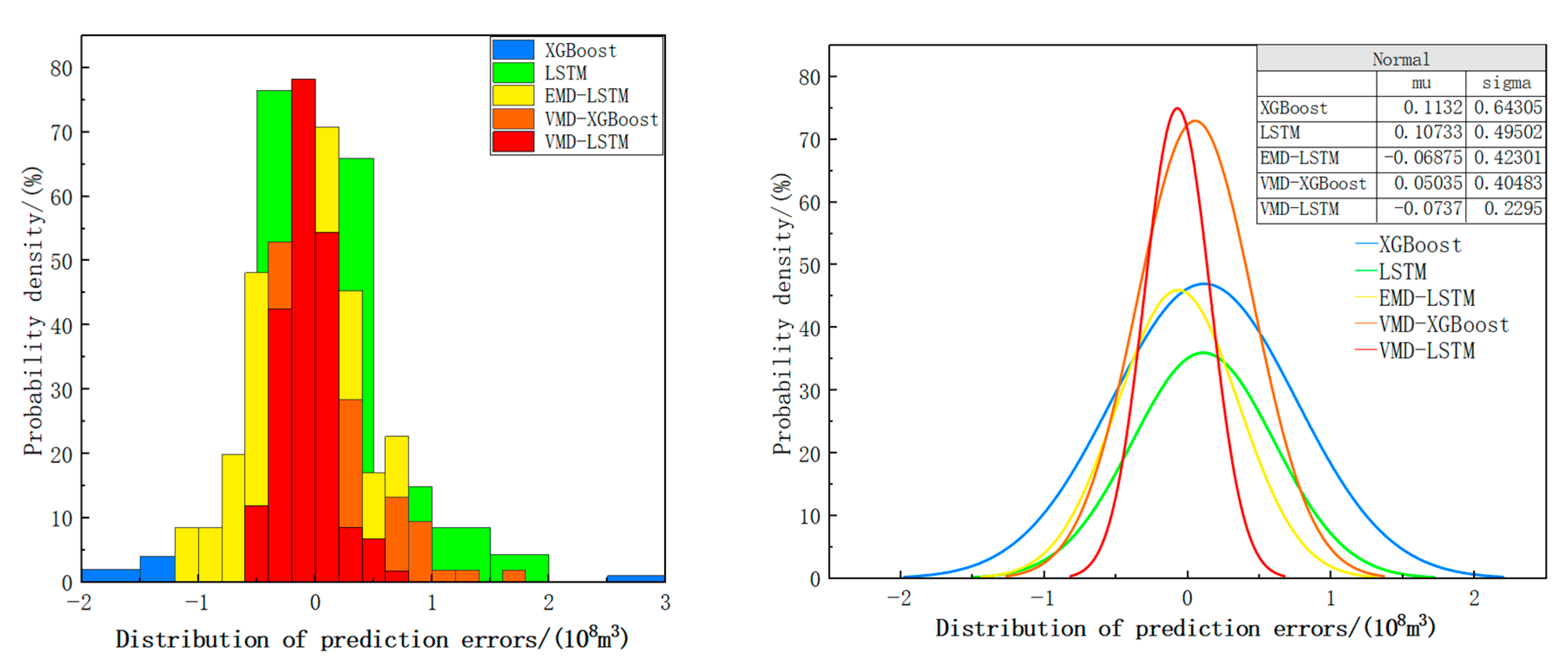
3.3. Comparing Single and Hybrid Forecasting Models
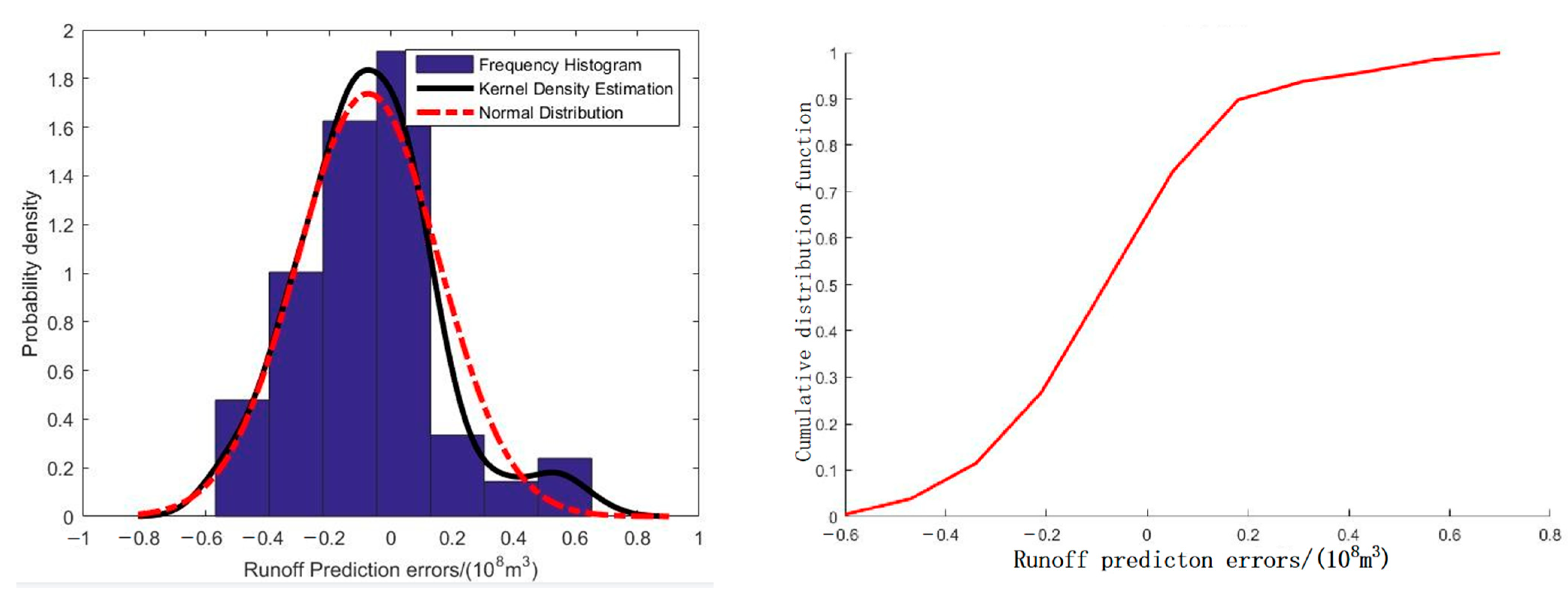
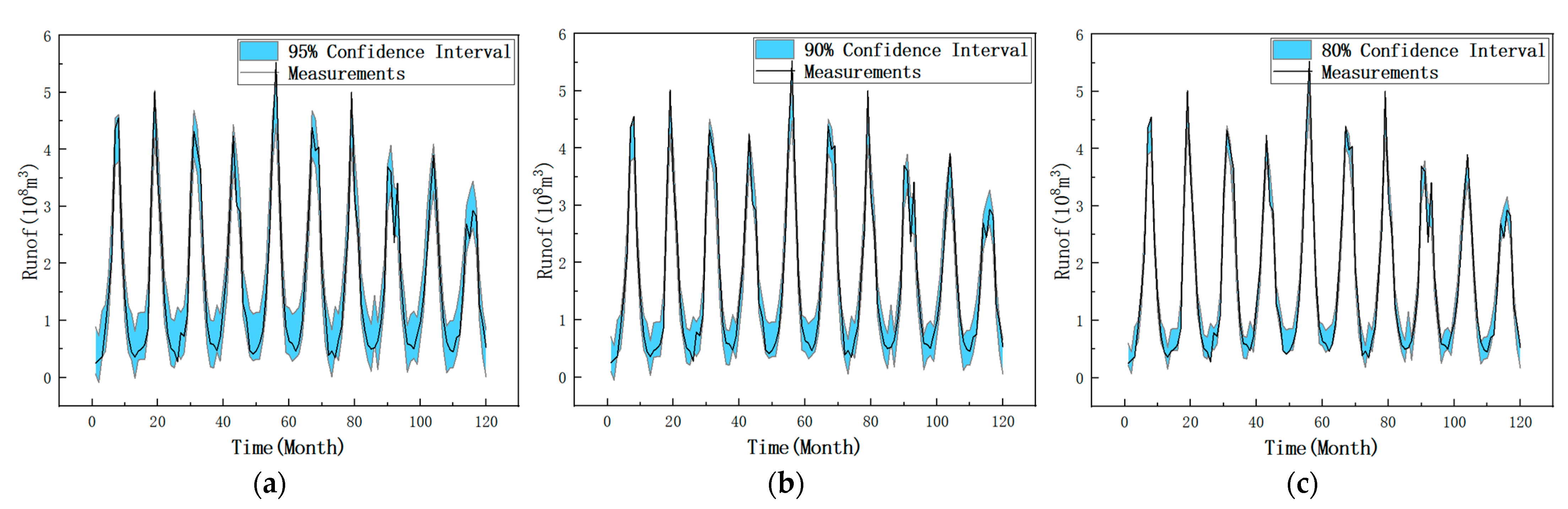
3.4. Runoff Interval Simulation
4. Discussion
5. Conclusions
- (1)
- The VMD method can effectively reduce the non-stationarity of hydrological time series, extract important hydrological feature information, and significantly improve the accuracy of runoff predictions. Compared with EMD, VMD can better control center frequency aliasing and noise levels.
- (2)
- Based on the MI method, the constructed VMD-LSTM model can effectively determine the input characteristics for deep learning. Overall, the proposed model performs well in runoff predictions. However, it should be noted that the accumulation of forecast errors for each subsequence affects the forecast result.
- (3)
- In interval prediction, the proposed model also yields satisfactory results. The prediction interval coverage and the simulation accuracy are high, and the average width is small. Interval prediction can be used to quantify the uncertainty of runoff predictions, estimate reasonable fluctuation ranges, and provide a certain reference for the establishment of hydrological prediction models and water resource management plans.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Wang, W.C.; Chau, K.W.; Cheng, C.T.; Qiu, L. A comparison of performance of several artificial intelligence methods for forecasting monthly discharge time series. J. Hydrol. 2009, 374, 294–306. [Google Scholar] [CrossRef]
- Zhang, Y.; Chiew, F.H.S.; Zhang, L.; Li, H. Use of Remotely Sensed Actual Evapotranspiration to Improve Rainfall-Runoff Modeling in Southeast Australia. J. Hydrometeorol. 2009, 10, 969–980. [Google Scholar] [CrossRef]
- Jiang, D.; Li, L.; Li, J. Runoff variation affected by precipitation change and human activity in Hailiutu River basin, China. Chin. J. Popul. Resour. Environ. 2021, 12, 116–122. [Google Scholar]
- Qiu, L.; Peng, D.; Xu, Z.; Liu, W. Identification of the impacts of climate changes and human activities on runoff in the upper and middle reaches of the Heihe River basin, China. J. Water Clim. Chang. 2016, 7, 251–262. [Google Scholar] [CrossRef]
- Qin, Y.; Sun, X.; Li, B.; Merz, B. A nonlinear hybrid model to assess the impacts of climate variability and human activities on runoff at different time scales. Stoch. Environ. Res. Risk Assess. 2021, 35, 1917–1929. [Google Scholar] [CrossRef]
- Li, C.; Zhu, L.; He, Z.; Gao, H.; Qu, X. Runoff Prediction Method Based on Adaptive Elman Neural Network. Water 2019, 11, 1113. [Google Scholar] [CrossRef]
- Young, C.-C.; Liu, W.-C.; Wu, M.-C. A physically based and machine learning hybrid approach for accurate rainfall-runoff modeling during extreme typhoon events. Appl. Soft. Comput. 2017, 53, 205–216. [Google Scholar] [CrossRef]
- Liu, Y.; Zhang, T.; Kang, A.; Li, J.; Lei, X. Research on Runoff Simulations Using Deep-Learning Methods. Sustainability 2021, 13, 1336. [Google Scholar] [CrossRef]
- Pathiraja, S.; Moradkhani, H.; Marshall, L.; Sharma, A.; Geenens, G. Data-driven model uncertainty estimation in hydrologic data assimilation. Water Resour. Res. 2018, 54, 1252–1280. [Google Scholar] [CrossRef]
- Ghaith, M.; Siam, A.; Li, Z.; El-Dakhakhni, W. Hybrid hydrological data-driven approach for daily streamflow forecasting. J. Hydrol. Eng. 2020, 25, 04019063. [Google Scholar] [CrossRef]
- Yuan, R.; Cai, S.; Liao, W.; Lei, X.; Xu, Y. Daily Runoff Forecasting Using Ensemble Empirical Mode Decomposition and Long Short-Term Memory. Front. Earth Sci. 2021, 9, 621780. [Google Scholar] [CrossRef]
- Ghanbarzadeh, M.; Aminghafari, M. A novel wavelet artificial neural networks method to predict non-stationary time series. Commun. Stat. Theory Methods 2020, 49, 864–878. [Google Scholar] [CrossRef]
- Wang, H.; Wu, X.; Gholinia, F. Forecasting hydropower generation by GFDL-CM3 climate model and hybrid hydrological-Elman neural network model based on Improved Sparrow Search Algorithm (ISSA). Concurr. Comput. Pract. Exp. 2021, 33, e6476. [Google Scholar] [CrossRef]
- Kelleher, J.D. Deep Learning; MIT Press: Cambridge, MA, USA, 2019. [Google Scholar]
- Li, Z.; Kang, L.; Zhou, L.; Zhu, M. Deep learning framework with time series analysis methods for runoff prediction. Water 2021, 13, 575. [Google Scholar] [CrossRef]
- Sherstinsky, A. Fundamentals of recurrent neural network (RNN) and long short-term memory (LSTM) network. Phys. D Nonlinear Phenom. 2020, 404, 132306. [Google Scholar] [CrossRef]
- Kratzert, F.; Klotz, D.; Brenner, C.; Schulz, K.; Herrnegger, M. Rainfall–runoff modelling using long short-term memory (LSTM) networks. Hydrol. Earth Syst. Sci. 2018, 22, 6005–6022. [Google Scholar] [CrossRef]
- Yuan, X.; Chen, C.; Lei, X.; Yuan, Y.; Muhammad Adnan, R. Monthly runoff forecasting based on LSTM–ALO model. Stoch. Environ. Res. Risk Assess. 2018, 32, 2199–2212. [Google Scholar] [CrossRef]
- Li, W.; Kiaghadi, A.; Dawson, C. High temporal resolution rainfall–runoff modeling using long-short-term-memory (LSTM) networks. Neural Comput. Appl. 2021, 33, 1261–1278. [Google Scholar] [CrossRef]
- Xue, H.; Liu, J.; Dong, G.; Zhang, C.; Jia, D. Runoff Estimation in the Upper Reaches of the Heihe River Using an LSTM Model with Remote Sensing Data. Remote Sens. 2022, 14, 2488. [Google Scholar] [CrossRef]
- Seo, Y.; Kim, S.; Singh, V.P. Machine Learning Models Coupled with Variational Mode Decomposition: A New Approach for Modeling Daily Rainfall-Runoff. Atmosphere 2018, 9, 251. [Google Scholar] [CrossRef]
- Lu, J.; Li, A. Monthly Runoff Prediction Using Wavelet Transform and Fast Resource Optimization Network (Fron) Algorithm. J. Phys. Conf. Ser. 2019, 1302, 042005. [Google Scholar] [CrossRef]
- Ding, Z.; Zhang, J.; Xie, G. LS-SVM forecast model of precipitation and runoff based on EMD. In Proceedings of the Sixth International Conference on Natural Computation, Yantai, China, 10–12 August 2010. [Google Scholar]
- Feng, Z.-K.; Niu, W.-J.; Tang, Z.-Y.; Jiang, Z.-Q.; Xu, Y.; Liu, Y.; Zhang, H.-R. Monthly runoff time series prediction by variational mode decomposition and support vector machine based on quantum-behaved particle swarm optimization. J. Hydrol. 2020, 583, 124627. [Google Scholar] [CrossRef]
- Zhao, X.; Chen, X.; Yuan, X. Application of data-driven model based on empirical mode decomposition for runoff forecasting. Syst. Eng. 2014, 32, 150–154. [Google Scholar]
- Li, B.J.; Sun, G.L.; Liu, Y.; Wang, W.C.; Huang, X.D. Monthly Runoff Forecasting Using Variational Mode Decomposition Coupled with Gray Wolf Optimizer-Based Long Short-term Memory Neural Networks. Water Resour. Manag. 2022, 36, 2095–2115. [Google Scholar] [CrossRef]
- Muhammad, S.; Li, X.; Bashir, H.; Azam, M.I. A Hybrid Model for Runoff Prediction Using Variational Mode Decomposition and Artificial Neural Network. Water Resour. 2021, 48, 701–712. [Google Scholar] [CrossRef]
- Zhu, S.; Zhou, J.; Ye, L.; Meng, C. Streamflow estimation by support vector machine coupled with different methods of time series decomposition in the upper reaches of Yangtze River, China. Environ. Earth Sci. 2016, 75, 531.1–531.12. [Google Scholar] [CrossRef]
- Zuo, G.; Luo, J.; Wang, N.; Lian, Y.; He, X. Decomposition ensemble model based on variational mode decomposition and long short-term memory for streamflow forecasting. J. Hydrol. 2020, 585, 124776. [Google Scholar] [CrossRef]
- Kasiviswanathan, K.; Cibin, R.; Sudheer, K.; Chaubey, I. Constructing prediction interval for artificial neural network rainfall runoff models based on ensemble simulations. J. Hydrol. 2013, 499, 275–288. [Google Scholar] [CrossRef]
- Chen, X.; Lai, C.S.; Ng, W.W.Y.; Pan, K.; Zhong, C. A stochastic sensitivity-based multi-objective optimization method for short-term wind speed interval prediction. Int. J. Mach. Learn. Cybern. 2021, 12, 2579–2590. [Google Scholar] [CrossRef]
- Kiefer, M.; Heimel, M.; Breß, S.; Markl, V. Estimating join selectivities using bandwidth-optimized kernel density models. Proc. VLDB Endow. 2017, 10, 2085–2096. [Google Scholar] [CrossRef]
- Yang, X.; Xue, M.; Ning, K.; Maihemuti, M. Probability Interval Prediction of Wind Power Based on KDE Method With Rough Sets and Weighted Markov Chain. IEEE Access 2018, 6, 51556–51565. [Google Scholar] [CrossRef]
- Du, B.; Huang, S.; Guo, J.; Tang, H.; Wang, L.; Zhou, S. Interval forecasting for urban water demand using PSO optimized KDE distribution and LSTM neural networks. Appl. Soft Comput. 2022, 122, 108875. [Google Scholar] [CrossRef]
- Zhang, L.; Xie, L.; Han, Q.; Wang, Z.; Huang, C. Probability Density Forecasting of Wind Speed Based on Quantile Regression and Kernel Density Estimation. Energies 2020, 13, 6125. [Google Scholar] [CrossRef]
- Zhang, L.; Su, F.; Yang, D.; Hao, Z.; Tong, K. Discharge regime and simulation for the upstream of major rivers over Tibetan Plateau. J. Geophys. Res. D. Atmos. JGR 2013, 118, 118. [Google Scholar] [CrossRef]
- Cheng, G.D.; Xiao, H.L.; Xu, Z.M.; Li, J.X.; Lu, M.F. Water Issue and Its Countermeasure in the Inland River Basins of Northwest China—A Case Study in Heihe River Basin. J. Glaciol. Geocryol. 2006, 28, 8. [Google Scholar]
- Wang, J.; Meng, J.J. Characteristics and Tendencies of Annual Runoff Variations in the Heihe River Basin During the Past 60 years. Sci. Geogr. Sin. 2008, 28, 83–88. [Google Scholar]
- Wang, Y.; Yang, D.; Lei, H.; Yang, H. Impact of cryosphere hydrological processes on the river runoff in the upper reaches of Heihe River. J. Hydraul. Eng. 2015, 46, 1064–1071. [Google Scholar] [CrossRef]
- Chen, D.; Jin, G.; Zhang, Q.; Arowolo, A.O.; Li, Y. Water ecological function zoning in Heihe River Basin, Northwest China. Phys. Chem. Earth 2016, 96, 74–83. [Google Scholar] [CrossRef]
- Dragomiretskiy, K.; Zosso, D. Variational mode decomposition. IEEE Trans. Signal Process. 2013, 62, 531–544. [Google Scholar] [CrossRef]
- Zhou, M.; Hu, T.; Bian, K.; Lai, W.; Hu, F.; Hamrani, O.; Zhu, Z. Short-Term Electric Load Forecasting Based on Variational Mode Decomposition and Grey Wolf Optimization. Energies 2021, 14, 4890. [Google Scholar] [CrossRef]
- Naik, J.; Dash, S.; Dash, P.K.; Bisoi, R. Short term wind power forecasting using hybrid variational mode decomposition and multi-kernel regularized pseudo inverse neural network. Renew. Energy 2018, 118, 180–212. [Google Scholar] [CrossRef]
- Banik, A.; Behera, C.; Sarathkumar, T.V.; Goswami, A.K. Uncertain wind power forecasting using LSTM-based prediction interval. IET Renew. Power Gener. 2020, 14, 2657–2667. [Google Scholar] [CrossRef]
- Božić, M.; Stojanović, M.; Stajić, Z.; Floranović, N. Mutual Information-Based Inputs Selection for Electric Load Time Series Forecasting. Entropy 2013, 15, 926–942. [Google Scholar] [CrossRef]
- Lv, N.; Liang, X.; Chen, C.; Zhou, Y.; Wang, H. A Long Short-Term Memory Cyclic model With Mutual Information For Hydrology Forecasting: A Case Study in the Xixian Basin. Adv. Water Resour. 2020, 141, 103622. [Google Scholar] [CrossRef]
- Kraskov, A.; Stögbauer, H.; Grassberger, P. Estimating mutual information. Physical Rev. E 2004, 69, 066138. [Google Scholar] [CrossRef]
- Chen, J.; Wu, Z.; Zhang, J.A.; Li, F.A. Mutual information-based dropout: Learning deep relevant feature representation architectures. Neurocomputing 2019, 361, 173–184. [Google Scholar] [CrossRef]
- Li, G.; Zhao, X.; Fan, C.; Fang, X.; Li, F.; Wu, Y. Assessment of long short-term memory and its modifications for enhanced short-term building energy predictions—ScienceDirect. J. Build. Eng. 2021, 43, 103182. [Google Scholar] [CrossRef]
- Hochreiter, S.; Schmidhuber, J. Long Short-Term Memory. Neural Comput. 1997, 9, 1735–1780. [Google Scholar] [CrossRef]
- Xiang, Z.; Yan, J.; Demir, I. A rainfall-runoff model with LSTM-based sequence-to-sequence learning. Water Resour. Res. 2020, 56, e2019WR025326. [Google Scholar] [CrossRef]
- Xu, Y.; Hu, C.; Wu, Q.; Jian, S.; Li, Z.; Chen, Y.; Zhang, G.; Zhang, Z.; Wang, S. Research on particle swarm optimization in LSTM neural networks for rainfall-runoff simulation. J. Hydrol. 2022, 608, 127553. [Google Scholar] [CrossRef]
- Terrell, G.R.; Scott, D.W. Variable kernel density estimation. Ann. Stat. 1992, 20, 1236–1265. [Google Scholar] [CrossRef]
- Zhou, B.; Ma, X.; Luo, Y.; Yang, D. Wind power prediction based on LSTM networks and nonparametric kernel density estimation. IEEE Access 2019, 7, 165279–165292. [Google Scholar] [CrossRef]
- Pan, C.; Tan, J.; Feng, D. Prediction intervals estimation of solar generation based on gated recurrent unit and kernel density estimation. Neurocomputing 2021, 453, 552–562. [Google Scholar] [CrossRef]
- Jiang, Y.; Huang, G.; Yang, Q.; Yan, Z.; Zhang, C. A novel probabilistic wind speed prediction approach using real time refined variational model decomposition and conditional kernel density estimation. Energy Convers. Manag. 2019, 185, 758–773. [Google Scholar] [CrossRef]
- Peel, S.; Wilson, L.J. Modeling the distribution of precipitation forecasts from the Canadian ensemble prediction system using kernel density estimation. Weather. Forecast. 2008, 23, 575–595. [Google Scholar] [CrossRef]
- Bai, M.; Zhao, X.; Long, Z.; Liu, J.; Yu, D. Short-term probabilistic photovoltaic power forecast based on deep convolutional long short-term memory network and kernel density estimation. arXiv 2021, arXiv:2107.01343. [Google Scholar]
- Zhanga, J.; Yan, Z.; Zhanga, X.; Ming, Y.; Yangb, J. Developing a Long Short-Term Memory (LSTM) based model for predicting water table depth in agricultural areas. J. Hydrol. 2018, 561, 918–929. [Google Scholar] [CrossRef]
- Wang, X.; Wang, Y.; Yuan, P.; Wang, L.; Cheng, D. An adaptive daily runoff forecast model using VMD-LSTM-PSO hybrid approach. Hydrol. Sci. J. 2021, 66, 1488–1502. [Google Scholar] [CrossRef]
- Yang, H.; Chao, J.; Shi, K.; Liu, S. Fault Information Extraction Method for Rolling Bearings Based on VMD Parameter Estimation. Bearing 2016, 10, 49–52. [Google Scholar]
- Chen, S.; Ren, M.; Sun, W. Combining two-stage decomposition based machine learning methods for annual runoff forecasting. J. Hydrol. 2021, 603, 126945. [Google Scholar] [CrossRef]
- Niu, H.; Xu, K.; Wang, W. A hybrid stock price index forecasting model based on variational mode decomposition and LSTM network. Appl. Intell. 2020, 50, 4296–4309. [Google Scholar] [CrossRef]
- Zhang, K.; Ma, P.; Cui, Z.; Xing, T.; Qi, C.; Ning, G.; Amp, E. Ultra-short term wind power output interval forecast model based on ASD-KDE algorithm. Ningxia Electr. Power 2018, 2018, 8. [Google Scholar]
- Zhao, M.; Zhang, Y.; Hu, T.; Wang, P. Interval Prediction Method for Solar Radiation Based on Kernel Density Estimation and Machine Learning. Complexity 2022, 2022, 7495651. [Google Scholar] [CrossRef]
| Category | Sub-Category | Advantages | Limitations |
|---|---|---|---|
| Process-driven models | Conceptual models (tank model, storage function) | Relatively easy to calculate; can express various runoff patterns | Parameters lack physical meaning |
| Physical models (distributed models) | Runoff process is expressed in detail; reflects topography and rainfall distribution | Required data are difficult to obtain; model building is time consuming | |
| Data-driven models | Time-series models (AR, ARMA, ARIMA, etc.) | Models are easily constructed | Cannot simulate complex and nonlinear runoff |
| Machine learning (linear regression, SVM, ANN, RNN, etc.) | Strong ability to deal with nonlinear problems | Calculation process is “black box”; requires a considerable amount of data |
| Runoff Sample | Length/Months | Mean/108 m3 | Standard Deviation/108 m3 | Coefficient of Variation | Skewness |
|---|---|---|---|---|---|
| Total | 480 | 1.49 | 1.256 | 0.842 | 1.31 |
| Training period | 360 | 1.417 | 1.216 | 0.858 | 0.92 |
| Verification period | 120 | 1.715 | 1.351 | 0.788 | 1.2 |
| Model | R | RMSE | NSE |
|---|---|---|---|
| XGBoost | 0.879 | 0.65 | 0.766 |
| LSTM | 0.951 | 0.522 | 0.849 |
| EMD-LSTM | 0.95 | 0.427 | 0.899 |
| VMD-XGBoost | 0.979 | 0.406 | 0.909 |
| VMD-LSTM | 0.988 | 0.24 | 0.968 |
| Confidence Interval/% | Estimation Error Interval |
|---|---|
| 95 | [−0.4252, 0.3983] |
| 90 | [−0.3863, 0.2189] |
| 80 | [−0.2645, 0.1148] |
| Model | Confidence Interval/% | Number of Measured Values within the Interval | PICP | MPIW |
|---|---|---|---|---|
| XGBoost | 95 | 98 | 0.8167 | 1.5615 |
| 90 | 86 | 0.7167 | 1.3678 | |
| 80 | 72 | 0.6 | 1.0125 | |
| LSTM | 95 | 96 | 0.8 | 1.4012 |
| 90 | 89 | 0.7417 | 1.2924 | |
| 80 | 74 | 0.6167 | 0.9085 | |
| EMD-LSTM | 95 | 106 | 0.8833 | 1.1137 |
| 90 | 97 | 0.8083 | 0.9124 | |
| 80 | 86 | 0.7166 | 0.6114 | |
| VMD-XGBoost | 95 | 106 | 0.8833 | 1.0685 |
| 90 | 99 | 0.825 | 0.8861 | |
| 80 | 87 | 0.725 | 0.5124 | |
| VMD-LSTM | 95 | 116 | 0.9667 | 0.8235 |
| 90 | 109 | 0.9083 | 0.6052 | |
| 80 | 92 | 0.7667 | 0.3793 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xue, H.; Wu, H.; Dong, G.; Gao, J. A Hybrid Forecasting Model to Simulate the Runoff of the Upper Heihe River. Sustainability 2023, 15, 7819. https://doi.org/10.3390/su15107819
Xue H, Wu H, Dong G, Gao J. A Hybrid Forecasting Model to Simulate the Runoff of the Upper Heihe River. Sustainability. 2023; 15(10):7819. https://doi.org/10.3390/su15107819
Chicago/Turabian StyleXue, Huazhu, Hui Wu, Guotao Dong, and Jianjun Gao. 2023. "A Hybrid Forecasting Model to Simulate the Runoff of the Upper Heihe River" Sustainability 15, no. 10: 7819. https://doi.org/10.3390/su15107819
APA StyleXue, H., Wu, H., Dong, G., & Gao, J. (2023). A Hybrid Forecasting Model to Simulate the Runoff of the Upper Heihe River. Sustainability, 15(10), 7819. https://doi.org/10.3390/su15107819






