Power Quality Enhancement of Grid-Connected Renewable Systems Using a Matrix-Pencil-Based Active Power Filter
Abstract
1. Introduction
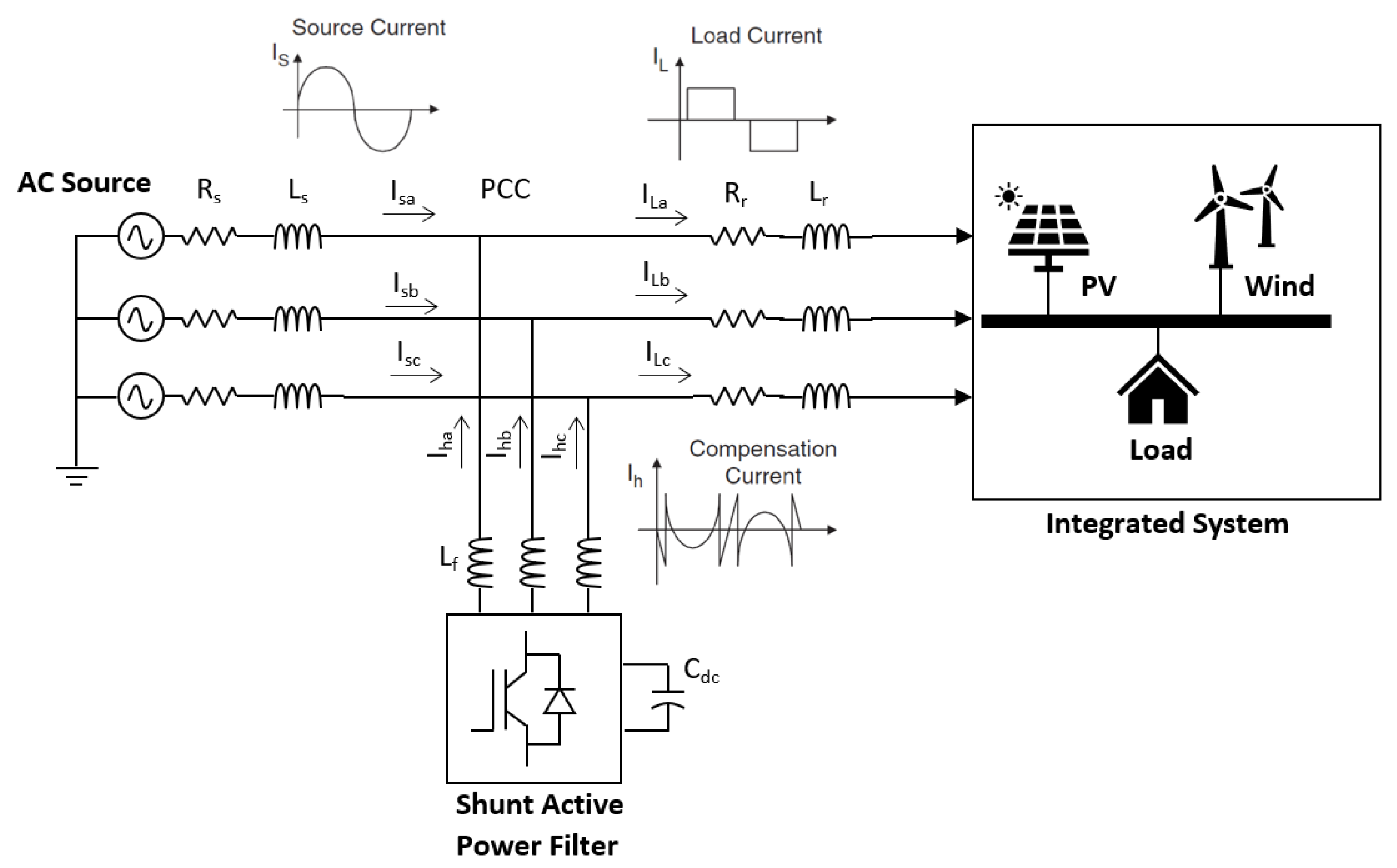
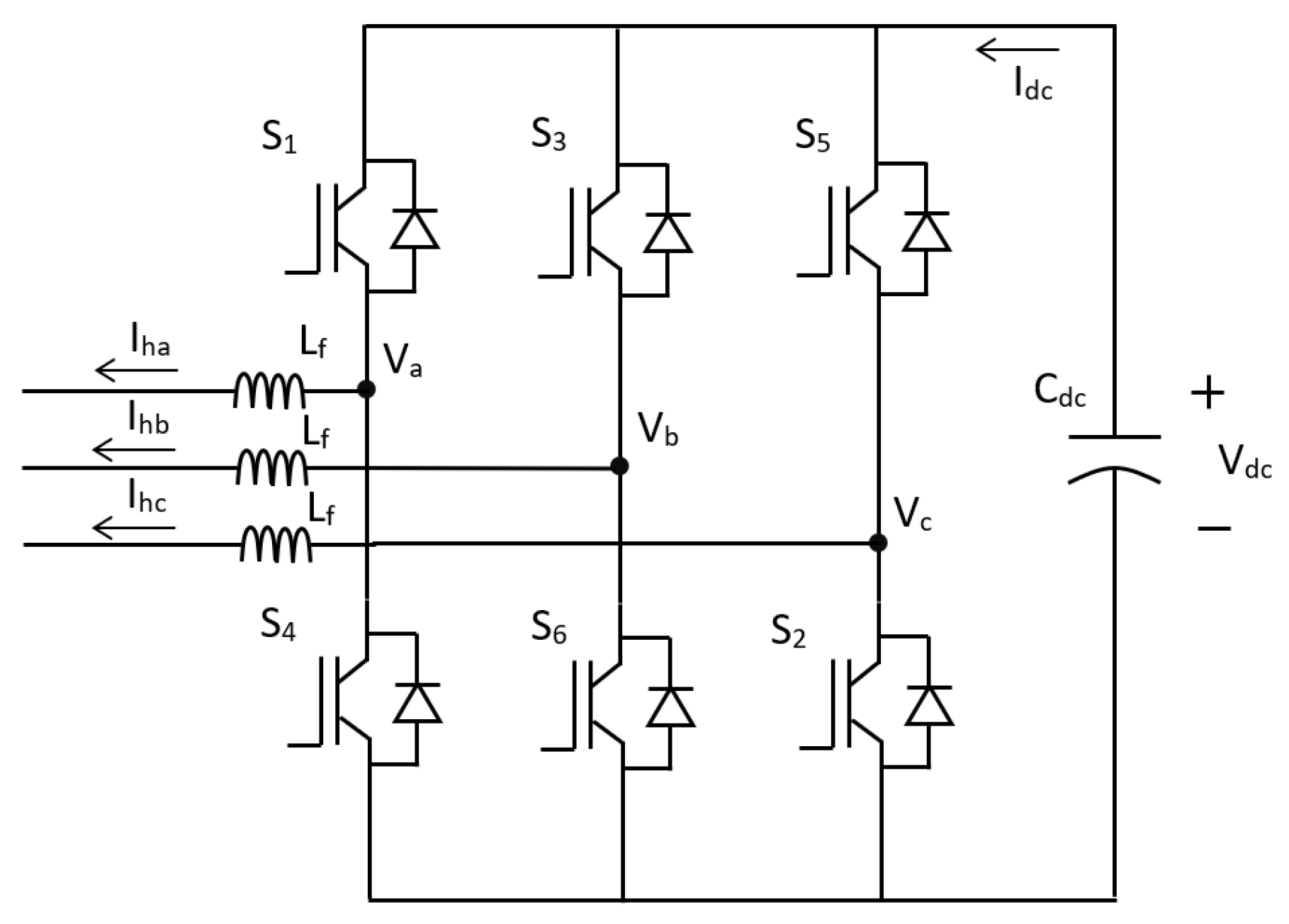
2. Structure of SAPF
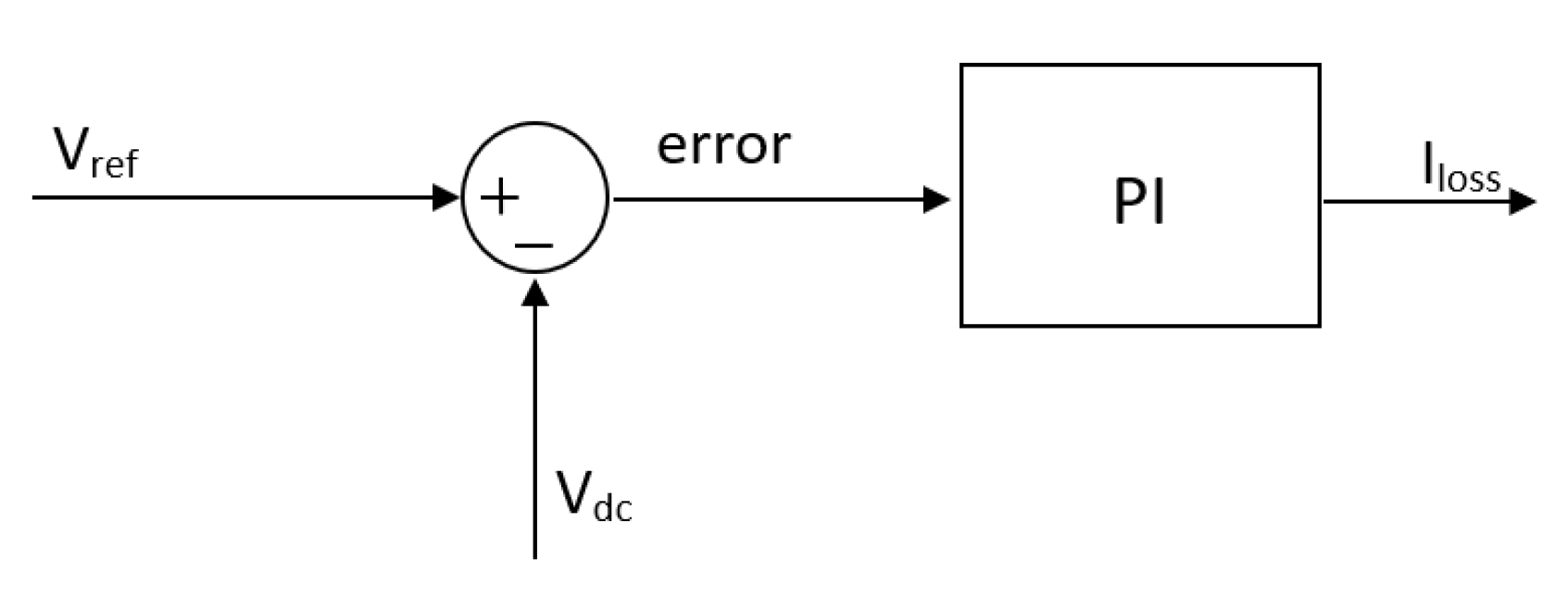
3. The DC Link
4. Integrating the loss current in MPM formulation
4.1. Signal Model
4.2. The Matrix Pencil Method
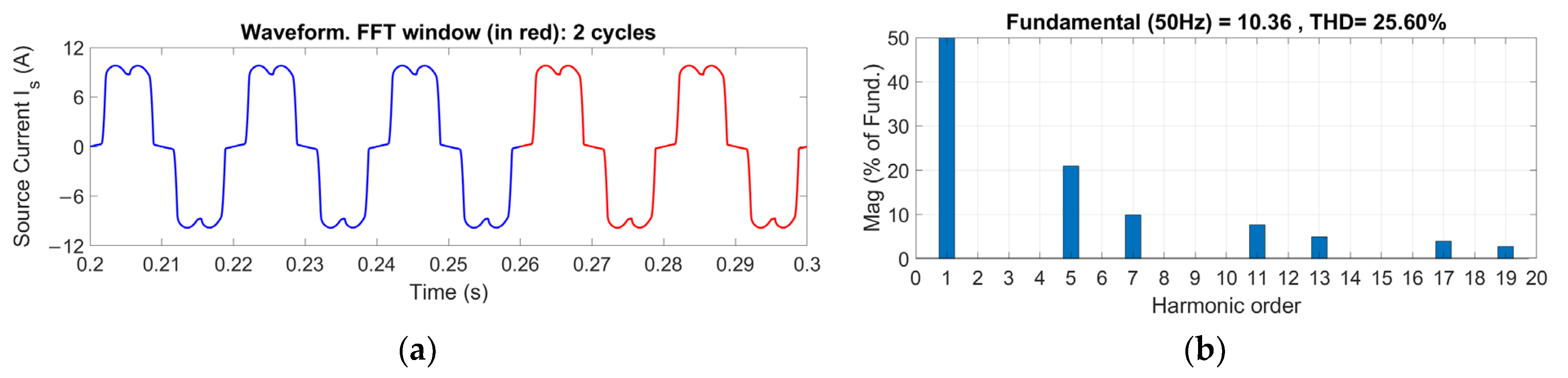
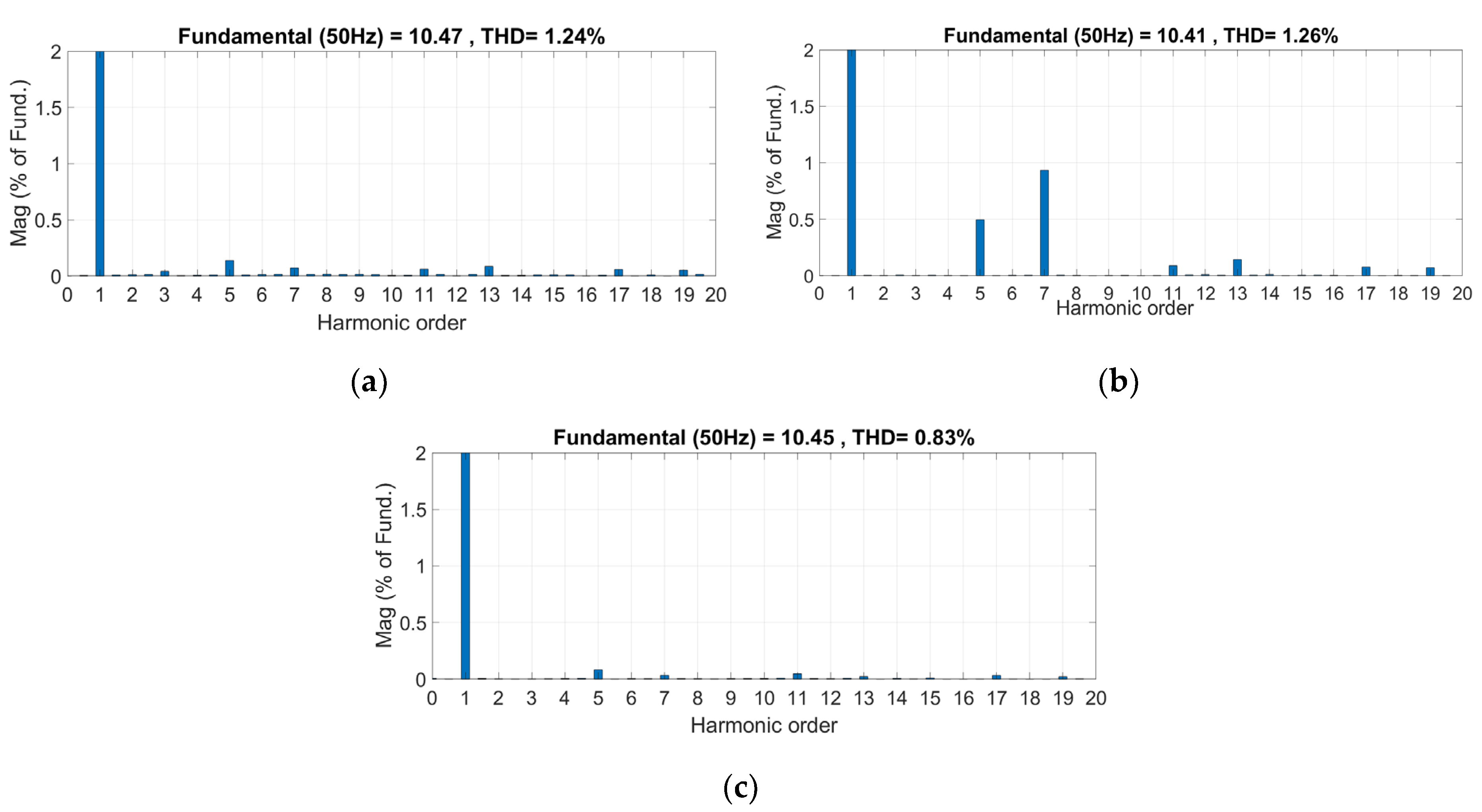
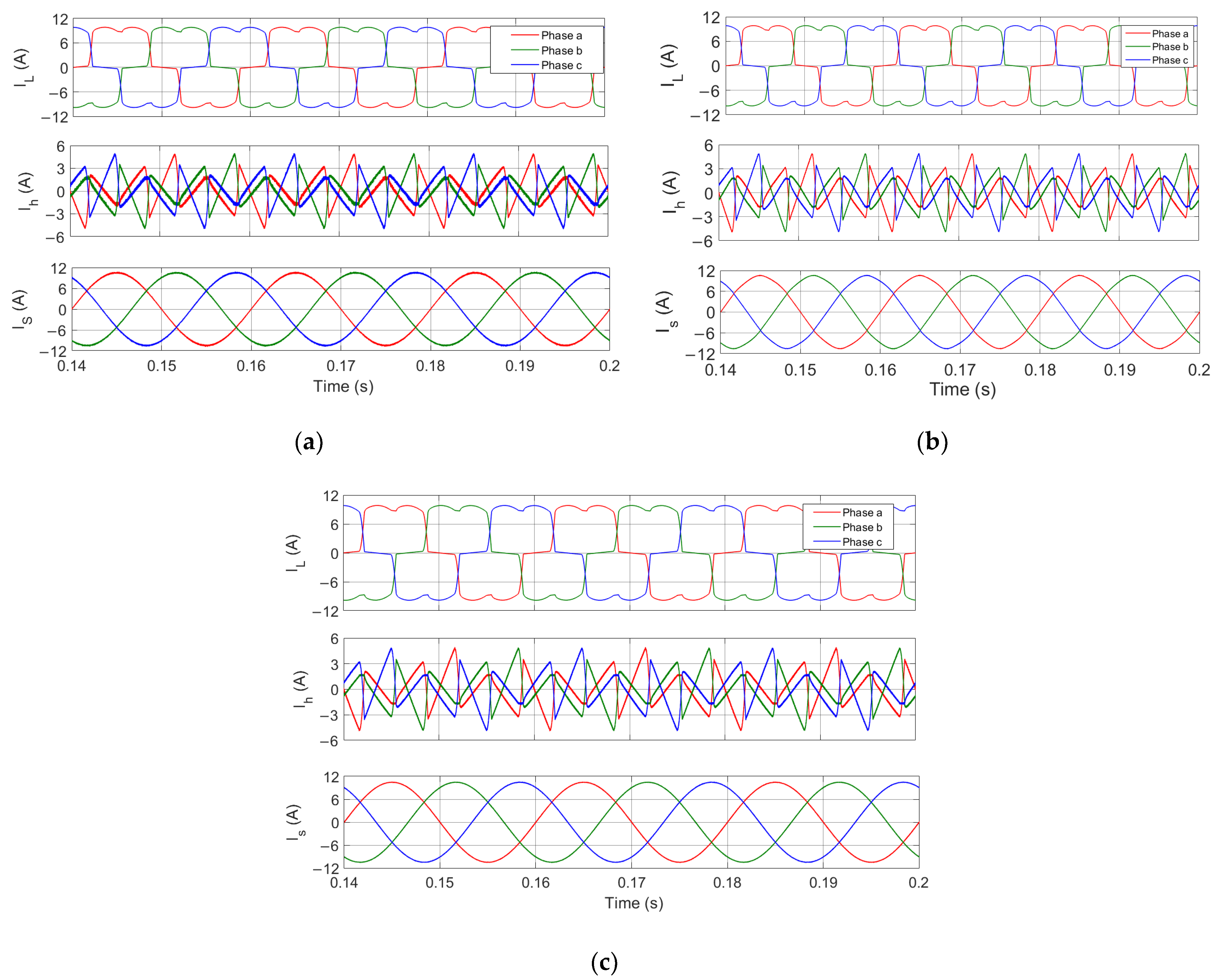
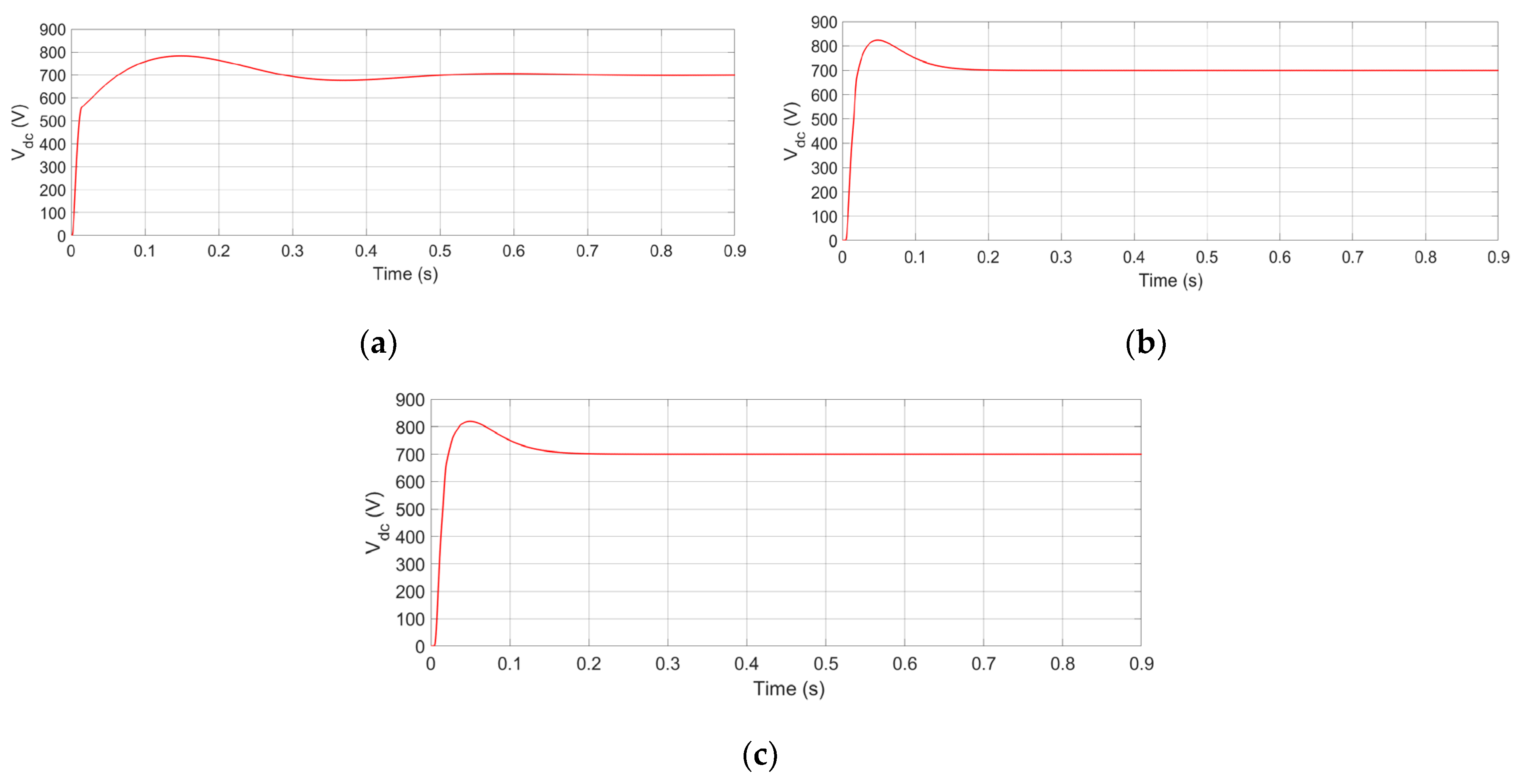
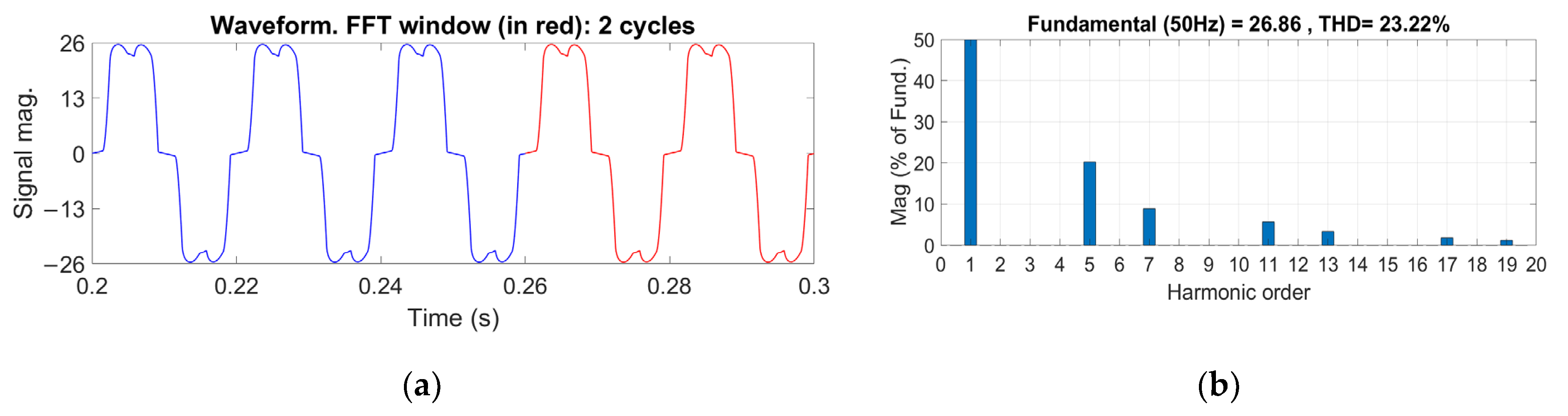
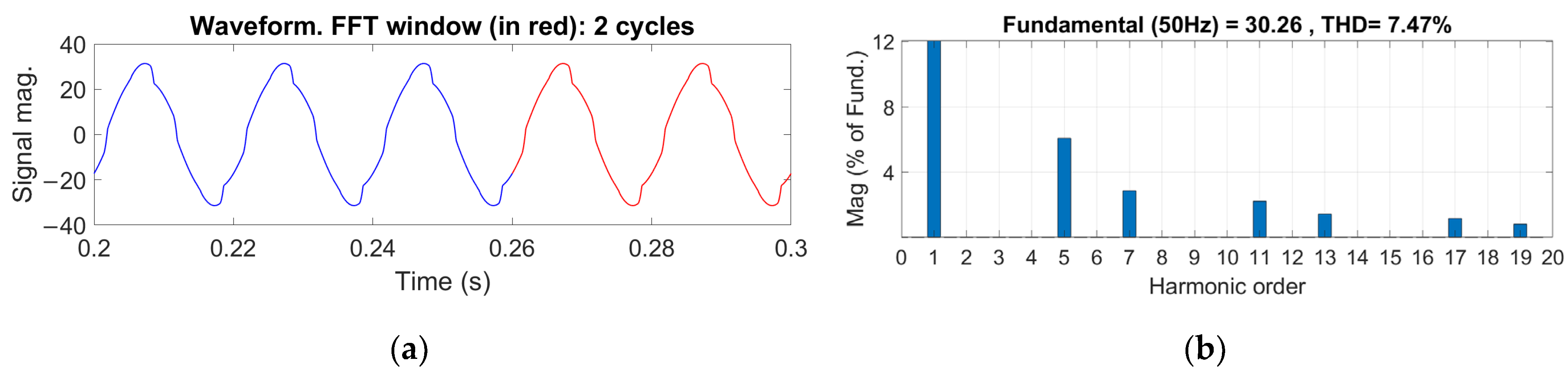
5. Simulation Results and Discussion
5.1. Battery DC Link
5.2. Capacitor DC Link
5.3. Dynamic Response under Capacitor DC Link
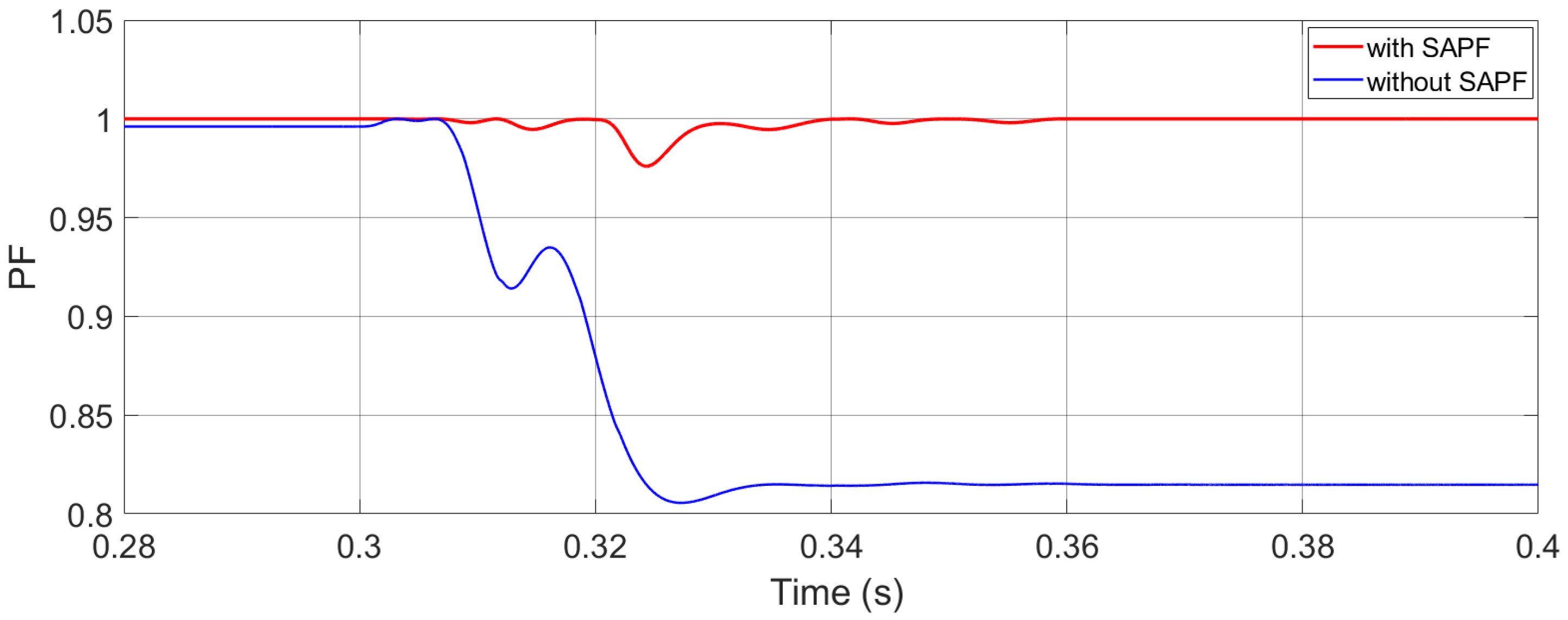
5.4. Power Factor Correction under Capacitor DC Link
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Jayaram, J.; Srinivasan, M.; Prabaharan, N.; Senjyu, T. Design of Decentralized Hybrid Microgrid Integrating Multiple Renewable Energy Sources with Power Quality Improvement. Sustainability 2022, 14, 7777. [Google Scholar] [CrossRef]
- Munir, H.; Zou, J.; Xie, C.; Guerrero, J. Cooperation of Voltage Controlled Active Power Filter with Grid-Connected DGs in Microgrid. Sustainability 2018, 11, 154. [Google Scholar] [CrossRef]
- Boukezata, B.; Chaoui, A.; Gaubert, J.-P.; Hachemi, M. Power Quality Improvement by an Active Power Filter in Grid-Connected Photovoltaic Systems with Optimized Direct Power Control Strategy. Electr. Power Compon. Syst. 2016, 44, 2036–2047. [Google Scholar] [CrossRef]
- Kumar, R.; Bansal, H.O. Shunt Active Power Filter: Current Status of Control Techniques and Its Integration to Renewable Energy Sources. Sustain. Cities Soc. 2018, 42, 574–592. [Google Scholar] [CrossRef]
- Rao, S.N.V.B.; Kumar, Y.V.P.; Pradeep, D.J.; Reddy, C.P.; Flah, A.; Kraiem, H.; Al-Asad, J.F. Power Quality Improvement in Renewable-Energy-Based Microgrid Clusters Using Fuzzy Space Vector PWM Controlled Inverter. Sustainability 2022, 14, 4663. [Google Scholar] [CrossRef]
- Sharma, A.; Rajpurohit, B.S.; Singh, S.N. A Review on Economics of Power Quality: Impact, Assessment and Mitigation. Renew. Sustain. Energy Rev. 2018, 88, 363–372. [Google Scholar] [CrossRef]
- Afonso, J.L.; Tanta, M.; Pinto, J.G.O.; Monteiro, L.F.C.; Machado, L.; Sousa, T.J.C.; Monteiro, V. A Review on Power Electronics Technologies for Power Quality Improvement. Energies 2021, 14, 8585. [Google Scholar] [CrossRef]
- Puhan, P.S.; Ray, P.K.; Pottapinjara, S. Performance Analysis of Shunt Active Filter for Harmonic Compensation under Various Non-Linear Loads. Int. J. Emerg. Electr. Power Syst. 2021, 22, 21–29. [Google Scholar] [CrossRef]
- Marian, P.K. Modeling and Control of Power Electronics Converter System for Power Quality Improvements; Elsevier: Amsterdam, The Netherlands, 2018; pp. 31–84. ISBN 9780128145685. [Google Scholar]
- Kashif, M.; Hossain, M.J.; Fernandez, E.; Taghizadeh, S.; Sharma, V.; Ali, S.M.N.; Irshad, U.B. A Fast Time-Domain Current Harmonic Extraction Algorithm for Power Quality Improvement Using Three-Phase Active Power Filter. IEEE Access 2020, 8, 103539–103549. [Google Scholar] [CrossRef]
- Das, S.R.; Ray, P.K.; Sahoo, A.K.; Ramasubbareddy, S.; Babu, T.S.; Kumar, N.M.; Elavarasan, R.M.; Mihet-Popa, L. A Comprehensive Survey on Different Control Strategies and Applications of Active Power Filters for Power Quality Improvement. Energies 2021, 14, 4589. [Google Scholar] [CrossRef]
- Kumar, R.S.; Christopher Raj, I.G.; Saravanan, S.; Leninpugalhanthi, P.; Pandiyan, P. Impact of Power Quality Issues in Residential Systems. In Power Quality in Modern Power Systems; Elsevier: Amsterdam, The Netherlands, 2021; pp. 163–191. ISBN 9780128233467. [Google Scholar]
- Tareen, W.U.; Mekhilef, S.; Seyedmahmoudian, M.; Horan, B. Active Power Filter (APF) for Mitigation of Power Quality Issues in Grid Integration of Wind and Photovoltaic Energy Conversion System. Renew. Sustain. Energy Rev. 2017, 70, 635–655. [Google Scholar] [CrossRef]
- Imam, A.A.; Sreerama Kumar, R.; Al-Turki, Y.A. Modeling and Simulation of a PI Controlled Shunt Active Power Filter for Power Quality Enhancement Based on P-Q Theory. Electronics 2020, 9, 637. [Google Scholar] [CrossRef]
- Tham, Z.Y.; Hoon, Y.; Mohd Radzi, M.A. Synchronous Reference Frame with Finite Impulse Response Filter for Operation of Single-Phase Shunt Active Power Filter. MATEC Web Conf. 2021, 335, 02004. [Google Scholar] [CrossRef]
- Qazi, S.H.; Mustafa, M.W.B.; Soomro, S.; Larik, R.M. Comparison of Reference Signal Extraction Methods for Active Power Filter to Mitigate Load Harmonics from Wind Turbine Generator. In Proceedings of the 2015 IEEE Conference on Energy Conversion (CENCON), Johor Bahru, Malaysia, 19–20 October 2015; pp. 463–468. [Google Scholar]
- Büyük, M.; İnci, M.; Tan, A.; Tümay, M. Improved Instantaneous Power Theory Based Current Harmonic Extraction for Unbalanced Electrical Grid Conditions. Electr. Power Syst. Res. 2019, 177, 106014. [Google Scholar] [CrossRef]
- Chen, D.; Xiao, L.; Yan, W.; Li, Y.; Guo, Y. A Harmonics Detection Method Based on Triangle Orthogonal Principle for Shunt Active Power Filter. Energy Rep. 2021, 7, 98–104. [Google Scholar] [CrossRef]
- Hoon, Y.; Mohd Radzi, M.; Hassan, M.; Mailah, N. A Dual-Function Instantaneous Power Theory for Operation of Three-Level Neutral-Point-Clamped Inverter-Based Shunt Active Power Filter. Energies 2018, 11, 1592. [Google Scholar] [CrossRef]
- Terriche, Y.; Golestan, S.; Guerrero, J.M.; Kerdoune, D.; Vasquez, J.C. Matrix Pencil Method-based Reference Current Generation for Shunt Active Power Filters. IET Power Electron. 2018, 11, 772–780. [Google Scholar] [CrossRef]
- El Ghaly, A.; Tarnini, M.; Moubayed, N.; Chahine, K. A Filter-Less Time-Domain Method for Reference Signal Extraction in Shunt Active Power Filters. Energies 2022, 15, 5568. [Google Scholar] [CrossRef]
- Thentral, T.M.T.; Palanisamy, R.; Usha, S.; Vishnuram, P.; Bajaj, M.; Sharma, N.K.; Khan, B.; Kamel, S. The Improved Unified Power Quality Conditioner with the Modular Multilevel Converter for Power Quality Improvement. Int. Trans. Electr. Energy Syst. 2022, 2022, 1–15. [Google Scholar] [CrossRef]
- Srilakshmi, K.; Sujatha, C.N.; Balachandran, P.K.; Mihet-Popa, L.; Kumar, N.U. Optimal Design of an Artificial Intelligence Controller for Solar-Battery Integrated UPQC in Three Phase Distribution Networks. Sustainability 2022, 14, 13992. [Google Scholar] [CrossRef]
- Huang, C.; Liu, Y.; Song, W.; Liu, K. Designing and Simulation of a Novel Active Power Filter Based on FXLMS Method. In Proceedings of the 2017 IEEE Electrical Design of Advanced Packaging and Systems Symposium (EDAPS), Haining, China, 14–16 December 2017; pp. 1–3. [Google Scholar]
- Musa, S.; Radzi, M.; Hizam, H.; Wahab, N.; Hoon, Y.; Zainuri, M. Modified Synchronous Reference Frame Based Shunt Active Power Filter with Fuzzy Logic Control Pulse Width Modulation Inverter. Energies 2017, 10, 758. [Google Scholar] [CrossRef]
- Hoon, Y.; Mohd Radzi, M.; Hassan, M.; Mailah, N. DC-Link Capacitor Voltage Regulation for Three-Phase Three-Level Inverter-Based Shunt Active Power Filter with Inverted Error Deviation Control. Energies 2016, 9, 533. [Google Scholar] [CrossRef]
- Wang, Y.; Wang, Y.; Chen, S.-Z.; Zhang, G.; Zhang, Y. A Simplified Minimum DC-Link Voltage Control Strategy for Shunt Active Power Filters. Energies 2018, 11, 2407. [Google Scholar] [CrossRef]
- Zainuri, M.A.A.M.; Radzi, M.A.M.; Soh, A.C.; Mariun, N.; Rahim, N.A. DC-link Capacitor Voltage Control for Single-phase Shunt Active Power Filter with Step Size Error Cancellation in Self-charging Algorithm. IET Power Electron. 2016, 9, 323–335. [Google Scholar] [CrossRef]
- Dian, R.; Xu, W.; Mu, C. Improved Negative Sequence Current Detection and Control Strategy for H-Bridge Three-Level Active Power Filter. IEEE Trans. Appl. Supercond. 2016, 26, 1–5. [Google Scholar] [CrossRef]
- Cao, X.; Zhou, S.; Li, J.; Zhang, S. A DC Voltage Control Strategy for Active Power Filter. TOEEJ 2016, 10, 166–180. [Google Scholar] [CrossRef][Green Version]
- Chen, M.-H. Development of Shunt-Type Three-Phase Active Power Filter with Novel Adaptive Control for Wind Generators. Sci. World J. 2015, 2015, 1–10. [Google Scholar] [CrossRef]
- Rameshkumar, K.; Indragandhi, V. Overview of Reference Current Extraction Techniques in Single Phase Shunt. Int. J. Emerg. Technol. 2020, 26, 689–698. [Google Scholar]
- Li, H.; Liu, Y.; Yang, J. A Novel FCS-MPC Method of Multi-Level APF Is Proposed to Improve the Power Quality in Renewable Energy Generation Connected to the Grid. Sustainability 2021, 13, 4094. [Google Scholar] [CrossRef]
- Chahine, K. Towards Automatic Setup of Non Intrusive Appliance Load Monitoring—Feature Extraction and Clustering. IJECE 2019, 9, 1002–1011. [Google Scholar] [CrossRef]
- Qiu, R.C.; Lu, I.-T. Multipath Resolving with Frequency Dependence for Wide-Band Wireless Channel Modeling. IEEE Trans. Veh. Technol. 1999, 48, 273–285. [Google Scholar] [CrossRef]
- McClure, M.; Qiu, R.C.; Carin, L. On the Superresolution Identification of Observables from Swept-Frequency Scattering Data. IEEE Trans. Antennas Propagat. 1997, 45, 631–641. [Google Scholar] [CrossRef]
- Fernandez del Rio, J.E.; Catedra-Perez, M.F. The Matrix Pencil Method for Two-Dimensional Direction of Arrival Estimation Employing an L-Shaped Array. IEEE Trans. Antennas Propagat. 1997, 45, 1693–1694. [Google Scholar] [CrossRef]
- Chahine, K.; Baltazart, V.; Wang, Y. Interpolation-Based Matrix Pencil Method for Parameter Estimation of Dispersive Media in Civil Engineering. Signal Process. 2010, 90, 2567–2580. [Google Scholar] [CrossRef]
- Chahine, K.; Baltazart, V.; Wang, Y. Parameter Estimation of Dispersive Media Using the Matrix Pencil Method with Interpolated Mode Vectors. IET Signal Process. 2011, 5, 397–406. [Google Scholar] [CrossRef]
- Chahine, K.; Baltazart, V.; Wang, Y. Parameter Estimation of Damped Power-Law Phase Signals via a Recursive and Alternately Projected Matrix Pencil Method. IEEE Trans. Antennas Propagat. 2011, 59, 1207–1216. [Google Scholar] [CrossRef]







| Circuit Parameters | Parameter Value |
|---|---|
| Frequency | 50 Hz |
| Supply phase voltage peak value | 220 V |
| Source impedance (Rs, Ls) | 0.15 Ω, 0.03 mH |
| Line impedance (Rr, Lr) | 1 Ω, 1 mH |
| Coupling reactance | 3 mH |
| DC-link capacitance (Cdc) | 3000 µF |
| DC-link voltage reference (Vref) | 700 V |
| Load 1 impedance (RL, LL) | 40 Ω, 2 mH |
| Extraction Technique | % THD of Source Current | ||
|---|---|---|---|
| Hysteresis | PWM | SVPWM | |
| IRPT | 1.74% | 1.24% | 1.39% |
| SRF | 1.46% | 1.26% | 1.41% |
| MPM | 1.22% | 0.83% | 0.93% |
| Extraction Technique | % THD of Source Current | ||
|---|---|---|---|
| Hysteresis | PWM | SVPWM | |
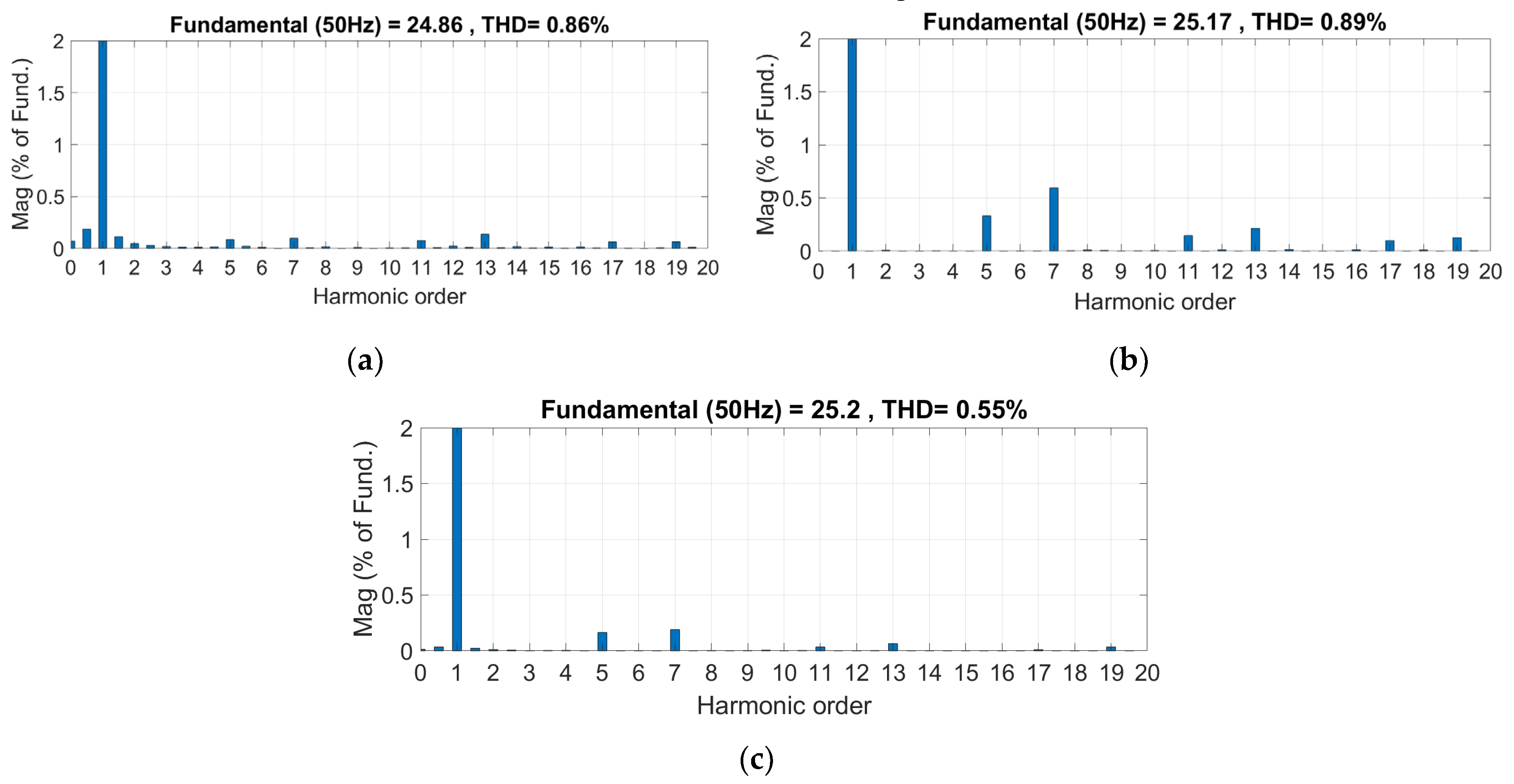
| IRPT | 1.74% | 1.21% | 1.37% |
| SRF | 1.61% | 1.43% | 1.54% |
| MPM | 1.21% | 0.85% | 0.93% |
| Extraction Technique | % THD of Source Current | ||
|---|---|---|---|
| Hysteresis | PWM | SVPWM | |
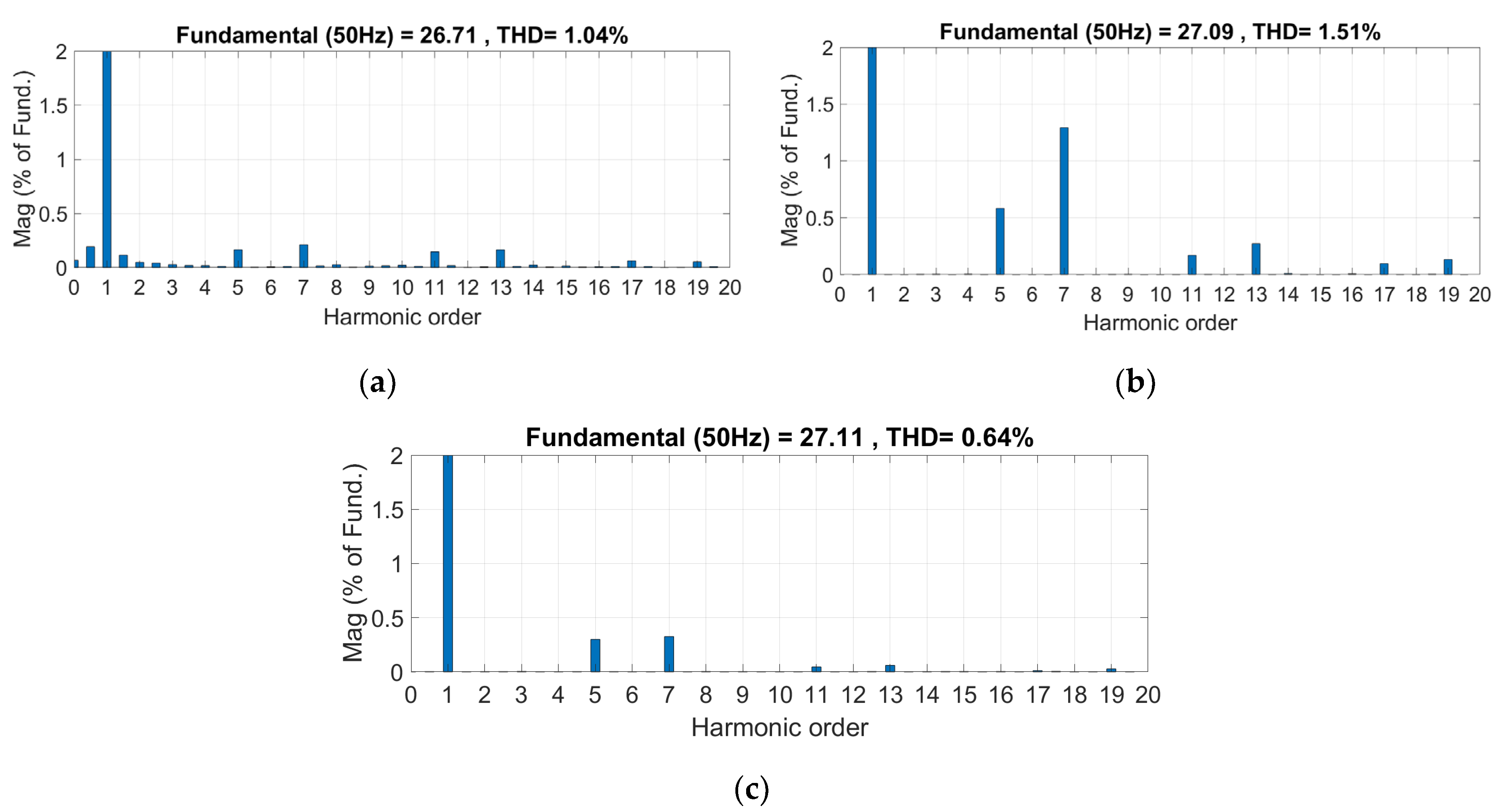
| IRPT | 1.04% | 0.85% | 0.88% |
| SRF | 1.51% | 1.52% | 1.61% |
| MPM | 0.64% | 0.52% | 0.55% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chahine, K.; Tarnini, M.; Moubayed, N.; El Ghaly, A. Power Quality Enhancement of Grid-Connected Renewable Systems Using a Matrix-Pencil-Based Active Power Filter. Sustainability 2023, 15, 887. https://doi.org/10.3390/su15010887
Chahine K, Tarnini M, Moubayed N, El Ghaly A. Power Quality Enhancement of Grid-Connected Renewable Systems Using a Matrix-Pencil-Based Active Power Filter. Sustainability. 2023; 15(1):887. https://doi.org/10.3390/su15010887
Chicago/Turabian StyleChahine, Khaled, Mohamad Tarnini, Nazih Moubayed, and Abdallah El Ghaly. 2023. "Power Quality Enhancement of Grid-Connected Renewable Systems Using a Matrix-Pencil-Based Active Power Filter" Sustainability 15, no. 1: 887. https://doi.org/10.3390/su15010887
APA StyleChahine, K., Tarnini, M., Moubayed, N., & El Ghaly, A. (2023). Power Quality Enhancement of Grid-Connected Renewable Systems Using a Matrix-Pencil-Based Active Power Filter. Sustainability, 15(1), 887. https://doi.org/10.3390/su15010887









