Two Terminal Instantaneous Power-Based Fault Classification and Location Techniques for Transmission Lines
Abstract
1. Introduction
- The proposed technique is implemented on the IEEE-9 bus system, which is an entirely different system to that used in the previous research.
- The fault locations are identified and located with less than 0.45% error. However, in the previous studies, the error in fault location was up to more than 5%.
- More parameters were required in the previous research to reduce the percentage error in fault location like fault inception angle, fault distance, and resistance. Here, the proposed technique is quite simple, and fault distance is sufficient to produce the desired results.
- The proposed technique helps us to prepare the datasets that could be used to train the machine learning algorithms so that a new fault type and location could be identified with the trained algorithm. However, there is no such information available in previous research.
- The proposed technique and the previous technique are both threshold-independent. However, the proposed technique is more independent of the variations of the system parameters, resulting in more accuracy for fault identification and location.
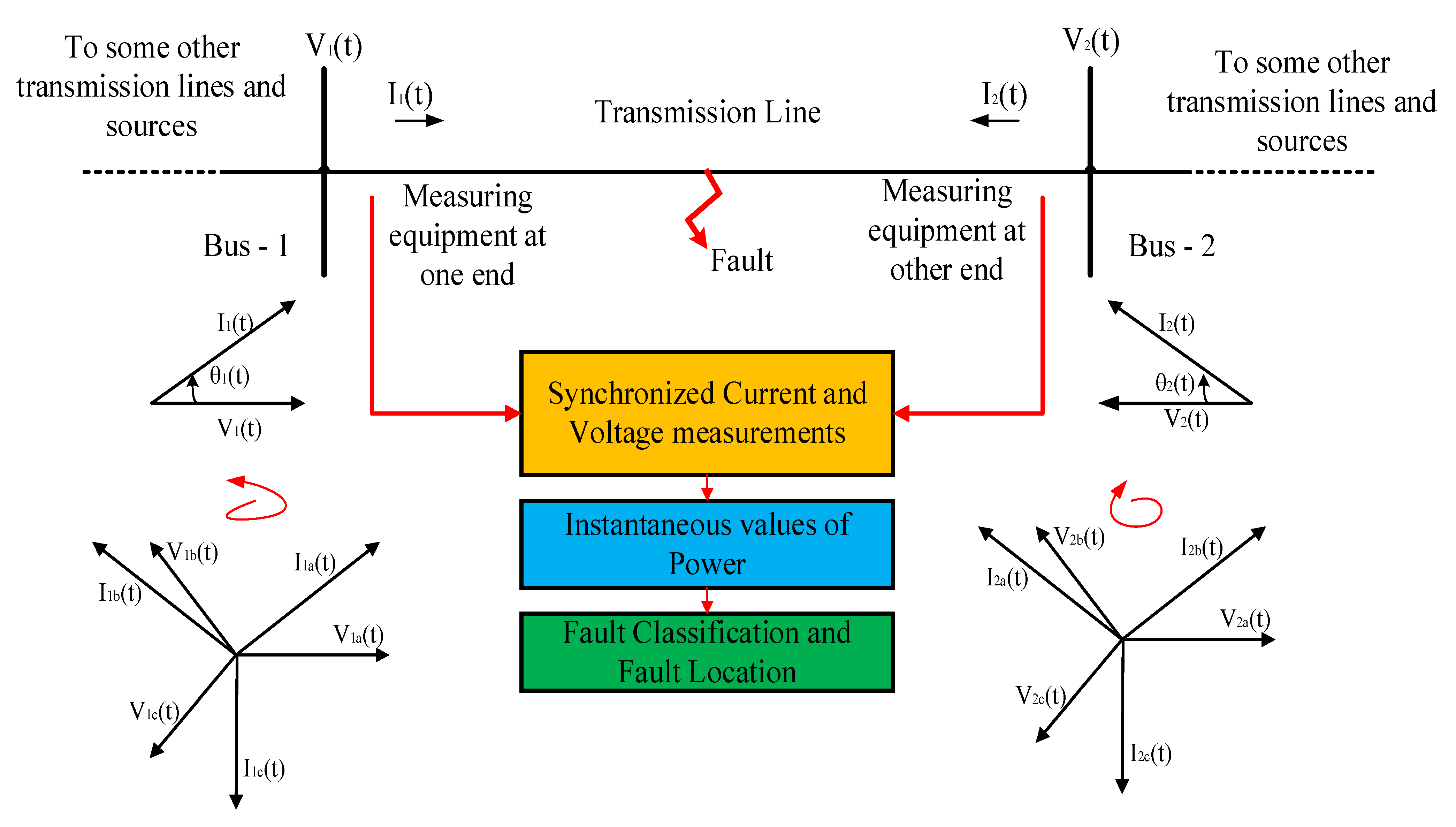
2. Proposed Method for Fault Analysis and Location
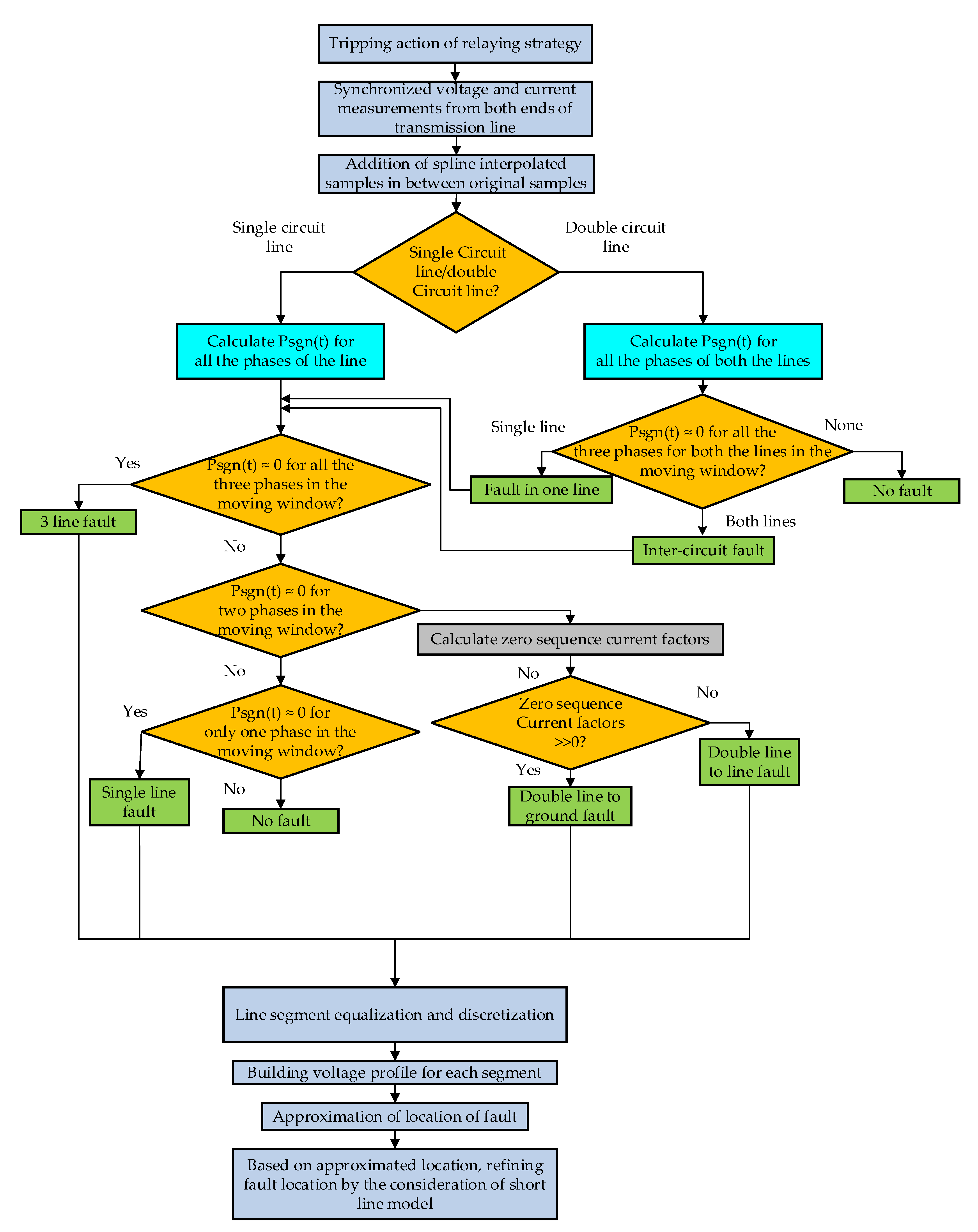
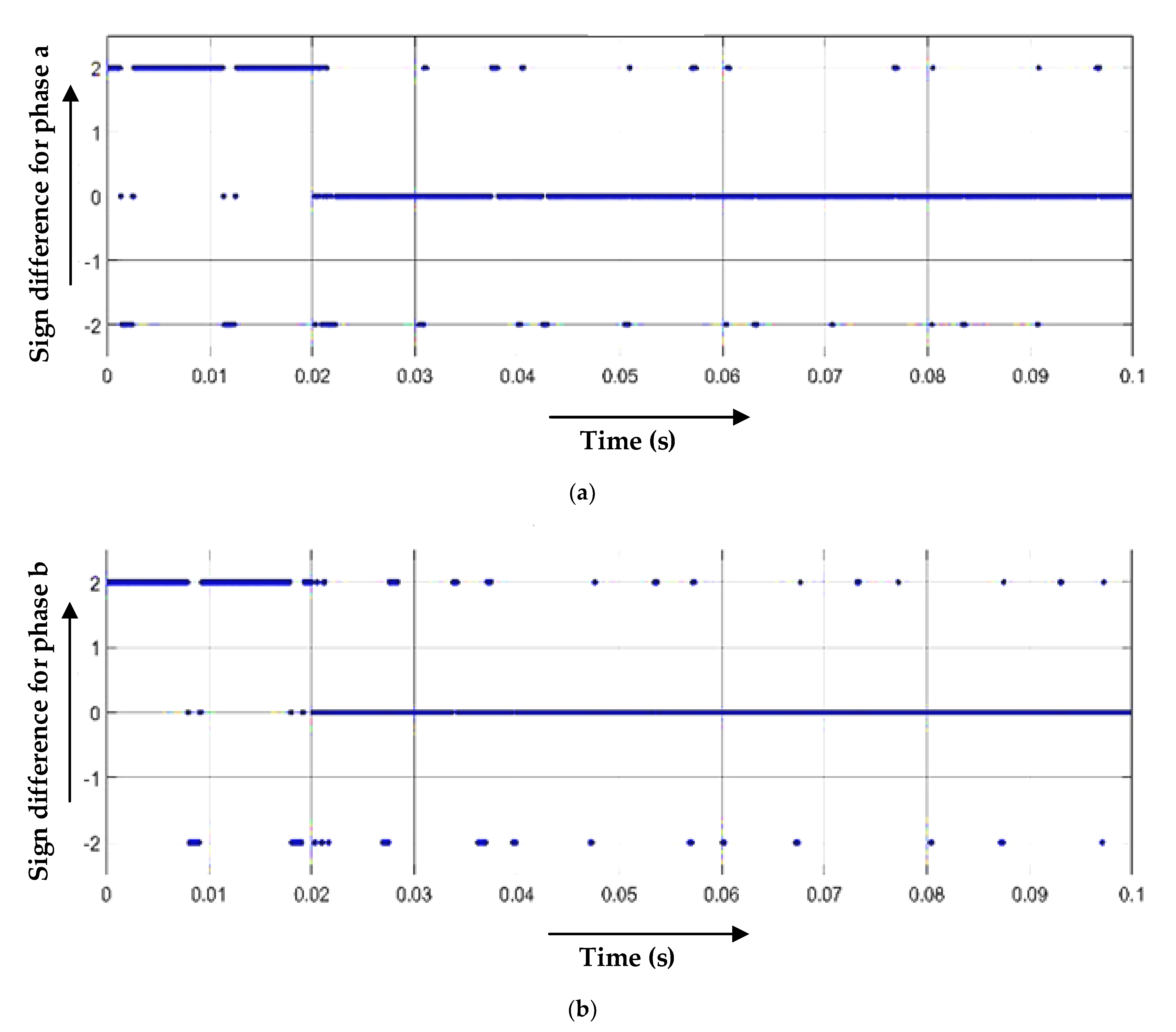
2.1. Detection of Fault and Fault Type Classification
2.1.1. Case 1
2.1.2. Case 2
3. Results and Discussions
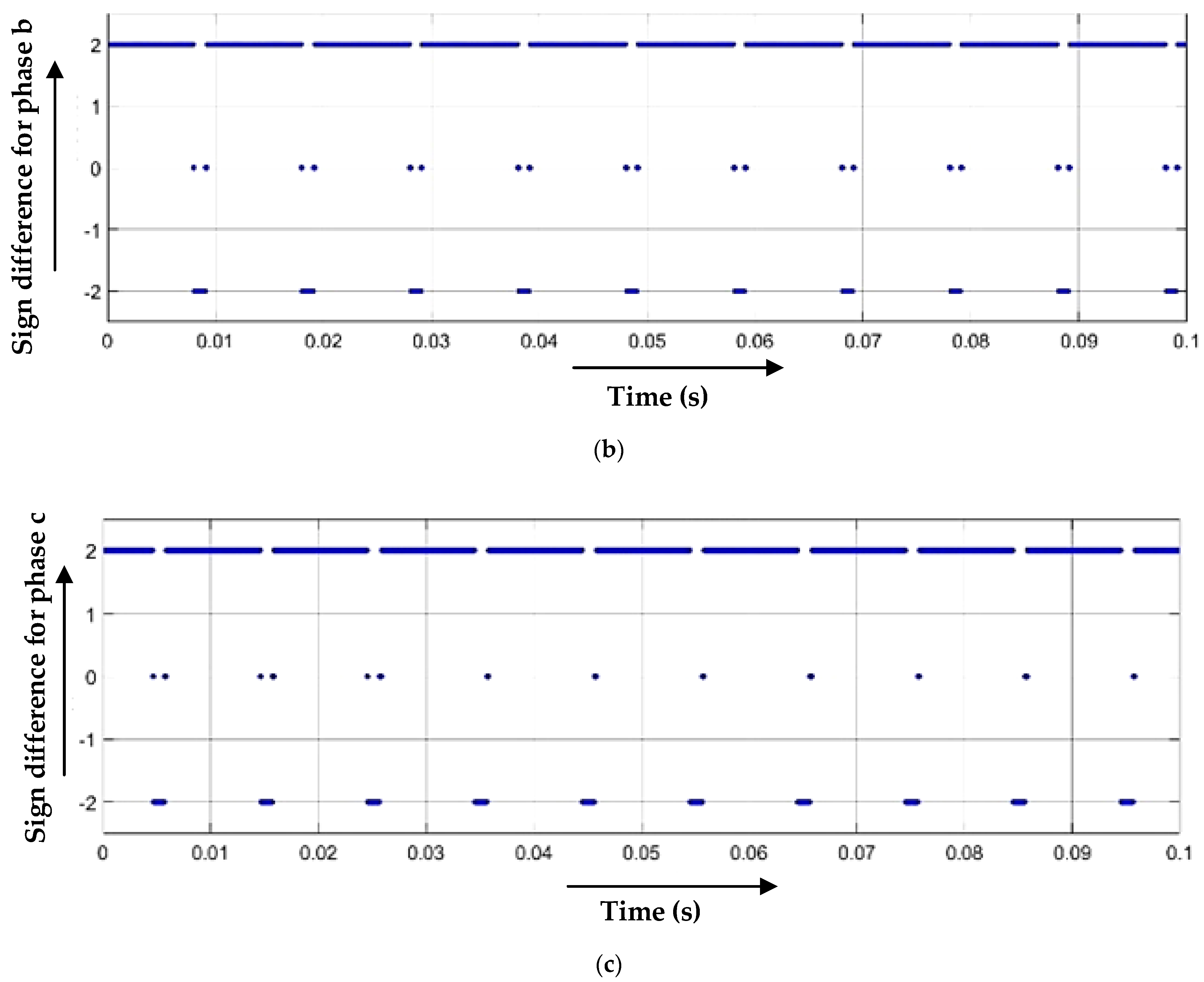
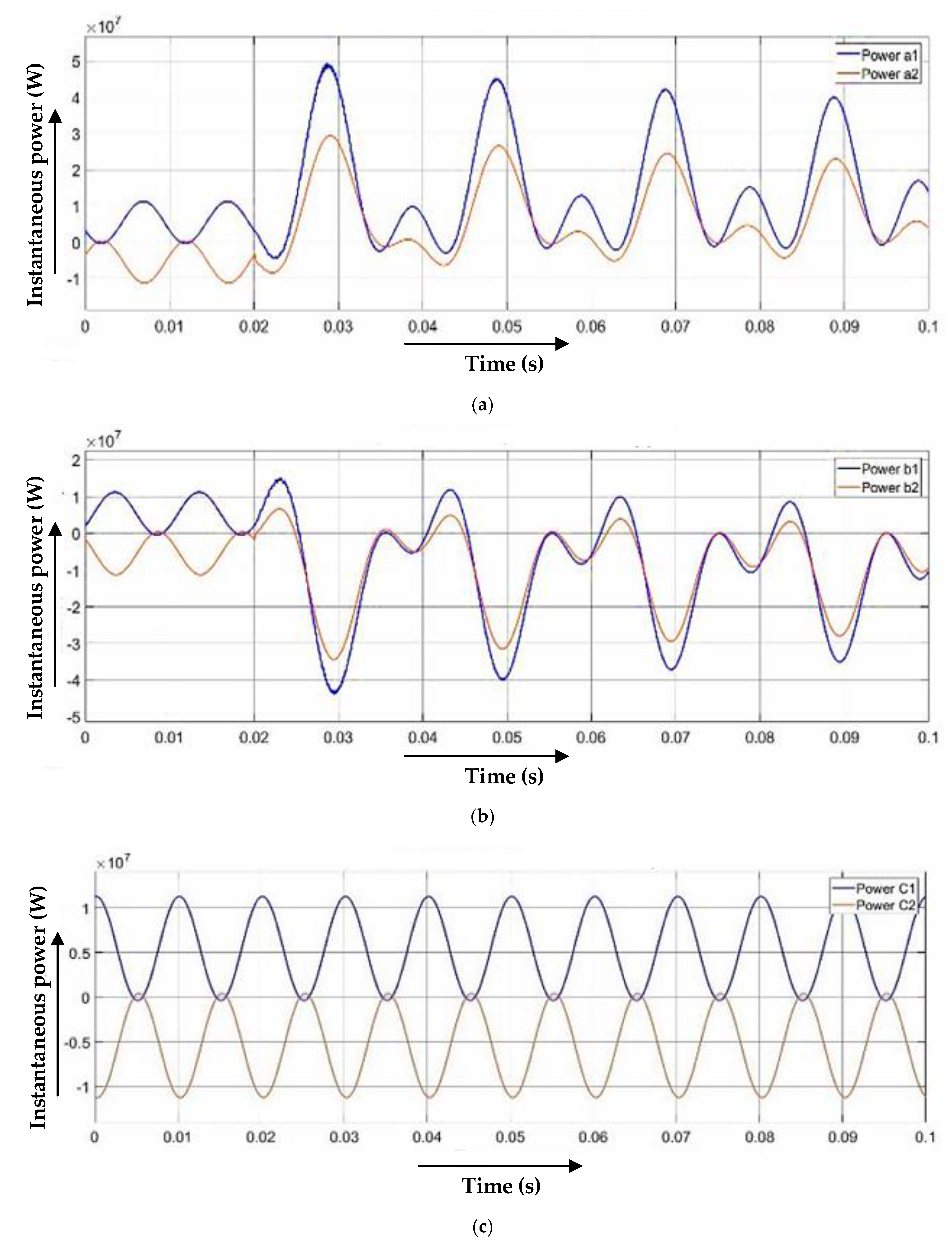
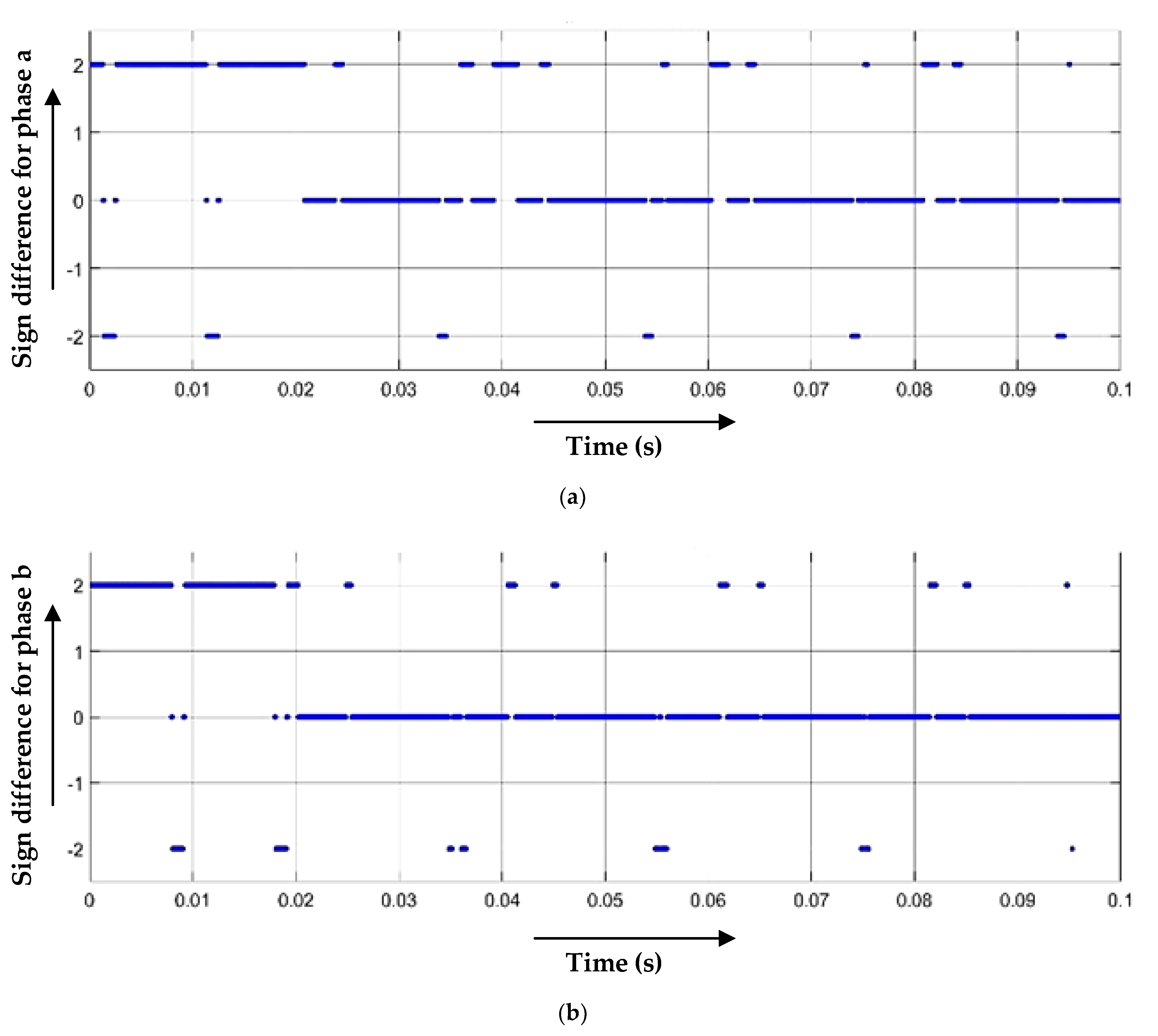
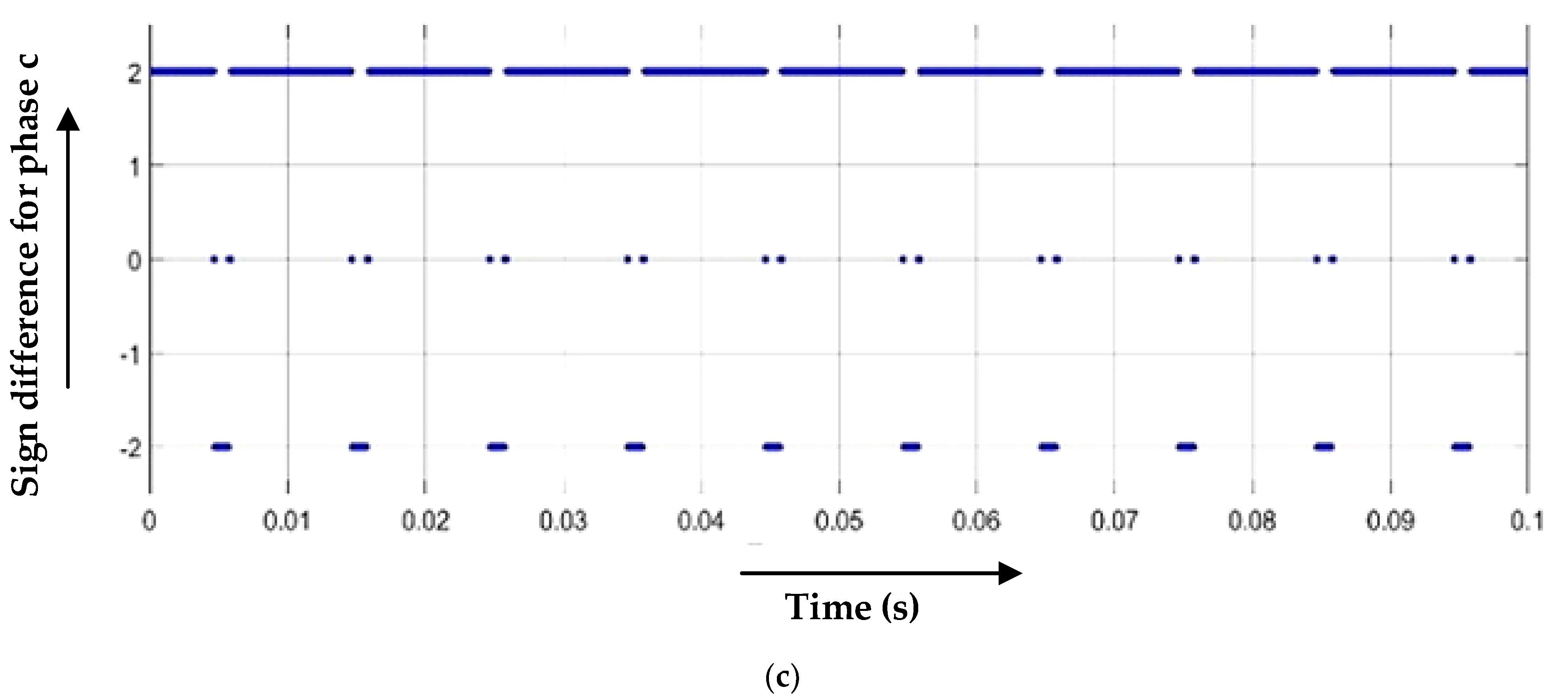
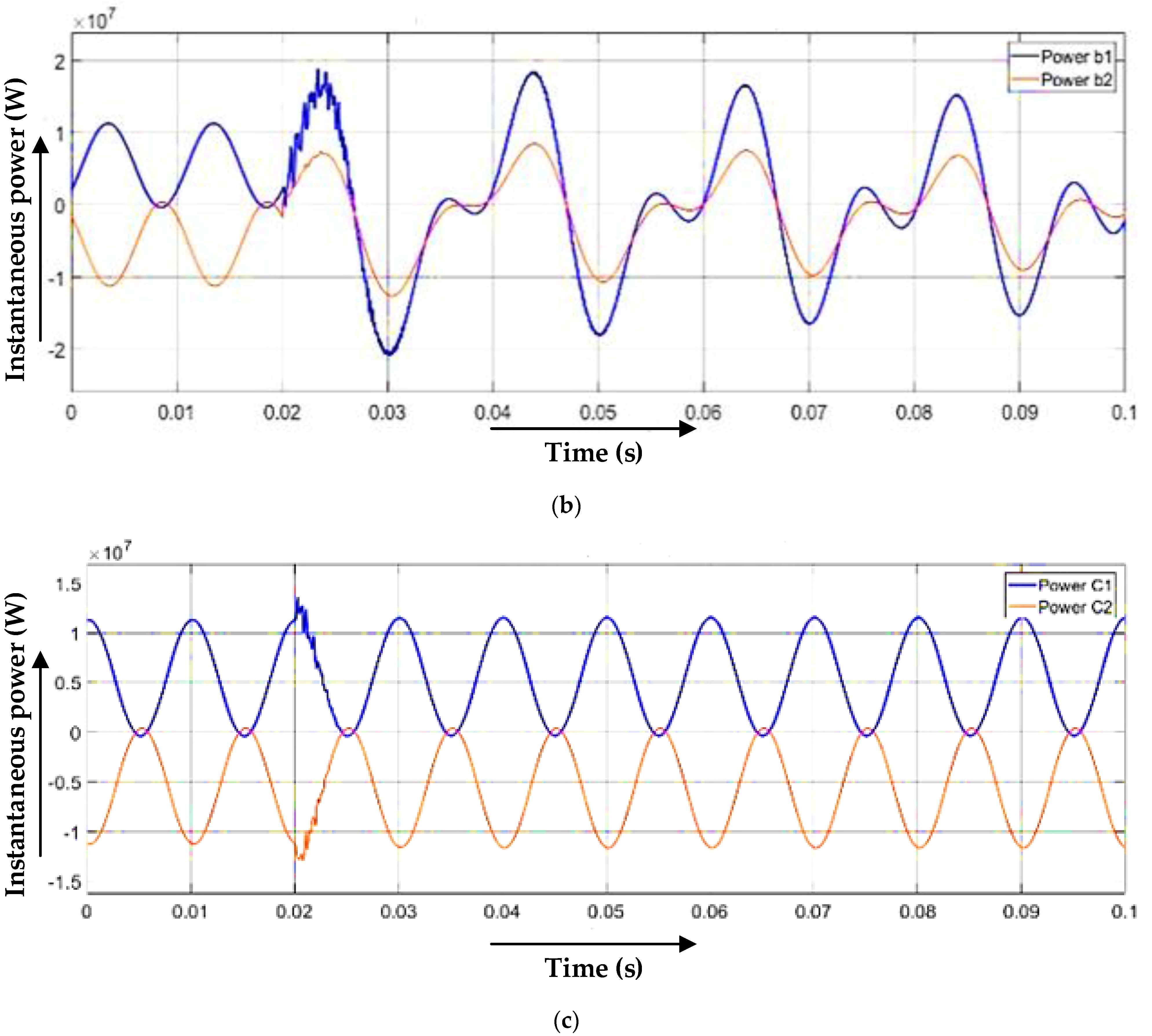
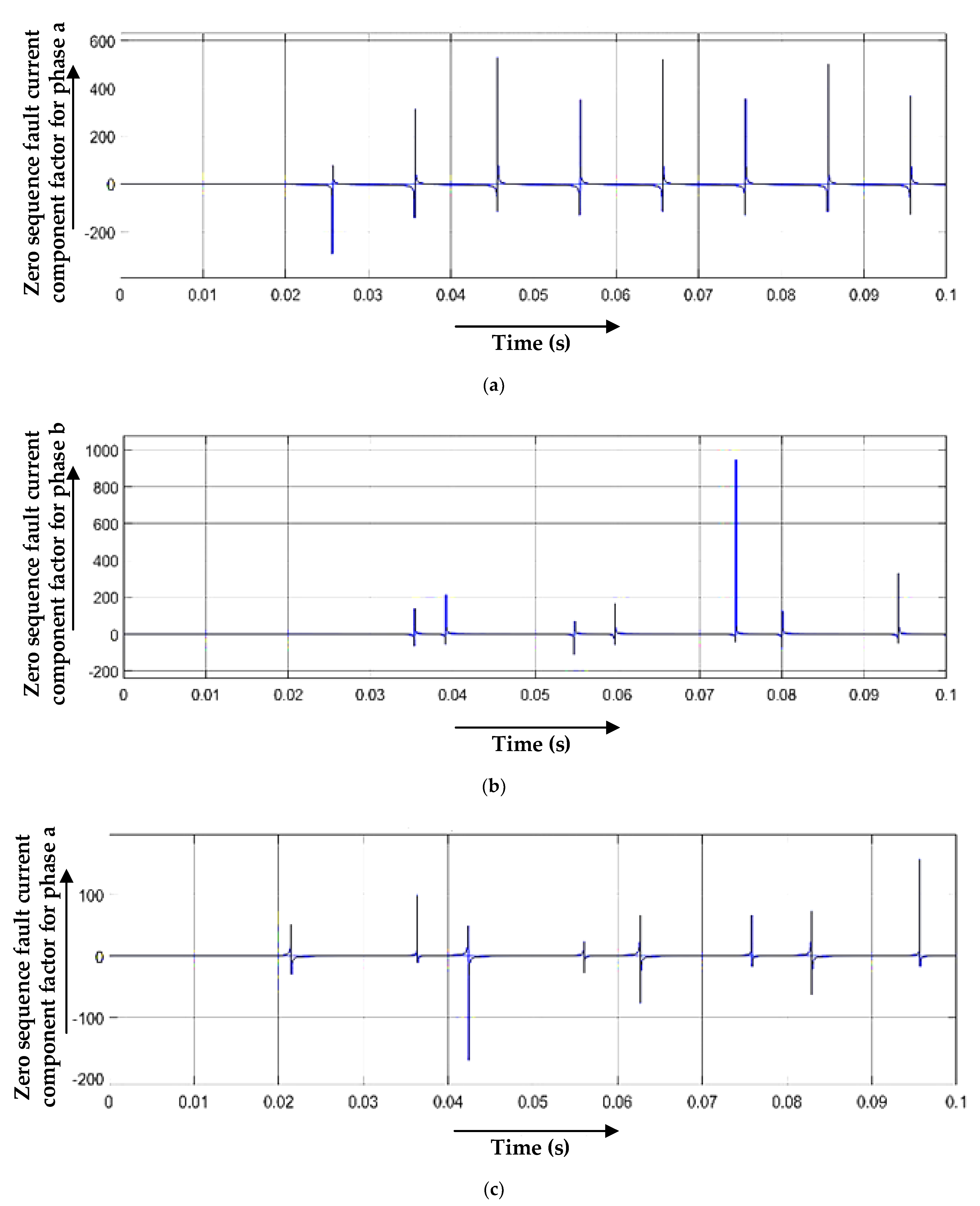
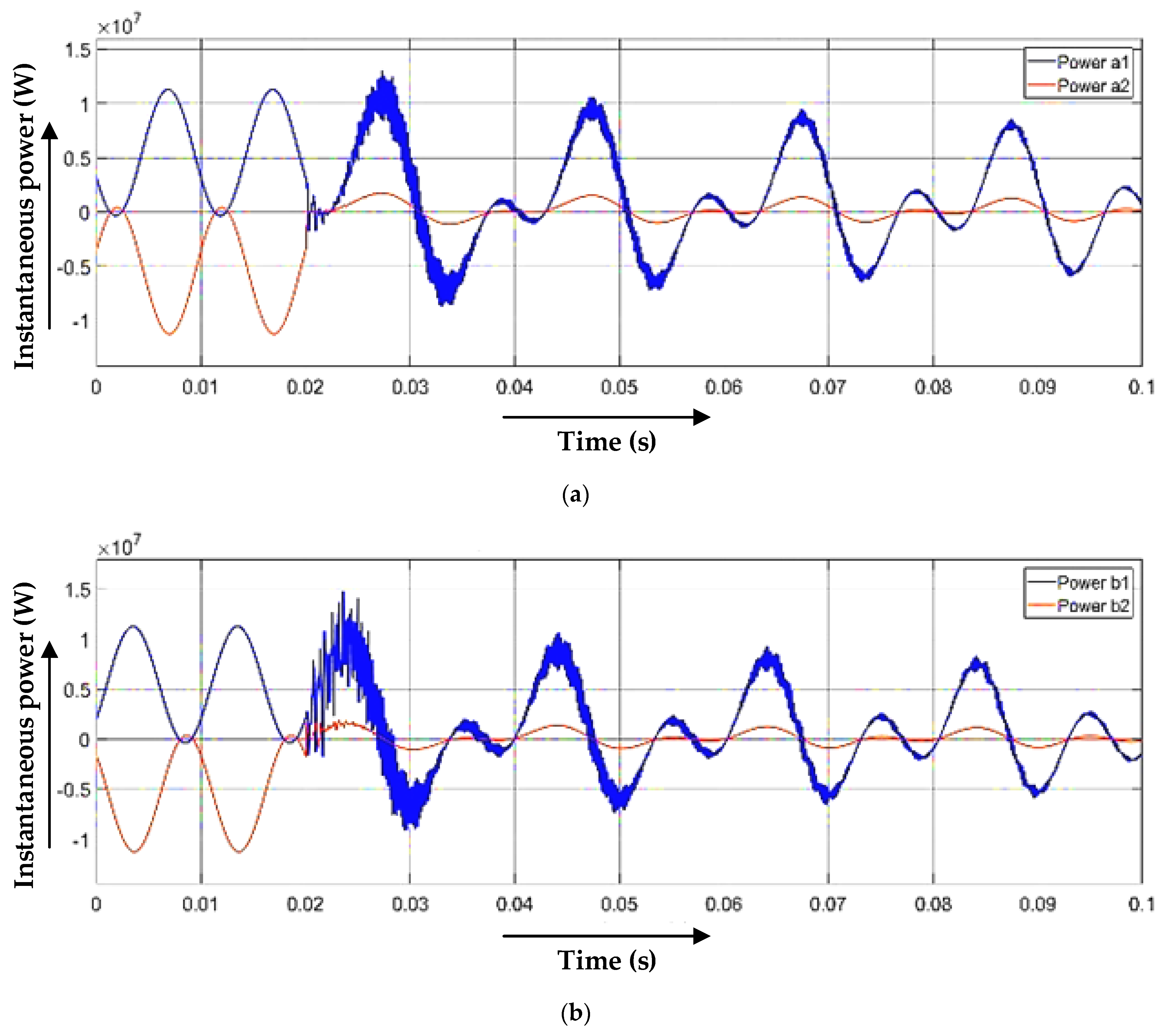
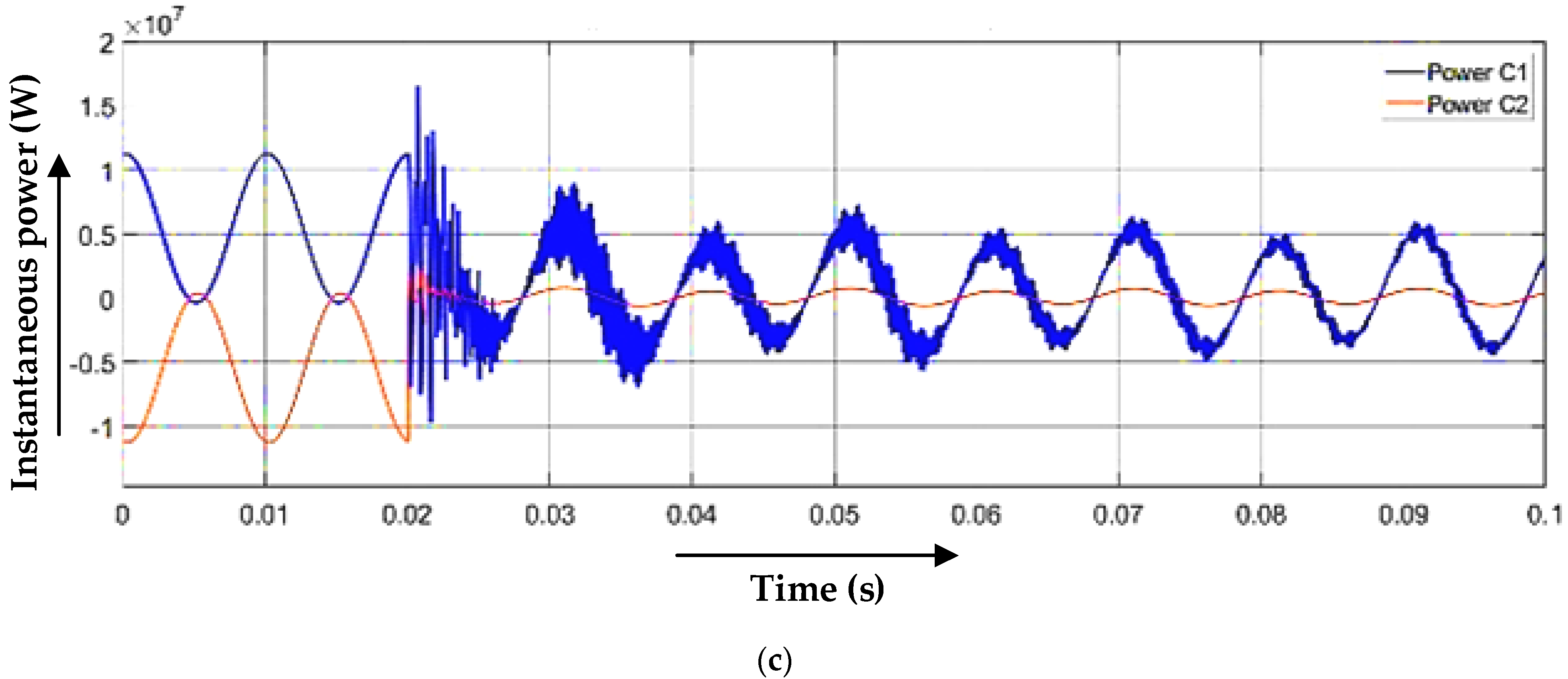
3.1. Single Line-to-Ground Fault
3.2. Line-to-Line Fault
3.3. Double-Line-to-Ground Fault
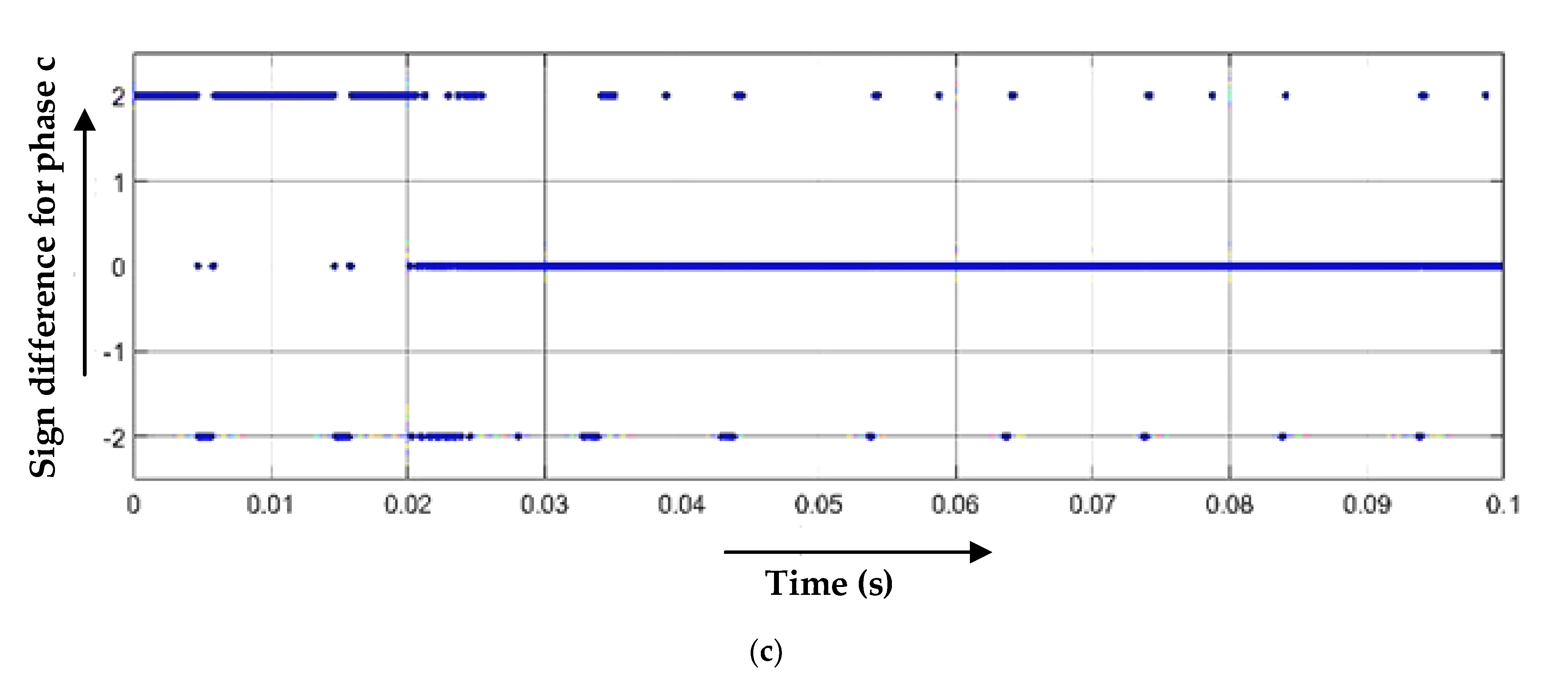
3.4. Line-to-Line and Line Fault (Three-Line Fault)
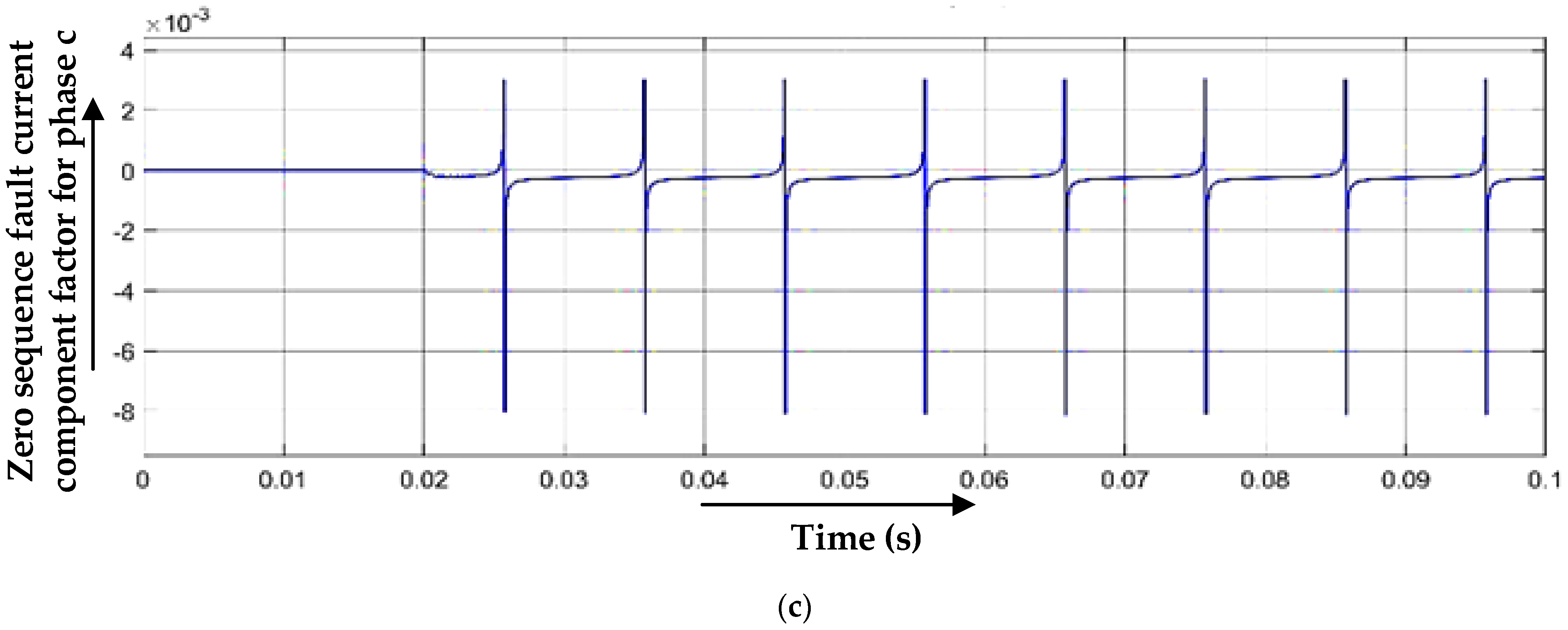
4. Location of Faults
5. Research Outcomes and Limitations
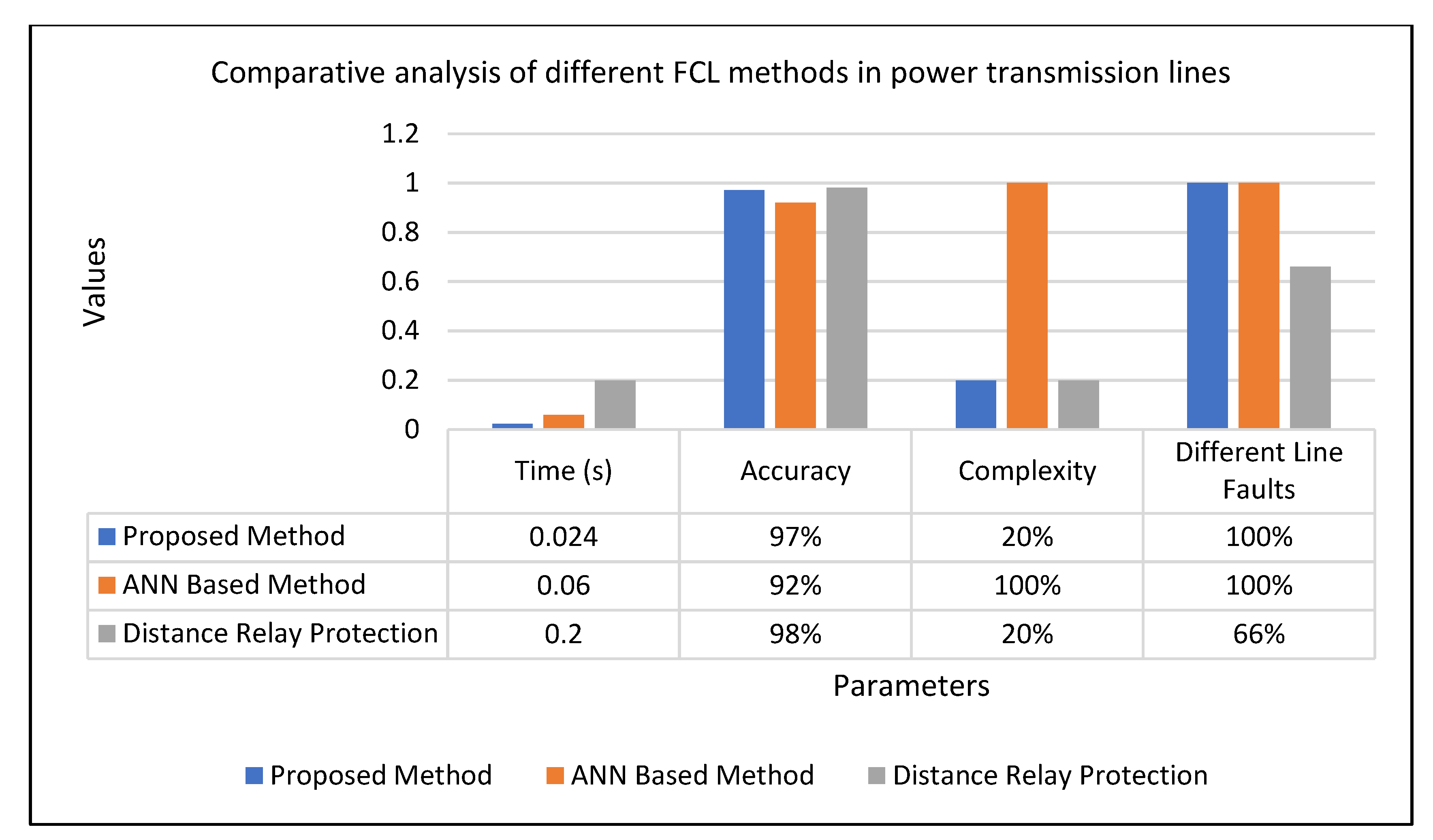
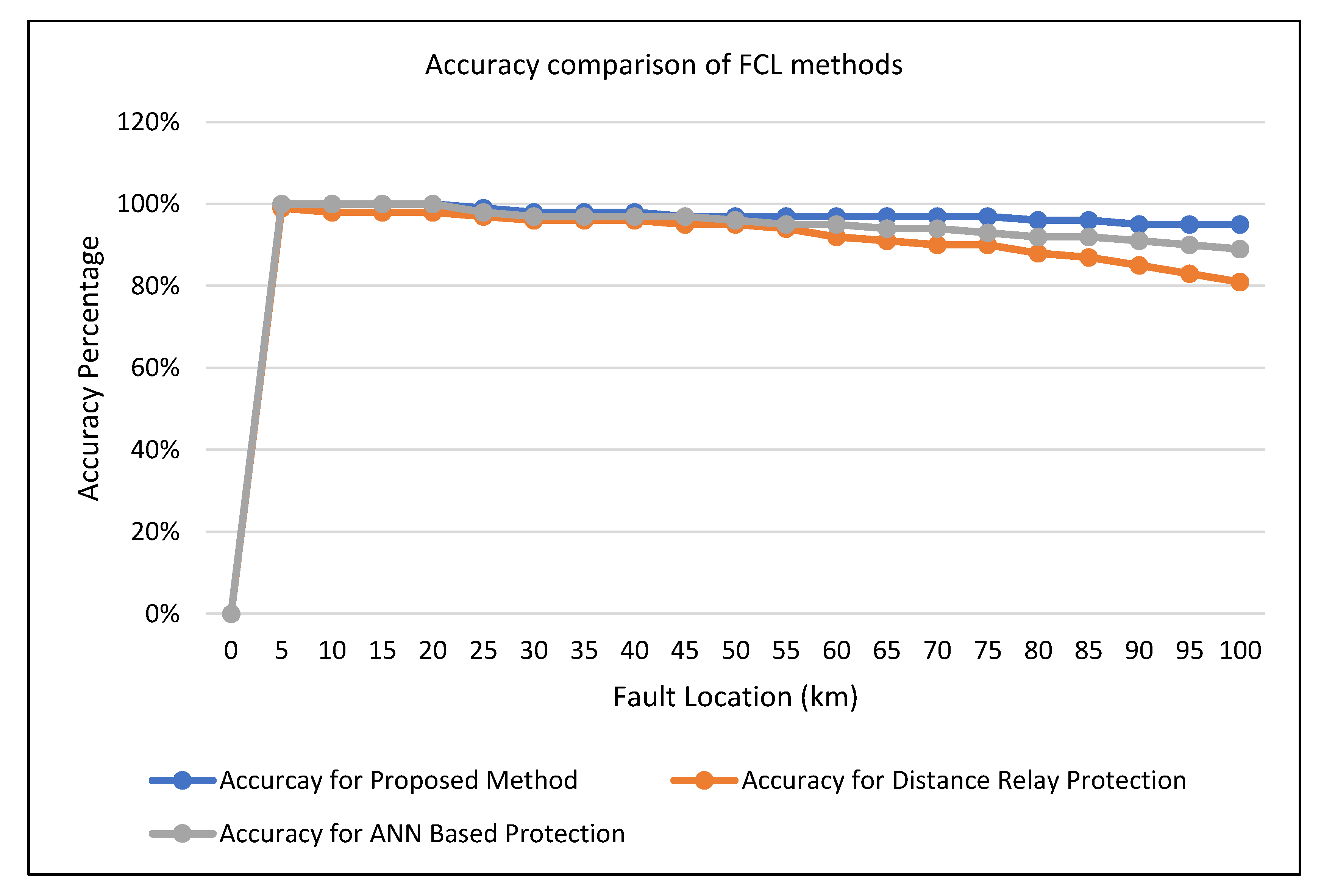
6. Comparative Analysis
7. Conclusions
- It does not require threshold comparison and requires only voltage and current samples from both ends of the line.
- It detects the fault in a very short time, and its fast response does not affect its accuracy.
- It can discriminate between faulty and non-faulty conditions.
- It can operate well with modern relays. The operation of the relay does not affect its performance.
- The rapidness makes this technique an ideal candidate for the power system integrated with renewable energy sources. In addition to this, peer-to-peer energy trading can be offered with the implementation of this technique.
- This technique is implemented on the IEEE-9 bus system for various types of faults and various fault locations. Its performance is not affected by any parameter of the system. This property highlights its effectiveness on any type of system.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Sachdev, M.S.; Baribeau, M.A. A New Algorithm for Digital Impedance Relays. IEEE Trans. Power Appar. Syst. 1979, PAS-98, 2232–2240. [Google Scholar] [CrossRef]
- Girgis, A.A. A New Kalman Filtering Based Digital Distance Relay. IEEE Trans. Power Appar. Syst. 1982, PAS-101, 3471–3480. [Google Scholar] [CrossRef]
- Takagi, T.; Yamakoshi, Y.; Baba, J.; Uemura, K.; Sakaguchi, T. A New Algorithm of an Accurate Fault Location for EHV/UHV Transmission Lines: Part II-Laplace Transform Method. IEEE Trans. Power Appar. Syst. 1982, PAS-10, 564–573. [Google Scholar] [CrossRef]
- Johns, A.T.; Jamali, S. Accurate Fault Location Technique for Power Transmission Lines. IEE Proc. C Gener. Transm. Distrib. 1990, 137, 395–402. [Google Scholar] [CrossRef]
- Hussain, A.; Kim, C.-H.; Admasie, S. An intelligent islanding detection of distribution networks with synchronous machine DG using ensemble learning and canonical methods. IET Gener. Transm. Distrib. 2021, 15, 3242–3255. [Google Scholar] [CrossRef]
- Poeltl, A.; Frohlich, K. Two New Methods for Very Fast Fault Type Detection by Means of Parameter Fitting and Artificial Neural Networks. IEEE Trans. Power Deliv. 1999, 14, 1269–1275. [Google Scholar] [CrossRef]
- Saha, M.M.; Izykowski, J.; Rosolowski, E.; Kasztenny, B. A New Accurate Fault Locating Algorithm for Series Compensated Lines. IEEE Trans. Power Deliv. 1999, 14, 789–797. [Google Scholar] [CrossRef]
- Youssef, O.A.S. Combined Fuzzy-Logic Wavelet-Based Fault Classification Technique for Power System Relaying. IEEE Trans. Power Deliv. 2004, 19, 582–589. [Google Scholar] [CrossRef]
- Kezunovic, M.; Perunicic, B. Automated Transmission Line Fault Analysis Using Synchronized Sampling at Two Ends. In IEEE Trans. Power Syst.; 1996; Volume 11, pp. 441–447. [Google Scholar] [CrossRef]
- Gopalakrishnan, A.; Kezunovic, M.; McKenna, S.M.; Hamai, D.M. Fault Location Using the Distributed Parameter Transmission Line Model. IEEE Trans. Power Deliv. 2000, 15, 1169–1174. [Google Scholar] [CrossRef]
- Muzzammel, R. Machine Learning Based Fault Diagnosis in HVDC Transmission Lines. In Intelligent Technologies and Applications; Bajwa, I.S., Kamareddine, F., Costa, A., Eds.; Communications in Computer and Information Science; Springer: Singapore, 2019. [Google Scholar] [CrossRef]
- Muzzammel, R. Traveling Waves-Based Method for Fault Estimation in HVDC Transmission System. Energies 2019, 12, 3614. [Google Scholar] [CrossRef]
- Muzzammel, R. Restricted Boltzmann Machines Based Fault Estimation in Multi Terminal HVDC Transmission System. In Intelligent Technologies and Applications; Bajwa, I.S., Sibalija, T., Jawawi, D.N.A., Eds.; Communications in Computer and Information Science; Springer: Singapore, 2020. [Google Scholar] [CrossRef]
- Muzzammel, R.; Raza, A. Low Impedance Fault Identification and Classification Based on Boltzmann Machine Learning for HVDC Transmission Systems. J. Mod. Power Syst. Clean Energy 2021, 10, 440–449. [Google Scholar] [CrossRef]
- Muzzammel, R.; Raza, A. Fault Classification and Location in MT-HVDC Systems Based on Machine. In Artificial Intelligence Applications in Electrical Transmission and Distribution Systems Protection; Taylor and Francis: Boca, Raton, 2021. [Google Scholar]
- Muzzammel, R.; Raza, A. A Support Vector Machine Learning-Based Protection Technique for MT-HVDC Systems. Energies 2020, 13, 6668. [Google Scholar] [CrossRef]
- Salat, R.; Osowski, S. Accurate Fault Location in the Power Transmission Line Using Support Vector Machine Approach. IEEE Trans. Power Syst. 2004, 19, 979–986. [Google Scholar] [CrossRef]
- Muzzammel, R.; Raza, A.; Hussain, M.R.; Abbas, G.; Ahmed, I.; Qayyum, M.; Rasool, M.A.; Khaleel, M.A. MT–HVdc Systems Fault Classification and Location Methods Based on Traveling and Non-Traveling Waves—A Comprehensive Review. Appl. Sci. 2019, 9, 4760. [Google Scholar] [CrossRef]
- Brahma, S.M.; Girgis, A.A. Fault Location on a Transmission Line Using Synchronized Voltage Measurements. IEEE Trans. Power Deliv. 2004, 19, 1619–1622. [Google Scholar] [CrossRef]
- Das, B.; Reddy, J.V. Fuzzy-Logic-Based Fault Classification Scheme for Digital Distance Protection. IEEE Trans. Power Deliv. 2005, 20, 609–616. [Google Scholar] [CrossRef]
- Zhang, N.; Kexunovic, M. Coordinating Fuzzy ART Neural Networks to Improve Transmission Line Fault Detection and Classification. IEEE Power Engineering Society General Meeting; IEEE: San Francisco, CA, USA, 2005; Volume 1, pp. 734–740. [Google Scholar] [CrossRef]
- Jamil, M.; Sharma, S.K.; Singh, R. Fault Detection and Classification in Electrical Power Transmission System Using Artificial Neural Network. SpringerPlus 2015, 4, 334. [Google Scholar] [CrossRef]
- Jiang, J.-A.; Yang, J.-Z.; Lin, Y.-H.; Liu, C.-W.; Ma, J.-C. An adaptive PMU based fault detection/location technique for transmission lines. I. Theory and algorithms. In IEEE Trans. Power Deliv.; 2000; Volume 15, pp. 486–493. [Google Scholar] [CrossRef]
- Qingchao, Z.; Yao, Z.; Wennan, S.; Yixin, Y.; Zhigang, W. Fault Location of Two-Parallel Transmission Line for Non-Earth Fault Using One-Terminal Data. IEEE Power Engineering Society. 1999 Winter Meeting (Cat. No.99CH36233), IEEE: New York, NY, USA, 1999; Volume 2, 967. [Google Scholar] [CrossRef]
- Lin, S.; He, Z.Y.; Li, X.P.; Qian, Q.Q. Travelling Wave Time–Frequency Characteristic-Based Fault Location Method for Transmission Lines. IET Gener. Transm. Amp Distrib. 2012, 6, 764–772. [Google Scholar] [CrossRef]
- Yadav, A.; Swetapadma, A. A Novel Transmission Line Relaying Scheme for Fault Detection and Classification Using Wavelet Transform and Linear Discriminant Analysis. Ain Shams Eng. J. 2015, 6, 199–209. [Google Scholar] [CrossRef][Green Version]
- Mansouri, S.A.; Nematbakhsh, E.; Jordehi, A.R.; Tostado-Véliz, M.; Jurado, F.; Leonowicz, Z. A Risk-Based Bi-Level Bidding System to Manage Day-Ahead Electricity Market and Scheduling of Interconnected Microgrids in the presence of Smart Homes. 2022 IEEE International Conference on Environment and Electrical Engineering and 2022 IEEE Industrial and Commercial Power Systems Europe (EEEIC/I&CPS Europe) 2022; IEEE: Prague, Czech Republic, 2022; pp. 1–6. [Google Scholar]
- Mansouri, S.A.; Nematbakhsh, E.; Ahmarinejad, A.; Jordehi, A.R.; Javadi, M.S.; Marzband, M. A hierarchical scheduling framework for resilience enhancement of decentralized renewable-based microgrids considering proactive actions and mobile units. Renew. Sustain. Energy Rev. 2022, 168, 112854. [Google Scholar] [CrossRef]
- Nasir, M.; Jordehi, A.R.; Tostado-Véliz, M.; Tabar, V.S.; Mansouri, S.A.; Jurado, F. Operation of energy hubs with storage systems, solar, wind and biomass units connected to demand response aggregators. Sustain. Cities Soc. 2022, 83, 103974. [Google Scholar] [CrossRef]
- Matin, S.A.A.; Mansouri, S.A.; Bayat, M.; Jordehi, A.R.; Radmehr, P. A multi-objective bi-level optimization framework for dynamic maintenance planning of active distribution networks in the presence of energy storage systems. J. Energy Storage 2022, 52, 104762. [Google Scholar] [CrossRef]
- Mansouri, S.A.; Ahmarinejad, A.; Sheidaei, F.; Javadi, M.S.; Jordehi, A.R.; Nezhad, A.E.; Catalão, J.P.S. A multi-stage joint planning and operation model for energy hubs considering integrated demand response programs. Int. J. Electr. Power Energy Syst. 2022, 140, 108103. [Google Scholar] [CrossRef]
- Mansouri, S.A.; Ahmarinejad, A.; Javadi, M.S.; Nezhad, A.E.; Shafie-Khah, M.; Catalão, J.P.S. Demand response role for enhancing the flexibility of local energy systems. In Distributed Energy Resources in Local Integrated Energy Systems; Graditi, G., Di Somma, M., Eds.; Elsevier: Amsterdam, The Netherlands, 2021; pp. 279–313. [Google Scholar] [CrossRef]
- Dutta, P.; Esmaeilian, A.; Kezunovic, M. Transmission-Line Fault Analysis Using Synchronized Sampling. IEEE Trans. Power Deliv. 2014, 29, 942–950. [Google Scholar] [CrossRef]
- Lin, Y.-H.; Liu, C.-W.; Chen, C.-S. A New PMU-Based Fault Detection/Location Technique for Transmission Lines with Consideration of Arcing Fault Discrimination-Part II: Performance Evaluation. IEEE Trans. Power Deliv. 2004, 19, 1594–1601. [Google Scholar] [CrossRef]







| Fault Type | Actual Fault | Calculated Fault | % Error | ||
|---|---|---|---|---|---|
| Location Km (Line) | Time (s) | Time (s) | Location Km (Line) | ||
| ag | 25 (2–3) | 0.02 | 0.024 | 25.71 (2–3) | 0.43 |
| 50 (6–7) | 0.02 | 0.023 | 50.14 (6–7) | 0.07 | |
| 75 (4–3) | 0.02 | 0.024 | 74.53 (4–3) | 0.56 | |
| ab | 25 (4–3) | 0.02 | 0.023 | 24.81 (4–3) | 0.12 |
| 50 (7–9) | 0.02 | 0.022 | 49.58 (7–9) | 0.24 | |
| 75 (9–2) | 0.02 | 0.024 | 74.35 (9–2) | 0.43 | |
| abg | 25 (6–7) | 0.02 | 0.023 | 24.83 (6–7) | 0.15 |
| 75 (4–6) | 0.02 | 0.024 | 74.32 (4–6) | 0.45 | |
| 75 (4–3) | 0.02 | 0.024 | 74.58 (4–3) | 0.25 | |
| abc | 25 (2–3) | 0.02 | 0.022 | 26.53 (2–3) | 1.43 |
| 50 (4–3) | 0.02 | 0.022 | 50.54 (4–3) | 0.76 | |
| 75 (9–2) | 0.02 | 0.022 | 74.33 (9–2) | 0.45 | |
| Sr. No. | Parameters | Proposed Method | Distance Relay Protection | ANN |
|---|---|---|---|---|
| 1 | Accuracy | High accuracy (97%) | Inaccurate up to about 8% | High |
| 2 | Complexity | Low complexity | Difficult | Difficult |
| 3 | Time response | Very fast response | High | Response |
| 4 | Detection of types of faults | Can detect all types of faults | Can detect all types of faults | Yes, can detect the fault types |
| 5 | Detection of phase involved in faults | Yes, detect the faulty phase too | No | No |
| 6 | Detection of different linesaffected by the fault | Yes, can detect different lines affected by the fault | Only in some cases, like phase-to-phase faults | Yes, can detect different lines affected |
| 7 | Operational issues | Does not get affected by the other parameters of the system | Expensive protection relay tester is required | It requires so much domain knowledge from experts, time-consuming |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Muzzammel, R.; Arshad, R.; Raza, A.; Sobahi, N.; Alqasemi, U. Two Terminal Instantaneous Power-Based Fault Classification and Location Techniques for Transmission Lines. Sustainability 2023, 15, 809. https://doi.org/10.3390/su15010809
Muzzammel R, Arshad R, Raza A, Sobahi N, Alqasemi U. Two Terminal Instantaneous Power-Based Fault Classification and Location Techniques for Transmission Lines. Sustainability. 2023; 15(1):809. https://doi.org/10.3390/su15010809
Chicago/Turabian StyleMuzzammel, Raheel, Rabia Arshad, Ali Raza, Nebras Sobahi, and Umar Alqasemi. 2023. "Two Terminal Instantaneous Power-Based Fault Classification and Location Techniques for Transmission Lines" Sustainability 15, no. 1: 809. https://doi.org/10.3390/su15010809
APA StyleMuzzammel, R., Arshad, R., Raza, A., Sobahi, N., & Alqasemi, U. (2023). Two Terminal Instantaneous Power-Based Fault Classification and Location Techniques for Transmission Lines. Sustainability, 15(1), 809. https://doi.org/10.3390/su15010809







